Tangentens ligning og normalen til grafen til funksjonen. online kalkulator
Eksempel 1 Gitt en funksjon f(x) = 3x 2 + 4x– 5. La oss skrive likningen av tangenten til grafen til funksjonen f(x) ved punktet av grafen med abscissen x 0 = 1.
Løsning. Funksjonsderiverte f(x) finnes for enhver x R . La oss finne det:
= (3x 2 + 4x– 5)′ = 6 x + 4.
Deretter f(x 0) = f(1) = 2; (x 0) = = 10. Tangentligningen har formen:
y = (x 0) (x – x 0) + f(x 0),
y = 10(x – 1) + 2,
y = 10x – 8.
Svar. y = 10x – 8.
Eksempel 2 Gitt en funksjon f(x) = x 3 – 3x 2 + 2x+ 5. La oss skrive likningen av tangenten til grafen til funksjonen f(x), parallelt med linjen y = 2x – 11.
Løsning. Funksjonsderiverte f(x) finnes for enhver x R . La oss finne det:
= (x 3 – 3x 2 + 2x+ 5)′ = 3 x 2 – 6x + 2.
Siden tangenten til grafen til funksjonen f(x) på punktet med abscissen x 0 er parallell med linjen y = 2x– 11, så er helningen 2, dvs. ( x 0) = 2. Finn denne abscissen fra betingelsen at 3 x– 6x 0 + 2 = 2. Denne likheten er kun gyldig for x 0 = 0 og x 0 = 2. Siden i begge tilfeller f(x 0) = 5, deretter den rette linjen y = 2x + b berører grafen til funksjonen enten ved punktet (0; 5) eller ved punktet (2; 5).
I det første tilfellet er den numeriske likheten sann 5 = 2×0 + b, hvor b= 5, og i det andre tilfellet er den numeriske likheten sann 5 = 2 × 2 + b, hvor b = 1.
Så det er to tangenter y = 2x+ 5 og y = 2x+ 1 til grafen til funksjonen f(x) parallelt med linjen y = 2x – 11.
Svar. y = 2x + 5, y = 2x + 1.
Eksempel 3 Gitt en funksjon f(x) = x 2 – 6x+ 7. La oss skrive likningen av tangenten til grafen til funksjonen f(x) passerer gjennom punktet EN (2; –5).
Løsning. Fordi f(2) –5, så poenget EN hører ikke til grafen til funksjonen f(x). La x 0 - abscisse av berøringspunktet.
Funksjonsderiverte f(x) finnes for enhver x R . La oss finne det:
= (x 2 – 6x+ 1)′ = 2 x – 6.
Deretter f(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 - 6. Tangentligningen har formen:
y = (2x 0 – 6)(x – x 0) + x– 6x+ 7,
y = (2x 0 – 6)x– x+ 7.
Siden punktet EN hører til tangenten, så er den numeriske likheten sann
–5 = (2x 0 – 6)×2– x+ 7,
hvor x 0 = 0 eller x 0 = 4. Dette betyr at gjennom punktet EN det er mulig å tegne to tangenter til grafen til funksjonen f(x).
Hvis x 0 = 0, så har tangentligningen formen y = –6x+ 7. Hvis x 0 = 4, så har tangentligningen formen y = 2x – 9.
Svar. y = –6x + 7, y = 2x – 9.
Eksempel 4 Oppgitte funksjoner f(x) = x 2 – 2x+ 2 og g(x) = –x 2 - 3. La oss skrive ligningen for fellestangens til grafene til disse funksjonene.
Løsning. La x 1 - abscisse av kontaktpunktet til ønsket linje med grafen til funksjonen f(x), A x 2 - abscisse av kontaktpunktet på samme linje med grafen til funksjonen g(x).
Funksjonsderiverte f(x) finnes for enhver x R . La oss finne det:
= (x 2 – 2x+ 2)′ = 2 x – 2.
Deretter f(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 - 2. Tangentligningen har formen:
y = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,
y = (2x 1 – 2)x – x+ 2. (1)
La oss finne den deriverte av funksjonen g(x):
= (–x 2 – 3)′ = –2 x.
I denne artikkelen vil vi analysere alle typer problemer for å finne
La oss huske geometrisk betydning av derivatet: hvis en tangent er tegnet til grafen til en funksjon i et punkt, så er hellingen til tangenten (lik tangens til vinkelen mellom tangenten og den positive retningen til aksen) lik den deriverte av funksjonen ved poenget.


Ta et vilkårlig punkt på tangenten med koordinater:

Og tenk på en rettvinklet trekant:

I denne trekanten 
Herfra 

Dette er ligningen for tangenten tegnet til grafen til funksjonen i punktet.
For å skrive likningen til tangenten trenger vi bare å kjenne likningen til funksjonen og punktet der tangenten er tegnet. Da kan vi finne og .
Det er tre hovedtyper av tangentligningsproblemer.
1. Gitt et kontaktpunkt
2. Gitt stigningskoeffisienten til tangenten, det vil si verdien av den deriverte av funksjonen i punktet.
3. Gitt koordinatene til punktet som tangenten er trukket gjennom, men som ikke er et tangentpunkt.
La oss se på hver type problem.
1 . Skriv ligningen for tangenten til grafen til funksjonen ![]() på punktet .
på punktet .
![]() .
.
b) Finn verdien av den deriverte ved punktet . Først finner vi den deriverte av funksjonen
![]()
![]()
Bytt de funnet verdiene inn i tangentligningen:
![]()
La oss åpne parentesene på høyre side av ligningen. Vi får:
Svar: .
2. Finn abscissen til punktene der funksjonene tangerer grafen ![]() parallelt med x-aksen.
parallelt med x-aksen.
Hvis tangenten er parallell med x-aksen, er vinkelen mellom tangenten og den positive retningen til aksen null, så tangenten til stigningstallet til tangenten er null. Så verdien av den deriverte av funksjonen ![]() ved kontaktpunktene er null.
ved kontaktpunktene er null.
a) Finn den deriverte av funksjonen ![]() .
.
![]()
b) Lik den deriverte med null og finn verdiene der tangenten er parallell med aksen:
![]()

Vi likestiller hver faktor til null, vi får:
Svar: 0;3;5
3 . Skriv tangenslikninger til grafen til en funksjon , parallell rett .
Tangenten er parallell med linjen. Helningen til denne rette linjen er -1. Siden tangenten er parallell med denne linjen, er stigningen til tangenten også -1. Det er vi kjenner stigningen til tangenten, og dermed verdien av derivatet ved kontaktpunktet.
Dette er den andre typen problem for å finne tangentligningen.
Så vi får en funksjon og verdien av den deriverte ved kontaktpunktet.
a) Finn punktene der den deriverte av funksjonen er lik -1.
La oss først finne den deriverte ligningen.

La oss sette likhetstegn mellom den deriverte og tallet -1.

Finn verdien av funksjonen ved punktet.
![]()
(etter tilstand)
![]() .
.
b) Finn ligningen for tangenten til grafen til funksjonen i punktet .
Finn verdien av funksjonen ved punktet.
![]()
(etter tilstand).
Bytt inn disse verdiene i tangentligningen:
![]() .
.
Svar:
4. Skriv en likning for en tangent til en kurve , passerer gjennom et punkt
Sjekk først om punktet ikke er et berøringspunkt. Hvis punktet er et tangentpunkt, hører det til grafen til funksjonen, og dets koordinater må tilfredsstille funksjonens ligning. Bytt ut koordinatene til punktet i funksjonens ligning.
Title="1sqrt(8-3^2)">. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и !} er ikke et kontaktpunkt.
Dette er den siste typen problem for å finne tangentligningen. Første ting vi må finne abscissen til kontaktpunktet.
La oss finne verdien.
La være kontaktpunktet. Punktet tilhører tangenten til grafen til funksjonen. Hvis vi erstatter koordinatene til dette punktet i tangentligningen, får vi riktig likhet:
 .
.
Verdien av funksjonen i punktet er  .
.
Finn verdien av den deriverte av funksjonen i punktet .
La oss først finne den deriverte av funksjonen. Dette .

Den deriverte i et punkt er  .
.
La oss erstatte uttrykkene for og inn i likningen til tangenten. Vi får ligningen for:

La oss løse denne ligningen.
Reduser telleren og nevneren for brøken med 2:

Vi bringer høyre side av ligningen til en fellesnevner. Vi får:

Forenkle telleren til brøken og multipliser begge deler med - dette uttrykket er strengt tatt større enn null.
Vi får ligningen

La oss løse det. For å gjøre dette, firer vi begge deler og går til systemet.
Title="delim(lbrace)(matrise(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0) ) ))( )">!}
La oss løse den første ligningen.
![]()
![]()
Vi løser den andregradsligningen, vi får
Den andre roten tilfredsstiller ikke betingelsen title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}
La oss skrive likningen av tangenten til kurven i punktet . For å gjøre dette, erstatter vi verdien i ligningen  Vi har allerede spilt det inn.
Vi har allerede spilt det inn.

![]()
Svar:
.
På det nåværende utviklingsstadiet av utdanning er en av hovedoppgavene dannelsen av en kreativt tenkende personlighet. Evnen til kreativitet hos studenter kan bare utvikles hvis de er systematisk involvert i det grunnleggende om forskningsaktiviteter. Grunnlaget for at studentene skal bruke sine kreative krefter, evner og talenter er dannet fullverdig kunnskap og ferdigheter. I denne forbindelse er problemet med å danne et system med grunnleggende kunnskap og ferdigheter for hvert emne i skolematematikkkurset av ikke liten betydning. Samtidig bør fullverdige ferdigheter være det didaktiske målet ikke for individuelle oppgaver, men for deres nøye gjennomtenkte system. I videste forstand forstås et system som et sett av interrelaterte samvirkende elementer som har integritet og en stabil struktur.
Tenk på en metodikk for å lære elevene hvordan de kan tegne en likning av en tangent til en funksjonsgraf. I hovedsak er alle oppgaver for å finne tangentligningen redusert til behovet for å velge fra settet (skjær, familie) av linjer de av dem som tilfredsstiller et visst krav - de tangerer grafen til en bestemt funksjon. I dette tilfellet kan settet med linjer som valget utføres fra spesifiseres på to måter:
a) et punkt som ligger på xOy-planet (sentral blyant av linjer);
b) vinkelkoeffisient (parallell bunt av linjer).
I denne forbindelse, når vi studerte emnet "Tangent til grafen til en funksjon" for å isolere elementene i systemet, identifiserte vi to typer oppgaver:
1) oppgaver på en tangent gitt av et punkt den passerer gjennom;
2) oppgaver på en tangent gitt av skråningen.
Å lære å løse problemer på en tangent ble utført ved hjelp av algoritmen foreslått av A.G. Mordkovich. Dens grunnleggende forskjell fra de allerede kjente er at abscissen til tangentpunktet er angitt med bokstaven a (i stedet for x0), i forbindelse med hvilken tangentligningen har formen
y \u003d f (a) + f "(a) (x - a)
(sammenlign med y \u003d f (x 0) + f "(x 0) (x - x 0)). Denne metodiske teknikken, etter vår mening, lar elevene raskt og enkelt innse hvor koordinatene til det gjeldende punktet er skrevet i den generelle tangentligningen, og hvor er kontaktpunktene.
Algoritme for å kompilere likningen av tangenten til grafen til funksjonen y = f(x)
1. Angi abscissen til kontaktpunktet med bokstaven a.
2. Finn f(a).
3. Finn f "(x) og f "(a).
4. Erstatt de funnet tallene a, f (a), f "(a) i den generelle ligningen for tangenten y \u003d f (a) \u003d f "(a) (x - a).
Denne algoritmen kan kompileres på grunnlag av studentenes uavhengige utvalg av operasjoner og rekkefølgen av deres utførelse.
Praksis har vist at den konsistente løsningen av hver av nøkkeloppgavene ved hjelp av algoritmen lar deg danne muligheten til å skrive likningen av tangenten til grafen til funksjonen i trinn, og trinnene i algoritmen tjener som sterke punkter for handlinger . Denne tilnærmingen tilsvarer teorien om gradvis dannelse av mentale handlinger utviklet av P.Ya. Galperin og N.F. Talyzina.
I den første typen oppgaver ble to nøkkeloppgaver identifisert:
- tangenten går gjennom et punkt som ligger på kurven (oppgave 1);
- tangenten går gjennom et punkt som ikke ligger på kurven (Oppgave 2).
Oppgave 1. Lik tangenten til grafen til funksjonen ![]() ved punktet M(3; – 2).
ved punktet M(3; – 2).
Løsning. Punktet M(3; – 2) er kontaktpunktet, siden
1. a = 3 - abscisse av berøringspunktet.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 er tangentligningen.
Oppgave 2. Skriv likningene til alle tangentene til grafen til funksjonen y = - x 2 - 4x + 2, som går gjennom punktet M(- 3; 6).
 Løsning. Punktet M(– 3; 6) er ikke et tangentpunkt, siden f(– 3) 6 (fig. 2).
Løsning. Punktet M(– 3; 6) er ikke et tangentpunkt, siden f(– 3) 6 (fig. 2).
2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - tangentligning.
Tangenten går gjennom punktet M(– 3; 6), derfor tilfredsstiller dens koordinater tangensligningen.
6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a 1 = - 4, a 2 = - 2.
Hvis a = – 4, er tangentligningen y = 4x + 18.
Hvis a \u003d - 2, har tangentligningen formen y \u003d 6.
I den andre typen vil nøkkeloppgavene være følgende:
- tangenten er parallell med en rett linje (oppgave 3);
- tangenten går i en eller annen vinkel til den gitte linjen (Oppgave 4).
Oppgave 3. Skriv likningene til alle tangenter til grafen til funksjonen y \u003d x 3 - 3x 2 + 3, parallelt med linjen y \u003d 9x + 1.
1. a - abscisse av berøringspunktet.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.
 Men på den annen side, f "(a) \u003d 9 (parallellismetilstand). Så vi må løse ligningen 3a 2 - 6a \u003d 9. Dens røtter a \u003d - 1, a \u003d 3 (fig. 3).
Men på den annen side, f "(a) \u003d 9 (parallellismetilstand). Så vi må løse ligningen 3a 2 - 6a \u003d 9. Dens røtter a \u003d - 1, a \u003d 3 (fig. 3).
4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9 (x + 1);
y = 9x + 8 er tangentligningen;
1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9 (x - 3);
y = 9x – 24 er tangentligningen.
 Oppgave 4. Skriv tangenslikningen til grafen til funksjonen y = 0,5x 2 - 3x + 1, passerer i en vinkel på 45 ° til den rette linjen y = 0 (fig. 4).
Oppgave 4. Skriv tangenslikningen til grafen til funksjonen y = 0,5x 2 - 3x + 1, passerer i en vinkel på 45 ° til den rette linjen y = 0 (fig. 4).
Løsning. Fra betingelsen f "(a) \u003d tg 45 ° finner vi a: a - 3 \u003d 1 ^ a \u003d 4.
1. a = 4 - abscisse av berøringspunktet.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).
y \u003d x - 7 - ligningen til tangenten.
Det er lett å vise at løsningen av ethvert annet problem reduseres til løsningen av ett eller flere nøkkelproblemer. Tenk på følgende to problemer som et eksempel.
 1. Skriv tangentlikningene til parablen y = 2x 2 - 5x - 2, hvis tangentene skjærer hverandre i rett vinkel og en av dem berører parablen i punktet med abscissen 3 (fig. 5).
1. Skriv tangentlikningene til parablen y = 2x 2 - 5x - 2, hvis tangentene skjærer hverandre i rett vinkel og en av dem berører parablen i punktet med abscissen 3 (fig. 5).
Løsning. Siden abscissen til kontaktpunktet er gitt, reduseres den første delen av løsningen til nøkkelproblemet 1.
1. a \u003d 3 - abscissen til kontaktpunktet til en av sidene av den rette vinkelen.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - ligningen til den første tangenten.
La a være helningen til den første tangenten. Siden tangentene er vinkelrette, er helningsvinkelen til den andre tangenten. Fra ligningen y = 7x – 20 av den første tangenten har vi tg a = 7. Finn
![]()
Dette betyr at helningen til den andre tangenten er .
Den videre løsningen er redusert til nøkkeloppgave 3.
La B(c; f(c)) være tangentpunktet til den andre linjen, da
1. - abscisse av det andre kontaktpunktet.
2. ![]()
3. ![]()
4. ![]()
![]() er ligningen til den andre tangenten.
er ligningen til den andre tangenten.
Merk. Vinkelkoeffisienten til tangenten kan lettere finnes hvis elevene kjenner forholdet mellom koeffisientene til vinkelrette linjer k 1 k 2 = - 1.
2. Skriv likningene til alle vanlige tangenter til funksjonsgrafer
 Løsning. Oppgaven er redusert til å finne abscissen til kontaktpunktene til de vanlige tangentene, det vil si å løse nøkkelproblemet 1 i en generell form, sette sammen et ligningssystem og deretter løse det (fig. 6).
Løsning. Oppgaven er redusert til å finne abscissen til kontaktpunktene til de vanlige tangentene, det vil si å løse nøkkelproblemet 1 i en generell form, sette sammen et ligningssystem og deretter løse det (fig. 6).
1. La a være abscissen til berøringspunktet som ligger på grafen til funksjonen y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.
1. La c være abscissen til tangentpunktet som ligger på grafen til funksjonen ![]()
2. ![]()
3. f "(c) = c.
4.
Siden tangentene er vanlige, altså

Så y = x + 1 og y = - 3x - 3 er vanlige tangenter.
Hovedmålet med oppgavene som vurderes er å forberede studentene på selverkjennelse av typen nøkkeloppgave når de løser mer komplekse oppgaver som krever visse forskningsferdigheter (evnen til å analysere, sammenligne, generalisere, sette frem en hypotese osv.). Slike oppgaver inkluderer enhver oppgave der nøkkeloppgaven er inkludert som en komponent. La oss som et eksempel se på problemet (inverst til oppgave 1) med å finne en funksjon fra familien til dens tangenter.
3. For hvilke b og c er linjene y \u003d x og y \u003d - 2x tangent til grafen til funksjonen y \u003d x 2 + bx + c?
La t være abscissen til kontaktpunktet til linjen y = x med parabelen y = x 2 + bx + c; p er abscissen til kontaktpunktet til linjen y = - 2x med parabelen y = x 2 + bx + c. Da vil tangentligningen y = x ha formen y = (2t + b)x + c - t 2 , og tangentligningen y = - 2x vil ha formen y = (2p + b)x + c - p 2 .
Komponer og løs et ligningssystem

Svar: ![]()
Tenk på følgende figur:
Den viser en funksjon y = f(x) som er differensierbar i punktet a. Merket punkt M med koordinater (a; f(a)). Gjennom et vilkårlig punkt P(a + ∆x; f(a + ∆x)) på grafen, tegnes en sekant MP.
Hvis nå punktet P forskyves langs grafen til punktet M, vil den rette linjen MP rotere rundt punktet M. I dette tilfellet vil ∆x tendere til null. Herfra kan vi formulere definisjonen av en tangent til grafen til en funksjon.
Tangent til funksjonsgraf
Tangenten til grafen til funksjonen er grenseposisjonen til sekanten når økningen av argumentet har en tendens til null. Det skal forstås at eksistensen av den deriverte av funksjonen f i punktet x0 betyr at det på dette punktet av grafen er tangent til ham.
I dette tilfellet vil stigningstallet til tangenten være lik den deriverte av denne funksjonen på dette punktet f’(x0). Dette er den geometriske betydningen av derivatet. Tangenten til grafen til funksjonen f som kan differensieres i punktet x0 er en rett linje som går gjennom punktet (x0;f(x0)) og har en helning f’(x0).
Tangentligning
La oss prøve å få ligningen for tangenten til grafen til en funksjon f i punktet A(x0; f(x0)). Ligningen av en rett linje med en helning k har følgende form:
Siden helningen vår er lik den deriverte f'(x0), så vil ligningen ha følgende form: y = f'(x0)*x + b.
La oss nå beregne verdien av b. For å gjøre dette bruker vi det faktum at funksjonen går gjennom punkt A.
f(x0) = f’(x0)*x0 + b, herfra uttrykker vi b og får b = f(x0) - f’(x0)*x0.
Vi erstatter den resulterende verdien i tangentligningen:
y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).
y = f(x0) + f'(x0)*(x - x0).
Tenk på følgende eksempel: finn ligningen for tangenten til grafen til funksjonen f (x) \u003d x 3 - 2 * x 2 + 1 ved punktet x \u003d 2.
2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.
3. f'(x) = 3*x 2 - 4*x.
4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.
5. Erstatt de oppnådde verdiene i tangentformelen, vi får: y = 1 + 4*(x - 2). Ved å åpne parentesene og bringe like termer, får vi: y = 4*x - 7.
Svar: y = 4*x - 7.
Generelt skjema for kompilering av tangentligningen til grafen til funksjonen y = f(x):
1. Bestem x0.
2. Beregn f(x0).
3. Beregn f'(x)
Dette matematikkprogrammet finner ligningen for tangenten til grafen til funksjonen \(f(x) \) ved et brukerspesifisert punkt \(a \).
Programmet viser ikke bare tangentligningen, men viser også prosessen med å løse problemet.
Denne nettbaserte kalkulatoren kan være nyttig for elever på videregående skole når de forbereder seg til prøver og eksamener, når de tester kunnskap før Unified State Examination, og for foreldre å kontrollere løsningen av mange problemer i matematikk og algebra. Eller kanskje det er for dyrt for deg å ansette en veileder eller kjøpe nye lærebøker? Eller vil du bare få matte- eller algebraleksene dine gjort så raskt som mulig? I dette tilfellet kan du også bruke våre programmer med en detaljert løsning.
På denne måten kan du gjennomføre din egen opplæring og/eller opplæring av dine yngre brødre eller søstre, samtidig som utdanningsnivået innen oppgavefeltet som skal løses økes.
Hvis du trenger å finne den deriverte av en funksjon, så har vi oppgaven Finn derivert for dette.
Hvis du ikke er kjent med reglene for innføring av funksjoner, anbefaler vi at du gjør deg kjent med dem.
Skriv inn funksjonsuttrykket \(f(x)\) og tallet \(a\) Finn Tangent-ligning Det ble funnet at noen skript som trengs for å løse denne oppgaven ikke ble lastet inn, og det kan hende at programmet ikke fungerer.
Du kan ha AdBlock aktivert.
I dette tilfellet, deaktiver den og oppdater siden.
JavaScript må være aktivert for at løsningen skal vises.
Her er instruksjoner for hvordan du aktiverer JavaScript i nettleseren din.
Fordi Det er mange mennesker som ønsker å løse problemet, forespørselen din står i kø.
Etter noen sekunder vil løsningen vises nedenfor.
Vennligst vent sek...
Hvis du oppdaget en feil i løsningen, så kan du skrive om det i tilbakemeldingsskjemaet .
Ikke glem angi hvilken oppgave du bestemmer hva skriv inn i feltene.
Våre spill, puslespill, emulatorer:
Litt teori.
Helning av en rett linje
Husk at grafen til den lineære funksjonen \(y=kx+b\) er en rett linje. Tallet \(k=tg \alpha \) kalles hellingen av en rett linje, og vinkelen \(\alpha \) er vinkelen mellom denne linjen og okseaksen
Hvis \(k>0\), så \(0 Hvis \(kLigningen til tangenten til grafen til funksjonen
Hvis punktet M (a; f (a)) tilhører grafen til funksjonen y \u003d f (x), og hvis det på dette punktet er mulig å tegne en tangent til grafen til funksjonen som ikke er vinkelrett på x-aksen, så følger det av den geometriske betydningen av den deriverte at stigningstallet til tangenten er lik f "(a). Deretter vil vi utvikle en algoritme for å kompilere likningen av tangenten til grafen til enhver funksjon.
La funksjonen y \u003d f (x) og punktet M (a; f (a)) på grafen til denne funksjonen gis; la det være kjent at f "(a) eksisterer. La oss komponere likningen av tangenten til grafen til en gitt funksjon i et gitt punkt. Denne likningen, som ligningen til enhver rett linje som ikke er parallell med y-aksen , har formen y \u003d kx + b, så problemet er å finne verdiene til koeffisientene k og b.
Alt er klart med skråningen k: det er kjent at k \u003d f "(a). For å beregne verdien av b, bruker vi det faktum at den ønskede rette linjen går gjennom punktet M (a; f (a)) Dette betyr at hvis vi erstatter koordinatene til punktet M inn i ligningen til en rett linje, får vi den riktige likheten: \ (f (a) \u003d ka + b \), dvs. \ (b \u003d f (a) ) - ka \).
Det gjenstår å erstatte de funnet verdiene til koeffisientene k og b i ligningen til en rett linje:
Vi mottok ligningen for tangenten til grafen til funksjonen\(y = f(x) \) ved punktet \(x=a \).
Algoritme for å finne ligningen for tangenten til grafen til funksjonen \(y=f(x)\)
1. Angi abscissen til kontaktpunktet med bokstaven \ (a \)
2. Beregn \(f(a)\)
3. Finn \(f"(x) \) og beregn \(f"(a) \)
4. Bytt inn de funnet tallene \ (a, f (a), f "(a) \) med formelen \ (y \u003d f (a) + f "(a) (x-a) \)
 Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler
Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler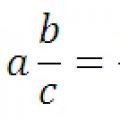 Konvertering av desimaltall til vanlige brøker
Konvertering av desimaltall til vanlige brøker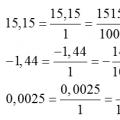 Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler
Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler