Det er tre vektorer i rommet. Koordinater og vektorer
Første ledd i dette kapitlet kan betraktes som en fortsettelse av skolegeometrikurset. Vi husker hoveddefinisjonene knyttet til begrepet vektor.
Et par prikker kalles ryddig, hvis du kan si om dem hvilken av dem som er den første, hvilken er den andre. Et ordnet poengpar definerer regissert segment.
Definisjon 1. Et rettet segment vil bli kalt vektor. Det første punktet i et ordnet par kalles start vektor, og den andre - dens slutt.
For å angi en vektor brukes notasjonen: , hvor EN– vektorpåføringspunkt (vektorens begynnelse), punkt I er slutten av vektoren; eller  ; eller EN
.
; eller EN
.
En vektor hvis begynnelse og slutt er den samme kalles null vektor og betegnet 0 .
Avstanden mellom starten og slutten av en vektor kalles dens lang(og modul eller absolutt verdi). Lengden til en vektor er betegnet med |  |, eller | EN
|, eller |
|, eller | EN
|, eller |  |.
|.
Definisjon 2. Vektorer kalles kollineær, hvis de er plassert på samme linje eller på parallelle linjer, dvs. det er en linje som de er parallelle med. Vektorene kalles koplanar hvis det finnes et plan som de er parallelle med.
Definisjon 3. To vektorer kalles lik hvis de er collineære, har samme retning og har samme lengde.
H  Figur 1 viser vektorer for hvilke en av likhetsbetingelsene er brutt: vektorene er ikke-kollineære (fig. 1 EN), er vektorene rettet mot forskjellige sider(Figur 1 b), har vektorer forskjellig lengde (fig. 1 V).
Figur 1 viser vektorer for hvilke en av likhetsbetingelsene er brutt: vektorene er ikke-kollineære (fig. 1 EN), er vektorene rettet mot forskjellige sider(Figur 1 b), har vektorer forskjellig lengde (fig. 1 V).
Legg merke til følgende egenskaper for likhetsrelasjonen mellom vektorer:
1.
 (refleksivitet).
(refleksivitet).
2. Hvis  , Det
, Det  (symmetri).
(symmetri).
3. Hvis  Og
Og  , Det
, Det  (transitivitet).
(transitivitet).
4. Hvis  , Det
, Det  .
.
5. For eventuelle poeng EN,
B,
C det er bare ett poeng D slik at  .
.
De tre første egenskapene kan erstattes med følgende formulering: likhetsrelasjonen er en ekvivalensrelasjon.
Merk at begrepet likhet av vektorer skiller seg betydelig fra begrepet likhet, for eksempel tall. Hvert tall er bare lik seg selv, med andre ord kan to like tall under alle omstendigheter betraktes som ett og samme tall. Med vektorer er situasjonen annerledes: per definisjon er det forskjellige, men like vektorer. Vi kan utsette en vektor lik den gitte fra et hvilket som helst punkt.
Ta litt vektor  og betrakt settet av alle vektorer lik vektoren
og betrakt settet av alle vektorer lik vektoren  . Dette settet kalles ekvivalensklasse generert av vektoren
. Dette settet kalles ekvivalensklasse generert av vektoren  . Vektor
. Vektor  er en representant for ekvivalensklassen.
er en representant for ekvivalensklassen.
Definisjon 4. gratis vektor EN vi vil kalle settet av alle vektorer lik vektoren EN , dvs. hele ekvivalensklassen.
Det er kjent fra skolegeometrikurset at en vektor kan betraktes som en parallell oversettelse. Denne definisjonen kan også betraktes som definisjonen av en fri vektor.
For en fri vektor, som for tall, betyr likhet en match: to vektorer er like hvis og bare hvis de er samme vektor. I det følgende mener vi med begrepet vektor en fri vektor.
Vurder lineære operasjoner på vektorer. Lineære operasjoner er addisjon av vektorer og multiplikasjon av en vektor med et tall.
OM
en
B
b
 C
C

 Og
Og  (dvs. flytt slutten EN
og start b
til et vilkårlig punkt I). Deretter vektoren
(dvs. flytt slutten EN
og start b
til et vilkårlig punkt I). Deretter vektoren  kalt sum vektorer og betegnet en
+ b
(Fig. 2).
kalt sum vektorer og betegnet en
+ b
(Fig. 2).
MED  egenskaper for vektoraddisjonsoperasjonen:
egenskaper for vektoraddisjonsoperasjonen:
For alle vektorer EN Og b sum en + b også en vektor (lukking).
For alle vektorer EN Og b utført en + b = b + en (kommutativitet).
For alle vektorer EN , b Og Med utført en + (b + Med ) = (en + b ) + Med (assosiativitet).
Settet med vektorer har en nullvektor 0 , som har egenskapen: 0 + EN = EN for enhver vektor EN . Med hensyn til kommutativitet kan vi skrive 0 + EN = 0 + EN = EN (eksistensen av en nullvektor).
For enhver vektor EN det er en vektor - EN , slik at
EN + (–EN ) = (–EN ) + EN = 0
(eksistensen av den motsatte vektoren).
Definisjon 6. Vektor produktEN på et reelt tall kalles α hvilken som helst vektor b , som tilfredsstiller vilkårene:
a) | b | = |α| ∙ | en |;
b) vektor b kolineært til vektoren EN ;
c) vektorer EN Og b er rettet på samme måte hvis α > 0 og motsatt hvis α< 0.
Vektor produkt EN tallet α er betegnet med α EN .
Fra forløpet av lineær algebra er de enkleste egenskapene til vektorrom kjent, som selvfølgelig gjelder for vektorer på planet og i rommet. For eksempel unikheten til nullelementet, unikheten til det motsatte elementet, likheten - EN = (–1)EN og andre.
Egenskaper for multiplikasjon av en vektor med et tall:
1. For alle tall α og β og hvilken som helst vektor EN ekte likestilling
(α β) EN = α (β EN ).
2. Å multiplisere en vektor med én endrer ikke denne vektoren 1 ∙ EN = EN .
3. For enhver vektor EN kjører 0 ∙ EN = 0 .
4. For et hvilket som helst tall α, α ∙ 0 = 0 .
Egenskaper som forbinder operasjonene addisjon og multiplikasjon med et tall:
1. For alle tall α, β og hvilken som helst vektor EN utført
(α + β) EN = α EN + β EN
(fordeling med hensyn til addisjon av tall).
2. For eventuelle vektorer EN Og b og et hvilket som helst tall α,
α ( EN + b ) = α EN + α b
(distributivitet med hensyn til vektoraddisjon).
Definisjon 7. forskjell to vektorer EN Og b kalles summen av vektoren EN og en vektor motsatt b , dvs. EN – b = en + (–b ).
Ved å definere subtraksjon av vektorer i form av addisjon, vil vi ikke betrakte subtraksjon som en egen operasjon. Det gir heller ingen mening å vurdere operasjonen med å dele en vektor med et tall, som kan defineres som multiplikasjonen av en vektor med det resiproke av et gitt tall.
En vektor er et rettet segment av en rett linje i det euklidiske rom, der den ene enden (punkt A) kalles begynnelsen av vektoren, og den andre enden (punkt B) kalles slutten av vektoren (fig. 1). . Vektorer er angitt:

Hvis begynnelsen og slutten av vektoren er den samme, kalles vektoren null vektor og betegnet 0 .
Eksempel. La begynnelsen av vektoren i todimensjonalt rom ha koordinater EN(12,6) , og enden av vektoren er koordinatene B(12.6). Da er vektoren en nullvektor.
Kutt lengde AB kalt modul (lang, normen) vektor og er betegnet med | en|. En vektor med lengde lik én kalles enhetsvektor. I tillegg til modulen er en vektor karakterisert ved en retning: en vektor har en retning fra EN Til B. En vektor kalles en vektor, motsatte vektor.

De to vektorene kalles kollineær hvis de ligger på samme linje eller på parallelle linjer. I fig. 3 røde vektorer er kollineære siden de ligger på samme rette linje, og de blå vektorene er kollineære, fordi de ligger på parallelle linjer. To kollineære vektorer kalt like rettet hvis endene deres ligger på samme side av linjen som forbinder begynnelsen. To kollineære vektorer kalles motsatte retninger hvis endene deres ligger på motsatte sider av linjen som forbinder begynnelsen. Hvis to kollineære vektorer ligger på samme linje, kalles de likt rettet hvis en av strålene dannet av den ene vektoren fullstendig inneholder strålen dannet av den andre vektoren. Ellers kalles vektorene motsatt rettet. I figur 3 er de blå vektorene i samme retning og de røde vektorene er i motsatt retning.

De to vektorene kalles lik hvis de har like moduler og er like rettet. I fig.2 er vektorene like pga deres moduler er like og har samme retning.
Vektorene kalles koplanar hvis de ligger på samme plan eller i parallelle plan.
I n I et dimensjonalt vektorrom, vurder settet av alle vektorer hvis startpunkt sammenfaller med opprinnelsen. Deretter kan vektoren skrives i følgende form:
| (1) |
Hvor x 1, x 2, ..., x n vektorendepunktkoordinater x.
Vektoren skrevet på formen (1) kalles rad vektor, og vektoren skrevet som
| (2) |
kalt kolonnevektor.
Antall n kalt dimensjon (i rekkefølge) vektor. Hvis ![]() så kalles vektoren null vektor(fordi startpunktet til vektoren
så kalles vektoren null vektor(fordi startpunktet til vektoren ![]() ). To vektorer x Og y er like hvis og bare hvis deres korresponderende elementer er like.
). To vektorer x Og y er like hvis og bare hvis deres korresponderende elementer er like.
Koordinater og vektorer. Omfattende guide (2019)
I denne artikkelen vil du og jeg begynne en diskusjon om én "tryllestav" som vil tillate deg å redusere mange problemer i geometri til enkel aritmetikk. Denne "staven" kan gjøre livet ditt mye enklere, spesielt når du føler deg usikker på å bygge romlige figurer, seksjoner osv. Alt dette krever en viss fantasi og praktiske ferdigheter. Metoden, som vi vil begynne å vurdere her, vil tillate deg å abstrahere nesten fullstendig fra alle slags geometriske konstruksjoner og resonnement. Metoden kalles "koordinatmetode". I denne artikkelen vil vi vurdere følgende spørsmål:
- Koordinat fly
- Punkter og vektorer på planet
- Bygge en vektor fra to punkter
- Vektorlengde (avstand mellom to punkter).
- Midtpunktskoordinater
- Punktprodukt av vektorer
- Vinkel mellom to vektorer
Jeg tror du allerede har gjettet hvorfor koordinatmetoden kalles det? Det er sant at det fikk et slikt navn, siden det ikke opererer med geometriske objekter, men med deres numeriske egenskaper(koordinater). Og selve transformasjonen, som gjør det mulig å gå fra geometri til algebra, består i å innføre et koordinatsystem. Hvis den opprinnelige figuren var flat, er koordinatene todimensjonale, og hvis figuren er tredimensjonale, så er koordinatene tredimensjonale. I denne artikkelen vil vi kun vurdere det todimensjonale tilfellet. Og hovedformålet med artikkelen er å lære deg hvordan du bruker noen grunnleggende teknikker for koordinatmetoden (de viser seg noen ganger å være nyttige når du løser problemer i planimetri i del B av Unified State Examination). De følgende to delene om dette emnet er viet diskusjonen om metoder for å løse problemer C2 (problemet med stereometri).
Hvor ville det være logisk å begynne å diskutere koordinatmetoden? Sannsynligvis med konseptet om et koordinatsystem. Husk når du møtte henne første gang. Det virker for meg som i 7. klasse, da du fant ut om eksistensen lineær funksjon, For eksempel. La meg minne deg på at du bygget det punkt for punkt. Husker du? Du valgte et vilkårlig tall, erstattet det i formelen og regnet ut på denne måten. For eksempel hvis, da, hvis, da osv. Hva fikk du som resultat? Og du fikk poeng med koordinater: og. Deretter tegnet du et "kryss" (koordinatsystem), valgte en skala på det (hvor mange celler du vil ha som et enkelt segment) og markerte punktene du mottok på det, som du deretter koblet med en rett linje, det resulterende linje er grafen til funksjonen.
Det er et par ting som må forklares litt mer detaljert:
1. Du velger et enkelt segment av bekvemmelighetshensyn, slik at alt passer fint og kompakt inn i bildet
2. Det antas at aksen går fra venstre mot høyre, og aksen går fra bunn til topp
3. De skjærer hverandre i rett vinkel, og skjæringspunktet kalles origo. Den er merket med en bokstav.
4. I posten av koordinaten til et punkt, for eksempel, til venstre i parentes er koordinaten til punktet langs aksen, og til høyre langs aksen. Spesielt betyr ganske enkelt at poenget
5. For å sette et hvilket som helst punkt på koordinataksen, må du spesifisere koordinatene (2 tall)
6. For ethvert punkt som ligger på aksen,
7. For ethvert punkt som ligger på aksen,
8. Aksen kalles x-aksen
9. Aksen kalles y-aksen
La oss nå ta neste steg med deg: marker to punkter. Koble disse to punktene med en linje. Og la oss sette pilen som om vi tegnet et segment fra punkt til punkt: det vil si at vi skal gjøre segmentet vårt rettet!

Husker du hva et annet navn for et regissert segment er? Det er riktig, det kalles en vektor!
Så hvis vi kobler en prikk til en prikk, og begynnelsen vil være punkt A, og slutten vil være punkt B, da får vi en vektor. Du gjorde også denne konstruksjonen i 8. klasse, husker du?
Det viser seg at vektorer, som punkter, kan betegnes med to tall: disse tallene kalles koordinatene til vektoren. Spørsmål: tror du det er nok for oss å kjenne koordinatene til begynnelsen og slutten av vektoren for å finne dens koordinater? Det viser seg at ja! Og det er veldig enkelt å gjøre:
Derfor, siden punktet i vektoren er begynnelsen og slutten, har vektoren følgende koordinater:
For eksempel hvis, så koordinatene til vektoren
La oss nå gjøre det motsatte, finne koordinatene til vektoren. Hva må vi endre for dette? Ja, du må bytte begynnelsen og slutten: nå vil begynnelsen av vektoren være på et punkt, og slutten på et punkt. Deretter:
Se nøye, hva er forskjellen mellom vektorer og? Deres eneste forskjell er tegnene i koordinatene. De er motsatte. Dette faktum er skrevet slik:
Noen ganger, hvis det ikke er spesifikt oppgitt hvilket punkt som er begynnelsen av vektoren, og hvilket som er slutten, er vektorene ikke angitt med to store bokstaver, men en liten bokstav, for eksempel: , etc.
Nå litt øve på og finn koordinatene til følgende vektorer:
Undersøkelse:
Nå løser du problemet litt vanskeligere:
En vektortorus med on-cha-scrap på et punkt har co-eller-di-on-you. Finn-di-te abs-cis-su poeng.
Det samme er ganske prosaisk: La være koordinatene til punktet. Deretter
Jeg kompilerte systemet ved å bestemme hva koordinatene til en vektor er. Da har punktet koordinater. Vi er interessert i abscissen. Deretter
Svar:
Hva annet kan du gjøre med vektorer? Ja, nesten alt er det samme som med vanlige tall (bortsett fra at du ikke kan dele, men du kan multiplisere på to måter, hvorav den ene skal diskuteres her litt senere)
- Vektorer kan stables med hverandre
- Vektorer kan trekkes fra hverandre
- Vektorer kan multipliseres (eller divideres) med et vilkårlig tall som ikke er null
- Vektorer kan multipliseres med hverandre
Alle disse operasjonene er ganske visuelle geometrisk representasjon. For eksempel, trekanten (eller parallellogram) regelen for addisjon og subtraksjon:



En vektor strekker seg eller krymper eller endrer retning når multiplisert eller delt med et tall:

Men her vil vi være interessert i spørsmålet om hva som skjer med koordinatene.
1. Når vi adderer (subtraherer) to vektorer, legger vi til (subtraherer) deres koordinater element for element. Det er:
2. Når du multipliserer (deler) en vektor med et tall, blir alle dens koordinater multiplisert (delt) med dette tallet:
For eksempel:
· Finn-di-summen av ko-eller-di-nat århundre-til-ra.

La oss først finne koordinatene til hver av vektorene. Begge har samme opphav - opprinnelsespunktet. Endene deres er forskjellige. Deretter, . Nå beregner vi koordinatene til vektoren Da er summen av koordinatene til den resulterende vektoren lik.
Svar:
Løs nå følgende problem selv:
· Finn summen av koordinatene til vektoren

Vi sjekker:
La oss nå vurdere følgende problem: vi har to punkter på koordinatplan. Hvordan finne avstanden mellom dem? La det første punktet være, og det andre. La oss betegne avstanden mellom dem som . La oss lage følgende tegning for klarhet:

Hva jeg har gjort? Jeg koblet for det første sammen punktene og, og tegnet også en linje parallelt med aksen fra punktet, og tegnet en linje parallelt med aksen fra punktet. Skjærte de seg på et tidspunkt og dannet en fantastisk figur? Hvorfor er hun fantastisk? Ja, du og jeg vet nesten alt om høyre trekant. Vel, Pythagoras teorem, helt klart. Det ønskede segmentet er hypotenusen til denne trekanten, og segmentene er bena. Hva er koordinatene til punktet? Ja, de er lette å finne fra bildet: Siden segmentene er parallelle med aksene og henholdsvis lengdene deres er enkle å finne: hvis vi betegner lengdene til segmentene, henholdsvis gjennom, så
La oss nå bruke Pythagoras teorem. Vi vet lengden på bena, vi finner hypotenusen:
Dermed er avstanden mellom to punkter rotsummen av kvadrerte forskjeller fra koordinatene. Eller - avstanden mellom to punkter er lengden på segmentet som forbinder dem. Det er lett å se at avstanden mellom punktene ikke er avhengig av retningen. Deretter:
Av dette trekker vi tre konklusjoner:
La oss øve litt på å beregne avstanden mellom to punkter:
For eksempel hvis, så er avstanden mellom og
Eller la oss gå annerledes: Finn koordinatene til vektoren
Og finn lengden på vektoren:
Som du kan se, er det det samme!
Tren nå litt på egenhånd:
Oppgave: Finn avstanden mellom de gitte punktene:
Vi sjekker:
Her er et par flere problemer for samme formel, selv om de høres litt annerledes ut:
1. Finn-di-te kvadratet av lengden av øyelokket-til-ra.

2. Nai-di-te firkant av øyelokkets lengde-til-ra

Jeg tipper du kan håndtere dem lett? Vi sjekker:
1. Og dette er for oppmerksomhet) Vi har allerede funnet koordinatene til vektorene før: . Da har vektoren koordinater. Kvadraten på lengden vil være:
2. Finn koordinatene til vektoren
Da er kvadratet av lengden
Ikke noe komplisert, ikke sant? Enkel aritmetikk, ikke noe mer.
Følgende gåter kan ikke entydig klassifiseres, de er snarere for generell lærdom og evnen til å tegne enkle bilder.
1. Finn-di-de sinus av vinkelen på-clo-on-fra-cut, koble-en-n-th-th-punkt, med abscisse-aksen.
 Og
Og
Hvordan skal vi gjøre det her? Du må finne sinusen til vinkelen mellom og aksen. Og hvor kan vi se etter sinusen? Det stemmer, i en rettvinklet trekant. Så hva må vi gjøre? Bygg denne trekanten!

Siden koordinatene til punktet og, så er segmentet likt, og segmentet. Vi må finne sinusen til vinkelen. La meg minne deg på at sinus er forholdet mellom det motsatte benet og hypotenusen
Hva har vi igjen å gjøre? Finn hypotenusen. Du kan gjøre det på to måter: ved å bruke Pythagoras teorem (bena er kjent!) eller ved å bruke formelen for avstanden mellom to punkter (faktisk den samme som den første metoden!). Jeg vil gå den andre veien:
Svar:
Den neste oppgaven vil virke enda enklere for deg. Hun - på koordinatene til punktet.
Oppgave 2. Fra punktet senkes per-pen-di-kular ned på abs-ciss-aksen. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
La oss lage en tegning:

Basen til perpendikulæren er punktet der den skjærer x-aksen (aksen) for meg er dette et punkt. Figuren viser at den har koordinater: . Vi er interessert i abscissen - det vil si "X"-komponenten. Hun er likestilt.
Svar: .
Oppgave 3. Under betingelsene i forrige oppgave, finn summen av avstandene fra punktet til koordinataksene.
Oppgaven er generelt elementær hvis du vet hva avstanden fra et punkt til aksene er. Du vet? Jeg håper, men jeg minner deg likevel om:
Så på tegningen min, som ligger litt høyere, har jeg allerede avbildet en slik vinkelrett? Hvilken akse er det? til aksen. Og hva er lengden da? Hun er likestilt. Tegn nå en vinkelrett på aksen selv og finn lengden. Det blir likt, ikke sant? Da er summen deres lik.
Svar: .
Oppgave 4. I betingelsene for oppgave 2, finn ordinaten til punktet symmetrisk med punktet om x-aksen.
Jeg tror du intuitivt forstår hva symmetri er? Veldig mange gjenstander har det: mange bygninger, bord, fly, mange geometriske figurer: kule, sylinder, firkant, rombe osv. Grovt sett kan symmetri forstås slik: en figur består av to (eller flere) like halvdeler. Denne symmetrien kalles aksial. Hva er da en akse? Dette er nøyaktig linjen langs hvilken figuren relativt sett kan "skjæres" i identiske halvdeler (i dette bildet er symmetriaksen rett):

La oss nå gå tilbake til oppgaven vår. Vi vet at vi ser etter et punkt som er symmetrisk rundt aksen. Da er denne aksen symmetriaksen. Så vi må merke et punkt slik at aksen kutter segmentet i to like deler. Prøv å markere et slikt punkt selv. Sammenlign nå med min løsning:

Gjorde du det samme? Fint! På funnpunktet er vi interessert i ordinaten. Hun er likestilt
Svar:
Fortell meg nå, etter å ha tenkt et sekund, hva blir abscissen til punktet som er symmetrisk til punkt A om y-aksen? Hva er svaret ditt? Korrekt svar: .
I generell sak Regelen kan skrives slik:
Et punkt som er symmetrisk til et punkt rundt x-aksen har koordinatene:
Et punkt som er symmetrisk til et punkt rundt y-aksen har koordinater:
Vel, nå er det virkelig skummelt. oppgave: Finn koordinatene til et punkt som er symmetrisk til et punkt, i forhold til origo. Du tenker først selv, og så ser du på tegningen min!

Svar:
Nå parallellogram problem:
Oppgave 5: Poengene er ver-shi-na-mi-pa-ral-le-lo-gram-ma. Finn-dee-te eller-dee-on-tu poeng.

Du kan løse dette problemet på to måter: logikk og koordinatmetoden. Jeg skal først bruke koordinatmetoden, og så skal jeg fortelle deg hvordan du kan bestemme annerledes.
Det er helt klart at abscissen til punktet er lik. (den ligger på vinkelrett tegnet fra punktet til x-aksen). Vi må finne ordinaten. La oss dra nytte av det faktum at figuren vår er et parallellogram, som betyr det. Finn lengden på segmentet ved å bruke formelen for avstanden mellom to punkter:
Vi senker vinkelrett som forbinder punktet med aksen. Skjæringspunktet er angitt med en bokstav.

Lengden på segmentet er lik. (finn problemet selv, der vi diskuterte dette øyeblikket), så vil vi finne lengden på segmentet ved å bruke Pythagoras teorem:
Lengden på segmentet er nøyaktig den samme som ordinaten.
Svar: .
En annen løsning (jeg skal bare gi et bilde som illustrerer det)

Løsningsfremgang:
1. Bruk
2. Finn punktkoordinater og lengde
3. Bevis det.
En annen klippelengdeproblem:
Punktene er-la-yut-xia top-shi-on-mi tri-angle-no-ka. Finn lengden på midtlinjen hans, par-ral-lel-noy.

Husker du hva det er midtlinje triangel? Da er denne oppgaven elementær for deg. Hvis du ikke husker det, vil jeg minne deg på: midtlinjen i en trekant er en linje som forbinder midtpunktene til motsatte sider. Den er parallell med basen og lik halvparten av den.
Basen er et segment. Vi måtte se etter lengden tidligere, den er lik. Da er lengden på midtlinjen halvparten så lang og lik.
Svar: .
Kommentar: Dette problemet kan løses på en annen måte, som vi skal se på litt senere.
I mellomtiden, her er noen få oppgaver for deg, tren på dem, de er ganske enkle, men de hjelper deg med å "fylle hånden" ved å bruke koordinatmetoden!
1. Punktene vises-la-yut-xia top-shi-on-mi tra-pe-tion. Finn lengden på midtlinjen.

2. Poeng og yav-la-yut-xia ver-shi-na-mi pa-ral-le-lo-gram-ma. Finn-dee-te eller-dee-on-tu poeng.

3. Finn lengden fra kuttet, koble det andre punktet og

4. Finn-di-te området for-den-røde-shen-noy fi-gu-ry på ko-eller-di-nat-noy flyet.

5. En sirkel sentrert ved na-cha-le ko-or-di-nat går gjennom et punkt. Finn-de-te hennes ra-di-bart.

6. Nai-di-te ra-di-us sirkel-no-sti, beskriv-san-noy nær den rette vinkelen-no-ka, toppene-shi-ny av noe-ro-go har co-eller - di-na-du med-fra-svar-men

Løsninger:
1. Det er kjent at midtlinjen til en trapes er lik halvparten av summen av dens baser. Basen er lik, men basen. Deretter
Svar:
2. Den enkleste måten å løse dette problemet på er å legge merke til det (parallelogramregelen). Regn ut koordinatene til vektorene og er ikke vanskelig: . Når vektorer legges til, legges koordinatene til. Har så koordinater. Punktet har de samme koordinatene, siden begynnelsen av vektoren er et punkt med koordinater. Vi er interessert i ordinaten. Hun er likestilt.
Svar:
3. Vi handler umiddelbart i henhold til formelen for avstanden mellom to punkter:
Svar:
4. Se på bildet og si, mellom hvilke to figurer er det skraverte området "klemt"? Den er klemt mellom to firkanter. Da er arealet til den ønskede figuren lik arealet til den store firkanten minus arealet til den lille. Side liten firkant er et linjestykke som forbinder punkter og lengden er
Da er arealet av den lille firkanten
Vi gjør det samme med en stor firkant: siden er et segment som forbinder punktene og lengden er lik
Da er arealet av det store torget
Arealet til den ønskede figuren er funnet av formelen:
Svar:
5. Hvis sirkelen har origo som senter og går gjennom et punkt, vil radiusen være nøyaktig lik lengde segment (lag en tegning og du vil forstå hvorfor dette er åpenbart). Finn lengden på dette segmentet:
Svar:
6. Det er kjent at radiusen til en sirkel omskrevet rundt et rektangel er lik halvparten av diagonalen. La oss finne lengden på en av de to diagonalene (tross alt, i et rektangel er de like!)
Svar:
Vel, klarte du alt? Det var ikke så vanskelig å finne ut av det, var det? Det er bare én regel her - å kunne lage et visuelt bilde og ganske enkelt "lese" alle dataene fra det.
Vi har veldig lite igjen. Det er bokstavelig talt to punkter til som jeg ønsker å diskutere.
La oss prøve å løse dette enkle problemet. La to poeng og gis. Finn koordinatene til midten av segmentet. Løsningen på dette problemet er som følger: la punktet være det ønskede midten, så har det koordinater:
Det er: koordinater til midten av segmentet = aritmetisk gjennomsnitt av de tilsvarende koordinatene til endene av segmentet.
Denne regelen er veldig enkel og forårsaker vanligvis ikke vanskeligheter for elevene. La oss se i hvilke problemer og hvordan det brukes:
1. Finn-di-te eller-di-na-tu se-re-di-us fra-cut, koble-nya-yu-th-th-th-punkt og

2. Punktene er yav-la-yut-xia ver-shi-na-mi-che-you-reh-coal-no-ka. Finn-di-te eller-di-na-tu-punkter for re-re-se-che-niya av dia-go-on-lei hans.

3. Finn-di-te abs-cis-su av sentrum av sirkelen, beskriv-san-noy nær rektangelet-no-ka, toppene-shi-vi har noe-ro-go co-or-di- na-du med-fra-veterinær-stvenno-men.

Løsninger:
1. Den første oppgaven er bare en klassiker. Vi handler umiddelbart ved å bestemme midtpunktet til segmentet. Hun har koordinater. Ordinaten er lik.
Svar:
2. Det er lett å se at den gitte firkanten er et parallellogram (til og med en rombe!). Du kan bevise det selv ved å beregne lengdene på sidene og sammenligne dem med hverandre. Hva vet jeg om et parallellogram? Dens diagonaler er halvert av skjæringspunktet! Aha! Så hva er skjæringspunktet mellom diagonalene? Dette er midten av noen av diagonalene! Jeg vil spesielt velge diagonalen. Da har punktet koordinater. Ordinaten til punktet er lik.
Svar:
3. Hva er sentrum av sirkelen omskrevet rundt rektangelet? Det faller sammen med skjæringspunktet mellom diagonalene. Hva vet du om diagonalene til et rektangel? De er like og skjæringspunktet er delt i to. Oppgaven er redusert til den forrige. Ta for eksempel diagonalen. Så hvis er midten av den omskrevne sirkelen, så er midten. Jeg ser etter koordinater: Abscissen er lik.
Svar:
Nå skal du øve litt på egenhånd, jeg vil bare gi svarene på hver oppgave slik at du kan sjekke deg selv.
1. Nai-di-te ra-di-us sirkel-no-sti, beskriv-san-noy nær trekanten-no-ka, toppen av noen-ro-go har ko-eller-di -no misters

2. Finn-di-te eller-di-na-tu sentrum av sirkelen, beskriv san-noy nær trekanten-no-ka, toppene-shi-vi har noe-ro-go koordinater
3. Hva slags ra-di-y-sa skal det være en sirkel med senter i et punkt slik at den berører abs-ciss-aksen?

4. Finn-di-te eller-di-på-det punktet for re-re-se-che-ing av aksen og fra-cut, koble-nya-yu-th-th-punkt og

Svar:
Har alt ordnet seg? Jeg håper virkelig på det! Nå - siste push. Vær spesielt forsiktig. Materialet som jeg nå skal forklare er direkte relatert ikke bare til enkle oppgaver til koordinatmetoden fra del B, men forekommer også overalt i oppgave C2.
Hvilke av løftene mine har jeg ennå ikke holdt? Husker du hvilke operasjoner på vektorer jeg lovet å introdusere og hvilke jeg til slutt introduserte? Er jeg sikker på at jeg ikke har glemt noe? Glemte! Jeg glemte å forklare hva multiplikasjon av vektorer betyr.
Det er to måter å multiplisere en vektor med en vektor. Avhengig av den valgte metoden vil vi få gjenstander av en annen karakter:
Vektorproduktet er ganske vanskelig. Hvordan du gjør det og hvorfor det er nødvendig, vil vi diskutere med deg i neste artikkel. Og i dette vil vi fokusere på det skalære produktet.
Det er allerede to måter som lar oss beregne det:
Som du gjettet, bør resultatet være det samme! Så la oss først se på den første måten:
Prikk produktet gjennom koordinatene
Finn: - vanlig notasjon for punktprodukt
Formelen for beregningen er som følger:
Det er skalært produkt= summen av produkter av vektorkoordinater!
Eksempel:
Finn-dee-te

Løsning:
Finn koordinatene til hver av vektorene:
Vi beregner skalarproduktet med formelen:
Svar:
Du skjønner, absolutt ingenting komplisert!
Vel, prøv det selv:
Finn-di-te scalar-noe pro-fra-ve-de-nie århundre-til-grøft og

Klarte du deg? Kanskje han la merke til et lite triks? La oss sjekke:
Vektorkoordinater, som i forrige oppgave! Svar: .
I tillegg til koordinaten er det en annen måte å beregne skalarproduktet på, nemlig gjennom lengdene på vektorene og cosinus til vinkelen mellom dem:
Angir vinkelen mellom vektorene og.
Det vil si at skalarproduktet er lik produktet av lengdene til vektorene og cosinus til vinkelen mellom dem.
Hvorfor trenger vi denne andre formelen, hvis vi har den første, som er mye enklere, er det i det minste ingen cosinus i den. Og vi trenger det slik at vi fra den første og andre formelen kan utlede hvordan vi finner vinkelen mellom vektorer!
La Så husk formelen for lengden til en vektor!
Så hvis jeg kobler disse dataene inn i prikkproduktformelen, får jeg:
Men på en annen måte:
Så hva har vi? Vi har nå en formel for å beregne vinkelen mellom to vektorer! Noen ganger, for korthets skyld, er det også skrevet slik:
Det vil si at algoritmen for å beregne vinkelen mellom vektorer er som følger:
- Vi beregner skalarproduktet gjennom koordinatene
- Finn lengdene på vektorer og gang dem
- Del resultatet av punkt 1 med resultatet av punkt 2
La oss øve med eksempler:
1. Finn vinkelen mellom øyelokkene-til-ra-mi og. Gi svaret i grader.

2. Under betingelsene i forrige oppgave, finn cosinus mellom vektorene
La oss gjøre dette: Jeg skal hjelpe deg med å løse det første problemet, og prøve å gjøre det andre selv! Bli enige? Så la oss starte!
1. Disse vektorene er våre gamle venner. Vi har allerede vurdert deres skalarprodukt, og det var likt. Koordinatene deres er: , . Så finner vi lengdene deres:
Så ser vi etter cosinus mellom vektorene:
Hva er cosinus til vinkelen? Dette er hjørnet.
Svar:
Vel, løs nå det andre problemet selv, og sammenlign! Jeg vil bare gi en veldig kort løsning:
2. har koordinater, har koordinater.
La være vinkelen mellom vektorene og da
Svar:
Det skal bemerkes at oppgavene direkte på vektorene og metoden for koordinater i del B eksamensarbeid ganske sjelden. De aller fleste C2-problemene kan imidlertid enkelt løses ved å innføre et koordinatsystem. Så du kan vurdere denne artikkelen som et grunnlag, på grunnlag av hvilket vi vil lage ganske vanskelige konstruksjoner som vi trenger å løse utfordrende oppgaver.
KOORDINATER OG VEKTORER. MELLOMNIVÅ
Du og jeg fortsetter å studere metoden for koordinater. I den siste delen utledet vi en serie viktige formler, som tillater:
- Finn vektorkoordinater
- Finn lengden på en vektor (alternativt: avstanden mellom to punkter)
- Legg til, trekk fra vektorer. multiplisere dem med ekte nummer
- Finn midtpunktet til et segment
- Beregn prikkprodukt av vektorer
- Finn vinkelen mellom vektorer
Hele koordinatmetoden passer selvsagt ikke inn i disse 6 punktene. Det ligger til grunn for en slik vitenskap som analytisk geometri, som du vil bli kjent med på universitetet. Jeg vil bare bygge et grunnlag som lar deg løse problemer i en enkelt stat. eksamen. Vi fant ut oppgavene til del B i Nå er det på tide å gå videre til kvalitet nytt nivå! Denne artikkelen vil bli viet til en metode for å løse de C2-problemene der det ville være rimelig å bytte til koordinatmetoden. Denne rimeligheten bestemmes av hva som må finnes i problemet, og hvilket tall som er oppgitt. Så jeg ville brukt koordinatmetoden hvis spørsmålene er:
- Finn vinkelen mellom to plan
- Finn vinkelen mellom en linje og et plan
- Finn vinkelen mellom to linjer
- Finn avstanden fra et punkt til et fly
- Finn avstanden fra et punkt til en linje
- Finn avstanden fra en rett linje til et plan
- Finn avstanden mellom to linjer
Hvis tallet gitt i tilstanden til problemet er et revolusjonslegeme (kule, sylinder, kjegle ...)
Egnede tall for koordinatmetoden er:
- kuboid
- Pyramide (trekantet, firkantet, sekskantet)
Også etter min erfaring det er uaktuelt å bruke koordinatmetoden for:
- Finne områdene til seksjoner
- Beregninger av volum av kropper
Imidlertid bør det umiddelbart bemerkes at tre "ugunstige" situasjoner for koordinatmetoden er ganske sjeldne i praksis. I de fleste oppgaver kan den bli din redningsmann, spesielt hvis du ikke er særlig sterk i tredimensjonale konstruksjoner (som noen ganger er ganske intrikate).
Hva er alle tallene jeg har listet opp ovenfor? De er ikke lenger flate, for eksempel en firkant, trekant, sirkel, men voluminøse! Følgelig må vi ikke vurdere et todimensjonalt, men et tredimensjonalt koordinatsystem. Den bygges ganske enkelt: bare i tillegg til abscissen og ordinatene, vil vi introdusere en annen akse, applikataksen. Figuren viser skjematisk deres relative posisjon:

Alle av dem er gjensidig vinkelrette, krysser på ett punkt, som vi vil kalle opprinnelsen. Abscisseaksen, som før, vil bli betegnet, ordinataksen - , og den introduserte applikataksen - .
Hvis hvert punkt på planet tidligere var preget av to tall - abscissen og ordinaten, er hvert punkt i rommet allerede beskrevet av tre tall - abscissen, ordinaten, applikatet. For eksempel:

Følgelig er punktets abscisse lik, ordinaten er , og applikatet er .
Noen ganger kalles abscissen til et punkt også projeksjonen av punktet på abscisseaksen, ordinaten er projeksjonen av punktet på ordinataksen, og applikatet er projeksjonen av punktet på applikataksen. Følgelig, hvis et punkt er gitt da, et punkt med koordinater:
kalt projeksjon av et punkt på et plan
kalt projeksjon av et punkt på et plan
Et naturlig spørsmål dukker opp: er alle formlene som er utledet for det todimensjonale tilfellet gyldige i rommet? Svaret er ja, de er rettferdige og har samme utseende. For en liten detalj. Jeg tror du allerede har gjettet hvilken. I alle formler må vi legge til ett begrep til som er ansvarlig for applikataksen. Nemlig.
1. Hvis to poeng er gitt: , så:
- Vektorkoordinater:
- Avstand mellom to punkter (eller vektorlengde)
- Midten av segmentet har koordinater
2. Hvis to vektorer er gitt: og, da:
- Punktproduktet deres er:
- Cosinus til vinkelen mellom vektorene er:
Plassen er imidlertid ikke så enkel. Som du forstår, introduserer tillegget av en koordinat til en betydelig variasjon i spekteret av figurer som "lever" i dette rommet. Og for videre fortelling må jeg introdusere noen, grovt sett, "generalisering" av den rette linjen. Denne "generaliseringen" vil være et fly. Hva vet du om fly? Prøv å svare på spørsmålet, hva er et fly? Det er veldig vanskelig å si. Imidlertid forestiller vi oss alle intuitivt hvordan det ser ut:

Grovt sett er dette et slags endeløst "blad" som kastes ut i verdensrommet. "Uendelig" skal forstås at planet strekker seg i alle retninger, det vil si at arealet er lik uendelig. Denne forklaringen "på fingrene" gir imidlertid ikke den minste idé om flyets struktur. Og vi vil være interessert i det.
La oss huske en av geometriens grunnleggende aksiomer:
- En rett linje går gjennom to forskjellige punkter på et plan, dessuten bare ett:

Eller dens analoge i verdensrommet:

Selvfølgelig husker du hvordan du utleder ligningen til en rett linje fra to gitte punkter, dette er ikke i det hele tatt vanskelig: hvis det første punktet har koordinater: og det andre, vil ligningen til den rette linjen være som følger:
Du gikk gjennom dette i 7. klasse. I verdensrommet ser likningen til en rett linje slik ut: la oss ha to punkter med koordinater: , så har likningen til en rett linje som går gjennom dem formen:
For eksempel går en linje gjennom punkter:
Hvordan skal dette forstås? Dette skal forstås som følger: et punkt ligger på en linje hvis koordinatene tilfredsstiller følgende system:
Vi vil ikke være veldig interessert i ligningen til en rett linje, men vi må ta hensyn til det veldig viktige konseptet med retningsvektoren til en rett linje. - enhver vektor som ikke er null som ligger på en gitt linje eller parallelt med den.

For eksempel er begge vektorene retningsvektorer av en rett linje. La være et punkt som ligger på en rett linje, og være dens retningsvektor. Da kan ligningen til en rett linje skrives på følgende form:
Nok en gang vil jeg ikke være veldig interessert i ligningen til en rett linje, men jeg trenger virkelig at du husker hva en retningsvektor er! En gang til: det er en hvilken som helst vektor som ikke er null som ligger på en linje, eller parallelt med den.
Ta ut trepunktsligningen til et plan er ikke lenger så triviell, og vanligvis vurderes ikke denne problemstillingen i kurset videregående skole. Men til ingen nytte! Denne teknikken er avgjørende når vi tyr til koordinatmetoden for å løse komplekse problemer. Jeg antar imidlertid at du er full av lyst til å lære noe nytt? Dessuten vil du kunne imponere læreren din ved universitetet når det viser seg at du allerede vet hvordan du bruker teknikken som vanligvis studeres i løpet av analytisk geometri. Så la oss komme i gang.
Ligningen til et plan er ikke så forskjellig fra ligningen til en rett linje på et plan, den har nemlig formen:
noen tall (ikke alle lik null), men variabler, for eksempel: osv. Som du kan se, er ligningen til et plan ikke veldig forskjellig fra ligningen til en rett linje (lineær funksjon). Men husker du hva vi kranglet med deg? Vi sa at hvis vi har tre punkter som ikke ligger på en rett linje, blir flyets ligning unikt gjenopprettet fra dem. Men hvordan? Jeg skal prøve å forklare deg.
Siden planligningen er:
Og punktene tilhører dette planet, så når vi erstatter koordinatene til hvert punkt i ligningen til planet, bør vi få riktig identitet:
Dermed er det behov for å løse tre ligninger allerede med ukjente! Dilemma! Imidlertid kan vi alltid anta det (for dette må vi dele med). Dermed får vi tre ligninger med tre ukjente:
Vi vil imidlertid ikke løse et slikt system, men skrive ut det kryptiske uttrykket som følger av det:
Ligning av et plan som går gjennom tre gitte punkter
\[\venstre| (\begin(array)(*(20)(c))(x - (x_0))&((x_1) - (x_0))&((x_2) - (x_0))\\(y - (y_0) )&((y_1) - (y_0))&((y_2) - (y_0))\\(z - (z_0))&((z_1) - (z_0))&((z_2) - (z_0)) \end(array)) \right| = 0\]
Stoppe! Hva annet er dette? En veldig uvanlig modul! Objektet du ser foran deg har imidlertid ingenting med modulen å gjøre. Dette objektet kalles en tredjeordens determinant. Fra nå av, når du arbeider med metoden for koordinater på et fly, vil du ofte komme over disse determinantene. Hva er en tredjeordens determinant? Merkelig nok er det bare et tall. Det gjenstår å forstå hvilket spesifikt tall vi vil sammenligne med determinanten.
La oss først skrive tredjeordens determinanten i mer generelt syn:
Hvor er noen tall. Med den første indeksen mener vi dessuten radnummeret, og med indeksen - kolonnenummeret. For eksempel betyr det at det gitte tallet er i skjæringspunktet mellom den andre raden og den tredje kolonnen. La oss sette neste spørsmål: hvordan skal vi beregne en slik determinant? Det vil si, hvilket spesifikt tall vil vi sammenligne det med? For determinanten av nøyaktig tredje orden er det en heuristisk (visuell) trekantregel, den ser slik ut:

- Produktet av elementene i hoveddiagonalen (fra øverst til venstre til nederst til høyre) produktet av elementene som danner den første trekanten "vinkelrett" på hoveddiagonalen produktet av elementene som danner den andre trekanten "vinkelrett" på hoveddiagonalen diagonal
- Produktet av elementene i den sekundære diagonalen (fra øvre høyre hjørne til nedre venstre) produktet av elementene som danner den første trekanten "vinkelrett" av den sekundære diagonalen produktet av elementene som danner den andre trekanten "vinkelrett" av den sekundære diagonalen
- Da er determinanten lik forskjellen mellom verdiene oppnådd på trinnet og
Hvis vi skriver alt dette i tall, får vi følgende uttrykk:
Du trenger imidlertid ikke å huske beregningsmetoden i dette skjemaet, det er nok å bare holde trekantene i hodet og selve ideen om hva som legges til hva og hva som deretter trekkes fra hva).
La oss illustrere trekantmetoden med et eksempel:
1. Regn ut determinanten:
La oss finne ut hva vi legger til og hva vi trekker fra:
Begreper som kommer med et "pluss":
Dette er hoveddiagonalen: produktet av elementene er
Den første trekanten, "vinkelrett på hoveddiagonalen: produktet av elementene er
Den andre trekanten, "vinkelrett på hoveddiagonalen: produktet av elementene er
Vi legger til tre tall:
Begreper som kommer med et "minus"
Dette er en sidediagonal: produktet av elementene er
Den første trekanten, "vinkelrett på den sekundære diagonalen: produktet av elementene er
Den andre trekanten, "vinkelrett på den sekundære diagonalen: produktet av elementene er
Vi legger til tre tall:
Alt som gjenstår å gjøre er å trekke fra summen av plussleddene summen av minusleddene:
Dermed,
Som du kan se, er det ikke noe komplisert og overnaturlig i beregningen av tredjeordens determinanter. Det er rett og slett viktig å huske på trekanter og ikke gjøre regnefeil. Prøv nå å beregne selv:
Vi sjekker:
- Den første trekanten vinkelrett på hoveddiagonalen:
- Den andre trekanten vinkelrett på hoveddiagonalen:
- Summen av plussvilkårene:
- Første trekant vinkelrett på sidediagonalen:
- Den andre trekanten, vinkelrett på sidediagonalen:
- Summen av ledd med minus:
- Summen av plussledd minus summen av minusledd:
Her er et par flere determinanter for deg, beregn verdiene deres selv og sammenlign med svarene:
Svar:
Vel, stemte alt? Flott, da kan du gå videre! Hvis det er vanskeligheter, er mitt råd dette: på Internett er det en haug med programmer for å beregne determinanten på nettet. Alt du trenger er å komme opp med din egen determinant, beregne den selv, og deretter sammenligne den med det programmet beregner. Og så videre til resultatene begynner å stemme. Jeg er sikker på at dette øyeblikket ikke vil vente lenge på seg!
La oss nå gå tilbake til determinanten som jeg skrev ut da jeg snakket om ligningen til et fly som passerer gjennom tre gitt poeng:
Alt du trenger å gjøre er å beregne verdien direkte (ved hjelp av trekantmetoden) og sette resultatet lik null. Naturligvis, siden de er variabler, vil du få et uttrykk som avhenger av dem. Det er dette uttrykket som vil være ligningen til et plan som går gjennom tre gitte punkter som ikke ligger på en rett linje!
La oss illustrere dette med et enkelt eksempel:
1. Konstruer ligningen til planet som går gjennom punktene
Vi komponerer en determinant for disse tre punktene:
Forenkling:
Nå beregner vi det direkte i henhold til regelen om trekanter:
\[(\left| (\begin(array)(*(20)(c))(x + 3)&2&6\\(y - 2)&0&1\\(z + 1)&5&0\end(array)) \ høyre| = \left((x + 3) \right) \cdot 0 \cdot 0 + 2 \cdot 1 \cdot \left((z + 1) \right) + \left((y - 2) \right) \cdot 5 \cdot 6 - )\]
Dermed er ligningen til planet som går gjennom punktene:
Prøv nå å løse ett problem selv, og så vil vi diskutere det:
2. Finn ligningen til planet som går gjennom punktene
Vel, la oss diskutere løsningen nå:
Vi tar en determinant:
Og beregne verdien:
Da har ligningen til planet formen:
Eller, for å redusere med, får vi:
Nå to oppgaver for selvkontroll:
- Konstruer ligningen til et plan som går gjennom tre punkter:
Svar:
Stemte alt? Igjen, hvis det er visse vanskeligheter, så er mitt råd dette: ta tre poeng fra hodet ditt (med stor sannsynlighet vil de ikke ligge på en rett linje), bygg et fly på dem. Og så sjekk deg selv på nettet. For eksempel på nettstedet:
Men ved hjelp av determinanter vil vi konstruere ikke bare ligningen til planet. Husk at jeg fortalte deg at for vektorer er ikke bare punktproduktet definert. Det er også en vektor, samt et blandet produkt. Og hvis skalarproduktet av to vektorer vil være et tall, vil vektorproduktet til to vektorer være en vektor, og denne vektoren vil være vinkelrett på de gitte:

Og modulen blir det lik areal parallellogram bygget på vektorer og. Denne vektoren vi må beregne avstanden fra et punkt til en linje. Hvordan kan vi beregne kryssproduktet til vektorer og om deres koordinater er gitt? Determinanten for den tredje orden kommer oss igjen til hjelp. Men før jeg går videre til algoritmen for å beregne kryssproduktet, må jeg gjøre en liten lyrisk digresjon.
Denne digresjonen gjelder basisvektorene.
Skjematisk er de vist i figuren:

Hvorfor tror du de kalles grunnleggende? Faktum er at:
Eller på bildet:

Gyldigheten av denne formelen er åpenbar, fordi:
vektor produkt
Nå kan jeg begynne å introdusere kryssproduktet:
Vektorproduktet av to vektorer er en vektor som beregnes i henhold til følgende regel:
La oss nå gi noen eksempler på beregning av kryssproduktet:
Eksempel 1: Finn kryssproduktet av vektorer:
Løsning: Jeg tar en determinant:
Og jeg regner det ut:
Nå, fra å skrive gjennom basisvektorer, vil jeg gå tilbake til den vanlige vektornotasjonen:
Dermed:
Prøv nå.
Klar? Vi sjekker:
Og tradisjonelt to oppgaver å kontrollere:
- Finn kryssproduktet til følgende vektorer:
- Finn kryssproduktet til følgende vektorer:
Svar:
Blandet produkt av tre vektorer
Den siste konstruksjonen jeg trenger er det blandede produktet av tre vektorer. Det, som en skalar, er et tall. Det er to måter å beregne det på. - gjennom determinanten, - gjennom det blandede produktet.
La oss nemlig si at vi har tre vektorer:
Deretter kan det blandede produktet av tre vektorer, betegnet med, beregnes som:
1. - det vil si at det blandede produktet er skalarproduktet av en vektor og vektorproduktet av to andre vektorer
For eksempel er det blandede produktet av tre vektorer:
Prøv å beregne det selv ved hjelp av vektorproduktet og sørg for at resultatene stemmer overens!
Igjen, to eksempler uavhengig avgjørelse:
Svar:
Valg av koordinatsystem
Vel, nå har vi alt nødvendig kunnskapsgrunnlag for å løse komplekse stereometriske problemer i geometri. Men før jeg går direkte videre til eksemplene og algoritmene for å løse dem, tror jeg at det vil være nyttig å dvele ved følgende spørsmål: hvordan nøyaktig velg et koordinatsystem for en bestemt figur. Det er tross alt valget relativ posisjon koordinatsystemer og figurer i rommet vil til syvende og sist avgjøre hvor tungvinte beregningene blir.
Jeg minner deg om at vi i denne delen vurderer følgende former:
- kuboid
- Rett prisme (trekantet, sekskantet ...)
- Pyramide (trekantet, firkantet)
- Tetraeder (samme som trekantet pyramide)
For en kube eller kube anbefaler jeg følgende konstruksjon:

Det vil si at jeg vil plassere figuren "i hjørnet". Kuben og boksen er veldig gode figurer. For dem kan du alltid enkelt finne koordinatene til hjørnene. For eksempel, hvis (som vist på bildet)

da er toppunktkoordinatene:
Selvfølgelig trenger du ikke å huske dette, men husk hvordan du best plasserer kuben eller kuboid- ønskelig.
rett prisme
Prisme er en mer skadelig figur. Du kan ordne det i rommet på forskjellige måter. Jeg tror imidlertid følgende er det beste alternativet:
Trekantet prisme:

Det vil si at vi legger en av sidene av trekanten helt på aksen, og en av toppunktene faller sammen med opprinnelsen.
Sekskantet prisme:

Det vil si at en av toppunktene faller sammen med origo, og en av sidene ligger på aksen.
Firkantet og sekskantet pyramide:

En situasjon som ligner på en kube: vi kombinerer to sider av basen med koordinataksene, vi kombinerer en av toppunktene med origo. Den eneste lille vanskeligheten vil være å beregne koordinatene til punktet.
For en sekskantet pyramide - det samme som for et sekskantet prisme. Hovedoppgaven vil igjen være å finne koordinatene til toppunktet.

Tetraeder (trekantet pyramide)

Situasjonen er veldig lik den jeg ga for det trekantede prismet: ett toppunkt faller sammen med origo, en side ligger på koordinataksen.
Vel, nå er du og jeg endelig nær ved å begynne å løse problemer. Fra det jeg sa helt i begynnelsen av artikkelen, kan du trekke følgende konklusjon: de fleste C2-oppgaver faller inn i 2 kategorier: problemer for vinkelen og problemer for avstanden. Først vil vi vurdere problemer for å finne en vinkel. De er på sin side delt inn i følgende kategorier (ettersom kompleksiteten øker):
Problemer med å finne hjørner
- Finne vinkelen mellom to linjer
- Finne vinkelen mellom to plan
La oss vurdere disse problemene sekvensielt: la oss starte med å finne vinkelen mellom to rette linjer. Kom igjen, husk, bestemte du og jeg ikke lignende eksempler Tidligere? Du husker, fordi vi allerede hadde noe lignende ... Vi lette etter en vinkel mellom to vektorer. Jeg minner deg om at hvis to vektorer er gitt: og da er vinkelen mellom dem funnet fra relasjonen:
Nå har vi et mål – å finne vinkelen mellom to rette linjer. La oss gå til det "flate bildet":

Hvor mange vinkler får vi når to linjer krysser hverandre? Allerede ting. Riktignok er bare to av dem ikke like, mens andre er vertikale for dem (og derfor sammenfaller med dem). Så hvilken vinkel bør vi vurdere vinkelen mellom to rette linjer: eller? Her er regelen: vinkelen mellom to rette linjer er alltid ikke mer enn grader. Det vil si at fra to vinkler vil vi alltid velge vinkelen med den minste gradsmål. Det vil si at i dette bildet er vinkelen mellom de to linjene lik. For ikke å bry seg med å finne den minste av de to vinklene hver gang, foreslo snedige matematikere å bruke modulen. Dermed bestemmes vinkelen mellom to rette linjer av formelen:
Du, som en oppmerksom leser, burde ha hatt et spørsmål: hvor får vi egentlig disse tallene som vi trenger for å beregne cosinus til en vinkel? Svar: vi tar dem fra retningsvektorene til linjene! Dermed er algoritmen for å finne vinkelen mellom to linjer som følger:
- Vi bruker formel 1.
Eller mer detaljert:
- Vi leter etter koordinatene til retningsvektoren til den første rette linjen
- Vi ser etter koordinatene til retningsvektoren til den andre linjen
- Beregn modulen til deres skalarprodukt
- Vi ser etter lengden på den første vektoren
- Vi ser etter lengden på den andre vektoren
- Multipliser resultatene fra punkt 4 med resultatene fra punkt 5
- Vi deler resultatet av punkt 3 med resultatet av punkt 6. Vi får cosinus til vinkelen mellom linjene
- Hvis gitt resultat lar deg beregne vinkelen nøyaktig, vi ser etter den
- Ellers skriver vi gjennom arccosine
Vel, nå er tiden inne for å gå videre til oppgavene: Jeg vil demonstrere løsningen av de to første i detalj, jeg vil presentere løsningen av en annen i korthet, og jeg vil bare gi svar på de to siste oppgavene, du må gjør alle beregningene for dem selv.
Oppgaver:
1. I høyre tet-ra-ed-re, finn-di-te vinkelen mellom deg-så-den tet-ra-ed-ra og me-di-a-noy bo-ko-how-siden.
2. I høyre-forover seks-kull-pi-ra-mi-de, hundre-ro-na-os-no-va-niya er på en eller annen måte like, og sideribbene er like, finn vinkelen mellom den rette linjer og.
3. Lengdene på alle kantene på den høyrehendte fire-du-rech-kull-noy pi-ra-mi-dy er lik hverandre. Finn vinkelen mellom de rette linjene og hvis fra-re-zok - du-så-det gitt pi-ra-mi-dy, er punktet se-re-di-på hennes bo-ko- th ribben
4. På kanten av kuben fra-me-che-til et punkt slik at Finn-di-te vinkelen mellom de rette linjene og
5. Pek - se-re-di-på kantene av kuben Nai-di-te vinkelen mellom de rette linjene og.
Det er ikke tilfeldig at jeg plasserte oppgavene i denne rekkefølgen. Mens du ennå ikke har hatt tid til å begynne å navigere i koordinatmetoden, vil jeg selv analysere de mest "problematiske" figurene, og jeg vil la deg håndtere den enkleste kuben! Etter hvert må du lære deg å jobbe med alle figurene, jeg skal øke kompleksiteten i oppgavene fra emne til emne.
La oss begynne å løse problemer:
1. Tegn et tetraeder, plasser det i koordinatsystemet som jeg foreslo tidligere. Siden tetraederet er regelmessig, er alle flatene (inkludert basen) vanlige trekanter. Siden vi ikke får oppgitt lengden på siden, kan jeg ta det likt. Jeg tror du forstår at vinkelen egentlig ikke vil avhenge av hvor mye tetraederet vårt vil bli "strukket"?. Jeg vil også tegne høyden og medianen i tetraederet. Underveis skal jeg tegne basen (den kommer også godt med for oss).

Jeg må finne vinkelen mellom og. Hva vet vi? Vi kjenner bare koordinaten til punktet. Så vi må finne flere koordinater til punktene. Nå tenker vi: et punkt er et skjæringspunkt mellom høyder (eller halveringslinjer eller medianer) til en trekant. En prikk er et forhøyet punkt. Poenget er midtpunktet av segmentet. Så må vi til slutt finne: koordinatene til punktene: .
La oss starte med det enkleste: punktkoordinater. Se på figuren: Det er tydelig at applikasjonen til et punkt er lik null (punktet ligger på et plan). Ordinaten er lik (fordi den er medianen). Det er vanskeligere å finne abscissen. Dette gjøres imidlertid enkelt på grunnlag av Pythagoras teorem: Betrakt en trekant. Hypotenusen er lik, og en av bena er lik. Da:
Endelig har vi:
La oss nå finne koordinatene til punktet. Det er klart at dens applikasjon igjen er lik null, og ordinaten er den samme som den til et punkt, det vil si. La oss finne abscissen. Dette gjøres ganske trivielt hvis man husker det høyder likesidet trekant skjæringspunktet er delt i forhold teller fra toppen. Siden: , deretter den ønskede abscissen til punktet, lik lengden segment er lik: . Dermed er koordinatene til punktet:
La oss finne koordinatene til punktet. Det er tydelig at abscissen og ordinaten sammenfaller med punktets abscisse og ordinat. Og applikasjonen er lik lengden på segmentet. - dette er et av bena i trekanten. Hypotenusen til en trekant er et segment - et ben. Det er søkt etter av de grunnene jeg har fremhevet med fet skrift:
Poenget er midtpunktet av segmentet. Da må vi huske formelen for koordinatene til midten av segmentet:
Det er det, nå kan vi se etter koordinatene til retningsvektorene:
Vel, alt er klart: vi erstatter alle dataene i formelen:
Dermed,
Svar:
Du bør ikke være redd for slike "forferdelige" svar: for problemer C2 er dette en vanlig praksis. Jeg vil heller bli overrasket over det "vakre" svaret i denne delen. Dessuten, som du merket, tyr jeg praktisk talt ikke til noe annet enn Pythagoras teorem og egenskapen til høydene til en likesidet trekant. Det vil si at for å løse det stereometriske problemet brukte jeg det aller minste av stereometri. Gevinsten i dette «slukkes» delvis ved ganske tungvinte beregninger. Men de er ganske algoritmiske!
2. Tegn en vanlig sekskantet pyramide sammen med koordinatsystemet, samt dens base:

Vi må finne vinkelen mellom linjene og. Dermed er vår oppgave redusert til å finne koordinatene til punktene: . Vi finner koordinatene til de tre siste fra den lille tegningen, og vi finner koordinaten til toppunktet gjennom koordinaten til punktet. Mye jobb, men må komme i gang!
a) Koordinat: det er tydelig at applikatet og ordinaten er null. La oss finne abscissen. For å gjøre dette, vurder en rettvinklet trekant. Akk, i den kjenner vi bare hypotenusen, som er lik. Vi vil prøve å finne benet (fordi det er klart at to ganger lengden på benet vil gi oss abscissen til punktet). Hvordan kan vi se etter det? La oss huske hva slags figur vi har ved bunnen av pyramiden? Dette er en vanlig sekskant. Hva betyr det? Dette betyr at alle sider og alle vinkler er like. Vi må finne et slikt hjørne. Noen ideer? Det er mange ideer, men det er en formel:
Summen av vinklene til en regulær n-gon er .
Dermed er summen av vinklene til en vanlig sekskant grader. Da er hver av vinklene lik:
La oss se på bildet igjen. Det er tydelig at segmentet er halveringslinjen til vinkelen. Da er vinkelen grader. Deretter:
Hvor da.
Så den har koordinater
b) Nå kan vi enkelt finne koordinaten til punktet: .
c) Finn koordinatene til punktet. Siden abscissen faller sammen med lengden på segmentet, er den lik. Å finne ordinaten er heller ikke veldig vanskelig: hvis vi kobler sammen punktene og og angir skjæringspunktet for linjen, si for. (gjør det selv enkel konstruksjon). Da er ordinaten til punkt B lik summen av lengdene til segmentene. La oss se på trekanten igjen. Deretter
Da siden Da har punktet koordinater
d) Finn nå koordinatene til punktet. Tenk på et rektangel og bevis at koordinatene til punktet er:
e) Det gjenstår å finne koordinatene til toppunktet. Det er tydelig at abscissen og ordinaten sammenfaller med punktets abscisse og ordinat. La oss finne en app. Siden da. Tenk på en rettvinklet trekant. Av tilstanden til problemet, sidekanten. Dette er hypotenusen til trekanten min. Da er høyden på pyramiden beinet.
Da har punktet koordinater:
Det er det, jeg har koordinatene til alle punkter av interesse for meg. Jeg ser etter koordinatene til retningsvektorene til de rette linjene:
Vi ser etter vinkelen mellom disse vektorene:
Svar:
Igjen, når jeg løste dette problemet, brukte jeg ingen sofistikerte triks, bortsett fra formelen for summen av vinklene til en vanlig n-gon, samt definisjonen av cosinus og sinus til en rettvinklet trekant.
3. Siden vi igjen ikke får oppgitt lengdene på kantene i pyramiden, vil jeg telle dem lik en. Derfor, siden ALLE kanter, og ikke bare sidekantene, er like med hverandre, så ligger det ved bunnen av pyramiden og meg en firkant, og sideflater er rette trekanter. La oss skildre en slik pyramide, så vel som basen på et fly, og markere alle dataene gitt i teksten til problemet:

Vi leter etter vinkelen mellom og. Jeg skal gjøre veldig korte beregninger når jeg ser etter koordinatene til punktene. Du må "dekryptere" dem:
b) - midten av segmentet. Hennes koordinater:
c) Jeg vil finne lengden på segmentet ved hjelp av Pythagoras teorem i en trekant. Jeg vil finne ved Pythagoras teorem i en trekant.
Koordinater:
d) - midten av segmentet. Dens koordinater er
e) Vektorkoordinater
f) Vektorkoordinater
g) Ser etter en vinkel:
Kuben er den enkleste figuren. Jeg er sikker på at du kan finne ut av det selv. Svarene på oppgave 4 og 5 er som følger:
Finne vinkelen mellom en linje og et plan
Vel, tiden for enkle gåter er over! Nå blir eksemplene enda vanskeligere. For å finne vinkelen mellom en linje og et plan, går vi frem som følger:
- Ved å bruke tre punkter bygger vi likningen til planet
,
ved å bruke en tredjeordens determinant. - Ved to punkter ser vi etter koordinatene til retningsvektoren til den rette linjen:
- Vi bruker formelen for å beregne vinkelen mellom en rett linje og et plan:
Som du kan se, er denne formelen veldig lik den vi brukte for å finne vinklene mellom to linjer. Strukturen på høyre side er akkurat den samme, og til venstre ser vi nå etter en sinus, og ikke en cosinus, som før. Vel, en ekkel handling ble lagt til - søket etter flyets ligning.
La oss ikke skrinlegge løse eksempler:
1. Os-no-va-ni-em straight-min premie-vi er-la-et-xia like-men-fattig-ren-ny triangel-nick du-med-den premien-vi er like. Finn vinkelen mellom den rette linjen og planet
2. I en rektangulær pa-ral-le-le-pi-pe-de fra West Nai-di-te vinkelen mellom den rette linjen og planet
3. I det høyrehendte sekskullprismet er alle kanter like. Finn vinkelen mellom den rette linjen og planet.
4. I høyre trekantet pi-ra-mi-de med os-but-va-ni-em fra vest for ribben Nai-di-te vinkel, ob-ra-zo-van -ny plan av os -no-va-niya og straight-my, som går gjennom se-re-di-na av ribbeina og
5. Lengdene på alle kantene på den høyre firkantede pi-ra-mi-dy med toppen er lik hverandre. Finn vinkelen mellom den rette linjen og planet, hvis punktet er se-re-di-på bo-ko-i-th-kanten av pi-ra-mi-dy.
Igjen vil jeg løse de to første problemene i detalj, den tredje - kort, og de to siste lar jeg deg løse på egen hånd. I tillegg måtte du allerede forholde deg til trekantet og firkantede pyramider, men med prismer - ikke ennå.
Løsninger:
1. Tegn et prisme, samt dets base. La oss kombinere det med koordinatsystemet og merke alle dataene som er gitt i problemstillingen:

Jeg beklager noe manglende overholdelse av proporsjoner, men for å løse problemet er dette faktisk ikke så viktig. Flyet er bare "bakveggen" til prismet mitt. Det er nok å bare gjette at ligningen til et slikt plan har formen:
Dette kan imidlertid også vises direkte:
Vi velger vilkårlige tre punkter på dette planet: for eksempel .
La oss lage ligningen til flyet:
Øvelse for deg: beregn denne determinanten selv. Har du lyktes? Da har ligningen til planet formen:
Eller rett og slett
Dermed,
For å løse eksemplet må jeg finne koordinatene til retningsvektoren til den rette linjen. Siden punktet falt sammen med origo, vil vektorens koordinater ganske enkelt falle sammen med koordinatene til punktet. For å gjøre dette finner vi først koordinatene til punktet.
For å gjøre dette, vurder en trekant. La oss tegne en høyde (det er også en median og en halveringslinje) fra toppen. Siden er ordinaten til punktet lik. For å finne abscissen til dette punktet, må vi beregne lengden på segmentet. Ved Pythagoras teorem har vi:
Da har punktet koordinater:
En prikk er en "hevet" på en prikk:
Så koordinatene til vektoren:
Svar:
Som du kan se, er det ingenting grunnleggende vanskelig å løse slike problemer. Faktisk forenkler "rettheten" til en figur som et prisme prosessen litt mer. La oss nå gå videre til neste eksempel:
2. Vi tegner et parallellepiped, tegner et plan og en rett linje i det, og tegner også den nedre basen separat:

Først finner vi ligningen til planet: Koordinatene til de tre punktene som ligger i det:
(de to første koordinatene fås på en åpenbar måte, og du finner enkelt den siste koordinaten fra bildet fra punktet). Så komponerer vi ligningen til planet:
Vi beregner:
Vi leter etter koordinatene til retningsvektoren: Det er tydelig at dens koordinater sammenfaller med koordinatene til punktet, er det ikke? Hvordan finne koordinater? Dette er koordinatene til punktet, hevet langs applikataksen med én! . Da ser vi etter ønsket vinkel:
Svar:
3. Tegn en vanlig sekskantet pyramide, og tegn deretter et plan og en rett linje i den.

Her er det til og med problematisk å tegne et fly, for ikke å snakke om løsningen på dette problemet, men koordinatmetoden bryr seg ikke! Det er i allsidigheten dens største fordel ligger!
Flyet går gjennom tre punkter: . Vi ser etter deres koordinater:
1) . Vis koordinatene for de to siste punktene selv. Du må løse problemet med en sekskantet pyramide for dette!
2) Vi bygger likningen til planet:
Vi ser etter koordinatene til vektoren: . (Se problemet med trekantet pyramide igjen!)
3) Vi ser etter en vinkel:
Svar:
Som du kan se, er det ikke noe overnaturlig vanskelig i disse oppgavene. Du må bare være veldig forsiktig med røttene. Til de to siste problemene vil jeg bare gi svar:
Som du kan se, er teknikken for å løse problemer den samme overalt: hovedoppgaven er å finne koordinatene til toppunktene og erstatte dem med noen formler. Det gjenstår for oss å vurdere en annen klasse problemer for å beregne vinkler, nemlig:
Beregne vinkler mellom to plan
Løsningsalgoritmen vil være som følger:
- For tre punkter ser vi etter ligningen til det første planet:
- For de tre andre punktene ser vi etter ligningen til det andre planet:
- Vi bruker formelen:
Som du kan se, er formelen veldig lik de to foregående, ved hjelp av disse lette vi etter vinkler mellom rette linjer og mellom en rett linje og et plan. Så å huske denne vil ikke være vanskelig for deg. La oss hoppe rett inn i problemet:
1. En hundre-ro-på grunnlag av det høyre trekantede prismet er lik, og dia-go-nalen til sideflaten er lik. Finn vinkelen mellom planet og planet for premiens base.
2. I høyre-forover fire-du-re-kull-noy pi-ra-mi-de, alle kantene på noen er like, finn sinusen til vinkelen mellom planet og planet Ko-Stu, som går gjennom poenget med per-pen-di-ku-lyar-men rett-my.
3. I et vanlig firekullprisme er sidene til os-no-va-nia like, og sidekantene like. På kanten fra-me-che-til poenget slik at. Finn vinkelen mellom planene og
4. I det høyre firkantede prismet er sidene på basene like, og sidekantene er like. På kanten fra-meg-che-til et punkt slik at Finn vinkelen mellom planene og.
5. I kuben finner du co-si-nus til vinkelen mellom planene og
Problemløsninger:
1. Jeg tegner den riktige (ved basen er en likesidet trekant) trekantet prisme og jeg merker på den flyene som vises i tilstanden til problemet:

Vi må finne likningene til to plan: Grunnligningen oppnås trivielt: du kan lage den tilsvarende determinanten for tre punkter, men jeg lager likningen med en gang:
La oss nå finne ligningen Punktet har koordinater Punktet - Siden - medianen og høyden til trekanten, er det lett å finne ved Pythagoras teorem i en trekant. Da har punktet koordinater: Finn applikatet til punktet For å gjøre dette, tenk på en rettvinklet trekant
Da får vi følgende koordinater: Vi komponerer likningen til planet.
Vi beregner vinkelen mellom planene:
Svar:
2. Lage en tegning:
Det vanskeligste er å forstå hva slags mystisk fly det er, som passerer gjennom et punkt vinkelrett. Vel, det viktigste er hva er det? Det viktigste er oppmerksomhet! Faktisk er linjen vinkelrett. Linjen er også vinkelrett. Da vil flyet som går gjennom disse to linjene være vinkelrett på linjen, og vil forresten passere gjennom punktet. Dette flyet går også gjennom toppen av pyramiden. Så ønsket fly - Og flyet er allerede gitt til oss. Vi ser etter koordinater til punkter.
Vi finner koordinaten til punktet gjennom punktet. Det er lett å utlede fra en liten tegning at koordinatene til punktet blir som følger: Hva gjenstår nå å finne for å finne koordinatene til toppen av pyramiden? Må fortsatt beregne høyden. Dette gjøres ved å bruke det samme Pythagoras teorem: først, bevis det (trivielt fra små trekanter som danner en firkant ved bunnen). Siden etter betingelse har vi:
Nå er alt klart: toppunktkoordinater:
Vi komponerer likningen til planet:
Du er allerede en ekspert på å beregne determinanter. Du vil enkelt motta:
Eller på annen måte (hvis vi multipliserer begge delene med roten av to)
La oss nå finne ligningen til flyet:
(Du har vel ikke glemt hvordan vi får ligningen til flyet, ikke sant? Hvis du ikke forstår hvor denne minusen kom fra, så gå tilbake til definisjonen av flyets ligning! Det viste seg bare alltid at min flyet tilhørte opprinnelsen!)
Vi beregner determinanten:
(Du legger kanskje merke til at ligningen til planet falt sammen med ligningen til den rette linjen som går gjennom punktene og! Tenk hvorfor!)
Nå beregner vi vinkelen:
Vi må finne sinusen:
Svar:
3. Et vanskelig spørsmål: hva er et rektangulært prisme, hva synes du? Det er bare et velkjent parallellepiped for deg! Tegner med en gang! Du kan til og med ikke skildre basen separat, det er liten nytte av det her:

Flyet, som vi bemerket tidligere, er skrevet som en ligning:
Nå lager vi et fly
Vi komponerer umiddelbart ligningen til planet:
Ser etter en vinkel
Nå er svarene på de to siste problemene:
Vel, nå er det på tide å ta en pause, for du og jeg er flotte og har gjort en god jobb!
Koordinater og vektorer. Avansert nivå
I denne artikkelen vil vi diskutere med deg en annen klasse problemer som kan løses ved hjelp av koordinatmetoden: avstandsproblemer. Vi vil nemlig vurdere følgende tilfeller:
- Beregning av avstanden mellom skjeve linjer.
Jeg har bestilt de gitte oppgavene etter hvert som deres kompleksitet øker. Det enkleste er å finne pek til plan avstand og det vanskeligste er å finne avstand mellom kryssende linjer. Selv om selvfølgelig ingenting er umulig! La oss ikke utsette og umiddelbart gå videre til vurderingen av den første klassen av problemer:
Beregne avstanden fra et punkt til et plan
Hva trenger vi for å løse dette problemet?
1. Punktkoordinater
Så, så snart vi får alle nødvendige data, bruker vi formelen:
Du bør allerede vite hvordan vi bygger flyets ligning fra de tidligere problemene som jeg analyserte i den siste delen. La oss sette i gang med en gang. Ordningen er som følger: 1, 2 - Jeg hjelper deg med å bestemme, og i noen detalj, 3, 4 - bare svaret, du tar avgjørelsen selv og sammenligner. Startet!
Oppgaver:
1. Gitt en kube. Kantlengden på kuben er Finn-di-te avstand fra se-re-di-ny fra kutt til flatt
2. Gitt rett-vil-naya fire-du-rekh-kull-naya pi-ra-mi-da Bo-ko-voe kanten hundre-ro-på os-no-va-nia er lik. Finn-di-de avstandene fra et punkt til et plan der - se-re-di-på kantene.
3. I den høyre trekantede pi-ra-mi-de med os-but-va-ni-em er den andre kanten lik, og hundre-ro-on os-no-vaniya er lik. Finn-di-disse avstandene fra toppen til flyet.
4. I det høyrehendte sekskullprismet er alle kanter like. Finn-di-disse avstandene fra et punkt til et plan.
Løsninger:
1. Tegn en kube med enkeltkanter, bygg et segment og et plan, angir midten av segmentet med bokstaven
 .
.
Først, la oss starte med en enkel en: Finn koordinatene til et punkt. Siden da (husk koordinatene til midten av segmentet!)
Nå setter vi sammen ligningen til planet på tre punkter
\[\venstre| (\begin(array)(*(20)(c))x&0&1\\y&1&0\\z&1&1\end(array)) \right| = 0\]
Nå kan jeg begynne å finne avstanden:
2. Vi starter på nytt med en tegning, der vi markerer alle dataene!
For en pyramide ville det være nyttig å tegne basen separat.

Selv det faktum at jeg tegner som en kyllingpote vil ikke hindre oss i å enkelt løse dette problemet!
Nå er det enkelt å finne koordinatene til et punkt
Siden koordinatene til punktet
2. Siden koordinatene til punktet a er midten av segmentet, da
Vi kan enkelt finne koordinatene til ytterligere to punkter på planet. Vi komponerer likningen til planet og forenkler den:
\[\venstre| (\venstre| (\begin(array)(*(20)(c))x&1&(\frac(3)(2))\\y&0&(\frac(3)(2))\\z&0&(\frac( (\sqrt 3 ))(2))\end(array)) \right|) \right| = 0\]
Siden punktet har koordinater: , så beregner vi avstanden:
Svar (veldig sjelden!):
Vel, forsto du? Det virker for meg at alt her er like teknisk som i eksemplene vi vurderte med deg i forrige del. Så jeg er sikker på at hvis du mestrer det materialet, vil det ikke være vanskelig for deg å løse de resterende to problemene. Jeg skal bare gi deg svarene:
Beregne avstanden fra en linje til et fly
Det er faktisk ikke noe nytt her. Hvordan kan en linje og et plan plasseres i forhold til hverandre? De har alle muligheter: å krysse, eller en rett linje er parallell med planet. Hva tror du er avstanden fra linjen til planet som den gitte linjen skjærer? Det virker for meg som det er klart at en slik avstand er lik null. Uinteressant sak.

Det andre tilfellet er vanskeligere: her er avstanden allerede null. Men siden linjen er parallell med planet, er hvert punkt på linjen like langt fra dette planet:

Dermed:
Og dette betyr at oppgaven min er redusert til den forrige: vi leter etter koordinatene til et hvilket som helst punkt på linjen, vi ser etter flyets ligning, vi beregner avstanden fra punktet til planet. Faktisk er slike oppgaver i eksamen ekstremt sjeldne. Jeg klarte å finne bare ett problem, og dataene i det var slik at koordinatmetoden ikke var særlig anvendelig på det!
La oss nå gå videre til en annen, mye viktigere problemklasse:
Beregne avstanden fra et punkt til en linje
Hva trenger vi?
1. Koordinatene til punktet vi ser etter avstanden fra:
2. Koordinater til ethvert punkt som ligger på en rett linje
3. Retningsvektorkoordinater til den rette linjen
Hvilken formel bruker vi?
Hva betyr nevneren til denne brøken for deg, så det burde være klart: dette er lengden på retningsvektoren til den rette linjen. Her er en veldig vanskelig teller! Uttrykket betyr modulen (lengden) til vektorproduktet av vektorer og Hvordan beregne vektorproduktet, studerte vi i forrige del av arbeidet. Oppdater kunnskapen din, det vil være veldig nyttig for oss nå!
Dermed vil algoritmen for å løse problemer være som følger:
1. Vi leter etter koordinatene til punktet vi leter etter avstanden fra:
2. Vi ser etter koordinatene til ethvert punkt på linjen som vi ser etter avstanden til:
3. Bygge en vektor
4. Vi bygger retningsvektoren til en rett linje
5. Regn ut kryssproduktet
6. Vi ser etter lengden på den resulterende vektoren:
7. Beregn avstanden:
Vi har mye arbeid, og eksemplene blir ganske komplekse! Så fokuser nå all oppmerksomheten din!
1. Dana er en høyrehendt trekantet pi-ra-mi-da med et toppunkt. Ett hundre-ro-på os-no-va-niya pi-ra-mi-dy er lik, you-so-ta er lik. Finn-di-disse avstandene fra se-re-di-ny av bo-ko-th-kanten til den rette linjen, der punktene og er se-re-di-ny av ribbeina og co-fra-vet -stven-men.
2. Lengdene på ribbene og rettvinklet-no-para-ral-le-le-pi-pe-da er henholdsvis like, og Finn-di-te avstand fra topp-shi-ny til rett-my
3. I det høyre sekskullprismet er alle kantene på en sverm like finn-di-avstanden fra et punkt til en rett linje
Løsninger:
1. Vi lager en pen tegning, der vi merker alle dataene:

Vi har mye arbeid for deg! Jeg vil først beskrive med ord hva vi vil se etter og i hvilken rekkefølge:
1. Koordinater av punkter og
2. Punktkoordinater
3. Koordinater av punkter og
4. Koordinater til vektorer og
5. Kryssproduktet deres
6. Vektorlengde
7. Lengden på vektorproduktet
8. Avstand fra til
Vel, vi har mye arbeid å gjøre! La oss brette opp ermene!
1. For å finne koordinatene til pyramidens høyde, må vi kjenne koordinatene til punktet. Dens applikat er null, og ordinaten er lik abscissen. Til slutt fikk vi koordinatene:
Punktkoordinater
2. - midten av segmentet
3. - midten av segmentet
midtpunkt
4.Koordinater
Vektorkoordinater
5. Regn ut vektorproduktet:

6. Lengden på vektoren: den enkleste måten er å erstatte at segmentet er midtlinjen i trekanten, som betyr at den er lik halve grunnflaten. Så.
7. Vi vurderer lengden på vektorproduktet:
8. Finn til slutt avstanden:
Puh, det er alt! Jeg skal fortelle deg ærlig: løsningen på dette problemet tradisjonelle metoder(via builds) ville være mye raskere. Men her reduserte jeg alt til en ferdig algoritme! Jeg tror at løsningsalgoritmen er klar for deg? Derfor vil jeg be deg løse de resterende to problemene på egen hånd. Sammenligne svar?
Igjen, jeg gjentar: det er lettere (raskere) å løse disse problemene gjennom konstruksjoner, heller enn å ty til koordinere metode. Jeg har demonstrert denne løsningen bare for å vise deg universell metode, som gjør at "ingenting kan fullføres".
Til slutt, vurder Siste klasse oppgaver:
Beregning av avstanden mellom skjeve linjer
Her vil algoritmen for å løse problemer være lik den forrige. Hva vi har:
3. Enhver vektor som forbinder punktene på den første og andre linjen:
Hvordan finner vi avstanden mellom linjene?
Formelen er:
Telleren er modulen til det blandede produktet (vi introduserte det i forrige del), og nevneren er den samme som i forrige formel (modulen til vektorproduktet til retningsvektorene til linjene, avstanden mellom vi ser etter).
Jeg vil minne deg på det

Deretter avstandsformelen kan skrives om som:
Del denne determinanten med determinanten! Selv om jeg, for å være ærlig, ikke er i humør for vitser her! Denne formelen, faktisk, er veldig tungvint og fører til ganske kompliserte beregninger. Hvis jeg var deg, ville jeg bare brukt det som en siste utvei!
La oss prøve å løse noen problemer ved å bruke metoden ovenfor:
1. I det høyre trekantede prismet er alle kantene på en eller annen måte like, finn avstanden mellom de rette linjene og.
2. Gitt et rett-for-formet trekantet prisme, er alle kantene på os-no-va-niya til noen lik Se-che-tion, som går gjennom den andre ribben og se-re-di-nu ribbeina er yav-la-et-sya square-ra-tom. Finn-di-te dis-sto-I-nie mellom straight-we-mi og
Jeg bestemmer det første, og basert på det bestemmer du det andre!
1. Jeg tegner et prisme og markerer linjene og

Punkt C-koordinater: deretter
Punktkoordinater
Vektorkoordinater
Punktkoordinater
Vektorkoordinater
Vektorkoordinater
\[\left((B,\overrightarrow (A(A_1)) \overrightarrow (B(C_1)) ) \right) = \venstre| (\begin(array)(*(20)(l))(\begin(array)(*(20)(c))0&1&0\end(array)\\(\begin(array)(*(20) (c))0&0&1\end(array))\\(\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \frac(1) (2))&1\end(array))\end(array)) \right| = \frac((\sqrt 3 ))(2)\]
Vi tar for oss kryssproduktet mellom vektorene og
\[\overhøyrepil (A(A_1)) \cdot \overhøyrepil (B(C_1)) = \venstre| \begin(array)(l)\begin(array)(*(20)(c))(\overrightarrow i )&(\overrightarrow j )&(\overrightarrow k )\end(array)\\\begin(array )(*(20)(c))0&0&1\end(array)\\\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \ frac(1)(2))&1\end(array)\end(array) \right| - \frac((\sqrt 3 ))(2)\overhøyrepil k + \frac(1)(2)\overhøyrepil i \]
Nå vurderer vi lengden:
Svar:
Prøv nå å fullføre den andre oppgaven nøye. Svaret på det vil være:.
Koordinater og vektorer. Kort beskrivelse og grunnleggende formler
En vektor er et rettet segment. - begynnelsen av vektoren, - slutten av vektoren.
Vektoren er betegnet med eller.
Absolutt verdi vektor - lengden på segmentet som representerer vektoren. Utpekt som.
Vektorkoordinater:
,
hvor er endene av vektoren \displaystyle a .
Sum av vektorer:.
Produktet av vektorer:
Punktprodukt av vektorer:
Endelig fikk jeg tak i et omfattende og etterlengtet tema analytisk geometri. Først litt om denne seksjonen høyere matematikk…. Nå husket du sikkert skolegeometrikurset med mange teoremer, deres bevis, tegninger osv. Hva du skal skjule, et uelsket og ofte uklart emne for en betydelig andel av elevene. Analytisk geometri kan merkelig nok virke mer interessant og tilgjengelig. Hva betyr adjektivet "analytisk"? To stemplede matematiske fraser dukker umiddelbart opp: "grafisk løsningsmetode" og " analytisk metode løsninger". Grafisk metode, selvfølgelig, er forbundet med konstruksjon av grafer, tegninger. Analytisk samme metode innebærer problemløsning hovedsakelig gjennom algebraiske operasjoner. I denne forbindelse er algoritmen for å løse nesten alle problemer med analytisk geometri enkel og gjennomsiktig, den er ofte ganske nøyaktig å bruke nødvendige formler- og svaret er klart! Nei, selvfølgelig, det vil ikke klare seg uten tegninger i det hele tatt, dessuten for bedre forståelse materiale, vil jeg prøve å gi dem utover nødvendighet.
Det åpne kurset med leksjoner i geometri hevder ikke å være teoretisk fullstendighet, det er fokusert på å løse praktiske problemer. Jeg vil i mine forelesninger ta med kun det som fra mitt ståsted er viktig i praksis. Hvis du trenger en mer fullstendig referanse på en underseksjon, anbefaler jeg følgende ganske tilgjengelig litteratur:
1) En ting som, uten spøk, er kjent for flere generasjoner: Skolebok i geometri, forfattere - L.S. Atanasyan og Company. Denne skolegarderobshengeren har allerede tålt 20 (!) nyutgivelser, som selvfølgelig ikke er grensen.
2) Geometri i 2 bind. Forfattere L.S. Atanasyan, Bazylev V.T.. Dette er litteratur for videregående skole, du vil trenge første bind. Sjeldne oppgaver kan falle utenfor synsfeltet mitt, og veiledningen vil være til uvurderlig hjelp.
Begge bøkene er gratis å laste ned online. I tillegg kan du bruke mitt arkiv med ferdige løsninger, som finnes på siden Last ned eksempler på høyere matematikk.
Fra verktøy Jeg tilbyr igjen min egen utvikling - Software pakke på analytisk geometri, noe som i stor grad vil forenkle livet og spare mye tid.
Det forutsettes at leseren er kjent med grunnleggende geometriske begreper og figurer: punkt, linje, plan, trekant, parallellogram, parallellepiped, terning, etc. Det er tilrådelig å huske noen teoremer, i det minste Pythagoras teorem, hallo repeatere)
Og nå vil vi sekvensielt vurdere: konseptet med en vektor, handlinger med vektorer, vektorkoordinater. Videre anbefaler jeg å lese den viktigste artikkelen Punktprodukt av vektorer, i tillegg til Vektor og blandet produkt av vektorer. Den lokale oppgaven vil ikke være overflødig - Inndeling av segmentet i denne forbindelse. Basert på informasjonen ovenfor kan du ligning av en rett linje i et plan Med de enkleste eksempler på løsninger, som vil tillate lære hvordan du løser problemer i geometri. Følgende artikler er også nyttige: Ligning av et plan i rommet, Ligninger av en rett linje i rommet, Grunnleggende problemer på linjen og planet , andre deler av analytisk geometri. Naturligvis vil standardoppgaver bli vurdert underveis.
Konseptet med en vektor. gratis vektor
La oss først gjenta skoledefinisjonen av en vektor. Vektor kalt regissert et segment der begynnelsen og slutten er indikert:
I denne saken begynnelsen av segmentet er punktet, slutten av segmentet er punktet. Selve vektoren er betegnet med . Retning er viktig, hvis du omorganiserer pilen til den andre enden av segmentet, får du en vektor, og dette er allerede helt annen vektor. Det er praktisk å identifisere konseptet med en vektor med bevegelse fysisk kropp: enig, å gå inn dørene til instituttet eller å gå ut dørene til instituttet er helt andre ting.
Det er praktisk å vurdere individuelle punkter på et fly, plass som den såkalte null vektor. En slik vektor har samme ende og begynnelse.
!!! Merk: Her og nedenfor kan du anta at vektorene ligger i samme plan eller du kan anta at de befinner seg i rommet - essensen av materialet som presenteres er gyldig for både planet og rommet.
Betegnelser: Mange gjorde umiddelbart oppmerksom på en pinne uten pil i betegnelsen og sa at de også satte en pil øverst! Det stemmer, du kan skrive med en pil: , men tillatt og post som jeg skal bruke senere. Hvorfor? Tilsynelatende har en slik vane utviklet seg fra praktiske hensyn, skytterne mine på skolen og universitetet viste seg å være for mangfoldige og shaggy. I pedagogisk litteratur noen ganger bryr de seg ikke med kileskrift i det hele tatt, men markerer bokstavene i fet skrift: , og antyder dermed at dette er en vektor.
Det var stilen, og nå om måtene å skrive vektorer på:
1) Vektorer kan skrives med to store latinske bokstaver: ![]() og så videre. Mens den første bokstaven Nødvendigvis angir startpunktet til vektoren, og den andre bokstaven angir endepunktet til vektoren.
og så videre. Mens den første bokstaven Nødvendigvis angir startpunktet til vektoren, og den andre bokstaven angir endepunktet til vektoren.
2) Vektorer er også skrevet med små latinske bokstaver:
Spesielt kan vektoren vår omdannes for korthets skyld med små latinsk bokstav.
Lengde eller modul ikke-null vektor kalles lengden på segmentet. Lengden på nullvektoren er null. Logisk sett.
Lengden til en vektor er angitt med modulo-tegnet: ,
Hvordan finne lengden på en vektor, vil vi lære (eller gjenta, for hvem hvordan) litt senere.
Det var elementær informasjon om vektoren, kjent for alle skolebarn. I analytisk geometri, den såkalte gratis vektor.
Hvis det er ganske enkelt - vektor kan tegnes fra et hvilket som helst punkt:
Vi er vant til å kalle slike vektorer like (definisjonen av like vektorer vil bli gitt nedenfor), men rent med matematisk poeng visjon er SAMME VEKTOR eller gratis vektor. Hvorfor gratis? Fordi i løpet av å løse problemer, kan du "feste" en eller annen vektor til et hvilket som helst punkt på flyet eller rommet du trenger. Dette er en veldig kul eiendom! Se for deg en vektor med vilkårlig lengde og retning - den kan "klones" et uendelig antall ganger og når som helst i verdensrommet, faktisk eksisterer den OVERALT. Det er et slikt studentordtak: Hver foreleser i f ** u i vektoren. Tross alt, ikke bare et vittig rim, alt er matematisk riktig - en vektor kan festes der også. Men ikke skynd deg å glede deg, studentene selv lider oftere =)
Så, gratis vektor- Dette en haug med identiske retningssegmenter. Skoledefinisjonen av en vektor, gitt i begynnelsen av avsnittet: "Et rettet segment kalles en vektor ...", innebærer spesifikk retningssegment hentet fra gitt sett, som er knyttet til et bestemt punkt i flyet eller rommet.
Det skal bemerkes at fra et fysikksynspunkt er konseptet med en fri vektor generelt feil, og vektorens anvendelsespunkt betyr noe. Faktisk er et direkte slag av samme kraft på nesen eller pannen nok til å utvikle mitt dumme eksempel medfører forskjellige konsekvenser. Derimot, ikke gratis vektorer finnes også i løpet av vyshmat (ikke gå dit :)).
Handlinger med vektorer. Kollinearitet av vektorer
I skolekurs geometri vurderer en rekke handlinger og regler med vektorer: addisjon etter trekantregelen, addisjon etter parallellogramregelen, regelen for forskjellen av vektorer, multiplikasjon av en vektor med et tall, skalarproduktet av vektorer, etc. Som et frø gjentar vi to regler som er spesielt relevante for å løse problemer med analytisk geometri.
Regel for addisjon av vektorer i henhold til regelen for trekanter
Vurder to vilkårlige ikke-null vektorer og: 
Det er nødvendig å finne summen av disse vektorene. På grunn av det faktum at alle vektorer anses som frie, utsetter vi vektoren fra slutt vektor: 
Summen av vektorer er vektoren. For en bedre forståelse av regelen, er det lurt å investere i den fysisk mening: la en kropp lage en bane langs vektoren, og deretter langs vektoren. Da er summen av vektorene vektoren til den resulterende banen som starter ved avgangspunktet og slutter ved ankomstpunktet. En lignende regel er formulert for summen av et hvilket som helst antall vektorer. Som de sier, kan kroppen gå sin vei sterkt i sikksakk, eller kanskje på autopilot - langs den resulterende sumvektoren.
Forresten, hvis vektoren er utsatt fra start vektor , så får vi ekvivalenten parallellogramregel tillegg av vektorer.
Først om vektorers kollinearitet. De to vektorene kalles kollineær hvis de ligger på samme linje eller på parallelle linjer. Grovt sett er det det parallelle vektorer. Men i forhold til dem brukes alltid adjektivet "collinear".
Se for deg to kollineære vektorer. Hvis pilene til disse vektorene er rettet i samme retning, kalles slike vektorer samveis. Hvis pilene ser i forskjellige retninger, vil vektorene være det motsatt rettet.
Betegnelser: kollinearitet av vektorer skrives med det vanlige parallellisme-ikonet: , mens detaljering er mulig: (vektorer er co-dirigert) eller (vektorer er rettet motsatt).
arbeid av en ikke-null vektor av et tall er en vektor hvis lengde er lik , og vektorene og er co-rettet mot og motsatt rettet mot .
Regelen for å multiplisere en vektor med et tall er lettere å forstå med et bilde: 
Vi forstår mer detaljert:
1 retning. Hvis multiplikatoren er negativ, så vektoren endrer retning til det motsatte.
2) Lengde. Hvis faktoren er inneholdt i eller , så lengden på vektoren avtar. Så lengden på vektoren er to ganger mindre enn lengden på vektoren. Hvis modulo multiplikatoren er større enn én, så lengden på vektoren øker i tide.
3) Vær oppmerksom på at alle vektorer er kollineære, mens en vektor uttrykkes gjennom en annen, for eksempel . Det motsatte er også sant: hvis en vektor kan uttrykkes i form av en annen, så er slike vektorer nødvendigvis kollineære. Dermed: hvis vi multipliserer en vektor med et tall, får vi kollineær(i forhold til originalen) vektor.
4) Vektorene er codirectional. Vektorene og er også codirectional. Enhver vektor i den første gruppen er motsatt av hvilken som helst vektor i den andre gruppen.
Hvilke vektorer er like?
To vektorer er like hvis de er codirectional og har samme lengde . Merk at co-direction innebærer at vektorene er kollineære. Definisjonen vil være unøyaktig (redundant) hvis du sier: "To vektorer er like hvis de er kollineære, co-directed og har samme lengde."
Fra synspunktet til konseptet med en fri vektor, like vektorer er samme vektor som diskutert i forrige avsnitt.
Vektorkoordinater på flyet og i verdensrommet
Det første punktet er å vurdere vektorer på et plan. La oss skildre den kartesiske rektangulært system koordinater og fra origo setter vi til side enkelt vektorer og:

Vektorer og ortogonal. Ortogonal = vinkelrett. Jeg anbefaler å sakte bli vant til begrepene: i stedet for parallellitet og perpendikularitet bruker vi ordene hhv. kolinearitet Og ortogonalitet.
Betegnelse: ortogonalitet av vektorer skrives med det vanlige vinkelrett tegnet, for eksempel: .
De betraktede vektorene kalles koordinatvektorer eller orts. Disse vektorene dannes basis på overflaten. Hva som ligger til grunn tror jeg er intuitivt klart for mange, flere detaljert informasjon finner du i artikkelen Lineær (ikke) avhengighet av vektorer. Vektor basis.Med enkle ord definerer grunnlaget og opprinnelsen til koordinatene hele systemet - dette er et slags grunnlag som et fullt og rikt geometrisk liv koker på.
Noen ganger kalles det konstruerte grunnlaget ortonormal basis av planet: "orto" - fordi koordinatvektorene er ortogonale, betyr adjektivet "normalisert" enhet, dvs. lengdene på basisvektorene er lik én.
Betegnelse: grunnlaget er vanligvis skrevet i parentes, innenfor hvilke i streng rekkefølge basisvektorer er listet opp, for eksempel: . Koordinatvektorer det er forbudt bytte plass.
Noen plan vektor den eneste måten uttrykt som: ![]() , Hvor - tall, som kalles vektorkoordinater på dette grunnlaget. Men selve uttrykket
, Hvor - tall, som kalles vektorkoordinater på dette grunnlaget. Men selve uttrykket ![]() kalt vektor nedbrytningbasis .
kalt vektor nedbrytningbasis .
Middag servert:

La oss starte med den første bokstaven i alfabetet: . Tegningen viser tydelig at når vektoren dekomponeres når det gjelder grunnlaget, brukes de som nettopp er vurdert:
1) regelen for multiplikasjon av en vektor med et tall: og ;
2) addisjon av vektorer etter trekantregelen: .
Sett nå vektoren mentalt til side fra et hvilket som helst annet punkt på flyet. Det er ganske åpenbart at hans korrupsjon vil «ubønnhørlig følge ham». Her er den, vektorens frihet - vektoren "bærer alt med deg." Denne egenskapen er selvfølgelig sann for enhver vektor. Det er morsomt at selve basisvektorene (frie) ikke må settes til side fra origo, den ene kan for eksempel tegnes nederst til venstre, og den andre øverst til høyre, og ingenting vil endre seg fra dette! Det er sant at du ikke trenger å gjøre dette, fordi læreren også vil vise originalitet og tegne deg et "pass" på et uventet sted.
Vektorer , illustrerer nøyaktig regelen for å multiplisere en vektor med et tall, vektoren er samrettet med basisvektoren , vektoren er rettet motsatt av basisvektoren . For disse vektorene er en av koordinatene lik null, den kan skrives omhyggelig som følger:
Og basisvektorene er forresten slik: (faktisk uttrykkes de gjennom seg selv).
Og endelig: , . Forresten, hva er vektorsubtraksjon, og hvorfor fortalte jeg deg ikke om subtraksjonsregelen? Et sted i lineær algebra, jeg husker ikke hvor, jeg la merke til at subtraksjon er spesielt tilfelle addisjon. Så utvidelsene til vektorene "de" og "e" er rolig skrevet som en sum: ![]() . Omorganiser begrepene stedvis og følg tegningen hvor tydelig den gode gamle addisjonen av vektorer i henhold til trekantregelen fungerer i disse situasjonene.
. Omorganiser begrepene stedvis og følg tegningen hvor tydelig den gode gamle addisjonen av vektorer i henhold til trekantregelen fungerer i disse situasjonene.
Vurderes dekomponering av formen ![]() noen ganger kalt en vektornedbrytning i systemet ort(dvs. i systemet av enhetsvektorer). Men dette er ikke den eneste måten å skrive en vektor på, følgende alternativ er vanlig:
noen ganger kalt en vektornedbrytning i systemet ort(dvs. i systemet av enhetsvektorer). Men dette er ikke den eneste måten å skrive en vektor på, følgende alternativ er vanlig:
Eller med et likhetstegn:
Selve basisvektorene er skrevet som følger: og
Det vil si at koordinatene til vektoren er angitt i parentes. I praktiske oppgaver brukes alle tre opptaksmulighetene.
Jeg tvilte på om jeg skulle snakke, men likevel vil jeg si: vektorkoordinater kan ikke omorganiseres. Strengt på første plass skriv ned koordinaten som tilsvarer enhetsvektor , strengt tatt på andreplass skriv ned koordinaten som tilsvarer enhetsvektoren . Faktisk, og er to forskjellige vektorer.
Vi fant ut koordinatene på flyet. Vurder nå vektorer i tredimensjonalt rom, alt er nesten det samme her! Bare én koordinat til vil bli lagt til. Det er vanskelig å utføre tredimensjonale tegninger, så jeg vil begrense meg til en vektor, som jeg for enkelhets skyld vil utsette fra opprinnelsen: 
Noen vektor tredimensjonalt rom Kan den eneste måten
ekspandere på ortonormal basis: ![]() , hvor er koordinatene til vektoren (tallet) i det gitte grunnlaget.
, hvor er koordinatene til vektoren (tallet) i det gitte grunnlaget.
Eksempel fra bildet: ![]() . La oss se hvordan vektorhandlingsreglene fungerer her. Først multipliserer du en vektor med et tall: (rød pil), (grønn pil) og (magenta pil). For det andre, før du er et eksempel på å legge til flere, i dette tilfelle av tre, vektorer: . Sumvektoren starter ved startpunktet (begynnelsen av vektoren ) og ender opp ved det endelige ankomstpunktet (enden av vektoren ).
. La oss se hvordan vektorhandlingsreglene fungerer her. Først multipliserer du en vektor med et tall: (rød pil), (grønn pil) og (magenta pil). For det andre, før du er et eksempel på å legge til flere, i dette tilfelle av tre, vektorer: . Sumvektoren starter ved startpunktet (begynnelsen av vektoren ) og ender opp ved det endelige ankomstpunktet (enden av vektoren ).
Alle vektorer av tredimensjonalt rom er selvfølgelig også gratis, prøv å mentalt utsette vektoren fra et hvilket som helst annet punkt, og du vil forstå at utvidelsen "blir med den."
på samme måte flat sak, i tillegg til å skrive ![]() versjoner med braketter er mye brukt: enten .
versjoner med braketter er mye brukt: enten .
Hvis en (eller to) koordinatvektorer mangler i utvidelsen, settes nuller i stedet. Eksempler:
vektor (omhyggelig ![]() ) - skrive ned ;
) - skrive ned ;
vektor (omhyggelig ![]() ) - skrive ned ;
) - skrive ned ;
vektor (omhyggelig ![]() ) - skrive ned .
) - skrive ned .
Basisvektorer skrives som følger:
Her er kanskje alle minimum teoretisk kunnskap nødvendig for å løse problemer med analytisk geometri. Kanskje det er for mange begreper og definisjoner, så jeg anbefaler dummies å lese og forstå på nytt denne informasjonen en gang til. Og det vil være nyttig for enhver leser fra tid til annen å referere til grunnleggende leksjon for bedre forståelse av materialet. Kollinearitet, ortogonalitet, ortonormal basis, vektordekomponering - disse og andre begreper vil ofte bli brukt i det følgende. Jeg bemerker at materialene på nettstedet ikke er nok til å bestå en teoretisk test, et kollokvium i geometri, siden jeg nøye krypterer alle teoremer (og uten bevis) - til skade for vitenskapelig stil presentasjon, men et pluss for din forståelse av emnet. For detaljert teoretisk informasjon ber jeg deg bøye deg for professor Atanasyan.
La oss nå gå videre til den praktiske delen:
De enkleste problemene med analytisk geometri.
Handlinger med vektorer i koordinater
Oppgavene som vil bli vurdert, det er svært ønskelig å lære å løse dem helt automatisk, og formlene huske, ikke engang huske det med vilje, de vil huske det selv =) Dette er veldig viktig, fordi på det enkleste elementære eksempler andre analytiske geometriproblemer er basert, og det ville være irriterende å bruke ekstra tid på å spise bønder. Du trenger ikke å feste de øverste knappene på skjorten, mange ting er kjent for deg fra skolen.
Presentasjonen av materialet vil følge et parallelt forløp – både for flyet og for rommet. Av den grunn at alle formlene ... vil du se selv.
Hvordan finne en vektor gitt to poeng?
Hvis to punkter på planet og er gitt, har vektoren følgende koordinater: ![]()
Hvis to punkter i rommet og er gitt, har vektoren følgende koordinater:
Det er, fra koordinatene til enden av vektoren du må trekke fra de tilsvarende koordinatene vektor start.
Trening: For de samme punktene, skriv ned formlene for å finne koordinatene til vektoren. Formler på slutten av leksjonen.
Eksempel 1
Gitt to punkter i flyet og . Finn vektorkoordinater
Løsning: i henhold til den tilsvarende formelen:
Alternativt kan følgende notasjon brukes:
Esteter vil avgjøre slik:
Personlig er jeg vant til den første versjonen av plata.
Svar:
I henhold til betingelsen var det ikke nødvendig å bygge en tegning (som er typisk for problemer med analytisk geometri), men for å forklare noen punkter til dummies, vil jeg ikke være for lat: 
Må forstås forskjellen mellom punktkoordinater og vektorkoordinater:
Punktkoordinater er de vanlige koordinatene i et rektangulært koordinatsystem. Jeg tror alle vet hvordan man plotter punkter på koordinatplanet siden klasse 5-6. Hvert punkt har en streng plass på flyet, og de kan ikke flyttes hvor som helst.
Koordinatene til samme vektor er dens utvidelse med hensyn til grunnlaget, i dette tilfellet. Enhver vektor er gratis, derfor kan vi om nødvendig enkelt utsette den fra et annet punkt i flyet. Interessant, for vektorer kan du ikke bygge akser i det hele tatt, et rektangulært koordinatsystem, du trenger bare et grunnlag, i dette tilfellet, en ortonormal basis av planet.
Registreringene av punktkoordinater og vektorkoordinater ser ut til å være like: , og følelse av koordinater absolutt annerledes, og du bør være godt klar over denne forskjellen. Denne forskjellen gjelder selvfølgelig også for plass.
Mine damer og herrer, vi fyller våre hender:
Eksempel 2
a) Gitt poeng og . Finn vektorer og .
b) Poeng gis ![]() Og . Finn vektorer og .
Og . Finn vektorer og .
c) Gitt poeng og . Finn vektorer og .
d) Poeng gis. Finn vektorer ![]() .
.
Kanskje nok. Dette er eksempler for en uavhengig avgjørelse, prøv å ikke overse dem, det vil lønne seg ;-). Tegninger er ikke nødvendig. Løsninger og svar på slutten av leksjonen.
Hva er viktig for å løse problemer med analytisk geometri? Det er viktig å være EKSTREMT FORSIKTIG for å unngå den mesterlige feilen "to pluss to er lik null". Jeg beklager på forhånd hvis jeg har gjort en feil =)
Hvordan finne lengden på et segment?
Lengden, som allerede nevnt, er indikert med modultegnet.
Hvis to punkter på planet og er gitt, kan lengden på segmentet beregnes ved hjelp av formelen
Hvis to punkter i rommet og er gitt, kan lengden på segmentet beregnes med formelen
Merk: Formlene forblir korrekte hvis de tilsvarende koordinatene byttes: og , men det første alternativet er mer standard
Eksempel 3
Løsning: i henhold til den tilsvarende formelen:
Svar: ![]()
For klarhetens skyld vil jeg lage en tegning 
Linjestykke - det er ikke en vektor, og du kan selvfølgelig ikke flytte den hvor som helst. I tillegg, hvis du fullfører tegningen i målestokk: 1 enhet. \u003d 1 cm (to tetradceller), så kan svaret kontrolleres med en vanlig linjal ved direkte å måle lengden på segmentet.
Ja, løsningen er kort, men den har et par til viktige poeng Jeg vil gjerne presisere:
Først, i svaret setter vi dimensjonen: "enheter". Tilstanden sier ikke HVA det er, millimeter, centimeter, meter eller kilometer. Derfor vil den generelle formuleringen være en matematisk kompetent løsning: "enheter" - forkortet som "enheter".
For det andre, la oss gjenta skolematerialet, som ikke bare er nyttig for det aktuelle problemet:
Følg med på viktig teknikk
– tar multiplikatoren ut under roten. Som et resultat av beregningene fikk vi resultatet og god matematisk stil innebærer å ta multiplikatoren ut under roten (hvis mulig). Prosessen ser mer detaljert slik ut: ![]() . Å la svaret ligge i skjemaet vil selvsagt ikke være en feil – men det er definitivt en feil og et tungtveiende argument for nitpicking fra lærerens side.
. Å la svaret ligge i skjemaet vil selvsagt ikke være en feil – men det er definitivt en feil og et tungtveiende argument for nitpicking fra lærerens side.
Her er andre vanlige tilfeller: 
Ofte under roten viser det seg nok stort antall, For eksempel . Hvordan være i slike tilfeller? På kalkulatoren sjekker vi om tallet er delelig med 4:. Ja, del helt opp, slik: ![]() . Eller kanskje tallet kan deles på 4 igjen? . Dermed:
. Eller kanskje tallet kan deles på 4 igjen? . Dermed: ![]() . Det siste sifferet i tallet er oddetall, så å dele med 4 for tredje gang er tydeligvis ikke mulig. Prøver å dele på ni: . Som et resultat:
. Det siste sifferet i tallet er oddetall, så å dele med 4 for tredje gang er tydeligvis ikke mulig. Prøver å dele på ni: . Som et resultat:
Klar.
Konklusjon: hvis vi under roten får et helt ikke-ekstraherbart tall, så prøver vi å ta ut faktoren fra under roten - på kalkulatoren sjekker vi om tallet er delelig med: 4, 9, 16, 25, 36, 49, etc.
I løpet av å løse ulike problemer finner man ofte røtter, prøv alltid å trekke ut faktorer fra under roten for å unngå lavere poengsum og unødvendige problemer med å sluttføre løsningene dine i henhold til lærerens bemerkning.
La oss gjenta kvadreringen av røttene og andre krefter samtidig: 
Reglene for handlinger med grader i generell form finner du i en skolebok om algebra, men jeg tror at alt eller nesten alt allerede er klart fra eksemplene gitt.
Oppgave for en uavhengig løsning med et segment i rommet:
Eksempel 4
Gitt poeng og . Finn lengden på segmentet.
Løsning og svar på slutten av leksjonen.
Hvordan finne lengden på en vektor?
Hvis en planvektor er gitt, beregnes lengden ved hjelp av formelen.
Hvis en romvektor er gitt, beregnes lengden ved hjelp av formelen ![]() .
.
 Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler
Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler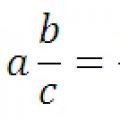 Konvertering av desimaltall til vanlige brøker
Konvertering av desimaltall til vanlige brøker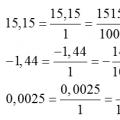 Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler
Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler