Funksjonstyper og deres egenskaper. Grunnleggende begreper og egenskaper ved funksjoner

Definisjon: En numerisk funksjon er en korrespondanse som tilordnes hvert tall x fra et gitt sett entall y.

Betegnelse:

der x er en uavhengig variabel (argument), y er en avhengig variabel (funksjon). Settet med verdier x kalles domenet til funksjonen (betegnet D(f)). Settet med verdier y kalles funksjonens rekkevidde (betegnet med E(f)). Grafen til en funksjon er settet med punkter i planet med koordinater (x, f(x))

Måter å sette en funksjon på.

analytisk metode (ved hjelp av en matematisk formel);
tabellmetode (ved hjelp av en tabell);
beskrivende metode (ved hjelp av en verbal beskrivelse);
grafisk metode (ved hjelp av en graf).

Grunnleggende egenskaper funksjoner.

1. Partall og oddetall

En funksjon kalles selv om
– definisjonsdomenet til funksjonen er symmetrisk i forhold til null
f(-x) = f(x)

Grafen til en jevn funksjon er symmetrisk om aksen 0y

En funksjon kalles oddetvis
– definisjonsdomenet til funksjonen er symmetrisk i forhold til null
– for enhver x fra definisjonsdomenet f(-x) = -f(x)

Grafen til en oddetallsfunksjon er symmetrisk om opprinnelsen.

2. Periodisitet

Funksjonen f(x) kalles periodisk med en periode hvis for en hvilken som helst x fra definisjonsdomenet f(x) = f(x+T) = f(x-T) .

Rute periodisk funksjon består av uendelig repeterende identiske fragmenter.

3. Monotoni (øke, redusere)

Funksjonen f(x) øker på settet P hvis for noen x 1 og x 2 fra dette settet, slik at x 1

Funksjonen f(x) er avtagende på settet P hvis for noen x 1 og x 2 fra dette settet, slik at x 1 f(x 2) .

4. Ytterligheter

Punktet X max kalles maksimumspunktet for funksjonen f (x) hvis for alle x fra et eller annet nabolag X max , ulikheten f (x) f (X max) er tilfredsstilt.

Verdien Y max =f(X max) kalles maksimum for denne funksjonen.

X maks - maksimumspunkt
Max har et maksimum

Punktet X min kalles minimumspunktet for funksjonen f (x) hvis for alle x fra et eller annet nabolag X min, er ulikheten f (x) f (X min) tilfredsstilt.

Verdien av Y min =f(X min) kalles minimum av denne funksjonen.

X min - minimumspunkt
Y min - minimum

X min , X max - ekstremumpunkter
Y min , Y max - ekstrema.

5. Funksjonsnuller

Nullpunktet til funksjonen y = f(x) er verdien av argumentet x der funksjonen forsvinner: f(x) = 0.

X 1, X 2, X 3 er nuller for funksjonen y = f(x).

Oppgaver og tester om emnet "Grunnleggende egenskaper til en funksjon"

Funksjonsegenskaper - Numeriske funksjoner Karakter 9
Leksjoner: 2 oppgaver: 11 prøver: 1
Egenskaper til logaritmer - Demonstrerende og logaritmisk funksjon 11. klasse
Leksjoner: 2 oppgaver: 14 prøver: 1
Kvadratrotfunksjon, dens egenskaper og graf - Funksjon kvadratrot. Kvadratrotegenskaper Grad 8
Leksjoner: 1 oppgaver: 9 prøver: 1
Potensfunksjoner, deres egenskaper og grafer – Grader og røtter. Strømfunksjoner 11. klasse
Leksjoner: 4 oppgaver: 14 prøver: 1
Funksjoner - Viktige emner til gjentakelse av eksamen matematikk
Oppgaver: 24

Etter å ha studert dette emnet, bør du kunne finne definisjonsdomenet til forskjellige funksjoner, bestemme monotonisitetsintervallene til en funksjon ved å bruke grafer, og undersøke funksjoner for partall og oddetall. Vurder løsningen av slike problemer i de følgende eksemplene.

Eksempler.

1. Finn domenet til funksjonen.

Løsning: omfanget av funksjonen er funnet fra betingelsen

Personvernet ditt er viktig for oss. Av denne grunn har vi utviklet en personvernerklæring som beskriver hvordan vi bruker og lagrer informasjonen din. Vennligst les vår personvernerklæring og gi oss beskjed hvis du har spørsmål.

Innsamling og bruk av personopplysninger

Personopplysninger refererer til data som kan brukes til å identifisere eller kontakte en bestemt person.

Du kan bli bedt om å oppgi din personlige informasjon når som helst når du kontakter oss.

Følgende er noen eksempler på hvilke typer personopplysninger vi kan samle inn og hvordan vi kan bruke slik informasjon.

Hvilken personlig informasjon samler vi inn:

Når du sender inn en søknad på nettstedet, kan vi samle inn ulike opplysninger, inkludert navn, telefonnummer, adresse E-post etc.

Hvordan vi bruker dine personopplysninger:

Samlet av oss personlig informasjon lar oss kontakte deg og informere deg om unike tilbud, kampanjer og andre arrangementer og kommende arrangementer.
Fra tid til annen kan vi bruke din personlige informasjon til å sende deg viktige meldinger og kommunikasjoner.
Vi kan også bruke personopplysninger til interne formål, som å gjennomføre revisjoner, dataanalyser og ulike undersøkelser for å forbedre tjenestene vi leverer og gi deg anbefalinger angående våre tjenester.
Hvis du deltar i en premietrekning, konkurranse eller lignende insentiv, kan vi bruke informasjonen du gir til å administrere slike programmer.

Offentliggjøring til tredjeparter

Vi utleverer ikke informasjon mottatt fra deg til tredjeparter.

Unntak:

Om nødvendig - i samsvar med loven, rettsorden, i rettssaker, og/eller basert på offentlige forespørsler eller forespørsler fra offentlige etater på den russiske føderasjonens territorium - oppgi din personlige informasjon. Vi kan også avsløre informasjon om deg hvis vi fastslår at slik avsløring er nødvendig eller hensiktsmessig av hensyn til sikkerhet, rettshåndhevelse eller andre offentlige interesser.
Ved en omorganisering, fusjon eller salg kan vi overføre personopplysningene vi samler inn til den aktuelle tredjeparts etterfølgeren.

Beskyttelse av personopplysninger

Vi tar forholdsregler - inkludert administrative, tekniske og fysiske - for å beskytte din personlige informasjon mot tap, tyveri og misbruk, samt mot uautorisert tilgang, avsløring, endring og ødeleggelse.

Opprettholde personvernet ditt på bedriftsnivå

For å sikre at din personlige informasjon er sikker, kommuniserer vi personvern- og sikkerhetspraksis til våre ansatte og håndhever strengt personvernpraksis.

Funksjonens omfang og rekkevidde. I elementær matematikk studeres funksjoner bare på settet reelle tall R.Dette betyr at funksjonsargumentet bare kan ta på de reelle verdiene som funksjonen er definert for, dvs. den aksepterer også bare virkelige verdier. Masse av X alle gyldige gyldige verdier av argumentet x, som funksjonen for y= f(x) er definert, kalt funksjonsomfang. Masse av Y alle reelle verdier y som funksjonen aksepterer kalles funksjonsområde. Nå kan du gi mer presis definisjon funksjoner: regel(lov) for korrespondanse mellom settene X og Y, som for hvert element fra settetX kan finne ett og bare ett element fra mengden Y, kalles en funksjon.

Det følger av denne definisjonen at en funksjon anses som gitt hvis:

Omfanget av funksjonen er satt X ;

Omfanget av funksjonen er satt Y ;

Reglen (loven) av korrespondanse er kjent, og slik at for hver

Bare én funksjonsverdi kan bli funnet for en argumentverdi.

Dette kravet om funksjonens unikhet er obligatorisk.

monoton funksjon. Hvis for to verdier av argumentet x 1 og x 2 i betingelsen x 2 > x 1 følger f(x 2) > f(x 1), deretter funksjonen f(x) er kalt økende; hvis for noen x 1 og x 2 i betingelsen x 2 > x 1 følger f(x 2) < f(x 1), deretter funksjonen f(x) er kalt avtar. En funksjon som bare øker eller bare reduseres kalles monotont.

Begrensede og ubegrensede funksjoner. Funksjonen kalles begrenset hvis det er slikt positivt tall M hva | f(x) | M for alle verdier x . Hvis det ikke finnes et slikt nummer, er funksjonen det ubegrenset.

EKSEMPLER.

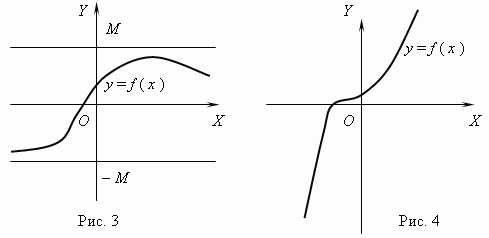
Funksjonen som er avbildet i fig. 3 er avgrenset, men ikke monoton. Funksjonen i figur 4 er akkurat det motsatte, monoton, men ubegrenset. (Vennligst forklar dette!)

Kontinuerlige og diskontinuerlige funksjoner. Funksjon y = f (x) er kalt kontinuerlige på punktetx = en, hvis:

1) funksjonen er definert for x = en, dvs. f (en) finnes;

2) eksisterer avgrenset grense lim f (x) ;

x→en

(Se "Begrensninger for funksjoner")

3) f (en) = lim f (x) .

x→en

Hvis minst en av disse betingelsene ikke er oppfylt, kalles funksjonen opp diskontinuerlig på punktet x = en.

Hvis funksjonen er kontinuerlig i alle punkter i definisjonsdomenet, da heter det kontinuerlig funksjon.

Partall og odde funksjoner. Hvis for noen x f(- x) = f (x), så kalles funksjonen til og med; hvis det gjør det: f(- x) = - f (x), så kalles funksjonen merkelig. Rute jevn funksjonsymmetrisk om Y-aksen(Fig.5), en graf merkelig funksjon Simmetrikk om opprinnelsen(Fig. 6).

Periodisk funksjon. Funksjon f (x) - tidsskrift hvis det er slikt ikke-null Antall T til hva noen x fra omfanget av funksjonsdefinisjonen finner sted: f (x + T) = f (x). Slik minst nummeret ringes opp funksjonsperiode. Alle trigonometriske funksjoner er periodiske.

EKSEMPEL 1. Bevis den synden x har en periode på 2.

LØSNING Vi vet at synd ( x+ 2n) = synd x, hvor n= 0, ± 1, ± 2, …

Derfor legger du til 2 n til sinusargumentet

Endrer verdien. Er det et annet nummer med dette

Samme eiendom?

La oss late som det P- et slikt tall, dvs. likestilling:

Synd ( x+P) = synd x,

Gyldig for alle verdier x. Men så har den det

Beliggenhet og x= / 2, dvs.

synd(/2 + P) = synd / 2 = 1.

Men ifølge reduksjonsformelen synd ( / 2 + P) = cos P. Deretter

Det følger av de to siste likhetene at cos P= 1, men vi

Vi vet at dette er sant bare når P = 2n. Siden den minste

Et tall som ikke er null av 2 n er 2, så dette tallet

Og det er en syndperiode x. Det er på samme måte bevist at 2 fra n er, så dette er perioden synd 2 x.

Funksjonen null. Verdien av argumentet som funksjonen er lik 0 for kalles null (root) funksjoner. En funksjon kan ha flere nuller, for eksempel funksjonen y = x (x + 1) (x-3) har tre nuller: x= 0, x= -1, x= 3. Geometrisk funksjon null - er abscissen til skjæringspunktet for grafen til funksjonen med aksen X .

Figur 7 viser grafen til funksjonen med nuller: x= en, x = b og x= c.

Asymptote. Hvis grafen til en funksjon nærmer seg en bestemt rett linje på ubestemt tid når den beveger seg bort fra origo, kalles denne rette linjen asymptote.

Funksjonsnuller
Nullpunktet til funksjonen er verdien X, hvor funksjonen blir 0, det vil si f(x)=0.

Nullpunkter er skjæringspunktene for grafen til funksjonen med aksen Åh.

Funksjonsparitet
En funksjon kalles selv om for noen X fra definisjonsdomenet, likheten f(-x) = f(x)

En jevn funksjon er symmetrisk om aksen OU

Odd funksjon
En funksjon kalles odd hvis for noen X fra definisjonsdomenet er likheten f(-x) = -f(x) tilfredsstilt.

En oddetallsfunksjon er symmetrisk med hensyn til origo.
En funksjon som verken er partall eller oddetall kalles en generell funksjon.

Funksjonsøkning
Funksjonen f(x) kalles økende if større verdi argumentet tilsvarer den større verdien av funksjonen, dvs.

Reduserende funksjon
Funksjonen f(x) kalles avtagende hvis den større verdien av argumentet tilsvarer den mindre verdien av funksjonen, dvs.

Intervallene som funksjonen enten bare avtar eller bare øker kalles intervaller av monotoni. Funksjonen f(x) har 3 intervaller med monotonisitet:

Finn intervaller med monotonitet ved hjelp av tjenesten Intervaller med økende og minkende funksjoner

Lokalt maksimum
Punktum x 0 kalt et punkt lokalt maksimum, hvis for noen X fra et område av et punkt x 0 følgende ulikhet gjelder: f(x 0) > f(x)

Lokalt minimum
Punktum x 0 kalt et punkt lokalt minimum, hvis for noen X fra et område av et punkt x 0 følgende ulikhet gjelder: f(x 0)< f(x).

Lokale maksimumspoeng og lokale minimumspoeng kalles lokale ekstremumpunkter.

lokale ekstremumpunkter.

Funksjon Periodisitet
Funksjonen f(x) kalles periodisk, med punktum T, hvis for noen X f(x+T) = f(x) .

Konstansintervaller
Intervaller der funksjonen enten bare er positiv eller kun negativ kalles intervaller med konstant fortegn.

Funksjonskontinuitet
En funksjon f(x) kalles kontinuerlig i et punkt x 0 hvis grensen for funksjonen er x → x 0 er lik verdien fungerer på dette tidspunktet, dvs. .