1 สัญลักษณ์แห่งความเท่าเทียมกันของรูปสามเหลี่ยมเรียกว่า เครื่องหมายที่สามของความเท่าเทียมกันของรูปสามเหลี่ยม
ท่ามกลาง จำนวนมากรูปหลายเหลี่ยมซึ่งโดยพื้นฐานแล้วจะเป็นเส้นขาดแบบปิดและไม่ตัดกัน สามเหลี่ยมคือรูปที่มีมุมน้อยที่สุด กล่าวอีกนัยหนึ่ง นี่คือรูปหลายเหลี่ยมที่ง่ายที่สุด แต่ถึงแม้จะเรียบง่าย แต่ร่างนี้ก็เต็มไปด้วยความลึกลับมากมายและ การค้นพบที่น่าสนใจซึ่งได้รับการส่องสว่าง ส่วนพิเศษคณิตศาสตร์-เรขาคณิต วินัยนี้เริ่มสอนในโรงเรียนตั้งแต่ชั้นประถมศึกษาปีที่ 7 และมีหัวข้อ "สามเหลี่ยม" ให้ที่นี่ ความสนใจเป็นพิเศษ- เด็ก ๆ ไม่เพียงเรียนรู้กฎเกี่ยวกับรูปร่างเท่านั้น แต่ยังเปรียบเทียบโดยศึกษาเครื่องหมายที่ 1, 2 และ 3 ของความเท่าเทียมกันของรูปสามเหลี่ยม
รู้จักกันครั้งแรก
กฎข้อแรกที่เด็กนักเรียนเรียนรู้มีดังนี้: ผลรวมของค่าของทุกมุมของสามเหลี่ยมเท่ากับ 180 องศา เพื่อยืนยันสิ่งนี้ ก็เพียงพอแล้วที่จะใช้ไม้โปรแทรกเตอร์เพื่อวัดแต่ละจุดยอดและบวกค่าผลลัพธ์ทั้งหมดเข้าด้วยกัน ด้วยเหตุนี้ เมื่อทราบปริมาณสองปริมาณแล้ว จึงง่ายต่อการระบุปริมาณที่สาม ตัวอย่างเช่น: ในรูปสามเหลี่ยม มุมหนึ่งเป็น 70° และอีกมุมเป็น 85° แล้วมุมที่สามจะมีขนาดเท่าใด
180 - 85 - 70 = 25.
คำตอบ: 25°
ปัญหาอาจซับซ้อนมากขึ้นหากระบุค่ามุมเพียงค่าเดียว และค่าที่สองจะบอกเฉพาะค่าที่มากกว่าหรือน้อยกว่าจำนวนเท่าหรือจำนวนเท่าเท่านั้น
ในรูปสามเหลี่ยมเพื่อกำหนดคุณสมบัติบางอย่างสามารถวาดเส้นพิเศษได้ซึ่งแต่ละเส้นมีชื่อของตัวเอง:
- ความสูง - เส้นตรงตั้งฉากที่ลากจากจุดยอดไปด้านตรงข้าม
- ความสูงทั้งสามวาดพร้อมกันตัดกันที่กึ่งกลางของรูปสร้างออร์โธเซนเตอร์ซึ่งสามารถวางได้ทั้งภายในและภายนอกขึ้นอยู่กับประเภทของสามเหลี่ยม
- ค่ามัธยฐาน - เส้นที่เชื่อมต่อจุดยอดกับตรงกลางของฝั่งตรงข้าม
- จุดตัดของค่ามัธยฐานคือจุดแรงโน้มถ่วงซึ่งอยู่ภายในร่าง
- เส้นแบ่งครึ่ง - เส้นที่วิ่งจากจุดยอดไปยังจุดตัดกับด้านตรงข้าม จุดตัดของเส้นแบ่งครึ่งสามจุดคือจุดศูนย์กลางของวงกลมที่ถูกจารึกไว้
ความจริงง่ายๆ เกี่ยวกับสามเหลี่ยม

สามเหลี่ยมก็เหมือนกับรูปร่างอื่นๆ ที่จะมีลักษณะและคุณสมบัติเป็นของตัวเอง ดังที่ได้กล่าวไปแล้ว ตัวเลขนี้เป็นรูปหลายเหลี่ยมที่ง่ายที่สุด แต่มีคุณสมบัติเฉพาะของตัวเอง:
- มุมที่มีค่ามากกว่าจะอยู่ตรงข้ามกับด้านที่ยาวที่สุดเสมอ และในทางกลับกัน
- มุมที่เท่ากันอยู่ตรงข้ามกับด้านที่เท่ากัน ตัวอย่างนี้คือสามเหลี่ยมหน้าจั่ว
- ผลรวมของมุมภายในจะเท่ากับ 180° เสมอ ซึ่งได้แสดงตัวอย่างไว้แล้ว
- เมื่อด้านหนึ่งของรูปสามเหลี่ยมขยายออกไปเกินขอบเขต มุมภายนอกจะถูกสร้างขึ้นซึ่งจะเป็นมุมดังกล่าวเสมอไป เท่ากับผลรวมมุมที่ไม่อยู่ติดกัน
- ด้านใดด้านหนึ่งจะน้อยกว่าผลรวมของอีกสองด้านเสมอ แต่จะมากกว่าผลต่าง
ประเภทของรูปสามเหลี่ยม
ขั้นตอนต่อไปของการทำความรู้จักคือการกำหนดกลุ่มที่สามเหลี่ยมที่นำเสนออยู่ การเป็นประเภทใดประเภทหนึ่งขึ้นอยู่กับขนาดของมุมของรูปสามเหลี่ยม

- หน้าจั่ว - มีสองด้านเท่ากันซึ่งเรียกว่าด้านข้างส่วนที่สามในกรณีนี้ทำหน้าที่เป็นฐานของรูป มุมที่ฐานของสามเหลี่ยมนั้นเท่ากัน และค่ามัธยฐานที่ดึงมาจากจุดยอดคือเส้นแบ่งครึ่งและความสูง
- ถูกต้องหรือ สามเหลี่ยมด้านเท่า, เป็นสิ่งที่ทุกด้านเท่ากัน
- สี่เหลี่ยม: มุมหนึ่งของมันคือ 90° ในกรณีนี้ ด้านที่อยู่ตรงข้ามมุมนี้เรียกว่าด้านตรงข้ามมุมฉาก และอีกสองด้านเรียกว่าขา
- สามเหลี่ยมเฉียบพลัน - ทุกมุมน้อยกว่า 90°
- ป้าน - มุมใดมุมหนึ่งที่มากกว่า 90°
ความเท่าเทียมกันและความคล้ายคลึงของรูปสามเหลี่ยม
ในระหว่างกระบวนการเรียนรู้ พวกเขาไม่เพียงแต่พิจารณารูปเดียวเท่านั้น แต่ยังเปรียบเทียบรูปสามเหลี่ยมสองรูปด้วย และอันนี้ก็ดูเหมือนว่า ธีมเรียบง่ายมีกฎและทฤษฎีบทมากมายซึ่งสามารถพิสูจน์ได้ว่าตัวเลขที่เป็นปัญหานั้นเป็นรูปสามเหลี่ยมที่เท่ากัน เกณฑ์ความเท่าเทียมกันของรูปสามเหลี่ยมมีคำจำกัดความดังนี้ รูปสามเหลี่ยมจะเท่ากันถ้าด้านและมุมที่ตรงกันเท่ากัน ด้วยความเท่าเทียมกัน หากคุณวางตัวเลขสองตัวนี้ทับกัน เส้นทั้งหมดของพวกมันจะมาบรรจบกัน นอกจากนี้ตัวเลขยังสามารถคล้ายกันโดยเฉพาะอย่างยิ่งซึ่งนำไปใช้ได้จริง ตัวเลขที่เหมือนกันต่างกันเพียงขนาดเท่านั้น เพื่อที่จะได้ข้อสรุปเกี่ยวกับรูปสามเหลี่ยมที่นำเสนอต้องเป็นไปตามเงื่อนไขข้อใดข้อหนึ่งต่อไปนี้:
- มุมสองมุมของรูปหนึ่งมีค่าเท่ากับสองมุมของอีกรูปหนึ่ง
- ด้านทั้งสองของด้านหนึ่งเป็นสัดส่วนกับทั้งสองด้านของสามเหลี่ยมที่สอง และมุมที่เกิดจากด้านทั้งสองเท่ากัน
- ด้านทั้งสามของรูปที่สองจะเหมือนกับรูปแรก
แน่นอนว่าเพื่อความเท่าเทียมกันที่เถียงไม่ได้ซึ่งจะไม่ทำให้เกิดข้อสงสัยแม้แต่น้อยจำเป็นต้องมีค่าเท่ากันขององค์ประกอบทั้งหมดของตัวเลขทั้งสองอย่างไรก็ตามด้วยการใช้ทฤษฎีบทงานจะง่ายขึ้นอย่างมากและมีเพียงไม่กี่เท่านั้น เงื่อนไขได้รับอนุญาตให้พิสูจน์ความเท่าเทียมกันของรูปสามเหลี่ยมได้

สัญญาณแรกของความเท่าเทียมกันของรูปสามเหลี่ยม
ปัญหาในหัวข้อนี้ได้รับการแก้ไขโดยอาศัยการพิสูจน์ทฤษฎีบท ซึ่งมีลักษณะดังนี้: “หากด้านสองด้านของสามเหลี่ยมและมุมที่เป็นรูปสามเหลี่ยมเท่ากันกับสองด้านและมุมของสามเหลี่ยมอีกรูปหนึ่ง ตัวเลขก็จะเท่ากับ กันและกัน."
การพิสูจน์ทฤษฎีบทเกี่ยวกับเครื่องหมายแรกของความเท่าเทียมกันของรูปสามเหลี่ยมฟังดูเป็นอย่างไร ทุกคนรู้ดีว่าสองส่วนจะเท่ากันหากมีความยาวเท่ากัน หรือวงกลมจะเท่ากันหากมีรัศมีเท่ากัน และในกรณีของรูปสามเหลี่ยมนั้นมีสัญญาณหลายอย่างซึ่งเราสามารถสรุปได้ว่าตัวเลขนั้นเหมือนกันซึ่งสะดวกมากที่จะใช้ในการแก้ปัญหาทางเรขาคณิตต่างๆ
สิ่งที่ทฤษฎีบท "สัญญาณแรกของความเท่าเทียมกันของสามเหลี่ยม" ฟังดูอธิบายไว้ข้างต้น แต่นี่คือข้อพิสูจน์:
- สมมติว่าสามเหลี่ยม ABC และ A 1 B 1 C 1 มีด้านเท่ากัน AB และ A 1 B 1 และดังนั้น BC และ B 1 C 1 และมุมที่เกิดจากด้านเหล่านี้มีขนาดเท่ากันนั่นคือพวกมันเท่ากัน จากนั้น โดยการซ้อน △ ABC บน △ A 1 B 1 C 1 เราจะได้ความบังเอิญของเส้นตรงและจุดยอดทั้งหมด ตามมาว่ารูปสามเหลี่ยมเหล่านี้เหมือนกันทุกประการและมีค่าเท่ากัน
ทฤษฎีบท "เครื่องหมายแรกของความเท่าเทียมกันของสามเหลี่ยม" เรียกอีกอย่างว่า "ด้านสองด้านและมุม" จริงๆแล้วนี่คือสาระสำคัญของมัน

ทฤษฎีบทเกี่ยวกับเครื่องหมายที่สอง
สัญญาณแห่งความเท่าเทียมกันประการที่สองได้รับการพิสูจน์ในลักษณะเดียวกัน การพิสูจน์นั้นขึ้นอยู่กับความจริงที่ว่าเมื่อตัวเลขซ้อนทับกัน พวกมันจะตรงกันทุกจุดยอดและทุกด้าน และทฤษฎีบทมีดังต่อไปนี้: “ หากด้านหนึ่งและสองมุมในรูปแบบที่มันมีส่วนร่วมนั้นสอดคล้องกับด้านและสองมุมของสามเหลี่ยมที่สอง ตัวเลขเหล่านี้จะเหมือนกันนั่นคือเท่ากัน”
เครื่องหมายที่สามและหลักฐาน
หากทั้ง 2 และ 1 สัญญาณแห่งความเท่าเทียมกันของรูปสามเหลี่ยมเกี่ยวข้องกับทั้งด้านข้างและมุมของรูป แล้วอันที่ 3 หมายถึงด้านข้างเท่านั้น ดังนั้น ทฤษฎีบทจึงมีสูตรดังนี้ “ถ้าทุกด้านของสามเหลี่ยมอันหนึ่งเท่ากับสามด้านของสามเหลี่ยมอันที่สอง รูปทั้งสองก็จะเหมือนกัน”
เพื่อพิสูจน์ทฤษฎีบทนี้ เราจำเป็นต้องเจาะลึกคำจำกัดความของความเท่าเทียมกันโดยละเอียดมากขึ้น โดยพื้นฐานแล้วสำนวน "สามเหลี่ยมเท่ากัน" หมายความว่าอย่างไร ตัวตนบอกว่าหากคุณวางซ้อนรูปหนึ่งทับอีกรูปหนึ่ง องค์ประกอบทั้งหมดจะตรงกัน ซึ่งจะเป็นไปได้เฉพาะเมื่อด้านและมุมเท่ากันเท่านั้น ในเวลาเดียวกัน มุมตรงข้ามกับด้านใดด้านหนึ่งซึ่งเท่ากับมุมของสามเหลี่ยมอีกด้าน จะเท่ากับจุดยอดที่สอดคล้องกันของรูปที่สอง ควรสังเกตว่า ณ จุดนี้การพิสูจน์สามารถแปลเป็น 1 เกณฑ์สำหรับความเท่าเทียมกันของรูปสามเหลี่ยมได้อย่างง่ายดาย หากไม่สังเกตลำดับดังกล่าว ความเท่าเทียมกันของรูปสามเหลี่ยมก็เป็นไปไม่ได้เลย ยกเว้นในกรณีที่เป็นตัวเลขนั้น ภาพสะท้อนอันดับแรก.
สามเหลี่ยมมุมฉาก

โครงสร้างของรูปสามเหลี่ยมดังกล่าวจะมีจุดยอดที่มีมุม 90° เสมอ ดังนั้น ข้อความต่อไปนี้จึงเป็นจริง:
- สามเหลี่ยมที่มีมุมฉากจะเท่ากันถ้าขาของอันหนึ่งเหมือนกันกับขาของอันที่สอง
- ตัวเลขจะเท่ากันถ้าด้านตรงข้ามมุมฉากและขาข้างหนึ่งเท่ากัน
- สามเหลี่ยมดังกล่าวจะเท่ากันถ้าขาและ มุมแหลมเหมือนกัน
เครื่องหมายนี้หมายถึง เพื่อพิสูจน์ทฤษฎีบทพวกเขาใช้การประยุกต์ใช้ตัวเลขต่อกันอันเป็นผลมาจากการที่สามเหลี่ยมพับด้วยขาเพื่อให้เส้นตรงสองเส้นออกมาโดยมีด้าน CA และ CA 1
การประยุกต์ใช้ในทางปฏิบัติ
ในกรณีส่วนใหญ่ ในทางปฏิบัติ จะใช้เครื่องหมายแรกของความเท่าเทียมกันของรูปสามเหลี่ยม ในความเป็นจริง หัวข้อเกรด 7 ที่ดูเรียบง่ายเกี่ยวกับเรขาคณิตและแผนผังยังใช้ในการคำนวณความยาวของสายโทรศัพท์ เช่น โดยไม่ต้องวัดพื้นที่ที่จะผ่านไป การใช้ทฤษฎีบทนี้ทำให้ง่ายต่อการคำนวณที่จำเป็นเพื่อกำหนดความยาวของเกาะที่ตั้งอยู่กลางแม่น้ำโดยไม่ต้องว่ายน้ำข้ามไป เสริมรั้วให้แข็งแรงโดยวางคานในช่วงเพื่อแบ่งออกเป็นสามเหลี่ยมสองอันเท่าๆ กัน หรือคำนวณ องค์ประกอบที่ซับซ้อนงานช่างไม้หรือเมื่อคำนวณระบบโครงหลังคาระหว่างการก่อสร้าง

สัญญาณแรกของความเท่าเทียมกันของรูปสามเหลี่ยมนั้นใช้กันอย่างแพร่หลายในชีวิต "ผู้ใหญ่" ที่แท้จริง แม้ว่าใน ปีการศึกษานี่เป็นหัวข้อที่ดูน่าเบื่อและไม่จำเป็นสำหรับหลายๆ คน
เกณฑ์ที่สามสำหรับความเท่าเทียมกันของรูปสามเหลี่ยมทั้งสามด้านถูกกำหนดไว้ในรูปแบบของทฤษฎีบท
ทฤษฎีบท : ถ้าด้านทั้งสามของสามเหลี่ยมด้านหนึ่งเท่ากันกับสามด้านของสามเหลี่ยมอีกด้านตามลำดับ แสดงว่าสามเหลี่ยมนั้นเท่ากันทุกประการ
การพิสูจน์.พิจารณา ΔABC และ ΔA 1 B 1 C 1 โดยที่ AB = A 1 B 1 , AC = A 1 C 1 , BC = B 1 C 1 ให้เราพิสูจน์ว่า ΔABC=ΔA 1 B 1 C 1
ให้ ABC และ A 1 B 1 C 1 เป็นรูปสามเหลี่ยมโดยมี AB=A 1 B 1 , AC=A 1 C 1 , BC=B 1 C 1 . กำหนด ∆ABC บน ∆A 1 B 1 C 1 เพื่อให้จุดยอด A อยู่ในแนวเดียวกับ A 1 และจุดยอด B และ B 1 และจุดยอด C และ C 1 อยู่ในแนวเดียวกัน ด้านที่แตกต่างกันจากเส้นตรง A 1 B 1 เป็นไปได้สามกรณี: 1) รังสี C 1 C ผ่านภายในมุม A 1 C 1 B 1 (รูปที่ a)); 2) รังสี C 1 C เกิดขึ้นพร้อมกับด้านใดด้านหนึ่งของมุมนี้ (รูปที่ b)); รังสี C 1 C ผ่านนอกมุม A 1 C 1 B 1 (รูปที่ c)) ลองพิจารณากรณีแรกกัน เนื่องจากตามเงื่อนไขของทฤษฎีบท ด้าน AC และ A 1 C 1, BC และ B 1 C 1 เท่ากัน ดังนั้นสามเหลี่ยม A 1 C 1 C และ B 1 C 1 C จึงเป็นหน้าจั่ว ตามทฤษฎีบทเกี่ยวกับคุณสมบัติของมุมของสามเหลี่ยมหน้าจั่ว Ðl = Ð2, Ð3 = Ð4 ดังนั้น ÐA 1 CB 1 = =ÐA 1 C 1 B 1 ดังนั้น AC=A 1 C 1, BC=B 1 C 1, РС = РС 1 ดังนั้น รูปสามเหลี่ยม ABC และ A 1 B 1 C 1 จึงเท่ากันตามเครื่องหมายแรกของความเท่าเทียมกันของรูปสามเหลี่ยม
เขียนบนกระดาน:
ที่ให้ไว้:∆ABC, ∆A 1 B 1 C 1 , AB=A 1 B 1 , AC=A 1 C 1 , BC=B 1 C 1
 พิสูจน์:∆ABC=∆A 1 B 1 C 1
พิสูจน์:∆ABC=∆A 1 B 1 C 1
การพิสูจน์.กำหนด ∆ABC บน ∆A 1 B 1 C 1 โดยที่ A →A 1 และ B → B 1 และ C และ C 1 อยู่บนด้านตรงข้ามของเส้นตรง A 1 B 1 ลองพิจารณากรณีหนึ่ง ลำแสง C 1 C ผ่านเข้าไปใน RA 1 C 1 B 1 (รูปที่ a))
AC = A 1 C 1, BC = B 1 C 1 ∙> ΔA 1 C 1 C และ ΔB 1 C 1 C - เท่ากัน ⦁> Ðl = Ð2, Ð3 = Ð4 (ตามธรรมชาติของมุมจะเท่ากับ Δ), fast> ÐA 1 CB 1 =ÐA 1 C 1 B 1 ∙> AC=A 1 C 1 , BC=B 1 C 1 , ÐС = РС 1 สีม่วง>
ΔABC=ΔA 1 B 1 C 1 ตามเครื่องหมายแรกของความเท่าเทียมกันของรูปสามเหลี่ยม
2.รูปสี่เหลี่ยมขนมเปียกปูน ความหมาย คุณสมบัติ สัญญาณ
 รูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมขนมเปียกปูนชนิดหนึ่ง
รูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมขนมเปียกปูนชนิดหนึ่ง
คำนิยาม: สี่เหลี่ยมขนมเปียกปูนเป็นสี่เหลี่ยมด้านขนานที่ทุกด้านเท่ากัน
รูปนี้แสดงสี่เหลี่ยมด้านขนาน ABCD โดยมี AB=BC=CD=DA ตามคำนิยาม สี่เหลี่ยมด้านขนานนี้คือสี่เหลี่ยมขนมเปียกปูน AC และ ВD เป็นเส้นทแยงมุมของสี่เหลี่ยมขนมเปียกปูน เนื่องจากสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมด้านขนาน คุณสมบัติและคุณลักษณะทั้งหมดของสี่เหลี่ยมด้านขนานจึงใช้ได้
คุณสมบัติ:
1) ในรูปสี่เหลี่ยมขนมเปียกปูน มุมตรงข้ามจะเท่ากัน (ÐA=ÐC, ÐB=ÐD)
2) เส้นทแยงมุมของสี่เหลี่ยมขนมเปียกปูนจะถูกแบ่งครึ่งตามจุดตัด (บีโอ=โอดี, AO=โอค)
3) เส้นทแยงมุมของสี่เหลี่ยมขนมเปียกปูนตั้งฉากกันและมุมของมันถูกแบ่งออกเป็นสองส่วน (AC DV, РАБО=РОВС, ADО=РОDC, рBСО=РDСО, РДАО=РУАО) ( คุณสมบัติพิเศษ)
4) ผลรวมของมุมที่อยู่ประชิดด้านหนึ่งเท่ากับ 180 0 (ÐA+ÐB= ÐC+ÐD=ÐB+ÐC=ÐA+ÐD=180 0)
สัญญาณ รูปสี่เหลี่ยมขนมเปียกปูน:
1) ถ้าเส้นทแยงมุมของสี่เหลี่ยมด้านขนานตั้งฉากกัน สี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมขนมเปียกปูน
2) ถ้าเส้นทแยงมุมของสี่เหลี่ยมด้านขนานแบ่งครึ่งมุมของมัน แสดงว่าสี่เหลี่ยมด้านขนานนั้นเป็นรูปสี่เหลี่ยมขนมเปียกปูน
3) ถ้าทุกด้านของสี่เหลี่ยมด้านขนานเท่ากัน แสดงว่าเป็นสี่เหลี่ยมขนมเปียกปูน
เขียนบนกระดาน
คุณสมบัติ:
1) ÐA=ÐC, ÐB=ÐD 2) บีโอ=โอดี, เอโอ=โอซี
3) AC DV, РАБО=РОВС, ADО=РОDC, рBСО=РDСО, РДАО=РВАО
4) ÐA+ÐB= ÐC+ÐD=ÐB+ÐC=ÐA+ÐD=180 0
ประโยคสนทนาคือ สัญญาณ รูปสี่เหลี่ยมขนมเปียกปูน:
1 ) ถ้า ABCD เป็นรูปสี่เหลี่ยมขนมเปียกปูนขนาน m และ AC DB แล้ว ABCD เป็นรูปสี่เหลี่ยมขนมเปียกปูน
2) ถ้า ABCD เป็นเส้นขนาน และ AC และ DB เป็นเส้นแบ่งครึ่ง ดังนั้น ABCD จะเป็นสี่เหลี่ยมขนมเปียกปูน
3) ถ้า ABCD เป็นรูปสี่เหลี่ยมขนมเปียกปูน และ AC=DB และ BC=AD แล้ว ABCD เป็นรูปสี่เหลี่ยมขนมเปียกปูน
งาน.
ว่ากันว่าสามเหลี่ยมสองรูปจะเท่ากันทุกประการหากนำมารวมกันได้โดยการทับซ้อนกัน รูปที่ 1 แสดงสามเหลี่ยมเท่ากัน ABC และ A 1 B 1 C 1 สามเหลี่ยมเหล่านี้แต่ละรูปสามารถซ้อนทับกันเพื่อให้เข้ากันได้อย่างสมบูรณ์ นั่นคือจุดยอดและด้านข้างเข้ากันได้เป็นคู่ เห็นได้ชัดว่ามุมของสามเหลี่ยมเหล่านี้จะจับคู่กันด้วย
ดังนั้น หากสามเหลี่ยมสองรูปเท่ากันทุกประการ องค์ประกอบ (เช่น ด้านและมุม) ของสามเหลี่ยมด้านหนึ่งจะเท่ากับองค์ประกอบของสามเหลี่ยมอีกด้านตามลำดับ โปรดทราบว่า วี สามเหลี่ยมเท่ากันเทียบกับด้านที่เท่ากันตามลำดับ(เช่น ทับซ้อนกันเมื่อซ้อนทับ) มุมที่เท่ากันโกหกและกลับ: ตรงข้ามกันตามลำดับ มุมเท่ากันอยู่ ด้านที่เท่ากัน.
ตัวอย่างเช่น ในรูปสามเหลี่ยมเท่ากัน ABC และ A 1 B 1 C 1 ดังแสดงในรูปที่ 1 ซึ่งอยู่ตรงข้ามด้านเท่ากัน AB และ A 1 B 1 ตามลำดับ จะมีมุมเท่ากัน C และ C 1 เราจะแสดงถึงความเท่าเทียมกันของสามเหลี่ยม ABC และ A 1 B 1 C 1 ดังนี้: Δ ABC = Δ A 1 B 1 C 1 ปรากฎว่าสามารถสร้างความเท่าเทียมกันของสามเหลี่ยมสองรูปได้โดยการเปรียบเทียบองค์ประกอบบางส่วน
ทฤษฎีบท 1 สัญญาณแรกของความเท่าเทียมกันของรูปสามเหลี่ยมถ้าสองด้านและมุมระหว่างสองด้านของสามเหลี่ยมหนึ่งเท่ากันกับสองด้านและมุมระหว่างสองด้านของสามเหลี่ยมอื่นตามลำดับ แสดงว่าสามเหลี่ยมนั้นเท่ากันทุกประการ (รูปที่ 2)
การพิสูจน์. พิจารณารูปสามเหลี่ยม ABC และ A 1 B 1 C 1 โดยที่ AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (ดูรูปที่ 2) ให้เราพิสูจน์ว่า Δ ABC = Δ A 1 B 1 C 1 .
เนื่องจาก ∠ A = ∠ A 1 ดังนั้น สามเหลี่ยม ABC สามารถซ้อนทับบนสามเหลี่ยม A 1 B 1 C 1 เพื่อให้จุดยอด A จัดอยู่ในแนวเดียวกับจุดยอด A 1 และด้าน AB และ AC ซ้อนทับบนรังสี A 1 B 1 และ A 1 ตามลำดับ ค 1. เนื่องจาก AB = A 1 B 1, AC = A 1 C 1 ดังนั้นด้าน AB จะอยู่ในแนวเดียวกันกับด้าน A 1 B 1 และด้าน AC จะอยู่ในแนวเดียวกันกับด้าน A 1 C 1; โดยเฉพาะจุด B และ B 1, C และ C 1 จะตรงกัน ดังนั้นด้าน BC และ B 1 C 1 จะเรียงกัน ดังนั้น สามเหลี่ยม ABC และ A 1 B 1 C 1 เข้ากันได้อย่างสมบูรณ์ ซึ่งหมายความว่าพวกมันเท่ากัน
ทฤษฎีบทที่ 2 ได้รับการพิสูจน์ในลักษณะเดียวกันโดยใช้วิธีการซ้อนทับ
ทฤษฎีบท 2 เครื่องหมายที่สองของความเท่าเทียมกันของรูปสามเหลี่ยมหากด้านหนึ่งและมุมสองมุมที่อยู่ติดกันของสามเหลี่ยมหนึ่งเท่ากันกับด้านและสองมุมที่อยู่ติดกันของสามเหลี่ยมอื่นตามลำดับ แสดงว่าสามเหลี่ยมนั้นเท่ากันทุกประการ (รูปที่ 34)
ความคิดเห็น จากทฤษฎีบทที่ 2 จึงมีการสร้างทฤษฎีบทที่ 3 ขึ้นมา
ทฤษฎีบท 3 ผลรวมของมุมภายในสองมุมใดๆ ของรูปสามเหลี่ยมจะน้อยกว่า 180°
ทฤษฎีบทที่ 4 ต่อจากทฤษฎีบทสุดท้าย
ทฤษฎีบท 4 มุมภายนอกของรูปสามเหลี่ยมมีค่ามากกว่ามุมใดๆ มุมภายในไม่ได้อยู่ติดกัน
ทฤษฎีบท 5 เครื่องหมายที่สามของความเท่าเทียมกันของรูปสามเหลี่ยมถ้าด้านสามด้านของสามเหลี่ยมด้านหนึ่งเท่ากันกับด้านสามด้านของสามเหลี่ยมอีกด้านตามลำดับ แล้วสามเหลี่ยมนั้นจะเท่ากันทุกประการ ()
ตัวอย่างที่ 1ในรูปสามเหลี่ยม ABC และ DEF (รูปที่ 4)
∠ A = ∠ E, AB = 20 ซม., AC = 18 ซม., DE = 18 ซม., EF = 20 ซม. เปรียบเทียบสามเหลี่ยม ABC และ DEF มุมในรูปสามเหลี่ยม DEF คืออะไร เท่ากับมุมใน?
สารละลาย. สามเหลี่ยมเหล่านี้จะเท่ากันตามเครื่องหมายแรก มุม F ของสามเหลี่ยม DEF เท่ากับมุม B สามเหลี่ยมเอบีซีเนื่องจากมุมเหล่านี้อยู่ตรงข้ามกับด้านที่เท่ากันของ DE และ AC
ตัวอย่างที่ 2ส่วน AB และ CD (รูปที่ 5) ตัดกันที่จุด O ซึ่งอยู่ตรงกลางของแต่ละส่วน ความยาวของส่วน BD คือเท่าใด ถ้าส่วน AC คือ 6 เมตร
สารละลาย.
สามเหลี่ยม AOC และ BOD เท่ากัน (ตามเกณฑ์แรก): ∠ AOC = ∠ BOD (แนวตั้ง), AO = OB, CO = OD (ตามเงื่อนไข)
จากความเท่ากันของรูปสามเหลี่ยมเหล่านี้ แสดงว่าด้านของรูปสามเหลี่ยมเท่ากัน นั่นคือ AC = BD แต่เนื่องจากตามเงื่อนไข AC = 6 m ดังนั้น BD = 6 m
เครื่องหมายที่สองของความเท่าเทียมกันของรูปสามเหลี่ยม
ถ้าด้านหนึ่งและมุมสองมุมที่อยู่ติดกันของสามเหลี่ยมหนึ่งเท่ากันกับด้านหนึ่งและสองมุมที่อยู่ติดกันของสามเหลี่ยมอีกรูปหนึ่งตามลำดับ แสดงว่าสามเหลี่ยมนั้นเท่ากันทุกประการ
MN = PR N = R M = P
ในการพิสูจน์เครื่องหมายแรก คุณต้องแน่ใจว่าสามเหลี่ยมจะเท่ากันเพียงพอหรือไม่ จะสามารถนำมารวมกันทั้งหมดได้หรือไม่
1. เนื่องจาก MN = PR ดังนั้นส่วนเหล่านี้จึงรวมกันหากจุดสิ้นสุดรวมกัน
2. เนื่องจาก N = R และ M = P รังสี \(MK\) และ \(NK\) จะทับซ้อนรังสี \(PT\) และ \(RT\) ตามลำดับ
3. ถ้ารังสีเกิดขึ้นพร้อมกัน จุดตัด \(K\) และ \(T\) จะตรงกัน
4. จุดยอดทั้งหมดของสามเหลี่ยมอยู่ในแนวเดียวกัน นั่นคือ Δ MNK และ Δ PRT อยู่ในแนวเดียวกันอย่างสมบูรณ์ ซึ่งหมายความว่าทั้งสองเท่ากัน
เครื่องหมายที่สามของความเท่าเทียมกันของรูปสามเหลี่ยม
ถ้าด้านสามด้านของสามเหลี่ยมด้านหนึ่งเท่ากันกับสามด้านของสามเหลี่ยมอีกด้านตามลำดับ แสดงว่าสามเหลี่ยมนั้นเท่ากันทุกประการ

MN = PR KN = TR MK = PT
ลองรวมสามเหลี่ยม Δ MNK และ Δ PRT อีกครั้งโดยการทับซ้อนกัน และตรวจสอบให้แน่ใจว่าด้านที่เท่ากันตรงกันรับประกันว่ามุมที่สอดคล้องกันของสามเหลี่ยมเหล่านี้จะเท่ากันและจะตรงกันโดยสมบูรณ์

ให้เรารวมส่วนที่เหมือนกัน \(MK\) และ \(PT\) เข้าด้วยกัน สมมติว่าจุด \(N\) และ \(R\) ไม่ตรงกัน
ให้ \(O\) เป็นจุดกึ่งกลางของส่วน \(NR\) จากข้อมูลนี้ MN = PR, KN = TR สามเหลี่ยม \(MNR\) และ \(KNR\) เป็นหน้าจั่วด้วย พื้นดินทั่วไป\(NR\)
ดังนั้น ค่ามัธยฐาน \(MO\) และ \(KO\) คือความสูง ซึ่งหมายความว่าค่ามัธยฐานตั้งฉากกับ \(NR\) เส้น \(MO\) และ \(KO\) ไม่ตรงกัน เนื่องจากจุด \(M\), \(K\), \(O\) ไม่ได้อยู่บนบรรทัดเดียวกัน แต่ผ่านจุด \(O\) ของเส้นตรง \(NR\) จะสามารถลากเส้นตั้งฉากได้เพียงเส้นเดียวเท่านั้น เรามาถึงความขัดแย้งแล้ว
ได้รับการพิสูจน์แล้วว่าจุดยอด \(N\) และ \(R\) จะต้องตรงกัน
เครื่องหมายที่สามช่วยให้เราเรียกสามเหลี่ยมนี้ว่าเป็นรูปที่แข็งแกร่งและมั่นคงมากซึ่งบางครั้งพวกเขาก็พูดอย่างนั้น สามเหลี่ยม - ร่างแข็ง - ถ้าความยาวของด้านไม่เปลี่ยนแปลง มุมก็ไม่เปลี่ยนเช่นกัน ตัวอย่างเช่น รูปสี่เหลี่ยมขนมเปียกปูนไม่มีคุณสมบัตินี้ ดังนั้นการรองรับและป้อมปราการต่างๆ จึงทำให้เป็นรูปสามเหลี่ยม



แต่ผู้คนประเมินและเน้นย้ำถึงความมั่นคงที่แปลกประหลาด ความมั่นคง และความสมบูรณ์แบบของตัวเลข \(3\) มาเป็นเวลานาน
เทพนิยายพูดถึงเรื่องนี้
ที่นั่นเราพบกับ "หมีสามตัว", "สามลม", "หมูน้อยสามตัว", "สามสหาย", "สามพี่น้อง", "ชายผู้โชคดีสามคน", "ช่างฝีมือสามคน", "เจ้าชายสามคน", "เพื่อนทั้งสาม", “สามฮีโร่” ฯลฯ
มีความพยายามสามครั้ง "คำแนะนำสามประการ" "คำแนะนำสามประการ" "การประชุมสามครั้ง" สำเร็จ "ความปรารถนาสามประการ" จะต้องอดทน "สามวัน" "สามคืน" "สามปี" ผ่านไป “สามรัฐ” “สามอาณาจักรใต้ดิน” ทนต่อ “การทดสอบสามประการ” แล่นผ่าน “สามทะเล”
 ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ
ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ คำประสมที่มีสระเชื่อมกัน
คำประสมที่มีสระเชื่อมกัน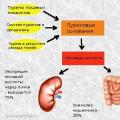 กรดยูริกในเลือด: บรรทัดฐานและการเบี่ยงเบน, เหตุใดจึงเพิ่มขึ้น, อาหารเพื่อลดกรด ผลิตภัณฑ์สุดท้ายของการเผาผลาญไนโตรเจนคือ
กรดยูริกในเลือด: บรรทัดฐานและการเบี่ยงเบน, เหตุใดจึงเพิ่มขึ้น, อาหารเพื่อลดกรด ผลิตภัณฑ์สุดท้ายของการเผาผลาญไนโตรเจนคือ