การหารเศษส่วนทศนิยมเป็นแบบสองชั้น วิธีหารจำนวนธรรมชาติด้วยทศนิยมและกลับกัน

37. หารด้วย ทศนิยม

งาน.พื้นที่ของสี่เหลี่ยมผืนผ้าคือ 2.88 dm 2 และความกว้างของมันคือ 0.8 dm ความยาวของสี่เหลี่ยมคืออะไร?

สารละลาย ตั้งแต่ 2.88 dm 2 \u003d 288 cm 2 และ 0.8 dm \u003d 8 cm ความยาวของสี่เหลี่ยมผืนผ้าคือ 288: 8 นั่นคือ 36 cm \u003d 3.6 dm เราพบตัวเลข 3.6 โดยที่ 3.6 0.8 = 2.88 มันคือผลหารของ 2.88 หารด้วย 0.8

คำตอบ 3.6 สามารถหาได้โดยไม่ต้องแปลงเดซิเมตรเป็นเซนติเมตร ในการทำเช่นนี้ ให้คูณตัวหาร 0.8 และเงินปันผล 2.88 ด้วย 10 (นั่นคือ ย้ายเครื่องหมายจุลภาคไปทางขวาในตัวเลขหนึ่งหลัก) และหาร 28.8 ด้วย 8 อีกครั้ง เราได้:

การหารตัวเลขด้วยทศนิยม, จำเป็น:
1) ในตัวหารและตัวหาร ให้เลื่อนเครื่องหมายจุลภาคไปทางขวาตามจำนวนหลักที่มีหลังจุดทศนิยมในตัวหาร
2) หลังจากนั้นทำการหารด้วยจำนวนธรรมชาติ

ตัวอย่าง 1หาร 12.096 ด้วย 2.24 ลองย้ายเครื่องหมายจุลภาค 2 หลักไปทางขวาในเงินปันผลและตัวหาร เราได้ตัวเลข 1209.6 และ 224

ตั้งแต่นั้นมา และ .

ตัวอย่าง 2หาร 4.5 ด้วย 0.125 ที่นี่จำเป็นต้องย้ายเครื่องหมายจุลภาค 3 หลักไปทางขวาในตัวปันผลและตัวหาร เนื่องจากเงินปันผลมีตัวเลขอยู่หลังจุดทศนิยมเพียงตัวเดียว เราจะบวกศูนย์สองตัวทางด้านขวา หลังจากย้ายเครื่องหมายจุลภาค เราได้ตัวเลข 4500 และ 125

ตั้งแต่นั้นมา และ .

ตัวอย่างที่ 1 และ 2 แสดงว่าเมื่อหารจำนวนด้วย ไม่ เศษส่วนที่เหมาะสมตัวเลขนี้ลดลงหรือไม่เปลี่ยนแปลง และเมื่อหารด้วยเศษส่วนทศนิยมที่ถูกต้อง จะเพิ่มขึ้น:, ก.

หาร 2.467 ด้วย 0.01 หลังจากย้ายเครื่องหมายจุลภาคในตัวปันผลและตัวหารด้วยเลข 2 หลักไปทางขวา เราจะได้ผลหารเป็น 246.7: 1 นั่นคือ 246.7 ดังนั้น และ 2.467: 0.01 = 246.7 จากที่นี่เราได้รับกฎ:

ในการหารทศนิยมด้วย 0.1; 0.01; 0.001คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยตัวเลขให้มากที่สุดเท่าที่มีศูนย์หน้าหน่วยในตัวหาร (นั่นคือ คูณด้วย 10, 100, 1000)

หากมีตัวเลขไม่เพียงพอ ก่อนอื่นคุณต้องบวกศูนย์สองสามตัวที่ส่วนท้ายของเศษส่วน

ตัวอย่างเช่น, .

1443. หาผลหารและทดสอบโดยการคูณ:

ก) 0.8: 0.5; ข) 3.51: 2.7; ค) 14.335: 0.61.

1444. ค้นหาผลหารและทดสอบตามการหาร:

ก) 0.096: 0.12; 6) 0.126:0.9; ค) 42.105: 3.5.

1445. ดำเนินการกอง:

1446. เขียนนิพจน์:

ก) ผลหารของการหารผลรวมของ a และ 2.6 ด้วยผลต่างของ b และ 8.5
b) ผลรวมของผลหาร x และ 3.7 และผลหาร 3.1 และ y

1447 อ่านนิพจน์:

ก) ม.: 12.8 - น: 4.9; b) (x + 0.7): (y + 3.4); ค) (ก: ข) (8: ค).

1448. ก้าวชาย 0.8 ม. ต้องเดินกี่ก้าวถึง 100 ม.?

1449. Alyosha เดินทางโดยรถไฟ 162.5 กม. ใน 2.6 ชั่วโมง รถไฟเร็วแค่ไหน?

1450. จงหามวลน้ำแข็ง 1 ซม. 3 ถ้ามวลน้ำแข็ง 3.5 ซม. 3 เท่ากับ 3.08 ก.

1451. เชือกถูกตัดเป็นสองส่วน ความยาวของส่วนหนึ่งเท่ากับ 3.25 ม. และอีกส่วนหนึ่งมีความยาว 1.3 เท่าของส่วนแรก ความยาวของเชือกคืออะไร?

1452 ชุดแรกรวมแป้ง 6.72 กก. ซึ่งมากกว่าชุดที่สอง 2.4 เท่า รวมแป้งกี่กิโลกรัมในถุงทั้งสอง?

1453 บอริยาใช้เวลาเตรียมบทเรียนน้อยกว่าการเดิน 3.5 เท่า Borya ใช้เวลานานแค่ไหนในการเดินและเตรียมบทเรียนหากการเดินใช้เวลา 2.8 ชั่วโมง?

ในบทช่วยสอนนี้ เราจะพิจารณาการดำเนินการเหล่านี้ทีละรายการ

เนื้อหาบทเรียน

การบวกทศนิยม

อย่างที่เราทราบ ทศนิยมมีส่วนจำนวนเต็มและเศษส่วน เมื่อเพิ่มทศนิยม ส่วนของจำนวนเต็มและเศษส่วนจะถูกเพิ่มแยกกัน

ตัวอย่างเช่น ลองบวกทศนิยม 3.2 และ 5.3 การเพิ่มเศษส่วนทศนิยมในคอลัมน์จะสะดวกกว่า

อันดับแรก เราเขียนเศษส่วนสองส่วนนี้ในคอลัมน์ ในขณะที่ส่วนจำนวนเต็มต้องอยู่ใต้ส่วนจำนวนเต็ม และเศษส่วนใต้เศษส่วน ในโรงเรียนข้อกำหนดนี้เรียกว่า "จุลภาคภายใต้เครื่องหมายจุลภาค".

ลองเขียนเศษส่วนในคอลัมน์เพื่อให้ลูกน้ำอยู่ใต้ลูกน้ำ:

เราเริ่มเพิ่มส่วนที่เป็นเศษส่วน: 2 + 3 \u003d 5. เราเขียนห้าในส่วนที่เป็นเศษส่วนของคำตอบของเรา:

ตอนนี้เราบวกส่วนจำนวนเต็ม: 3 + 5 = 8 เราเขียนแปดในส่วนจำนวนเต็มของคำตอบของเรา:

ตอนนี้เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค การทำเช่นนี้เราทำตามกฎอีกครั้ง "จุลภาคภายใต้เครื่องหมายจุลภาค":

ได้คำตอบ 8.5 ดังนั้นนิพจน์ 3.2 + 5.3 จึงเท่ากับ 8.5

อันที่จริงไม่ใช่ทุกอย่างจะง่ายอย่างที่เห็นในแวบแรก ที่นี่ก็มีข้อผิดพลาดซึ่งตอนนี้เราจะพูดถึง

ตำแหน่งทศนิยม

ทศนิยมเช่นเดียวกับตัวเลขทั่วไปมีตัวเลขของตัวเอง เหล่านี้เป็นตำแหน่งที่สิบ ที่ร้อย ที่หนึ่งพัน ในกรณีนี้ ตัวเลขจะเริ่มต้นหลังจุดทศนิยม

หลักแรกหลังจุดทศนิยมรับผิดชอบตำแหน่งที่สิบ หลักที่สองหลังจุดทศนิยมสำหรับตำแหน่งที่ร้อย หลักที่สามหลังจากจุดทศนิยมสำหรับหลักพัน

ตัวเลขในเศษส่วนทศนิยมเก็บบางส่วน ข้อมูลที่เป็นประโยชน์. โดยเฉพาะอย่างยิ่ง พวกเขารายงานว่ามีกี่ส่วนในสิบ ร้อย และในพันที่เป็นทศนิยม

ตัวอย่างเช่น พิจารณาทศนิยม 0.345

ตำแหน่งที่ไตรตั้งอยู่เรียกว่า อันดับที่สิบ

ตำแหน่งที่สี่ตั้งอยู่เรียกว่า ที่ร้อย

ตำแหน่งที่ห้าตั้งอยู่เรียกว่า พัน

ลองดูที่รูปนี้ เราเห็นว่าในหมวดสิบมีสาม นี่แสดงให้เห็นว่ามีสามในสิบของเศษส่วนทศนิยม 0.345

ถ้าเราบวกเศษส่วนแล้วเราจะได้เศษทศนิยมเดิม 0.345

จะเห็นได้ว่าตอนแรกเราได้คำตอบแล้ว แต่แปลงเป็นทศนิยมแล้วได้ 0.345

เมื่อบวกเศษส่วนทศนิยม หลักการและกฎเดียวกันจะถูกปฏิบัติตามเมื่อบวกเลขธรรมดา การบวกเศษส่วนทศนิยมเกิดขึ้นจากตัวเลข: ในสิบจะเพิ่มเป็นสิบ, จากร้อยถึงหนึ่งในร้อย, ในพันถึงหนึ่งในพัน

ดังนั้นเมื่อบวกเศษทศนิยม จึงต้องปฏิบัติตามกฎ "จุลภาคภายใต้เครื่องหมายจุลภาค". เครื่องหมายจุลภาคที่อยู่ใต้เครื่องหมายจุลภาคให้ลำดับเดียวกันกับที่เพิ่มหนึ่งในสิบเป็นสิบ จากร้อยถึงหนึ่งในร้อย

ตัวอย่าง 1ค้นหาค่าของนิพจน์ 1.5 + 3.4

ก่อนอื่น เราเพิ่มส่วนที่เป็นเศษส่วน 5 + 4 = 9 เราเขียนเก้าในส่วนที่เป็นเศษส่วนของคำตอบของเรา:

ตอนนี้เราบวกส่วนจำนวนเต็ม 1 + 3 = 4 เราเขียนสี่ในส่วนจำนวนเต็มของคำตอบของเรา:

ตอนนี้เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการดำเนินการนี้ เราปฏิบัติตามกฎ "comma under a comma" อีกครั้ง:

ได้คำตอบ 4.9 ดังนั้นค่าของนิพจน์ 1.5 + 3.4 คือ 4.9

ตัวอย่าง 2ค้นหาค่าของนิพจน์: 3.51 + 1.22

เราเขียนนิพจน์นี้ในคอลัมน์โดยปฏิบัติตามกฎ "comma under a comma"

ก่อนอื่นเพิ่มส่วนที่เป็นเศษส่วน คือ ส่วนร้อย 1+2=3 เราเขียนสามส่วนในส่วนที่ร้อยของคำตอบของเรา:

ตอนนี้เพิ่มหนึ่งในสิบของ 5+2=7 เราเขียนเจ็ดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เพิ่มทั้งส่วน 3+1=4 เราเขียนสี่ในส่วนทั้งหมดของคำตอบของเรา:

เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค โดยปฏิบัติตามกฎ "เครื่องหมายจุลภาคภายใต้เครื่องหมายจุลภาค":

ได้คำตอบ 4.73 ดังนั้นค่าของนิพจน์ 3.51 + 1.22 คือ 4.73

3,51 + 1,22 = 4,73

เช่นเดียวกับตัวเลขธรรมดา เมื่อบวกเศษส่วนทศนิยม . ในกรณีนี้ คำตอบจะถูกเขียนหนึ่งหลัก และส่วนที่เหลือจะถูกโอนไปยังหลักถัดไป

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 2.65 + 3.27

เราเขียนนิพจน์นี้ในคอลัมน์:

เพิ่มหนึ่งในร้อยของ 5+7=12 หมายเลข 12 จะไม่พอดีกับส่วนที่ร้อยของคำตอบของเรา ดังนั้นในส่วนที่ร้อย เราเขียนเลข 2 และโอนหน่วยไปยังบิตถัดไป:

ตอนนี้เราบวกหนึ่งในสิบของ 6+2=8 บวกหน่วยที่เราได้รับจากการดำเนินการก่อนหน้านี้ เราได้ 9 เราเขียนหมายเลข 9 ในหนึ่งในสิบของคำตอบของเรา:

ตอนนี้เพิ่มทั้งส่วน 2+3=5 เราเขียนหมายเลข 5 ในส่วนจำนวนเต็มของคำตอบของเรา:

ได้คำตอบ 5.92 ดังนั้นค่าของนิพจน์ 2.65 + 3.27 คือ 5.92

2,65 + 3,27 = 5,92

ตัวอย่างที่ 4ค้นหาค่าของนิพจน์ 9.5 + 2.8

เขียนนิพจน์นี้ในคอลัมน์

เราบวกส่วนที่เป็นเศษส่วน 5 + 8 = 13 ตัวเลข 13 จะไม่พอดีกับส่วนที่เป็นเศษส่วนของคำตอบ ดังนั้นก่อนอื่นให้เขียนเลข 3 แล้วโอนหน่วยไปยังหลักถัดไป หรือโอนไปยังจำนวนเต็ม ส่วนหนึ่ง:

ตอนนี้เราบวกส่วนจำนวนเต็ม 9+2=11 บวกหน่วยที่เราได้รับจากการดำเนินการก่อนหน้านี้ เราได้ 12 เราเขียนหมายเลข 12 ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 12.3 ดังนั้นค่าของนิพจน์ 9.5 + 2.8 คือ 12.3

9,5 + 2,8 = 12,3

เมื่อบวกเศษส่วนทศนิยม จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองจะต้องเท่ากัน หากมีตัวเลขไม่เพียงพอ ตำแหน่งเหล่านี้ในส่วนที่เป็นเศษส่วนจะเต็มไปด้วยศูนย์

ตัวอย่างที่ 5. ค้นหาค่าของนิพจน์: 12.725 + 1.7

ก่อนเขียนนิพจน์นี้ในคอลัมน์ เรามาทำให้จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองเท่ากันก่อน เศษส่วนทศนิยม 12.725 มีสามหลักหลังจุดทศนิยม ในขณะที่เศษส่วน 1.7 มีเพียงหนึ่ง ดังนั้นในเศษส่วน 1.7 ในตอนท้าย คุณต้องบวกศูนย์สองตัว แล้วเราจะได้เศษส่วน 1,700. ตอนนี้คุณสามารถเขียนนิพจน์นี้ในคอลัมน์และเริ่มคำนวณ:

เพิ่มหนึ่งในพันของ 5+0=5 เราเขียนหมายเลข 5 ในส่วนที่พันของคำตอบของเรา:

เพิ่มหนึ่งในร้อยของ 2+0=2 เราเขียนหมายเลข 2 ในส่วนที่ร้อยของคำตอบของเรา:

เพิ่มหนึ่งในสิบของ 7+7=14 หมายเลข 14 จะไม่พอดีกับหนึ่งในสิบของคำตอบของเรา ดังนั้นเราจึงเขียนหมายเลข 4 ก่อนและโอนหน่วยไปยังบิตถัดไป:

ตอนนี้เราบวกส่วนจำนวนเต็ม 12+1=13 บวกหน่วยที่เราได้รับจากการดำเนินการก่อนหน้านี้ เราได้ 14 เราเขียนหมายเลข 14 ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 14,425 ดังนั้นค่าของนิพจน์ 12.725+1.700 คือ 14.425

12,725+ 1,700 = 14,425

การลบทศนิยม

เมื่อลบเศษส่วนทศนิยม คุณต้องปฏิบัติตามกฎเดียวกันกับเมื่อบวก: "เครื่องหมายจุลภาคภายใต้เครื่องหมายจุลภาค" และ "จำนวนหลักหลังจุดทศนิยมเท่ากัน"

ตัวอย่าง 1ค้นหาค่าของนิพจน์ 2.5 - 2.2

เราเขียนนิพจน์นี้ในคอลัมน์โดยปฏิบัติตามกฎ "comma under comma":

เราคำนวณส่วนที่เป็นเศษส่วน 5−2=3 เราเขียนหมายเลข 3 ในส่วนที่สิบของคำตอบของเรา:

คำนวณส่วนจำนวนเต็ม 2−2=0 เราเขียนศูนย์ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้คำตอบ 0.3 ดังนั้นค่าของนิพจน์ 2.5 - 2.2 เท่ากับ 0.3

2,5 − 2,2 = 0,3

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 7.353 - 3.1

ในนิพจน์นี้ ปริมาณที่แตกต่างกันตัวเลขหลังจุดทศนิยม ในเศษส่วน 7.353 มีตัวเลขสามหลักหลังจุดทศนิยม และในเศษส่วนที่ 3.1 มีเพียงตัวเดียว ซึ่งหมายความว่าในเศษส่วนที่ 3.1 ต้องเติมศูนย์สองตัวที่ส่วนท้ายเพื่อให้จำนวนหลักในเศษส่วนทั้งสองเท่ากัน แล้วเราจะได้ 3,100.

ตอนนี้คุณสามารถเขียนนิพจน์นี้ในคอลัมน์และคำนวณได้:

ได้คำตอบ 4,253 ดังนั้นค่าของนิพจน์ 7.353 − 3.1 คือ 4.253

7,353 — 3,1 = 4,253

เช่นเดียวกับตัวเลขทั่วไป บางครั้งคุณจะต้องยืมหนึ่งตัวจากบิตที่อยู่ติดกัน หากการลบไม่สามารถทำได้

ตัวอย่างที่ 3หาค่าของนิพจน์ 3.46 − 2.39

ลบหนึ่งในร้อยของ 6-9 จากหมายเลข 6 อย่าลบหมายเลข 9 ดังนั้นคุณต้องนำหน่วยจากหลักที่อยู่ติดกัน เมื่อยืมหนึ่งจากหลักที่อยู่ใกล้เคียง หมายเลข 6 จะกลายเป็นหมายเลข 16 ตอนนี้ เราสามารถคำนวณหนึ่งในร้อยของ 16−9=7 ได้ เราเขียนเจ็ดในส่วนที่ร้อยของคำตอบของเรา:

ตอนนี้ลบสิบ เนื่องจากเราใช้หนึ่งหน่วยในหมวดที่สิบ ตัวเลขที่อยู่ตรงนั้นจึงลดลงหนึ่งหน่วย กล่าวอีกนัยหนึ่ง ตำแหน่งที่สิบตอนนี้ไม่ใช่หมายเลข 4 แต่เป็นหมายเลข 3 ลองคำนวณหนึ่งในสิบของ 3−3=0 กัน เราเขียนศูนย์ในส่วนที่สิบของคำตอบของเรา:

ตอนนี้ลบส่วนจำนวนเต็ม 3−2=1 เราเขียนหน่วยในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 1.07 ดังนั้นค่าของนิพจน์ 3.46−2.39 จึงเท่ากับ 1.07

3,46−2,39=1,07

ตัวอย่างที่ 4. ค้นหาค่าของนิพจน์ 3−1.2

ตัวอย่างนี้ลบทศนิยมจากจำนวนเต็ม ลองเขียนนิพจน์นี้ในคอลัมน์เพื่อให้ ทั้งส่วนเศษส่วนทศนิยม 1.23 อยู่ใต้เลข 3

ทีนี้มาทำจำนวนหลักหลังจุดทศนิยมกัน เมื่อต้องการทำสิ่งนี้ หลังจากเลข 3 ให้ใส่เครื่องหมายจุลภาคและเพิ่มศูนย์หนึ่งตัว:

ตอนนี้ลบสิบ: 0−2 อย่าลบเลข 2 จากศูนย์ ดังนั้น คุณต้องนำหน่วยจากหลักที่อยู่ติดกัน โดยการยืมหนึ่งตัวจากหลักที่อยู่ติดกัน 0 จะกลายเป็นตัวเลข 10 ตอนนี้คุณสามารถคำนวณหนึ่งในสิบของ 10−2=8 ได้แล้ว เราเขียนแปดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้ลบส่วนทั้งหมด ก่อนหน้านี้เลข 3 อยู่ในจำนวนเต็ม แต่เรายืมหนึ่งหน่วยจากมัน เป็นผลให้มันกลายเป็นหมายเลข 2 ดังนั้นเราจึงลบ 1 จาก 2 2-1=1 เราเขียนหน่วยในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 1.8 ดังนั้นค่าของนิพจน์ 3−1.2 คือ 1.8

การคูณทศนิยม

การคูณทศนิยมนั้นง่ายและสนุก ในการคูณทศนิยม คุณต้องคูณมันเหมือนตัวเลขปกติ โดยไม่สนใจเครื่องหมายจุลภาค

เมื่อได้รับคำตอบแล้ว จำเป็นต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสอง จากนั้นนับจำนวนหลักทางด้านขวาของคำตอบและใส่เครื่องหมายจุลภาค

ตัวอย่าง 1ค้นหาค่าของนิพจน์ 2.5 × 1.5

เราคูณเศษส่วนทศนิยมเหล่านี้เป็นตัวเลขธรรมดา โดยไม่สนใจเครื่องหมายจุลภาค หากต้องการละเว้นเครื่องหมายจุลภาค คุณสามารถจินตนาการได้ชั่วคราวว่าไม่มีเครื่องหมายจุลภาค:

เราได้ 375 ในตัวเลขนี้ จำเป็นต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วนของ 2.5 และ 1.5 ในเศษส่วนแรกมีหนึ่งหลักหลังจุดทศนิยมในเศษส่วนที่สองก็มีหนึ่งตัวเช่นกัน รวมเป็นสองจำนวน

เรากลับไปที่หมายเลข 375 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 3.75 ดังนั้นค่าของนิพจน์ 2.5 × 1.5 คือ 3.75

2.5 x 1.5 = 3.75

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 12.85 × 2.7

ลองคูณทศนิยมเหล่านี้โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้ 34695 ในตัวเลขนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องคำนวณจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วนของ 12.85 และ 2.7 ในเศษส่วน 12.85 มีตัวเลขสองหลักหลังจุดทศนิยม ในเศษส่วนที่ 2.7 มีหนึ่งหลัก - รวมเป็นสามหลัก

เรากลับไปที่หมายเลข 34695 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสามหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 34,695 ดังนั้นค่าของนิพจน์ 12.85 × 2.7 คือ 34.695

12.85 x 2.7 = 34.695

การคูณทศนิยมด้วยจำนวนปกติ

บางครั้งมีบางสถานการณ์ที่คุณต้องคูณเศษส่วนทศนิยมด้วยจำนวนปกติ

ในการคูณทศนิยมกับจำนวนปกติ คุณต้องคูณมันโดยไม่คำนึงถึงเครื่องหมายจุลภาคในทศนิยม เมื่อได้รับคำตอบแล้ว จำเป็นต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทศนิยม จากนั้นในคำตอบ ให้นับจำนวนหลักทางขวาและใส่เครื่องหมายจุลภาค

ตัวอย่างเช่น คูณ 2.54 ด้วย 2

เราคูณเศษส่วนทศนิยม 2.54 ด้วยจำนวนปกติ 2 โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้หมายเลข 508 ในตัวเลขนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.54 เศษส่วน 2.54 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 508 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 5.08 ดังนั้นค่าของนิพจน์ 2.54 × 2 คือ 5.08

2.54 x 2 = 5.08

การคูณทศนิยมด้วย 10, 100, 1000

การคูณทศนิยมด้วย 10, 100 หรือ 1,000 ทำได้ในลักษณะเดียวกับการคูณทศนิยมด้วยตัวเลขปกติ จำเป็นต้องทำการคูณโดยละเว้นเครื่องหมายจุลภาคในเศษส่วนทศนิยม จากนั้นในคำตอบ ให้แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วน โดยนับจำนวนหลักทางด้านขวาเนื่องจากมีตัวเลขอยู่หลังจุดทศนิยมในทศนิยม เศษส่วน

ตัวอย่างเช่น คูณ 2.88 ด้วย 10

ลองคูณเศษทศนิยม 2.88 ด้วย 10 โดยไม่สนใจเครื่องหมายจุลภาคในเศษทศนิยม:

เราได้ 2880 ในตัวเลขนี้ คุณต้องแยกส่วนทั้งหมดออกจากเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษ 2.88 เราจะเห็นว่าในเศษ 2.88 มีเลขหลังจุดทศนิยมสองหลัก

เรากลับไปที่หมายเลข 2880 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 28.80 เราทิ้งศูนย์สุดท้าย - เราได้ 28.8 ดังนั้นค่าของนิพจน์ 2.88 × 10 คือ 28.8

2.88 x 10 = 28.8

มีวิธีที่สองในการคูณเศษส่วนทศนิยมด้วย 10, 100, 1000 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยข้อเท็จจริงที่ว่าเครื่องหมายจุลภาคในเศษส่วนทศนิยมเคลื่อนไปทางขวาด้วยจำนวนหลักมากเท่ากับศูนย์ในตัวคูณ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 2.88×10 ด้วยวิธีนี้ เราจะดูที่ตัวประกอบ 10 ทันทีโดยไม่ได้คำนวณอะไรเลย เราสนใจว่าเลขศูนย์อยู่ในนั้นกี่ตัว เราเห็นว่ามันมีศูนย์หนึ่งตัว ในเศษ 2.88 เราย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เราได้ 28.8

2.88 x 10 = 28.8

ลองคูณ 2.88 ด้วย 100 ดูตัวประกอบ 100 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราจะเห็นว่ามันมีศูนย์สองตัว ตอนนี้ในเศษ 2.88 เราย้ายจุดทศนิยมไปทางขวาด้วยตัวเลขสองหลัก เราได้288

2.88 x 100 = 288

ลองคูณ 2.88 ด้วย 1000 กัน. เราดูที่ตัวประกอบ 1000 ทันที. เราสนใจว่าเลขศูนย์อยู่ในนั้นกี่ตัว. เราเห็นว่ามันมีศูนย์สามตัว ตอนนี้ในเศษ 2.88 เราย้ายจุดทศนิยมไปทางขวาด้วยตัวเลขสามหลัก ตัวเลขตัวที่สามไม่อยู่ ดังนั้นเราจึงบวกศูนย์อีกตัวหนึ่ง เป็นผลให้เราได้ 2880

2.88 x 1,000 = 2880

คูณทศนิยมด้วย 0.1 0.01 และ 0.001

การคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 ทำงานในลักษณะเดียวกับการคูณทศนิยมด้วยทศนิยม จำเป็นต้องคูณเศษส่วนเหมือนตัวเลขธรรมดา แล้วใส่เครื่องหมายจุลภาคในคำตอบ โดยนับจำนวนหลักทางด้านขวาให้มากที่สุดเท่าที่จะมีตัวเลขอยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

ตัวอย่างเช่น คูณ 3.25 ด้วย 0.1

เราคูณเศษส่วนเหล่านี้เหมือนตัวเลขธรรมดาโดยไม่สนใจเครื่องหมายจุลภาค:

เราได้ 325 ในตัวเลขนี้ คุณต้องแยกส่วนทั้งหมดออกจากเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องคำนวณจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วนของ 3.25 และ 0.1 ในเศษ 3.25 มีตัวเลขสองหลักหลังจุดทศนิยม ในเศษ 0.1 มีหนึ่งหลัก รวมเป็นสามตัวเลข

เรากลับไปที่หมายเลข 325 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสามหลักทางด้านขวาและใส่เครื่องหมายจุลภาค นับสามหลักแล้วพบว่าเลขหมด ในกรณีนี้ คุณต้องเพิ่มศูนย์หนึ่งตัวและใส่เครื่องหมายจุลภาค:

เราได้คำตอบ 0.325 ดังนั้นค่าของนิพจน์ 3.25 × 0.1 คือ 0.325

3.25 x 0.1 = 0.325

มีวิธีที่สองในการคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยข้อเท็จจริงที่ว่าเครื่องหมายจุลภาคในเศษส่วนทศนิยมเคลื่อนไปทางซ้ายด้วยตัวเลขมากที่สุดเท่าที่มีศูนย์ในตัวคูณ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 3.25 × 0.1 ด้วยวิธีนี้ เราจะดูที่ตัวประกอบ 0.1 ทันทีโดยไม่ให้การคำนวณใดๆ เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราเห็นว่ามันมีหนึ่งศูนย์ ตอนนี้ในเศษ 3.25 เราย้ายจุดทศนิยมไปทางซ้ายหนึ่งหลัก ย้ายเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลัก เราจะเห็นว่าไม่มีตัวเลขก่อนหน้าสามหลักอีกต่อไป ในกรณีนี้ ให้เพิ่มศูนย์หนึ่งตัวแล้วใส่เครื่องหมายจุลภาค เป็นผลให้เราได้รับ0.325

3.25 x 0.1 = 0.325

ลองคูณ 3.25 ด้วย 0.01 ดูตัวคูณของ 0.01 ทันที เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราจะเห็นว่ามันมีศูนย์สองตัว ตอนนี้ในเศษส่วน 3.25 เราย้ายเครื่องหมายจุลภาคไปทางซ้ายด้วยตัวเลขสองหลัก เราได้ 0.0325

3.25 x 0.01 = 0.0325

ลองคูณ 3.25 ด้วย 0.001 ดูตัวคูณของ 0.001 ทันที เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราเห็นว่ามันมีศูนย์สามตัว ตอนนี้ในเศษ 3.25 เราย้ายจุดทศนิยมไปทางซ้ายด้วยตัวเลขสามหลัก เราได้ 0.00325

3.25 × 0.001 = 0.00325

อย่าสับสนการคูณทศนิยมด้วย 0.1, 0.001 และ 0.001 ด้วยการคูณด้วย 10, 100, 1000 ข้อผิดพลาดทั่วไปคนส่วนใหญ่

เมื่อคูณด้วย 10, 100, 1000 เครื่องหมายจุลภาคจะถูกย้ายไปทางขวาด้วยจำนวนหลักมากเท่ากับศูนย์ในตัวคูณ

และเมื่อคูณด้วย 0.1, 0.01 และ 0.001 เครื่องหมายจุลภาคจะถูกย้ายไปทางซ้ายตามจำนวนหลักมากเท่ากับศูนย์ในตัวคูณ

หากจำยากในตอนแรก คุณสามารถใช้วิธีแรกซึ่งทำการคูณเหมือนกับตัวเลขธรรมดา ในคำตอบ คุณจะต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนโดยนับจำนวนหลักทางด้านขวาให้มากที่สุดเท่าที่จะมีตัวเลขอยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

การหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า ระดับสูง.

ในบทเรียนก่อนหน้านี้เรากล่าวว่าเมื่อทำการหาร น้อยลงยิ่งไปกว่านั้น จะได้เศษส่วน ในตัวเศษซึ่งเป็นเงินปันผล และตัวส่วนเป็นตัวหาร

ตัวอย่างเช่น ในการแบ่งแอปเปิ้ลหนึ่งผลออกเป็นสองผล คุณต้องเขียน 1 (แอปเปิ้ลหนึ่งผล) ในตัวเศษ และเขียน 2 (เพื่อนสองคน) ในตัวส่วน ผลที่ได้คือเศษส่วน ดังนั้นเพื่อนแต่ละคนจะได้รับแอปเปิ้ล กล่าวอีกนัยหนึ่งคือครึ่งแอปเปิ้ล เศษส่วนคือคำตอบของปัญหา วิธีแยกแอปเปิ้ลหนึ่งลูกระหว่างสองลูก

ปรากฎว่าคุณสามารถแก้ปัญหานี้ต่อไปได้หากคุณหาร 1 ด้วย 2 ท้ายที่สุด แท่งเศษส่วนในเศษส่วนใดๆ หมายถึงการหาร ซึ่งหมายความว่าการหารนี้เป็นเศษส่วนด้วย แต่อย่างไร? เราเคยชินกับความจริงที่ว่าเงินปันผลมากกว่าตัวหารเสมอ และที่นี่ตรงกันข้าม แบ่งได้ ตัวหารน้อย.

ทุกอย่างจะชัดเจนขึ้นถ้าเราจำได้ว่าเศษส่วนหมายถึงการทุบ หาร หาร ซึ่งหมายความว่าหน่วยสามารถแบ่งออกเป็นส่วนต่างๆ ได้มากเท่าที่คุณต้องการ ไม่ใช่แค่เป็นสองส่วนเท่านั้น

เมื่อหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า จะได้รับเศษส่วนทศนิยม ซึ่งส่วนจำนวนเต็มจะเป็น 0 (ศูนย์) เศษส่วนสามารถเป็นอะไรก็ได้

ลองหาร 1 ด้วย 2 ลองแก้ตัวอย่างนี้ด้วยมุม:

หนึ่งไม่สามารถแบ่งออกเป็นสองเช่นนั้น หากคุณถามคำถาม "มีกี่สองในหนึ่ง" คำตอบจะเป็น 0 ดังนั้นในส่วนตัวเราเขียน 0 และใส่เครื่องหมายจุลภาค:

ตามปกติแล้ว เราจะคูณผลหารด้วยตัวหารเพื่อดึงเศษที่เหลือออกมา:

ช่วงเวลาได้มาถึงเมื่อหน่วยสามารถแบ่งออกเป็นสองส่วน เมื่อต้องการทำสิ่งนี้ ให้เพิ่มอีกศูนย์ทางด้านขวาของอันที่ได้รับ:

เราได้ 10 เราหาร 10 ด้วย 2 เราได้ 5 เราเขียนห้าในส่วนเศษส่วนของคำตอบของเรา:

ตอนนี้เรานำส่วนที่เหลือสุดท้ายออกเพื่อทำการคำนวณให้สมบูรณ์ คูณ 5 ด้วย 2 เราได้ 10

เราได้คำตอบ 0.5 ดังนั้นเศษส่วนคือ 0.5

แอปเปิ้ลครึ่งลูกสามารถเขียนโดยใช้เศษทศนิยม 0.5 หากเราเพิ่มสองส่วนนี้ (0.5 และ 0.5) เราจะได้แอปเปิ้ลเดิมทั้งลูกอีกครั้ง:

จุดนี้สามารถเข้าใจได้เช่นกันถ้าเราจินตนาการว่า 1 ซม. แบ่งออกเป็นสองส่วนอย่างไร ถ้าคุณแบ่ง 1 เซนติเมตรออกเป็น 2 ส่วน คุณจะได้ 0.5 ซม.

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 4:5

มีกี่ห้าในสี่? ไม่เลย. เราเขียนในส่วนตัว 0 และใส่เครื่องหมายจุลภาค:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียนศูนย์ใต้สี่ ลบศูนย์นี้ออกจากเงินปันผลทันที:

ทีนี้มาเริ่มแบ่ง (แบ่ง) สี่ส่วนเป็น 5 ส่วนกัน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของ 4 เราบวกศูนย์ และหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดเป็นการส่วนตัว

เราทำตัวอย่างให้สมบูรณ์โดยคูณ 8 ด้วย 5 และรับ 40:

เราได้คำตอบ 0.8. ดังนั้นค่าของนิพจน์ 4: 5 คือ 0.8

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 5: 125

จำนวน 125 ในห้ามีกี่ตัว? ไม่เลย. เราเขียน 0 เป็นการส่วนตัวและใส่เครื่องหมายจุลภาค:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียน 0 ใต้ห้า ลบทันทีจากห้า 0

ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) ห้าส่วนออกเป็น 125 ส่วนกัน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของห้านี้ เราเขียนศูนย์:

หาร 50 ด้วย 125 ตัวเลข 125 ใน 50 มีกี่ตัว? ไม่เลย. ดังนั้นในผลหาร เราเขียน 0 . อีกครั้ง

เราคูณ 0 ด้วย 125 เราได้ 0 เราเขียนศูนย์นี้ภายใต้ 50 ลบ 0 จาก 50 . ทันที

ตอนนี้เราแบ่งหมายเลข 50 เป็น 125 ส่วน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของ 50 เราจะเขียนศูนย์อีกตัวหนึ่ง:

หาร 500 ด้วย 125 จำนวน 125 ในจำนวน 500 มีกี่จำนวน ในจำนวน 500 มีสี่ตัวเลข 125 เราเขียนสี่เป็นส่วนตัว:

เราเติมตัวอย่างให้สมบูรณ์โดยคูณ 4 ด้วย 125 และรับ 500

เราได้คำตอบ 0.04 ดังนั้นค่าของนิพจน์ 5: 125 คือ 0.04

การหารตัวเลขโดยไม่เหลือเศษ

ดังนั้น ให้ใส่เครื่องหมายจุลภาคในผลหารหลังหน่วย ซึ่งแสดงว่าการหารของส่วนจำนวนเต็มสิ้นสุดลง และเราดำเนินการในส่วนที่เป็นเศษส่วน:

เพิ่มศูนย์ในส่วนที่เหลือ 4

ตอนนี้เราหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดเป็นส่วนตัว:

40−40=0. ได้รับ 0 ส่วนที่เหลือ การแบ่งส่วนจึงเสร็จสมบูรณ์ การหาร 9 ด้วย 5 ได้ผลลัพธ์เป็นทศนิยม 1.8:

9: 5 = 1,8

ตัวอย่าง 2. หาร 84 ด้วย 5 โดยไม่มีเศษ

ก่อนอื่นเราหาร 84 ด้วย 5 ตามปกติด้วยเศษ:

ได้รับในส่วนตัว 16 และอีก 4 ในยอดคงเหลือ ตอนนี้เราหารเศษนี้ด้วย 5 เราใส่เครื่องหมายจุลภาคในไพรเวต แล้วบวก 0 ให้กับเศษที่เหลือ 4

ตอนนี้เราหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดในผลหารหลังจุดทศนิยม:

และกรอกตัวอย่างโดยตรวจสอบว่ายังเหลืออยู่หรือไม่:

การหารทศนิยมด้วยจำนวนปกติ

เศษส่วนทศนิยมอย่างที่เราทราบประกอบด้วยจำนวนเต็มและเศษส่วน เมื่อหารเศษส่วนทศนิยมด้วยจำนวนปกติ ขั้นแรกคุณต้อง:

หารส่วนจำนวนเต็มของเศษส่วนทศนิยมด้วยตัวเลขนี้
หลังจากแบ่งส่วนจำนวนเต็มแล้ว คุณต้องใส่เครื่องหมายจุลภาคในส่วนไพรเวตทันทีและทำการคำนวณต่อไป เช่นเดียวกับการหารธรรมดา

ตัวอย่างเช่น ลองหาร 4.8 ด้วย 2

ลองเขียนตัวอย่างนี้เป็นมุม:

ทีนี้ลองหารส่วนทั้งหมดด้วย 2 กัน สี่หารด้วยสองเป็นสอง เราเขียนผีสางเป็นการส่วนตัวและใส่เครื่องหมายจุลภาคทันที:

ตอนนี้เราคูณผลหารด้วยตัวหารแล้วดูว่าเหลือเศษจากการหารหรือไม่:

4-4=0. ส่วนที่เหลือเป็นศูนย์ เรายังไม่ได้เขียนศูนย์ เนื่องจากการแก้ปัญหายังไม่เสร็จสิ้น จากนั้นเราคำนวณต่อไปเช่นเดียวกับการหารธรรมดา ลง 8 แล้วหารด้วย 2

8: 2 = 4 เราเขียนสี่ในผลหารแล้วคูณด้วยตัวหารทันที:

ได้คำตอบ 2.4 ค่านิพจน์ 4.8: 2 เท่ากับ 2.4

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 8.43:3

เราหาร 8 ด้วย 3 เราได้ 2 ใส่เครื่องหมายจุลภาคหลังสองทันที:

ตอนนี้เราคูณผลหารด้วยตัวหาร 2 × 3 = 6 เราเขียนหกภายใต้แปดและหาเศษที่เหลือ:

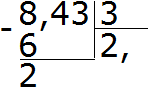
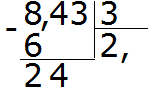
เราหาร 24 ด้วย 3 ได้ 8 เราเขียนแปดเป็นส่วนตัว เราคูณมันด้วยตัวหารทันทีเพื่อค้นหาส่วนที่เหลือของการหาร:

24-24=0. ส่วนที่เหลือเป็นศูนย์ Zero ยังไม่ได้บันทึก ใช้เงินปันผลสามตัวสุดท้ายแล้วหารด้วย 3 เราจะได้ 1 คูณ 1 ด้วย 3 ทันทีเพื่อให้ตัวอย่างนี้สมบูรณ์:

ได้คำตอบ 2.81 ดังนั้นค่าของนิพจน์ 8.43: 3 เท่ากับ 2.81

การหารทศนิยมด้วยทศนิยม

ในการหารเศษส่วนทศนิยมให้เป็นเศษส่วนทศนิยม ในเงินปันผลและในตัวหาร ให้ย้ายเครื่องหมายจุลภาคไปทางขวาด้วยจำนวนหลักเดียวกับที่อยู่หลังจุดทศนิยมในตัวหาร แล้วหารด้วยจำนวนปกติ

ตัวอย่างเช่น หาร 5.95 ด้วย 1.7

ลองเขียนนิพจน์นี้เป็นมุม

ตอนนี้ ในตัวหารและตัวหาร เราย้ายเครื่องหมายจุลภาคไปทางขวาด้วยจำนวนหลักเดียวกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีหนึ่งหลักหลังจุดทศนิยม ดังนั้นเราต้องย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลักในเงินปันผลและในตัวหาร การโอน:

หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักแล้ว เศษทศนิยม 5.95 จะกลายเป็นเศษส่วน 59.5 และเศษทศนิยม 1.7 หลังจากที่เลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักแล้ว กลายเป็นเลข 17 ปกติ และเรารู้วิธีหารเศษส่วนทศนิยมด้วยจำนวนปกติแล้ว การคำนวณเพิ่มเติมนั้นไม่ยาก:

เครื่องหมายจุลภาคถูกย้ายไปทางขวาเพื่ออำนวยความสะดวกในการแบ่ง สิ่งนี้ได้รับอนุญาตเนื่องจากข้อเท็จจริงที่ว่าเมื่อคูณหรือหารเงินปันผลและตัวหารด้วยจำนวนเดียวกัน ผลหารจะไม่เปลี่ยนแปลง มันหมายความว่าอะไร?

นี่เป็นหนึ่งใน คุณสมบัติที่น่าสนใจแผนก. เรียกว่าทรัพย์สินส่วนตัว พิจารณานิพจน์ 9: 3 = 3 หากในนิพจน์นี้ เงินปันผลและตัวหารถูกคูณหรือหารด้วยตัวเลขเดียวกัน ผลหาร 3 จะไม่เปลี่ยนแปลง

ลองคูณเงินปันผลและตัวหารด้วย 2 แล้วดูว่าเกิดอะไรขึ้น:

(9 × 2) : (3 × 2) = 18: 6 = 3

ดังจะเห็นได้จากตัวอย่าง ความฉลาดไม่เปลี่ยนแปลง

สิ่งเดียวกันนี้จะเกิดขึ้นเมื่อเราใส่เครื่องหมายจุลภาคในตัวปันผลและในตัวหาร ในตัวอย่างก่อนหน้านี้ โดยที่เราหาร 5.91 ด้วย 1.7 เราย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลักในตัวหารและตัวหาร หลังจากย้ายเครื่องหมายจุลภาค เศษ 5.91 จะถูกแปลงเป็นเศษส่วน 59.1 และเศษส่วน 1.7 จะถูกแปลงเป็นเลข 17 ตามปกติ

อันที่จริงภายในกระบวนการนี้ การคูณด้วย 10 เกิดขึ้น นี่คือสิ่งที่ดูเหมือน:

5.91 × 10 = 59.1

ดังนั้นจำนวนหลักหลังจุดทศนิยมในตัวหารจึงขึ้นอยู่กับว่าตัวหารและตัวหารจะคูณด้วยอะไร กล่าวอีกนัยหนึ่ง จำนวนหลักหลังจุดทศนิยมในตัวหารจะเป็นตัวกำหนดจำนวนหลักในการจ่ายเงินปันผล และในตัวหาร เครื่องหมายจุลภาคจะถูกย้ายไปทางขวา

การหารทศนิยมด้วย 10, 100, 1000

การหารทศนิยมด้วย 10, 100 หรือ 1,000 ทำได้ในลักษณะเดียวกับ . ตัวอย่างเช่น ลองหาร 2.1 ด้วย 10 ลองแก้ตัวอย่างนี้ด้วยมุม:

แต่ยังมีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือเครื่องหมายจุลภาคในตัวปันผลจะถูกย้ายไปทางซ้ายด้วยตัวเลขมากที่สุดเท่าที่มีเลขศูนย์ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 2.1: 10. เราดูที่ตัวแบ่ง เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราจะเห็นว่ามีศูนย์หนึ่งตัว ในการหาร 2.1 คุณต้องเลื่อนเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลัก เราย้ายเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลักและเห็นว่าไม่มีตัวเลขเหลืออยู่ ในกรณีนี้ เราจะบวกศูนย์อีกหนึ่งตัวก่อนตัวเลข เป็นผลให้เราได้รับ 0.21

ลองหาร 2.1 ด้วย 100 มีศูนย์สองตัวในจำนวน 100 ดังนั้นในการหาร 2.1 คุณต้องย้ายเครื่องหมายจุลภาคไปทางซ้ายด้วยตัวเลขสองหลัก:

2,1: 100 = 0,021

ลองหาร 2.1 ด้วย 1000 มีศูนย์สามตัวในจำนวน 1000 ดังนั้นในการหาร 2.1 คุณต้องย้ายเครื่องหมายจุลภาคไปทางซ้ายด้วยตัวเลขสามหลัก:

2,1: 1000 = 0,0021

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001 ทำได้ในลักษณะเดียวกับ . ในการจ่ายเงินปันผลและในตัวหาร คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยจำนวนหลักมากเท่ากับที่มีหลังจุดทศนิยมในตัวหาร

ตัวอย่างเช่น ลองหาร 6.3 ด้วย 0.1 ก่อนอื่น เราย้ายเครื่องหมายจุลภาคในตัวหารและในตัวหารไปทางขวาด้วยจำนวนหลักเดียวกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีหนึ่งหลักหลังจุดทศนิยม ดังนั้นเราจึงย้ายเครื่องหมายจุลภาคในตัวปันผลและตัวหารไปทางขวาหนึ่งหลัก

หลังจากย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เศษส่วนทศนิยม 6.3 จะกลายเป็นตัวเลขปกติ 63 และเศษส่วนทศนิยม 0.1 หลังจากย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก จะกลายเป็นหนึ่ง และการหาร 63 ด้วย 1 นั้นง่ายมาก:

ดังนั้นค่าของนิพจน์ 6.3: 0.1 เท่ากับ 63

แต่ยังมีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือเครื่องหมายจุลภาคในเงินปันผลจะถูกโอนไปทางขวาด้วยตัวเลขมากที่สุดเท่าที่มีศูนย์ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 6.3:0.1. มาดูตัวแบ่งกัน เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราจะเห็นว่ามีศูนย์หนึ่งตัว ในการหาร 6.3 คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลัก เราย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลักและรับ63

ลองหาร 6.3 ด้วย 0.01 ตัวหาร 0.01 มีศูนย์สองตัว ในการหาร 6.3 คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยตัวเลขสองหลัก แต่ในการจ่ายเงินปันผลจะมีตัวเลขอยู่หลังจุดทศนิยมเพียงตัวเดียว ในกรณีนี้จะต้องเพิ่มศูนย์อีกหนึ่งตัวในตอนท้าย เป็นผลให้เราได้รับ 630

ลองหาร 6.3 ด้วย 0.001 ตัวหารของ 0.001 มีศูนย์สามตัว ดังนั้นในการหาร 6.3 คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยตัวเลขสามหลัก:

6,3: 0,001 = 6300

งานสำหรับโซลูชันอิสระ

คุณชอบบทเรียนหรือไม่?
เข้าร่วมกับเรา กลุ่มใหม่ Vkontakte และเริ่มรับการแจ้งเตือนเกี่ยวกับบทเรียนใหม่

§ 107. การบวกเศษส่วนทศนิยม

การบวกทศนิยมทำได้ในลักษณะเดียวกับการบวกจำนวนเต็ม ลองดูสิ่งนี้พร้อมตัวอย่าง

1) 0.132 + 2.354. มาลงนามข้อตกลงกัน

ที่นี่จากการเพิ่ม 2 ในพันกับ 4 ในพัน เราได้ 6 ในพัน;
จากการเพิ่ม 3 ในร้อยกับ 5 ในร้อย มันกลายเป็น 8 ในร้อย;
จากการเพิ่ม 1 ในสิบกับ 3 ในสิบ -4 ในสิบและ
จากการเพิ่มจำนวนเต็ม 0 กับจำนวนเต็ม 2 จำนวน - 2 จำนวนเต็ม

2) 5,065 + 7,83.

ไม่มีหนึ่งในพันในระยะที่สอง ดังนั้นจึงเป็นสิ่งสำคัญที่จะไม่ทำผิดพลาดเมื่อลงนามในข้อกำหนดภายใต้กันและกัน

3) 1,2357 + 0,469 + 2,08 + 3,90701.

ที่นี่ เมื่อบวกในพัน เราจะได้ 21,000 เราเขียน 1 ภายใต้หลักพัน และ 2 บวกกับหลักร้อย ดังนั้นในตำแหน่งที่ร้อย เราได้เงื่อนไขต่อไปนี้: 2 + 3 + 6 + 8 + 0; โดยรวมแล้วพวกเขาให้ 19 ในร้อย เราเซ็น 9 อันภายใต้ร้อย และ 1 ถูกนับเป็นหนึ่งในสิบ ฯลฯ

ดังนั้น เมื่อเพิ่มเศษส่วนทศนิยม ต้องสังเกตลำดับต่อไปนี้: เศษส่วนถูกเซ็นชื่อหนึ่งภายใต้ส่วนอื่น ดังนั้นในทุกพจน์ ตัวเลขเดียวกันจะอยู่ใต้กันและกัน และเครื่องหมายจุลภาคทั้งหมดอยู่ในคอลัมน์แนวตั้งเดียวกัน ทางด้านขวาของตำแหน่งทศนิยมของคำศัพท์บางคำพวกเขาระบุอย่างน้อยทางจิตใจจำนวนศูนย์ดังกล่าวเพื่อให้คำศัพท์ทั้งหมดที่อยู่หลังจุดทศนิยมมี เบอร์เดียวกันตัวเลข จากนั้น ทำการบวกด้วยตัวเลข โดยเริ่มจากด้านขวา และในจำนวนผลลัพธ์ เครื่องหมายจุลภาคจะถูกวางในคอลัมน์แนวตั้งเดียวกันกับที่อยู่ในเงื่อนไขเหล่านี้

§ 108. การลบเศษส่วนทศนิยม

การลบทศนิยมทำได้ในลักษณะเดียวกับการลบจำนวนเต็ม ขอแสดงนี้ด้วยตัวอย่าง

1) 9.87 - 7.32. มาลงชื่อ subtrahend ภายใต้ minuend เพื่อให้หน่วยของตัวเลขเดียวกันอยู่ใต้กันและกัน:

2) 16.29 - 4.75. มาลงชื่อ subtrahend ภายใต้ minuend ดังตัวอย่างแรก:

หากต้องการลบหนึ่งในสิบ เราต้องนำหน่วยทั้งหมดหนึ่งหน่วยจาก 6 และแบ่งออกเป็นสิบ

3) 14.0213-5.350712. มาลงชื่อ subtrahend ภายใต้ minuend:

การลบได้ดำเนินการดังนี้: เนื่องจากเราไม่สามารถลบ 2 ในล้านจาก 0 ได้ เราจึงควรอ้างถึงหลักที่ใกล้ที่สุดทางซ้าย นั่นคือ ถึงหลักแสน แต่มีศูนย์อยู่ในตำแหน่งหลักแสนเช่นกัน ดังนั้นเราจึงนำ 1 หมื่นจาก 3 หมื่น และเราแบ่งเป็นแสนหนึ่งแสน เราได้หนึ่งแสนในจำนวนนี้ เหลือ 9 แสนในหมวดหนึ่งแสน และ 1 แสนถูกบดเป็นล้าน เราได้ 10 ล้าน ดังนั้น ในสามหลักสุดท้าย เราได้: ล้าน 10, แสน 9, หมื่น 2 เพื่อความชัดเจนและความสะดวกมากขึ้น (อย่าลืม) ตัวเลขเหล่านี้จะถูกเขียนบนตัวเลขเศษส่วนที่สอดคล้องกันของค่าลดหย่อน ตอนนี้เราสามารถเริ่มลบได้ เราลบ 2 ในล้านจาก 10 ในล้าน เราได้ 8 ในล้าน ลบ 1 แสนจาก 9 แสน เราได้ 8 แสน ฯลฯ

ดังนั้น เมื่อลบเศษส่วนทศนิยม จะสังเกตในลำดับต่อไปนี้: การลบจะถูกเซ็นชื่อภายใต้การย่อส่วน เพื่อให้ตัวเลขเดียวกันอยู่ด้านล่างอีกตัวหนึ่ง และเครื่องหมายจุลภาคทั้งหมดอยู่ในคอลัมน์แนวตั้งเดียวกัน ทางด้านขวาพวกเขาแอตทริบิวต์อย่างน้อยทางจิตใจในการลดลงหรือลบศูนย์จำนวนมากเพื่อให้มีจำนวนหลักเท่ากันจากนั้นลบด้วยตัวเลขโดยเริ่มจากด้านขวาและในผลต่างให้ใส่เครื่องหมายจุลภาคใน คอลัมน์แนวตั้งเดียวกันกับที่มันถูกย่อและลบ

§ 109. การคูณเศษส่วนทศนิยม

ลองพิจารณาตัวอย่างการคูณเศษส่วนทศนิยม

ในการหาผลคูณของตัวเลขเหล่านี้ เราสามารถให้เหตุผลได้ดังนี้: หากตัวประกอบเพิ่มขึ้น 10 เท่า ตัวประกอบทั้งสองจะเป็นจำนวนเต็ม และเราสามารถคูณตามกฎสำหรับการคูณจำนวนเต็มได้ แต่เรารู้ว่าเมื่อปัจจัยใดปัจจัยหนึ่งเพิ่มขึ้นหลายครั้ง ผลิตภัณฑ์จะเพิ่มขึ้นในปริมาณเท่ากัน ซึ่งหมายความว่าจำนวนที่จะได้รับจากการคูณตัวประกอบจำนวนเต็ม เช่น 28 คูณ 23 มีค่ามากกว่าผลคูณจริง 10 เท่า และเพื่อให้ได้ งานจริงคุณต้องลดจำนวนสินค้าที่พบลง 10 เท่า ดังนั้นที่นี่คุณต้องทำการคูณด้วย 10 หนึ่งครั้งและการหารด้วย 10 หนึ่งครั้ง แต่การคูณและการหารด้วย 10 ทำได้โดยการย้ายเครื่องหมายจุลภาคไปทางขวาและซ้ายด้วยเครื่องหมายเดียว ดังนั้น คุณต้องทำสิ่งนี้: ในตัวคูณ ให้ย้ายเครื่องหมายจุลภาคไปทางขวาด้วยหนึ่งเครื่องหมาย จากนั้นจะเท่ากับ 23 จากนั้นคุณต้องคูณจำนวนเต็มผลลัพธ์:

สินค้าชิ้นนี้ใหญ่กว่าของแท้ 10 เท่า ดังนั้นจึงต้องลดลง 10 เท่า โดยเราจะย้ายเครื่องหมายจุลภาคไปทางซ้ายหนึ่งอักขระ ดังนั้นเราจึงได้รับ

28 2,3 = 64,4.

เพื่อวัตถุประสงค์ในการตรวจสอบ คุณสามารถเขียนเศษส่วนทศนิยมด้วยตัวส่วนและดำเนินการตามกฎสำหรับการคูณเศษส่วนสามัญ กล่าวคือ

2) 12,27 0,021.

ความแตกต่างระหว่างตัวอย่างนี้กับตัวอย่างก่อนหน้าคือที่นี่ ตัวประกอบทั้งสองแสดงด้วยเศษส่วนทศนิยม แต่ที่นี่ ในกระบวนการคูณ เราจะไม่ใส่ใจกับเครื่องหมายจุลภาค นั่นคือ เราจะเพิ่มตัวคูณชั่วคราว 100 เท่า และตัวคูณด้วย 1,000 เท่า ซึ่งจะทำให้ผลคูณเพิ่มขึ้น 100,000 เท่า ดังนั้น เมื่อคูณ 1227 ด้วย 21 เราได้:

1 227 21 = 25 767.

เมื่อพิจารณาว่าผลลัพธ์ที่ได้นั้นมากกว่าของจริง 100,000 เท่า ตอนนี้เราต้องลดมันลง 100,000 เท่าโดยใส่เครื่องหมายจุลภาคลงไปอย่างเหมาะสม เราจะได้:

32,27 0,021 = 0,25767.

มาตรวจสอบกัน:

ดังนั้น ในการคูณเศษส่วนทศนิยมสองทศนิยม ก็เพียงพอแล้ว โดยไม่ต้องสนใจเครื่องหมายจุลภาค ให้คูณพวกมันเป็นจำนวนเต็ม และในผลคูณให้คั่นด้วยเครื่องหมายจุลภาคทางด้านขวาของตำแหน่งทศนิยมมากเท่ากับที่มีในตัวคูณและใน ปัจจัยด้วยกัน

ที่ ตัวอย่างสุดท้ายผลิตภัณฑ์ที่มีทศนิยมห้าตำแหน่ง หากไม่ต้องการความแม่นยำมากกว่านี้ ให้ทำการปัดเศษทศนิยม เมื่อปัดเศษ คุณควรใช้กฎเดียวกับที่ระบุไว้สำหรับจำนวนเต็ม

§ 110. การคูณโดยใช้ตาราง

บางครั้งการคูณทศนิยมสามารถทำได้โดยใช้ตาราง เพื่อจุดประสงค์นี้ ตัวอย่างเช่น คุณสามารถใช้ตารางสูตรคูณเหล่านั้นได้ ตัวเลขสองหลักที่ได้ให้คำอธิบายไว้ก่อนหน้านี้

1) คูณ 53 ด้วย 1.5

เราจะคูณ 53 ด้วย 15 ในตาราง ผลิตภัณฑ์นี้เท่ากับ 795 เราพบผลคูณของ 53 คูณ 15 แต่ตัวประกอบที่สองของเราน้อยกว่า 10 เท่า ซึ่งหมายความว่าผลิตภัณฑ์ต้องลดลง 10 เท่า กล่าวคือ

53 1,5 = 79,5.

2) คูณ 5.3 ด้วย 4.7

อันดับแรก ลองหาผลคูณของ 53 คูณ 47 ในตาราง มันจะเป็น 2491 แต่เนื่องจากเราเพิ่มตัวคูณและตัวคูณด้วยทั้งหมด 100 เท่า ดังนั้นผลลัพธ์ที่ได้จึงมากกว่าที่ควรจะเป็น 100 เท่า ดังนั้นเราต้องลดผลิตภัณฑ์นี้ลง 100 เท่า:

5,3 4,7 = 24,91.

3) คูณ 0.53 ด้วย 7.4

อันดับแรกเราพบผลิตภัณฑ์ 53 คูณ 74 ในตาราง นี่จะเท่ากับ 3,922 แต่เนื่องจากเราเพิ่มตัวคูณขึ้น 100 เท่า และตัวคูณ 10 เท่า ผลิตภัณฑ์จึงเพิ่มขึ้น 1,000 เท่า ดังนั้นตอนนี้เราต้องลดมันลง 1,000 เท่า:

0,53 7,4 = 3,922.

§ 111. การหารทศนิยม

เราจะดูการหารทศนิยมตามลำดับนี้:

1. หารทศนิยมโดย จำนวนเต็ม,

1. การหารเศษส่วนทศนิยมด้วยจำนวนเต็ม

1) หาร 2.46 ด้วย 2.

เราหารด้วยจำนวนเต็มแรก 2 ตัว ตามด้วยหลักสิบและหลักร้อย

2) หาร 32.46 ด้วย 3.

32,46: 3 = 10,82.

เราหาร 3 สิบด้วย 3 แล้วเราก็เริ่มหาร 2 หน่วยด้วย 3; เนื่องจากจำนวนหน่วยของเงินปันผล (2) น้อยกว่าตัวหาร (3) เราจึงต้องใส่ 0 ลงในผลหาร ต่อไป ที่เหลือเรารื้อถอน 4 ใน 10 และหาร 24 ในสิบด้วย 3; ได้รับในส่วนตัว 8 ในสิบและสุดท้ายแบ่ง 6 ในร้อย

3) หาร 1.2345 ด้วย 5.

1,2345: 5 = 0,2469.

ในที่นี้ ในผลหารในตอนแรก จำนวนเต็มศูนย์ปรากฏออกมา เนื่องจากจำนวนเต็มหนึ่งตัวหารด้วย 5 ไม่ลงตัว

4) หาร 13.58 ด้วย 4.

ลักษณะเฉพาะของตัวอย่างนี้คือเมื่อเราได้ 9 ในร้อยในส่วนตัว จากนั้นพบส่วนที่เหลือเท่ากับ 2 ในร้อย เราแบ่งส่วนที่เหลือนี้ออกเป็นพัน ได้ 20,000 และนำการหารมาจนสิ้นสุด

กฎ.การหารเศษส่วนทศนิยมด้วยจำนวนเต็มดำเนินการในลักษณะเดียวกับการหารจำนวนเต็ม และเศษที่เป็นผลลัพธ์จะถูกแปลงเป็นเศษส่วนทศนิยม มีขนาดเล็กลงเรื่อยๆ การหารจะดำเนินต่อไปจนกว่าส่วนที่เหลือจะเป็นศูนย์

2. หารเศษส่วนทศนิยมด้วยเศษส่วนทศนิยม

1) หาร 2.46 ด้วย 0.2

เรารู้วิธีหารเศษส่วนทศนิยมด้วยจำนวนเต็มแล้ว ลองคิดดูว่าถ้าสิ่งนี้ คดีใหม่ดิวิชั่นที่จะลดไปก่อนหน้านี้? ครั้งหนึ่ง เราพิจารณาคุณสมบัติที่โดดเด่นของผลหาร ซึ่งประกอบด้วยข้อเท็จจริงที่ว่ามันยังคงไม่เปลี่ยนแปลงในขณะที่เพิ่มหรือลดเงินปันผลและตัวหารด้วยจำนวนเท่าเดิม เราจะทำการหารจำนวนที่เสนอให้เราได้อย่างง่ายดายหากตัวหารเป็นจำนวนเต็ม ในการทำเช่นนี้ก็เพียงพอที่จะเพิ่ม 10 เท่าและเพื่อให้ได้ผลหารที่ถูกต้องจำเป็นต้องเพิ่มเงินปันผลเป็นจำนวนเท่าเดิมนั่นคือ 10 เท่า จากนั้นการหารของตัวเลขเหล่านี้จะถูกแทนที่ด้วยการหารของตัวเลขดังกล่าว:

และไม่จำเป็นต้องทำการแก้ไขใดๆ เป็นการส่วนตัว

มาทำส่วนนี้กันเถอะ:

ดังนั้น 2.46: 0.2 = 12.3

2) หาร 1.25 ด้วย 1.6

เราเพิ่มตัวหาร (1.6) 10 เท่า เพื่อไม่ให้ผลหารเปลี่ยนแปลงเราเพิ่มเงินปันผล 10 เท่า จำนวนเต็ม 12 จำนวนหารด้วย 16 ไม่ลงตัว เราจึงเขียนด้วยผลหาร 0 และหาร 125 ในสิบด้วย 16 เราได้ 7 ในสิบของผลหารและเศษเป็น 13 เราแบ่ง 13 ในสิบเป็นร้อยโดยกำหนดศูนย์และหาร 130 ในร้อยด้วย 16 เป็นต้น . ให้ความสนใจกับสิ่งต่อไปนี้:

a) เมื่อไม่ได้รับจำนวนเต็มในผลหารแล้วจำนวนเต็มศูนย์จะถูกเขียนแทน

b) เมื่อหลังจากนำตัวเลขของเงินปันผลไปยังส่วนที่เหลือแล้วได้ตัวเลขที่ไม่สามารถหารด้วยตัวหารได้ศูนย์จะถูกเขียนลงในผลหาร

c) เมื่อหลังจากลบหลักสุดท้ายของการจ่ายเงินปันผล การหารไม่สิ้นสุด จากนั้นโดยการกำหนดศูนย์ให้กับเศษที่เหลือ การหารจะดำเนินต่อไป

d) หากเงินปันผลเป็นจำนวนเต็ม เมื่อหารด้วยเศษส่วนทศนิยม การเพิ่มขึ้นจะดำเนินการโดยการกำหนดศูนย์ให้กับมัน

ดังนั้น ในการหารตัวเลขด้วยเศษส่วนทศนิยม คุณต้องทิ้งเครื่องหมายจุลภาคในตัวหาร แล้วเพิ่มเงินปันผลให้มากที่สุดเท่าที่ตัวหารเพิ่มขึ้นเมื่อเครื่องหมายจุลภาคถูกทิ้งลงไป จากนั้นจึงทำการหารตาม กฎการหารเศษส่วนทศนิยมด้วยจำนวนเต็ม

§ 112 ผลหารโดยประมาณ

ในย่อหน้าก่อนหน้านี้ เราพิจารณาการหารของเศษส่วนทศนิยม และในตัวอย่างทั้งหมดที่เราแก้ไข การหารถูกทำให้สิ้นสุด กล่าวคือ ได้ผลหารที่แน่นอน อย่างไรก็ตาม ในกรณีส่วนใหญ่ ไม่สามารถหาผลหารที่แน่นอนได้ ไม่ว่าเราจะขยายการแบ่งออกไปไกลแค่ไหนก็ตาม นี่เป็นกรณีหนึ่ง: หาร 53 ด้วย 101

เราได้รับเลขผลหารห้าหลักแล้ว แต่การหารยังไม่สิ้นสุด และไม่มีความหวังที่จะสิ้นสุด เนื่องจากตัวเลขที่เราพบก่อนเริ่มปรากฏในส่วนที่เหลือ ตัวเลขจะถูกทำซ้ำในผลหารด้วย: แน่นอนหลังจากหมายเลข 7 หมายเลข 5 จะปรากฏขึ้น จากนั้น 2 และต่อไปเรื่อย ๆ โดยไม่มีที่สิ้นสุด ในกรณีเช่นนี้ การหารจะถูกขัดจังหวะและจำกัดเฉพาะตัวเลขสองสามหลักแรกของผลหาร ส่วนตัวนี้เรียกว่า โดยประมาณวิธีดำเนินการหารในกรณีนี้เราจะแสดงพร้อมตัวอย่าง

ปล่อยให้ต้องหาร 25 ด้วย 3 เห็นได้ชัดว่าผลหารที่แน่นอนซึ่งแสดงเป็นจำนวนเต็มหรือเศษทศนิยมไม่สามารถหาได้จากการหารดังกล่าว ดังนั้น เราจะหาผลหารโดยประมาณ:

25: 3 = 8 และเศษเหลือ 1

ผลหารโดยประมาณคือ 8; แน่นอนว่ามันน้อยกว่าผลหารที่แน่นอน เพราะเหลือ 1 เพื่อให้ได้ผลหารที่แน่นอน คุณต้องบวกผลหารโดยประมาณที่พบ นั่นคือ 8 เศษส่วนที่เกิดจากการหารเศษที่เหลือ เท่ากับ 1 คูณ 3; มันจะเป็นเศษส่วน 1/3 ดังนั้นผลหารที่แน่นอนจึงแสดง คละจำนวน 8 1 / 3 . เนื่องจาก 1/3 เป็นเศษส่วนที่เหมาะสม นั่นคือเศษส่วน น้อยกว่าหนึ่ง, ละทิ้งมัน, เราถือว่า ข้อผิดพลาด, ที่ น้อยกว่าหนึ่ง. ส่วนตัว 8 will ผลหารโดยประมาณถึงหนึ่งที่มีข้อเสียเปรียบหากเราใช้ 9 แทน 8 เราก็อนุญาตให้มีข้อผิดพลาดที่น้อยกว่าหนึ่งเนื่องจากเราจะไม่เพิ่มหน่วยทั้งหมด แต่ 2 / 3 เจตจำนงส่วนตัวเช่นนี้ ผลหารโดยประมาณถึงหนึ่งที่มีส่วนเกิน

ลองมาอีกตัวอย่างตอนนี้ ปล่อยให้มันต้องหาร 27 ด้วย 8 เนื่องจากที่นี่เราจะไม่ได้ผลหารที่แน่นอนที่แสดงเป็นจำนวนเต็ม เราจะมองหาผลหารโดยประมาณ:

27: 8 = 3 และเศษ 3

ข้อผิดพลาดคือ 3 / 8 ซึ่งน้อยกว่าหนึ่ง ซึ่งหมายความว่าพบผลหารโดยประมาณ (3) ได้ถึง 1 รายการที่มีข้อเสียเปรียบ เราแบ่งส่วนต่อไป: เราแบ่งส่วนที่เหลือจาก 3 เป็นสิบ เราได้ 30 ในสิบ; ลองหารด้วย 8

เราอยู่ในที่ส่วนตัวในจุดที่สิบ 3 และในส่วนที่เหลือข. หากเราจำกัดตัวเองไว้ที่หมายเลข 3.3 โดยเฉพาะ และละทิ้ง 6 ส่วนที่เหลือ เราจะอนุญาตให้มีข้อผิดพลาดน้อยกว่าหนึ่งในสิบ ทำไม เพราะจะได้ผลหารที่แน่นอนเมื่อเราบวกกับ 3.3 ผลลัพธ์ของการหาร 6 ในสิบด้วย 8; จากส่วนนี้จะเป็น 6/80 ซึ่งน้อยกว่าหนึ่งในสิบ (ตรวจสอบ!) ดังนั้น หากเราจำกัดตัวเองให้เหลือหนึ่งในสิบของผลหาร เราก็สามารถพูดได้ว่าเราพบผลหารแล้ว แม่นยำถึงหนึ่งในสิบ(มีข้อเสีย).

ทำการหารต่อไปเพื่อหาทศนิยมอีกหนึ่งตำแหน่ง ในการทำเช่นนี้ เราแบ่ง 6 ในสิบเป็นร้อย และรับ 60 ในร้อย ลองหารด้วย 8

ในที่ส่วนตัวที่สามมันกลายเป็น 7 และในส่วนที่เหลือ 4 ในร้อย; หากเราทิ้งมัน แสดงว่าเรายอมให้ผิดพลาดน้อยกว่าหนึ่งในร้อย เพราะ 4 ในร้อยหารด้วย 8 นั้นน้อยกว่าหนึ่งในร้อย ในกรณีเช่นนี้ จะมีการกล่าวถึงผลหาร แม่นยำถึงหนึ่งร้อย(มีข้อเสีย).

ในตัวอย่างที่เรากำลังพิจารณาอยู่ คุณสามารถหาผลหารที่แน่นอน ซึ่งแสดงเป็นเศษส่วนทศนิยม เมื่อต้องการทำเช่นนี้ ก็เพียงพอแล้วที่จะแบ่งเศษที่เหลือ 4 ในร้อยเป็นพันแล้วหารด้วย 8

อย่างไรก็ตาม ในกรณีส่วนใหญ่ มันเป็นไปไม่ได้ที่จะได้รับผลหารที่แน่นอนและเราต้องจำกัดตัวเองให้มีค่าใกล้เคียงกัน ตอนนี้เราจะพิจารณาตัวอย่างดังกล่าว:

40: 7 = 5,71428571...

จุดที่ท้ายตัวเลขแสดงว่าการหารยังไม่สมบูรณ์ กล่าวคือ ความเท่าเทียมกันเป็นค่าโดยประมาณ โดยปกติความเท่าเทียมกันโดยประมาณจะเขียนดังนี้:

40: 7 = 5,71428571.

เราหาผลหารด้วยทศนิยมแปดตำแหน่ง แต่ถ้าไม่ต้องการความแม่นยำมากขนาดนั้น เราสามารถจำกัดตัวเองให้อยู่ในส่วนทั้งหมดของผลหารได้ นั่นคือ ตัวเลข 5 (แม่นยำกว่าคือ 6); เพื่อความแม่นยำที่มากขึ้น ควรพิจารณาหนึ่งในสิบและผลหารที่นำมาเท่ากับ 5.7 ถ้าด้วยเหตุผลบางอย่างความแม่นยำนี้ไม่เพียงพอ เราสามารถหยุดที่ส่วนร้อยและรับ 5.71 เป็นต้น มาเขียนผลหารแต่ละรายการและตั้งชื่อพวกมันกัน

ผลหารโดยประมาณแรกสูงถึง 6

ที่สอง » » » ถึงหนึ่งในสิบ 5.7

ที่สาม » » » มากถึงหนึ่งร้อย 5.71

ที่สี่ » » » มากถึงหนึ่งในพันของ 5.714

ดังนั้น ในการหาผลหารโดยประมาณถึงบางส่วน ตัวอย่างเช่น ทศนิยมตำแหน่งที่ 3 (กล่าวคือ มากถึงหนึ่งในพัน) การหารจะหยุดทันทีที่พบเครื่องหมายนี้ ในกรณีนี้ เราต้องจำกฎที่กำหนดไว้ใน § 40

§ 113. ปัญหาที่ง่ายที่สุดสำหรับความสนใจ

หลังจากศึกษาเศษส่วนทศนิยมแล้ว เราจะแก้ปัญหาเปอร์เซ็นต์เพิ่มอีกเล็กน้อย

ปัญหาเหล่านี้คล้ายกับที่เราแก้ไขในแผนกเศษส่วนธรรมดา แต่ตอนนี้ เราจะเขียนส่วนที่ร้อยเป็นเศษส่วนทศนิยม นั่นคือ โดยไม่มีตัวส่วนกำหนดไว้อย่างชัดเจน

ก่อนอื่น คุณต้องสามารถเปลี่ยนจากเศษส่วนธรรมดาไปเป็นเศษส่วนทศนิยมได้อย่างง่ายดายด้วยตัวส่วน 100 ในการทำเช่นนี้ คุณต้องหารตัวเศษด้วยตัวส่วน:

ตารางด้านล่างแสดงให้เห็นว่าตัวเลขที่มีสัญลักษณ์ % (เปอร์เซ็นต์) ถูกแทนที่ด้วยทศนิยมที่มีตัวส่วนเป็น 100 อย่างไร:

ตอนนี้ขอพิจารณาปัญหาเล็กน้อย

1. การหาเปอร์เซ็นต์ ให้หมายเลข.

ภารกิจที่ 1มีเพียง 1,600 คนอาศัยอยู่ในหมู่บ้านเดียว จำนวนบุตร วัยเรียนเป็น 25% ของ จำนวนทั้งหมดผู้อยู่อาศัย หมู่บ้านนี้มีเด็กวัยเรียนกี่คน?

ในปัญหานี้ คุณต้องหา 25% หรือ 0.25 ของ 1,600 ปัญหาได้รับการแก้ไขโดยการคูณ:

1,600 0.25 = 400 (เด็ก)

ดังนั้น 25% ของ 1,600 คือ 400

เพื่อความเข้าใจที่ชัดเจนของงานนี้ เป็นการดีที่จะระลึกว่าทุก ๆ ร้อยประชากรมีเด็กวัยเรียน 25 คน ดังนั้น ในการหาจำนวนเด็กในวัยเรียนทั้งหมด ก่อนอื่นให้ค้นหาว่ามีกี่ร้อยใน 1600 (16) แล้วคูณ 25 ด้วยจำนวนหลายร้อย (25 x 16 = 400) วิธีนี้ทำให้คุณสามารถตรวจสอบความถูกต้องของโซลูชันได้

ภารกิจที่ 2ธนาคารออมสินให้ผู้ฝาก 2% ของรายได้ต่อปี ผู้ฝากที่ฝากเงินจะได้รับรายได้เท่าใดต่อปี: ก) 200 รูเบิล? ข) 500 รูเบิล? ค) 750 รูเบิล? ง) 1,000 รูเบิล?

ในทั้งสี่กรณีในการแก้ปัญหานั้นจำเป็นต้องคำนวณ 0.02 ของจำนวนที่ระบุนั่นคือ แต่ละตัวเลขเหล่านี้จะต้องคูณด้วย 0.02 มาทำกัน:

ก) 200 0.02 = 4 (รูเบิล)

b) 500 0.02 = 10 (รูเบิล)

c) 750 0.02 = 15 (รูเบิล)

ง) 1,000 0.02 = 20 (รูเบิล)

แต่ละกรณีเหล่านี้สามารถตรวจสอบได้โดยการพิจารณาดังต่อไปนี้ ธนาคารออมสินให้ผู้ฝาก 2% ของรายได้ นั่นคือ 0.02 ของจำนวนเงินที่ออม หากจำนวนเงินคือ 100 รูเบิล ดังนั้น 0.02 ของมันจะเป็น 2 รูเบิล ซึ่งหมายความว่าทุก ๆ ร้อยจะนำผู้ฝาก 2 รูเบิล รายได้. ดังนั้นในแต่ละกรณีที่พิจารณา มันก็เพียงพอแล้วที่จะหาว่ามีกี่ร้อยในจำนวนที่กำหนดและคูณ 2 รูเบิลด้วยจำนวนนี้หลายร้อย ในตัวอย่าง ก) หลายร้อย 2 ดังนั้น

2 2 \u003d 4 (รูเบิล)

ในตัวอย่าง d) หลายร้อยคือ 10 ซึ่งหมายถึง

2 10 \u003d 20 (รูเบิล)

2. การหาตัวเลขตามเปอร์เซ็นต์

ภารกิจที่ 1ในฤดูใบไม้ผลิ โรงเรียนมีนักเรียน 54 คน ซึ่งคิดเป็น 6% ของจำนวนนักเรียนทั้งหมด สมัยก่อนมีนักเรียนกี่คน ปีการศึกษา?

ให้เราชี้แจงความหมายของปัญหานี้ก่อน โรงเรียนมีนักเรียน 54 คน ซึ่งคิดเป็น 6% ของจำนวนนักเรียนทั้งหมด หรืออีกนัยหนึ่งคือ 6 ในร้อย (0.06) ของนักเรียนทั้งหมดในโรงเรียน เราจึงรู้จักนักเรียนบางคน แสดงเป็นตัวเลข(54) และเศษส่วน (0.06) จากเศษส่วนนี้ เราต้องหาจำนวนเต็ม ดังนั้นต่อหน้าเรา งานธรรมดาเพื่อหาตัวเลขด้วยเศษส่วน (§90 p.6) ปัญหาประเภทนี้แก้ไขโดยการแบ่ง:

ซึ่งหมายความว่ามีนักเรียน 900 คนในโรงเรียน

การตรวจสอบปัญหาดังกล่าวมีประโยชน์โดยการแก้ปัญหาผกผันเช่น หลังจากแก้ปัญหาแล้วอย่างน้อยคุณควรแก้ปัญหาประเภทแรก (หาเปอร์เซ็นต์ของตัวเลขที่กำหนด): นำตัวเลขที่พบ ( 900) ตามที่กำหนดและหาเปอร์เซ็นต์ที่ระบุในปัญหาที่แก้ไขได้จากมัน กล่าวคือ:

900 0,06 = 54.

ภารกิจที่ 2ครอบครัวใช้เงิน 780 รูเบิลเป็นค่าอาหารในเดือนนั้น ซึ่งคิดเป็น 65% ของรายได้ต่อเดือนของพ่อ กำหนดรายได้ต่อเดือนของเขา

งานนี้มีความหมายเดียวกับงานก่อนหน้านี้ มันให้ส่วนหนึ่งของรายได้ต่อเดือนซึ่งแสดงเป็นรูเบิล (780 รูเบิล) และระบุว่าส่วนนี้คือ 65% หรือ 0.65 ของรายได้ทั้งหมด และที่ต้องการคือรายได้ทั้งหมด:

780: 0,65 = 1 200.

ดังนั้นรายได้ที่ต้องการคือ 1200 รูเบิล

3. การหาเปอร์เซ็นต์ของตัวเลข

ภารกิจที่ 1ที่ ห้องสมุดโรงเรียนเพียง 6,000 เล่ม ในจำนวนนี้มีหนังสือเกี่ยวกับคณิตศาสตร์ 1,200 เล่ม เปอร์เซ็นต์ หนังสือคณิตศาสตร์ทำขึ้นจากหนังสือทั้งหมดในห้องสมุด?

เราได้พิจารณาปัญหาประเภทนี้แล้ว (§97) และได้ข้อสรุปว่าในการคำนวณเปอร์เซ็นต์ของตัวเลขสองตัวนั้น คุณต้องหาอัตราส่วนของตัวเลขเหล่านี้แล้วคูณด้วย 100

ในปัญหาของเรา เราต้องหา เปอร์เซ็นต์ตัวเลข 1,200 และ 6,000

ก่อนอื่นเราหาอัตราส่วนของพวกเขาแล้วคูณด้วย 100:

ดังนั้น เปอร์เซ็นต์ของตัวเลข 1,200 และ 6,000 คือ 20 กล่าวอีกนัยหนึ่ง หนังสือคณิตศาสตร์คิดเป็น 20% ของจำนวนหนังสือทั้งหมด

ในการตรวจสอบเราแก้ ปัญหาผกผัน: พบ 20% ของ 6,000:

6 000 0,2 = 1 200.

ภารกิจที่ 2โรงงานควรได้รับถ่านหิน 200 ตัน ส่งมอบแล้ว 80 ตัน ถ่านหินส่งถึงโรงงานกี่เปอร์เซ็นต์?

ปัญหานี้ถามว่าเปอร์เซ็นต์หนึ่ง (80) เป็นของอีกจำนวนหนึ่ง (200) อัตราส่วนของตัวเลขเหล่านี้จะเท่ากับ 80/200 ลองคูณด้วย 100:

ซึ่งหมายความว่ามีการส่งมอบถ่านหิน 40%

สี่เหลี่ยมผืนผ้า?

วิธีการแก้. ตั้งแต่ 2.88 dm2 \u003d 288 cm2 และ 0.8 dm \u003d 8 cm ความยาวของสี่เหลี่ยมผืนผ้าคือ 288: 8 นั่นคือ 36 cm \u003d 3.6 dm เราพบตัวเลข 3.6 โดยที่ 3.6 0.8 = 2.88 มันคือผลหารของ 2.88 หารด้วย 0.8

พวกเขาเขียน: 2.88: 0.8 = 3.6

คำตอบ 3.6 สามารถหาได้โดยไม่ต้องแปลงเดซิเมตรเป็นเซนติเมตร ในการทำเช่นนี้ ให้คูณตัวหาร 0.8 และเงินปันผล 2.88 ด้วย 10 (นั่นคือ ย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลัก) และหาร 28.8 ด้วย 8 อีกครั้ง เราได้: 28.8: 8 = 3.6

ในการหารตัวเลขด้วยเศษส่วนทศนิยม คุณต้อง:

1) ในตัวหารและตัวหาร ให้เลื่อนเครื่องหมายจุลภาคไปทางขวาตามจำนวนหลักที่มีหลังจุดทศนิยมในตัวหาร
2) หลังจากนั้นทำการหารด้วยจำนวนธรรมชาติ

ตัวอย่าง 1หาร 12.096 ด้วย 2.24 ย้ายเครื่องหมายจุลภาค 2 หลักไปทางขวาในตัวปันผลและตัวหาร เราได้ตัวเลข 1209.6 และ 224 ตั้งแต่ 1209.6: 224 = 5.4 จากนั้น 12.096: 2.24 = 5.4

จากตัวอย่างที่ 1 และ 2 จะเห็นได้ว่าเมื่อจำนวนหารด้วยเศษส่วนที่ไม่เหมาะสม จำนวนนี้จะลดลงหรือไม่เปลี่ยนแปลง และเมื่อหารด้วยเศษส่วนทศนิยมที่เหมาะสม จะเพิ่มขึ้น: 12.096\u003e 5.4 และ 4.5< 36.

หาร 2.467 ด้วย 0.01 หลังจากย้ายเครื่องหมายจุลภาคในตัวปันผลและตัวหารด้วยเลข 2 หลักไปทางขวา เราจะได้ผลหารเป็น 246.7: 1 นั่นคือ 246.7

ดังนั้น และ 2.467: 0.01 = 246.7 จากที่นี่เราได้รับกฎ:

ในการหารทศนิยมด้วย 0.1; 0.01; 0.001 จำเป็นต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยตัวเลขมากที่สุดเท่าที่มีเลขศูนย์อยู่ด้านหน้าหน่วยในตัวหาร (นั่นคือ คูณด้วย 10, 100, 1000)

หากมีจำนวนไม่เพียงพอ ต้องระบุต่อท้ายก่อน เศษส่วนศูนย์ไม่กี่

ตัวอย่างเช่น 56.87: 0.0001 = 56.8700: 0.0001 = 568,700

กำหนดกฎการหารเศษส่วนทศนิยม: ด้วยเศษทศนิยม โดย 0.1; 0.01; 0.001.
จำนวนใดที่สามารถคูณเพื่อแทนที่การหารด้วย 0.01?

1443. หาผลหารและทดสอบโดยการคูณ:

ก) 0.8: 0.5; ข) 3.51: 2.7; ค) 14.335: 0.61.

1444. ค้นหาผลหารและทดสอบตามการหาร:

ก) 0.096: 0.12; ข) 0.126: 0.9; ค) 42.105: 3.5.

ก) 7.56: 0.6; g) 6.944: 3.2; ม.) 14.976: 0.72;
ข) 0.161: 0.7; ซ) 0.0456: 3.8; o) 168.392: 5.6;
ค) 0.468: 0.09; ผม) 0.182: 1.3; น) 24.576: 4.8;
ง) 0.00261: 0.03; ญ) 131.67: 5.7; ป) 16.51: 1.27;
จ) 0.824: 0.8; ฎ) 189.54: 0.78; ค) 46.08: 0.384;
จ) 10.5: 3.5; ม.) 636: 0.12; ท) 22.256: 20.8.

1446. เขียนนิพจน์:

ก) 10 - 2.4x = 3.16; จ) 4.2p - p = 5.12;
b) (y + 26.1) 2.3 = 70.84; ฉ) 8.2t - 4.4t = 38.38;
ค) (z - 1.2): 0.6 = 21.1; g) (10.49 - s): 4.02 = 0.805;
ง) 3.5m + m = 9.9; ชั่วโมง) 9k - 8.67k = 0.6699

1460 มีน้ำมันเบนซิน 119.88 ตันในสองถัง ในถังแรกมีน้ำมันเบนซินมากกว่าถังที่สอง 1.7 เท่า แต่ละถังมีน้ำมันเบนซินเท่าไหร่?

1461. เก็บเกี่ยวกะหล่ำปลีได้ 87.36 ตันจากสามแปลง ในเวลาเดียวกัน มีการเก็บรวบรวมจากส่วนแรกมากกว่า 1.4 เท่า และจากส่วนที่สองมากกว่าส่วนที่สาม 1.8 เท่า แต่ละแปลงเก็บกะหล่ำปลีได้กี่ตัน?

1462. จิงโจ้ต่ำกว่ายีราฟ 2.4 เท่า และยีราฟสูงกว่าจิงโจ้ 2.52 เมตร ยีราฟสูงเท่าไหร่และจิงโจ้สูงเท่าไหร่

1463 คนเดินเท้าสองคนอยู่ห่างจากกัน 4.6 กม. พวกเขาเดินไปหากันและพบกันใน 0.8 ชั่วโมง หาความเร็วของคนเดินเท้าแต่ละคนถ้าความเร็วของหนึ่งในนั้นคือ 1.3 เท่าของความเร็วของอีกคนหนึ่ง

1464. ทำดังต่อไปนี้:

ก) (130.2 - 30.8) 2.8 - 21.84:
ข) 8.16: (1.32 + 3.48) - 0.345;
ค) 3.712: (7 - 3.8) + 1.3 (2.74 + 0.66);
ง) (3.4: 1.7 + 0.57: 1.9) 4.9 + 0.0825: 2.75;
จ) (4.44: 3.7 - 0.56: 2.8): 0.25 - 0.8;
ฉ) 10.79: 8.3 0.7 - 0.46 3.15: 6.9.

1465. จินตนาการ เศษส่วนร่วมเป็นทศนิยมและหาค่า สำนวน:

1466. คำนวณด้วยวาจา:

ก) 25.5: 5; ข) 9 0.2; ค) 0.3: 2; ง) 6.7 - 2.3;
1,5: 3; 1 0,1; 2:5; 6- 0,02;
4,7: 10; 16 0,01; 17,17: 17; 3,08 + 0,2;
0,48: 4; 24 0,3; 25,5: 25; 2,54 + 0,06;
0,9:100; 0,5 26; 0,8:16; 8,2-2,2.

1467. หางาน:

ก) 0.1 0.1; ง) 0.4 0.4; กรัม) 0.7 0.001;
ข) 1.3 1.4; จ) 0.06 0.8; ซ) 100 0.09;
ค) 0.3 0.4; ฉ) 0.01 100; ผม) 0.3 0.3 0.3

1468. ค้นหา: 0.4 ของจำนวน 30; 0.5 หมายเลข 18; 0.1 หมายเลข 6.5; 2.5 หมายเลข 40; 0.12 จำนวน 100; 0.01 จาก 1,000

1469. ความหมายของนิพจน์ 5683.25a กับ a = 10 คืออะไร; 0.1; 0.01; 100; 0.001; 1,000; 0.00001?

1470. ลองนึกดูว่าตัวเลขใดเป็นตัวเลขที่แน่นอน ซึ่งเป็นค่าประมาณ:

ก) มีนักเรียน 32 คนในชั้นเรียน
b) ระยะทางจากมอสโกถึงเคียฟคือ 900 กม.
c) parallelepiped มี 12 ขอบ
ง) ความยาวของโต๊ะ 1.3 ม.
จ) ประชากรของมอสโกคือ 8 ล้านคน
ฉ) 0.5 กก. แป้งในถุง;
g) พื้นที่ของเกาะคิวบาคือ 105,000 km2;
ซ) มี 10,000 เล่มในห้องสมุดโรงเรียน
i) หนึ่งช่วงเท่ากับ 4 vershok และ vershok เท่ากับ 4.45 ซม. (vershok
ความยาวของพรรคนิ้วชี้)

1471. ค้นหาวิธีแก้ปัญหาความไม่เท่าเทียมกันสามวิธี:

ก) 1.2< х < 1,6; в) 0,001 < х < 0,002;
ข) 2.1< х< 2,3; г) 0,01 <х< 0,011.

1472. เปรียบเทียบโดยไม่ต้องคำนวณค่าของนิพจน์:

ก) 24 0.15 และ (24 - 15): 100;

b) 0.084 0.5 และ (84 5): 10,000
อธิบายคำตอบของคุณ.

1473. ปัดเศษตัวเลข:

1474. ดำเนินการแผนก:

ก) 22.7: 10; 23.3:10; 3.14:10; 9.6:10;
ข) 304: 100; 42.5:100; 2.5:100; 0.9:100; 0.03:100;
ค) 143.4: 12; 1.488:124; 0.3417: 34; 159.9:235; 65.32:568.

1475 นักปั่นจักรยานออกจากหมู่บ้านด้วยความเร็ว 12 กม./ชม. หลังจากผ่านไป 2 ชั่วโมง นักปั่นจักรยานอีกคนก็ออกจากหมู่บ้านเดียวกันไปในทิศทางตรงกันข้าม
และความเร็วของวินาทีคือ 1.25 เท่าของความเร็วครั้งแรก ระยะห่างระหว่างพวกเขา 3.3 ชั่วโมงหลังจากนักปั่นคนที่สองออกไปคืออะไร?

1476 ความเร็วของเรือคือ 8.5 กม./ชม. และความเร็วกระแสน้ำ 1.3 กม./ชม. เรือจะเดินทางไปกับกระแสได้ไกลแค่ไหนใน 3.5 ชั่วโมง? เรือจะเดินทางต้นน้ำได้ไกลแค่ไหนใน 5.6 ชั่วโมง?

1477 โรงงานผลิตชิ้นส่วน 3.75,000 ชิ้นและขายในราคา 950 รูเบิล ชิ้น ค่าใช้จ่ายของโรงงานสำหรับการผลิตส่วนหนึ่งมีจำนวน 637.5 รูเบิล หากำไรจากโรงงานจากการขายชิ้นส่วนเหล่านี้

1478. ความกว้างของสี่เหลี่ยมด้านขนานคือ 7.2 ซม. ซึ่งก็คือ หาปริมาตรของช่องนี้แล้วปัดคำตอบเป็นจำนวนเต็มที่ใกล้เคียงที่สุด

1479. สมเด็จพระสันตะปาปาคาร์โลสัญญาว่าจะให้ Piero 4 ทหารทุกวัน และ Pinocchio 1 ทหารในวันแรก และอีก 1 ทหารทุกวันถัดไปถ้าเขาประพฤติตนดี Pinocchio ขุ่นเคือง: เขาตัดสินใจว่าไม่ว่าเขาจะพยายามมากแค่ไหนก็ตามเขาก็ไม่สามารถได้รับ Solido ได้มากเท่ากับ Pierrot ลองคิดดูว่าพิน็อกคิโอพูดถูกหรือไม่

1480 กระดาน 231 ม. ต่อตู้ 3 ตู้และชั้นหนังสือ 9 ชั้น และวัสดุเข้าตู้มากกว่าชั้นวางถึง 4 เท่า บอร์ดไปที่ตู้กี่เมตรและถึงชั้นวางกี่เมตร?

1481. แก้ปัญหา:
1) ตัวเลขแรกคือ 6.3 และเป็นตัวเลขที่สอง ตัวเลขที่สามคือตัวที่สอง ค้นหาตัวเลขที่สองและสาม

2) หมายเลขแรกคือ 8.1 ตัวเลขที่สองมาจากหมายเลขแรกและจากหมายเลขที่สาม ค้นหาตัวเลขที่สองและสาม

1482. ค้นหาค่าของนิพจน์:

1) (7 - 5,38) 2,5;

2) (8 - 6,46) 1,5.

1483. หาค่าของส่วนตัว:

ก) 17.01: 6.3; ง) 1.4245: 3.5; ก) 0.02976: 0.024;
ข) 1.598: 4.7; จ) 193.2: 8.4; ซ) 11.59: 3.05;
ค) 39.156: 7.8; จ) 0.045: 0.18; ผม) 74.256: 18.2.

1484 เส้นทางจากบ้านไปโรงเรียน 1.1 กม. สาวครอบคลุมเส้นทางนี้ใน 0.25 ชั่วโมง สาวเดินเร็วแค่ไหน?

1485. ในอพาร์ตเมนต์แบบสองห้อง พื้นที่ของห้องหนึ่งคือ 20.64 ตร.ม. และพื้นที่ของอีกห้องหนึ่งน้อยกว่า 2.4 เท่า หาพื้นที่ของทั้งสองห้องนี้ด้วยกัน

1486 เครื่องยนต์ใช้เชื้อเพลิง 111 ลิตรใน 7.5 ชั่วโมง เครื่องยนต์จะใช้น้ำมันกี่ลิตรใน 1.8 ชั่วโมง?
1487 ชิ้นส่วนโลหะที่มีปริมาตร 3.5 dm3 มีมวล 27.3 กก. อีกชิ้นทำด้วยโลหะชนิดเดียวกันมีน้ำหนัก 10.92 กก. ส่วนที่สองมีปริมาตรเท่าใด

1488 น้ำมันเบนซิน 2.28 ตันถูกเทลงในถังผ่านท่อสองท่อ น้ำมันเบนซิน 3.6 ตันต่อชั่วโมงไหลผ่านท่อแรกและเปิดได้ 0.4 ชั่วโมง น้ำมันเบนซิน 0.8 ตันน้อยกว่าท่อแรกเข้ามาต่อชั่วโมงผ่านท่อที่สอง ท่อที่สองเปิดนานแค่ไหน?

1489. แก้สมการ:

ก) 2.136: (1.9 - x) = 7.12; c) 0.2t + 1.7t - 0.54 = 0.22;
b) 4.2 (0.8 + y) = 8.82; ง) 5.6g - 2z - 0.7z + 2.65 = 7.

1490. สินค้าที่มีน้ำหนัก 13.3 ตันถูกแจกจ่ายให้กับรถสามคัน รถคันแรกบรรทุกได้มากกว่า 1.3 เท่าและคันที่สอง - มากกว่ารถคันที่สาม 1.5 เท่า รถแต่ละคันบรรทุกสินค้าได้กี่ตัน?

1491. คนเดินเท้าสองคนออกจากที่เดียวกันพร้อมกันในทิศทางตรงกันข้าม หลังจาก 0.8 ชั่วโมง ระยะห่างระหว่างพวกเขาเท่ากับ 6.8 กม. ความเร็วของคนเดินถนนคนหนึ่งคือ 1.5 เท่าของความเร็วของอีกคนหนึ่ง หาความเร็วของคนเดินเท้าแต่ละคน

1492. ทำสิ่งต่อไปนี้:

ก) (21.2544: 0.9 + 1.02 3.2): 5.6;
b) 4.36: (3.15 + 2.3) + (0.792 - 0.78) 350;
ค) (3.91: 2.3 5.4 - 4.03) 2.4;
ง) 6.93: (0.028 + 0.36 4.2) - 3.5

พ.ศ. 1493 หมอมาโรงเรียนและนำซีรั่ม 0.25 กก. มาฉีดวัคซีน เขาสามารถฉีดเด็กได้กี่คนหากการฉีดแต่ละครั้งต้องใช้เซรั่ม 0.002 กิโลกรัม?

1494 นำขนมปังขิง 2.8 ตันมาที่ร้าน ก่อนอาหารกลางวันจะขายคุกกี้ขนมปังขิงเหล่านี้ ขายขนมปังขิงเหลือกี่ตัน?

1495. ผ้าผืนหนึ่งถูกตัดออก 5.6 ม. ถ้าผ้าชิ้นนี้ถูกตัดออกจะมีผ้ากี่เมตร?

น. VILENKIN, V. I. ZHOKHOV, A. S. CHESNOKOV, S. I. SHVARTSBURD, คณิตศาสตร์เกรด 5, ตำราเรียนสำหรับสถาบันการศึกษา

ในบทความนี้ เราจะวิเคราะห์การดำเนินการที่สำคัญดังกล่าวโดยใช้เศษส่วนทศนิยมเป็นการหาร ขั้นแรก เรากำหนดหลักการทั่วไป จากนั้นเราจะวิเคราะห์วิธีหารเศษส่วนทศนิยมตามคอลัมน์ให้เป็นเศษส่วนอื่นๆ และให้เป็นจำนวนธรรมชาติ ต่อไป เราจะวิเคราะห์การหารเศษส่วนธรรมดาเป็นทศนิยมและในทางกลับกัน และในตอนท้าย เราจะมาดูวิธีการหารเศษส่วนที่ลงท้ายด้วย 0, 1, 0, 01, 100, 10 เป็นต้น

ที่นี่เราใช้เฉพาะกรณีที่มีเศษส่วนบวก หากมีเครื่องหมายลบก่อนเศษส่วน คุณจำเป็นต้องศึกษาเนื้อหาเกี่ยวกับการหารจำนวนตรรกยะและจำนวนจริง

Yandex.RTB R-A-339285-1

เศษส่วนทศนิยมทั้งจำนวนจำกัดและเป็นระยะเป็นเพียงรูปแบบพิเศษของการเขียนเศษส่วนธรรมดา ดังนั้นหลักการเดียวกันนี้จึงนำไปใช้กับเศษส่วนสามัญที่สอดคล้องกัน ดังนั้นเราจึงลดกระบวนการทั้งหมดของการหารเศษส่วนทศนิยมเพื่อแทนที่ด้วยทศนิยมธรรมดา ตามด้วยการคำนวณด้วยวิธีที่เรารู้จักอยู่แล้ว มาดูตัวอย่างเฉพาะกัน

ตัวอย่าง 1

หาร 1.2 ด้วย 0.48

วิธีการแก้

เราเขียนเศษส่วนทศนิยมในรูปของเศษส่วนสามัญ เราจะสามารถ:

1 , 2 = 12 10 = 6 5

0 , 48 = 48 100 = 12 25 .

ดังนั้นเราต้องหาร 6 5 ด้วย 12 25 . พวกเราเชื่อว่า:

1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2

จากผลลัพธ์เศษส่วนที่ไม่ถูกต้อง คุณสามารถเลือกส่วนทั้งหมดและรับจำนวนคละ 2 1 2 หรือคุณสามารถแสดงเป็นเศษส่วนทศนิยมเพื่อให้ตรงกับตัวเลขเดิม: 5 2 \u003d 2, 5 วิธีการทำเช่นนี้เราได้เขียนไว้ก่อนหน้านี้

ตอบ: 1 , 2: 0 , 48 = 2 , 5 .

ตัวอย่าง 2

คำนวณจำนวนที่จะเป็น 0 , (504) 0 , 56

วิธีการแก้

อันดับแรก เราต้องแปลงเศษส่วนทศนิยมเป็นระยะเป็นเศษส่วนธรรมดา

0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111

หลังจากนั้น เราจะแปลเศษส่วนทศนิยมสุดท้ายเป็นรูปแบบอื่น: 0, 56 = 56 100 ตอนนี้เรามีตัวเลขสองตัวซึ่งจะทำให้เราสามารถคำนวณที่จำเป็นได้ง่าย:

0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 100 56 = 100 111

เราได้ผลลัพธ์ที่เราสามารถแปลงเป็นทศนิยมได้ เมื่อต้องการทำสิ่งนี้ ให้แบ่งตัวเศษด้วยตัวส่วนโดยใช้วิธีคอลัมน์:

ตอบ: 0 , (504) : 0 , 56 = 0 , (900) .

หากในตัวอย่างการหาร เราพบเศษส่วนทศนิยมที่ไม่เป็นคาบ เราจะทำตัวต่างไปเล็กน้อย เราไม่สามารถนำมันมาเป็นเศษส่วนธรรมดาทั่วไปได้ ดังนั้นเมื่อทำการหาร เราต้องปัดเศษขึ้นเป็นตัวเลขที่แน่นอนก่อน การดำเนินการนี้จะต้องดำเนินการทั้งกับเงินปันผลและตัวหาร: เราจะปัดเศษเศษส่วนที่มีอยู่หรือเป็นงวดที่มีอยู่เพื่อความถูกต้อง

ตัวอย่างที่ 3

หาเท่าไหร่จะได้เป็น 0, 779 ... / 1, 5602.

วิธีการแก้

ก่อนอื่น เราปัดเศษทั้งสองส่วนให้เป็นร้อย นี่คือวิธีที่เราเปลี่ยนจากเศษส่วนที่ไม่เกิดซ้ำแบบอนันต์ไปเป็นทศนิยมจำกัดจำนวน:

0 , 779 … ≈ 0 , 78

1 , 5602 ≈ 1 , 56

เราสามารถคำนวณต่อและรับผลลัพธ์โดยประมาณ: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78100: 156100 = 78100 100156 = 78156 = 12 = 0.5

ความแม่นยำของผลลัพธ์จะขึ้นอยู่กับระดับของการปัดเศษ

ตอบ: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .

วิธีหารจำนวนธรรมชาติด้วยทศนิยมและกลับกัน

วิธีการหารในกรณีนี้เกือบจะเหมือนกัน: เราแทนที่เศษส่วนจำกัดและเชิงคาบด้วยเศษธรรมดา และปัดเศษอนันต์ที่ไม่ใช่คาบออก เริ่มจากตัวอย่างการหารด้วยจำนวนธรรมชาติและเศษส่วนทศนิยม

ตัวอย่างที่ 4

หาร 2.5 ด้วย 45

วิธีการแก้

ลองนำ 2, 5 มาอยู่ในรูปของเศษส่วนสามัญ: 255 10 \u003d 51 2 ต่อไป เราแค่ต้องหารมันด้วยจำนวนธรรมชาติ เรารู้แล้วว่าต้องทำอย่างไร:

25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30

หากเราแปลผลลัพธ์เป็นสัญกรณ์ทศนิยม เราก็จะได้ 0 , 5 (6)

ตอบ: 25 , 5: 45 = 0 , 5 (6) .

วิธีการหารด้วยคอลัมน์นั้นดีไม่เพียงแต่สำหรับจำนวนธรรมชาติเท่านั้น โดยการเปรียบเทียบ เราสามารถใช้มันเป็นเศษส่วนได้เช่นกัน ด้านล่างเราจะระบุลำดับของการกระทำที่ต้องทำเพื่อสิ่งนี้

คำจำกัดความ 1

ในการหารคอลัมน์เศษส่วนทศนิยมด้วยจำนวนธรรมชาติ คุณต้อง:

1. เพิ่มศูนย์สองสามตัวให้กับเศษส่วนทศนิยมทางด้านขวา (สำหรับการหาร เราสามารถเพิ่มจำนวนเท่าใดก็ได้ที่เราต้องการ)

2. หารเศษส่วนทศนิยมด้วยจำนวนธรรมชาติโดยใช้อัลกอริทึม เมื่อการหารส่วนจำนวนเต็มของเศษส่วนสิ้นสุดลง เราจะใส่เครื่องหมายจุลภาคในผลหารที่เป็นผลลัพธ์แล้วนับต่อไป

ผลลัพธ์ของการหารดังกล่าวอาจเป็นเศษส่วนทศนิยมที่มีขอบเขตจำกัดหรือเป็นช่วงอนันต์ก็ได้ ขึ้นอยู่กับส่วนที่เหลือ: หากเป็นศูนย์ ผลลัพธ์จะมีขอบเขต และหากส่วนที่เหลือเริ่มซ้ำ คำตอบจะเป็นเศษส่วนเป็นระยะ

ยกตัวอย่างงานสองสามอย่างและลองทำขั้นตอนเหล่านี้ด้วยตัวเลขเฉพาะ

ตัวอย่างที่ 5

คำนวณว่าจะได้เท่าไหร่ 65 , 14 4 .

วิธีการแก้

เราใช้วิธีคอลัมน์ ในการทำเช่นนี้ ให้บวกเลขศูนย์สองตัวเข้ากับเศษส่วนแล้วได้เศษส่วนทศนิยม 65, 1400 ซึ่งจะเท่ากับค่าเดิม ตอนนี้เราเขียนคอลัมน์สำหรับการหารด้วย 4:

ผลลัพธ์ที่ได้จะเป็นผลมาจากการหารส่วนจำนวนเต็มที่ต้องการ เราใส่เครื่องหมายจุลภาคคั่นและดำเนินการต่อ:

เรามาถึงศูนย์ที่เหลือแล้ว กระบวนการหารจึงเสร็จสิ้น

ตอบ: 65 , 14: 4 = 16 , 285 .

ตัวอย่างที่ 6

หาร 164.5 ด้วย 27.

วิธีการแก้

เราแบ่งส่วนเศษส่วนก่อนและรับ:

เราแยกตัวเลขผลลัพธ์ด้วยเครื่องหมายจุลภาคแล้วหารต่อ:

เราเห็นว่าส่วนที่เหลือเริ่มทำซ้ำเป็นระยะ และตัวเลขเก้า สอง และห้าเริ่มสลับกันในความฉลาด เราจะหยุดตรงนั้นและเขียนคำตอบเป็นเศษส่วนเป็นระยะ 6, 0 (925) .

ตอบ: 164 , 5: 27 = 6 , 0 (925) .

การหารดังกล่าวสามารถลดขั้นตอนในการค้นหาเศษส่วนทศนิยมส่วนตัวและจำนวนธรรมชาติที่อธิบายไว้ข้างต้น ในการทำเช่นนี้ เราต้องคูณเงินปันผลและตัวหารด้วย 10, 100 เป็นต้น เพื่อให้ตัวหารกลายเป็นจำนวนธรรมชาติ จากนั้นเราดำเนินการตามลำดับการกระทำข้างต้น วิธีนี้เป็นไปได้เนื่องจากคุณสมบัติของการหารและการคูณ ในรูปแบบตัวอักษร เราเขียนมันแบบนี้:

a: b = (a 10) : (b 10) , a: b = (a 100) : (b 100) เป็นต้น

มากำหนดกฎกัน:

คำจำกัดความ 2

ในการหารเศษส่วนทศนิยมด้วยทศนิยมอื่น คุณต้อง:

1. ย้ายเครื่องหมายจุลภาคในตัวปันผลและตัวหารไปทางขวาด้วยจำนวนอักขระที่จำเป็นในการเปลี่ยนตัวหารให้เป็นจำนวนธรรมชาติ หากไม่มีสัญญาณเพียงพอในการจ่ายเงินปันผล เราจะบวกศูนย์ทางด้านขวา

2. หลังจากนั้น เราหารเศษส่วนด้วยคอลัมน์ตามจำนวนธรรมชาติที่ได้

ลองดูที่ปัญหาเฉพาะ

ตัวอย่าง 7

หาร 7, 287 ด้วย 2, 1

วิธีแก้ไข: ในการทำให้ตัวหารเป็นจำนวนธรรมชาติ เราต้องย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งอักขระ เราก็เลยหารเศษส่วนทศนิยม 72, 87 ด้วย 21. ลองเขียนตัวเลขที่ได้รับในคอลัมน์แล้วคำนวณ

ตอบ: 7 , 287: 2 , 1 = 3 , 47

ตัวอย่างที่ 8

คำนวณ 16 , 3 0 , 021 .

วิธีการแก้

เราจะต้องย้ายเครื่องหมายจุลภาคเป็นสามหลัก มีตัวเลขไม่เพียงพอในตัวหารสำหรับสิ่งนี้ ซึ่งหมายความว่าคุณต้องใช้เลขศูนย์เพิ่มเติม เราคิดว่าผลลัพธ์ที่ได้จะเป็น:

เราเห็นการทำซ้ำเป็นระยะของสารตกค้าง 4 , 19 , 1 , 10 , 16 , 13 ผลหารจะทำซ้ำ 1 , 9 , 0 , 4 , 7 และ 5 จากนั้นผลลัพธ์ของเราคือทศนิยมเป็นระยะ 776 , (190476)

ตอบ: 16 , 3: 0 , 021 = 776 , (190476)

วิธีที่อธิบายโดยเราช่วยให้คุณทำสิ่งที่ตรงกันข้าม นั่นคือ หารจำนวนธรรมชาติด้วยเศษส่วนทศนิยมสุดท้าย เรามาดูกันว่ามันทำอย่างไร

ตัวอย่างที่ 9

คำนวณจำนวนที่จะเป็น 3 5 , 4 .

วิธีการแก้

แน่นอน เราจะต้องย้ายเครื่องหมายจุลภาคไปทางขวาทีละอักขระ หลังจากนั้นเราสามารถเริ่มหาร 30 , 0 ด้วย 54 . มาเขียนข้อมูลในคอลัมน์และคำนวณผลลัพธ์กัน:

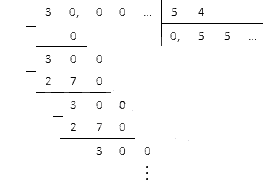
การทำซ้ำส่วนที่เหลือทำให้เราได้ตัวเลข 0 , (5) ซึ่งเป็นทศนิยมเป็นระยะ

ตอบ: 3: 5 , 4 = 0 , (5) .

วิธีหารทศนิยมด้วย 1000, 100, 10 เป็นต้น

ตามกฎที่ศึกษาแล้วสำหรับการหารเศษส่วนธรรมดาหารเศษส่วนเป็นหมื่นหลักพันคล้ายกับการคูณด้วย 1/1000, 1/100, 1/10 เป็นต้น ปรากฎว่าทำการหารใน กรณีนี้เพียงย้ายเครื่องหมายจุลภาคไปยังจำนวนหลักที่ต้องการ หากมีจำนวนค่าไม่เพียงพอในการถ่ายโอน คุณต้องเพิ่มจำนวนศูนย์ที่ต้องการ

ตัวอย่าง 10

ดังนั้น 56, 21: 10 = 5, 621 และ 0, 32: 100,000 = 0, 0000032

ในกรณีของทศนิยมอนันต์ เราก็ทำเช่นเดียวกัน

ตัวอย่าง 11

ตัวอย่างเช่น 3 , (56) : 1000 = 0 , 003 (56) และ 593 , 374 ... : 100 = 5 , 93374 ... .

วิธีหารทศนิยมด้วย 0.001, 0.01, 0.1 เป็นต้น

โดยใช้กฎเดียวกัน เราสามารถหารเศษส่วนด้วยค่าที่ระบุได้ การกระทำนี้จะคล้ายกับการคูณด้วย 1000 , 100 , 10 ตามลำดับ ในการดำเนินการนี้ เราย้ายเครื่องหมายจุลภาคเป็นตัวเลขหนึ่ง สอง หรือสามหลัก ขึ้นอยู่กับเงื่อนไขของปัญหา และเพิ่มศูนย์หากมีตัวเลขในตัวเลขไม่เพียงพอ

ตัวอย่างที่ 12

ตัวอย่างเช่น 5, 739: 0, 1 = 57, 39 และ 0, 21: 0, 00001 = 21,000

กฎนี้ยังใช้กับทศนิยมอนันต์ เราแนะนำให้คุณระมัดระวังเฉพาะช่วงเวลาของเศษส่วนที่ได้รับในคำตอบเท่านั้น

ดังนั้น 7 , 5 (716) : 0 , 01 = 757 , (167) เพราะหลังจากที่เราย้ายเครื่องหมายจุลภาคเป็นทศนิยม 7 , 5716716716 ... ตัวเลขสองหลักทางขวา เราได้ 757 , 167167 ... .

ถ้าเรามีเศษส่วนไม่เป็นระยะในตัวอย่าง ทุกอย่างก็จะง่ายขึ้น: 394 , 38283 ... : 0 , 001 = 394382 , 83 ... .

วิธีหารจำนวนคละหรือเศษส่วนร่วมด้วยทศนิยมและในทางกลับกัน

เรายังลดการดำเนินการนี้เป็นการดำเนินการด้วยเศษส่วนธรรมดา เมื่อต้องการทำเช่นนี้ ให้แทนที่ตัวเลขทศนิยมด้วยเศษส่วนธรรมดาที่เกี่ยวข้อง และเขียนจำนวนคละเป็นเศษส่วนที่ไม่เหมาะสม

หากเราหารเศษส่วนที่ไม่ใช่ระยะด้วยจำนวนปกติหรือจำนวนคละ เราต้องทำตรงกันข้าม โดยแทนที่เศษส่วนธรรมดาหรือจำนวนคละด้วยเศษส่วนทศนิยมที่สอดคล้องกัน

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter