พิจารณาตัวอย่างการแบ่ง เศษส่วนทศนิยมในแง่นี้

ตัวอย่าง.

หารทศนิยม 1.2 ด้วยทศนิยม 0.48

วิธีการแก้.

ตอบ:

1,2:0,48=2,5 .

ตัวอย่าง.

หารทศนิยมเป็นระยะ 0.(504) ด้วยทศนิยม 0.56 .

วิธีการแก้.

ลองแปลเศษส่วนทศนิยมเป็นระยะ ๆ เป็นแบบธรรมดา: นอกจากนี้เรายังแปลเศษทศนิยมสุดท้าย 0.56 เป็นทศนิยมธรรมดาเรามี 0.56 \u003d 56/100 ตอนนี้ เราสามารถย้ายจากการหารทศนิยมเดิมเป็นการหารเศษส่วนธรรมดาและเสร็จสิ้นการคำนวณ: .

มาแปลที่ได้รับ เศษส่วนร่วมเป็นเศษส่วนทศนิยมโดยการหารตัวเศษด้วยตัวส่วนด้วยคอลัมน์:

ตอบ:

0,(504):0,56=0,(900) .

หลักการหารเศษส่วนทศนิยมที่ไม่เป็นคาบเป็นอนันต์แตกต่างจากหลักการหารเศษส่วนทศนิยมจำกัดและเป็นระยะ เนื่องจากเศษส่วนทศนิยมที่ไม่ซ้ำกันไม่สามารถแปลงเป็นเศษส่วนธรรมดาได้ การหารเศษส่วนทศนิยมที่ไม่เป็นคาบเป็นอนันต์จะลดลงเหลือเศษส่วนทศนิยมจำกัดซึ่งจะดำเนินการ ปัดเศษตัวเลขจนถึงระดับหนึ่ง ยิ่งกว่านั้น หากหนึ่งในตัวเลขที่ใช้หารเป็นเศษส่วนทศนิยมที่มีจำกัดหรือเป็นคาบ ก็จะถูกปัดเศษให้เป็นตัวเลขเดียวกันกับเศษทศนิยมที่ไม่เป็นคาบด้วย

ตัวอย่าง.

หารทศนิยมที่ไม่เกิดซ้ำแบบอนันต์ 0.779... ด้วยทศนิยมสุดท้าย 1.5602

วิธีการแก้.

ก่อนอื่น คุณต้องปัดเศษทศนิยมเพื่อเปลี่ยนจากการหารเศษส่วนทศนิยมที่ไม่ซ้ำแบบอนันต์ เป็นการหารเศษส่วนทศนิยมที่มีจำกัด เราสามารถปัดเศษเป็นร้อยได้ 0.779…≈0.78 และ 1.5602≈1.56 ดังนั้น 0.779…:1.5602≈0.78:1.56= 78/100:156/100=78/100 100/156= 78/156=1/2=0,5 .

ตอบ:

0,779…:1,5602≈0,5 .

การหารจำนวนธรรมชาติด้วยเศษส่วนทศนิยมและกลับกัน

สาระสำคัญของแนวทางการหารจำนวนธรรมชาติด้วยเศษส่วนทศนิยมและการหารเศษส่วนทศนิยมด้วย ตัวเลขธรรมชาติไม่ต่างจากแก่นแท้ของการหารเศษส่วนทศนิยม นั่นคือ เศษส่วนจำกัดและเศษส่วนเป็นระยะถูกแทนที่ด้วยเศษส่วนธรรมดา และอนันต์ เศษส่วนไม่เป็นระยะจะถูกปัดเศษขึ้น

เพื่อเป็นตัวอย่าง ให้พิจารณาตัวอย่างการหารเศษส่วนทศนิยมด้วยจำนวนธรรมชาติ

ตัวอย่าง.

หารเศษทศนิยม 25.5 ด้วยจำนวนธรรมชาติ 45

วิธีการแก้.

การแทนที่เศษส่วนทศนิยม 25.5 ด้วยเศษส่วนสามัญ 255/10=51/2 การหารจะลดลงจนหารเศษส่วนธรรมดาด้วยจำนวนธรรมชาติ: . เศษส่วนผลลัพธ์ สัญกรณ์ทศนิยมมีรูปแบบ 0.5(6)

ตอบ:

25,5:45=0,5(6) .

การหารเศษส่วนทศนิยมด้วยจำนวนธรรมชาติด้วยคอลัมน์

การหารเศษส่วนทศนิยมสุดท้ายด้วยจำนวนธรรมชาติทำได้โดยสะดวกโดยคอลัมน์หนึ่งโดยการเปรียบเทียบกับการหารด้วยคอลัมน์ของจำนวนธรรมชาติ นี่คือกฎการแบ่ง

ถึง หารทศนิยมด้วยจำนวนธรรมชาติด้วยคอลัมน์, จำเป็น:

• เพิ่มตัวเลขทางขวาสองสามหลักในเศษทศนิยมที่หารได้ 0 (ในระหว่างการหาร ถ้าจำเป็น คุณสามารถเพิ่มศูนย์จำนวนเท่าใดก็ได้ แต่อาจไม่จำเป็นต้องใช้ศูนย์เหล่านี้)
• ทำการหารด้วยคอลัมน์ของเศษส่วนทศนิยมด้วยจำนวนธรรมชาติตามกฎทั้งหมดสำหรับการหารด้วยคอลัมน์ของตัวเลขธรรมชาติ แต่เมื่อการหารส่วนจำนวนเต็มของเศษส่วนทศนิยมเสร็จสมบูรณ์แล้วในส่วนส่วนตัวคุณต้อง ใส่เครื่องหมายจุลภาคและดำเนินการหารต่อ

สมมุติว่าผลจากการหารเศษส่วนทศนิยมจำกัดด้วยจำนวนธรรมชาติ จะได้เศษส่วนทศนิยมสุดท้ายหรือเศษส่วนทศนิยมเป็นคาบอนันต์ก็ได้ แท้จริงแล้วหลังจากหารทศนิยมที่ไม่ใช่ 0 ทั้งหมดแล้ว เงินปันผล, เราจะได้เศษ 0 อย่างใดอย่างหนึ่ง และเราก็ได้เศษทศนิยมสุดท้าย หรือเศษจะเริ่มซ้ำเป็นระยะ และเราจะได้เศษทศนิยมแบบเป็นระยะ

มาจัดการกับความซับซ้อนทั้งหมดของการหารเศษส่วนทศนิยมเป็นจำนวนธรรมชาติด้วยคอลัมน์เมื่อแก้ตัวอย่าง

ตัวอย่าง.

หารทศนิยม 65.14 ด้วย 4 .

วิธีการแก้.

ลองทำการหารเศษส่วนทศนิยมด้วยจำนวนธรรมชาติตามคอลัมน์ ลองบวกเลขศูนย์สองตัวทางด้านขวาในบันทึกของเศษส่วน 65.14 ในขณะที่เราได้เศษทศนิยมเท่ากับ 65.1400 (ดูเศษส่วนทศนิยมที่เท่ากันและไม่เท่ากัน) ตอนนี้คุณสามารถเริ่มหารส่วนจำนวนเต็มของเศษส่วนทศนิยม 65.1400 ด้วยจำนวนธรรมชาติ 4 ด้วยคอลัมน์:

การหารส่วนจำนวนเต็มของเศษทศนิยมเสร็จสมบูรณ์ ที่นี่คุณต้องใส่จุดทศนิยมและทำการหารต่อ:

เรามาเหลือ 0 ในขั้นตอนนี้ การหารด้วยคอลัมน์จะสิ้นสุดลง เป็นผลให้เรามี 65.14:4=16.285

ตอบ:

65,14:4=16,285 .

ตัวอย่าง.

หาร 164.5 ด้วย 27.

วิธีการแก้.

ลองหารเศษส่วนทศนิยมด้วยจำนวนธรรมชาติด้วยคอลัมน์ หลังจากหารส่วนจำนวนเต็มแล้ว จะได้ภาพดังนี้

ตอนนี้เราใส่เครื่องหมายจุลภาคเป็นส่วนตัวและดำเนินการต่อด้วยคอลัมน์:

ตอนนี้เห็นได้ชัดว่าเศษของ 25, 7 และ 16 ได้เริ่มทำซ้ำในขณะที่ตัวเลข 9, 2 และ 5 ถูกทำซ้ำในผลหาร การหารทศนิยม 164.5 ด้วย 27 ทำให้เราได้จุดทศนิยมเป็นระยะ 6.0(925)

ตอบ:

164,5:27=6,0(925) .

การหารเศษส่วนทศนิยมด้วยคอลัมน์

การหารเศษส่วนทศนิยมด้วยเศษส่วนทศนิยมสามารถลดลงได้เป็นการหารเศษส่วนทศนิยมด้วยจำนวนธรรมชาติด้วยคอลัมน์ ในการทำเช่นนี้ เงินปันผลและตัวหารจะต้องคูณด้วยตัวเลข 10 หรือ 100 หรือ 1,000 เป็นต้น เพื่อให้ตัวหารกลายเป็นจำนวนธรรมชาติ แล้วหารด้วยจำนวนธรรมชาติด้วยคอลัมน์ เราสามารถทำได้เนื่องจากคุณสมบัติของการหารและการคูณ เนื่องจาก a:b=(a 10):(b 10) , a:b=(a 100):(b 100) เป็นต้น

กล่าวอีกนัยหนึ่ง หารทศนิยมลงท้ายด้วยทศนิยมลงท้าย, ความต้องการ:

• ในตัวปันผลและตัวหาร ให้ย้ายเครื่องหมายจุลภาคไปทางขวาทีละอักขระตามหลังจุดทศนิยมในตัวหาร ถ้าในขณะเดียวกัน เงินปันผลมีอักขระไม่เพียงพอที่จะย้ายเครื่องหมายจุลภาค คุณต้องเพิ่ม จำนวนเงินที่ต้องการศูนย์ทางด้านขวา
• หลังจากนั้น ทำการหารด้วยคอลัมน์ของเศษส่วนทศนิยมด้วยจำนวนธรรมชาติ

พิจารณาเมื่อแก้ตัวอย่าง การนำกฎนี้ไปหารด้วยเศษส่วนทศนิยม

ตัวอย่าง.

ทำการหารคอลัมน์ 7.287 คูณ 2.1

วิธีการแก้.

ลองย้ายเครื่องหมายจุลภาคในเศษส่วนทศนิยมเหล่านี้ไปทางขวาหนึ่งหลัก ซึ่งจะทำให้เราสามารถไปจากการหารเศษส่วนทศนิยม 7.287 ด้วยเศษทศนิยม 2.1 เพื่อหารเศษส่วนทศนิยม 72.87 ด้วยจำนวนธรรมชาติ 21 มาหารด้วยคอลัมน์กัน:

ตอบ:

7,287:2,1=3,47 .

ตัวอย่าง.

หารทศนิยม 16.3 ด้วยทศนิยม 0.021

วิธีการแก้.

ย้ายเครื่องหมายจุลภาคในตัวปันผลและตัวหารไปทางขวา 3 หลัก เห็นได้ชัดว่า มีตัวเลขในตัวหารไม่เพียงพอสำหรับใส่เครื่องหมายจุลภาค ดังนั้น ให้เพิ่มจำนวนศูนย์ที่ต้องการทางด้านขวากัน ทีนี้ลองหารคอลัมน์ของเศษส่วน 16300.0 ด้วยจำนวนธรรมชาติ 21:

จากนี้ไป ส่วนที่เหลือ 4, 19, 1, 10, 16 และ 13 จะเริ่มทำซ้ำ ซึ่งหมายความว่าตัวเลข 1, 9, 0, 4, 7 และ 6 ในผลหารจะทำซ้ำเช่นกัน เป็นผลให้เราได้รับเศษส่วนทศนิยมเป็นระยะ 776,(190476) .

ตอบ:

16,3:0,021=776,(190476) .

โปรดทราบว่ากฎที่เปล่งเสียงทำให้คุณสามารถหารจำนวนธรรมชาติด้วยเศษส่วนทศนิยมสุดท้ายด้วยคอลัมน์

ตัวอย่าง.

หารจำนวนธรรมชาติ 3 ด้วยเศษส่วนทศนิยม 5.4

วิธีการแก้.

หลังจากย้ายเครื่องหมายจุลภาคไปทางขวา 1 หลัก เรามาหารตัวเลข 30.0 ด้วย 54 มาหารด้วยคอลัมน์กัน:
.

กฎนี้ยังสามารถนำไปใช้เมื่อหารเศษส่วนทศนิยมอนันต์ด้วย 10, 100, .... ตัวอย่างเช่น 3,(56):1000=0.003(56) และ 593.374…:100=5.93374…

หารทศนิยมด้วย 0.1, 0.01, 0.001 เป็นต้น

ตั้งแต่ 0.1 \u003d 1/10, 0.01 \u003d 1/100 เป็นต้น จากกฎการหารด้วยเศษส่วนธรรมดาที่หารเศษส่วนทศนิยมด้วย 0.1, 0.01, 0.001 เป็นต้น . มันเหมือนกับการคูณทศนิยมที่กำหนดด้วย 10 , 100 , 1000 เป็นต้น ตามลำดับ

กล่าวอีกนัยหนึ่ง ในการหารเศษส่วนทศนิยมด้วย 0.1, 0.01, ... คุณต้องเลื่อนเครื่องหมายจุลภาคไปทางขวาด้วย 1, 2, 3, ... หลัก และหากมีตัวเลขในเศษทศนิยมไม่เพียงพอ ย้ายเครื่องหมายจุลภาค จากนั้นคุณต้องเพิ่มตัวเลขที่ต้องการลงในศูนย์ที่ถูกต้อง

ตัวอย่างเช่น 5.739:0.1=57.39 และ 0.21:0.00001=21,000

สามารถใช้กฎเดียวกันนี้เมื่อหารทศนิยมอนันต์ด้วย 0.1, 0.01, 0.001 เป็นต้น ในขณะเดียวกันก็ควรระมัดระวังการแบ่งส่วนให้มาก เศษส่วนเป็นระยะเพื่อไม่ให้เข้าใจผิดกับคาบของเศษส่วนซึ่งได้มาจากการหาร ตัวอย่างเช่น 7.5(716):0.01=757,(167) เนื่องจากหลังจากย้ายเครื่องหมายจุลภาคในระเบียนเศษทศนิยม 7.5716716716 ... ตัวเลขสองหลักทางขวา เรามีบันทึก 757.167167 ... . ด้วยทศนิยมที่ไม่เป็นระยะอนันต์ ทุกอย่างง่ายกว่า: 394,38283…:0,001=394382,83… .

การหารเศษส่วนหรือจำนวนคละด้วยทศนิยมและในทางกลับกัน

การหารเศษส่วนร่วมหรือจำนวนคละด้วยทศนิยมที่มีจำนวนจำกัดหรือทศนิยมที่เกิดซ้ำ หรือหารทศนิยมที่มีจำกัดหรือที่เกิดซ้ำด้วยเศษส่วนร่วมหรือ คละจำนวนให้เหลือการหารเศษส่วนธรรมดา เมื่อต้องการทำเช่นนี้ เศษส่วนทศนิยมจะถูกแทนที่ด้วยเศษส่วนธรรมดาที่สอดคล้องกัน และจำนวนคละจะแสดงเป็นเศษส่วนที่ไม่เหมาะสม

เมื่อทำการหารเศษส่วนทศนิยมที่ไม่เป็นคาบเป็นอนันต์ด้วยเศษส่วนธรรมดาหรือจำนวนคละ และในทางกลับกัน เราควรทำการหารเศษส่วนทศนิยมโดยแทนที่เศษส่วนธรรมดาหรือจำนวนคละด้วยเศษส่วนทศนิยมที่สอดคล้องกัน

บรรณานุกรม.

• คณิตศาสตร์: การศึกษา สำหรับ 5 เซลล์ การศึกษาทั่วไป สถาบัน / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartburd - ฉบับที่ 21 ลบแล้ว - M.: Mnemosyne, 2007. - 280 p.: ill. ไอเอสบีเอ็น 5-346-00699-0
• คณิตศาสตร์.ชั้นประถมศึกษาปีที่ 6: ตำราเรียน เพื่อการศึกษาทั่วไป สถาบัน / [น. ยะ. Vilenkin และอื่น ๆ ]. - ครั้งที่ 22 รายได้ - M.: Mnemosyne, 2008. - 288 p.: ill. ไอ 978-5-346-00897-2
• พีชคณิต:หนังสือเรียน สำหรับ 8 เซลล์ การศึกษาทั่วไป สถาบัน / [อ. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; เอ็ด S.A. Telyakovsky. - ครั้งที่ 16 - ม. : การศึกษา, 2551. - 271 น. : ป่วย. - ไอ 978-5-09-019243-9
• Gusev V. A. , Mordkovich A. G.คณิตศาสตร์ (คู่มือสำหรับผู้สมัครเข้าโรงเรียนเทคนิค): Proc. เบี้ยเลี้ยง.- ม.; สูงกว่า รร. 2527-351 น.

37. หารทศนิยม

งาน.พื้นที่ของสี่เหลี่ยมผืนผ้าคือ 2.88 dm 2 และความกว้างของมันคือ 0.8 dm ความยาวของสี่เหลี่ยมคืออะไร?

สารละลาย ตั้งแต่ 2.88 dm 2 \u003d 288 cm 2 และ 0.8 dm \u003d 8 cm ความยาวของสี่เหลี่ยมผืนผ้าคือ 288: 8 นั่นคือ 36 cm \u003d 3.6 dm เราพบตัวเลข 3.6 โดยที่ 3.6 0.8 = 2.88 มันคือผลหารของ 2.88 หารด้วย 0.8

คำตอบ 3.6 สามารถหาได้โดยไม่ต้องแปลงเดซิเมตรเป็นเซนติเมตร ในการทำเช่นนี้ ให้คูณตัวหาร 0.8 และเงินปันผล 2.88 ด้วย 10 (นั่นคือ ย้ายเครื่องหมายจุลภาคไปทางขวาในตัวเลขหนึ่งหลัก) และหาร 28.8 ด้วย 8 อีกครั้ง เราได้:

การหารตัวเลขด้วยทศนิยม, จำเป็น:
1) ในตัวหารและตัวหาร ให้เลื่อนเครื่องหมายจุลภาคไปทางขวาตามจำนวนหลักที่มีหลังจุดทศนิยมในตัวหาร
2) หลังจากนั้นทำการหารด้วยจำนวนธรรมชาติ

ตัวอย่าง 1หาร 12.096 ด้วย 2.24 ลองย้ายเครื่องหมายจุลภาค 2 หลักไปทางขวาในเงินปันผลและตัวหาร เราได้ตัวเลข 1209.6 และ 224

ตั้งแต่นั้นมา และ .

ตัวอย่าง 2หาร 4.5 ด้วย 0.125 ที่นี่จำเป็นต้องย้ายเครื่องหมายจุลภาค 3 หลักไปทางขวาในตัวปันผลและตัวหาร เนื่องจากเงินปันผลมีตัวเลขอยู่หลังจุดทศนิยมเพียงตัวเดียว เราจะบวกศูนย์สองตัวทางด้านขวา หลังจากย้ายเครื่องหมายจุลภาค เราได้ตัวเลข 4500 และ 125

ตั้งแต่นั้นมา และ .

ตัวอย่างที่ 1 และ 2 แสดงว่าเมื่อหารจำนวนด้วย เศษส่วนที่ไม่เหมาะสมตัวเลขนี้ลดลงหรือไม่เปลี่ยนแปลง และเมื่อหารด้วยเศษส่วนทศนิยมที่ถูกต้อง จะเพิ่มขึ้น:, ก.

หาร 2.467 ด้วย 0.01 หลังจากย้ายเครื่องหมายจุลภาคในตัวปันผลและตัวหารด้วยเลข 2 หลักไปทางขวา เราจะได้ผลหารเป็น 246.7: 1 นั่นคือ 246.7 ดังนั้น และ 2.467: 0.01 = 246.7 จากที่นี่เราได้รับกฎ:

ในการหารทศนิยมด้วย 0.1; 0.01; 0.001คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยตัวเลขให้มากที่สุดเท่าที่มีศูนย์หน้าหน่วยในตัวหาร (นั่นคือ คูณด้วย 10, 100, 1000)

หากมีตัวเลขไม่เพียงพอ ก่อนอื่นคุณต้องบวกศูนย์สองสามตัวที่ส่วนท้ายของเศษส่วน

ตัวอย่างเช่น, .

1443. หาผลหารและทดสอบโดยการคูณ:

ก) 0.8: 0.5; ข) 3.51: 2.7; ค) 14.335: 0.61.

1444. หาผลหารและทดสอบโดยหาร:

ก) 0.096: 0.12; 6) 0.126:0.9; ค) 42.105: 3.5.

1445. ดำเนินการแผนก:

1446. เขียนนิพจน์:

ก) ผลหารของการหารผลรวมของ a และ 2.6 ด้วยผลต่างของ b และ 8.5
b) ผลรวมของผลหาร x และ 3.7 และผลหาร 3.1 และ y

1447 อ่านนิพจน์:

ก) ม.: 12.8 - น: 4.9; b) (x + 0.7): (y + 3.4); ค) (ก: ข) (8: ค)

1448. ก้าวชาย 0.8 ม. ต้องเดินกี่ก้าวถึง 100 ม.?

1449. Alyosha เดินทางโดยรถไฟ 162.5 กม. ใน 2.6 ชั่วโมง รถไฟเร็วแค่ไหน?

1450. จงหามวลน้ำแข็ง 1 ซม. 3 ถ้ามวลน้ำแข็ง 3.5 ซม. 3 เท่ากับ 3.08 ก.

1451. เชือกถูกตัดเป็นสองส่วน ความยาวของส่วนหนึ่งเท่ากับ 3.25 ม. และอีกส่วนหนึ่งมีความยาว 1.3 เท่าของส่วนแรก ความยาวของเชือกคืออะไร?

1452 ชุดแรกรวมแป้ง 6.72 กก. ซึ่งมากกว่าชุดที่สอง 2.4 เท่า รวมแป้งกี่กิโลกรัมในถุงทั้งสอง?

1453 บอริยาใช้เวลาเตรียมบทเรียนน้อยกว่าการเดิน 3.5 เท่า Borya ใช้เวลานานแค่ไหนในการเดินและเตรียมบทเรียนหากการเดินใช้เวลา 2.8 ชั่วโมง?

การหารด้วยทศนิยมจะเหมือนกับการหารด้วยจำนวนธรรมชาติ

กฎการหารตัวเลขด้วยเศษส่วนทศนิยม

ในการหารตัวเลขด้วยเศษส่วนทศนิยม จำเป็นทั้งในเงินปันผลและในตัวหารเพื่อย้ายเครื่องหมายจุลภาคไปทางขวาให้มากที่สุดเท่าที่มีอยู่ในตัวหารหลังจุดทศนิยม หลังจากนั้นหารด้วยจำนวนธรรมชาติ

ตัวอย่าง.

ทำการหารด้วยทศนิยม:

ในการหารด้วยเศษส่วนทศนิยม คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาให้มากที่สุดเท่าที่เป็นไปได้ทั้งในตัวหารและตัวหารตามที่อยู่หลังจุดทศนิยมในตัวหาร นั่นคือด้วยเครื่องหมายเดียว เราได้รับ: 35.1: 1.8 \u003d 351: 18 ตอนนี้เราทำการหารด้วยมุม เป็นผลให้เราได้รับ: 35.1: 1.8 = 19.5

2) 14,76: 3,6

ในการหารเศษส่วนทศนิยมทั้งในเงินปันผลและในตัวหาร ให้เลื่อนเครื่องหมายจุลภาคไปทางขวาด้วยเครื่องหมายเดียว: 14.76: 3.6 \u003d 147.6: 36 ตอนนี้เราดำเนินการกับจำนวนธรรมชาติ ผลลัพธ์: 14.76: 3.6 = 4.1

ในการหารด้วยเศษส่วนทศนิยมของจำนวนธรรมชาติ จำเป็นทั้งในเงินปันผลและในตัวหารเพื่อย้ายอักขระไปทางขวามากที่สุดเท่าที่มีในตัวหารหลังจุดทศนิยม เนื่องจากในกรณีนี้ไม่ได้เขียนเครื่องหมายจุลภาคในตัวหาร เราจึงเติมจำนวนอักขระที่ขาดหายไปด้วยศูนย์: 70: 1.75 \u003d 7000: 175 เราหารจำนวนธรรมชาติที่เป็นผลลัพธ์ด้วยมุม: 70: 1.75 \u003d 7000: 175 \u003d 40.

4) 0,1218: 0,058

ในการหารเศษทศนิยมหนึ่งให้เป็นอีกเศษหนึ่ง เราย้ายเครื่องหมายจุลภาคไปทางขวา ทั้งในเงินปันผลและในตัวหารด้วยตัวเลขมากที่สุดเท่าที่มีในตัวหารหลังจุดทศนิยม นั่นคือ ตัวเลขสามหลัก ดังนั้น 0.1218: 0.058 \u003d 121.8: 58 การหารด้วยเศษส่วนทศนิยมถูกแทนที่ด้วยการหารด้วยจำนวนธรรมชาติ เราแบ่งปันมุม เรามี: 0.1218: 0.058 = 121.8: 58 = 2.1

5) 0,0456: 3,8

ในบทช่วยสอนนี้ เราจะพิจารณาการดำเนินการเหล่านี้ทีละรายการ

เนื้อหาบทเรียน

การบวกทศนิยม

อย่างที่เราทราบ ทศนิยมมีส่วนจำนวนเต็มและเศษส่วน เมื่อเพิ่มทศนิยม ส่วนของจำนวนเต็มและเศษส่วนจะถูกเพิ่มแยกกัน

ตัวอย่างเช่น ลองบวกทศนิยม 3.2 และ 5.3 การเพิ่มเศษส่วนทศนิยมในคอลัมน์จะสะดวกกว่า

อันดับแรก เราเขียนเศษส่วนสองส่วนนี้ในคอลัมน์ ในขณะที่ส่วนจำนวนเต็มต้องอยู่ใต้ส่วนจำนวนเต็ม และเศษส่วนใต้ส่วนที่เป็นเศษส่วน ในโรงเรียนข้อกำหนดนี้เรียกว่า "จุลภาคภายใต้เครื่องหมายจุลภาค".

ลองเขียนเศษส่วนในคอลัมน์เพื่อให้ลูกน้ำอยู่ใต้ลูกน้ำ:

เราเริ่มเพิ่มส่วนที่เป็นเศษส่วน: 2 + 3 \u003d 5. เราเขียนห้าในส่วนที่เป็นเศษส่วนของคำตอบของเรา:

ตอนนี้เราบวกส่วนจำนวนเต็ม: 3 + 5 = 8 เราเขียนแปดในส่วนจำนวนเต็มของคำตอบของเรา:

ตอนนี้เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค การทำเช่นนี้เราทำตามกฎอีกครั้ง "จุลภาคภายใต้เครื่องหมายจุลภาค":

ได้คำตอบ 8.5 ดังนั้นนิพจน์ 3.2 + 5.3 จึงเท่ากับ 8.5

อันที่จริงไม่ใช่ทุกอย่างจะง่ายอย่างที่เห็นในแวบแรก ที่นี่ก็มีข้อผิดพลาดซึ่งตอนนี้เราจะพูดถึง

ตำแหน่งทศนิยม

ทศนิยมเช่นเดียวกับตัวเลขทั่วไปมีตัวเลขของตัวเอง เหล่านี้เป็นตำแหน่งที่สิบ ที่ร้อย ที่หนึ่งพัน ในกรณีนี้ ตัวเลขจะเริ่มต้นหลังจุดทศนิยม

หลักแรกหลังจุดทศนิยมรับผิดชอบตำแหน่งที่สิบ หลักที่สองหลังจุดทศนิยมสำหรับตำแหน่งที่ร้อย หลักที่สามหลังจากจุดทศนิยมสำหรับหลักพัน

ตัวเลขในเศษส่วนทศนิยมเก็บบางส่วน ข้อมูลที่เป็นประโยชน์. โดยเฉพาะอย่างยิ่ง พวกเขารายงานว่ามีกี่ส่วนในสิบ ร้อย และในพันที่เป็นทศนิยม

ตัวอย่างเช่น พิจารณาทศนิยม 0.345

ตำแหน่งที่ไตรตั้งอยู่เรียกว่า อันดับที่สิบ

ตำแหน่งที่สี่ตั้งอยู่เรียกว่า ที่ร้อย

ตำแหน่งที่ทั้งห้าตั้งอยู่เรียกว่า พัน

ลองดูที่รูปนี้ เราเห็นว่าในหมวดสิบมีสาม นี่แสดงให้เห็นว่ามีสามในสิบของเศษส่วนทศนิยม 0.345

ถ้าเราบวกเศษส่วนแล้วเราจะได้เศษทศนิยมเดิม 0.345

จะเห็นได้ว่าตอนแรกเราได้คำตอบแล้ว แต่แปลงเป็นทศนิยมแล้วได้ 0.345

เมื่อบวกเศษส่วนทศนิยม หลักการและกฎเดียวกันจะถูกปฏิบัติตามเมื่อบวกเลขธรรมดา การบวกเศษส่วนทศนิยมเกิดขึ้นจากตัวเลข: ในสิบจะเพิ่มเป็นสิบ, จากร้อยถึงหนึ่งในร้อย, ในพันถึงหนึ่งในพัน

ดังนั้น เมื่อบวกเศษทศนิยม จึงต้องปฏิบัติตามกฎ "จุลภาคภายใต้เครื่องหมายจุลภาค". เครื่องหมายจุลภาคที่อยู่ใต้เครื่องหมายจุลภาคให้ลำดับเดียวกันกับที่เพิ่มหนึ่งในสิบเป็นสิบ จากร้อยถึงหนึ่งในร้อย

ตัวอย่าง 1ค้นหาค่าของนิพจน์ 1.5 + 3.4

ก่อนอื่น เราเพิ่มส่วนที่เป็นเศษส่วน 5 + 4 = 9 เราเขียนเก้าในส่วนที่เป็นเศษส่วนของคำตอบของเรา:

ตอนนี้เราบวกส่วนจำนวนเต็ม 1 + 3 = 4 เราเขียนสี่ในส่วนจำนวนเต็มของคำตอบของเรา:

ตอนนี้เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการดำเนินการนี้ เราปฏิบัติตามกฎ "comma under a comma" อีกครั้ง:

ได้คำตอบ 4.9 ดังนั้นค่าของนิพจน์ 1.5 + 3.4 คือ 4.9

ตัวอย่าง 2ค้นหาค่าของนิพจน์: 3.51 + 1.22

เราเขียนนิพจน์นี้ในคอลัมน์โดยปฏิบัติตามกฎ "comma under a comma"

ก่อนอื่นเพิ่มส่วนที่เป็นเศษส่วน คือ ส่วนร้อย 1+2=3 เราเขียนสามส่วนในส่วนที่ร้อยของคำตอบของเรา:

ตอนนี้เพิ่มหนึ่งในสิบของ 5+2=7 เราเขียนเจ็ดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เพิ่มทั้งส่วน 3+1=4 เราเขียนสี่ในส่วนทั้งหมดของคำตอบของเรา:

เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค โดยปฏิบัติตามกฎ "เครื่องหมายจุลภาคภายใต้เครื่องหมายจุลภาค":

ได้คำตอบ 4.73 ดังนั้นค่าของนิพจน์ 3.51 + 1.22 คือ 4.73

3,51 + 1,22 = 4,73

เช่นเดียวกับตัวเลขธรรมดา เมื่อบวกเศษส่วนทศนิยม . ในกรณีนี้ คำตอบจะถูกเขียนหนึ่งหลัก และส่วนที่เหลือจะถูกโอนไปยังหลักถัดไป

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 2.65 + 3.27

เราเขียนนิพจน์นี้ในคอลัมน์:

เพิ่มหนึ่งในร้อยของ 5+7=12 หมายเลข 12 จะไม่พอดีกับส่วนที่ร้อยของคำตอบของเรา ดังนั้นในส่วนที่ร้อย เราเขียนเลข 2 และโอนหน่วยไปยังบิตถัดไป:

ตอนนี้เราบวกหนึ่งในสิบของ 6+2=8 บวกหน่วยที่เราได้รับจากการดำเนินการก่อนหน้านี้ เราได้ 9 เราเขียนหมายเลข 9 ในหนึ่งในสิบของคำตอบของเรา:

ตอนนี้เพิ่มทั้งส่วน 2+3=5 เราเขียนหมายเลข 5 ในส่วนจำนวนเต็มของคำตอบของเรา:

ได้คำตอบ 5.92 ดังนั้นค่าของนิพจน์ 2.65 + 3.27 คือ 5.92

2,65 + 3,27 = 5,92

ตัวอย่างที่ 4ค้นหาค่าของนิพจน์ 9.5 + 2.8

เขียนนิพจน์นี้ในคอลัมน์

เราบวกส่วนที่เป็นเศษส่วน 5 + 8 = 13 ตัวเลข 13 จะไม่พอดีกับส่วนที่เป็นเศษส่วนของคำตอบ ดังนั้นอันดับแรกให้เขียนเลข 3 ลงไป แล้วโอนหน่วยไปที่หลักถัดไป หรือโอนไปยังจำนวนเต็ม ส่วนหนึ่ง:

ตอนนี้เราบวกส่วนจำนวนเต็ม 9+2=11 บวกหน่วยที่เราได้รับจากการดำเนินการก่อนหน้านี้ เราได้ 12 เราเขียนหมายเลข 12 ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 12.3 ดังนั้นค่าของนิพจน์ 9.5 + 2.8 คือ 12.3

9,5 + 2,8 = 12,3

เมื่อบวกเศษส่วนทศนิยม จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองจะต้องเท่ากัน หากมีตัวเลขไม่เพียงพอ ตำแหน่งเหล่านี้ในส่วนที่เป็นเศษส่วนจะเต็มไปด้วยศูนย์

ตัวอย่างที่ 5. ค้นหาค่าของนิพจน์: 12.725 + 1.7

ก่อนเขียนนิพจน์นี้ในคอลัมน์ เรามาทำให้จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองเท่ากันก่อน เศษส่วนทศนิยม 12.725 มีสามหลักหลังจุดทศนิยม ในขณะที่เศษส่วน 1.7 มีเพียงหนึ่ง ดังนั้นในเศษส่วน 1.7 ในตอนท้าย คุณต้องบวกศูนย์สองตัว แล้วเราจะได้เศษส่วน 1,700. ตอนนี้คุณสามารถเขียนนิพจน์นี้ในคอลัมน์และเริ่มคำนวณ:

เพิ่มหนึ่งในพันของ 5+0=5 เราเขียนหมายเลข 5 ในส่วนที่พันของคำตอบของเรา:

เพิ่มหนึ่งในร้อยของ 2+0=2 เราเขียนหมายเลข 2 ในส่วนที่ร้อยของคำตอบของเรา:

เพิ่มหนึ่งในสิบของ 7+7=14 หมายเลข 14 จะไม่พอดีกับหนึ่งในสิบของคำตอบของเรา ดังนั้นเราจึงเขียนหมายเลข 4 ก่อนและโอนหน่วยไปยังบิตถัดไป:

ตอนนี้เราบวกส่วนจำนวนเต็ม 12+1=13 บวกหน่วยที่เราได้รับจากการดำเนินการก่อนหน้านี้ เราได้ 14 เราเขียนหมายเลข 14 ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 14,425 ดังนั้นค่าของนิพจน์ 12.725+1.700 คือ 14.425

12,725+ 1,700 = 14,425

การลบทศนิยม

เมื่อลบเศษส่วนทศนิยม คุณต้องปฏิบัติตามกฎเดียวกันกับเมื่อบวก: "เครื่องหมายจุลภาคภายใต้เครื่องหมายจุลภาค" และ "จำนวนหลักหลังจุดทศนิยมเท่ากัน"

ตัวอย่าง 1ค้นหาค่าของนิพจน์ 2.5 - 2.2

เราเขียนนิพจน์นี้ในคอลัมน์โดยปฏิบัติตามกฎ "comma under comma":

เราคำนวณส่วนที่เป็นเศษส่วน 5−2=3 เราเขียนหมายเลข 3 ในส่วนที่สิบของคำตอบของเรา:

คำนวณส่วนจำนวนเต็ม 2−2=0 เราเขียนศูนย์ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้คำตอบ 0.3 ดังนั้นค่าของนิพจน์ 2.5 - 2.2 เท่ากับ 0.3

2,5 − 2,2 = 0,3

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 7.353 - 3.1

ในนิพจน์นี้ ปริมาณที่แตกต่างกันตัวเลขหลังจุดทศนิยม ในเศษส่วน 7.353 มีตัวเลขสามหลักหลังจุดทศนิยม และในเศษส่วนที่ 3.1 มีเพียงตัวเดียว ซึ่งหมายความว่าในเศษส่วนที่ 3.1 ต้องเติมศูนย์สองตัวที่ส่วนท้ายเพื่อให้จำนวนหลักในเศษส่วนทั้งสองเท่ากัน แล้วเราจะได้ 3,100.

ตอนนี้คุณสามารถเขียนนิพจน์นี้ในคอลัมน์และคำนวณได้:

ได้คำตอบ 4,253 ดังนั้นค่าของนิพจน์ 7.353 − 3.1 คือ 4.253

7,353 — 3,1 = 4,253

เช่นเดียวกับตัวเลขทั่วไป บางครั้งคุณจะต้องยืมหนึ่งตัวจากบิตที่อยู่ติดกัน หากการลบไม่สามารถทำได้

ตัวอย่างที่ 3หาค่าของนิพจน์ 3.46 − 2.39

ลบหนึ่งในร้อยของ 6-9 จากหมายเลข 6 อย่าลบหมายเลข 9 ดังนั้นคุณต้องนำหน่วยจากหลักที่อยู่ติดกัน เมื่อยืมหนึ่งจากหลักที่อยู่ใกล้เคียง หมายเลข 6 จะกลายเป็นหมายเลข 16 ตอนนี้ เราสามารถคำนวณหนึ่งในร้อยของ 16−9=7 ได้ เราเขียนเจ็ดในส่วนที่ร้อยของคำตอบของเรา:

ตอนนี้ลบสิบ เนื่องจากเราใช้หนึ่งหน่วยในหมวดที่สิบ ตัวเลขที่อยู่ตรงนั้นจึงลดลงหนึ่งหน่วย กล่าวอีกนัยหนึ่ง ตำแหน่งที่สิบตอนนี้ไม่ใช่หมายเลข 4 แต่เป็นหมายเลข 3 ลองคำนวณหนึ่งในสิบของ 3−3=0 กัน เราเขียนศูนย์ในส่วนที่สิบของคำตอบของเรา:

ตอนนี้ลบส่วนจำนวนเต็ม 3−2=1 เราเขียนหน่วยในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 1.07 ดังนั้นค่าของนิพจน์ 3.46−2.39 จึงเท่ากับ 1.07

3,46−2,39=1,07

ตัวอย่างที่ 4. ค้นหาค่าของนิพจน์ 3−1.2

ตัวอย่างนี้ลบทศนิยมจากจำนวนเต็ม ลองเขียนนิพจน์นี้ในคอลัมน์เพื่อให้ ทั้งส่วนเศษส่วนทศนิยม 1.23 อยู่ใต้เลข 3

ทีนี้มาทำจำนวนหลักหลังจุดทศนิยมกัน เมื่อต้องการทำสิ่งนี้ หลังจากเลข 3 ให้ใส่เครื่องหมายจุลภาคและเพิ่มศูนย์หนึ่งตัว:

ตอนนี้ลบสิบ: 0−2 อย่าลบเลข 2 จากศูนย์ ดังนั้น คุณต้องนำหน่วยจากหลักที่อยู่ติดกัน โดยการยืมหนึ่งตัวจากหลักที่อยู่ติดกัน 0 จะกลายเป็นตัวเลข 10 ตอนนี้คุณสามารถคำนวณหนึ่งในสิบของ 10−2=8 ได้แล้ว เราเขียนแปดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้ลบส่วนทั้งหมด ก่อนหน้านี้เลข 3 อยู่ในจำนวนเต็ม แต่เรายืมหนึ่งหน่วยจากมัน เป็นผลให้มันกลายเป็นหมายเลข 2 ดังนั้นเราจึงลบ 1 จาก 2 2-1=1 เราเขียนหน่วยในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 1.8 ดังนั้นค่าของนิพจน์ 3−1.2 คือ 1.8

การคูณทศนิยม

การคูณทศนิยมนั้นง่ายและสนุก ในการคูณทศนิยม คุณต้องคูณมันเหมือนตัวเลขปกติ โดยไม่สนใจเครื่องหมายจุลภาค

เมื่อได้รับคำตอบแล้ว จำเป็นต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสอง จากนั้นนับจำนวนหลักทางด้านขวาของคำตอบและใส่เครื่องหมายจุลภาค

ตัวอย่าง 1ค้นหาค่าของนิพจน์ 2.5 × 1.5

เราคูณเศษส่วนทศนิยมเหล่านี้เป็นตัวเลขธรรมดา โดยไม่สนใจเครื่องหมายจุลภาค หากต้องการละเว้นเครื่องหมายจุลภาค คุณสามารถจินตนาการได้ชั่วคราวว่าไม่มีเครื่องหมายจุลภาค:

เราได้ 375 ในตัวเลขนี้ จำเป็นต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วนของ 2.5 และ 1.5 ในเศษส่วนแรกมีหนึ่งหลักหลังจุดทศนิยมในเศษส่วนที่สองก็มีหนึ่งตัวเช่นกัน รวมเป็นสองจำนวน

เรากลับไปที่หมายเลข 375 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 3.75 ดังนั้นค่าของนิพจน์ 2.5 × 1.5 คือ 3.75

2.5 x 1.5 = 3.75

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 12.85 × 2.7

ลองคูณทศนิยมเหล่านี้โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้ 34695 ในตัวเลขนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องคำนวณจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วนของ 12.85 และ 2.7 ในเศษส่วน 12.85 มีตัวเลขสองหลักหลังจุดทศนิยม ในเศษส่วนที่ 2.7 มีหนึ่งหลัก - รวมเป็นสามหลัก

เรากลับไปที่หมายเลข 34695 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสามหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 34,695 ดังนั้นค่าของนิพจน์ 12.85 × 2.7 คือ 34.695

12.85 x 2.7 = 34.695

การคูณทศนิยมด้วยจำนวนปกติ

บางครั้งมีบางสถานการณ์ที่คุณต้องคูณเศษส่วนทศนิยมด้วยจำนวนปกติ

ในการคูณทศนิยมกับจำนวนปกติ คุณต้องคูณมันโดยไม่คำนึงถึงเครื่องหมายจุลภาคในทศนิยม เมื่อได้รับคำตอบแล้ว จำเป็นต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทศนิยม จากนั้นในคำตอบ ให้นับจำนวนหลักทางขวาและใส่เครื่องหมายจุลภาค

ตัวอย่างเช่น คูณ 2.54 ด้วย 2

เราคูณเศษส่วนทศนิยม 2.54 ด้วยจำนวนปกติ 2 โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้หมายเลข 508 ในตัวเลขนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.54 เศษส่วน 2.54 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 508 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 5.08 ดังนั้นค่าของนิพจน์ 2.54 × 2 คือ 5.08

2.54 x 2 = 5.08

การคูณทศนิยมด้วย 10, 100, 1000

การคูณทศนิยมด้วย 10, 100 หรือ 1,000 ทำได้ในลักษณะเดียวกับการคูณทศนิยมด้วยตัวเลขปกติ จำเป็นต้องทำการคูณโดยละเว้นเครื่องหมายจุลภาคในเศษส่วนทศนิยม จากนั้นในคำตอบ ให้แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วน โดยนับจำนวนหลักทางด้านขวาเนื่องจากมีตัวเลขอยู่หลังจุดทศนิยมในทศนิยม เศษส่วน

ตัวอย่างเช่น คูณ 2.88 ด้วย 10

ลองคูณเศษทศนิยม 2.88 ด้วย 10 โดยไม่สนใจเครื่องหมายจุลภาคในเศษทศนิยม:

เราได้ 2880 ในตัวเลขนี้ คุณต้องแยกส่วนทั้งหมดออกจากเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษ 2.88 เราจะเห็นว่าในเศษ 2.88 มีเลขหลังจุดทศนิยมสองหลัก

เรากลับไปที่หมายเลข 2880 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากด้านขวาและใส่เครื่องหมายจุลภาค:

ได้คำตอบ 28.80 เราทิ้งศูนย์สุดท้าย - เราได้ 28.8 ดังนั้นค่าของนิพจน์ 2.88 × 10 คือ 28.8

2.88 x 10 = 28.8

มีวิธีที่สองในการคูณเศษส่วนทศนิยมด้วย 10, 100, 1000 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยข้อเท็จจริงที่ว่าเครื่องหมายจุลภาคในเศษส่วนทศนิยมเคลื่อนไปทางขวาด้วยจำนวนหลักมากเท่ากับศูนย์ในตัวคูณ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 2.88×10 ด้วยวิธีนี้ เราจะดูที่ตัวประกอบ 10 ทันทีโดยไม่ได้คำนวณอะไรเลย เราสนใจว่าเลขศูนย์อยู่ในนั้นกี่ตัว เราเห็นว่ามันมีศูนย์หนึ่งตัว ในเศษ 2.88 เราย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เราได้ 28.8

2.88 x 10 = 28.8

ลองคูณ 2.88 ด้วย 100 ดูตัวประกอบ 100 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราจะเห็นว่ามันมีศูนย์สองตัว ตอนนี้ในเศษ 2.88 เราย้ายจุดทศนิยมไปทางขวาด้วยตัวเลขสองหลัก เราได้288

2.88 x 100 = 288

ลองคูณ 2.88 ด้วย 1000 กัน. เราดูที่ตัวประกอบ 1000 ทันที. เราสนใจว่าเลขศูนย์อยู่ในนั้นกี่ตัว. เราเห็นว่ามันมีศูนย์สามตัว ตอนนี้ในเศษ 2.88 เราย้ายจุดทศนิยมไปทางขวาด้วยตัวเลขสามหลัก ตัวเลขตัวที่สามไม่อยู่ ดังนั้นเราจึงบวกศูนย์อีกตัวหนึ่ง เป็นผลให้เราได้ 2880

2.88 x 1,000 = 2880

คูณทศนิยมด้วย 0.1 0.01 และ 0.001

การคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 ทำงานในลักษณะเดียวกับการคูณทศนิยมด้วยทศนิยม จำเป็นต้องคูณเศษส่วนเหมือนตัวเลขธรรมดา แล้วใส่เครื่องหมายจุลภาคในคำตอบ โดยนับจำนวนหลักทางด้านขวาให้มากที่สุดเท่าที่จะมีตัวเลขอยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

ตัวอย่างเช่น คูณ 3.25 ด้วย 0.1

เราคูณเศษส่วนเหล่านี้เหมือนตัวเลขธรรมดาโดยไม่สนใจเครื่องหมายจุลภาค:

เราได้ 325 ในตัวเลขนี้ คุณต้องแยกส่วนทั้งหมดออกจากเศษส่วนด้วยเครื่องหมายจุลภาค ในการทำเช่นนี้ คุณต้องคำนวณจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วนของ 3.25 และ 0.1 ในเศษ 3.25 มีตัวเลขสองหลักหลังจุดทศนิยม ในเศษ 0.1 มีหนึ่งหลัก รวมเป็นสามตัวเลข

เรากลับไปที่หมายเลข 325 และเริ่มเลื่อนจากขวาไปซ้าย เราต้องนับสามหลักทางด้านขวาและใส่เครื่องหมายจุลภาค นับสามหลักแล้วพบว่าเลขหมด ในกรณีนี้ คุณต้องเพิ่มศูนย์หนึ่งตัวและใส่เครื่องหมายจุลภาค:

เราได้คำตอบ 0.325 ดังนั้นค่าของนิพจน์ 3.25 × 0.1 คือ 0.325

3.25 x 0.1 = 0.325

มีวิธีที่สองในการคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยข้อเท็จจริงที่ว่าเครื่องหมายจุลภาคในเศษส่วนทศนิยมเคลื่อนไปทางซ้ายด้วยตัวเลขมากที่สุดเท่าที่มีศูนย์ในตัวคูณ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 3.25 × 0.1 ด้วยวิธีนี้ เราจะดูที่ตัวประกอบ 0.1 ทันทีโดยไม่ให้การคำนวณใดๆ เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราเห็นว่ามันมีศูนย์หนึ่งตัว ตอนนี้ในเศษ 3.25 เราย้ายจุดทศนิยมไปทางซ้ายหนึ่งหลัก ย้ายเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลัก เราจะเห็นว่าไม่มีตัวเลขก่อนหน้าสามหลักอีกต่อไป ในกรณีนี้ ให้เพิ่มศูนย์หนึ่งตัวแล้วใส่เครื่องหมายจุลภาค เป็นผลให้เราได้รับ0.325

3.25 x 0.1 = 0.325

ลองคูณ 3.25 ด้วย 0.01 ดูตัวคูณของ 0.01 ทันที เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราจะเห็นว่ามันมีศูนย์สองตัว ตอนนี้ในเศษส่วน 3.25 เราย้ายเครื่องหมายจุลภาคไปทางซ้ายด้วยตัวเลขสองหลัก เราได้ 0.0325

3.25 x 0.01 = 0.0325

ลองคูณ 3.25 ด้วย 0.001 ดูตัวคูณของ 0.001 ทันที เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราเห็นว่ามันมีศูนย์สามตัว ตอนนี้ในเศษ 3.25 เราย้ายจุดทศนิยมไปทางซ้ายด้วยตัวเลขสามหลัก เราได้ 0.00325

3.25 × 0.001 = 0.00325

อย่าสับสนการคูณทศนิยมด้วย 0.1, 0.001 และ 0.001 ด้วยการคูณด้วย 10, 100, 1000 ข้อผิดพลาดทั่วไปคนส่วนใหญ่

เมื่อคูณด้วย 10, 100, 1000 เครื่องหมายจุลภาคจะถูกย้ายไปทางขวาด้วยจำนวนหลักมากเท่ากับศูนย์ในตัวคูณ

และเมื่อคูณด้วย 0.1, 0.01 และ 0.001 เครื่องหมายจุลภาคจะถูกย้ายไปทางซ้ายตามจำนวนหลักมากเท่ากับศูนย์ในตัวคูณ

หากจำยากในตอนแรก คุณสามารถใช้วิธีแรกซึ่งทำการคูณเหมือนกับตัวเลขธรรมดา ในคำตอบ คุณจะต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนโดยนับจำนวนหลักทางด้านขวาให้มากที่สุดเท่าที่จะมีตัวเลขอยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

การหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า ระดับสูง.

ในบทเรียนก่อนหน้านี้เรากล่าวว่าเมื่อทำการหาร น้อยลงยิ่งไปกว่านั้น จะได้เศษส่วน ในตัวเศษซึ่งเป็นเงินปันผล และตัวส่วนเป็นตัวหาร

ตัวอย่างเช่น ในการแบ่งแอปเปิ้ลหนึ่งผลออกเป็นสองผล คุณต้องเขียน 1 (แอปเปิ้ลหนึ่งผล) ในตัวเศษ และเขียน 2 (เพื่อนสองคน) ในตัวส่วน ผลที่ได้คือเศษส่วน ดังนั้นเพื่อนแต่ละคนจะได้รับแอปเปิ้ล กล่าวอีกนัยหนึ่งคือครึ่งแอปเปิ้ล เศษส่วนคือคำตอบของปัญหา วิธีแยกแอปเปิ้ลหนึ่งลูกระหว่างสองลูก

ปรากฎว่าคุณสามารถแก้ปัญหานี้ต่อไปได้หากคุณหาร 1 ด้วย 2 ท้ายที่สุด แท่งเศษส่วนในเศษส่วนใดๆ หมายถึงการหาร ซึ่งหมายความว่าการหารนี้เป็นเศษส่วนด้วย แต่อย่างไร? เราเคยชินกับความจริงที่ว่าเงินปันผลมากกว่าตัวหารเสมอ และในทางกลับกัน เงินปันผลน้อยกว่าตัวหาร

ทุกอย่างจะชัดเจนขึ้นถ้าเราจำได้ว่าเศษส่วนหมายถึงการทุบ หาร หาร ซึ่งหมายความว่าหน่วยสามารถแบ่งออกเป็นส่วนต่างๆ ได้มากเท่าที่คุณต้องการ ไม่ใช่แค่เป็นสองส่วนเท่านั้น

เมื่อหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า จะได้รับเศษส่วนทศนิยม ซึ่งส่วนจำนวนเต็มจะเป็น 0 (ศูนย์) เศษส่วนสามารถเป็นอะไรก็ได้

ลองหาร 1 ด้วย 2 ลองแก้ตัวอย่างนี้ด้วยมุม:

หนึ่งไม่สามารถแบ่งออกเป็นสองเช่นนั้น หากคุณถามคำถาม "มีกี่สองในหนึ่ง" คำตอบจะเป็น 0 ดังนั้นในส่วนตัวเราเขียน 0 และใส่เครื่องหมายจุลภาค:

ตามปกติแล้ว เราจะคูณผลหารด้วยตัวหารเพื่อดึงเศษที่เหลือออกมา:

ช่วงเวลาได้มาถึงเมื่อหน่วยสามารถแบ่งออกเป็นสองส่วน เมื่อต้องการทำสิ่งนี้ ให้เพิ่มอีกศูนย์ทางด้านขวาของอันที่ได้รับ:

เราได้ 10 เราหาร 10 ด้วย 2 เราได้ 5 เราเขียนห้าในส่วนเศษส่วนของคำตอบของเรา:

ตอนนี้เรานำส่วนที่เหลือสุดท้ายออกเพื่อทำการคำนวณให้สมบูรณ์ คูณ 5 ด้วย 2 เราได้ 10

เราได้คำตอบ 0.5 ดังนั้นเศษส่วนคือ 0.5

แอปเปิ้ลครึ่งลูกสามารถเขียนโดยใช้เศษทศนิยม 0.5 หากเราเพิ่มสองส่วนนี้ (0.5 และ 0.5) เราจะได้แอปเปิ้ลเดิมทั้งลูกอีกครั้ง:

จุดนี้สามารถเข้าใจได้เช่นกันถ้าเราจินตนาการว่า 1 ซม. แบ่งออกเป็นสองส่วนอย่างไร ถ้าคุณแบ่ง 1 เซนติเมตรออกเป็น 2 ส่วน คุณจะได้ 0.5 ซม.

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 4:5

มีกี่ห้าในสี่? ไม่เลย. เราเขียนในส่วนตัว 0 และใส่เครื่องหมายจุลภาค:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียนศูนย์ใต้สี่ ลบศูนย์นี้ออกจากเงินปันผลทันที:

ทีนี้มาเริ่มแบ่ง (แบ่ง) สี่ส่วนเป็น 5 ส่วนกัน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของ 4 เราบวกศูนย์ และหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดเป็นการส่วนตัว

เราทำตัวอย่างให้สมบูรณ์โดยคูณ 8 ด้วย 5 และรับ 40:

เราได้คำตอบ 0.8. ดังนั้นค่าของนิพจน์ 4: 5 คือ 0.8

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 5: 125

จำนวน 125 ในห้ามีกี่ตัว? ไม่เลย. เราเขียน 0 เป็นการส่วนตัวและใส่เครื่องหมายจุลภาค:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียน 0 ใต้ห้า ลบทันทีจากห้า 0

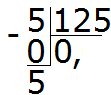
ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) ห้าส่วนออกเป็น 125 ส่วนกัน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของห้านี้ เราเขียนศูนย์:

หาร 50 ด้วย 125 ตัวเลข 125 ใน 50 มีกี่ตัว? ไม่เลย. ดังนั้นในผลหาร เราเขียน 0 . อีกครั้ง

เราคูณ 0 ด้วย 125 เราได้ 0 เราเขียนศูนย์นี้ภายใต้ 50 ลบ 0 จาก 50 . ทันที

ตอนนี้เราแบ่งหมายเลข 50 เป็น 125 ส่วน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของ 50 เราจะเขียนศูนย์อีกตัวหนึ่ง:

หาร 500 ด้วย 125 จำนวน 125 ในจำนวน 500 มีกี่จำนวน ในจำนวน 500 มีสี่ตัวเลข 125 เราเขียนสี่เป็นส่วนตัว:

เราเติมตัวอย่างให้สมบูรณ์โดยคูณ 4 ด้วย 125 และรับ 500

เราได้คำตอบ 0.04 ดังนั้นค่าของนิพจน์ 5: 125 คือ 0.04

การหารตัวเลขโดยไม่เหลือเศษ

ดังนั้น ให้ใส่เครื่องหมายจุลภาคในผลหารหลังหน่วย ซึ่งแสดงว่าการหารของส่วนจำนวนเต็มสิ้นสุดลง และเราดำเนินการในส่วนที่เป็นเศษส่วน:

เพิ่มศูนย์ในส่วนที่เหลือ 4

ตอนนี้เราหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดเป็นส่วนตัว:

40−40=0. ได้รับ 0 ส่วนที่เหลือ การแบ่งส่วนจึงเสร็จสมบูรณ์ การหาร 9 ด้วย 5 ได้ผลลัพธ์เป็นทศนิยม 1.8:

9: 5 = 1,8

ตัวอย่าง 2. หาร 84 ด้วย 5 โดยไม่เหลือเศษ

ก่อนอื่นเราหาร 84 ด้วย 5 ตามปกติด้วยเศษ:

ได้รับในส่วนตัว 16 และอีก 4 ในยอดคงเหลือ ตอนนี้เราหารเศษนี้ด้วย 5 เราใส่เครื่องหมายจุลภาคในไพรเวต แล้วบวก 0 ให้กับเศษที่เหลือ 4

ตอนนี้เราหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดในผลหารหลังจุดทศนิยม:

และกรอกตัวอย่างโดยตรวจสอบว่ายังเหลืออยู่หรือไม่:

การหารทศนิยมด้วยจำนวนปกติ

เศษส่วนทศนิยมอย่างที่เราทราบประกอบด้วยจำนวนเต็มและเศษส่วน เมื่อหารเศษส่วนทศนิยมด้วยจำนวนปกติ ขั้นแรกคุณต้อง:

• หารส่วนจำนวนเต็มของเศษส่วนทศนิยมด้วยตัวเลขนี้
• หลังจากแบ่งส่วนจำนวนเต็มแล้ว คุณต้องใส่เครื่องหมายจุลภาคในส่วนไพรเวตทันทีและทำการคำนวณต่อไป เช่นเดียวกับการหารธรรมดา

ตัวอย่างเช่น ลองหาร 4.8 ด้วย 2

ลองเขียนตัวอย่างนี้เป็นมุม:

ทีนี้ลองหารส่วนทั้งหมดด้วย 2 กัน สี่หารด้วยสองเป็นสอง เราเขียนผีสางเป็นการส่วนตัวและใส่เครื่องหมายจุลภาคทันที:

ตอนนี้เราคูณผลหารด้วยตัวหารแล้วดูว่าเหลือเศษจากการหารหรือไม่:

4-4=0. ส่วนที่เหลือเป็นศูนย์ เรายังไม่ได้เขียนศูนย์ เนื่องจากการแก้ปัญหายังไม่เสร็จสิ้น จากนั้นเราคำนวณต่อไปเช่นเดียวกับการหารธรรมดา ลง 8 แล้วหารด้วย 2

8: 2 = 4 เราเขียนสี่ในผลหารแล้วคูณด้วยตัวหารทันที:

ได้คำตอบ 2.4 ค่านิพจน์ 4.8: 2 เท่ากับ 2.4

ตัวอย่าง 2ค้นหาค่าของนิพจน์ 8.43:3

เราหาร 8 ด้วย 3 เราได้ 2 ใส่เครื่องหมายจุลภาคหลังสองทันที:

ตอนนี้เราคูณผลหารด้วยตัวหาร 2 × 3 = 6 เราเขียนหกภายใต้แปดและหาเศษที่เหลือ:

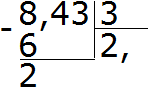
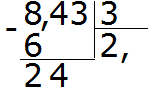
เราหาร 24 ด้วย 3 ได้ 8 เราเขียนแปดเป็นส่วนตัว เราคูณมันด้วยตัวหารทันทีเพื่อค้นหาส่วนที่เหลือของการหาร:

24-24=0. ส่วนที่เหลือเป็นศูนย์ Zero ยังไม่ได้บันทึก ใช้เงินปันผลสามตัวสุดท้ายแล้วหารด้วย 3 เราจะได้ 1 คูณ 1 ด้วย 3 ทันทีเพื่อให้ตัวอย่างนี้สมบูรณ์:

ได้คำตอบ 2.81 ดังนั้นค่าของนิพจน์ 8.43: 3 เท่ากับ 2.81

การหารทศนิยมด้วยทศนิยม

ในการหารเศษส่วนทศนิยมให้เป็นเศษส่วนทศนิยม ในเงินปันผลและในตัวหาร ให้ย้ายเครื่องหมายจุลภาคไปทางขวาด้วยจำนวนหลักเดียวกับที่อยู่หลังจุดทศนิยมในตัวหาร แล้วหารด้วยตัวเลขปกติ

ตัวอย่างเช่น หาร 5.95 ด้วย 1.7

ลองเขียนนิพจน์นี้เป็นมุม

ตอนนี้ ในตัวหารและตัวหาร เราย้ายเครื่องหมายจุลภาคไปทางขวาด้วยจำนวนหลักเดียวกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีหนึ่งหลักหลังจุดทศนิยม ดังนั้นเราต้องย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลักในเงินปันผลและในตัวหาร การโอน:

หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักแล้ว เศษทศนิยม 5.95 จะกลายเป็นเศษส่วน 59.5 และเศษทศนิยม 1.7 หลังจากที่เลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักแล้ว ก็เปลี่ยนเป็นเลข 17 ตามปกติ และเรารู้วิธีหารเศษส่วนทศนิยมด้วยจำนวนปกติแล้ว การคำนวณเพิ่มเติมนั้นไม่ยาก:

เครื่องหมายจุลภาคถูกย้ายไปทางขวาเพื่ออำนวยความสะดวกในการแบ่ง สิ่งนี้ได้รับอนุญาตเนื่องจากข้อเท็จจริงที่ว่าเมื่อคูณหรือหารเงินปันผลและตัวหารด้วยจำนวนเดียวกัน ผลหารจะไม่เปลี่ยนแปลง มันหมายความว่าอะไร?

นี่เป็นหนึ่งใน คุณสมบัติที่น่าสนใจแผนก. เรียกว่าทรัพย์สินส่วนตัว พิจารณานิพจน์ 9: 3 = 3 หากในนิพจน์นี้ เงินปันผลและตัวหารถูกคูณหรือหารด้วยตัวเลขเดียวกัน ผลหาร 3 จะไม่เปลี่ยนแปลง

ลองคูณเงินปันผลและตัวหารด้วย 2 แล้วดูว่าเกิดอะไรขึ้น:

(9 × 2) : (3 × 2) = 18: 6 = 3

ดังจะเห็นได้จากตัวอย่าง ความฉลาดไม่เปลี่ยนแปลง

สิ่งเดียวกันนี้จะเกิดขึ้นเมื่อเราใส่เครื่องหมายจุลภาคในตัวปันผลและในตัวหาร ในตัวอย่างก่อนหน้านี้ โดยที่เราหาร 5.91 ด้วย 1.7 เราย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลักในตัวหารและตัวหาร หลังจากย้ายเครื่องหมายจุลภาค เศษ 5.91 จะถูกแปลงเป็นเศษส่วน 59.1 และเศษส่วน 1.7 จะถูกแปลงเป็นเลข 17 ตามปกติ

อันที่จริงภายในกระบวนการนี้ การคูณด้วย 10 เกิดขึ้น นี่คือสิ่งที่ดูเหมือน:

5.91 × 10 = 59.1

ดังนั้นจำนวนหลักหลังจุดทศนิยมในตัวหารจึงขึ้นอยู่กับว่าตัวหารและตัวหารจะคูณด้วยอะไร กล่าวอีกนัยหนึ่ง จำนวนหลักหลังจุดทศนิยมในตัวหารจะเป็นตัวกำหนดจำนวนหลักในการจ่ายเงินปันผล และในตัวหาร เครื่องหมายจุลภาคจะถูกย้ายไปทางขวา

การหารทศนิยมด้วย 10, 100, 1000

การหารทศนิยมด้วย 10, 100 หรือ 1,000 ทำได้ในลักษณะเดียวกับ . ตัวอย่างเช่น ลองหาร 2.1 ด้วย 10 ลองแก้ตัวอย่างนี้ด้วยมุม:

แต่ยังมีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือเครื่องหมายจุลภาคในตัวปันผลจะถูกย้ายไปทางซ้ายด้วยตัวเลขมากที่สุดเท่าที่มีเลขศูนย์ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 2.1: 10. เราดูที่ตัวแบ่ง เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราจะเห็นว่ามีหนึ่งศูนย์ ในการหาร 2.1 คุณต้องเลื่อนเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลัก เราย้ายเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลักและเห็นว่าไม่มีตัวเลขเหลืออยู่ ในกรณีนี้ เราจะบวกศูนย์อีกหนึ่งตัวก่อนตัวเลข เป็นผลให้เราได้รับ 0.21

ลองหาร 2.1 ด้วย 100 มีศูนย์สองตัวในจำนวน 100 ดังนั้นในการหาร 2.1 คุณต้องย้ายเครื่องหมายจุลภาคไปทางซ้ายด้วยตัวเลขสองหลัก:

2,1: 100 = 0,021

ลองหาร 2.1 ด้วย 1000 มีศูนย์สามตัวในจำนวน 1000 ดังนั้นในการหาร 2.1 คุณต้องย้ายเครื่องหมายจุลภาคไปทางซ้ายด้วยตัวเลขสามหลัก:

2,1: 1000 = 0,0021

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001 ทำได้ในลักษณะเดียวกับ . ในการจ่ายเงินปันผลและในตัวหาร คุณต้องเลื่อนเครื่องหมายจุลภาคไปทางขวาตามจำนวนหลักที่มีตามหลังจุดทศนิยมในตัวหาร

ตัวอย่างเช่น ลองหาร 6.3 ด้วย 0.1 ก่อนอื่น เราย้ายเครื่องหมายจุลภาคในตัวหารและในตัวหารไปทางขวาด้วยจำนวนหลักเดียวกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีหนึ่งหลักหลังจุดทศนิยม ดังนั้นเราจึงย้ายเครื่องหมายจุลภาคในตัวปันผลและตัวหารไปทางขวาหนึ่งหลัก

หลังจากย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เศษส่วนทศนิยม 6.3 จะกลายเป็นตัวเลขปกติ 63 และเศษส่วนทศนิยม 0.1 หลังจากย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก จะกลายเป็นหนึ่ง และการหาร 63 ด้วย 1 นั้นง่ายมาก:

ดังนั้นค่าของนิพจน์ 6.3: 0.1 เท่ากับ 63

แต่ยังมีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือเครื่องหมายจุลภาคในเงินปันผลจะถูกโอนไปทางขวาด้วยตัวเลขมากที่สุดเท่าที่มีศูนย์ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 6.3:0.1. มาดูตัวแบ่งกัน เราสนใจว่ามีเลขศูนย์อยู่ในนั้นกี่ตัว เราจะเห็นว่ามีหนึ่งศูนย์ ในการหาร 6.3 คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลัก เราย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลักและรับ63

ลองหาร 6.3 ด้วย 0.01 ตัวหาร 0.01 มีศูนย์สองตัว ในการหาร 6.3 คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยตัวเลขสองหลัก แต่ในการจ่ายเงินปันผลจะมีตัวเลขอยู่หลังจุดทศนิยมเพียงตัวเดียว ในกรณีนี้จะต้องเพิ่มศูนย์อีกหนึ่งตัวในตอนท้าย เป็นผลให้เราได้รับ 630

ลองหาร 6.3 ด้วย 0.001 ตัวหารของ 0.001 มีศูนย์สามตัว ดังนั้นในการหาร 6.3 คุณต้องย้ายเครื่องหมายจุลภาคไปทางขวาด้วยตัวเลขสามหลัก:

6,3: 0,001 = 6300

งานสำหรับโซลูชันอิสระ

คุณชอบบทเรียนหรือไม่?
เข้าร่วมกับเรา กลุ่มใหม่ Vkontakte และเริ่มรับการแจ้งเตือนเกี่ยวกับบทเรียนใหม่

ในบทเรียนที่แล้ว เราได้เรียนรู้วิธีบวกและลบเศษส่วนทศนิยม (ดูบทเรียน " การบวกและการลบเศษส่วนทศนิยม") ในเวลาเดียวกัน พวกเขาประเมินว่าการคำนวณนั้นง่ายขึ้นมากเพียงใดเมื่อเทียบกับเศษส่วน "สองชั้น" ปกติ

ขออภัย ด้วยการคูณและหารเศษส่วนทศนิยม ผลกระทบนี้จะไม่เกิดขึ้น ในบางกรณี สัญกรณ์ทศนิยมอาจทำให้การดำเนินการเหล่านี้ซับซ้อน

ขั้นแรก มาแนะนำคำจำกัดความใหม่ เราจะพบเขาค่อนข้างบ่อยและไม่เพียงแต่ในบทเรียนนี้

ส่วนสำคัญของตัวเลขคือทุกอย่างระหว่างตัวเลขตัวแรกและตัวสุดท้ายที่ไม่ใช่ศูนย์ รวมถึงตัวอย่าง มันเป็นเรื่องของเกี่ยวกับตัวเลขเท่านั้นไม่คำนึงถึงจุดทศนิยม

ตัวเลขที่รวมอยู่ในส่วนสำคัญของจำนวนนั้นเรียกว่าตัวเลขที่มีนัยสำคัญ สามารถทำซ้ำได้และเท่ากับศูนย์

ตัวอย่างเช่น พิจารณาเศษส่วนทศนิยมหลายๆ ส่วนและเขียนส่วนที่มีนัยสำคัญที่เกี่ยวข้อง:

1. 91.25 → 9125 (ตัวเลขสำคัญ: 9; 1; 2; 5);
2. 0.008241 → 8241 (ตัวเลขสำคัญ: 8; 2; 4; 1);
3. 15.0075 → 150075 (ตัวเลขสำคัญ: 1; 5; 0; 0; 7; 5);
4. 0.0304 → 304 (ตัวเลขสำคัญ: 3; 0; 4);
5. 3000 → 3 (มีตัวเลขสำคัญเพียงตัวเดียว: 3)

โปรดทราบ: ศูนย์ภายในส่วนสำคัญของตัวเลขจะไม่ไปไหน เราได้พบสิ่งที่คล้ายกันแล้วเมื่อเราเรียนรู้การแปลงเศษส่วนทศนิยมให้เป็นทศนิยม (ดูบทเรียน " เศษส่วนทศนิยม")

ประเด็นนี้สำคัญมาก และมีข้อผิดพลาดเกิดขึ้นบ่อยครั้งจนฉันจะเผยแพร่การทดสอบในหัวข้อนี้ในอนาคตอันใกล้ หมั่นฝึกฝน! และเราซึ่งติดอาวุธด้วยแนวคิดของส่วนสำคัญ อันที่จริง เราจะดำเนินการตามหัวข้อของบทเรียน

การคูณทศนิยม

การคูณประกอบด้วยสามขั้นตอนติดต่อกัน:

1. สำหรับเศษส่วนแต่ละส่วน ให้จดส่วนที่มีนัยสำคัญ คุณจะได้รับจำนวนเต็มธรรมดาสองจำนวน - โดยไม่มีตัวส่วนและจุดทศนิยม
2. คูณตัวเลขเหล่านี้ด้วยวิธีที่สะดวก โดยตรงถ้าตัวเลขมีขนาดเล็กหรืออยู่ในคอลัมน์ เราได้ส่วนสำคัญของเศษส่วนที่ต้องการ
3. ค้นหาตำแหน่งและจำนวนหลักที่จุดทศนิยมถูกเลื่อนในเศษส่วนดั้งเดิมเพื่อให้ได้ส่วนที่มีนัยสำคัญที่สอดคล้องกัน ทำการย้อนกลับในส่วนสำคัญที่ได้รับในขั้นตอนก่อนหน้า

ผมขอเตือนคุณอีกครั้งว่าศูนย์ที่ด้านข้างของส่วนสำคัญจะไม่ถูกนำมาพิจารณา การละเว้นกฎนี้ทำให้เกิดข้อผิดพลาด

1. 0.28 12.5;
2. 6.3 1.08;
3. 132.5 0.0034;
4. 0.0108 1600.5;
5. 5.25 10,000.

เราทำงานกับนิพจน์แรก: 0.28 12.5

1. ลองเขียนส่วนสำคัญของตัวเลขจากนิพจน์นี้: 28 และ 125;
2. ผลิตภัณฑ์ของพวกเขา: 28 125 = 3500;
3. ในตัวคูณแรก จุดทศนิยมจะเลื่อนไปทางขวา 2 หลัก (0.28 → 28) และในหลักที่สอง - อีก 1 หลัก โดยรวมแล้วจำเป็นต้องเลื่อนไปทางซ้ายด้วยตัวเลขสามหลัก: 3500 → 3.500 = 3.5

ทีนี้มาจัดการกับนิพจน์ 6.3 1.08

1. มาเขียนส่วนสำคัญกัน: 63 และ 108;
2. ผลิตภัณฑ์ของพวกเขา: 63 108 = 6804;
3. อีกครั้ง เลื่อนไปทางขวาสองครั้ง: ทีละ 2 และ 1 หลักตามลำดับ ทั้งหมด - อีกครั้งทางขวา 3 หลัก ดังนั้นการเลื่อนย้อนกลับจะเป็น 3 หลักทางซ้าย: 6804 → 6.804 คราวนี้ไม่มีศูนย์ในตอนท้าย

เราได้นิพจน์ที่สาม: 132.5 0.0034

1. ส่วนสำคัญ: 1325 และ 34;
2. ผลิตภัณฑ์ของพวกเขา: 1325 34 = 45,050;
3. ในเศษส่วนแรก จุดทศนิยมไปทางขวา 1 หลัก และในส่วนที่สอง - มากถึง 4 ทั้งหมด: 5 ทางด้านขวา เราทำการเลื่อน 5 ไปทางซ้าย: 45050 → .45050 = 0.4505 ศูนย์จะถูกลบออกในตอนท้ายและเพิ่มที่ด้านหน้าเพื่อไม่ให้จุดทศนิยม "เปล่า"

นิพจน์ต่อไปนี้: 0.0108 1600.5

1. เราเขียนส่วนสำคัญ: 108 และ 16 005;
2. เราคูณมัน: 108 16 005 = 1 728 540;
3. เรานับตัวเลขหลังจุดทศนิยม: ในตัวเลขแรกมี 4 ในวินาที - 1 ทั้งหมด - อีกครั้ง 5. เรามี: 1,728,540 → 17.28540 = 17.2854 ในตอนท้าย ศูนย์ "พิเศษ" จะถูกลบออก

สุดท้าย นิพจน์สุดท้าย: 5.25 10,000

1. ส่วนสำคัญ: 525 และ 1;
2. เราคูณมัน: 525 1 = 525;
3. เศษส่วนแรกเลื่อนไปทางขวา 2 หลัก และเศษส่วนที่สองเลื่อนไปทางซ้าย 4 หลัก (10,000 → 1.0000 = 1) รวม 4 − 2 = 2 หลักทางซ้าย เราทำการย้อนกลับทางขวา 2 หลัก: 525, → 52 500 (เราต้องเพิ่มศูนย์)

ให้ความสนใจกับ ตัวอย่างสุดท้าย: เนื่องจากจุดทศนิยมเคลื่อนที่ไปในทิศทางที่ต่างกัน การเลื่อนทั้งหมดจึงผ่านส่วนต่าง นี้มันมาก จุดสำคัญ! นี่เป็นอีกตัวอย่างหนึ่ง:

พิจารณาตัวเลข 1.5 และ 12,500 เรามี: 1.5 → 15 (เลื่อนไปทางขวา 1); 12 500 → 125 (เลื่อน 2 ไปทางซ้าย) เรา "ก้าว" 1 หลักไปทางขวาแล้ว 2 หลักไปทางซ้าย เป็นผลให้เราก้าว 2 − 1 = 1 หลักไปทางซ้าย

ทศนิยม

ดิวิชั่นอาจจะเยอะที่สุด การดำเนินการที่ซับซ้อน. แน่นอน คุณสามารถกระทำโดยการเปรียบเทียบกับการคูณ: แบ่งส่วนสำคัญ แล้ว "ย้าย" จุดทศนิยม แต่ในกรณีนี้ มีรายละเอียดปลีกย่อยหลายอย่างที่ปฏิเสธการประหยัดที่อาจเกิดขึ้น

ลองดูอัลกอริธึมทั่วไปที่ยาวกว่าเล็กน้อย แต่น่าเชื่อถือกว่ามาก:

1. แปลงทศนิยมทั้งหมดให้เป็นเศษส่วนร่วม ด้วยการฝึกฝนเพียงเล็กน้อย ขั้นตอนนี้จะใช้เวลาไม่กี่วินาที
2. หารเศษส่วนที่เกิดขึ้นด้วยวิธีคลาสสิก กล่าวอีกนัยหนึ่งให้คูณเศษส่วนแรกด้วย "inverted" วินาที (ดูบทเรียน " การคูณและการหารเศษส่วนตัวเลข");
3. หากเป็นไปได้ ให้ส่งคืนผลลัพธ์เป็นทศนิยม ขั้นตอนนี้รวดเร็วเช่นกัน เพราะบ่อยครั้งที่ตัวส่วนมีกำลังสิบอยู่แล้ว

งาน. ค้นหาค่าของนิพจน์:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

เราพิจารณานิพจน์แรก ขั้นแรก ให้แปลงเศษส่วนโอบีเป็นทศนิยม:

เราทำเช่นเดียวกันกับนิพจน์ที่สอง ตัวเศษของเศษส่วนแรกจะถูกย่อยสลายเป็นตัวประกอบอีกครั้ง:

มีจุดสำคัญในตัวอย่างที่สามและสี่: หลังจากกำจัดสัญกรณ์ทศนิยมแล้ว เศษส่วนที่ยกเลิกได้จะปรากฏขึ้น อย่างไรก็ตาม เราจะไม่ดำเนินการลดหย่อนนี้

ตัวอย่างสุดท้ายน่าสนใจเพราะตัวเศษของเศษส่วนที่สองเป็นจำนวนเฉพาะ ไม่มีอะไรจะแยกตัวประกอบในที่นี้ ดังนั้นเราจึงถือว่า "ว่างเปล่า":

บางครั้งผลการหารเป็นจำนวนเต็ม (ฉันกำลังพูดถึงตัวอย่างสุดท้าย) ในกรณีนี้ จะไม่มีการดำเนินการขั้นตอนที่สามเลย

นอกจากนี้ เมื่อทำการหาร เศษส่วน "น่าเกลียด" มักจะปรากฏที่ไม่สามารถแปลงเป็นทศนิยมได้ นี่คือจุดที่การหารแตกต่างจากการคูณ โดยที่ผลลัพธ์จะแสดงในรูปแบบทศนิยมเสมอ แน่นอน ในกรณีนี้ ขั้นตอนสุดท้ายจะไม่ทำอีก

ให้ความสนใจกับตัวอย่างที่ 3 และ 4 ด้วย ในนั้น เราจงใจไม่ลดเศษส่วนธรรมดาที่ได้จากทศนิยม ไม่งั้นจะทำให้ยากขึ้น ปัญหาผกผัน- การแสดงคำตอบสุดท้ายในรูปแบบทศนิยมอีกครั้ง

ข้อควรจำ: คุณสมบัติพื้นฐานของเศษส่วน (เช่นเดียวกับกฎอื่นๆ ในวิชาคณิตศาสตร์) ไม่ได้หมายความว่าจะต้องนำไปใช้ทุกที่และทุกเวลา ในทุกโอกาส