สูตรการกระจายตัวของตัวแปรสุ่ม ความแปรปรวนและค่าเบี่ยงเบนมาตรฐานใน MS EXCEL

อย่างไรก็ตาม คุณลักษณะนี้เพียงอย่างเดียวไม่เพียงพอที่จะศึกษา ตัวแปรสุ่ม. ลองนึกภาพมือปืนสองคนที่กำลังยิงไปที่เป้าหมาย คนหนึ่งยิงแม่นและยิงใกล้จุดศูนย์กลาง และอีกคนหนึ่ง ... แค่สนุกและไม่ได้เล็ง แต่ที่ตลกคือ เฉลี่ยผลลัพธ์จะเหมือนกับการยิงครั้งแรก! สถานการณ์นี้แสดงให้เห็นตามเงื่อนไขโดยตัวแปรสุ่มต่อไปนี้:

"สไนเปอร์" มูลค่าที่คาดหวังเท่ากันอย่างไรก็ตามและ บุคลิกที่น่าสนใจ»: - มันก็เป็นศูนย์เช่นกัน!

จึงต้องคำนวณว่าไกลแค่ไหน กระจัดกระจายสัญลักษณ์แสดงหัวข้อย่อย (ค่าของตัวแปรสุ่ม) เทียบกับจุดศูนย์กลางของเป้าหมาย (ความคาดหวัง) ดีและ กระเจิงแปลจากภาษาละตินเท่านั้นเป็น การกระจายตัว .

เรามาดูกันว่าคุณลักษณะเชิงตัวเลขนี้ถูกกำหนดอย่างไรในตัวอย่างหนึ่งของบทเรียนที่ 1:

ที่นั่นเราพบความคาดหวังทางคณิตศาสตร์ที่น่าผิดหวังสำหรับเกมนี้ และตอนนี้เราต้องคำนวณความแปรปรวนของมัน ซึ่ง หมายถึงผ่าน .

มาดูกันว่าการชนะ/แพ้นั้น "กระจัดกระจาย" มากเพียงใดเมื่อเทียบกับค่าเฉลี่ย แน่นอน สำหรับสิ่งนี้เราต้องคำนวณ ความแตกต่างระหว่าง ค่าของตัวแปรสุ่มและเธอ ความคาดหวังทางคณิตศาสตร์:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

ตอนนี้ดูเหมือนว่าจะจำเป็นต้องสรุปผลลัพธ์ แต่วิธีนี้ไม่ดี - เพราะการแกว่งไปทางซ้ายจะตัดกันโดยมีการแกว่งไปทางขวา ตัวอย่างเช่น มือปืน "มือสมัครเล่น" (ตัวอย่างด้านบน)ความแตกต่างจะเป็น และเมื่อเพิ่มเข้าไป พวกเขาจะให้ศูนย์ ดังนั้นเราจะไม่ได้ค่าประมาณการกระเจิงของการยิงของเขา

เพื่อขจัดความรำคาญนี้ ให้พิจารณา โมดูลความแตกต่าง แต่ด้วยเหตุผลทางเทคนิค วิธีการได้หยั่งรากเมื่อถูกยกกำลังสอง สะดวกกว่าในการจัดเรียงโซลูชันในตาราง:

และนี่ก็ขอให้คำนวณ ค่าเฉลี่ยถ่วงน้ำหนักค่าของส่วนเบี่ยงเบนกำลังสอง มันคืออะไร? มันเป็นของพวกเขา มูลค่าที่คาดหวังซึ่งเป็นการวัดการกระเจิง:

– คำนิยามการกระจายตัว เป็นที่ชัดเจนทันทีจากคำจำกัดความที่ว่า ความแปรปรวนไม่สามารถเป็นลบได้- รับทราบเพื่อการปฏิบัติ!

มาจำกันว่าจะหาความคาดหวังได้อย่างไร คูณผลต่างกำลังสองด้วยความน่าจะเป็นที่สอดคล้องกัน (ต่อตาราง):
- เปรียบเปรย นี่คือ "แรงฉุด"
และสรุปผล:

คุณไม่คิดหรือว่าเมื่อเทียบกับเบื้องหลังของการชนะ ผลลัพธ์กลับกลายเป็นว่าใหญ่เกินไป? ถูกต้อง - เรากำลังยกกำลังสอง และเพื่อกลับไปยังมิติของเกม เราต้องหาสแควร์รูท ค่านี้เรียกว่า ส่วนเบี่ยงเบนมาตรฐาน และเขียนแทนด้วยอักษรกรีก "ซิกมา":

บางครั้งความหมายนี้เรียกว่า ส่วนเบี่ยงเบนมาตรฐาน .

ความหมายของมันคืออะไร? หากเราเบี่ยงเบนจากการคาดหมายทางคณิตศาสตร์ไปทางซ้ายและทางขวาโดยค่าเฉลี่ย ส่วนเบี่ยงเบนมาตรฐาน:

– จากนั้นค่าที่น่าจะเป็นไปได้มากที่สุดของตัวแปรสุ่มจะถูก "เข้มข้น" ในช่วงเวลานี้ สิ่งที่เราเห็นจริง:

อย่างไรก็ตาม มันเกิดขึ้นที่ในการวิเคราะห์การกระเจิงมักจะดำเนินการกับแนวคิดของการกระจายตัว เรามาดูกันว่ามันหมายถึงอะไรเกี่ยวกับเกม หากในกรณีของนักแม่นปืน เรากำลังพูดถึง "ความแม่นยำ" ของการยิงที่สัมพันธ์กับจุดศูนย์กลางของเป้าหมาย การกระจายตัวมีลักษณะสองประการดังนี้:

ประการแรก เห็นได้ชัดว่าเมื่ออัตราเพิ่มขึ้น ความแปรปรวนก็เพิ่มขึ้นเช่นกัน ตัวอย่างเช่น หากเราเพิ่มขึ้น 10 เท่า ความคาดหมายทางคณิตศาสตร์จะเพิ่มขึ้น 10 เท่า และความแปรปรวนจะเพิ่มขึ้น 100 เท่า (ทันทีที่มันเป็นค่ากำลังสอง). แต่โปรดทราบว่ากฎของเกมไม่เปลี่ยนแปลง! เฉพาะอัตราที่มีการเปลี่ยนแปลง พูดคร่าวๆ เราเคยเดิมพัน 10 รูเบิล ตอนนี้ 100

ประการที่สอง มากกว่า จุดที่น่าสนใจคือความแปรปรวนเป็นตัวกำหนดลักษณะของเกม จิตใจแก้ไขอัตราเกม ในระดับหนึ่งและดูว่ามีอะไรอยู่ที่นี่:

เกมที่มีความแปรปรวนต่ำเป็นเกมที่ระมัดระวัง ผู้เล่นมักจะเลือกแผนการที่น่าเชื่อถือที่สุด โดยที่เขาจะไม่แพ้/ชนะมากเกินไปในคราวเดียว ตัวอย่างเช่น ระบบสีแดง/ดำในรูเล็ต (ดูตัวอย่างที่ 4 ของบทความ ตัวแปรสุ่ม) .

เกมที่มีความแปรปรวนสูง เธอมักจะถูกเรียกว่า การกระจายตัวเกม. นี่คือรูปแบบการเล่นที่ท้าทายหรือดุดัน โดยผู้เล่นเลือกรูปแบบ "อะดรีนาลีน" อย่างน้อยก็จำไว้ "มาร์ติงเกล"ซึ่งผลรวมที่เดิมพันเป็นลำดับความสำคัญมากกว่าเกม "เงียบ" ของย่อหน้าก่อนหน้า

สถานการณ์ในโป๊กเกอร์เป็นสิ่งบ่งชี้: มีสิ่งที่เรียกว่า แน่นผู้เล่นที่มักจะระมัดระวังและ "สั่น" กับเงินในเกม (แบ๊งค์). ไม่น่าแปลกใจเลยที่เงินทุนของพวกเขาไม่ผันผวนมากนัก (ความแปรปรวนต่ำ) ในทางกลับกัน หากผู้เล่นมีความแปรปรวนสูงก็จะเป็นผู้รุกราน เขามักจะเสี่ยง วางเดิมพันขนาดใหญ่ และสามารถทำลายธนาคารขนาดใหญ่และพังทลายได้

สิ่งเดียวกันนี้เกิดขึ้นใน Forex และอื่นๆ - มีตัวอย่างมากมาย

ยิ่งกว่านั้นในทุกกรณี ไม่สำคัญว่าเกมจะจ่ายเพนนีหรือหลายพันดอลลาร์ ทุกระดับมีผู้เล่นที่มีความแปรปรวนต่ำและสูง สำหรับการชนะโดยเฉลี่ยอย่างที่เราจำได้ "รับผิดชอบ" มูลค่าที่คาดหวัง.

คุณอาจสังเกตเห็นว่าการค้นหาความแปรปรวนเป็นกระบวนการที่ยาวนานและต้องใช้ความอุตสาหะ แต่คณิตศาสตร์นั้นใจกว้าง:

สูตรการหาความแปรปรวน

สูตรนี้ได้มาจากคำจำกัดความของความแปรปรวนโดยตรง และเรานำมันเข้าสู่การหมุนเวียนทันที ฉันจะคัดลอกจานกับเกมของเราจากด้านบน:

และความคาดหวังที่พบ

เราคำนวณความแปรปรวนด้วยวิธีที่สอง อันดับแรก หาการคาดหมายทางคณิตศาสตร์ - กำลังสองของตัวแปรสุ่ม โดย คำจำกัดความของความคาดหวังทางคณิตศาสตร์:

ที่ กรณีนี้:

ดังนั้นตามสูตร:

อย่างที่พวกเขาพูด รู้สึกถึงความแตกต่าง และในทางปฏิบัติจะดีกว่าถ้าใช้สูตร (เว้นแต่เงื่อนไขจะเป็นอย่างอื่น)

เราเชี่ยวชาญเทคนิคการแก้ปัญหาและการออกแบบ:

ตัวอย่างที่ 6

หาค่าความคาดหมาย ความแปรปรวน และค่าเบี่ยงเบนมาตรฐานทางคณิตศาสตร์

งานนี้พบได้ทุกที่และตามกฎแล้วไปโดยไม่มีความหมายที่มีความหมาย
คุณสามารถจินตนาการถึงหลอดไฟหลายดวงที่มีตัวเลขที่ส่องสว่างในบ้านบ้าที่มีความเป็นไปได้บางอย่าง :)

วิธีการแก้: สะดวกในการสรุปการคำนวณหลักในตาราง ขั้นแรก เราเขียนข้อมูลเริ่มต้นในสองบรรทัดบน จากนั้นเราคำนวณผลิตภัณฑ์ จากนั้นจึงรวมผลรวมในคอลัมน์ด้านขวา:

อันที่จริงเกือบทุกอย่างพร้อมแล้ว ในบรรทัดที่สาม มีการวาดความคาดหวังทางคณิตศาสตร์สำเร็จรูป: .

การกระจายตัวคำนวณโดยสูตร:

และสุดท้าย ค่าเบี่ยงเบนมาตรฐาน:
- โดยส่วนตัวแล้ว ฉันมักจะปัดเศษทศนิยม 2 ตำแหน่ง

การคำนวณทั้งหมดสามารถทำได้โดยใช้เครื่องคิดเลข และดียิ่งขึ้นไปอีก - ใน Excel:

มันยากที่จะผิดพลาดที่นี่ :)

ตอบ:

ผู้ที่ต้องการสามารถทำให้ชีวิตของพวกเขาง่ายขึ้นและใช้ประโยชน์จากของฉัน เครื่องคิดเลข (การสาธิต)ซึ่งไม่เพียงแค่แก้ได้ทันที งานนี้แต่ยังสร้าง กราฟิกเฉพาะเรื่อง (มาเร็ว ๆ นี้). โปรแกรมสามารถ ดาวน์โหลดในห้องสมุด– หากคุณได้ดาวน์โหลดอย่างน้อยหนึ่ง สื่อการศึกษาหรือได้รับ อีกทางหนึ่ง. ขอบคุณสำหรับการสนับสนุนโครงการ!

งานสองสามอย่างสำหรับ โซลูชันอิสระ:

ตัวอย่าง 7

คำนวณความแปรปรวนของตัวแปรสุ่มของตัวอย่างก่อนหน้าตามคำจำกัดความ

และตัวอย่างที่คล้ายกัน:

ตัวอย่างที่ 8

ตัวแปรสุ่มแบบไม่ต่อเนื่องกำหนดโดยกฎการแจกแจงของมันเอง:

ใช่ ค่าของตัวแปรสุ่มอาจมีขนาดใหญ่มาก (ตัวอย่างจาก งานจริง) และที่นี่ ถ้าเป็นไปได้ ให้ใช้ Excel อีกอย่างในตัวอย่างที่ 7 มันเร็วกว่า น่าเชื่อถือกว่า และน่าพอใจมากกว่า

คำตอบและคำตอบที่ด้านล่างของหน้า

ในตอนท้ายของบทเรียนส่วนที่ 2 เราจะวิเคราะห์อีกครั้งหนึ่ง งานทั่วไปบางคนอาจพูดว่า rebus เล็ก ๆ :

ตัวอย่างที่ 9

ตัวแปรสุ่มแบบไม่ต่อเนื่องสามารถรับได้เพียงสองค่าเท่านั้น: และ , และ ทราบความน่าจะเป็น ความคาดหวังทางคณิตศาสตร์ และความแปรปรวน

วิธีการแก้: เริ่มจากความน่าจะเป็นที่ไม่รู้จักกันก่อน เนื่องจากตัวแปรสุ่มสามารถรับค่าได้เพียงสองค่า ดังนั้นผลรวมของความน่าจะเป็นของเหตุการณ์ที่เกี่ยวข้องกัน:

และตั้งแต่นั้นเป็นต้นมา

มันยังคงค้นหา ... พูดง่าย :) แต่เอาล่ะมันเริ่มแล้ว ตามคำจำกัดความของความคาดหวังทางคณิตศาสตร์:
- แทนที่ค่าที่รู้จัก:

- และไม่มีอะไรมากไปจากสมการนี้ ยกเว้นว่าคุณสามารถเขียนมันใหม่ในทิศทางปกติ:

หรือ:

อู๋ ขั้นตอนถัดไปฉันคิดว่าคุณสามารถเดาได้ มาสร้างและแก้ไขระบบกันเถอะ:

ทศนิยม- แน่นอนว่านี่เป็นความอัปยศอย่างสมบูรณ์ คูณสมการทั้งสองด้วย 10:

และหารด้วย 2:

นั่นดีกว่ามาก จากสมการที่ 1 เราแสดง:
(วิธีนี้ง่ายกว่า)- แทนที่ในสมการที่ 2:

เรากำลังสร้าง กำลังสองและทำให้เข้าใจง่าย:

เราคูณด้วย:

ผลที่ตามมา, สมการกำลังสอง, ค้นหาการเลือกปฏิบัติ:
- สมบูรณ์แบบ!

และเราได้รับสองวิธีแก้ไข:

1) ถ้า , แล้ว ;

2) ถ้า , แล้ว .

ค่าคู่แรกเป็นไปตามเงื่อนไข ด้วยความน่าจะเป็นสูง ทุกอย่างถูกต้อง แต่ถึงกระนั้น เราเขียนกฎการแจกจ่าย:

และดำเนินการตรวจสอบ กล่าวคือ ค้นหาความคาดหวัง:

ในหลายกรณี จำเป็นต้องแนะนำอีกเรื่องหนึ่ง ลักษณะเชิงตัวเลขเพื่อวัดระดับ กระจาย กระจายค่า, นำมาเป็นตัวแปรสุ่ม ξ รอบความคาดหวังทางคณิตศาสตร์

คำนิยาม.ความแปรปรวนของตัวแปรสุ่ม ξ เรียกว่าหมายเลข

ดี= M(ξ-M ξ) 2 . (1)

กล่าวอีกนัยหนึ่งการกระจายตัวคือความคาดหวังทางคณิตศาสตร์ของการเบี่ยงเบนกำลังสองของค่าตัวแปรสุ่มจากค่าเฉลี่ย

เรียกว่า ตารางการเบี่ยงเบน

ปริมาณ ξ .

ถ้าลักษณะการกระจายตัว ขนาดเฉลี่ยส่วนเบี่ยงเบนกำลังสอง ξ จาก Mξ,แล้วนับได้เป็นบางตัว ลักษณะเฉลี่ยค่าเบี่ยงเบนเองอย่างแม่นยำมากขึ้นขนาดของ | ξ-Mξ |.

คำจำกัดความ (1) หมายถึงคุณสมบัติสองประการต่อไปนี้ของการกระจายตัว

1. การกระจายตัว ค่าคงที่เท่ากับศูนย์ ซึ่งค่อนข้างสอดคล้องกับความหมายทางสายตาของการกระจายตัว เป็น "การวัดการแพร่กระจาย"

แท้จริงแล้วถ้า

ξ \u003d C,แล้ว Mξ = Cและนั่นก็หมายความว่า Dξ = M(C-C) 2 = เอ็ม 0 = 0.

2. เมื่อคูณตัวแปรสุ่ม ξ บน ค่าคงที่ด้วยความแปรปรวนของมันคูณด้วย C 2

D(Cξ .)) = ค 2 ดี . (3)

จริงๆ

D(Cξ) = M(C .)

= ม(C .

3. มีสูตรคำนวณความแปรปรวนดังต่อไปนี้:

. (4)

การพิสูจน์สูตรนี้สืบเนื่องมาจากคุณสมบัติของการคาดหมายทางคณิตศาสตร์

เรามี:

4. ถ้าค่า ξ 1 และ ξ 2 เป็นอิสระ จากนั้นความแปรปรวนของผลรวมจะเท่ากับผลรวมของความแปรปรวน:

การพิสูจน์ . ในการพิสูจน์ เราใช้คุณสมบัติของการคาดหมายทางคณิตศาสตร์ อนุญาต Mξ 1 = ม 1 , Mξ 2 = ม 2 แล้ว.

สูตร (5) ได้รับการพิสูจน์แล้ว

เนื่องจากความแปรปรวนของตัวแปรสุ่ม โดยนิยาม การคาดหมายทางคณิตศาสตร์ของค่า ( ξ-m) 2 , โดยที่ ม = Mξ ,จากนั้นในการคำนวณความแปรปรวน คุณสามารถใช้สูตรที่ได้รับในส่วนที่ 7 บทที่ II

ดังนั้นถ้า ξ มี DSV ที่มีกฎหมายการจัดจำหน่าย

x 1	x 2	...
พี 1	พี 2	...

แล้วเราจะได้:

. (7)

ถ้า ξ ตัวแปรสุ่มต่อเนื่องที่มีความหนาแน่นการกระจาย พี(x)จากนั้นเราได้รับ:

ดี= . (8)

หากใช้สูตร (4) ในการคำนวณความแปรปรวน ก็สามารถหาสูตรอื่นๆ ได้ กล่าวคือ:

, (9)

ถ้าค่า ξ ไม่ต่อเนื่องและ

ดี= , (10)

ถ้า ξ กระจายอย่างหนาแน่น พี(x).

ตัวอย่างที่ 1 . ให้ค่า ξ มีการกระจายอย่างสม่ำเสมอบนเซ็กเมนต์ [ a,b]. ใช้สูตร (10) เราได้รับ:

สามารถแสดงว่าความแปรปรวนของตัวแปรสุ่มกระจายตามกฎปกติที่มีความหนาแน่น

พี(x)= , (11)

เท่ากับ σ 2

อธิบายความหมายของพารามิเตอร์ σ ที่รวมอยู่ในนิพจน์ความหนาแน่น (11) for กฎหมายปกติ; σ มีค่าเฉลี่ย ส่วนเบี่ยงเบนมาตรฐานปริมาณ ξ.

ตัวอย่างที่ 2 . ค้นหาความแปรปรวนของตัวแปรสุ่ม ξ กระจายตามกฎทวินาม

วิธีการแก้ . การใช้แทน ξ ในรูปแบบ

ξ = ξ 1 + ξ 2 + น(ดูตัวอย่างที่ 2 §7 ch. II) และนำสูตรมาบวกความแปรปรวนของ ตัวแปรอิสระ, เราได้รับ

ดξ = ด 1 + ด 2 + เหนียง .

การกระจายของปริมาณใด ๆ ξi (ผม= 1,2, น) คำนวณโดยตรง:

Dξi = M(ξi .)) 2 - (ฉัน) 2 = 0 2 q+ 1 2 พี- พี 2 = พี(1-พี) = pq.

ในที่สุดเราก็ได้

ดี= npq, ที่ไหน q = 1 -p.

สำหรับข้อมูลที่จัดกลุ่ม การกระจายตัวของสารตกค้าง - ค่าเฉลี่ยของ ความแปรปรวนภายในกลุ่ม:

โดยที่ σ 2 j คือความแปรปรวนภายในกลุ่มของกลุ่ม j -th

สำหรับข้อมูลที่ไม่ได้จัดกลุ่ม การกระจายตัวของสารตกค้างเป็นการวัดความแม่นยําโดยประมาณ กล่าวคือ การประมาณเส้นการถดถอยกับข้อมูลเดิม:
โดยที่ y(t) คือการคาดการณ์ตามสมการแนวโน้ม y เสื้อ – ชุดเริ่มต้นของไดนามิก; n คือจำนวนคะแนน p คือจำนวนสัมประสิทธิ์ของสมการถดถอย (จำนวนตัวแปรอธิบาย)
ในตัวอย่างนี้เรียกว่า ค่าประมาณความแปรปรวนที่ไม่เอนเอียง.

ตัวอย่าง # 1 การกระจายคนงานของสามองค์กรของหนึ่งสมาคมตามหมวดหมู่ภาษีมีลักษณะตามข้อมูลต่อไปนี้:

หมวดหมู่ค่าจ้างแรงงาน	จำนวนคนงานในสถานประกอบการ
	องค์กร 1	องค์กร 2	องค์กร 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

กำหนด:
1. การกระจายตัวสำหรับแต่ละองค์กร (การกระจายภายในกลุ่ม);
2. ค่าเฉลี่ยของการกระจายภายในกลุ่ม
3. การกระจายตัวระหว่างกลุ่ม
4. ผลต่างทั้งหมด.

วิธีการแก้.
ก่อนดำเนินการแก้ไขปัญหา คุณจำเป็นต้องค้นหาว่าคุณลักษณะใดมีประสิทธิภาพและคุณลักษณะใดเป็นแฟกทอเรียล ในตัวอย่างที่พิจารณา คุณลักษณะที่มีผลคือ "หมวดหมู่ภาษี" และคุณลักษณะปัจจัยคือ "หมายเลข (ชื่อ) ขององค์กร"
จากนั้นเรามีสามกลุ่ม (องค์กร) ซึ่งจำเป็นต้องคำนวณค่าเฉลี่ยของกลุ่มและความแปรปรวนภายในกลุ่ม:

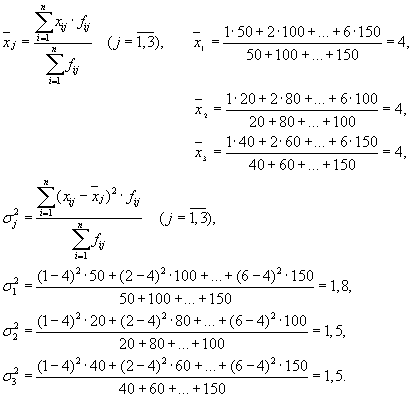
บริษัท	ค่าเฉลี่ยของกลุ่ม	ความแปรปรวนภายในกลุ่ม
1	4	1,8

ค่าเฉลี่ยของความแปรปรวนภายในกลุ่ม ( การกระจายตัวของสารตกค้าง) คำนวณโดยสูตร:

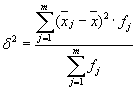
ที่คุณสามารถคำนวณ:
หรือ:

แล้ว:
การกระจายทั้งหมดจะเท่ากับ: s 2 \u003d 1.6 + 0 \u003d 1.6
ค่าความแปรปรวนรวมสามารถคำนวณได้โดยใช้หนึ่งในสองสูตรต่อไปนี้:

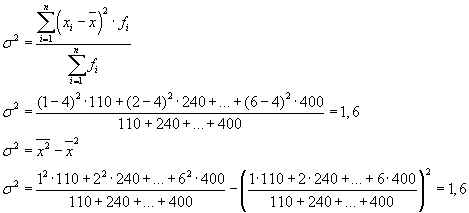
เมื่อแก้ปัญหาในทางปฏิบัติ เรามักจะต้องจัดการกับเครื่องหมายที่ใช้ค่าทางเลือกเพียงสองค่าเท่านั้น ในกรณีนี้ พวกเขาไม่ได้พูดถึงน้ำหนักของค่าเฉพาะของจุดสนใจ แต่เกี่ยวกับส่วนแบ่งโดยรวม หากสัดส่วนของหน่วยประชากรที่มีลักษณะภายใต้การศึกษาแสดงด้วย " R"และไม่ครอบครอง - ผ่าน" q” จากนั้นสามารถคำนวณการกระจายโดยสูตร:
s 2 = p×q

ตัวอย่าง # 2 ตามข้อมูลการพัฒนาคนงานหกคนในกองพลน้อย ให้กำหนดความแปรปรวนระหว่างกลุ่มและประเมินผลกระทบของกะการทำงานที่มีต่อผลิตภาพแรงงานของพวกเขา หากความแปรปรวนทั้งหมดเท่ากับ 12.2

จำนวนกองพลทำงาน	ผลงานชิ้น
	ในกะแรก	ในกะที่ 2
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

วิธีการแก้. ข้อมูลเบื้องต้น

X	f1	f2	ฉ 3	f4	f5	f6	ทั้งหมด
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
ทั้งหมด	31	33	37	37	40	38

จากนั้นเรามี 6 กลุ่มซึ่งจำเป็นต้องคำนวณค่าเฉลี่ยของกลุ่มและความแปรปรวนภายในกลุ่ม
1. หาค่าเฉลี่ยของแต่ละกลุ่ม.







2. หาค่าเฉลี่ยกำลังสองของแต่ละกลุ่ม.







เราสรุปผลการคำนวณในตาราง:

หมายเลขกลุ่ม	ค่าเฉลี่ยของกลุ่ม	ความแปรปรวนภายในกลุ่ม
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. ความแปรปรวนภายในกลุ่มกำหนดลักษณะการเปลี่ยนแปลง (การเปลี่ยนแปลง) ของลักษณะที่ศึกษา (ผลลัพธ์) ภายในกลุ่มภายใต้อิทธิพลของปัจจัยทั้งหมด ยกเว้นปัจจัยที่อยู่ภายใต้การจัดกลุ่ม:
เราคำนวณค่าเฉลี่ยของการกระจายภายในกลุ่มโดยใช้สูตร:


4. ความแปรปรวนระหว่างกลุ่มแสดงลักษณะการเปลี่ยนแปลง (ความแปรผัน) ของลักษณะที่ศึกษา (ผลลัพธ์) ภายใต้อิทธิพลของปัจจัย (ลักษณะแฟกทอเรียล) ที่อยู่ภายใต้การจัดกลุ่ม
การกระจายตัวระหว่างกลุ่มถูกกำหนดเป็น:

ที่ไหน


แล้ว

ผลต่างทั้งหมดแสดงลักษณะการเปลี่ยนแปลง (การเปลี่ยนแปลง) ของลักษณะที่ศึกษา (ผลลัพธ์) ภายใต้อิทธิพลของปัจจัยทั้งหมด (ลักษณะแฟกทอเรียล) โดยไม่มีข้อยกเว้น โดยเงื่อนไขของปัญหาจะเท่ากับ 12.2
ความสัมพันธ์เชิงประจักษ์วัดว่าความผันผวนทั้งหมดของแอตทริบิวต์ที่เป็นผลลัพธ์นั้นเกิดจากปัจจัยที่ศึกษามากเพียงใด นี่คืออัตราส่วนของความแปรปรวนแฟกทอเรียลต่อความแปรปรวนทั้งหมด:

เรากำหนดความสัมพันธ์เชิงประจักษ์:

ความสัมพันธ์ระหว่างจุดสนใจอาจอ่อนแอหรือแข็งแกร่ง (ใกล้เคียง) เกณฑ์ของพวกเขาได้รับการประเมินในระดับแชดด็อค:
0.1 0.3 0.5 0.7 0.9 ในตัวอย่างของเรา ความสัมพันธ์ระหว่างคุณลักษณะ Y ปัจจัย X นั้นอ่อนแอ
สัมประสิทธิ์ความมุ่งมั่น

มากำหนดสัมประสิทธิ์ของการกำหนด:

ดังนั้น 0.67% ของความผันแปรเกิดจากความแตกต่างระหว่างคุณลักษณะ และ 99.37% เกิดจากปัจจัยอื่นๆ
บทสรุป: ในกรณีนี้ ผลลัพธ์ของคนงานไม่ได้ขึ้นอยู่กับงานในกะเฉพาะ เช่น อิทธิพลของกะการทำงานที่มีต่อผลิตภาพแรงงานไม่มีนัยสำคัญและเกิดจากปัจจัยอื่นๆ

ตัวอย่าง #3 อิงจากค่าเฉลี่ย ค่าจ้างและค่าเบี่ยงเบนยกกำลังสองจากค่าของมันสำหรับคนทำงานสองกลุ่ม ให้หาค่าความแปรปรวนทั้งหมดโดยใช้กฎสำหรับการบวกความแปรปรวน:

วิธีการแก้:
ค่าเฉลี่ยของผลต่างภายในกลุ่ม

การกระจายตัวระหว่างกลุ่มถูกกำหนดเป็น:


ความแปรปรวนทั้งหมดจะเป็น: 480 + 13824 = 14304

ตัวบ่งชี้ทั่วไปหลักของการเปลี่ยนแปลงในสถิติคือการกระจายตัวและส่วนเบี่ยงเบนมาตรฐาน

การกระจายตัว มัน เลขคณิต ส่วนเบี่ยงเบนกำลังสองของค่าคุณลักษณะแต่ละค่าจากค่าเฉลี่ยทั้งหมด ความแปรปรวนมักจะเรียกว่ากำลังสองเฉลี่ยของส่วนเบี่ยงเบนและแสดงแทน  2 . ขึ้นอยู่กับข้อมูลเริ่มต้น ความแปรปรวนสามารถคำนวณได้จากค่าเฉลี่ยเลขคณิต แบบง่าย หรือแบบถ่วงน้ำหนัก:

 การกระจายตัวแบบไม่ถ่วงน้ำหนัก (แบบง่าย)

 ความแปรปรวนถ่วงน้ำหนัก

ส่วนเบี่ยงเบนมาตรฐาน เป็นลักษณะทั่วไปของมิติสัมบูรณ์ รูปแบบต่างๆ ลักษณะโดยรวม มันถูกแสดงในหน่วยเดียวกับเครื่องหมาย (เป็นเมตร, ตัน, เปอร์เซ็นต์, เฮกตาร์, ฯลฯ )

ค่าเบี่ยงเบนมาตรฐานคือรากที่สองของความแปรปรวนและเขียนแทนด้วย :

 ส่วนเบี่ยงเบนมาตรฐานไม่ถ่วงน้ำหนัก

 ค่าเบี่ยงเบนมาตรฐานถ่วงน้ำหนัก

ค่าเบี่ยงเบนมาตรฐานเป็นตัววัดความน่าเชื่อถือของค่าเฉลี่ย ยิ่งค่าเบี่ยงเบนมาตรฐานน้อยกว่า ค่าเฉลี่ยเลขคณิตจะสะท้อนประชากรทั้งหมดได้ดีกว่า

การคำนวณค่าเบี่ยงเบนมาตรฐานนำหน้าด้วยการคำนวณค่าความแปรปรวน

ขั้นตอนการคำนวณความแปรปรวนถ่วงน้ำหนักมีดังนี้:

1) กำหนดค่าเฉลี่ยถ่วงน้ำหนักเลขคณิต:

2) คำนวณค่าเบี่ยงเบนของตัวเลือกจากค่าเฉลี่ย:

3) ยกกำลังส่วนเบี่ยงเบนของแต่ละตัวเลือกจากค่าเฉลี่ย:

4) คูณค่าเบี่ยงเบนกำลังสองด้วยน้ำหนัก (ความถี่):

5) สรุปผลงานที่ได้รับ:

6) จำนวนผลลัพธ์หารด้วยผลรวมของน้ำหนัก:

ตัวอย่าง 2.1

คำนวณค่าเฉลี่ยถ่วงน้ำหนักเลขคณิต:

ค่าเบี่ยงเบนจากค่าเฉลี่ยและกำลังสองแสดงในตาราง มานิยามความแปรปรวนกัน:

ส่วนเบี่ยงเบนมาตรฐานจะเท่ากับ:

หากข้อมูลต้นทางถูกนำเสนอเป็นช่วงเวลา ชุดจำหน่าย จากนั้นคุณต้องกำหนดค่าที่ไม่ต่อเนื่องของคุณลักษณะ จากนั้นใช้วิธีที่อธิบายไว้

ตัวอย่าง 2.2

ให้เราแสดงการคำนวณความแปรปรวนสำหรับชุดช่วงเวลาเกี่ยวกับข้อมูลเกี่ยวกับการกระจายพื้นที่หว่านของฟาร์มส่วนรวมด้วยผลผลิตข้าวสาลี

ค่าเฉลี่ยเลขคณิตคือ:

ลองคำนวณความแปรปรวน:

6.3. การคำนวณการกระจายตามสูตรสำหรับข้อมูลแต่ละส่วน

เทคนิคการคำนวณ การกระจายตัว ซับซ้อนและ คุณค่ามหาศาลตัวเลือกและความถี่อาจยุ่งยาก การคำนวณสามารถทำให้ง่ายขึ้นได้โดยใช้คุณสมบัติการกระจาย

การกระจายมีคุณสมบัติดังต่อไปนี้

1. การลดลงหรือเพิ่มขึ้นในน้ำหนัก (ความถี่) ของคุณลักษณะตัวแปรตามจำนวนครั้งที่กำหนดจะไม่เปลี่ยนการกระจาย

2. ลดหรือเพิ่มค่าคุณลักษณะแต่ละค่าด้วยค่าคงที่เท่ากัน แต่การกระจายตัวไม่เปลี่ยนแปลง

3. ลดหรือเพิ่มค่าคุณสมบัติแต่ละค่าตามจำนวนครั้งที่กำหนด kลดหรือเพิ่มความแปรปรวนตามลำดับใน k 2 ครั้ง ส่วนเบี่ยงเบนมาตรฐาน  ใน kครั้งหนึ่ง.

4. ความแปรปรวนของจุดสนใจที่สัมพันธ์กับค่าที่กำหนดเองมักจะมากกว่าความแปรปรวนที่สัมพันธ์กับค่าเฉลี่ยเลขคณิตด้วยกำลังสองของผลต่างระหว่างค่าเฉลี่ยและค่าที่กำหนดเอง:

ถ้า แต่ 0 แล้วเราก็มาถึงความเท่าเทียมกันดังต่อไปนี้:

กล่าวคือ ความแปรปรวนของจุดสนใจเท่ากับผลต่างระหว่างค่าเฉลี่ยกำลังสองของค่าคุณลักษณะและกำลังสองของค่าเฉลี่ย

แต่ละคุณสมบัติสามารถใช้เดี่ยวๆ หรือใช้ร่วมกับคุณสมบัติอื่นๆ เมื่อคำนวณความแปรปรวน

ขั้นตอนการคำนวณความแปรปรวนนั้นง่าย:

1) กำหนด เลขคณิต :

2) ยกกำลังสองค่าเฉลี่ยเลขคณิต:

3) ยกกำลังส่วนเบี่ยงเบนของแต่ละตัวแปรในซีรีส์:

X ผม 2 .

4) ค้นหาผลรวมของตัวเลือกกำลังสอง:

5) หารผลรวมของกำลังสองของตัวเลือกด้วยจำนวนของมัน นั่นคือ กำหนดกำลังสองเฉลี่ย:

6) กำหนดความแตกต่างระหว่างกำลังสองเฉลี่ยของจุดสนใจและกำลังสองของค่าเฉลี่ย:

ตัวอย่าง 3.1เรามีข้อมูลต่อไปนี้เกี่ยวกับประสิทธิภาพการทำงานของพนักงาน:

มาทำการคำนวณต่อไปนี้:

การกระจายตัวของตัวแปรสุ่มคือการวัดการแพร่กระจายของค่าของตัวแปรนี้ ความแปรปรวนเล็กน้อยหมายความว่าค่าต่างๆ ถูกจัดกลุ่มอยู่ใกล้กัน ความแปรปรวนขนาดใหญ่บ่งบอกถึงค่าที่กระจัดกระจายอย่างมาก แนวคิดของการกระจายตัวของตัวแปรสุ่มถูกใช้ในสถิติ ตัวอย่างเช่น หากคุณเปรียบเทียบความแปรปรวนของค่าของสองปริมาณ (เช่น ผลการสังเกตของผู้ป่วยชายและหญิง) คุณสามารถทดสอบความสำคัญของตัวแปรบางตัวได้ ความแปรปรวนยังใช้ในการสร้าง แบบจำลองทางสถิติเนื่องจากความแปรปรวนเล็กน้อยอาจเป็นสัญญาณว่าคุณมีค่ามากเกินไป

ขั้นตอน

การคำนวณความแปรปรวนตัวอย่าง

1. บันทึกค่าตัวอย่างในกรณีส่วนใหญ่ นักสถิติจะมีเฉพาะกลุ่มตัวอย่างบางกลุ่มเท่านั้น ตัวอย่างเช่นตามกฎแล้วนักสถิติจะไม่วิเคราะห์ค่าใช้จ่ายในการบำรุงรักษารถยนต์ทุกคันในรัสเซีย - พวกเขาวิเคราะห์ สุ่มตัวอย่างจากรถหลายพันคัน ตัวอย่างดังกล่าวจะช่วยกำหนดต้นทุนเฉลี่ยต่อคัน แต่ส่วนใหญ่แล้วมูลค่าที่ได้จะห่างไกลจากของจริง

   • ตัวอย่างเช่น ลองวิเคราะห์จำนวนขนมปังที่ขายในร้านกาแฟใน 6 วัน โดยสุ่มลำดับ ตัวอย่างมี มุมมองถัดไป: 17, 15, 23, 7, 9, 13 นี่เป็นตัวอย่าง ไม่ใช่ประชากร เพราะเราไม่มีข้อมูลขนมปังที่ขายในแต่ละวันที่เปิดร้านกาแฟ
   • หากคุณได้รับประชากรและไม่ใช่ตัวอย่างค่า ให้ข้ามไปยังส่วนถัดไป

2. เขียนสูตรคำนวณความแปรปรวนตัวอย่างการกระจายตัวคือการวัดการแพร่กระจายของค่าของปริมาณบางอย่าง ยิ่งค่าการกระจายตัวเป็นศูนย์มากเท่าใด ค่าต่างๆ จะถูกจัดกลุ่มไว้ใกล้กันมากขึ้นเท่านั้น เมื่อทำงานกับตัวอย่างค่า ให้ใช้สูตรต่อไปนี้เพื่อคำนวณความแปรปรวน:

   • s 2 (\displaystyle s^(2)) = ∑[(x ฉัน (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))] / (n - 1)
   • s 2 (\displaystyle s^(2))คือการกระจายตัว การกระจายตัววัดเป็น ตารางหน่วยการวัด
   • x ฉัน (\displaystyle x_(i))- แต่ละค่าในตัวอย่าง
   • x ฉัน (\displaystyle x_(i))คุณต้องลบ x̅ ยกกำลังสอง แล้วบวกผลลัพธ์
   • x̅ – ค่าเฉลี่ยตัวอย่าง (ค่าเฉลี่ยตัวอย่าง)
   • n คือจำนวนค่าในกลุ่มตัวอย่าง

3. คำนวณค่าเฉลี่ยตัวอย่างมันแสดงเป็น x̅ ค่าเฉลี่ยตัวอย่างคำนวณเหมือนค่าเฉลี่ยเลขคณิตปกติ: บวกค่าทั้งหมดในตัวอย่างแล้วหารผลลัพธ์ด้วยจำนวนค่าในกลุ่มตัวอย่าง

   • ในตัวอย่างของเรา เพิ่มค่าในตัวอย่าง: 15 + 17 + 23 + 7 + 9 + 13 = 84
     ตอนนี้หารผลลัพธ์ด้วยจำนวนค่าในกลุ่มตัวอย่าง (ในตัวอย่างของเราคือ 6): 84 ÷ 6 = 14
     ค่าเฉลี่ยตัวอย่าง x̅ = 14
   • ค่าเฉลี่ยตัวอย่างคือค่ากลางที่มีการกระจายค่าในกลุ่มตัวอย่าง หากค่าในกลุ่มตัวอย่างรอบค่าเฉลี่ยตัวอย่าง ความแปรปรวนจะมีน้อย มิฉะนั้นการกระจายตัวจะมีขนาดใหญ่

4. ลบค่าเฉลี่ยตัวอย่างออกจากแต่ละค่าในกลุ่มตัวอย่างตอนนี้คำนวณส่วนต่าง x ฉัน (\displaystyle x_(i))- x̅ โดยที่ x ฉัน (\displaystyle x_(i))- แต่ละค่าในตัวอย่าง ผลลัพธ์แต่ละรายการที่ได้รับจะระบุขอบเขตที่ค่าใดค่าหนึ่งเบี่ยงเบนไปจากค่าเฉลี่ยตัวอย่าง นั่นคือ ค่านี้อยู่ห่างจากค่าเฉลี่ยตัวอย่างมากเพียงใด

   • ในตัวอย่างของเรา:
     x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
     x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
     x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
     x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
     x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
     x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
   • ความถูกต้องของผลลัพธ์ที่ได้นั้นง่ายต่อการตรวจสอบ เนื่องจากผลรวมต้องเท่ากับศูนย์ สิ่งนี้เกี่ยวข้องกับคำจำกัดความของค่าเฉลี่ยเนื่องจาก ค่าลบ(ระยะทางจากค่าเฉลี่ยถึงค่าที่น้อยกว่า) ได้รับการชดเชยอย่างเต็มที่ ค่าบวก(ระยะทางจากค่าเฉลี่ยไปจนถึงค่ามาก)

5. ตามที่ระบุไว้ข้างต้น ผลรวมของความแตกต่าง x ฉัน (\displaystyle x_(i))- x̅ ต้องเท่ากับศูนย์ หมายความว่า ความแปรปรวนเฉลี่ยมีค่าเท่ากับศูนย์เสมอซึ่งไม่ได้ให้ความคิดใด ๆ เกี่ยวกับการแพร่กระจายของค่าของปริมาณที่แน่นอน เพื่อแก้ปัญหานี้ ยกกำลังสองส่วนต่างออก x ฉัน (\displaystyle x_(i))- x̅. ซึ่งจะส่งผลให้คุณได้รับเพียง ตัวเลขบวกซึ่งเมื่อเพิ่มแล้วจะไม่ให้ 0

   • ในตัวอย่างของเรา:
     (x 1 (\displaystyle x_(1))-x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
     (x 2 (\displaystyle (x_(2))-x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
     9 2 = 81
     (-7) 2 = 49
     (-5) 2 = 25
     (-1) 2 = 1
   • คุณพบกำลังสองของความแตกต่างแล้ว - x̅) 2 (\displaystyle ^(2))สำหรับแต่ละค่าในตัวอย่าง

6. คำนวณผลรวมของผลต่างกำลังสองนั่นคือ หาส่วนของสูตรที่เขียนดังนี้ ∑[( x ฉัน (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))]. ในที่นี้เครื่องหมาย Σ หมายถึงผลรวมของผลต่างกำลังสองสำหรับแต่ละค่า x ฉัน (\displaystyle x_(i))ในตัวอย่าง คุณได้พบความแตกต่างกำลังสองแล้ว (x ฉัน (\displaystyle (x_(i))-x̅) 2 (\displaystyle ^(2))สำหรับแต่ละค่า x ฉัน (\displaystyle x_(i))ในตัวอย่าง; ตอนนี้เพียงแค่เพิ่มสี่เหลี่ยมเหล่านี้

   • ในตัวอย่างของเรา: 9 + 1 + 81 + 49 + 25 + 1 = 166 .

7. หารผลลัพธ์ด้วย n - 1 โดยที่ n คือจำนวนค่าในกลุ่มตัวอย่างเมื่อไม่นานมานี้ ในการคำนวณความแปรปรวนตัวอย่าง นักสถิติเพียงหารผลลัพธ์ด้วย n; ในกรณีนี้ คุณจะได้ค่าเฉลี่ยของความแปรปรวนกำลังสอง ซึ่งเหมาะสำหรับการอธิบายความแปรปรวนของกลุ่มตัวอย่างที่กำหนด แต่จำไว้ว่าตัวอย่างใด ๆ เป็นเพียงส่วนเล็ก ๆ ประชากรค่า หากคุณใช้ตัวอย่างอื่นและทำการคำนวณแบบเดียวกัน คุณจะได้ผลลัพธ์ที่ต่างออกไป เมื่อมันปรากฏออกมา การหารด้วย n - 1 (ไม่ใช่แค่ n) ให้มากกว่า ประมาณการที่แม่นยำความแปรปรวนของประชากร ซึ่งเป็นสิ่งที่คุณสนใจ การหารด้วย n - 1 กลายเป็นเรื่องธรรมดา ดังนั้นจึงรวมอยู่ในสูตรสำหรับคำนวณความแปรปรวนของตัวอย่าง

   • ในตัวอย่างของเรา ตัวอย่างประกอบด้วย 6 ค่า นั่นคือ n = 6
     ความแปรปรวนตัวอย่าง = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2

8. ความแตกต่างระหว่างความแปรปรวนและค่าเบี่ยงเบนมาตรฐานโปรดทราบว่าสูตรประกอบด้วยเลขชี้กำลัง ดังนั้นความแปรปรวนจะถูกวัดเป็นหน่วยกำลังสองของค่าที่วิเคราะห์ บางครั้งค่าดังกล่าวค่อนข้างยากที่จะดำเนินการ ในกรณีเช่นนี้ ให้ใช้ค่าเบี่ยงเบนมาตรฐานซึ่งเท่ากับ รากที่สองจากการกระจายตัว นั่นคือเหตุผลที่ความแปรปรวนตัวอย่างแสดงเป็น s 2 (\displaystyle s^(2)), แ ส่วนเบี่ยงเบนมาตรฐานตัวอย่าง - อย่างไร s (\displaystyle s).

   • ในตัวอย่างของเรา ค่าเบี่ยงเบนมาตรฐานของตัวอย่างคือ: s = √33.2 = 5.76

   การคำนวณความแปรปรวนของประชากร

   1. วิเคราะห์ชุดค่าบางชุดชุดประกอบด้วยค่าทั้งหมดของปริมาณที่พิจารณา ตัวอย่างเช่น ถ้าคุณศึกษาอายุของผู้อยู่อาศัย ภูมิภาคเลนินกราดจากนั้นประชากรจะรวมถึงอายุของผู้อยู่อาศัยในพื้นที่นี้ทั้งหมด ในกรณีที่ทำงานกับการรวม ขอแนะนำให้สร้างตารางและป้อนค่าของการรวมลงในตาราง พิจารณาตัวอย่างต่อไปนี้:

      • มีพิพิธภัณฑ์สัตว์น้ำ 6 แห่งในห้องหนึ่ง พิพิธภัณฑ์สัตว์น้ำแต่ละแห่งมีปลาจำนวนดังต่อไปนี้:
        x 1 = 5 (\displaystyle x_(1)=5)
        x 2 = 5 (\displaystyle x_(2)=5)
        x 3 = 8 (\displaystyle x_(3)=8)
        x 4 = 12 (\displaystyle x_(4)=12)
        x 5 = 15 (\displaystyle x_(5)=15)
        x 6 = 18 (\displaystyle x_(6)=18)

   2. เขียนสูตรคำนวณความแปรปรวนของประชากรเนื่องจากประชากรมีค่าทั้งหมดของปริมาณที่แน่นอน สูตรต่อไปนี้จึงช่วยให้คุณได้ค่าที่แน่นอนของความแปรปรวนของประชากร ในการแยกแยะความแปรปรวนของประชากรออกจากความแปรปรวนตัวอย่าง (ซึ่งเป็นเพียงการประมาณการ) นักสถิติใช้ตัวแปรต่างๆ:

      • σ 2 (\displaystyle ^(2)) = (∑(x ฉัน (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / น
      • σ 2 (\displaystyle ^(2))- ความแปรปรวนของประชากร (อ่านว่า "ซิกมากำลังสอง") การกระจายตัววัดเป็นหน่วยตารางหน่วย
      • x ฉัน (\displaystyle x_(i))- แต่ละค่าในการรวม
      • Σ เป็นเครื่องหมายของผลรวม นั่นคือสำหรับแต่ละค่า x ฉัน (\displaystyle x_(i))ลบ μ ยกกำลังสอง แล้วบวกผลลัพธ์
      • μ คือค่าเฉลี่ยประชากร
      • n คือจำนวนค่าในประชากรทั่วไป

   3. คำนวณค่าเฉลี่ยประชากรเมื่อทำงานกับประชากรทั่วไป ค่าเฉลี่ยจะแสดงเป็น μ (mu) ค่าเฉลี่ยประชากรคำนวณเป็นค่าเฉลี่ยเลขคณิต: รวมค่าทั้งหมดในประชากรแล้วหารผลลัพธ์ด้วยจำนวนค่าในประชากร

      • โปรดทราบว่าค่าเฉลี่ยไม่ได้คำนวณเป็นค่าเฉลี่ยเลขคณิตเสมอไป
      • ในตัวอย่างของเรา ค่าเฉลี่ยประชากร: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5

   4. ลบค่าเฉลี่ยประชากรออกจากแต่ละค่าในประชากรยิ่งค่าผลต่างเข้าใกล้ศูนย์มากเท่าใด ค่าเฉพาะก็จะยิ่งใกล้ค่าเฉลี่ยประชากรมากขึ้นเท่านั้น ค้นหาความแตกต่างระหว่างแต่ละค่าในประชากรและค่าเฉลี่ย แล้วคุณจะได้ดูการกระจายของค่านั้นก่อน

      • ในตัวอย่างของเรา:
        x 1 (\displaystyle x_(1))- μ = 5 - 10.5 = -5.5
        x 2 (\displaystyle x_(2))- μ = 5 - 10.5 = -5.5
        x 3 (\displaystyle x_(3))- μ = 8 - 10.5 = -2.5
        x 4 (\displaystyle x_(4))- μ = 12 - 10.5 = 1.5
        x 5 (\displaystyle x_(5))- μ = 15 - 10.5 = 4.5
        x 6 (\displaystyle x_(6))- μ = 18 - 10.5 = 7.5

   5. ยกกำลังสองผลลัพธ์ที่คุณได้รับค่าความแตกต่างจะเป็นทั้งค่าบวกและค่าลบ หากคุณใส่ค่าเหล่านี้บนเส้นจำนวน ค่าเหล่านี้จะอยู่ทางขวาและซ้ายของค่าเฉลี่ยประชากร ไม่เหมาะสำหรับการคำนวณความแปรปรวนเนื่องจากเป็นบวกและ ตัวเลขติดลบชดเชยซึ่งกันและกัน ดังนั้น ยกกำลังสองส่วนต่างเพื่อให้ได้จำนวนบวกโดยเฉพาะ

      • ในตัวอย่างของเรา:
        (x ฉัน (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))สำหรับแต่ละค่าประชากร (จาก i = 1 ถึง i = 6):
        (-5,5)2 (\displaystyle ^(2)) = 30,25
        (-5,5)2 (\displaystyle ^(2)), ที่ไหน x n (\displaystyle x_(n)) – ค่าสุดท้ายในประชากรทั่วไป
      • ในการคำนวณค่าเฉลี่ยของผลลัพธ์ที่ได้ คุณต้องหาผลรวมแล้วหารด้วย n: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / น
      • ตอนนี้เรามาเขียนคำอธิบายข้างต้นโดยใช้ตัวแปร: (∑( x ฉัน (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n และรับสูตรการคำนวณความแปรปรวนของประชากร