สูตรการหาผลรวมของตัวเลขในการก้าวหน้าทางคณิตศาสตร์ ความก้าวหน้าทางคณิตศาสตร์
ถ้าเป็นจำนวนธรรมชาติทุกจำนวน n จับคู่จำนวนจริง หนึ่ง แล้วพวกเขาก็บอกว่าได้รับ ลำดับหมายเลข :
ก 1 , ก 2 , ก 3 , . . . , หนึ่ง , . . . .
ดังนั้น ลำดับตัวเลขจึงเป็นฟังก์ชันของอาร์กิวเมนต์ธรรมชาติ
ตัวเลข ก 1 เรียกว่า เทอมแรกของลำดับ , ตัวเลข ก 2 — เทอมที่สองของลำดับ , ตัวเลข ก 3 — ที่สาม และอื่น ๆ ตัวเลข หนึ่ง เรียกว่า สมาชิกคนที่ n ของลำดับ และจำนวนธรรมชาติ n — หมายเลขของเขา .
จากสมาชิกสองคนที่อยู่ติดกัน หนึ่ง และ หนึ่ง +1 สมาชิกลำดับ หนึ่ง +1 เรียกว่า ภายหลัง (สัมพันธ์กับ หนึ่ง ) ก หนึ่ง — ก่อนหน้า (สัมพันธ์กับ หนึ่ง +1 ).
ในการกำหนดลำดับ คุณต้องระบุวิธีการที่ช่วยให้คุณค้นหาสมาชิกของลำดับด้วยตัวเลขใดก็ได้
บ่อยครั้งมีการระบุลำดับโดยใช้ สูตรเทอมที่ n นั่นคือสูตรที่ช่วยให้คุณกำหนดสมาชิกของลำดับตามหมายเลขของมันได้
ตัวอย่างเช่น,
สูตรสามารถกำหนดลำดับของเลขคี่บวกได้
หนึ่ง= 2ไม่มี 1,
และลำดับการสลับกัน 1 และ -1 - สูตร
ข n = (-1)n +1 . ◄
สามารถกำหนดลำดับได้ สูตรเกิดซ้ำ, นั่นคือ สูตรที่แสดงสมาชิกใดๆ ของลำดับ โดยเริ่มจากบางส่วน จนถึงสมาชิกก่อนหน้า (หนึ่งตัวหรือมากกว่า)
ตัวอย่างเช่น,
ถ้า ก 1 = 1 , ก หนึ่ง +1 = หนึ่ง + 5
ก 1 = 1,
ก 2 = ก 1 + 5 = 1 + 5 = 6,
ก 3 = ก 2 + 5 = 6 + 5 = 11,
ก 4 = ก 3 + 5 = 11 + 5 = 16,
ก 5 = ก 4 + 5 = 16 + 5 = 21.
ถ้า 1= 1, 2 = 1, หนึ่ง +2 = หนึ่ง + หนึ่ง +1 , จากนั้นเจ็ดเทอมแรกของลำดับตัวเลขจะถูกสร้างดังนี้:
1 = 1,
2 = 1,
3 = 1 + 2 = 1 + 1 = 2,
4 = 2 + 3 = 1 + 2 = 3,
5 = 3 + 4 = 2 + 3 = 5,
ก 6 = ก 4 + ก 5 = 3 + 5 = 8,
ก 7 = ก 5 + ก 6 = 5 + 8 = 13. ◄
ลำดับได้ สุดท้าย และ ไม่มีที่สิ้นสุด .
ลำดับที่เรียกว่า สุดยอด ถ้ามีสมาชิกจำนวนจำกัด ลำดับที่เรียกว่า ไม่มีที่สิ้นสุด ถ้ามีสมาชิกจำนวนมากอย่างไม่สิ้นสุด
ตัวอย่างเช่น,
ลำดับของจำนวนธรรมชาติสองหลัก:
10, 11, 12, 13, . . . , 98, 99
สุดท้าย.
ลำดับของจำนวนเฉพาะ:
2, 3, 5, 7, 11, 13, . . .
ไม่มีที่สิ้นสุด ◄
ลำดับที่เรียกว่า เพิ่มขึ้น ถ้าสมาชิกแต่ละคนเริ่มตั้งแต่ตัวที่สองมากกว่าสมาชิกก่อนหน้า
ลำดับที่เรียกว่า ลดลง ถ้าสมาชิกแต่ละคนเริ่มตั้งแต่ตัวที่สองน้อยกว่าสมาชิกก่อนหน้า
ตัวอย่างเช่น,
2, 4, 6, 8, . . . , 2n, . . . — ลำดับที่เพิ่มขึ้น;
1, 1 / 2 , 1 / 3 , 1 / 4 , . . . , 1 /n, . . . - ลำดับที่ลดลง ◄
ลำดับที่องค์ประกอบไม่ลดลงเมื่อจำนวนเพิ่มขึ้น หรือในทางกลับกัน ไม่เพิ่มขึ้น เรียกว่า ลำดับที่ซ้ำซากจำเจ .
โดยเฉพาะอย่างยิ่งลำดับแบบโมโนโทนิกคือลำดับที่เพิ่มขึ้นและลำดับที่ลดลง
ความก้าวหน้าทางคณิตศาสตร์
ความก้าวหน้าทางคณิตศาสตร์ คือลำดับที่สมาชิกแต่ละตัวเริ่มต้นจากตัวที่สองมีค่าเท่ากับสมาชิกตัวก่อนหน้าซึ่งมีการเพิ่มจำนวนเดียวกันเข้าไป
ก 1 , ก 2 , ก 3 , . . . , หนึ่ง, . . .
คือความก้าวหน้าทางคณิตศาสตร์หากเป็นจำนวนธรรมชาติใดๆ n ตรงตามเงื่อนไข:
หนึ่ง +1 = หนึ่ง + ง,
ที่ไหน ง - จำนวนหนึ่ง
ดังนั้น ความแตกต่างระหว่างเงื่อนไขที่ตามมาและเงื่อนไขก่อนหน้าของความก้าวหน้าทางคณิตศาสตร์ที่กำหนดจึงเป็นค่าคงที่เสมอ:
2 - ก 1 = 3 - ก 2 = . . . = หนึ่ง +1 - หนึ่ง = ง.
ตัวเลข ง เรียกว่า ความแตกต่างของความก้าวหน้าทางคณิตศาสตร์.
เพื่อกำหนดความก้าวหน้าทางคณิตศาสตร์ ก็เพียงพอแล้วที่จะระบุเทอมแรกและผลต่างของมัน
ตัวอย่างเช่น,
ถ้า ก 1 = 3, ง = 4 จากนั้นเราจะพบพจน์ห้าคำแรกของลำดับดังนี้:
1 =3,
2 = 1 + ง = 3 + 4 = 7,
3 = 2 + ง= 7 + 4 = 11,
4 = 3 + ง= 11 + 4 = 15,
ก 5 = ก 4 + ง= 15 + 4 = 19. ◄
สำหรับความก้าวหน้าทางคณิตศาสตร์กับเทอมแรก ก 1 และความแตกต่าง ง ของเธอ n
หนึ่ง = 1 + (n- 1)ง.
ตัวอย่างเช่น,
ค้นหาระยะที่สามสิบของความก้าวหน้าทางคณิตศาสตร์
1, 4, 7, 10, . . .
1 =1, ง = 3,
30 = 1 + (30 - 1)ง = 1 + 29· 3 = 88. ◄
n-1 = 1 + (n- 2)ง,
หนึ่ง= 1 + (n- 1)ง,
หนึ่ง +1 = ก 1 + nd,
เห็นได้ชัดว่า
| หนึ่ง=
| n-1 + n+1
|
| 2
|
สมาชิกแต่ละคนของการก้าวหน้าทางคณิตศาสตร์ เริ่มจากวินาที จะเท่ากับค่าเฉลี่ยเลขคณิตของสมาชิกก่อนหน้าและสมาชิกที่ตามมา
ตัวเลข a, b และ c เป็นพจน์ที่ต่อเนื่องกันของความก้าวหน้าทางคณิตศาสตร์บางอย่าง ถ้าหากหนึ่งในนั้นเท่ากับค่าเฉลี่ยเลขคณิตของอีกสองตัวเท่านั้น
ตัวอย่างเช่น,
หนึ่ง = 2n- 7 เป็นการก้าวหน้าทางคณิตศาสตร์
ลองใช้ข้อความข้างต้น เรามี:
หนึ่ง = 2n- 7,
n-1 = 2(ไม่มี 1) - 7 = 2n- 9,
n+1 = 2(n+ 1) - 7 = 2n- 5.
เพราะฉะนั้น,
| n+1 + n-1
| =
| 2n- 5 + 2n- 9
| = 2n- 7 = หนึ่ง,
|
| 2
| 2
|
◄
โปรดทราบว่า n เทอมที่ 3 ของความก้าวหน้าทางคณิตศาสตร์สามารถพบได้ไม่เพียงแต่ผ่านเท่านั้น ก 1 แต่ยังรวมถึงก่อนหน้านี้ด้วย เค
หนึ่ง = เค + (n- เค)ง.
ตัวอย่างเช่น,
สำหรับ ก 5 สามารถเขียนลงไปได้
5 = 1 + 4ง,
5 = 2 + 3ง,
5 = 3 + 2ง,
5 = 4 + ง. ◄
หนึ่ง = ไม่เป็นไร + เคดี,
หนึ่ง = เอ็น+เค - เคดี,
เห็นได้ชัดว่า
| หนึ่ง=
| ก นะเค
+ก ไม่มี+เค
|
| 2
|
สมาชิกใดๆ ของความก้าวหน้าทางคณิตศาสตร์ โดยเริ่มจากวินาที จะเท่ากับครึ่งหนึ่งของผลรวมของสมาชิกที่มีระยะห่างเท่ากันของความก้าวหน้าทางคณิตศาสตร์นี้
นอกจากนี้ สำหรับความก้าวหน้าทางคณิตศาสตร์ใดๆ จะมีความเท่าเทียมกันดังต่อไปนี้:
a m + a n = a k + a l,
ม. + n = k + ล.
ตัวอย่างเช่น,
ในการก้าวหน้าทางคณิตศาสตร์
1) ก 10 = 28 = (25 + 31)/2 = (ก 9 + ก 11 )/2;
2) 28 = 10 = 3 + 7ง= 7 + 7 3 = 7 + 21 = 28;
3) 10= 28 = (19 + 37)/2 = (ก 7 + 13)/2;
4) 2 + 12 = 5 + 9, เพราะ
ก 2 + 12= 4 + 34 = 38,
5 + 9 = 13 + 25 = 38. ◄
ส= ก 1 + ก 2 + ก 3 + - -+ หนึ่ง,
อันดับแรก n เงื่อนไขของความก้าวหน้าทางคณิตศาสตร์เท่ากับผลคูณของผลรวมครึ่งหนึ่งของเงื่อนไขสุดขั้วและจำนวนเงื่อนไข:
จากนี้โดยเฉพาะจะตามมาว่าหากคุณต้องการรวมคำศัพท์
เค, เค +1 , . . . , หนึ่ง,
ดังนั้นสูตรก่อนหน้านี้จะคงโครงสร้างไว้:
ตัวอย่างเช่น,
ในการก้าวหน้าทางคณิตศาสตร์ 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .
ส 10 = 1 + 4 + . . . + 28 = (1 + 28) · 10/2 = 145;
10 + 13 + 16 + 19 + 22 + 25 + 28 = ส 10 - ส 3 = (10 + 28 ) · (10 - 4 + 1)/2 = 133. ◄
ถ้าให้ความก้าวหน้าทางคณิตศาสตร์แล้ว ปริมาณ ก 1 , หนึ่ง, ง, nและส n เชื่อมต่อกันด้วยสองสูตร:
ดังนั้นหากให้ค่าของสามปริมาณเหล่านี้จากนั้นค่าที่สอดคล้องกันของอีกสองปริมาณจะถูกกำหนดจากสูตรเหล่านี้รวมกันเป็นระบบสองสมการที่ไม่ทราบค่าสองตัว
ความก้าวหน้าทางคณิตศาสตร์เป็นลำดับที่ซ้ำซากจำเจ ในกรณีนี้:
- ถ้า ง > 0 แล้วมันก็เพิ่มขึ้น;
- ถ้า ง < 0 ก็กำลังลดลง;
- ถ้า ง = 0 จากนั้นลำดับก็จะหยุดนิ่ง
ความก้าวหน้าทางเรขาคณิต
ความก้าวหน้าทางเรขาคณิต คือลำดับที่สมาชิกแต่ละตัวเริ่มจากตัวที่สองมีค่าเท่ากับตัวก่อนหน้าคูณด้วยจำนวนเดียวกัน
ข 1 , ข 2 , ข 3 , . . . , บีเอ็น, . . .
คือความก้าวหน้าทางเรขาคณิตหากเป็นจำนวนธรรมชาติใดๆ n ตรงตามเงื่อนไข:
บีเอ็น +1 = บีเอ็น · ถาม,
ที่ไหน ถาม ≠ 0 - จำนวนหนึ่ง
ดังนั้น อัตราส่วนของเทอมต่อมาของความก้าวหน้าทางเรขาคณิตที่กำหนดต่อเทอมก่อนหน้าจึงเป็นจำนวนคงที่:
ข 2 / ข 1 = ข 3 / ข 2 = . . . = บีเอ็น +1 / บีเอ็น = ถาม.
ตัวเลข ถาม เรียกว่า ตัวส่วนของความก้าวหน้าทางเรขาคณิต.
ในการกำหนดความก้าวหน้าทางเรขาคณิต การระบุเทอมแรกและตัวส่วนก็เพียงพอแล้ว
ตัวอย่างเช่น,
ถ้า ข 1 = 1, ถาม = -3 จากนั้นเราจะพบพจน์ห้าคำแรกของลำดับดังนี้:
ข 1 = 1,
ข 2 = ข 1 · ถาม = 1 · (-3) = -3,
ข 3 = ข 2 · ถาม= -3 · (-3) = 9,
ข 4 = ข 3 · ถาม= 9 · (-3) = -27,
ข 5 = ข 4 · ถาม= -27 · (-3) = 81. ◄
ข 1 และตัวส่วน ถาม ของเธอ n คำที่ 3 สามารถพบได้โดยใช้สูตร:
บีเอ็น = ข 1 · qn -1 .
ตัวอย่างเช่น,
หาเทอมที่ 7 ของความก้าวหน้าทางเรขาคณิต 1, 2, 4, . . .
ข 1 = 1, ถาม = 2,
ข 7 = ข 1 · ถาม 6 = 1 2 6 = 64. ◄
บีเอ็น-1 = ข 1 · qn -2 ,
บีเอ็น = ข 1 · qn -1 ,
บีเอ็น +1 = ข 1 · qn,
เห็นได้ชัดว่า
บีเอ็น 2 = บีเอ็น -1 · บีเอ็น +1 ,
สมาชิกแต่ละคนของความก้าวหน้าทางเรขาคณิต เริ่มต้นจากวินาที เท่ากับค่าเฉลี่ยเรขาคณิต (สัดส่วน) ของสมาชิกก่อนหน้าและสมาชิกต่อๆ ไป
เนื่องจากการสนทนาก็เป็นจริงเช่นกัน ข้อความต่อไปนี้จึงถือเป็น:
ตัวเลข a, b และ c เป็นพจน์ที่ต่อเนื่องกันของความก้าวหน้าทางเรขาคณิต ถ้าหากกำลังสองของหนึ่งในนั้นเท่ากับผลคูณของอีกสองตัว นั่นคือ หนึ่งในตัวเลขนั้นเป็นค่าเฉลี่ยเรขาคณิตของอีกสองตัว
ตัวอย่างเช่น,
ให้เราพิสูจน์ว่าลำดับที่กำหนดโดยสูตร บีเอ็น= -3 2 n คือความก้าวหน้าทางเรขาคณิต ลองใช้ข้อความข้างต้น เรามี:
บีเอ็น= -3 2 n,
บีเอ็น -1 = -3 2 n -1 ,
บีเอ็น +1 = -3 2 n +1 .
เพราะฉะนั้น,
บีเอ็น 2 = (-3 2 n) 2 = (-3 2 n -1 ) · (-3 · 2 n +1 ) = บีเอ็น -1 · บีเอ็น +1 ,
ซึ่งพิสูจน์ข้อความที่ต้องการ ◄
โปรดทราบว่า n เทอมที่ 3 ของความก้าวหน้าทางเรขาคณิตสามารถพบได้ไม่เพียงแต่ผ่านเท่านั้น ข 1 แต่ยังรวมถึงสมาชิกคนก่อนหน้าด้วย ข ซึ่งก็เพียงพอที่จะใช้สูตร
บีเอ็น = ข · qn - เค.
ตัวอย่างเช่น,
สำหรับ ข 5 สามารถเขียนลงไปได้
ข 5 = ข 1 · ถาม 4 ,
ข 5 = ข 2 · คำถามที่ 3,
ข 5 = ข 3 · คำถามที่ 2,
ข 5 = ข 4 · ถาม. ◄
บีเอ็น = ข · qn - เค,
บีเอ็น = บีเอ็น - เค · คิวเค,
เห็นได้ชัดว่า
บีเอ็น 2 = บีเอ็น - เค· บีเอ็น + เค
กำลังสองของเทอมใดๆ ของความก้าวหน้าทางเรขาคณิต โดยเริ่มจากวินาทีนั้น จะเท่ากับผลคูณของเงื่อนไขของความก้าวหน้านี้ซึ่งมีระยะห่างเท่ากัน
นอกจากนี้ สำหรับความก้าวหน้าทางเรขาคณิตใดๆ ความเท่าเทียมกันจะเป็นจริง:
ข ม· บีเอ็น= ข· ข,
ม+ n= เค+ ล.
ตัวอย่างเช่น,
ในความก้าวหน้าทางเรขาคณิต
1) ข 6 2 = 32 2 = 1024 = 16 · 64 = ข 5 · ข 7 ;
2) 1024 = ข 11 = ข 6 · ถาม 5 = 32 · 2 5 = 1024;
3) ข 6 2 = 32 2 = 1024 = 8 · 128 = ข 4 · ข 8 ;
4) ข 2 · ข 7 = ข 4 · ข 5 , เพราะ
ข 2 · ข 7 = 2 · 64 = 128,
ข 4 · ข 5 = 8 · 16 = 128. ◄
ส= ข 1 + ข 2 + ข 3 + . . . + บีเอ็น
อันดับแรก n สมาชิกของความก้าวหน้าทางเรขาคณิตที่มีตัวส่วน ถาม ≠ 0 คำนวณโดยสูตร:
และเมื่อไร ถาม = 1 - ตามสูตร
ส= ไม่มี 1
โปรดทราบว่าหากคุณต้องการสรุปข้อกำหนด
ข, ข +1 , . . . , บีเอ็น,
จากนั้นจึงใช้สูตร:
| ส- เอสเค -1 = ข + ข +1 + . . . + บีเอ็น = ข · | 1 - qn -
เค +1
| . |
| 1 - ถาม
|
ตัวอย่างเช่น,
ในความก้าวหน้าทางเรขาคณิต 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .
ส 10 = 1 + 2 + . . . + 512 = 1 · (1 - 2 10) / (1 - 2) = 1023;
64 + 128 + 256 + 512 = ส 10 - ส 6 = 64 · (1 - 2 10-7+1) / (1 - 2) = 960. ◄
ถ้าให้ความก้าวหน้าทางเรขาคณิต แสดงว่าปริมาณ ข 1 , บีเอ็น, ถาม, nและ ส เชื่อมต่อกันด้วยสองสูตร:
ดังนั้นหากให้ค่าของสามปริมาณใด ๆ เหล่านี้จากนั้นค่าที่สอดคล้องกันของปริมาณอีกสองปริมาณจะถูกกำหนดจากสูตรเหล่านี้รวมกันเป็นระบบสมการสองสมการที่ไม่ทราบค่าสองตัว
สำหรับความก้าวหน้าทางเรขาคณิตกับเทอมแรก ข 1 และตัวส่วน ถาม สิ่งต่อไปนี้จะเกิดขึ้น คุณสมบัติของความน่าเบื่อ :
- ความก้าวหน้าจะเพิ่มขึ้นหากตรงตามเงื่อนไขข้อใดข้อหนึ่งต่อไปนี้:
ข 1 > 0 และ ถาม> 1;
ข 1 < 0 และ 0 < ถาม< 1;
- ความก้าวหน้าจะลดลงหากตรงตามเงื่อนไขข้อใดข้อหนึ่งต่อไปนี้:
ข 1 > 0 และ 0 < ถาม< 1;
ข 1 < 0 และ ถาม> 1.
ถ้า ถาม< 0 จากนั้นความก้าวหน้าทางเรขาคณิตจะสลับกัน: พจน์ที่เป็นเลขคี่จะมีเครื่องหมายเดียวกันกับเทอมแรก และเทอมที่มีเลขคู่จะมีเครื่องหมายตรงกันข้าม เห็นได้ชัดว่าความก้าวหน้าทางเรขาคณิตแบบสลับกันนั้นไม่ใช่เรื่องซ้ำซากจำเจ
สินค้าชิ้นแรก n เงื่อนไขของความก้าวหน้าทางเรขาคณิตสามารถคำนวณได้โดยใช้สูตร:
พี= ข 1 · ข 2 · ข 3 · . . . · บีเอ็น = (ข 1 · บีเอ็น) n / 2 .
ตัวอย่างเช่น,
1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 = (1 · 128) 8/2 = 128 4 = 268 435 456;
3 · 6 · 12 · 24 · 48 = (3 · 48) 5/2 = (144 1/2) 5 = 12 5 = 248 832.◄
ลดความก้าวหน้าทางเรขาคณิตอย่างไม่สิ้นสุด
ลดความก้าวหน้าทางเรขาคณิตอย่างไม่สิ้นสุด เรียกว่าความก้าวหน้าทางเรขาคณิตอนันต์ซึ่งมีโมดูลัสตัวส่วนน้อยกว่า 1 นั่นคือ
|ถาม| < 1 .
โปรดทราบว่าความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดอาจไม่ใช่ลำดับที่ลดลง มันเหมาะกับโอกาส
1 < ถาม< 0 .
ด้วยตัวส่วนดังกล่าว ลำดับจึงสลับกัน ตัวอย่างเช่น,
1, - 1 / 2 , 1 / 4 , - 1 / 8 , . . . .
ผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด ตั้งชื่อหมายเลขที่ผลรวมของหมายเลขแรกเข้าใกล้โดยไม่มีขีดจำกัด n สมาชิกของความก้าวหน้าโดยเพิ่มจำนวนได้ไม่จำกัด n - จำนวนนี้มีจำกัดเสมอและแสดงเป็นสูตร
| ส= ข 1 + ข 2 + ข 3 + . . . = | ข 1
| . |
| 1 - ถาม
|
ตัวอย่างเช่น,
10 + 1 + 0,1 + 0,01 + . . . = 10 / (1 - 0,1) = 11 1 / 9 ,
10 - 1 + 0,1 - 0,01 + . . . = 10 / (1 + 0,1) = 9 1 / 11 . ◄
ความสัมพันธ์ระหว่างความก้าวหน้าทางคณิตศาสตร์และเรขาคณิต
ความก้าวหน้าทางคณิตศาสตร์และเรขาคณิตมีความสัมพันธ์กันอย่างใกล้ชิด ลองดูเพียงสองตัวอย่าง
ก 1 , ก 2 , ก 3 , . . . ง , ที่
ข 1 , ข 2 , ข 3 , . . . ข d .
ตัวอย่างเช่น,
1, 3, 5, . . . - ความก้าวหน้าทางคณิตศาสตร์ที่มีความแตกต่าง 2 และ
7 1 , 7 3 , 7 5 , . . . - ความก้าวหน้าทางเรขาคณิตพร้อมตัวส่วน 7 2 . ◄
ข 1 , ข 2 , ข 3 , . . . - ความก้าวหน้าทางเรขาคณิตพร้อมตัวส่วน ถาม , ที่
เข้าสู่ระบบ ข 1, เข้าสู่ระบบ ข 2, เข้าสู่ระบบ ข 3, . . . - ความก้าวหน้าทางคณิตศาสตร์ที่มีความแตกต่าง เข้าสู่ระบบถาม .
ตัวอย่างเช่น,
2, 12, 72, . . . - ความก้าวหน้าทางเรขาคณิตพร้อมตัวส่วน 6 และ
แอลจี 2, แอลจี 12, แอลจี 72, . . . - ความก้าวหน้าทางคณิตศาสตร์ที่มีความแตกต่าง แอลจี 6 . ◄
ระดับรายการ
ความก้าวหน้าทางคณิตศาสตร์ ทฤษฎีโดยละเอียดพร้อมตัวอย่าง (2019)
ลำดับหมายเลข
เรามานั่งลงและเริ่มเขียนตัวเลขกันดีกว่า ตัวอย่างเช่น:
คุณสามารถเขียนตัวเลขใดก็ได้ และอาจมีได้มากเท่าที่คุณต้องการ (ในกรณีของเราก็มีอยู่แล้ว) ไม่ว่าเราจะเขียนตัวเลขไปกี่จำนวน เราก็บอกได้เสมอว่าอันไหนเป็นอันแรก อันไหนเป็นอันที่สอง และต่อๆ ไปจนถึงตัวสุดท้าย นั่นคือ เราสามารถนับเลขได้ นี่คือตัวอย่างลำดับตัวเลข:
ลำดับหมายเลข
ตัวอย่างเช่น สำหรับลำดับของเรา:
หมายเลขที่กำหนดจะเฉพาะกับหมายเลขเดียวในลำดับเท่านั้น กล่าวอีกนัยหนึ่ง ไม่มีตัวเลขสามวินาทีในลำดับ ตัวเลขที่สอง (เช่นตัวเลขที่ th) จะเหมือนกันเสมอ
จำนวนที่มีจำนวนเรียกว่าเทอมที่ 3 ของลำดับ
โดยปกติเราเรียกลำดับทั้งหมดด้วยตัวอักษรบางตัว (เช่น) และสมาชิกแต่ละคนของลำดับนี้จะเป็นตัวอักษรเดียวกัน โดยมีดัชนีเท่ากับจำนวนสมาชิกนี้:
ในกรณีของเรา: 
สมมติว่าเรามีลำดับตัวเลขซึ่งความแตกต่างระหว่างตัวเลขที่อยู่ติดกันเท่ากันและเท่ากัน
ตัวอย่างเช่น: 
ฯลฯ
ลำดับตัวเลขนี้เรียกว่าความก้าวหน้าทางคณิตศาสตร์
คำว่า "ความก้าวหน้า" ถูกนำมาใช้โดยนักเขียนชาวโรมันชื่อ Boethius ย้อนกลับไปในศตวรรษที่ 6 และเป็นที่เข้าใจในความหมายที่กว้างกว่าว่าเป็นลำดับตัวเลขที่ไม่มีที่สิ้นสุด ชื่อ "เลขคณิต" โอนมาจากทฤษฎีสัดส่วนต่อเนื่องที่ชาวกรีกโบราณศึกษา
นี่คือลำดับตัวเลข ซึ่งสมาชิกแต่ละตัวจะเท่ากับลำดับก่อนหน้าที่บวกเข้ากับหมายเลขเดียวกัน จำนวนนี้เรียกว่าผลต่างของความก้าวหน้าทางคณิตศาสตร์และถูกกำหนดไว้
พยายามพิจารณาว่าลำดับตัวเลขใดเป็นความก้าวหน้าทางคณิตศาสตร์ และลำดับใดไม่ใช่:
ก)
ข)
ค)
ง)
เข้าใจแล้ว? ลองเปรียบเทียบคำตอบของเรา:
เป็นความก้าวหน้าทางคณิตศาสตร์ - b, c
ไม่ใช่ความก้าวหน้าทางคณิตศาสตร์ - a, d
กลับไปที่ความก้าวหน้าที่กำหนด () แล้วลองค้นหาค่าของเทอมที่ 3 ของมัน มีอยู่ สองวิธีที่จะค้นหามัน
1. วิธีการ
เราสามารถบวกเลขความก้าวหน้าเข้ากับค่าก่อนหน้าได้จนกว่าเราจะถึงระยะที่ 3 ของความก้าวหน้า เป็นการดีที่เราไม่มีอะไรจะสรุปมากนัก - มีเพียงสามค่าเท่านั้น:
ดังนั้นเทอมที่ 3 ของความก้าวหน้าทางคณิตศาสตร์ที่อธิบายไว้จึงเท่ากับ
2. วิธีการ
จะเป็นอย่างไรถ้าเราจำเป็นต้องค้นหามูลค่าของระยะที่ 3 ของความก้าวหน้า? การบวกจะใช้เวลามากกว่าหนึ่งชั่วโมง และไม่ใช่ความจริงที่ว่าเราจะไม่ทำผิดพลาดเมื่อบวกตัวเลข
แน่นอนว่านักคณิตศาสตร์ได้คิดค้นวิธีที่ไม่จำเป็นต้องเพิ่มผลต่างของความก้าวหน้าทางคณิตศาสตร์ให้กับค่าก่อนหน้า ลองดูภาพที่วาดให้ละเอียดยิ่งขึ้น... แน่นอนคุณได้สังเกตเห็นรูปแบบบางอย่างแล้ว ได้แก่:
ตัวอย่างเช่น ลองดูว่าค่าของเทอมที่ 3 ของความก้าวหน้าทางคณิตศาสตร์นี้ประกอบด้วยเท่าใด: 
กล่าวอีกนัยหนึ่ง:
พยายามหาค่าของสมาชิกของความก้าวหน้าทางคณิตศาสตร์ที่กำหนดด้วยตัวเองด้วยวิธีนี้
คุณคำนวณแล้วหรือยัง? เปรียบเทียบบันทึกย่อของคุณกับคำตอบ:
โปรดทราบว่าคุณได้ตัวเลขเดียวกันกับวิธีก่อนหน้าทุกประการ เมื่อเราเพิ่มเงื่อนไขของความก้าวหน้าทางคณิตศาสตร์เป็นค่าก่อนหน้าตามลำดับ
เรามาลอง "ลดความเป็นตัวตน" ของสูตรนี้ - มาวางไว้ในรูปแบบทั่วไปแล้วจะได้:
|
สมการความก้าวหน้าทางคณิตศาสตร์ |
ความก้าวหน้าทางคณิตศาสตร์สามารถเพิ่มหรือลดลงได้
เพิ่มขึ้น- ความก้าวหน้าซึ่งแต่ละมูลค่าที่ตามมาของข้อกำหนดจะมากกว่าค่าก่อนหน้า
ตัวอย่างเช่น:
จากมากไปน้อย- ความก้าวหน้าซึ่งแต่ละค่าของข้อกำหนดที่ตามมาจะน้อยกว่าค่าก่อนหน้า
ตัวอย่างเช่น:
สูตรที่ได้รับใช้ในการคำนวณเงื่อนไขทั้งในเงื่อนไขที่เพิ่มขึ้นและลดลงของความก้าวหน้าทางคณิตศาสตร์
มาตรวจสอบสิ่งนี้ในทางปฏิบัติ
เราได้รับความก้าวหน้าทางคณิตศาสตร์ซึ่งประกอบด้วยตัวเลขต่อไปนี้: มาตรวจสอบกันว่าตัวเลขลำดับที่ 3 ของความก้าวหน้าทางคณิตศาสตร์นี้จะเป็นอย่างไรหากเราใช้สูตรของเราในการคำนวณ:

ตั้งแต่นั้นมา:
ดังนั้นเราจึงมั่นใจว่าสูตรดำเนินการทั้งในการลดลงและเพิ่มความก้าวหน้าทางคณิตศาสตร์
พยายามค้นหาเงื่อนไขที่ th และ th ของความก้าวหน้าทางคณิตศาสตร์นี้ด้วยตัวเอง
ลองเปรียบเทียบผลลัพธ์:
คุณสมบัติความก้าวหน้าทางคณิตศาสตร์
มาทำให้ปัญหาซับซ้อนขึ้น - เราจะได้คุณสมบัติของความก้าวหน้าทางคณิตศาสตร์
สมมติว่าเราได้รับเงื่อนไขต่อไปนี้:
- ความก้าวหน้าทางคณิตศาสตร์ ค้นหาค่า
ง่าย ๆ ที่คุณพูดและเริ่มนับตามสูตรที่คุณรู้อยู่แล้ว:
ให้เอ่อแล้ว:
จริงอย่างแน่นอน ปรากฎว่าเราพบก่อนแล้วจึงบวกเข้ากับตัวเลขแรกแล้วได้สิ่งที่เรากำลังมองหา ถ้าความก้าวหน้าแสดงด้วยค่าเล็กๆ ก็ไม่มีอะไรซับซ้อน แต่จะเกิดอะไรขึ้นถ้าเราได้รับตัวเลขในเงื่อนไขล่ะ? ยอมรับว่ามีความเป็นไปได้ที่จะเกิดข้อผิดพลาดในการคำนวณ
ทีนี้ลองคิดดูว่าจะสามารถแก้ไขปัญหานี้ในขั้นตอนเดียวโดยใช้สูตรใดๆ ได้หรือไม่? ใช่แน่นอน และนั่นคือสิ่งที่เราจะพยายามนำเสนอออกมาในตอนนี้
ให้เราแสดงคำที่ต้องการของความก้าวหน้าทางคณิตศาสตร์เนื่องจากสูตรในการค้นหาที่เรารู้จัก - นี่เป็นสูตรเดียวกับที่เราได้รับตั้งแต่ต้น:
, แล้ว:
- ระยะก่อนหน้าของความก้าวหน้าคือ:
- ระยะต่อไปของความก้าวหน้าคือ:
เรามาสรุปข้อกำหนดก่อนหน้าและถัดไปของความก้าวหน้า:
ปรากฎว่าผลรวมของเงื่อนไขก่อนหน้าและเงื่อนไขถัดไปของความก้าวหน้าคือค่าสองเท่าของเงื่อนไขความก้าวหน้าที่อยู่ระหว่างพวกเขา กล่าวอีกนัยหนึ่ง หากต้องการค้นหาค่าของเทอมความก้าวหน้าด้วยค่าก่อนหน้าและค่าต่อเนื่องที่ทราบ คุณจะต้องบวกค่าเหล่านั้นแล้วหารด้วย
ใช่แล้ว เราได้เลขเดียวกัน มารักษาความปลอดภัยของวัสดุกันเถอะ คำนวณมูลค่าสำหรับความก้าวหน้าด้วยตัวเอง ไม่ยากเลย
ทำได้ดี! คุณรู้เกือบทุกอย่างเกี่ยวกับความก้าวหน้า! ยังคงต้องหาสูตรเพียงสูตรเดียวเท่านั้น ซึ่งตามตำนานสามารถอนุมานได้อย่างง่ายดายโดยหนึ่งในนักคณิตศาสตร์ที่ยิ่งใหญ่ที่สุดตลอดกาล "ราชาแห่งนักคณิตศาสตร์" - Karl Gauss...
เมื่อ Carl Gauss อายุ 9 ขวบ ครูคนหนึ่งซึ่งยุ่งอยู่กับการตรวจสอบงานของนักเรียนในชั้นเรียนอื่น ได้มอบหมายงานในชั้นเรียนดังต่อไปนี้: “คำนวณผลรวมของจำนวนธรรมชาติทั้งหมดตั้งแต่ ถึง (ตามแหล่งอื่นถึง) รวม” ลองนึกภาพความประหลาดใจของครูเมื่อนักเรียนคนหนึ่งของเขา (นี่คือคาร์ล เกาส์) นาทีต่อมาให้คำตอบที่ถูกต้องกับงาน ในขณะที่เพื่อนร่วมชั้นของผู้บ้าระห่ำส่วนใหญ่ได้รับผลลัพธ์ที่ผิดหลังจากคำนวณมาเป็นเวลานาน...
คาร์ล เกาส์ วัยหนุ่มสังเกตเห็นรูปแบบบางอย่างที่คุณสามารถสังเกตได้ง่ายเช่นกัน
สมมติว่าเรามีความก้าวหน้าทางคณิตศาสตร์ที่ประกอบด้วยเทอมที่ -: เราจำเป็นต้องค้นหาผลรวมของเงื่อนไขเหล่านี้ของการก้าวหน้าทางคณิตศาสตร์ แน่นอนว่า เราสามารถรวมค่าทั้งหมดด้วยตนเอง แต่จะเกิดอะไรขึ้นถ้างานนั้นต้องการหาผลรวมของเงื่อนไขตามที่เกาส์กำลังมองหา?
ให้เราบรรยายถึงความก้าวหน้าที่มอบให้เรา ดูตัวเลขที่ไฮไลต์อย่างใกล้ชิดแล้วลองดำเนินการทางคณิตศาสตร์ต่างๆ กับตัวเลขเหล่านั้น 
คุณลองแล้วหรือยัง? คุณสังเกตเห็นอะไร? ขวา! ผลรวมของพวกเขาเท่ากัน

ทีนี้บอกหน่อยเถอะว่าความก้าวหน้าที่มอบให้เรามีทั้งหมดกี่คู่? แน่นอนว่าครึ่งหนึ่งของตัวเลขทั้งหมดนั่นเอง
จากข้อเท็จจริงที่ว่าผลรวมของสองเทอมของการก้าวหน้าทางคณิตศาสตร์เท่ากัน และคู่ที่คล้ายกันเท่ากัน เราจึงได้ผลลัพธ์ว่าผลรวมทั้งหมดเท่ากับ:
.
ดังนั้น สูตรสำหรับผลรวมของเทอมแรกของความก้าวหน้าทางคณิตศาสตร์จะเป็นดังนี้:
ในปัญหาบางอย่างเราไม่รู้คำศัพท์ที่ 3 แต่เรารู้ถึงความแตกต่างของความก้าวหน้า ลองแทนสูตรของเทอมที่ 3 ลงในสูตรผลรวม
คุณได้อะไร?
ทำได้ดี! ตอนนี้กลับมาที่ปัญหาที่ Carl Gauss ถาม: คำนวณด้วยตัวคุณเองว่าผลรวมของตัวเลขที่เริ่มต้นจาก -th เท่ากับเท่าใด และผลรวมของตัวเลขที่เริ่มต้นจาก -th
คุณได้รับเท่าไหร่?
เกาส์พบว่าผลรวมของพจน์เท่ากัน และผลรวมของพจน์นั้น นั่นคือสิ่งที่คุณตัดสินใจ?
ในความเป็นจริง สูตรสำหรับผลรวมของเทอมของความก้าวหน้าทางคณิตศาสตร์ได้รับการพิสูจน์โดยนักวิทยาศาสตร์ชาวกรีกโบราณ ไดโอแฟนตัส ย้อนกลับไปในศตวรรษที่ 3 และตลอดเวลานี้ คนที่มีไหวพริบได้ใช้คุณสมบัติของความก้าวหน้าทางคณิตศาสตร์อย่างเต็มที่
ตัวอย่างเช่น ลองนึกภาพอียิปต์โบราณและโครงการก่อสร้างที่ใหญ่ที่สุดในยุคนั้น - การก่อสร้างปิรามิด... รูปภาพแสดงด้านใดด้านหนึ่ง 
คุณพูดว่าความก้าวหน้าอยู่ที่ไหน? มองให้ดีและหารูปแบบจำนวนบล็อกทรายในแต่ละแถวของกำแพงพีระมิด 
ทำไมไม่ก้าวหน้าทางคณิตศาสตร์? คำนวณจำนวนบล็อกที่จำเป็นในการสร้างกำแพงด้านหนึ่งหากวางอิฐบล็อกไว้ที่ฐาน ฉันหวังว่าคุณจะไม่นับในขณะที่เลื่อนนิ้วไปบนหน้าจอ คุณจำสูตรสุดท้ายและทุกสิ่งที่เราพูดเกี่ยวกับความก้าวหน้าทางคณิตศาสตร์ได้ไหม
ในกรณีนี้ ความคืบหน้าจะเป็นดังนี้:
ความแตกต่างความก้าวหน้าทางคณิตศาสตร์
จำนวนเงื่อนไขของการก้าวหน้าทางคณิตศาสตร์
เรามาแทนที่ข้อมูลของเราเป็นสูตรสุดท้าย (คำนวณจำนวนบล็อกได้ 2 วิธี)
วิธีที่ 1
วิธีที่ 2
และตอนนี้คุณสามารถคำนวณบนมอนิเตอร์ได้: เปรียบเทียบค่าที่ได้รับกับจำนวนบล็อกที่อยู่ในปิรามิดของเรา เข้าใจแล้ว? ทำได้ดีมาก คุณเชี่ยวชาญผลรวมของเทอมที่ n ของความก้าวหน้าทางคณิตศาสตร์แล้ว
แน่นอนว่าคุณไม่สามารถสร้างปิรามิดจากบล็อกที่ฐานได้ แต่จากอะไรล่ะ? ลองคำนวณว่าต้องใช้อิฐทรายจำนวนเท่าใดในการสร้างกำแพงด้วยเงื่อนไขนี้
คุณจัดการหรือไม่?
คำตอบที่ถูกต้องคือบล็อก:
การฝึกอบรม
งาน:
- Masha กำลังมีรูปร่างดีสำหรับฤดูร้อน เธอเพิ่มจำนวนท่าสควอชทุกวัน Masha จะทำ squats กี่ครั้งในหนึ่งสัปดาห์ถ้าเธอทำ squats ในการฝึกซ้อมครั้งแรก?
- ผลรวมของเลขคี่ทั้งหมดที่มีอยู่เป็นเท่าใด
- เมื่อจัดเก็บบันทึก ตัวบันทึกจะซ้อนกันในลักษณะที่แต่ละชั้นบนสุดมีบันทึกหนึ่งรายการน้อยกว่าบันทึกก่อนหน้า อิฐหนึ่งก้อนมีท่อนไม้กี่ท่อน ถ้ารากฐานของท่อนไม้เป็นท่อนไม้?
คำตอบ:
- ให้เรากำหนดพารามิเตอร์ของความก้าวหน้าทางคณิตศาสตร์ ในกรณีนี้
(สัปดาห์ = วัน)คำตอบ:ในสองสัปดาห์ Masha ควรทำ squats วันละครั้ง
- เลขคี่ตัวแรก เลขสุดท้าย
ความแตกต่างความก้าวหน้าทางคณิตศาสตร์
อย่างไรก็ตาม จำนวนเลขคี่คือครึ่งหนึ่ง เราจะมาตรวจสอบข้อเท็จจริงนี้โดยใช้สูตรในการหาเทอมที่ 3 ของความก้าวหน้าทางคณิตศาสตร์:ตัวเลขประกอบด้วยเลขคี่
ลองแทนที่ข้อมูลที่มีอยู่ลงในสูตร:คำตอบ:ผลรวมของเลขคี่ทั้งหมดที่อยู่ในนั้นมีค่าเท่ากัน
- เรามาจำปัญหาเกี่ยวกับปิรามิดกันดีกว่า สำหรับกรณีของเรา a เนื่องจากแต่ละเลเยอร์บนสุดจะลดลงหนึ่งบันทึก ดังนั้นโดยรวมแล้วจะมีหลายเลเยอร์ นั่นก็คือ
ลองแทนที่ข้อมูลลงในสูตร:คำตอบ:มีท่อนซุงอยู่ในการก่ออิฐ
มาสรุปกัน
- - ลำดับตัวเลขที่ความแตกต่างระหว่างตัวเลขที่อยู่ติดกันเท่ากันและเท่ากัน มันอาจจะเพิ่มขึ้นหรือลดลงก็ได้
- การหาสูตรเทอมที่ 3 ของความก้าวหน้าทางคณิตศาสตร์เขียนโดยสูตร - โดยที่ คือจำนวนตัวเลขในความก้าวหน้า
- คุณสมบัติของสมาชิกของความก้าวหน้าทางคณิตศาสตร์- - โดยที่คือจำนวนตัวเลขที่กำลังดำเนินอยู่
- ผลรวมของเงื่อนไขของความก้าวหน้าทางคณิตศาสตร์สามารถพบได้สองวิธี:
โดยที่คือจำนวนค่า
ความก้าวหน้าทางคณิตศาสตร์ ระดับกลาง
ลำดับหมายเลข
ลองนั่งลงและเริ่มเขียนตัวเลขกัน ตัวอย่างเช่น:
คุณสามารถเขียนตัวเลขใดๆ ก็ได้ และจะมีได้มากเท่าที่คุณต้องการ แต่เราสามารถพูดได้เสมอว่าอันไหนเป็นอันดับแรก อันไหนเป็นที่สอง และอื่น ๆ นั่นคือเราสามารถนับพวกมันได้ นี่คือตัวอย่างลำดับตัวเลข
ลำดับหมายเลขคือชุดตัวเลขซึ่งแต่ละชุดสามารถกำหนดหมายเลขเฉพาะได้
กล่าวอีกนัยหนึ่ง แต่ละหมายเลขสามารถเชื่อมโยงกับจำนวนธรรมชาติจำนวนหนึ่งและเป็นจำนวนเฉพาะได้ และเราจะไม่กำหนดหมายเลขนี้ให้กับหมายเลขอื่นจากชุดนี้
ตัวเลขที่มีตัวเลขเรียกว่าสมาชิกตัวที่ 2 ของลำดับ
โดยปกติเราเรียกลำดับทั้งหมดด้วยตัวอักษรบางตัว (เช่น) และสมาชิกแต่ละคนของลำดับนี้จะเป็นตัวอักษรเดียวกัน โดยมีดัชนีเท่ากับจำนวนสมาชิกนี้:
จะสะดวกมากหากบางสูตรสามารถระบุเทอมที่ 3 ของลำดับได้ ยกตัวอย่างสูตร
กำหนดลำดับ:
และสูตรก็มีลำดับดังนี้:
ตัวอย่างเช่น ความก้าวหน้าทางคณิตศาสตร์คือลำดับ (เทอมแรกในที่นี้มีค่าเท่ากัน และผลต่างคือ) หรือ (, ส่วนต่าง)
สูตรเทอมที่ n
เราเรียกสูตรที่เกิดซ้ำซึ่งในการหาเทอมที่ 3 คุณจำเป็นต้องรู้คำก่อนหน้าหรือหลายคำก่อนหน้านี้:
หากต้องการค้นหาระยะที่ 3 ของความก้าวหน้าโดยใช้สูตรนี้ เราจะต้องคำนวณเก้าค่าก่อนหน้า เช่น ปล่อยให้มัน. แล้ว:
ตอนนี้ชัดเจนแล้วว่าสูตรคืออะไร?
ในแต่ละบรรทัดที่เราบวกเข้าไป คูณด้วยตัวเลขจำนวนหนึ่ง อันไหน? ง่ายมาก: นี่คือจำนวนสมาชิกปัจจุบันลบ:
ตอนนี้สะดวกขึ้นมากแล้วใช่ไหม? เราตรวจสอบ:
ตัดสินใจด้วยตัวเอง:
ในการก้าวหน้าทางคณิตศาสตร์ ให้ค้นหาสูตรสำหรับเทอมที่ n และค้นหาเทอมที่ร้อย
สารละลาย:
เทอมแรกมีค่าเท่ากัน ความแตกต่างคืออะไร? นี่คือสิ่งที่:
(เหตุนี้จึงเรียกว่าความแตกต่างเพราะเท่ากับผลต่างของระยะต่อเนื่องของการก้าวหน้า)
ดังนั้นสูตร:
จากนั้นเทอมที่ร้อยจะเท่ากับ:
ผลรวมของจำนวนธรรมชาติทั้งหมดตั้งแต่ ถึง คืออะไร?
ตามตำนาน คาร์ล เกาส์ นักคณิตศาสตร์ผู้ยิ่งใหญ่ เมื่อตอนอายุ 9 ขวบ คำนวณจำนวนนี้ในเวลาไม่กี่นาที เขาสังเกตเห็นว่าผลรวมของเลขตัวแรกและตัวสุดท้ายเท่ากัน ผลรวมของเลขที่สองและเลขสุดท้ายเท่ากัน ผลรวมของเลขที่สามและเลข 3 จากท้ายสุดเท่ากัน เป็นต้น มีคู่ดังกล่าวทั้งหมดกี่คู่? ถูกต้อง ครึ่งหนึ่งของจำนวนทั้งหมดนั่นเอง ดังนั้น,
สูตรทั่วไปสำหรับผลรวมของเทอมแรกของความก้าวหน้าทางคณิตศาสตร์จะเป็น:
ตัวอย่าง:
ค้นหาผลรวมของตัวคูณสองหลักทั้งหมด
สารละลาย:
ตัวเลขแรกคือสิ่งนี้ แต่ละหมายเลขที่ตามมาจะได้มาจากการเพิ่มหมายเลขก่อนหน้า ดังนั้นตัวเลขที่เราสนใจจะสร้างความก้าวหน้าทางคณิตศาสตร์ด้วยเทอมแรกและผลต่าง
สูตรของเทอมที่ 3 สำหรับความก้าวหน้านี้:
มีคำศัพท์กี่คำที่อยู่ในความก้าวหน้าหากทุกคำต้องเป็นเลขสองหลัก?
ง่ายมาก: .
ระยะสุดท้ายของความก้าวหน้าจะเท่ากัน จากนั้นผลรวม:
คำตอบ: .
ตอนนี้ตัดสินใจด้วยตัวเอง:
- ทุกวันนักกีฬาจะวิ่งมากกว่าวันก่อนหน้า เขาจะวิ่งรวมกี่กิโลเมตรในหนึ่งสัปดาห์ถ้าเขาวิ่ง km m ในวันแรก?
- นักปั่นจักรยานเดินทางหลายกิโลเมตรทุกวันมากกว่าวันก่อนหน้า วันแรกเดินทาง กม. เขาต้องเดินทางกี่วันจึงจะครบหนึ่งกิโลเมตร? วันสุดท้ายของการเดินทางเขาจะเดินทางกี่กิโลเมตร?
- ราคาตู้เย็นในร้านค้าลดลงเท่ากันทุกปี พิจารณาว่าราคาตู้เย็นลดลงเท่าใดในแต่ละปีหากขายเป็นรูเบิลหกปีต่อมาขายเป็นรูเบิล
คำตอบ:
- สิ่งที่สำคัญที่สุดคือการจดจำความก้าวหน้าทางคณิตศาสตร์และกำหนดพารามิเตอร์ ในกรณีนี้ (สัปดาห์ = วัน) คุณต้องพิจารณาผลรวมของเงื่อนไขแรกของความก้าวหน้านี้:
.
คำตอบ: - นี่คือสิ่งที่ได้รับ: จะต้องพบ
แน่นอนว่าคุณต้องใช้สูตรผลรวมเดียวกันกับในปัญหาก่อนหน้านี้:
.
แทนค่า:เห็นได้ชัดว่ารูตไม่พอดี ดังนั้นคำตอบก็คือ
ลองคำนวณเส้นทางที่เดินทางในวันสุดท้ายโดยใช้สูตรของเทอมที่ 3:
(กม.)
คำตอบ: - ที่ให้ไว้: . หา: .
ไม่มีอะไรง่ายไปกว่านี้อีกแล้ว:
(ถู).
คำตอบ:
ความก้าวหน้าทางคณิตศาสตร์ สั้น ๆ เกี่ยวกับสิ่งสำคัญ
นี่คือลำดับตัวเลขซึ่งความแตกต่างระหว่างตัวเลขที่อยู่ติดกันจะเท่ากันและเท่ากัน
ความก้าวหน้าทางคณิตศาสตร์สามารถเพิ่ม () และลด ()
ตัวอย่างเช่น:
สูตรการหาเทอมที่ n ของความก้าวหน้าทางคณิตศาสตร์
เขียนโดยสูตร โดยที่ คือจำนวนตัวเลขที่กำลังดำเนินอยู่
คุณสมบัติของสมาชิกของความก้าวหน้าทางคณิตศาสตร์
ช่วยให้คุณสามารถค้นหาคำศัพท์ของความก้าวหน้าได้อย่างง่ายดายหากทราบคำศัพท์ใกล้เคียง - โดยที่จำนวนตัวเลขในความก้าวหน้าคือจำนวนใด
ผลรวมของเงื่อนไขความก้าวหน้าทางคณิตศาสตร์
มีสองวิธีในการค้นหาจำนวนเงิน:
จำนวนค่าอยู่ที่ไหน
จำนวนค่าอยู่ที่ไหน
แนวคิดเรื่องลำดับตัวเลขบอกเป็นนัยว่าจำนวนธรรมชาติแต่ละจำนวนสอดคล้องกับค่าจริงบางค่า ชุดตัวเลขดังกล่าวอาจเป็นแบบใดก็ได้หรือมีคุณสมบัติบางอย่าง - ความก้าวหน้า ในกรณีหลัง แต่ละองค์ประกอบที่ตามมา (สมาชิก) ของลำดับสามารถคำนวณได้โดยใช้องค์ประกอบก่อนหน้า
ความก้าวหน้าทางคณิตศาสตร์คือลำดับของค่าตัวเลขที่สมาชิกที่อยู่ใกล้เคียงต่างกันด้วยจำนวนเดียวกัน (องค์ประกอบทั้งหมดของซีรีส์เริ่มจากอันดับที่ 2 มีคุณสมบัติคล้ายกัน) ตัวเลขนี้ซึ่งเป็นผลต่างระหว่างพจน์ก่อนหน้าและพจน์ถัดไป เป็นค่าคงที่และเรียกว่าผลต่างของความก้าวหน้า
ความแตกต่างระหว่างความก้าวหน้า: คำจำกัดความ
พิจารณาลำดับที่ประกอบด้วยค่า j A = a(1), a(2), a(3), a(4) ... a(j), j เป็นของเซตของจำนวนธรรมชาติ N เลขคณิต ความก้าวหน้า ตามคำจำกัดความ คือลำดับ โดยที่ a(3) – a(2) = a(4) – a(3) = a(5) – a(4) = … = a(j) – ก(เจ-1) = ง. ค่า d คือความแตกต่างที่ต้องการของความก้าวหน้านี้
ง = ก(เจ) – ก(เจ-1)
ไฮไลท์:
- ความก้าวหน้าที่เพิ่มขึ้น ในกรณีนี้ d > 0 ตัวอย่าง: 4, 8, 12, 16, 20, ...
- ความก้าวหน้าลดลงแล้วง< 0. Пример: 18, 13, 8, 3, -2, …
ความก้าวหน้าที่แตกต่างกันและองค์ประกอบโดยพลการ
หากทราบเงื่อนไขการก้าวหน้าโดยพลการ 2 ข้อ (i-th, k-th) ดังนั้นความแตกต่างสำหรับลำดับที่กำหนดสามารถถูกกำหนดตามความสัมพันธ์:
a(i) = a(k) + (i – k)*d ซึ่งหมายถึง d = (a(i) – a(k))/(i-k)
ความแตกต่างของความก้าวหน้าและระยะแรก
นิพจน์นี้จะช่วยกำหนดค่าที่ไม่รู้จักเฉพาะในกรณีที่ทราบจำนวนองค์ประกอบลำดับเท่านั้น
ความแตกต่างของความก้าวหน้าและผลรวม
ผลรวมของความก้าวหน้าคือผลรวมของเงื่อนไข ในการคำนวณมูลค่ารวมขององค์ประกอบ j แรก ให้ใช้สูตรที่เหมาะสม:
S(j) =((a(1) + a(j))/2)*j แต่เนื่องจาก a(j) = a(1) + d(j – 1) จากนั้น S(j) = ((a(1) + a(1) + d(j – 1))/2)*j=(( 2a(1) + d(– 1))/2)*j
เมื่อเรียนพีชคณิตในโรงเรียนมัธยม (ชั้นประถมศึกษาปีที่ 9) หนึ่งในหัวข้อที่สำคัญคือการศึกษาลำดับตัวเลขซึ่งรวมถึงความก้าวหน้า - เรขาคณิตและเลขคณิต ในบทความนี้ เราจะดูความก้าวหน้าทางคณิตศาสตร์และตัวอย่างพร้อมคำตอบ
ความก้าวหน้าทางคณิตศาสตร์คืออะไร?
เพื่อให้เข้าใจสิ่งนี้ จำเป็นต้องกำหนดความก้าวหน้าในคำถาม พร้อมทั้งเตรียมสูตรพื้นฐานที่จะใช้ในการแก้ปัญหาในภายหลัง
เลขคณิตหรือเป็นชุดของจำนวนตรรกยะเรียงลำดับ ซึ่งสมาชิกแต่ละตัวจะแตกต่างจากจำนวนก่อนหน้าด้วยค่าคงที่ ค่านี้เรียกว่าส่วนต่าง นั่นคือการรู้จักสมาชิกของชุดตัวเลขที่เรียงลำดับและความแตกต่างคุณสามารถคืนค่าความก้าวหน้าทางคณิตศาสตร์ทั้งหมดได้
ลองยกตัวอย่าง ลำดับตัวเลขต่อไปนี้จะเป็นความก้าวหน้าทางคณิตศาสตร์: 4, 8, 12, 16, ... เนื่องจากความแตกต่างในกรณีนี้คือ 4 (8 - 4 = 12 - 8 = 16 - 12) แต่ชุดของตัวเลข 3, 5, 8, 12, 17 ไม่สามารถนำมาประกอบกับประเภทของความก้าวหน้าที่กำลังพิจารณาได้อีกต่อไปเนื่องจากความแตกต่างนั้นไม่ใช่ค่าคงที่ (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12)

สูตรสำคัญ
ให้เรานำเสนอสูตรพื้นฐานที่จำเป็นในการแก้ปัญหาโดยใช้ความก้าวหน้าทางคณิตศาสตร์ ให้เราแสดงด้วยสัญลักษณ์ a n สมาชิกตัวที่ n ของลำดับ โดยที่ n เป็นจำนวนเต็ม เราแสดงความแตกต่างด้วยตัวอักษรละติน d ดังนั้นนิพจน์ต่อไปนี้จึงถูกต้อง:
- เพื่อกำหนดค่าของเทอมที่ n สูตรต่อไปนี้มีความเหมาะสม: a n = (n-1)*d+a 1
- วิธีหาผลรวมของ n เทอมแรก: S n = (a n +a 1)*n/2
เพื่อให้เข้าใจตัวอย่างความก้าวหน้าทางคณิตศาสตร์ด้วยเฉลยในชั้นประถมศึกษาปีที่ 9 ก็เพียงพอที่จะจำสูตรทั้งสองนี้ได้เนื่องจากปัญหาประเภทใด ๆ ที่อยู่ระหว่างการพิจารณานั้นขึ้นอยู่กับการใช้งาน คุณควรจำไว้ว่าส่วนต่างของความก้าวหน้าถูกกำหนดโดยสูตร: d = a n - a n-1
ตัวอย่างที่ 1: การค้นหาสมาชิกที่ไม่รู้จัก

เราจะยกตัวอย่างง่ายๆ ของความก้าวหน้าทางคณิตศาสตร์และสูตรที่จำเป็นต้องใช้ในการแก้โจทย์
ให้ลำดับ 10, 8, 6, 4, ... คุณต้องหาคำศัพท์ห้าคำในนั้น
จากเงื่อนไขของปัญหาก็เป็นไปตามที่ทราบ 4 คำแรกแล้ว ห้าสามารถกำหนดได้สองวิธี:
- ก่อนอื่นมาคำนวณความแตกต่างกันก่อน เรามี: d = 8 - 10 = -2 ในทำนองเดียวกัน คุณสามารถพาสมาชิกอีกสองคนมายืนอยู่ข้างๆ กันก็ได้ ตัวอย่างเช่น d = 4 - 6 = -2 เนื่องจากเป็นที่ทราบกันว่า d = a n - a n-1 ดังนั้น d = a 5 - a 4 ซึ่งเราได้รับ: a 5 = a 4 + d เราแทนค่าที่ทราบ: a 5 = 4 + (-2) = 2
- วิธีที่สองยังต้องอาศัยความรู้เกี่ยวกับความแตกต่างของความก้าวหน้าที่เป็นปัญหา ดังนั้นคุณต้องพิจารณาก่อนดังที่แสดงไว้ด้านบน (d = -2) เมื่อรู้ว่าเทอมแรก a 1 = 10 เราใช้สูตรสำหรับจำนวน n ของลำดับ เรามี: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2*n เมื่อแทน n = 5 ลงในนิพจน์สุดท้าย เราจะได้: a 5 = 12-2 * 5 = 2
อย่างที่คุณเห็น ทั้งสองวิธีนำไปสู่ผลลัพธ์เดียวกัน โปรดทราบว่าในตัวอย่างนี้ ผลต่างความก้าวหน้า d เป็นค่าลบ ลำดับดังกล่าวเรียกว่าการลดลง เนื่องจากแต่ละเทอมถัดไปจะน้อยกว่าลำดับก่อนหน้า
ตัวอย่างที่ 2: ความแตกต่างในความก้าวหน้า
ทีนี้มาทำให้งานซับซ้อนขึ้นอีกหน่อย ยกตัวอย่างวิธีค้นหาความแตกต่างของความก้าวหน้าทางคณิตศาสตร์
เป็นที่ทราบกันว่าในการก้าวหน้าทางพีชคณิตบางเทอม เทอมที่ 1 เท่ากับ 6 และเทอมที่ 7 เท่ากับ 18 จำเป็นต้องค้นหาความแตกต่างและคืนค่าลำดับนี้เป็นเทอมที่ 7
ลองใช้สูตรเพื่อกำหนดคำที่ไม่รู้จัก: a n = (n - 1) * d + a 1 ลองแทนที่ข้อมูลที่ทราบจากเงื่อนไขลงไปนั่นคือตัวเลข a 1 และ 7 เรามี: 18 = 6 + 6 * d จากนิพจน์นี้ คุณสามารถคำนวณความแตกต่างได้อย่างง่ายดาย: d = (18 - 6) /6 = 2 ดังนั้นเราจึงได้ตอบส่วนแรกของปัญหาแล้ว
ในการคืนลำดับให้เป็นเทอมที่ 7 คุณควรใช้คำจำกัดความของการก้าวหน้าทางพีชคณิต นั่นคือ a 2 = a 1 + d, a 3 = a 2 + d และอื่นๆ เป็นผลให้เรากู้คืนลำดับทั้งหมด: a 1 = 6, a 2 = 6 + 2=8, 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , 6 = 14 + 2 = 16, 7 = 18
ตัวอย่างที่ 3: วาดความก้าวหน้า

มาทำให้ปัญหาซับซ้อนยิ่งขึ้น ตอนนี้เราต้องตอบคำถามว่าจะหาความก้าวหน้าทางคณิตศาสตร์ได้อย่างไร สามารถให้ตัวอย่างต่อไปนี้: ให้ตัวเลขสองตัวเช่น - 4 และ 5 มีความจำเป็นต้องสร้างความก้าวหน้าทางพีชคณิตเพื่อให้มีคำศัพท์อีกสามคำอยู่ระหว่างคำเหล่านี้
ก่อนที่คุณจะเริ่มแก้ไขปัญหานี้ คุณต้องเข้าใจว่าตัวเลขที่ให้มาจะอยู่ในตำแหน่งใดในความก้าวหน้าในอนาคต เนื่องจากจะมีคำศัพท์อีกสามคำระหว่างกัน ดังนั้น 1 = -4 และ 5 = 5 เมื่อสร้างสิ่งนี้แล้ว เราจึงไปยังปัญหาซึ่งคล้ายกับปัญหาก่อนหน้า อีกครั้ง สำหรับเทอมที่ n เราใช้สูตร เราได้: a 5 = a 1 + 4 * d จาก: d = (ก 5 - ก 1)/4 = (5 - (-4)) / 4 = 2.25 สิ่งที่เราได้มานี้ไม่ใช่ค่าจำนวนเต็มของความแตกต่าง แต่เป็นจำนวนตรรกยะ ดังนั้นสูตรสำหรับการก้าวหน้าทางพีชคณิตจึงยังคงเหมือนเดิม
ทีนี้มาเพิ่มความแตกต่างที่พบให้กับ 1 และเรียกคืนเงื่อนไขที่ขาดหายไปของความก้าวหน้า เราได้รับ: a 1 = - 4, a 2 = - 4 + 2.25 = - 1.75, a 3 = -1.75 + 2.25 = 0.5, a 4 = 0.5 + 2.25 = 2.75, a 5 = 2.75 + 2.25 = 5 ซึ่งใกล้เคียงกัน ด้วยเงื่อนไขของปัญหา
ตัวอย่างที่ 4: ระยะแรกของความก้าวหน้า

เราจะยกตัวอย่างความก้าวหน้าทางคณิตศาสตร์พร้อมเฉลยต่อไป ในปัญหาก่อนหน้านี้ทั้งหมด ทราบจำนวนแรกของความก้าวหน้าทางพีชคณิต ทีนี้ลองพิจารณาปัญหาประเภทอื่น: ให้ระบุตัวเลขสองตัว โดยที่ 15 = 50 และ 43 = 37 จำเป็นต้องค้นหาว่าลำดับนี้ขึ้นต้นด้วยตัวเลขใด
สูตรที่ใช้จนถึงขณะนี้ถือว่าความรู้เกี่ยวกับ 1 และ d ในคำชี้แจงปัญหา ไม่มีใครทราบเกี่ยวกับตัวเลขเหล่านี้ อย่างไรก็ตาม เราจะเขียนนิพจน์สำหรับแต่ละเทอมเกี่ยวกับข้อมูลที่มีอยู่: a 15 = a 1 + 14 * d และ 43 = a 1 + 42 * d เราได้รับสมการสองสมการซึ่งมีปริมาณที่ไม่ทราบจำนวน 2 ปริมาณ (a 1 และ d) ซึ่งหมายความว่าปัญหาจะลดลงเหลือเพียงการแก้ระบบสมการเชิงเส้น
วิธีที่ง่ายที่สุดในการแก้ระบบนี้คือแสดง 1 ในแต่ละสมการ แล้วเปรียบเทียบนิพจน์ผลลัพธ์ สมการแรก: a 1 = a 15 - 14 * d = 50 - 14 * d; สมการที่สอง: a 1 = a 43 - 42 * d = 37 - 42 * d เมื่อเทียบนิพจน์เหล่านี้เราจะได้: 50 - 14 * d = 37 - 42 * d ดังนั้นความแตกต่าง d = (37 - 50) / (42 - 14) = - 0.464 (ให้ทศนิยม 3 ตำแหน่งเท่านั้น)
เมื่อรู้ d แล้ว คุณสามารถใช้ 2 สำนวนข้างต้นเป็น 1 ได้ ตัวอย่างเช่น อย่างแรก: a 1 = 50 - 14 * d = 50 - 14 * (- 0.464) = 56.496
หากมีข้อสงสัยเกี่ยวกับผลลัพธ์ที่ได้ก็สามารถตรวจสอบได้ เช่น กำหนดระยะความก้าวหน้าที่ 43 ซึ่งระบุไว้ในเงื่อนไข เราได้: a 43 = a 1 + 42 * d = 56.496 + 42 * (- 0.464) = 37.008 ข้อผิดพลาดเล็กน้อยเกิดจากการใช้การปัดเศษเป็นพันในการคำนวณ
ตัวอย่างหมายเลข 5: จำนวนเงิน
ตอนนี้เรามาดูตัวอย่างต่างๆ พร้อมคำตอบสำหรับผลรวมของความก้าวหน้าทางคณิตศาสตร์กัน
ให้แสดงความก้าวหน้าเชิงตัวเลขของแบบฟอร์มต่อไปนี้: 1, 2, 3, 4, ..., จะคำนวณผลรวมของ 100 ของตัวเลขเหล่านี้ได้อย่างไร?
ด้วยการพัฒนาเทคโนโลยีคอมพิวเตอร์จึงเป็นไปได้ที่จะแก้ไขปัญหานี้นั่นคือการเพิ่มตัวเลขทั้งหมดตามลำดับซึ่งคอมพิวเตอร์จะทำทันทีที่มีคนกดปุ่ม Enter อย่างไรก็ตามปัญหาสามารถแก้ไขได้ทางจิตหากคุณใส่ใจกับความจริงที่ว่าชุดตัวเลขที่นำเสนอนั้นเป็นความก้าวหน้าทางพีชคณิตและผลต่างเท่ากับ 1 เมื่อใช้สูตรสำหรับผลรวมเราจะได้: S n = n * ( ก 1 + ก n) / 2 = 100 * (1 + 100) / 2 = 5050
เป็นที่น่าสนใจที่ทราบว่าปัญหานี้เรียกว่า "เกาส์เซียน" เพราะเมื่อต้นศตวรรษที่ 18 ชาวเยอรมันผู้โด่งดังซึ่งอายุเพียง 10 ปีเท่านั้นสามารถแก้ปัญหาในหัวได้ภายในไม่กี่วินาที เด็กชายไม่ทราบสูตรสำหรับผลรวมของการก้าวหน้าทางพีชคณิต แต่เขาสังเกตว่าถ้าคุณบวกตัวเลขที่ท้ายลำดับเป็นคู่ คุณจะได้ผลลัพธ์เหมือนเดิมเสมอ นั่นคือ 1 + 100 = 2 + 99 = 3 + 98 = ... และเนื่องจากผลรวมเหล่านี้จะเท่ากับ 50 (100/2) พอดี ดังนั้นเพื่อให้ได้คำตอบที่ถูกต้อง ก็เพียงพอที่จะคูณ 50 ด้วย 101

ตัวอย่างที่ 6: ผลรวมของเงื่อนไขตั้งแต่ n ถึง m
อีกตัวอย่างทั่วไปของผลรวมของความก้าวหน้าทางคณิตศาสตร์มีดังต่อไปนี้: เมื่อพิจารณาชุดตัวเลข: 3, 7, 11, 15, ... คุณต้องค้นหาว่าผลรวมของคำศัพท์ตั้งแต่ 8 ถึง 14 จะเท่ากับเท่าใด .
ปัญหาได้รับการแก้ไขในสองวิธี วิธีแรกเกี่ยวข้องกับการค้นหาคำศัพท์ที่ไม่รู้จักตั้งแต่ 8 ถึง 14 แล้วจึงรวมคำศัพท์ตามลำดับ เนื่องจากมีคำศัพท์ไม่มาก วิธีการนี้จึงใช้แรงงานคนไม่มาก อย่างไรก็ตามมีการเสนอให้แก้ไขปัญหานี้โดยใช้วิธีที่สองซึ่งเป็นสากลมากกว่า
แนวคิดคือการหาสูตรสำหรับผลรวมของการก้าวหน้าทางพีชคณิตระหว่างพจน์ m และ n โดยที่ n > m เป็นจำนวนเต็ม สำหรับทั้งสองกรณี เราจะเขียนนิพจน์สองนิพจน์เพื่อสรุปผลรวม:
- S ม. = ม. * (ม. + ก 1) / 2
- S n = n * (a n + a 1) / 2
เนื่องจาก n > m เห็นได้ชัดว่าผลรวมที่สองรวมผลรวมแรกด้วย ข้อสรุปสุดท้ายหมายความว่าถ้าเราหาผลต่างระหว่างผลรวมเหล่านี้แล้วบวกคำว่า a m ลงไป (ในกรณีที่นำผลต่างมาลบออกจากผลรวม S n) เราก็จะได้คำตอบที่จำเป็นของปัญหา เรามี: S mn = S n - S m + a m =n * (a 1 + a n) / 2 - m *(a 1 + a m)/2 + a m = a 1 * (n - m) / 2 + a n * n/2 + ม. * (1- ม./2) จำเป็นต้องแทนที่สูตรสำหรับ n และ a m ในนิพจน์นี้ จากนั้นเราจะได้: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - ม. / 2) = ก 1 * (น - ม. + 1) + ง * n * (n - 1) / 2 + ง *(3 * ม. - ม. 2 - 2) / 2
สูตรผลลัพธ์ค่อนข้างยุ่งยาก แต่ผลรวม S mn ขึ้นอยู่กับ n, m, 1 และ d เท่านั้น ในกรณีของเรา a 1 = 3, d = 4, n = 14, m = 8 เมื่อแทนตัวเลขเหล่านี้ เราจะได้: S mn = 301

ดังที่เห็นได้จากวิธีแก้ปัญหาข้างต้น ปัญหาทั้งหมดจะขึ้นอยู่กับความรู้เกี่ยวกับนิพจน์สำหรับเทอมที่ n และสูตรสำหรับผลรวมของเซตของเทอมแรก ก่อนที่จะเริ่มแก้ไขปัญหาใดๆ เหล่านี้ ขอแนะนำให้คุณอ่านเงื่อนไขอย่างละเอียด ทำความเข้าใจอย่างชัดเจนถึงสิ่งที่คุณต้องค้นหา จากนั้นจึงดำเนินการแก้ไขปัญหาต่อไป
เคล็ดลับอีกประการหนึ่งคือการมุ่งมั่นเพื่อความเรียบง่าย กล่าวคือ หากคุณสามารถตอบคำถามได้โดยไม่ต้องใช้การคำนวณทางคณิตศาสตร์ที่ซับซ้อน คุณก็จำเป็นต้องทำเช่นนั้น เนื่องจากในกรณีนี้ โอกาสที่จะทำผิดพลาดมีน้อยกว่า ตัวอย่างเช่นในตัวอย่างของความก้าวหน้าทางคณิตศาสตร์ด้วยวิธีแก้ปัญหาหมายเลข 6 เราสามารถหยุดที่สูตร S mn = n * (a 1 + a n) / 2 - m * (a 1 + a m) / 2 + a m และ แบ่งปัญหาโดยรวมออกเป็นงานย่อยแยกกัน (ในกรณีนี้ ให้หาพจน์ a n และ a m ก่อน)
หากคุณมีข้อสงสัยเกี่ยวกับผลลัพธ์ที่ได้ ขอแนะนำให้ตรวจสอบดังที่ได้ดำเนินการไปแล้วในตัวอย่างบางส่วนที่ให้ไว้ เราพบวิธีค้นหาความก้าวหน้าทางคณิตศาสตร์ ถ้าคุณเข้าใจ มันก็ไม่ใช่เรื่องยากขนาดนั้น
หลายคนเคยได้ยินเกี่ยวกับความก้าวหน้าทางคณิตศาสตร์ แต่ไม่ใช่ทุกคนที่จะมีความคิดที่ดีว่ามันคืออะไร ในบทความนี้ เราจะให้คำจำกัดความที่เกี่ยวข้อง และพิจารณาคำถามว่าจะค้นหาความแตกต่างของความก้าวหน้าทางคณิตศาสตร์ได้อย่างไร พร้อมยกตัวอย่างจำนวนหนึ่ง
คำจำกัดความทางคณิตศาสตร์
ดังนั้น หากเรากำลังพูดถึงความก้าวหน้าทางคณิตศาสตร์หรือพีชคณิต (แนวคิดเหล่านี้นิยามสิ่งเดียวกัน) นั่นหมายความว่ามีชุดตัวเลขจำนวนหนึ่งที่เป็นไปตามกฎต่อไปนี้: ทุก ๆ สองตัวเลขที่อยู่ติดกันในชุดต่างกันด้วยค่าเดียวกัน ในทางคณิตศาสตร์มันเขียนดังนี้:
ในที่นี้ n หมายถึงจำนวนขององค์ประกอบ a n ในลำดับ และตัวเลข d คือผลต่างของความก้าวหน้า (ชื่อตามมาจากสูตรที่นำเสนอ)
การรู้ความแตกต่าง d หมายถึงอะไร? ว่าตัวเลขข้างเคียง “ไกล” แค่ไหน อย่างไรก็ตาม ความรู้เกี่ยวกับ d ถือเป็นเงื่อนไขที่จำเป็นแต่ไม่เพียงพอในการพิจารณา (ฟื้นฟู) ความก้าวหน้าทั้งหมด คุณจำเป็นต้องรู้ตัวเลขอีกตัวหนึ่งซึ่งอาจเป็นองค์ประกอบใดๆ ก็ตามของอนุกรมที่เป็นปัญหาได้ เช่น 4, a10 แต่ตามกฎแล้วจะใช้ตัวเลขแรกซึ่งก็คือ 1
สูตรการกำหนดองค์ประกอบความก้าวหน้า
โดยทั่วไป ข้อมูลข้างต้นเพียงพอที่จะดำเนินการแก้ไขปัญหาเฉพาะได้แล้ว อย่างไรก็ตาม ก่อนที่จะให้ความก้าวหน้าทางคณิตศาสตร์และจำเป็นต้องค้นหาความแตกต่าง เราจะนำเสนอสูตรที่มีประโยชน์สองสามสูตร ซึ่งจะช่วยอำนวยความสะดวกในกระบวนการแก้ไขปัญหาที่ตามมา
เป็นเรื่องง่ายที่จะแสดงให้เห็นว่าองค์ประกอบใดๆ ของลำดับที่มีหมายเลข n สามารถหาได้ดังนี้:
n = 1 + (n - 1) * d
แน่นอนว่าใครๆ ก็สามารถตรวจสอบสูตรนี้ได้ด้วยการค้นหาง่ายๆ: หากคุณแทนที่ n = 1 คุณจะได้องค์ประกอบแรก หากคุณแทนที่ n = 2 นิพจน์จะให้ผลรวมของตัวเลขแรกและผลต่าง ไปเรื่อยๆ

เงื่อนไขของปัญหาต่างๆ ประกอบขึ้นในลักษณะที่ว่า เมื่อพิจารณาคู่ของตัวเลขที่รู้จัก และตัวเลขที่ได้รับในลำดับด้วย จำเป็นต้องสร้างชุดตัวเลขใหม่ทั้งหมด (ค้นหาผลต่างและองค์ประกอบแรก) ตอนนี้เราจะแก้ไขปัญหานี้ในรูปแบบทั่วไป
ดังนั้น ให้ระบุองค์ประกอบสองตัวที่มีตัวเลข n และ m เมื่อใช้สูตรที่ได้รับข้างต้น คุณสามารถสร้างระบบสมการได้สองสมการ:
n = 1 + (n - 1) * d;
ก. = ก. 1 + (ม. - 1) * ง
ในการค้นหาปริมาณที่ไม่ทราบ เราจะใช้เทคนิคง่ายๆ ที่รู้จักกันดีในการแก้ระบบดังกล่าว: ลบด้านซ้ายและขวาเป็นคู่ ความเท่าเทียมกันจะยังคงใช้ได้ เรามี:
n = 1 + (n - 1) * d;
n - a m = (n - 1) * d - (m - 1) * d = d * (n - m)
ดังนั้นเราจึงได้แยกสิ่งที่ไม่รู้จักออกไป (a 1) ตอนนี้เราสามารถเขียนนิพจน์สุดท้ายเพื่อกำหนด d:
d = (a n - a m) / (n - m) โดยที่ n > m
เราได้รับสูตรง่ายๆ: ในการคำนวณความแตกต่าง d ตามเงื่อนไขของปัญหา จำเป็นต้องใช้อัตราส่วนของความแตกต่างระหว่างองค์ประกอบเองกับหมายเลขซีเรียลเท่านั้น ควรให้ความสนใจประเด็นสำคัญประการหนึ่ง: ความแตกต่างระหว่างสมาชิก "รุ่นพี่" และ "รุ่นน้อง" นั่นคือ n > m ("รุ่นพี่" หมายถึงการยืนห่างจากจุดเริ่มต้นของลำดับ ค่าสัมบูรณ์ของมันสามารถเป็นได้ทั้ง องค์ประกอบ "จูเนียร์" มากกว่าหรือน้อยกว่า)
นิพจน์สำหรับส่วนต่าง d ความก้าวหน้าควรถูกแทนที่ลงในสมการใดๆ ที่ตอนเริ่มต้นของการแก้ปัญหาเพื่อให้ได้ค่าของเทอมแรก

ในยุคของการพัฒนาเทคโนโลยีคอมพิวเตอร์ของเรา เด็กนักเรียนจำนวนมากพยายามค้นหาวิธีแก้ปัญหาสำหรับการมอบหมายงานของตนบนอินเทอร์เน็ต ดังนั้นจึงมักมีคำถามประเภทนี้เกิดขึ้น: ค้นหาความแตกต่างของความก้าวหน้าทางคณิตศาสตร์ทางออนไลน์ สำหรับคำขอดังกล่าว เครื่องมือค้นหาจะส่งคืนหน้าเว็บจำนวนหนึ่ง โดยไปที่ซึ่งคุณจะต้องป้อนข้อมูลที่ทราบจากเงื่อนไข (ซึ่งอาจเป็นได้สองเงื่อนไขของความก้าวหน้าหรือผลรวมของจำนวนที่แน่นอน ) และได้รับคำตอบทันที อย่างไรก็ตามแนวทางในการแก้ปัญหานี้ไม่เกิดผลในแง่ของการพัฒนาและความเข้าใจของนักเรียนในสาระสำคัญของงานที่ได้รับมอบหมาย
วิธีแก้ปัญหาโดยไม่ต้องใช้สูตร

มาแก้ปัญหาแรกโดยไม่ต้องใช้สูตรที่กำหนดเลย ให้องค์ประกอบของอนุกรมได้รับ: a6 = 3, a9 = 18 ค้นหาผลต่างของความก้าวหน้าทางคณิตศาสตร์
องค์ประกอบที่รู้จักจะยืนชิดกันเป็นแถว ต้องบวกส่วนต่าง d เข้ากับค่าที่น้อยที่สุดกี่ครั้งเพื่อให้ได้ค่าที่ใหญ่ที่สุด? สามครั้ง (ครั้งแรกที่เพิ่ม d เราจะได้องค์ประกอบที่ 7 ครั้งที่สอง - ที่แปดในที่สุดครั้งที่สาม - ที่เก้า) ต้องบวกเลขอะไรเป็นสามครั้งจึงจะได้ 18? นี่คือหมายเลขห้า จริงหรือ:
ดังนั้น ผลต่างที่ไม่ทราบ d = 5
แน่นอนว่าการแก้ปัญหาสามารถทำได้โดยใช้สูตรที่เหมาะสม แต่ก็ไม่ได้ตั้งใจ คำอธิบายโดยละเอียดเกี่ยวกับวิธีแก้ปัญหาควรเป็นตัวอย่างที่ชัดเจนและชัดเจนว่าความก้าวหน้าทางคณิตศาสตร์คืออะไร
งานที่คล้ายกับงานก่อนหน้า
ตอนนี้เรามาแก้ไขปัญหาที่คล้ายกัน แต่เปลี่ยนข้อมูลอินพุต ดังนั้น คุณควรหาว่า a3 = 2, a9 = 19 หรือไม่
แน่นอนว่าคุณสามารถใช้วิธีแก้ไขปัญหาแบบ "เผชิญหน้า" ได้อีกครั้ง แต่เนื่องจากองค์ประกอบของอนุกรมได้รับซึ่งค่อนข้างห่างไกลจากกัน วิธีการนี้จึงไม่สะดวกนัก แต่การใช้สูตรผลลัพธ์จะนำเราไปสู่คำตอบอย่างรวดเร็ว:
d = (ก 9 - ก 3) / (9 - 3) = (19 - 2) / (6) = 17 / 6 กลับไปยัง 2.83
ที่นี่เราได้ปัดเศษตัวเลขสุดท้ายแล้ว ขอบเขตที่การปัดเศษนี้นำไปสู่ข้อผิดพลาดสามารถตัดสินได้โดยการตรวจสอบผลลัพธ์:
9 = 3 + 2.83 + 2.83 + 2.83 + 2.83 + 2.83 + 2.83 = 18.98
ผลลัพธ์นี้แตกต่างเพียง 0.1% จากค่าที่กำหนดในเงื่อนไข ดังนั้นการปัดเศษที่ใช้เป็นร้อยที่ใกล้ที่สุดจึงถือเป็นตัวเลือกที่ประสบความสำเร็จ
ปัญหาเกี่ยวกับการประยุกต์สูตรสำหรับเทอม

ลองพิจารณาตัวอย่างคลาสสิกของปัญหาเพื่อระบุ d ที่ไม่รู้จัก: ค้นหาผลต่างของความก้าวหน้าทางคณิตศาสตร์หาก a1 = 12, a5 = 40
เมื่อระบุลำดับพีชคณิตที่ไม่รู้จักจำนวนสองตัว และหนึ่งในนั้นคือองค์ประกอบ a 1 คุณไม่จำเป็นต้องคิดนาน แต่ควรใช้สูตรสำหรับพจน์ n ทันที ในกรณีนี้เรามี:
5 = 1 + d * (5 - 1) => d = (5 - 1) / 4 = (40 - 12) / 4 = 7
เราได้รับจำนวนที่แน่นอนเมื่อทำการหาร ดังนั้นจึงไม่มีประเด็นในการตรวจสอบความถูกต้องของผลลัพธ์ที่คำนวณได้ดังที่ทำในย่อหน้าก่อนหน้า
มาแก้ปัญหาที่คล้ายกันอีกปัญหาหนึ่ง: เราจำเป็นต้องค้นหาผลต่างของความก้าวหน้าทางคณิตศาสตร์หาก a1 = 16, a8 = 37
เราใช้แนวทางที่คล้ายกับวิธีก่อนหน้าและได้รับ:
8 = 1 + d * (8 - 1) => d = (8 - 1) / 7 = (37 - 16) / 7 = 3
คุณควรรู้อะไรอีกบ้างเกี่ยวกับความก้าวหน้าทางคณิตศาสตร์?
นอกจากปัญหาในการค้นหาความแตกต่างที่ไม่ทราบค่าหรือองค์ประกอบแต่ละส่วนแล้ว ยังมักจำเป็นต้องแก้ปัญหาผลรวมของเทอมแรกของลำดับด้วย การพิจารณาปัญหาเหล่านี้อยู่นอกเหนือขอบเขตของบทความ อย่างไรก็ตาม เพื่อความสมบูรณ์ของข้อมูล เราขอนำเสนอสูตรทั่วไปสำหรับผลรวมของตัวเลข n ชุด:
∑ n i = 1 (ai) = n * (a 1 + n) / 2
 สมการลอการิทึม
สมการลอการิทึม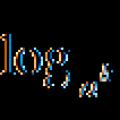 เทคนิคการแก้สมการลอการิทึม
เทคนิคการแก้สมการลอการิทึม การวิเคราะห์ตนเองของครูนักบำบัดการพูด
การวิเคราะห์ตนเองของครูนักบำบัดการพูด