ศึกษาการเคลื่อนที่ของวัตถุที่ถูกโยนในมุมหนึ่งไปยังแนวนอน การเคลื่อนไหวของวัตถุที่ถูกโยนทำมุมกับขอบฟ้า การคำนวณระยะการบิน
คำแนะนำ
ปล่อยให้วัตถุถูกโยนในมุม α ไปยังขอบฟ้าด้วยความเร็วเริ่มต้น v0 ให้พิกัดเริ่มต้นของร่างกายเป็นศูนย์: x(0)=0, y(0)=0 ในการฉายภาพลงบนแกนพิกัด ความเร็วเริ่มต้นจะถูกแบ่งออกเป็นสององค์ประกอบ: v0(x) และ v0(y) ความเร็วเท่ากันโดยทั่วไป ตามแกน Ox ความเร็วจะถือว่าคงที่ตามอัตภาพ ในขณะที่ตามแกน Oy ความเร็วจะเปลี่ยนไปภายใต้อิทธิพลของ ความเร่งของแรงโน้มถ่วง g สามารถวัดได้ประมาณ 10 m/s²
มุม α ที่ร่างกายถูกขว้างนั้นไม่ได้เกิดขึ้นโดยบังเอิญ คุณสามารถอธิบายความเร็วเริ่มต้นในแกนพิกัดได้ ดังนั้น v0(x)=v0·cos(α), v0(y)=v0·sin(α) ตอนนี้เราสามารถรับฟังก์ชันของส่วนประกอบพิกัดของความเร็วได้แล้ว: v(x)=const=v0(x)=v0·cos(α), v(y)=v0(y)-g·t=v0·sin( α)-g· เสื้อ.
พิกัด x และ y ของร่างกายขึ้นอยู่กับเวลา t ดังนั้น เราสามารถสร้างสมการการพึ่งพาได้สองสมการ: x=x0+v0(x) t+a(x) t²/2, y=y0+v0(y) t+a(y) t²/2 เนื่องจาก x0=0, a(x)=0 จากนั้น x=v0(x) t=v0 cos(α) t เป็นที่ทราบกันว่า y0=0, a(y)=-g (เครื่องหมาย “ ” ปรากฏขึ้นเนื่องจากทิศทางความเร่งของแรงโน้มถ่วง g และทิศทางบวกของแกน Oy อยู่ตรงข้ามกัน) ดังนั้น y=v0·sin(α)·t-g·t²/2
เวลาบินสามารถแสดงได้จากสูตรความเร็ว โดยรู้ว่า ณ จุดสูงสุดร่างกายหยุดชั่วขณะหนึ่ง (v = 0) และระยะเวลา "ขึ้น" และ "ลง" เท่ากัน ดังนั้น เมื่อแทน v(y)=0 ลงในสมการ v(y)=v0·sin(α)-g·t จะได้ว่า: 0=v0·sin(α)-g·t(p) โดยที่ t (p) – เวลาสูงสุด “t จุดยอด” ดังนั้น t(p)=v0·sin(α)/g เวลาบินทั้งหมดจะแสดงเป็น t=2·v0·sin(α)/g
สูตรเดียวกันนี้สามารถหาได้ในอีกทางหนึ่งทางคณิตศาสตร์ จากสมการของพิกัด y=v0·sin(α)·t-g·t²/2 สมการนี้สามารถเขียนใหม่ได้ในรูปแบบที่มีการปรับเปลี่ยนเล็กน้อย: y=-g/2·t²+v0·sin(α)·t จะเห็นได้ว่านี่คือการพึ่งพากำลังสอง โดยที่ y คือฟังก์ชัน t คืออาร์กิวเมนต์ จุดยอดของพาราโบลาที่อธิบายวิถีโคจรคือจุด t(p)=[-v0·sin(α)]/[-2g/2] ลบและสองหักล้างกัน ดังนั้น t(p)=v0·sin(α)/g หากเราแสดงความสูงสูงสุดเป็น H และจำไว้ว่าจุดสูงสุดคือจุดยอดของพาราโบลาที่วัตถุเคลื่อนที่ ดังนั้น H=y(t(p))=v0²sin²(α)/2g นั่นคือเพื่อให้ได้ความสูง คุณต้องแทนที่ "จุดยอด" ลงในสมการของพิกัด y
ดังนั้น เวลาบินจึงเขียนเป็น t=2·v0·sin(α)/g หากต้องการเปลี่ยน คุณจะต้องเปลี่ยนความเร็วเริ่มต้นและมุมเอียงตามลำดับ ยิ่งความเร็วสูง ร่างกายก็จะบินได้นานขึ้น เมื่อทำมุมจะค่อนข้างซับซ้อนกว่า เพราะเวลาไม่ได้ขึ้นอยู่กับมุมนั้นเอง แต่ขึ้นอยู่กับไซน์ของมันด้วย ค่าไซน์ที่เป็นไปได้สูงสุด - เอกภาพ - ทำได้ที่มุมเอียง 90° ซึ่งหมายความว่าร่างกายจะบินได้ไกลที่สุดเมื่อถูกเหวี่ยงขึ้นในแนวตั้ง
ระยะการบินคือพิกัด x สุดท้าย หากเราแทนเวลาบินที่พบแล้วลงในสมการ x=v0·cos(α)·t ก็จะพบว่า L=2v0²sin(α)cos(α)/g เป็นเรื่องง่าย ตรงนี้เราสามารถใช้สูตรมุมคู่ตรีโกณมิติ 2sin(α)cos(α)=sin(2α) จากนั้น L=v0²sin(2α)/g ไซน์ของอัลฟ่าสองตัวจะเท่ากับหนึ่งเมื่อ 2α=n/2, α=n/4 ดังนั้น ระยะการบินจะสูงสุดหากลำตัวถูกเหวี่ยงไปที่มุม 45°
หากวัตถุถูกโยนในมุมหนึ่งจนถึงขอบฟ้า ขณะบินวัตถุนั้นจะถูกกระทำโดยแรงโน้มถ่วงและแรงต้านอากาศ หากละเลยแรงต้านทาน แรงเดียวที่เหลืออยู่คือแรงโน้มถ่วง ดังนั้นเนื่องจากกฎข้อที่ 2 ของนิวตัน ร่างกายจึงเคลื่อนที่ด้วยความเร่งเท่ากับความเร่งของแรงโน้มถ่วง เส้นโครงความเร่งบนแกนพิกัด ax = 0, ay = - g
รูปที่ 1 ลักษณะทางจลนศาสตร์ของวัตถุที่ถูกโยนทำมุมกับแนวนอน
การเคลื่อนไหวที่ซับซ้อนใดๆ ของจุดวัสดุสามารถแสดงเป็นการซ้อนทับของการเคลื่อนไหวอิสระตามแนวแกนพิกัด และประเภทของการเคลื่อนที่อาจแตกต่างกันไปในทิศทางของแกนต่างๆ ในกรณีของเรา การเคลื่อนที่ของวัตถุที่บินสามารถแสดงเป็นการซ้อนทับของการเคลื่อนไหวอิสระสองแบบ: การเคลื่อนที่สม่ำเสมอตามแนวแกนนอน (แกน X) และการเคลื่อนที่ด้วยความเร่งสม่ำเสมอตามแนวแกนตั้ง (แกน Y) (รูปที่ 1) .
การคาดคะเนความเร็วของร่างกายจึงเปลี่ยนไปตามเวลาดังนี้
![]()
โดยที่ $v_0$ คือความเร็วเริ่มต้น $(\mathbf \alpha )$ คือมุมการขว้าง
ด้วยการเลือกแหล่งกำเนิดของเรา พิกัดเริ่มต้น (รูปที่ 1) คือ $x_0=y_0=0$ จากนั้นเราจะได้รับ:
 (1)
(1)
มาวิเคราะห์สูตร (1) กัน ให้เรากำหนดเวลาการเคลื่อนไหวของร่างกายที่ถูกโยน เมื่อต้องการทำสิ่งนี้ ให้ตั้งค่าพิกัด y เท่ากับศูนย์ เพราะ ในขณะที่ลงจอดความสูงของร่างกายเป็นศูนย์ จากที่นี่เราจะทราบเวลาเที่ยวบิน:
ค่าครั้งที่สองที่ความสูงเป็นศูนย์จะเป็นศูนย์ซึ่งสอดคล้องกับช่วงเวลาของการขว้างนั่นคือ ค่านี้ยังมีความหมายทางกายภาพด้วย
เราได้ระยะการบินจากสูตรแรก (1) ช่วงการบินคือค่าของพิกัด x ที่จุดสิ้นสุดของการบิน กล่าวคือ ในเวลาเท่ากับ $t_0$ แทนค่า (2) ลงในสูตรแรก (1) เราจะได้:
จากสูตรนี้จะเห็นได้ว่าระยะการบินสูงสุดอยู่ที่มุมการขว้าง 45 องศา
ความสูงในการยกสูงสุดของตัวโยนสามารถรับได้จากสูตรที่สอง (1) ในการทำเช่นนี้ คุณต้องแทนที่ค่าเวลาเท่ากับครึ่งหนึ่งของเวลาการบิน (2) ลงในสูตรนี้ เนื่องจาก ระดับความสูงของการบินอยู่ที่จุดกึ่งกลางของวิถีโคจร เราได้รับการคำนวณ
จากสมการ (1) เราสามารถหาสมการวิถีการเคลื่อนที่ของร่างกายได้ เช่น สมการที่เกี่ยวข้องกับพิกัด x และ y ของร่างกายระหว่างการเคลื่อนไหว เมื่อต้องการทำเช่นนี้ คุณต้องแสดงเวลาจากสมการแรก (1):
และแทนที่มันลงในสมการที่สอง จากนั้นเราจะได้รับ:
![]()
สมการนี้คือสมการวิถีการเคลื่อนที่ จะเห็นได้ว่านี่คือสมการของพาราโบลาที่มีกิ่งก้านลงมา ดังระบุด้วยเครื่องหมาย "-" หน้าเทอมกำลังสอง โปรดทราบว่ามุมการขว้าง $\alpha $ และฟังก์ชันของมันคือค่าคงที่ที่นี่ นั่นคือ ตัวเลขคงที่
ร่างกายถูกโยนด้วยความเร็ว v0 ที่มุม $(\mathbf \alpha )$ ไปยังแนวนอน เวลาบิน $t = 2 วินาที Hmax ตัวจะสูงขนาดไหน?
$$t_B = 2 ส$$ $$H_สูงสุด - ?$$

กฎการเคลื่อนที่ของร่างกายมีรูปแบบดังนี้
$$\left\( \begin(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \right.$ $
เวกเตอร์ความเร็วเริ่มต้นสร้างมุม $(\mathbf \alpha )$ กับแกน OX เพราะฉะนั้น,
\ \ \
ก้อนหินถูกโยนลงมาจากยอดเขาด้วยมุม = 30$()^\circ$ ด้วยความเร็วเริ่มต้นที่ $v_0 = 6 m/s$ มุมระนาบเอียง = 30$()^\circ$ หินจะตกลงจากจุดขว้างไกลแค่ไหน?
$$ \alpha =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

ลองวางจุดกำเนิดของพิกัดที่จุดขว้าง OX - ตามระนาบเอียงลง OY - ตั้งฉากกับระนาบเอียงขึ้นไป ลักษณะทางจลนศาสตร์ของการเคลื่อนไหว:
กฎการเคลื่อนที่:
$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(array) \right.$$ \
แทนที่ค่าผลลัพธ์ $t_В$ เราจะพบ $S$:
นี่เป็นงานที่สร้างสรรค์สำหรับชั้นเรียนปริญญาโทด้านวิทยาการคอมพิวเตอร์สำหรับเด็กนักเรียนที่ FEFU
วัตถุประสงค์ของภารกิจคือค้นหาว่าวิถีการเคลื่อนที่ของร่างกายจะเปลี่ยนไปอย่างไรหากคำนึงถึงแรงต้านของอากาศ จำเป็นต้องตอบคำถามว่าระยะการบินจะยังคงถึงค่าสูงสุดที่มุมขว้าง 45° หรือไม่ หากคำนึงถึงแรงต้านอากาศ
ส่วน “การวิจัยเชิงวิเคราะห์” จะสรุปทฤษฎี คุณสามารถข้ามส่วนนี้ได้ แต่ส่วนใหญ่ควรชัดเจนสำหรับคุณเพราะ... โอคุณเรียนรู้สิ่งนี้ส่วนใหญ่ในโรงเรียน
ส่วน "การศึกษาเชิงตัวเลข" ประกอบด้วยคำอธิบายของอัลกอริทึมที่ต้องนำไปใช้กับคอมพิวเตอร์ อัลกอริธึมนั้นเรียบง่ายและกระชับ ดังนั้นทุกคนควรจะสามารถทำได้
การวิจัยเชิงวิเคราะห์
ขอแนะนำระบบพิกัดสี่เหลี่ยมดังแสดงในรูป ในช่วงเวลาเริ่มต้นวัตถุมีมวล มตั้งอยู่ที่จุดกำเนิด เวกเตอร์ความเร่งอิสระตกมีทิศทางในแนวตั้งลงในแนวตั้งและมีพิกัด (0, - ก).- เวกเตอร์ความเร็วเริ่มต้น ลองขยายเวกเตอร์นี้เป็นฐาน:
ลองเขียนกฎข้อที่สองของนิวตัน:
ความเร่งในแต่ละช่วงเวลาคืออัตราการเปลี่ยนแปลงความเร็ว (ทันที) กล่าวคือ อนุพันธ์ของความเร็วเทียบกับเวลา:
ดังนั้นกฎข้อที่ 2 ของนิวตันจึงสามารถเขียนใหม่ได้ดังนี้
โดยที่เป็นผลจากแรงทั้งหมดที่กระทำต่อร่างกาย
เนื่องจากแรงโน้มถ่วงและแรงต้านอากาศกระทำต่อร่างกายแล้ว  .
.
เราจะพิจารณาสามกรณี:
1) แรงต้านอากาศคือ 0: .
2) แรงต้านอากาศนั้นทิศทางตรงข้ามกับเวกเตอร์ความเร็ว และขนาดของมันจะแปรผันตามความเร็ว: ![]() .
.
3) แรงต้านอากาศนั้นทิศทางตรงข้ามกับเวกเตอร์ความเร็ว และขนาดของมันเป็นสัดส่วนกับกำลังสองของความเร็ว: ![]() .
.
เรามาพิจารณากรณีที่ 1 กันก่อน
ในกรณีนี้  , หรือ .
, หรือ . 
มันเป็นไปตามนั้น ![]() (การเคลื่อนที่ด้วยความเร่งสม่ำเสมอ)
(การเคลื่อนที่ด้วยความเร่งสม่ำเสมอ)
เพราะ ( ร- เวกเตอร์รัศมี) แล้ว  .
.
จากที่นี่  .
.
สูตรนี้ไม่มีอะไรมากไปกว่าสูตรที่คุ้นเคยสำหรับกฎการเคลื่อนที่ของร่างกายในระหว่างการเคลื่อนที่ด้วยความเร่งสม่ำเสมอ
ตั้งแต่นั้นเป็นต้นมา  .
.
เมื่อพิจารณาแล้วว่าทั้งสองอย่าง ![]() เราได้รับความเท่าเทียมกันแบบสเกลาร์จากความเท่าเทียมกันของเวกเตอร์สุดท้าย:
เราได้รับความเท่าเทียมกันแบบสเกลาร์จากความเท่าเทียมกันของเวกเตอร์สุดท้าย:

ให้เราวิเคราะห์สูตรผลลัพธ์
มาหากัน. เวลาบินร่างกาย การทำให้เท่าเทียมกัน ยถึงศูนย์ เราได้


จากสูตรนี้ จะได้ว่าระยะการบินสูงสุดอยู่ที่
ตอนนี้เรามาหากัน สมการของแทรคเตอร์ตัวถัง- เมื่อต้องการทำเช่นนี้ ให้เราแสดง ทีผ่าน x

และลองแทนที่นิพจน์ผลลัพธ์ด้วย ทีสู่ความเท่าเทียมกันเพื่อ ย.

ฟังก์ชันผลลัพธ์ ย(x) เป็นฟังก์ชันกำลังสอง กราฟของมันคือพาราโบลา ซึ่งมีกิ่งก้านชี้ลงด้านล่าง
มีการอธิบายการเคลื่อนไหวของวัตถุโดยทำมุมกับขอบฟ้า (โดยไม่คำนึงถึงแรงต้านของอากาศ) ในวิดีโอนี้
พิจารณากรณีที่สอง: ![]() .
.
กฎข้อที่สองใช้แบบฟอร์ม  ,
,
จากที่นี่  .
.
ให้เราเขียนความเท่าเทียมกันนี้ในรูปแบบสเกลาร์:

เราได้รับ สมการเชิงอนุพันธ์เชิงเส้นสองสมการ.
สมการแรกมีคำตอบ
![]()
ซึ่งสามารถตรวจสอบได้โดยการแทนที่ฟังก์ชันนี้ลงในสมการ วีเอ็กซ์และสู่สภาวะเริ่มต้น ![]() .
.
โดยที่ e = 2.718281828459... คือเลขของออยเลอร์
สมการที่สองมีคำตอบ
เพราะ ![]() ,
,
![]() จากนั้นเมื่อมีแรงต้านอากาศ การเคลื่อนไหวของร่างกายมีแนวโน้มที่จะสม่ำเสมอ ตรงกันข้ามกับกรณีที่ 1 เมื่อความเร็วเพิ่มขึ้นอย่างไม่มีขีดจำกัด
จากนั้นเมื่อมีแรงต้านอากาศ การเคลื่อนไหวของร่างกายมีแนวโน้มที่จะสม่ำเสมอ ตรงกันข้ามกับกรณีที่ 1 เมื่อความเร็วเพิ่มขึ้นอย่างไม่มีขีดจำกัด
วิดีโอต่อไปนี้บอกว่านักดิ่งพสุธาจะเคลื่อนที่ด้วยความเร็วขั้นแรก จากนั้นจึงเริ่มเคลื่อนที่เท่าๆ กัน (แม้กระทั่งก่อนที่ร่มชูชีพจะเปิดออกด้วยซ้ำ)
เรามาค้นหาสำนวนสำหรับ xและ ย.
เพราะ x(0) = 0, ย(0) = 0 แล้ว


เรายังต้องพิจารณากรณีที่ 3 เมื่อใด
กฎข้อที่สองของนิวตันมีรูปแบบ
 , หรือ
, หรือ  .
.ในรูปแบบสเกลาร์ สมการนี้มีลักษณะดังนี้:

นี้ ระบบสมการเชิงอนุพันธ์ไม่เชิงเส้น- ระบบนี้ไม่สามารถแก้ไขได้อย่างชัดเจน ดังนั้นจึงจำเป็นต้องใช้การจำลองเชิงตัวเลข
การศึกษาเชิงตัวเลข
ในหัวข้อที่แล้ว เราเห็นว่าในสองกรณีแรก กฎการเคลื่อนที่ของวัตถุสามารถได้รับในรูปแบบที่ชัดเจน อย่างไรก็ตามในกรณีที่สาม จำเป็นต้องแก้ไขปัญหาเชิงตัวเลข การใช้วิธีเชิงตัวเลขเราจะได้ผลลัพธ์โดยประมาณเท่านั้น แต่เราจะค่อนข้างพอใจกับความแม่นยำเพียงเล็กน้อย (อย่างไรก็ตาม ไม่สามารถเขียนจำนวน π หรือรากที่สองของ 2 ได้อย่างแม่นยำ ดังนั้นเมื่อคำนวณ พวกเขาจะใช้ตัวเลขจำนวนจำกัด ซึ่งก็เพียงพอแล้ว)เราจะพิจารณากรณีที่สองเมื่อสูตรกำหนดแรงต้านทานอากาศ ![]() - สังเกตว่าเมื่อไร. เค= 0 เราได้กรณีแรก
- สังเกตว่าเมื่อไร. เค= 0 เราได้กรณีแรก
ความเร็วของร่างกาย ![]() เป็นไปตามสมการต่อไปนี้:
เป็นไปตามสมการต่อไปนี้:

องค์ประกอบความเร่งเขียนไว้ทางด้านซ้ายของสมการเหล่านี้  .
.
จำไว้ว่าความเร่งคืออัตราการเปลี่ยนแปลงความเร็ว (ขณะนั้น) ซึ่งก็คืออนุพันธ์ของความเร็วเทียบกับเวลา
ทางด้านขวามือของสมการจะมีส่วนประกอบของความเร็ว ดังนั้นสมการเหล่านี้แสดงให้เห็นว่าอัตราการเปลี่ยนแปลงความเร็วสัมพันธ์กับความเร็วอย่างไร
ลองหาคำตอบของสมการเหล่านี้โดยใช้วิธีตัวเลข เมื่อต้องการทำเช่นนี้ เราจะแนะนำแกนเวลา ตาข่าย: ลองเลือกตัวเลขและพิจารณาช่วงเวลาของแบบฟอร์ม: .
งานของเราคือการคำนวณค่าโดยประมาณ ![]() ที่โหนดกริด
ที่โหนดกริด
ให้เราแทนที่ความเร่งในสมการ ( ความเร็วทันทีการเปลี่ยนแปลงความเร็ว) โดย ความเร็วเฉลี่ยการเปลี่ยนแปลงความเร็วโดยคำนึงถึงการเคลื่อนไหวของร่างกายในช่วงเวลาหนึ่ง:

ทีนี้ลองแทนที่การประมาณที่ได้รับลงในสมการของเรา


สูตรที่ได้ช่วยให้เราคำนวณค่าของฟังก์ชันได้ ![]() ที่โหนดกริดถัดไป หากทราบค่าของฟังก์ชันเหล่านี้ที่โหนดกริดก่อนหน้า
ที่โหนดกริดถัดไป หากทราบค่าของฟังก์ชันเหล่านี้ที่โหนดกริดก่อนหน้า
โดยใช้วิธีการที่อธิบายไว้เราสามารถรับตารางค่าโดยประมาณของส่วนประกอบความเร็วได้
วิธีค้นหากฎการเคลื่อนที่ของร่างกาย ได้แก่ ตารางค่าพิกัดโดยประมาณ x(ที), ย(ที- เช่นเดียวกัน!
เรามี
ค่าของ vx[j] เท่ากับค่าของฟังก์ชัน และค่าเดียวกันสำหรับอาร์เรย์อื่นๆ
ตอนนี้สิ่งที่เหลืออยู่คือการเขียนลูปภายในซึ่งเราจะคำนวณ vx ผ่านค่าที่คำนวณไว้แล้ว vx[j] และเช่นเดียวกันกับอาร์เรย์ที่เหลือ วงจรก็จะเป็น เจตั้งแต่ 1 ถึง เอ็น.
อย่าลืมกำหนดค่าเริ่มต้น vx, vy, x, y ตามสูตร x 0 = 0, ย 0 = 0.
ใน Pascal และ C มีฟังก์ชัน sin(x) และ cos(x) สำหรับคำนวณไซน์และโคไซน์ โปรดทราบว่าฟังก์ชันเหล่านี้รับอาร์กิวเมนต์เป็นเรเดียน
คุณต้องสร้างกราฟการเคลื่อนไหวของร่างกายในระหว่างนั้น เค= 0 และ เค> 0 และเปรียบเทียบกราฟผลลัพธ์ กราฟสามารถสร้างได้ใน Excel
โปรดทราบว่าสูตรการคำนวณนั้นเรียบง่ายมากจนคุณสามารถใช้เฉพาะ Excel ในการคำนวณและไม่ได้ใช้ภาษาการเขียนโปรแกรมด้วยซ้ำ
อย่างไรก็ตาม ในอนาคต คุณจะต้องแก้ไขปัญหาใน CATS ซึ่งคุณจะต้องคำนวณเวลาและช่วงการบินของร่างกาย ซึ่งคุณไม่สามารถทำได้หากไม่มีภาษาการเขียนโปรแกรม
โปรดทราบว่าคุณสามารถ ทดสอบโปรแกรมของคุณและตรวจสอบกราฟของคุณโดยเปรียบเทียบผลการคำนวณเมื่อใด เค= 0 ด้วยสูตรที่แน่นอนที่ให้ไว้ในส่วน “การศึกษาเชิงวิเคราะห์”
ทดลองกับโปรแกรมของคุณ ตรวจสอบให้แน่ใจว่าหากไม่มีแรงต้านอากาศ ( เค= 0) ระยะการบินสูงสุดที่ความเร็วเริ่มต้นคงที่ทำได้ที่มุม 45°
แล้วความต้านทานต่ออากาศล่ะ? ระยะการบินสูงสุดทำได้ที่มุมใด?
รูปแสดงวิถีการเคลื่อนที่ของร่างกาย ณ โวลต์ 0 = 10 ม./วินาที, α = 45°, ก= 9.8 เมตรต่อวินาที 2, ม= 1 กก. เค= 0 และ 1 ได้มาจากการจำลองเชิงตัวเลขที่ Δ ที = 0,01.

คุณสามารถทำความคุ้นเคยกับผลงานที่ยอดเยี่ยมของนักเรียนเกรด 10 จาก Troitsk ซึ่งนำเสนอในการประชุม "Start in Science" ในปี 2554 งานนี้อุทิศให้กับการสร้างแบบจำลองการเคลื่อนไหวของลูกเทนนิสที่ขว้างในมุมหนึ่งถึงขอบฟ้า (โดยคำนึงถึงอากาศ) ความต้านทาน). ใช้ทั้งการสร้างแบบจำลองเชิงตัวเลขและการทดลองเต็มรูปแบบ
ดังนั้นงานที่สร้างสรรค์นี้จะช่วยให้คุณได้ทำความคุ้นเคยกับวิธีการสร้างแบบจำลองทางคณิตศาสตร์และตัวเลขซึ่งใช้ในทางปฏิบัติอย่างแข็งขัน แต่มีการศึกษาน้อยที่โรงเรียน ตัวอย่างเช่นวิธีการเหล่านี้ใช้ในการดำเนินโครงการนิวเคลียร์และอวกาศในสหภาพโซเวียตในช่วงกลางศตวรรษที่ 20
 สมการลอการิทึม
สมการลอการิทึม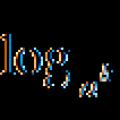 เทคนิคการแก้สมการลอการิทึม
เทคนิคการแก้สมการลอการิทึม การวิเคราะห์ตนเองของครูนักบำบัดการพูด
การวิเคราะห์ตนเองของครูนักบำบัดการพูด