วิธีค้นหาตัวส่วนของความก้าวหน้าทางเรขาคณิต ลดความก้าวหน้าทางเรขาคณิตอย่างไม่สิ้นสุด
ลำดับตัวเลข VI
§ l48 ผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด
จนถึงตอนนี้ เมื่อพูดถึงผลรวม เรามักจะถือว่าจำนวนพจน์ในผลรวมเหล่านี้มีจำกัด (เช่น 2, 15, 1,000 เป็นต้น) แต่เมื่อแก้ไขปัญหาบางอย่าง (โดยเฉพาะ คณิตศาสตร์ที่สูงขึ้น) เราจะต้องจัดการกับผลรวมของพจน์จำนวนอนันต์
ส= ก 1 + ก 2 + ... + ก n + ... . (1)
จำนวนเงินเหล่านี้คืออะไร? ตามคำนิยาม ผลรวมของเงื่อนไขจำนวนอนันต์ ก 1 , ก 2 , ..., ก n , ... เรียกว่าลิมิตของผลรวม S n อันดับแรก n ตัวเลขเมื่อใด n -> ∞ :
ส=ส n = (ก 1 + ก 2 + ... + ก n ). (2)
แน่นอนว่าขีดจำกัด (2) อาจมีหรือไม่มีก็ได้ ดังนั้นพวกเขาจึงบอกว่าผลรวม (1) มีอยู่หรือไม่มีอยู่
เราจะทราบได้อย่างไรว่าผลรวม (1) มีอยู่ในแต่ละกรณีหรือไม่? วิธีแก้ปัญหาทั่วไปปัญหานี้อยู่นอกเหนือขอบเขตของโปรแกรมของเรา อย่างไรก็ตาม มีสิ่งหนึ่งที่สำคัญ กรณีพิเศษซึ่งตอนนี้เราต้องพิจารณา เราจะพูดถึงการสรุปเงื่อนไขของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด
อนุญาต ก 1 , ก 1 ถาม , ก 1 ถาม 2, ... คือความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด ซึ่งหมายความว่า | ถาม |< 1. Сумма первых n เงื่อนไขของความก้าวหน้านี้เท่ากัน
จากทฤษฎีบทหลักเกี่ยวกับขีดจำกัด ตัวแปร(ดูมาตรา 136) เราได้รับ:
แต่ 1 = 1, ก qn = 0 ดังนั้น
ดังนั้น ผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด เท่ากับเทอมแรกของความก้าวหน้านี้ หารด้วย 1 ลบตัวส่วนของความก้าวหน้านี้
1) ผลรวมของความก้าวหน้าทางเรขาคณิต 1, 1/3, 1/9, 1/27, ... เท่ากับ
และผลรวมของความก้าวหน้าทางเรขาคณิตคือ 12 -6; 3; - 3 / 2 , ... เท่ากัน
2) เรียบง่าย เศษส่วนเป็นระยะ 0.454545 ... แปลงเป็นธรรมดา
เพื่อแก้ปัญหานี้ ลองจินตนาการดู เศษส่วนที่กำหนดในรูปแบบ ผลรวมอนันต์:
ด้านขวาความเท่าเทียมกันนี้คือผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด เทอมแรกมีค่าเท่ากับ 45/100 และตัวส่วนคือ 1/100 นั่นเป็นเหตุผล
โดยใช้วิธีการที่อธิบายไว้ก็เป็นไปได้ที่จะได้รับ กฎทั่วไปการแปลงเศษส่วนคาบอย่างง่ายให้เป็นเศษส่วนธรรมดา (ดูบทที่ II, § 38):
ในการแปลงเศษส่วนคาบอย่างง่ายให้เป็นเศษส่วนธรรมดา คุณต้องทำสิ่งต่อไปนี้: ใส่จุดในตัวเศษ ทศนิยมและตัวส่วนคือตัวเลขที่ประกอบด้วยเก้าคูณจำนวนเท่าที่มีหลักในช่วงเวลาของเศษส่วนทศนิยม
3) แปลงเศษส่วนคาบผสม 0.58333 .... เป็นเศษส่วนสามัญ
ลองจินตนาการถึงเศษส่วนนี้ว่าเป็นผลรวมอนันต์:
ทางด้านขวาของความเท่าเทียมกันนี้ พจน์ทั้งหมดเริ่มต้นจาก 3/1000 ก่อให้เกิดความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด เทอมแรกเท่ากับ 3/1000 และตัวส่วนคือ 1/10 นั่นเป็นเหตุผล
เมื่อใช้วิธีการที่อธิบายไว้ สามารถรับกฎทั่วไปสำหรับการแปลงเศษส่วนคาบแบบผสมเป็นเศษส่วนสามัญได้ (ดูบทที่ II, § 38) เราจงใจไม่นำเสนอที่นี่ ไม่จำเป็นต้องจำกฎที่ยุ่งยากนี้ การรู้ว่าเศษส่วนคาบแบบผสมใดๆ สามารถแสดงเป็นผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดและจำนวนหนึ่งจะมีประโยชน์มากกว่ามาก และสูตร
แน่นอนว่าคุณต้องจำไว้เพื่อผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด
เพื่อเป็นแบบฝึกหัด เราขอแนะนำให้คุณหันไปใช้ปัญหาหมายเลข 301 § 38 อีกครั้ง นอกเหนือจากปัญหาหมายเลข 995-1000 ที่ระบุด้านล่าง
แบบฝึกหัด
995 ผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดเรียกว่าอะไร?
996 ค้นหาผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด:
997. มีค่าเท่าไร เอ็กซ์ ความก้าวหน้า
มันลดลงอย่างไม่สิ้นสุดเหรอ? จงหาผลรวมของความก้าวหน้าดังกล่าว
998.ว สามเหลี่ยมด้านเท่ากับด้านข้าง ก สามเหลี่ยมใหม่ถูกจารึกไว้โดยเชื่อมต่อจุดกึ่งกลางของด้านข้าง สามเหลี่ยมใหม่จะถูกจารึกไว้ในสามเหลี่ยมนี้ในลักษณะเดียวกัน และเป็นเช่นนี้ไปเรื่อยๆ
ก) ผลรวมของเส้นรอบวงของสามเหลี่ยมเหล่านี้ทั้งหมด
b) ผลรวมของพื้นที่ของพวกเขา
999.เหลี่ยมมีข้าง ก จารึกไว้โดยการต่อจุดกึ่งกลางด้านข้าง จัตุรัสใหม่- สี่เหลี่ยมจัตุรัสนี้ถูกจารึกไว้ในลักษณะเดียวกัน และไม่มีที่สิ้นสุด หาผลรวมของเส้นรอบรูปของกำลังสองเหล่านี้กับผลรวมของพื้นที่
1,000 เขียนความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่มีที่สิ้นสุด โดยผลรวมของมันเท่ากับ 25/4 และผลรวมของกำลังสองของพจน์ของมันเท่ากับ 625/24
จำนวนนี้เรียกว่าตัวหารของความก้าวหน้าทางเรขาคณิต กล่าวคือ แต่ละเทอมจะแตกต่างจากเทอมก่อนหน้าด้วย q คูณ (เราจะถือว่า q ≠ 1 ไม่เช่นนั้นทุกอย่างจะไม่สำคัญเกินไป) มันไม่ยากที่จะเห็นสิ่งนั้น สูตรทั่วไปเทอมที่ n ของความก้าวหน้าทางเรขาคณิต b n = b 1 q n – 1 ; พจน์ที่มีตัวเลข b n และ b m ต่างกันด้วย q n – m คูณเข้าแล้ว อียิปต์โบราณไม่เพียงแต่รู้เลขคณิตเท่านั้น แต่ยังรู้จักความก้าวหน้าทางเรขาคณิตด้วย ตัวอย่างเช่น นี่คือปัญหาจากกระดาษปาปิรัส Rhind: “หน้าเจ็ดหน้ามีแมวเจ็ดตัว แมวแต่ละตัวกินหนูเจ็ดตัว หนูแต่ละตัวกินข้าวโพดเจ็ดรวง และข้าวบาร์เลย์แต่ละรวงสามารถปลูกข้าวบาร์เลย์ได้เจ็ดถัง ตัวเลขในชุดนี้มีจำนวนเท่าใดและผลรวมมีจำนวนเท่าใด
 |
|
ข้าว. 1. ปัญหาความก้าวหน้าทางเรขาคณิตของอียิปต์โบราณ |
งานนี้เกิดขึ้นซ้ำหลายครั้งโดยมีความแตกต่างกันในหมู่ชนชาติอื่น ๆ ในเวลาอื่น เช่น เขียนไว้ในศตวรรษที่ 13 “หนังสือลูกคิด” โดยเลโอนาร์โดแห่งปิซา (ฟีโบนัชชี) มีปัญหาเรื่องหญิงชรา 7 คนปรากฏตัวระหว่างเดินทางไปโรม (เห็นได้ชัดว่าเป็นผู้แสวงบุญ) แต่ละคนมีล่อ 7 ตัว แต่ละตัวมี 7 ถุง แต่ละถุง มีขนมปัง 7 ก้อน แต่ละก้อนมีมีด 7 เล่ม แต่ละก้อนมีฝัก 7 เล่ม ปัญหาถามว่ามีวัตถุกี่ชิ้น
ผลรวมของเทอม n แรกของความก้าวหน้าทางเรขาคณิต S n = b 1 (q n – 1) / (q – 1) . สูตรนี้สามารถพิสูจน์ได้เช่นนี้: S n = b 1 + b 1 q + b 1 q 2 + b 1 q 3 + ... + b 1 q n – 1
เพิ่มตัวเลข b 1 qn ไปที่ S n และรับ:
|
จากที่นี่ S n (q – 1) = b 1 (q n – 1) และเราได้สูตรที่จำเป็น
อยู่บนแผ่นดินเหนียวแผ่นหนึ่งแล้ว บาบิโลนโบราณมีอายุย้อนกลับไปถึงศตวรรษที่ 6 พ.ศ e. มีผลรวม 1 + 2 + 2 2 + 2 3 + ... + 2 9 = 2 10 – 1 จริง เช่นเดียวกับในหลายกรณี เราไม่รู้ว่าชาวบาบิโลนรู้ข้อเท็จจริงนี้ได้อย่างไร .
การเพิ่มขึ้นอย่างรวดเร็วของความก้าวหน้าทางเรขาคณิตในหลายวัฒนธรรม โดยเฉพาะอย่างยิ่งในอินเดีย ถูกนำมาใช้ซ้ำแล้วซ้ำอีกเป็นสัญลักษณ์ที่มองเห็นถึงความกว้างใหญ่ของจักรวาล ในตำนานอันโด่งดังเกี่ยวกับการปรากฏตัวของหมากรุก ผู้ปกครองเปิดโอกาสให้นักประดิษฐ์เลือกรางวัลด้วยตัวเอง และเขาขอจำนวนเมล็ดข้าวสาลีที่จะได้รับหากวางอันหนึ่งไว้ที่สี่เหลี่ยมแรกของกระดานหมากรุก สองอันบน ครั้งที่สอง สี่ในสาม แปดในสี่ และอื่นๆ แต่ละครั้งจำนวนจะเพิ่มเป็นสองเท่า Vladyka คิดว่าอย่างน้อยที่สุดเรากำลังพูดถึงถุงสองสามใบ แต่เขาคำนวณผิด เห็นได้ง่ายว่าสำหรับกระดานหมากรุกทั้ง 64 ช่องนักประดิษฐ์จะต้องได้รับเมล็ดพืช (2 64 - 1) ซึ่งแสดงเป็นตัวเลข 20 หลัก แม้ว่าคุณจะหว่านพื้นผิวโลกทั้งหมด แต่ก็ต้องใช้เวลาอย่างน้อย 8 ปีในการรวบรวม ปริมาณที่ต้องการธัญพืช ตำนานนี้บางครั้งถูกตีความว่าเป็นการบ่งบอกถึงความเป็นไปได้ที่แทบไม่มีขีดจำกัดที่ซ่อนอยู่ในเกมหมากรุก
จะเห็นว่าตัวเลขนี้เป็น 20 หลักจริงๆ:
2 64 = 2 4 ∙ (2 10) 6 = 16 ∙ 1,024 6 data 16 ∙ 1,000 6 = 1.6∙10 19 (การคำนวณที่แม่นยำยิ่งขึ้นจะให้ 1.84∙10 19) แต่ฉันสงสัยว่าคุณจะพบว่าตัวเลขนี้ลงท้ายด้วยเลขอะไร?
ความก้าวหน้าทางเรขาคณิตอาจเพิ่มขึ้นได้หากตัวส่วนมากกว่า 1 ในค่าสัมบูรณ์ หรือลดลงหากน้อยกว่า 1 ใน กรณีหลังจำนวน q n สำหรับ n ที่มีขนาดใหญ่เพียงพอสามารถมีขนาดเล็กลงได้โดยพลการ แม้ว่าความก้าวหน้าทางเรขาคณิตที่เพิ่มขึ้นจะเพิ่มขึ้นอย่างรวดเร็วอย่างไม่คาดคิด แต่ความก้าวหน้าทางเรขาคณิตที่ลดลงก็จะลดลงอย่างรวดเร็วเช่นกัน
ยิ่ง n มีขนาดใหญ่เท่าใด จำนวน q n ก็จะยิ่งแตกต่างจากศูนย์ และยิ่งผลรวมของเงื่อนไข n ของความก้าวหน้าทางเรขาคณิตยิ่งใกล้มากขึ้น S n = b 1 (1 – q n) / (1 – q) ถึงตัวเลข S = b 1 / ( 1 – คิว) (เช่น เอฟ.เวียดให้เหตุผลแบบนี้) เลข S เรียกว่าผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด อย่างไรก็ตาม เป็นเวลาหลายศตวรรษมาแล้วที่คำถามว่าอะไรคือความหมายของการสรุปความก้าวหน้าทางเรขาคณิตทั้งหมด พร้อมด้วยจำนวนคำศัพท์ที่ไม่มีที่สิ้นสุด นั้นยังไม่ชัดเจนเพียงพอสำหรับนักคณิตศาสตร์
ความก้าวหน้าทางเรขาคณิตที่ลดลงสามารถเห็นได้ เช่น ใน aporias ของ Zeno เรื่อง “Half Division” และ “Achilles and the Tortoise” ในกรณีแรกแสดงให้เห็นชัดเจนว่าถนนทั้งเส้น (สมมุติว่ามีความยาว 1) คือผลรวมของส่วนต่างๆ ที่เป็นจำนวนอนันต์ 1/2, 1/4, 1/8 เป็นต้น แน่นอนว่านี่เป็นกรณีจาก มุมมองของความคิดเกี่ยวกับ จำนวนเงินสุดท้ายความก้าวหน้าทางเรขาคณิตที่ไม่มีที่สิ้นสุด แล้วนี่จะเป็นไปได้ยังไงล่ะ?
|
ข้าว. 2. ความก้าวหน้าด้วยค่าสัมประสิทธิ์ 1/2 |
ใน aporia เกี่ยวกับจุดอ่อน สถานการณ์มีความซับซ้อนกว่าเล็กน้อย เนื่องจากในตัวส่วนของความก้าวหน้าไม่ใช่ 1/2 แต่เป็นจำนวนอื่น ตัวอย่างเช่น ให้จุดอ่อนวิ่งด้วยความเร็ว v เต่าเคลื่อนที่ด้วยความเร็ว u และระยะห่างเริ่มต้นระหว่างพวกมันคือ l จุดอ่อนจะครอบคลุมระยะทางนี้ในเวลา l/v และในช่วงเวลานี้เต่าจะเคลื่อนที่เป็นระยะทาง lu/v เมื่อจุดอ่อนวิ่งส่วนนี้ ระยะห่างระหว่างเขากับเต่าจะเท่ากับ l (u /v) 2 เป็นต้น ปรากฎว่าการไล่ตามเต่าหมายถึงการค้นหาผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดกับเทอมแรก l และตัวส่วน u /v ผลรวมนี้ - ส่วนที่จุดอ่อนจะวิ่งไปยังจุดนัดพบกับเต่าในที่สุด - เท่ากับ l / (1 – u /v) = lv / (v – u) แต่ขอย้ำอีกครั้งว่าจะตีความผลลัพธ์นี้อย่างไรและเหตุใดจึงสมเหตุสมผลมาเป็นเวลานานแล้วยังไม่ชัดเจนนัก
|
ข้าว. 3. ความก้าวหน้าทางเรขาคณิตโดยมีค่าสัมประสิทธิ์ 2/3 |
อาร์คิมิดีสใช้ผลรวมของความก้าวหน้าทางเรขาคณิตเพื่อกำหนดพื้นที่ของส่วนของพาราโบลา ให้ส่วนของพาราโบลานี้คั่นด้วยคอร์ด AB และปล่อยให้แทนเจนต์ที่จุด D ของพาราโบลาขนานกับ AB ให้ C เป็นจุดกึ่งกลางของ AB, E เป็นจุดกึ่งกลางของ AC, F เป็นจุดกึ่งกลางของ CB ลองวาดเส้นขนานกับ DC ผ่านจุด A, E, F, B; ให้เส้นสัมผัสที่ลากที่จุด D ตัดกันเส้นเหล่านี้ที่จุด K, L, M, N มาวาดส่วน AD และ DB กัน ให้เส้น EL ตัดกับเส้น AD ที่จุด G และพาราโบลาที่จุด H เส้น FM ตัดกับเส้น DB ที่จุด Q และพาราโบลาที่จุด R ตาม ทฤษฎีทั่วไปส่วนรูปกรวย DC คือเส้นผ่านศูนย์กลางของพาราโบลา (นั่นคือ ส่วนที่ขนานกับแกน) มันและแทนเจนต์ที่จุด D สามารถทำหน้าที่เป็นแกนพิกัด x และ y ซึ่งสมการของพาราโบลาเขียนเป็น y 2 = 2px (x คือระยะห่างจาก D ไปยังจุดใดๆ ของเส้นผ่านศูนย์กลางที่กำหนด y คือความยาวของ ส่วนขนานกับแทนเจนต์ที่กำหนดจากจุดเส้นผ่านศูนย์กลางนี้ไปยังจุดใดจุดหนึ่งบนพาราโบลาเอง)
โดยอาศัยสมการพาราโบลา DL 2 = 2 ∙ p ∙ LH, DK 2 = 2 ∙ p ∙ KA และเนื่องจาก DK = 2DL ดังนั้น KA = 4LH เพราะ KA = 2LG, LH = HG พื้นที่เซกเมนต์ ADB ของพาราโบลาเท่ากับพื้นที่สามเหลี่ยม ΔADB และพื้นที่ของเซกเมนต์ AHD และ DRB รวมกัน ในทางกลับกัน พื้นที่ของเซ็กเมนต์ AHD จะเท่ากับพื้นที่ของสามเหลี่ยม AHD และเซ็กเมนต์ที่เหลือ AH และ HD ในทำนองเดียวกัน โดยแต่ละส่วนคุณสามารถดำเนินการเดียวกันได้ - แบ่งออกเป็นสามเหลี่ยม (Δ) และ สองส่วนที่เหลือ () ฯลฯ :
พื้นที่ของสามเหลี่ยม ΔAHD เท่ากับครึ่งหนึ่งของพื้นที่ของสามเหลี่ยม ΔALD (มี พื้นดินทั่วไป AD และความสูงแตกต่างกันด้วยปัจจัย 2) ซึ่งในทางกลับกันจะเท่ากับครึ่งหนึ่งของพื้นที่สามเหลี่ยม ΔAKD และครึ่งหนึ่งของพื้นที่ของสามเหลี่ยม ΔACD ดังนั้น พื้นที่ของสามเหลี่ยม ΔAHD เท่ากับหนึ่งในสี่ของพื้นที่ของสามเหลี่ยม ΔACD ในทำนองเดียวกัน พื้นที่ของสามเหลี่ยม ΔDRB เท่ากับหนึ่งในสี่ของพื้นที่สามเหลี่ยม ΔDFB ดังนั้น พื้นที่ของสามเหลี่ยม ΔAHD และ ΔDRB เมื่อนำมารวมกันจะเท่ากับหนึ่งในสี่ของพื้นที่ของสามเหลี่ยม ΔADB ทำซ้ำการดำเนินการนี้เมื่อนำไปใช้กับกลุ่ม AH, HD, DR และ RB จะเลือกสามเหลี่ยมจากพวกเขา พื้นที่ซึ่งเมื่อนำมารวมกันจะน้อยกว่าพื้นที่สามเหลี่ยม ΔAHD และ ΔDRB 4 เท่า เมื่อนำมารวมกัน และ จึงน้อยกว่าพื้นที่ของสามเหลี่ยม ΔADB 16 เท่า และอื่นๆ:
ดังนั้น อาร์คิมิดีสจึงพิสูจน์ว่า “ทุกๆ ส่วนระหว่างเส้นตรงและพาราโบลาประกอบขึ้นเป็นสี่ในสามของรูปสามเหลี่ยมซึ่งมีฐานเท่ากันและมีความสูงเท่ากัน”
>>คณิตศาสตร์: ความก้าวหน้าทางเรขาคณิต
เพื่อความสะดวกของผู้อ่าน ย่อหน้านี้ถูกสร้างขึ้นตามแผนเดียวกันกับที่เราติดตามในย่อหน้าก่อนหน้า
1. แนวคิดพื้นฐาน
คำนิยาม.ลำดับตัวเลข สมาชิกทั้งหมดจะแตกต่างจาก 0 และสมาชิกแต่ละคนโดยเริ่มจากสมาชิกตัวที่สองได้รับจากสมาชิกก่อนหน้าโดยการคูณด้วยจำนวนเดียวกัน เรียกว่าความก้าวหน้าทางเรขาคณิต ในกรณีนี้ เลข 5 เรียกว่าตัวหารของความก้าวหน้าทางเรขาคณิต
ดังนั้นความก้าวหน้าทางเรขาคณิตจึงเป็นลำดับตัวเลข (bn) ที่กำหนดซ้ำโดยความสัมพันธ์
เป็นไปได้ไหมที่จะดูลำดับตัวเลขและพิจารณาว่าเป็นความก้าวหน้าทางเรขาคณิตหรือไม่? สามารถ. หากคุณมั่นใจว่าอัตราส่วนของสมาชิกใดๆ ในลำดับต่อสมาชิกก่อนหน้านั้นคงที่ แสดงว่าคุณมีความก้าวหน้าทางเรขาคณิต
ตัวอย่างที่ 1
1, 3, 9, 27, 81,... .
ข 1 = 1, คิว = 3
ตัวอย่างที่ 2
ซึ่งเป็นความก้าวหน้าทางเรขาคณิตที่ได้
ตัวอย่างที่ 3
ซึ่งเป็นความก้าวหน้าทางเรขาคณิตที่ได้
ตัวอย่างที่ 4
8, 8, 8, 8, 8, 8,....
นี่คือความก้าวหน้าทางเรขาคณิตโดยที่ b 1 - 8, q = 1
โปรดทราบว่าลำดับนี้เป็นความก้าวหน้าทางคณิตศาสตร์ด้วย (ดูตัวอย่างที่ 3 จากมาตรา 15)
ตัวอย่างที่ 5
2,-2,2,-2,2,-2.....
นี่คือความก้าวหน้าทางเรขาคณิตโดยที่ b 1 = 2, q = -1
แน่นอนว่าความก้าวหน้าทางเรขาคณิตคือลำดับที่เพิ่มขึ้นถ้า b 1 > 0, q > 1 (ดูตัวอย่างที่ 1) และลำดับที่ลดลงถ้า b 1 > 0, 0< q < 1 (см. пример 2).
เพื่อระบุว่าลำดับ (bn) เป็นความก้าวหน้าทางเรขาคณิต บางครั้งการใช้สัญลักษณ์ต่อไปนี้ก็สะดวก:
ไอคอนจะแทนที่วลี “ความก้าวหน้าทางเรขาคณิต”
ให้เราสังเกตคุณสมบัติที่น่าสนใจอย่างหนึ่งและในเวลาเดียวกันก็ค่อนข้างชัดเจนของความก้าวหน้าทางเรขาคณิต:
ถ้าเป็นลำดับ 
คือความก้าวหน้าทางเรขาคณิต ตามด้วยลำดับของกำลังสอง เช่น 
เป็นความก้าวหน้าทางเรขาคณิต
ในการก้าวหน้าทางเรขาคณิตครั้งที่สอง เทอมแรกเท่ากับ และเท่ากับ q 2
หากในความก้าวหน้าทางเรขาคณิตเราละทิ้งพจน์ทั้งหมดที่ตามหลัง bn เราก็จะได้ความก้าวหน้าทางเรขาคณิตที่มีขอบเขตจำกัด 
ในย่อหน้าถัดไปของย่อหน้านี้เราจะพิจารณามากที่สุด คุณสมบัติที่สำคัญความก้าวหน้าทางเรขาคณิต
2. สูตรสำหรับเทอมที่ n ของความก้าวหน้าทางเรขาคณิต
พิจารณาความก้าวหน้าทางเรขาคณิต 
ตัวส่วน q เรามี:
ไม่ใช่เรื่องยากที่จะเดาว่าสำหรับจำนวนใดๆ n ความเท่าเทียมกันนั้นเป็นจริง
นี่คือสูตรสำหรับเทอมที่ n ของความก้าวหน้าทางเรขาคณิต
ความคิดเห็น
ถ้าคุณอ่าน หมายเหตุสำคัญจากย่อหน้าที่แล้วและทำความเข้าใจแล้วจึงลองพิสูจน์สูตร (1) โดยใช้วิธี การเหนี่ยวนำทางคณิตศาสตร์คล้ายกับที่ทำกับสูตรเทอมที่ n ความก้าวหน้าทางคณิตศาสตร์.
ลองเขียนสูตรสำหรับเทอมที่ n ของความก้าวหน้าทางเรขาคณิตอีกครั้ง
และแนะนำสัญกรณ์: เราได้ y = mq 2 หรือรายละเอียดเพิ่มเติม 
อาร์กิวเมนต์ x มีอยู่ในเลขชี้กำลัง ดังนั้นฟังก์ชันนี้จึงเรียกว่าฟังก์ชันเลขชี้กำลัง ซึ่งหมายความว่าความก้าวหน้าทางเรขาคณิตถือได้ว่าเป็นฟังก์ชันเลขชี้กำลังที่กำหนดบนเซต N ของจำนวนธรรมชาติ ในรูป 96a แสดงกราฟของฟังก์ชัน Fig. 966 - กราฟฟังก์ชัน 
ในทั้งสองกรณีเรามี จุดที่แยกได้(โดยที่แอบซิสซา x = 1, x = 2, x = 3 ฯลฯ) นอนอยู่บนเส้นโค้งที่แน่นอน (ทั้งสองร่างแสดงเส้นโค้งเดียวกัน เพียงแต่อยู่ในตำแหน่งที่แตกต่างกันและแสดงในระดับที่ต่างกัน) เส้นโค้งนี้เรียกว่าเส้นโค้งเอ็กซ์โปเนนเชียล อ่านเพิ่มเติมเกี่ยวกับ ฟังก์ชันเลขชี้กำลังและตารางงานของเธอ เราจะคุยกันในหลักสูตรพีชคณิตชั้นประถมศึกษาปีที่ 11
กลับไปที่ตัวอย่างที่ 1-5 จากย่อหน้าก่อนหน้า
1) 1, 3, 9, 27, 81,... . นี่คือความก้าวหน้าทางเรขาคณิตโดยที่ b 1 = 1, q = 3 มาสร้างสูตรสำหรับเทอมที่ n กัน 
2) 
นี่คือความก้าวหน้าทางเรขาคณิต ซึ่งมาสร้างสูตรสำหรับเทอมที่ n กันดีกว่า 
ซึ่งเป็นความก้าวหน้าทางเรขาคณิตที่ได้ 
มาสร้างสูตรสำหรับเทอมที่ n กัน 
4) 8, 8, 8, ..., 8, ... . นี่คือความก้าวหน้าทางเรขาคณิตโดยที่ b 1 = 8, q = 1 มาสร้างสูตรสำหรับเทอมที่ n กัน 
5) 2, -2, 2, -2, 2, -2,.... นี่คือความก้าวหน้าทางเรขาคณิต โดยที่ b 1 = 2, q = -1 มาสร้างสูตรสำหรับเทอมที่ n กัน 
ตัวอย่างที่ 6
เมื่อพิจารณาถึงความก้าวหน้าทางเรขาคณิต
ในทุกกรณี คำตอบจะขึ้นอยู่กับสูตรของเทอมที่ n ของความก้าวหน้าทางเรขาคณิต
a) เราได้รับ n = 6 ในสูตรสำหรับเทอมที่ n ของความก้าวหน้าทางเรขาคณิต
ข) เรามี
เนื่องจาก 512 = 2 9 เราได้ n - 1 = 9, n = 10
ง) เรามี
ตัวอย่างที่ 7
ความแตกต่างระหว่างเทอมที่เจ็ดและห้าของความก้าวหน้าทางเรขาคณิตคือ 48 ผลรวมของเทอมที่ห้าและหกของความก้าวหน้าก็คือ 48 เช่นกัน ค้นหาเทอมที่สิบสองของความก้าวหน้านี้
ขั้นแรก.การสร้างแบบจำลองทางคณิตศาสตร์
เงื่อนไขของปัญหาสามารถเขียนโดยย่อได้ดังนี้:
เมื่อใช้สูตรสำหรับเทอมที่ n ของความก้าวหน้าทางเรขาคณิต เราจะได้:
จากนั้นเงื่อนไขที่สองของปัญหา (b 7 - b 5 = 48) สามารถเขียนเป็นได้
เงื่อนไขที่สามของปัญหา (b 5 + b 6 = 48) สามารถเขียนเป็น
เป็นผลให้เราได้รับระบบสมการสองสมการที่มีตัวแปรสองตัว b 1 และ q:
ซึ่งเมื่อรวมกับเงื่อนไข 1) ที่เขียนไว้ข้างบนนี้ก็คือ แบบจำลองทางคณิตศาสตร์งาน
ขั้นตอนที่สอง
การทำงานกับโมเดลที่คอมไพล์แล้ว เมื่อทำให้ด้านซ้ายของสมการทั้งสองของระบบเท่ากันเราได้:
(เราหารทั้งสองข้างของสมการด้วยนิพจน์ที่ไม่เป็นศูนย์ b 1 q 4)
จากสมการ q 2 - q - 2 = 0 เราพบว่า q 1 = 2, q 2 = -1 เราได้แทนค่า q = 2 ลงในสมการที่สองของระบบ 
แทนค่า q = -1 ลงในสมการที่สองของระบบเราจะได้ b 1 1 0 = 48; สมการนี้ไม่มีคำตอบ
ดังนั้น b 1 =1, q = 2 - คู่นี้คือคำตอบของระบบสมการที่คอมไพล์แล้ว
ตอนนี้เราสามารถเขียนความก้าวหน้าทางเรขาคณิตเกี่ยวกับเรื่องนั้นได้ เรากำลังพูดถึงในปัญหา: 1, 2, 4, 8, 16, 32, ... .
ขั้นตอนที่สาม
ตอบคำถามปัญหา. คุณต้องคำนวณ b 12 เรามี
คำตอบ: ข 12 = 2048
3. สูตรสำหรับผลรวมของเทอมของความก้าวหน้าทางเรขาคณิตอันจำกัด
ปล่อยให้มีความก้าวหน้าทางเรขาคณิตอันจำกัด
ให้เราแสดงด้วย S n ผลรวมของเงื่อนไขนั่นคือ
ขอให้เราได้สูตรในการหาจำนวนนี้
เริ่มจากจุดเริ่มต้นกันก่อน กรณีง่ายๆเมื่อ q = 1 จากนั้นความก้าวหน้าทางเรขาคณิต b 1 , b 2 , b 3 ,..., bn ประกอบด้วยตัวเลข n เท่ากับ b 1 เช่น ความก้าวหน้าดูเหมือน b 1, b 2, b 3, ..., b 4 ผลรวมของตัวเลขเหล่านี้คือ nb 1
ให้ตอนนี้ q = 1 ในการค้นหา S n เราใช้เทคนิคประดิษฐ์: เราทำการเปลี่ยนแปลงนิพจน์ S n q เรามี:
เมื่อทำการแปลง ประการแรก เราใช้คำจำกัดความของความก้าวหน้าทางเรขาคณิต ตามนั้น (ดูบรรทัดที่สามของการให้เหตุผล) ประการที่สองพวกเขาเพิ่มและลบซึ่งเป็นเหตุผลว่าทำไมความหมายของสำนวนจึงไม่เปลี่ยนแปลง (ดูบรรทัดที่สี่ของการให้เหตุผล) ประการที่สาม เราใช้สูตรสำหรับเทอมที่ n ของความก้าวหน้าทางเรขาคณิต:
จากสูตร (1) เราพบว่า:
นี่คือสูตรสำหรับผลรวมของเทอม n ของความก้าวหน้าทางเรขาคณิต (สำหรับกรณีที่ q = 1)
ตัวอย่างที่ 8
ด้วยความก้าวหน้าทางเรขาคณิตอันจำกัด
ก) ผลรวมของเงื่อนไขของความก้าวหน้า; b) ผลรวมของกำลังสองของเงื่อนไข
b) ข้างต้น (ดูหน้า 132) เราได้สังเกตแล้วว่าหากเงื่อนไขทั้งหมดของความก้าวหน้าทางเรขาคณิตยกกำลังสอง เราจะได้ความก้าวหน้าทางเรขาคณิตที่มีเทอมแรก b 2 และตัวส่วน q 2 จากนั้นผลรวมของเงื่อนไขทั้งหกของความก้าวหน้าใหม่จะถูกคำนวณโดย
ตัวอย่างที่ 9
ค้นหาเทอมที่ 8 ของความก้าวหน้าทางเรขาคณิตที่ต้องการ
อันที่จริงเราได้พิสูจน์ทฤษฎีบทต่อไปนี้แล้ว
ลำดับตัวเลขคือความก้าวหน้าทางเรขาคณิต ก็ต่อเมื่อกำลังสองของแต่ละเทอม ยกเว้นทฤษฎีบทแรก (และสุดท้าย ในกรณีของลำดับจำกัด) เท่ากับผลคูณของเทอมก่อนหน้าและเทอมต่อๆ ไป (a คุณสมบัติเฉพาะของความก้าวหน้าทางเรขาคณิต)
ตอนนี้ให้เราพิจารณาคำถามเกี่ยวกับการสรุปความก้าวหน้าทางเรขาคณิตอันไม่มีที่สิ้นสุด ให้เราเรียกผลรวมบางส่วนของความก้าวหน้าอันไม่มีที่สิ้นสุดที่กำหนดว่าผลรวมของเทอมแรก ให้เราแสดงผลรวมบางส่วนด้วยสัญลักษณ์
สำหรับทุกความก้าวหน้าอันไม่มีที่สิ้นสุด
เราสามารถเขียนลำดับ (รวมถึงอนันต์) ของผลรวมบางส่วนได้
ปล่อยให้ลำดับที่เพิ่มขึ้นอย่างไม่จำกัดมีขีดจำกัด
ในกรณีนี้ ตัวเลข S ซึ่งก็คือขีดจำกัดของผลรวมบางส่วนของความก้าวหน้า เรียกว่าผลรวมของความก้าวหน้าที่ไม่สิ้นสุด เราจะพิสูจน์ว่าความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดมีผลรวมเสมอ และเราจะได้สูตรสำหรับผลรวมนี้ (เรายังแสดงได้ว่าถ้าความก้าวหน้าแบบไม่มีที่สิ้นสุดไม่มีผลรวม มันก็ไม่มีอยู่จริง)
ให้เราเขียนนิพจน์ผลรวมบางส่วนเป็นผลรวมของเงื่อนไขความก้าวหน้าตามสูตร (91.1) และพิจารณาขีดจำกัดของผลรวมบางส่วนที่
จากทฤษฎีบทที่ 89 เป็นที่ทราบกันว่าสำหรับความก้าวหน้าที่ลดลง ดังนั้นเราจึงพบการใช้ทฤษฎีบทขีดจำกัดผลต่าง
(ที่นี่ใช้กฎเช่นกัน: ปัจจัยคงที่อยู่นอกเครื่องหมายจำกัด) การดำรงอยู่ได้รับการพิสูจน์แล้ว และในขณะเดียวกันก็ได้รับสูตรสำหรับผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด:
ความเท่าเทียมกัน (92.1) สามารถเขียนในรูปแบบได้เช่นกัน
มันอาจดูขัดแย้งกันตรงนี้ว่าจำนวนเงิน จำนวนอนันต์เงื่อนไขได้รับการกำหนดมูลค่าสุดท้ายที่ชัดเจนมาก
สามารถยกตัวอย่างที่ชัดเจนเพื่ออธิบายสถานการณ์นี้ได้ พิจารณารูปสี่เหลี่ยมจัตุรัสที่มีด้านข้าง เท่ากับหนึ่ง(รูปที่ 72) แบ่งสี่เหลี่ยมจัตุรัสนี้ด้วยเส้นแนวนอนออกเป็นสองส่วนเท่า ๆ กันและ ส่วนบนนำไปใช้กับด้านล่างเพื่อให้เป็นรูปสี่เหลี่ยมผืนผ้าที่มีด้าน 2 และ . หลังจากนั้นเราจะแบ่งครึ่งขวาของสี่เหลี่ยมผืนผ้านี้อีกครั้งด้วยเส้นแนวนอนและแนบส่วนบนกับส่วนล่าง (ดังแสดงในรูปที่ 72) ด้วยการดำเนินกระบวนการนี้ต่อไป เรากำลังเปลี่ยนแปลงอยู่ตลอดเวลา จัตุรัสเดิมโดยมีพื้นที่เท่ากับ 1 ให้มีขนาดเท่ากัน (เป็นรูปบันไดที่มีขั้นบันไดบาง)
ด้วยความต่อเนื่องที่ไม่มีที่สิ้นสุดของกระบวนการนี้ พื้นที่ทั้งหมดของสี่เหลี่ยมจัตุรัสจะแบ่งออกเป็นจำนวนเทอมที่ไม่สิ้นสุด - พื้นที่ของสี่เหลี่ยมที่มีฐานเท่ากับ 1 และความสูง พื้นที่ของสี่เหลี่ยมก่อให้เกิดความก้าวหน้าที่ลดลงอย่างไม่สิ้นสุดอย่างแม่นยำ
คืออย่างที่ใครๆ คาดคิด เท่ากับพื้นที่ของสี่เหลี่ยมจัตุรัส
ตัวอย่าง. ค้นหาผลรวมของความก้าวหน้าที่ไม่สิ้นสุดต่อไปนี้:
วิธีแก้ไข ก) เราสังเกตว่าความก้าวหน้านี้ ดังนั้นเราจึงพบโดยใช้สูตร (92.2)
b) ในที่นี้หมายความว่าเราใช้สูตรเดียวกัน (92.2) ที่เรามี
c) เราพบว่าความก้าวหน้านี้จึงไม่มีผลรวม
ในย่อหน้าที่ 5 มีการแสดงการใช้สูตรสำหรับผลรวมของเงื่อนไขของความก้าวหน้าที่ลดลงอย่างไม่สิ้นสุดในการแปลงเศษส่วนทศนิยมเป็นงวดเป็นเศษส่วนสามัญ
แบบฝึกหัด
1. ผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดคือ 3/5 และผลรวมของสี่เทอมแรกคือ 13/27 ค้นหาพจน์แรกและตัวส่วนของความก้าวหน้า
2. ค้นหาตัวเลขสี่ตัวที่ก่อให้เกิดความก้าวหน้าทางเรขาคณิตสลับกัน โดยเทอมที่สองน้อยกว่าตัวแรกคูณ 35 และเทอมที่สามมากกว่าตัวเลขที่สี่คูณ 560
3.แสดงว่าถ้าเป็นลำดับ
ก่อให้เกิดความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด จากนั้นจึงเกิดลำดับ
สำหรับสิ่งใดก็ตาม มันก่อให้เกิดความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด คำกล่าวนี้จะเป็นจริงเมื่อใด
หาสูตรสำหรับผลคูณของเทอมของความก้าวหน้าทางเรขาคณิต
คณิตศาสตร์คืออะไรผู้คนควบคุมธรรมชาติและตนเอง
นักคณิตศาสตร์โซเวียตนักวิชาการ A.N. โคลโมโกรอฟ
ความก้าวหน้าทางเรขาคณิต
นอกจากปัญหาเกี่ยวกับความก้าวหน้าทางคณิตศาสตร์แล้ว ปัญหาที่เกี่ยวข้องกับแนวคิดเรื่องความก้าวหน้าทางเรขาคณิตก็เป็นเรื่องปกติในการสอบเข้าวิชาคณิตศาสตร์ด้วย สำหรับ โซลูชั่นที่ประสบความสำเร็จปัญหาดังกล่าวต้องอาศัยความรู้เกี่ยวกับคุณสมบัติของความก้าวหน้าทางเรขาคณิตและทักษะที่ดีในการใช้งาน
บทความนี้มีเนื้อหาเกี่ยวกับการนำเสนอคุณสมบัติพื้นฐานของความก้าวหน้าทางเรขาคณิต ตัวอย่างของการแก้ปัญหาทั่วไปมีให้ไว้ที่นี่ด้วย, ยืมมาจากงานสอบเข้าวิชาคณิตศาสตร์
ให้เราทราบก่อน คุณสมบัติพื้นฐานความก้าวหน้าทางเรขาคณิตและการจดจำมากที่สุด สูตรสำคัญและงบ, ที่เกี่ยวข้องกับแนวคิดนี้
คำนิยาม.ลำดับตัวเลขเรียกว่าความก้าวหน้าทางเรขาคณิต ถ้าแต่ละตัวเลขเริ่มจากวินาที เท่ากับตัวเลขก่อนหน้า คูณด้วยตัวเลขเดียวกัน จำนวนนี้เรียกว่าตัวหารของความก้าวหน้าทางเรขาคณิต
สำหรับความก้าวหน้าทางเรขาคณิตสูตรถูกต้อง
, (1)
ที่ไหน . สูตร (1) เรียกว่าสูตรของเทอมทั่วไปของความก้าวหน้าทางเรขาคณิต และสูตร (2) แสดงถึงคุณสมบัติหลักของความก้าวหน้าทางเรขาคณิต: แต่ละเทอมของความก้าวหน้าเกิดขึ้นพร้อมกับค่าเฉลี่ยเรขาคณิตของเทอมข้างเคียง และ
บันทึก, เป็นเพราะคุณสมบัตินี้เองที่ทำให้ความก้าวหน้าที่เป็นปัญหาเรียกว่า "เรขาคณิต"
สูตรข้างต้น (1) และ (2) มีรูปแบบทั่วไปดังนี้:
, (3)
เพื่อคำนวณจำนวนเงินอันดับแรก เงื่อนไขความก้าวหน้าทางเรขาคณิตใช้สูตร
ถ้าเราแสดงว่า แล้ว
ที่ไหน . เนื่องจาก สูตร (6) เป็นลักษณะทั่วไปของสูตร (5)
ในกรณีที่เมื่อใดและ ความก้าวหน้าทางเรขาคณิตกำลังลดลงอย่างไม่สิ้นสุด เพื่อคำนวณจำนวนเงินสำหรับเงื่อนไขทั้งหมดของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด จะใช้สูตรนี้
. (7)
ตัวอย่างเช่น , โดยใช้สูตร (7) ที่เราสามารถแสดงได้, อะไร
ที่ไหน . ความเท่าเทียมกันเหล่านี้ได้มาจากสูตร (7) ภายใต้เงื่อนไขว่า , (ความเท่าเทียมกันครั้งแรก) และ , (ความเท่าเทียมกันที่สอง)
ทฤษฎีบท.ถ้าอย่างนั้น
การพิสูจน์. ถ้าอย่างนั้น
ทฤษฎีบทได้รับการพิสูจน์แล้ว
มาดูตัวอย่างการแก้ปัญหาในหัวข้อ "ความก้าวหน้าทางเรขาคณิต" กันดีกว่า
ตัวอย่างที่ 1ให้ไว้: , และ . หา .
สารละลาย.หากเราใช้สูตร (5) แล้ว
คำตอบ: .
ตัวอย่างที่ 2ช่างมัน. หา .
สารละลาย.เนื่องจาก และ เราใช้สูตร (5), (6) และรับระบบสมการ
ถ้าสมการที่สองของระบบ (9) หารด้วยสมการแรกแล้วหรือ สืบต่อจากนี้ไปว่า - ลองพิจารณาสองกรณี
1. ถ้า จากสมการแรกของระบบ (9) ที่เรามี.
2. ถ้าอย่างนั้น .
ตัวอย่างที่ 3ให้ และ . หา .
สารละลาย.จากสูตร (2) เป็นไปตามนั้น หรือ . ตั้งแต่ แล้ว หรือ .
ตามเงื่อนไข. อย่างไรก็ตาม ดังนั้น. ตั้งแต่และ ตรงนี้เรามีระบบสมการ
ถ้าสมการที่สองของระบบหารด้วยสมการแรก แล้ว หรือ
เนื่องจากสมการนี้มีรากที่เหมาะสมเฉพาะตัว ในกรณีนี้จะเป็นไปตามสมการแรกของระบบ
โดยคำนึงถึงสูตรบัญชี (7) ที่เราได้รับ
คำตอบ: .
ตัวอย่างที่ 4ให้ไว้: และ . หา .
สารละลาย.ตั้งแต่นั้นมา.
ตั้งแต่ แล้ว หรือ
ตามสูตร (2) เราได้ ในเรื่องนี้เราได้รับจากความเท่าเทียมกัน (10) หรือ
อย่างไรก็ตามตามเงื่อนไขดังนั้น
ตัวอย่างที่ 5เป็นที่ทราบกันว่า หา .
สารละลาย. ตามทฤษฎีบท เรามีความเท่าเทียมกันสองประการ
ตั้งแต่ แล้ว หรือ . เพราะว่าแล้ว.
คำตอบ: .
ตัวอย่างที่ 6ให้ไว้: และ . หา .
สารละลาย.โดยคำนึงถึงสูตรบัญชี (5) ที่เราได้รับ
ตั้งแต่นั้นมา. ตั้งแต่ และ จากนั้น .
ตัวอย่างที่ 7ช่างมัน. หา .
สารละลาย.ตามสูตร (1) เราสามารถเขียนได้
ดังนั้นเราจึงมี หรือ . เป็นที่รู้กันว่า และ ดังนั้น และ .
คำตอบ: .
ตัวอย่างที่ 8หาตัวส่วนของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดถ้า
และ .
สารละลาย. จากสูตร (7) เป็นไปตามนี้และ - จากที่นี่และจากเงื่อนไขของปัญหาเราได้ระบบสมการ
ถ้าสมการแรกของระบบเป็นกำลังสอง, แล้วหารสมการผลลัพธ์ด้วยสมการที่สองแล้วเราก็ได้
หรือ .
คำตอบ: .
ตัวอย่างที่ 9ค้นหาค่าทั้งหมดที่ลำดับ , , เป็นความก้าวหน้าทางเรขาคณิต
สารละลาย.ให้ และ . ตามสูตร (2) ซึ่งกำหนดคุณสมบัติหลักของความก้าวหน้าทางเรขาคณิต เราสามารถเขียนได้ หรือ
จากตรงนี้เราจะได้สมการกำลังสอง, ซึ่งมีรากอยู่และ .
มาตรวจสอบกันดีกว่า: ถ้าแล้ว และ ;
ถ้า แล้ว และในกรณีแรกที่เรามี
และ และในวินาที – และ
คำตอบ: , .ตัวอย่างที่ 10
, (11)
แก้สมการ
ที่ไหน และ .
จากสูตร (7) เป็นไปตามนี้, อะไร - ในเรื่องนี้สมการ (11) จะอยู่ในรูปแบบหรือ - รากที่เหมาะสม สมการกำลังสองเป็น
คำตอบ: .
ตัวอย่างที่ 11ป ความสม่ำเสมอ ตัวเลขบวก ทำให้เกิดความก้าวหน้าทางคณิตศาสตร์, ก – ความก้าวหน้าทางเรขาคณิตและที่นี่ หา .
สารละลาย.เพราะ ลำดับเลขคณิต, ที่ (คุณสมบัติหลักของความก้าวหน้าทางคณิตศาสตร์) เพราะแล้วหรือ สืบเนื่องมาจากเรื่องนี้ ว่าความก้าวหน้าทางเรขาคณิตมีรูปแบบ- ตามสูตร (2)แล้วเราก็เขียนลงไป
ตั้งแต่ และ จากนั้น - ในกรณีนี้คือนิพจน์ใช้แบบฟอร์มหรือ. ตามเงื่อนไข ดังนั้นจากสมการเราได้รับแนวทางแก้ไขปัญหาเฉพาะที่อยู่ระหว่างการพิจารณา, เช่น. -
คำตอบ: .
ตัวอย่างที่ 12คำนวณผลรวม
. (12)
สารละลาย. คูณความเท่าเทียมกันทั้งสองข้าง (12) ด้วย 5 แล้วได้
หากเราลบ (12) ออกจากนิพจน์ผลลัพธ์, ที่
หรือ .
ในการคำนวณเราจะแทนที่ค่าลงในสูตร (7) และรับ . ตั้งแต่นั้นมา.
คำตอบ: .
ตัวอย่างการแก้ปัญหาที่ให้ไว้นี้จะเป็นประโยชน์ต่อผู้สมัครในการเตรียมตัว การสอบเข้า- เพื่อศึกษาวิธีการแก้ไขปัญหาอย่างลึกซึ้งยิ่งขึ้น, ที่เกี่ยวข้องกับความก้าวหน้าทางเรขาคณิต, สามารถใช้ อุปกรณ์ช่วยสอนจากรายการวรรณกรรมแนะนำ
1. รวบรวมปัญหาทางคณิตศาสตร์สำหรับผู้สมัครเข้าศึกษาในวิทยาลัย / อ. มิ.ย. สแกนวิ – อ.: มีร์ และการศึกษา, 2556. – 608 หน้า
2. สุพรรณ วี.พี. คณิตศาสตร์สำหรับนักเรียนมัธยมปลาย: ส่วนเพิ่มเติม หลักสูตรของโรงเรียน- – ม.: เลนันด์ / URSS, 2014. – 216 น.
3. เมดินสกี้ เอ็ม.เอ็ม. หลักสูตรเต็มคณิตศาสตร์เบื้องต้นในปัญหาและแบบฝึกหัด เล่ม 2: ลำดับหมายเลขและความก้าวหน้า – ม.: บรรณาธิการ, 2558 – 208 น.
ยังมีคำถามอยู่ใช่ไหม?
หากต้องการความช่วยเหลือจากครูสอนพิเศษ ให้ลงทะเบียน
เว็บไซต์ เมื่อคัดลอกเนื้อหาทั้งหมดหรือบางส่วน จำเป็นต้องมีลิงก์ไปยังแหล่งที่มา
สมการลอการิทึม
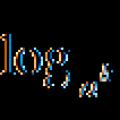เทคนิคการแก้สมการลอการิทึม
การวิเคราะห์ตนเองของครูนักบำบัดการพูด