หลักการของการกระทำน้อยที่สุดเกิดขึ้นได้อย่างไร? หลักการของการกระทำน้อยที่สุด

เมื่อข้าพเจ้าเรียนรู้หลักธรรมนี้ครั้งแรก ข้าพเจ้ามีความรู้สึกลึกลับบางอย่าง ดูเหมือนว่าธรรมชาติจะผ่านเส้นทางการเคลื่อนไหวของระบบที่เป็นไปได้ทั้งหมดอย่างลึกลับและเลือกเส้นทางที่ดีที่สุด

วันนี้ฉันอยากจะพูดถึงหลักการทางฟิสิกส์ที่น่าทึ่งที่สุดข้อหนึ่ง - หลักการของการกระทำน้อยที่สุด

พื้นหลัง

ตั้งแต่สมัยกาลิเลโอ เป็นที่รู้กันว่าวัตถุต่างๆ ที่ไม่ได้ถูกกระทำโดยแรงใดๆ จะเคลื่อนที่เป็นเส้นตรง กล่าวคือ ไปตามเส้นทางที่สั้นที่สุด รังสีของแสงก็เดินทางเป็นเส้นตรงเช่นกัน

เมื่อสะท้อนแสง แสงยังเคลื่อนที่ในลักษณะเดินทางจากจุดหนึ่งไปยังอีกจุดหนึ่งด้วยวิธีที่สั้นที่สุดเท่าที่จะเป็นไปได้ ในภาพ เส้นทางที่สั้นที่สุดจะเป็นเส้นทางสีเขียว ซึ่งมุมตกกระทบเท่ากับมุมสะท้อน เส้นทางอื่นๆ เช่น สีแดง จะยาวกว่า

วิธีนี้สามารถพิสูจน์ได้ง่าย ๆ โดยการสะท้อนเส้นทางของรังสีที่อยู่ด้านตรงข้ามของกระจก จะแสดงเป็นเส้นประในภาพ

จะเห็นได้ว่าเส้นทางสีเขียว ACB กลายเป็น ACB ทางตรง' และเส้นทางสีแดงจะกลายเป็นเส้นขาด ADB’ ซึ่งแน่นอนว่ายาวกว่าเส้นสีเขียว

ในปี 1662 ปิแอร์ แฟร์มาต์เสนอว่าความเร็วแสงในสสารหนาแน่น เช่น แก้ว นั้นน้อยกว่าในอากาศ ก่อนหน้านี้ เวอร์ชันของเดส์การตส์ได้รับการยอมรับโดยทั่วไป โดยความเร็วแสงในสสารจะต้องมากกว่าในอากาศเพื่อให้ได้กฎการหักเหที่ถูกต้อง สำหรับแฟร์มาต์ การสันนิษฐานว่าแสงสามารถเคลื่อนที่ได้เร็วกว่าในตัวกลางที่มีความหนาแน่นมากกว่าในตัวกลางทำให้บริสุทธิ์นั้นดูไม่เป็นธรรมชาติ ดังนั้นเขาจึงสันนิษฐานว่าทุกสิ่งทุกอย่างตรงกันข้ามและพิสูจน์ให้เห็นถึงสิ่งมหัศจรรย์ - ด้วยการสันนิษฐานนี้ แสงจะหักเหในลักษณะที่จะไปถึงจุดหมายปลายทางโดยใช้เวลาน้อยที่สุด

อีกครั้ง สีเขียวแสดงเส้นทางที่ลำแสงเดินทางไปตามจริง เส้นทางที่ทำเครื่องหมายด้วยสีแดงเป็นเส้นทางที่สั้นที่สุด แต่ไม่ใช่เส้นทางที่เร็วที่สุด เนื่องจากแสงมีเส้นทางที่ยาวกว่าเพื่อเดินทางผ่านกระจกและช้ากว่า เส้นทางที่เร็วที่สุดคือเส้นทางที่แท้จริงของลำแสง

ข้อเท็จจริงทั้งหมดนี้ชี้ให้เห็นว่าธรรมชาติกระทำในลักษณะที่มีเหตุผล แสงและวัตถุจะเคลื่อนไหวได้อย่างเหมาะสมที่สุด โดยใช้ความพยายามน้อยที่สุด แต่ความพยายามเหล่านี้เป็นอย่างไรและจะคำนวณอย่างไรยังคงเป็นปริศนา

ในปี ค.ศ. 1744 มอเปอร์ทุยส์ได้นำเสนอแนวคิดเรื่อง "การกระทำ" และกำหนดหลักการที่ว่าวิถีโคจรที่แท้จริงของอนุภาคแตกต่างจากที่อื่นตรงที่แรงกระทำนั้นน้อยมาก อย่างไรก็ตาม มอเพอร์ทุยส์เองก็ไม่สามารถให้คำจำกัดความที่ชัดเจนว่าการกระทำนี้หมายถึงอะไร สูตรทางคณิตศาสตร์ที่เข้มงวดของหลักการของการกระทำน้อยที่สุดได้รับการพัฒนาแล้วโดยนักคณิตศาสตร์คนอื่นๆ - ออยเลอร์, ลากรองจ์ และในที่สุดก็มอบให้โดยวิลเลียม แฮมิลตัน:

ในภาษาคณิตศาสตร์ หลักการของการกระทำน้อยที่สุดมีการกำหนดไว้ค่อนข้างสั้น แต่ผู้อ่านบางคนอาจไม่เข้าใจความหมายของสัญกรณ์ที่ใช้ ฉันต้องการพยายามอธิบายหลักการนี้ให้ชัดเจนและเรียบง่ายยิ่งขึ้น

ร่างกายอิสระ

ลองจินตนาการว่าคุณกำลังนั่งอยู่ในรถ ณ จุดหนึ่ง และ ณ เวลานี้ คุณได้รับมอบหมายงานง่ายๆ ในเวลาหนึ่ง นั่นคือ คุณต้องขับรถไปยังจุดนั้นก่อน

น้ำมันสำหรับรถยนต์มีราคาแพง และแน่นอนว่าคุณคงอยากใช้จ่ายให้น้อยที่สุดเท่าที่จะเป็นไปได้ รถของคุณถูกสร้างขึ้นโดยใช้เทคโนโลยีขั้นสูงล่าสุดและสามารถเร่งความเร็วหรือเบรกได้เร็วเท่าที่คุณต้องการ อย่างไรก็ตาม มันได้รับการออกแบบในลักษณะที่ว่ายิ่งวิ่งได้เร็วเท่าไรก็ยิ่งสิ้นเปลืองเชื้อเพลิงมากขึ้นเท่านั้น นอกจากนี้ปริมาณการใช้เชื้อเพลิงยังแปรผันตามกำลังสองของความเร็วอีกด้วย หากคุณขับเร็วเป็นสองเท่า คุณจะสิ้นเปลืองเชื้อเพลิงมากขึ้น 4 เท่าในช่วงเวลาเดียวกัน นอกจากความเร็วแล้ว อัตราสิ้นเปลืองเชื้อเพลิงยังส่งผลต่อน้ำหนักของรถด้วย ยิ่งรถเราหนักเท่าไหร่ก็ยิ่งกินน้ำมันมากขึ้นเท่านั้น ปริมาณการใช้เชื้อเพลิงของรถเราในแต่ละช่วงเวลาเท่ากันนั่นคือ เท่ากับพลังงานจลน์ของรถทุกประการ

แล้วจะขับรถอย่างไรให้ถึงที่หมายตามเวลาที่กำหนดและใช้น้ำมันให้น้อยที่สุด? ชัดเจนว่าคุณต้องเดินเป็นเส้นตรง เมื่อระยะทางเดินทางเพิ่มขึ้น น้ำมันก็จะสิ้นเปลืองไม่น้อย จากนั้นคุณสามารถเลือกกลยุทธ์ที่แตกต่างกันได้ เช่นสามารถไปถึงจุดล่วงหน้าได้อย่างรวดเร็วและนั่งรอจนกว่าจะถึงเวลา ความเร็วในการขับขี่และการสิ้นเปลืองน้ำมันเชื้อเพลิงในแต่ละช่วงเวลาจะสูง แต่เวลาในการขับขี่ก็จะลดลงเช่นกัน บางทีการสิ้นเปลืองเชื้อเพลิงโดยรวมอาจไม่มากนัก หรือคุณสามารถขับเท่าๆ กันด้วยความเร็วเท่ากัน เพื่อที่คุณจะได้มาถึงทันเวลาโดยไม่ต้องเร่งรีบ หรือขับส่วนหนึ่งของทางให้เร็วและขับช้ากว่านั้น วิธีที่ดีที่สุดที่จะไปคืออะไร?

ปรากฎว่าวิธีที่ดีที่สุดและประหยัดที่สุดในการขับขี่คือการขับขี่ด้วยความเร็วคงที่ เพื่อให้ถึงจุดหมายปลายทางตามเวลาที่กำหนด ตัวเลือกอื่นจะสิ้นเปลืองน้ำมันเชื้อเพลิงมากขึ้น คุณสามารถตรวจสอบได้ด้วยตัวเองโดยใช้ตัวอย่างต่างๆ เหตุผลก็คือการสิ้นเปลืองน้ำมันเชื้อเพลิงเพิ่มขึ้นตามกำลังสองของความเร็ว ดังนั้น เมื่อความเร็วเพิ่มขึ้น การสิ้นเปลืองน้ำมันเชื้อเพลิงจะเพิ่มขึ้นเร็วกว่าเวลาในการขับขี่ที่ลดลง และการสิ้นเปลืองน้ำมันเชื้อเพลิงโดยรวมก็เพิ่มขึ้นเช่นกัน

ดังนั้นเราจึงพบว่าหากรถยนต์ในแต่ละช่วงเวลาใช้เชื้อเพลิงตามสัดส่วนของพลังงานจลน์ของมัน วิธีที่ประหยัดที่สุดในการเดินทางจากจุดหนึ่งไปยังอีกจุดหนึ่งตามเวลาที่กำหนดคือการขับรถอย่างสม่ำเสมอและเป็นเส้นตรงอย่างแน่นอน วิธีที่ร่างกายเคลื่อนไหวโดยไม่มีแรงมากระทำ วิธีการขับขี่แบบอื่นจะส่งผลให้อัตราการสิ้นเปลืองน้ำมันเชื้อเพลิงโดยรวมสูงขึ้น

ในสนามแรงโน้มถ่วง

ตอนนี้เรามาปรับปรุงรถของเรากันหน่อย มาติดเครื่องยนต์ไอพ่นเข้ากับมันเพื่อให้บินได้อย่างอิสระในทุกทิศทาง โดยทั่วไปแล้ว การออกแบบยังคงเหมือนเดิม ดังนั้นการสิ้นเปลืองน้ำมันเชื้อเพลิงจึงยังคงเป็นสัดส่วนอย่างเคร่งครัดกับพลังงานจลน์ของรถ หากตอนนี้มอบหมายให้บินจากจุดหนึ่งไปยังอีกจุดหนึ่งแล้วมาถึงจุดหนึ่งในเวลาหนึ่งแล้ววิธีที่ประหยัดที่สุดเช่นเดิมแน่นอนคือการบินสม่ำเสมอและเป็นเส้นตรงเพื่อที่จะสิ้นสุด ขึ้นตรงเวลาที่กำหนด สิ่งนี้สอดคล้องกับการเคลื่อนไหวอย่างอิสระของร่างกายในพื้นที่สามมิติอีกครั้ง

อย่างไรก็ตาม มีการติดตั้งอุปกรณ์ที่ผิดปกติในรถยนต์รุ่นล่าสุด อุปกรณ์นี้สามารถผลิตเชื้อเพลิงได้อย่างแท้จริงจากไม่มีอะไรเลย แต่การออกแบบนั้นยิ่งรถอยู่สูงเท่าไร อุปกรณ์ก็จะผลิตเชื้อเพลิงได้มากขึ้นเท่านั้น การผลิตเชื้อเพลิงเป็นสัดส่วนโดยตรงกับระดับความสูงที่รถตั้งอยู่ในปัจจุบัน นอกจากนี้ ยิ่งรถมีน้ำหนักมาก อุปกรณ์ก็จะยิ่งมีประสิทธิภาพมากขึ้น และผลิตเชื้อเพลิงได้มากขึ้น และการผลิตจะเป็นสัดส่วนโดยตรงกับน้ำหนักของรถ อุปกรณ์กลายเป็นว่าการผลิตเชื้อเพลิงเท่ากับ (โดยที่ความเร่งของการตกอย่างอิสระ) คือ พลังงานศักย์ของรถยนต์

ปริมาณการใช้เชื้อเพลิงในแต่ละช่วงเวลาจะเท่ากับพลังงานจลน์ลบด้วยพลังงานศักย์ของรถยนต์ (ลบด้วยพลังงานศักย์เนื่องจากอุปกรณ์ที่ติดตั้งผลิตเชื้อเพลิงและไม่สิ้นเปลือง) ตอนนี้งานของเราในการเคลื่อนย้ายรถระหว่างจุดต่างๆ อย่างมีประสิทธิภาพที่สุดกลายเป็นเรื่องยากมากขึ้น การเคลื่อนที่สม่ำเสมอเป็นเส้นตรงกลับกลายเป็นว่าไม่ได้ผลดีที่สุดในกรณีนี้ ปรากฎว่าเป็นการดีที่สุดที่จะเพิ่มระดับความสูงเล็กน้อย อยู่ที่นั่นสักพัก ใช้เชื้อเพลิงมากขึ้น จากนั้นจึงลงมาที่จุด ด้วยวิถีการบินที่ถูกต้อง การผลิตเชื้อเพลิงทั้งหมดเนื่องจากการไต่ระดับจะครอบคลุมต้นทุนเชื้อเพลิงเพิ่มเติมสำหรับการเพิ่มความยาวของเส้นทางและการเพิ่มความเร็ว หากคุณคำนวณอย่างรอบคอบ วิธีที่ประหยัดที่สุดสำหรับรถยนต์คือการบินในพาราโบลาในวิถีโคจรเดียวกันทุกประการและด้วยความเร็วเท่ากันทุกประการกับก้อนหินที่บินในสนามโน้มถ่วงของโลก

มันคุ้มค่าที่จะชี้แจงที่นี่ แน่นอน คุณสามารถขว้างก้อนหินจากจุดหนึ่งได้หลายวิธีเพื่อให้หินถึงจุดนั้น แต่คุณต้องโยนมันในลักษณะที่เมื่อออกจากจุดในขณะนั้นแล้วก็จะถึงจุดนั้นในขณะนั้น การเคลื่อนไหวนี้จะประหยัดที่สุดสำหรับรถของเรา

ฟังก์ชันลากรองจ์และหลักการของการกระทำน้อยที่สุด

ตอนนี้เราสามารถถ่ายโอนการเปรียบเทียบนี้ไปยังร่างกายจริงได้ อัตราการสิ้นเปลืองเชื้อเพลิงที่คล้ายคลึงกันสำหรับตัวถังเรียกว่าฟังก์ชันลากรองจ์หรือลากรองจ์ (เพื่อเป็นเกียรติแก่ลากรองจ์) และเขียนแทนด้วยตัวอักษร . ลากรองจ์แสดงให้เห็นว่าร่างกายใช้ "เชื้อเพลิง" มากเพียงใดในเวลาที่กำหนด สำหรับวัตถุที่เคลื่อนที่ในสนามศักย์ ลากรองจ์จะเท่ากับพลังงานจลน์ลบด้วยพลังงานศักย์

อะนาล็อกของปริมาณเชื้อเพลิงทั้งหมดที่ใช้ตลอดระยะเวลาการเคลื่อนไหวคือ ค่าลากรองจ์ที่สะสมตลอดระยะเวลาการเคลื่อนไหวเรียกว่า "การกระทำ"

หลักการของการกระทำน้อยที่สุดคือร่างกายเคลื่อนไหวในลักษณะที่การกระทำ (ซึ่งขึ้นอยู่กับวิถีการเคลื่อนไหว) น้อยที่สุด ในเวลาเดียวกันเราต้องไม่ลืมว่ามีการระบุเงื่อนไขเริ่มต้นและเงื่อนไขสุดท้ายไว้เช่น ที่ซึ่งกายอยู่ ณ ขณะนั้นและขณะแห่งกาลนั้น

ในกรณีนี้ ร่างกายไม่จำเป็นต้องเคลื่อนที่ในสนามโน้มถ่วงสม่ำเสมอซึ่งเราพิจารณาสำหรับรถของเรา สามารถพิจารณาสถานการณ์ที่แตกต่างกันโดยสิ้นเชิงได้ ร่างกายสามารถแกว่งไปมาบนแถบยางยืด แกว่งบนลูกตุ้ม หรือบินรอบดวงอาทิตย์ ในกรณีทั้งหมดนี้ ร่างกายจะเคลื่อนที่ในลักษณะที่จะลด "การสิ้นเปลืองเชื้อเพลิงทั้งหมด" เช่น การกระทำ.

หากระบบประกอบด้วยวัตถุหลายชิ้น ลากรองจ์ของระบบดังกล่าวจะเท่ากับพลังงานจลน์รวมของวัตถุทั้งหมดลบด้วยพลังงานศักย์รวมของวัตถุทั้งหมด และขอย้ำอีกครั้งว่าวัตถุทั้งหมดจะเคลื่อนไหวพร้อมกันเพื่อให้ผลกระทบของระบบทั้งหมดในระหว่างการเคลื่อนไหวนั้นน้อยที่สุด

มันไม่ง่ายอย่างนั้น

จริงๆ แล้ว ฉันโกงนิดหน่อยโดยบอกว่าร่างกายมักจะเคลื่อนไหวในลักษณะที่ลดการกระทำลง แม้ว่าสิ่งนี้จะเป็นจริงในหลายกรณี แต่ก็เป็นไปได้ที่จะนึกถึงสถานการณ์ที่การกระทำนั้นไม่ได้เกิดขึ้นเพียงเล็กน้อยเท่านั้น

เช่น ลองเอาลูกบอลมาวางไว้ในที่ว่าง ในระยะหนึ่งเราจะวางกำแพงยางยืด สมมติว่าเราต้องการให้ลูกบอลไปจบลงที่จุดเดิมหลังจากผ่านไประยะหนึ่ง ภายใต้เงื่อนไขที่กำหนด ลูกบอลสามารถเคลื่อนที่ได้สองวิธี ประการแรก มันสามารถอยู่กับที่ได้อย่างง่ายดาย ประการที่สอง คุณสามารถดันมันไปทางผนังได้ ลูกบอลจะลอยไปชนกำแพง กระเด็นออกไป แล้วกลับมา เห็นได้ชัดว่าคุณสามารถผลักมันด้วยความเร็วที่มันกลับมาในเวลาที่เหมาะสม

เป็นไปได้ทั้งสองตัวเลือกสำหรับการเคลื่อนที่ของลูกบอล แต่การกระทำในกรณีที่สองจะยิ่งใหญ่กว่าเพราะตลอดเวลานี้ลูกบอลจะเคลื่อนที่ด้วยพลังงานจลน์ที่ไม่เป็นศูนย์

เราจะรักษาหลักการของการกระทำน้อยที่สุดให้ถูกต้องในสถานการณ์เช่นนี้ได้อย่างไร? เราจะพูดถึงเรื่องนี้ใน

ในเราได้พิจารณาหลักการทางกายภาพที่น่าทึ่งที่สุดข้อหนึ่งโดยย่อ - หลักการของการกระทำน้อยที่สุด และหยุดที่ตัวอย่างที่ดูเหมือนจะขัดแย้งกับหลักการนั้น ในบทความนี้ เราจะดูหลักการนี้โดยละเอียดมากขึ้นอีกเล็กน้อย และดูว่าเกิดอะไรขึ้นในตัวอย่างนี้

คราวนี้เราจะต้องเรียนคณิตศาสตร์เพิ่มอีกนิดหน่อย อย่างไรก็ตาม ฉันจะพยายามนำเสนอส่วนหลักของบทความในระดับประถมศึกษาอีกครั้ง ฉันจะเน้นจุดสีที่เข้มงวดและซับซ้อนมากขึ้นเล็กน้อย สามารถข้ามได้โดยไม่กระทบต่อความเข้าใจพื้นฐานของบทความ

เงื่อนไขขอบเขต

เราจะเริ่มต้นด้วยวัตถุที่ง่ายที่สุด - ลูกบอลเคลื่อนที่อย่างอิสระในอวกาศโดยไม่มีแรงกระทำ ดังที่ทราบกันว่าลูกบอลดังกล่าวเคลื่อนที่สม่ำเสมอและเป็นเส้นตรง เพื่อความง่าย สมมติว่ามันเคลื่อนที่ไปตามแกน:

ตามกฎแล้วเพื่ออธิบายการเคลื่อนไหวอย่างถูกต้อง จึงมีการระบุเงื่อนไขเริ่มต้น เช่น กำหนดไว้ว่า ณ เวลาเริ่มแรกลูกบอลอยู่ในจุดที่มีการประสานงานและมีความเร็ว เมื่อกำหนดเงื่อนไขเริ่มต้นในรูปแบบนี้แล้วเราจะกำหนดการเคลื่อนที่ต่อไปของลูกบอลอย่างไม่น่าสงสัย - มันจะเคลื่อนที่ด้วยความเร็วคงที่และตำแหน่ง ณ ขณะนั้นจะเท่ากับตำแหน่งเริ่มต้นบวกกับความเร็วคูณด้วยเวลาที่ผ่านไป : . วิธีการตั้งค่าเงื่อนไขเริ่มต้นนี้เป็นไปตามธรรมชาติและคุ้นเคยเป็นอย่างดี เราได้ระบุข้อมูลที่จำเป็นทั้งหมดเกี่ยวกับการเคลื่อนที่ของลูกบอลในช่วงเวลาเริ่มต้น จากนั้นการเคลื่อนที่จะถูกกำหนดตามกฎของนิวตัน

อย่างไรก็ตาม นี่ไม่ใช่วิธีเดียวที่จะระบุการเคลื่อนที่ของลูกบอลได้ อีกทางเลือกหนึ่งคือการกำหนดตำแหน่งของลูกบอลในเวลาที่ต่างกันสองเวลา และ เหล่านั้น. ถามสิ่งนั้น:

1) ในขณะที่ลูกบอลอยู่ ณ จุดหนึ่ง (พร้อมพิกัด)
2) ขณะที่ลูกบอลอยู่ ณ จุดนั้น (โดยมีพิกัด )

สำนวน "อยู่ที่จุด" ไม่ได้หมายความว่าลูกบอลอยู่นิ่งที่จุดนั้น ในช่วงเวลานั้นเขาสามารถบินผ่านจุดนั้นได้ ซึ่งหมายความว่าตำแหน่งในขณะนั้นตรงกับจุดนั้น เช่นเดียวกับประเด็น

เงื่อนไขทั้งสองนี้ยังกำหนดการเคลื่อนที่ของลูกบอลโดยเฉพาะอีกด้วย การเคลื่อนไหวของมันคำนวณได้ง่าย เพื่อให้เป็นไปตามเงื่อนไขทั้งสอง ความเร็วของลูกบอลจะต้องเป็นอย่างชัดเจน ตำแหน่งของลูกบอล ณ เวลานั้นจะเท่ากับตำแหน่งเริ่มต้นอีกครั้งบวกกับความเร็วคูณด้วยเวลาที่ผ่านไป:

โปรดทราบว่าในเงื่อนไขของปัญหาเราไม่จำเป็นต้องตั้งค่าความเร็วเริ่มต้น ถูกกำหนดโดยเฉพาะจากเงื่อนไข 1) และ 2)

การตั้งค่าเงื่อนไขในลักษณะที่สองดูผิดปกติ อาจไม่ชัดเจนว่าเหตุใดจึงจำเป็นต้องถามพวกเขาในแบบฟอร์มนี้เลย อย่างไรก็ตาม โดยหลักการของการดำเนินการน้อยที่สุด จะใช้เงื่อนไขในรูปแบบ 1) และ 2) ไม่ใช่ในรูปแบบการระบุตำแหน่งเริ่มต้นและความเร็วเริ่มต้น

เส้นทางที่มีการกระทำน้อยที่สุด

ทีนี้ลองพูดนอกเรื่องเล็กน้อยจากการเคลื่อนที่อย่างอิสระของลูกบอลและพิจารณาปัญหาทางคณิตศาสตร์ล้วนๆต่อไปนี้ สมมติว่าเรามีลูกบอลที่เราสามารถเคลื่อนที่ด้วยตนเองในแบบที่เราต้องการได้ ในกรณีนี้ เราต้องปฏิบัติตามเงื่อนไข 1) และ 2) เหล่านั้น. ในช่วงเวลาระหว่างนั้นและเราต้องเคลื่อนจากจุดหนึ่งไปยังอีกจุดหนึ่ง ซึ่งสามารถทำได้ในรูปแบบที่แตกต่างกันโดยสิ้นเชิง เราจะเรียกแต่ละวิธีดังกล่าวว่าวิถีการเคลื่อนที่ของลูกบอล และสามารถอธิบายได้ด้วยฟังก์ชันของตำแหน่งลูกบอลเทียบกับเวลา ลองวาดเส้นวิถีเหล่านี้หลายๆ เส้นบนกราฟตำแหน่งของลูกบอลเทียบกับเวลา:

เช่น เราสามารถเคลื่อนลูกบอลด้วยความเร็วเท่ากันกับ (วิถีสีเขียว) หรือเราจะเก็บไว้ที่จุดครึ่งหนึ่งของเวลาแล้วเลื่อนไปยังจุดด้วยความเร็วสองเท่า (วิถีสีน้ำเงิน) คุณสามารถเคลื่อนไปในทิศทางตรงกันข้ามได้ก่อน แล้วจึงย้ายไปที่ (วิถีสีน้ำตาล) สามารถเลื่อนไปมาได้(เส้นทางสีแดง) โดยทั่วไป คุณสามารถเคลื่อนย้ายได้ตามที่คุณต้องการ ตราบใดที่เป็นไปตามเงื่อนไข 1) และ 2)

สำหรับแต่ละวิถีนั้นเราสามารถเชื่อมโยงตัวเลขได้ ในตัวอย่างของเรา กล่าวคือ ในกรณีที่ไม่มีแรงใด ๆ ที่กระทำต่อลูกบอล จำนวนนี้จะเท่ากับพลังงานจลน์ที่สะสมทั้งหมดตลอดระยะเวลาการเคลื่อนที่ในช่วงเวลาระหว่าง และ และ เรียกว่าการกระทำ

ในกรณีนี้คำว่า “สะสม” พลังงานจลน์ไม่ได้สื่อความหมายได้แม่นยำนัก ในความเป็นจริง พลังงานจลน์ไม่ได้สะสมอยู่ที่ใดเลย การสะสมนั้นใช้เพื่อคำนวณการกระทำของวิถีเท่านั้น ในทางคณิตศาสตร์มีแนวคิดที่ดีมากสำหรับการสะสมดังกล่าว - อินทิกรัล:

การกระทำมักจะระบุด้วยตัวอักษร สัญลักษณ์หมายถึงพลังงานจลน์ อินทิกรัลนี้หมายความว่าการกระทำจะเท่ากับพลังงานจลน์ที่สะสมของลูกบอลในช่วงเวลาตั้งแต่ ถึง

ตัวอย่างเช่น ลองใช้ลูกบอลมวล 1 กิโลกรัม กำหนดเงื่อนไขขอบเขตและคำนวณการกระทำสำหรับวิถีการเคลื่อนที่สองแบบที่แตกต่างกัน ให้จุดอยู่ห่างจากจุด 1 เมตร และเวลาอยู่ห่างจากเวลา 1 วินาที เหล่านั้น. เราต้องเคลื่อนลูกบอลซึ่ง ณ เวลาเริ่มต้นอยู่ที่จุด ในหนึ่งวินาทีไปยังระยะ 1 เมตรตามแนวแกน

ในตัวอย่างแรก (วิถีสีเขียว) เราเคลื่อนลูกบอลอย่างสม่ำเสมอ นั่นคือ ด้วยความเร็วเท่ากัน ซึ่งแน่นอนว่าควรจะเท่ากับ m/s พลังงานจลน์ของลูกบอลในแต่ละช่วงเวลาเท่ากับ: = 1/2 J ในหนึ่งวินาที พลังงานจลน์ 1/2 J จะสะสม เหล่านั้น. การกระทำสำหรับวิถีดังกล่าวเท่ากับ: J s

ตอนนี้เราอย่าเพิ่งเคลื่อนลูกบอลจากจุดหนึ่งไปยังอีกจุดหนึ่งทันที แต่ให้ค้างไว้ที่จุดหนึ่งเป็นเวลาครึ่งวินาที จากนั้นให้เคลื่อนไปยังจุดเท่าๆ กันในช่วงเวลาที่เหลือ ในช่วงครึ่งวินาทีแรก ลูกบอลอยู่นิ่งและพลังงานจลน์ของลูกบอลเป็นศูนย์ ดังนั้นการมีส่วนร่วมในการกระทำของวิถีส่วนนี้จึงเป็นศูนย์เช่นกัน ครึ่งวินาทีหลังเราเคลื่อนลูกบอลด้วยความเร็วสองเท่า: m/s พลังงานจลน์จะเท่ากับ = 2 J การมีส่วนร่วมของช่วงเวลานี้ต่อการกระทำจะเท่ากับ 2 J คูณครึ่งวินาทีนั่นคือ 1 เจ ดังนั้น การกระทำทั้งหมดสำหรับวิถีดังกล่าวจึงเท่ากับ J

ในทำนองเดียวกัน วิถีอื่นใดที่มีเงื่อนไขขอบเขต 1) และ 2) ที่เรากำหนดไว้นั้นสอดคล้องกับจำนวนที่แน่นอนซึ่งเท่ากับการกระทำสำหรับวิถีนี้ ในบรรดาวิถีดังกล่าว มีวิถีที่กระทำน้อยที่สุด พิสูจน์ได้ว่าวิถีนี้เป็นวิถีสีเขียวคือ การเคลื่อนไหวของลูกบอลสม่ำเสมอ สำหรับวิถีอื่นๆ ไม่ว่าจะยากแค่ไหน การกระทำก็จะมากกว่า 1/2

ในทางคณิตศาสตร์ การเปรียบเทียบแต่ละฟังก์ชันของจำนวนหนึ่งเรียกว่าฟังก์ชัน บ่อยครั้งในปัญหาทางฟิสิกส์และคณิตศาสตร์ที่คล้ายกับของเราเกิดขึ้นเช่น เพื่อค้นหาฟังก์ชันที่มีค่าของฟังก์ชันหนึ่งมีค่าน้อยที่สุด ตัวอย่างเช่น ปัญหาประการหนึ่งที่มีความสำคัญทางประวัติศาสตร์อย่างมากต่อการพัฒนาคณิตศาสตร์ก็คือปัญหาของบาคิสโตโครน เหล่านั้น. หาเส้นโค้งที่ลูกบอลกลิ้งเร็วที่สุด ขอย้ำอีกครั้ง แต่ละเส้นโค้งสามารถแสดงด้วยฟังก์ชัน h(x) และแต่ละฟังก์ชันสามารถเชื่อมโยงกับตัวเลขได้ ในกรณีนี้คือเวลาในการกลิ้งลูกบอล อีกครั้ง ปัญหาอยู่ที่การค้นหาฟังก์ชันที่มีค่าของฟังก์ชันน้อยที่สุด สาขาวิชาคณิตศาสตร์ที่เกี่ยวข้องกับปัญหาดังกล่าวเรียกว่าแคลคูลัสของการแปรผัน

หลักการของการกระทำน้อยที่สุด

ในตัวอย่างที่กล่าวถึงข้างต้น เรามีวิถีพิเศษสองวิถีที่ได้รับในสองวิธีที่แตกต่างกัน

วิถีแรกได้มาจากกฎฟิสิกส์และสอดคล้องกับวิถีที่แท้จริงของลูกบอลอิสระซึ่งไม่มีแรงกระทำและเงื่อนไขขอบเขตระบุไว้ในรูปแบบ 1) และ 2)

วิถีที่สองได้มาจากปัญหาทางคณิตศาสตร์ในการค้นหาวิถีที่มีเงื่อนไขขอบเขตที่กำหนด 1) และ 2) ซึ่งมีการกระทำน้อยที่สุด

หลักการกระทำน้อยที่สุด ระบุว่า วิถีทั้งสองนี้ต้องตรงกัน กล่าวอีกนัยหนึ่ง หากทราบว่าลูกบอลเคลื่อนที่ไปในลักษณะที่เงื่อนไขขอบเขต 1) และ 2) เป็นไปตามนั้น ก็จำเป็นต้องเคลื่อนที่ไปตามวิถีซึ่งมีการกระทำน้อยที่สุดเมื่อเทียบกับวิถีอื่นที่มีขอบเขตเดียวกัน เงื่อนไข.

บางคนอาจมองว่านี่เป็นเพียงเรื่องบังเอิญ มีปัญหามากมายที่วิถีโคจรและเส้นตรงสม่ำเสมอปรากฏขึ้น อย่างไรก็ตาม หลักการของการกระทำน้อยที่สุดกลายเป็นหลักการทั่วไป ซึ่งใช้ได้ในสถานการณ์อื่น เช่น การเคลื่อนที่ของลูกบอลในสนามโน้มถ่วงสม่ำเสมอ ในการทำเช่นนี้ คุณเพียงแค่ต้องแทนที่พลังงานจลน์ด้วยความแตกต่างระหว่างพลังงานจลน์และพลังงานศักย์ ความแตกต่างนี้เรียกว่าฟังก์ชันลากรองจ์หรือลากรองจ์ และการกระทำจะเท่ากับผลรวมลากรองจ์ที่สะสมไว้ ที่จริงแล้ว ฟังก์ชัน Lagrange มีข้อมูลที่จำเป็นทั้งหมดเกี่ยวกับคุณสมบัติไดนามิกของระบบ

หากเราปล่อยลูกบอลในสนามโน้มถ่วงสม่ำเสมอในลักษณะที่ลูกบอลผ่านจุดหนึ่ง ณ เวลาหนึ่งและมาถึงจุดหนึ่ง ณ เวลาหนึ่งทันที ดังนั้น ตามกฎของนิวตัน ลูกบอลจะลอยไปตามพาราโบลา พาราโบลานี้จะตรงกับวิถีที่การกระทำจะน้อยที่สุด

ดังนั้น สำหรับวัตถุที่เคลื่อนที่ในสนามศักย์ เช่น ในสนามโน้มถ่วงของโลก ฟังก์ชันลากรองจ์จะเท่ากับ: พลังงานจลน์ขึ้นอยู่กับความเร็วของร่างกาย และพลังงานศักย์ขึ้นอยู่กับตำแหน่งของร่างกาย เช่น พิกัด ในกลศาสตร์การวิเคราะห์ ชุดพิกัดทั้งชุดที่กำหนดตำแหน่งของระบบมักจะแสดงด้วยตัวอักษรตัวเดียว สำหรับลูกบอลที่เคลื่อนที่อย่างอิสระในสนามโน้มถ่วง หมายถึง พิกัด และ

เพื่อระบุอัตราการเปลี่ยนแปลงของปริมาณใดๆ ในฟิสิกส์ บ่อยครั้งมักใส่จุดไว้เหนือปริมาณนี้ ตัวอย่างเช่น แสดงถึงอัตราการเปลี่ยนแปลงพิกัด หรืออีกนัยหนึ่ง คือ ความเร็วของร่างกายในทิศทาง เมื่อใช้แบบแผนเหล่านี้ ความเร็วของลูกบอลของเราในกลศาสตร์การวิเคราะห์จะแสดงเป็น เหล่านั้น. ย่อมาจากส่วนประกอบของความเร็ว

เนื่องจากฟังก์ชันลากรองจ์ขึ้นอยู่กับความเร็วและพิกัด และยังสามารถขึ้นอยู่กับเวลาได้อย่างชัดเจน (ขึ้นอยู่กับเวลาอย่างชัดเจนหมายความว่าค่าจะแตกต่างกันในเวลาที่ต่างกัน สำหรับความเร็วและตำแหน่งของลูกบอลเท่ากัน) ดังนั้นการกระทำโดยทั่วไปจะถูกเขียน เช่น

ไม่น้อยเสมอไป

อย่างไรก็ตาม ในตอนท้ายของส่วนก่อนหน้านี้ เราได้ดูตัวอย่างที่เห็นได้ชัดว่าหลักการของการดำเนินการน้อยที่สุดไม่ได้ผล ในการทำเช่นนี้ เราหยิบลูกบอลฟรีอีกครั้งโดยไม่มีแรงกระทำใด ๆ และวางกำแพงสปริงไว้ข้างๆ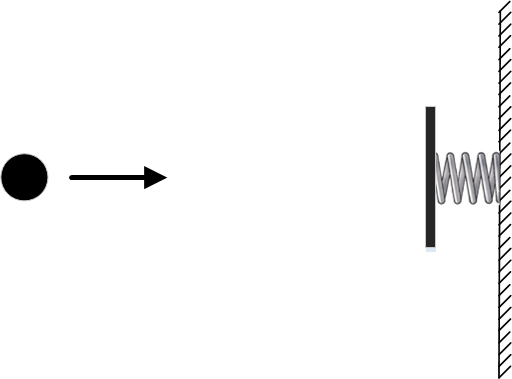

เรากำหนดเงื่อนไขขอบเขตดังกล่าวว่าจุดและตรงกัน เหล่านั้น. ทั้งขณะและขณะเวลาลูกบอลต้องอยู่จุดเดียวกัน วิถีที่เป็นไปได้ประการหนึ่งคือลูกบอลหยุดนิ่ง เหล่านั้น. ตลอดระยะเวลาระหว่างนั้นและเขาจะยืนอยู่ตรงจุดนั้น พลังงานจลน์และพลังงานศักย์ในกรณีนี้จะเท่ากับศูนย์ ดังนั้นการกระทำของวิถีโคจรก็จะเท่ากับศูนย์เช่นกัน

พูดอย่างเคร่งครัด พลังงานศักย์สามารถวัดได้ไม่เท่ากับศูนย์ แต่เป็นจำนวนเท่าใดก็ได้ เนื่องจากความแตกต่างของพลังงานศักย์ที่จุดต่างๆ ในอวกาศเป็นสิ่งสำคัญ อย่างไรก็ตาม การเปลี่ยนแปลงค่าพลังงานศักย์ไม่ส่งผลต่อการค้นหาวิถีที่มีการเคลื่อนไหวน้อยที่สุด เพียงแต่ว่าสำหรับวิถีทั้งหมด ค่าการกระทำจะเปลี่ยนเป็นตัวเลขเดียวกัน และวิถีที่มีการกระทำขั้นต่ำจะยังคงเป็นวิถีที่มีการกระทำขั้นต่ำ เพื่อความสะดวกสำหรับลูกบอลของเราเราจะเลือกพลังงานศักย์เท่ากับศูนย์

วิถีทางกายภาพที่เป็นไปได้อีกประการหนึ่งที่มีเงื่อนไขขอบเขตเดียวกันคือวิถีที่ลูกบอลบินไปทางขวาก่อนโดยผ่านจุดนั้นไปตามเวลา จากนั้นเขาก็ชนกับสปริง บีบอัด สปริงยืดตัว ผลักลูกบอลกลับ และมันก็บินผ่านจุดนั้นอีกครั้ง คุณสามารถเลือกความเร็วของลูกบอลเพื่อให้มันกระเด้งออกจากกำแพงและผ่านจุดนั้นไปในขณะนั้น การกระทำบนวิถีดังกล่าวจะเท่ากับพลังงานจลน์ที่สะสมไว้ในระหว่างการบินระหว่างจุดกับกำแพงและด้านหลัง จะมีช่วงระยะเวลาหนึ่งที่ลูกบอลจะบีบอัดสปริงและพลังงานศักย์ของมันจะเพิ่มขึ้น และในช่วงเวลานี้ พลังงานศักย์จะส่งผลเสียต่อการกระทำ แต่ระยะเวลาดังกล่าวจะไม่นานมากและจะไม่ลดผลกระทบอย่างมีนัยสำคัญ

รูปนี้แสดงวิถีการเคลื่อนที่ของลูกบอลที่เป็นไปได้ทางกายภาพ วิถีสีเขียวสอดคล้องกับลูกบอลที่อยู่นิ่ง ในขณะที่วิถีสีน้ำเงินสอดคล้องกับลูกบอลที่กระดอนจากกำแพงสปริง

อย่างไรก็ตาม มีเพียงอันเดียวเท่านั้นที่มีผลน้อยที่สุด กล่าวคืออันแรก! วิถีที่สองมีการกระทำมากขึ้น ปรากฎว่าในปัญหานี้ มีวิถีที่เป็นไปได้ทางกายภาพสองวิถี และมีเพียงวิถีเดียวเท่านั้นที่มีการเคลื่อนไหวน้อยที่สุด เหล่านั้น. ในกรณีนี้ หลักการของการดำเนินการน้อยที่สุดใช้ไม่ได้ผล

จุดคงที่

เพื่อให้เข้าใจถึงสิ่งที่เกิดขึ้นที่นี่ เราลองละเลยหลักการของการดำเนินการน้อยที่สุดในตอนนี้ และไปยังฟังก์ชันธรรมดาต่อไป ลองใช้ฟังก์ชันแล้ววาดกราฟของมัน:

บนกราฟ ฉันทำเครื่องหมายจุดพิเศษสี่จุดเป็นสีเขียว ประเด็นเหล่านี้มีอะไรเหมือนกัน? ลองจินตนาการว่ากราฟของฟังก์ชันเป็นสไลด์จริงที่ลูกบอลสามารถหมุนได้ จุดที่กำหนดทั้งสี่จุดมีความพิเศษคือถ้าวางลูกบอลตรงจุดนี้จะไม่กลิ้งไปไหน ที่จุดอื่นๆ เช่น จุด E เขาจะไม่สามารถยืนนิ่งได้และจะเริ่มไถลลง จุดดังกล่าวเรียกว่านิ่ง การค้นหาจุดดังกล่าวเป็นงานที่มีประโยชน์ เนื่องจากฟังก์ชันสูงสุดหรือต่ำสุดใดๆ หากไม่มีจุดหักคม จะต้องเป็นจุดที่อยู่นิ่งเสมอ

หากเราจำแนกจุดเหล่านี้ได้แม่นยำยิ่งขึ้น จุด A คือค่าต่ำสุดสัมบูรณ์ของฟังก์ชัน เช่น ค่าของมันน้อยกว่าค่าฟังก์ชันอื่นๆ จุด B ไม่ใช่ค่าสูงสุดหรือค่าต่ำสุดและเรียกว่าจุดอาน จุด C เรียกว่าค่าสูงสุดในพื้นที่ เช่น ค่าในนั้นมากกว่าจุดใกล้เคียงของฟังก์ชัน และจุด D คือค่าต่ำสุดในพื้นที่ เช่น ค่าในนั้นน้อยกว่าจุดใกล้เคียงของฟังก์ชัน

การค้นหาประเด็นดังกล่าวดำเนินการโดยสาขาวิชาคณิตศาสตร์ที่เรียกว่าการวิเคราะห์ทางคณิตศาสตร์ มิฉะนั้น บางครั้งเรียกว่าการวิเคราะห์แบบไม่จำกัด เนื่องจากสามารถทำงานกับปริมาณที่จำกัดได้ จากมุมมองของการวิเคราะห์ทางคณิตศาสตร์ จุดคงที่มีคุณสมบัติพิเศษอย่างหนึ่งซึ่งพบได้ เพื่อทำความเข้าใจว่าคุณสมบัตินี้คืออะไร เราต้องเข้าใจว่าฟังก์ชันนี้มีลักษณะอย่างไรที่ระยะห่างจากจุดเหล่านี้น้อยมาก ในการทำเช่นนี้ เราจะใช้กล้องจุลทรรศน์และมองผ่านจุดของเรา รูปภาพนี้แสดงให้เห็นว่าฟังก์ชันจะมีลักษณะอย่างไรในบริเวณใกล้เคียงกับจุดต่างๆ ที่มีกำลังขยายต่างกัน

จะเห็นได้ว่าเมื่อใช้กำลังขยายที่สูงมาก (เช่น สำหรับการเบี่ยงเบนเล็กน้อย x) จุดที่อยู่นิ่งจะดูเหมือนกันทุกประการและแตกต่างจากจุดที่ไม่อยู่นิ่งอย่างมาก เป็นเรื่องง่ายที่จะเข้าใจว่าความแตกต่างนี้คืออะไร - กราฟของฟังก์ชันที่จุดที่นิ่งจะกลายเป็นเส้นแนวนอนอย่างเคร่งครัดเมื่อเพิ่มขึ้น และที่จุดที่ไม่คงที่จะกลายเป็นเส้นเอียง นั่นคือสาเหตุที่ลูกบอลที่ติดตั้งอยู่กับที่จะไม่กลิ้งออกไป

แนวนอนของฟังก์ชันที่จุดที่อยู่นิ่งสามารถแสดงได้แตกต่างกัน: ฟังก์ชันที่จุดที่อยู่นิ่งนั้นในทางปฏิบัติแล้วจะไม่เปลี่ยนแปลงโดยมีการเปลี่ยนแปลงเล็กน้อยในการโต้แย้ง แม้ว่าจะเปรียบเทียบกับการเปลี่ยนแปลงในการโต้แย้งก็ตาม ฟังก์ชันที่จุดที่ไม่คงที่ซึ่งมีการเปลี่ยนแปลงเล็กน้อยจะเปลี่ยนไปตามสัดส่วนการเปลี่ยนแปลง และความชันของฟังก์ชันมากขึ้น ฟังก์ชันจะเปลี่ยนไปมากขึ้นเมื่อ ในความเป็นจริง เมื่อฟังก์ชันเพิ่มขึ้น มันก็จะกลายเป็นเหมือนเส้นสัมผัสของกราฟ ณ จุดที่ต้องการมากขึ้นเรื่อยๆ

ในภาษาคณิตศาสตร์ที่เข้มงวด นิพจน์ "ในทางปฏิบัติแล้วฟังก์ชันจะไม่เปลี่ยนแปลง ณ จุดที่มีการเปลี่ยนแปลงเพียงเล็กน้อย" หมายความว่าอัตราส่วนของการเปลี่ยนแปลงในฟังก์ชันและการเปลี่ยนแปลงในอาร์กิวเมนต์มีแนวโน้มเป็น 0 เนื่องจากมีแนวโน้มเป็น 0:

$$display$$\lim_(∆x \to 0) \frac (∆y(x_0))(∆x) = \lim_(x \to 0) \frac (y(x_0+∆x)-y(x_0) )(∆x) = 0$$แสดง$$

สำหรับจุดที่ไม่คงที่ อัตราส่วนนี้มีแนวโน้มเป็นจำนวนที่ไม่เป็นศูนย์ ซึ่งเท่ากับค่าแทนเจนต์ของความชันของฟังก์ชัน ณ จุดนี้ จำนวนเดียวกันนี้เรียกว่าอนุพันธ์ของฟังก์ชันที่จุดที่กำหนด อนุพันธ์ของฟังก์ชันแสดงให้เห็นว่าฟังก์ชันเปลี่ยนแปลงเร็วเพียงใดรอบจุดที่กำหนดโดยมีการเปลี่ยนแปลงเล็กน้อยในการโต้แย้ง ดังนั้น จุดคงที่คือจุดที่อนุพันธ์ของฟังก์ชันเท่ากับ 0

วิถีนิ่ง

โดยการเปรียบเทียบกับจุดที่อยู่กับที่ เราสามารถแนะนำแนวคิดเกี่ยวกับวิถีการเคลื่อนที่แบบคงที่ได้ ให้เราจำไว้ว่าแต่ละวิถีสอดคล้องกับค่าการกระทำบางอย่าง เช่น หมายเลขบางอย่าง จากนั้นอาจมีวิถีโคจรที่สำหรับวิถีที่อยู่ใกล้กับมันโดยมีเงื่อนไขขอบเขตเดียวกันค่าการกระทำที่สอดคล้องกันจะไม่แตกต่างจากการกระทำของวิถีการเคลื่อนที่ที่อยู่นิ่ง วิถีดังกล่าวเรียกว่านิ่ง กล่าวอีกนัยหนึ่ง วิถีโคจรใด ๆ ที่ใกล้กับวิถีนิ่งจะมีค่าการกระทำที่แตกต่างจากการกระทำของวิถีการเคลื่อนที่นี้น้อยมาก

อีกครั้งในภาษาคณิตศาสตร์ "แตกต่างกันเล็กน้อย" มีความหมายที่ชัดเจนดังต่อไปนี้ สมมติว่าเรามีฟังก์ชันที่กำหนดสำหรับฟังก์ชันที่มีเงื่อนไขขอบเขตที่ต้องการ 1) และ 2) เช่น และ . ให้เราสมมติว่าวิถีโคจรอยู่นิ่ง

เราสามารถใช้ฟังก์ชันอื่นใดที่จะรับค่าเป็นศูนย์ที่ส่วนท้ายเช่น = = 0 ลองใช้ตัวแปรซึ่งเราจะทำให้เล็กลงเรื่อยๆ จากฟังก์ชันทั้งสองนี้และตัวแปร เราสามารถเขียนฟังก์ชันที่สามได้ ซึ่งจะเป็นไปตามเงื่อนไขขอบเขตและด้วย เมื่อลดลง วิถีที่สอดคล้องกับฟังก์ชันจะเข้าใกล้วิถีมากขึ้น

ยิ่งไปกว่านั้น สำหรับวิถีการเคลื่อนที่แบบคงที่ที่มีค่าฟังก์ชันน้อยสำหรับวิถีการเคลื่อนที่จะแตกต่างจากค่าฟังก์ชันเพียงเล็กน้อยแม้จะเปรียบเทียบกับ เหล่านั้น.

$$display$$\lim_(ε \to 0) \frac (S(x"(t))-S(x(t)))ε=\lim_(ε \to 0) \frac (S(x( t)+εg(t))-S(x(t)))ε = 0$$แสดง$$

นอกจากนี้ สิ่งนี้ควรเป็นจริงสำหรับวิถีใดๆ ที่ตรงตามเงื่อนไขขอบเขต = = 0

การเปลี่ยนแปลงในการทำงานโดยมีการเปลี่ยนแปลงเล็กน้อยในฟังก์ชัน (แม่นยำยิ่งขึ้นส่วนเชิงเส้นของการเปลี่ยนแปลงในการทำงานซึ่งเป็นสัดส่วนกับการเปลี่ยนแปลงในฟังก์ชัน) เรียกว่าการเปลี่ยนแปลงของฟังก์ชันและแสดงด้วย . ชื่อ "แคลคูลัสของการแปรผัน" มาจากคำว่า "การแปรผัน"

สำหรับวิถีวิถีนิ่ง การเปลี่ยนแปลงของฟังก์ชัน

วิธีการหาฟังก์ชันคงที่ (ไม่เพียงแต่สำหรับหลักการของการกระทำน้อยที่สุดเท่านั้น แต่ยังสำหรับปัญหาอื่นๆ อีกมากมาย) ถูกค้นพบโดยนักคณิตศาสตร์สองคน ได้แก่ ออยเลอร์และลากรองจ์ ปรากฎว่าฟังก์ชันคงที่ซึ่งมีฟังก์ชันแสดงด้วยอินทิกรัลที่คล้ายกับอินทิกรัลกระทำ ต้องเป็นไปตามสมการหนึ่ง ซึ่งปัจจุบันเรียกว่าสมการออยเลอร์-ลากรองจ์

หลักการนิ่ง

สถานการณ์ที่มีการดำเนินการขั้นต่ำสำหรับวิถีจะคล้ายกับสถานการณ์ที่มีขั้นต่ำสำหรับฟังก์ชัน เพื่อให้วิถีโคจรมีผลกระทบน้อยที่สุด จะต้องเป็นวิถีโคจรที่อยู่นิ่ง อย่างไรก็ตาม ไม่ใช่ว่าวิถีการเคลื่อนที่แบบคงที่ทั้งหมดจะเป็นวิถีการเคลื่อนที่ขั้นต่ำ ตัวอย่างเช่น วิถีโคจรที่อยู่นิ่งอาจมีผลกระทบในท้องถิ่นน้อยที่สุด เหล่านั้น. การกระทำของมันจะน้อยกว่าวิถีวิถีใกล้เคียงอื่นๆ อย่างไรก็ตาม ที่ไหนสักแห่งที่ห่างไกล อาจมีวิถีอื่นที่การกระทำจะยิ่งน้อยลงไปอีก

ปรากฎว่าวัตถุจริงอาจไม่จำเป็นต้องเคลื่อนที่ไปตามวิถีโดยออกแรงน้อยที่สุด พวกเขาสามารถเคลื่อนที่ไปตามชุดวิถีพิเศษที่กว้างขึ้น กล่าวคือ วิถีการเคลื่อนที่ที่อยู่นิ่ง เหล่านั้น. วิถีที่แท้จริงของร่างกายจะต้องหยุดนิ่งอยู่เสมอ ดังนั้นหลักการของการกระทำน้อยที่สุดจึงเรียกว่าหลักการของการกระทำที่อยู่นิ่งมากกว่า อย่างไรก็ตาม ตามประเพณีที่กำหนดไว้ มักเรียกกันว่าหลักการของการกระทำน้อยที่สุด ซึ่งไม่เพียงแต่หมายถึงความเรียบง่ายเท่านั้น แต่ยังรวมถึงความคงที่ของวิถีด้วย

ตอนนี้เราสามารถเขียนหลักการของการกระทำที่อยู่กับที่ในภาษาคณิตศาสตร์ได้ตามที่มักจะเขียนในตำราเรียน: .

นี่คือพิกัดทั่วไปเช่น ชุดตัวแปรที่กำหนดตำแหน่งของระบบโดยไม่ซ้ำกัน
- อัตราการเปลี่ยนแปลงพิกัดทั่วไป
- ฟังก์ชันลากรองจ์ ซึ่งขึ้นอยู่กับพิกัดทั่วไป ความเร็ว และอาจรวมถึงเวลาด้วย
- การกระทำที่ขึ้นอยู่กับวิถีเฉพาะของระบบ (เช่น บน )

วิถีที่แท้จริงของระบบนั้นอยู่นิ่งนั่นคือ สำหรับพวกเขาแล้วการกระทำที่หลากหลาย

หากเรากลับมาดูตัวอย่างด้วยลูกบอลและกำแพงยางยืด คำอธิบายสถานการณ์นี้ในตอนนี้จะง่ายมาก ภายใต้เงื่อนไขขอบเขตที่กำหนดว่าลูกบอลจะต้องจบลงที่จุดหนึ่งทั้งเวลาและเวลา มีวิถีวิถีการเคลื่อนที่สองเส้น และลูกบอลสามารถเคลื่อนที่ไปตามวิถีเหล่านี้ได้จริงๆ หากต้องการเลือกวิถีใดวิถีหนึ่งอย่างชัดเจน คุณสามารถกำหนดเงื่อนไขเพิ่มเติมในการเคลื่อนที่ของลูกบอลได้ เช่น บอกว่าลูกบอลควรกระเด็นออกจากกำแพง จากนั้นวิถีจะถูกกำหนดอย่างชัดเจน

ผลที่ตามมาที่น่าทึ่งบางประการเป็นไปตามหลักการของการกระทำที่น้อยที่สุด (คงที่มากขึ้น) ซึ่งเราจะพูดถึงในส่วนต่อไป

พวกเขาเชื่อฟัง ดังนั้นหลักการนี้จึงเป็นหนึ่งในข้อกำหนดสำคัญของฟิสิกส์ยุคใหม่ สมการการเคลื่อนที่ที่ได้จากความช่วยเหลือเรียกว่าสมการออยเลอร์-ลากรองจ์

หลักการแรกของหลักการนี้มอบให้โดย P. Maupertuis ในปีนั้น โดยชี้ให้เห็นถึงธรรมชาติสากลของมันทันที โดยพิจารณาว่าใช้ได้กับทัศนศาสตร์และกลศาสตร์ จากหลักการนี้เขาได้กฎแห่งการสะท้อนและการหักเหของแสง

เรื่องราว

มอเพอร์ทุยส์มาถึงหลักการนี้จากความรู้สึกที่ว่าความสมบูรณ์แบบของจักรวาลจำเป็นต้องมีเศรษฐกิจในธรรมชาติและขัดแย้งกับการใช้พลังงานที่ไร้ประโยชน์ การเคลื่อนไหวตามธรรมชาติจะต้องทำให้มีปริมาณขั้นต่ำที่แน่นอน สิ่งที่เขาต้องทำคือค้นหาคุณค่านี้ซึ่งเขายังคงทำต่อไป มันเป็นผลคูณของระยะเวลา (เวลา) ของการเคลื่อนที่ภายในระบบเป็นสองเท่าของค่า ซึ่งปัจจุบันเราเรียกว่าพลังงานจลน์ของระบบ

ออยเลอร์ (อิน. "Réflexions sur quelques loix générales de la ธรรมชาติ", 1748) ใช้หลักการของการกระทำให้น้อยที่สุด โดยเรียกการกระทำว่า "ความพยายาม" การแสดงออกของมันในสถิตยศาสตร์สอดคล้องกับสิ่งที่เราเรียกว่าพลังงานศักย์ ดังนั้น การดำเนินการน้อยที่สุดในสถิตยศาสตร์จึงเทียบเท่ากับสภาวะพลังงานศักย์ขั้นต่ำสำหรับการกำหนดค่าสมดุล

ในกลศาสตร์คลาสสิก

หลักการของการกระทำน้อยที่สุดทำหน้าที่เป็นพื้นฐานและเป็นพื้นฐานมาตรฐานของสูตรกลศาสตร์ลากรองจ์และแฮมิลตัน

ก่อนอื่นเรามาดูการก่อสร้างดังนี้: กลศาสตร์ลากรองจ์- จากตัวอย่างของระบบทางกายภาพที่มีระดับความเป็นอิสระหนึ่งระดับ ขอให้เราระลึกว่าการกระทำนั้นเป็นการทำงานที่เกี่ยวข้องกับพิกัด (ทั่วไป) (ในกรณีของระดับความอิสระหนึ่งระดับ - หนึ่งพิกัด) นั่นคือมันแสดงออกผ่าน โดยที่แต่ละเวอร์ชันที่เป็นไปได้ของฟังก์ชันจะเชื่อมโยงกับจำนวนหนึ่ง - การกระทำ (ในแง่นี้เราสามารถพูดได้ว่าการกระทำในฐานะฟังก์ชันเป็นกฎที่ช่วยให้ฟังก์ชันใด ๆ ที่กำหนดสามารถคำนวณจำนวนที่กำหนดไว้อย่างดี - เช่นกัน เรียกว่าการกระทำ) การกระทำดูเหมือนว่า:

ลากรองจ์ของระบบอยู่ที่ไหน ขึ้นอยู่กับพิกัดทั่วไป อนุพันธ์อันดับแรกเมื่อเทียบกับเวลา และอาจตรงต่อเวลาอย่างชัดเจนด้วย หากระบบมีระดับความเป็นอิสระมากกว่า ลากรองจ์จะขึ้นอยู่กับพิกัดทั่วไปจำนวนมากขึ้นและอนุพันธ์อันดับแรกเมื่อเทียบกับเวลา ดังนั้นการกระทำจึงเป็นฟังก์ชันสเกลาร์ขึ้นอยู่กับวิถีการเคลื่อนที่ของร่างกาย

ความจริงที่ว่าการกระทำนั้นเป็นสเกลาร์ทำให้ง่ายต่อการเขียนในพิกัดทั่วไปใด ๆ สิ่งสำคัญคือตำแหน่ง (การกำหนดค่า) ของระบบนั้นมีลักษณะที่ชัดเจนอย่างชัดเจน (ตัวอย่างเช่นแทนที่จะเป็นพิกัดคาร์ทีเซียน สิ่งเหล่านี้สามารถเป็นขั้วได้ พิกัด ระยะห่างระหว่างจุดของระบบ มุมหรือฟังก์ชัน ฯลฯ .ง.)

การกระทำสามารถคำนวณได้สำหรับวิถีโคจรที่กำหนดเองโดยสมบูรณ์ ไม่ว่ามันจะ “ดุร้าย” และ “ผิดธรรมชาติ” แค่ไหนก็ตาม อย่างไรก็ตาม ในกลศาสตร์คลาสสิก ในบรรดาวิถีที่เป็นไปได้ทั้งหมด มีเพียงวิถีเดียวเท่านั้นที่ร่างกายจะไปได้จริง หลักการกระทำนิ่งให้คำตอบสำหรับคำถามว่าร่างกายจะเคลื่อนไหวอย่างไร:

ซึ่งหมายความว่าหากให้ลากรองจ์ของระบบ จากนั้นใช้แคลคูลัสของการแปรผัน เราจะสามารถกำหนดได้อย่างชัดเจนว่าวัตถุจะเคลื่อนที่อย่างไรโดยหาสมการการเคลื่อนที่ในขั้นแรก นั่นคือ สมการออยเลอร์-ลากรองจ์ แล้วจึงแก้สมการเหล่านั้น สิ่งนี้ช่วยให้ไม่เพียงแต่สรุปการกำหนดสูตรของกลศาสตร์อย่างจริงจังเท่านั้น แต่ยังสามารถเลือกพิกัดที่สะดวกที่สุดสำหรับปัญหาเฉพาะแต่ละข้อ ไม่จำกัดเพียงพิกัดคาร์ทีเซียน ซึ่งจะมีประโยชน์มากในการรับสมการที่ง่ายและแก้ไขได้ง่ายที่สุด

ฟังก์ชันแฮมิลตันของระบบนี้อยู่ที่ไหน - (ทั่วไป) พิกัด - แรงกระตุ้นผัน (ทั่วไป) ซึ่งรวมกันแสดงลักษณะเฉพาะของสถานะไดนามิกของระบบในแต่ละช่วงเวลาที่กำหนด และแต่ละอันเป็นฟังก์ชันของเวลา จึงแสดงลักษณะวิวัฒนาการ (การเคลื่อนไหว) ของระบบ ในกรณีนี้ เพื่อให้ได้สมการการเคลื่อนที่ของระบบในรูปแบบของสมการบัญญัติของแฮมิลตัน จำเป็นต้องเปลี่ยนแปลงการกระทำที่เขียนในลักษณะนี้อย่างอิสระสำหรับทุกคน และ

ควรสังเกตว่าหากจากเงื่อนไขของปัญหาโดยหลักการแล้วสามารถค้นหากฎการเคลื่อนที่ได้ก็จะเป็นไปโดยอัตโนมัติ ไม่หมายความว่า เป็นไปได้ที่จะสร้างฟังก์ชันที่รับค่าคงที่ระหว่างการเคลื่อนที่จริง ตัวอย่างคือการเคลื่อนที่ร่วมกันของประจุไฟฟ้าและโมโนโพล (ประจุแม่เหล็ก) ในสนามแม่เหล็กไฟฟ้า สมการการเคลื่อนที่ไม่สามารถหาได้จากหลักการของการกระทำที่อยู่นิ่ง ในทำนองเดียวกัน ระบบแฮมิลตันบางระบบมีสมการการเคลื่อนที่ที่ไม่สามารถหาได้จากหลักการนี้

ตัวอย่าง

ตัวอย่างเล็กๆ น้อยๆ ช่วยในการประเมินการใช้หลักการทำงานผ่านสมการออยเลอร์-ลากรองจ์ อนุภาคอิสระ (มวล มและความเร็ว โวลต์) ในปริภูมิแบบยุคลิดเคลื่อนที่เป็นเส้นตรง เมื่อใช้สมการออยเลอร์-ลากรองจ์ สามารถแสดงเป็นพิกัดเชิงขั้วได้ดังนี้ ในกรณีที่ไม่มีศักย์ไฟฟ้า ฟังก์ชันลากรองจ์จะเท่ากับพลังงานจลน์เท่านั้น

ในระบบพิกัดตั้งฉาก

ในพิกัดเชิงขั้ว พลังงานจลน์และฟังก์ชันลากรองจ์จึงกลายเป็น

ส่วนประกอบรัศมีและเชิงมุมของสมการจะกลายเป็นตามลำดับ:

การแก้สมการทั้งสองนี้

ต่อไปนี้เป็นสัญลักษณ์แบบมีเงื่อนไขสำหรับการอินทิเกรตฟังก์ชันหลายฟังก์ชันอย่างไม่สิ้นสุดเหนือวิถีทั้งหมด x(t) และเป็นค่าคงที่ของพลังค์ ให้เราเน้นย้ำว่าตามหลักการแล้ว การกระทำในรูปเลขชี้กำลังจะปรากฏขึ้น (หรือสามารถปรากฏได้) เองเมื่อศึกษาตัวดำเนินการวิวัฒนาการในกลศาสตร์ควอนตัม แต่สำหรับระบบที่มีอะนาล็อกแบบคลาสสิก (ไม่ใช่ควอนตัม) ที่แน่นอน มันจะเท่ากับ การกระทำแบบคลาสสิกตามปกติ

การวิเคราะห์ทางคณิตศาสตร์ของนิพจน์นี้ในขีดจำกัดแบบคลาสสิก - สำหรับขนาดใหญ่เพียงพอ นั่นคือ สำหรับการแกว่งที่เร็วมากของเลขชี้กำลังเชิงจินตภาพ - แสดงให้เห็นว่าวิถีโคจรที่เป็นไปได้ส่วนใหญ่อย่างท่วมท้นในอินทิกรัลนี้จะหักล้างซึ่งกันและกันในขีดจำกัด (อย่างเป็นทางการที่ ) สำหรับเกือบทุกเส้นทาง มีเส้นทางที่การเปลี่ยนเฟสจะตรงกันข้าม และจะรวมกันเป็นศูนย์ เฉพาะวิถีที่การกระทำใกล้กับค่าสูงสุด (สำหรับระบบส่วนใหญ่ - ต่ำสุด) จะไม่ลดลง นี่เป็นข้อเท็จจริงทางคณิตศาสตร์ล้วนๆ จากทฤษฎีฟังก์ชันของตัวแปรเชิงซ้อน ตัวอย่างเช่น วิธีเฟสคงที่จะขึ้นอยู่กับวิธีนั้น

ผลก็คือ อนุภาคจะเคลื่อนที่ไปพร้อมๆ กันตามวิถีโคจรทั้งหมดตามข้อตกลงอย่างสมบูรณ์กับกฎกลศาสตร์ควอนตัม แต่ภายใต้สภาวะปกติ วิถีโคจรที่อยู่ใกล้กับการเคลื่อนที่ (นั่นคือ แบบคลาสสิก) เท่านั้นมีส่วนทำให้เกิดค่าที่สังเกตได้ เนื่องจากกลศาสตร์ควอนตัมแปลงร่างเป็นกลศาสตร์คลาสสิกด้วยขีดจำกัดของพลังงานสูง เราจึงสามารถสรุปได้ว่านี่คือ ที่มาทางกลควอนตัมของหลักการคลาสสิกของความคงที่ของการกระทำ.

ในทฤษฎีสนามควอนตัม

ในทฤษฎีสนามควอนตัม หลักการของการกระทำนิ่งก็ประสบความสำเร็จเช่นกัน ความหนาแน่นลากรองจ์ที่นี่รวมตัวดำเนินการของสนามควอนตัมที่สอดคล้องกันด้วย แม้ว่ามันจะถูกต้องมากกว่าในสาระสำคัญ (ยกเว้นขีด จำกัด แบบคลาสสิกและกึ่งคลาสสิกบางส่วน) ที่จะไม่พูดเกี่ยวกับหลักการของความคงที่ของการกระทำ แต่เกี่ยวกับการบูรณาการไฟน์แมนตามวิถีในการกำหนดค่าหรือพื้นที่เฟสของฟิลด์เหล่านี้โดยใช้ ความหนาแน่นลากรองจ์ที่เพิ่งกล่าวถึง

ลักษณะทั่วไปเพิ่มเติม

ในวงกว้างยิ่งขึ้น การกระทำถูกเข้าใจว่าเป็นฟังก์ชันที่กำหนดการแมปจากพื้นที่การกำหนดค่าไปยังชุดของจำนวนจริง และโดยทั่วไป การกระทำนั้นไม่จำเป็นต้องเป็นอินทิกรัล เนื่องจากการกระทำที่ไม่ใช่ในพื้นที่นั้นเป็นไปได้ตามหลักการ อย่างน้อยที่สุด ในทางทฤษฎี นอกจากนี้ พื้นที่การกำหนดค่าไม่จำเป็นต้องเป็นพื้นที่ฟังก์ชัน เนื่องจากสามารถมีเรขาคณิตที่ไม่สับเปลี่ยนได้

หลักการของการกระทำน้อยที่สุด ซึ่งคิดค้นขึ้นครั้งแรกโดยจาโคบี คล้ายคลึงกับหลักการของแฮมิลตัน แต่มีความทั่วไปน้อยกว่าและพิสูจน์ได้ยากกว่า หลักการนี้ใช้ได้เฉพาะในกรณีที่ฟังก์ชันการเชื่อมต่อและแรงไม่ขึ้นอยู่กับเวลาและเมื่อใด ดังนั้นจึงมีส่วนสำคัญของพลังชีวิต

อินทิกรัลนี้มีรูปแบบ:

หลักการของแฮมิลตันที่ระบุไว้ข้างต้นระบุว่าการแปรผันของอินทิกรัล

จะเท่ากับศูนย์เมื่อมีการเปลี่ยนการเคลื่อนที่ตามจริงไปเป็นการเคลื่อนที่แบบปิดอนันต์อื่นๆ ซึ่งจะถ่ายโอนระบบจากตำแหน่งเริ่มต้นเดียวกันไปยังตำแหน่งสุดท้ายเดียวกันในช่วงเวลาเดียวกัน

ในทางกลับกัน หลักการของจาโคบีเป็นการแสดงออกถึงคุณสมบัติของการเคลื่อนไหวที่ไม่ขึ้นอยู่กับเวลา Jacobi พิจารณาถึงส่วนสำคัญ

การกำหนดการกระทำ หลักการที่เขาตั้งขึ้นระบุว่าความแปรผันของอินทิกรัลนี้เป็นศูนย์เมื่อเราเปรียบเทียบการเคลื่อนที่ที่แท้จริงของระบบกับการเคลื่อนที่ในระยะใกล้อนันต์อื่นๆ ที่นำระบบจากตำแหน่งเริ่มต้นเดียวกันไปยังตำแหน่งสุดท้ายเดียวกัน ในกรณีนี้ เราไม่ได้ใส่ใจกับช่วงเวลาที่ใช้ แต่เราสังเกตสมการ (1) กล่าวคือ สมการกำลังคนที่มีค่าคงที่ h เท่ากันกับการเคลื่อนที่จริง

เงื่อนไขที่จำเป็นสำหรับตัวนำส่วนปลายสุด โดยทั่วไปจะหมายถึงค่าอินทิกรัลขั้นต่ำ (2) จึงเป็นที่มาของชื่อการกระทำที่น้อยที่สุด เงื่อนไขขั้นต่ำดูเหมือนจะเป็นธรรมชาติที่สุด เนื่องจากค่าของ T นั้นเป็นค่าบวก ดังนั้นอินทิกรัล (2) จึงต้องมีค่าต่ำสุดด้วย การมีอยู่ของค่าขั้นต่ำสามารถพิสูจน์ได้อย่างเข้มงวดหากเพียงช่วงเวลาน้อยพอ การพิสูจน์ตำแหน่งนี้สามารถพบได้ในหลักสูตรทฤษฎีพื้นผิวที่มีชื่อเสียงของ Darboux อย่างไรก็ตาม เราจะไม่นำเสนอสิ่งนี้ที่นี่ และจะจำกัดตัวเองให้อยู่ในภาวะนั้นเท่านั้น

432. การพิสูจน์หลักการของการกระทำน้อยที่สุด

ในการคำนวณจริง เราพบปัญหาอย่างหนึ่งที่ไม่มีอยู่ในการพิสูจน์ทฤษฎีบทของแฮมิลตัน ตัวแปร t จะไม่เป็นอิสระจากการเปลี่ยนแปลงอีกต่อไป ดังนั้นการเปลี่ยนแปลงของ q i และ q สัมพันธ์กับการแปรผันของ t ด้วยความสัมพันธ์ที่ซับซ้อนซึ่งตามมาจากสมการ (1) วิธีที่ง่ายที่สุดในการแก้ไขปัญหานี้คือการเปลี่ยนตัวแปรอิสระโดยเลือกตัวแปรที่มีค่าอยู่ระหว่างขีดจำกัดคงที่ซึ่งไม่ขึ้นอยู่กับเวลา ให้ k เป็นตัวแปรอิสระตัวใหม่ โดยถือว่าลิมิตไม่ขึ้นอยู่กับ t เมื่อย้ายระบบ พารามิเตอร์และ t จะเป็นฟังก์ชันของตัวแปรนี้

ให้ตัวอักษรที่มีจำนวนเฉพาะ q แสดงถึงอนุพันธ์ของพารามิเตอร์ q เทียบกับเวลา

เนื่องจากการเชื่อมต่อตามสมมติฐานไม่ได้ขึ้นอยู่กับเวลา พิกัดคาร์ทีเซียน x, y, z จึงเป็นฟังก์ชันของ q ที่ไม่มีเวลา ดังนั้นอนุพันธ์ของพวกมันจะเป็นฟังก์ชันเอกพันธ์เชิงเส้นของ q และ 7 จะเป็นรูปแบบกำลังสองเอกพันธ์ของ q ซึ่งสัมประสิทธิ์เป็นฟังก์ชันของ q เรามี

เพื่อแยกแยะอนุพันธ์ของ q ตามเวลา เราแสดงโดยใช้วงเล็บ (q) อนุพันธ์ของ q ที่นำมาด้วยความเคารพและวางไว้ตามนี้

แล้วเราจะมี

และอินทิกรัล (2) ซึ่งแสดงผ่านตัวแปรอิสระ A ใหม่จะอยู่ในรูปแบบ

อนุพันธ์สามารถกำจัดออกได้โดยใช้ทฤษฎีบทพลังชีวิต แท้จริงแล้วกำลังคนที่สำคัญจะเป็นเช่นนั้น

แทนที่นิพจน์นี้ลงในสูตร เราจะลดอินทิกรัล (2) ลงในแบบฟอร์ม

การนิยามการกระทำแบบอินทิกรัลจึงเกิดขึ้นในรูปแบบสุดท้าย (3) ฟังก์ชันจำนวนเต็มคือรากที่สองของรูปแบบกำลังสองของปริมาณ

ให้เราแสดงให้เห็นว่าสมการเชิงอนุพันธ์ของส่วนปลายของอินทิกรัล (3) ตรงกับสมการลากรองจ์ สมการของเอ็กซ์ตรีมซึ่งขึ้นอยู่กับสูตรทั่วไปของแคลคูลัสของการแปรผันจะเป็น:

ลองคูณสมการด้วย 2 และทำการหาอนุพันธ์บางส่วนโดยคำนึงถึงว่าไม่มี จากนั้นเราจะได้ถ้าเราไม่เขียนดัชนี

นี่คือสมการของเอ็กซ์ตรีมที่แสดงออกมาในรูปของตัวแปรอิสระ ภารกิจตอนนี้คือการกลับไปยังตัวแปรอิสระ

เนื่องจาก Γ เป็นฟังก์ชันเอกพันธ์ของดีกรี 2 ของ และเป็นฟังก์ชันเอกพันธ์ของดีกรี 1 เราจึงได้

ในทางกลับกัน ทฤษฎีบทพลังชีวิตสามารถประยุกต์ใช้กับปัจจัยของอนุพันธ์ในสมการสุดขั้ว ซึ่งนำไปสู่การทดแทนดังที่เราเห็นข้างต้น

จากการทดแทนทั้งหมด สมการของเอ็กซ์ตรีมจึงลดลงเหลืออยู่ในรูปแบบ

เรามาถึงสมการลากรองจ์แล้ว

433. กรณีที่ไม่มีแรงขับเคลื่อน

ในกรณีที่ไม่มีแรงขับเคลื่อนก็มีสมการพลังชีวิตเราก็มี

เงื่อนไขสำหรับอินทิกรัลให้มีค่าน้อยที่สุดในกรณีนี้คือค่าที่สอดคล้องกันของ -10 จะต้องน้อยที่สุด ดังนั้น เมื่อไม่มีแรงผลักดัน ในบรรดาการเคลื่อนไหวทั้งหมดที่พลังชีวิตรักษาค่าที่กำหนดไว้เท่าเดิม การเคลื่อนไหวที่แท้จริงคือการเคลื่อนไหวที่ถ่ายโอนระบบจากตำแหน่งเริ่มต้นไปยังตำแหน่งสุดท้ายในเวลาอันสั้นที่สุด

ถ้าระบบลดลงเหลือจุดหนึ่งที่เคลื่อนที่บนพื้นผิวที่อยู่นิ่ง การเคลื่อนไหวที่เกิดขึ้นจริงในบรรดาการเคลื่อนไหวทั้งหมดบนพื้นผิวซึ่งดำเนินการด้วยความเร็วเท่ากัน จะเป็นการเคลื่อนที่ที่จุดเคลื่อนที่จากตำแหน่งเริ่มต้นไปยังตำแหน่งสุดท้ายใน สั้นที่สุด

ระยะเวลา กล่าวอีกนัยหนึ่ง จุดหนึ่งอธิบายบนพื้นผิวถึงเส้นที่สั้นที่สุดระหว่างตำแหน่งทั้งสองของมัน กล่าวคือ เส้นเนื้อที่

434 หมายเหตุ

หลักการของการกระทำน้อยที่สุดถือว่าระบบมีระดับความอิสระหลายระดับ เนื่องจากหากมีระดับความอิสระเพียงระดับเดียว สมการเดียวก็เพียงพอที่จะกำหนดการเคลื่อนที่ เนื่องจากการเคลื่อนไหวในกรณีนี้สามารถถูกกำหนดโดยสมการของพลังชีวิตได้อย่างสมบูรณ์ ดังนั้นการเคลื่อนไหวที่แท้จริงจะเป็นการเคลื่อนไหวเดียวที่เป็นไปตามสมการนี้ และดังนั้นจึงไม่สามารถเปรียบเทียบกับการเคลื่อนไหวอื่น ๆ ได้

P. Maupertuis) ในปี 1744 ชี้ให้เห็นถึงธรรมชาติสากลของมันทันที และพิจารณาว่ามันใช้ได้กับทัศนศาสตร์และกลไก จากหลักการนี้เขาได้กฎแห่งการสะท้อนและการหักเหของแสง

YouTube สารานุกรม

• 1 / 5

  การวิจัยทางคณิตศาสตร์และการพัฒนาหลักการของแฟร์มาต์ดำเนินการโดย Christiaan Huygens หลังจากนั้นนักวิทยาศาสตร์ที่ใหญ่ที่สุดแห่งศตวรรษที่ 17 ก็อภิปรายหัวข้อนี้อย่างแข็งขัน ไลบ์นิซได้นำแนวคิดพื้นฐานของการกระทำมาสู่ฟิสิกส์ในปี ค.ศ. 1669 ว่า “การกระทำที่เป็นทางการของการเคลื่อนที่นั้นเป็นสัดส่วน ... กับผลคูณของปริมาณสสาร ระยะทางที่วัตถุเคลื่อนที่ และความเร็ว”

  ควบคู่ไปกับการวิเคราะห์พื้นฐานของกลศาสตร์ได้มีการพัฒนาวิธีการแก้ไขปัญหาที่หลากหลาย ไอแซก นิวตันใน “Mathematical Principles of Natural Philosophy” (1687) ได้วางและแก้ไขปัญหาการแปรผันข้อแรก นั่นคือ การค้นหารูปแบบหนึ่งของการปฏิวัติที่เคลื่อนที่ในตัวกลางต้านทานตามแนวแกนของมัน ซึ่งความต้านทานจะประสบน้อยที่สุด ปัญหาการเปลี่ยนแปลงอื่น ๆ ปรากฏขึ้นเกือบจะพร้อมกัน: ปัญหาของ brachistochrone (1696) รูปแบบของสายโซ่ ฯลฯ

  เหตุการณ์แตกหักเกิดขึ้นในปี ค.ศ. 1744 Leonhard Euler ตีพิมพ์ผลงานทั่วไปเรื่องแรกเกี่ยวกับแคลคูลัสของการแปรผัน (“วิธีการค้นหาเส้นโค้งที่มีคุณสมบัติสูงสุดหรือต่ำสุด”) และ Pierre-Louis de Maupertuis ในบทความของเขาเรื่อง “การคืนดีของกฎต่างๆ ของธรรมชาติที่จนบัดนี้ดูเหมือนจะเข้ากันไม่ได้ ” ได้ให้สูตรแรกเกี่ยวกับหลักการของการกระทำน้อยที่สุด: “เส้นทางที่ตามมาด้วยแสงคือเส้นทางที่ปริมาณของการกระทำจะน้อยที่สุด” เขาแสดงให้เห็นถึงการปฏิบัติตามกฎนี้ทั้งในการสะท้อนและการหักเหของแสง เพื่อตอบสนองต่อบทความของมอเพอร์ทุยส์ ออยเลอร์ได้ตีพิมพ์ผลงาน (ในปีเดียวกัน ค.ศ. 1744) เรื่อง "การกำหนดการเคลื่อนที่ของวัตถุที่ถูกโยนในตัวกลางที่ไม่ต้านทานโดยวิธีแม็กซิมาและมินิมา" และในงานนี้เขาได้มอบให้กับมอเพอร์ทุยส์ หลักการ ลักษณะทางกลทั่วไป: “เนื่องจากปรากฏการณ์ทางธรรมชาติทั้งหมดเป็นไปตามกฎบางประการ ถ้ามีกฎสูงสุดหรือต่ำสุด ไม่ต้องสงสัยเลยว่าสำหรับเส้นโค้งที่อธิบายวัตถุที่ถูกโยน เมื่อมีแรงใดๆ กระทำต่อสิ่งเหล่านั้น จะมีคุณสมบัติบางประการของ สูงสุดหรือต่ำสุด ออยเลอร์ได้กำหนดกฎนี้เพิ่มเติม: วิถีการเคลื่อนที่ของวัตถุบรรลุผลขั้นต่ำ ∫ m v d s (\displaystyle \int mv\ ds)- จากนั้นเขาก็ประยุกต์ใช้มัน โดยได้กฎการเคลื่อนที่ในสนามโน้มถ่วงสม่ำเสมอและในกรณีอื่นๆ อีกหลายกรณี

  ในปี 1746 ในงานใหม่ Maupertuis เห็นด้วยกับความเห็นของออยเลอร์ และได้ประกาศหลักการของเขาฉบับทั่วไปที่สุดว่า "เมื่อการเปลี่ยนแปลงบางอย่างเกิดขึ้นในธรรมชาติ ปริมาณของการดำเนินการที่จำเป็นสำหรับการเปลี่ยนแปลงนี้จะเป็นไปได้น้อยที่สุด ปริมาณของการกระทำเป็นผลคูณของมวลของวัตถุด้วยความเร็วและระยะทางที่วัตถุเคลื่อนที่” ในการอภิปรายอย่างกว้างขวางที่ตามมา ออยเลอร์สนับสนุนลำดับความสำคัญของมอเปอร์ทุยส์ และโต้แย้งถึงธรรมชาติที่เป็นสากลของกฎหมายใหม่: “พลศาสตร์และอุทกพลศาสตร์ทั้งหมดสามารถเปิดเผยได้อย่างง่ายดายอย่างน่าอัศจรรย์ผ่านวิธีการสูงสุดและต่ำสุดเพียงอย่างเดียว”

  ขั้นใหม่เริ่มต้นขึ้นในปี 1760-1761 เมื่อโจเซฟ หลุยส์ ลากรองจ์แนะนำแนวคิดที่เข้มงวดของการแปรผันของฟังก์ชัน ทำให้แคลคูลัสของการแปรผันมีรูปแบบที่ทันสมัย ​​และขยายหลักการของการกระทำน้อยที่สุดไปยังระบบกลไกตามอำเภอใจ (นั่นคือ ไม่เพียงแต่ คะแนนวัสดุฟรี) นี่เป็นจุดเริ่มต้นของกลศาสตร์การวิเคราะห์ การวางนัยทั่วไปเพิ่มเติมของหลักการนี้ดำเนินการโดยคาร์ล กุสตาฟ เจค็อบ จาโคบีในปี พ.ศ. 2380 โดยเขาพิจารณาปัญหาในเชิงเรขาคณิต โดยเป็นการค้นหาส่วนปลายสุดของปัญหาการแปรผันในพื้นที่โครงแบบด้วยหน่วยเมตริกที่ไม่ใช่แบบยุคลิด โดยเฉพาะอย่างยิ่ง Jacobi ชี้ให้เห็นว่าในกรณีที่ไม่มีแรงภายนอก วิถีของระบบจะแสดงเส้น geodesic ในพื้นที่การกำหนดค่า

  วิธีการของแฮมิลตันได้รับการพิสูจน์แล้วว่าเป็นสากลและมีประสิทธิภาพสูงในแบบจำลองทางคณิตศาสตร์ของฟิสิกส์ โดยเฉพาะอย่างยิ่งสำหรับกลศาสตร์ควอนตัม พลังการเรียนรู้ของมันได้รับการยืนยันในการสร้างทฤษฎีสัมพัทธภาพทั่วไป เมื่อเดวิด ฮิลเบิร์ตใช้หลักการของแฮมิลตันในการหาสมการสุดท้ายของสนามโน้มถ่วง (1915)

  ในกลศาสตร์คลาสสิก

  หลักการของการกระทำน้อยที่สุดทำหน้าที่เป็นพื้นฐานและเป็นพื้นฐานมาตรฐานของสูตรกลศาสตร์ลากรองจ์และแฮมิลตัน

  ก่อนอื่นเรามาดูการก่อสร้างดังนี้: กลศาสตร์ลากรองจ์- จากตัวอย่างของระบบทางกายภาพที่มีระดับความเป็นอิสระหนึ่งระดับ ให้เราระลึกว่าการกระทำนั้นเป็นการทำงานที่เกี่ยวข้องกับพิกัด (ทั่วไป) (ในกรณีของระดับความอิสระหนึ่งระดับ - หนึ่งพิกัด) นั่นคือมันแสดงออกผ่าน q (t) (\displaystyle q(t))ดังนั้นทุกตัวแปรที่เป็นไปได้ของฟังก์ชัน q (t) (\displaystyle q(t))มีการเปรียบเทียบจำนวนหนึ่ง - การกระทำ (ในแง่นี้เราสามารถพูดได้ว่าการกระทำในฐานะหน้าที่เป็นกฎที่อนุญาตให้มีฟังก์ชันที่กำหนด q (t) (\displaystyle q(t))คำนวณจำนวนที่เฉพาะเจาะจงมาก - เรียกอีกอย่างว่าการกระทำ) การกระทำดูเหมือนว่า:

  S [ q ] = ∫ L (q (t) , q ˙ (t) , t) d t , (\displaystyle S[q]=\int (\mathcal (L))(q(t),(\dot ( ฏ))(t),t)dt,)

  ที่ไหน L (q (t) , q ˙ (t) , t) (\displaystyle (\mathcal (L))(q(t),(\dot (q))(t),t))คือลากรองจ์ของระบบ ขึ้นอยู่กับพิกัดทั่วไป คิว (\displaystyle q), อนุพันธ์ครั้งแรก q ˙ (\displaystyle (\dot (q)))และอาจชัดเจนจากเวลาด้วย เสื้อ (\displaystyle เสื้อ)- หากระบบมีระดับความเป็นอิสระมากขึ้น n (\displaystyle n)ดังนั้นลากรองจ์จะขึ้นอยู่กับพิกัดทั่วไปจำนวนมากกว่า q i (t) , i = 1 , 2 , … , n (\displaystyle q_(i)(t),\ i=1,2,\dots ,n)และอนุพันธ์ครั้งแรก ดังนั้นการกระทำจึงเป็นฟังก์ชันสเกลาร์ขึ้นอยู่กับวิถีการเคลื่อนที่ของร่างกาย

  ความจริงที่ว่าการกระทำนั้นเป็นสเกลาร์ทำให้ง่ายต่อการเขียนในพิกัดทั่วไปใด ๆ สิ่งสำคัญคือตำแหน่ง (การกำหนดค่า) ของระบบนั้นมีลักษณะที่ชัดเจนอย่างชัดเจน (ตัวอย่างเช่นแทนที่จะเป็นพิกัดคาร์ทีเซียน สิ่งเหล่านี้สามารถเป็นขั้วได้ พิกัด ระยะห่างระหว่างจุดของระบบ มุมหรือฟังก์ชัน ฯลฯ .ง.)

  การกระทำสามารถคำนวณได้สำหรับวิถีโคจรตามอำเภอใจโดยสมบูรณ์ q (t) (\displaystyle q(t))ไม่ว่ามันจะ “ดุร้าย” และ “ผิดธรรมชาติ” แค่ไหนก็ตาม อย่างไรก็ตาม ในกลศาสตร์คลาสสิก ในบรรดาวิถีที่เป็นไปได้ทั้งหมด มีเพียงวิถีเดียวเท่านั้นที่ร่างกายจะไปได้จริง หลักการกระทำนิ่งให้คำตอบสำหรับคำถามว่าร่างกายจะเคลื่อนไหวอย่างไร:

  ซึ่งหมายความว่าหากให้ลากรองจ์ของระบบ จากนั้นใช้แคลคูลัสของการแปรผัน เราจะสามารถระบุได้อย่างชัดเจนว่าร่างกายจะเคลื่อนไหวอย่างไร โดยขั้นแรกได้สมการการเคลื่อนที่ - สมการออยเลอร์-ลากรองจ์ แล้วจึงแก้สมการเหล่านั้น สิ่งนี้ช่วยให้ไม่เพียงแต่สรุปการกำหนดสูตรของกลศาสตร์อย่างจริงจังเท่านั้น แต่ยังสามารถเลือกพิกัดที่สะดวกที่สุดสำหรับปัญหาเฉพาะแต่ละข้อ ไม่จำกัดเพียงพิกัดคาร์ทีเซียน ซึ่งจะมีประโยชน์มากในการรับสมการที่ง่ายและแก้ไขได้ง่ายที่สุด

  S [ p , q ] = ∫ (∑ i p i d q i − H (q , p , t) d t) = ∫ (∑ i p i q ˙ i − H (q , p , t)) d t , (\displaystyle S=\int (\ ใหญ่ ()\sum _(i)p_(i)dq_(i)-(\mathcal (H))(q,p,t)dt(\big))=\int (\big ()\sum _( i)p_(i)(\dot (q))_(i)-(\mathcal (H))(q,p,t)(\big))dt,)

  ที่ไหน H (q , p , t) ≡ H (q 1 , q 2 , … , q N , p 1 , p 2 , … , p N , t) (\displaystyle (\mathcal (H))(q,p, t)\equiv (\mathcal (H))(q_(1),q_(2),\dots ,q_(N),p_(1),p_(2),\dots ,p_(N),t) )- ฟังก์ชั่นแฮมิลตันของระบบนี้ q ≡ q 1 , q 2 , … , q N (\displaystyle q\equiv q_(1),q_(2),\dots ,q_(N))- (ทั่วไป) พิกัด p ≡ p 1 , p 2 , … , p N (\displaystyle p\equiv p_(1),p_(2),\dots ,p_(N))- แรงกระตุ้น (ทั่วไป) ที่เกี่ยวข้องกับมัน ซึ่งร่วมกันแสดงลักษณะเฉพาะของสถานะไดนามิกของระบบในแต่ละช่วงเวลาที่กำหนด และแต่ละอันเป็นฟังก์ชันของเวลา ดังนั้น จึงแสดงลักษณะวิวัฒนาการ (การเคลื่อนไหว) ของระบบ ในกรณีนี้ เพื่อให้ได้สมการการเคลื่อนที่ของระบบในรูปแบบของสมการบัญญัติของแฮมิลตัน จำเป็นต้องเปลี่ยนแปลงการกระทำที่เขียนในลักษณะนี้โดยอิสระสำหรับทุกคน q ฉัน (\displaystyle q_(i))และ พี ฉัน (\displaystyle p_(i)).

  ควรสังเกตว่าหากจากเงื่อนไขของปัญหาโดยหลักการแล้วสามารถค้นหากฎการเคลื่อนที่ได้ก็จะเป็นไปโดยอัตโนมัติ ไม่หมายความว่า เป็นไปได้ที่จะสร้างฟังก์ชันที่รับค่าคงที่ระหว่างการเคลื่อนที่จริง ตัวอย่างคือการเคลื่อนที่ร่วมกันของประจุไฟฟ้าและโมโนโพล (ประจุแม่เหล็ก) ในสนามแม่เหล็กไฟฟ้า สมการการเคลื่อนที่ไม่สามารถหาได้จากหลักการของการกระทำที่อยู่นิ่ง ในทำนองเดียวกัน ระบบแฮมิลตันบางระบบมีสมการการเคลื่อนที่ที่ไม่สามารถหาได้จากหลักการนี้

  ตัวอย่าง

  ตัวอย่างเล็กๆ น้อยๆ ช่วยในการประเมินการใช้หลักการทำงานผ่านสมการออยเลอร์-ลากรองจ์ อนุภาคอิสระ (มวล มและความเร็ว โวลต์) ในปริภูมิแบบยุคลิดเคลื่อนที่เป็นเส้นตรง เมื่อใช้สมการออยเลอร์-ลากรองจ์ สามารถแสดงเป็นพิกัดเชิงขั้วได้ดังนี้ ในกรณีที่ไม่มีศักย์ไฟฟ้า ฟังก์ชันลากรองจ์จะเท่ากับพลังงานจลน์เท่านั้น

  1 2 m v 2 = 1 2 m (x ˙ 2 + y ˙ 2) (\displaystyle (\frac (1)(2))mv^(2)=(\frac (1)(2))m\left( (\จุด (x))^(2)+(\จุด (y))^(2)\right)) ψ = ∫ [D x ] อี (i S [ x ] / ℏ) .

  (\displaystyle \psi =\int e^(((iS[x])/(\hbar )))\,.) ที่นี่∫ [ D x ] (\displaystyle \int ) เป็นสัญกรณ์แบบมีเงื่อนไขสำหรับการอินทิเกรตฟังก์ชันหลายฟังก์ชันอย่างไม่สิ้นสุดบนวิถีทั้งหมด x(t) และℏ (\displaystyle \hbar )

  - ค่าคงตัวของพลังค์ ให้เราเน้นย้ำว่าตามหลักการแล้ว การกระทำในรูปเลขชี้กำลังจะปรากฏขึ้น (หรือสามารถปรากฏได้) เองเมื่อศึกษาตัวดำเนินการวิวัฒนาการในกลศาสตร์ควอนตัม แต่สำหรับระบบที่มีอะนาล็อกแบบคลาสสิก (ไม่ใช่ควอนตัม) ที่แน่นอน มันจะเท่ากับ การกระทำแบบคลาสสิกตามปกติ การวิเคราะห์ทางคณิตศาสตร์ของนิพจน์นี้ในขีดจำกัดแบบคลาสสิก - สำหรับขนาดใหญ่เพียงพอ S / ℏ (\รูปแบบการแสดงผล S/\hbar ) กล่าวคือ ด้วยการแกว่งของเลขชี้กำลังจินตภาพอย่างรวดเร็ว - แสดงให้เห็นว่าวิถีโคจรที่เป็นไปได้ส่วนใหญ่อย่างท่วมท้นในอินทิกรัลนี้หักล้างกันในขีดจำกัด (อย่างเป็นทางการที่ S / ℏ → ∞ (\displaystyle S/\hbar \rightarrow \infty )