การปรับให้เรียบแบบเอ็กซ์โปเนนเชียลทำงานอย่างไร วิธีการปรับให้เรียบแบบเอ็กซ์โพเนนเชียล
งานการคาดการณ์สร้างขึ้นจากการเปลี่ยนแปลงของข้อมูลบางส่วนเมื่อเวลาผ่านไป (ยอดขาย อุปสงค์ อุปทาน GDP การปล่อยคาร์บอน ประชากร ...) และคาดการณ์การเปลี่ยนแปลงเหล่านี้ในอนาคต น่าเสียดายที่ข้อมูลในอดีตระบุว่าแนวโน้มอาจถูกละเมิดโดยหลาย ๆ คน สถานการณ์ที่ไม่คาดฝัน. ดังนั้นข้อมูลในอนาคตจึงอาจแตกต่างจากที่เกิดขึ้นในอดีตอย่างมาก นี่คือปัญหาของการพยากรณ์
อย่างไรก็ตาม มีเทคนิค (เรียกว่าการปรับให้เรียบแบบเอกซ์โปเนนเชียล) ที่ช่วยให้ไม่เพียงแต่พยายามทำนายอนาคตเท่านั้น แต่ยังสามารถแสดงความไม่แน่นอนของทุกสิ่งที่เกี่ยวข้องกับการคาดการณ์เป็นตัวเลขได้ด้วย การแสดงตัวเลขของความไม่แน่นอนโดยการสร้างช่วงคาดการณ์เป็นสิ่งที่ประเมินค่าไม่ได้อย่างแท้จริง แต่มักถูกมองข้ามในโลกของการพยากรณ์
ดาวน์โหลดบันทึกในรูปแบบหรือตัวอย่างในรูปแบบ
ข้อมูลเบื้องต้น
สมมติว่าคุณเป็นแฟนของลอร์ดออฟเดอะริงส์และได้ผลิตและจำหน่ายดาบมาสามปีแล้ว (รูปที่ 1) มาแสดงการขายแบบกราฟิกกันเถอะ (รูปที่ 2) ความต้องการเพิ่มขึ้นสองเท่าในสามปี - นี่อาจเป็นเทรนด์หรือไม่? เราจะกลับมาที่แนวคิดนี้ในภายหลัง มียอดเขาและหุบเขาหลายแห่งบนแผนภูมิ ซึ่งอาจเป็นสัญญาณของฤดูกาล โดยเฉพาะช่วงเดือนที่ 12, 24 และ 36 ซึ่งตรงกับเดือนธันวาคม แต่อาจจะเป็นแค่เรื่องบังเอิญ? ลองหากัน

การทำให้เรียบแบบเอ็กซ์โพเนนเชียลอย่างง่าย
วิธีการ การทำให้เรียบแบบทวีคูณขึ้นอยู่กับการทำนายอนาคตจากข้อมูลในอดีต ซึ่งการสังเกตที่ใหม่กว่ามีน้ำหนักมากกว่าการที่เก่ากว่า การถ่วงน้ำหนักดังกล่าวเป็นไปได้เนื่องจากค่าคงที่การปรับให้เรียบ วิธีการปรับให้เรียบแบบเอกซ์โปเนนเชียลวิธีแรกที่เราจะลองเรียกว่าการปรับให้เรียบแบบเอกซ์โปเนนเชียลอย่างง่าย (PES) การทำให้เรียบแบบทวีคูณ, ส.). ใช้ค่าคงที่การปรับให้เรียบเพียงค่าเดียว
การทำให้เรียบแบบเอกซ์โพเนนเชียลอย่างง่ายจะถือว่าอนุกรมเวลาข้อมูลของคุณมีสององค์ประกอบ: ระดับ (หรือค่าเฉลี่ย) และข้อผิดพลาดรอบค่านั้น ไม่มีแนวโน้มหรือความผันผวนตามฤดูกาล - มีเพียงระดับที่อุปสงค์ผันผวน ล้อมรอบด้วยข้อผิดพลาดเล็กน้อยที่นี่และที่นั่น ด้วยการให้ความสำคัญกับข้อสังเกตที่ใหม่กว่า TEC อาจทำให้เกิดการเปลี่ยนแปลงในระดับนี้ ในภาษาของสูตร
ความต้องการ ณ เวลา t = ระดับ + ข้อผิดพลาดแบบสุ่มใกล้ระดับที่เวลา t
แล้วคุณจะหาค่าโดยประมาณของระดับได้อย่างไร? หากเรายอมรับค่าเวลาทั้งหมดว่ามีค่าเท่ากัน เราก็ควรคำนวณค่าเฉลี่ยของมัน อย่างไรก็ตาม นี่เป็นความคิดที่ไม่ดี ควรให้น้ำหนักกับข้อสังเกตล่าสุดมากกว่านี้
มาสร้างระดับกัน คำนวณพื้นฐานสำหรับปีแรก:
ระดับ 0 = ความต้องการเฉลี่ยสำหรับปีแรก (เดือนที่ 1-12)
สำหรับความต้องการดาบ มันคือ 163 เราใช้ระดับ 0 (163) เป็นการคาดการณ์ความต้องการสำหรับเดือนที่ 1 ความต้องการในเดือนที่ 1 คือ 165 ซึ่งเป็นดาบ 2 เล่มที่อยู่เหนือระดับ 0 ควรปรับปรุงการประมาณค่าพื้นฐาน สมการเรียบเลขชี้กำลังอย่างง่าย:
ระดับ 1 = ระดับ 0 + ไม่กี่เปอร์เซ็นต์ × (อุปสงค์ 1 - ระดับ 0)
ระดับ 2 = ระดับ 1 + ไม่กี่เปอร์เซ็นต์ × (อุปสงค์ 2 - ระดับ 1)
เป็นต้น "ไม่กี่เปอร์เซ็นต์" เรียกว่าค่าคงที่การปรับให้เรียบ และเขียนแทนด้วยอัลฟา สามารถเป็นตัวเลขใดก็ได้ตั้งแต่ 0 ถึง 100% (0 ถึง 1) คุณจะได้เรียนรู้วิธีเลือกค่าอัลฟ่าในภายหลัง ใน กรณีทั่วไปค่าสำหรับจุดต่าง ๆ ในเวลา:
ระดับงวดปัจจุบัน = ระดับงวดก่อนหน้า +
อัลฟ่า × (อุปสงค์งวดปัจจุบัน - ระดับงวดก่อนหน้า)
ความต้องการในอนาคตเท่ากับระดับที่คำนวณล่าสุด (รูปที่ 3) เนื่องจากคุณไม่รู้ว่าอัลฟ่าคืออะไร ให้ตั้งค่าเซลล์ C2 เป็น 0.5 เพื่อเริ่มต้น หลังจากสร้างโมเดลแล้ว ให้หาอัลฟาที่ทำให้ผลรวมของกำลังสองของข้อผิดพลาดคือ E2 (หรือ ส่วนเบี่ยงเบนมาตรฐาน– F2) น้อยที่สุด เมื่อต้องการทำเช่นนี้ ให้เรียกใช้ตัวเลือก หาทางออก. ในการทำเช่นนี้ให้ไปที่เมนู ข้อมูล –> หาทางออกและตั้งค่าในหน้าต่าง ตัวเลือกการค้นหาโซลูชันค่าที่ต้องการ (รูปที่ 4) หากต้องการแสดงผลการคาดการณ์บนแผนภูมิ ก่อนอื่นให้เลือกช่วง A6:B41 และสร้างแผนภูมิเส้นอย่างง่าย จากนั้นคลิกขวาที่ไดอะแกรม เลือกตัวเลือก เลือกข้อมูลในหน้าต่างที่เปิดขึ้น ให้สร้างแถวที่สองและแทรกการคาดคะเนจากช่วง A42:B53 ลงไป (รูปที่ 5)



บางทีคุณอาจมีแนวโน้ม
เพื่อทดสอบสมมติฐานนี้ก็เพียงพอแล้ว การถดถอยเชิงเส้นภายใต้ข้อมูลอุปสงค์และทำการทดสอบค่า t ในการเพิ่มขึ้นของเส้นแนวโน้มนี้ (ดังใน ) หากความชันของเส้นไม่เป็นศูนย์และมีนัยสำคัญทางสถิติ (ในการทดสอบของนักเรียน ค่า รน้อยกว่า 0.05) ข้อมูลมีแนวโน้ม (ภาพที่ 6)

เราใช้ฟังก์ชัน LINEST ซึ่งจะคืนค่า 10 สถิติเชิงพรรณนา(หากคุณไม่เคยใช้ฟังก์ชันนี้มาก่อน ฉันแนะนำ) และฟังก์ชัน INDEX ซึ่งช่วยให้คุณ "ดึง" เฉพาะสถิติที่จำเป็นสามรายการเท่านั้น ไม่ใช่ทั้งชุด ปรากฎว่าความชันคือ 2.54 และมีความสำคัญเนื่องจากการทดสอบของนักเรียนแสดงให้เห็นว่า 0.000000012 นั้นน้อยกว่า 0.05 อย่างมีนัยสำคัญ ดังนั้นจึงมีแนวโน้มและยังคงรวมไว้ในการคาดการณ์
Exponential Holt ปรับให้เรียบด้วยการแก้ไขแนวโน้ม
มักถูกเรียกว่าการปรับให้เรียบแบบเอกซ์โปเนนเชียลสองเท่าเนื่องจากมีพารามิเตอร์การปรับให้เรียบสองตัวคืออัลฟ่าแทนที่จะเป็นหนึ่งตัว หากลำดับเวลามีแนวโน้มเชิงเส้น ดังนั้น:
ความต้องการเมื่อเวลาผ่านไป t = ระดับ + t × แนวโน้ม + ค่าเบี่ยงเบนแบบสุ่มระดับ ณ เวลา t
Holt Exponential Smoothing พร้อมการแก้ไขแนวโน้มมีสมการใหม่สองสมการ สมการหนึ่งสำหรับระดับในขณะที่เคลื่อนไปข้างหน้าในเวลา และอีกสมการสำหรับแนวโน้ม สมการระดับประกอบด้วยอัลฟาพารามิเตอร์การปรับให้เรียบ และสมการแนวโน้มประกอบด้วยแกมมา นี่คือลักษณะของสมการระดับใหม่:
ระดับ 1 = ระดับ 0 + แนวโน้ม 0 + อัลฟา × (อุปสงค์ 1 - (ระดับ 0 + แนวโน้ม 0))
โปรดทราบว่า ระดับ 0 + แนวโน้ม 0เป็นเพียงการพยากรณ์แบบขั้นตอนเดียวจากค่าเดิมเป็นเดือนที่ 1 ดังนั้น ความต้องการ 1 – (ระดับ 0 + แนวโน้ม 0)เป็นการเบี่ยงเบนขั้นเดียว ดังนั้นสมการการประมาณระดับพื้นฐานจะเป็นดังนี้:
ระดับของงวดปัจจุบัน = ระดับของงวดก่อนหน้า + แนวโน้มของงวดก่อนหน้า + อัลฟ่า × (อุปสงค์ของงวดปัจจุบัน - (ระดับของงวดก่อนหน้า) + แนวโน้มของงวดก่อนหน้า))
สมการอัพเดทเทรนด์:
เทรนด์งวดปัจจุบัน = เทรนด์งวดก่อนหน้า + แกมมา × อัลฟา × (อุปสงค์งวดปัจจุบัน – (ระดับงวดก่อนหน้า) + เทรนด์งวดก่อนหน้า))
การปรับโฮลท์ให้เรียบใน Excel นั้นคล้ายกับการปรับให้เรียบอย่างง่าย (รูปที่ 7) และตามที่กล่าวไว้ข้างต้น เป้าหมายคือการหาค่าสัมประสิทธิ์สองตัวในขณะที่ลดผลรวมของข้อผิดพลาดกำลังสองให้น้อยที่สุด (รูปที่ 8) ในการรับระดับเดิมและค่าแนวโน้ม (ในเซลล์ C5 และ D5 ในรูปที่ 7) ให้สร้างแผนภูมิสำหรับการขาย 18 เดือนแรกและเพิ่มเส้นแนวโน้มพร้อมสมการ ป้อนค่าแนวโน้มเริ่มต้นที่ 0.8369 และระดับเริ่มต้นที่ 155.88 ลงในเซลล์ C5 และ D5 ข้อมูลพยากรณ์สามารถแสดงเป็นกราฟิกได้ (รูปที่ 9)

ข้าว. 7. Exponential Holt ปรับให้เรียบด้วยการแก้ไขแนวโน้ม หากต้องการขยายภาพ ให้คลิกขวาที่ภาพแล้วเลือก เปิดรูปภาพในแท็บใหม่


ค้นหารูปแบบในข้อมูล
มีวิธีทดสอบความแข็งแกร่งของโมเดลการทำนาย - เพื่อเปรียบเทียบข้อผิดพลาดกับตัวเองโดยเลื่อนทีละขั้นตอน (หรือหลายขั้นตอน) หากความเบี่ยงเบนเป็นแบบสุ่ม ก็จะไม่สามารถปรับปรุงโมเดลได้ อย่างไรก็ตาม อาจมีปัจจัยตามฤดูกาลในข้อมูลความต้องการ แนวคิดของข้อผิดพลาดที่สัมพันธ์กับเวอร์ชันของตัวเองในช่วงเวลาต่างๆ เรียกว่า ความสัมพันธ์อัตโนมัติ (สำหรับข้อมูลเพิ่มเติมเกี่ยวกับความสัมพันธ์อัตโนมัติ โปรดดูที่ ) ในการคำนวณความสัมพันธ์อัตโนมัติ ให้เริ่มด้วยข้อมูลข้อผิดพลาดของการคาดการณ์สำหรับแต่ละช่วงเวลา (ย้ายคอลัมน์ F ในรูปที่ 7 ไปยังคอลัมน์ B ในรูปที่ 10) กำหนดต่อไป ข้อผิดพลาดเฉลี่ยการคาดการณ์ (รูปที่ 10 เซลล์ B39 สูตรในเซลล์: =AVERAGE(B3:B38)) ในคอลัมน์ C ให้คำนวณค่าเบี่ยงเบนของข้อผิดพลาดในการคาดการณ์จากค่าเฉลี่ย สูตรในเซลล์ C3: =B3-B$39 ถัดไป เลื่อนคอลัมน์ C ไปทางขวาและเลื่อนแถวลงตามลำดับ สูตรในเซลล์ D39: =SUMPRODUCT($C3:$C38,D3:D38), D41: =D39/$C39, D42: =2/SQRT(36), D43: =-2/SQRT(36)

“การเคลื่อนที่แบบซิงโครนัส” กับคอลัมน์ C หมายถึงอะไรสำหรับคอลัมน์ D:O ตัวอย่างเช่น ถ้าคอลัมน์ C และ D เป็นซิงโครนัส ดังนั้นจำนวนที่เป็นลบในคอลัมน์หนึ่งจะต้องเป็นลบในอีกคอลัมน์หนึ่ง เป็นบวกในคอลัมน์หนึ่ง , คิดบวกในเพื่อน. ซึ่งหมายความว่าผลรวมของผลิตภัณฑ์ของทั้งสองคอลัมน์จะมีนัยสำคัญ (ผลต่างสะสม) หรือ ซึ่งเหมือนกัน ยิ่งค่าในช่วง D41:O41 ถึงศูนย์ยิ่งใกล้ ความสัมพันธ์ของคอลัมน์ (ตามลำดับจาก D ถึง O) กับคอลัมน์ C ก็จะยิ่งต่ำลง (รูปที่ 11)

ความสัมพันธ์อัตโนมัติหนึ่งรายการอยู่เหนือค่าวิกฤต ข้อผิดพลาดในการเลื่อนปีมีความสัมพันธ์กับตัวมันเอง ซึ่งหมายถึงรอบฤดูกาล 12 เดือน และไม่น่าแปลกใจเลย หากคุณดูที่กราฟอุปสงค์ (รูปที่ 2) ปรากฎว่ามีความต้องการสูงสุดทุกวันคริสต์มาสและลดลงในเดือนเมษายนถึงพฤษภาคม พิจารณาเทคนิคการพยากรณ์ที่คำนึงถึงฤดูกาล
การทำให้เรียบ Holt-Winters แบบเลขชี้กำลังแบบทวีคูณ
วิธีการนี้เรียกว่าการคูณ (จากการคูณ - การคูณ) เพราะมันใช้การคูณเพื่อพิจารณาฤดูกาล:
ความต้องการ ณ เวลา t = (ระดับ + t × แนวโน้ม) × การปรับตามฤดูกาล ณ เวลา t × การปรับที่ไม่สม่ำเสมอใดๆ ที่เหลืออยู่ซึ่งเราไม่สามารถอธิบายได้
การปรับให้เรียบของ Holt-Winters เรียกอีกอย่างว่าการปรับให้เรียบแบบทวีคูณเอกซ์โปเนนเชียล เนื่องจากมีพารามิเตอร์การปรับให้เรียบสามค่า (อัลฟา แกมมา และเดลต้า ปัจจัยตามฤดูกาล) ตัวอย่างเช่น หากมีรอบฤดูกาล 12 เดือน:
การคาดการณ์รายเดือน 39 = (ระดับ 36 + 3 × แนวโน้ม 36) x ฤดูกาล 27
เมื่อวิเคราะห์ข้อมูล จำเป็นต้องค้นหาว่าแนวโน้มในชุดข้อมูลคืออะไรและอะไรคือฤดูกาล ในการคำนวณด้วยวิธี Holt-Winters คุณต้อง:
- ข้อมูลย้อนหลังที่ราบรื่นโดยใช้วิธีค่าเฉลี่ยเคลื่อนที่
- เปรียบเทียบอนุกรมเวลาเวอร์ชันที่ราบรื่นกับต้นฉบับเพื่อรับค่าประมาณของฤดูกาลอย่างคร่าวๆ
- รับข้อมูลใหม่โดยไม่มีองค์ประกอบตามฤดูกาล
- ค้นหาการประมาณระดับและแนวโน้มตามข้อมูลใหม่นี้
เริ่มด้วยข้อมูลดั้งเดิม (คอลัมน์ A และ B ในรูปที่ 12) และเพิ่มคอลัมน์ C ด้วยค่าที่ปรับให้เรียบตามค่าเฉลี่ยเคลื่อนที่ เนื่องจากฤดูกาลมีรอบ 12 เดือน คุณจึงควรใช้ค่าเฉลี่ย 12 เดือน มีปัญหาเล็กน้อยกับค่าเฉลี่ยนี้ 12 เป็นเลขคู่ หากคุณปรับความต้องการให้เรียบในเดือนที่ 7 ควรพิจารณาความต้องการเฉลี่ยจากเดือนที่ 1 ถึง 12 หรือตั้งแต่ 2 ถึง 13 เพื่อจัดการกับความยากลำบากนี้ เราจำเป็นต้องทำให้ความต้องการราบรื่นขึ้นโดยใช้ "ค่าเฉลี่ยเคลื่อนที่ 2x12" นั่นคือ ใช้ครึ่งหนึ่งของสองค่าเฉลี่ยจากเดือนที่ 1 ถึง 12 และ 2 ถึง 13 สูตรในเซลล์ C8 คือ: =(AVERAGE(B3:B14)+AVERAGE(B2:B13))/2

ไม่สามารถรับข้อมูลที่ราบรื่นสำหรับเดือนที่ 1–6 และ 31–36 เนื่องจากมีระยะเวลาก่อนหน้าและถัดไปไม่เพียงพอ เพื่อความชัดเจน ข้อมูลต้นฉบับและข้อมูลที่ปรับให้เรียบสามารถแสดงในไดอะแกรม (รูปที่ 13)

ตอนนี้ในคอลัมน์ D ให้หารค่าเดิมด้วยค่าที่ปรับให้เรียบเพื่อให้ได้ค่าประมาณของการปรับตามฤดูกาล (คอลัมน์ D ในรูปที่ 12) สูตรในเซลล์ D8: =B8/C8 บันทึกการเพิ่มขึ้น 20% เหนืออุปสงค์ปกติในเดือน 12 และ 24 (ธันวาคม) ในขณะที่มีการลดลงในฤดูใบไม้ผลิ เทคนิคการทำให้เรียบนี้ให้คุณสองคน การประมาณจุดในแต่ละเดือน (รวม 24 เดือน) คอลัมน์ E คือค่าเฉลี่ยของตัวประกอบสองตัวนี้ สูตรในเซลล์ E1 คือ: =AVERAGE(D14,D26) เพื่อความชัดเจน ระดับความผันผวนตามฤดูกาลสามารถแสดงเป็นกราฟิกได้ (รูปที่ 14)

ตอนนี้คุณสามารถรับการปรับข้อมูลสำหรับ ความผันผวนตามฤดูกาล. สูตรในเซลล์ G1: =B2/E2 สร้างกราฟจากข้อมูลในคอลัมน์ G เติมเส้นแนวโน้ม แสดงสมการแนวโน้มบนแผนภูมิ (รูปที่ 15) และใช้ค่าสัมประสิทธิ์ในการคำนวณในภายหลัง

รูปร่าง ใบใหม่ดังแสดงในรูป 16. แทนค่าในช่วง E5:E16 จากรูปที่ 12 พื้นที่ E2:E13 นำค่า C16 และ D16 จากสมการของเส้นแนวโน้มในรูปที่ 15. ตั้งค่าของค่าคงที่การปรับให้เรียบเริ่มต้นที่ประมาณ 0.5 ขยายค่าในแถว 17 ในช่วงเดือนที่ 1 ถึง 36 เรียกใช้ หาทางออกเพื่อเพิ่มค่าสัมประสิทธิ์การปรับให้เรียบ (รูปที่ 18) สูตรในเซลล์ B53: =(C$52+(A53-A$52)*D$52)*E41


ในการคาดการณ์คุณต้องตรวจสอบความสัมพันธ์อัตโนมัติ (รูปที่ 18) เนื่องจากค่าทั้งหมดอยู่ระหว่างขอบเขตบนและล่าง คุณเข้าใจว่าโมเดลทำงานได้ดีในการทำความเข้าใจโครงสร้างของค่าอุปสงค์

สร้างช่วงความเชื่อมั่นสำหรับการคาดการณ์
ดังนั้นเราจึงมีการคาดการณ์ที่ค่อนข้างได้ผล คุณจะกำหนดขอบเขตบนและล่างที่สามารถใช้เดาได้อย่างสมจริงได้อย่างไร การจำลองแบบมอนติคาร์โลที่คุณเคยพบมาแล้ว (ดูเพิ่มเติม ) จะช่วยคุณได้ในเรื่องนี้ ประเด็นคือการสร้างสถานการณ์ในอนาคตของพฤติกรรมอุปสงค์และกำหนดกลุ่มที่ 95% ตกอยู่ในนั้น
นำออกจากแผ่น การคาดการณ์ของ Excelจากเซลล์ B53:B64 (ดูรูปที่ 17) คุณจะเขียนความต้องการที่นั่นตามการจำลอง หลังสามารถสร้างได้โดยใช้ฟังก์ชัน NORMINV สำหรับเดือนต่อๆ ไป คุณเพียงแค่ต้องระบุค่าเฉลี่ย (0) การแจกแจงมาตรฐาน (10.37 จากเซลล์ $H$2) และ หมายเลขสุ่มจาก 0 ถึง 1 ฟังก์ชันจะส่งกลับค่าเบี่ยงเบนด้วยความน่าจะเป็นที่สอดคล้องกับเส้นโค้งรูประฆัง ใส่การจำลองข้อผิดพลาดแบบขั้นตอนเดียวในเซลล์ G53: =NORMINV(RAND();0;H$2) การขยายสูตรนี้ลงไปที่ G64 ช่วยให้คุณจำลองข้อผิดพลาดในการคาดการณ์สำหรับการพยากรณ์แบบขั้นตอนเดียว 12 เดือน (รูปที่ 19) ค่าการจำลองของคุณจะแตกต่างจากที่แสดงในรูป (นั่นเป็นเหตุผลว่าทำไมจึงเป็นการจำลอง!)

ด้วย Forecast Error คุณมีทุกสิ่งที่จำเป็นในการอัปเดตระดับ แนวโน้ม และปัจจัยตามฤดูกาล ดังนั้น เลือกเซลล์ C52:F52 และยืดเซลล์ไปที่แถว 64 ดังนั้น คุณจึงมีข้อผิดพลาดในการคาดการณ์จำลองและการคาดการณ์เอง จากสิ่งที่ตรงกันข้ามเป็นไปได้ที่จะทำนายค่าความต้องการ ใส่สูตรลงในเซลล์ B53: =F53+G53 และขยายเป็น B64 (รูปที่ 20 ช่วง B53:F64) ตอนนี้คุณสามารถกดปุ่ม F9 ทุกครั้งที่อัปเดตการคาดการณ์ วางผลลัพธ์ของการจำลอง 1,000 รายการในเซลล์ A71:L1070 แต่ละครั้งจะย้ายค่าจากช่วง B53:B64 ไปยังช่วง A71:L71, A72:L72, ... A1070:L1070 ถ้ามันรบกวนคุณ เขียนโค้ด VBA

ตอนนี้คุณมี 1,000 สถานการณ์สำหรับแต่ละเดือน และคุณสามารถใช้ฟังก์ชัน PERCENTILE เพื่อรับขอบเขตบนและล่างในช่วงกลางของช่วงความเชื่อมั่น 95% ในเซลล์ A66 สูตรคือ: =PERCENTILE(A71:A1070,0.975) และในเซลล์ A67: =PERCENTILE(A71:A1070,0.025)
ตามปกติ เพื่อความชัดเจนสามารถนำเสนอข้อมูลใน รูปแบบกราฟิก(รูปที่ 21)

มีจุดที่น่าสนใจสองจุดบนแผนภูมิ:
- ขอบของข้อผิดพลาดเพิ่มขึ้นตามเวลา มันสมเหตุสมผล ความไม่แน่นอนสะสมทุกเดือน
- ในทำนองเดียวกัน ข้อผิดพลาดจะเพิ่มขึ้นในชิ้นส่วนที่ตกลงมาในช่วงเวลาที่มีความต้องการเพิ่มขึ้นตามฤดูกาล เมื่อตกรุ่นต่อมา ข้อผิดพลาดจะลดขนาดลง
อ้างอิงเนื้อหาจากหนังสือของ John Foreman – อ.: Alpina Publisher, 2016. – ส. 329–381
ค่าเฉลี่ยเคลื่อนที่ช่วยให้คุณปรับข้อมูลให้ราบรื่นได้อย่างสมบูรณ์แบบ แต่ข้อเสียเปรียบหลักคือแต่ละค่าในแหล่งข้อมูลมีน้ำหนักเท่ากัน ตัวอย่างเช่น สำหรับค่าเฉลี่ยเคลื่อนที่ที่ใช้ระยะเวลาหกสัปดาห์ แต่ละค่าสำหรับแต่ละสัปดาห์จะได้รับ 1/6 ของน้ำหนัก สำหรับสถิติที่รวบรวมบางค่า ค่าล่าสุดจะมีน้ำหนักมากกว่า ดังนั้นการปรับให้เรียบแบบเอกซ์โปเนนเชียลจึงถูกนำมาใช้เพื่อให้ข้อมูลล่าสุดมีน้ำหนักมากขึ้น ดังนั้นปัญหาทางสถิตินี้จึงได้รับการแก้ไข
สูตรการคำนวณวิธีการปรับให้เรียบแบบเอ็กซ์โพเนนเชียลใน Excel
รูปภาพด้านล่างแสดงรายงานความต้องการสำหรับผลิตภัณฑ์เฉพาะเป็นเวลา 26 สัปดาห์ คอลัมน์ความต้องการประกอบด้วยข้อมูลเกี่ยวกับปริมาณสินค้าที่ขาย ในคอลัมน์ "การคาดการณ์" - สูตร:
คอลัมน์ "ค่าเฉลี่ยเคลื่อนที่" กำหนดความต้องการที่คาดการณ์ไว้ ซึ่งคำนวณโดยใช้การคำนวณตามปกติของค่าเฉลี่ยเคลื่อนที่โดยมีระยะเวลา 6 สัปดาห์:

ในคอลัมน์สุดท้าย "การคาดการณ์" ด้วยสูตรที่อธิบายไว้ข้างต้น วิธีการปรับข้อมูลให้เรียบแบบเอกซ์โปเนนเชียลถูกนำมาใช้ซึ่งค่าของสัปดาห์ที่ผ่านมามีน้ำหนักมากกว่าค่าก่อนหน้า
ค่าสัมประสิทธิ์ "Alpha:" ถูกป้อนในเซลล์ G1 ซึ่งหมายถึงน้ำหนักของการกำหนดให้กับข้อมูลล่าสุด ใน ตัวอย่างนี้มันมีมูลค่า 30% น้ำหนักที่เหลืออีก 70% จะกระจายไปยังข้อมูลที่เหลือ นั่นคือค่าที่สองในแง่ของความเกี่ยวข้อง (จากขวาไปซ้าย) มีน้ำหนักเท่ากับ 30% ของน้ำหนัก 70% ที่เหลือ - นี่คือ 21% ค่าที่สามมีน้ำหนักเท่ากับ 30% ของส่วนที่เหลือ จาก 70% ของน้ำหนัก - 14.7% และอื่น ๆ .
พล็อตการปรับให้เรียบแบบเอกซ์โปเนนเชียล
รูปภาพด้านล่างแสดงกราฟอุปสงค์ ค่าเฉลี่ยเคลื่อนที่ และการคาดการณ์การปรับให้เรียบแบบเอ็กซ์โพเนนเชียล ซึ่งสร้างขึ้นจากค่าดั้งเดิม:

โปรดทราบว่าการคาดการณ์การปรับให้เรียบแบบเอ็กซ์โพเนนเชียลนั้นตอบสนองต่อการเปลี่ยนแปลงของอุปสงค์มากกว่าเส้นค่าเฉลี่ยเคลื่อนที่
ข้อมูลสำหรับสัปดาห์ก่อนหน้าที่ต่อเนื่องกันจะคูณด้วยปัจจัยอัลฟา และผลลัพธ์จะถูกเพิ่มไปยังเปอร์เซ็นต์น้ำหนักที่เหลือคูณด้วยค่าที่คาดการณ์ไว้ก่อนหน้า
9 5. วิธีการปรับให้เรียบแบบเอ็กซ์โปเนนเชียล การเลือกค่าคงที่การปรับให้เรียบ
เมื่อใช้วิธี กำลังสองน้อยที่สุดเพื่อกำหนดแนวโน้มการทำนาย (แนวโน้ม) จะสันนิษฐานล่วงหน้าว่าข้อมูลย้อนหลังทั้งหมด (การสังเกต) มีเนื้อหาข้อมูลเดียวกัน เห็นได้ชัดว่าการพิจารณาขั้นตอนการลดราคาจะมีเหตุผลมากกว่า ข้อมูลพื้นฐานนั่นคือความไม่เท่าเทียมกันของข้อมูลเหล่านี้สำหรับการพัฒนาการคาดการณ์ สิ่งนี้ทำได้ในวิธีการปรับให้เรียบแบบเอ็กซ์โปเนนเชียลโดยการให้ค่าการสังเกตล่าสุดของอนุกรมเวลา (นั่นคือ ค่าที่อยู่ก่อนระยะเวลารอคอยการคาดการณ์ทันที) มี "น้ำหนัก" ที่มีนัยสำคัญมากกว่าเมื่อเทียบกับการสังเกตครั้งแรก ข้อดีของวิธีการทำให้เรียบแบบเอกซ์โพเนนเชียลควรรวมถึงความเรียบง่ายของการดำเนินการคำนวณและความยืดหยุ่นในการอธิบายการเปลี่ยนแปลงของกระบวนการต่างๆ วิธีการนี้พบแอปพลิเคชั่นที่ดีที่สุดสำหรับการดำเนินการคาดการณ์ระยะกลาง
5.1. สาระสำคัญของวิธีการทำให้เรียบแบบเอ็กซ์โปเนนเชียล
สาระสำคัญของวิธีการคือว่า ซีรีย์ไดนามิกถูกปรับให้เรียบด้วย "ค่าเฉลี่ยเคลื่อนที่" ที่ถ่วงน้ำหนัก ซึ่งน้ำหนักเป็นไปตามกฎเลขชี้กำลัง กล่าวอีกนัยหนึ่ง ยิ่งห่างจากจุดสิ้นสุดของอนุกรมเวลาเป็นจุดที่คำนวณค่าเฉลี่ยเคลื่อนที่แบบถ่วงน้ำหนัก ยิ่ง "ต้องมีส่วนร่วม" ในการพัฒนาการคาดการณ์น้อยลงเท่านั้น
ให้ชุดไดนามิกดั้งเดิมประกอบด้วยระดับ (ส่วนประกอบชุด) y t , t = 1 , 2 ,...,n สำหรับแต่ละระดับต่อเนื่องของซีรีส์นี้
(ม อนุกรมไดนามิกที่มีขั้นตอนเท่ากับหนึ่ง ถ้า m เป็นเลขคี่ และควรใช้ระดับเป็นเลขคี่ เนื่องจากในกรณีนี้ ค่าระดับที่คำนวณได้จะอยู่ตรงกลางของช่วงการปรับให้เรียบ และง่ายต่อการแทนที่ค่าจริงด้วยค่านั้น ดังนั้น สามารถเขียนสูตรต่อไปนี้เพื่อกำหนดค่าเฉลี่ยเคลื่อนที่: t+ ξ t+ ξ ∑ ฉัน ∑ ฉัน ผม= t−ξ ผม= t−ξ 2ξ + 1 โดยที่ y t คือค่าของค่าเฉลี่ยเคลื่อนที่สำหรับโมเมนต์ t (t = 1 , 2 ,...,n ); y i คือค่าจริงของระดับในขณะ i ; i คือเลขลำดับของระดับในช่วงการปรับให้เรียบ ค่าของ ξ ถูกกำหนดจากระยะเวลาของช่วงการปรับให้เรียบ เพราะว่า ม = 2 ξ +1 สำหรับม. คี่แล้ว ξ = ม. 2 − 1 . การคำนวณค่าเฉลี่ยเคลื่อนที่สำหรับระดับจำนวนมากสามารถทำได้ง่ายขึ้นโดยการกำหนดค่าต่อเนื่องของค่าเฉลี่ยเคลื่อนที่แบบเรียกซ้ำ: y t= y t− 1 + yt + ξ − y t − (ξ + 1 ) 2ξ + 1 แต่ด้วยข้อเท็จจริงที่ว่าการสังเกตครั้งล่าสุดจำเป็นต้องให้ "น้ำหนัก" มากขึ้น ค่าเฉลี่ยเคลื่อนที่จึงจำเป็นต้องตีความให้แตกต่างออกไป มันอยู่ในความจริงที่ว่าค่าที่ได้รับจากการหาค่าเฉลี่ยไม่ได้แทนที่เทอมกลางของช่วงเวลาเฉลี่ย แต่เทอมสุดท้าย ดังนั้น นิพจน์สุดท้ายสามารถเขียนใหม่เป็น มิ = มิ + 1 y i− y i− ม ที่นี่ ค่าเฉลี่ยเคลื่อนที่ที่เกี่ยวข้องกับจุดสิ้นสุดของช่วงเวลา จะแสดงด้วยสัญลักษณ์ใหม่ M i โดยพื้นฐานแล้ว M i เท่ากับ y t เลื่อน ξ ไปทางขวา นั่นคือ M i = y t + ξ โดยที่ i = t + ξ พิจารณาว่า M i − 1 เป็นค่าประมาณของ y i − m นิพจน์ (5.1) สามารถเขียนใหม่ในรูปแบบ y ฉัน+ 1 ฉัน − 1 , M ฉันกำหนดโดยนิพจน์ (5.1) โดยที่ M i คือค่าประมาณ ถ้าการคำนวณ (5.2) ซ้ำเมื่อมีข้อมูลใหม่เข้ามา และเขียนใหม่ในรูปแบบอื่น จากนั้นเราจะได้ฟังก์ชันการสังเกตที่ราบรื่น: Q i= α y i+ (1 − α ) Q i− 1 , หรือในรูปแบบที่เทียบเท่า Q t= α y t+ (1 − α ) Q t− 1 การคำนวณที่ดำเนินการโดยนิพจน์ (5.3) พร้อมการสังเกตใหม่แต่ละครั้งเรียกว่าการปรับให้เรียบแบบเอ็กซ์โปเนนเชียล ในนิพจน์สุดท้าย เพื่อแยกความแตกต่างของการทำให้เรียบแบบเอกซ์โปเนนเชียลจากค่าเฉลี่ยเคลื่อนที่ จะใช้สัญลักษณ์ Q แทน M ค่า α ซึ่งก็คือ อะนาล็อกของ m 1 เรียกว่าค่าคงที่การปรับให้เรียบ ค่าของ α อยู่ใน ช่วงเวลา [ 0 , 1 ] . ถ้า α แสดงเป็นอนุกรม α + α(1 − α) + α(1 − α) 2 + α(1 − α) 3 + ... + α(1 − α) n , เป็นเรื่องง่ายที่จะเห็นว่า "น้ำหนัก" ลดลงอย่างทวีคูณในเวลา ตัวอย่างเช่น สำหรับ α = 0 , 2 เราได้ 0,2 + 0,16 + 0,128 + 0,102 + 0,082 + … ผลรวมของอนุกรมมีแนวโน้มที่จะเป็นเอกภาพ และเงื่อนไขของผลรวมจะลดลงตามเวลา ค่าของ Q t ในนิพจน์ (5.3) คือค่าเฉลี่ยเอกซ์โปเนนเชียลของลำดับที่หนึ่ง นั่นคือค่าเฉลี่ยที่ได้รับโดยตรงจาก ปรับข้อมูลการสังเกตให้เรียบ (การปรับให้เรียบหลัก) บางครั้ง เมื่อพัฒนาแบบจำลองทางสถิติ การคำนวณค่าเฉลี่ยเลขชี้กำลังของคำสั่งซื้อที่สูงขึ้นจะมีประโยชน์ นั่นคือ ค่าเฉลี่ยที่ได้จากการทำให้เรียบแบบเลขชี้กำลังซ้ำๆ สัญลักษณ์ทั่วไปในรูปแบบเรียกซ้ำของค่าเฉลี่ยเลขชี้กำลังของคำสั่ง k คือ Q t (k)= α Q t (k− 1 )+ (1 − α ) Q t (− k1 ) ค่าของ k แปรผันภายใน 1, 2, …, p ,p+1 โดยที่ p คือลำดับของพหุนามเชิงทำนาย (เชิงเส้น กำลังสอง และอื่นๆ) ตามสูตรนี้ นิพจน์สำหรับค่าเฉลี่ยเลขชี้กำลังของลำดับที่หนึ่ง สอง และสาม Q t (1 )= α y t + (1 − α ) Q t (− 1 1 ); Q t (2 )= α Q t (1 )+ (1 − α ) Q t (− 2 1 ); Q t (3 )= α Q t (2 )+ (1 − α ) Q t (− 3 1 ) 5.2. การหาค่าพารามิเตอร์ของตัวแบบทำนายโดยใช้วิธีการปรับให้เรียบแบบเอ็กซ์โปเนนเชียล เห็นได้ชัดว่าในการพัฒนาค่าการทำนายตามชุดไดนามิกโดยใช้วิธีการทำให้เรียบแบบเอ็กซ์โปเนนเชียล จำเป็นต้องคำนวณค่าสัมประสิทธิ์ของสมการแนวโน้มผ่านค่าเฉลี่ยแบบเอ็กซ์โปเนนเชียล ค่าประมาณของค่าสัมประสิทธิ์ถูกกำหนดโดยทฤษฎีบทพื้นฐานของ Brown-Meyer ซึ่งเกี่ยวข้องกับค่าสัมประสิทธิ์ของพหุนามเชิงทำนายกับค่าเฉลี่ยเลขชี้กำลังของคำสั่งที่สอดคล้องกัน: (−
1
) aˆp α (1 − α )∞ −α
)
j (p − 1 + j ) ! ∑จ พี = 0 พี! (k− 1 ) !j = 0 โดยที่ aˆ p คือค่าประมาณของค่าสัมประสิทธิ์ของพหุนามของดีกรี p . ค่าสัมประสิทธิ์พบได้จากการแก้ระบบ (p + 1 ) ของสมการ сp + 1 ไม่ทราบ ดังนั้นสำหรับโมเดลเชิงเส้น aˆ 0 = 2 Q เสื้อ (1 ) − Q เสื้อ (2 ) ; aˆ 1 = 1 − α α (Q t (1 )− Q t (2 )) ; สำหรับแบบจำลองกำลังสอง aˆ 0 = 3 (Q เสื้อ (1 )− Q เสื้อ (2 )) + Q เสื้อ (3 ); aˆ 1 =1 − α α [ (6 −5 α ) Q t (1 ) −2 (5 −4 α ) Q t (2 ) +(4 −3 α ) Q t (3 ) ] ; aˆ 2 = (1 − α α ) 2 [ Q t (1 )− 2 Q t (2 )+ Q t (3 )] . การคาดการณ์จะดำเนินการตามพหุนามที่เลือกตามลำดับสำหรับแบบจำลองเชิงเส้น ˆyt + τ = aˆ0 + aˆ1 τ ; สำหรับแบบจำลองกำลังสอง ˆyt + τ = aˆ0 + aˆ1 τ + aˆ 2 2 τ 2 , โดยที่ τ คือขั้นตอนการทำนาย ควรสังเกตว่าค่าเฉลี่ยเลขชี้กำลัง Q t (k ) สามารถคำนวณได้ด้วยพารามิเตอร์ที่รู้จัก (เลือก) เท่านั้น โดยรู้เงื่อนไขเริ่มต้น Q 0 (k ) การประมาณค่าเงื่อนไขเริ่มต้น โดยเฉพาะอย่างยิ่งสำหรับแบบจำลองเชิงเส้น ถาม(1)=ก 1 − α Q(2 ) = a − 2 (1 − α ) ก สำหรับแบบจำลองกำลังสอง ถาม(1)=ก 1 − α + (1 − α )(2 − α ) 2(1−α ) (1− α )(3− 2α ) ถาม 0(2 ) = a 0− 2α 2 ถาม(3)=ก 3(1−α ) (1 − α )(4 − 3 α ) โดยที่ค่าสัมประสิทธิ์ a 0 และ 1 คำนวณโดยวิธีกำลังสองน้อยที่สุด ค่าของพารามิเตอร์การปรับให้เรียบ α คำนวณโดยสูตรโดยประมาณ α ≈ ม. 2 + 1, โดยที่ m คือจำนวนของการสังเกต (ค่า) ในช่วงการปรับให้เรียบ ลำดับการคำนวณค่าพยากรณ์แสดงใน การคำนวณสัมประสิทธิ์ของอนุกรมโดยวิธีกำลังสองน้อยที่สุด การกำหนดช่วงเวลาการปรับให้เรียบ การคำนวณค่าคงที่การปรับให้เรียบ การคำนวณเงื่อนไขเริ่มต้น การคำนวณค่าเฉลี่ยเลขชี้กำลัง การคำนวณค่าประมาณ a 0 , a 1 เป็นต้น การคำนวณค่าพยากรณ์ของชุดข้อมูล ข้าว. 5.1. ลำดับการคำนวณค่าพยากรณ์ ตัวอย่างเช่น พิจารณาขั้นตอนการรับค่าคาดการณ์ของเวลาทำงานของผลิตภัณฑ์ ซึ่งแสดงตามเวลาระหว่างความล้มเหลว ข้อมูลเริ่มต้นสรุปไว้ในตาราง 5.1. เราเลือกแบบจำลองการพยากรณ์เชิงเส้นในรูปแบบ y t = a 0 + a 1 τ วิธีแก้ปัญหาเป็นไปได้ด้วยค่าเริ่มต้นต่อไปนี้: 0 , 0 = 64, 2; 1 , 0 = 31.5; α = 0.305 ตารางที่ 5.1 ข้อมูลเบื้องต้น หมายเลขสังเกต t ความยาวขั้นตอน การคาดคะเน τ MTBF, y (ชั่วโมง) สำหรับค่าเหล่านี้ ค่าสัมประสิทธิ์ "ปรับให้เรียบ" ที่คำนวณได้สำหรับ y 2 ค่าจะเท่ากัน = α Q (1 )− Q (2 )= 97 , 9 ; [ ถาม (1) - ถาม (2) 31,
9 , 1−α ภายใต้เงื่อนไขเริ่มต้น 1 − α ก 0 , 0 − 1, 0 = −7
,
6
1 − α = −79
,
4
และค่าเฉลี่ยเลขชี้กำลัง Q (1 )= α y + (1 − α ) Q (1 ) 25,
2;
ถาม(2) = α Q (1 ) + (1 −α ) Q (2 ) = −47 , 5 . จากนั้นสูตรจะคำนวณค่า "ปรับให้เรียบ" y 2 ถามฉัน (1 ) ถามฉัน (2 ) 0 ,ผม 1 ,i ใช่ ดังนั้น (ตารางที่ 5.2) โมเดลการทำนายเชิงเส้นจึงมีรูปแบบ ˆy เสื้อ + τ = 224.5+ 32τ . ให้เราคำนวณค่าที่คาดการณ์ไว้สำหรับระยะเวลารอคอยสินค้า 2 ปี (τ = 1 ), 4 ปี (τ = 2 ) และอื่น ๆ ระยะเวลาระหว่างความล้มเหลวของผลิตภัณฑ์ (ตาราง 5.3) ตารางที่ 5.3 ค่าพยากรณ์ˆy t สมการ เสื้อ+2 เสื้อ+4 เสื้อ+6 เสื้อ+8 เสื้อ+20 การถดถอย (τ = 1) (τ=2) (τ = 3) (τ=5) τ =
ˆy t = 224.5+ 32τ ควรสังเกตว่าสูตรสามารถคำนวณ "น้ำหนัก" ทั้งหมดของค่า m สุดท้ายของอนุกรมเวลาได้ ค = 1 − (ม. (− 1 ) ม. ) . ม.+ 1 ดังนั้น สำหรับการสังเกตสองชุดสุดท้าย (m = 2 ) ค่า c = 1 − (2 2 − + 1 1 ) 2 = 0 667 . 5.3. การเลือกเงื่อนไขเริ่มต้นและการกำหนดค่าคงที่การปรับให้เรียบ ดังมาจากสำนวน Q t= α y t+ (1 − α ) Q t− 1 , เมื่อดำเนินการปรับให้เรียบแบบเอ็กซ์โปเนนเชียล จำเป็นต้องทราบค่าเริ่มต้น (ก่อนหน้า) ของฟังก์ชันที่ปรับให้เรียบ ในบางกรณี การสังเกตครั้งแรกสามารถใช้เป็นค่าเริ่มต้น บ่อยครั้งมากขึ้น เงื่อนไขเริ่มต้นถูกกำหนดตามนิพจน์ (5.4) และ (5.5) ในกรณีนี้ ค่า a 0 , 0 ,a 1 , 0 และ 2 , 0 ถูกกำหนดโดยวิธีกำลังสองน้อยที่สุด หากเราไม่เชื่อถือค่าเริ่มต้นที่เลือกจริง ๆ แล้วโดยการสังเกตค่าคงที่การปรับให้เรียบ α ถึง k ที่มีค่ามาก เราจะนำมา "น้ำหนัก" ของค่าเริ่มต้นจนถึงค่า (1 − α ) k<<
α
, и оно будет практически забыто. Наоборот, если мы уверены в правильности выбранного начального значения и неизменности модели в течение определенного отрезка времени в будущем,α
может быть выбрано малым (близким к 0). ดังนั้น การเลือกค่าคงที่การปรับให้เรียบ (หรือจำนวนการสังเกตในค่าเฉลี่ยเคลื่อนที่) จึงเกี่ยวข้องกับการแลกเปลี่ยน โดยปกติตามที่แสดงให้เห็นในทางปฏิบัติ ค่าคงที่การปรับให้เรียบจะอยู่ในช่วงตั้งแต่ 0.01 ถึง 0.3 เป็นที่ทราบกันดีว่าทรานซิชั่นหลายอันอนุญาตให้เราหาค่าประมาณโดยประมาณของ α ข้อแรกต่อจากเงื่อนไขที่ว่าค่าเฉลี่ยเคลื่อนที่และค่าเฉลี่ยแบบเอ็กซ์โปเนนเชียลมีค่าเท่ากัน α \u003d ม. 2 + 1 โดยที่ m คือจำนวนของการสังเกตในช่วงการปรับให้เรียบ วิธีการอื่นๆ เกี่ยวข้องกับความแม่นยำของการคาดการณ์ ดังนั้นจึงเป็นไปได้ที่จะกำหนด α ตามความสัมพันธ์ของเมเยอร์: α ≈ S y , โดยที่ S y คือข้อผิดพลาดมาตรฐานของแบบจำลอง S 1 คือค่าเฉลี่ยความคลาดเคลื่อนกำลังสองของอนุกรมเดิม อย่างไรก็ตาม การใช้อัตราส่วนหลังมีความซับซ้อนเนื่องจากข้อเท็จจริงที่ว่ามันยากมากที่จะระบุ S y และ S 1 จากข้อมูลเริ่มต้นได้อย่างน่าเชื่อถือ บ่อยครั้งที่พารามิเตอร์การปรับให้เรียบและในเวลาเดียวกันค่าสัมประสิทธิ์ 0 , 0 และ a 0 , 1 ได้รับเลือกว่าเหมาะสมที่สุดขึ้นอยู่กับเกณฑ์ S 2 = α ∑ ∞ (1 − α ) j [ yij − ˆyij ] 2 → นาที เจ=0 โดยการแก้ระบบพีชคณิตของสมการซึ่งได้มาจากการเทียบอนุพันธ์ให้เป็นศูนย์ ∂ส2 ∂ส2 ∂ส2 ∂a0, 0 ∂ ก 1, 0 ∂a2, 0 ดังนั้น สำหรับแบบจำลองการคาดการณ์เชิงเส้น เกณฑ์เริ่มต้นจะเท่ากับ S 2 = α ∑ ∞ (1 − α ) j [ yij − a0 , 0 − a1 , 0 τ ] 2 → นาที เจ=0 วิธีแก้ปัญหาของระบบนี้ด้วยความช่วยเหลือของคอมพิวเตอร์ไม่มีปัญหาใด ๆ สำหรับตัวเลือกที่สมเหตุสมผลของ α คุณยังสามารถใช้ขั้นตอนการทำให้เรียบแบบทั่วไป ซึ่งช่วยให้คุณได้รับความสัมพันธ์ต่อไปนี้ที่เกี่ยวข้องกับความแปรปรวนที่คาดการณ์และพารามิเตอร์การปรับให้เรียบสำหรับแบบจำลองเชิงเส้น: S p 2 ≈[ 1 + α β ] 2 [ 1 +4 β +5 β 2 +2 α (1 +3 β ) τ +2 α 2 τ 3 ] S y 2 สำหรับแบบจำลองกำลังสอง S p 2≈ [ 2 α + 3 α 3+ 3 α 2τ ] S y 2, โดยที่ β =
1
−
α
;สย– การประมาณ RMS ของชุดไดนามิกเริ่มต้น จุดมุ่งหมายการศึกษาในหัวข้อนี้เป็นการสร้างพื้นฐานสำหรับการฝึกอบรมผู้จัดการในสาขาพิเศษ 080507 ในด้านการสร้างแบบจำลองของงานต่าง ๆ ในสาขาเศรษฐศาสตร์การสร้างแนวทางที่เป็นระบบในการตั้งค่าและแก้ปัญหาการพยากรณ์ของนักเรียน . หลักสูตรที่นำเสนอนี้จะช่วยให้ผู้เชี่ยวชาญสามารถปรับตัวเข้ากับการปฏิบัติงานได้อย่างรวดเร็ว สำรวจข้อมูลและวรรณกรรมทางวิทยาศาสตร์และทางเทคนิคในสาขาเฉพาะทางของตนได้ดีขึ้น และตัดสินใจได้อย่างมั่นใจมากขึ้นที่เกิดขึ้นในการทำงานของตน หลัก งานการศึกษาหัวข้อคือ: นักเรียนได้รับความรู้ทางทฤษฎีเชิงลึกเกี่ยวกับการประยุกต์ใช้แบบจำลองการคาดการณ์ การได้รับทักษะที่มั่นคงในการปฏิบัติงานวิจัย ความสามารถในการแก้ปัญหาทางวิทยาศาสตร์ที่ซับซ้อนที่เกี่ยวข้องกับแบบจำลองอาคาร รวมถึงแบบจำลองหลายมิติ ความสามารถในการวิเคราะห์เชิงตรรกะ ผลลัพธ์ที่ได้และกำหนดแนวทางเพื่อหาทางออกที่ยอมรับได้ วิธีที่ค่อนข้างง่ายในการระบุแนวโน้มการพัฒนาคือการทำให้อนุกรมเวลาราบรื่น กล่าวคือแทนที่ระดับจริงด้วยระดับที่คำนวณได้ซึ่งมีความแปรผันน้อยกว่าข้อมูลต้นฉบับ เรียกว่าการแปลงที่สอดคล้องกัน การกรอง. ลองพิจารณาวิธีการปรับให้เรียบหลายวิธี เป้าหมายของการทำให้ราบรื่นคือการสร้างแบบจำลองการคาดการณ์สำหรับช่วงเวลาในอนาคตตามการสังเกตในอดีต ในวิธีการหาค่าเฉลี่ยอย่างง่าย ค่าของตัวแปรจะถูกใช้เป็นข้อมูลเริ่มต้น วายณ เวลาใดเวลาหนึ่ง ทีและค่าพยากรณ์ถูกกำหนดเป็นค่าเฉลี่ยอย่างง่ายสำหรับช่วงเวลาถัดไป สูตรการคำนวณมีรูปแบบ ที่ไหน นจำนวนการสังเกต ในกรณีที่มีการสังเกตใหม่ ควรนำการพยากรณ์ที่ได้รับใหม่มาพิจารณาสำหรับการพยากรณ์สำหรับช่วงเวลาถัดไปด้วย เมื่อใช้วิธีนี้ การคาดการณ์จะดำเนินการโดยการเฉลี่ยข้อมูลก่อนหน้าทั้งหมด อย่างไรก็ตาม ข้อเสียของการพยากรณ์ดังกล่าวคือความยากในการใช้งานในแบบจำลองแนวโน้ม วิธีนี้ขึ้นอยู่กับการแสดงซีรีส์เป็นผลรวมของแนวโน้มที่ค่อนข้างราบรื่นและส่วนประกอบแบบสุ่ม วิธีการนี้ขึ้นอยู่กับแนวคิดในการคำนวณค่าทางทฤษฎีตามการประมาณในท้องถิ่น เพื่อสร้างการประมาณแนวโน้ม ณ จุดหนึ่ง ทีโดยค่าของอนุกรมจากช่วงเวลา
คำนวณค่าทางทฤษฎีของอนุกรม วิธีที่แพร่หลายที่สุดในการปฏิบัติของชุดการปรับให้เรียบคือกรณีที่น้ำหนักทั้งหมดสำหรับองค์ประกอบของช่วงเวลา
มีค่าเท่ากัน ด้วยเหตุนี้จึงเรียกวิธีนี้ว่า วิธีค่าเฉลี่ยเคลื่อนที่เนื่องจากเมื่อดำเนินการตามขั้นตอน หน้าต่างที่มีความกว้าง (ม.2+1)ตลอดทั้งแถว ความกว้างของหน้าต่างมักจะเป็นเลขคี่ เนื่องจากค่าทางทฤษฎีถูกคำนวณสำหรับค่ากลาง: จำนวนเทอม k = 2 ม. + 1ด้วยจำนวนระดับที่เท่ากันทางซ้ายและขวาของช่วงเวลานั้น ที สูตรสำหรับการคำนวณค่าเฉลี่ยเคลื่อนที่ในกรณีนี้ใช้แบบฟอร์ม: การกระจายตัวของค่าเฉลี่ยเคลื่อนที่ถูกกำหนดเป็น σ 2 /k,ผ่านที่ไหน σ2หมายถึงความแปรปรวนของเงื่อนไขดั้งเดิมของซีรีส์ และ เคช่วงเวลาการปรับให้เรียบ ดังนั้น ยิ่งช่วงการปรับให้เรียบมากเท่าใด ค่าเฉลี่ยของข้อมูลก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น และแนวโน้มที่เปลี่ยนแปลงก็จะยิ่งน้อยลงเท่านั้น บ่อยครั้งที่การปรับให้เรียบจะดำเนินการกับสมาชิกสาม ห้าและเจ็ดคนของซีรีส์ดั้งเดิม ในกรณีนี้ ควรพิจารณาคุณลักษณะต่อไปนี้ของค่าเฉลี่ยเคลื่อนที่: หากเราพิจารณาชุดที่มีการขึ้นลงเป็นระยะของความยาวคงที่ เมื่อปรับให้เรียบตามค่าเฉลี่ยเคลื่อนที่ที่มีช่วงปรับให้เรียบเท่ากับหรือหลายช่วงของช่วงเวลา ความผันผวนจะถูกกำจัดอย่างสมบูรณ์ บ่อยครั้งที่การปรับให้เรียบตามค่าเฉลี่ยเคลื่อนที่จะแปลงชุดข้อมูลอย่างรุนแรงจนแนวโน้มการพัฒนาที่ระบุปรากฏเฉพาะในเงื่อนไขทั่วไปที่สุด ในขณะที่มีขนาดเล็กลงแต่สำคัญสำหรับรายละเอียดการวิเคราะห์ (คลื่น เส้นโค้ง ฯลฯ) จะหายไป หลังจากปรับให้เรียบ บางครั้งคลื่นเล็กๆ สามารถเปลี่ยนทิศทางไปยัง "หลุม" ตรงข้าม ปรากฏขึ้นแทนที่ "ยอดเขา" และในทางกลับกัน ทั้งหมดนี้ต้องใช้ความระมัดระวังในการใช้ค่าเฉลี่ยเคลื่อนที่อย่างง่ายและบังคับให้มองหาวิธีการอธิบายที่ละเอียดยิ่งขึ้น วิธีค่าเฉลี่ยเคลื่อนที่ไม่ได้ให้ค่าแนวโน้มสำหรับค่าแรกและค่าสุดท้าย มสมาชิกแถว ข้อบกพร่องนี้จะเห็นได้ชัดเจนโดยเฉพาะในกรณีที่ความยาวของแถวมีขนาดเล็ก ค่าเฉลี่ยเลขชี้กำลัง y tเป็นตัวอย่างของค่าเฉลี่ยถ่วงน้ำหนักแบบอสมมาตรที่คำนึงถึงระดับอายุของข้อมูล: ข้อมูล "เก่ากว่า" ที่มีน้ำหนักน้อยกว่าจะเข้าสู่สูตรเพื่อคำนวณค่าที่เรียบของระดับของชุดข้อมูล ที่นี่
ค่าเฉลี่ยเลขชี้กำลังแทนค่าที่สังเกตได้ของอนุกรม y t(การปรับให้เรียบเกี่ยวข้องกับข้อมูลทั้งหมดที่ได้รับจนถึงช่วงเวลาปัจจุบัน ที), α
พารามิเตอร์การปรับให้เรียบซึ่งแสดงลักษณะน้ำหนักของการสังเกต (ล่าสุด) ในปัจจุบัน 0< α
<1. วิธีการนี้ใช้ในการทำนายอนุกรมเวลาที่ไม่หยุดนิ่งโดยมีการเปลี่ยนแปลงระดับและความชันแบบสุ่ม เมื่อเราย้ายออกจากช่วงเวลาปัจจุบันไปสู่อดีต น้ำหนักของคำศัพท์ที่สอดคล้องกันของอนุกรมจะลดลงอย่างรวดเร็ว (แบบทวีคูณ) และแทบไม่มีผลใดๆ ต่อค่าของ เป็นเรื่องง่ายที่จะเห็นว่าความสัมพันธ์สุดท้ายช่วยให้เราตีความค่าเฉลี่ยเลขชี้กำลังได้ดังต่อไปนี้: ถ้า
การทำนายค่าอนุกรม y tแล้วความแตกต่างคือข้อผิดพลาดในการคาดการณ์ ดังนั้นคำทำนายสำหรับจุดต่อไปในเวลา เสื้อ+1คำนึงถึงสิ่งที่เป็นที่รู้จักในขณะนี้ ทีข้อผิดพลาดในการคาดการณ์ ตัวเลือกการปรับให้เรียบ α
เป็นตัวถ่วง. ถ้า α
ใกล้เคียงกับความสามัคคี จากนั้นการคาดการณ์จะคำนึงถึงขนาดของข้อผิดพลาดของการพยากรณ์ครั้งล่าสุดอย่างมีนัยสำคัญ สำหรับค่าเล็กน้อย α
ค่าที่คาดการณ์ไว้ใกล้เคียงกับการคาดการณ์ครั้งก่อน การเลือกพารามิเตอร์การปรับให้เรียบเป็นปัญหาที่ค่อนข้างซับซ้อน ข้อควรพิจารณาโดยทั่วไปมีดังนี้ วิธีการนี้ดีสำหรับการทำนายอนุกรมที่ราบรื่นเพียงพอ ในกรณีนี้ เราสามารถเลือกค่าคงที่การปรับให้เรียบได้โดยการลดข้อผิดพลาดในการคาดคะเนล่วงหน้า 1 ขั้นที่ประเมินจากช่วงที่สามสุดท้ายของซีรีส์ให้เหลือน้อยที่สุด ผู้เชี่ยวชาญบางคนไม่แนะนำให้ใช้พารามิเตอร์การปรับให้เรียบที่มีค่ามาก บนมะเดื่อ 3.1 แสดงตัวอย่างอนุกรมที่ปรับให้เรียบโดยใช้วิธีการปรับให้เรียบแบบเอกซ์โปเนนเชียลสำหรับ α=
0,1. ข้าว. 3.1. ผลลัพธ์ของการทำให้เรียบแบบเอ็กซ์โปเนนเชียลที่ α
=0,1 วิธีนี้คำนึงถึงแนวโน้มเชิงเส้นในท้องถิ่นที่มีอยู่ในอนุกรมเวลา หากมีแนวโน้มสูงขึ้นในอนุกรมเวลา ควบคู่ไปกับการประมาณระดับปัจจุบัน การประมาณค่าความชันก็เป็นสิ่งจำเป็นเช่นกัน ในเทคนิค Holt ค่าระดับและความชันจะถูกปรับให้เรียบโดยตรงโดยใช้ค่าคงที่ที่แตกต่างกันสำหรับแต่ละพารามิเตอร์ ค่าคงที่การปรับให้เรียบทำให้คุณสามารถประเมินระดับปัจจุบันและความชันได้ ปรับปรุงทุกครั้งที่มีการสังเกตใหม่ วิธี Holt ใช้สูตรการคำนวณสามสูตร: (3.2)
(3.3)
(3.4)
ที่ไหน α, β
ปรับค่าคงที่ให้เรียบจากช่วงเวลา สมการ (3.2) คล้ายกับสมการ (3.1) สำหรับการทำให้เรียบแบบเอกซ์โปเนนเชียลอย่างง่าย ยกเว้นคำที่มีแนวโน้ม คงที่ β
จำเป็นต้องทำให้การประมาณแนวโน้มราบรื่น ในสมการพยากรณ์ (3.3) ค่าประมาณแนวโน้มจะคูณด้วยจำนวนงวด รซึ่งอิงตามการคาดการณ์ จากนั้นผลิตภัณฑ์นี้จะถูกเพิ่มในระดับปัจจุบันของข้อมูลที่ราบรื่น ถาวร α
และ β
ถูกเลือกตามอัตวิสัยหรือโดยลดข้อผิดพลาดในการทำนายให้น้อยที่สุด ยิ่งมีการใช้ค่าน้ำหนักมากเท่าใด การตอบสนองต่อการเปลี่ยนแปลงอย่างต่อเนื่องก็จะยิ่งเร็วขึ้นเท่านั้น และข้อมูลก็จะราบรื่นยิ่งขึ้น น้ำหนักที่น้อยลงทำให้โครงสร้างของค่าที่เรียบนั้นแบนน้อยลง บนมะเดื่อ 3.2 แสดงตัวอย่างการปรับอนุกรมให้เรียบโดยใช้วิธี Holt สำหรับค่าต่างๆ α
และ β
เท่ากับ 0.1 ข้าว. 3.2. ผลการทำให้เรียบ Holt หากมีความผันผวนตามฤดูกาลในโครงสร้างข้อมูล จะใช้แบบจำลองการปรับให้เรียบแบบเอ็กซ์โปเนนเชียลแบบสามพารามิเตอร์ที่เสนอโดย Winters เพื่อลดข้อผิดพลาดในการคาดการณ์ วิธีการนี้เป็นส่วนขยายของโมเดล Holt ก่อนหน้านี้ เพื่ออธิบายความผันแปรของฤดูกาล จึงมีการใช้สมการเพิ่มเติมที่นี่ และวิธีนี้อธิบายไว้อย่างครบถ้วนโดยใช้สมการสี่ตัว: (3.5)
(3.6)
(3.7)
(3.8)
ที่ไหน α, β,
γ
การปรับให้เรียบอย่างต่อเนื่องสำหรับระดับ แนวโน้ม และฤดูกาล ตามลำดับ ส- ระยะเวลาของช่วงความผันผวนตามฤดูกาล สมการ (3.5) แก้ไขอนุกรมที่เรียบ ในสมการนี้ คำนี้จะคำนึงถึงฤดูกาลในข้อมูลดั้งเดิม หลังจากคำนึงถึงฤดูกาลและแนวโน้มในสมการ (3.6), (3.7) แล้ว การประมาณการจะราบรื่นและมีการพยากรณ์ในสมการ (3.8) เช่นเดียวกับในวิธีการก่อนหน้านี้ ตุ้มน้ำหนัก α, β, γ
สามารถเลือกได้ตามอัตวิสัยหรือโดยลดข้อผิดพลาดในการทำนายให้น้อยที่สุด ก่อนใช้สมการ (3.5) จำเป็นต้องกำหนดค่าเริ่มต้นสำหรับซีรี่ส์ที่เรียบ ล, แนวโน้ม ที ทีค่าสัมประสิทธิ์ฤดูกาล เซนต์. โดยปกติแล้ว ค่าเริ่มต้นของอนุกรมที่ปรับให้เรียบจะเท่ากับการสังเกตครั้งแรก จากนั้นแนวโน้มจะเป็นศูนย์ และค่าสัมประสิทธิ์ตามฤดูกาลจะถูกตั้งค่าเท่ากับหนึ่ง บนมะเดื่อ 3.3 แสดงตัวอย่างการปรับอนุกรมให้เรียบโดยใช้วิธี Winters ข้าว. 3.3. ผลลัพธ์ของการเกลี่ยให้เรียบด้วยวิธีวินเทอร์ส บ่อยครั้งที่อนุกรมเวลามีแนวโน้มเชิงเส้น (แนวโน้ม) สมมติว่าเป็นแนวโน้มเชิงเส้น คุณจะต้องสร้างเส้นตรงที่จะสะท้อนการเปลี่ยนแปลงไดนามิกอย่างแม่นยำที่สุดในช่วงเวลาที่กำลังพิจารณา มีหลายวิธีในการสร้างเส้นตรง แต่วัตถุประสงค์ส่วนใหญ่จากมุมมองที่เป็นทางการคือการสร้างโดยอิงจากผลรวมของการเบี่ยงเบนเชิงลบและบวกของค่าเริ่มต้นของซีรีส์จากเส้นตรงให้น้อยที่สุด เส้นตรงในระบบสองพิกัด (x, y)สามารถกำหนดเป็นจุดตัดของพิกัดใดพิกัดหนึ่งได้ ที่และมุมเอียงกับแกน เอ็กซ์สมการของเส้นตรงดังกล่าวจะมีลักษณะดังนี้ เพื่อให้เส้นตรงสะท้อนวิถีไดนามิก จำเป็นต้องลดผลรวมของความเบี่ยงเบนในแนวดิ่งให้เหลือน้อยที่สุด เมื่อใช้เป็นเกณฑ์ในการประมาณการการลดลงของผลรวมของการเบี่ยงเบนอย่างง่าย ผลลัพธ์ที่ได้จะไม่ค่อยดีนัก เนื่องจากค่าลบและค่าเบี่ยงเบนบวกจะหักล้างกันเอง การลดผลรวมของค่าสัมบูรณ์ให้น้อยที่สุดไม่ได้นำไปสู่ผลลัพธ์ที่น่าพอใจเนื่องจากการประมาณพารามิเตอร์ในกรณีนี้ไม่เสถียรและยังมีปัญหาในการคำนวณในการใช้ขั้นตอนการประมาณค่าดังกล่าว ดังนั้นขั้นตอนที่ใช้บ่อยที่สุดคือการลดผลรวมของการเบี่ยงเบนกำลังสองให้น้อยที่สุดหรือ วิธีกำลังสองน้อยที่สุด(ม.ป.ป). เนื่องจากชุดของค่าเริ่มต้นมีความผันผวน แบบจำลองของชุดข้อมูลจะมีข้อผิดพลาด ซึ่งช่องสี่เหลี่ยมจะต้องย่อให้เล็กสุด โดยที่ y ฉันสังเกตค่า; y i * ค่าทางทฤษฎีของแบบจำลอง;
หมายเลขการสังเกต เมื่อสร้างแบบจำลองแนวโน้มของอนุกรมเวลาดั้งเดิมโดยใช้แนวโน้มเชิงเส้น เราจะถือว่าเป็นเช่นนั้น หารสมการแรกด้วย น, เรามาถึงที่ต่อไป แทนนิพจน์ผลลัพธ์ลงในสมการที่สองของระบบ (3.10) สำหรับค่าสัมประสิทธิ์ ข *เราได้รับ: ตัวอย่างเช่นในรูป 3.4 แสดงกราฟการถดถอยเชิงเส้นระหว่างกำลังของรถ เอ็กซ์และค่าใช้จ่าย ที่. ข้าว. 3.4. พล็อตการถดถอยเชิงเส้น สมการสำหรับกรณีนี้คือ: ที่=1455,3 + 13,4 เอ็กซ์. การวิเคราะห์ด้วยสายตาของตัวเลขนี้แสดงให้เห็นว่าสำหรับการสังเกตจำนวนหนึ่งมีความเบี่ยงเบนอย่างมีนัยสำคัญจากเส้นโค้งทางทฤษฎี กราฟที่เหลือแสดงในรูปที่ 3.5. ข้าว. 3.5. แผนภูมิสารตกค้าง การวิเคราะห์ส่วนที่เหลือของเส้นการถดถอยสามารถให้การวัดที่เป็นประโยชน์ว่าการถดถอยโดยประมาณสะท้อนข้อมูลจริงได้ดีเพียงใด การถดถอยที่ดีคือการอธิบายความแปรปรวนจำนวนมาก ในทางกลับกัน การถดถอยที่ไม่ดีจะไม่ติดตามความผันผวนจำนวนมากในข้อมูลต้นฉบับ เป็นที่ชัดเจนโดยสัญชาตญาณว่าข้อมูลเพิ่มเติมใด ๆ จะช่วยปรับปรุงโมเดล เช่น ลดส่วนที่อธิบายไม่ได้ของการแปรผันของตัวแปร ที่. ในการวิเคราะห์การถดถอย เราจะแยกย่อยความแปรปรวนออกเป็นส่วนประกอบ เห็นได้ชัดว่า พจน์สุดท้ายจะเท่ากับศูนย์ เนื่องจากเป็นผลรวมของเศษเหลือ เราจึงได้ผลลัพธ์ดังนี้ ที่ไหน SS0, SS1, SS2กำหนดผลรวม การถดถอย และผลรวมที่เหลือของกำลังสองตามลำดับ ผลรวมการถดถอยของกำลังสองวัดส่วนของความแปรปรวนที่อธิบายโดยความสัมพันธ์เชิงเส้น ส่วนที่เหลืออยู่ของการกระจาย ไม่ได้อธิบายโดยการพึ่งพาเชิงเส้น ผลรวมแต่ละรายการมีลักษณะตามจำนวนองศาอิสระ (HR) ที่สอดคล้องกัน ซึ่งจะกำหนดจำนวนหน่วยข้อมูลที่ไม่ขึ้นต่อกัน กล่าวอีกนัยหนึ่ง อัตราการเต้นของหัวใจเกี่ยวข้องกับจำนวนการสังเกต นและจำนวนพารามิเตอร์ที่คำนวณจากผลรวมของพารามิเตอร์เหล่านี้ กรณีที่อยู่ระหว่างการพิจารณาให้คำนวณ SS0
กำหนดค่าคงที่เดียวเท่านั้น (ค่าเฉลี่ย) ดังนั้นอัตราการเต้นของหัวใจสำหรับ SS0
จะ (น– 1),
อัตราการเต้นของหัวใจสำหรับ SS 2 - (น - 2)และอัตราการเต้นของหัวใจสำหรับ เอสเอส 1จะ n - (n - 1)=1เนื่องจากมี n - 1 จุดคงที่ในสมการถดถอย เช่นเดียวกับผลรวมของกำลังสอง อัตราการเต้นของหัวใจสัมพันธ์กัน ผลรวมของกำลังสองที่เกี่ยวข้องกับการสลายตัวของความแปรปรวน ร่วมกับอัตราการเต้นของหัวใจที่สอดคล้องกัน สามารถใส่ไว้ในตารางการวิเคราะห์ความแปรปรวนที่เรียกว่า (ตาราง ANOVA ANalysis Of VAriance) (ตาราง 3.1) ตารางที่ 3.1 ตาราง ANOVA แหล่งที่มา ผลรวมของกำลังสอง สี่เหลี่ยมจัตุรัสขนาดกลาง การถดถอย SS2/ (n-2) เรากำหนดโดยใช้ตัวย่อที่แนะนำสำหรับผลรวมของกำลังสอง ค่าสัมประสิทธิ์การตัดสินใจเป็นอัตราส่วนของผลรวมการถดถอยของกำลังสองต่อผลรวมกำลังสองทั้งหมด เช่น (3.13)
ค่าสัมประสิทธิ์ของการกำหนดจะวัดสัดส่วนของความแปรปรวนในตัวแปร วายซึ่งสามารถอธิบายได้โดยใช้ข้อมูลเกี่ยวกับความแปรปรวนของตัวแปรอิสระ x.ค่าสัมประสิทธิ์การกำหนดเปลี่ยนจากศูนย์เมื่อ เอ็กซ์ไม่ส่งผลกระทบ วายเป็นหนึ่งเดียวเมื่อมีการเปลี่ยนแปลง วายอธิบายอย่างครบถ้วนโดยการเปลี่ยนแปลง x. การทำนายที่ดีที่สุดคือการทำนายที่มีความแปรปรวนน้อยที่สุด ในกรณีของเรา การหาค่ากำลังสองน้อยที่สุดแบบธรรมดาจะสร้างการทำนายที่ดีที่สุดของวิธีการทั้งหมดที่ให้ค่าประมาณที่ไม่เอนเอียงตามสมการเชิงเส้น ข้อผิดพลาดในการคาดการณ์ที่เกี่ยวข้องกับขั้นตอนการคาดการณ์อาจมาจากแหล่งที่มาสี่แหล่ง ประการแรก ลักษณะสุ่มของข้อผิดพลาดเพิ่มเติมที่จัดการโดยการถดถอยเชิงเส้นทำให้มั่นใจได้ว่าการคาดการณ์จะเบี่ยงเบนจากค่าจริง แม้ว่าแบบจำลองจะถูกระบุอย่างถูกต้องและทราบพารามิเตอร์อย่างแม่นยำ ประการที่สอง กระบวนการประมาณค่าเองทำให้เกิดข้อผิดพลาดในการประมาณค่าพารามิเตอร์ ซึ่งแทบจะไม่สามารถเท่ากับค่าจริงได้ แม้ว่าค่าเหล่านั้นจะเท่ากับค่าเฉลี่ยก็ตาม ประการที่สาม ในกรณีของการคาดการณ์แบบมีเงื่อนไข (ในกรณีที่ไม่ทราบค่าที่แน่นอนของตัวแปรอิสระ) ข้อผิดพลาดจะถูกนำมาใช้กับการคาดการณ์ของตัวแปรอธิบาย ประการที่สี่ ข้อผิดพลาดอาจปรากฏขึ้นเนื่องจากข้อมูลจำเพาะของรุ่นไม่ถูกต้อง ด้วยเหตุนี้จึงสามารถจำแนกแหล่งที่มาของข้อผิดพลาดได้ดังนี้: เราจะพิจารณาการคาดการณ์แบบไม่มีเงื่อนไข เมื่อตัวแปรอิสระสามารถทำนายได้ง่ายและแม่นยำ เราเริ่มพิจารณาปัญหาคุณภาพการคาดการณ์ด้วยสมการถดถอยคู่ คำแถลงปัญหาในกรณีนี้สามารถกำหนดได้ดังนี้ สิ่งที่จะเป็นการคาดการณ์ที่ดีที่สุด y T+1 โดยมีเงื่อนไขว่าในแบบจำลอง y = a + bxตัวเลือก กและ ขโดยประมาณและมูลค่า xT+1เป็นที่รู้จัก. จากนั้นค่าที่ทำนายสามารถกำหนดเป็น ข้อผิดพลาดการคาดการณ์จะเป็น ข้อผิดพลาดการคาดการณ์มีสองคุณสมบัติ: ความแปรปรวนที่เกิดขึ้นนั้นมีค่าน้อยที่สุดในบรรดาค่าประมาณที่เป็นไปได้ทั้งหมดตามสมการเชิงเส้น แม้ว่า กและ b เป็นที่ทราบกันดีว่าข้อผิดพลาดในการพยากรณ์ปรากฏขึ้นเนื่องจากข้อเท็จจริงที่ว่า ที่ T+1อาจไม่อยู่ในเส้นถดถอยเนื่องจากข้อผิดพลาด ε T+1เป็นไปตามการแจกแจงแบบปกติโดยมีค่าเฉลี่ยและความแปรปรวนเป็นศูนย์ σ2. ในการตรวจสอบคุณภาพของการคาดการณ์ เราแนะนำค่าที่ทำให้เป็นมาตรฐาน ช่วงความเชื่อมั่น 95% สามารถกำหนดได้ดังนี้: ที่ไหน เบต้า 0.05ควอไทล์ของการแจกแจงแบบปกติ ขอบเขตของช่วง 95% สามารถกำหนดได้ดังนี้ โปรดทราบว่าในกรณีนี้คือความกว้าง ช่วงความมั่นใจไม่ได้ขึ้นอยู่กับขนาด เอ็กซ์,และขอบเขตของช่วงเวลาเป็นเส้นตรงขนานกับเส้นถดถอย บ่อยครั้งมากขึ้น เมื่อสร้างเส้นการถดถอยและตรวจสอบคุณภาพของการคาดการณ์ จำเป็นต้องประเมินไม่เพียงแต่พารามิเตอร์การถดถอยเท่านั้น แต่ยังรวมถึงความแปรปรวนของข้อผิดพลาดในการคาดการณ์ด้วย สามารถแสดงได้ว่าในกรณีนี้ความแปรปรวนของข้อผิดพลาดขึ้นอยู่กับค่า () โดยที่ค่าเฉลี่ยของตัวแปรอิสระ นอกจากนี้ ยิ่งซีรีย์ยาวมากเท่าไหร่ การคาดการณ์ก็ยิ่งแม่นยำมากขึ้นเท่านั้น ข้อผิดพลาดในการคาดการณ์จะลดลงหากค่าของ X T+1 ใกล้เคียงกับค่าเฉลี่ยของตัวแปรอิสระ และในทางกลับกัน เมื่อย้ายออกจากค่าเฉลี่ย การคาดการณ์จะมีความแม่นยำน้อยลง บนมะเดื่อ 3.6 แสดงผลการทำนายโดยใช้สมการถดถอยเชิงเส้นสำหรับ 6 ช่วงเวลาข้างหน้าพร้อมกับช่วงความเชื่อมั่น ข้าว. 3.6. การทำนายการถดถอยเชิงเส้น ดังจะเห็นได้จากรูป 3.6 เส้นถดถอยนี้อธิบายข้อมูลเดิมได้ไม่ดีนัก: มีความแปรผันมากเมื่อเทียบกับเส้นประกอบ คุณภาพของแบบจำลองยังสามารถตัดสินได้จากสิ่งที่เหลืออยู่ ซึ่งด้วยแบบจำลองที่น่าพอใจ ควรได้รับการแจกจ่ายโดยประมาณตามกฎหมายปกติ บนมะเดื่อ 3.7 แสดงกราฟของส่วนที่เหลือซึ่งสร้างขึ้นโดยใช้มาตราส่วนความน่าจะเป็น รูปที่ 3.7 แผนภูมิสารตกค้าง เมื่อใช้มาตราส่วนดังกล่าว ข้อมูลที่เป็นไปตามกฎหมายปกติควรอยู่บนเส้นตรง จากรูปต่อไปนี้ จุดที่จุดเริ่มต้นและจุดสิ้นสุดของระยะเวลาการสังเกตค่อนข้างเบี่ยงเบนไปจากเส้นตรง ซึ่งบ่งชี้ว่าแบบจำลองที่เลือกมีคุณภาพสูงไม่เพียงพอในรูปแบบของสมการการถดถอยเชิงเส้น ในตาราง ตาราง 3.2 แสดงผลการคาดการณ์ (คอลัมน์ที่สอง) พร้อมกับช่วงความเชื่อมั่น 95% (คอลัมน์ที่สามล่างและสี่บนตามลำดับ) ตารางที่ 3.2 ผลการพยากรณ์ ในการถดถอยหลายตัวแปร ข้อมูลสำหรับแต่ละกรณีรวมถึงค่าของตัวแปรตามและตัวแปรอิสระแต่ละตัว ตัวแปรตาม ยเป็นตัวแปรสุ่มที่เกี่ยวข้องกับตัวแปรอิสระโดยมีความสัมพันธ์ดังนี้ ที่จะต้องกำหนดค่าสัมประสิทธิ์การถดถอย ε
องค์ประกอบข้อผิดพลาดที่สอดคล้องกับการเบี่ยงเบนของค่าของตัวแปรตามจากอัตราส่วนจริง (สันนิษฐานว่าข้อผิดพลาดนั้นเป็นอิสระและมีการแจกแจงแบบปกติโดยมีค่าเฉลี่ยเป็นศูนย์และความแปรปรวนที่ไม่รู้จัก σ
). สำหรับชุดข้อมูลที่กำหนด สามารถหาค่าประมาณของสัมประสิทธิ์การถดถอยได้โดยใช้วิธีกำลังสองน้อยที่สุด หากค่าประมาณ OLS แสดงด้วย ฟังก์ชันการถดถอยที่เกี่ยวข้องจะมีลักษณะดังนี้: ส่วนที่เหลือเป็นค่าประมาณขององค์ประกอบข้อผิดพลาดและคล้ายกับส่วนที่เหลือในกรณีของการถดถอยเชิงเส้นอย่างง่าย การวิเคราะห์ทางสถิติของแบบจำลองการถดถอยหลายตัวแปรดำเนินการในลักษณะเดียวกับการวิเคราะห์การถดถอยเชิงเส้นอย่างง่าย แพ็คเกจมาตรฐานของโปรแกรมทางสถิติทำให้สามารถรับการประมาณค่ากำลังสองน้อยที่สุดสำหรับพารามิเตอร์แบบจำลอง การประมาณค่าข้อผิดพลาดมาตรฐาน ได้อีกด้วยค่า ที- สถิติเพื่อตรวจสอบความสำคัญของข้อกำหนดแต่ละข้อของแบบจำลองการถดถอยและค่า ฉ- สถิติเพื่อทดสอบความสำคัญของการพึ่งพาการถดถอย รูปแบบของการแยกผลรวมกำลังสองในกรณีของ multivariate regression จะคล้ายกับนิพจน์ (3.13) แต่อัตราส่วนของอัตราการเต้นของหัวใจจะเป็นดังนี้ ขอย้ำอีกครั้งว่า นคือปริมาณการสังเกต และ เคจำนวนตัวแปรในโมเดล ความแปรปรวนโดยรวมของตัวแปรตามประกอบด้วยสององค์ประกอบ: ความแปรปรวนที่อธิบายโดยตัวแปรอิสระผ่านฟังก์ชันการถดถอยและความแปรปรวนที่อธิบายไม่ได้ ตาราง ANOVA สำหรับกรณีของการถดถอยหลายตัวแปรจะมีรูปแบบแสดงในตาราง 3.3. ตารางที่ 3.3 ตาราง ANOVA แหล่งที่มา ผลรวมของกำลังสอง สี่เหลี่ยมจัตุรัสขนาดกลาง การถดถอย SS2/ (n-k-1) ตัวอย่างของการถดถอยหลายตัวแปร เราจะใช้ข้อมูลจากแพ็คเกจ Statistica (ไฟล์ข้อมูล ยากจน.สถา).ข้อมูลที่นำเสนอมาจากการเปรียบเทียบผลการสำรวจสำมะโนปี พ.ศ. 2503 และ พ.ศ. 2513 สำหรับการสุ่มตัวอย่าง 30 ประเทศ ชื่อประเทศถูกป้อนเป็นชื่อสตริง และชื่อของตัวแปรทั้งหมดในไฟล์นี้แสดงอยู่ด้านล่าง: POP_CHNG
การเปลี่ยนแปลงของประชากรในปี 2503-2513; N_EMPLD
จำนวนแรงงานในภาคการเกษตร เปอร์เซ็นต์ PT_POOR ของครอบครัวที่อาศัยอยู่ต่ำกว่าเส้นความยากจน อัตราภาษี TAX_RATE; PT_PHONE เปอร์เซ็นต์ของอพาร์ทเมนท์ที่มีโทรศัพท์ PT_RURAL เปอร์เซ็นต์ของประชากรในชนบท AGE วัยกลางคน ในฐานะตัวแปรตาม เราเลือกคุณลักษณะ Pt_แย่และเป็นอิสระ - ส่วนที่เหลือทั้งหมด ค่าสัมประสิทธิ์การถดถอยที่คำนวณได้ระหว่างตัวแปรที่เลือกแสดงไว้ในตาราง 3.4 ตารางที่ 3.4 ค่าสัมประสิทธิ์การถดถอย ตารางนี้แสดงค่าสัมประสิทธิ์การถดถอย ( ใน) และค่าสัมประสิทธิ์การถดถอยมาตรฐาน ( เบต้า). ด้วยความช่วยเหลือของสัมประสิทธิ์ ในมีการกำหนดรูปแบบของสมการถดถอยซึ่งในกรณีนี้มีรูปแบบ: การรวมไว้ทางด้านขวาของตัวแปรเหล่านี้เท่านั้นเกิดจากการที่คุณสมบัติเหล่านี้เท่านั้นที่มีค่าความน่าจะเป็น รน้อยกว่า 0.05 (ดูคอลัมน์ที่สี่ของตาราง 3.4) 1. บทบัญญัติเกี่ยวกับระเบียบวิธีพื้นฐาน วิธีการทำให้เรียบแบบเอกซ์โพเนนเชียลอย่างง่ายใช้ค่าเฉลี่ยเคลื่อนที่แบบถ่วงน้ำหนัก (แบบเอ็กซ์โพเนนเชียล) ของการสังเกตก่อนหน้านี้ทั้งหมด แบบจำลองนี้มักใช้กับข้อมูลที่จำเป็นในการประเมินการมีอยู่ของความสัมพันธ์ระหว่างตัวบ่งชี้ที่วิเคราะห์ (แนวโน้ม) หรือการพึ่งพาข้อมูลที่วิเคราะห์ จุดประสงค์ของการทำให้เรียบแบบเอกซ์โปเนนเชียลคือการประเมินสถานะปัจจุบัน ซึ่งผลลัพธ์จะเป็นตัวกำหนดการคาดการณ์ในอนาคตทั้งหมด การปรับให้เรียบแบบเอ็กซ์โปเนนเชียลการอัปเดตโมเดลอย่างต่อเนื่องเนื่องจากข้อมูลล่าสุด วิธีนี้ขึ้นอยู่กับการหาค่าเฉลี่ย (ปรับให้เรียบ) อนุกรมเวลาของการสังเกตที่ผ่านมาในทิศทางลง (แบบทวีคูณ) นั่นคือเหตุการณ์ในภายหลังมีน้ำหนักมากขึ้น น้ำหนักถูกกำหนดดังนี้: สำหรับการสังเกตครั้งล่าสุด น้ำหนักจะเป็นค่า α สำหรับค่าสุดท้าย - (1-α) สำหรับค่าที่อยู่ก่อนหน้า - (1-α) 2 เป็นต้น ในรูปแบบที่ราบรื่น การคาดการณ์ใหม่ (สำหรับช่วงเวลา t + 1) สามารถแสดงเป็นค่าเฉลี่ยถ่วงน้ำหนักของการสังเกตปริมาณครั้งล่าสุด ณ เวลา t และการคาดการณ์ก่อนหน้าสำหรับช่วงเวลาเดียวกัน t ยิ่งไปกว่านั้น น้ำหนัก α ถูกกำหนดให้กับค่าที่สังเกตได้ และน้ำหนัก (1- α) ถูกกำหนดให้กับการคาดการณ์ สันนิษฐานว่าเป็น 0< α<1. Это правило в общем виде можно записать следующим образом. การคาดการณ์ใหม่ = [α*(การสังเกตครั้งสุดท้าย)]+[(1- α)*การคาดการณ์ล่าสุด] ค่าที่คาดการณ์สำหรับช่วงเวลาถัดไปอยู่ที่ไหน α คือค่าคงที่การปรับให้เรียบ Y t คือการสังเกตค่าสำหรับช่วงเวลาปัจจุบัน t; การคาดการณ์ที่ราบรื่นก่อนหน้านี้ของค่านี้สำหรับช่วงเวลา t การปรับให้เรียบแบบเอกซ์โพเนนเชียลเป็นขั้นตอนสำหรับการแก้ไขผลการพยากรณ์อย่างต่อเนื่องในแง่ของการพัฒนาล่าสุด ค่าคงที่การปรับให้เรียบ α เป็นปัจจัยถ่วงน้ำหนัก มูลค่าที่แท้จริงของมันถูกกำหนดโดยขอบเขตที่การสังเกตในปัจจุบันควรมีอิทธิพลต่อค่าที่ทำนายไว้ หาก α มีค่าใกล้เคียงกับ 1 การคาดการณ์จะคำนึงถึงค่าของข้อผิดพลาดของการพยากรณ์ครั้งล่าสุด ในทางกลับกัน สำหรับค่าเล็กน้อยของ α ค่าที่คาดการณ์ไว้จะใกล้เคียงกับการคาดการณ์ก่อนหน้ามากที่สุด สามารถคิดได้ว่าเป็นค่าเฉลี่ยถ่วงน้ำหนักของการสังเกตที่ผ่านมาทั้งหมด โดยน้ำหนักจะลดลงแบบทวีคูณตาม "อายุ" ของข้อมูล ตารางที่ 2.1 การเปรียบเทียบอิทธิพลของค่าคงที่การปรับให้เรียบที่แตกต่างกัน ค่าคงที่ α เป็นกุญแจสำคัญในการวิเคราะห์ข้อมูล หากต้องการให้ค่าที่คาดการณ์ไว้มีความเสถียรและการเบี่ยงเบนแบบสุ่มจะถูกปรับให้เรียบ จำเป็นต้องเลือกค่าขนาดเล็กของ α ค่าคงที่ α จำนวนมากเหมาะสมหากคุณต้องการการตอบสนองอย่างรวดเร็วต่อการเปลี่ยนแปลงในสเปกตรัมการสังเกต 2. ตัวอย่างการปฏิบัติของการทำให้เรียบแบบเอ็กซ์โปเนนเชียล มีการนำเสนอข้อมูลของ บริษัท ในแง่ของปริมาณการขาย (พันหน่วย) เป็นเวลาเจ็ดปีค่าคงที่การปรับให้เรียบจะเท่ากับ 0.1 และ 0.6 ข้อมูลเป็นเวลา 7 ปีเป็นส่วนทดสอบ มีความจำเป็นต้องประเมินประสิทธิภาพของแต่ละรุ่น สำหรับการทำให้ซีรีย์เรียบแบบเอ็กซ์โปเนนเชียล ค่าเริ่มต้นจะเท่ากับ 500 (ค่าแรกของข้อมูลจริงหรือค่าเฉลี่ยสำหรับช่วงเวลา 3-5 จะถูกบันทึกในค่าที่เรียบสำหรับไตรมาสที่ 2) ตารางที่ 2.2 ข้อมูลเบื้องต้น บนมะเดื่อ 2.1 แสดงการทำนายตามการปรับให้เรียบแบบเอ็กซ์โปเนนเชียลด้วยค่าคงที่การปรับให้เรียบที่ 0.1 ข้าว. 2.1. การทำให้เรียบแบบเอ็กซ์โปเนนเชียล โซลูชันใน Excel 1. เลือกเมนู "เครื่องมือ" - "การวิเคราะห์ข้อมูล" จากรายการเครื่องมือวิเคราะห์ เลือกการปรับให้เรียบแบบเอ็กซ์โปเนนเชียล หากไม่มีการวิเคราะห์ข้อมูลในเมนู "เครื่องมือ" คุณต้องติดตั้ง "แพ็คเกจการวิเคราะห์" ในการดำเนินการนี้ ให้ค้นหารายการ "การตั้งค่า" ใน "พารามิเตอร์" และในกล่องโต้ตอบที่ปรากฏขึ้น ให้ทำเครื่องหมายที่ช่องสำหรับ "แพ็คเกจการวิเคราะห์" คลิกตกลง 2. กล่องโต้ตอบที่แสดงในรูป 2.2. 3. ในฟิลด์ "ช่วงเวลาการป้อนข้อมูล" ให้ป้อนค่าของข้อมูลเริ่มต้น (บวกหนึ่งเซลล์ว่าง) 4. เลือกช่องทำเครื่องหมาย "ป้ายกำกับ" (หากช่วงอินพุตมีชื่อคอลัมน์) 5. ป้อนค่า (1-α) ในฟิลด์ปัจจัยหน่วง 6. ในฟิลด์ "ช่วงเวลาการป้อนข้อมูล" ให้ป้อนค่าของเซลล์ที่คุณต้องการดูค่าที่ได้รับ 7. ทำเครื่องหมายในช่อง "ตัวเลือก" - "เอาต์พุตกราฟ" เพื่อสร้างโดยอัตโนมัติ ข้าว. 2.2. กล่องโต้ตอบสำหรับการทำให้เรียบแบบเอ็กซ์โปเนนเชียล 3. งานของห้องปฏิบัติการ มีข้อมูลเบื้องต้นเกี่ยวกับปริมาณการผลิตของสถานประกอบการผลิตน้ำมันเป็นเวลา 2 ปี ซึ่งแสดงในตารางที่ 2.3: ตารางที่ 2.3 ข้อมูลเบื้องต้น ดำเนินการปรับให้เรียบแบบเอ็กซ์โพเนนเชียลของซีรีส์ ใช้ค่าสัมประสิทธิ์การทำให้เรียบแบบเอ็กซ์โพเนนเชียลเท่ากับ 0.1; 0.2; 0.3 แสดงความคิดเห็นเกี่ยวกับผลลัพธ์ คุณสามารถใช้สถิติที่แสดงในภาคผนวก 1


หัวข้อ 3. การทำให้ราบรื่นและการพยากรณ์อนุกรมเวลาตามโมเดลแนวโน้ม
3.1. ค่าเฉลี่ยอย่างง่าย

3.2. วิธีเฉลี่ยเคลื่อนที่

3.3. การทำให้เรียบแบบเอ็กซ์โปเนนเชียล

(ต้นฉบับ 1 ชุด; 2 ชุดเรียบ; 3 ส่วนที่เหลือ)3.4. การทำให้เรียบแบบเอ็กซ์โปเนนเชียล
ตามแนวโน้ม (วิธี Holt)
![]()

ที่ α
= 0,1
และ β
= 0,1
3.5. การปรับให้เรียบแบบเอ็กซ์โปเนนเชียลด้วยเทรนด์และความผันแปรของฤดูกาล (วิธีฤดูหนาว)

 .
.

ที่ α
= 0,1
;β
= 0.1; γ = 0.1(1- แถวเดิม 2 แถวเรียบ 3 ที่เหลือ)3.6. การคาดการณ์ตามโมเดลแนวโน้ม
![]() ที่ไหน เอ-จุดตัด; ขมุมเอียง
ที่ไหน เอ-จุดตัด; ขมุมเอียง
![]()

3.7. ตรวจสอบความพอดีของรุ่น


![]()
![]()
3.8. โมเดลพยากรณ์การถดถอย
![]()
![]() .
.




3.9. แบบจำลองการถดถอยพหุตัวแปร

บรรณานุกรม
เวลา มูลค่าที่แท้จริง (ตามจริง) ค่าที่ราบรื่น ข้อผิดพลาดในการคาดการณ์
ปี หนึ่งในสี่ 0,1
0,1
เก่ง ตามสูตร
#ไม่มี
0,00
500,00
-150,00
485,00
485,00
-235,00
461,50
461,50
-61,50
455,35
455,35
-5,35
454,82
454,82
-104,82
444,33
444,33
-244,33
419,90
419,90
-119,90
407,91
407,91
-57,91
402,12
402,12
-202,12
381,91
381,91
-231,91
358,72
358,72
41,28
362,84
362,84
187,16
381,56
381,56
-31,56
378,40
378,40
-128,40
365,56
365,56
184,44
384,01
384,01
165,99
400,61
400,61
-0,61
400,55
400,55
-50,55
395,49
395,49
204,51
415,94
415,94
334,06
449,35
449,35
50,65
454,41
454,41
-54,41
448,97
448,97
201,03
469,07
469,07
380,93


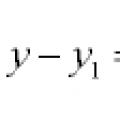 สมการเส้นและเส้นโค้งในระนาบ
สมการเส้นและเส้นโค้งในระนาบ สมการเอกพันธ์ทั่วไป สมการเอกพันธ์ทั่วไปของอันดับสอง
สมการเอกพันธ์ทั่วไป สมการเอกพันธ์ทั่วไปของอันดับสอง ขอบคุณเครื่องหมายจุลภาคเนื่องจากข้อเท็จจริงที่ว่าในพวกเขา
ขอบคุณเครื่องหมายจุลภาคเนื่องจากข้อเท็จจริงที่ว่าในพวกเขา