วิธีการบวกและลบเวกเตอร์ คุณสมบัติของการคูณเวกเตอร์ด้วยตัวเลข

เพื่อการแสดงกฎธรรมชาติที่ถูกต้องในฟิสิกส์ จำเป็นต้องมีเครื่องมือทางคณิตศาสตร์ที่เหมาะสม

ในเรขาคณิตและฟิสิกส์ มีปริมาณที่มีลักษณะเฉพาะและ ค่าตัวเลขและทิศทาง

ขอแนะนำให้แสดงเป็นส่วนกำกับหรือ เวกเตอร์.

ค่าดังกล่าวมีจุดเริ่มต้น (แสดงด้วยจุด) และจุดสิ้นสุดซึ่งระบุด้วยลูกศร ความยาวของส่วนเรียกว่า (ความยาว)

• ความเร็ว;
• การเร่งความเร็ว;
• ชีพจร;
• ความแข็งแกร่ง;
• ช่วงเวลา;
• ความแข็งแกร่ง;
• ย้าย;
• ความแรงของสนาม ฯลฯ

พิกัดเครื่องบิน

มากำหนดส่วนบนระนาบจากจุด A (x1, y1) ไปยังจุด B (x2, y2) พิกัด a (a1, a2) คือตัวเลข a1=x2-x1, a2=y2-y1

โมดูลคำนวณโดยใช้ทฤษฎีบทพีทาโกรัส:

เวกเตอร์ศูนย์มีจุดเริ่มต้นและจุดสิ้นสุด พิกัดและความยาวเป็น 0

ผลรวมของเวกเตอร์

มีอยู่ กฎหลายข้อในการคำนวณจำนวนเงิน

• กฎสามเหลี่ยม
• กฎรูปหลายเหลี่ยม
• กฎสี่เหลี่ยมด้านขนาน

กฎการบวกเวกเตอร์สามารถอธิบายได้โดยใช้ปัญหาจากไดนามิกและกลไก พิจารณาการเพิ่มเวกเตอร์ตามกฎสามเหลี่ยมโดยใช้ตัวอย่างของแรงที่กระทำต่อวัตถุจุดและการกระจัดของวัตถุในอวกาศอย่างต่อเนื่อง

สมมุติว่าร่างกายเคลื่อนที่จากจุด A ไปยังจุด B ก่อน จากนั้นจากจุด B ไปยังจุด C การกระจัดขั้นสุดท้ายคือส่วนที่กำกับจากจุดเริ่มต้น A ไปยังจุดสิ้นสุด C

ผลลัพธ์ของการกระจัดสองครั้งหรือผลรวม s = s1+ s2 วิธีการดังกล่าวเรียกว่า กฎสามเหลี่ยม.

ลูกศรเรียงกันเป็นลูกโซ่ถ้าจำเป็นให้ทำการถ่ายโอนแบบขนาน ส่วนทั้งหมดปิดลำดับ จุดเริ่มต้นเกิดขึ้นพร้อมกับการเริ่มต้นของครั้งแรก จุดสิ้นสุด - กับการสิ้นสุดของครั้งสุดท้าย ในตำราต่างประเทศ วิธีนี้เรียกว่า "หางต่อหัว".

พิกัดของผลลัพธ์ c = a + b เท่ากับผลรวมของพิกัดที่สอดคล้องกันของเงื่อนไข c (a1+ b1, a2+ b2)

ผลรวมของเวกเตอร์ขนาน (คอลิเนียร์) ถูกกำหนดโดยกฎสามเหลี่ยมเช่นกัน

ถ้าส่วนเริ่มต้นสองส่วนตั้งฉากกัน ผลลัพธ์ของการบวกของพวกมันคือด้านตรงข้ามมุมฉากของ สามเหลี่ยมมุมฉาก. ความยาวของผลรวมคำนวณโดยใช้ทฤษฎีบทพีทาโกรัส

ตัวอย่าง:

• ความเร็วของร่างกายโยนในแนวนอน ตั้งฉากอัตราเร่ง ตกฟรี.
• พร้อมชุดยูนิฟอร์ม การเคลื่อนที่แบบหมุน ความเร็วสายร่างกายตั้งฉากกับความเร่งสู่ศูนย์กลาง

การบวกเวกเตอร์สามตัวขึ้นไปผลิตตาม กฎรูปหลายเหลี่ยม, "หางต่อหัว"

สมมุติว่ากำลัง F1 และ F2 ถูกนำไปใช้กับเนื้อหาจุด

ประสบการณ์พิสูจน์ว่าผลรวมของแรงเหล่านี้เทียบเท่ากับการกระทำของแรงหนึ่งที่พุ่งไปตามแนวทแยงมุมตามสี่เหลี่ยมด้านขนานที่สร้างขึ้นบนแรงเหล่านี้ แรงลัพธ์นี้เท่ากับผลรวมของพวกมัน F \u003d F1 + F 2 วิธีการบวกข้างต้นเรียกว่า กฎสี่เหลี่ยมด้านขนาน.

ความยาวในกรณีนี้คำนวณโดยสูตร

โดยที่ θ คือมุมระหว่างด้าน

กฎรูปสามเหลี่ยมและสี่เหลี่ยมด้านขนานสามารถใช้แทนกันได้ ในทางฟิสิกส์ กฎสี่เหลี่ยมด้านขนานมักใช้มากกว่า เนื่องจากปริมาณของแรง ความเร็ว และความเร่งโดยตรงมักใช้กับวัตถุจุดหนึ่ง ในระบบพิกัด 3 มิติ กฎของกล่องจะมีผลบังคับใช้

องค์ประกอบพีชคณิต

1. การเพิ่มเป็นการดำเนินการแบบไบนารี: คุณสามารถเพิ่มได้ครั้งละหนึ่งคู่เท่านั้น
2. การสับเปลี่ยน: ผลรวมจากการเปลี่ยนเงื่อนไขไม่เปลี่ยนแปลง a + b = b + a สิ่งนี้ชัดเจนจากกฎสี่เหลี่ยมด้านขนาน: เส้นทแยงมุมจะเท่ากันเสมอ
3. สมาคม: ผลรวมของจำนวนเวกเตอร์ตามอำเภอใจไม่ได้ขึ้นอยู่กับลำดับของการบวก (a + b) + c = a + (b + c)
4. การรวมเวกเตอร์ศูนย์จะไม่เปลี่ยนทิศทางหรือความยาว: a +0= a
5. สำหรับแต่ละเวกเตอร์จะมี ตรงข้าม. ผลรวมของพวกมันเท่ากับศูนย์ a +(-a)=0 และความยาวเท่ากัน

การลบส่วนที่กำกับจะเทียบเท่ากับการบวกสิ่งที่ตรงกันข้าม พิกัดจะเท่ากับส่วนต่างของพิกัดที่สอดคล้องกัน ความยาวคือ:

สำหรับการลบ คุณสามารถใช้กฎสามเหลี่ยมที่แก้ไข

การคูณด้วยสเกลาร์

ผลของการคูณด้วยสเกลาร์คือเวกเตอร์

พิกัดผลิตภัณฑ์ได้มาจากการคูณด้วยพิกัดที่สอดคล้องกันของแหล่งกำเนิดด้วยสเกลาร์

สเกลาร์ - ค่าตัวเลขด้วยเครื่องหมายบวกหรือลบ มากกว่าหรือน้อยกว่าหนึ่ง

ตัวอย่าง สเกลาร์ในวิชาฟิสิกส์:

• น้ำหนัก;
• เวลา;
• ค่าใช้จ่าย;
• ความยาว;
• สี่เหลี่ยม;
• ปริมาณ;
• ความหนาแน่น;
• อุณหภูมิ;
• พลังงาน.

ตัวอย่าง:

• การกระจัดของวัตถุที่เคลื่อนที่สม่ำเสมอเท่ากับผลคูณของเวลาและความเร็ว s = vt
• โมเมนตัมของวัตถุคือมวลคูณด้วยความเร็ว p = mv
• กฎข้อที่สองของนิวตัน ผลคูณของมวลกายและความเร่งคือ ที่แนบมาแรงลัพธ์ ma=F
• แรงที่กระทำต่ออนุภาคที่มีประจุในสนามไฟฟ้าเป็นสัดส่วนกับประจุ F = qE

ผลคูณสเกลาร์ของส่วนกำกับ a และ b เท่ากับผลคูณของโมดูลและโคไซน์ของมุมระหว่างพวกมัน ผลคูณสเกลาร์ของส่วนตั้งฉากซึ่งกันและกันมีค่าเท่ากับศูนย์

ตัวอย่าง:

งานคือ ผลิตภัณฑ์สเกลาร์แรงและการกระจัด A = Fs

X และ yเรียกว่าเวกเตอร์ zดังนั้น z+y=x.

ตัวเลือกที่ 1.จุดเริ่มต้นของเวกเตอร์ทั้งหมดตรงกับจุดกำเนิด

ให้เราสร้างผลต่างของเวกเตอร์และ .

เพื่อพลอตผลต่างของเวกเตอร์ z=x-yคุณต้องเพิ่มเวกเตอร์ xตรงข้ามกับ yเวกเตอร์ คุณ". ตรงข้าม Vector คุณ"ถูกสร้างขึ้นอย่างง่าย:

เวกเตอร์ คุณ"อยู่ตรงข้ามกับเวกเตอร์ y, เพราะ y+y"= 0 โดยที่ 0 เป็นเวกเตอร์ว่างที่มีขนาดเหมาะสม ถัดไป ดำเนินการเพิ่มเวกเตอร์ xและ คุณ":

จากนิพจน์ (1) จะเห็นได้ว่าการสร้างความแตกต่างของเวกเตอร์ การคำนวณความแตกต่างของพิกัดที่สอดคล้องกันของเวกเตอร์ก็เพียงพอแล้ว xและ y.

ข้าว. หนึ่ง

ในรูป 1 ในปริภูมิสองมิติแสดงถึงความแตกต่างของเวกเตอร์ x=(10,3) และ y=(2,4).

คำนวณ z=x-y=(10-3,3-4)=(7,-1). ให้เราเปรียบเทียบผลลัพธ์ที่ได้กับการตีความทางเรขาคณิต แน่นอน หลังจากสร้างเวกเตอร์แล้ว คุณ"และการเคลื่อนที่ขนานของจุดเริ่มต้นของเวกเตอร์ คุณ"ถึงจุดสิ้นสุดของเวกเตอร์ x, เราได้เวกเตอร์ ย""และหลังจากเพิ่มเวกเตอร์ xและ ย"", เราได้เวกเตอร์ z.

ตัวเลือกที่ 2จุดเริ่มต้นของเวกเตอร์นั้นไม่แน่นอน

ข้าว. 2

ในรูป 2 ในปริภูมิสองมิติคือความแตกต่างของเวกเตอร์ x=ABและ y=ซีดี, ที่ไหน อา(1,0), บี(11,3), ค(1,2), ดี(3.6) ในการคำนวณเวกเตอร์ z=x-y, สร้างขึ้นตรงข้ามกับเวกเตอร์ yเวกเตอร์ คุณ":

ต่อไป คุณต้องเพิ่มเวกเตอร์ xและ คุณ". เวกเตอร์ คุณ"เคลื่อนที่ขนานกันจนจุด ค"ตรงกับจุด บี. การทำเช่นนี้จะคำนวณความแตกต่างในพิกัดของจุด บีและ จาก.

ov ก่อนอื่นคุณต้องเข้าใจแนวคิดเช่นการเลื่อนเวกเตอร์จากจุดที่กำหนด

คำจำกัดความ 1

หากจุด $A$ เป็นจุดเริ่มต้นของเวกเตอร์ $\overrightarrow(a)$ เวกเตอร์ $\overrightarrow(a)$ จะถูกแยกจากจุด $A$ (รูปที่ 1)

รูปที่ 1 $\overrightarrow(a)$ แปลงจากจุด $A$

เราแนะนำทฤษฎีบทต่อไปนี้:

ทฤษฎีบท 1

จากจุดใดๆ $K$ เราสามารถวาดเวกเตอร์ $\overrightarrow(a)$ และเพียงอันเดียวเท่านั้น

การพิสูจน์.

การดำรงอยู่:มีสองกรณีที่ต้องพิจารณาที่นี่:

เวกเตอร์ $\overrightarrow(a)$ เป็นศูนย์

ในกรณีนี้ เห็นได้ชัดว่าเวกเตอร์ที่ต้องการคือเวกเตอร์ $\overrightarrow(KK)$

เวกเตอร์ $\overrightarrow(a)$ ไม่ใช่ศูนย์

ให้จุด $A$ แทนจุดเริ่มต้นของเวกเตอร์ $\overrightarrow(a)$ และจุด $B$ แสดงถึงจุดสิ้นสุดของเวกเตอร์ $\overrightarrow(a)$ ให้เราลากเส้น $b$ ผ่านจุด $K$ ขนานกับเวกเตอร์$\overrightarrow(a)$. ให้เราพลอตส่วน $\left|KL\right|=|AB|$ and $\left|KM\right|=|AB|$ บนเส้นตรงนี้ พิจารณาเวกเตอร์ $\overrightarrow(KL)$ และ $\overrightarrow(KM)$ จากเวกเตอร์ทั้งสองนี้ เวกเตอร์ที่ต้องการจะเป็นเวกเตอร์ที่กำกับร่วมกับเวกเตอร์ $\overrightarrow(a)$ (รูปที่ 2)

รูปที่ 2 ภาพประกอบของทฤษฎีบท 1

เอกลักษณ์:เอกลักษณ์ตามมาทันทีจากการก่อสร้างที่ดำเนินการในส่วนย่อย "การดำรงอยู่"

ทฤษฎีบทได้รับการพิสูจน์แล้ว

การลบเวกเตอร์ กฎข้อที่หนึ่ง

ให้เราได้เวกเตอร์ $\overrightarrow(a)$ และ $\overrightarrow(b)$

คำจำกัดความ 2

ความแตกต่างของเวกเตอร์สองตัว $\overrightarrow(a)$ และ $\overrightarrow(b)$ เป็นเวกเตอร์ $\overrightarrow(c)$ ซึ่งเมื่อเพิ่มลงในเวกเตอร์ $\overrightarrow(b)$ แล้ว จะให้เวกเตอร์ $\ overrightarrow(a)$ นั่นคือ

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

การกำหนด:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

เราจะพิจารณาการสร้างความแตกต่างของเวกเตอร์สองตัวโดยใช้ปัญหา

ตัวอย่าง 1

ให้เวกเตอร์ $\overrightarrow(a)$ และ $\overrightarrow(b)$ สร้างเวกเตอร์ $\overrightarrow(a)-\overrightarrow(b)$

วิธีการแก้.

ให้เราสร้างจุด $O$ โดยพลการและพล็อตเวกเตอร์ $\overrightarrow(OA)=\overrightarrow(a)$ และ $\overrightarrow(OB)=\overrightarrow(b)$ จากจุดนั้น เชื่อมต่อจุด $B$ กับจุด $A$ เราจะได้เวกเตอร์ $\overrightarrow(BA)$ (รูปที่ 3)

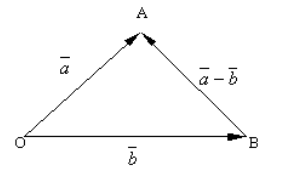
รูปที่ 3 ความแตกต่างของเวกเตอร์สองตัว

จากกฎสามเหลี่ยมในการสร้างผลรวมของเวกเตอร์สองตัว เราจะเห็นว่า

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

จากคำจำกัดความที่ 2 เราจะได้สิ่งนั้น

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

ตอบ:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

จากปัญหานี้ เราได้รับกฎต่อไปนี้ในการค้นหาความแตกต่างของเวกเตอร์สองตัว หากต้องการค้นหาความแตกต่าง $\overrightarrow(a)-\overrightarrow(b)$ ที่คุณต้องการจาก จุดโดยพลการ$O$ กันเวกเตอร์ $\overrightarrow(OA)=\overrightarrow(a)$ and $\overrightarrow(OB)=\overrightarrow(b)$ และรวมจุดสิ้นสุดของเวกเตอร์ที่สองกับจุดสิ้นสุดของเวกเตอร์แรก

การลบเวกเตอร์ กฎข้อที่สอง

จำแนวคิดต่อไปนี้ที่เราต้องการ

คำจำกัดความ 3

เวกเตอร์ $\overrightarrow(a_1)$ ถูกเรียกโดยพลการสำหรับเวกเตอร์ $\overrightarrow(a)$ หากเวกเตอร์เหล่านี้มีทิศทางตรงกันข้ามและมีความยาวเท่ากัน

การกำหนด:เวกเตอร์ $(-\overrightarrow(a))$ อยู่ตรงข้ามกับเวกเตอร์ $\overrightarrow(a)$

ในการที่จะแนะนำกฎข้อที่สองสำหรับผลต่างของเวกเตอร์สองตัว เราต้องแนะนำและพิสูจน์ทฤษฎีบทต่อไปนี้ก่อน

ทฤษฎีบท 2

สำหรับเวกเตอร์สองตัวใด ๆ $\overrightarrow(a)$ และ $\overrightarrow(b)$ ความเท่าเทียมกันต่อไปนี้ถือ:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

การพิสูจน์.

ตามคำจำกัดความที่ 2 เรามี

เพิ่มเวกเตอร์ $\left(-\overrightarrow(b)\right)$ ลงในเวกเตอร์ $\left(-\overrightarrow(b)\right)$ จะได้

เนื่องจากเวกเตอร์ $\overrightarrow(b)$ และ $\left(-\overrightarrow(b)\right)$ อยู่ตรงข้าม ดังนั้น $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ ลูกศรขวา (0)$ เรามี

ทฤษฎีบทได้รับการพิสูจน์แล้ว

จากทฤษฎีบทนี้ เราได้รับกฎต่อไปนี้สำหรับความแตกต่างของเวกเตอร์สองตัว: ในการหาความแตกต่าง $\overrightarrow(a)-\overrightarrow(b)$ เราต้องเลื่อนเวกเตอร์ $\overrightarrow(OA)=\overrightarrow( a)$ จากจุดที่กำหนด $O$ จากนั้นจากจุดที่ได้รับ $A$ ให้เลื่อนเวกเตอร์ $\overrightarrow(AB)=-\overrightarrow(b)$ และเชื่อมต่อจุดเริ่มต้นของเวกเตอร์แรกกับจุดสิ้นสุดของ เวกเตอร์ที่สอง

ตัวอย่างปัญหาแนวคิดความแตกต่างของเวกเตอร์

ตัวอย่าง 2

ให้ $ADCD$ เป็นสี่เหลี่ยมด้านขนานที่มีเส้นทแยงมุมตัดกันที่ $O$ $\overrightarrow(AB)=\overrightarrow(a)$, $\overrightarrow(AD)=\overrightarrow(b)$ (รูปที่ 4). แสดงเวกเตอร์ต่อไปนี้ในรูปของ $\overrightarrow(a)$ และ $\overrightarrow(b)$:

ก) $\overrightarrow(DC)+\overrightarrow(CB)$

b) $\overrightarrow(BO)-\overrightarrow(OC)$

รูปที่ 4 สี่เหลี่ยมด้านขนาน

วิธีการแก้.

ก) เราบวกตามกฎสามเหลี่ยมเราจะได้

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

จากกฎข้อแรกสำหรับผลต่างของเวกเตอร์สองตัว เราจะได้

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

b) ตั้งแต่ $\overrightarrow(OC)=\overrightarrow(AO)$ เราจะได้

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

โดยทฤษฎีบท 2 เรามี

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

ใช้กฎสามเหลี่ยมในที่สุดเราก็มี

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

ov ก่อนอื่นคุณต้องเข้าใจแนวคิดเช่นการเลื่อนเวกเตอร์จากจุดที่กำหนด

คำจำกัดความ 1

หากจุด $A$ เป็นจุดเริ่มต้นของเวกเตอร์ $\overrightarrow(a)$ เวกเตอร์ $\overrightarrow(a)$ จะถูกแยกจากจุด $A$ (รูปที่ 1)

รูปที่ 1 $\overrightarrow(a)$ แปลงจากจุด $A$

เราแนะนำทฤษฎีบทต่อไปนี้:

ทฤษฎีบท 1

จากจุดใดๆ $K$ เราสามารถวาดเวกเตอร์ $\overrightarrow(a)$ และเพียงอันเดียวเท่านั้น

การพิสูจน์.

การดำรงอยู่:มีสองกรณีที่ต้องพิจารณาที่นี่:

เวกเตอร์ $\overrightarrow(a)$ เป็นศูนย์

ในกรณีนี้ เห็นได้ชัดว่าเวกเตอร์ที่ต้องการคือเวกเตอร์ $\overrightarrow(KK)$

เวกเตอร์ $\overrightarrow(a)$ ไม่ใช่ศูนย์

ให้จุด $A$ แทนจุดเริ่มต้นของเวกเตอร์ $\overrightarrow(a)$ และจุด $B$ แสดงถึงจุดสิ้นสุดของเวกเตอร์ $\overrightarrow(a)$ ให้เราลากเส้น $b$ ขนานกับเวกเตอร์ $\overrightarrow(a)$ ผ่านจุด $K$ ให้เราพลอตส่วน $\left|KL\right|=|AB|$ and $\left|KM\right|=|AB|$ บนเส้นตรงนี้ พิจารณาเวกเตอร์ $\overrightarrow(KL)$ และ $\overrightarrow(KM)$ จากเวกเตอร์ทั้งสองนี้ เวกเตอร์ที่ต้องการจะเป็นเวกเตอร์ที่กำกับร่วมกับเวกเตอร์ $\overrightarrow(a)$ (รูปที่ 2)

รูปที่ 2 ภาพประกอบของทฤษฎีบท 1

เอกลักษณ์:เอกลักษณ์ตามมาทันทีจากการก่อสร้างที่ดำเนินการในส่วนย่อย "การดำรงอยู่"

ทฤษฎีบทได้รับการพิสูจน์แล้ว

การลบเวกเตอร์ กฎข้อที่หนึ่ง

ให้เราได้เวกเตอร์ $\overrightarrow(a)$ และ $\overrightarrow(b)$

คำจำกัดความ 2

ความแตกต่างของเวกเตอร์สองตัว $\overrightarrow(a)$ และ $\overrightarrow(b)$ เป็นเวกเตอร์ $\overrightarrow(c)$ ซึ่งเมื่อเพิ่มลงในเวกเตอร์ $\overrightarrow(b)$ แล้ว จะให้เวกเตอร์ $\ overrightarrow(a)$ นั่นคือ

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

การกำหนด:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

เราจะพิจารณาการสร้างความแตกต่างของเวกเตอร์สองตัวโดยใช้ปัญหา

ตัวอย่าง 1

ให้เวกเตอร์ $\overrightarrow(a)$ และ $\overrightarrow(b)$ สร้างเวกเตอร์ $\overrightarrow(a)-\overrightarrow(b)$

วิธีการแก้.

ให้เราสร้างจุด $O$ โดยพลการและพล็อตเวกเตอร์ $\overrightarrow(OA)=\overrightarrow(a)$ และ $\overrightarrow(OB)=\overrightarrow(b)$ จากจุดนั้น เชื่อมต่อจุด $B$ กับจุด $A$ เราจะได้เวกเตอร์ $\overrightarrow(BA)$ (รูปที่ 3)

รูปที่ 3 ความแตกต่างของเวกเตอร์สองตัว

จากกฎสามเหลี่ยมในการสร้างผลรวมของเวกเตอร์สองตัว เราจะเห็นว่า

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

จากคำจำกัดความที่ 2 เราจะได้สิ่งนั้น

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

ตอบ:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

จากปัญหานี้ เราได้รับกฎต่อไปนี้ในการค้นหาความแตกต่างของเวกเตอร์สองตัว เพื่อหาความแตกต่าง $\overrightarrow(a)-\overrightarrow(b)$ จากจุด $O$ โดยพลการ เราต้องแยกเวกเตอร์ $\overrightarrow(OA)=\overrightarrow(a)$ and $\overrightarrow( OB)=\overrightarrow(b )$ และเชื่อมต่อจุดสิ้นสุดของเวกเตอร์ที่สองกับจุดสิ้นสุดของเวกเตอร์แรก

การลบเวกเตอร์ กฎข้อที่สอง

จำแนวคิดต่อไปนี้ที่เราต้องการ

คำจำกัดความ 3

เวกเตอร์ $\overrightarrow(a_1)$ ถูกเรียกโดยพลการสำหรับเวกเตอร์ $\overrightarrow(a)$ หากเวกเตอร์เหล่านี้มีทิศทางตรงกันข้ามและมีความยาวเท่ากัน

การกำหนด:เวกเตอร์ $(-\overrightarrow(a))$ อยู่ตรงข้ามกับเวกเตอร์ $\overrightarrow(a)$

ในการที่จะแนะนำกฎข้อที่สองสำหรับผลต่างของเวกเตอร์สองตัว เราต้องแนะนำและพิสูจน์ทฤษฎีบทต่อไปนี้ก่อน

ทฤษฎีบท 2

สำหรับเวกเตอร์สองตัวใด ๆ $\overrightarrow(a)$ และ $\overrightarrow(b)$ ความเท่าเทียมกันต่อไปนี้ถือ:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

การพิสูจน์.

ตามคำจำกัดความที่ 2 เรามี

เพิ่มเวกเตอร์ $\left(-\overrightarrow(b)\right)$ ลงในเวกเตอร์ $\left(-\overrightarrow(b)\right)$ จะได้

เนื่องจากเวกเตอร์ $\overrightarrow(b)$ และ $\left(-\overrightarrow(b)\right)$ อยู่ตรงข้าม ดังนั้น $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ ลูกศรขวา (0)$ เรามี

ทฤษฎีบทได้รับการพิสูจน์แล้ว

จากทฤษฎีบทนี้ เราได้รับกฎต่อไปนี้สำหรับความแตกต่างของเวกเตอร์สองตัว: ในการหาความแตกต่าง $\overrightarrow(a)-\overrightarrow(b)$ เราต้องเลื่อนเวกเตอร์ $\overrightarrow(OA)=\overrightarrow( a)$ จากจุดที่กำหนด $O$ จากนั้นจากจุดที่ได้รับ $A$ ให้เลื่อนเวกเตอร์ $\overrightarrow(AB)=-\overrightarrow(b)$ และเชื่อมต่อจุดเริ่มต้นของเวกเตอร์แรกกับจุดสิ้นสุดของ เวกเตอร์ที่สอง

ตัวอย่างปัญหาแนวคิดความแตกต่างของเวกเตอร์

ตัวอย่าง 2

ให้ $ADCD$ เป็นสี่เหลี่ยมด้านขนานที่มีเส้นทแยงมุมตัดกันที่ $O$ $\overrightarrow(AB)=\overrightarrow(a)$, $\overrightarrow(AD)=\overrightarrow(b)$ (รูปที่ 4). แสดงเวกเตอร์ต่อไปนี้ในรูปของ $\overrightarrow(a)$ และ $\overrightarrow(b)$:

ก) $\overrightarrow(DC)+\overrightarrow(CB)$

b) $\overrightarrow(BO)-\overrightarrow(OC)$

รูปที่ 4 สี่เหลี่ยมด้านขนาน

วิธีการแก้.

ก) เราบวกตามกฎสามเหลี่ยมเราจะได้

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

จากกฎข้อแรกสำหรับผลต่างของเวกเตอร์สองตัว เราจะได้

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

b) ตั้งแต่ $\overrightarrow(OC)=\overrightarrow(AO)$ เราจะได้

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

โดยทฤษฎีบท 2 เรามี

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

ใช้กฎสามเหลี่ยมในที่สุดเราก็มี

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

วิธีการเพิ่มเวกเตอร์นั้นไม่ชัดเจนสำหรับนักเรียนเสมอไป เด็กไม่รู้ว่าอะไรอยู่เบื้องหลังพวกเขา คุณเพียงแค่ต้องจดจำกฎเกณฑ์และไม่ต้องคิดถึงแก่นแท้ ดังนั้นจึงเป็นเรื่องอย่างแม่นยำเกี่ยวกับหลักการบวกและการลบปริมาณเวกเตอร์ที่ต้องการความรู้จำนวนมาก

การเพิ่มเวกเตอร์สองตัวขึ้นไปจะส่งผลให้เกิดเวกเตอร์อื่นเสมอ ยิ่งไปกว่านั้น มันจะเหมือนเดิมเสมอ โดยไม่คำนึงถึงตำแหน่งที่รับสัญญาณ

บ่อยที่สุดใน หลักสูตรโรงเรียนเรขาคณิตพิจารณาการบวกเวกเตอร์สองตัว สามารถทำได้ตามกฎของรูปสามเหลี่ยมหรือสี่เหลี่ยมด้านขนาน ภาพวาดเหล่านี้ดูแตกต่าง แต่ผลลัพธ์ของการกระทำเหมือนกัน

การบวกตามกฎของรูปสามเหลี่ยมทำอย่างไร?

ใช้เมื่อเวกเตอร์ไม่ใช่คอลลิเนียร์ กล่าวคือไม่นอนบนเส้นเดียวกันหรือขนานกัน

ในกรณีนี้ ต้องเลื่อนเวกเตอร์แรกจากจุดใดจุดหนึ่ง จากจุดสิ้นสุดจะต้องวาดขนานและเท่ากับวินาที ผลลัพธ์จะเป็นเวกเตอร์ที่เริ่มต้นจากจุดเริ่มต้นของอันแรกและสิ้นสุดที่จุดสิ้นสุดของวินาที ภาพวาดดูเหมือนสามเหลี่ยม ดังนั้นชื่อของกฎ

หากเวกเตอร์เป็นแบบ collinear ก็สามารถใช้กฎนี้ได้เช่นกัน เฉพาะภาพวาดเท่านั้นที่จะอยู่ในบรรทัดเดียว

การเพิ่มสี่เหลี่ยมด้านขนานทำอย่างไร?

อีกแล้วเหรอ? ใช้เฉพาะกับ เวกเตอร์ collinear. การก่อสร้างดำเนินการตามหลักการที่แตกต่างกัน ทั้งที่จุดเริ่มต้นก็เหมือนกัน เราต้องเลื่อนเวกเตอร์แรกออกไป และจากจุดเริ่มต้น - ครั้งที่สอง ให้กรอกสี่เหลี่ยมด้านขนานและวาดเส้นทแยงมุมจากจุดเริ่มต้นของเวกเตอร์ทั้งสอง เธอจะเป็นผล นี่คือวิธีการเพิ่มเวกเตอร์ตามกฎสี่เหลี่ยมด้านขนาน

จนถึงตอนนี้มีสอง แต่ถ้ามี 3 หรือ 10 ตัวล่ะ? ใช้เคล็ดลับต่อไปนี้

กฎรูปหลายเหลี่ยมนำไปใช้อย่างไรและเมื่อใด

หากคุณต้องการเพิ่มเวกเตอร์ซึ่งมากกว่าสอง คุณไม่ควรกลัว ก็เพียงพอแล้วที่จะวางพวกเขาทั้งหมดตามลำดับและเชื่อมต่อจุดเริ่มต้นของโซ่กับจุดสิ้นสุด เวกเตอร์นี้จะเป็นผลรวมที่ต้องการ

คุณสมบัติใดที่ถูกต้องสำหรับการดำเนินการกับเวกเตอร์

เกี่ยวกับเวกเตอร์ศูนย์ซึ่งอ้างว่าเมื่อเพิ่มเข้าไปแล้วจะได้รับของเดิม

เกี่ยวกับเวกเตอร์ตรงข้ามนั่นคือประมาณหนึ่งที่มีทิศทางตรงกันข้ามและมีค่าเท่ากันในค่าสัมบูรณ์ ผลรวมของพวกเขาจะเป็นศูนย์

เกี่ยวกับการสลับสับเปลี่ยนของการบวกสิ่งที่ได้รับรู้ตั้งแต่ โรงเรียนประถมศึกษา. การเปลี่ยนตำแหน่งของเงื่อนไขจะไม่เปลี่ยนแปลงผลลัพธ์ กล่าวอีกนัยหนึ่ง ไม่สำคัญว่าจะเลื่อนเวกเตอร์ใดก่อน คำตอบจะยังคงถูกต้องและไม่ซ้ำกัน

เกี่ยวกับการเชื่อมโยงของการบวกกฎหมายนี้อนุญาตให้คุณเพิ่มเวกเตอร์ใดๆ จากสามตัวเป็นคู่และเพิ่มหนึ่งในสามเข้าไปได้ ถ้าเราเขียนสิ่งนี้โดยใช้สัญลักษณ์ เราจะได้สิ่งต่อไปนี้:

แรก + (ที่สอง + สาม) = วินาที + (ที่หนึ่ง + ที่สาม) = ที่สาม + (ที่หนึ่ง + วินาที)

สิ่งที่ทราบเกี่ยวกับความแตกต่างของเวกเตอร์?

ไม่มีการดำเนินการลบแยกต่างหาก นี่เป็นเพราะความจริงที่ว่าในความเป็นจริงนอกจากนี้ มีเพียงคนที่สองเท่านั้นที่ได้รับทิศทางตรงกันข้าม จากนั้นทุกอย่างก็เสร็จสิ้นราวกับว่ามีการพิจารณาการเพิ่มเวกเตอร์ ดังนั้นพวกเขาแทบไม่พูดถึงความแตกต่างของพวกเขา

เพื่อให้การทำงานง่ายขึ้นด้วยการลบ กฎสามเหลี่ยมได้รับการแก้ไข ตอนนี้ (เมื่อลบ) เวกเตอร์ที่สองจะต้องเลื่อนจากจุดเริ่มต้นของอันแรก คำตอบจะเป็นคำตอบที่เชื่อมจุดสิ้นสุดของ minuend กับมัน แม้ว่าจะเลื่อนตามที่อธิบายไว้ก่อนหน้านี้ได้ แต่เพียงเปลี่ยนทิศทางของวินาที

จะหาผลรวมและความแตกต่างของเวกเตอร์ในพิกัดได้อย่างไร

ในปัญหาจะได้รับพิกัดของเวกเตอร์และจำเป็นต้องค้นหาค่าสำหรับค่าสุดท้าย ในกรณีนี้ไม่จำเป็นต้องดำเนินการก่อสร้าง นั่นคือ คุณสามารถใช้สูตรง่ายๆ ที่อธิบายกฎสำหรับการเพิ่มเวกเตอร์ พวกเขามีลักษณะเช่นนี้:

a(x, y, z) + b(k, l, m) = c(x+k, y+l, z+m);

a (x, y, z) -ใน (k, l, m) \u003d c (x-k, y-l, z-m)

มันง่ายที่จะเห็นว่าจำเป็นต้องเพิ่มหรือลบพิกัดนั้นขึ้นอยู่กับงานเฉพาะ

ตัวอย่างแรกพร้อมวิธีแก้ปัญหา

สภาพ. กำหนดสี่เหลี่ยม ABCD ด้านข้างมีขนาด 6 และ 8 ซม. จุดตัดของเส้นทแยงมุมจะมีตัวอักษร O กำกับอยู่ ซึ่งจำเป็นต้องคำนวณความแตกต่างระหว่างเวกเตอร์ AO และ VO

วิธีการแก้. ก่อนอื่นคุณต้องวาดเวกเตอร์เหล่านี้ พวกมันถูกนำจากจุดยอดของสี่เหลี่ยมผืนผ้าไปยังจุดตัดของเส้นทแยงมุม

หากคุณดูภาพวาดอย่างใกล้ชิด คุณจะเห็นว่าเวกเตอร์อยู่ในแนวเดียวกันแล้ว เพื่อให้ส่วนที่สองสัมผัสกับจุดสิ้นสุดของอันแรก เป็นเพียงว่าทิศทางของเขาผิด มันต้องเริ่มจากจุดนี้ นี่คือถ้ามีการเพิ่มเวกเตอร์และในปัญหา - การลบ หยุด. การกระทำนี้หมายความว่าคุณต้องบวกเวกเตอร์ตรงข้าม ดังนั้น VO ต้องถูกแทนที่ด้วย OB และปรากฎว่าเวกเตอร์สองตัวได้สร้างด้านคู่หนึ่งจากกฎสามเหลี่ยมแล้ว ดังนั้นผลลัพธ์ของการบวก นั่นคือ ความแตกต่างที่ต้องการ คือเวกเตอร์ AB

และตรงกับด้านข้างของสี่เหลี่ยม ในการบันทึกคำตอบที่เป็นตัวเลข คุณจะต้องมีสิ่งต่อไปนี้ วาดรูปสี่เหลี่ยมผืนผ้าตามยาวโดยให้ด้านที่ยาวที่สุดอยู่ในแนวนอน การนับจุดยอดเริ่มจากด้านล่างซ้ายและทวนเข็มนาฬิกา จากนั้นความยาวของเวกเตอร์ AB จะเท่ากับ 8 ซม.

ตอบ. ความแตกต่างระหว่าง AO และ VO คือ 8 ซม.

ตัวอย่างที่สองและวิธีแก้ปัญหาโดยละเอียด

สภาพ. รูปสี่เหลี่ยมขนมเปียกปูน ABCD มีเส้นทแยงมุม 12 และ 16 ซม. จุดตัดของพวกมันจะมีตัวอักษร O กำกับ คำนวณความยาวของเวกเตอร์ที่เกิดจากความแตกต่างระหว่างเวกเตอร์ AO และ BO

วิธีการแก้. ให้การกำหนดจุดยอดของรูปสี่เหลี่ยมขนมเปียกปูนเหมือนกับในปัญหาก่อนหน้า ในทำนองเดียวกันกับคำตอบของตัวอย่างแรก ปรากฎว่าผลต่างที่ต้องการเท่ากับเวกเตอร์ AB และไม่ทราบความยาวของมัน การแก้ปัญหาลดลงเหลือเพียงการคำนวณด้านใดด้านหนึ่งของรูปสี่เหลี่ยมขนมเปียกปูน

เพื่อจุดประสงค์นี้ คุณต้องพิจารณาสามเหลี่ยม ABO เป็นรูปสี่เหลี่ยมผืนผ้าเพราะเส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูนตัดกันที่มุม 90 องศา และขาของมันมีขนาดเท่ากับครึ่งหนึ่งของเส้นทแยงมุม นั่นคือ 6 และ 8 ซม. ด้านที่ค้นหาในโจทย์ตรงกับด้านตรงข้ามมุมฉากในสามเหลี่ยมนี้

หากต้องการค้นหา คุณต้องมีทฤษฎีบทพีทาโกรัส กำลังสองของด้านตรงข้ามมุมฉากจะเป็น เท่ากับผลรวมหมายเลข 6 2 และ 8 2 . หลังจากการยกกำลังสอง ค่าที่ได้คือ 36 และ 64 ผลรวมคือ 100 ด้านตรงข้ามมุมฉากคือ 10 ซม.

ตอบ. ความแตกต่างระหว่างเวกเตอร์ AO และ VO คือ 10 ซม.

ตัวอย่างที่สามพร้อมวิธีแก้ปัญหาโดยละเอียด

สภาพ. คำนวณผลต่างและผลรวมของเวกเตอร์สองตัว พิกัดของพวกเขาเป็นที่ทราบกันดีอยู่แล้ว: อันแรกมี 1 และ 2 อันที่สองมี 4 และ 8

วิธีการแก้. ในการหาผลรวม คุณต้องเพิ่มพิกัดที่หนึ่งและที่สองเป็นคู่ ผลลัพธ์จะเป็นตัวเลข 5 และ 10 คำตอบจะเป็นเวกเตอร์ที่มีพิกัด (5; 10)

สำหรับความแตกต่าง คุณต้องลบพิกัด หลังจากดำเนินการนี้แล้ว จะได้รับหมายเลข -3 และ -6 พวกมันจะเป็นพิกัดของเวกเตอร์ที่ต้องการ

ตอบ. ผลรวมของเวกเตอร์คือ (5; 10) ส่วนต่างคือ (-3; -6)

ตัวอย่างที่สี่

สภาพ. ความยาวของเวกเตอร์ AB คือ 6 ซม., BC - 8 ซม. ส่วนที่สองอยู่ห่างจากจุดสิ้นสุดของอันแรกในมุม 90 องศา คำนวณ: ก) ความแตกต่างระหว่างโมดูลของเวกเตอร์ BA และ BC และโมดูลของความแตกต่างระหว่าง BA และ BC; b) ผลรวมของโมดูลเดียวกันและโมดูลัสของผลรวม

วิธีแก้ไข: ก) ความยาวของเวกเตอร์มีอยู่แล้วในปัญหา ดังนั้นจึงไม่ยากที่จะคำนวณความแตกต่าง 6 - 8 = -2. สถานการณ์ที่มีโมดูลัสต่างกันค่อนข้างซับซ้อนกว่า ก่อนอื่นคุณต้องหาว่าเวกเตอร์ใดที่จะเป็นผลจากการลบ เพื่อจุดประสงค์นี้ ควรแยกเวกเตอร์ BA ซึ่งมุ่งไปที่ ฝั่งตรงข้ามเอบี. จากนั้นวาดเวกเตอร์ BC จากจุดสิ้นสุดของมัน โดยชี้ไปในทิศทางตรงกันข้ามกับจุดเดิม ผลลัพธ์ของการลบคือเวกเตอร์ CA โมดูลัสของมันสามารถคำนวณได้โดยใช้ทฤษฎีบทพีทาโกรัส การคำนวณอย่างง่ายนำไปสู่ค่า 10 ซม.

b) ผลรวมของโมดูลของเวกเตอร์คือ 14 ซม. เพื่อหาคำตอบที่สอง จำเป็นต้องมีการแปลงบางส่วน เวกเตอร์ BA อยู่ตรงข้ามกับที่กำหนด - AB เวกเตอร์ทั้งสองถูกชี้นำจากจุดเดียวกัน ในสถานการณ์นี้ คุณสามารถใช้กฎสี่เหลี่ยมด้านขนานได้ ผลลัพธ์ของการบวกจะเป็นเส้นทแยงมุมและไม่ใช่แค่สี่เหลี่ยมด้านขนาน แต่เป็นสี่เหลี่ยม เส้นทแยงมุมเท่ากัน ซึ่งหมายความว่าโมดูลัสของผลรวมเท่ากับในย่อหน้าก่อนหน้า

คำตอบ: ก) -2 และ 10 ซม. b) 14 และ 10 ซม.