คุณรู้สูตรการสร้างความแตกต่างพื้นฐานอะไรบ้าง อนุพันธ์ กฎและสูตรการสร้างความแตกต่าง
ตารางอนุพันธ์ ฟังก์ชั่นเบื้องต้น
คำจำกัดความ 1
การคำนวณอนุพันธ์เรียกว่า ความแตกต่าง.
แสดงถึงอนุพันธ์ $y"$ หรือ $\frac(dy)(dx)$
หมายเหตุ 1
ในการค้นหาอนุพันธ์ของฟังก์ชัน ตามกฎพื้นฐานของการหาอนุพันธ์ ฟังก์ชันนั้นจะถูกแปลงเป็นฟังก์ชันอื่น
ลองดูที่ตารางอนุพันธ์ ให้เราใส่ใจกับความจริงที่ว่าฟังก์ชันหลังจากค้นหาอนุพันธ์แล้วจะถูกเปลี่ยนเป็นฟังก์ชันอื่น
ข้อยกเว้นเพียงอย่างเดียวคือ $y=e^x$ ซึ่งจะกลายเป็นตัวมันเอง
กฎเกณฑ์สำหรับการแยกอนุพันธ์
บ่อยครั้งเมื่อค้นหาอนุพันธ์ คุณไม่เพียงต้องดูตารางอนุพันธ์ แต่ก่อนอื่นให้ใช้กฎของการสร้างความแตกต่างและการพิสูจน์อนุพันธ์ของผลิตภัณฑ์ จากนั้นจึงใช้ตารางอนุพันธ์ของฟังก์ชันพื้นฐานเท่านั้น
1. ค่าคงที่ถูกนำออกจากเครื่องหมายอนุพันธ์
$C$ เป็นค่าคงที่
ตัวอย่างที่ 1
แยกความแตกต่างของฟังก์ชัน $y=7x^4$
สารละลาย.
ค้นหา $y"=(7x^4)"$ นำตัวเลข $7$ ออกจากเครื่องหมายอนุพันธ์ เราจะได้:
$y"=(7x^4)"=7(x^4)"=$
เมื่อใช้ตารางคุณจะต้องค้นหาค่าอนุพันธ์ของฟังก์ชันกำลัง:
$=7 \cdot 4x^3=$
ให้เราแปลงผลลัพธ์เป็นรูปแบบที่ยอมรับในวิชาคณิตศาสตร์:
คำตอบ:$28x^3$.
2. อนุพันธ์ของผลรวม (ผลต่าง) เท่ากับผลรวม (ผลต่าง) ของอนุพันธ์:
$(u \pm v)"=u" \pm v"$.
ตัวอย่างที่ 2
แยกฟังก์ชัน $y=7+x-5x^3+4 \sin x-9\sqrt(x^2)+\frac(4)(x^4) -11\cot x$
สารละลาย.
$y"=(7+x-5x^5+4 \sin x-9\sqrt(x^2)+\frac(4)(x^4) -11\เตียง x)"=$
เราใช้กฎในการหาความแตกต่างของผลรวมและผลต่างของอนุพันธ์:
$=(7)"+(x)"-(5x^5)"+(4 \บาป x)"-(9\sqrt(x^2))"+(\frac(4)(x^4) )"-(11\เตียง x)"=$
โปรดทราบว่าเมื่อสร้างความแตกต่าง พลังและรากทั้งหมดจะต้องถูกแปลงให้อยู่ในรูปแบบ $x^(\frac(a)(b))$;
ลองนำค่าคงที่ทั้งหมดออกจากเครื่องหมายอนุพันธ์:
$=(7)"+(x)"-(5x^5)"+(4\บาป x)"-(9x^(\frac(2)(5)))"+(4x^(-4) )"-(11\เตียง x)"=$
$=(7)"+(x)"-5(x^5)"+4(\บาป x)"-9(x^(\frac(2)(5)))"+4(x^( -4))"-11(\เตียง x)"=$
เมื่อเข้าใจกฎของการสร้างความแตกต่างแล้ว บางส่วน (เช่น สองข้อสุดท้าย) จึงถูกนำไปใช้พร้อมกันเพื่อหลีกเลี่ยงการเขียนสำนวนที่ยาวขึ้นใหม่
เราได้รับนิพจน์จากฟังก์ชันพื้นฐานภายใต้เครื่องหมายอนุพันธ์ ลองใช้ตารางอนุพันธ์:
$=0+1-5 \cdot 5x^4+4\cos x-9 \cdot \frac(2)(5) x^(-\frac(3)(5))+12x^(-5)- 11 \cdot \frac(-1)(\sin^2 x)=$
มาแปลงเป็นรูปแบบที่ยอมรับกันในวิชาคณิตศาสตร์:
$=1-25x^4+4 \cos x-\frac(18)(5\sqrt(x^3))+\frac(12)(x^5) +\frac(11)(\sin^2 x)$
โปรดทราบว่าเมื่อค้นหาผลลัพธ์แล้วเงื่อนไขด้วย พลังเศษส่วนแปลงเป็นรากและลบ - เป็นเศษส่วน
คำตอบ: $1-25x^4+4 \cos x-\frac(18)(5\sqrt(x^3))+\frac(12)(x^5) +\frac(11)(\sin^2 x )$
3. สูตรอนุพันธ์ของผลคูณของฟังก์ชัน:
$(ยูวี)"=u" วี+ยูวี"$.
ตัวอย่างที่ 3
แยกความแตกต่างของฟังก์ชัน $y=x^(11) \ln x$
สารละลาย.
ขั้นแรก เราใช้กฎในการคำนวณอนุพันธ์ของผลคูณของฟังก์ชัน จากนั้นจึงใช้ตารางอนุพันธ์:
$y"=(x^(11) \ln x)"=(x^(11))" \ln x+x^(11) (\lnтx)"=11x^(10) \ln x+x^ (11) \cdot \frac(1)(x)=11x^(10) \ln x-\frac(x^(11))(x)=11x^(10) \ln x-x^(10)=x ^(10) (11 \ln x-1)$
คำตอบ: $x^(10) (11 \ln x-1)$.
4. สูตรอนุพันธ์ของฟังก์ชันบางส่วน:
$(\frac(u)(v))"=\frac(u" v-uv")(v^2)$.
ตัวอย่างที่ 4
แยกความแตกต่างของฟังก์ชัน $y=\frac(3x-8)(x^5-7)$
สารละลาย.
$y"=(\frac(3x-8)(x^5-7))"=$
ตามกฎลำดับความสำคัญ การดำเนินการทางคณิตศาสตร์ขั้นแรกเราทำการหาร จากนั้นจึงบวกและลบ ดังนั้นเราจึงใช้กฎในการคำนวณอนุพันธ์ของผลหารก่อน:
$=\frac((3x-8)" (x^5-7)-(3x-8) (x^5-7)")((x^5-7)^2) =$
ลองใช้กฎของผลรวมและอนุพันธ์ส่วนต่าง เปิดวงเล็บและทำให้นิพจน์ง่ายขึ้น:
$=\frac(3(x^5-7)-5x^4 (3x-8))((x^5-7)^2) =\frac(3x^5-21-15x^5+40x^ 4)((x^5-7)^2) =\frac(-12x^5+40x^4-21)((x^5-7)^2)$
คำตอบ:$\frac(-12x^5+40x^4-21)((x^5-7)^2)$.
ตัวอย่างที่ 5
ลองแยกความแตกต่างของฟังก์ชัน $y=\frac(x^7-2x+3)(x)$ กัน
สารละลาย.
ฟังก์ชัน y คือผลหารของสองฟังก์ชัน ดังนั้นคุณจึงใช้กฎในการคำนวณอนุพันธ์ของผลหารได้ แต่ในกรณีนี้ คุณจะได้ฟังก์ชันที่ยุ่งยาก เพื่อให้ฟังก์ชันนี้ง่ายขึ้น คุณสามารถหารตัวเศษด้วยเทอมของตัวส่วนตามเทอม:
$y=\frac(x^7-13x+9)(x)=x^6-13+\frac(9)(x)$.
ให้เราใช้กฎเพื่อแยกความแตกต่างระหว่างผลรวมและผลต่างของฟังก์ชันกับฟังก์ชันแบบง่าย:
$y"=(x^6-13+\frac(9)(x))"=(x^6)"+(-13)"+9(x^(-1))"=6x^5+ 0+9 \cdot (-x^(-2))=$
$=6x^5-\frac(9)(x^2)$.
คำตอบ: $6x^5-\frac(9)(x^2)$.
1. (f(h(x))) "= f" (h(x)) x ∙ h"(x)
2. (บาป x) " = cos x
3. (cos x) " = - บาป x
4. (tg x) " = 1/cos 2 x
5. (ctg x) " = 1/บาป 2 x
6. (a x) " = a x ∙ ln a
7. (อี x) " = อี x
8. (ล x) " = 1/x
9. (บันทึก a x) " = 1/ x ∙ ln a a
10. (อาร์กซิน x) " = 1/
11. (อาร์คคอส x) " = -1/
12. (ส่วนโค้ง x) " = 1/ 1+x 2
13. (อาร์คซีทีจี x) " = -1/1+x 2
ตัวอย่าง. คำนวณอนุพันธ์
y = บาป 3 (1-x 2)
y"= (บาป 3 (1-x 2))"* (บาป (1-x 2))"* (1-x 2)" = 3 บาป 2 (1-x 2) * cos (1-x 2) ) * (-2x) =
6x * บาป 2 (1-x 2) * cos (1-x 2)
คำนิยาม. ปล่อยให้ฟังก์ชัน y = f(x), x Є(a;b) สามารถหาอนุพันธ์ได้ ณ จุดใดจุดหนึ่ง x o Є(a;b) เช่น ที่จุด x o มีอยู่ จำกัด ลิมΔf(x o) / Δx = f"’ (x o)
ดังนั้นเราจึงได้ Δ f(x o) / Δx = f’(x o) + α โดยที่ α เป็นค่าที่น้อยที่สุดสำหรับ Δ x→0 นั่นคือ ลิม α = 0
นี่หมายถึง Δ f(x o) = f"" (x o) ∙ Δx + α∙ Δx
เทอมที่สองนั้นน้อยมากสำหรับ Δx→0 ดังนั้น d f(x o)= f " (x o)∙ Δx หรือ
ตัวอย่าง. คำนวณส่วนต่างของฟังก์ชัน y = x 2 + cos 3x - 5
ได = (x 2 + cos 3x – 5)"dx = (2x – 3 บาป 3x) dx
คำนิยาม. ฟังก์ชันดิฟเฟอเรนเชียล f(x) ที่กำหนดในช่วงเวลาหนึ่ง x เรียกว่าแอนติเดริเวทีฟสำหรับฟังก์ชัน f(x) ที่กำหนดในช่วงเวลาเดียวกัน ถ้าสำหรับ x ทั้งหมดจากช่วงเวลานี้ F"(x) = f(x) หรือ d F(x) = ฉ(x) * dx
คำนิยาม. เซตของแอนติเดริเวทีฟทั้งหมดสำหรับฟังก์ชัน f(x) ซึ่งกำหนดในช่วง x เรียกว่า not อินทิกรัลที่แน่นอนจากฟังก์ชัน f(x) ในช่วงเวลานี้และเขียนแทนด้วยสัญลักษณ์
∫ f(x) dx = f(x) + C โดยที่ F(x) คือแอนติเดริเวทีฟ
C คือค่าคงที่อนุพันธ์
เพื่อคำนวณ อินทิกรัลไม่ จำกัดมีตารางอินทิกรัลพื้นฐาน (ดูตำราคณิตศาสตร์สำหรับโรงเรียนเทคนิคโดย I.I. Valuta) หน้า 251)
ตัวอย่าง. หา
1. ∫(4x 3 – 6x 2 + 2x + 3)dx = ∫4x 3 dx - ∫6x 2 dx + ∫2xdx + ∫3dx = 4 x 4 /4 – 6 x 3 /3 + 2 x 2 /2 +
2. ∫(5x 4 – 8/cos 2 x + 3√x + 1) dx = ∫ 5x 4 dx – ∫8/cos 2 x * dx + ∫3√x dx + ∫dx =
5 * x 5 /5 – 8 * TG x + 3 x 3/2 / 3/2 + x + C = x 5 - 8 TG x + 2x√x + x + C
3. ∫2 3x * 3 x dx = ∫(2 3 * 3) x dx = ∫ 24 x dx = 24 x / ln 24 + C
คำนิยาม. เพิ่มขั้น F(b) – F (a) ใดๆ ของ ฟังก์ชันต้านอนุพันธ์ f(x) + C เมื่ออาร์กิวเมนต์เปลี่ยนจาก x = a เป็น x = b เรียกว่าอินทิกรัลจำกัดจาก a ถึง b ของฟังก์ชัน f(x) และเขียนแทนด้วย f(x) dx = F(x) = F(b) – F(a) และเรียกว่าสูตรนิวตัน-ไลบ์นิซ
ตัวอย่าง. คำนวณ
1. ∫ (x 2 – 3x + 7)dx = ( x 3 - 3/2 x 2 + 7x) | = (1/3 * 2 3 – 3/2 * 2 2 + 7*2) – (1/3 *(-1) 3 -
3/2 (-1) 2 + 7*(-1)) = 19,5
คำนิยาม. รูปที่ล้อมรอบด้วยกราฟของฟังก์ชัน y = f(x) ส่วนและเส้นตรง x = a และ x = b เรียกว่าสี่เหลี่ยมคางหมูโค้ง
S= ∫ f(x) dx = F(b) – F(a)
ตัวอย่าง. คำนวณพื้นที่ของรูปที่ล้อมรอบด้วย y = ½ x 2 + 1 y = 0 x = -2 x = 3
 |
S= ∫ (1/2 x 2 + 1) dx = (1/6 x 3 + x) | = (1/6 * 3 3 +3) -
- (1/6 (-2) 3 – 2) = 10 5/6
หัวข้อ 1.2. สมการเชิงอนุพันธ์สามัญ
การแก้ปัญหาต่างๆโดยใช้วิธีการ การสร้างแบบจำลองทางคณิตศาสตร์ลงมาเพื่อค้นหาฟังก์ชันที่ไม่รู้จักจากสมการที่มีตัวแปรอิสระ ฟังก์ชันที่ต้องการ และอนุพันธ์ของฟังก์ชันนี้ สมการดังกล่าวเรียกว่าอนุพันธ์
คำนิยาม. การแก้สมการเชิงอนุพันธ์คือฟังก์ชันใดๆ ที่กลับตัว สมการที่กำหนดสู่ตัวตน
ในเชิงสัญลักษณ์ สมการเชิงอนุพันธ์เขียนดังนี้:
F(x, y, y" , y"", .....y (h)) = 0
2x + y – 3y"= 0 y" 2 – 4 = 0, sin y"= cos xy, y"" = 2x คือสมการเชิงอนุพันธ์
คำจำกัดความที่ 2 ลำดับของสมการเชิงอนุพันธ์คือ ลำดับสูงสุดอนุพันธ์ที่รวมอยู่ในสมการนี้
xy" + y – 2 = 0 – สมการอันดับหนึ่ง
y"" + 7y"- 3y = 0 – สมการลำดับที่สาม
คำจำกัดความ 3 สมการเชิงอนุพันธ์อันดับหนึ่งคือสมการในรูปแบบ F(x, y, y") = 0
y"= f(x, y) คือสมการอันดับหนึ่งที่แก้ได้ด้วยอนุพันธ์
คำจำกัดความ 4. คำตอบเฉพาะใดๆ ของสมการเชิงอนุพันธ์เรียกว่าคำตอบบางส่วน
คำจำกัดความ 5. ฟังก์ชั่น กำหนดโดยสูตร y = (e (x,C) หรือ y = y(x,C) – แทน วิธีแก้ปัญหาทั่วไป โซลูชั่นดิฟเฟอเรนเชียล F(x, y, y") = 0 หรือ
ปัญหาคอชี่. เมื่อแก้ไขปัญหาเฉพาะเจาะจง มักจะจำเป็นต้องเลือกคำตอบของสมการเชิงอนุพันธ์จากชุดคำตอบทั้งชุดว่าคำตอบใดคือคำตอบของคำถามที่ตั้งไว้ เพื่อแยกเส้นโค้งอินทิกรัลที่แยกออกจากชุดการแก้ปัญหาทั้งหมด จึงมีการกำหนดเงื่อนไขเริ่มต้นที่เรียกว่าเงื่อนไขเริ่มต้น
ในกรณีของสมการเชิงอนุพันธ์อันดับหนึ่ง y" = f(x, y) เงื่อนไขเริ่มต้นสำหรับการแก้ปัญหา y = y(x) เข้าใจว่าเป็นเงื่อนไขที่ y = y o สำหรับ x = x o นั่นคือ y (x o) = y o โดยที่ x o และ y o ได้รับตัวเลข (ข้อมูลเริ่มต้น) โดยที่สำหรับ x = x o และ y = y o ฟังก์ชัน f(x, y) สมเหตุสมผล นั่นคือ f(x o, y) มี O)
คำจำกัดความ 6. ปัญหาในการหาคำตอบเฉพาะของสมการเชิงอนุพันธ์ที่ตรงตามเงื่อนไขที่กำหนด เงื่อนไขเริ่มต้นเรียกว่าปัญหาคอชี
ในกรณีของสมการเชิงอนุพันธ์อันดับหนึ่ง ปัญหาคอชีมีสูตรดังนี้: หาคำตอบ y = y(x) ของสมการ y" = f(x, y) โดยเป็นไปตามเงื่อนไขเริ่มต้นสำหรับข้อมูลตั้งต้นที่กำหนด ( x โอ โย)
y (x o) = y o หรือในอีกรูปแบบหนึ่ง y x = x0 = y o โดยที่ x o, y o จะได้รับเป็นตัวเลข
คำจำกัดความ 7. สมการเชิงอนุพันธ์เรียกว่าสมการที่มีตัวแปรที่แยกกันได้หากมี มุมมองถัดไป: y"= f 1 (x) f 2 (y) หรือ
dy/f 2 (y) = f 1 (x) dx
ทฤษฎีบท: ถ้าอินทิกรัล ∫dy/f 2 (y) และ ∫ f 1 (x) dx มีอยู่ อินทิกรัลทั่วไปของสมการตัวแปรที่แยกจากกันจะได้มาจากสมการ
F 2 (y) = F 1 (x) + C โดยที่ F 2 (y) และ F 1 (x) คือแอนติเดริเวทีฟของฟังก์ชัน 1/f 2 (y) และ f 1 (x) ตามลำดับ
เมื่อตัดสินใจ สมการเชิงอนุพันธ์ด้วยการแยกตัวแปร คุณสามารถใช้อัลกอริทึมต่อไปนี้:
1) แยกตัวแปร (คำนึงถึงเงื่อนไขเมื่อสามารถทำได้)
2) การรวมสมการที่ได้รับกับตัวแปรที่แยกจากกันทีละเทอมค้นหาอินทิกรัลทั่วไป
3) ค้นหาว่าสมการนั้นมีคำตอบที่ไม่สามารถหาได้จากอินทิกรัลทั่วไปหรือไม่
4) ค้นหา อินทิกรัลบางส่วน(หรือสารละลาย) เป็นไปตามเงื่อนไขเริ่มต้น (ถ้าจำเป็น)
ตัวอย่าง. ค้นหาคำตอบเฉพาะของสมการ 2yy" = 1-3x 2 ถ้า y o = 3 ที่ x o =1
นี่คือสมการตัวแปรที่แยกออกจากกัน ลองจินตนาการว่ามันเป็นดิฟเฟอเรนเชียล:
ดังนั้น 2y * dy = (1-3 x 2) dx
เราอินทิเกรตทั้งสองด้านของความเสมอภาคสุดท้าย หา ∫ 2y * dy = ∫ (1-3x 2) dx เราจะได้ y 2 = x – x 3 + C การแทนที่ ค่าเริ่มต้น y o = 3 x o =1 เราพบ
C: 9 = 1-1+C เช่น ค = 9
ดังนั้นอินทิกรัลบางส่วนที่ต้องการจะเป็น y 2 = x – x 3 + 9 หรือ
x 3 + y 2 – x – 9 = 0
หัวข้อ 1.4. แถว.
คำจำกัดความ 1. ชุดตัวเลขเรียกว่า การแสดงออกของรูป
a 1 + a 2 + …a n + ………. โดยที่ 1, a 2, ……a n เป็นตัวเลขที่อยู่ในระบบตัวเลขจำนวนหนึ่ง
สำหรับการกำหนดอนุกรมแบบย่อ จะใช้เครื่องหมายผลรวม Σ และ
คือ 1 + a 2 + …a n + ……….= Σ a n
คำจำกัดความ 2. ตัวเลข a 1, a 2, ... และ n, ..... เรียกว่าสมาชิกของอนุกรม และ n เรียกว่าเป็นคำทั่วไปของอนุกรม
คำจำกัดความ 3 อนุกรมหนึ่งเรียกว่าการลู่เข้าหากลำดับของผลรวมบางส่วน S 1, S 2, S 3 .........S n, ...... มาบรรจบกันเช่น หากมีขอบเขตจำกัด
เลข S เรียกว่าผลรวมของอนุกรม หากไม่มี Lim S n หรือ Lim S n = ∞ แสดงว่าอนุกรมนั้น
ชั่วโมง →∞ ชั่วโมง →∞
เรียกว่าไดเวอร์เจนต์และไม่มีการกำหนดค่าตัวเลขให้
ทฤษฎีบท 1 ถ้าอนุกรมมาบรรจบกัน คำศัพท์ทั่วไปของอนุกรม a n จะมีค่าเป็นศูนย์
หากไม่มี Lim a n ≠ 0 หรือขีดจำกัดนี้ อนุกรมจะลู่ออก
ทฤษฎีบท 2 ให้อนุกรม a 1 + a 2 + …a n + ……….
มี + 1 มี + 1
สมมติว่า Lim มีอยู่จริงและ Lim = P
ชั่วโมง →∞ n ชั่วโมง →∞ n
1) ถ้า ป<1, то ряд сходится
2) ถ้า P>1 แสดงว่าอนุกรมลู่ออก
คำจำกัดความ 3 ชุดข้อมูลที่มีทั้งพจน์เชิงบวกและเชิงลบเรียกว่าแบบปกติ
คำจำกัดความ 4 ซีรีส์ปกติเรียกว่าการลู่เข้าอย่างสมบูรณ์หากซีรีส์มาบรรจบกัน
|ก 1 | + |ก 2 | - n | + ………. ประกอบด้วยโมดูลของสมาชิก
คำจำกัดความ 5. อนุกรม a 1 + a 2 + …a n + ………. เรียกว่าการลู่เข้าแบบมีเงื่อนไข ถ้ามันมาบรรจบกัน และอนุกรม |a 1 | + |ก 2 | - n | + ………. ประกอบด้วยโมดูลของสมาชิก แตกต่าง
คำจำกัดความ 6. อนุกรมหนึ่งเรียกว่าสลับกัน ถ้าพจน์บวกและลบติดตามกันสลับกัน (a 1 + a 2 + a 3 – a 4 +…..+(-1) n +1 *
ทฤษฎีบท 3 ชุดของสัญญาณสลับมาบรรจบกันถ้า:
1) เงื่อนไขของโมดูลัสลดลง
ก 1 ≥ ก 2 ≥ … ≥a n ≥ ……..
2) คำทั่วไปของมันมีแนวโน้มเป็นศูนย์
ในกรณีนี้ ผลรวม S ของอนุกรมเป็นไปตามความไม่เท่าเทียมกัน 0≤ S ≤a 1
คำจำกัดความ 7. ให้ u 1 (x), u 2 (x),.....u n (x) ... เป็นลำดับของฟังก์ชัน
การแสดงออกของรูปแบบ Σ u n (x) = u 1 (x), u 2 (x),.....u n (x) + เรียกว่าอนุกรมฟังก์ชัน
คำจำกัดความ 8. อนุกรมฟังก์ชันเรียกว่าการลู่เข้าที่จุด x o ถ้า
ชุดตัวเลขΣ คุณ n (x o) = คุณ 1 (x o), คุณ 2 (x o),.....คุณ n (x o) + ......
ที่ได้จากอนุกรมฟังก์ชันโดยการแทนที่ x = x o เป็นอนุกรมลู่เข้า นี้เรียกว่าจุดบรรจบของซีรีส์
คำนิยาม 9 ซีรีย์พาวเวอร์เรียกว่า ช่วงการทำงานใจดี
Σ n (x-x o) n = a o + a 1 (x-x o), a 2 (x-x o) 2 ,.....a n (x-x o) n + ......
โดยที่ x เป็นตัวแปรอิสระ x o เป็นจำนวนคงที่ และ o, a 1, a 2, ... และ n ..... เป็นสัมประสิทธิ์คงที่
ส่วนที่ 2.1 พื้นฐานของคณิตศาสตร์ไม่ต่อเนื่อง
หัวข้อ 2.1. ชุดและความสัมพันธ์ คุณสมบัติของความสัมพันธ์ การดำเนินงานในชุด
เซตเป็นแนวคิดพื้นฐานของทฤษฎีเซตซึ่งถูกนำมาใช้โดยไม่มีคำจำกัดความ อย่างน้อยที่สุด สิ่งที่ทราบเกี่ยวกับเซตก็คือประกอบด้วยองค์ประกอบต่างๆ
 เซต A เรียกว่า
เซต A เรียกว่า
รูปที่ 1
วิธีการระบุชุด:
1. โดยการโอน ได้แก่ รายการองค์ประกอบ
2. ขั้นตอนการสร้างที่อธิบายวิธีการรับองค์ประกอบของชุดจากองค์ประกอบที่ได้รับแล้วหรือวัตถุอื่น ๆ ในกรณีนี้ องค์ประกอบของเซตคือออบเจ็กต์ทั้งหมดที่สามารถสร้างได้โดยใช้ขั้นตอนดังกล่าว
3. คำอธิบายคุณสมบัติลักษณะเฉพาะที่องค์ประกอบต้องมี
ชุด ในรูปแบบต่างๆเซต N ของทั้งหมด ตัวเลขธรรมชาติ 1, 2, 3…..
ก) ไม่สามารถระบุเซต N เป็นรายการได้เนื่องจากค่าอนันต์
b) ขั้นตอนการสร้างประกอบด้วยกฎสองข้อ:
1) 1 โอ เอ็น ; 2) ถ้า n О N ดังนั้น n + 1 О N
ค) คำอธิบาย คุณสมบัติลักษณะองค์ประกอบของเซต N:
N = (x; x – จำนวนเต็ม จำนวนบวก}
การดำเนินงานในชุด
1.  การรวมกันของเซต A และ B เรียกว่า
การรวมกันของเซต A และ B เรียกว่า
ชุดที่ประกอบด้วยองค์ประกอบเหล่านั้นทั้งหมด
ซึ่งอยู่ในชุดอย่างน้อยหนึ่งชุด
A, B. (รูปที่ 2)
รูปที่ 2
2. เรียกว่าจุดตัดของเซต A และ B
 ชุดที่ประกอบด้วยองค์ประกอบเหล่านั้นทั้งหมดเท่านั้น
ชุดที่ประกอบด้วยองค์ประกอบเหล่านั้นทั้งหมดเท่านั้น
ซึ่งเป็นของทั้ง A และ B (ภาพที่ 3)
รูปที่ 3
3. ความแตกต่างของเซต A และ B คือเซต
องค์ประกอบทั้งหมดเหล่านั้นและเฉพาะองค์ประกอบเหล่านั้นของ A เท่านั้น
รูปที่ 4
4.  ส่วนเติมเต็ม (ถึง B) ของเซต A เรียกว่า B
ส่วนเติมเต็ม (ถึง B) ของเซต A เรียกว่า B
|
รูปที่ 5
ดำเนินการกับเซต A = (a, b, c, d) และ B = (c,d,f.g,h)
A U B =(a, b, c, d, e, f.g,h)
ก ∩ B = (ค, ง)
การดำเนินการเสริมในชุด A และ B ไม่สามารถทำได้ เช่น ชุดสากลไม่ได้กำหนดไว้
ความสัมพันธ์เป็นวิธีหนึ่งในการระบุความสัมพันธ์ระหว่างองค์ประกอบของเซต การศึกษาและใช้บ่อยที่สุดคือสิ่งที่เรียกว่าความสัมพันธ์แบบระเหยและแบบสองคู่
สามารถระบุความสัมพันธ์ได้:
รายการ;
เมทริกซ์
คุณสมบัติของความสัมพันธ์
ให้ R เป็นความสัมพันธ์บนเซต M, R ≤ M x M แล้ว:
1. R จะสะท้อนกลับได้ถ้า R a คงไว้สำหรับ Î M ใดๆ
2. R มีฤทธิ์ต้านการสะท้อนแสง ถ้า a Î M แต่ละตัวไม่ถือเป็น R a
3. R มีความสมมาตรถ้า R b หมายถึงbRа
4. R เป็นแบบแอนติสมมาตร ถ้า aRb และ bRa บอกเป็นนัยว่า a=b กล่าวคือ เนื่องจากไม่มีองค์ประกอบที่แตกต่างกัน a และ b (a≠b) aRb และ bRa จะค้างไว้พร้อมกัน
5. R เป็นสกรรมกริยาถ้า aRb และ bRa หมายถึง aRc
หัวข้อที่ 2.2 แนวคิดพื้นฐานของทฤษฎีกราฟ
การแสดงกราฟิกวี ในความหมายกว้างๆ– การแสดงภาพใดๆ ของระบบ กระบวนการ ปรากฏการณ์ที่กำลังศึกษาบนเครื่องบิน สิ่งเหล่านี้อาจรวมถึงภาพวาด ภาพวาด กราฟคุณลักษณะ แผนที่ตำแหน่ง ผังกระบวนการ ไดอะแกรม ฯลฯ
การแสดงกราฟิกเป็นวิธีที่สะดวกในการแสดงเนื้อหา แนวคิดต่างๆเกี่ยวข้องกับวิธีการอื่น ๆ ของการนำเสนออย่างเป็นทางการ
คลาสของวัตถุที่ทรงพลังและได้รับการศึกษามากที่สุดที่เกี่ยวข้องกับการแสดงกราฟิกคือสิ่งที่เรียกว่ากราฟ
ทฤษฎีกราฟมีการนำไปประยุกต์ใช้มากมาย เนื่องจากด้านหนึ่งเป็นภาษาที่มองเห็นได้และเข้าใจได้ และอีกด้านหนึ่งสะดวกสำหรับการวิจัยอย่างเป็นทางการ
การแสดงภาพกราฟิกในความหมายแคบเป็นคำอธิบายของระบบ กระบวนการ หรือปรากฏการณ์ที่กำลังศึกษาโดยใช้ทฤษฎีกราฟในรูปแบบของชุดของวัตถุสองประเภท: จุดยอดและเส้นที่เชื่อมต่อกัน - ขอบหรือส่วนโค้ง
คำจำกัดความ: กราฟ D คือชุดของสองชุด: จุดยอด V และขอบ E ระหว่างองค์ประกอบที่กำหนดความสัมพันธ์ระหว่างเหตุการณ์ - แต่ละขอบ E บังเอิญเท่ากับจุดยอดสองจุด v", v"" V ที่เชื่อมต่อกัน
นอกจากนี้เกี่ยวกับทฤษฎีกราฟเกี่ยวกับองค์ประกอบของกราฟคุณสามารถทำความคุ้นเคยกับประเภทของกราฟและพิจารณาการดำเนินการกับกราฟเหล่านั้นได้คุณสามารถศึกษาส่วนที่ 3 "ทฤษฎีกราฟ" หน้า 195-214 ในหนังสือเรียนสำหรับศตวรรษที่ 21 แก้ไขโดย G.I. Moskinov “ คณิตศาสตร์ไม่ต่อเนื่อง”
สำหรับ การศึกษาด้วยตนเองหัวข้อ 3.1. พื้นฐานของทฤษฎีความน่าจะเป็นและ สถิติทางคณิตศาสตร์- ความน่าจะเป็น ทฤษฎีบทการบวกและคูณความน่าจะเป็น หัวข้อ 3.2. ตัวแปรสุ่ม ฟังก์ชันการกระจายตัว หัวข้อ 3.3. ความคาดหวังและความแปรปรวน ตัวแปรสุ่ม- คุณสามารถใช้วรรณกรรมต่อไปนี้: V.S. Shchipacheva “ความรู้พื้นฐาน คณิตศาสตร์ที่สูงขึ้น" เช่นเดียวกับ I.P. Natanson หลักสูตรระยะสั้นคณิตศาสตร์ขั้นสูงหรือ N.V. Bogomolov บทเรียนภาคปฏิบัติในวิชาคณิตศาสตร์
ปล่อยให้ฟังก์ชัน y = f(x) ถูกกำหนดไว้ในช่วง X อนุพันธ์ฟังก์ชัน y = f(x) ที่จุด x o เรียกว่าลิมิต
=
![]() .
.
ถ้าจำกัดขนาดนี้ มีจำกัด,จากนั้นจึงเรียกฟังก์ชัน f(x) หาความแตกต่างได้ตรงจุด x โอ- ยิ่งกว่านั้น ปรากฎว่าจำเป็นต้องต่อเนื่องกัน ณ จุดนี้
หากขีดจำกัดที่พิจารณาเท่ากับ (หรือ - ) ให้ถือว่าฟังก์ชันอยู่ที่จุดนั้น เอ็กซ์ โอมีความต่อเนื่อง เราจะบอกว่าฟังก์ชัน f(x) มี ณ จุดนั้น เอ็กซ์ โอ อนุพันธ์อนันต์.
อนุพันธ์จะแสดงด้วยสัญลักษณ์
y , f (x o), , .
การหาอนุพันธ์เรียกว่า ความแตกต่างฟังก์ชั่น ความหมายทางเรขาคณิตของอนุพันธ์ก็คืออนุพันธ์คือ ความลาดชันสัมผัสเส้นโค้ง y=f(x) ที่จุดที่กำหนด เอ็กซ์ โอ ; ความหมายทางกายภาพ -คืออนุพันธ์ของเส้นทางเทียบกับเวลาคือ ความเร็วทันทีย้ายจุดที่ การเคลื่อนไหวตรง s = s(t) ณ เวลา t o
ถ้า กับ - จำนวนคงที่และ u = u(x), v = v(x) เป็นฟังก์ชันหาอนุพันธ์ได้ ดังนั้นกฎการหาอนุพันธ์ต่อไปนี้จึงใช้ได้:
1) (ค) " = 0, (ลูกบาศ์ก) " = ลูกบาศ์ก";
2) (ยู+วี)" = ยู"+วี";
3) (ยูวี)" = ยู"วี+วี"ยู;
4) (u/v)" = (u"v-v"u)/v 2;
5) ถ้า y = f(u), u = (x) เช่น y = ฉ((x)) - ฟังก์ชั่นที่ซับซ้อนหรือ การซ้อนทับประกอบด้วยฟังก์ชันหาอนุพันธ์ และ f จากนั้น , หรือ
6) ถ้าสำหรับฟังก์ชัน y = f(x) มีฟังก์ชันหาอนุพันธ์แบบผกผัน x = g(y) และ 0 แล้ว
ขึ้นอยู่กับคำจำกัดความของอนุพันธ์และกฎของการสร้างความแตกต่าง คุณสามารถรวบรวมรายการอนุพันธ์แบบตารางของฟังก์ชันพื้นฐานหลักได้
1. (คุณ )" = คุณ 1 คุณ" ( ร).
2. (คุณ)" = คุณ lna คุณ".
3. (อี ยู)" = อี ยู".
4. (log a u)" = u"/(u ln a)
5. (คุณ)" = คุณ"/u.
6. (บาป u)" = cos u u".
7. (เพราะคุณ)" = - บาป คุณ คุณ".
8. (tg u)" = 1/ cos 2 u u".
9. (ctg u)" = - u" / บาป 2 คุณ.
10. (อาร์คซิน u)" = u" / .
11. (อาร์คคอส u)" = - u" / .
12. (arctg u)" = u"/(1 + u 2).
13. (arcctg u)" = - u"/(1 + u 2).
ลองคำนวณอนุพันธ์ของนิพจน์กำลัง-เลขชี้กำลัง y=u v , (u>0) โดยที่ คุณและ โวลต์สาระสำคัญของฟังก์ชันจาก เอ็กซ์มีอนุพันธ์ ณ จุดที่กำหนด คุณ",วี".
เมื่อหาลอการิทึมของความเท่าเทียมกัน y=u v เราจะได้ ln y = v ln u
การเทียบอนุพันธ์ด้วยความเคารพ เอ็กซ์จากทั้งสองด้านของผลลัพธ์ที่เท่าเทียมกันโดยใช้กฎ 3, 5 และสูตรอนุพันธ์ ฟังก์ชันลอการิทึมเราจะมี:
y"/y = vu"/u +v" ln u, ที่ไหน y" = y (vu"/u +v" ln u)
(u v)"=u v (vu"/u+v" ln u), u > 0.
ตัวอย่างเช่น ถ้า y = x sin x แล้ว y" = x sin x (sin x/x + cos x ln x)
ถ้าฟังก์ชัน y = f(x) สามารถหาอนุพันธ์ได้ ณ จุดนั้น x, เช่น. มีอนุพันธ์จำกัด ณ จุดนี้ คุณ"จากนั้น = y"+ โดยที่ 0 ที่ х 0; ดังนั้น y = y" х + x
ส่วนหลักของการเพิ่มฟังก์ชันซึ่งเป็นเส้นตรงเทียบกับ x เรียกว่า ส่วนต่าง ฟังก์ชั่นและเขียนแทนด้วย dy: dy = y" х หากเราใส่ y=x ในสูตรนี้ เราจะได้ dx = x"х = 1х =х ดังนั้น dy=y"dx นั่นคือสัญลักษณ์ สำหรับสัญกรณ์อนุพันธ์สามารถมองเป็นเศษส่วนได้
การเพิ่มฟังก์ชัน ยคือการเพิ่มขึ้นของพิกัดของเส้นโค้ง และส่วนต่าง d ยคือการเพิ่มขึ้นตามลำดับของแทนเจนต์
ให้เราค้นหาฟังก์ชัน y=f(x) อนุพันธ์ของมัน y = f (x) อนุพันธ์ของอนุพันธ์นี้เรียกว่าอนุพันธ์อันดับสอง ฟังก์ชัน f(x) หรืออนุพันธ์อันดับสอง ![]() .
.
และถูกกำหนดไว้
ต่อไปนี้ถูกกำหนดและกำหนดในลักษณะเดียวกัน:
-
![]() ,
,
อนุพันธ์อันดับสาม
![]()
อนุพันธ์อันดับสี่ - และโดยทั่วไป
-
![]() .
.
อนุพันธ์ลำดับที่ n.15. ตัวอย่างที่ 3
สารละลาย.คำนวณอนุพันธ์ของฟังก์ชัน y=(3x 3 -2x+1)sin x
ตามกฎข้อที่ 3 y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1)คอส x 3.16 ตัวอย่าง
สารละลาย.- ค้นหา y", y = tan x + ![]() =
=
![]()
![]() .
.
อนุพันธ์ลำดับที่ n.17. เมื่อใช้กฎในการแยกผลรวมและผลหาร เราได้: y"=(tgx + )" = (tgx)" + ()" = + หาอนุพันธ์ฟังก์ชั่นที่ซับซ้อน
สารละลาย. y= , u=x 4 +1. ![]() .
.
หา
อนุพันธ์ กฎและสูตรการสร้างความแตกต่าง อนุพันธ์ปล่อยให้ฟังก์ชัน y = f(x) ถูกกำหนดไว้ในช่วง X
= ![]() .
.
ฟังก์ชัน y = f(x) ที่จุด x o เรียกว่าลิมิต มีจำกัด,ถ้าจำกัดขนาดนี้ หาความแตกต่างได้จากนั้นจึงเรียกฟังก์ชัน f(x) ตรงจุด xo
- ยิ่งกว่านั้น ปรากฎว่าจำเป็นต้องต่อเนื่องกัน ณ จุดนี้ หากขีดจำกัดที่พิจารณาเท่ากับ ¥ (หรือ - ¥) ให้ถือว่าฟังก์ชัน ณ จุดนั้น xo มีความต่อเนื่อง เราจะบอกว่าฟังก์ชัน f(x) มี ณ จุดนั้น.
x o อนุพันธ์อนันต์
y ¢, f ¢(x o), , .
การหาอนุพันธ์เรียกว่า ความแตกต่างฟังก์ชั่น ความหมายทางเรขาคณิตอนุพันธ์คืออนุพันธ์คือความชันของเส้นสัมผัสเส้นโค้ง y=f(x) ที่จุดที่กำหนด หากขีดจำกัดที่พิจารณาเท่ากับ ¥ (หรือ - ¥) ให้ถือว่าฟังก์ชัน ณ จุดนั้น; ความหมายทางกายภาพ - คืออนุพันธ์ของเส้นทางเทียบกับเวลาคือความเร็วชั่วขณะของจุดที่เคลื่อนที่ระหว่างการเคลื่อนที่เป็นเส้นตรง s = s(t) ในขณะนี้ t o
ถ้า กับเป็นจำนวนคงที่ และ u = u(x), v = v(x) เป็นฟังก์ชันหาอนุพันธ์ได้ ดังนั้นกฎการหาอนุพันธ์ต่อไปนี้จึงใช้ได้:
1) (ค) " = 0, (ลูกบาศ์ก) " = ลูกบาศ์ก";
2) (ยู+วี)" = ยู"+วี";
3) (ยูวี)" = ยู"วี+วี"ยู;
4) (u/v)" = (u"v-v"u)/v 2;
5) ถ้า y = f(u), u = j(x) เช่น y = ฉ(เจ(x)) - ฟังก์ชั่นที่ซับซ้อนหรือ การซ้อนทับประกอบด้วยฟังก์ชันหาอนุพันธ์ j และ f จากนั้น , หรือ
6) ถ้าสำหรับฟังก์ชัน y = f(x) มีฟังก์ชันหาอนุพันธ์แบบผกผัน x = g(y) และ ¹ 0 แล้ว
ขึ้นอยู่กับคำจำกัดความของอนุพันธ์และกฎของการสร้างความแตกต่าง คุณสามารถรวบรวมรายการอนุพันธ์แบบตารางของฟังก์ชันพื้นฐานหลักได้
1. (ม.)" = ม. ม.- 1 คุณ" (ม. О ร).
2. (a u)" = a u lna× u".
3. (อี ยู)" = อี ยู".
4. (log a u)" = u"/(u ln a)
5. (คุณ)" = คุณ"/u.
6. (บาป u)" = cos u× u".
7. (เพราะคุณ)" = - บาป u× u"
8. (tg u)" = 1/ cos 2 u× u".
9. (ctg u)" = - u" / บาป 2 คุณ.
10. (อาร์คซิน u)" = u" / .
11. (อาร์คคอส u)" = - u" / .
12. (arctg u)" = u"/(1 + u 2).
13. (arcctg u)" = - u"/(1 + u 2).
ลองคำนวณอนุพันธ์ของนิพจน์กำลัง-เลขชี้กำลัง y=u v , (u>0) โดยที่ คุณและ โวลต์สาระสำคัญของฟังก์ชันจาก เอ็กซ์มีอนุพันธ์ ณ จุดที่กำหนด คุณ",วี".
เมื่อหาลอการิทึมของความเท่าเทียมกัน y=u v เราจะได้ ln y = v ln u
การเทียบอนุพันธ์ด้วยความเคารพ เอ็กซ์จากทั้งสองด้านของผลลัพธ์ที่เท่าเทียมกันโดยใช้กฎ 3, 5 และสูตรสำหรับอนุพันธ์ของฟังก์ชันลอการิทึมเราจะได้:
y"/y = vu"/u +v" ln u, ที่ไหน y" = y (vu"/u +v" ln u)
(u v)"=u v (vu"/u+v" ln u), u > 0.
ตัวอย่างเช่น ถ้า y = x sin x แล้ว y" = x sin x (sin x/x + cos x× ln x)
ถ้าฟังก์ชัน y = f(x) สามารถหาอนุพันธ์ได้ ณ จุดนั้น x, เช่น. มีอนุพันธ์จำกัด ณ จุดนี้ คุณ"จากนั้น = y"+a โดยที่ a®0 ที่ Dх® 0; ดังนั้น D y = y" Dх + a x
ส่วนหลักเรียกว่าการเพิ่มฟังก์ชันเชิงเส้นเทียบกับ Dx ฟังก์ชันดิฟเฟอเรนเชียลและเขียนแทนด้วย dy: dy = y" Dx ถ้าเราใส่ y=x ในสูตรนี้ เราจะได้ dx = x"Dx = 1×Dx = Dx ดังนั้น dy=y"dx กล่าวคือ สัญลักษณ์ที่ใช้แทนอนุพันธ์ ถือได้ว่าเป็นเศษส่วน
ฟังก์ชัน D เพิ่มขึ้น ยคือการเพิ่มขึ้นของพิกัดของเส้นโค้ง และส่วนต่าง d ยคือการเพิ่มลำดับของแทนเจนต์
ให้เราค้นหาฟังก์ชัน y=f(x) อนุพันธ์ของมัน y ¢= f ¢(x) อนุพันธ์ของอนุพันธ์นี้เรียกว่า อนุพันธ์อันดับสองฟังก์ชัน f(x) หรือ อนุพันธ์อันดับสองและถูกกำหนดไว้ ![]() .
.
ต่อไปนี้ถูกกำหนดและกำหนดในลักษณะเดียวกัน:
อนุพันธ์อันดับสาม - ![]() ,
,
อนุพันธ์อันดับสี่ - ![]()
และโดยทั่วไป อนุพันธ์ลำดับที่ n - ![]() .
.
ตัวอย่างที่ 3.15. คำนวณอนุพันธ์ของฟังก์ชัน y=(3x 3 -2x+1)×sin x
สารละลาย.ตามกฎข้อที่ 3 y"=(3x 3 -2x+1)"×sin x + (3x 3 -2x+1)×(sin x)" =
= (9x 2 -2)ซิน x + (3x 3 -2x+1)คอส x
ตัวอย่างที่ 3.16- ค้นหา y", y = tan x +
สารละลาย.เมื่อใช้กฎในการแยกผลรวมและผลหาร เราได้: y"=(tgx + )" = (tgx)" + ()" = + ![]() =
= ![]()
![]() .
.
ตัวอย่างที่ 3.17.
ค้นหาอนุพันธ์ของฟังก์ชันเชิงซ้อน y=,
คุณ=x 4 +1.
สารละลาย.ตามกฎการหาความแตกต่างของฟังก์ชันเชิงซ้อน เราจะได้: y" x =y " u u" x =()" u (x 4 +1)" x =(2u + เนื่องจาก u=x 4 +1 ดังนั้น
(2x4+2+ ![]() .
.
ตัวอย่างที่ 3.18.
สารละลาย.ลองจินตนาการว่าฟังก์ชัน y= เป็นการซ้อนทับของฟังก์ชันสองฟังก์ชัน: y = e u และ u = x 2 เรามี: y" x =y " u u" x = (e u)" u (x 2)" x = eu ×2x x2แทน คุณ, เราได้ y=2x .
ตัวอย่างที่ 3.19. ค้นหาอนุพันธ์ของฟังก์ชัน y=ln sin x
สารละลาย.ให้เราแสดงว่า u=sin x จากนั้นอนุพันธ์ของฟังก์ชันเชิงซ้อน y=ln u คำนวณโดยสูตร y" = (ln u)" u (sin x)" x = ![]() .
.
ตัวอย่าง 3.20.ค้นหาอนุพันธ์ของฟังก์ชัน y=
สารละลาย.กรณีของฟังก์ชันที่ซับซ้อนที่ได้รับอันเป็นผลมาจากการซ้อนทับหลายครั้งได้รับการแก้ไขโดยการใช้กฎข้อที่ 5 ตามลำดับ:
![]()
 .
.
ตัวอย่างที่ 3.21- คำนวณอนุพันธ์ y=ln  .
.
สารละลาย.เมื่อหาลอการิทึมและใช้คุณสมบัติของลอการิทึมเราจะได้:
y=5/3ln(x 2 +4) +7/3ln(3x-1)-2/3ln(6x 3 +1)-1/3tg 5x
เมื่อแยกความแตกต่างทั้งสองด้านของความเสมอภาคสุดท้าย เราได้:
สุดขั้วของฟังก์ชัน
ฟังก์ชัน y=f(x) ถูกเรียก เพิ่มขึ้น (ลดลง) ในช่วงเวลาหนึ่ง ถ้าเป็น x 1< x 2 выполняется неравенство f(x 1) < f (x 2) (f(x 1) >ฉ(x 2)).
หากฟังก์ชันหาอนุพันธ์ y = f(x) เพิ่มขึ้น (ลดลง) ในช่วงเวลาหนึ่ง ดังนั้นอนุพันธ์ของฟังก์ชันหาอนุพันธ์ในช่วงเวลานี้ f ¢(x) > 0 (f ¢(x)< 0).
จุด xoเรียกว่า จุด สูงสุดในท้องถิ่น (ขั้นต่ำ) ฟังก์ชัน f(x) ถ้ามีพื้นที่ใกล้เคียงของจุด xoสำหรับทุกจุดที่ความไม่เท่าเทียมกัน f(x) £ f(x о) (f(x) ³ f(x о)) เป็นจริง
เรียกว่าจุดสูงสุดและต่ำสุด จุดสุดขั้วและค่าของฟังก์ชันที่จุดเหล่านี้คือค่าของมัน สุดขั้ว
เงื่อนไขที่จำเป็นสำหรับสุดขั้ว- ถ้าตรงประเด็น xoคือจุดปลายสุดของฟังก์ชัน f(x) ดังนั้น f ¢(x о) = 0 หรือ f ¢(x о) ไม่มีอยู่จริง จุดดังกล่าวเรียกว่า วิกฤต,และฟังก์ชันนั้นถูกกำหนดไว้ที่จุดวิกฤติ ควรค้นหาจุดสุดขีดของฟังก์ชันท่ามกลางจุดวิกฤต
เงื่อนไขแรกเพียงพออนุญาต xo - จุดวิกฤติ- ถ้า f ¢ (x) เมื่อผ่านจุดนั้น xoเปลี่ยนเครื่องหมายบวกเป็นลบแล้วถึงจุดนั้น xoฟังก์ชันมีค่าสูงสุด ไม่เช่นนั้นจะมีค่าต่ำสุด หากเมื่อผ่านจุดวิกฤต อนุพันธ์ไม่เปลี่ยนเครื่องหมาย ให้ไปที่จุดนั้น xoไม่มีความสุดขั้ว
เงื่อนไขที่สองเพียงพอปล่อยให้ฟังก์ชัน f(x) มีอนุพันธ์
f ¢ (x) ใกล้กับจุด xoและอนุพันธ์อันดับสอง ณ จุดนั้นเอง xo- ถ้า f ¢(x о) = 0, >0 (<0), то точка xoคือจุดต่ำสุด (สูงสุด) ในพื้นที่ของฟังก์ชัน f(x) ถ้า =0 คุณต้องใช้เงื่อนไขแรกเพียงพอหรือใช้อนุพันธ์ที่สูงกว่า
บนเซ็กเมนต์ ฟังก์ชัน y = f(x) สามารถเข้าถึงค่าต่ำสุดหรือสูงสุดได้ที่จุดวิกฤติหรือที่ส่วนท้ายของเซ็กเมนต์
ตัวอย่างที่ 3.22ค้นหาสุดขั้วของฟังก์ชัน f(x) = 2x 3 - 15x 2 + 36x - 14
สารละลาย.เนื่องจาก f ¢ (x) = 6x 2 - 30x +36 = 6(x -2)(x - 3) ดังนั้นจุดวิกฤตของฟังก์ชัน x 1 = 2 และ x 2 = 3 Extrema สามารถอยู่ที่เท่านั้น จุดเหล่านี้ เนื่องจากเมื่อผ่านจุด x 1 = 2 อนุพันธ์จะเปลี่ยนเครื่องหมายจากบวกเป็นลบ จากนั้น ณ จุดนี้ฟังก์ชันจะมีค่าสูงสุด เมื่อผ่านจุด x 2 = 3 อนุพันธ์จะเปลี่ยนเครื่องหมายจากลบเป็นบวก ดังนั้นที่จุด x 2 = 3 ฟังก์ชันจึงมีค่าต่ำสุด เมื่อคำนวณค่าของฟังก์ชันที่จุด x 1 = 2 และ x 2 = 3 เราจะพบจุดสุดขีดของฟังก์ชัน: สูงสุด f(2) = 14 และต่ำสุด f(3) = 13
ตัวอย่างที่ 3.23จำเป็นต้องสร้างพื้นที่เป็นรูปสี่เหลี่ยมผืนผ้าใกล้กำแพงหินโดยกั้นรั้ว 3 ด้านด้วยลวดตาข่าย และด้านที่ 4 ติดกับผนัง สำหรับสิ่งนี้ก็มี กเมตรเชิงเส้นของตาข่าย ไซต์จะมีพื้นที่ที่ใหญ่ที่สุดในอัตราส่วนเท่าใด
สารละลาย.ให้เราแสดงด้านข้างของชานชาลาด้วย xและ ย- พื้นที่ของไซต์คือ S = xy อนุญาต ย- นี่คือความยาวของด้านที่อยู่ติดกับผนัง จากนั้นตามเงื่อนไข ความเท่าเทียมกัน 2x + y = a ที่ต้องคงไว้ ดังนั้น y = a - 2x และ S = x(a - 2x) โดยที่ 0 £ x £ a/2 (ความยาวและความกว้างของแพดไม่สามารถเป็นค่าลบได้) S ¢ = a - 4x, a - 4x = 0 ที่ x = a/4 ดังนั้น
y = ก - 2×ก/4 =ก/2 เนื่องจาก x = a/4 เป็นจุดวิกฤติจุดเดียว ลองตรวจสอบว่าสัญญาณของอนุพันธ์เปลี่ยนแปลงไปเมื่อผ่านจุดนี้หรือไม่ ที่เอ็กซ์< a/4 S ¢ >0 และสำหรับ x >a/4 S ¢<0, значит, в точке x=a/4 функция S имеет максимум. Значение функции S(a/4) = a/4(a - a/2) = a 2 /8 (кв. ед).
เนื่องจาก S เปิดต่อเนื่องและค่าของมันที่ปลาย S(0) และ S(a/2) เท่ากับศูนย์ ค่าที่พบจะเป็นค่าที่ใหญ่ที่สุดของฟังก์ชัน ดังนั้น อัตราส่วนภาพที่เหมาะสมที่สุดของไซต์ภายใต้เงื่อนไขที่กำหนดของปัญหาคือ y = 2x
ตัวอย่างที่ 3.24จำเป็นต้องผลิตถังทรงกระบอกปิดที่มีความจุ V=16p » 50 ม. 3 . ขนาดของถังควรมีขนาดเท่าใด (รัศมี R และความสูง H) เพื่อให้ใช้วัสดุในปริมาณน้อยที่สุดในการผลิต
สารละลาย.พื้นที่ผิวทั้งหมดของทรงกระบอกคือ S = 2pR(R+H) เรารู้ปริมาตรของทรงกระบอก V = pR 2 N Þ N = V/pR 2 =16p/ pR 2 = 16/ R 2 นี่หมายถึง S(R) = 2p(R 2 +16/R) เราพบอนุพันธ์ของฟังก์ชันนี้:
S ¢(R) = 2p(2R- 16/R 2) = 4p (R- 8/R 2) S ¢(R) = 0 ที่ R 3 = 8 ดังนั้น
R = 2, H = 16/4 = 4
ในสูตรด้านล่างทั้งหมดจะมีตัวอักษร คุณและ โวลต์มีการระบุฟังก์ชันหาอนุพันธ์ของตัวแปรอิสระ x: ,  และในรูปแบบตัวอักษร ก, ค, เอ็น- คงที่:
และในรูปแบบตัวอักษร ก, ค, เอ็น- คงที่:
1. ![]()
3. 
4. 
5. 
6. 
สูตรที่เหลือเขียนทั้งสำหรับฟังก์ชันของตัวแปรอิสระและสำหรับฟังก์ชันที่ซับซ้อน:
8. 
9. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
7ก. 
8ก. 
9ก. 
11ก. 
12ก. 
13ก. 
16ก. 
17ก. 
มีการจดบันทึกโดยละเอียดขณะแก้ไขตัวอย่างด้านล่าง อย่างไรก็ตาม คุณควรเรียนรู้ที่จะแยกแยะโดยไม่ต้องป้อนข้อมูลระหว่างกลาง
ตัวอย่างที่ 1ค้นหาอนุพันธ์ของฟังก์ชัน  .
.
สารละลาย. ฟังก์ชันนี้คือผลรวมของฟังก์ชันเชิงพีชคณิต เราแยกความแตกต่างโดยใช้สูตร 3, 5, 7 และ 8:


ตัวอย่างที่ 2ค้นหาอนุพันธ์ของฟังก์ชัน 
สารละลาย. เราได้รับสูตร 6, 3, 7 และ 1
ตัวอย่างที่ 3ค้นหาอนุพันธ์ของฟังก์ชัน  และคำนวณมูลค่าของมันได้ที่
และคำนวณมูลค่าของมันได้ที่ 
สารละลาย. นี่คือฟังก์ชันที่ซับซ้อนซึ่งมีอาร์กิวเมนต์ระดับกลาง เรามีสูตร 7a และ 10
 .
.
ตัวอย่างที่ 4ค้นหาอนุพันธ์ของฟังก์ชัน  .
.
สารละลาย. นี่คือฟังก์ชันที่ซับซ้อนซึ่งมีอาร์กิวเมนต์ระดับกลาง เราได้รับสูตร 3, 5, 7a, 11, 16a
ตัวอย่างที่ 5ค้นหาอนุพันธ์ของฟังก์ชัน  .
.
สารละลาย. เราแยกความแตกต่างฟังก์ชันนี้โดยใช้สูตร 6, 12, 3 และ 1:



ตัวอย่างที่ 6ค้นหาอนุพันธ์ของฟังก์ชัน  และคำนวณค่าของมันได้ที่
และคำนวณค่าของมันได้ที่
สารละลาย. ขั้นแรกเราแปลงฟังก์ชันโดยใช้คุณสมบัติของลอการิทึม:

ตอนนี้เราแยกความแตกต่างโดยใช้สูตร 3, 16a, 7 และ 1:


 .
.
ลองคำนวณมูลค่าของอนุพันธ์ที่
ตัวอย่างที่ 7หาอนุพันธ์ของฟังก์ชันแล้วคำนวณค่าได้ที่
สารละลาย. เราใช้สูตร 6, 3, 14a, 9a, 5 และ 1:


 .
.
ลองคำนวณมูลค่าของอนุพันธ์ได้ที่:
 .
.
ความหมายทางเรขาคณิตของอนุพันธ์
อนุพันธ์ของฟังก์ชันมีการตีความทางเรขาคณิตที่เรียบง่ายและสำคัญ
ถ้าฟังก์ชั่น  แยกแยะได้ตรงจุด เอ็กซ์จากนั้นกราฟของฟังก์ชันนี้จะมีแทนเจนต์อยู่ที่จุดที่สอดคล้องกัน และค่าสัมประสิทธิ์เชิงมุมของแทนเจนต์จะเท่ากับค่าของอนุพันธ์ ณ จุดที่เป็นปัญหา
แยกแยะได้ตรงจุด เอ็กซ์จากนั้นกราฟของฟังก์ชันนี้จะมีแทนเจนต์อยู่ที่จุดที่สอดคล้องกัน และค่าสัมประสิทธิ์เชิงมุมของแทนเจนต์จะเท่ากับค่าของอนุพันธ์ ณ จุดที่เป็นปัญหา
ความชันของเส้นสัมผัสกันที่ลากไปยังกราฟของฟังก์ชัน  ณ จุด ( เอ็กซ์ 0 , ที่ 0) เท่ากับค่าอนุพันธ์ของฟังก์ชันที่ x = x 0 เช่น
ณ จุด ( เอ็กซ์ 0 , ที่ 0) เท่ากับค่าอนุพันธ์ของฟังก์ชันที่ x = x 0 เช่น  .
.
สมการของแทนเจนต์นี้คือ
ตัวอย่างที่ 8- เขียนสมการแทนเจนต์ให้กับกราฟของฟังก์ชัน  ที่จุด A (3.6)
ที่จุด A (3.6)
สารละลาย. ในการหาความชันของแทนเจนต์ เราจะหาอนุพันธ์ของฟังก์ชันนี้:
เอ็กซ์= 3:
สมการแทนเจนต์มีรูปแบบ
 , หรือ
, หรือ  , เช่น.
, เช่น. 
ตัวอย่างที่ 9เขียนสมการแทนเจนต์ที่วาดลงบนกราฟของฟังก์ชันที่จุดด้วยแอบซิสซา x=2.
สารละลาย. ก่อนอื่น เรามาค้นหาพิกัดของจุดสัมผัสกันก่อน เนื่องจากจุด A อยู่บนเส้นโค้ง พิกัดจึงเป็นไปตามสมการของเส้นโค้ง เช่น
 ;
;  .
.
สมการของแทนเจนต์ที่ลากไปยังเส้นโค้ง ณ จุดจะมีรูปแบบ  - เพื่อหาความชันของแทนเจนต์ เราจะหาอนุพันธ์ได้:
- เพื่อหาความชันของแทนเจนต์ เราจะหาอนุพันธ์ได้:
 .
.
ความชันของแทนเจนต์เท่ากับค่าอนุพันธ์ของฟังก์ชันที่ เอ็กซ์= 2:

สมการแทนเจนต์คือ:
 ,
,  , เช่น.
, เช่น. 
ความหมายทางกายภาพของอนุพันธ์หากร่างกายเคลื่อนที่เป็นเส้นตรงตามกฎหมาย s=s(ต) จากนั้นในช่วงระยะเวลาหนึ่ง (จากช่วงเวลานั้น ทีจนถึงขณะนี้ ![]() ) มันจะเดินทางได้ไกลพอสมควร จากนั้นจะมีความเร็วเฉลี่ยในการเคลื่อนที่ในช่วงระยะเวลาหนึ่ง
) มันจะเดินทางได้ไกลพอสมควร จากนั้นจะมีความเร็วเฉลี่ยในการเคลื่อนที่ในช่วงระยะเวลาหนึ่ง
ความเร็วการเคลื่อนไหวของร่างกายในช่วงเวลาหนึ่งๆ ทีเรียกว่าขีดจำกัดของอัตราส่วนของเส้นทางต่อการเพิ่มเวลา เมื่อการเพิ่มเวลามีแนวโน้มเป็นศูนย์:
 .
.
ดังนั้นอนุพันธ์ของเวลาของเส้นทาง s ทีเท่ากับความเร็วของการเคลื่อนที่เป็นเส้นตรงของร่างกายในช่วงเวลาที่กำหนด:
 .
.
อัตราของกระบวนการทางกายภาพ เคมี และกระบวนการอื่นๆ ยังแสดงโดยใช้อนุพันธ์อีกด้วย
อนุพันธ์ของฟังก์ชัน  เท่ากับอัตราการเปลี่ยนแปลงของฟังก์ชันนี้สำหรับค่าที่กำหนดของอาร์กิวเมนต์ เอ็กซ์:
เท่ากับอัตราการเปลี่ยนแปลงของฟังก์ชันนี้สำหรับค่าที่กำหนดของอาร์กิวเมนต์ เอ็กซ์:

ตัวอย่างที่ 10สูตรกำหนดกฎการเคลื่อนที่ของจุดในเส้นตรง  (s - เป็นเมตร, t - เป็นวินาที) จงหาความเร็วของจุดเมื่อสิ้นสุดวินาทีแรก
(s - เป็นเมตร, t - เป็นวินาที) จงหาความเร็วของจุดเมื่อสิ้นสุดวินาทีแรก
สารละลาย. ความเร็วของจุด ณ เวลาที่กำหนด เท่ากับอนุพันธ์ของเส้นทาง สตามเวลา ที:
 ,
,
ดังนั้น ความเร็วของจุดที่สิ้นสุดวินาทีแรกคือ 9 เมตร/วินาที
ตัวอย่างที่ 11ร่างที่เหวี่ยงขึ้นไปในแนวตั้งจะเคลื่อนไหวตามกฎข้อใด โวลต์ 0 - ความเร็วเริ่มต้น ก- การเร่งความเร็วของการตกอย่างอิสระของร่างกาย ค้นหาความเร็วของการเคลื่อนไหวนี้ในช่วงเวลาใดก็ได้ ที- ร่างกายจะใช้เวลานานแค่ไหนในการขึ้น และจะสูงได้แค่ไหนหาก โวลต์ 0= 40 เมตร/วินาที?
สารละลาย. ความเร็วของการเคลื่อนที่ของจุด ณ เวลาหนึ่งๆ ทีเท่ากับอนุพันธ์ของเส้นทาง สตามเวลา เสื้อ:
 .
.
เมื่อถึงจุดสูงสุด ความเร็วของร่างกายจะเป็นศูนย์:
,  , ,
, ,  ,
, ![]() กับ.
กับ.
มากกว่า 40/ กวินาทีที่ร่างกายสูงขึ้น
, ![]() ม.
ม.
อนุพันธ์อันดับสอง
อนุพันธ์ของฟังก์ชัน  ในกรณีทั่วไปเป็นฟังก์ชันของ เอ็กซ์- ถ้าเราคำนวณอนุพันธ์ของฟังก์ชันนี้ เราจะได้อนุพันธ์อันดับสองหรืออนุพันธ์อันดับสองของฟังก์ชัน
ในกรณีทั่วไปเป็นฟังก์ชันของ เอ็กซ์- ถ้าเราคำนวณอนุพันธ์ของฟังก์ชันนี้ เราจะได้อนุพันธ์อันดับสองหรืออนุพันธ์อันดับสองของฟังก์ชัน  .
.
อนุพันธ์อันดับสองฟังก์ชั่น  เรียกว่าอนุพันธ์ของอนุพันธ์อันดับหนึ่ง
เรียกว่าอนุพันธ์ของอนุพันธ์อันดับหนึ่ง  .
.
อนุพันธ์อันดับสองของฟังก์ชันแสดงด้วยสัญลักษณ์ตัวใดตัวหนึ่ง - , , . ดังนั้น,  .
.
อนุพันธ์ของคำสั่งใด ๆ ถูกกำหนดและแสดงไว้ในทำนองเดียวกัน ตัวอย่างเช่น อนุพันธ์อันดับสาม:
 หรือ
หรือ  ,
,
ตัวอย่างที่ 12  .
.
สารละลาย. ก่อนอื่น ลองหาอนุพันธ์อันดับแรกกันก่อน
ตัวอย่างที่ 13ค้นหาอนุพันธ์อันดับสองของฟังก์ชัน  และคำนวณมูลค่าของมันได้ที่ x=2.
และคำนวณมูลค่าของมันได้ที่ x=2.
สารละลาย. ก่อนอื่น เรามาค้นหาอนุพันธ์อันดับแรกกันก่อน:
เมื่อสร้างความแตกต่างอีกครั้ง เราจะพบอนุพันธ์อันดับสอง:
ให้เราคำนวณมูลค่าของอนุพันธ์อันดับสองที่ x=2- เรามี
ความหมายทางกายภาพของอนุพันธ์อันดับสอง
หากร่างกายเคลื่อนไหวเป็นเส้นตรงตามกฎหมาย ส = ส(ที)แล้วอนุพันธ์อันดับสองของเส้นทาง สตามเวลา ทีเท่ากับความเร่งของร่างกายในช่วงเวลาหนึ่งๆ เสื้อ:

ดังนั้นอนุพันธ์อันดับ 1 แสดงถึงความเร็วของกระบวนการหนึ่ง และอนุพันธ์อันดับ 2 แสดงถึงลักษณะความเร่งของกระบวนการเดียวกัน
ตัวอย่างที่ 14จุดเคลื่อนที่เป็นเส้นตรงตามกฎหมาย ![]() - จงหาความเร็วและความเร่งของการเคลื่อนที่
- จงหาความเร็วและความเร่งของการเคลื่อนที่  .
.
สารละลาย. ความเร็วของการเคลื่อนไหวของร่างกาย ณ เวลาหนึ่งจะเท่ากับอนุพันธ์ของเส้นทาง สตามเวลา เสื้อและความเร่งเป็นอนุพันธ์อันดับสองของเส้นทาง สตามเวลา ที- เราพบ:
 - แล้ว ;
- แล้ว ;
- แล้ว 
ตัวอย่างที่ 15ความเร็วของการเคลื่อนที่เป็นเส้นตรงจะเป็นสัดส่วนกับรากที่สองของระยะทางที่เคลื่อนที่ได้ (เช่น ในการตกอย่างอิสระ) พิสูจน์ว่าการเคลื่อนไหวนี้เกิดขึ้นภายใต้อิทธิพลของแรงคงที่
สารละลาย. ตามกฎของนิวตัน แรง F ที่ทำให้เกิดการเคลื่อนที่นั้นแปรผันตามความเร่ง กล่าวคือ
 หรือ
หรือ 
ตามเงื่อนไข  - เราพบการสร้างความแตกต่างความเท่าเทียมกันนี้
- เราพบการสร้างความแตกต่างความเท่าเทียมกันนี้

ดังนั้นกำลังรักษาการ  .
.
การประยุกต์อนุพันธ์ในการศึกษาฟังก์ชัน.
1) เงื่อนไขในการเพิ่มฟังก์ชัน: ฟังก์ชันหาอนุพันธ์ y = f(x) จะเพิ่มขึ้นแบบซ้ำซากในช่วงเวลา X ถ้าหากอนุพันธ์ของมันมากกว่าศูนย์เท่านั้น กล่าวคือ y = ฉ(x) ฉ’(x) > 0- เงื่อนไขนี้ในเชิงเรขาคณิตหมายความว่า แทนเจนต์ของกราฟของฟังก์ชันนี้ก่อให้เกิดมุมแหลมโดยมีทิศทางบวกไปยังแกน oX
2) เงื่อนไขสำหรับฟังก์ชันที่ลดลง: ฟังก์ชันหาอนุพันธ์ y = f(x) ลดลงแบบซ้ำซากในช่วงเวลา X ถ้าหากอนุพันธ์ของมันมีค่าน้อยกว่าศูนย์เท่านั้น เช่น
y = ฉ(x)↓ f’(x) เงื่อนไขนี้ในเชิงเรขาคณิตหมายถึงว่าเส้นสัมผัสของกราฟของฟังก์ชันนี้ก่อตัวขึ้น มุมป้านโดยมีทิศทางบวกของแกนโอ้)
3) เงื่อนไขสำหรับความคงตัวของฟังก์ชัน:ฟังก์ชันหาอนุพันธ์ y = f(x) คงที่ในช่วง X ถ้าหากอนุพันธ์ของมันเท่ากับศูนย์เท่านั้น เช่น y = ฉ(x) - ค่าคงที่ ฉ'(x) = 0 .เงื่อนไขนี้ในเชิงเรขาคณิตหมายความว่าแทนเจนต์กับกราฟของฟังก์ชันนี้ขนานกับแกน oX นั่นคือ α = 0)
เอ็กซ์ตรีมของฟังก์ชัน
คำจำกัดความ 1: เรียกจุด x = x 0 จุดต่ำสุดฟังก์ชัน y = f(x) หากจุดนี้มีย่านใกล้เคียงที่ทุกจุด (ยกเว้นจุดนั้นเอง) เป็นไปตามความไม่เท่าเทียมกัน f(x)> f(x 0)
คำจำกัดความ 2:เรียกจุด x = x 0 จุดสูงสุดฟังก์ชัน y = f(x) หากจุดนี้มีย่านใกล้เคียงที่ทุกจุด (ยกเว้นจุดนั้นเอง) เป็นไปตามความไม่เท่าเทียมกัน f(x)< f(x 0).
คำจำกัดความที่ 3: จุดต่ำสุดหรือสูงสุดของฟังก์ชันเรียกว่าจุด สุดขั้ว- ค่าของฟังก์ชัน ณ จุดนี้เรียกว่าค่าสุดขีด
หมายเหตุ: 1. ค่าสูงสุด (ต่ำสุด) ไม่จำเป็นต้องเป็นค่าที่ใหญ่ที่สุด (น้อยที่สุด) ของฟังก์ชัน
2. ฟังก์ชันสามารถมีค่าสูงสุดหรือต่ำสุดได้หลายค่า
3. ฟังก์ชันที่กำหนดไว้ในช่วงเวลาหนึ่งสามารถเข้าถึงได้ถึงจุดสุดขีดเท่านั้น จุดภายในส่วนนี้
5) ข้อกำหนดเบื้องต้นสุดขีด:ถ้าฟังก์ชัน y = f(x) มีปลายสุดที่จุด x = x 0 แล้ว ณ จุดนี้อนุพันธ์จะเป็นศูนย์หรือไม่มีเลย จุดเหล่านี้เรียกว่า จุดวิกฤติประเภทที่ 1.
6) เงื่อนไขที่เพียงพอการมีอยู่ของฟังก์ชันสุดขั้ว:ปล่อยให้ฟังก์ชัน y = f(x) ต่อเนื่องกันในช่วง X และมีจุดวิกฤตแบบแรก x = x 0 ภายในช่วงเวลานี้ จากนั้น:
ก) ถ้าจุดนี้มีพื้นที่ใกล้เคียงสำหรับ x< х 0 f’(x) < 0, а при x>x 0 f’(x) > 0 แล้ว x = x 0 คือจุด ขั้นต่ำฟังก์ชัน y = f(x);
b) ถ้าจุดนี้มีพื้นที่ใกล้เคียงสำหรับ x< х 0 f’(x) >0 และสำหรับ x> x 0
ฉ'(x)< 0, то х = х 0 является точкой สูงสุดฟังก์ชัน y = f(x);
c) หากจุดนี้มีพื้นที่ใกล้เคียงโดยทั้งทางขวาและทางซ้ายของจุด x 0 สัญญาณของอนุพันธ์เหมือนกัน จากนั้นที่จุด x 0 จะไม่มีจุดสุดโต่ง
ช่วงเวลาของฟังก์ชันที่ลดลงหรือเพิ่มขึ้นเรียกว่าช่วงเวลา ความน่าเบื่อ
คำจำกัดความ 1:เรียกว่าเส้นโค้ง y = f(x) นูนลงในช่วงเวลาก< х <в, если она лежит выше касательной в любой точке этого промежутка и кривая у = f(x) называется นูนขึ้นในช่วงเวลาก< х <в, если она лежит ниже касательной в любой точке этого промежутка.
คำจำกัดความ 2:เรียกว่าช่วงเวลาที่กราฟของฟังก์ชันนูนขึ้นหรือลง ช่วงเวลานูนกราฟิกฟังก์ชั่น
สภาพที่เพียงพอสำหรับความนูนของเส้นโค้งกราฟของฟังก์ชันหาอนุพันธ์ Y = f(x) คือ นูนขึ้นในช่วงเวลาก< х <в, если f”(x) < 0 и นูนลง, ถ้า f”(x) > 0
คำจำกัดความ 1:จุดที่อนุพันธ์อันดับสองเป็นศูนย์หรือไม่มีเรียกว่า จุดวิกฤติประเภทที่สอง.
คำจำกัดความ 2:จุดบนกราฟของฟังก์ชัน Y = f(x) ซึ่งแยกช่วงนูนของทิศทางตรงกันข้ามของกราฟนี้เรียกว่าจุด โรคติดเชื้อ
จุดเปลี่ยน
ตามกฎข้อที่ 3 y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1)คอส x: กำหนดฟังก์ชัน y = x 3 - 2x 2 + 6x - 4 ตรวจสอบฟังก์ชันเพื่อหาช่วงของความน่าเบื่อและจุดสุดขั้ว กำหนดทิศทางของความนูนและจุดเปลี่ยนเว้า
วิธีแก้: 1. ค้นหาโดเมนของคำจำกัดความของฟังก์ชัน: D(y) = ;
2. มาหาอนุพันธ์อันดับหนึ่งกัน: y’ = 3x 2 - 4x+ 6;
3. มาแก้สมการกัน: y’ = 0, 3x 2 - 4x+ 6 = 0, D 0 จากนั้นสมการนี้ไม่มีคำตอบ ดังนั้นจึงไม่มีจุดสุดขั้ว y’ จากนั้นฟังก์ชันจะเพิ่มขึ้นทั่วทั้งขอบเขตคำจำกัดความ
4. ค้นหาอนุพันธ์อันดับสอง: y” = 6x - 4;
5. แก้สมการ: y” = 0, 6x - 4 = 0, x =
คำตอบ: ( ; - ) - จุดเปลี่ยนเว้า ฟังก์ชันจะนูนขึ้นที่ x และนูนขึ้นที่ x
เส้นกำกับ
1. คำจำกัดความ: เส้นกำกับของเส้นโค้งคือเส้นตรงที่กราฟของฟังก์ชันที่กำหนดเข้าใกล้โดยไม่มีขีดจำกัด
2. ประเภทของเส้นกำกับ:
1) เส้นกำกับแนวตั้ง- กราฟของฟังก์ชัน y = f(x) มีเส้นกำกับแนวตั้ง ถ้า สมการเส้นกำกับแนวตั้งมีรูปแบบ x = a
2) เส้นกำกับแนวนอน- กราฟของฟังก์ชัน y = f(x) มีเส้นกำกับแนวนอนถ้า ![]() - สมการเส้นกำกับแนวนอนมีรูปแบบ y = b
- สมการเส้นกำกับแนวนอนมีรูปแบบ y = b
ตัวอย่างที่ 1: สำหรับฟังก์ชัน y = ค้นหาเส้นกำกับ
3) เส้นกำกับเฉียงเส้นตรง y = kx + b เรียกว่าเส้นกำกับเอียงของกราฟของฟังก์ชัน y = f(x) ถ้า ค่าของ k และ b คำนวณโดยใช้สูตร: k = ; ข = .
สารละลาย: ![]() จากนั้น y = 0 - เส้นกำกับแนวนอน;
จากนั้น y = 0 - เส้นกำกับแนวนอน;
![]() (ตั้งแต่ x - 3 ≠ 0, x ≠3) ดังนั้น x = 3 จึงเป็นเส้นกำกับแนวตั้ง
(ตั้งแต่ x - 3 ≠ 0, x ≠3) ดังนั้น x = 3 จึงเป็นเส้นกำกับแนวตั้ง ![]() ,ท. e. k = 0 ดังนั้นเส้นโค้งจึงไม่มีเส้นกำกับเฉียง
,ท. e. k = 0 ดังนั้นเส้นโค้งจึงไม่มีเส้นกำกับเฉียง
ตัวอย่างที่ 2: สำหรับฟังก์ชัน y = ค้นหาเส้นกำกับ
วิธีแก้: x 2 - 25 ≠ 0 สำหรับ x ≠ ± 5 จากนั้น x = 5 และ x = - 5 เป็นเส้นกำกับแนวนอน
y = ดังนั้นเส้นโค้งไม่มีเส้นกำกับแนวตั้ง
เค = ; b = เช่น y = 5x - เส้นกำกับเฉียง
ตัวอย่างฟังก์ชันการลงจุด.
ตัวอย่างที่ 1
สำรวจฟังก์ชันและสร้างกราฟของฟังก์ชัน y = x 3 - 6x 2 + 9x - 3
1. ค้นหาโดเมนของคำจำกัดความของฟังก์ชัน: D(y) = R
y(- x) = (- x) 3 - 6·(- x) 2 + 9·(-x) - 3 = - x 3 - 6x 2 - 9x - 3 = - (x 3 + 6x 2 + 9x + 3) กล่าวคือ
(y = x 5 - x 3 - คี่, y = x 4 + x 2 - คู่)
3. ไม่เป็นระยะๆ
4. ค้นหาจุดตัดด้วยแกนพิกัด: ถ้า x = 0 ดังนั้น y = - 3 (0; - 3)
ถ้า Y = 0 แสดงว่า x หาได้ยาก
5. มาหาเส้นกำกับของกราฟของฟังก์ชันกันดีกว่า: ไม่มีเส้นกำกับแนวตั้งเพราะว่า ไม่มีค่า x ที่ฟังก์ชันไม่แน่นอน y = คือ ไม่มีเส้นกำกับแนวนอน
k = นั่นคือไม่มีเส้นกำกับแบบเฉียง
6. เราศึกษาฟังก์ชันสำหรับช่วงเวลาของความน่าเบื่อและสุดขั้ว: y’ = 3x 2 - 12x + 9,
y’= 0. 3x 2 - 12x + 9 = 0 x 1 = 1; x 2 = 3 - จุดวิกฤตของประเภทที่ 1
มาดูสัญญาณของอนุพันธ์กันดีกว่า: y’(0) = 9 > 0; คุณ'(2) = - 3< 0; y’(4) = 9 > 0
y สูงสุด = y(1) = 1, (1;1) - จุดสูงสุด; y min = y(3) = - 3, (3; - 3) - จุดต่ำสุด, ฟังก์ชัน y สำหรับ x และ y ![]() .
.
7. เราตรวจสอบฟังก์ชันสำหรับช่วงนูนและจุดเปลี่ยนเว้า:
y” = (y’)’ = (3x 2 - 12x + 9)’ = 6x - 12, y” = 0, 6x - 12 = 0 x = 2 - จุดวิกฤติของประเภทที่ 1
ให้เราพิจารณาสัญญาณของอนุพันธ์อันดับสอง: y”(0) = - 12< 0; y”(3) = 6 > 0
Y(2) = - 1 (2; - 1) - จุดเปลี่ยนเว้า ฟังก์ชันจะนูนขึ้นที่ x และนูนลงที่ x
8. ประเด็นเพิ่มเติม:
| เอ็กซ์ | - 1 | |
| ที่ | - 19 |
9. มาสร้างกราฟของฟังก์ชันกันดีกว่า:
สำรวจฟังก์ชันและสร้างกราฟของฟังก์ชัน y =
1. มาหาโดเมนของคำจำกัดความของฟังก์ชันกันดีกว่า: 1 - x ≠ 0, x ≠ 1, D(y) =
2. เรามาดูกันว่า ฟังก์ชั่นนี้คู่หรือคี่: ![]() ,
,
y(- x) ≠ y(x) - ไม่เป็นคู่ และ y(- x) ≠ - y(x) - ไม่แปลก
3. ไม่เป็นระยะๆ
4. ค้นหาจุดตัดด้วยแกนพิกัด: x = 0 จากนั้น y = - 2; y = 0 แล้ว ![]() เช่น (0; - 2); -
เช่น (0; - 2); -
5. เรามาค้นหาเส้นกำกับของกราฟของฟังก์ชันกัน: เพราะว่า x ≠ 1 จากนั้นเส้นตรง x = 1 จะเป็นเส้นกำกับแนวตั้ง
 สมการลอการิทึม
สมการลอการิทึม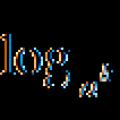 เทคนิคการแก้สมการลอการิทึม
เทคนิคการแก้สมการลอการิทึม การวิเคราะห์ตนเองของครูนักบำบัดการพูด
การวิเคราะห์ตนเองของครูนักบำบัดการพูด