คำจำกัดความคลาสสิกของทฤษฎีความน่าจะเป็น ความน่าจะเป็นแบบคลาสสิกและคุณสมบัติของมัน
ความน่าจะเป็นของเหตุการณ์เป็นที่เข้าใจกันว่ามีอยู่บ้าง ลักษณะเชิงตัวเลขโอกาสที่เหตุการณ์นี้จะเกิดขึ้น มีหลายวิธีในการพิจารณาความน่าจะเป็น
ความน่าจะเป็นของเหตุการณ์ กเรียกว่าอัตราส่วนของจำนวนผลลัพธ์ที่เอื้ออำนวยต่อเหตุการณ์นี้ จำนวนทั้งหมดเป็นไปได้เท่าเทียมกันทั้งหมดเข้ากันไม่ได้ ผลลัพธ์เบื้องต้น, รวมตัวกันเป็นกลุ่มสมบูรณ์. ดังนั้นความน่าจะเป็นของเหตุการณ์ กถูกกำหนดโดยสูตร
ที่ไหน ม– จำนวนผลลัพธ์เบื้องต้นที่น่าพอใจ ก, n– จำนวนผลการทดสอบเบื้องต้นที่เป็นไปได้ทั้งหมด
ตัวอย่างที่ 3.1ในการทดลองขว้าง ลูกเต๋าจำนวนผลลัพธ์ทั้งหมด nเท่ากับ 6 และทั้งหมดเป็นไปได้เท่ากัน ให้จัดงาน กหมายถึง การปรากฏของเลขคู่ จากนั้นสำหรับเหตุการณ์นี้ผลลัพธ์ที่ดีจะเป็นเลข 2, 4, 6 เลขของพวกเขาคือ 3 ดังนั้นความน่าจะเป็นของเหตุการณ์นี้ กเท่ากับ
![]()
ตัวอย่างที่ 3.2ความน่าจะเป็นที่ตัวเลขสองหลักที่เลือกโดยการสุ่มจะมีตัวเลขเหมือนกันคือเท่าไร?
ตัวเลขสองหลักเป็นตัวเลขตั้งแต่ 10 ถึง 99 มีทั้งหมด 90 หมายเลข ตัวเลขที่เหมือนกันมี 9 หมายเลข (ได้แก่ หมายเลข 11, 22, ..., 99) ตั้งแต่ใน ในกรณีนี้ ม=9, n=90 แล้ว ![]()
ที่ไหน ก– เหตุการณ์ “ตัวเลขที่มีตัวเลขเท่ากัน”
ตัวอย่างที่ 3.3ในชุดมี 10 ส่วน 7 ชิ้นเป็นมาตรฐาน ค้นหาความน่าจะเป็นที่จากหกส่วนที่สุ่มมา มี 4 ส่วนที่เป็นค่ามาตรฐาน
จำนวนผลการทดสอบเบื้องต้นที่เป็นไปได้ทั้งหมดจะเท่ากับจำนวนวิธีที่สามารถแยก 6 ส่วนออกจาก 10 ส่วนได้ กล่าวคือ จำนวนชุดค่าผสมของ 10 องค์ประกอบจาก 6 องค์ประกอบในแต่ละส่วน ให้เรากำหนดจำนวนผลลัพธ์ที่เป็นประโยชน์ต่อเหตุการณ์ที่เราสนใจ ก(ในบรรดาชิ้นส่วนที่นำมาหกชิ้นนั้นมีชิ้นส่วนมาตรฐาน 4 ชิ้น) ชิ้นส่วนมาตรฐานสี่ชิ้นสามารถนำมาจากชิ้นส่วนมาตรฐานเจ็ดชิ้นได้ด้วยวิธีที่แตกต่างกัน ในเวลาเดียวกัน ส่วนที่เหลือ 6-4=2 ส่วนจะต้องไม่ได้มาตรฐาน แต่คุณสามารถนำส่วนที่ไม่ได้มาตรฐานสองส่วนจาก 10-7=3 ส่วนที่ไม่ได้มาตรฐานด้วยวิธีที่ต่างกัน ดังนั้นจำนวนผลลัพธ์ที่ดีจึงเท่ากับ
จากนั้นความน่าจะเป็นที่ต้องการจะเท่ากับ

คุณสมบัติต่อไปนี้เป็นไปตามคำจำกัดความของความน่าจะเป็น:
1. ความน่าจะเป็นของเหตุการณ์ที่เชื่อถือได้มีค่าเท่ากับหนึ่ง
แท้จริงแล้ว หากเหตุการณ์นั้นเชื่อถือได้ ผลการทดสอบเบื้องต้นทุกประการก็สนับสนุนเหตุการณ์นั้น ในกรณีนี้ m=n ดังนั้น
![]()
2. ความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้คือศูนย์
อันที่จริง ถ้าเหตุการณ์หนึ่งเป็นไปไม่ได้ ก็ไม่มีผลลัพธ์เบื้องต้นของการทดสอบใดที่สนับสนุนเหตุการณ์นั้น ในกรณีนี้ก็หมายถึง
![]()
3. ความน่าจะเป็น เหตุการณ์สุ่มมี จำนวนบวกล้อมรอบระหว่างศูนย์ถึงหนึ่ง
แท้จริงแล้วมีเพียงส่วนหนึ่งของจำนวนผลลัพธ์เบื้องต้นของการทดสอบทั้งหมดเท่านั้นที่ได้รับการสนับสนุนจากเหตุการณ์สุ่ม ในกรณีนี้< ม< n, หมายถึง 0 < m/n < 1 เช่น 0< พี(เอ) < 1. Итак, вероятность любого события удовлетворяет двойному неравенству
การสร้างทฤษฎีความน่าจะเป็นที่สมบูรณ์ตามหลักตรรกะนั้นขึ้นอยู่กับคำจำกัดความเชิงสัจพจน์ของเหตุการณ์สุ่มและความน่าจะเป็นของมัน ในระบบสัจพจน์ที่เสนอโดย A. N. Kolmogorov แนวคิดที่ไม่ได้กำหนดนั้นเป็นเหตุการณ์เบื้องต้นและความน่าจะเป็น ต่อไปนี้เป็นสัจพจน์ที่กำหนดความน่าจะเป็น:
1. ทุกงาน กจับคู่ไม่เป็นลบ จำนวนจริง พี(เอ)- จำนวนนี้เรียกว่าความน่าจะเป็นของเหตุการณ์ ก.
2. ความน่าจะเป็นของเหตุการณ์ที่เชื่อถือได้มีค่าเท่ากับหนึ่ง
3. ความน่าจะเป็นของการเกิดเหตุการณ์ที่เข้ากันไม่ได้อย่างน้อยหนึ่งเหตุการณ์จะเท่ากับผลรวมของความน่าจะเป็นของเหตุการณ์เหล่านี้
จากสัจพจน์เหล่านี้ คุณสมบัติของความน่าจะเป็นและการพึ่งพาระหว่างกันนั้นได้มาเป็นทฤษฎีบท
คำถามทดสอบตัวเอง
1. คุณลักษณะเชิงตัวเลขของความเป็นไปได้ที่เหตุการณ์จะเกิดขึ้นชื่ออะไร?
2. ความน่าจะเป็นของเหตุการณ์คืออะไร?
3. ความน่าจะเป็นของเหตุการณ์ที่เชื่อถือได้คือเท่าไร?
4. ความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้คืออะไร?
5. อะไรคือขีดจำกัดของความน่าจะเป็นของเหตุการณ์สุ่ม?
6. อะไรคือขีดจำกัดของความน่าจะเป็นของเหตุการณ์ใดๆ?
7. คำจำกัดความของความน่าจะเป็นแบบใดเรียกว่าคลาสสิก?
สถาบันการศึกษาเทศบาล
โรงยิมหมายเลข 6
ในหัวข้อ " คำจำกัดความคลาสสิกความน่าจะเป็น"
จบโดยนักเรียนชั้นประถมศึกษาปีที่ 8 "B"
คลีมันโตวา อเล็กซานดรา.
ครูคณิตศาสตร์: Videnkina V. A.
โวโรเนซ, 2008
หลายเกมใช้ลูกเต๋า ลูกบาศก์มี 6 ด้าน แต่ละด้านมีจำนวนจุดที่แตกต่างกัน ตั้งแต่ 1 ถึง 6 ผู้เล่นทอยลูกเต๋าและดูว่าด้านที่ตกมีกี่จุด (ด้านที่อยู่ด้านบน) . บ่อยครั้ง จุดบนใบหน้าของลูกบาศก์จะถูกแทนที่ด้วยตัวเลขที่สอดคล้องกัน จากนั้นพวกเขาบอกว่าทอยเลข 1, 2 หรือ 6 การโยนลูกเต๋าถือได้ว่าเป็นการทดลอง การทดลอง การทดสอบ และผลลัพธ์ที่ได้รับ คือผลการทดสอบหรือ เหตุการณ์เบื้องต้น- ผู้คนสนใจที่จะคาดเดาเหตุการณ์นี้หรือเหตุการณ์นั้นและทำนายผลลัพธ์ พวกเขาสามารถทำนายอะไรได้บ้างเมื่อพวกเขาทอยลูกเต๋า? ตัวอย่างเช่น:
1) เหตุการณ์ A - ทอยหมายเลข 1, 2, 3, 4, 5 หรือ 6
2) เหตุการณ์ B - หมายเลข 7, 8 หรือ 9 ปรากฏขึ้น
3) เหตุการณ์ C - หมายเลข 1 ปรากฏขึ้น
เหตุการณ์ A ที่คาดการณ์ไว้ในกรณีแรกจะเกิดขึ้นอย่างแน่นอน โดยทั่วไปแล้ว เหตุการณ์ที่จะเกิดขึ้นแน่นอนในประสบการณ์นั้นๆ เรียกว่า เหตุการณ์ที่เชื่อถือได้ .
เหตุการณ์ B ที่คาดการณ์ไว้ในกรณีที่สองจะไม่เกิดขึ้น มันเป็นไปไม่ได้เลย โดยทั่วไป เหตุการณ์ที่ไม่สามารถเกิดขึ้นในประสบการณ์ที่กำหนดเรียกว่า เหตุการณ์ที่เป็นไปไม่ได้ .
และเหตุการณ์ C ที่ทำนายไว้ในกรณีที่สามจะเกิดขึ้นหรือไม่เกิดขึ้น? เราไม่สามารถตอบคำถามนี้ได้อย่างแน่ชัด เนื่องจากข้อ 1 อาจหลุดหรือไม่ก็ได้ เหตุการณ์ที่อาจจะเกิดขึ้นหรืออาจไม่เกิดขึ้นในประสบการณ์นั้นๆ เรียกว่า เหตุการณ์สุ่ม .
เมื่อนึกถึงเหตุการณ์ที่น่าเชื่อถือ เรามักจะไม่ใช้คำว่า “อาจจะ” ตัวอย่างเช่น หากวันนี้เป็นวันพุธ พรุ่งนี้ก็เป็นวันพฤหัสบดี นี่ถือเป็นเหตุการณ์ที่เชื่อถือได้ ในวันพุธ เราจะไม่พูดว่า: “พรุ่งนี้อาจเป็นวันพฤหัสบดี” เราจะพูดสั้น ๆ และชัดเจน: “พรุ่งนี้เป็นวันพฤหัสบดี” จริงอยู่ถ้าเรามีความโน้มเอียงที่จะ วลีที่สวยงามจากนั้นเราสามารถพูดได้ว่า: “ด้วยความน่าจะเป็นร้อยเปอร์เซ็นต์ฉันบอกว่าพรุ่งนี้เป็นวันพฤหัสบดี” ในทางตรงกันข้าม ถ้าวันนี้เป็นวันพุธ การเริ่มวันศุกร์ในวันพรุ่งนี้ก็เป็นไปไม่ได้ เมื่อประเมินเหตุการณ์นี้ในวันพุธ เราสามารถพูดได้ว่า “ฉันแน่ใจว่าพรุ่งนี้ไม่ใช่วันศุกร์” หรือนี่: “เหลือเชื่อเลยที่พรุ่งนี้เป็นวันศุกร์” ถ้าเรามีแนวโน้มที่จะใช้วลีที่สวยงาม เราสามารถพูดได้ว่า: “ความน่าจะเป็นที่พรุ่งนี้เป็นวันศุกร์จะเป็นศูนย์” ดังนั้นเหตุการณ์ที่เชื่อถือได้คือเหตุการณ์ที่เกิดขึ้นภายใต้เงื่อนไขที่กำหนด ด้วยความน่าจะเป็นร้อยเปอร์เซ็นต์(เช่น เกิดขึ้นใน 10 กรณีจาก 10 กรณี, ใน 100 กรณีจาก 100 กรณี เป็นต้น) เหตุการณ์ที่เป็นไปไม่ได้คือเหตุการณ์ที่ไม่เคยเกิดขึ้นภายใต้เงื่อนไขที่กำหนด ด้วยความน่าจะเป็นเป็นศูนย์ .
แต่น่าเสียดาย (และอาจจะโชคดี) ไม่ใช่ทุกสิ่งในชีวิตที่ชัดเจนและแม่นยำนัก มันจะเป็นเช่นนั้นตลอดไป (เหตุการณ์บางอย่าง) มันจะไม่มีวันเป็น (เหตุการณ์ที่เป็นไปไม่ได้) บ่อยครั้งที่เราต้องเผชิญกับเหตุการณ์สุ่ม ซึ่งบางเหตุการณ์ก็มีโอกาสเป็นไปได้มากกว่า และเหตุการณ์อื่นๆ มีโอกาสน้อยกว่า โดยปกติแล้วผู้คนจะใช้คำว่า "มีโอกาสมากขึ้น" หรือ "มีโอกาสน้อยกว่า" ตามที่พวกเขาพูดโดยไม่ได้ตั้งใจตามสิ่งที่พวกเขาเรียกว่า สามัญสำนึก- แต่บ่อยครั้งที่การประมาณการดังกล่าวไม่เพียงพอเนื่องจากสิ่งสำคัญคือต้องรู้ นานแค่ไหนเปอร์เซ็นต์อาจเป็นเหตุการณ์สุ่มหรือ กี่ครั้งเหตุการณ์สุ่มเหตุการณ์หนึ่งมีแนวโน้มมากกว่าเหตุการณ์อื่น กล่าวอีกนัยหนึ่ง เราต้องการความแม่นยำ เชิงปริมาณคุณต้องสามารถระบุลักษณะความน่าจะเป็นด้วยตัวเลขได้
เราได้ดำเนินการขั้นตอนแรกในทิศทางนี้แล้ว เราบอกว่าความน่าจะเป็นของเหตุการณ์บางอย่างที่เกิดขึ้นนั้นมีลักษณะดังนี้ หนึ่งร้อยเปอร์เซ็นต์และความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้จะเกิดขึ้นคือ ศูนย์- เนื่องจาก 100% เท่ากับ 1 ผู้คนจึงเห็นด้วยกับสิ่งต่อไปนี้:
1) ความน่าจะเป็นของเหตุการณ์ที่เชื่อถือได้ถือว่าเท่ากัน 1;
2) ความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้ถือว่าเท่ากัน 0.
จะคำนวณความน่าจะเป็นของเหตุการณ์สุ่มได้อย่างไร? ท้ายที่สุดมันก็เกิดขึ้น โดยบังเอิญซึ่งหมายความว่าไม่เป็นไปตามกฎหมาย อัลกอริธึม หรือสูตร ปรากฎว่าในโลกของการสุ่มมีกฎหมายบางข้อที่อนุญาตให้คำนวณความน่าจะเป็นได้ นี่คือสาขาหนึ่งของคณิตศาสตร์ที่เรียกว่า - ทฤษฎีความน่าจะเป็น .
คณิตศาสตร์เกี่ยวข้องกับ แบบอย่างปรากฏการณ์ความเป็นจริงบางอย่างรอบตัวเรา ในบรรดาแบบจำลองทั้งหมดที่ใช้ในทฤษฎีความน่าจะเป็น เราจะจำกัดตัวเองให้อยู่เพียงแบบจำลองที่ง่ายที่สุด
รูปแบบความน่าจะเป็นแบบคลาสสิก
หากต้องการค้นหาความน่าจะเป็นของเหตุการณ์ A เมื่อทำการทดลอง คุณควร:
1) ค้นหาหมายเลข N ของผลลัพธ์ที่เป็นไปได้ทั้งหมด ประสบการณ์นี้;
2) ยอมรับสมมติฐานที่ว่าผลลัพธ์ทั้งหมดเหล่านี้มีโอกาสเท่าเทียมกัน
3) หาจำนวน N(A) ของผลลัพธ์การทดลองที่มีเหตุการณ์ A เกิดขึ้น
4) หาผลหาร ; มันจะเท่ากับความน่าจะเป็นของเหตุการณ์ A
เป็นธรรมเนียมที่จะต้องแสดงถึงความน่าจะเป็นของเหตุการณ์ A: P(A) คำอธิบายสำหรับการกำหนดนี้ง่ายมาก: คำว่า "ความน่าจะเป็น" ในภาษาฝรั่งเศสคือ ความน่าจะเป็นในภาษาอังกฤษ– ความน่าจะเป็น.การกำหนดใช้อักษรตัวแรกของคำ
เมื่อใช้สัญกรณ์นี้ ความน่าจะเป็นของเหตุการณ์ A ตามโครงร่างคลาสสิกสามารถพบได้โดยใช้สูตร
พี(ก)=.
บ่อยครั้งทุกประเด็นของโครงการความน่าจะเป็นแบบคลาสสิกข้างต้นจะแสดงออกมาเป็นวลีเดียวที่ค่อนข้างยาว
คำจำกัดความคลาสสิกของความน่าจะเป็น
ความน่าจะเป็นของเหตุการณ์ A ในระหว่างการทดสอบบางอย่างคืออัตราส่วนของจำนวนผลลัพธ์อันเป็นผลมาจากเหตุการณ์ A ที่เกิดขึ้นกับจำนวนผลลัพธ์ที่เป็นไปได้ทั้งหมดเท่ากันของการทดสอบนี้
ตัวอย่างที่ 1- ค้นหาความน่าจะเป็นที่ด้วยการโยนลูกเต๋าหนึ่งครั้งผลลัพธ์จะเป็น: ก) 4; ข) 5; วี) เลขคู่แว่นตา; d) จำนวนคะแนนที่มากกว่า 4; e) จำนวนคะแนนที่หารด้วยสามไม่ลงตัว
สารละลาย- โดยรวมแล้วมีผลลัพธ์ที่เป็นไปได้ทั้งหมด N=6 รายการ: การหลุดออกจากหน้าลูกบาศก์ด้วยจำนวนคะแนนเท่ากับ 1, 2, 3, 4, 5 หรือ 6 เราเชื่อว่าไม่มีผลลัพธ์ใดที่ได้เปรียบเหนือผลลัพธ์อื่น ๆ กล่าวคือ เรา ยอมรับสมมติฐานที่ว่าความเท่าเทียมกันของผลลัพธ์เหล่านี้
ก) ในผลลัพธ์ประการหนึ่ง เหตุการณ์ A ที่เราสนใจจะเกิดขึ้น—หมายเลข 4 จะปรากฏขึ้น ซึ่งหมายความว่า N(A)=1 และ
ป ( ก )= =.
b) วิธีแก้ไขและคำตอบเหมือนกับในย่อหน้าก่อนหน้า
c) เหตุการณ์ B ที่เราสนใจจะเกิดขึ้นตรงที่ สามกรณีเมื่อจำนวนแต้มเป็น 2, 4 หรือ 6 ซึ่งหมายความว่า
เอ็น ( บี )=3 และ ป ( บี )==.
d) เหตุการณ์ C ที่เราสนใจจะเกิดขึ้นในสองกรณีที่จำนวนคะแนนคือ 5 หรือ 6 ซึ่งหมายความว่า
เอ็น ( ค ) =2 และ Р(С)=.
e) จากตัวเลขที่เป็นไปได้หกตัวที่จับได้ สี่ (1, 2, 4 และ 5) ไม่สามารถหารด้วยสามได้ และอีกสอง (3 และ 6) ที่เหลือหารด้วยสามลงตัว ซึ่งหมายความว่าเหตุการณ์ที่เราสนใจเกิดขึ้นในสี่ในหกที่เป็นไปได้และน่าจะเป็นไปได้เท่ากันและน่าจะเป็นไปได้เท่ากันของผลลัพธ์ของการทดลอง ดังนั้นคำตอบจึงกลายเป็นว่า
- - ข) ; วี) ; ช) ; ง)ลูกเต๋าจริงอาจแตกต่างจากลูกบาศก์ในอุดมคติ (แบบจำลอง) ดังนั้นเพื่ออธิบายพฤติกรรมของมันจึงจำเป็นต้องมีแบบจำลองที่แม่นยำและมีรายละเอียดมากขึ้นโดยคำนึงถึงข้อดีของด้านหนึ่งเหนืออีกด้านหนึ่งการมีแม่เหล็กที่เป็นไปได้ ฯลฯ แต่ “ปีศาจอยู่ในรายละเอียด” และความแม่นยำมากขึ้นมีแนวโน้มที่จะนำไปสู่ความซับซ้อนมากขึ้น และการได้รับคำตอบจะกลายเป็นปัญหา เราจำกัดตัวเองให้พิจารณาแบบจำลองความน่าจะเป็นที่ง่ายที่สุด โดยที่ผลลัพธ์ที่เป็นไปได้ทั้งหมดมีความน่าจะเป็นเท่ากัน
หมายเหตุ 1- ลองดูอีกตัวอย่างหนึ่ง คำถามที่ถูกถาม: “ความน่าจะเป็นที่จะได้ทอยลูกเต๋าแบบสามต่อหนึ่งคืออะไร?” นักเรียนตอบว่า “ความน่าจะเป็นคือ 0.5” และเขาอธิบายคำตอบของเขา: “สามคนจะขึ้นมาหรือไม่ก็ตาม ซึ่งหมายความว่ามีผลลัพธ์ทั้งหมดสองรายการ และหนึ่งในนั้นคือเหตุการณ์ที่เราสนใจเกิดขึ้น เมื่อใช้แผนความน่าจะเป็นแบบคลาสสิก เราได้คำตอบ 0.5” มีข้อผิดพลาดในการให้เหตุผลนี้หรือไม่? เมื่อมองแวบแรกไม่มี อย่างไรก็ตาม มันยังคงมีอยู่และเป็นพื้นฐาน ใช่ จริงๆ แล้ว สามคนจะเกิดขึ้นหรือไม่ก็ตาม กล่าวคือ ด้วยคำจำกัดความของผลลัพธ์ของการทอย N=2 เป็นความจริงเช่นกันที่ N(A) = 1 และแน่นอนว่าเป็นความจริงเช่นกัน
=0.5 นั่นคือ คำนึงถึงสามจุดของโครงการความน่าจะเป็น แต่การดำเนินการตามจุดที่ 2) มีข้อสงสัย แน่นอน จากมุมมองทางกฎหมายล้วนๆ เรามีสิทธิ์ที่จะเชื่อว่าการทอยสามก็มีแนวโน้มที่จะไม่หลุดพอๆ กัน แต่เราจะคิดเช่นนั้นโดยไม่ละเมิดสมมติฐานตามธรรมชาติของเราเองเกี่ยวกับ "ความเหมือนกัน" ของขอบได้หรือไม่ ไม่แน่นอน! ที่นี่เรากำลังจัดการกับการใช้เหตุผลที่ถูกต้องภายในโมเดลที่แน่นอน แต่โมเดลนี้เอง "ผิด" ไม่สอดคล้องกับปรากฏการณ์จริงหมายเหตุ 2- เมื่อพูดถึงความน่าจะเป็น อย่ามองข้ามสถานการณ์สำคัญต่อไปนี้ ถ้าเราบอกว่าตอนโยนลูกเต๋าความน่าจะเป็นที่จะได้หนึ่งแต้มก็คือ
นี่ไม่ได้หมายความว่าการทอยลูกเต๋า 6 ครั้งคุณจะได้หนึ่งแต้มอย่างแน่นอน โยนลูกเต๋า 12 ครั้งคุณจะได้หนึ่งแต้มสองเท่าอย่างแน่นอน การโยนลูกเต๋า 18 ครั้งคุณจะได้หนึ่งแต้มพอดีสามแต้ม ครั้ง ฯลฯ คำนี้น่าจะเป็นการเก็งกำไร เราถือว่าสิ่งที่น่าจะเกิดขึ้นมากที่สุด บางทีถ้าเราทอยลูกเต๋า 600 ครั้ง แต้มหนึ่งก็จะขึ้นมา 100 ครั้ง หรือประมาณ 100 แต้มทฤษฎีสั้น ๆ
ในการเปรียบเทียบเหตุการณ์ในเชิงปริมาณตามระดับความเป็นไปได้ของการเกิดขึ้น จะมีการแนะนำการวัดเชิงตัวเลข ซึ่งเรียกว่าความน่าจะเป็นของเหตุการณ์ ความน่าจะเป็นของเหตุการณ์สุ่มคือตัวเลขที่แสดงการวัดความเป็นไปได้ของเหตุการณ์ที่เกิดขึ้น
ปริมาณที่กำหนดความสำคัญของเหตุผลวัตถุประสงค์ที่คาดว่าจะเกิดเหตุการณ์นั้น มีลักษณะเฉพาะด้วยความน่าจะเป็นของเหตุการณ์ ต้องเน้นย้ำว่าความน่าจะเป็นเป็นปริมาณวัตถุประสงค์ที่มีอยู่อย่างเป็นอิสระจากผู้รู้และถูกกำหนดเงื่อนไขโดยเงื่อนไขทั้งหมดที่มีส่วนทำให้เกิดเหตุการณ์
คำอธิบายที่เราให้ไว้สำหรับแนวคิดเรื่องความน่าจะเป็นนั้นไม่ใช่ คำจำกัดความทางคณิตศาสตร์เนื่องจากพวกเขาไม่ได้กำหนดแนวคิดนี้ในเชิงปริมาณ มีคำจำกัดความหลายประการของความน่าจะเป็นของเหตุการณ์สุ่ม ซึ่งใช้กันอย่างแพร่หลายในการแก้ปัญหาเฉพาะ (คลาสสิก สัจพจน์ สถิติ ฯลฯ)
คำจำกัดความคลาสสิกของความน่าจะเป็นของเหตุการณ์ลดแนวคิดนี้ลงเหลือแนวคิดเบื้องต้นเกี่ยวกับเหตุการณ์ที่เป็นไปได้ที่เท่าเทียมกัน ซึ่งไม่อยู่ภายใต้คำจำกัดความอีกต่อไป และถือว่ามีความชัดเจนโดยสัญชาตญาณ ตัวอย่างเช่น หากลูกเต๋าเป็นลูกบาศก์เนื้อเดียวกัน การสูญเสียหน้าใดๆ ของลูกบาศก์นี้ก็จะเป็นเหตุการณ์ที่เป็นไปได้เท่าเทียมกัน
ให้เหตุการณ์ที่น่าเชื่อถือถูกแบ่งออกเป็นกรณีที่เป็นไปได้เท่าๆ กัน โดยผลรวมจะเป็นเหตุการณ์นั้น นั่นคือกรณีที่พังทลายลงเรียกว่าเป็นผลดีต่อเหตุการณ์เนื่องจากการปรากฏตัวของหนึ่งในนั้นทำให้มั่นใจได้ว่าจะเกิดขึ้น
ความน่าจะเป็นของเหตุการณ์จะแสดงด้วยสัญลักษณ์
ความน่าจะเป็นของเหตุการณ์จะเท่ากับอัตราส่วนของจำนวนกรณีที่เป็นประโยชน์ต่อเหตุการณ์นั้น จากจำนวนกรณีที่เป็นไปได้ที่ไม่ซ้ำกัน เป็นไปได้เท่ากัน และเข้ากันไม่ได้ ต่อจำนวน เช่น
นี่คือคำจำกัดความคลาสสิกของความน่าจะเป็น ดังนั้น ในการค้นหาความน่าจะเป็นของเหตุการณ์ เมื่อพิจารณาผลลัพธ์ต่างๆ ของการทดสอบแล้ว จำเป็นต้องค้นหาชุดของกรณีที่เป็นไปได้เฉพาะ เป็นไปได้เท่าเทียมกัน และเข้ากันไม่ได้ คำนวณจำนวนทั้งหมด n จำนวนกรณี m ที่เป็นประโยชน์ เหตุการณ์ที่กำหนด จากนั้นจึงทำการคำนวณโดยใช้สูตรข้างต้น
ความน่าจะเป็นของเหตุการณ์เท่ากับอัตราส่วนของจำนวน เหตุการณ์ที่ดีผลลัพธ์ของการทดสอบเรียกว่าจำนวนผลลัพธ์ทั้งหมดของการทดสอบ ความน่าจะเป็นแบบคลาสสิกเหตุการณ์สุ่ม
มันเป็นไปตามคำนิยาม คุณสมบัติดังต่อไปนี้ความน่าจะเป็น:
คุณสมบัติ 1. ความน่าจะเป็นของเหตุการณ์ที่เชื่อถือได้มีค่าเท่ากับหนึ่ง
คุณสมบัติ 2 ความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้คือศูนย์
คุณสมบัติ 3 ความน่าจะเป็นของเหตุการณ์สุ่มเป็นจำนวนบวกระหว่างศูนย์ถึงหนึ่ง
คุณสมบัติ 4. ความน่าจะเป็นที่เหตุการณ์จะเกิดเป็นกลุ่มที่สมบูรณ์จะมีค่าเท่ากับหนึ่ง
คุณสมบัติ 5. ความน่าจะเป็นที่จะเกิดขึ้น เหตุการณ์ตรงกันข้ามถูกกำหนดในลักษณะเดียวกับความน่าจะเป็นของการเกิดเหตุการณ์ A
จำนวนคดีที่สนับสนุนให้เกิดเหตุการณ์ตรงกันข้าม ดังนั้น ความน่าจะเป็นที่เหตุการณ์ตรงกันข้ามจะเกิดขึ้นจะเท่ากับความแตกต่างระหว่างความสามัคคีและความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้น:
ข้อได้เปรียบที่สำคัญของคำจำกัดความคลาสสิกของความน่าจะเป็นของเหตุการณ์คือด้วยความช่วยเหลือ ความน่าจะเป็นของเหตุการณ์สามารถกำหนดได้โดยไม่ต้องใช้ประสบการณ์ แต่ขึ้นอยู่กับการใช้เหตุผลเชิงตรรกะ
เมื่อตรงตามเงื่อนไขที่กำหนด เหตุการณ์ที่เชื่อถือได้จะเกิดขึ้นอย่างแน่นอน แต่เหตุการณ์ที่เป็นไปไม่ได้จะไม่เกิดขึ้นอย่างแน่นอน ในบรรดาเหตุการณ์ที่อาจหรือไม่อาจเกิดขึ้นเมื่อมีการสร้างเงื่อนไขขึ้นมา การเกิดขึ้นของบางเหตุการณ์สามารถนับได้ด้วยเหตุผลที่ดี และการเกิดขึ้นของเหตุการณ์อื่นๆ ที่มีเหตุผลน้อยกว่า ตัวอย่างเช่น หากในโกศมีลูกบอลสีขาวมากกว่าลูกบอลสีดำ ก็มีเหตุผลมากกว่าที่จะหวังว่าจะมีลักษณะเป็นลูกบอลสีขาวเมื่อสุ่มออกมาจากโกศมากกว่าที่จะมีลักษณะเป็นลูกบอลสีดำ
ตัวอย่างการแก้ปัญหา
ตัวอย่างที่ 1
กล่องหนึ่งประกอบด้วยลูกบอลสีขาว 8 ลูก สีดำ 4 ลูก และสีแดง 7 ลูก สุ่มจับลูกบอล 3 ลูก ค้นหาความน่าจะเป็นของเหตุการณ์ต่อไปนี้: – สุ่มลูกบอลสีแดงอย่างน้อย 1 ลูก – มีลูกบอลสีเดียวกันอย่างน้อย 2 ลูก – มีลูกบอลสีแดงอย่างน้อย 1 ลูกและลูกบอลสีขาว 1 ลูก
การแก้ปัญหา
เราค้นหาจำนวนผลการทดสอบทั้งหมดเป็นจำนวนชุดค่าผสมขององค์ประกอบ 19 (8+4+7) ของ 3:
ลองหาความน่าจะเป็นของเหตุการณ์กัน– สุ่มลูกบอลสีแดงอย่างน้อย 1 ลูก (1,2 หรือ 3 ลูกสีแดง)
ความน่าจะเป็นที่ต้องการ:
ให้จัดงาน– มีลูกบอลสีเดียวกันอย่างน้อย 2 ลูก (ลูกบอลสีขาว 2 หรือ 3 ลูก, ลูกบอลสีดำ 2 หรือ 3 ลูก และลูกบอลสีแดง 2 หรือ 3 ลูก)
จำนวนผลลัพธ์ที่เอื้อต่อเหตุการณ์:
ความน่าจะเป็นที่ต้องการ:
ให้จัดงาน– มีอย่างน้อยหนึ่งสีแดงและ 1 ลูกบอลสีขาว
(1 แดง, 1 ขาว, 1 ดำหรือ 1 แดง, 2 ขาวหรือ 2 แดง, 1 ขาว)
จำนวนผลลัพธ์ที่เอื้อต่อเหตุการณ์:
ความน่าจะเป็นที่ต้องการ:
คำตอบ: P(A)=0.773;P(C)=0.7688; ป(ล)=0.6068
ตัวอย่างที่ 2
มีการโยนลูกเต๋าสองลูก จงหาความน่าจะเป็นที่ผลรวมของคะแนนจะเท่ากับ 5 เป็นอย่างน้อย
สารละลาย
ให้กิจกรรมมีคะแนนอย่างน้อย 5
ลองใช้คำจำกัดความคลาสสิกของความน่าจะเป็น:
จำนวนผลการทดสอบที่เป็นไปได้ทั้งหมด
จำนวนการทดลองที่สนับสนุนเหตุการณ์ที่สนใจ
ด้านที่หล่นของลูกเต๋าลูกแรก มีหนึ่งแต้ม สองแต้ม... หกแต้มอาจปรากฏขึ้น ในทำนองเดียวกัน ผลลัพธ์ที่เป็นไปได้หกประการเมื่อทอยลูกที่สอง แต่ละผลลัพธ์ของการขว้างลูกเต๋าลูกแรกสามารถนำมารวมกับผลลัพธ์ของลูกที่สองได้ ดังนั้น จำนวนผลการทดสอบเบื้องต้นที่เป็นไปได้ทั้งหมดจะเท่ากับจำนวนตำแหน่งที่มีการทำซ้ำ (ตัวเลือกที่มีตำแหน่ง 2 องค์ประกอบจากชุดเล่มที่ 6):
ลองหาความน่าจะเป็นของเหตุการณ์ตรงข้ามกัน - ผลรวมคะแนนน้อยกว่า 5
การรวมกันของคะแนนที่ดรอปต่อไปนี้จะสนับสนุนกิจกรรม:
| № | กระดูกที่ 1 | กระดูกที่ 2 | 1 | 1 | 1 | 2 | 1 | 2 | 3 | 2 | 1 | 4 | 3 | 1 | 5 | 1 | 3 |
อธิบาย คำจำกัดความทางเรขาคณิตความน่าจะเป็นและแนวทางแก้ไขปัญหาการประชุมที่รู้จักกันดี
ทฤษฎีความน่าจะเป็น - วิทยาศาสตร์คณิตศาสตร์ศึกษารูปแบบปรากฏการณ์สุ่ม การเกิดขึ้นของทฤษฎีนี้เกิดขึ้นตั้งแต่กลางศตวรรษที่ 17 และมีความเกี่ยวข้องกับชื่อของ Huygens, Pascal, Fermat, J. Bernoulli
เราจะเรียกผลลัพธ์ที่ไม่สามารถแยกย่อยได้... ของเหตุการณ์เบื้องต้นของการทดลองบางอย่าง และผลรวมของผลลัพธ์เหล่านั้น
(จำกัด) พื้นที่ของเหตุการณ์เบื้องต้น หรือพื้นที่ของผลลัพธ์
ตัวอย่างที่ 21. ก) เมื่อขว้างลูกเต๋า พื้นที่ของเหตุการณ์เบื้องต้นประกอบด้วยหกจุด:
b) โยนเหรียญสองครั้งติดต่อกัน
โดยที่ G คือ "แขนเสื้อ" P คือ "โครงตาข่าย" และจำนวนผลลัพธ์ทั้งหมด
c) โยนเหรียญจนเห็น "ตราแผ่นดิน" ครั้งแรกจากนั้น
ในกรณีนี้เรียกว่าพื้นที่ไม่ต่อเนื่องของเหตุการณ์เบื้องต้น
โดยปกติแล้ว เราไม่สนใจว่าผลลัพธ์เฉพาะเจาะจงใดเกิดขึ้นจากการทดลอง แต่สนใจว่าผลลัพธ์นั้นเป็นของส่วนย่อยของผลลัพธ์ทั้งหมดหรือไม่ ชุดย่อยทั้งหมดเหล่านี้ซึ่งตามเงื่อนไขการทดลอง การตอบสนองของหนึ่งในสองประเภทที่เป็นไปได้: "ผลลัพธ์" หรือ "ผลลัพธ์" เราจะเรียกว่าเหตุการณ์
ในตัวอย่างที่ 21 b) set = (GG, GR, RG) คือเหตุการณ์ที่มี "ตราแผ่นดิน" ปรากฏขึ้นอย่างน้อยหนึ่งรายการ เหตุการณ์ประกอบด้วยผลลัพธ์เบื้องต้น 3 ประการของอวกาศดังนั้น
ผลรวมของสองเหตุการณ์คือเหตุการณ์ที่ประกอบด้วยการปฏิบัติตามเหตุการณ์หรือเหตุการณ์
การผลิตงานกิจกรรมคืองานที่ประกอบด้วยการดำเนินกิจกรรมและงานกิจกรรมร่วมกัน
สิ่งที่ตรงกันข้ามกับเหตุการณ์คือเหตุการณ์ที่ประกอบด้วยการไม่ปรากฏตัวและเป็นส่วนเสริมของเหตุการณ์นั้น
เซตหนึ่งเรียกว่าเหตุการณ์ที่เชื่อถือได้ เซตว่างเรียกว่าเหตุการณ์ที่เป็นไปไม่ได้
หากแต่ละเหตุการณ์เกิดขึ้นพร้อม ๆ กัน ให้เขียนและพูดสิ่งที่อยู่ข้างหน้าหรือเกี่ยวข้อง
เหตุการณ์และกล่าวกันว่าเทียบเท่าถ้าและ
คำนิยาม. ความน่าจะเป็นของเหตุการณ์คือตัวเลขเท่ากับอัตราส่วนของจำนวนผลลัพธ์เบื้องต้นที่ประกอบขึ้นเป็นเหตุการณ์ต่อจำนวนผลลัพธ์เบื้องต้นทั้งหมด
กรณีของเหตุการณ์ที่น่าจะเป็นไปได้เท่ากัน (เรียกว่า "คลาสสิก" ดังนั้นความน่าจะเป็น
เรียกว่า "คลาสสิค"
เหตุการณ์เบื้องต้น (ผลลัพธ์ของประสบการณ์) ที่รวมอยู่ในเหตุการณ์เรียกว่า “เป็นผลดี”
คุณสมบัติของความน่าจะเป็นแบบคลาสสิก:
ถ้า (และเป็นเหตุการณ์ที่เข้ากันไม่ได้)
ตัวอย่างที่ 22 (ปัญหาไฮเกนส์) ในโกศมีลูกบอลสีขาว 2 ลูกและสีดำ 4 ลูก นักพนันคนหนึ่งเดิมพันกับอีกคนหนึ่งว่าในบรรดาลูกบอลที่สุ่มออกมา 3 ลูกนั้น จะมีลูกสีขาวเพียงลูกเดียวเท่านั้น โอกาสของผู้โต้แย้งมีความสัมพันธ์กันอย่างไร?
โซลูชันที่ 1 (ดั้งเดิม) ในกรณีนี้ การทดสอบ = (หยิบลูกบอลออกมา 3 ลูก) และเหตุการณ์เป็นผลดีต่อผู้โต้แย้งคนใดคนหนึ่ง:
= (ได้ลูกบอลสีขาวหนึ่งลูกพอดี)
เนื่องจากลำดับการหยิบลูกบอลทั้งสามลูกนั้นไม่สำคัญ
สามารถรับลูกบอลสีขาวได้หนึ่งลูกในกรณีและลูกบอลสีดำสองลูก - จากนั้นตามกฎพื้นฐานของการรวมกัน ดังนั้น a ด้วยคุณสมบัติที่ห้าของความน่าจะเป็น ดังนั้น

โซลูชันที่ 2 มาสร้างแผนผังผลลัพธ์ที่น่าจะเป็นกันดีกว่า:

ตัวอย่างที่ 23 พิจารณากระปุกออมสินซึ่งมีเหรียญเหลืออยู่สี่เหรียญ - เหรียญละ 3 ใน 2 รูเบิล และอีกอันสำหรับ 5 รูเบิล เรานำเหรียญสองเหรียญออกมา
สารละลาย. ก) การแยกสองครั้งติดต่อกัน (พร้อมผลตอบแทน) สามารถนำไปสู่ผลลัพธ์ต่อไปนี้:
ความน่าจะเป็นของผลลัพธ์แต่ละอย่างเป็นเท่าไหร่?

ตารางแสดงกรณีที่เป็นไปได้ทั้งหมด 16 กรณี
เพราะฉะนั้น,
ต้นไม้ต่อไปนี้นำไปสู่ผลลัพธ์เดียวกัน:

b) การสกัดสองครั้งติดต่อกัน (โดยไม่ทำซ้ำ) สามารถนำไปสู่ผลลัพธ์สามประการต่อไปนี้:

ตารางแสดงผลลัพธ์ที่เป็นไปได้ทั้งหมด:
เพราะฉะนั้น,
ต้นไม้ที่สอดคล้องกันนำไปสู่ผลลัพธ์เดียวกัน:

ตัวอย่างที่ 24 (ปัญหาเดอเมียร์) คนสองคนเล่นเกมทอยลูกเต๋าเพื่อชัยชนะสูงสุดห้าครั้ง เกมจะหยุดลงเมื่อเกมแรกชนะสี่เกม และเกมที่สองชนะสามเกม ในกรณีนี้ควรแบ่งการเดิมพันเริ่มต้นอย่างไร?
สารละลาย. Let event = (เป็นผู้เล่นคนแรกที่ได้รับรางวัล) จากนั้นแผนผังผลตอบแทนที่น่าจะเป็นสำหรับผู้เล่นคนแรกจะเป็นดังนี้:
ดังนั้นควรแบ่งการเดิมพันสามส่วนให้กับผู้เล่นคนแรก และส่วนหนึ่งให้กับผู้เล่นคนที่สอง
ให้เราสาธิตประสิทธิผลของการแก้ปัญหาความน่าจะเป็นโดยใช้กราฟโดยใช้ตัวอย่างต่อไปนี้ ซึ่งเราพิจารณาใน§1 (ตัวอย่างที่ 2)
ตัวอย่างที่ 25 การเลือกใช้ “โต๊ะนับ” ยุติธรรมหรือไม่
สารละลาย. มาสร้างแผนผังผลลัพธ์ที่น่าจะเป็นกันดีกว่า:

ดังนั้นเมื่อเล่น “เกมนับ” การยืนอันดับสองจะได้กำไรมากกว่า
ใน การตัดสินใจครั้งล่าสุดใช้การตีความกราฟของทฤษฎีบทการบวกและการคูณความน่าจะเป็น:
และโดยเฉพาะอย่างยิ่ง
ถ้า และ เป็นเหตุการณ์ที่เข้ากันไม่ได้
และถ้าและ - เหตุการณ์อิสระ
ความน่าจะเป็นแบบคงที่
คำจำกัดความคลาสสิกเมื่อพิจารณาถึงปัญหาที่ซับซ้อน ต้องเผชิญกับความยากลำบากในลักษณะที่ผ่านไม่ได้ โดยเฉพาะอย่างยิ่งในบางกรณีอาจไม่สามารถระบุกรณีที่เป็นไปได้เท่าเทียมกันได้ แม้แต่ในกรณีของเหรียญ ดังที่เราทราบ มีความเป็นไปได้ไม่เท่ากันที่ "ขอบ" จะหลุดออกมา ซึ่งจากการพิจารณาทางทฤษฎีไม่สามารถประเมินได้ (ใคร ๆ ก็สามารถพูดได้ว่าไม่น่าเป็นไปได้และการพิจารณานี้ค่อนข้าง ใช้ได้จริง). ดังนั้นแม้ในช่วงเริ่มต้นของทฤษฎีความน่าจะเป็น จึงมีการนำเสนอคำจำกัดความ "ความถี่" ทางเลือกของความน่าจะเป็น กล่าวอย่างเป็นทางการ ความน่าจะเป็นสามารถกำหนดเป็นขีดจำกัดความถี่ของการสังเกตเหตุการณ์ A โดยถือว่าการสังเกตเป็นเนื้อเดียวกัน (นั่นคือ ความเหมือนกันของเงื่อนไขการสังเกตทั้งหมด) และความเป็นอิสระจากกัน:
โดยที่คือจำนวนการสังเกต และคือจำนวนครั้งของเหตุการณ์
ถึงแม้ว่า คำจำกัดความนี้ค่อนข้างบ่งบอกถึงวิธีการประมาณค่าความน่าจะเป็นที่ไม่ทราบ - โดย ปริมาณมากการสังเกตที่เป็นเนื้อเดียวกันและเป็นอิสระ - อย่างไรก็ตามคำจำกัดความนี้สะท้อนถึงเนื้อหาของแนวคิดเรื่องความน่าจะเป็น กล่าวคือ หากความน่าจะเป็นที่กำหนดให้กับเหตุการณ์เป็นการวัดความเป็นไปได้อย่างเป็นกลาง นั่นหมายความว่าภายใต้เงื่อนไขที่ตายตัวและการทำซ้ำซ้ำๆ เราควรได้รับความถี่ของการเกิดขึ้นใกล้กับ (ยิ่งใกล้มากเท่าใดก็ยิ่งสังเกตได้มากขึ้นเท่านั้น) จริงๆ แล้ว นี่คือความหมายดั้งเดิมของแนวคิดเรื่องความน่าจะเป็น มันขึ้นอยู่กับมุมมองเชิงวัตถุนิยมเกี่ยวกับปรากฏการณ์ทางธรรมชาติ กฎหมายที่เรียกว่าจะกล่าวถึงด้านล่าง จำนวนมากที่ให้ พื้นฐานทางทฤษฎี(ภายในกรอบของแนวทางเชิงสัจพจน์สมัยใหม่ที่สรุปไว้ด้านล่าง) รวมถึงการประมาณค่าความถี่ของความน่าจะเป็น
สถาบันการศึกษาเทศบาล
โรงยิมหมายเลข 6
ในหัวข้อ “คำจำกัดความคลาสสิกของความน่าจะเป็น”
จบโดยนักเรียนชั้นประถมศึกษาปีที่ 8 "B"
คลีมันโตวา อเล็กซานดรา.
ครูคณิตศาสตร์: Videnkina V. A.
โวโรเนซ, 2008
หลายเกมใช้ลูกเต๋า ลูกบาศก์มี 6 ด้าน แต่ละด้านมีจำนวนจุดที่แตกต่างกัน - ตั้งแต่ 1 ถึง 6 ผู้เล่นทอยลูกเต๋าและดูว่าด้านที่ตกมีกี่จุด (ด้านที่อยู่ด้านบน) . บ่อยครั้ง จุดบนใบหน้าของลูกบาศก์จะถูกแทนที่ด้วยหมายเลขที่สอดคล้องกัน แล้วพูดถึงการหมุน 1, 2 หรือ 6 การขว้างลูกเต๋าถือได้ว่าเป็นการทดลอง การทดลอง การทดสอบ และผลลัพธ์ที่ได้คือ ผลการทดสอบหรือเหตุการณ์เบื้องต้น ผู้คนสนใจที่จะคาดเดาเหตุการณ์นี้หรือเหตุการณ์นั้นและทำนายผลลัพธ์ พวกเขาสามารถทำนายอะไรได้บ้างเมื่อพวกเขาทอยลูกเต๋า? ตัวอย่างเช่น:
- เหตุการณ์ A—ทอยหมายเลข 1, 2, 3, 4, 5 หรือ 6
- เหตุการณ์ B—ทอยหมายเลข 7, 8 หรือ 9;
- เหตุการณ์ C—หมายเลข 1 ปรากฏขึ้น
เหตุการณ์ A ที่คาดการณ์ไว้ในกรณีแรกจะเกิดขึ้นอย่างแน่นอน โดยทั่วไปแล้ว เหตุการณ์ที่จะเกิดขึ้นแน่นอนในประสบการณ์นั้นๆ เรียกว่า เหตุการณ์ที่เชื่อถือได้.
เหตุการณ์ B ที่คาดการณ์ไว้ในกรณีที่สองจะไม่เกิดขึ้น มันเป็นไปไม่ได้เลย โดยทั่วไป เหตุการณ์ที่ไม่สามารถเกิดขึ้นในประสบการณ์ที่กำหนดเรียกว่า เหตุการณ์ที่เป็นไปไม่ได้.
และเหตุการณ์ C ที่ทำนายไว้ในกรณีที่สามจะเกิดขึ้นหรือไม่เกิดขึ้น? เราไม่สามารถตอบคำถามนี้ได้อย่างแน่ชัด เนื่องจากข้อ 1 อาจหลุดหรือไม่ก็ได้ เหตุการณ์ที่อาจจะเกิดขึ้นหรืออาจไม่เกิดขึ้นในประสบการณ์นั้นๆ เรียกว่า เหตุการณ์สุ่ม.
เมื่อนึกถึงเหตุการณ์ที่น่าเชื่อถือ เรามักจะไม่ใช้คำว่า “อาจจะ” ตัวอย่างเช่น หากวันนี้เป็นวันพุธ พรุ่งนี้ก็เป็นวันพฤหัสบดี นี่ถือเป็นเหตุการณ์ที่เชื่อถือได้ ในวันพุธ เราจะไม่พูดว่า: “พรุ่งนี้อาจเป็นวันพฤหัสบดี” เราจะพูดสั้น ๆ และชัดเจน: “พรุ่งนี้เป็นวันพฤหัสบดี” จริงอยู่ที่ถ้าเรามีแนวโน้มที่จะใช้วลีที่สวยงามเราสามารถพูดได้ว่า: “ด้วยความน่าจะเป็นร้อยเปอร์เซ็นต์ฉันบอกว่าพรุ่งนี้เป็นวันพฤหัสบดี” ในทางตรงกันข้าม ถ้าวันนี้เป็นวันพุธ การเริ่มวันศุกร์ในวันพรุ่งนี้ก็เป็นไปไม่ได้ เมื่อประเมินเหตุการณ์นี้ในวันพุธ เราสามารถพูดได้ว่า “ฉันแน่ใจว่าพรุ่งนี้ไม่ใช่วันศุกร์” หรือนี่: “เหลือเชื่อเลยที่พรุ่งนี้เป็นวันศุกร์” ถ้าเรามีแนวโน้มที่จะใช้วลีที่สวยงาม เราสามารถพูดได้ว่า: “ความน่าจะเป็นที่พรุ่งนี้เป็นวันศุกร์จะเป็นศูนย์” ดังนั้นเหตุการณ์ที่เชื่อถือได้คือเหตุการณ์ที่เกิดขึ้นภายใต้เงื่อนไขที่กำหนด ด้วยความน่าจะเป็นร้อยเปอร์เซ็นต์(เช่น เกิดขึ้นใน 10 กรณีจาก 10 กรณี, ใน 100 กรณีจาก 100 กรณี เป็นต้น) เหตุการณ์ที่เป็นไปไม่ได้คือเหตุการณ์ที่ไม่เคยเกิดขึ้นภายใต้เงื่อนไขที่กำหนด ด้วยความน่าจะเป็นเป็นศูนย์.
แต่น่าเสียดาย (และอาจจะโชคดี) ไม่ใช่ทุกสิ่งในชีวิตที่ชัดเจนและแม่นยำนัก มันจะเป็นเช่นนั้นตลอดไป (เหตุการณ์บางอย่าง) มันจะไม่มีวันเป็น (เหตุการณ์ที่เป็นไปไม่ได้) บ่อยครั้งที่เราต้องเผชิญกับเหตุการณ์สุ่ม ซึ่งบางเหตุการณ์ก็มีโอกาสเป็นไปได้มากกว่า และเหตุการณ์อื่นๆ มีโอกาสน้อยกว่า โดยปกติแล้วผู้คนจะใช้คำว่า "มีโอกาสมากขึ้น" หรือ "มีโอกาสน้อยกว่า" ตามที่พวกเขาพูดโดยไม่ได้ตั้งใจโดยอาศัยสิ่งที่เรียกว่าสามัญสำนึก แต่บ่อยครั้งที่การประมาณการดังกล่าวไม่เพียงพอเนื่องจากสิ่งสำคัญคือต้องรู้ นานแค่ไหนเปอร์เซ็นต์อาจเป็นเหตุการณ์สุ่มหรือ กี่ครั้งเหตุการณ์สุ่มเหตุการณ์หนึ่งมีแนวโน้มมากกว่าเหตุการณ์อื่น กล่าวอีกนัยหนึ่ง เราต้องการความแม่นยำ เชิงปริมาณคุณต้องสามารถระบุลักษณะความน่าจะเป็นด้วยตัวเลขได้
เราได้ดำเนินการขั้นตอนแรกในทิศทางนี้แล้ว เราบอกว่าความน่าจะเป็นของเหตุการณ์บางอย่างที่เกิดขึ้นนั้นมีลักษณะดังนี้ หนึ่งร้อยเปอร์เซ็นต์และความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้จะเกิดขึ้นคือ ศูนย์- เนื่องจาก 100% เท่ากับ 1 ผู้คนจึงเห็นด้วยกับสิ่งต่อไปนี้:
- ความน่าจะเป็นของเหตุการณ์ที่เชื่อถือได้ถือว่าเท่ากัน 1;
- ความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้ถือว่าเท่ากัน 0.
จะคำนวณความน่าจะเป็นของเหตุการณ์สุ่มได้อย่างไร? ท้ายที่สุดมันก็เกิดขึ้น โดยบังเอิญซึ่งหมายความว่าไม่เป็นไปตามกฎหมาย อัลกอริธึม หรือสูตร ปรากฎว่าในโลกของการสุ่มมีกฎหมายบางข้อที่อนุญาตให้คำนวณความน่าจะเป็นได้ นี่คือสาขาหนึ่งของคณิตศาสตร์ที่เรียกว่า - ทฤษฎีความน่าจะเป็น.
คณิตศาสตร์เกี่ยวข้องกับ แบบอย่างปรากฏการณ์ความเป็นจริงบางอย่างรอบตัวเรา ในบรรดาแบบจำลองทั้งหมดที่ใช้ในทฤษฎีความน่าจะเป็น เราจะจำกัดตัวเองให้อยู่เพียงแบบจำลองที่ง่ายที่สุด
รูปแบบความน่าจะเป็นแบบคลาสสิก
หากต้องการค้นหาความน่าจะเป็นของเหตุการณ์ A เมื่อทำการทดลอง คุณควร:
1) ค้นหาหมายเลข N ของผลลัพธ์ที่เป็นไปได้ทั้งหมดของการทดลองนี้
2) ยอมรับสมมติฐานที่ว่าผลลัพธ์ทั้งหมดเหล่านี้มีโอกาสเท่าเทียมกัน
3) หาจำนวน N(A) ของผลลัพธ์การทดลองที่มีเหตุการณ์ A เกิดขึ้น
4) หาผลหาร ; มันจะเท่ากับความน่าจะเป็นของเหตุการณ์ A
เป็นธรรมเนียมที่จะต้องแสดงถึงความน่าจะเป็นของเหตุการณ์ A: P(A) คำอธิบายสำหรับการกำหนดนี้ง่ายมาก: คำว่า "ความน่าจะเป็น" ในภาษาฝรั่งเศสคือ ความน่าจะเป็นในภาษาอังกฤษ- ความน่าจะเป็น.การกำหนดใช้อักษรตัวแรกของคำ
เมื่อใช้สัญกรณ์นี้ ความน่าจะเป็นของเหตุการณ์ A ตามโครงร่างคลาสสิกสามารถพบได้โดยใช้สูตร
พี(ก)=.
บ่อยครั้งทุกประเด็นของโครงการความน่าจะเป็นแบบคลาสสิกข้างต้นจะแสดงออกมาเป็นวลีเดียวที่ค่อนข้างยาว
คำจำกัดความคลาสสิกของความน่าจะเป็น
ความน่าจะเป็นของเหตุการณ์ A ในระหว่างการทดสอบบางอย่างคืออัตราส่วนของจำนวนผลลัพธ์อันเป็นผลมาจากเหตุการณ์ A ที่เกิดขึ้นกับจำนวนผลลัพธ์ที่เป็นไปได้ทั้งหมดเท่ากันของการทดสอบนี้
ตัวอย่างที่ 1- ค้นหาความน่าจะเป็นที่ด้วยการโยนลูกเต๋าหนึ่งครั้งผลลัพธ์จะเป็น: ก) 4; ข) 5; c) จำนวนคะแนนเท่ากัน d) จำนวนคะแนนที่มากกว่า 4; e) จำนวนคะแนนที่หารด้วยสามไม่ลงตัว
สารละลาย- โดยรวมแล้วมีผลลัพธ์ที่เป็นไปได้ทั้งหมด N=6 รายการ: การหลุดออกจากหน้าลูกบาศก์ด้วยจำนวนคะแนนเท่ากับ 1, 2, 3, 4, 5 หรือ 6 เราเชื่อว่าไม่มีผลลัพธ์ใดที่ได้เปรียบเหนือผลลัพธ์อื่น ๆ กล่าวคือ เรา ยอมรับสมมติฐานที่ว่าความเท่าเทียมกันของผลลัพธ์เหล่านี้
ก) ในผลลัพธ์ประการหนึ่ง เหตุการณ์ที่เราสนใจ A จะเกิดขึ้น—หมายเลข 4 จะปรากฏขึ้น ซึ่งหมายความว่า N(A)=1 และ
ป(ก)= =.
b) วิธีแก้ไขและคำตอบเหมือนกับในย่อหน้าก่อนหน้า
c) เหตุการณ์ B ที่เราสนใจจะเกิดขึ้นในสามกรณีอย่างแน่นอนเมื่อจำนวนคะแนนคือ 2, 4 หรือ 6 ซึ่งหมายความว่า
เอ็น(บี)=3 และป(บี)==.
d) เหตุการณ์ C ที่เราสนใจจะเกิดขึ้นในสองกรณีที่จำนวนคะแนนคือ 5 หรือ 6 ซึ่งหมายความว่า
เอ็น(ค) =2 และ Р(С)=.
e) จากตัวเลขที่เป็นไปได้หกตัวที่จับได้ สี่ (1, 2, 4 และ 5) ไม่สามารถหารด้วยสามได้ และอีกสอง (3 และ 6) ที่เหลือหารด้วยสามลงตัว ซึ่งหมายความว่าเหตุการณ์ที่เราสนใจเกิดขึ้นในสี่ในหกที่เป็นไปได้และน่าจะเป็นไปได้เท่ากันและน่าจะเป็นไปได้เท่ากันของผลลัพธ์ของการทดลอง ดังนั้นคำตอบจึงกลายเป็นว่า
คำตอบ: ก) ; ข) ; วี) ; ช) ; ง)
ลูกเต๋าจริงอาจแตกต่างจากลูกบาศก์ในอุดมคติ (แบบจำลอง) ดังนั้นเพื่ออธิบายพฤติกรรมของมันจึงจำเป็นต้องมีแบบจำลองที่แม่นยำและมีรายละเอียดมากขึ้นโดยคำนึงถึงข้อดีของด้านหนึ่งเหนืออีกด้านหนึ่งการมีแม่เหล็กที่เป็นไปได้ ฯลฯ แต่ “ปีศาจอยู่ในรายละเอียด” และความแม่นยำมากขึ้นมีแนวโน้มที่จะนำไปสู่ความซับซ้อนมากขึ้น และการได้รับคำตอบจะกลายเป็นปัญหา เราจำกัดตัวเองให้พิจารณาแบบจำลองความน่าจะเป็นที่ง่ายที่สุด โดยที่ผลลัพธ์ที่เป็นไปได้ทั้งหมดมีความน่าจะเป็นเท่ากัน
หมายเหตุ 1- ลองดูอีกตัวอย่างหนึ่ง คำถามที่ถูกถาม: “ความน่าจะเป็นที่จะได้ทอยลูกเต๋าแบบสามต่อหนึ่งคืออะไร?” นักเรียนตอบว่า “ความน่าจะเป็นคือ 0.5” และเขาอธิบายคำตอบของเขา: “สามคนจะขึ้นมาหรือไม่ก็ตาม ซึ่งหมายความว่ามีผลลัพธ์ทั้งหมดสองรายการ และหนึ่งในนั้นคือเหตุการณ์ที่เราสนใจเกิดขึ้น เมื่อใช้แผนความน่าจะเป็นแบบคลาสสิก เราได้คำตอบ 0.5” มีข้อผิดพลาดในการให้เหตุผลนี้หรือไม่? เมื่อมองแวบแรกไม่มี อย่างไรก็ตาม มันยังคงมีอยู่และเป็นพื้นฐาน ใช่ จริงๆ แล้ว สามคนจะเกิดขึ้นหรือไม่ก็ตาม กล่าวคือ ด้วยคำจำกัดความของผลลัพธ์ของการทอย N=2 เป็นความจริงเช่นกันที่ N(A) = 1 และแน่นอนว่า =0.5 กล่าวคือ คำนึงถึงจุดสามจุดของแผนความน่าจะเป็น แต่การบรรลุผลตามจุดที่ 2) ยังคงเป็นที่น่าสงสัย แน่นอน จากมุมมองทางกฎหมายล้วนๆ เรามีสิทธิ์ที่จะเชื่อว่าการทอยสามก็มีแนวโน้มที่จะไม่หลุดพอๆ กัน แต่เราจะคิดเช่นนั้นโดยไม่ละเมิดสมมติฐานตามธรรมชาติของเราเองเกี่ยวกับ "ความเหมือนกัน" ของขอบได้หรือไม่ ไม่แน่นอน! ที่นี่เรากำลังจัดการกับการใช้เหตุผลที่ถูกต้องภายในโมเดลที่แน่นอน แต่โมเดลนี้เอง "ผิด" ไม่สอดคล้องกับปรากฏการณ์จริง
หมายเหตุ 2- เมื่อพูดถึงความน่าจะเป็น อย่ามองข้ามสถานการณ์สำคัญต่อไปนี้ ถ้าเราบอกว่าตอนทอยลูกเต๋า ความน่าจะเป็นที่จะได้หนึ่งแต้มเท่ากับคูณ คุณจะได้หนึ่งแต้มเท่ากับสามครั้งพอดี เป็นต้น คำนี้น่าจะเป็นคำคาดเดา เราถือว่าสิ่งที่น่าจะเกิดขึ้นมากที่สุด บางทีถ้าเราทอยลูกเต๋า 600 ครั้ง แต้มหนึ่งก็จะขึ้นมา 100 ครั้ง หรือประมาณ 100 แต้ม
ทฤษฎีความน่าจะเป็นเกิดขึ้นในศตวรรษที่ 17 เมื่อทำการวิเคราะห์ต่างๆ การพนัน- ดังนั้นจึงไม่น่าแปลกใจที่ตัวอย่างแรกๆ มีลักษณะขี้เล่น จากตัวอย่างที่มีลูกเต๋า มาดูการสุ่มจับฉลากกันดีกว่า เล่นไพ่จากดาดฟ้า
ตัวอย่างที่ 2- จากสำรับไพ่ 36 ใบ จะมีการสุ่มไพ่ 3 ใบพร้อมกัน ความน่าจะเป็นที่จะไม่มีราชินีโพดำในหมู่พวกเขาคืออะไร?
สารละลาย- เรามีธาตุอยู่ 36 ธาตุ เราเลือกองค์ประกอบสามประการโดยลำดับที่ไม่สำคัญ ซึ่งหมายความว่าเป็นไปได้ที่จะได้รับผลลัพธ์ N=C เราจะดำเนินการตามรูปแบบความน่าจะเป็นแบบคลาสสิก กล่าวคือ เราจะถือว่าผลลัพธ์ทั้งหมดเหล่านี้มีความน่าจะเป็นที่เท่าเทียมกัน
ยังคงต้องคำนวณความน่าจะเป็นที่ต้องการโดยใช้คำจำกัดความแบบคลาสสิก:
ความน่าจะเป็นที่ไพ่สามใบที่เลือกจะมีคือเท่าใด ราชินีแห่งโพดำ- จำนวนผลลัพธ์ดังกล่าวทั้งหมดนั้นคำนวณได้ไม่ยาก คุณเพียงแค่ต้องลบผลลัพธ์ทั้งหมดที่ไม่มีราชินีโพดำออกจากผลลัพธ์ทั้งหมด นั่นคือ ลบจำนวน N(A) ที่พบในตัวอย่างที่ 3 จากนั้น ตามแผนความน่าจะเป็นแบบคลาสสิก ผลต่าง N-N(A) ควรหารด้วย N นี่คือสิ่งที่เราได้รับ:
เราเห็นว่ามีความเชื่อมโยงบางอย่างระหว่างความน่าจะเป็นของสองเหตุการณ์ ถ้าเหตุการณ์ A ไม่มีราชินีโพดำ และเหตุการณ์ B อยู่ในไพ่สามใบที่เลือก
P(B)= 1—P(A)
ป(ก)+พี(B)=1.
น่าเสียดายที่ในความเท่าเทียมกัน P(A)+P(B)=1 ไม่มีข้อมูลเกี่ยวกับความเชื่อมโยงระหว่างเหตุการณ์ A และ B; เราต้องคำนึงถึงความสัมพันธ์นี้ไว้ จะสะดวกกว่าถ้าให้ชื่อและการกำหนดชื่อเหตุการณ์ B ล่วงหน้าเพื่อระบุความเกี่ยวข้องกับ A อย่างชัดเจน
คำจำกัดความ 1. เหตุการณ์ Bเรียกว่า ตรงข้ามงาน Aและแสดงว่า B=Ā ถ้าเหตุการณ์ B เกิดขึ้น ก็ต่อเมื่อเหตุการณ์ A ไม่เกิดขึ้นเท่านั้น
ตทฤษฎีบท 1- ในการค้นหาความน่าจะเป็นของเหตุการณ์ตรงกันข้าม ให้ลบความน่าจะเป็นของเหตุการณ์นั้นออกจากเอกภาพ: P(Ā)= 1—P(A) ในความเป็นจริง,
ในทางปฏิบัติ พวกเขาคำนวณสิ่งที่หาง่ายกว่า: P(A) หรือ P(Ā) หลังจากนั้น ให้ใช้สูตรจากทฤษฎีบทและค้นหา P(Ā) = 1 - P(A) หรือ P(A) = 1 - P(Ā) ตามลำดับ
วิธีการแก้ไขปัญหาเฉพาะมักใช้โดย "การแจงนับกรณี" เมื่อเงื่อนไขของปัญหาถูกแบ่งออกเป็นกรณีที่แยกกันซึ่งแต่ละกรณีจะพิจารณาแยกกัน ตัวอย่างเช่น “ถ้าคุณไปทางขวา คุณจะสูญเสียม้าของคุณ ถ้าคุณไปทางตรง คุณจะแก้ปัญหาตามทฤษฎีความน่าจะเป็น ถ้าคุณไปทางซ้าย ….” หรือเมื่อสร้างกราฟของฟังก์ชัน y=│x+1│—│2x—5│ พิจารณากรณี x
ตัวอย่างที่ 3- จากทั้งหมด 50 คะแนน มี 17 คะแนนอยู่ในนั้น สีฟ้าและ 13 นิ้ว ส้ม- ค้นหาความน่าจะเป็นที่จุดที่เลือกแบบสุ่มจะถูกแรเงา
สารละลาย- มีการแรเงาทั้งหมด 30 คะแนนจาก 50 ซึ่งหมายความว่าความน่าจะเป็นคือ = 0.6
คำตอบ: 0.6.
อย่างไรก็ตาม ลองดูตัวอย่างง่ายๆ นี้ให้ละเอียดยิ่งขึ้น ให้เหตุการณ์ A เป็นจุดที่เลือกเป็นสีน้ำเงิน และเหตุการณ์ B กำหนดให้จุดที่เลือกเป็นสีส้ม ตามเงื่อนไข เหตุการณ์ A และ B ไม่สามารถเกิดขึ้นพร้อมกันได้
ให้เราแสดงเหตุการณ์ที่เราสนใจด้วยตัวอักษร C เหตุการณ์ C จะเกิดขึ้นก็ต่อเมื่อเกิดขึ้นเท่านั้น อย่างน้อยหนึ่งเหตุการณ์ A หรือ B- เป็นที่ชัดเจนว่า N(C)= N(A)+N(B)
ให้เราหารทั้งสองด้านของความเท่าเทียมกันด้วย N ซึ่งเป็นจำนวนผลลัพธ์ที่เป็นไปได้ทั้งหมดของการทดลองนี้ เราได้รับ
เรากำลังดำเนินการอยู่ ตัวอย่างง่ายๆเราวิเคราะห์สถานการณ์ที่สำคัญและเกิดขึ้นบ่อยครั้ง มีชื่อพิเศษสำหรับมัน
คำจำกัดความ 2- มีการเรียกเหตุการณ์ A และ B เข้ากันไม่ได้หากไม่สามารถเกิดขึ้นพร้อมกันได้
ทฤษฎีบท 2- ความน่าจะเป็นที่จะมีเหตุการณ์ที่เข้ากันไม่ได้อย่างน้อยหนึ่งในสองเหตุการณ์จะเท่ากับผลรวมของความน่าจะเป็น
เมื่อแปลทฤษฎีบทนี้เป็น ภาษาคณิตศาสตร์มีความจำเป็นต้องตั้งชื่อและกำหนดเหตุการณ์อย่างใดอย่างหนึ่งซึ่งประกอบด้วยการเกิดขึ้นของเหตุการณ์ A และ B ที่กำหนดอย่างน้อยหนึ่งในสองเหตุการณ์ดังกล่าวเรียกว่าผลรวมของเหตุการณ์ A และ B และแสดงว่า A + B
ถ้า A และ B เข้ากันไม่ได้ ดังนั้น P(A+B)=P(A)+P(B)
ในความเป็นจริง,
สะดวกในการอธิบายความไม่เข้ากันของเหตุการณ์ A และ B ด้วยภาพวาด หากผลลัพธ์ทั้งหมดของการทดลองเป็นจุดที่กำหนดในรูป เหตุการณ์ A และ B ก็คือเหตุการณ์บางส่วน เซตย่อย ชุดที่ให้มา - ความเข้ากันไม่ได้ของ A และ B หมายความว่าเซตย่อยทั้งสองนี้ไม่ได้ตัดกัน ตัวอย่างทั่วไปเหตุการณ์ที่เข้ากันไม่ได้—เหตุการณ์ A ใดๆ และเหตุการณ์ตรงกันข้าม Ā
แน่นอนว่าทฤษฎีบทนี้เป็นจริงสำหรับสาม สี่ และสำหรับใดๆ ก็ตาม จำนวนจำกัดเหตุการณ์ที่เข้ากันไม่ได้เป็นคู่ ความน่าจะเป็นของผลรวมของจำนวนเหตุการณ์ที่เข้ากันไม่ได้แบบคู่จะเท่ากับผลรวมของความน่าจะเป็นของเหตุการณ์เหล่านี้ข้อความสำคัญนี้สอดคล้องกับวิธีการแก้ไขปัญหาแบบ “เป็นกรณีไป” อย่างแม่นยำ
อาจมีความสัมพันธ์ การขึ้นต่อกัน การเชื่อมต่อ ฯลฯ ระหว่างเหตุการณ์ที่เกิดขึ้นอันเป็นผลมาจากประสบการณ์บางอย่างและระหว่างความน่าจะเป็นของเหตุการณ์เหล่านี้ ตัวอย่างเช่น เหตุการณ์สามารถ "เพิ่ม" ได้ และความน่าจะเป็นของผลรวมของเหตุการณ์ที่เข้ากันไม่ได้จะเท่ากัน ถึงผลรวมของความน่าจะเป็น
โดยสรุป ให้เราอภิปรายคำถามพื้นฐานต่อไปนี้: เป็นไปได้หรือไม่ พิสูจน์ความน่าจะเป็นที่จะได้หัวในการโยนเหรียญ 1 เหรียญคือ
คำตอบคือไม่ โดยทั่วไปแล้ว คำถามนั้นไม่ถูกต้อง ความหมายที่แท้จริงของคำว่า "พิสูจน์" นั้นไม่ชัดเจน ท้ายที่สุดแล้ว เรามักจะพิสูจน์บางสิ่งบางอย่างภายใต้กรอบของบางอย่างเสมอ โมเดลซึ่งกฎเกณฑ์ กฎสัจพจน์ สูตร ทฤษฎีบท ฯลฯ เป็นที่ทราบกันดีอยู่แล้ว เรากำลังพูดถึงเกี่ยวกับเหรียญในจินตนาการ "ในอุดมคติ" เหตุใดจึงถือว่าเป็นอุดมคติ เพราะ ตามคำจำกัดความความน่าจะเป็นที่จะได้ "ก้อย" เท่ากับความน่าจะเป็นที่จะได้ "หัว" และโดยหลักการแล้วเราสามารถพิจารณาแบบจำลองที่ความน่าจะเป็นที่จะ "ก้อย" ตกลงนั้นมากกว่าความน่าจะเป็นที่จะ "หัว" ล้มถึง 2 เท่าหรือน้อยกว่า 3 เท่า เป็นต้น จากนั้นคำถามก็เกิดขึ้น: เราเลือกจากเหตุผลอะไร รูปแบบการโยนเหรียญที่เป็นไปได้หลายแบบ แบบใดแบบหนึ่งซึ่งผลลัพธ์ของการโยนทั้งสองแบบมีโอกาสเท่ากัน?
คำตอบที่ตรงไปตรงมาคือ: “แต่ง่ายกว่า ชัดเจนกว่า และเป็นธรรมชาติมากกว่าสำหรับเรา!” แต่ยังมีข้อโต้แย้งที่สำคัญกว่านั้นด้วย พวกเขามาจากการปฏิบัติ หนังสือเรียนเกี่ยวกับทฤษฎีความน่าจะเป็นส่วนใหญ่มีตัวอย่างมากมายของนักธรรมชาติวิทยาชาวฝรั่งเศส เจ. บุฟฟ่อน (ศตวรรษที่ 18) และเค. เพียร์สัน นักคณิตศาสตร์และนักสถิติชาวอังกฤษ ( ปลาย XIXค.) ผู้โยนเหรียญ 4,040 และ 24,000 ครั้ง ตามลำดับ และนับจำนวนหัวหรือก้อย พวกเขาขึ้นนำได้ในปี 1992 และ 11998 ครั้ง ตามลำดับ ถ้าคุณนับ ความถี่การสูญเสีย“ก้อย” ปรากฎว่า = = 0.493069... สำหรับบุฟฟ่อน และ = 0.4995 สำหรับเพียร์สัน ธรรมเกิดขึ้น สมมติฐานด้วยการเพิ่มจำนวนการโยนเหรียญอย่างไม่จำกัด ความถี่ของก้อยและความถี่ของหัวจะเพิ่มขึ้นเข้าใกล้ 0.5 สมมติฐานนี้ซึ่งอิงจากข้อมูลเชิงปฏิบัติเป็นพื้นฐานในการเลือกแบบจำลองที่มีผลลัพธ์ที่น่าจะเป็นไปได้เท่าเทียมกัน
ตอนนี้เราสามารถสรุปได้ แนวคิดพื้นฐาน— ความน่าจะเป็นของเหตุการณ์สุ่มซึ่งคำนวณภายในแบบจำลองที่ง่ายที่สุด— รูปแบบความน่าจะเป็นแบบคลาสสิก. สำคัญทั้งทางทฤษฎีและทางปฏิบัติก็มีแนวคิด เหตุการณ์ตรงกันข้ามและสูตร P(Ā)= 1—P(A) เพื่อค้นหาความน่าจะเป็นของเหตุการณ์ดังกล่าว
ในที่สุดเราก็ได้พบกัน เหตุการณ์ที่เข้ากันไม่ได้ และด้วยสูตร
P(A+B)=P(A)+P(B),
P(A+B+C)= P(A)+P(B)+P(C)
ช่วยให้คุณค้นหาความน่าจะเป็น จำนวนเงินเหตุการณ์ดังกล่าว
อ้างอิง
1.กิจกรรม ความน่าจะเป็น การประมวลผลทางสถิติข้อมูล: เพิ่ม ย่อหน้าสำหรับหลักสูตรพีชคณิตเกรด 7-9 สถาบันการศึกษา/ A.G. Mordkovich, P.V. Semenov - 4th ed. - M.: Mnemosyne, 2006. - 112 หน้า: ป่วย
2.คุณ N. Makarychev, N. G. Mindyuk “พีชคณิต องค์ประกอบของสถิติและทฤษฎีความน่าจะเป็น”—มอสโก, “โปรสเวชเชนี”, 2006
 ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ
ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ คำประสมที่มีสระเชื่อมกัน
คำประสมที่มีสระเชื่อมกัน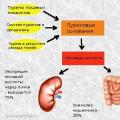 กรดยูริกในเลือด: บรรทัดฐานและการเบี่ยงเบน, เหตุใดจึงเพิ่มขึ้น, อาหารเพื่อลดกรด ผลิตภัณฑ์สุดท้ายของการเผาผลาญไนโตรเจนคือ
กรดยูริกในเลือด: บรรทัดฐานและการเบี่ยงเบน, เหตุใดจึงเพิ่มขึ้น, อาหารเพื่อลดกรด ผลิตภัณฑ์สุดท้ายของการเผาผลาญไนโตรเจนคือ