โคไซน์ของมุมระหว่างระนาบสองระนาบ การหามุมระหว่างระนาบ (มุมไดฮีดรัล)

เป้าหมาย:

• พัฒนาความสามารถในการพิจารณาแนวทางต่าง ๆ ในการแก้ปัญหาและวิเคราะห์ "ผล" ของการใช้วิธีการเหล่านี้ในการแก้ปัญหา
• พัฒนาความสามารถของนักเรียนในการเลือกวิธีการแก้ปัญหาตามความชอบทางคณิตศาสตร์ของพวกเขา โดยอาศัยความรู้ที่มั่นคงและทักษะที่มีความมั่นใจมากขึ้น
• พัฒนาความสามารถในการจัดทำแผนขั้นตอนต่อเนื่องเพื่อให้บรรลุผล
• พัฒนาความสามารถในการปรับขั้นตอนและการคำนวณทั้งหมด
• ทำซ้ำและแก้ไข ธีมต่างๆและปัญหาของ stereometry และ planimetry โครงสร้าง stereometric ทั่วไปที่เกี่ยวข้องกับการแก้ปัญหาในปัจจุบัน
• พัฒนาความคิดเชิงพื้นที่

• การวิเคราะห์ วิธีการต่างๆการแก้ปัญหา: วิธีเวกเตอร์พิกัด, การประยุกต์ใช้ทฤษฎีบทโคไซน์, การประยุกต์ใช้ทฤษฎีบทสามตั้งฉาก;
• เปรียบเทียบข้อดีและข้อเสียของแต่ละวิธี
• การทำซ้ำคุณสมบัติของลูกบาศก์, ปริซึมสามเหลี่ยม, หกเหลี่ยมปกติ;
• การเตรียมตัวสอบ
• การพัฒนาความเป็นอิสระในการตัดสินใจ

โครงร่างบทเรียน

ลูกบาศก์ ABCDA 1 B 1 C 1 D 1มีขอบ 1 จุด O - ศูนย์หน้า เอบีซีดี.

ก) มุมระหว่างเส้น A 1 Dและ BO;

b) ระยะห่างจากจุด บีถึงตรงกลางของการตัด A 1 D.

จุดตัดสินใจ ก)

มาใส่คิวบ์ของเรากันเถอะ ระบบสี่เหลี่ยมพิกัดดังรูป จุดยอด A 1 (1; 0; 1), D (1; 1; 0), B 1 (0; 0; 1), O (½; ½; 0)

เวกเตอร์ทิศทางของเส้น A 1 Dและ B1O:

(0; 1; -1) และ (½; ½; -1);

สูตรพบมุมที่ต้องการ φ ระหว่างกัน:

cos∠φ = ,
โดยที่ ∠φ = 30°

2 ทาง. เราใช้ทฤษฎีบทโคไซน์

1) ลากเส้นตรง ที่ 1 Cขนานกับเส้นตรง A 1 D. มุม CB1Oจะเป็นที่ต้องการ

2) จากสามเหลี่ยมมุมฉาก BB 1Oตามทฤษฎีบทพีทาโกรัส:

3) ตามกฎของโคไซน์จากรูปสามเหลี่ยม CB1Oคำนวณมุม CB1O:

cos CB 1 O = , มุมที่ต้องการคือ 30°

ความคิดเห็น เมื่อแก้โจทย์แบบที่ 2 จะเห็นได้ว่าตามทฤษฎีบทสามฉากตั้งฉาก ซัง 1 = 90°ดังนั้นจากสี่เหลี่ยม ∆ CB1Oนอกจากนี้ยังง่ายต่อการคำนวณโคไซน์ของมุมที่ต้องการ

จุดตัดสินใจ b)

1 ทาง. ลองใช้สูตรระยะห่างระหว่างจุดสองจุด

ให้ประเด็น อี- กลาง A 1 Dแล้วพิกัด E (1; 1/2; ½), B (0; 0; 0).

พ.ศ.= .

2 ทาง. ตามทฤษฎีบทพีทาโกรัส

จากสี่เหลี่ยม ∆ BAEกับทางตรง BAEหา เป็น = .

ทางขวา ปริซึมสามเหลี่ยม ABCA 1 B 1 C 1ขอบทั้งหมดเท่ากัน เอ. หามุมระหว่างเส้น ABและ A 1 C.

1 ทาง. วิธีเวกเตอร์พิกัด

พิกัดของจุดยอดของปริซึมในระบบสี่เหลี่ยมเมื่อปริซึมตั้งอยู่ ดังรูป: A (0; 0; 0), B (a; ; 0), A 1 (0; 0; a), C (0; a; 0)

เวกเตอร์ทิศทางของเส้น A 1 Cและ AB:

(0; ก; -ก)และ (a; ; 0} ;

cos φ = ;

2 ทาง. เราใช้กฎของโคไซน์

เราพิจารณา ∆ A 1 B 1 C, โดยที่ A 1 B 1 || AB. เรามี

cos φ = .

(จากการรวบรวม Unified State Exam-2012. คณิตศาสตร์: ทั่วไป ตัวเลือกการสอบเอ็ด A.L. Semenova, I.V. Yashchenko)

ในปริซึมหกเหลี่ยมปกติ ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, ขอบทั้งหมดมีค่าเท่ากับ 1, จงหาระยะห่างจากจุดนั้น อีตรง บี 1 ซี 1.

1 ทาง. วิธีเวกเตอร์พิกัด

1) วางปริซึมในระบบพิกัดสี่เหลี่ยมโดยวางแกนพิกัดดังแสดงในรูป SS 1, SWและ CEตั้งฉากเป็นคู่ ดังนั้นแกนพิกัดจึงสามารถกำหนดทิศทางไปตามพวกมันได้ เราได้รับพิกัด:

ค 1 (0; 0; 1), E (; 0; 0), B 1 (0; 1; 1).

2) ค้นหาพิกัดของเวกเตอร์ทิศทางสำหรับเส้น จาก 1 ถึง 1และ ซี 1 อี:

(0;1;0), (;0;-1).

3) หาโคไซน์ของมุมระหว่าง จาก 1 ถึง 1และ ซี 1 อีโดยใช้ ผลิตภัณฑ์สเกลาร์เวกเตอร์ และ :

cos β = = 0 => β = 90° => C 1 E คือระยะทางที่ต้องการ

4)ค 1 อี \u003d \u003d 2

สรุป: ความรู้ แนวทางต่างๆการแก้ปัญหา stereometric ทำให้คุณสามารถเลือกวิธีการที่ต้องการสำหรับนักเรียนคนใดก็ได้เช่น สิ่งหนึ่งที่นักเรียนมั่นใจ ช่วยหลีกเลี่ยงข้อผิดพลาด นำไปสู่การแก้ปัญหาที่ประสบความสำเร็จ และทำคะแนนได้ดีในการสอบ วิธีการประสานงานมีข้อได้เปรียบเหนือวิธีการอื่น ๆ ที่ต้องใช้การพิจารณาและการมองเห็นแบบสามมิติน้อยกว่า และขึ้นอยู่กับการใช้สูตรที่มีการเปรียบเทียบเชิงวางแผนและเชิงพีชคณิตหลายอย่างที่นักเรียนคุ้นเคยมากกว่า

รูปแบบของบทเรียนเป็นการผสมผสานระหว่างคำอธิบายของครูกับผลงานส่วนหน้าของนักเรียน

รูปทรงหลายเหลี่ยมที่อยู่ระหว่างการพิจารณาจะแสดงบนหน้าจอโดยใช้เครื่องฉายภาพ ซึ่งทำให้สามารถเปรียบเทียบได้ วิธีต่างๆโซลูชั่น

การบ้าน : แก้โจทย์ที่ 3 ให้แตกต่างออกไป เช่น ใช้ทฤษฎีบทตั้งฉากสามตัว .

วรรณกรรม

1. Ershova A.P. , Goloborodko V.V. อิสระและ ข้อสอบในเรขาคณิตสำหรับเกรด 11 - M.: ILEKSA, - 2010. - 208 p.

2. เรขาคณิต 10-11: หนังสือเรียนสำหรับ สถาบันการศึกษา: ระดับพื้นฐานและโปรไฟล์ / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev และอื่น ๆ - ม.: การศึกษา, 2550. - 256 หน้า

3. USE-2012 คณิตศาสตร์: ตัวเลือกการสอบทั่วไป: 10 ตัวเลือก / ed. A.L. Semenova, I.V. ยาชเชนโก – ม.: การศึกษาแห่งชาติ, 2554. - 112 น. - (USE-2012. FIPI - โรงเรียน).

บทความกล่าวถึงการหามุมระหว่างระนาบ หลังจากนำคำจำกัดความมาเราจะตั้งภาพประกอบกราฟิกพิจารณา วิธีละเอียดหาได้โดยวิธีพิกัด เราได้สูตรสำหรับการตัดกันระนาบซึ่งรวมถึงพิกัด เวกเตอร์ปกติ.

Yandex.RTB R-A-339285-1

เนื้อหาจะใช้ข้อมูลและแนวคิดที่เคยศึกษาในบทความเกี่ยวกับระนาบและเส้นในอวกาศ ในการเริ่มต้น มีความจำเป็นต้องดำเนินการต่อไปในการให้เหตุผลที่ช่วยให้มีแนวทางที่แน่นอนในการกำหนดมุมระหว่างระนาบที่ตัดกันสองระนาบ

ให้ระนาบตัดกันสองระนาบ γ 1 และ γ 2 ทางแยกของพวกเขาจะใช้ชื่อค. การสร้างระนาบ χ เชื่อมต่อกับจุดตัดของระนาบเหล่านี้ เครื่องบิน χ ผ่านจุด M เป็นเส้นตรง c เครื่องบิน γ 1 และ γ 2 จะตัดกันโดยใช้ระนาบ χ เรายอมรับการกำหนดเส้นที่ตัดกัน γ 1 และ χ สำหรับเส้น a และตัด γ 2 และ χ สำหรับเส้น b เราได้จุดตัดของเส้น a และ b ให้จุด M

ตำแหน่งของจุด M ไม่ส่งผลต่อมุมระหว่างเส้นตัดกัน a และ b และจุด M อยู่บนเส้น c ที่ระนาบ χ ผ่าน

จำเป็นต้องสร้างระนาบ χ 1 ตั้งฉากกับเส้น c และแตกต่างจากระนาบ χ . จุดตัดของระนาบ γ 1 และ γ 2 ด้วยความช่วยเหลือของ χ 1 จะใช้การกำหนดเส้น a 1 และ b 1 .

จะเห็นได้ว่าเมื่อสร้าง χ และ χ 1 เส้น a และ b ตั้งฉากกับเส้น c จากนั้น a 1, b 1 จะตั้งฉากกับเส้น c การหาเส้น a และ 1 ในระนาบ γ 1 ที่มีฉากตั้งฉากกับเส้น c ถือว่าขนานกัน ในทำนองเดียวกัน ตำแหน่งของ b และ b 1 ในระนาบ γ 2 ที่มีความตั้งฉากของเส้น c แสดงถึงความขนานกัน ซึ่งหมายความว่าจำเป็นต้องทำการถ่ายโอนแบบขนานของระนาบ χ 1 ถึง χ โดยที่เราจะได้เส้นตรงสองเส้น a และ a 1 , b และ b 1 . เราได้มุมระหว่างเส้นตัดกัน a และ b 1 เท่ากับมุมตัดกันเส้น a และ b

พิจารณารูปด้านล่าง

การตัดสินนี้พิสูจน์โดยข้อเท็จจริงที่ว่าระหว่างเส้นตัดกัน a และ b มีมุมที่ไม่ขึ้นกับตำแหน่งของจุด M นั่นคือจุดตัด เส้นเหล่านี้อยู่ในระนาบ γ 1 และ γ 2 . อันที่จริง มุมที่ได้นั้นถือได้ว่าเป็นมุมระหว่างระนาบที่ตัดกันสองระนาบ

มาดูการกำหนดมุมระหว่างระนาบที่ตัดกันที่มีอยู่ γ 1 และ γ 2 กัน

คำจำกัดความ 1

มุมระหว่างระนาบตัดกันสองระนาบ γ 1 และ γ 2เรียกมุมที่เกิดจากจุดตัดของเส้น a และ b โดยที่ระนาบ γ 1 และ γ 2 ตัดกับระนาบ χ ตั้งฉากกับเส้น c

พิจารณารูปด้านล่าง

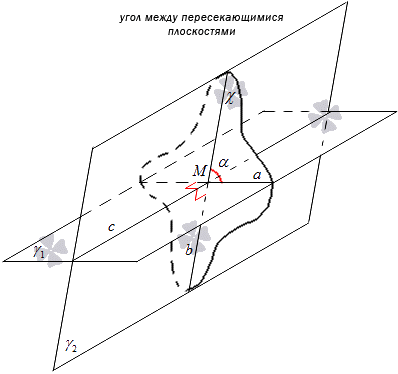
คำจำกัดความอาจถูกส่งในรูปแบบอื่น ที่จุดตัดของระนาบ γ 1 และ γ 2 โดยที่ c คือเส้นที่พวกมันตัดกัน ให้ทำเครื่องหมายที่จุด M ซึ่งลากเส้น a และ b ตั้งฉากกับเส้น c และนอนอยู่ในระนาบ γ 1 และ γ 2 แล้วมุมระหว่างเส้น a และ b จะเป็นมุมระหว่างระนาบ ในทางปฏิบัติ วิธีนี้ใช้ได้กับการสร้างมุมระหว่างระนาบ

ที่ทางแยกจะเกิดมุมที่มีค่าน้อยกว่า 90 องศา นั่นคือ องศาวัดมุมใช้ได้ในช่วงเวลาประเภทนี้ (0, 90] . ในเวลาเดียวกันระนาบเหล่านี้เรียกว่าตั้งฉากหากมีการสร้างมุมฉากที่ทางแยกมุมระหว่างระนาบคู่ขนานถือเป็นศูนย์

วิธีปกติในการหามุมระหว่างระนาบที่ตัดกันคือดำเนินการก่อสร้างเพิ่มเติม ซึ่งช่วยในการกำหนดได้อย่างแม่นยำ และสามารถทำได้โดยใช้เครื่องหมายของความเท่าเทียมกันหรือความคล้ายคลึงกันของรูปสามเหลี่ยม ไซน์ โคไซน์ของมุม

พิจารณาแก้ปัญหาโดยใช้ตัวอย่างจาก ใช้งานบล็อก C 2 .

ตัวอย่าง 1

ถาม ทรงลูกบาศก์ A B C D A 1 B 1 C 1 D 1 โดยที่ด้าน A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, จุด E แยกด้าน A A 1 ในอัตราส่วน 4: 3 หามุมระหว่างระนาบ A B C และ B E D 1

วิธีการแก้

เพื่อความชัดเจนคุณต้องวาดรูป เราได้รับสิ่งนั้น

จำเป็นต้องมีการแสดงภาพเพื่อให้สะดวกยิ่งขึ้นในการทำงานกับมุมระหว่างระนาบ

เราให้คำจำกัดความของเส้นตรงที่ระนาบ A B C และ B E D 1 ตัดกัน จุด B เป็นจุดร่วม ต้องหาอีกละ จุดร่วมทางแยก พิจารณาเส้น D A และ D 1 E ซึ่งอยู่ในระนาบเดียวกัน A D D 1 ตำแหน่งของพวกมันไม่ได้บ่งบอกถึงความขนาน ซึ่งหมายความว่าพวกมันมีจุดตัดร่วม

อย่างไรก็ตาม สาย D A อยู่ในระนาบ A B C และ D 1 E ใน B E D 1 . ดังนั้นเราจึงได้รับว่าเส้น ดี อาและ D 1 อีมีจุดตัดร่วมซึ่งเป็นเรื่องปกติสำหรับเครื่องบิน A B C และ B E D 1 . ระบุจุดตัดของเส้น ดี อาและ D 1 E จดหมาย F. จากที่นี่เราจะได้ B F เป็นเส้นตรงที่ระนาบ A B C และ B E D 1 ตัดกัน

พิจารณารูปด้านล่าง

เพื่อให้ได้คำตอบ จำเป็นต้องสร้างเส้นตรงที่อยู่ในระนาบ A B C และ B E D 1 โดยมีทางผ่านผ่านจุดที่อยู่บนเส้น B F และตั้งฉากกับมัน จากนั้นมุมผลลัพธ์ระหว่างเส้นเหล่านี้จะถือเป็นมุมที่ต้องการระหว่างระนาบ A B C และ B E D 1

จากนี้จะเห็นได้ว่าจุด A คือการฉายของจุด E ลงบนระนาบ A B C จำเป็นต้องลากเส้นตัดกับเส้น B F ที่มุมฉากที่จุด M จะเห็นว่าเส้นตรง A M คือการฉายภาพของเส้น E M ลงบนระนาบ A B C ตามทฤษฎีบทเกี่ยวกับฉากตั้งฉากเหล่านั้น A M ⊥ B F . พิจารณารูปด้านล่าง

∠ A M E คือมุมที่ต้องการที่เกิดจากระนาบ A B C และ B E D 1 จากผลสามเหลี่ยม A E M ที่ได้ เราสามารถหาไซน์ โคไซน์ หรือแทนเจนต์ของมุม หลังจากนั้นมุมนั้นเอง มีเพียงสองด้านที่รู้จักเท่านั้น โดยเงื่อนไข เรามีว่าความยาวของ A E ถูกพบในลักษณะนี้: เส้น A A 1 หารด้วยจุด E ในอัตราส่วน 4: 3 ซึ่งหมายความว่าความยาวทั้งหมดของเส้นคือ 7 ส่วน แล้ว A E \u003d 4 ส่วน เราพบ A.M.

ต้องพิจารณา สามเหลี่ยมมุมฉากเอ บี เอฟ เรามีมุมฉาก A ที่มีความสูง A M จากเงื่อนไข A B \u003d 2 เราจะสามารถหาความยาว A F โดยความคล้ายคลึงกันของสามเหลี่ยม D D 1 F และ A E F เราได้ A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

จำเป็นต้องหาความยาวของด้าน B F จากสามเหลี่ยม A B F โดยใช้ทฤษฎีบทพีทาโกรัส เราได้ BF   = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . ความยาวของด้าน A M หาได้จากพื้นที่สามเหลี่ยม A B F เรามีพื้นที่ที่สามารถเท่ากับทั้ง S A B C = 1 2 · A B · A F และ S A B C = 1 2 · B F · A M

เราได้ A M = A B A F B F = 2 4 2 5 = 4 5 5

จากนั้นเราสามารถหาค่าแทนเจนต์ของมุมของสามเหลี่ยม A E M ได้:

t ก ∠ A M E = A E A M = 4 4 5 5 = 5

มุมที่ต้องการได้จากจุดตัดของระนาบ A B C และ B E D 1 เท่ากับ a r c t g 5 จากนั้นเมื่อทำให้ง่ายขึ้น เราจะได้ a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

ตอบ: a r c t g 5 = a r c บาป 30 6 = a r c cos 6 6 .

บางกรณีของการหามุมระหว่างเส้นตัดกันนั้นใช้ พิกัดเครื่องบินเกี่ยวกับ xy z และวิธีการพิกัด ลองพิจารณาในรายละเอียดเพิ่มเติม

หากพบปัญหาเมื่อจำเป็นต้องหามุมระหว่างระนาบที่ตัดกัน γ 1 และ γ 2 เราจะระบุมุมที่ต้องการด้วย α

แล้ว ระบบที่กำหนดพิกัดแสดงว่าเรามีพิกัดของเวกเตอร์ปกติของระนาบที่ตัดกัน γ 1 และ γ 2 . จากนั้นเราแสดงว่า n 1 → = n 1 x , n 1 y , n 1 z เป็นเวกเตอร์ปกติของระนาบ γ 1 และ n 2 → = (n 2 x , n 2 y , n 2 z) - สำหรับ เครื่องบิน γ 2 . พิจารณาการหามุมที่อยู่ระหว่างระนาบเหล่านี้โดยละเอียดตามพิกัดของเวกเตอร์

จำเป็นต้องกำหนดเส้นตรงที่ระนาบ γ 1 และ γ 2 ตัดกับตัวอักษร c ในแนวเดียวกับที่เรามีจุด M ซึ่งเราวาดระนาบ χ ตั้งฉากกับ c เครื่องบิน χ ตามเส้น a และ b ตัดกับระนาบ γ 1 และ γ 2 ที่จุด M . จากคำจำกัดความที่ว่ามุมระหว่างระนาบที่ตัดกัน γ 1 และ γ 2 เท่ากับมุมของเส้นตัดกัน a และ b ที่เป็นของระนาบเหล่านี้ ตามลำดับ

ในระนาบ χ เราแยกเวกเตอร์ปกติออกจากจุด M และแทนค่า n 1 → และ n 2 → เวกเตอร์ n 1 → อยู่บนเส้นตั้งฉากกับเส้น a และเวกเตอร์ n 2 → บนเส้นตั้งฉากกับเส้น b เราจึงได้สิ่งนั้น ให้เครื่องบินχ มีเวกเตอร์ตั้งฉากของเส้น a เท่ากับ n 1 → และสำหรับเส้นตรง b เท่ากับ n 2 → พิจารณารูปด้านล่าง

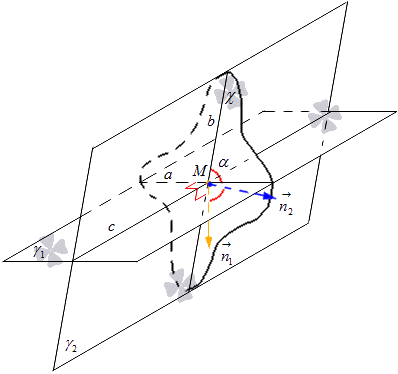
จากที่นี่ เราได้สูตรที่เราสามารถคำนวณไซน์ของมุมของเส้นตัดกันโดยใช้พิกัดของเวกเตอร์ เราพบว่าโคไซน์ของมุมระหว่างเส้น a และ b เท่ากับโคไซน์ระหว่างระนาบที่ตัดกัน γ 1 และ γ 2 ได้มาจาก สูตรคอสα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 , โดยที่เรามี n 1 → = (n 1 x , n 1 y , n 1 z) และ n 2 → = (n 2 x , n 2 y , n 2 z) คือพิกัดของ เวกเตอร์ของระนาบที่แสดง

มุมระหว่างเส้นตัดกันคำนวณโดยใช้สูตร

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

ตัวอย่าง 2

ตามเงื่อนไขจะได้รับ А В С D A 1 B 1 C 1 D 1 แบบขนาน , โดยที่ A B \u003d 2, A D \u003d 3, A A 1 \u003d 7 และจุด E แยกด้าน A A 1 4: 3 หามุมระหว่างระนาบ A B C และ B E D 1

วิธีการแก้

สังเกตได้จากสภาพที่ด้านข้างตั้งฉากเป็นคู่ ซึ่งหมายความว่าจำเป็นต้องแนะนำระบบพิกัด O x y z ที่มีจุดยอดที่จุด C และแกนพิกัด O x, O y, O z จำเป็นต้องวางทิศทางไว้ที่ด้านที่เหมาะสม พิจารณารูปด้านล่าง

เครื่องบินตัดกัน เอ บี ซีและ บี อี ดี 1สร้างมุมซึ่งสามารถพบได้โดยสูตร 2 x 2 + n 2 y 2 + n 2 z 2 โดยที่ n 1 → = (n 1 x , n 1 y , n 1 z) และ n 2 → = (n 2 x , n 2 y , n 2 z ) เป็นเวกเตอร์ปกติของระนาบเหล่านี้ มีความจำเป็นต้องกำหนดพิกัด จากรูปจะเห็นว่า แกนพิกัดเกี่ยวกับ x y เกิดขึ้นพร้อมกันในระนาบ A B C ซึ่งหมายความว่าพิกัดของเวกเตอร์ปกติ k → เท่ากับค่า n 1 → = k → = (0, 0, 1) .

เวกเตอร์ปกติของระนาบ B E D 1 เป็นผลิตภัณฑ์เวกเตอร์ของ B E → และ B D 1 → โดยที่พิกัดจะพบ จุดสุดขีด B, E, D 1 ซึ่งพิจารณาจากสภาพของปัญหา

เราได้ B (0 , 3 , 0) , D 1 (2 , 0 , 7) เพราะ A E E A 1 = 4 3 จากพิกัดของจุด A 2 , 3 , 0 , A 1 2 , 3 , 7 เราพบ E 2 , 3 , 4 เราได้ B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)

จำเป็นต้องแทนที่พิกัดที่พบลงในสูตรเพื่อคำนวณมุมผ่านโคไซน์ส่วนโค้ง เราได้รับ

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

วิธีการพิกัดให้ผลลัพธ์ที่คล้ายคลึงกัน

ตอบ: a rc cos 6 6 .

ปัญหาสุดท้ายได้รับการพิจารณาเพื่อหามุมระหว่างระนาบที่ตัดกับสมการที่ทราบของระนาบ

ตัวอย่างที่ 3

คำนวณไซน์ โคไซน์ของมุม และค่าของมุมที่เกิดจากเส้นตัดกันสองเส้น ซึ่งกำหนดไว้ในระบบพิกัด O x y z และกำหนดโดยสมการ 2 x - 4 y + z + 1 = 0 และ 3 y - z - 1 = 0 .

วิธีการแก้

เมื่อเรียนหัวข้อ สมการทั่วไปเส้นของรูปแบบ A x + B y + C z + D = 0 แสดงว่า A, B, C เป็นสัมประสิทธิ์เท่ากับพิกัดของเวกเตอร์ปกติ ดังนั้น n 1 → = 2 , - 4 , 1 และ n 2 → = 0 , 3 , - 1 เป็นเวกเตอร์ปกติของเส้นที่กำหนด

จำเป็นต้องแทนที่พิกัดของเวกเตอร์ปกติของระนาบเป็นสูตรสำหรับคำนวณมุมที่ต้องการของระนาบที่ตัดกัน แล้วเราจะได้สิ่งนั้น

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

ดังนั้นเราจึงมีว่าโคไซน์ของมุมอยู่ในรูปแบบ cos α = 13 210 . มุมของเส้นตัดกันจะไม่เป็นมุมป้าน แทนที่ใน เอกลักษณ์ตรีโกณมิติ, เราได้ค่าของไซน์ของมุมเท่ากับนิพจน์ เราคำนวณแล้วได้สิ่งนั้น

บาป α = 1 - cos 2 α = 1 - 13 210 = 41 210

ตอบ:บาป α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c บาป 41 210 .

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter

ในงาน C2 ในวิชาคณิตศาสตร์ ส่วนใหญ่คุณต้องแก้ปัญหาที่คุณต้องพิจารณา:

1. ระยะห่างระหว่างจุดสองจุด
2. ระยะทางจากจุดถึงเส้น
3. ระยะทางจากจุดไปยังเครื่องบิน
4. ระยะห่างระหว่างเส้นตัดกัน
5. มุมระหว่างสองเส้น
6. มุมระหว่างเส้นกับระนาบ
7. มุมระหว่างระนาบ

งานเป็นพื้นฐานถ้าคุณทำตามอัลกอริทึมสำหรับการแก้ C2 และจำหลัก คุณสมบัติตรีโกณมิติเช่นคุณสมบัติของเส้นทแยงมุมหรือพื้นที่ผิวของรูปทรงหลายเหลี่ยม งานสนับสนุนจะช่วยให้คุณจำคุณสมบัติพื้นฐานเหล่านี้ได้

ทีนี้มาดูอัลกอริธึมกัน

1. ในการกำหนดระยะห่างระหว่างจุดสองจุด A และ B เราใช้หนึ่งในสองวิธี:

• เรารวม AB ไว้ในสามเหลี่ยมแล้วหาความยาวเป็นด้านของสามเหลี่ยม
• ตามสูตร

ยิ่งไปกว่านั้น ในความคิดของฉัน วิธีการประสานงานนั้นง่ายที่สุด เพียงแต่จำเป็นต้องกำหนดพิกัดของแต่ละจุดให้ถูกต้องเท่านั้น

2. ในการกำหนดระยะทางจากจุดหนึ่งไปยังอีกเส้นหนึ่ง ให้คำนวณ

• เท่ากับความยาวของส่วนตั้งฉาก ถ้าเป็นไปได้ที่จะรวมส่วนนี้ไว้ในสามเหลี่ยมบางอันเป็นหนึ่งในความสูง

โดยใช้วิธีพิกัดโดยใช้สูตรคำนวณพื้นที่ โดยระยะที่ต้องการจะเป็นความสูงและ

3. ระยะทางจากจุดหนึ่งถึงระนาบคือ

• ความยาวของเส้นตั้งฉากลดลงจากจุดนี้ไปยังระนาบ ในการทำเช่นนี้ ให้สร้างส่วนที่ตั้งฉากกับระนาบและลอดผ่านอย่างระมัดระวัง คะแนนที่กำหนด. ระยะทางที่ต้องการจะเท่ากับความสูงของรูปทรงหลายเหลี่ยมใหม่ที่เกิดขึ้น
• โดยใช้วิธีพิกัด

สมการหาได้จากการแทนพิกัดของจุดสามจุดที่เป็นของระนาบนี้

• ใช้วิธีเวกเตอร์

ในการทำเช่นนี้ คุณต้องจำกฎสำหรับการบวกและลบเวกเตอร์ที่ผลิตภัณฑ์ เวกเตอร์ตั้งฉากเท่ากับศูนย์

• โดยใช้วิธีปริมาตร หากมีพีระมิด ABCM ระยะทางจากจุด M ถึงระนาบที่มีสามเหลี่ยม ABC จะถูกคำนวณโดยสูตร

• โดยวิธีอ้างอิงปัญหาสามารถดูได้

4. ระยะห่างระหว่างเส้นข้ามสามารถแก้ไขได้โดยใช้

4.1. วิธีการคำนวณทีละขั้นตอน:

• สร้างฉากตั้งฉากร่วมกันของเส้นตรงสองเส้นตัดกันและหาความยาวของมัน
• สร้างระนาบที่มีเส้นหนึ่งเส้นและขนานกับอีกเส้นหนึ่ง จากนั้นระยะทางที่ต้องการจะเท่ากับระยะทางจากจุดไปยังเส้นตรงที่สร้างขึ้นในระนาบ
• ล้อมรอบเส้นที่กำหนดในระนาบคู่ขนานที่ผ่านเส้นเอียงที่กำหนด หาระยะห่างระหว่างระนาบเหล่านี้
• สร้างระนาบตั้งฉากกับหนึ่งในเส้นเหล่านี้ และสร้างการฉายภาพมุมฉากของเส้นที่สอง

4.2. วิธีพิกัดเวกเตอร์

• หาพิกัดของปลายของส่วนที่เป็นแนวตั้งฉากร่วมกันของเส้นตัดกันสองเส้น
• การหาระยะห่างระหว่างจุดสองจุด

4.3. วิธีเวกเตอร์
เราลดปัญหาในการกำหนดความยาวของเวกเตอร์ที่อยู่ในแนวตั้งฉากซึ่งเป็นฉากตั้งฉากร่วมกันของเส้นตัดกันสองเส้น

6. มุมระหว่างเส้นกับระนาบถูกกำหนดโดยการรวมไว้ในสามเหลี่ยมมุมฉากเป็นมุมแหลมมุมหนึ่งหรือโดยวิธีเวคเตอร์-โคออร์ดิเนเตอร์

หรือ

วิธีกำหนดมุมระหว่างระนาบจะถูกพิจารณาในบทเรียนถัดไป อัลกอริธึมเหล่านี้สำหรับการแก้ปัญหา C2 ช่วยให้เข้าใจวิธีการแก้ปัญหาได้อย่างครอบคลุม "เพื่อช่วยเหลือนิตยสารนักเรียนสำหรับนักเรียนและผู้ปกครอง" อ่านเพิ่มเติม: http://education-club.ru/#ixzz2IXf5GOJU

7. มุมระหว่างระนาบ(วิธีทางเรขาคณิต)

• 1. หาเส้นตรงที่ระนาบตัดกัน
• 2. เลือกจุดบนเส้นนี้แล้ววาดสองเส้นตั้งฉากกับมันโดยนอนอยู่ในระนาบเหล่านี้ หรือวาดระนาบตั้งฉากกับเส้นตัดของระนาบ
• 3. ค้นหาฟังก์ชันตรีโกณมิติของมุมที่เกิดขึ้นจากเส้นตั้งฉากกับเส้นตัดของระนาบ ตามกฎแล้ว เราทำสิ่งนี้ผ่านรูปสามเหลี่ยมซึ่งรวมถึงมุมที่ต้องการ
• 4. ในคำตอบ ให้เขียนค่าของมุมหรือ ฟังก์ชันตรีโกณมิติมุม.

มุมระหว่างระนาบ วิธีการประสานงาน งาน C2

ระนาบตัดกันสองระนาบสร้างมุมไดฮีดรัลเท่ากันสองคู่:

ค่าของมุมไดฮีดรัลวัดจากค่าของมุมเชิงเส้นที่สอดคล้องกัน

ในการสร้างมุมเชิงเส้นของมุมไดฮีดรัล คุณต้องอยู่บนเส้นตัดของระนาบ จุดโดยพลการและในระนาบแต่ละระนาบวาดรังสีมายังจุดนี้ในแนวตั้งฉากกับเส้นตัดของระนาบ มุมที่เกิดจากรังสีเหล่านี้คือมุมเชิงเส้นของมุมไดฮีดรัล:

ค่าของมุมระหว่างระนาบคือค่าของมุมไดฮีดรัลที่น้อยกว่าหนึ่งปี

ให้ระนาบของเราและให้โดยสมการ:

โคไซน์ของมุมระหว่างระนาบหาได้จากสูตรต่อไปนี้:

ในคำตอบ เราเขียน เนื่องจากค่าของมุมระหว่างระนาบคือค่าของมุมไดฮีดรัลที่เล็กกว่า

ในปริซึมสี่เหลี่ยมปกติ ด้วยด้านฐานเท่ากับ 12 และสูง 21 จุด M จะถูกนำไปที่ขอบ จุด K ถูกถ่ายที่ขอบเพื่อให้ หามุมระหว่างระนาบกับระนาบ.

มาวาดรูปกันเถอะ เนื่องจากเราจะใช้วิธีพิกัด เราจะแนะนำระบบพิกัดทันที: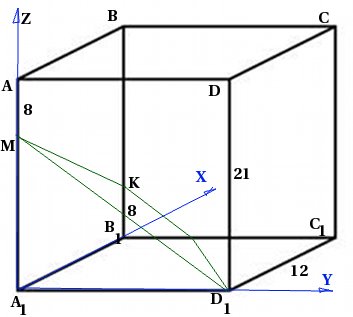

ตอนนี้เรากำลังเผชิญกับงานเขียนสมการของระนาบและระนาบ

ฉันอธิบายอัลกอริทึมโดยละเอียดสำหรับการค้นหาสมการของระนาบโดยใช้สามจุด

หลังจากที่เราหาสัมประสิทธิ์ในระนาบและสมการระนาบแล้ว เราก็แทนที่พวกมันลงในสูตรเพื่อหาโคไซน์ของมุมระหว่างระนาบ แล้วหามุม

ฉันแนะนำให้คุณดูวิดีโอวิธีแก้ปัญหาโดยละเอียดสำหรับปัญหานี้:

งานอื่นจาก Inna Vladimirovna Feldman

บทเรียนวิดีโอ "วิธีการประสานงานในการแก้ปัญหา c-2"

บทที่ 2 http://youtu.be/dKQWG8OZRGo
บทที่ 3 http://youtu.be/ddgr0PnbFno
บทที่ 4 http://youtu.be/n6yx2pQC0Lo
บทที่ 5 http://youtu.be/JkWbxAw1YLI
บทที่ 6 http://youtu.be/gybIqCMKBi
บทที่ 7 http://youtu.be/_LpARpYxp5g
บทที่ 8 http://youtu.be/XJhyZQoofD8

มุมระหว่างระนาบสองระนาบที่แตกต่างกันสามารถกำหนดได้สำหรับ ตำแหน่งสัมพัทธ์เครื่องบิน

กรณีเล็กน้อยคือถ้าระนาบขนานกัน จากนั้นมุมระหว่างพวกมันจะเท่ากับศูนย์

กรณีที่ไม่สำคัญถ้าเครื่องบินตัดกัน กรณีนี้เป็นหัวข้อที่จะอภิปรายต่อไป อันดับแรก เราต้องการแนวคิดของมุมไดฮีดรัล

9.1 มุมไดฮีดรัล

มุมไดฮีดรัลคือระนาบครึ่งระนาบสองระนาบที่มีเส้นตรงร่วมกัน (ซึ่งเรียกว่าขอบของมุมไดฮีดรัล) ในรูป 50 แสดงมุมไดฮีดรัลที่เกิดจากระนาบครึ่งระนาบและ ขอบของมุมไดฮีดรัลนี้เป็นเส้นร่วมของครึ่งระนาบที่กำหนด

ข้าว. 50. มุมไดฮีดรัล

มุมไดฮีดรัลสามารถวัดเป็นองศาหรือเรเดียนในหนึ่งคำ ป้อนค่าเชิงมุมของมุมไดฮีดรัล นี้จะทำในวิธีต่อไปนี้

ที่ขอบของมุมไดฮีดรัลที่เกิดจากระนาบครึ่งระนาบและเราใช้จุดใดจุดหนึ่ง M ลองวาดรังสี MA และ MB ตามลำดับในระนาบครึ่งระนาบเหล่านี้และตั้งฉากกับขอบ (รูปที่ 51)

ข้าว. 51. มุมไดฮีดรัลมุมเชิงเส้น

มุมที่ได้ AMB คือมุมเชิงเส้นของมุมไดฮีดรัล มุม " = \AMB คือค่าเชิงมุมของมุมไดฮีดรัลของเราอย่างแม่นยำ

คำนิยาม. ขนาดเชิงมุมของมุมไดฮีดรัลคือขนาดของมุมเชิงเส้นของมุมไดฮีดรัลที่กำหนด

มุมเชิงเส้นทั้งหมดของมุมไดฮีดรัลมีค่าเท่ากัน (หลังจากทั้งหมด พวกมันได้มาจากการเลื่อนขนานกัน) นั่นเป็นเหตุผลที่ นิยามนี้ถูกต้อง: ค่า "ไม่ได้ขึ้นอยู่กับ ทางเลือกเฉพาะจุด M บนขอบของมุมไดฮีดรัล

9.2 การกำหนดมุมระหว่างระนาบ

เมื่อระนาบสองระนาบตัดกัน จะได้มุมไดฮีดรัลสี่มุม ถ้าทุกคนมี มีค่าเท่ากัน(โดย 90) จากนั้นเครื่องบินจะเรียกว่าตั้งฉาก มุมระหว่างระนาบจะเท่ากับ 90 .

หากมุมไดฮีดรัลไม่เหมือนกันทั้งหมด (นั่นคือมีสองมุมแหลมและมุมป้านสองมุม) มุมระหว่างระนาบจะเป็นค่าของมุมไดฮีดรัลเฉียบพลัน (รูปที่ 52)

ข้าว. 52. มุมระหว่างระนาบ

9.3 ตัวอย่างการแก้ปัญหา

ลองพิจารณาสามงาน อย่างแรกนั้นง่าย อันที่สองและสามอยู่ที่ระดับ C2 โดยประมาณในการสอบวิชาคณิตศาสตร์

ภารกิจที่ 1 ค้นหามุมระหว่างสองหน้าของจัตุรมุขปกติ

วิธีการแก้. ให้ ABCD เป็นจัตุรมุขปกติ ลองวาดค่ามัธยฐาน AM และ DM ของใบหน้าที่เกี่ยวข้องกัน รวมถึงความสูงของจัตุรมุข DH (รูปที่ 53)

ข้าว. 53. สู่ปัญหา 1

เป็นค่ามัธยฐาน AM และ DM ก็เป็นความสูงของด้านเท่ากันหมด สามเหลี่ยม ABCและดีบีซี ดังนั้นมุม " = \AMD คือมุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากใบหน้า ABC และ DBC เราหาได้จากสามเหลี่ยม DHM:

			1AM

คำตอบ: arccos 1 3 .

ปัญหาที่ 2 ใน SABCD พีระมิดรูปสี่เหลี่ยมปกติ (มีจุดยอด S) ขอบด้านข้างจะเท่ากับด้านข้างของฐาน จุด K เป็นจุดกึ่งกลางของ edge SA หามุมระหว่างระนาบ

วิธีการแก้. เส้น BC ขนานกับ AD และขนานกับ ADS ระนาบ ดังนั้นระนาบ KBC จึงตัดระนาบ ADS ตามเส้นตรง KL ขนานกับ BC (รูปที่ 54)

ข้าว. 54. สู่ปัญหา2

ในกรณีนี้ KL จะขนานกับเส้น AD ด้วย เพราะฉะนั้น KL สายกลางสามเหลี่ยม ADS และจุด L เป็นจุดกึ่งกลางของ DS

วาดความสูงของปิรามิด SO ให้ N เป็นจุดกึ่งกลางของ DO จากนั้น LN จะเป็นเส้นกึ่งกลางของรูปสามเหลี่ยม DOS ดังนั้น LN k SO ดังนั้น LN จึงตั้งฉากกับระนาบ ABC

จากจุด N เราวาง NM ตั้งฉากกับเส้น BC เส้นตรง NM จะเป็นเส้นโครงของ LM เฉียงบนระนาบ ABC จากทฤษฎีบทตั้งฉากทั้งสามว่า LM ยังตั้งฉากกับ BC ด้วย

ดังนั้นมุม " = \LMN คือมุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากครึ่งระนาบ KBC และ ABC เราจะมองหามุมนี้จากสามเหลี่ยมมุมฉาก LMN

ให้ขอบพีระมิดเป็น a. ขั้นแรก หาความสูงของปิรามิด:

SO=p

วิธีการแก้. ให้ L เป็นจุดตัดของเส้น A1 K และ AB จากนั้นเครื่องบิน A1 KC ตัดกับระนาบ ABC ตามแนวเส้นตรง CL (รูปที่.55)

อา ค

ข้าว. 55. ปัญหา 3

สามเหลี่ยม A1 B1 K และ KBL เท่ากันทั้งขาและมุมแหลม ดังนั้นขาอีกข้างจึงเท่ากัน: A1 B1 = BL

พิจารณาสามเหลี่ยม ACL ในนั้น BA = BC = BL มุม CBL คือ 120 ; ดังนั้น \BCL = 30 นอกจากนี้ \BCA = 60 ดังนั้น \ACL = \BCA + \BCL = 90

แอลซี? เอซี. แต่เส้น AC คือการฉายภาพของเส้น A1 C ลงบนระนาบ ABC จากทฤษฎีบทฉากตั้งฉากทั้งสาม เราสรุปได้ว่า LC ? เอ1ซี.

ดังนั้นมุม A1 CA คือมุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากระนาบครึ่ง A1 KC และ ABC นี่คือมุมที่ต้องการ จากสามเหลี่ยมหน้าจั่ว A1 AC เราจะเห็นว่ามันเท่ากับ 45 .

\(\blacktriangleright\) มุมไดฮีดรัลคือมุมที่เกิดจากระนาบครึ่งสองระนาบและเส้นตรง \(a\) ซึ่งเป็นขอบเขตร่วมของพวกมัน

\(\blacktriangleright\) ในการหามุมระหว่างระนาบ \(\xi\) และ \(\pi\) คุณต้องหามุมเชิงเส้น เผ็ดหรือ ตรง) ของมุมไดฮีดรัลที่เกิดจากระนาบ \(\xi\) และ \(\pi\) :

ขั้นตอนที่ 1: ให้ \(\xi\cap\pi=a\) (เส้นตัดของระนาบ) ในระนาบ \(\xi\) เราทำเครื่องหมายจุดโดยพลการ \(F\) และวาด \(FA\perp a\) ;

ขั้นตอนที่ 2: วาด \(FG\perp \pi\) ;

ขั้นตอนที่ 3: ตาม TTP (\(FG\) - ตั้งฉาก, \(FA\) - เฉียง, \(AG\) - การฉายภาพ) เรามี: \(AG\perp a\) ;

ขั้นตอนที่ 4: มุม \(\angle FAG\) เรียกว่ามุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากระนาบ \(\xi\) และ \(\pi\)

โปรดทราบว่าสามเหลี่ยม \(AG\) เป็นสามเหลี่ยมมุมฉาก
โปรดทราบว่าเครื่องบิน \(AFG\) ที่สร้างขึ้นในลักษณะนี้ตั้งฉากกับทั้งระนาบ \(\xi\) และ \(\pi\) ดังนั้นจึงอาจกล่าวได้อีกนัยหนึ่งว่า มุมระหว่างระนาบ\(\xi\) และ \(\pi\) เป็นมุมระหว่างสองเส้นตัดกัน \(c\in \xi\) และ \(b\in\pi\) ก่อรูประนาบตั้งฉากกับ \(\xi\ ) และ \(\pi\)

งาน 1 #2875

ระดับงาน: ยากกว่าข้อสอบ

ดานา พีระมิดทรงสี่เหลี่ยมซึ่งขอบทั้งหมดเท่ากันและฐานเป็นรูปสี่เหลี่ยมจัตุรัส ค้นหา \(6\cos \alpha\) โดยที่ \(\alpha\) คือมุมระหว่างด้านที่อยู่ติดกัน

ให้ \(SABCD\) เป็นปิรามิดที่กำหนด (\(S\) เป็นจุดยอด) ซึ่งมีขอบเท่ากับ \(a\) ดังนั้น ทั้งหมด ใบหน้าด้านข้างเป็นสามเหลี่ยมด้านเท่า ค้นหามุมระหว่างใบหน้า \(SAD\) และ \(SCD\)

มาวาดกัน \(CH\perp SD\) เพราะ \(\สามเหลี่ยม SAD=\สามเหลี่ยม SCD\)จากนั้น \(AH\) ก็จะสูงเท่ากับ \(\triangle SAD\) ดังนั้น ตามคำจำกัดความ \(\angle AHC=\alpha\) เป็นมุมไดฮีดรัลเชิงเส้นระหว่างใบหน้า \(SAD\) และ \(SCD\)
เนื่องจากฐานเป็นรูปสี่เหลี่ยมจัตุรัส ดังนั้น \(AC=a\sqrt2\) โปรดทราบว่า \(CH=AH\) คือความสูง สามเหลี่ยมด้านเท่ากับด้านข้าง \(a\) ดังนั้น \(CH=AH=\frac(\sqrt3)2a\)
จากนั้นโดยทฤษฎีบทโคไซน์จาก \(\triangle AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

คำตอบ: -2

งาน 2 #2876

ระดับงาน: ยากกว่าข้อสอบ

เครื่องบิน \(\pi_1\) และ \(\pi_2\) ตัดกันที่มุมที่มีโคไซน์เท่ากับ \(0,2\) เครื่องบิน \(\pi_2\) และ \(\pi_3\) ตัดกันเป็นมุมฉาก และเส้นตัดของระนาบ \(\pi_1\) และ \(\pi_2\) ขนานกับเส้นตัดของ เครื่องบิน \(\pi_2\) และ \(\ pi_3\) ค้นหาไซน์ของมุมระหว่างระนาบ \(\pi_1\) และ \(\pi_3\)

ให้เส้นตัดของ \(\pi_1\) และ \(\pi_2\) เป็นเส้น \(a\) เส้นตัดของ \(\pi_2\) และ \(\pi_3\) เป็นเส้น \ (b\) และเส้นของทางแยก \(\pi_3\) และ \(\pi_1\) เป็นเส้นตรง \(c\) ตั้งแต่ \(a\parallel b\) จากนั้น \(c\parallel a\parallel b\) (ตามทฤษฎีบทจากส่วนของการอ้างอิงทางทฤษฎี "เรขาคณิตในอวกาศ" \(\rightarrow\) "ความรู้เบื้องต้นเกี่ยวกับสเตอริโอเมทรี, ความเท่าเทียม”)

ทำเครื่องหมายจุด \(A\in a, B\in b\) เพื่อให้ \(AB\perp a, AB\perp b\) (เป็นไปได้เพราะ \(a\parallel b\) ) หมายเหตุ \(C\in c\) ดังนั้น \(BC\perp c\) ดังนั้น \(BC\perp b\) จากนั้น \(AC\perp c\) และ \(AC\perp a\)
แน่นอน เนื่องจาก \(AB\perp b, BC\perp b\) ดังนั้น \(b\) จึงตั้งฉากกับระนาบ \(ABC\) เนื่องจาก \(c\parallel a\parallel b\) ดังนั้นเส้น \(a\) และ \(c\) จึงตั้งฉากกับระนาบ \(ABC\) และด้วยเหตุนี้เส้นใด ๆ จากระนาบนี้โดยเฉพาะ บรรทัด \ (AC\)

ดังนั้นจึงเป็นไปตามนั้น \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). ปรากฎว่า \(\triangle ABC\) เป็นรูปสี่เหลี่ยมผืนผ้า ซึ่งหมายความว่า \[\sin \angle BCA=\cos \angle BAC=0,2.\]

คำตอบ: 0.2

งาน 3 #2877

ระดับงาน: ยากกว่าข้อสอบ

เส้นที่กำหนด \(a, b, c\) ตัดกันที่จุดหนึ่ง และมุมระหว่างสองเส้นใด ๆ เท่ากับ \(60^\circ\) ค้นหา \(\cos^(-1)\alpha\) โดยที่ \(\alpha\) คือมุมระหว่างระนาบที่เกิดจากเส้น \(a\) และ \(c\) และระนาบที่เกิดจากเส้น \(b\ ) และ \(c\) ให้คำตอบเป็นองศา

ให้เส้นตัดกันที่จุด \(O\) เนื่องจากมุมระหว่างสองอันใดมีค่าเท่ากับ \(60^\circ\) ดังนั้นทั้งสามเส้นจึงไม่สามารถอยู่ในระนาบเดียวกันได้ ให้เราทำเครื่องหมายจุด \(A\) บนเส้น \(a\) และวาด \(AB\perp b\) และ \(AC\perp c\) แล้ว \(\สามเหลี่ยม AOB=\สามเหลี่ยม AOC\)เป็นสี่เหลี่ยมด้านตรงข้ามมุมฉากและมุมแหลม ดังนั้น \(OB=OC\) และ \(AB=AC\)
มาทำกันเถอะ \(AH\perp (BOC)\) จากนั้นตามทฤษฎีบทสามตั้งฉาก \(HC\perp c\) , \(HB\perp b\) ตั้งแต่ \(AB=AC\) แล้ว \(\สามเหลี่ยม AHB=\สามเหลี่ยม AHC\)เป็นรูปสี่เหลี่ยมผืนผ้าตามด้านตรงข้ามมุมฉากและขา ดังนั้น \(HB=HC\) ดังนั้น \(OH\) ​​​​คือเส้นแบ่งครึ่งของมุม \(BOC\) (เนื่องจากจุด \(H\) อยู่ห่างจากด้านข้างของมุมเท่ากัน)

โปรดทราบว่าด้วยวิธีนี้ เราได้สร้างมุมเชิงเส้นของมุมไดฮีดรัลที่เกิดจากระนาบที่เกิดจากเส้น \(a\) และ \(c\) และระนาบที่เกิดจากเส้น \(b\) และ \( ค\) . นี่คือมุม \(ACH\)

มาหามุมนี้ เนื่องจากเราเลือกจุด \(A\) โดยพลการ ให้เราเลือกจุดนั้นเพื่อว่า \(OA=2\) จากนั้นในรูปสี่เหลี่ยมผืนผ้า \(\triangle AOC\) : \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]เนื่องจาก \(OH\) ​​​​เป็น bisector ดังนั้น \(\angle HOC=30^\circ\) จึงอยู่ในรูปสี่เหลี่ยมผืนผ้า \(\triangle HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\]จากนั้นจากรูปสี่เหลี่ยมผืนผ้า \(\triangle ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

คำตอบ: 3

งาน 4 #2910

ระดับงาน: ยากกว่าข้อสอบ

เครื่องบิน \(\pi_1\) และ \(\pi_2\) ตัดกันตามเส้น \(l\) ซึ่งประกอบด้วยจุด \(M\) และ \(N\) เซ็กเมนต์ \(MA\) และ \(MB\) ตั้งฉากกับเส้น \(l\) และอยู่ในระนาบ \(\pi_1\) และ \(\pi_2\) ตามลำดับ และ \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) ค้นหา \(3\cos\alpha\) โดยที่ \(\alpha\) คือมุมระหว่างระนาบ \(\pi_1\) และ \(\pi_2\)

สามเหลี่ยม \(AMN\) เป็นมุมฉาก \(AN^2 = AM^2 + MN^2\) มาจากไหน \ สามเหลี่ยม \(BMN\) เป็นมุมฉาก \(BN^2 = BM^2 + MN^2\) มาจากไหน \ เราเขียนทฤษฎีบทโคไซน์สำหรับรูปสามเหลี่ยม \(AMB\): \ แล้ว \ เนื่องจากมุม \(\alpha\) ระหว่างระนาบคือ มุมแหลมและ \(\angle AMB\) เป็นป้าน ดังนั้น \(\cos\alpha=\dfrac5(12)\) แล้ว \

คำตอบ: 1.25

งาน 5 #2911

ระดับงาน: ยากกว่าข้อสอบ

\(ABCDA_1B_1C_1D_1\) เป็นสี่เหลี่ยมด้านขนาน \(ABCD\) เป็นสี่เหลี่ยมจัตุรัสที่มีด้าน \(a\) จุด \(M\) คือฐานของฉากตั้งฉากที่ตกลงมาจากจุด \(A_1\) ไปยังระนาบ \ ((ABCD)\) ยิ่งไปกว่านั้น \(M\) เป็นจุดตัดของเส้นทแยงมุมของสี่เหลี่ยมจัตุรัส \(ABCD\) เป็นที่ทราบกันดีว่า \(A_1M = \dfrac(\sqrt(3))(2)a\). ค้นหามุมระหว่างระนาบ \((ABCD)\) และ \((AA_1B_1B)\) ให้คำตอบเป็นองศา

เราสร้าง \(MN\) ตั้งฉากกับ \(AB\) ดังแสดงในรูป

เนื่องจาก \(ABCD\) เป็นสี่เหลี่ยมจัตุรัสที่มีด้าน \(a\) และ \(MN\perp AB\) และ \(BC\perp AB\) จากนั้น \(MN\parallel BC\) เนื่องจาก \(M\) เป็นจุดตัดของเส้นทแยงมุมของสี่เหลี่ยมจัตุรัส ดังนั้น \(M\) คือจุดกึ่งกลางของ \(AC\) ดังนั้น \(MN\) จึงเป็นเส้นกึ่งกลางและ \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) คือการฉายภาพของ \(A_1N\) ลงบนระนาบ \((ABCD)\) , และ \(MN\) ตั้งฉากกับ \(AB\) จากนั้น โดยสามทฤษฎีบทตั้งฉาก \( A_1N\) ตั้งฉากกับ \(AB \) และมุมระหว่างระนาบ \((ABCD)\) และ \((AA_1B_1B)\) คือ \(\angle A_1NM\)
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

คำตอบ: 60

งาน 6 #1854

ระดับงาน: ยากกว่าข้อสอบ

ในสี่เหลี่ยมจัตุรัส \(ABCD\) : \(O\) เป็นจุดตัดของเส้นทแยงมุม \(S\) ไม่ได้อยู่ในระนาบของสี่เหลี่ยม \(SO \perp ABC\) ค้นหามุมระหว่างระนาบ \(ASD\) และ \(ABC\) ถ้า \(SO = 5\) และ \(AB = 10\)

สามเหลี่ยมมุมฉาก \(\triangle SAO\) และ \(\triangle SDO\) มีค่าเท่ากันในสองด้านและมุมระหว่างพวกมัน (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) เพราะ \(O\) เป็นจุดตัดของเส้นทแยงมุมของสี่เหลี่ยมจัตุรัส \(SO\) คือ ด้านทั่วไป) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\triangle ASD\) คือหน้าจั่ว จุด \(K\) เป็นจุดกึ่งกลางของ \(AD\) จากนั้น \(SK\) คือความสูงในสามเหลี่ยม \(\triangle ASD\) และ \(OK\) คือความสูงในสามเหลี่ยม \ (AOD\) \(\ Rightarrow\) ระนาบ \(SOK\) ตั้งฉากกับระนาบ \(ASD\) และ \(ABC\) \(\Rightarrow\) \(\angle SKO\) เป็นมุมเชิงเส้นเท่ากับ ถึงมุมไดฮีดรัลที่ต้องการ

ใน \(\triangle SKO\) : \(ตกลง = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) เป็นสามเหลี่ยมมุมฉากหน้าจั่ว \(\Rightarrow\) \(\angle SKO = 45^\circ\)

คำตอบ: 45

งาน 7 #1855

ระดับงาน: ยากกว่าข้อสอบ

ในสี่เหลี่ยมจัตุรัส \(ABCD\) : \(O\) เป็นจุดตัดของเส้นทแยงมุม \(S\) ไม่ได้อยู่ในระนาบของสี่เหลี่ยม \(SO \perp ABC\) ค้นหามุมระหว่างระนาบ \(ASD\) และ \(BSC\) ถ้า \(SO = 5\) และ \(AB = 10\)

สามเหลี่ยมมุมฉาก \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) และ \(\triangle SOC\) มีค่าเท่ากันในสองด้านและมุมระหว่างพวกมัน (\(SO \perp ABC \) \(\ลูกศรขวา\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\) เพราะ \(O\) คือจุดตัดของเส้นทแยงมุมของสี่เหลี่ยมจัตุรัส \(SO\) คือด้านร่วม) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \(\triangle ASD\) และ \(\triangle BSC\) เป็นหน้าจั่ว จุด \(K\) เป็นจุดกึ่งกลางของ \(AD\) จากนั้น \(SK\) คือความสูงในสามเหลี่ยม \(\triangle ASD\) และ \(OK\) คือความสูงในสามเหลี่ยม \ (AOD\) \(\ Rightarrow\) เครื่องบิน \(SOK\) ตั้งฉากกับระนาบ \(ASD\) จุด \(L\) เป็นจุดกึ่งกลางของ \(BC\) จากนั้น \(SL\) คือความสูงในสามเหลี่ยม \(\triangle BSC\) และ \(OL\) คือความสูงในสามเหลี่ยม \ (BOC\) \(\ Rightarrow\) เครื่องบิน \(SOL\) (หรือที่รู้จักว่าเครื่องบิน \(SOK\) ) ตั้งฉากกับระนาบ \(BSC\) ดังนั้นเราจึงได้ \(\angle KSL\) เป็นมุมเชิงเส้นเท่ากับมุมไดฮีดรัลที่ต้องการ

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\ลูกศรขวา\) \(OL = 5\) ; \(SK = SL\) – ความสูงเท่ากัน สามเหลี่ยมหน้าจั่วซึ่งสามารถพบได้โดยใช้ทฤษฎีบทพีทาโกรัส: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). จะเห็นได้ว่า \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) สำหรับสามเหลี่ยม \(\triangle KSL\) ทฤษฎีบทสนทนาพีทาโกรัส \(\Rightarrow\) \(\triangle KSL\) – สามเหลี่ยมมุมฉาก \(\Rightarrow\) \(\angle KSL = 90^\circ\)

คำตอบ: 90

ตามกฎแล้วการเตรียมนักเรียนสำหรับการสอบคณิตศาสตร์เริ่มต้นด้วยการทำซ้ำสูตรพื้นฐานรวมถึงสูตรที่อนุญาตให้คุณกำหนดมุมระหว่างระนาบ แม้ว่าเรขาคณิตส่วนนี้จะมีรายละเอียดเพียงพอในกรอบของ หลักสูตรโรงเรียนผู้สำเร็จการศึกษาจำนวนมากจำเป็นต้องทำซ้ำเนื้อหาพื้นฐาน เมื่อเข้าใจถึงวิธีการหามุมระหว่างเครื่องบิน นักเรียนระดับมัธยมศึกษาตอนปลายจะสามารถคำนวณคำตอบที่ถูกต้องได้อย่างรวดเร็วในการแก้ปัญหาและนับคะแนนที่ดีจากการสอบรัฐแบบรวมศูนย์

ความแตกต่างหลัก

เพื่อให้คำถามเกี่ยวกับวิธีการหามุมไดฮีดรัลไม่ก่อให้เกิดปัญหา เราขอแนะนำให้คุณปฏิบัติตามอัลกอริธึมโซลูชันที่จะช่วยให้คุณรับมือกับงานในการสอบ

ก่อนอื่นคุณต้องกำหนดเส้นที่ระนาบตัดกัน

จากนั้นในบรรทัดนี้ คุณต้องเลือกจุดและวาดเส้นตั้งฉากสองจุด

ขั้นตอนต่อไปคือการหาฟังก์ชันตรีโกณมิติของมุมไดเฮดรัลซึ่งเกิดจากฉากตั้งฉาก การทำเช่นนี้สะดวกที่สุดด้วยความช่วยเหลือของรูปสามเหลี่ยมที่ได้ซึ่งมุมนั้นเป็นส่วนหนึ่ง

คำตอบจะเป็นค่าของมุมหรือฟังก์ชันตรีโกณมิติ

การเตรียมตัวสอบร่วมกับ Shkolkovo คือกุญแจสู่ความสำเร็จของคุณ

ระหว่างเรียนเมื่อวันก่อน สอบผ่านนักเรียนหลายคนประสบปัญหาในการหาคำจำกัดความและสูตรที่ให้คุณคำนวณมุมระหว่าง 2 ระนาบได้ หนังสือเรียนไม่ได้อยู่ใกล้แค่เอื้อมเสมอเมื่อจำเป็น และพบกับ สูตรที่จำเป็นและตัวอย่างการใช้งานที่ถูกต้อง รวมถึงการหามุมระหว่างระนาบบนอินเทอร์เน็ตออนไลน์ ซึ่งบางครั้งต้องใช้เวลามาก

ข้อเสนอพอร์ทัลคณิตศาสตร์ "Shkolkovo" แนวทางใหม่เพื่อเตรียมสอบราชการ ชั้นเรียนบนเว็บไซต์ของเราจะช่วยให้นักเรียนระบุส่วนที่ยากที่สุดสำหรับตนเองและเติมเต็มช่องว่างในความรู้

เราได้เตรียมและนำเสนอเนื้อหาที่จำเป็นทั้งหมดอย่างชัดเจน คำจำกัดความพื้นฐานและสูตรต่างๆ ได้แสดงไว้ในส่วน "การอ้างอิงเชิงทฤษฎี"

เพื่อให้ดูดซึมวัสดุได้ดีขึ้น เรายังแนะนำให้ฝึกแบบฝึกหัดที่เกี่ยวข้อง มีงานให้เลือกมากมาย องศาที่แตกต่างความซับซ้อน เช่น บน จะแสดงในส่วน "แคตตาล็อก" งานทั้งหมดมีอัลกอริธึมโดยละเอียดเพื่อค้นหาคำตอบที่ถูกต้อง รายการแบบฝึกหัดบนเว็บไซต์ได้รับการเสริมและปรับปรุงอย่างต่อเนื่อง

การฝึกหัดในการแก้ปัญหาที่จำเป็นต้องหามุมระหว่างระนาบสองระนาบ นักเรียนมีโอกาสที่จะบันทึกงานออนไลน์ใดๆ ไว้ใน "รายการโปรด" ด้วยเหตุนี้พวกเขาจะสามารถกลับไปหาเขาได้ จำนวนเงินที่ต้องการครั้งและหารือถึงแนวทางการตัดสินใจด้วย ครูโรงเรียนหรือติวเตอร์