งานหลักสูตร: สมการและอสมการพร้อมโมดูลการทดสอบแบบรวมศูนย์ การแก้ปัญหาความไม่เท่าเทียมกัน
บทความนี้ทุ่มเทให้กับวิธีการตัดสินใจ สมการที่แตกต่างกันและความไม่เท่าเทียมกันประกอบด้วย
ตัวแปรใต้เครื่องหมายโมดูลัส
ถ้าเจอสมการหรืออสมการกับมอดุลัสในข้อสอบก็แก้ได้ด้วยการ
โดยไม่รู้อะไรเลย วิธีการพิเศษและใช้เฉพาะคำจำกัดความของโมดูลเท่านั้น จริงมั้ย,
ซึ่งอาจใช้เวลาหนึ่งชั่วโมงครึ่งของเวลาอันมีค่าในการสอบ
นั่นเป็นเหตุผลที่เราต้องการบอกคุณเกี่ยวกับเทคนิคที่ทำให้การแก้ปัญหาดังกล่าวง่ายขึ้น
ก่อนอื่นให้เราจำไว้ว่า
ลองพิจารณาดู ประเภทต่างๆ สมการกับโมดูลัส- (เราจะไปสู่ความไม่เท่าเทียมกันในภายหลัง)
โมดูลทางด้านซ้าย หมายเลขทางด้านขวา
นี่เป็นกรณีที่ง่ายที่สุด มาแก้สมการ | x 2 − 5x + 4| = 4.
มีเพียงตัวเลขสองตัวเท่านั้นที่มีโมดูลเท่ากับสี่ เหล่านี้คือ 4 และ −4 ดังนั้นสมการ
เทียบเท่ากับการรวมกันของสองสิ่งง่าย ๆ:
x 2 − 5x+ 4 = 4 หรือ x 2 − 5x + 4 = −4.
สมการที่สองไม่มีคำตอบ วิธีแก้ปัญหาแรก: x= 0 และ x = 5.
คำตอบ: 0; 5.
ตัวแปรทั้งภายใต้โมดูลและโมดูลภายนอก
ที่นี่เราต้องขยายโมดูลตามคำจำกัดความ - - หรือคิด!
1. |2 − x| = 5 − 4x
สมการแบ่งออกเป็นสองกรณี ขึ้นอยู่กับเครื่องหมายของนิพจน์ใต้โมดูลัส
กล่าวอีกนัยหนึ่ง มันเทียบเท่ากับการรวมกันของสองระบบ:
![]()
แนวทางแก้ไขของระบบแรก: x= 1. ระบบที่สองไม่มีคำตอบ
คำตอบ: 1.
2 . x 2 + 4|x − 3| − 7x + 11 = 0.
กรณีแรก: x≥ 3. ถอดโมดูล:
ตัวเลข x 2 เป็นลบ ไม่เข้าเงื่อนไข x≥ 3 และดังนั้นจึงไม่ใช่รากของสมการดั้งเดิม
มาดูกันว่าตัวเลขเป็นไปตามเงื่อนไขนี้หรือไม่ x 1. ในการทำเช่นนี้ เราจะเขียนความแตกต่างและกำหนดเครื่องหมาย:
วิธี, x 1 มากกว่าสาม และดังนั้นจึงเป็นรากของสมการดั้งเดิม
กรณีที่สอง: x < 3. Снимаем модуль:
ตัวเลข x 3 มากกว่า และดังนั้นจึงไม่ตรงตามเงื่อนไข x < 3. Проверим x 4:
วิธี, x 4 คือรากของสมการดั้งเดิม
3. |2x 2 − 3x − 4| = 6x − 1.
การลบโมดูลตามคำจำกัดความ? มันน่ากลัวที่จะคิดเรื่องนี้ เพราะตัวแบ่งแยกไม่ใช่กำลังสองที่แน่นอน ลองใช้การพิจารณาต่อไปนี้กันดีกว่า: สมการในรูปแบบ |A| = B เทียบเท่ากับการรวมกันของสองระบบ:
![]()
สิ่งเดียวกัน แต่แตกต่างกันเล็กน้อย:
กล่าวอีกนัยหนึ่ง เราแก้สมการสองสมการ A = B และ A = −B จากนั้นเลือกรากที่ตรงตามเงื่อนไข B ≥ 0
มาเริ่มกันเลย ก่อนอื่นเราจะแก้สมการแรก:
จากนั้นเราก็แก้สมการที่สอง:
ในแต่ละกรณีเราจะตรวจสอบป้ายทางด้านขวา:
ดังนั้นจึงเหมาะสมเท่านั้น x 1 และ x 3 .
สมการกำลังสองที่มีการแทนที่ | x| = ที
มาแก้สมการกัน: x 2 + 2|x| − 3 = 0.
เพราะ x 2 = |x- 2 สะดวกในการเปลี่ยน | x| = ที- เราได้รับ:
![]()
คำตอบ: ±1
โมดูลัสเท่ากับโมดูลัส
เรากำลังพูดถึงสมการที่อยู่ในรูปแบบ |A| = |ข|. นี่คือของขวัญแห่งโชคชะตา ไม่มีการเปิดเผยโมดูลตามคำจำกัดความ! มันง่ายมาก:
ตัวอย่างเช่น พิจารณาสมการ: |3 x 2 + 5x − 9| = |6x+ 15|. มันเทียบเท่ากับชุดต่อไปนี้:
ยังคงต้องแก้สมการแต่ละชุดและจดคำตอบไว้
สองโมดูลขึ้นไป
มาแก้สมการกัน: | x − 1| − 2|x − 2| + 3|x − 3| = 4.
อย่ากังวลกับแต่ละโมดูลแยกกันและเปิดตามคำจำกัดความ - จะมีตัวเลือกมากเกินไป มีวิธีที่มีเหตุผลมากกว่านี้ - วิธีช่วงเวลา
นิพจน์ภายใต้โมดูลหายไป ณ จุดต่างๆ x = 1, x= 2 และ x= 3 จุดเหล่านี้จะแบ่งเส้นจำนวนออกเป็นสี่ช่อง (ช่วง) ทำเครื่องหมายจุดเหล่านี้บนเส้นจำนวนและวางเครื่องหมายสำหรับแต่ละนิพจน์ภายใต้โมดูลในช่วงเวลาผลลัพธ์ (ลำดับของเครื่องหมายเกิดขึ้นพร้อมกับลำดับของโมดูลที่เกี่ยวข้องในสมการ)

ดังนั้นเราจึงต้องพิจารณาสี่กรณี - เมื่อใด xจะอยู่ในแต่ละช่วงเวลา
กรณีที่ 1: x≥ 3. โมดูลทั้งหมดจะถูกลบออก "พร้อมเครื่องหมายบวก":
มูลค่าที่ได้รับ x= 5 เป็นไปตามเงื่อนไข x≥ 3 และดังนั้นจึงเป็นรากของสมการดั้งเดิม
กรณีที่ 2: 2 ≤ x≤ 3 โมดูลสุดท้ายจะถูกลบออก “ด้วยเครื่องหมายลบ”:
มูลค่าที่ได้รับ xเหมาะสมเช่นกัน - เป็นของช่วงเวลาที่เป็นปัญหา
กรณีที่ 3: 1 ≤ x≤ 2 โมดูลที่สองและสามจะถูกลบออก "ด้วยเครื่องหมายลบ":
เราได้รับความเท่าเทียมกันทางตัวเลขที่ถูกต้องสำหรับค่าใดๆ xจากช่วงเวลาที่พิจารณาไว้เป็นแนวทางแก้ไข สมการที่กำหนด.
กรณีที่ 4: x ≤ 1 ≤ 1 โมดูลที่สองและสามจะถูกลบออก "ด้วยเครื่องหมายลบ":
ไม่มีอะไรใหม่ เรารู้อยู่แล้วว่า x= 1 คือคำตอบ
คำตอบ: ∪ (5)
โมดูลภายในโมดูล
มาแก้สมการกันดีกว่า: ||3 − x| − 2x + 1| = 4x − 10.
เราเริ่มต้นด้วยการเปิดโมดูลภายใน
1) x≤ 3 เราได้รับ:
การแสดงออกภายใต้โมดูลัสหายไปที่ ประเด็นนี้เป็นของการพิจารณา
ระหว่าง. ดังนั้นเราจึงต้องวิเคราะห์สองกรณีย่อย
1.1) ในกรณีนี้เราได้รับ:
นี่คือความหมาย xไม่เหมาะสมเนื่องจากไม่อยู่ในช่วงพิจารณา
1.2) . แล้ว:
นี่คือความหมาย xไม่เหมาะเช่นกัน
แล้วเมื่อไหร่ล่ะ x≤ 3 ไม่มีวิธีแก้ปัญหา มาดูกรณีที่สองกันดีกว่า
2) x≥ 3 เรามี:
เราโชคดีที่นี่: การแสดงออก x+2 เป็นบวกในช่วงที่พิจารณา! ดังนั้นจะไม่มีกรณีย่อยอีกต่อไป: โมดูลจะถูกลบออก "พร้อมเครื่องหมายบวก":
นี่คือความหมาย xอยู่ในช่วงพิจารณาจึงเป็นรากของสมการเดิม
นี่คือวิธีแก้ปัญหาทั้งหมด ประเภทนี้- ขยายโมดูลที่ซ้อนกันทีละโมดูลโดยเริ่มจากโมดูลภายใน
อสมการกับโมดูลัส
ไม่มีแนวคิดใหม่ที่เป็นพื้นฐานเกิดขึ้นที่นี่ ทุกคน ความรู้ที่จำเป็นคุณเป็นเจ้าของแล้ว ดังนั้นเราจะวิเคราะห์เพียงสองปัญหาเท่านั้น ส่วนที่เหลือจะทำในชั้นเรียนและการบ้าน
1. 2|x − 4| + |3x + 5| ≥ 16.
1) x≥ 4 เรามี:
ความไม่เท่าเทียมกันที่เกิดขึ้นเป็นที่พอใจสำหรับทุกคนที่พิจารณา x≥ 4 กล่าวอีกนัยหนึ่งคือตัวเลขทั้งหมดจากช่วง
3) . เรามี:
เนื่องจาก − แล้วค่าทั้งหมด xจากช่วงเวลาที่เกิดจะทำหน้าที่เป็นวิธีแก้ปัญหาของความไม่เท่าเทียมกันดั้งเดิม
ยังคงต้องรวมชุดโซลูชันที่ได้รับในสามกรณีที่พิจารณา
2. |x 2 − 2x − 3| < 3x − 3.
นี่คือภารกิจที่ 6 ของส่วนทฤษฎีของบทที่ 8 ของหนังสือของ V. V. Tkachuk เรื่อง "คณิตศาสตร์สำหรับผู้สมัคร" ผู้เขียนแก้โดยใช้วิธีช่วงเวลา อย่าลืมตรวจสอบวิธีแก้ปัญหาของผู้เขียน!
โปรดทราบว่าวิธีการเป็นช่วงๆ ตรงนี้ไม่ยุ่งยากมาก เนื่องจากรากของกำลังสองตรีโนเมียลใต้โมดูลัสเป็นจำนวนเต็ม จะเกิดอะไรขึ้นถ้าการแบ่งแยกไม่ใช่กำลังสองที่แน่นอน? ตัวอย่างเช่น แทนที่ภายใต้โมดูลัส −3 ด้วย −5 ปริมาณงานคำนวณจะเพิ่มขึ้นอย่างมาก
เราจะแสดงวิธีแก้ไขปัญหานี้ให้คุณอีกวิธีหนึ่ง วิธีที่ไม่ขึ้นอยู่กับความหลากหลายของผู้ที่เลือกปฏิบัติ
อสมการของเรามีรูปแบบ |A|< B. Очевидны следующие утверждения.
ถ้า B ≤ 0 แสดงว่าอสมการไม่มีวิธีแก้ปัญหา
ถ้า B > 0 แสดงว่าอสมการจะเท่ากับอสมการสองเท่า −B< A < B или, что то же самое, системе
กล่าวอีกนัยหนึ่ง เราใช้จุดตัดของชุดคำตอบของระบบที่กำหนดกับชุดของคำตอบของอสมการ B > 0 นั่นคือเราแก้ระบบ
ในปัญหาของเราเราได้รับ:
ให้เราอธิบายชุดวิธีแก้ปัญหาสำหรับความไม่เท่าเทียมกันเหล่านี้ในรูป วิธีแก้ไขของอสมการแรก (สองเท่า) จะแสดงเป็นสีดำ สีเขียว- การแก้ปัญหาของจำนวนทั้งสิ้น สีฟ้า- แนวทางแก้ไขความไม่เท่าเทียมกันสุดท้ายของระบบ
วิธีแก้ของระบบคือจุดตัดกันของชุดเหล่านี้ ซึ่งก็คือชุดที่อยู่ด้านบนซึ่งมีเส้นทั้งสามสี มันเป็นร่มเงา
นี้ เครื่องคิดเลขคณิตศาสตร์ออนไลน์จะช่วยคุณได้ แก้สมการหรืออสมการด้วยโมดูลัส- โปรแกรมสำหรับ การแก้สมการและอสมการด้วยมอดูลิไม่เพียงแต่ให้คำตอบต่อปัญหาเท่านั้น แต่ยังนำไปสู่อีกด้วย วิธีแก้ปัญหาโดยละเอียดพร้อมคำอธิบาย, เช่น. แสดงกระบวนการรับผลลัพธ์
โปรแกรมนี้อาจเป็นประโยชน์สำหรับนักเรียนระดับมัธยมศึกษาตอนปลายในการเตรียมความพร้อม การทดสอบและการสอบเมื่อทดสอบความรู้ก่อนการสอบ Unified State เพื่อให้ผู้ปกครองได้ควบคุมการแก้ปัญหาต่างๆในวิชาคณิตศาสตร์และพีชคณิต หรืออาจจะแพงเกินไปสำหรับคุณที่จะจ้างครูสอนพิเศษหรือซื้อตำราเรียนใหม่ หรือคุณเพียงต้องการที่จะทำให้มันเสร็จโดยเร็วที่สุด?การบ้าน
ในวิชาคณิตศาสตร์หรือพีชคณิต? ในกรณีนี้ คุณสามารถใช้โปรแกรมของเราพร้อมวิธีแก้ปัญหาโดยละเอียดได้ ด้วยวิธีนี้คุณสามารถดำเนินการฝึกอบรมและ/หรือฝึกอบรมของคุณเองได้หรือน้องสาวในขณะที่ระดับการศึกษาในด้านปัญหาที่กำลังแก้ไขเพิ่มขึ้น
|x|หรือ เอบีเอส(x) - โมดูล x
แก้สมการหรืออสมการ
พบว่าไม่ได้โหลดสคริปต์บางตัวที่จำเป็นในการแก้ปัญหานี้ และโปรแกรมอาจไม่ทำงาน
คุณอาจเปิดใช้งาน AdBlock ไว้
JavaScript ถูกปิดใช้งานในเบราว์เซอร์ของคุณ
เพื่อให้วิธีแก้ปัญหาปรากฏขึ้น คุณต้องเปิดใช้งาน JavaScript
ต่อไปนี้เป็นคำแนะนำเกี่ยวกับวิธีเปิดใช้งาน JavaScript ในเบราว์เซอร์ของคุณ
เพราะ มีคนจำนวนมากยินดีแก้ไขปัญหา คำขอของคุณอยู่ในคิวแล้ว
ภายในไม่กี่วินาทีวิธีแก้ปัญหาจะปรากฏขึ้นด้านล่าง โปรดรอ
วินาที... ถ้าคุณสังเกตเห็นข้อผิดพลาดในการแก้ปัญหา
จากนั้นคุณสามารถเขียนเกี่ยวกับเรื่องนี้ในแบบฟอร์มคำติชม อย่าลืมระบุว่างานใด คุณตัดสินใจว่าอะไร.
เข้าไปในทุ่งนา
เกม ปริศนา อีมูเลเตอร์ของเรา:
ทฤษฎีเล็กน้อย
สมการและอสมการด้วยโมดูลัส
![]()
ในหลักสูตรพีชคณิตขั้นพื้นฐานของโรงเรียน คุณอาจพบกับสมการและอสมการที่ง่ายที่สุดด้วยโมดูลัส ในการแก้ปัญหาเหล่านี้ คุณสามารถใช้วิธีเรขาคณิตโดยยึดตามข้อเท็จจริงที่ว่า \(|x-a| \) คือระยะห่างบนเส้นจำนวนระหว่างจุด x และ a: \(|x-a| = \rho (x;\; a) \) ตัวอย่างเช่น ในการแก้สมการ \(|x-3|=2\) คุณต้องหาจุดบนเส้นจำนวนที่อยู่ห่างจากจุดที่ 3 ที่ระยะ 2 โดยมีจุดดังกล่าวสองจุด: \(x_1=1 \) และ \(x_2=5\) ![]()
การแก้อสมการ \(|2x+7|
แต่วิธีหลักในการแก้สมการและอสมการด้วยโมดูลัสนั้นเกี่ยวข้องกับสิ่งที่เรียกว่า "การเปิดเผยของโมดูลัสตามคำจำกัดความ":
ถ้า \(a \geq 0 \) ดังนั้น \(|a|=a \);
ถ้า \(a ตามกฎแล้ว สมการ (อสมการ) ที่มีมอดูลิลดลงเหลือเพียงเซตของสมการ (อสมการ) ที่ไม่มีเครื่องหมายโมดูลัส
นอกเหนือจากคำจำกัดความข้างต้นแล้ว ยังมีการใช้ข้อความต่อไปนี้:
1) ถ้า \(c > 0\) ดังนั้นสมการ \(|f(x)|=c \) จะเทียบเท่ากับเซตของสมการ: \(\left[\begin(array)(l) f(x )=c \\ f(x)=-c \end(อาร์เรย์)\right
2) ถ้า \(c > 0 \) แล้วความไม่เท่าเทียมกัน \(|f(x)| 3) ถ้า \(c \geq 0 \) แล้วความไม่เท่าเทียมกัน \(|f(x)| > c \) คือ เทียบเท่ากับเซตของอสมการ : \(\left[\begin(array)(l) f(x) c \end(array)\right. \) 4) ถ้าทั้งสองด้านมีความไม่เท่ากัน \(f(x)
ตัวอย่าง 1. แก้สมการ \(x^2 +2|x-1| -6 = 0\) ถ้า \(x-1 \geq 0\) แล้ว \(|x-1| = x-1\) และสมการที่กำหนด
ใช้แบบฟอร์ม
\(x^2 +2(x-1) -6 = 0 \ลูกศรขวา x^2 +2x -8 = 0 \)
ถ้า \(x-1 \(x^2 -2(x-1) -6 = 0 \ลูกศรขวา x^2 -2x -4 = 0 \)
1) ให้ \(x-1 \geq 0 \) เช่น \(x\geq 1\) จากสมการ \(x^2 +2x -8 = 0\) เราพบว่า \(x_1=2, \; x_2=-4\)
เงื่อนไข \(x \geq 1 \) เป็นไปตามค่า \(x_1=2\) เท่านั้น
2) ให้ \(x-1 ตอบ: \(2; \;\; 1-\sqrt(5) \)
ตัวอย่าง 2. แก้สมการ \(|x^2-6x+7| = \frac(5x-9)(3)\)วิธีแรก
(การขยายโมดูลตามคำจำกัดความ)
การให้เหตุผลตามตัวอย่างที่ 1 เราได้ข้อสรุปว่าสมการที่กำหนดจะต้องพิจารณาแยกกันหากตรงตามเงื่อนไขสองข้อ: \(x^2-6x+7 \geq 0 \) หรือ \(x^2-6x+7 1) ถ้า \(x^2-6x+7 \geq 0 \) ดังนั้น \(|x^2-6x+7| = x^2-6x+7 \) และสมการที่ให้มาจะอยู่ในรูปแบบ \(x ^2 -6x+7 = \frac(5x-9)(3) \ลูกศรขวา 3x^2-23x+30=0 \) ตัดสินใจเรื่องนี้แล้วสมการกำลังสอง
เราได้รับ: \(x_1=6, \; x_2=\frac(5)(3) \) มาดูกันว่าค่า \(x_1=6\) ตรงตามเงื่อนไข \(x^2-6x+7 \geq 0\) หรือไม่ เมื่อต้องการทำเช่นนี้ เรามาทดแทนกันค่าที่ระบุ วีอสมการกำลังสอง
- เราได้รับ: \(6^2-6 \cdot 6+7 \geq 0 \) เช่น \(7 \geq 0 \) คืออสมการที่แท้จริง
ซึ่งหมายความว่า \(x_1=6\) คือรากของสมการที่กำหนด
มาดูกันว่าค่า \(x_2=\frac(5)(3)\) ตรงตามเงื่อนไข \(x^2-6x+7 \geq 0\) หรือไม่ เมื่อต้องการทำเช่นนี้ ให้แทนที่ค่าที่ระบุลงในอสมการกำลังสอง เราได้รับ: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \) เช่น \(\frac(25)(9) -3 \geq 0 \) เป็นอสมการที่ไม่ถูกต้อง ซึ่งหมายความว่า \(x_2=\frac(5)(3)\) ไม่ใช่รากของสมการที่กำหนด 2) ถ้า \(x^2-6x+7 Value \(x_3=3\) ตรงตามเงื่อนไข \(x^2-6x+7 Value \(x_4=\frac(4)(3) \) ไม่ตรงตามเงื่อนไข เงื่อนไข \ (x^2-6x+7 ดังนั้น สมการที่ให้มามีสองราก: \(x=6, \; x=3 \)
วิธีที่สอง. ถ้าสมการ \(|f(x)| = h(x) \) ถูกกำหนดไว้ ดังนั้นด้วย \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(อาร์เรย์)\right \)สมการทั้งสองนี้ได้รับการแก้ไขข้างต้น (โดยใช้วิธีแรกในการแก้สมการที่กำหนด) รากของสมการมีดังนี้: \(6,\; \frac(5)(3),\; 3,\; \frac(4 )(3)\) เงื่อนไข \(\frac(5x-9)(3) \geq 0 \) จากสิ่งเหล่านี้
สี่ค่าพอใจเพียงสอง: 6 และ 3 ซึ่งหมายความว่าสมการที่กำหนดมีสองราก: \(x=6, \; x=3\)
1) มาสร้างกราฟของฟังก์ชัน \(y = |x^2-6x+7| \) กัน ก่อนอื่น เรามาสร้างพาราโบลา \(y = x^2-6x+7\) กันก่อน
เรามี \(x^2-6x+7 = (x-3)^2-2 \) กราฟของฟังก์ชัน \(y = (x-3)^2-2\) สามารถหาได้จากกราฟของฟังก์ชัน \(y = x^2 \) โดยเลื่อนไปทางขวา 3 หน่วยมาตราส่วน (ตาม แกน x) และลดลง 2 หน่วย (ตามแกน y)
เส้นตรง x=3 คือแกนของพาราโบลาที่เราสนใจ เป็นจุดควบคุมสำหรับการวางแผนที่แม่นยำยิ่งขึ้น สะดวกในการใช้จุด (3; -2) - จุดยอดของพาราโบลา จุด (0; 7) และจุด (6; 7) สมมาตรกับจุดนั้นสัมพันธ์กับแกนของพาราโบลา .

หากต้องการสร้างกราฟของฟังก์ชัน \(y = |x^2-6x+7| \) คุณต้องปล่อยส่วนต่างๆ ของพาราโบลาที่สร้างขึ้นซึ่งไม่ต่ำกว่าแกน x ไว้ไม่เปลี่ยนแปลง และสะท้อนส่วนนั้นของ พาราโบลาที่อยู่ต่ำกว่าแกน x สัมพันธ์กับแกน x
2) มาสร้างกราฟของฟังก์ชันเชิงเส้น \(y = \frac(5x-9)(3)\) กันดีกว่า สะดวกในการนำจุด (0; –3) และ (3; 2) เป็นจุดควบคุม. สิ่งสำคัญคือจุด x = 1.8 ของจุดตัดของเส้นตรงกับแกน abscissa จะอยู่ทางด้านขวาของจุดตัดด้านซ้ายของพาราโบลากับแกน abscissa - นี่คือจุด \(x=3-\ sqrt(2) \) (เนื่องจาก \(3-\sqrt(2 ) 3) เมื่อพิจารณาจากรูปวาด กราฟจะตัดกันที่จุดสองจุด - A(3; 2) และ B(6; 7) โดยแทนที่จุดขาดของสิ่งเหล่านี้ คะแนน x = 3 และ x = 6 ในสมการที่กำหนด เราเชื่อว่าในทั้งสองกรณี ในอีกค่าหนึ่ง จะได้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง ซึ่งหมายความว่าสมมติฐานของเราได้รับการยืนยัน - สมการมีสองราก: x = 3 และ x = 6 คำตอบ: 3;ความคิดเห็น
วิธีกราฟิก
ตัวอย่าง 2. แก้สมการ \(|x^2-6x+7| = \frac(5x-9)(3)\)
เพื่อความสง่างามทั้งหมดจึงไม่น่าเชื่อถือมากนัก ในตัวอย่างที่พิจารณา มันได้ผลเพียงเพราะว่ารากของสมการเป็นจำนวนเต็ม
![]()
ตัวอย่าง 3. แก้สมการ \(|2x-4|+|x+3| = 8\)
นิพจน์ 2x–4 กลายเป็น 0 ที่จุด x = 2 และนิพจน์ x + 3 กลายเป็น 0 ที่จุด x = –3 สองจุดนี้แบ่งเส้นจำนวนออกเป็นสามช่วง: \(x
พิจารณาช่วงแรก: \((-\infty; \; -3) \)
ถ้า x พิจารณาช่วงที่สอง: \([-3; \; 2) \)
ถ้า \(-3 \leq x พิจารณาช่วงที่สาม: \( พูดง่ายๆ ก็คือ โมดูลัสคือ “ตัวเลขที่ไม่มีเครื่องหมายลบ” และมันอยู่ในความเป็นคู่นี้อย่างแน่นอน (ในบางสถานที่คุณไม่จำเป็นต้องทำอะไรกับหมายเลขเดิม แต่ในบางสถานที่คุณจะต้องลบเครื่องหมายลบบางประเภทออก) นั่นคือจุดที่ความยากลำบากทั้งหมดอยู่ที่นักเรียนระดับเริ่มต้นยังมีอีกมาก
คำนิยาม. ให้จุด $a$ ถูกทำเครื่องหมายไว้บนเส้นจำนวน จากนั้นโมดูล $\left| x-a \right|$ คือระยะห่างจากจุด $x$ ถึงจุด $a$ บนเส้นนี้
หากคุณวาดภาพคุณจะได้สิ่งนี้:
 คำจำกัดความกราฟิกโมดูล
คำจำกัดความกราฟิกโมดูล ไม่ทางใดก็ทางหนึ่งจากคำจำกัดความของโมดูลจะติดตามทันที คุณสมบัติที่สำคัญ: โมดูลัสของตัวเลขจะเป็นปริมาณที่ไม่เป็นลบเสมอ- ข้อเท็จจริงนี้จะเป็นหัวข้อสีแดงที่ดำเนินไปตลอดการเล่าเรื่องทั้งหมดของเราในวันนี้
การแก้ปัญหาความไม่เท่าเทียมกัน วิธีช่วงเวลา
ทีนี้มาดูความไม่เท่าเทียมกันกัน มีพวกมันมากมาย แต่งานของเราตอนนี้คือต้องสามารถแก้ไขอย่างน้อยที่สุดก็ง่ายที่สุด สิ่งที่ลดความไม่เท่าเทียมกันเชิงเส้นเช่นเดียวกับวิธีช่วงเวลา
ฉันมีสองหัวข้อในหัวข้อนี้ บทเรียนใหญ่(โดยวิธีการที่มีประโยชน์มาก - ฉันแนะนำให้ศึกษา):
- วิธีช่วงเวลาสำหรับความไม่เท่าเทียมกัน (โดยเฉพาะดูวิดีโอ)
- อสมการเชิงตรรกศาสตร์แบบเศษส่วนเป็นบทเรียนที่กว้างขวางมาก แต่หลังจากนั้น คุณจะไม่มีคำถามใดๆ เลย
หากคุณรู้ทั้งหมดนี้ หากวลี "เปลี่ยนจากความไม่เท่าเทียมกันไปสู่สมการ" ไม่ได้ทำให้คุณมีความปรารถนาที่คลุมเครือที่จะชนกำแพงคุณก็พร้อมแล้ว: ยินดีต้อนรับสู่หัวข้อหลักของบทเรียน :)
1. อสมการของรูปแบบ “โมดูลัสน้อยกว่าฟังก์ชัน”
นี่เป็นหนึ่งในปัญหาที่พบบ่อยที่สุดเกี่ยวกับโมดูล จำเป็นต้องแก้ไขความไม่เท่าเทียมกันของแบบฟอร์ม:
\[\ซ้าย| ฉ\ขวา| \ltg\]
ฟังก์ชัน $f$ และ $g$ สามารถเป็นอะไรก็ได้ แต่โดยปกติแล้วจะเป็นพหุนาม ตัวอย่างของความไม่เท่าเทียมกันดังกล่าว:
\[\begin(align) & \left| 2x+3 \ขวา| \ltx+7; \\ & \ซ้าย| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0; \\ & \ซ้าย| ((x)^(2))-2\ซ้าย| x \right|-3 \right| \lt 2. \\\end(align)\]
พวกเขาทั้งหมดสามารถแก้ไขได้อย่างแท้จริงในบรรทัดเดียวตามรูปแบบต่อไปนี้:
\[\ซ้าย| ฉ\ขวา| \lt g\Rightarrow -g \lt f \lt g\quad \left(\ลูกศรขวา \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \right.\right)\]
เป็นเรื่องง่ายที่จะเห็นว่าเรากำจัดโมดูลออกไป แต่ในทางกลับกัน เราก็ได้รับความไม่เท่าเทียมกันสองเท่า (หรือซึ่งเป็นสิ่งเดียวกัน นั่นคือระบบของความไม่เท่าเทียมกันทั้งสอง) แต่การเปลี่ยนแปลงนี้คำนึงถึงทุกสิ่งอย่างแน่นอน ปัญหาที่เป็นไปได้: ถ้าตัวเลขใต้โมดูลัสเป็นบวก แสดงว่าวิธีนี้ได้ผล หากเป็นลบก็ยังใช้งานได้ และถึงแม้จะมีฟังก์ชันที่ไม่เพียงพอที่สุดแทนที่ $f$ หรือ $g$ วิธีการก็ยังใช้งานได้
โดยธรรมชาติแล้วคำถามก็เกิดขึ้น: ง่ายกว่านี้ไม่ได้เหรอ? น่าเสียดายที่มันเป็นไปไม่ได้ นี่คือจุดรวมของโมดูล
แต่พอมีปรัชญาแล้ว มาแก้ไขปัญหาสองสามข้อกัน:
งาน. แก้ความไม่เท่าเทียมกัน:
\[\ซ้าย| 2x+3 \ขวา| \lt x+7\]
สารละลาย. ดังนั้นเราจึงมีความไม่เท่าเทียมกันแบบคลาสสิกของรูปแบบ "โมดูลัสน้อยกว่า" - ไม่มีอะไรจะแปลงด้วยซ้ำ เราทำงานตามอัลกอริทึม:
\[\begin(align) & \left| ฉ\ขวา| \lt g\ลูกศรขวา -g \lt f \lt g; \\ & \ซ้าย| 2x+3 \ขวา| \lt x+7\ลูกศรขวา -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]
อย่ารีบเปิดวงเล็บที่มีเครื่องหมาย "ลบ" นำหน้า: ค่อนข้างเป็นไปได้ว่าคุณจะทำผิดพลาดที่น่ารังเกียจเนื่องจากความเร่งรีบของคุณ
\[-x-7 \lt 2x+3 \lt x+7\]
\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]
\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]
\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]
ปัญหาลดลงเหลือความไม่เท่าเทียมกันเบื้องต้นสองประการ ให้เราสังเกตคำตอบของพวกเขาบนเส้นจำนวนคู่ขนาน:
จุดตัดของชุด
จุดตัดของเซตเหล่านี้จะเป็นคำตอบ
คำตอบ: $x\in \left(-\frac(10)(3);4 \right)$
งาน. แก้ความไม่เท่าเทียมกัน:
\[\ซ้าย| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]
สารละลาย. งานนี้ยากขึ้นเล็กน้อย ขั้นแรก เรามาแยกโมดูลโดยเลื่อนเทอมที่สองไปทางขวา:
\[\ซ้าย| ((x)^(2))+2x-3 \right| \lt -3\left(x+1 \right)\]
เห็นได้ชัดว่าเรามีความไม่เท่าเทียมกันของรูปแบบ "โมดูลมีขนาดเล็กกว่า" อีกครั้งดังนั้นเราจึงกำจัดโมดูลโดยใช้อัลกอริธึมที่ทราบอยู่แล้ว:
\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]
ตอนนี้ให้ความสนใจ: บางคนจะบอกว่าฉันเป็นคนนิสัยไม่ดีกับวงเล็บทั้งหมดนี้ แต่ให้ฉันเตือนคุณอีกครั้งว่าเป้าหมายหลักของเราคือ แก้ความไม่เท่าเทียมกันให้ถูกต้องแล้วได้คำตอบ- ต่อมาเมื่อคุณเชี่ยวชาญทุกสิ่งที่อธิบายไว้ในบทเรียนนี้อย่างสมบูรณ์แล้ว คุณสามารถบิดเบือนมันได้เองตามที่คุณต้องการ: เปิดวงเล็บเหลี่ยม เพิ่มเครื่องหมายลบ ฯลฯ
ขั้นแรกเราจะกำจัดเครื่องหมายลบสองเท่าทางด้านซ้าย:
\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\ซ้าย(x+1 \ขวา)\]
ทีนี้มาเปิดวงเล็บทั้งหมดในอสมการสองเท่ากัน:
เรามาดูอสมการสองเท่ากันดีกว่า. คราวนี้การคำนวณจะจริงจังกว่านี้:
\[\left\( \begin(จัดแนว) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(จัดตำแหน่ง) \right.\]
\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( จัดตำแหน่ง)\right.\]
อสมการทั้งสองเป็นแบบกำลังสองและสามารถแก้ไขได้โดยใช้วิธีช่วงเวลา (นั่นคือเหตุผลที่ฉันพูดว่า: ถ้าคุณไม่รู้ว่าสิ่งนี้คืออะไร จะเป็นการดีกว่าที่จะไม่เข้าร่วมโมดูล) เรามาดูสมการในอสมการแรกกันดีกว่า:
\[\begin(align) & ((x)^(2))+5x=0; \\ & x\ซ้าย(x+5 \ขวา)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(จัดแนว)\]
อย่างที่คุณเห็น ผลลัพธ์ที่ได้คือสมการกำลังสองที่ไม่สมบูรณ์ ซึ่งสามารถแก้ไขได้ด้วยวิธีเบื้องต้น ทีนี้ลองดูอสมการที่สองของระบบ คุณจะต้องใช้ทฤษฎีบทของ Vieta ที่นั่น:
\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(จัดแนว)\]
เราทำเครื่องหมายตัวเลขผลลัพธ์บนเส้นคู่ขนานสองเส้น (แยกสำหรับความไม่เท่าเทียมกันครั้งแรกและแยกจากที่สอง):
อีกครั้ง เนื่องจากเรากำลังแก้ระบบอสมการ เราจึงสนใจจุดตัดของเซตสีเทา: $x\in \left(-5;-2 \right)$ นี่คือคำตอบ
คำตอบ: $x\in \left(-5;-2 \right)$
ฉันคิดว่าหลังจากตัวอย่างเหล่านี้ รูปแบบการแก้ปัญหามีความชัดเจนมาก:
- แยกโมดูลโดยการย้ายพจน์อื่นๆ ทั้งหมดไปไว้ฝั่งตรงข้ามของอสมการ ดังนั้นเราจึงได้ความไม่เท่าเทียมกันของรูปแบบ $\left| ฉ\ขวา| \ltg$.
- แก้ไขความไม่เท่าเทียมกันนี้ด้วยการกำจัดโมดูลตามโครงร่างที่อธิบายไว้ข้างต้น เมื่อถึงจุดหนึ่ง จำเป็นต้องย้ายจากความไม่เท่าเทียมกันสองเท่าไปเป็นระบบสองนิพจน์ที่เป็นอิสระ ซึ่งแต่ละนิพจน์สามารถแก้ไขได้แยกกันอยู่แล้ว
- สุดท้าย สิ่งที่เหลืออยู่ก็คือตัดผลเฉลยของนิพจน์อิสระทั้งสองนี้ - แค่นั้นเอง เราก็จะได้คำตอบสุดท้าย
อัลกอริธึมที่คล้ายกันมีอยู่สำหรับอสมการประเภทต่อไปนี้ เมื่อโมดูลัสมากกว่าฟังก์ชัน อย่างไรก็ตาม มี "แต่" ที่ร้ายแรงอยู่สองสามประการ เราจะพูดถึง "แต่" เหล่านี้ตอนนี้
2. อสมการของรูปแบบ “โมดูลัสมีค่ามากกว่าฟังก์ชัน”
พวกเขามีลักษณะเช่นนี้:
\[\ซ้าย| ฉ\ขวา| \gtg\]
คล้ายกับครั้งก่อน? ดูเหมือนว่า. แต่ปัญหาดังกล่าวได้รับการแก้ไขด้วยวิธีที่แตกต่างไปจากเดิมอย่างสิ้นเชิง อย่างเป็นทางการโครงการมีดังนี้:
\[\ซ้าย| ฉ\ขวา| \gt g\ลูกศรขวา \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]
กล่าวอีกนัยหนึ่ง เราจะพิจารณาสองกรณี:
- อันดับแรก เราเพียงเพิกเฉยต่อโมดูลและแก้ไขความไม่เท่าเทียมกันตามปกติ
- โดยพื้นฐานแล้ว เราจะขยายโมดูลด้วยเครื่องหมายลบ จากนั้นคูณทั้งสองข้างของอสมการด้วย −1 ขณะที่ฉันมีเครื่องหมายอยู่
ตัวเลือกจะรวมกัน วงเล็บเหลี่ยม, เช่น. เรามีข้อกำหนดสองประการรวมกันอยู่ตรงหน้าเรา
โปรดทราบอีกครั้ง: นี่ไม่ใช่ระบบ แต่เป็นระบบทั้งหมด ในคำตอบ ชุดต่างๆ จะรวมกันแทนที่จะตัดกัน- นี่คือความแตกต่างพื้นฐานจากประเด็นที่แล้ว!
โดยทั่วไปแล้ว นักเรียนหลายคนสับสนอย่างสิ้นเชิงกับสหภาพแรงงานและทางแยก ดังนั้นเรามาแก้ไขปัญหานี้กัน:
- "∪" คือสัญลักษณ์สหภาพ โดยพื้นฐานแล้วนี่คือตัวอักษร "U" ที่เก๋ไก๋ซึ่งส่งถึงเรา ภาษาอังกฤษและเป็นคำย่อของคำว่า “ยูเนี่ยน” คือ "สมาคม".
- "∩" คือป้ายทางแยก เรื่องไร้สาระนี้ไม่ได้มาจากที่ไหนเลย แต่ดูเหมือนเป็นสิ่งที่ตรงกันข้ามกับ “∪”
เพื่อให้จำได้ง่ายขึ้น เพียงวาดขาไปที่ป้ายเหล่านี้เพื่อทำแว่นตา (อย่ากล่าวหาว่าฉันส่งเสริมการติดยาและโรคพิษสุราเรื้อรัง: หากคุณศึกษาบทเรียนนี้อย่างจริงจัง แสดงว่าคุณติดยาแล้ว):
 ความแตกต่างระหว่างจุดตัดและการรวมกันของเซต
ความแตกต่างระหว่างจุดตัดและการรวมกันของเซต เมื่อแปลเป็นภาษารัสเซียหมายถึงสิ่งต่อไปนี้: สหภาพ (ผลรวม) รวมถึงองค์ประกอบจากทั้งสองชุดดังนั้นจึงไม่น้อยไปกว่าแต่ละชุด แต่จุดตัด (ระบบ) จะรวมเฉพาะองค์ประกอบที่พร้อมกันทั้งชุดแรกและชุดที่สอง ดังนั้นจุดตัดกันของเซตจึงไม่ใหญ่กว่าเซตต้นทาง
มันเลยชัดเจนขึ้น? นั่นเยี่ยมมาก เรามาฝึกกันต่อ
งาน. แก้ความไม่เท่าเทียมกัน:
\[\ซ้าย| 3x+1 \ขวา| \gt 5-4x\]
สารละลาย. เราดำเนินการตามโครงการ:
\[\ซ้าย| 3x+1 \ขวา| \gt 5-4x\ลูกศรขวา \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ ขวา.\]
เราแก้ไขความไม่เท่าเทียมกันแต่ละอย่างในประชากร:
\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]
\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]
\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]
เราทำเครื่องหมายแต่ละชุดผลลัพธ์บนเส้นจำนวน จากนั้นจึงรวมเข้าด้วยกัน:
ยูเนี่ยนของชุด
เห็นได้ชัดว่าคำตอบจะเป็น $x\in \left(\frac(4)(7);+\infty \right)$
คำตอบ: $x\in \left(\frac(4)(7);+\infty \right)$
งาน. แก้ความไม่เท่าเทียมกัน:
\[\ซ้าย| ((x)^(2))+2x-3 \right| \gt x\]
สารละลาย. ดี? ไม่มีอะไร - ทุกอย่างเหมือนกัน เราย้ายจากความไม่เท่าเทียมกันที่มีโมดูลัสไปสู่ชุดของความไม่เท่าเทียมกันสองประการ:
\[\ซ้าย| ((x)^(2))+2x-3 \right| \gt x\ลูกศรขวา \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]
เราแก้ไขทุกความไม่เท่าเทียมกัน น่าเสียดายที่รากที่นั่นจะไม่ดีนัก:
\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2) \\\end(จัดแนว)\]
ความไม่เท่าเทียมกันประการที่สองนั้นค่อนข้างจะรุนแรง:
\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2) \\\end(จัดแนว)\]
ตอนนี้คุณต้องทำเครื่องหมายตัวเลขเหล่านี้บนสองแกน - หนึ่งแกนสำหรับความไม่เท่าเทียมกันแต่ละอัน อย่างไรก็ตาม คุณต้องทำเครื่องหมายจุดตามลำดับที่ถูกต้อง: มากกว่า จำนวนที่มากขึ้นยิ่งเราเลื่อนจุดไปทางขวามากเท่าไร
และนี่คือการตั้งค่ารอเราอยู่ ถ้าทุกอย่างชัดเจนด้วยตัวเลข $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (เงื่อนไขในตัวเศษของตัวแรก เศษส่วนน้อยกว่าพจน์ในตัวเศษของวินาที ดังนั้นผลรวมจึงน้อยกว่าด้วย) โดยมีตัวเลข $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ ก็จะไม่มีปัญหาเช่นกัน (จำนวนบวกเป็นลบมากกว่าอย่างเห็นได้ชัด) จากนั้นสองสามอย่างสุดท้ายทุกอย่างก็ไม่ชัดเจน อันไหนมากกว่า: $\frac(-3+\sqrt(21))(2)$ หรือ $\frac(-1+\sqrt(13))(2)$? การวางจุดบนเส้นจำนวนและที่จริงแล้วคำตอบจะขึ้นอยู่กับคำตอบของคำถามนี้
ลองเปรียบเทียบกัน:
\[\begin(เมทริกซ์) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ วี -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(เมทริกซ์)\]
เราแยกรากได้จำนวนที่ไม่เป็นลบทั้งสองข้างของอสมการ ดังนั้นเราจึงมีสิทธิ์ยกกำลังสองทั้งสองข้าง:
\[\begin(เมทริกซ์) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \ 4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(เมทริกซ์)\]
ฉันคิดว่ามันไม่ใช่เรื่องง่ายที่ $4\sqrt(13) \gt 3$ ดังนั้น $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$ จุดสุดท้ายของแกนจะถูกวางดังนี้:
กรณีของรากที่น่าเกลียด
ฉันขอเตือนคุณว่าเรากำลังแก้ไขคอลเลคชัน ดังนั้นคำตอบจะเป็นการรวม ไม่ใช่จุดตัดของเซตที่แรเงา
คำตอบ: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty \right)$
อย่างที่คุณเห็น โครงการของเราใช้ได้ผลดีกับทั้งคู่ งานง่ายๆและสำหรับอันที่ยากมาก สิ่งเดียวเท่านั้น" จุดอ่อน“ในแนวทางนี้ คุณจะต้องเปรียบเทียบอย่างมีศักยภาพ จำนวนตรรกยะ(และเชื่อฉันเถอะ: มันไม่ใช่แค่รากเท่านั้น) แต่บทเรียนแยกต่างหาก (และจริงจังมาก) จะเน้นไปที่ประเด็นการเปรียบเทียบ และเราก็เดินหน้าต่อไป
3. ความไม่เท่าเทียมกันกับ "ก้อย" ที่ไม่เป็นลบ
ตอนนี้เรามาถึงส่วนที่น่าสนใจที่สุดแล้ว นี่คือความไม่เท่าเทียมกันของแบบฟอร์ม:
\[\ซ้าย| ฉ\ขวา| \gt \ซ้าย| ก\ขวา|\]
โดยทั่วไปแล้ว อัลกอริธึมที่เราจะพูดถึงตอนนี้นั้นถูกต้องสำหรับโมดูลเท่านั้น มันใช้ได้กับความไม่เท่าเทียมกันทั้งหมด โดยรับประกันว่านิพจน์ที่ไม่เป็นลบทางซ้ายและขวา:
จะทำอย่างไรกับงานเหล่านี้? เพียงจำไว้ว่า:
ในความไม่เท่าเทียมกับ "ก้อย" ที่ไม่เป็นลบสามารถยกทั้งสองฝ่ายเป็นค่าใดก็ได้ ระดับธรรมชาติ- ไม่มี ข้อ จำกัด เพิ่มเติมมันจะไม่เกิดขึ้น
ก่อนอื่นเราจะสนใจเรื่องการยกกำลังสอง - มันเผาโมดูลและรูท:
\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f \\\end(จัดแนว)\]
อย่าสับสนกับการหารากของกำลังสอง:
\[\sqrt(((f)^(2)))=\left| ฉ \right|\ne ฉ\]
เกิดข้อผิดพลาดนับไม่ถ้วนเมื่อนักเรียนลืมติดตั้งโมดูล! แต่นี่เป็นเรื่องราวที่แตกต่างไปจากเดิมอย่างสิ้นเชิง (สมการไร้เหตุผล) ดังนั้นเราจะไม่พูดถึงเรื่องนี้ในตอนนี้ มาแก้ไขปัญหาสองสามข้อกันดีกว่า:
งาน. แก้ความไม่เท่าเทียมกัน:
\[\ซ้าย| x+2 \right|\ge \left| 1-2x \ขวา|\]
สารละลาย. ลองสังเกตสองสิ่งทันที:
- นี่ไม่ใช่ความไม่เท่าเทียมกันที่เข้มงวด จุดบนเส้นจำนวนจะถูกแทง
- เห็นได้ชัดว่าความไม่เท่าเทียมกันทั้งสองด้านไม่เป็นลบ (นี่คือคุณสมบัติของโมดูล: $\left| f\left(x \right) \right|\ge 0$)
ดังนั้นเราจึงสามารถยกกำลังสองของความไม่เท่าเทียมกันทั้งสองด้านเพื่อกำจัดโมดูลัสและแก้ไขปัญหาโดยใช้วิธีช่วงเวลาปกติ:
\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)) \\\end(จัดแนว)\]
ในขั้นตอนสุดท้าย ฉันโกงนิดหน่อย: ฉันเปลี่ยนลำดับของคำศัพท์ โดยใช้ประโยชน์จากความเท่าเทียมกันของโมดูล (อันที่จริง ฉันคูณนิพจน์ $1-2x$ ด้วย −1)
\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ ขวา)\right)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]
เราแก้โดยใช้วิธีช่วงเวลา เรามาเปลี่ยนจากอสมการไปสู่สมการกัน:
\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3) \\\end(จัดแนว)\]
เราทำเครื่องหมายรากที่พบบนเส้นจำนวน อีกครั้ง: ทุกจุดถูกแรเงาเพราะอสมการเดิมไม่เข้มงวด!
กำจัดเครื่องหมายมอดุลัส
ฉันขอเตือนคุณสำหรับผู้ที่ดื้อรั้นเป็นพิเศษ: เรานำสัญญาณจากความไม่เท่าเทียมกันครั้งล่าสุดซึ่งเขียนไว้ก่อนที่จะไปสู่สมการ และเราทาสีทับพื้นที่ที่ต้องการในความไม่เท่าเทียมกันเดียวกัน ในกรณีของเราคือ $\left(x-3 \right)\left(3x+1 \right)\le 0$
นั่นคือทั้งหมดที่ ปัญหาได้รับการแก้ไขแล้ว
คำตอบ: $x\in \left[ -\frac(1)(3);3 \right]$.
งาน. แก้ความไม่เท่าเทียมกัน:
\[\ซ้าย| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]
สารละลาย. เราทำทุกอย่างเหมือนกัน ฉันจะไม่แสดงความคิดเห็น - แค่ดูลำดับของการกระทำ
ยกกำลังสอง:
\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left) |. ((x)^(2))+3x+4 \right|. \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \ขวา))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ ขวา))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\เลอ 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]
วิธีช่วงเวลา:
\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ ลูกศรขวา x=-1.5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\ลูกศรขวา \varnothing \\\end(จัดแนว)\]
มีเพียงรากเดียวบนเส้นจำนวน:
คำตอบคือช่วงเวลาทั้งหมด
คำตอบ: $x\in \left[ -1.5;+\infty \right)$.
บันทึกเล็กๆ น้อยๆ เกี่ยวกับงานสุดท้าย ตามที่นักเรียนคนหนึ่งของฉันระบุไว้อย่างถูกต้อง นิพจน์ย่อยทั้งสองในความไม่เท่าเทียมกันนี้เป็นเชิงบวกอย่างเห็นได้ชัด ดังนั้นจึงสามารถละเครื่องหมายโมดูลัสได้โดยไม่เป็นอันตรายต่อสุขภาพ
แต่นี่เป็นระดับการคิดที่แตกต่างอย่างสิ้นเชิงและเป็นแนวทางที่แตกต่าง - มันสามารถเรียกได้ว่าเป็นวิธีการของผลที่ตามมาอย่างมีเงื่อนไข เกี่ยวกับเรื่องนี้ - ในบทเรียนแยกต่างหาก ตอนนี้เรามาดูส่วนสุดท้ายของบทเรียนของวันนี้แล้วดูอัลกอริธึมสากลที่ใช้งานได้เสมอ แม้ว่าวิธีการก่อนหน้านี้ทั้งหมดจะไร้พลังก็ตาม :)
4. วิธีการแจงนับตัวเลือก
จะเกิดอะไรขึ้นถ้าเทคนิคทั้งหมดนี้ไม่ได้ช่วยอะไร? หากไม่สามารถลดความไม่เท่าเทียมกันเป็นหางที่ไม่เป็นลบได้หากไม่สามารถแยกโมดูลได้หากโดยทั่วไปมีความเจ็บปวดความโศกเศร้าความเศร้าโศก?
จากนั้น “ปืนใหญ่” ของคณิตศาสตร์ทั้งหมดก็มาถึงที่เกิดเหตุ ซึ่งเป็นวิธีแบบเดรัจฉาน สัมพันธ์กับอสมการกับโมดูลัส มีลักษณะดังนี้:
- เขียนนิพจน์ย่อยทั้งหมดและตั้งค่าให้เท่ากับศูนย์
- แก้สมการผลลัพธ์และทำเครื่องหมายรากที่พบในเส้นจำนวนหนึ่งเส้น
- เส้นตรงจะแบ่งออกเป็นหลายส่วน โดยแต่ละโมดูลจะมีป้ายตายตัวและเผยให้เห็นไม่ซ้ำกัน
- แก้ไขความไม่เท่าเทียมกันในแต่ละส่วนดังกล่าว (คุณสามารถพิจารณาขอบเขตรากที่ได้รับในขั้นตอนที่ 2 แยกกันเพื่อความน่าเชื่อถือ) รวมผลลัพธ์ - นี่จะเป็นคำตอบ :)
แล้วยังไงล่ะ? อ่อนแอ? อย่างง่ายดาย! เป็นเวลานานเท่านั้น มาดูในทางปฏิบัติ:
งาน. แก้ความไม่เท่าเทียมกัน:
\[\ซ้าย| x+2 \ขวา| \lt \ซ้าย| x-1 \right|+x-\frac(3)(2)\]
สารละลาย. เรื่องไร้สาระนี้ไม่ได้เดือดลงไปถึงความไม่เท่าเทียมกันเช่น $\left| ฉ\ขวา| \lt g$, $\ซ้าย| ฉ\ขวา| \gt g$ หรือ $\left| ฉ\ขวา| \lt \ซ้าย| g \right|$ ดังนั้นเราจึงดำเนินการล่วงหน้า
เราเขียนนิพจน์ submodular จัดให้เป็นศูนย์และค้นหาราก:
\[\begin(align) & x+2=0\ลูกศรขวา x=-2; \\ & x-1=0\ลูกศรขวา x=1 \\\end(จัดแนว)\]
โดยรวมแล้ว เรามีรากสองอันที่แบ่งเส้นจำนวนออกเป็นสามส่วน ซึ่งภายในแต่ละโมดูลจะถูกเปิดเผยโดยไม่ซ้ำกัน:
การแบ่งเส้นจำนวนด้วยศูนย์ของฟังก์ชันย่อย
มาดูแต่ละส่วนแยกกัน
1. ให้ $x \lt -2$. จากนั้นนิพจน์ย่อยทั้งสองจะเป็นค่าลบ และความไม่เท่าเทียมกันดั้งเดิมจะถูกเขียนใหม่ดังนี้:
\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1.5 \\ & -x-2 \lt -x+1+ x- 1.5 \\ & x \gt 1.5 \\\end (จัดแนว)\]
เรามีข้อจำกัดที่ค่อนข้างง่าย ลองตัดมันด้วยสมมติฐานเบื้องต้นว่า $x \lt -2$:
\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1.5 \\\end(align) \right.\Rightarrow x\in \varnothing \]
แน่นอนว่าตัวแปร $x$ ต้องไม่น้อยกว่า −2 และมากกว่า 1.5 ในเวลาเดียวกัน ไม่มีวิธีแก้ปัญหาในพื้นที่นี้
1.1. ให้เราพิจารณากรณีเส้นเขตแดนแยกกัน: $x=-2$ ลองแทนจำนวนนี้ลงในอสมการเดิมแล้วตรวจดู: จริงไหม?
\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=-2) ) \ \ & 0 \lt \ซ้าย| -3\ขวา|-2-1.5; \\ & 0 \lt 3-3.5; \\ & 0 \lt -0.5\ลูกศรขวา \varnothing \\\end(จัดแนว)\]
เห็นได้ชัดว่าห่วงโซ่การคำนวณทำให้เราเกิดความไม่เท่าเทียมกันที่ไม่ถูกต้อง ดังนั้น อสมการดั้งเดิมจึงเป็นเท็จเช่นกัน และ $x=-2$ จะไม่รวมอยู่ในคำตอบ
2. ให้ $-2 \lt x \lt 1$ โมดูลด้านซ้ายจะเปิดด้วยเครื่องหมาย "บวก" อยู่แล้ว แต่โมดูลด้านขวาจะยังคงเปิดด้วย "เครื่องหมายลบ" เรามี:
\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\end(จัดตำแหน่ง)\]
เราตัดกับข้อกำหนดเดิมอีกครั้ง:
\[\left\( \begin(align) & x \lt -2.5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]
และขอย้ำอีกครั้งว่าชุดของคำตอบนั้นว่างเปล่า เนื่องจากไม่มีตัวเลขใดที่ทั้งน้อยกว่า −2.5 และมากกว่า −2
2.1. และอีกครั้ง กรณีพิเศษ: $x=1$. เราแทนที่ความไม่เท่าเทียมกันดั้งเดิม:
\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=1)) \\ & \ซ้าย| 3\ขวา| \lt \ซ้าย| 0 \ขวา|+1-1.5; \\ & 3 \lt -0.5; \\ & 3 \lt -0.5\ลูกศรขวา \varnothing \\\end(จัดแนว)\]
เช่นเดียวกับ “กรณีพิเศษ” ก่อนหน้านี้ ตัวเลข $x=1$ ไม่ได้รวมอยู่ในคำตอบอย่างชัดเจน
3. ส่วนสุดท้ายของบรรทัด: $x \gt 1$ ที่นี่โมดูลทั้งหมดจะเปิดขึ้นโดยมีเครื่องหมายบวก:
\[\begin(จัดตำแหน่ง) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]
และอีกครั้งที่เราตัดกันเซตที่พบด้วยข้อจำกัดเดิม:
\[\left\( \begin(align) & x \gt 4.5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4.5;+\infty \right)\ ]
ในที่สุด! เราได้พบช่วงเวลาที่จะเป็นคำตอบ
คำตอบ: $x\in \left(4,5;+\infty \right)$
สุดท้ายนี้ มีหมายเหตุหนึ่งที่อาจช่วยคุณจากความผิดพลาดโง่ๆ เมื่อแก้ไขปัญหาจริง:
คำตอบของอสมการด้วยโมดูลัสมักจะแสดงถึงเซตต่อเนื่องบนเส้นจำนวน - ช่วงเวลาและเซ็กเมนต์ พบได้น้อยกว่ามาก จุดที่แยกได้- และบ่อยครั้งที่ขอบเขตของการแก้ปัญหา (จุดสิ้นสุดของส่วน) เกิดขึ้นพร้อมกับขอบเขตของช่วงที่พิจารณา
ดังนั้น หากไม่รวมขอบเขต ("กรณีพิเศษ" เดียวกันในคำตอบ พื้นที่ทางซ้ายและขวาของขอบเขตเหล่านี้แทบจะไม่รวมอยู่ในคำตอบเลย และในทางกลับกัน: เส้นขอบเข้าสู่คำตอบ ซึ่งหมายความว่าบางพื้นที่รอบ ๆ จะเป็นคำตอบด้วย
โปรดคำนึงถึงสิ่งนี้เมื่อตรวจสอบวิธีแก้ปัญหาของคุณ
สมการและอสมการกับโมดูลัส
หมายเหตุอธิบาย
หลักสูตรนี้เน้นการนำเสนออย่างเป็นระบบ สื่อการศึกษาเกี่ยวข้องกับแนวคิดเรื่องโมดูลัสของตัวเลขและแง่มุมของการประยุกต์ มันหารือ วิธีการต่างๆการแก้สมการและอสมการด้วยโมดูลัสตามนิยาม คุณสมบัติ และการตีความเชิงกราฟิก
หลักสูตรนี้มีเอกลักษณ์เฉพาะด้วยการปฐมนิเทศภาคปฏิบัติ โดยมีเนื้อหาหลักคือ วัตถุประสงค์การเรียนรู้- บ้างก็มอบให้ด้วย โซลูชั่นที่สมบูรณ์แสดงให้เห็นวิธีการหนึ่งหรือวิธีอื่น อื่น ๆ รวมอยู่ด้วยสำหรับ งานอิสระ- การนำเสนอ เทคนิคการปฏิบัติการแก้ปัญหาจะมาพร้อมกับความจำเป็น ข้อมูลทางทฤษฎี.
หลักสูตรนี้มีวัตถุประสงค์เพื่อพัฒนาให้นักเรียนมีความเข้าใจในโมดูลที่กว้างขึ้น นอกจากนี้งานต่างๆ การสอบแบบรวมในวิชาคณิตศาสตร์สมมุติว่ามีความสามารถในการทำงานกับโมดูล ดังนั้นบทบาทหลักของหลักสูตรนี้คือการเตรียมนักเรียนให้พร้อม สำเร็จลุล่วงได้การสอบแบบรวมรัฐ
แผนการศึกษาและเฉพาะเรื่อง
วัสดุสำหรับชั้นเรียน
บทที่ 1 การกำหนดโมดูลัสของตัวเลขและการประยุกต์ในการแก้สมการ
คำนิยาม- โมดูลัสของการไม่เป็นลบ จำนวนจริง เอ็กซ์โทรไปที่หมายเลขนี้เอง: | x | = เอ็กซ์- โมดูลัสของจำนวนจริงลบ x เรียกว่า หมายเลขตรงข้าม- x | = - x .
เขียนโดยย่อดังนี้:
|x | -
คำว่า "โมดูล" (จากภาษาละตินโมดูลัส - การวัด) ถูกนำมาใช้โดย นักคณิตศาสตร์ชาวอังกฤษ R. Cortes (1682-1716) และเครื่องหมายโมดูลัสถูกสร้างขึ้นโดยนักคณิตศาสตร์ชาวเยอรมัน K. Weierstrass (1815-1897) ในปี 1841 เมื่อใช้คำจำกัดความข้างต้น คุณสามารถแก้สมการและอสมการที่มีโมดูลัสได้ ตอนนี้เรามาดูบางส่วนกัน ตัวอย่างง่ายๆ.
ตัวอย่างที่ 1 แก้สมการ |3-3x|= -1
สารละลาย. ตามคุณสมบัติของโมดูล นิพจน์ | 3-3x | ไม่เป็นลบ ดังนั้นจึงไม่สามารถเท่ากับ (-1) ได้
คำตอบ. ไม่มีวิธีแก้ปัญหา
ตัวอย่างที่ 2. แก้สมการ | 3x -x 2 -2 | = 3x -x 2
สารละลาย. อย่าแก้สมการนี้เลย วิธีดั้งเดิมและสังเกตว่ามันมี มุมมองถัดไป:
|ก | = ก.
โปรดทราบว่าตามคำจำกัดความของโมดูล ความเท่าเทียมกันนี้จำเป็นต้องได้รับการตอบสนองเมื่อ A>0 และเมื่อ A<0 оно не может быть верным. Поэтому исходное уравнение равносильно квадратному неравенству 3х – х 2 - 2 >0 ซึ่งเราก็รู้วิธีแก้อยู่แล้ว
คำตอบ. -
ตัวอย่างที่ 3 แก้สมการ | x + 2 | - 2x – 1 |.
สารละลาย. ลองยกกำลังสองทั้งสองข้างของสมการกัน ซึ่งสามารถทำได้เพราะทั้งสองด้านของสมการดั้งเดิมไม่เป็นลบ เราได้รับ
- x + 2 | 2 = | 2x – 1 | 2.
แน่นอนว่าในสมการนี้เราสามารถลบโมดูลออกและเขียนสมการกำลังสองที่เทียบเท่าได้
(x + 2) 2 = (2x – 1) 2,
การเปลี่ยนแปลงที่เราได้รับ
x 2 + 4x + 4 = 4x 2 – 4x + 1, 3x 2 – 8x – 3 = 0
คำตอบ. ( -1/3 .3).
ตอนนี้เรามาดูงานแบบดั้งเดิมกันดีกว่า
แผนกต้อนรับหลักเมื่อแก้สมการและอสมการที่มีนิพจน์ |f(x)| ประกอบด้วยการเปิดเผยโมดูลตามคำนิยาม กล่าวคือ ทั้งภาค ค่าที่ยอมรับได้ M แบ่งออกเป็น 2 ชุดย่อย M 1 และ M 2 ดังกล่าวนั่นเอง
f (x)>0 สำหรับ x M 1 ทั้งหมด จากนั้น |f (x)| =ฉ(x)
ฉ(x)<0 для всех х ∊ М 2 ,тогда |f (x )| = - f (x )
ตัวอย่างที่ 4 แก้สมการ | 2x – 3 | = 3x – 7
สารละลาย. พิจารณากรณีต่างๆ: 1. 2x – 3 >0, 2x – 3 = 3x – 7, x = 4
2. 2x - 3<0, -2х + 3 = 3х- 7, х=2-не является корнем, т.к. при х=2 2х-3>0. คำตอบ: 4.
วิธีนี้ไม่ใช่วิธีเดียว เมื่อแก้สมการของแบบฟอร์ม
- ฉ(x) | = ก(x)
สองวิธีต่อไปนี้ใช้กันอย่างแพร่หลายที่สุด
มาตรฐานแรกนั้นขึ้นอยู่กับการเปิดเผยของโมดูลตามคำจำกัดความและประกอบด้วยการเปลี่ยนไปใช้ชุดระบบที่เทียบเท่ากัน
- ฉ(x) | = ก(x)
วิธีที่สองคือการย้ายจากสมการดั้งเดิมไปเป็นระบบที่เทียบเท่า
- ฉ(x) | = ก(x)
วิธีแรกควรใช้ในกรณี การแสดงออกที่ซับซ้อนสำหรับฟังก์ชัน g (x) และไม่ซับซ้อนมาก - สำหรับฟังก์ชัน f (x) ประการที่สองตรงกันข้ามควรใช้ถ้านิพจน์สำหรับ g (x) นั้นเรียบง่าย
ตัวอย่างที่ 5 แก้สมการ |x | = x - √2x +1 + 1 (ใช้วิธีแรก)
ตัวอย่างที่ 6 แก้สมการ 3|x 2 -2x -1| = 5x +1 (ใช้วิธีที่สอง)
อสมการของแบบฟอร์ม | ฉ(x) |< g (x ) гораздо удобнее решать, перейдя двойному неравенству или к равносильной ему системе двух неравенств
- ฉ(x) | ก.(x) -ก.(x) ฉ(x) ก.(x)
ในทำนองเดียวกันความไม่เท่าเทียมกันของแบบฟอร์ม
- ฉ(x) | ก.(เอ็กซ์)
แก้สมการ
3|ปี 2 – 6ปี + 7| = 5ป – 9 |x | - |x – 1| = 1 |x 2 – 1| = (x – 1)
x 2 + |x – 1| = 1 |x 2 + 2x – 3| = x 2 + x – 20
แก้ความไม่เท่าเทียมกัน
|2x – 5|< 3 |x 2 – 2x – 3| < 3x - 3
x 2 – 6 > |x | |3 - |x – 2| -< 1
บทที่ 2 วิธีช่วงสำหรับการแก้สมการและอสมการที่มีโมดูลัส
แก้สมการ | x -2| + |2x -3| = 5 การขยายโมดูลที่รวมอยู่ในสมการที่กำลังพิจารณาตามลำดับ เราจะต้องพิจารณาสี่ระบบและกรณีที่ไม่เหมาะสมอย่างเห็นได้ชัด และถ้ามีสามโมดูลขึ้นไปในสมการ จำนวนระบบก็จะเพิ่มขึ้นอีก ดังนั้น ในการแก้ปัญหาที่เกี่ยวข้องกับโมดูลตั้งแต่สองโมดูลขึ้นไป การใช้วิธีช่วงเวลาจึงมีเหตุผลมากกว่า
หากต้องการใช้วิธีการช่วงเวลาเมื่อแก้สมการด้วยโมดูล เส้นจำนวนจะต้องแบ่งออกเป็นช่วงเวลาในลักษณะที่ในแต่ละนิพจน์ submodular ทั้งหมดจะมีเครื่องหมายคงที่ ดังนั้นในแต่ละช่วงเวลา โมดูลทั้งหมดจะถูกเปิดเผยในลักษณะเฉพาะ
ตัวอย่างที่ 1. แก้สมการ | 3x +4| + 2|x -3| = 16
ให้เราทำเครื่องหมายบนแกนตัวเลขว่าจุด x = - 4/3 และ x = 3 ซึ่งนิพจน์ submodular หายไป ให้เราพิจารณาสัญญาณของการแสดงออก submodular ในช่วงเวลาผลลัพธ์สามช่วง
กรณีที่ 1 เมื่อ x>3 ทั้งสองโมดูลจะเปิดขึ้นโดยมีเครื่องหมาย “+” เราได้รับระบบ
x >3,
3x+4+2(x-3) = 16 x=18/5 (18/5>3)
กรณีที่ 2 ที่ -4/3 4/3 3x+4+2(-x+3) = 16 สมการของระบบนี้มีราก x=6 ซึ่งไม่เป็นไปตามความไม่เท่าเทียมกันของระบบ ดังนั้นจึงไม่ใช่รากของสมการที่กำหนด กรณีที่ 3 ที่เอ็กซ์< -4/3 оба модуля раскрываются со знаком «-«, получаем x< -4/3, 3x-4+(-x+3) = 16 ระบบนี้มีคำตอบเฉพาะ x = -14/5 คำตอบ:(-14/5; 18/5) ในกรณีส่วนใหญ่ วิธีแก้อสมการที่มีโมดูลัสจะถูกสร้างขึ้นในลักษณะเดียวกับการแก้สมการที่สอดคล้องกัน ข้อแตกต่างที่สำคัญคือหลังจากปลดปล่อยตัวเองจากโมดูลต่างๆ แล้ว เราจำเป็นต้องแก้ตามธรรมชาติ ไม่ใช่สมการ แต่เป็นความไม่เท่าเทียมกัน มีความแตกต่างอีกอย่างหนึ่ง หากเมื่อทำการแก้สมการ เราสามารถใช้การตรวจสอบความถูกต้องของวิธีแก้ปัญหาที่ได้รับได้อย่างกว้างขวาง ในกรณีที่เกิดความไม่เท่าเทียมกัน อาจเป็นเรื่องยากที่จะละทิ้งวิธีแก้ปัญหาที่ไม่เกี่ยวข้องโดยการตรวจสอบ ซึ่งหมายความว่าเมื่อแก้ไขอสมการ พวกเขาพยายามใช้การเปลี่ยนผ่านที่เทียบเท่ากันเป็นหลัก ตัวอย่างที่ 2 แก้สมการ |x – 4| + |x + 1|<7 สารละลาย. บนเส้นจำนวนจำเป็นต้องทำเครื่องหมายตัวเลข x=-1 และ x=4 ซึ่งนิพจน์ภายใต้เครื่องหมายโมดูลัสจะเปลี่ยนเป็นศูนย์ จากนั้นเราจะวางเครื่องหมายนิพจน์ไว้บนช่วงผลลัพธ์ทั้งสามช่วง (x-4) และ (x+1) - ชุดสัญญาณที่เกิดขึ้นจะแจ้งให้เราทราบว่ากรณีใดที่ต้องพิจารณา จากการขยายโมดูลในสามกรณีนี้ เราได้รับสามระบบ เราได้รับการแก้ปัญหาระบบเหล่านี้และรวมคำตอบเข้าด้วยกัน คำตอบ: (-2;5) แบบฝึกหัดสำหรับงานอิสระ แก้สมการ: - x – 1| + |x – 2| + |x – 3| = 4 |6 – 2x | + |3x + 7| - 2|4x + 11| = x – 3 | |3x – 1| - |2x + 1| - = 1 แก้ความไม่เท่าเทียมกัน: |x – 1| + |x + 2|< 3
|x – 1|< |2x
– 3| - |x
– 2| |x
2 – 3| + x
2 + x
< 7. บทที่ 4 การแก้สมการและอสมการด้วยโมดูลบนเส้นพิกัด เมื่อศึกษาระยะห่างระหว่างจุดสองจุด A(x 1) และ B(x 2) บนเส้นพิกัด สูตรจะได้มาจาก AB = | x 1 - x 2 |. เมื่อใช้สูตรนี้ คุณจะแก้สมการและอสมการในรูปแบบ |x – a | ได้ = ข , |x – ก | = |x – ข |, |x – ก | - x – a |>|x – b | ตลอดจนสมการและอสมการที่สามารถลดทอนลงได้ ตัวอย่างที่ 1 แก้สมการ |x – 3| = 1. สารละลาย. การแปลสมการนี้เป็น "ภาษาของระยะทาง" เราจะได้ประโยค "ระยะห่างจากจุดที่มีพิกัด x ไปยังจุดที่มีพิกัด 3 คือ 1" ต่อมาการแก้สมการลงมาเพื่อหาจุดที่อยู่ห่างจากจุดที่มีพิกัด 3 ที่ระยะ 1 ให้เราหันมาดูภาพประกอบทางเรขาคณิตกัน _______________________________________________________ รากของสมการคือตัวเลข 2 และ 4 ตัวอย่างที่ 2 แก้สมการ | 2x + 1 | = 3 ลดสมการนี้ให้อยู่ในรูปแบบ | x – (-1/2) | = 3/2 ใช้สูตรระยะทาง คำตอบ: -2;1. ตัวอย่างที่ 3: แก้สมการ |x + 2| = |x – 1|. สารละลาย. ลองเขียนสมการนี้ในรูปแบบ |x – (-2)| = |x – 1|. จากการพิจารณาทางเรขาคณิต ไม่ใช่เรื่องยากที่จะเข้าใจว่ารากของสมการสุดท้ายคือพิกัดของจุดที่อยู่ห่างจากจุดที่มีพิกัด 1 และ -2 เท่าๆ กัน คำตอบ: -0.5 ตัวอย่างที่ 4: แก้อสมการ |x – 1|<2. สารละลาย. จากแนวคิดทางเรขาคณิต เราได้ข้อสรุปว่าคำตอบของอสมการนี้คือพิกัดของจุดที่อยู่ห่างจากจุดที่มีพิกัด 1 น้อยกว่า 2 คำตอบ: (-1;3) แบบฝึกหัดสำหรับงานอิสระ - x – 2| = 0.4 | 10 – x |< 7 | x
+ 4 | = | x
– 4 | - x + 3 | = 0.7 | x + 1 | > 1 | x + 2.5| - x - 3.3| - x – 2.5|< 0,5 | x
+ 8 | >0.7 | x | - x – 2 | - x – 5 |< | x – 1 |
.
 คุณสมบัติทางเคมีของไซเลนซิลิคอนไฮไดรด์ 4
คุณสมบัติทางเคมีของไซเลนซิลิคอนไฮไดรด์ 4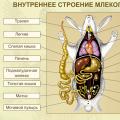 งานห้องปฏิบัติการ “โครงสร้างโครงกระดูกของสัตว์เลี้ยงลูกด้วยนม โครงสร้างภายนอกและภายในของงานห้องปฏิบัติการของสัตว์เลี้ยงลูกด้วยนม
งานห้องปฏิบัติการ “โครงสร้างโครงกระดูกของสัตว์เลี้ยงลูกด้วยนม โครงสร้างภายนอกและภายในของงานห้องปฏิบัติการของสัตว์เลี้ยงลูกด้วยนม Stolypin, Pyotr Arkadyevich - ชีวประวัติสั้น ๆ
Stolypin, Pyotr Arkadyevich - ชีวประวัติสั้น ๆ