ฟังก์ชันเชิงเส้นแบบแบ่งส่วนถูกกำหนดโดยสูตรที่หาได้ X=1 - จุดเปลี่ยนของสูตร

7
บทเรียนพีชคณิตในชั้นเรียน 9A อาจารย์ Mikitchuk Zh.N. MOU "โรงเรียนมัธยม ครั้งที่ 23"19.03.07หัวข้อบทเรียน: "ฟังก์ชันที่กำหนดแบบแยกส่วน" เป้าหมาย:

สรุปและพัฒนาความรู้ ทักษะ และความสามารถของนักเรียนในหัวข้อที่กำหนด อบรมนักเรียนให้ตั้งใจเรียน มีสมาธิ มีความเพียร มีความมั่นใจในความรู้ พัฒนาความสามารถในการคิด การคิดเชิงตรรกะ วัฒนธรรมการพูดความสามารถในการใช้ความรู้ทางทฤษฎี

อันเป็นผลมาจากหัวข้อทั่วไปนักเรียนควร ทราบ:

แนวคิดแบบแยกส่วน ฟังก์ชันที่กำหนด; สูตรของฟังก์ชันต่าง ๆ ชื่อที่เกี่ยวข้องและรูปภาพของกราฟ

สามารถ:

สร้างกราฟของฟังก์ชันที่กำหนดแบบแยกส่วน อ่านแผนภูมิ กำหนดฟังก์ชันวิเคราะห์ตามกราฟ

ระหว่างเรียน

I. ช่วงเวลาทางจิตใจและองค์กร เรามาเริ่มบทเรียนด้วยคำพูดของ D.K. Fadeev“ ไม่ว่าคุณจะแก้ปัญหาใดในตอนท้ายคุณจะมีช่วงเวลาที่มีความสุข - ความรู้สึกที่สนุกสนานของความสำเร็จเสริมสร้างศรัทธาในความแข็งแกร่งของคุณให้คำเหล่านี้ในบทเรียนของเราได้รับการยืนยันอย่างแท้จริง ครั้งที่สอง ตรวจการบ้าน. เริ่มบทเรียนตามปกติด้วยการตรวจสอบ d / z - ทำซ้ำนิยามของฟังก์ชันทีละส่วนและแผนการศึกษาฟังก์ชัน1). บนโต๊ะทำงานอธิบายโครงเรื่องของฟังก์ชันแบบแยกส่วนที่คุณประดิษฐ์ขึ้น (รูปที่ 1,2,3)2) การ์ด.#1. เรียงลำดับการศึกษาคุณสมบัติของฟังก์ชัน:

นูน; คู่คี่; ช่วงของค่า ข้อ จำกัด ; เสียงเดียว; ความต่อเนื่อง; ยิ่งใหญ่ที่สุดและ ค่าที่น้อยที่สุดฟังก์ชั่น; โดเมน.

หมายเลข 2 วาดกราฟของฟังก์ชันแบบแผน:

ก) y = kx + b, k0; ข) y = kx, k0;

ค) y = , k0.

3).งานปาก . - 2 นาที

ฟังก์ชันแยกส่วนคืออะไร?

ฟังก์ชันแยกส่วนคือฟังก์ชันที่กำหนดขึ้น สูตรที่แตกต่างกันในช่วงเวลาต่างๆ

ฟังก์ชันตามส่วนที่แสดงในรูปที่ 1,2,3 ประกอบด้วยฟังก์ชันใดบ้าง คุณรู้จักชื่อฟังก์ชันอะไรอีกบ้าง กราฟของฟังก์ชันที่เกี่ยวข้องเรียกว่าอะไร เป็นกราฟของฟังก์ชันใด ดังรูปที่ 4 หรือไม่ ทำไม

คำตอบ:ไม่เพราะ ตามนิยามของฟังก์ชัน แต่ละค่าของตัวแปรอิสระ x จะสัมพันธ์กับค่าเดียวของตัวแปรตาม y 4) การควบคุมตนเอง - 3 นาทีจากกราฟที่เสนอและสูตรที่เกี่ยวข้องซึ่งกำหนดฟังก์ชัน ให้เลือกกราฟที่ถูกต้อง จากจดหมายคำตอบที่ได้รับให้สร้างคำที่คุ้นเคย คำตอบ: GRAPH ที่ไหนในชีวิตในทางวิทยาศาสตร์ในชีวิตประจำวันเรายังพบคำว่า GRAPH อยู่หรือไม่ - กราฟของการพึ่งพามวลต่อปริมาตร - ปริมาตรต่อแรงกด - ตารางเวร - ตารางรถไฟ; การผลิตภาคอุตสาหกรรมในภูมิภาค Saratov ในช่วงปี 1980 ถึง 2002 .. ตามกราฟนี้ คุณสามารถติดตามการลดลงและการเติบโตของการผลิตในแต่ละปี - บอกฉันว่ากราฟของฟังก์ชันใดให้ข้อมูลนี้ คำตอบ: ฟังก์ชันแยกส่วน.สาม. ข้อความของหัวข้อจุดประสงค์ของบทเรียน หัวข้อบทเรียน:"ฟังก์ชันที่กำหนดแบบแยกส่วน" เป้า:- ในตัวอย่างฟังก์ชันที่กำหนดทีละส่วน ให้นึกถึงแผนการศึกษาฟังก์ชัน

ทำซ้ำขั้นตอนการสร้างฟังก์ชันที่กำหนดทีละส่วน ใช้ความรู้ทั่วไปในการแก้ปัญหาที่ไม่ได้มาตรฐาน

IV. การปรับปรุงความรู้ที่ได้รับก่อนหน้านี้ แนวคิดของฟังก์ชันพบเราครั้งแรกตอนเรียนอยู่ชั้นประถมศึกษาปีที่ 7 การพึ่งพาเชิงเส้น. จากมุมมองของการสร้างแบบจำลองกระบวนการจริง การพึ่งพาอาศัยกันนี้สอดคล้องกับกระบวนการที่เป็นเอกภาพ ตัวอย่าง: การเดินเท้าด้วย ความเร็วคงที่ทันเวลา t. สูตร: s \u003d vt, กราฟ - ส่วนของเส้นตรงที่อยู่ในไตรมาส I
ธีมหลักของเกรด 8 - ฟังก์ชันกำลังสองจำลองกระบวนการที่เร่งความเร็วอย่างสม่ำเสมอ ตัวอย่าง: สูตรที่คุณศึกษาในชั้นประถมศึกษาปีที่ 9 สำหรับการกำหนดความต้านทานของหลอดความร้อน (R) ที่กำลังคงที่ (P) และแรงดันไฟฟ้าที่แตกต่างกัน (U) สูตร R = 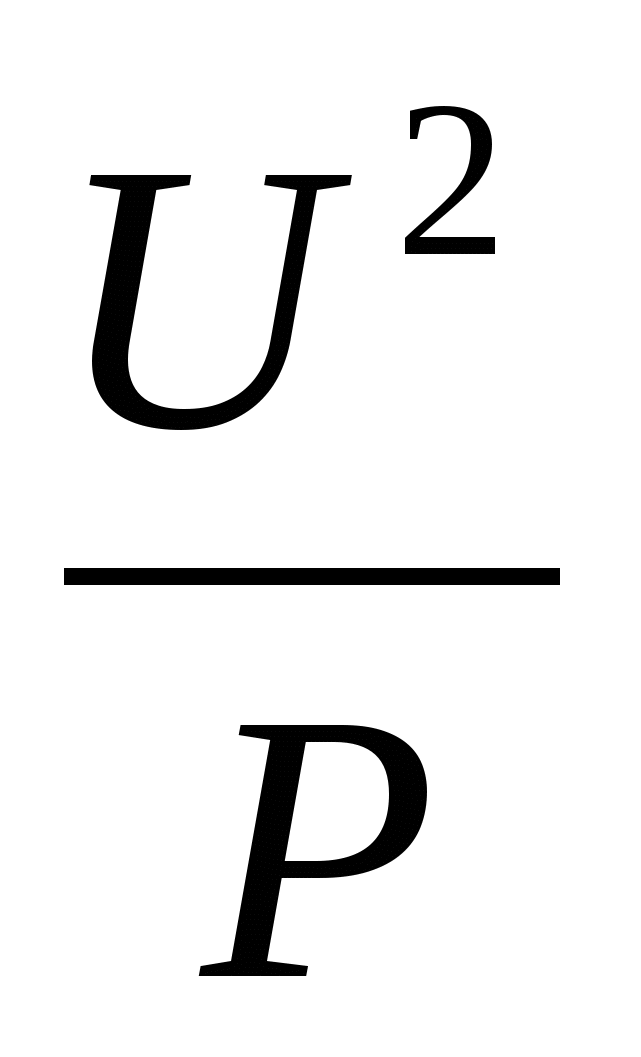กราฟเป็นกิ่งก้านของพาราโบลาซึ่งอยู่ในไตรมาสแรก
สำหรับ สามปีความรู้เรื่องฟังก์ชันของเราเพิ่มขึ้น จำนวนของฟังก์ชันที่ศึกษาเพิ่มขึ้น และชุดของงานสำหรับการแก้ปัญหาซึ่งต้องใช้กราฟถูกเติมเต็ม ตั้งชื่องานประเภทนี้ ... - การแก้สมการ- คำตอบของระบบสมการ- การแก้ปัญหาความไม่เท่าเทียมกัน- การศึกษาคุณสมบัติของฟังก์ชันV. การเตรียมนักเรียนสำหรับกิจกรรมทั่วไป. ลองนึกถึงงานประเภทหนึ่งคือการศึกษาคุณสมบัติของฟังก์ชันหรือการอ่านกราฟ หันไปหาตำรา หน้า 65 รูปที่ 20a จาก #250 ออกกำลังกาย:อ่านกราฟของฟังก์ชัน ขั้นตอนการตรวจสอบฟังก์ชันอยู่ข้างหน้าเรา 1. โดเมนนิยาม - (-∞; +∞)2. คู่, คี่ - ไม่คู่หรือคี่3. ความซ้ำซากจำเจ - เพิ่มขึ้น [-3; +∞) ลดลง[-5;-3], ค่าคงที่ (-∞; -5];4. จำกัด - จำกัด จากด้านล่าง5. ค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชัน - y naim = 0, y naib - ไม่มีอยู่6. ความต่อเนื่อง - ต่อเนื่องทั่วทั้งขอบเขตของคำนิยาม7. ช่วงของค่า - , นูนขึ้นและลง (-∞; -5] และ [-2; +∞).วี.ไอ. การผลิตซ้ำความรู้ในระดับใหม่ คุณรู้ว่าการลงจุดและการวิจัยกราฟ ฟังก์ชันแบบแยกส่วน, ได้รับการพิจารณาในส่วนที่สองของการสอบพีชคณิตในส่วนฟังก์ชันและประเมินด้วย 4 และ 6 คะแนน มาดูการรวบรวมงานกัน หน้า 119 - หมายเลข 4.19-1) วิธีแก้ปัญหา: 1) y \u003d - x, - ฟังก์ชันกำลังสอง, กราฟ - พาราโบลา, กิ่งก้านลง (a \u003d -1, a 0) x -2 -1 0 1 2 y -4 -1 0 1 4 2) y \u003d 3x - 10, - ฟังก์ชันเชิงเส้น, กราฟเป็นเส้นตรงมาทำตารางค่าต่างๆ กันx 3 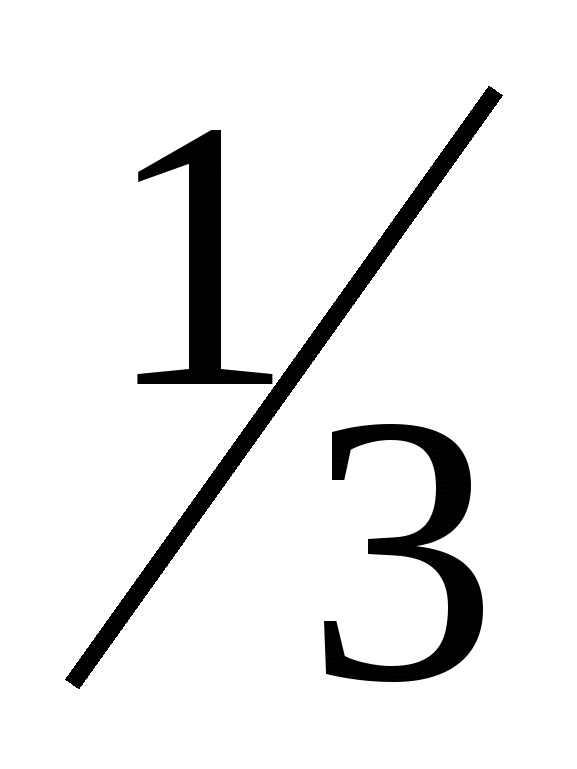3 y 0 -1 3) y \u003d -3x -10, - ฟังก์ชันเชิงเส้น กราฟเป็นเส้นตรงมาทำตารางค่าต่างๆ กัน x -3 -3 y 0 -1 4) เราสร้างกราฟของฟังก์ชันในระบบพิกัดเดียวและเลือกส่วนของกราฟตามช่วงเวลาที่กำหนด
ให้เราค้นหาจากกราฟที่ค่า x ค่าของฟังก์ชันไม่เป็นลบคำตอบ: f(x)  0 สำหรับ x = 0 และ สำหรับ  3 VII. ทำงานที่ไม่ได้มาตรฐาน ฉบับที่ 4.29-1), น. 121.สารละลาย: 1) ทางตรง (ซ้าย) y \u003d kx + b ผ่านจุด (-4;0) และ (-2;2) ดังนั้น -4 k + b = 0, -2 k + b = 2;
k \u003d 1, b \u003d 4, y \u003d x + 4 คำตอบ: x +4 ถ้า x -2 y = ถ้า -2  x 3 ปอนด์ 3 ถ้า x  3
VIII. การควบคุมความรู้ งั้นเรามาสรุปกันสักหน่อย เราทำซ้ำอะไรในบทเรียน แผนวิจัยฟังก์ชัน ขั้นตอนในการลงจุดกราฟฟังก์ชันแบบแยกส่วน การตั้งค่าฟังก์ชันเชิงวิเคราะห์ มาดูกันว่าคุณเรียนรู้เนื้อหานี้อย่างไร การทดสอบสำหรับ "4" - "5", "3" I option No. U
2 1 -1 -1 1 X

D(f) = , นูนขึ้นและลงโดย , นูนขึ้นและลงโดย , ลดลงโดย ________ จำกัดโดย ____________ อย่างน้อยไม่มีอยู่ ที่สูงสุด =_____ ต่อเนื่องตลอดโดเมนทั้งหมดของนิยาม E(f) = ____________ นูนขึ้นและลงและขึ้นเหนือโดเมนทั้งหมดของนิยาม

ย้อนกลับ

ความสนใจ! การแสดงตัวอย่างสไลด์มีวัตถุประสงค์เพื่อให้ข้อมูลเท่านั้น และอาจไม่ได้แสดงถึงขอบเขตทั้งหมดของงานนำเสนอ ถ้าคุณสนใจ งานนี้โปรดดาวน์โหลดเวอร์ชันเต็ม

หนังสือเรียน:พีชคณิตเกรด 8 แก้ไขโดย A. G. Mordkovich

ประเภทบทเรียน:การค้นพบความรู้ใหม่

เป้าหมาย:

สำหรับครู เป้าหมายได้รับการแก้ไขในแต่ละขั้นตอนของบทเรียน

สำหรับนักเรียน:

เป้าหมายของแต่ละบุคคล:

• เรียนรู้ที่จะแสดงความคิดของคุณอย่างชัดเจน ถูกต้อง และมีความสามารถ การเขียนเข้าใจความหมายของงาน
• เรียนรู้ที่จะใช้ความรู้และทักษะที่ได้รับในการแก้ปัญหาใหม่
• เรียนรู้ที่จะควบคุมกระบวนการและผลลัพธ์ของกิจกรรมของพวกเขา

เป้าหมายวัตถุประสงค์เมตา:

ในกิจกรรมการเรียนรู้:

• การพัฒนา การคิดอย่างมีตรรกะและคำพูดความสามารถในการยืนยันการตัดสินอย่างมีเหตุผลเพื่อดำเนินการจัดระบบอย่างง่าย
• เรียนรู้ที่จะตั้งสมมติฐาน การแก้ปัญหาเข้าใจความจำเป็นในการตรวจสอบ
• นำความรู้ไปใช้ใน สถานการณ์มาตรฐานเรียนรู้วิธีการทำงานให้เสร็จโดยอิสระ
• เพื่อดำเนินการถ่ายโอนความรู้ไปยังสถานการณ์ที่เปลี่ยนแปลงเพื่อดูงานในบริบทของสถานการณ์ที่เป็นปัญหา

ในกิจกรรมข้อมูลและการสื่อสาร:

• เรียนรู้ที่จะดำเนินการสนทนา ตระหนักถึงสิทธิในการแสดงความคิดเห็นที่แตกต่าง

ในกิจกรรมสะท้อนแสง:

• เรียนรู้ที่จะคาดการณ์ ผลที่เป็นไปได้การกระทำของพวกเขา
• เรียนรู้ที่จะขจัดสาเหตุของความยุ่งยาก

เป้าหมายของเรื่อง:

• เรียนรู้ว่าฟังก์ชันที่กำหนดแบบแยกส่วนคืออะไร
• เรียนรู้การตั้งค่าฟังก์ชันที่กำหนดทีละส่วนโดยวิเคราะห์ตามกราฟ

ระหว่างเรียน

1. การตัดสินใจด้วยตนเองเพื่อ กิจกรรมการเรียนรู้

วัตถุประสงค์ของเวที:

• รวมนักเรียนในกิจกรรมการเรียนรู้
• กำหนดเนื้อหาของบทเรียน: เราทำซ้ำหัวข้อของฟังก์ชันตัวเลขต่อไป

องค์กร กระบวนการศึกษาในขั้นตอนที่ 1:

T: เราทำอะไรในบทเรียนที่แล้ว?

D: เราทำซ้ำหัวข้อของฟังก์ชันตัวเลข

T: วันนี้เราจะทำซ้ำหัวข้อของบทเรียนก่อนหน้านี้ และวันนี้เราควรค้นหาสิ่งใหม่ ๆ ที่เราสามารถเรียนรู้เกี่ยวกับหัวข้อนี้

2. อัพเดทความรู้และแก้ไขข้อขัดข้องในการทำกิจกรรม

วัตถุประสงค์ของเวที:

• อัปเดต เนื้อหาการศึกษาจำเป็นและเพียงพอสำหรับการรับรู้เนื้อหาใหม่: จำสูตร ฟังก์ชันตัวเลขคุณสมบัติและวิธีการก่อสร้าง
• อัปเดต การดำเนินงานทางจิตจำเป็นและเพียงพอสำหรับการรับรู้เนื้อหาใหม่: การเปรียบเทียบ การวิเคราะห์ การวางนัยทั่วไป
• เพื่อแก้ไขปัญหาเฉพาะบุคคลในกิจกรรมสาธิตเป็นการส่วนตัว ระดับที่มีนัยสำคัญความไม่เพียงพอของความรู้ที่มีอยู่: งานของฟังก์ชันที่กำหนดทีละส่วนในการวิเคราะห์ เช่นเดียวกับการสร้างกราฟ

การจัดกระบวนการศึกษาในระยะที่ 2:

T: มีฟังก์ชันตัวเลขห้าตัวบนสไลด์ กำหนดประเภทของพวกเขา

1) เศษส่วนเหตุผล;

2) กำลังสอง;

3) ไม่มีเหตุผล;

4) ฟังก์ชั่นพร้อมโมดูล

5) พลังงาน

T: ตั้งชื่อสูตรที่สอดคล้องกัน

3) ;

4) ;

T: เรามาคุยกันว่าแต่ละค่าสัมประสิทธิ์มีบทบาทอย่างไรในสูตรเหล่านี้

D: ตัวแปร "l" และ "m" มีหน้าที่เลื่อนกราฟของฟังก์ชันเหล่านี้ไปทางซ้าย - ขวาและขึ้น - ลงตามลำดับ ค่าสัมประสิทธิ์ "k" ในฟังก์ชันแรกกำหนดตำแหน่งของกิ่งไฮเพอร์โบลา: k>0 - กิ่งอยู่ในไตรมาส I และ III, k< 0 - во II и IV четвертях, а коэффициент “а” определяет направление ветвей параболы: а>0 - สาขาพุ่งขึ้นและ< 0 - вниз).

2. สไลด์ 2

U: ตั้งค่าวิเคราะห์ฟังก์ชันที่มีกราฟแสดงในรูป (พิจารณาว่าพวกมันกำลังเคลื่อนที่ y=x 2) ครูเขียนคำตอบบนกระดาน

ง: 1) );

2);

3. สไลด์ 3

U: ตั้งค่าวิเคราะห์ฟังก์ชันที่มีกราฟแสดงในรูป (พิจารณาว่ากำลังเคลื่อนที่). ครูเขียนคำตอบบนกระดาน

4. สไลด์ 4

U: ใช้ผลลัพธ์ก่อนหน้านี้ ตั้งค่าวิเคราะห์ฟังก์ชันที่มีกราฟแสดงในรูป

3. การระบุสาเหตุของปัญหาและการกำหนดเป้าหมายของกิจกรรม

วัตถุประสงค์ของเวที:

• จัดระเบียบ ปฏิสัมพันธ์สื่อสารในระหว่างที่มีการระบุและแก้ไขคุณสมบัติเฉพาะของงานที่ทำให้เกิดความยากลำบากในกิจกรรมการศึกษา
• เห็นด้วยกับจุดประสงค์และหัวข้อของบทเรียน

การจัดกระบวนการศึกษาในระยะที่ 3:

ถาม: อะไรทำให้คุณมีปัญหา

D: มีกราฟแสดงอยู่บนหน้าจอ

T: จุดประสงค์ของบทเรียนของเราคืออะไร?

D: เพื่อเรียนรู้วิธีกำหนดชิ้นส่วนของฟังก์ชันเชิงวิเคราะห์

T: ระบุหัวข้อของบทเรียน (เด็กพยายามกำหนดหัวข้อด้วยตัวเอง ครูชี้แจง หัวข้อ: แบ่งตามหน้าที่ที่กำหนด)

4. สร้างโครงการเพื่อออกจากความยากลำบาก

วัตถุประสงค์ของเวที:

• จัดระเบียบการสื่อสารโต้ตอบเพื่อสร้างใหม่ โหมดของการกระทำขจัดสาเหตุของปัญหาที่ระบุ
• แก้ไข วิธีการใหม่การกระทำ

การจัดกระบวนการศึกษาในระยะที่ 4:

T: มาอ่านการบ้านอย่างละเอียดอีกครั้ง ขอให้ใช้ผลลัพธ์อะไรเป็นตัวช่วย

D: ก่อนหน้านี้เช่น ที่เขียนไว้บนกระดาน

T: บางทีสูตรเหล่านี้อาจเป็นคำตอบของงานนี้อยู่แล้ว?

D: ไม่เพราะ สูตรเหล่านี้กำหนดกำลังสองและ ฟังก์ชันตรรกยะและชิ้นส่วนจะแสดงบนสไลด์

ท: เรามาคุยกันว่าช่วงใดของแกน x ที่ตรงกับชิ้นส่วนของฟังก์ชันแรก

U: ถ้าอย่างนั้นวิธีวิเคราะห์ในการระบุฟังก์ชันแรกจะเป็นดังนี้: ถ้า

ถาม: ต้องทำอะไรเพื่อทำงานที่คล้ายกันให้สำเร็จ

D: จดสูตรและกำหนดว่าช่วงใดของแกน x ที่สอดคล้องกับชิ้นส่วนของฟังก์ชันนี้

5. การรวมหลักในการพูดภายนอก

วัตถุประสงค์ของเวที:

• แก้ไขเนื้อหาการศึกษาที่ศึกษาในการพูดภายนอก

การจัดกระบวนการศึกษาในระยะที่ 5:

7. รวมอยู่ในระบบความรู้และการทำซ้ำ

วัตถุประสงค์ของเวที:

• ฝึกทักษะการใช้เนื้อหาใหม่ควบคู่กับที่เรียนมา

การจัดกระบวนการศึกษาในระยะที่ 7:

Y: ตั้งค่าการวิเคราะห์ของฟังก์ชัน ซึ่งกราฟจะแสดงในรูป

8. การสะท้อนกิจกรรมในบทเรียน

วัตถุประสงค์ของเวที:

• เพื่อแก้ไขเนื้อหาใหม่ที่เรียนในบทเรียน
• ประเมินกิจกรรมของตนเองในห้องเรียน
• ขอบคุณเพื่อนร่วมชั้นที่ช่วยให้ได้รับผลของบทเรียน
• แก้ไขปัญหาที่ยังไม่ได้แก้ไขเป็นแนวทางสำหรับกิจกรรมการเรียนรู้ในอนาคต
• พูดคุยและจดการบ้าน

การจัดกระบวนการศึกษาในระยะที่ 8:

T: เราเรียนรู้อะไรในชั้นเรียนวันนี้

D: ด้วยฟังก์ชันที่กำหนดทีละส่วน

T: วันนี้เราเรียนรู้งานอะไร

D: ถาม สายพันธุ์นี้ทำหน้าที่วิเคราะห์

T: ยกมือขึ้น ใครเข้าใจหัวข้อบทเรียนวันนี้บ้าง? (ปรึกษาปัญหากับลูกที่เหลือ).

การบ้าน

• หมายเลข 21.12(ก, ค);
• หมายเลข 21.13(ก, ค);
• №22.41;
• №22.44.

กระบวนการจริงที่เกิดขึ้นในธรรมชาติสามารถอธิบายได้โดยใช้ฟังก์ชัน ดังนั้นเราจึงสามารถแยกแยะการไหลของกระบวนการหลักสองประเภทที่อยู่ตรงข้ามกัน - เหล่านี้คือ ค่อยเป็นค่อยไปหรือ ต่อเนื่องและ กระตุก(ตัวอย่างจะเป็นลูกบอลที่ตกลงมาและกระดอนขึ้น) แต่ถ้ามีกระบวนการที่ไม่ต่อเนื่องก็มีวิธีการพิเศษสำหรับคำอธิบาย เพื่อจุดประสงค์นี้ ฟังก์ชันที่มีความไม่ต่อเนื่อง การกระโดด จะถูกหมุนเวียน นั่นคือ ในส่วนต่าง ๆ ของเส้นตัวเลข ฟังก์ชันจะทำงานตามกฎหมายต่าง ๆ และตามด้วยสูตรต่าง ๆ แนวคิดของจุดความไม่ต่อเนื่องและความไม่ต่อเนื่องที่ถอดได้ถูกนำมาใช้

แน่นอนคุณได้เห็นฟังก์ชันที่กำหนดโดยสูตรต่างๆ แล้ว ขึ้นอยู่กับค่าของอาร์กิวเมนต์ เช่น

y \u003d (x - 3, กับ x\u003e -3;
(-(x - 3), สำหรับ x< -3.

ฟังก์ชันดังกล่าวเรียกว่า เป็นชิ้น ๆหรือ เป็นชิ้น ๆ. ส่วนของเส้นจำนวนกับสูตรงานต่างๆ ลองโทร ส่วนประกอบโดเมน. การรวมส่วนประกอบทั้งหมดเข้าด้วยกันคือโดเมนของฟังก์ชันทีละส่วน จุดที่แบ่งโดเมนของฟังก์ชันออกเป็นส่วนประกอบเรียกว่า จุดขอบเขต. สูตรที่กำหนดฟังก์ชันทีละส่วนในแต่ละโดเมนของคำจำกัดความจะถูกเรียก ฟังก์ชันขาเข้า. กราฟของฟังก์ชันที่กำหนดแบบแยกส่วนได้มาจากการรวมส่วนต่างๆ ของกราฟที่สร้างขึ้นในแต่ละช่วงเวลาของพาร์ติชัน

การออกกำลังกาย.

สร้างกราฟของฟังก์ชันทีละส่วน:

1) (-3, กับ -4 ≤ x< 0,
ฉ(x) = (0, สำหรับ x = 0,
(1 ที่ 0< x ≤ 5.

กราฟของฟังก์ชันแรกคือเส้นตรงที่ลากผ่านจุด y = -3 มันเริ่มต้นที่จุดที่มีพิกัด (-4; -3) ขนานกับแกน abscissa ไปยังจุดที่มีพิกัด (0; -3) กราฟของฟังก์ชันที่สองคือจุดที่มีพิกัด (0; 0) กราฟที่สามคล้ายกับกราฟแรก - เป็นเส้นตรงที่ผ่านจุด y \u003d 1 แต่อยู่ในพื้นที่ตั้งแต่ 0 ถึง 5 ตามแกน Ox

คำตอบ: รูปที่ 1

2) (3 ถ้า x ≤ -4,
f(x) = (|x 2 - 4|x| + 3| ถ้า -4< x ≤ 4,
(3 - (x - 4) 2 ถ้า x > 4.

พิจารณาแต่ละฟังก์ชันแยกจากกันและเขียนกราฟ

ดังนั้น f(x) = 3 เป็นเส้นตรงขนานกับแกน Ox แต่ต้องวาดในพื้นที่ที่ x ≤ -4 เท่านั้น

กราฟของฟังก์ชัน f(x) = |x 2 – 4|x| + 3| สามารถหาได้จากพาราโบลา y \u003d x 2 - 4x + 3 เมื่อสร้างกราฟแล้ว ส่วนของรูปที่อยู่เหนือแกน Ox จะต้องไม่เปลี่ยนแปลง และส่วนที่อยู่ใต้แกน abscissa จะต้องแสดงอย่างสมมาตรเมื่อเทียบกับแกน Ox จากนั้นแสดงส่วนของกราฟอย่างสมมาตรโดยที่
x ≥ 0 รอบแกน Oy สำหรับค่าลบ x กราฟที่ได้จากการเปลี่ยนแปลงทั้งหมดจะเหลือเพียงในพื้นที่ตั้งแต่ -4 ถึง 4 ตามแนว abscissa

กราฟของฟังก์ชันที่สามคือพาราโบลา ซึ่งมีกิ่งชี้ลง และจุดยอดอยู่ที่จุดที่มีพิกัด (4; 3) ภาพวาดจะแสดงในพื้นที่ที่ x > 4 เท่านั้น

คำตอบ: รูปที่ 2

3) (8 - (x + 6) 2 ถ้า x ≤ -6,
f(x) = (|x 2 – 6|x| + 8| ถ้า -6 ≤ x< 5,
(3 ถ้า x ≥ 5.

การสร้างฟังก์ชั่นที่เสนอทีละชิ้นนั้นคล้ายกับย่อหน้าก่อนหน้า ที่นี่ กราฟของสองฟังก์ชันแรกได้มาจากการแปลงพาราโบลา และกราฟของฟังก์ชันที่สามเป็นเส้นตรงขนานกับ Ox

คำตอบ: รูปที่ 3

4) พล็อตฟังก์ชัน y = x – |x| + (x – 1 – |x|/x) 2 .

สารละลาย.ขอบเขตของฟังก์ชันนี้คือทั้งหมด จำนวนจริงยกเว้นศูนย์ มาเปิดโมดูลกันเถอะ ในการทำเช่นนี้ ให้พิจารณาสองกรณี:

1) สำหรับ x > 0 เราจะได้ y = x - x + (x - 1 - 1) 2 = (x - 2) 2

2) สำหรับ x< 0 получим y = x + x + (x – 1 + 1) 2 = 2x + x 2 .

ดังนั้นเราจึงมีฟังก์ชันที่กำหนดทีละส่วน:

y = ((x - 2) 2 , สำหรับ x > 0;
( x 2 + 2x สำหรับ x< 0.

กราฟของฟังก์ชันทั้งสองคือพาราโบลา ซึ่งมีกิ่งก้านชี้ขึ้น

คำตอบ: รูปที่ 4

5) พล็อตฟังก์ชัน y = (x + |x|/x – 1) 2

สารละลาย.

จะเห็นว่าโดเมนของฟังก์ชันเป็นจำนวนจริงทั้งหมดยกเว้นศูนย์ หลังจากขยายโมดูลแล้ว เราจะได้ฟังก์ชันที่กำหนดทีละส่วน:

1) สำหรับ x > 0 เราจะได้ y = (x + 1 - 1) 2 = x 2

2) สำหรับ x< 0 получим y = (x – 1 – 1) 2 = (x – 2) 2 .

มาเขียนใหม่กันเถอะ

y \u003d (x 2 สำหรับ x\u003e 0;
((x – 2) 2 สำหรับ x< 0.

กราฟของฟังก์ชันเหล่านี้คือพาราโบลา

ตอบ รูปที่ 5

6) มีฟังก์ชันที่มีกราฟเป็น ระนาบพิกัดมันมี จุดร่วมกับสายไหน?

สารละลาย.

ใช่มี

ตัวอย่างจะเป็นฟังก์ชัน f(x) = x 3 อันที่จริง กราฟของพาราโบลาลูกบาศก์ตัดกับเส้นแนวตั้ง x = a ที่จุด (a; a 3) ให้สมการ y = kx + b เป็นเส้นตรง จากนั้นสมการ
x 3 - kx - b \u003d 0 มีรูทจริง x 0 (เนื่องจากพหุนามระดับคี่จะมีรูทจริงอย่างน้อยหนึ่งรูทเสมอ) ดังนั้น กราฟของฟังก์ชันจึงตัดกับเส้นตรง y \u003d kx + b เช่น ที่จุด (x 0; x 0 3)

ไซต์ที่มีการคัดลอกเนื้อหาทั้งหมดหรือบางส่วนจำเป็นต้องมีลิงก์ไปยังแหล่งที่มา

นิยามเชิงวิเคราะห์ของฟังก์ชัน

ฟังก์ชัน %%y = f(x), x \in X%% ที่กำหนด ด้วยวิธีวิเคราะห์ที่ชัดเจนหากมีการระบุสูตรที่ระบุลำดับของการดำเนินการทางคณิตศาสตร์ที่ต้องดำเนินการกับอาร์กิวเมนต์ %%x%% เพื่อรับค่า %%f(x)%% ของฟังก์ชันนี้

ตัวอย่าง

• %% y = 2 x^2 + 3x + 5, x \in \mathbb(R)%%;
• %% y = \frac(1)(x - 5), x \neq 5%%;
• %% y = \sqrt(x), x \geq 0%%

ตัวอย่างเช่น ในฟิสิกส์ที่มีความเร่งสม่ำเสมอ การเคลื่อนที่เป็นเส้นตรงความเร็วของร่างกายถูกกำหนดโดยสูตร %%v = v_0 + a t%% และสูตรสำหรับการเคลื่อนที่ %%s%% ของร่างกายอย่างสม่ำเสมอ การเคลื่อนไหวอย่างรวดเร็วในช่วงเวลาตั้งแต่ %%0%% ถึง %%t%% เขียนเป็น: %% s = s_0 + v_0 t + \frac(a t^2)(2) %%

ฟังก์ชันที่กำหนดทีละส่วน

ในบางครั้ง ฟังก์ชันภายใต้การพิจารณาสามารถกำหนดได้ด้วยสูตรหลายสูตรที่ทำงานในส่วนต่าง ๆ ของโดเมนของคำนิยาม ซึ่งอาร์กิวเมนต์ของฟังก์ชันจะเปลี่ยนไป ตัวอย่างเช่น $$ y = \begin(cases) x ^ 2,~ if~x< 0, \\ \sqrt{x},~ если~x \geq 0. \end{cases} $$

ฟังก์ชันประเภทนี้บางครั้งเรียกว่า ส่วนประกอบหรือ เป็นชิ้น ๆ. ตัวอย่างของฟังก์ชันดังกล่าวคือ %%y = |x|%%

ขอบเขตของฟังก์ชัน

หากมีการระบุฟังก์ชันด้วยวิธีการวิเคราะห์ที่ชัดเจนโดยใช้สูตร แต่ไม่ได้ระบุขอบเขตของฟังก์ชันในรูปแบบของชุด %%D%% ดังนั้น %%D%% เราจะหมายถึงชุดค่าของอาร์กิวเมนต์ %%x%% เสมอ ซึ่งสำหรับ สูตรที่กำหนดมีความหมาย ดังนั้นสำหรับฟังก์ชัน %%y = x^2%% โดเมนของนิยามคือชุด %%D = \mathbb(R) = (-\infty, +\infty)%% เนื่องจากอาร์กิวเมนต์ %%x%% สามารถรับค่าใดๆ เส้นจำนวน. และสำหรับฟังก์ชัน %%y = \frac(1)(\sqrt(1 - x^2))%% โดเมนของคำจำกัดความจะเป็นชุดของค่า %%x%% ที่ตอบสนองความไม่เท่าเทียมกัน %%1 - x^2 > 0%% เช่น %%D = (-1, 1)%%

ประโยชน์ของคำจำกัดความฟังก์ชันการวิเคราะห์ที่ชัดเจน

โปรดทราบว่าวิธีการวิเคราะห์ที่ชัดเจนในการกำหนดฟังก์ชันนั้นค่อนข้างกะทัดรัด (ตามกฎแล้วสูตรจะใช้พื้นที่น้อย) สร้างซ้ำได้ง่าย (เขียนสูตรได้ง่าย) และปรับให้เข้ากับการดำเนินการทางคณิตศาสตร์และการแปลงฟังก์ชันมากที่สุด

การดำเนินการเหล่านี้บางส่วน - เกี่ยวกับพีชคณิต (การบวก การคูณ ฯลฯ) - เป็นที่รู้จักกันดีจาก หลักสูตรของโรงเรียนคณิตศาสตร์, อื่น ๆ (ความแตกต่าง, การรวม) จะได้รับการศึกษาในอนาคต อย่างไรก็ตาม วิธีนี้ไม่ชัดเจนเสมอไป เนื่องจากธรรมชาติของการพึ่งพาฟังก์ชันในอาร์กิวเมนต์นั้นไม่ชัดเจนเสมอไป และบางครั้งจำเป็นต้องมีการคำนวณที่ยุ่งยากเพื่อค้นหาค่าของฟังก์ชัน (หากจำเป็น)

ข้อกำหนดฟังก์ชันโดยปริยาย

มีการกำหนดฟังก์ชัน %%y = f(x)%% ด้วยวิธีวิเคราะห์โดยปริยายถ้าให้ความสัมพันธ์ $$F(x,y) = 0 ~~~~~~~~~~(1)$$ เกี่ยวข้องกับค่าของฟังก์ชัน %%y%% และอาร์กิวเมนต์ %%x%% หากกำหนดค่าอาร์กิวเมนต์ เพื่อหาค่าของ %%y%% ที่สอดคล้องกับค่าเฉพาะของ %%x%% จำเป็นต้องแก้สมการ %%(1)%% เทียบกับ %%y%% ที่ค่าเฉพาะของ %%x%%

เมื่อสำหรับ ค่าที่กำหนดสมการ %%x%% %%(1)%% อาจไม่มีคำตอบหรือมีคำตอบมากกว่าหนึ่งคำตอบ ในกรณีแรก ตั้งค่า%%x%% ไม่อยู่ในขอบเขตของฟังก์ชันโดยปริยาย และในกรณีที่สองจะระบุ ฟังก์ชันหลายค่าซึ่งมีค่ามากกว่าหนึ่งค่าสำหรับค่าอาร์กิวเมนต์ที่กำหนด

โปรดทราบว่าหากสมการ %%(1)%% สามารถแก้ไขได้อย่างชัดเจนด้วยความเคารพ %%y = f(x)%% เราก็จะได้ฟังก์ชันเดียวกัน แต่กำหนดไว้แล้วด้วยวิธีการวิเคราะห์ที่ชัดเจน ดังนั้น สมการ %%x + y^5 - 1 = 0%%

และความเท่าเทียมกัน %%y = \sqrt(1 - x)%% กำหนดฟังก์ชันเดียวกัน

นิยามฟังก์ชันพาราเมตริก

เมื่อไม่ได้ระบุการพึ่งพาของ %%y%% บน %%x%% โดยตรง แต่เป็นการพึ่งพาของตัวแปรทั้งสอง %%x%% และ %%y%% ของตัวแปรเสริมตัวที่สามบางตัว %%t%% แทน ในรูปแบบ

$$ \begin(กรณี) x = \varphi(t),\\ y = \psi(t), \end(กรณี) ~~~t \in T \subseteq \mathbb(R), ~~~~~~~~~~(2) พาราเมตริกวิธีการตั้งค่าฟังก์ชั่น

จากนั้นตัวแปรเสริม %%t%% จะเรียกว่าพารามิเตอร์

หากเป็นไปได้ที่จะแยกพารามิเตอร์ %%t%% ออกจากสมการ %%(2)%% พารามิเตอร์เหล่านั้นจะมาถึงฟังก์ชันที่กำหนดโดยการพึ่งพาการวิเคราะห์อย่างชัดเจนหรือโดยปริยายของ %%y%% บน %%x%% ตัวอย่างเช่น จากความสัมพันธ์ $$ \begin(กรณี) x = 2 t + 5, \\ y = 4 t + 12, \end(กรณี), ~~~t \in \mathbb(R), $$ โดยไม่รวมพารามิเตอร์ %%t%% เราได้รับการพึ่งพา %%y = 2 x + 2%% ซึ่งกำหนดเส้นตรงในระนาบ %%xOy%%

ทางกราฟิก

ตัวอย่างของคำจำกัดความเชิงกราฟิกของฟังก์ชัน

ตัวอย่างข้างต้นแสดงให้เห็นว่าวิธีการวิเคราะห์ของการกำหนดฟังก์ชันนั้นสอดคล้องกับฟังก์ชันนั้น ภาพกราฟิก ซึ่งถือได้ว่าเป็นรูปแบบการอธิบายฟังก์ชันที่สะดวกและเห็นภาพ บางครั้งใช้ ทางกราฟิก การกำหนดฟังก์ชันเมื่อการพึ่งพา %%y%% บน %%x%% ถูกกำหนดโดยบรรทัดบนระนาบ %%xOy%% อย่างไรก็ตามเพื่อความชัดเจนทั้งหมดจะสูญเสียความแม่นยำเนื่องจากค่าของอาร์กิวเมนต์และค่าที่สอดคล้องกันของฟังก์ชันสามารถหาได้จากกราฟโดยประมาณเท่านั้น ข้อผิดพลาดที่เกิดขึ้นขึ้นอยู่กับขนาดและความแม่นยำของการวัด abscissa และการจัดตำแหน่งของแต่ละจุดของกราฟ ในอนาคต เราจะกำหนดบทบาทของกราฟของฟังก์ชันเพื่อแสดงพฤติกรรมของฟังก์ชันเท่านั้น ดังนั้น เราจะจำกัดตัวเองไว้ที่การสร้าง "ภาพร่าง" ของกราฟที่สะท้อนถึงคุณลักษณะหลักของฟังก์ชัน

วิธีตาราง

บันทึก วิธีตารางการกำหนดฟังก์ชันเมื่อค่าอาร์กิวเมนต์และค่าฟังก์ชันที่เกี่ยวข้องอยู่ในตารางในลำดับที่แน่นอน ตารางที่รู้จักกันดีถูกสร้างขึ้นเช่นนี้ ฟังก์ชันตรีโกณมิติตารางลอการิทึม ฯลฯ ในรูปแบบตารางแสดงความสัมพันธ์ระหว่างปริมาณที่วัดได้ที่ การศึกษาเชิงทดลองการสังเกตการทดสอบ

ข้อเสียของวิธีนี้คือความเป็นไปไม่ได้ที่จะกำหนดค่าของฟังก์ชันโดยตรงสำหรับค่าของอาร์กิวเมนต์ที่ไม่รวมอยู่ในตาราง หากมีความมั่นใจว่าค่าของอาร์กิวเมนต์ที่ไม่ได้แสดงในตารางเป็นของโดเมนของฟังก์ชันที่พิจารณา ค่าที่สอดคล้องกันของฟังก์ชันสามารถคำนวณได้โดยประมาณโดยใช้การประมาณค่าและการอนุมาน

ตัวอย่าง

x	3	5.1	10	12.5
ย	9	23	80	110

วิธีอัลกอริทึมและวาจาในการระบุฟังก์ชัน

สามารถตั้งค่าฟังก์ชั่นได้ อัลกอริทึม(หรือ แบบเป็นโปรแกรม) ในทางที่ใช้แพร่หลายในการคำนวณด้วยคอมพิวเตอร์.

สุดท้ายนี้ก็อาจจะสังเกตได้ อธิบาย(หรือ วาจา) วิธีการระบุฟังก์ชันเมื่อกฎสำหรับการจับคู่ค่าของฟังก์ชันกับค่าของอาร์กิวเมนต์แสดงเป็นคำพูด

ตัวอย่างเช่น ฟังก์ชัน %%[x] = m~\forall (x \in )