สมการผลต่างเชิงเส้นที่มีค่าสัมประสิทธิ์คงที่ สมการเชิงอนุพันธ์สำหรับหุ่นจำลอง

บ่อยครั้งที่การกล่าวถึงสมการเชิงอนุพันธ์ทำให้นักเรียนรู้สึกไม่เป็นที่พอใจ ทำไมสิ่งนี้ถึงเกิดขึ้น? บ่อยที่สุดเนื่องจากเมื่อศึกษาพื้นฐานของวัสดุจะมีช่องว่างความรู้เกิดขึ้นเนื่องจากการที่การศึกษาตัวกระจายต่อไปกลายเป็นเพียงการทรมาน ยังไม่แน่ชัดว่าจะทำอย่างไร ตัดสินใจอย่างไร จะเริ่มตรงไหน?

อย่างไรก็ตาม เราจะพยายามแสดงให้คุณเห็นว่าตัวกระจายกลิ่นนั้นไม่ยากอย่างที่คิด

แนวคิดพื้นฐานของทฤษฎีสมการเชิงอนุพันธ์

จากโรงเรียนเรารู้สมการที่ง่ายที่สุดซึ่งเราต้องค้นหาค่า x ที่ไม่รู้จัก โดยพื้นฐานแล้ว สมการเชิงอนุพันธ์แตกต่างเพียงเล็กน้อยจากพวกเขา - แทนที่จะเป็นตัวแปร เอ็กซ์ คุณต้องค้นหาฟังก์ชันในนั้น ใช่(x) ซึ่งจะทำให้สมการกลายเป็นอัตลักษณ์

สมการเชิงอนุพันธ์มีความสำคัญในทางปฏิบัติอย่างยิ่ง นี่ไม่ใช่คณิตศาสตร์เชิงนามธรรมที่ไม่เกี่ยวข้องกับโลกรอบตัวเรา กระบวนการทางธรรมชาติที่แท้จริงหลายอย่างอธิบายไว้โดยใช้สมการเชิงอนุพันธ์ ตัวอย่างเช่น การสั่นของสาย การเคลื่อนที่ของออสซิลเลเตอร์ฮาร์มอนิก โดยใช้สมการเชิงอนุพันธ์ในปัญหากลศาสตร์ ค้นหาความเร็วและความเร่งของร่างกาย อีกด้วย ธอมีการใช้กันอย่างแพร่หลายในด้านชีววิทยา เคมี เศรษฐศาสตร์ และวิทยาศาสตร์อื่นๆ อีกมากมาย

สมการเชิงอนุพันธ์ (ธอ) คือสมการที่มีอนุพันธ์ของฟังก์ชัน y(x) ตัวฟังก์ชันเอง ตัวแปรอิสระ และพารามิเตอร์อื่นๆ ในชุดค่าผสมต่างๆ

สมการเชิงอนุพันธ์มีหลายประเภท: สมการเชิงอนุพันธ์สามัญ สมการเชิงอนุพันธ์เชิงเส้นและไม่เชิงเส้น สมการเชิงอนุพันธ์แบบเอกพันธ์และแบบไม่เอกพันธ์ สมการเชิงอนุพันธ์ลำดับที่หนึ่งและสูงกว่า สมการเชิงอนุพันธ์ย่อย และอื่นๆ

การแก้สมการเชิงอนุพันธ์คือฟังก์ชันที่เปลี่ยนสมการให้มีเอกลักษณ์ มีวิธีแก้ไขปัญหาทั่วไปและเฉพาะสำหรับรีโมทคอนโทรล

ผลเฉลยทั่วไปของสมการเชิงอนุพันธ์คือชุดคำตอบทั่วไปที่เปลี่ยนสมการให้มีเอกลักษณ์เฉพาะตัว ผลเฉลยบางส่วนของสมการเชิงอนุพันธ์คือผลเฉลยที่ตรงตามเงื่อนไขเพิ่มเติมที่ระบุไว้ในตอนแรก

ลำดับของสมการเชิงอนุพันธ์ถูกกำหนดโดยลำดับสูงสุดของอนุพันธ์

สมการเชิงอนุพันธ์สามัญ

สมการเชิงอนุพันธ์สามัญเป็นสมการที่มีตัวแปรอิสระตัวเดียว

ลองพิจารณาสมการเชิงอนุพันธ์สามัญที่ง่ายที่สุดของลำดับแรก ดูเหมือนว่า:

สมการนี้สามารถแก้ไขได้โดยการรวมทางด้านขวามือเข้าด้วยกัน

ตัวอย่างของสมการดังกล่าว:

สมการที่แยกออกจากกัน

โดยทั่วไป สมการประเภทนี้จะมีลักษณะดังนี้:

นี่คือตัวอย่าง:

เมื่อแก้สมการดังกล่าว คุณจะต้องแยกตัวแปรต่างๆ ออกให้อยู่ในรูปแบบ:

หลังจากนี้ยังคงรวมทั้งสองส่วนเข้าด้วยกันและรับวิธีแก้ไข

สมการเชิงอนุพันธ์เชิงเส้นของลำดับแรก

สมการดังกล่าวมีลักษณะดังนี้:

โดยที่ p(x) และ q(x) คือฟังก์ชันบางส่วนของตัวแปรอิสระ และ y=y(x) คือฟังก์ชันที่ต้องการ นี่คือตัวอย่างของสมการดังกล่าว:

เมื่อแก้สมการดังกล่าว ส่วนใหญ่มักจะใช้วิธีการเปลี่ยนแปลงค่าคงที่ตามอำเภอใจหรือแสดงฟังก์ชันที่ต้องการเป็นผลคูณของฟังก์ชันอื่นอีกสองฟังก์ชัน y(x)=u(x)v(x)

ในการแก้สมการดังกล่าว จำเป็นต้องมีการเตรียมการบางอย่าง และจะค่อนข้างยากในการ "สรุป"

ตัวอย่างการแก้สมการเชิงอนุพันธ์ด้วยตัวแปรที่แยกไม่ออก

ดังนั้นเราจึงดูประเภทรีโมตคอนโทรลที่ง่ายที่สุด ตอนนี้เรามาดูวิธีแก้ปัญหาของหนึ่งในนั้นกัน ให้นี่เป็นสมการที่มีตัวแปรที่แยกกันไม่ออก

ก่อนอื่น มาเขียนอนุพันธ์ใหม่ในรูปแบบที่คุ้นเคยกว่านี้:

จากนั้นเราแบ่งตัวแปรนั่นคือในส่วนหนึ่งของสมการที่เรารวบรวม "ฉัน" ทั้งหมดและอีกส่วนหนึ่ง - "X":

ตอนนี้ยังคงรวมทั้งสองส่วนเข้าด้วยกัน:

เรารวมและรับคำตอบทั่วไปสำหรับสมการนี้:

แน่นอนว่าการแก้สมการเชิงอนุพันธ์ถือเป็นศิลปะอย่างหนึ่ง คุณต้องสามารถเข้าใจว่าสมการเป็นของประเภทใด และเรียนรู้ที่จะเห็นว่าการเปลี่ยนแปลงใดที่จำเป็นต้องทำเพื่อนำไปสู่รูปแบบใดรูปแบบหนึ่ง ไม่ต้องพูดถึงความสามารถในการแยกความแตกต่างและบูรณาการ และการจะประสบความสำเร็จในการแก้ปัญหา DE คุณต้องฝึกฝน (เช่นเดียวกับทุกสิ่ง) และหากคุณไม่มีเวลาทำความเข้าใจว่าสมการเชิงอนุพันธ์ได้รับการแก้ไขอย่างไร หรือปัญหาคอชี่ติดอยู่เหมือนกระดูกในลำคอ หรือคุณไม่รู้วิธีเตรียมการนำเสนออย่างเหมาะสม โปรดติดต่อผู้เขียนของเรา ในเวลาอันสั้น เราจะจัดเตรียมโซลูชันสำเร็จรูปและรายละเอียดให้กับคุณ โดยรายละเอียดที่คุณสามารถเข้าใจได้ตลอดเวลาที่สะดวกสำหรับคุณ ในระหว่างนี้ เราขอแนะนำให้ดูวิดีโอในหัวข้อ “วิธีแก้สมการเชิงอนุพันธ์”:

ให้เราพิจารณาสมการผลต่างของลำดับที่ n

y(k) = F(k) (92)

เช่นเดียวกับสมการเชิงอนุพันธ์ วิธีแก้จะถูกกำหนดไว้สำหรับสมการลำดับที่หนึ่งเสมอ และโดยทั่วไปแล้วจะไม่พบในสมการที่มีลำดับสูงกว่า

โซลูชั่นที่เป็นประโยชน์

พิจารณาสมการอันดับหนึ่งที่เป็นเนื้อเดียวกัน

1 (k)y(k+1) + 0 (k)y(k) = 0, (93)

โดยที่ 0 (k)≠0 และ 1 (k)≠0 สามารถเขียนใหม่ได้ในรูป

y(k+1) = ก(k)y(k) (94)

ที่ k=0,1,2...

y(1)=ก(0)y(0),

y(2)=ก(1)ก(0)y(0)

y(3)=ก(2)ก(1)ก(0)y(0)

หรือโดยทั่วไปแล้ว

ดังนั้นคำตอบทั่วไปของสมการ (94) ก็คือ

ขีดจำกัดล่างของผลิตภัณฑ์นั้นไม่จำกัดจำนวน เนื่องจากจำนวนปัจจัยคงที่ใดๆ a(0), a(1) และ a(2), ... สามารถนำมารวมกับค่าคงที่ใดๆ ก็ได้ C

การแก้สมการเอกพันธ์เหนือลำดับแรกในกรณีทั่วไปไม่ได้แสดงในรูปแบบของฟังก์ชันพื้นฐาน เนื่องจากขั้นตอนที่ใช้สมการ (81) และ (82) โดยมีค่าสัมประสิทธิ์ขึ้นอยู่กับ k สิ้นสุดลง หากรู้คำตอบอิสระของสมการทั้งหมดยกเว้นคำตอบเดียว ก็สามารถหาคำตอบที่เหลือได้ เช่นเดียวกับสมการเชิงอนุพันธ์ ในหลายกรณี เป็นไปได้ที่จะได้คำตอบที่ชัดเจน สมการของแบบฟอร์ม

n f(k + n)y(k + n) + ... + a 1 f (k + 1)y(k + 1) + n f(k)y(k) = 0,

โดยที่สัมประสิทธิ์ a i เป็นค่าคงที่ โดยการแทน z(k)=f(k)y(k) จะถูกลดลงเป็นสมการผลต่างด้วยสัมประสิทธิ์คงที่ ขั้นตอนบางส่วนจะคล้ายกับขั้นตอนที่ใช้สำหรับสมการเชิงอนุพันธ์ของออยเลอร์ แต่ในกรณีนี้ ตัวแปรตาม (แทนที่จะเป็นตัวแปรอิสระ) อาจถูกแทนที่ได้ วิธีนี้ใช้กันอย่างแพร่หลายในการแก้สมการด้วยสัมประสิทธิ์ตัวแปร

สมการเชิงอนุพันธ์ของระบบควบคุมอัตโนมัติ ระเบียบวิธีในการคอมไพล์สมการเชิงอนุพันธ์สำหรับระบบควบคุมอัตโนมัติ

หมายเหตุทั่วไป

ระบบควบคุมอัตโนมัติมีความหลากหลายตามวัตถุประสงค์และการออกแบบ พฤติกรรมของ ACS สามารถอธิบายได้ด้วยสมการเชิงอนุพันธ์ย่อยแบบธรรมดา สมการผลต่าง ฯลฯ

ACS ใด ๆ แสดงถึงชุดขององค์ประกอบแต่ละส่วนที่มีปฏิสัมพันธ์ระหว่างกันและเชื่อมต่อกันด้วยการเชื่อมต่อ ขั้นตอนแรกในการเขียนสมการเชิงอนุพันธ์สำหรับ ACS คือการแบ่งระบบออกเป็นองค์ประกอบเดี่ยวๆ และการเขียนสมการเชิงอนุพันธ์สำหรับองค์ประกอบเหล่านี้ สมการขององค์ประกอบและสมการของการเชื่อมต่อระหว่างแต่ละองค์ประกอบอธิบายกระบวนการในระบบควบคุม เช่น การเปลี่ยนแปลงตามเวลาของพิกัดทั้งหมดของระบบ เมื่อทราบสมการขององค์ประกอบและสมการของการเชื่อมต่อแล้ว จะสามารถเขียนบล็อกไดอะแกรมของ ACS ได้

แผนภาพโครงสร้างของ ACS แสดงถึงลักษณะทางเรขาคณิตของระบบเช่น แสดงให้เห็นว่าองค์ประกอบใดที่ ATS ประกอบด้วย และองค์ประกอบเหล่านี้เกี่ยวข้องกันอย่างไร สถานะของ ACS รวมถึงแต่ละองค์ประกอบที่รวมอยู่ในนั้นนั้นมีลักษณะเฉพาะด้วยตัวแปรอิสระจำนวนหนึ่ง ตัวแปรเหล่านี้อาจเป็นปริมาณทางไฟฟ้า (กระแส แรงดัน ฯลฯ) หรือปริมาณทางกล (ความเร็ว มุมการหมุน การเคลื่อนที่ ฯลฯ) โดยปกติแล้ว เพื่อระบุลักษณะสถานะของระบบหรือองค์ประกอบของระบบ พิกัดทั่วไปหนึ่งพิกัดจะถูกเลือกที่อินพุตของระบบหรือองค์ประกอบ (g(t)) และอีกหนึ่งพิกัดที่เอาต์พุต (x(t)) ในบางกรณี การแสดงดังกล่าวเป็นไปไม่ได้ เนื่องจากระบบหรือองค์ประกอบอาจมีปริมาณอินพุตและเอาต์พุตหลายรายการ ในระบบหลายมิติ เราสามารถพิจารณาปริมาณอินพุทและเอาท์พุทเวกเตอร์ที่มีขนาดตรงกัน ตามลำดับ กับจำนวนปริมาณอินพุทและเอาท์พุทของ ACS

การคอมไพล์และการทำให้เป็นเส้นตรงของสมการเชิงอนุพันธ์ องค์ประกอบของระบบ

เมื่อรวบรวมสมการเชิงอนุพันธ์สำหรับ ACS ภารกิจหลักคือการรวบรวมสมการเชิงอนุพันธ์สำหรับแต่ละองค์ประกอบของระบบ สมการของแต่ละองค์ประกอบจะถูกรวบรวมบนพื้นฐานของกฎทางกายภาพที่กำหนดลักษณะพฤติกรรมขององค์ประกอบ

เมื่อวาดสมการเชิงอนุพันธ์สำหรับองค์ประกอบ ACS เราควรพยายามอธิบายพฤติกรรมขององค์ประกอบที่กำหนดให้ถูกต้องที่สุด อย่างไรก็ตาม ความซับซ้อนของสมการที่เกิดขึ้นทำให้ยากต่อการศึกษาคุณสมบัติของคำตอบ ดังนั้นเมื่อเขียนสมการเชิงอนุพันธ์จึงจำเป็นต้องพยายามประนีประนอมอย่างสมเหตุสมผลระหว่างคำอธิบายพฤติกรรมขององค์ประกอบที่สมบูรณ์ที่สุดกับความเป็นไปได้ในการทบทวนและศึกษาสมการผลลัพธ์

หากอธิบายไดนามิกขององค์ประกอบด้วยสมการเชิงอนุพันธ์เชิงเส้น องค์ประกอบนี้จะถูกเรียก เชิงเส้นถ้าสมการเชิงอนุพันธ์ไม่เป็นเชิงเส้น องค์ประกอบนั้นจะถูกเรียก ไม่เชิงเส้น.

เพื่อให้การวิเคราะห์ง่ายขึ้น เมื่อเป็นไปได้ สมการเชิงอนุพันธ์แบบไม่เชิงเส้นจะถูกแทนที่ด้วยสมการเชิงเส้นโดยประมาณ ซึ่งคำตอบจะตรงกับคำตอบของสมการไม่เชิงเส้นที่มีระดับความแม่นยำเพียงพอ กระบวนการแทนที่สมการเชิงอนุพันธ์แบบไม่เชิงเส้นด้วยสมการเชิงเส้นนี้เรียกว่า การทำให้เป็นเส้นตรง.

ถ้าสมการเชิงอนุพันธ์ขององค์ประกอบไม่เชิงเส้นเนื่องจากลักษณะไม่เชิงเส้นขององค์ประกอบนั้น การทำให้สมการเชิงเส้นตรงจะลดลงเป็นการแทนที่ลักษณะไม่เชิงเส้นขององค์ประกอบนั้น x=φ(ก) ฟังก์ชันเชิงเส้นบางอย่าง x= เอจี+ ข- ในเชิงวิเคราะห์ การแทนที่นี้ทำโดยใช้การขยายฟังก์ชันของซีรีส์ Taylor x=φ(ก) ในบริเวณใกล้เคียงจุดที่สอดคล้องกับสถานะคงตัวและละทิ้งพจน์ทั้งหมดที่มีค่าเบี่ยงเบน ∆g ของค่าอินพุตขององค์ประกอบให้เป็นกำลังที่สูงกว่าตัวแรก ในเชิงเรขาคณิต นี่หมายถึงการแทนที่เส้นโค้ง x=φ(ก) แทนเจนต์ที่วาดไปยังเส้นโค้งที่จุด (x 0 , g 0) ซึ่งสอดคล้องกับสถานะคงที่ของการทำงานขององค์ประกอบ (รูปที่ 29) ในกรณีอื่นๆ การทำให้เป็นเส้นตรงจะดำเนินการโดยการวาดเส้นตัดที่เบี่ยงเบนไปจากฟังก์ชันเพียงเล็กน้อย x=φ(ก) ในช่วงที่ต้องการของการเปลี่ยนแปลงค่าอินพุตขององค์ประกอบ

นอกจากคุณลักษณะเชิงเส้นตรงแล้ว ยังมีคุณลักษณะที่ไม่สอดคล้องกับลักษณะเชิงเส้นตรงดังกล่าวด้วย ซึ่งรวมถึง คุณลักษณะที่ไม่สามารถขยายเป็นอนุกรม Taylor ได้ในบริเวณใกล้เคียงกับจุดสถานะคงตัว เราจะเรียกลักษณะดังกล่าวว่า ไม่เชิงเส้นอย่างมีนัยสำคัญ.

ให้เราพิจารณากระบวนการเชิงเส้นตรงของสมการองค์ประกอบไม่เชิงเส้นโดยใช้อนุกรมเทย์เลอร์ ให้อธิบายพฤติกรรมขององค์ประกอบด้วยสมการเชิงอนุพันธ์ไม่เชิงเส้น

F(x n , x ’ , x, g) = 0 (1) จากนั้นสถานะคงตัวขององค์ประกอบจะมีลักษณะเป็นสมการ F(0, 0, x, g) = 0 (2) ให้ g 0 และ x 0 เป็นค่าสถานะคงที่ จากนั้นพิกัด g และ x สามารถเขียนเป็น x = x 0 + ∆x, g = g 0 + ∆g โดยที่ ∆g และ ∆x เป็นส่วนเบี่ยงเบนของพิกัด g และ x จากสถานะคงตัว สมการ (1) ในการเบี่ยงเบนมีรูปแบบ:

F(∆x ’’ , ∆x ’ , x 0 + ∆x, ก. 0 + ∆g) = 0 (3)

ให้เราขยายด้านซ้ายของสมการ (3) ออกเป็นอนุกรมเทย์เลอร์ที่สัมพันธ์กับจุดสถานะคงตัว (0, 0, x 0, g 0):

อนุพันธ์บางส่วนทางด้านซ้ายของสมการ (4) แทนตัวเลขจำนวนหนึ่ง ค่าซึ่งขึ้นอยู่กับประเภทของฟังก์ชัน F(x '', x ', x, g) และค่าของพิกัด x 0 และก 0

เมื่อพิจารณาความเบี่ยงเบน ∆g, ∆x จากสถานะคงตัว รวมถึงอนุพันธ์ของพวกมันเมื่อเทียบกับเวลา ให้มีค่าน้อยและสมมติว่าฟังก์ชัน F(x '' , x ' , x, g) มีความราบรื่นเพียงพอเมื่อเทียบกับ ข้อโต้แย้งทั้งหมดในบริเวณใกล้เคียงจุดที่สอดคล้องกับสถานะคงตัว เราละทิ้งสมการ (4) พจน์ทั้งหมดที่มีการเบี่ยงเบน ∆g และ ∆x รวมถึงอนุพันธ์ของพวกมันในระดับที่สูงกว่าครั้งแรก สมการผลลัพธ์ (5) คือสมการเชิงอนุพันธ์เชิงเส้นที่มีค่าสัมประสิทธิ์คงที่ ,,,และเป็นผลจากการทำให้สมการเชิงเส้น (1)

เห็นได้ชัดว่า เงื่อนไขที่จำเป็นสำหรับการทำให้เป็นเส้นตรงคือความเป็นไปได้ในการขยายฟังก์ชัน F(x ’’ , x ' , x, g) ให้เป็นอนุกรมของ Taylor ในบริเวณใกล้เคียงกับจุดที่สอดคล้องกับสถานะคงตัว

กระบวนการเชิงเส้นตรงของสมการ (1) สามารถตีความทางเรขาคณิตได้ดังนี้ ในช่องว่างของตัวแปร x '' , x ' , x, g สมการ (1) กำหนดพื้นผิวที่แน่นอน การเปลี่ยนจากสมการ (1) ไปเป็นสมการเชิงเส้น (5) หมายถึงการแทนที่พื้นผิวด้วยระนาบแทนเจนต์ที่ลากไปยังพื้นผิว ณ จุดที่สอดคล้องกับสถานะคงตัว โดยปกติแล้ว ยิ่งความแตกต่างระหว่างจุดพื้นผิวและจุดระนาบมีขนาดเล็กลง ข้อผิดพลาดในการเปลี่ยนดังกล่าวก็จะยิ่งน้อยลงเท่านั้น สิ่งนี้เป็นจริงเฉพาะในบริเวณใกล้เคียงเล็กๆ ของสภาวะคงตัวเท่านั้น

แนวคิดเรื่องการควบคุมและการสังเกต

โดยปกติกระบวนการหรือวัตถุจะเรียกว่าสามารถควบคุมได้อย่างสมบูรณ์ หากสามารถถ่ายโอนจากสถานะที่แน่นอน x(t 0) ไปยังสถานะสมดุลที่ต้องการ x(t 1) ในช่วงเวลาจำกัด t 1 – t 0 กล่าวอีกนัยหนึ่ง กระบวนการสามารถควบคุมได้อย่างสมบูรณ์หากมีการดำเนินการควบคุม m(t) ซึ่งกำหนดไว้ในช่วงเวลาจำกัด t 0 ≤ t ≤ t 1 ซึ่งจะถ่ายโอนกระบวนการจากสถานะเริ่มต้น x(t 0) ไปยังที่ต้องการ สถานะสมดุล x(t 1) ในช่วงเวลา t 1 – เสื้อ 0 .

เงื่อนไขที่จำเป็นและเพียงพอสำหรับการควบคุมได้อย่างสมบูรณ์สำหรับกรณีระบบแยกสามารถกำหนดได้ดังนี้

กระบวนการแยกเชิงเส้นเชิงเส้นลำดับที่ n สามารถควบคุมได้อย่างสมบูรณ์หากและเฉพาะในกรณีที่เวกเตอร์

ส 1 = φ(-T)ชม(T)

ส 2 = φ(-T)ชม(T)

s n = φ(-T)ชม(T)

เป็นอิสระเชิงเส้น

เวกเตอร์เหล่านี้เกิดขึ้นเนื่องจากการเปลี่ยนแปลงต่อไปนี้

(t) = ขวาน(t) + d ม.(t)

โดยที่ m(t) เป็นเพียงการกระทำควบคุมเท่านั้น กรณีของการดำเนินการควบคุมเดียวจะถือว่าทำให้การตีความนิพจน์ผลลัพธ์ง่ายขึ้น สมการของสถานะการเปลี่ยนแปลงของกระบวนการมีรูปแบบ

โดยที่ φ(T) คือเมทริกซ์การเปลี่ยนแปลงกระบวนการและ
.

แนวคิดเรื่องความสามารถในการควบคุมสามารถตีความได้อีกแบบหนึ่งซึ่งจะช่วยให้เข้าใจได้ดีขึ้น ให้กระบวนการหลายมิติเชิงเส้นอธิบายด้วยสมการเชิงอนุพันธ์เวกเตอร์ (t) = Ax(t) + D m(t) โดยที่ x คือเวกเตอร์สถานะ n มิติ

m – เวกเตอร์มิติ r แสดงถึงการกระทำการควบคุม

A – เมทริกซ์กำลังสองของสัมประสิทธิ์ลำดับที่ n;

D – เมทริกซ์ควบคุมขนาด n×r

เมทริกซ์ A สามารถลดลงเป็นรูปแบบแนวทแยงได้

,

โดยที่ λ i คือค่าลักษณะเฉพาะของเมทริกซ์ A ของกระบวนการเชิงเส้นซึ่งถือว่าแตกต่างกันทั้งหมด

การใช้การทดแทน x=Tz เราเขียนสมการในรูปแบบมาตรฐาน

(t) = Λz(t) + ∆ ม.(t),

ที่ไหน
- เวกเตอร์ z จะถูกเรียกว่าเวกเตอร์สถานะมาตรฐาน

กระบวนการที่อธิบายโดยสมการ (t) = Ax(t) + D m(t) สามารถควบคุมได้ถ้าเมทริกซ์ ∆ ไม่มีแถวที่มีองค์ประกอบเป็นศูนย์ทั้งหมด พิกัดที่สอดคล้องกับแถวที่ไม่ใช่ศูนย์ ∆ ถือว่าถูกควบคุม

ตัวอย่าง:

หาสมการเชิงอนุพันธ์ของลูกตุ้มแรงเหวี่ยง ซึ่งใช้เป็นองค์ประกอบการตรวจจับในระบบควบคุมอัตโนมัติบางระบบ แผนภาพของลูกตุ้มแสดงในรูป ปริมาณอินพุตคือความเร็วเชิงมุม ω และปริมาณเอาต์พุตคือการกระจัด x ของแท่น เมื่อความเร็วในการหมุนเพิ่มขึ้น ลูกบอลจะเคลื่อนตัวออกไปภายใต้อิทธิพลของแรงเหวี่ยงหนีศูนย์และเคลื่อนแท่น แท่นยังได้รับผลกระทบจากแรงยืดหยุ่นของสปริง แรงหน่วง และแรงเฉื่อยอีกด้วย

ให้เราแนะนำสัญลักษณ์ต่อไปนี้: c – ค่าสัมประสิทธิ์ความแข็งของสปริง; k คือค่าสัมประสิทธิ์แรงเสียดทานแบบหนืด ม. – มวลของลูกบอล; M – มวลของชิ้นส่วนที่เกี่ยวข้องกับการเคลื่อนที่ของการเคลื่อนที่ตามแนวแกน OX ω – ความเร็วเชิงมุมของเพลา f 0 – แรงอัดล่วงหน้าของสปริง

ในการรวบรวมสมการเชิงอนุพันธ์ของลูกตุ้มแรงเหวี่ยง เราใช้สมการลากรองจ์ชนิดที่สอง:
(ฉัน = 1, 2,…, น) (*) ตามพิกัดทั่วไป x i เราเลือกพิกัดเอาต์พุต - การเคลื่อนที่ของแพลตฟอร์ม x ให้เราค้นหาการแสดงออกของพลังงานจลน์ T, พลังงานศักย์ P และฟังก์ชันการกระจาย R ของลูกตุ้มแรงเหวี่ยง จากรูปก็ชัดเจนว่า

ρ = r + l บาป α, x = 2a(1 – cos α)

พลังงานจลน์ของระบบ T = T 1 + T 2 + T 3 โดยที่ T 1 คือพลังงานจลน์ในการเคลื่อนที่แบบหมุนรอบแกน OX T 2 – พลังงานจลน์ของลูกบอลในการเคลื่อนที่แบบหมุนรอบจุด A และ A’; Т 3 – พลังงานจลน์ของมวลในการเคลื่อนที่เชิงแปลตามแนวแกน OX เรามี:

,

,
. (*1)

พลังงานศักย์ของลูกตุ้ม P = P 1 + P 2 + P 3 โดยที่ P 1 คือพลังงานศักย์ของมวลที่เคลื่อนที่ขนานกับแกน OX P 2 – พลังงานศักย์; P 3 – พลังงานศักย์ของสปริง สำหรับกรณีที่อยู่ระหว่างการพิจารณา เรามี:

,
,
. (*2)

ให้เราหาแรงกระจายทั่วไป Q R . เนื่องจากมีแดมเปอร์อยู่ แรงเสียดทานแบบแห้งจึงมีน้อยเมื่อเทียบกับแรงเสียดทานแบบหนืด และสามารถละเลยได้ ตามสูตรครับ
เราจะมี

. (*3)

ลองคำนวณค่าของแต่ละพจน์ที่รวมอยู่ในสมการลากรองจ์ (*):

,

,

.

ให้เราแทนที่นิพจน์ผลลัพธ์ลงในสมการลากรองจ์ประเภทที่สอง (*) จากนั้น

ให้เราแนะนำสัญกรณ์ต่อไปนี้:

,
,

; (*5)

. (*6)

เมื่อคำนึงถึงสัญกรณ์ที่ยอมรับแล้ว สมการของลูกตุ้มแรงเหวี่ยงจะถูกเขียนในรูปแบบ

สมการ (*7) เป็นสมการเชิงอนุพันธ์แบบไม่เชิงเส้น สถานะสมดุล (x 0, ω 0) เป็นวิธีแก้สมการ

ให้เราพิจารณาการแกว่งเล็กน้อยของลูกตุ้มสัมพันธ์กับสภาวะสมดุล

x = x 0 + ∆x, ω = ω 0 + ∆ω (*9)

ให้เราขยายฟังก์ชัน f 1 (x), f 2 (x), f 3 (x, ω) ให้เป็นอนุกรมเทย์เลอร์ในบริเวณใกล้เคียงกับสถานะสมดุล (x 0, ω 0)

โดยที่ฟังก์ชัน F 1 (∆x), F 2 (∆x), F 3 (∆x, ∆ω) มีลำดับความเล็กที่สูงกว่าเมื่อเปรียบเทียบกับ ∆x และ ∆ω เมื่อพิจารณาว่า x' = ∆x' และ x” = ∆x” และคำนึงถึงนิพจน์ (*8), (*9), (*10) สมการ (*7) สามารถเขียนใหม่ได้เป็น

ฟังก์ชั่นอยู่ที่ไหน

มีลำดับความเล็กที่สูงกว่าเมื่อเปรียบเทียบกับ
- วางฟังก์ชัน
เราได้รับสมการเชิงเส้นของการแกว่งของลูกตุ้มสัมพันธ์กับสถานะสมดุล (x 0, ω 0)

, (*11)

,

(*12)

.

ระบบที่มีลำดับอินพุตและเอาท์พุตเชื่อมต่อกันด้วยสมการผลต่างเชิงเส้นที่มีค่าสัมประสิทธิ์คงที่จะสร้างเซตย่อยของคลาสของระบบเชิงเส้นที่มีพารามิเตอร์คงที่ คำอธิบายของระบบ LPP ด้วยสมการผลต่างมีความสำคัญมาก เนื่องจากมักจะทำให้สามารถค้นพบวิธีที่มีประสิทธิภาพในการสร้างระบบดังกล่าวได้ นอกจากนี้ จากสมการความแตกต่าง ยังเป็นไปได้ที่จะกำหนดคุณลักษณะต่างๆ ของระบบที่กำลังพิจารณาได้ รวมถึงความถี่ธรรมชาติและความหลากหลายของมัน ลำดับของระบบ ความถี่ที่สอดคล้องกับอัตราขยายเป็นศูนย์ เป็นต้น

ในกรณีทั่วไปส่วนใหญ่ สมการผลต่างเชิงเส้นของลำดับที่ 2 ที่มีค่าสัมประสิทธิ์คงที่ซึ่งเกี่ยวข้องกับระบบที่สามารถรับรู้ได้ทางกายภาพจะมีรูปแบบดังนี้

(2.18)

โดยที่ค่าสัมประสิทธิ์และอธิบายระบบเฉพาะและ ลำดับของระบบที่แสดงถึงคุณสมบัติทางคณิตศาสตร์ของสมการผลต่างจะแสดงไว้ด้านล่างนี้ สมการ (2.18) เขียนในรูปแบบที่สะดวกสำหรับการแก้โดยวิธีทดแทนโดยตรง มีเงื่อนไขตั้งต้น [เช่น สำหรับ ] และลำดับอินพุต โดยใช้สูตร (2.18) คุณสามารถคำนวณลำดับเอาต์พุตสำหรับ เช่น สมการผลต่าง

(2.19)

ด้วยเงื่อนไขเริ่มต้นและสามารถแก้ไขได้ด้วยการทดแทนซึ่งจะทำให้

แม้ว่าการแก้สมการผลต่างด้วยการทดแทนโดยตรงจะมีประโยชน์ในบางกรณี แต่จะมีประโยชน์มากกว่ามากหากได้คำตอบที่ชัดเจนของสมการ วิธีการหาคำตอบดังกล่าวมีรายละเอียดอยู่ในบทความเกี่ยวกับสมการผลต่าง และจะอธิบายไว้เพียงภาพรวมคร่าวๆ เท่านั้น แนวคิดหลักอยู่ที่การหาคำตอบสองวิธีสำหรับสมการผลต่าง: แบบเอกพันธ์และแบบบางส่วน สารละลายที่เป็นเนื้อเดียวกันได้มาโดยการแทนที่ศูนย์สำหรับทุกพจน์ที่มีองค์ประกอบของลำดับอินพุต และกำหนดการตอบสนองเมื่อลำดับอินพุตเป็นศูนย์ โซลูชันประเภทนี้จะอธิบายคุณสมบัติพื้นฐานของระบบที่กำหนด วิธีแก้ปัญหาเฉพาะได้มาจากการเลือกประเภทของลำดับเอาต์พุตสำหรับลำดับอินพุตที่กำหนด เพื่อกำหนดค่าคงที่ตามอำเภอใจของสารละลายที่เป็นเนื้อเดียวกัน จะใช้เงื่อนไขเริ่มต้น ตัวอย่างเช่น ขอให้เราแก้สมการ (2.19) โดยใช้วิธีนี้ สมการเอกพันธ์มีรูปแบบ

(2.20)

เป็นที่ทราบกันดีว่าการแก้ลักษณะของสมการเอกพันธ์ที่สอดคล้องกับสมการผลต่างเชิงเส้นที่มีค่าสัมประสิทธิ์คงที่คือคำตอบของรูปแบบ ดังนั้นเราจึงได้การแทนที่ในสมการ (2.20) แทน

(2.21)

ลองค้นหาวิธีแก้ปัญหาเฉพาะที่สอดคล้องกับลำดับอินพุตในแบบฟอร์ม

(2.22)

จากสมการ (2.19) ที่เราได้รับ

เนื่องจากค่าสัมประสิทธิ์สำหรับองศาที่เท่ากันจะต้องเท่ากัน B, C และ D จึงต้องเท่ากัน

(2.24)

ดังนั้นคำตอบทั่วไปจึงมีรูปแบบ

(2.25)

ค่าสัมประสิทธิ์ถูกกำหนดจากเงื่อนไขเริ่มต้น จากที่ไหน และ

(2.26)

การตรวจสอบสารละลายแบบเลือกสรร (2.26) ที่แสดงถึงข้อตกลงที่สมบูรณ์กับโซลูชันโดยตรงที่ให้ไว้ข้างต้น ข้อได้เปรียบที่ชัดเจนของโซลูชัน (2.26) คือช่วยให้สามารถระบุ .

มะเดื่อ. 2.7. โครงการนำสมการผลต่างลำดับที่หนึ่งอย่างง่ายไปใช้

ความสำคัญของสมการผลต่างคือสมการจะกำหนดวิธีการสร้างระบบดิจิทัลโดยตรง ดังนั้นสมการผลต่างอันดับหนึ่งของรูปแบบทั่วไปที่สุด

สามารถทำได้โดยใช้วงจรดังรูป 2.7. บล็อก "ล่าช้า" ล่าช้าหนึ่งนับ รูปแบบของการออกแบบระบบนี้ ซึ่งใช้องค์ประกอบการหน่วงเวลาแยกต่างหากสำหรับลำดับอินพุตและเอาต์พุต เรียกว่ารูปแบบโดยตรง 1 ด้านล่างนี้เราจะกล่าวถึงวิธีการต่างๆ สำหรับการสร้างระบบดิจิทัลนี้และระบบดิจิทัลอื่นๆ

สมการผลต่างอันดับสองของรูปแบบทั่วไปที่สุด

มะเดื่อ. 2.8. โครงการนำสมการผลต่างอันดับสองไปใช้

สามารถทำได้โดยใช้วงจรดังรูป 2.8. วงจรนี้ยังใช้องค์ประกอบการหน่วงเวลาแยกต่างหากสำหรับลำดับอินพุตและเอาต์พุต

จากการนำเสนอเนื้อหาในบทนี้ในเวลาต่อมา จะเห็นได้ชัดว่าระบบลำดับที่หนึ่งและสองสามารถนำมาใช้ในการดำเนินการตามระบบลำดับที่สูงกว่าได้ เนื่องจากระบบลำดับหลังสามารถแสดงในรูปแบบของอนุกรมหรือขนานที่เชื่อมต่อลำดับที่หนึ่งและสอง ระบบ

V i r e f e r m o r e l a l i v e n ts ถูกเรียก สมการของแบบฟอร์ม

อันที่ต้องการอยู่ที่ไหนและ ฉ-ฟังก์ชันที่กำหนด การแทนที่ความแตกต่างอันจำกัดใน (2) ด้วยนิพจน์ผ่านค่าของฟังก์ชันที่ต้องการตาม (1) นำไปสู่สมการของรูปแบบ

ถ้า นั่นคือสมการ (3) มีทั้งจริงๆ และ จากนั้นจึงเรียกสมการ (3) สมการเชิงอนุพันธ์ลำดับที่ m หรือสมการเชิงอนุพันธ์ V o r m e l a l i n g i n g

(6)

ค่าคงที่ตามอำเภอใจอยู่ที่ไหน

3) คำตอบทั่วไปของสมการเชิงเส้นแบบไม่เอกพันธ์ (4) นำเสนอเป็นผลรวมของคำตอบเฉพาะของมันกับคำตอบทั่วไปของสมการเชิงเส้นเนื้อเดียวกัน (5)

คำตอบเฉพาะของสมการเอกพันธ์ (5) สามารถสร้างขึ้นได้โดยใช้วิธีแก้ปัญหาทั่วไป (6) ของสมการเอกพันธ์โดยการใช้วิธีการแปรผันของค่าคงที่ตามใจชอบ (ดูตัวอย่าง) ในกรณีของ R.u. โดยมีค่าสัมประสิทธิ์คงที่

เราสามารถค้นหาคำตอบบางส่วนที่เป็นอิสระเชิงเส้นได้โดยตรง เพื่อจุดประสงค์นี้ให้พิจารณาลักษณะเฉพาะ สมการ

และเสาะหารากของมัน ถ้ารากทั้งหมดเป็นแบบธรรมดา แสดงว่าฟังก์ชันต่างๆ

สร้างระบบการแก้สมการ (7) ที่เป็นอิสระเชิงเส้น ในกรณีที่ - รากของการคูณ ร,โซลูชันมีความเป็นอิสระเชิงเส้น

ถ้าสัมประสิทธิ์เป็น 0 , ก 1 , . . ., ที่จริงและสมการ (8) มีรากที่ซับซ้อน เป็นต้น รูตแบบง่าย จากนั้นแทนที่จะใช้โซลูชันที่ซับซ้อน โซลูชันจริงที่เป็นอิสระเชิงเส้นสองตัวจะมีความแตกต่างกัน

ให้มีร. อันดับ 2 ที่มีค่าสัมประสิทธิ์จริงคงที่

(9) ลักษณะเฉพาะ สมการ

มีราก

ในกรณีนี้ จะสะดวกในการเขียนคำตอบทั่วไปของสมการ (9) ในรูปแบบ

(10)

โดยที่ c 1 และ c 2 เป็นค่าคงที่ตามอำเภอใจ ถ้า และ เป็นรากคอนจูเกตที่ซับซ้อน:

จากนั้นการแสดงวิธีแก้ปัญหาทั่วไปอีกรูปแบบหนึ่งก็มีรูปแบบ

ในกรณีของหลายรูต สามารถหาคำตอบทั่วไปได้โดยส่งผ่านไปยังขีดจำกัดจาก (10) หรือ (11) ดูเหมือนว่า

เช่นเดียวกับในกรณีของสมการลำดับตามอำเภอใจสำหรับร. ใน ในลำดับที่ 2 เราสามารถพิจารณาปัญหาคอชีหรือปัญหาค่าขอบเขตต่างๆ ได้ ตัวอย่างเช่น สำหรับปัญหาคอชี่

การแก้สมการผลต่างเชิงเส้นธรรมดา

โดยมีค่าสัมประสิทธิ์คงที่

ความสัมพันธ์ระหว่างเอาต์พุตและอินพุตของระบบแยกเชิงเส้นสามารถอธิบายได้ด้วยสมการผลต่างเชิงเส้นธรรมดาที่มีค่าสัมประสิทธิ์คงที่

,

ที่ไหน ใช่แล้ว[n]- สัญญาณเอาท์พุตในขณะนี้ n,

เอ็กซ์[n]- สัญญาณเข้าในขณะนี้ n,

AI,ข– ค่าสัมประสิทธิ์คงที่

สามารถใช้สองวิธีในการแก้สมการดังกล่าว

• วิธีการโดยตรง
• วิธี Z – การแปลง

ขั้นแรก ลองพิจารณาแก้สมการผลต่างเชิงเส้นโดยใช้วิธีทางตรง

ผลเฉลยทั่วไปของสมการผลต่างเชิงเส้นที่ไม่เป็นเนื้อเดียวกัน (ที่มีด้านขวามือไม่เป็นศูนย์) จะเท่ากับผลรวมของ วิธีแก้ปัญหาทั่วไปสมการผลต่างเอกพันธ์เชิงเส้นและ โซลูชันส่วนตัวสมการที่ไม่เหมือนกัน

คำตอบทั่วไปของสมการผลต่างเอกพันธ์ ( ศูนย์-ป้อนข้อมูลการตอบสนอง) ใช่แล้ว [n]

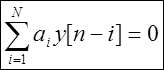
ถูกกำหนดให้เป็น

.

เราได้การแทนที่คำตอบนี้เป็นสมการเอกพันธ์

พหุนามดังกล่าวเรียกว่า พหุนามลักษณะเฉพาะระบบ เขามี เอ็นราก - รากอาจเป็นจริงหรือซับซ้อนก็ได้ และรากบางรากอาจเกิดขึ้นพร้อมกัน (หลายรายการ)

ถ้าราก มีจริงและแตกต่าง ดังนั้นคำตอบของสมการเอกพันธ์จึงมีรูปแบบ

ค่าสัมประสิทธิ์อยู่ที่ไหน

หากรากบางอย่างเช่น แล 1มีหลายหลาก มจากนั้นเงื่อนไขการแก้ปัญหาที่สอดคล้องกันจะอยู่ในรูปแบบ

หากค่าสัมประสิทธิ์ทั้งหมดของสมการเอกพันธ์และพหุนามลักษณะเฉพาะนั้นเป็นจำนวนจริง ดังนั้นเงื่อนไขสองข้อของการแก้ปัญหาที่สอดคล้องกับรากคอนจูเกตที่ซับซ้อนอย่างง่าย สามารถแสดง (เขียน) ในรูปแบบ โดยมีค่าสัมประสิทธิ์ เอ,บีถูกกำหนดโดยเงื่อนไขเริ่มต้น

ประเภทของโซลูชันส่วนตัว ใช่แล้ว [n]สมการขึ้นอยู่กับด้านขวา (สัญญาณอินพุต) และกำหนดตามตารางด้านล่าง

ตารางที่ 1. ประเภทของโซลูชันเฉพาะสำหรับลักษณะที่แตกต่างกันของด้านขวา

สัญญาณอินพุตเอ็กซ์[n]	โซลูชันส่วนตัวใช่แล้ว [n]
ก(คงที่)

การแก้สมการผลต่างเชิงเส้นด้วยวิธีการแปลง Z ประกอบด้วยการใช้ ซี– การแปลงเป็นสมการโดยใช้คุณสมบัติของความเป็นเส้นตรงและการเลื่อนเวลา ผลลัพธ์ที่ได้คือสมการพีชคณิตเชิงเส้นเทียบกับ ซี- รูปภาพของฟังก์ชั่นที่ต้องการ ย้อนกลับ ซี– การแปลงให้ผลลัพธ์ที่ต้องการในโดเมนเวลา เพื่อให้ได้การแปลง Z แบบผกผันมักใช้การสลายตัวของนิพจน์เชิงตรรกยะเป็นเศษส่วนอย่างง่าย (ประถมศึกษา) เนื่องจากการแปลงผกผันจากเศษส่วนประถมศึกษาที่แยกจากกันมีรูปแบบที่เรียบง่าย

โปรดทราบว่าหากต้องการย้ายไปยังโดเมนเวลา สามารถใช้วิธีอื่นในการคำนวณการแปลงรูป Z แบบผกผันได้

ตัวอย่าง- ให้เราพิจารณาการตอบสนอง (สัญญาณเอาท์พุต) ของระบบที่อธิบายโดยสมการผลต่างเชิงเส้นกับสัญญาณอินพุต

สารละลาย.

1. วิธีการแก้สมการโดยตรง

สมการเอกพันธ์ พหุนามลักษณะเฉพาะของมัน

รากของพหุนาม .

การแก้สมการเอกพันธ์

เนื่องจากเรากำหนดวิธีแก้ปัญหาเฉพาะในรูปแบบ .

แทนมันลงในสมการ

เพื่อหาค่าคงที่ ถึงยอมรับเถอะ n=2- แล้ว

หรือ K=2.33

ดังนั้นวิธีแก้ปัญหาเฉพาะ และคำตอบทั่วไปของสมการผลต่าง (1)

ลองหาค่าคงที่กัน ค 1และ ค 2- การทำเช่นนี้มาใส่กัน n=0แล้วจากสมการผลต่างเดิมที่เราได้รับ สำหรับสมการที่กำหนด

นั่นเป็นเหตุผลว่าทำไม จากการแสดงออก (1)

เพราะฉะนั้น,

.

จากนิพจน์ (1) สำหรับ n=1เรามี.
เราได้รับสมการสองสมการต่อไปนี้สำหรับ C 1 และ C 2

.

การแก้ระบบนี้ให้ค่าต่อไปนี้: C 1 = 0.486 และ C 2 = -0.816

ดังนั้นคำตอบทั่วไปของสมการนี้คือ

2. วิธีแก้ปัญหาโดยใช้วิธี Z – การแปลง

ลองใช้ Z - การแปลงจากสมการผลต่างดั้งเดิมโดยคำนึงถึงคุณสมบัติ (ทฤษฎีบท) ของการเปลี่ยนเวลา - เราได้รับ