รุกฆาต x y ความคาดหวังทางคณิตศาสตร์ ความหมาย ความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่มแบบไม่ต่อเนื่องและต่อเนื่อง ตัวอย่าง ความคาดหวังแบบมีเงื่อนไข การคำนวณ คุณสมบัติ ปัญหา การประมาณค่าความคาดหวัง การกระจายตัว ฟังก์ชันการกระจาย สูตร ตัวอย่าง

ความคาดหวังทางคณิตศาสตร์คือคำจำกัดความ

รุกฆาตที่รอคอยคือหนึ่งในแนวคิดที่สำคัญที่สุดในสถิติทางคณิตศาสตร์และทฤษฎีความน่าจะเป็นซึ่งกำหนดลักษณะการกระจายตัวของค่าหรือ ความน่าจะเป็น ตัวแปรสุ่ม- โดยทั่วไปจะแสดงเป็นค่าเฉลี่ยถ่วงน้ำหนักของพารามิเตอร์ที่เป็นไปได้ทั้งหมดของตัวแปรสุ่ม ใช้กันอย่างแพร่หลายในการวิเคราะห์ทางเทคนิค การวิจัย ชุดตัวเลข, การศึกษากระบวนการต่อเนื่องและระยะยาว เป็นสิ่งสำคัญในการประเมินความเสี่ยง ทำนายตัวบ่งชี้ราคาเมื่อทำการซื้อขายในตลาดการเงิน และใช้ในการพัฒนากลยุทธ์และวิธีการของกลยุทธ์การเล่นเกม ทฤษฎี การพนัน .

รุกฆาตรออยู่- นี้ค่าเฉลี่ยของตัวแปรสุ่ม การแจกแจง ความน่าจะเป็นตัวแปรสุ่มถือเป็นตัวแปรสุ่มในทฤษฎีความน่าจะเป็น

รุกฆาตที่รอคอยคือการวัดค่าเฉลี่ยของตัวแปรสุ่มในทฤษฎีความน่าจะเป็น รุกฆาตความคาดหวังของตัวแปรสุ่ม xแสดงโดย เอ็ม(เอ็กซ์).

ความคาดหวัง(ค่าเฉลี่ยประชากร) คือ

รุกฆาตที่รอคอยคือ

รุกฆาตที่รอคอยคือในทฤษฎีความน่าจะเป็น ค่าเฉลี่ยถ่วงน้ำหนักของค่าที่เป็นไปได้ทั้งหมดที่ตัวแปรสุ่มสามารถรับได้

รุกฆาตที่รอคอยคือผลรวมของผลคูณของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่มและความน่าจะเป็นของค่าเหล่านี้

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

รุกฆาตที่รอคอยคือประโยชน์โดยเฉลี่ยจากการตัดสินใจครั้งใดครั้งหนึ่ง โดยมีเงื่อนไขว่าการตัดสินใจดังกล่าวสามารถพิจารณาได้ภายในกรอบของทฤษฎีจำนวนมากและระยะทางไกล

รุกฆาตที่รอคอยคือในทฤษฎีการพนัน จำนวนเงินชนะที่นักเก็งกำไรสามารถรับหรือแพ้ได้โดยเฉลี่ยในการเดิมพันแต่ละครั้ง ในภาษาการพนัน นักเก็งกำไรบางครั้งเรียกว่า “ข้อได้เปรียบ” นักเก็งกำไร“ (หากเป็นผลบวกต่อนักเก็งกำไร) หรือ “เฮ้าส์เอจ” (หากเป็นผลลบต่อนักเก็งกำไร)

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

รุกฆาตที่รอคอยคือกำไรต่อการชนะคูณด้วยค่าเฉลี่ย กำไรลบขาดทุน คูณด้วยขาดทุนเฉลี่ย

ความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่มในทฤษฎีทางคณิตศาสตร์

หนึ่งในสิ่งสำคัญ ลักษณะเชิงตัวเลขตัวแปรสุ่มคือค่าที่คาดหวัง ให้เราแนะนำแนวคิดของระบบตัวแปรสุ่ม ลองพิจารณาชุดตัวแปรสุ่มที่เป็นผลลัพธ์ของการทดลองสุ่มเดียวกัน ถ้า เป็นหนึ่งในค่าที่เป็นไปได้ของระบบ เหตุการณ์จะสอดคล้องกับความน่าจะเป็นบางประการที่สอดคล้องกับสัจพจน์ของ Kolmogorov ฟังก์ชั่นที่กำหนดไว้สำหรับค่าที่เป็นไปได้ของตัวแปรสุ่มเรียกว่ากฎการแจกแจงร่วม ฟังก์ชั่นนี้ช่วยให้คุณคำนวณความน่าจะเป็นของเหตุการณ์ใด ๆ จาก โดยเฉพาะข้อต่อ กฎการแจกแจงของตัวแปรสุ่มและซึ่งรับค่าจากชุดและได้รับจากความน่าจะเป็น

คำว่า “เสื่อ.. ความคาดหวัง" ได้รับการแนะนำโดย Pierre Simon Marquis de Laplace (1795) และมาจากแนวคิดของ "มูลค่าที่คาดหวังของการชนะ" ซึ่งปรากฏครั้งแรกในศตวรรษที่ 17 ในทฤษฎีการพนันในงานของ Blaise Pascal และ Christiaan Huygens อย่างไรก็ตาม Pafnuty Lvovich Chebyshev (กลางศตวรรษที่ 19) เป็นผู้ให้ความเข้าใจทางทฤษฎีและการประเมินแนวคิดนี้อย่างสมบูรณ์เป็นครั้งแรก

กฎการแจกแจงของตัวแปรตัวเลขสุ่ม (ฟังก์ชันการแจกแจงและอนุกรมการแจกแจงหรือความหนาแน่นของความน่าจะเป็น) อธิบายพฤติกรรมของตัวแปรสุ่มได้อย่างสมบูรณ์ แต่ในปัญหาหลายประการ ก็เพียงพอที่จะทราบคุณลักษณะเชิงตัวเลขของปริมาณที่กำลังศึกษา (เช่น ค่าเฉลี่ยและความเบี่ยงเบนที่เป็นไปได้) เพื่อตอบคำถามที่ถูกตั้งไว้ คุณลักษณะเชิงตัวเลขหลักของตัวแปรสุ่ม ได้แก่ ค่าคาดหวัง ความแปรปรวน โหมด และค่ามัธยฐาน

ความคาดหวังของตัวแปรสุ่มแบบไม่ต่อเนื่องคือผลรวมของผลิตภัณฑ์ของค่าที่เป็นไปได้และความน่าจะเป็นที่สอดคล้องกัน บางครั้งก็สบถ ความคาดหวังเรียกว่าค่าเฉลี่ยถ่วงน้ำหนักเนื่องจากมีค่าประมาณเท่ากับค่าเฉลี่ยเลขคณิตของค่าที่สังเกตได้ของตัวแปรสุ่มที่ จำนวนมากการทดลอง จากคำจำกัดความของค่าคาดหวัง พบว่าค่าของมันต้องไม่น้อยกว่าค่าที่น้อยที่สุดที่เป็นไปได้ของตัวแปรสุ่ม และไม่มากกว่าค่าที่ใหญ่ที่สุด ค่าที่คาดหวังของตัวแปรสุ่มคือตัวแปรที่ไม่สุ่ม (ค่าคงที่)

การรุกฆาตรอเป็นเรื่องง่าย ความหมายทางกายภาพ: หากคุณวางมวลหน่วยบนเส้นตรง วางมวลจำนวนหนึ่งไว้ที่จุดใดจุดหนึ่ง (สำหรับการกระจายแบบไม่ต่อเนื่อง) หรือ "ทา" ด้วยความหนาแน่นที่แน่นอน (สำหรับการกระจายอย่างต่อเนื่องอย่างแน่นอน) จากนั้นจุดที่สอดคล้องกับความคาดหวัง จะเป็นพิกัดของ “จุดศูนย์ถ่วง” ของเส้นตรง

ค่าเฉลี่ยของตัวแปรสุ่มคือตัวเลขจำนวนหนึ่งซึ่งเสมือนเป็น "ค่าตัวแทน" และแทนที่ด้วยการคำนวณโดยประมาณโดยประมาณ เมื่อเราพูดว่า: “เวลาใช้งานหลอดไฟโดยเฉลี่ยคือ 100 ชั่วโมง” หรือ “จุดกระแทกโดยเฉลี่ยจะเลื่อนสัมพันธ์กับเป้าหมายไปทางขวา 2 ม.” เรากำลังระบุลักษณะตัวเลขที่แน่นอนของตัวแปรสุ่มที่อธิบายตำแหน่งของหลอดไฟ บนแกนตัวเลขเช่น "ลักษณะตำแหน่ง"

จากลักษณะของตำแหน่งในทฤษฎีความน่าจะเป็น บทบาทที่สำคัญเล่นค่าที่คาดหวังของตัวแปรสุ่ม ซึ่งบางครั้งเรียกว่าค่าเฉลี่ยของตัวแปรสุ่ม

พิจารณาตัวแปรสุ่ม เอ็กซ์มีค่าที่เป็นไปได้ x1, x2, …, xnด้วยความน่าจะเป็น p1, p2, …, พีเอ็น- เราจำเป็นต้องกำหนดลักษณะเฉพาะของตำแหน่งของค่าของตัวแปรสุ่มบนแกน abscissa ด้วยจำนวนหนึ่ง โดยคำนึงถึงว่าค่าเหล่านี้มีความน่าจะเป็นที่แตกต่างกัน เพื่อจุดประสงค์นี้ เป็นเรื่องปกติที่จะใช้สิ่งที่เรียกว่า "ค่าเฉลี่ยถ่วงน้ำหนัก" ของค่าต่างๆ ซีและแต่ละค่า xi ในระหว่างการหาค่าเฉลี่ยควรนำมาพิจารณาด้วย "น้ำหนัก" ตามสัดส่วนกับความน่าจะเป็นของค่านี้ ดังนั้นเราจะคำนวณค่าเฉลี่ยของตัวแปรสุ่ม เอ็กซ์ซึ่งเราแสดงถึง เอ็ม |เอ็กซ์|:

ค่าเฉลี่ยถ่วงน้ำหนักนี้เรียกว่าค่าคาดหวังของตัวแปรสุ่ม ดังนั้นเราจึงนำเสนอแนวคิดที่สำคัญที่สุดประการหนึ่งของทฤษฎีความน่าจะเป็น - แนวคิดทางคณิตศาสตร์ ความคาดหวัง เสื่อ. ความคาดหวังของตัวแปรสุ่มคือผลรวมของผลคูณของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่มและความน่าจะเป็นของค่าเหล่านี้

เสื่อ. กำลังรอตัวแปรสุ่ม เอ็กซ์เชื่อมต่อกันด้วยการพึ่งพาที่แปลกประหลาดกับค่าเฉลี่ยเลขคณิตของค่าที่สังเกตได้ของตัวแปรสุ่มในการทดลองจำนวนมาก การพึ่งพานี้เป็นประเภทเดียวกับการพึ่งพาระหว่างความถี่และความน่าจะเป็น กล่าวคือ ด้วยการทดลองจำนวนมาก ค่าเฉลี่ยเลขคณิตของค่าที่สังเกตได้ของตัวแปรสุ่มจะเข้าใกล้ (มาบรรจบกันในความน่าจะเป็น) กับคณิตศาสตร์ของมัน ซึ่งรอคอย. จากการมีความเชื่อมโยงระหว่างความถี่และความน่าจะเป็น เราสามารถสรุปได้ว่ามีความเชื่อมโยงที่คล้ายกันระหว่างค่าเฉลี่ยเลขคณิตกับความคาดหวังทางคณิตศาสตร์ อันที่จริงให้พิจารณาตัวแปรสุ่ม เอ็กซ์โดดเด่นด้วยชุดการจัดจำหน่าย:

ให้มันผลิตออกมา เอ็นการทดลองอิสระซึ่งในแต่ละอันมีค่า เอ็กซ์ยอมรับ ค่าเฉพาะ- สมมุติว่าค่านั้น x1ปรากฏขึ้น ม1ครั้ง คุณค่า x2ปรากฏขึ้น ตร.มครั้งหนึ่ง ในความหมายทั่วไป ซีปรากฏไมล์ครั้ง ให้เราคำนวณค่าเฉลี่ยเลขคณิตของค่าที่สังเกตได้ของค่า X ซึ่งตรงกันข้ามกับความคาดหวังทางคณิตศาสตร์ เอ็ม|เอ็กซ์|เราแสดงถึง ม*|X|:

ด้วยจำนวนการทดลองที่เพิ่มขึ้น เอ็นความถี่ ปี่จะเข้าใกล้ (มาบรรจบกันในความน่าจะเป็น) ความน่าจะเป็นที่สอดคล้องกัน ดังนั้นค่าเฉลี่ยเลขคณิตของค่าที่สังเกตได้ของตัวแปรสุ่ม เอ็ม|เอ็กซ์|เมื่อจำนวนการทดลองเพิ่มขึ้น มันจะเข้าใกล้ (มาบรรจบกันในความน่าจะเป็น) ให้เป็นค่าที่คาดหวัง การเชื่อมต่อที่กำหนดไว้ข้างต้นระหว่างค่าเฉลี่ยเลขคณิตและคณิตศาสตร์ ความคาดหวังคือเนื้อหาของกฎรูปแบบหนึ่งที่มีจำนวนมาก

เรารู้อยู่แล้วว่ากฎจำนวนมากทุกรูปแบบระบุถึงความจริงที่ว่าค่าเฉลี่ยบางค่ามีเสถียรภาพในการทดลองจำนวนมาก ที่นี่ เรากำลังพูดถึงเรื่องความเสถียรของค่าเฉลี่ยเลขคณิตจากการสังเกตหลายๆ ชุดที่มีปริมาณเท่ากัน ด้วยการทดลองจำนวนน้อย ค่าเฉลี่ยเลขคณิตของผลลัพธ์จะเป็นแบบสุ่ม ด้วยจำนวนการทดลองที่เพิ่มขึ้นอย่างเพียงพอ มันจะกลายเป็น "เกือบจะไม่สุ่ม" และเมื่อเสถียรแล้วจะเข้าใกล้ค่าคงที่ - mat ซึ่งรอคอย.

ความเสถียรของค่าเฉลี่ยจากการทดลองจำนวนมากสามารถตรวจสอบได้โดยง่ายจากการทดลอง ตัวอย่างเช่น เมื่อชั่งน้ำหนักร่างกายในห้องปฏิบัติการด้วยเครื่องชั่งที่แม่นยำ จากการชั่งน้ำหนัก เราก็จะได้ค่าใหม่ทุกครั้ง เพื่อลดข้อผิดพลาดในการสังเกต เราชั่งน้ำหนักร่างกายหลายครั้งและใช้ค่าเฉลี่ยเลขคณิตของค่าที่ได้รับ เป็นเรื่องง่ายที่จะเห็นว่าเมื่อจำนวนการทดลองเพิ่มขึ้น (การชั่งน้ำหนัก) ค่าเฉลี่ยเลขคณิตจะตอบสนองต่อการเพิ่มขึ้นนี้น้อยลงเรื่อยๆ และเมื่อมีการทดลองจำนวนมากเพียงพอ ในทางปฏิบัติก็หยุดการเปลี่ยนแปลง

ก็ควรสังเกตว่า ลักษณะที่สำคัญที่สุดตำแหน่งของตัวแปรสุ่ม - mat ความคาดหวัง - ไม่มีอยู่ในตัวแปรสุ่มทั้งหมด มันเป็นไปได้ที่จะสร้างตัวอย่างของตัวแปรสุ่มสำหรับเสื่อ ไม่มีความคาดหวังเนื่องจากผลรวมหรือปริพันธ์ที่สอดคล้องกันจะลู่ออก อย่างไรก็ตาม กรณีดังกล่าวไม่เป็นประโยชน์อย่างมากต่อการปฏิบัติ โดยทั่วไปแล้ว ตัวแปรสุ่มที่เราจัดการจะมีช่วงค่าที่เป็นไปได้ที่จำกัด และแน่นอนว่ามีความคาดหวังทางคณิตศาสตร์ด้วย

นอกเหนือจากคุณลักษณะที่สำคัญที่สุดของตำแหน่งของตัวแปรสุ่ม - ค่าคาดหวัง - ในทางปฏิบัติแล้ว บางครั้งมีการใช้คุณลักษณะอื่น ๆ ของตำแหน่ง โดยเฉพาะอย่างยิ่งโหมดและค่ามัธยฐานของตัวแปรสุ่ม

โหมดของตัวแปรสุ่มคือค่าที่เป็นไปได้มากที่สุด คำว่า "มูลค่าที่เป็นไปได้มากที่สุด" หากพูดอย่างเคร่งครัดใช้เฉพาะกับปริมาณที่ไม่ต่อเนื่องเท่านั้น สำหรับปริมาณต่อเนื่อง โหมดคือค่าที่ความหนาแน่นของความน่าจะเป็นสูงสุด ตัวเลขแสดงโหมดสำหรับตัวแปรสุ่มแบบไม่ต่อเนื่องและต่อเนื่องตามลำดับ

หากรูปหลายเหลี่ยมการกระจาย (เส้นโค้งการกระจาย) มีค่าสูงสุดมากกว่าหนึ่งค่า การแจกแจงจะเรียกว่า "หลายรูปแบบ"

บางครั้งมีการแจกแจงที่มีค่าต่ำสุดอยู่ตรงกลางมากกว่าค่าสูงสุด การแจกแจงดังกล่าวเรียกว่า "การต่อต้านกิริยา"

ใน กรณีทั่วไปโหมดและความคาดหวังคู่ของตัวแปรสุ่มไม่ตรงกัน ในกรณีพิเศษเมื่อการกระจายเป็นแบบสมมาตรและเป็นกิริยาช่วย (เช่น มีโหมด) และมีเสื่อ ความคาดหวังจึงเกิดขึ้นพร้อมกับโหมดและจุดศูนย์กลางสมมาตรของการแจกแจง

มักใช้คุณลักษณะตำแหน่งอื่น - สิ่งที่เรียกว่าค่ามัธยฐานของตัวแปรสุ่ม โดยทั่วไปคุณลักษณะนี้จะใช้เฉพาะกับตัวแปรสุ่มแบบต่อเนื่องเท่านั้น แม้ว่าจะสามารถกำหนดอย่างเป็นทางการสำหรับตัวแปรที่ไม่ต่อเนื่องก็ตาม ในเชิงเรขาคณิต ค่ามัธยฐานคือจุดขาดของจุดที่พื้นที่ล้อมรอบด้วยเส้นโค้งการกระจายถูกแบ่งออกเป็นครึ่งหนึ่ง

ในกรณีของการกระจายแบบโมดอลแบบสมมาตร ค่ามัธยฐานจะตรงกับเสื่อ ความคาดหวังและแฟชั่น

ค่าที่คาดหวังคือค่าเฉลี่ยของตัวแปรสุ่ม ซึ่งเป็นคุณลักษณะเชิงตัวเลขของการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม มากที่สุด ในลักษณะทั่วไปความคาดหวังรุกฆาตของตัวแปรสุ่ม เอ็กซ์(ญ)ถูกกำหนดให้เป็นอินทิกรัลของ Lebesgue ที่เกี่ยวข้องกับการวัดความน่าจะเป็น รในต้นฉบับ พื้นที่ความน่าจะเป็น:

เสื่อ. ความคาดหวังยังสามารถคำนวณได้จากอินทิกรัล Lebesgue ของ เอ็กซ์โดยการกระจายความน่าจะเป็น พิกเซลปริมาณ เอ็กซ์:

เป็นเรื่องปกติที่จะกำหนดแนวคิดของตัวแปรสุ่มด้วยความคาดหวังที่ไม่สิ้นสุด ตัวอย่างทั่วไปคือระยะเวลาในการส่งตัวกลับประเทศในการเดินสุ่มบางครั้ง

ด้วยความช่วยเหลือของเสื่อ ความคาดหวังถูกกำหนดโดยตัวเลขและ ลักษณะการทำงานการแจกแจง (เป็นการคาดหวังทางคณิตศาสตร์ของฟังก์ชันที่สอดคล้องกันจากตัวแปรสุ่ม) เช่น ฟังก์ชันการสร้าง ฟังก์ชันลักษณะเฉพาะ โมเมนต์ของลำดับใดๆ โดยเฉพาะการกระจายตัว ความแปรปรวนร่วม

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ความคาดหวังทางคณิตศาสตร์เป็นลักษณะของตำแหน่งของค่าของตัวแปรสุ่ม (ค่าเฉลี่ยของการแจกแจง) ในตำแหน่งนี้ ความคาดหวังทางคณิตศาสตร์ทำหน้าที่เป็นพารามิเตอร์การกระจาย "ทั่วไป" และบทบาทของมันจะคล้ายกับบทบาทของโมเมนต์คงที่ ซึ่งเป็นพิกัดของจุดศูนย์ถ่วงของการกระจายมวล ในกลศาสตร์ ความคาดหวังแตกต่างจากลักษณะตำแหน่งอื่น ๆ โดยมีการอธิบายการกระจายในแง่ทั่วไป - ค่ามัธยฐาน โหมด เสื่อ คุ้มค่ามากซึ่งมันและคุณลักษณะการกระเจิงที่สอดคล้องกัน - การกระจายตัว - มีอยู่ในทฤษฎีบทขีดจำกัดของทฤษฎีความน่าจะเป็น ความหมายของคู่รักที่คาดหวังนั้นได้รับการเปิดเผยอย่างเต็มที่โดยกฎแห่งจำนวนมาก (ความไม่เท่าเทียมกันของเชบีเชฟ) และกฎที่เข้มแข็งขึ้นของจำนวนมาก

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ความคาดหวังของตัวแปรสุ่มแบบไม่ต่อเนื่อง

ให้มีตัวแปรสุ่มบางตัวที่สามารถรับค่าตัวเลขได้หลายค่า (เช่น จำนวนแต้มเมื่อทอยลูกเต๋าอาจเป็น 1, 2, 3, 4, 5 หรือ 6) บ่อยครั้งในทางปฏิบัติสำหรับค่าดังกล่าวคำถามเกิดขึ้น: ต้องใช้ค่า "โดยเฉลี่ย" เท่าใดกับการทดสอบจำนวนมาก? รายได้เฉลี่ย (หรือขาดทุน) ของเราจากธุรกรรมที่มีความเสี่ยงแต่ละรายการจะเป็นเท่าใด

สมมติว่ามีลอตเตอรีบางชนิด เราต้องการเข้าใจว่าการเข้าร่วมจะทำกำไรหรือไม่ (หรือแม้กระทั่งเข้าร่วมซ้ำ ๆ เป็นประจำ) สมมติว่าตั๋วทุกใบที่สี่เป็นผู้ชนะ รางวัลจะเป็น 300 รูเบิล และตั๋วใดๆ จะเป็น 100 รูเบิล ด้วยจำนวนผู้เข้าร่วมที่มากมายไม่สิ้นสุด นี่คือสิ่งที่เกิดขึ้น เราจะแพ้ในสามในสี่ของกรณี ทุก ๆ การสูญเสียสามครั้งจะมีราคา 300 รูเบิล ในทุก ๆ สี่เราจะชนะ 200 รูเบิล (รางวัลหักค่าใช้จ่าย) นั่นคือสำหรับการมีส่วนร่วมสี่ครั้งเราเสียโดยเฉลี่ย 100 รูเบิลต่อหนึ่งครั้ง - โดยเฉลี่ย 25 ​​รูเบิล โดยรวมแล้วอัตราความเสียหายเฉลี่ยของเราจะอยู่ที่ 25 รูเบิลต่อตั๋ว

เราโยน ลูกเต๋า- ถ้าไม่โกง(ไม่เปลี่ยนจุดศูนย์ถ่วง ฯลฯ) แล้วเราจะได้คะแนนเฉลี่ยครั้งละกี่คะแนน? เนื่องจากแต่ละตัวเลือกมีโอกาสเท่ากัน เราจึงหาค่าเฉลี่ยเลขคณิตแล้วได้ 3.5 เนื่องจากนี่คือค่าเฉลี่ย จึงไม่จำเป็นต้องโกรธเคืองที่ไม่มีการหมุนรอบใดเป็นพิเศษจะให้ 3.5 แต้ม - ลูกบาศก์นี้ไม่มีหน้าที่มีตัวเลขเช่นนี้!

ตอนนี้เรามาสรุปตัวอย่างของเรา:

มาดูภาพที่เพิ่งให้มากัน ด้านซ้ายเป็นตารางการแจกแจงของตัวแปรสุ่ม ค่า X สามารถรับหนึ่งใน n ค่าที่เป็นไปได้ (แสดงในบรรทัดบนสุด) ไม่สามารถมีความหมายอื่นใดได้ ต่ำกว่าค่าที่เป็นไปได้แต่ละค่าคือความน่าจะเป็น ทางด้านขวาคือสูตร โดยที่ M(X) เรียกว่า mat ซึ่งรอคอย. ความหมายของค่านี้คือเมื่อมีการทดสอบจำนวนมาก (ด้วย ตัวอย่างขนาดใหญ่) ค่าเฉลี่ยจะมีแนวโน้มที่จะเป็นไปตามความคาดหวังเดียวกันนี้

กลับมาอีกครั้งกับการเล่นคิวบ์แบบเดิม เสื่อ. จำนวนคะแนนที่คาดหวังเมื่อขว้างคือ 3.5 (คำนวณด้วยตัวเองโดยใช้สูตรหากคุณไม่เชื่อฉัน) สมมติว่าคุณโยนมันสองสามครั้ง ผลลัพธ์คือ 4 และ 6 ค่าเฉลี่ยคือ 5 ซึ่งยังห่างไกลจาก 3.5 พวกเขาโยนมันอีกครั้ง ได้ 3 นั่นคือโดยเฉลี่ย (4 + 6 + 3)/3 = 4.3333... อยู่ไกลจากเสื่อมาก ความคาดหวัง ตอนนี้ทำการทดลองสุดมันส์ - หมุนลูกบาศก์ 1,000 ครั้ง! และถึงแม้ค่าเฉลี่ยจะไม่เท่ากับ 3.5 พอดีแต่ก็จะใกล้เคียงกัน

มาคำนวณเสื่อกัน กำลังรอลอตเตอรีที่อธิบายไว้ข้างต้น จานจะมีลักษณะดังนี้:

จากนั้นความคาดหวังรุกฆาตจะเป็นไปตามที่เรากำหนดไว้ข้างต้น:

อีกประการหนึ่งก็คือ การทำ "ด้วยมือ" โดยไม่มีสูตรคงเป็นเรื่องยากหากมีตัวเลือกมากกว่านี้ สมมติว่าจะมีตั๋วที่แพ้ 75% ตั๋วที่ชนะ 20% และ 5% โดยเฉพาะตั๋วที่ชนะ

ขณะนี้คุณสมบัติบางอย่างเป็นไปตามความคาดหวัง

เสื่อ. ความคาดหวังเป็นเส้นตรงง่ายที่จะพิสูจน์:

ตัวคูณคงที่สามารถนำออกไปเลยเครื่องหมายรุกฆาตได้ ความคาดหวังนั่นคือ:

นี่เป็นกรณีพิเศษของคุณสมบัติความเป็นเชิงเส้นของคู่คาดหวัง

ผลที่ตามมาอีกประการหนึ่งของความเป็นเส้นตรงของเสื่อ ความคาดหวัง:

นั่นคือเสื่อ ความคาดหวังของผลรวมของตัวแปรสุ่มเท่ากับผลรวมของความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่ม

ให้ X, Y เป็นตัวแปรสุ่มอิสระ, แล้ว:

นี่พิสูจน์ได้ง่ายเช่นกัน) การทำงาน เอ็กซ์วายตัวเองเป็นตัวแปรสุ่มและหากค่าเริ่มต้นสามารถรับได้ nและ มคุณค่าตามนั้นแล้ว เอ็กซ์วายสามารถรับค่า nm ได้ แต่ละค่าจะถูกคำนวณตามข้อเท็จจริงที่ว่าความน่าจะเป็นของเหตุการณ์อิสระจะถูกคูณ เป็นผลให้เราได้รับสิ่งนี้:

ความคาดหวังของตัวแปรสุ่มต่อเนื่อง

ตัวแปรสุ่มต่อเนื่องมีลักษณะเฉพาะเช่นความหนาแน่นของการแจกแจง (ความหนาแน่นของความน่าจะเป็น) โดยพื้นฐานแล้วจะระบุลักษณะสถานการณ์ที่ค่าบางค่าจากชุด ตัวเลขจริงตัวแปรสุ่มใช้เวลาบ่อยขึ้น บ้างก็น้อยลง ตัวอย่างเช่น ลองพิจารณากราฟนี้:

ที่นี่ เอ็กซ์- ตัวแปรสุ่มจริง ฉ(x)- ความหนาแน่นของการกระจาย ตัดสินโดย กำหนดการนี้ในระหว่างการทดลองค่า เอ็กซ์มักจะเป็นตัวเลขที่ใกล้ศูนย์ โอกาสมีเกิน 3 หรือจะเล็กลง -3 ค่อนข้างเป็นเชิงทฤษฎีล้วนๆ

หากทราบความหนาแน่นของการกระจาย ก็จะพบค่าที่คาดหวังได้ดังนี้:

สมมติว่ามีการกระจายแบบสม่ำเสมอ:

มาหารุกฆาตกันเถอะ ความคาดหวัง:

สิ่งนี้ค่อนข้างสอดคล้องกับความเข้าใจตามสัญชาตญาณ สมมติว่าถ้าเราได้รับจำนวนจริงสุ่มจำนวนมากที่มีการแจกแจงแบบสม่ำเสมอในแต่ละส่วน |0; 1| ดังนั้นค่าเฉลี่ยเลขคณิตควรอยู่ที่ประมาณ 0.5

คุณสมบัติของความคาดหวังทางคณิตศาสตร์ - ความเป็นเส้นตรง ฯลฯ ที่ใช้ได้กับตัวแปรสุ่มแบบไม่ต่อเนื่อง ก็สามารถใช้ได้ที่นี่เช่นกัน

ความสัมพันธ์ระหว่างความคาดหวังทางคณิตศาสตร์กับตัวชี้วัดทางสถิติอื่นๆ

ใน เชิงสถิติการวิเคราะห์พร้อมกับความคาดหวังทางคณิตศาสตร์ มีระบบตัวบ่งชี้ที่พึ่งพาซึ่งกันและกันซึ่งสะท้อนถึงความสม่ำเสมอของปรากฏการณ์และความมั่นคง กระบวนการ- ตัวบ่งชี้การเปลี่ยนแปลงมักไม่มีความหมายที่เป็นอิสระและใช้สำหรับการวิเคราะห์ข้อมูลเพิ่มเติม ข้อยกเว้นคือค่าสัมประสิทธิ์ของการแปรผันซึ่งเป็นลักษณะเฉพาะของความเป็นเนื้อเดียวกัน ข้อมูลสิ่งที่มีค่า เชิงสถิติลักษณะเฉพาะ

ระดับความแปรปรวนหรือความเสถียร กระบวนการในทางสถิติศาสตร์สามารถวัดได้โดยใช้ตัวชี้วัดหลายตัว

ตัวบ่งชี้ที่สำคัญที่สุดในการกำหนดลักษณะ ความแปรปรวนตัวแปรสุ่มคือ การกระจายตัวซึ่งมีความใกล้ชิดและเกี่ยวข้องโดยตรงกับเสื่อมากที่สุด ซึ่งรอคอย. พารามิเตอร์นี้ถูกใช้อย่างแข็งขันในการวิเคราะห์ทางสถิติประเภทอื่นๆ (การทดสอบสมมติฐาน การวิเคราะห์ความสัมพันธ์ระหว่างเหตุและผล ฯลฯ) เช่นเดียวกับค่าเบี่ยงเบนเชิงเส้นเฉลี่ย การกระจายตัวยังสะท้อนถึงการวัดการแพร่กระจายด้วย ข้อมูลรอบๆ ขนาดเฉลี่ย.

การแปลภาษาของสัญลักษณ์เป็นภาษาของคำจะเป็นประโยชน์ ปรากฎว่าความแปรปรวนคือ จัตุรัสกลางการเบี่ยงเบน นั่นคือคำนวณค่าเฉลี่ยก่อน จากนั้นนำความแตกต่างระหว่างมูลค่าดั้งเดิมและค่าเฉลี่ยแต่ละค่า ยกกำลังสอง บวก แล้วหารด้วยจำนวนค่าในประชากร ความแตกต่างระหว่างค่าแต่ละค่ากับค่าเฉลี่ยสะท้อนถึงการวัดความเบี่ยงเบน กำลังสองเพื่อให้การเบี่ยงเบนทั้งหมดกลายเป็นสิ่งเดียว ตัวเลขบวกและเพื่อหลีกเลี่ยงการทำลายล้างทางบวกและร่วมกัน การเบี่ยงเบนเชิงลบเมื่อสรุปแล้ว จากนั้น เมื่อพิจารณาค่าเบี่ยงเบนกำลังสอง เราก็เพียงคำนวณค่าเฉลี่ยเลขคณิต ค่าเฉลี่ย - สี่เหลี่ยม - ส่วนเบี่ยงเบน ส่วนเบี่ยงเบนจะถูกยกกำลังสองและคำนวณค่าเฉลี่ย คำตอบของคำว่า "การกระจายตัว" อันมหัศจรรย์นั้นมีเพียงสามคำเท่านั้น

อย่างไรก็ตามใน รูปแบบบริสุทธิ์เช่น ค่าเฉลี่ยเลขคณิต หรือ ไม่ใช้ความแปรปรวน ค่อนข้างเป็นตัวบ่งชี้เสริมและระดับกลางที่ใช้สำหรับการวิเคราะห์ทางสถิติประเภทอื่นๆ มันไม่มีหน่วยวัดปกติด้วยซ้ำ เมื่อพิจารณาจากสูตร นี่คือกำลังสองของหน่วยการวัดข้อมูลต้นฉบับ

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ให้เราวัดตัวแปรสุ่ม เอ็นเช่นเราวัดความเร็วลมสิบครั้งแล้วต้องการหาค่าเฉลี่ย ค่าเฉลี่ยเกี่ยวข้องกับฟังก์ชันการแจกแจงอย่างไร

หรือเราจะทอยลูกเต๋า จำนวนมากครั้งหนึ่ง. จำนวนแต้มที่จะปรากฏบนลูกเต๋าในการโยนแต่ละครั้งเป็นตัวแปรสุ่มและสามารถรับค่าธรรมชาติใดๆ ได้ตั้งแต่ 1 ถึง 6 ค่าเฉลี่ยเลขคณิตของแต้มที่หล่นซึ่งคำนวณสำหรับการโยนลูกเต๋าทั้งหมดก็เป็นตัวแปรสุ่มเช่นกัน แต่สำหรับขนาดใหญ่ เอ็นมันมีแนวโน้มที่จะเป็นตัวเลขที่เฉพาะเจาะจงมาก - รุกฆาต ซึ่งรอคอย ม- ใน ในกรณีนี้มx = 3.5

คุณได้รับคุณค่านี้มาได้อย่างไร? ให้เข้า เอ็นการทดสอบ n1เมื่อคุณได้รับ 1 แต้ม n2หนึ่งครั้ง - 2 คะแนนเป็นต้น จากนั้นจำนวนผลลัพธ์ที่จุดหนึ่งลดลง:

ในทำนองเดียวกันสำหรับผลลัพธ์เมื่อมีการทอยคะแนน 2, 3, 4, 5 และ 6

ตอนนี้ให้เราสมมติว่าเรารู้การแจกแจงของตัวแปรสุ่ม x นั่นคือเรารู้ว่าตัวแปรสุ่ม x รับค่า x1, x2,..., xk ด้วยความน่าจะเป็น p1, p2,..., pk .

ความคาดหวังทางคณิตศาสตร์ Mx ของตัวแปรสุ่ม x เท่ากับ:

ความคาดหวังทางคณิตศาสตร์ไม่ใช่การประมาณค่าตัวแปรสุ่มบางตัวที่สมเหตุสมผลเสมอไป ดังนั้นเพื่อประมาณค่าเฉลี่ย ค่าจ้างควรใช้แนวคิดเรื่องค่ามัธยฐานมากกว่า คือ ค่าที่จำนวนคนรับน้อยกว่าค่ามัธยฐาน เงินเดือนและใหญ่โตตรงกัน

ความน่าจะเป็น p1 ที่ตัวแปรสุ่ม x จะน้อยกว่า x1/2 และความน่าจะเป็น p2 ที่ตัวแปรสุ่ม x จะมากกว่า x1/2 จะเท่ากันและเท่ากับ 1/2 ค่ามัธยฐานไม่ได้ถูกกำหนดไว้โดยเฉพาะสำหรับการแจกแจงทั้งหมด

มาตรฐานหรือส่วนเบี่ยงเบนมาตรฐานในสถิติจะเรียกว่าระดับความเบี่ยงเบนของข้อมูลเชิงสังเกตหรือชุดจากค่า AVERAGE เขียนแทนด้วยตัวอักษร s หรือ s ค่าเบี่ยงเบนมาตรฐานเล็กน้อยบ่งชี้ว่ากลุ่มข้อมูลรอบๆ ค่าเฉลี่ย ในขณะที่ค่าเบี่ยงเบนมาตรฐานที่สูงบ่งชี้ว่าข้อมูลเริ่มต้นอยู่ห่างจากค่าเฉลี่ย ส่วนเบี่ยงเบนมาตรฐานเท่ากับ รากที่สองปริมาณที่เรียกว่าการกระจายตัว เป็นค่าเฉลี่ยของผลรวมของผลต่างกำลังสองของข้อมูลเริ่มต้นที่เบี่ยงเบนไปจากค่าเฉลี่ย ค่าเบี่ยงเบนมาตรฐานของตัวแปรสุ่มคือรากที่สองของความแปรปรวน:

ตัวอย่าง. ภายใต้เงื่อนไขการทดสอบเมื่อยิงไปที่เป้าหมาย ให้คำนวณการกระจายตัวและส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่ม:

การเปลี่ยนแปลง- ความผันผวน การเปลี่ยนแปลงของมูลค่าคุณลักษณะระหว่างหน่วยประชากร ค่าตัวเลขส่วนบุคคลของคุณลักษณะที่พบในประชากรที่กำลังศึกษาเรียกว่าค่าตัวแปร ค่าเฉลี่ยไม่เพียงพอสำหรับ คุณสมบัติครบถ้วนประชากรบังคับให้เราเสริมค่าเฉลี่ยด้วยตัวบ่งชี้ที่ช่วยให้เราสามารถประเมินความเป็นปกติของค่าเฉลี่ยเหล่านี้โดยการวัดความแปรปรวน (ความแปรปรวน) ของคุณลักษณะที่กำลังศึกษา ค่าสัมประสิทธิ์การเปลี่ยนแปลงคำนวณโดยใช้สูตร:

ช่วงของการเปลี่ยนแปลง(R) แสดงถึงความแตกต่างระหว่างค่าสูงสุดและต่ำสุดของคุณลักษณะในประชากรที่กำลังศึกษา ตัวบ่งชี้นี้ให้ประโยชน์สูงสุด ความคิดทั่วไปเกี่ยวกับความแปรปรวนของลักษณะที่ศึกษาตามที่แสดง ความแตกต่างระหว่างค่าสุดขีดของตัวเลือกเท่านั้น พึ่ง ค่าสุดขีดคุณลักษณะนี้ทำให้ขอบเขตของการเปลี่ยนแปลงมีอักขระสุ่มที่ไม่เสถียร

ค่าเบี่ยงเบนเชิงเส้นเฉลี่ยแสดงถึงค่าเฉลี่ยเลขคณิตของการเบี่ยงเบนสัมบูรณ์ (โมดูโล) ของค่าทั้งหมดของประชากรที่วิเคราะห์จากค่าเฉลี่ย:

ความคาดหวังทางคณิตศาสตร์ในทฤษฎีการพนัน

รุกฆาตที่รอคอยคือจำนวนเงินโดยเฉลี่ยที่นักเก็งกำไรการพนันสามารถชนะหรือแพ้ในการเดิมพันที่กำหนด นี่เป็นแนวคิดที่สำคัญมากสำหรับนักเก็งกำไรเนื่องจากเป็นพื้นฐานของการประเมินสถานการณ์การพนันส่วนใหญ่ รุกฆาตยังเป็นเครื่องมือที่เหมาะสมที่สุดสำหรับการวิเคราะห์รูปแบบการ์ดพื้นฐานและสถานการณ์การเล่นเกม

สมมติว่าคุณกำลังเล่นเกมเหรียญกับเพื่อน โดยเดิมพันเท่ากันที่ 1 ดอลลาร์ในแต่ละครั้ง ไม่ว่าจะเกิดอะไรขึ้นก็ตาม ก้อยหมายถึงคุณชนะ หัวที่คุณแพ้ อัตราต่อรองจะเป็นแบบหนึ่งต่อหนึ่ง ดังนั้นคุณเดิมพัน $1 ถึง $1 ดังนั้นความคาดหวังรุกฆาตของคุณจึงเท่ากับศูนย์เพราะว่า จากมุมมองทางคณิตศาสตร์ คุณไม่สามารถรู้ได้ว่าคุณจะขึ้นนำหรือแพ้หลังจากโยนสองครั้งหรือหลังจาก 200 ครั้ง

กำไรรายชั่วโมงของคุณเป็นศูนย์ เงินรางวัลรายชั่วโมงคือจำนวนเงินที่คุณคาดว่าจะชนะในหนึ่งชั่วโมง คุณสามารถโยนเหรียญได้ 500 ครั้งในหนึ่งชั่วโมง แต่คุณจะไม่ชนะหรือแพ้เพราะ... โอกาสของคุณไม่ใช่ทั้งบวกและลบ จากมุมมองของนักเก็งกำไรที่จริงจัง ระบบการเดิมพันนี้ไม่เลว แต่นี่เป็นเพียงการเสียเวลา

แต่สมมติว่ามีคนต้องการเดิมพัน $2 ต่อ $1 ของคุณในเกมเดียวกัน จากนั้นคุณจะมีความคาดหวังเป็นบวก 50 เซ็นต์จากการเดิมพันแต่ละครั้งทันที ทำไมต้อง 50 เซนต์- โดยเฉลี่ยแล้ว คุณจะชนะเดิมพันหนึ่งครั้งและแพ้ครั้งที่สอง เดิมพันก่อนแล้วคุณจะเสียเงิน 1 ดอลลาร์ เดิมพันครั้งที่สองแล้วคุณจะชนะ 2 ดอลลาร์ คุณเดิมพัน $1 สองครั้งและนำหน้า $1 ดังนั้นการเดิมพันหนึ่งดอลลาร์แต่ละครั้งของคุณจะทำให้คุณได้รับ 50 เซนต์.

หากเหรียญปรากฏ 500 ครั้งในหนึ่งชั่วโมง เงินรางวัลรายชั่วโมงของคุณจะอยู่ที่ 250 ดอลลาร์แล้ว เพราะ... โดยเฉลี่ยแล้วคุณสูญเสียไปหนึ่งอัน ดอลลาร์ 250 ครั้งและชนะสองครั้ง ดอลลาร์ 250 ครั้ง $500 ลบ $250 เท่ากับ $250 ซึ่งเป็นเงินรางวัลทั้งหมด โปรดทราบว่ามูลค่าที่คาดหวังซึ่งเป็นจำนวนเงินโดยเฉลี่ยที่คุณชนะต่อการเดิมพันคือ 50 เซ็นต์ คุณได้รับรางวัล $250 จากการเดิมพันหนึ่งดอลลาร์ 500 ครั้ง ซึ่งเท่ากับ 50 เซ็นต์ต่อการเดิมพัน

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

เสื่อ. การรอคอยไม่เกี่ยวอะไรกับผลลัพธ์ระยะสั้น คู่ต่อสู้ของคุณที่ตัดสินใจเดิมพัน 2 ดอลลาร์ต่อคุณ สามารถเอาชนะคุณได้ใน 10 ม้วนแรกติดต่อกัน แต่คุณมีความได้เปรียบในการเดิมพัน 2 ต่อ 1 สิ่งอื่นๆ ที่เท่าเทียมกัน จะได้รับ 50 เซ็นต์จากทุกๆ การเดิมพัน 1 ดอลลาร์ในสกุลเงินใดก็ได้ สถานการณ์. ไม่สำคัญว่าคุณจะชนะหรือแพ้เดิมพันหนึ่งรายการหรือหลายรายการ ตราบใดที่คุณมีเงินสดเพียงพอที่จะครอบคลุมค่าใช้จ่ายได้อย่างสบายๆ หากคุณยังคงเดิมพันในลักษณะเดิม เมื่อเวลาผ่านไป เงินรางวัลของคุณจะเข้าใกล้ผลรวมของความคาดหวังในการโยนแต่ละครั้ง

ทุกครั้งที่คุณวางเดิมพันที่ดีที่สุด (เดิมพันที่อาจกลายเป็นผลกำไรในระยะยาว) เมื่ออัตราต่อรองเข้าข้างคุณ คุณจะต้องชนะบางสิ่งจากสิ่งนั้น ไม่ว่าคุณจะแพ้หรือไม่ก็ตาม ให้มือ ในทางกลับกัน หากคุณเดิมพันฝ่ายรอง (การเดิมพันที่ไม่ได้ผลกำไรในระยะยาว) เมื่ออัตราต่อรองขัดแย้งกับคุณ คุณจะสูญเสียบางสิ่งไม่ว่าคุณจะชนะหรือแพ้ในมือก็ตาม

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

คุณวางเดิมพันด้วยผลลัพธ์ที่ดีที่สุดหากความคาดหวังของคุณเป็นบวก และจะเป็นเชิงบวกหากอัตราต่อรองอยู่ฝั่งคุณ เมื่อคุณวางเดิมพันด้วยผลลัพธ์ที่แย่ที่สุด คุณจะมีความคาดหวังเชิงลบ ซึ่งเกิดขึ้นเมื่ออัตราต่อรองขัดแย้งกับคุณ นักเก็งกำไรที่จริงจังจะเดิมพันเฉพาะผลลัพธ์ที่ดีที่สุดเท่านั้น หากเกิดเหตุการณ์เลวร้ายที่สุด พวกเขาก็จะพับ อัตราต่อรองหมายถึงอะไรในความโปรดปรานของคุณ? คุณอาจจบลงด้วยการชนะมากกว่าราคาต่อรองที่แท้จริง อัตราต่อรองที่แท้จริงของการลงจอดคือ 1 ต่อ 1 แต่คุณจะได้ 2 ต่อ 1 เนื่องจากอัตราส่วนอัตราต่อรอง ในกรณีนี้ อัตราต่อรองจะเข้าข้างคุณ คุณจะได้รับผลลัพธ์ที่ดีที่สุดอย่างแน่นอนโดยคาดหวังบวก 50 เซ็นต์ต่อการเดิมพัน

นี่คือตัวอย่างเสื่อที่ซับซ้อนมากขึ้น ความคาดหวัง เพื่อนเขียนตัวเลขตั้งแต่หนึ่งถึงห้าและเดิมพัน $5 กับ $1 ของคุณโดยที่คุณจะไม่เดาตัวเลขนั้น คุณควรยอมรับการเดิมพันดังกล่าวหรือไม่? คาดหวังอะไรที่นี่?

โดยเฉลี่ยแล้วคุณจะผิดสี่ครั้ง จากข้อมูลนี้ อัตราต่อรองที่คุณทายหมายเลขคือ 4 ต่อ 1 อัตราต่อรองที่คุณจะเสียเงินหนึ่งดอลลาร์ในครั้งเดียว อย่างไรก็ตาม คุณชนะ 5 ต่อ 1 โดยมีความเป็นไปได้ที่จะแพ้ 4 ต่อ 1 ดังนั้นอัตราต่อรองจึงเข้าข้างคุณ คุณสามารถเดิมพันและหวังว่าจะได้ผลลัพธ์ที่ดีที่สุด หากคุณทำการเดิมพันนี้ห้าครั้ง โดยเฉลี่ยคุณจะเสียเงิน $1 สี่ครั้งและชนะ $5 หนึ่งครั้ง ตามนี้ สำหรับความพยายามทั้งห้าครั้ง คุณจะได้รับ $1 โดยมีความคาดหวังทางคณิตศาสตร์เป็นบวกที่ 20 เซ็นต์ต่อการเดิมพัน

นักเก็งกำไรที่คาดหวังที่จะชนะมากกว่าที่เขาเดิมพัน ดังตัวอย่างข้างต้นกำลังเสี่ยง ในทางตรงกันข้าม เขาทำลายโอกาสเมื่อเขาคาดหวังว่าจะชนะน้อยกว่าที่เขาเดิมพัน นักเก็งกำไรที่วางเดิมพันอาจมีความคาดหวังเชิงบวกหรือเชิงลบก็ได้ ซึ่งขึ้นอยู่กับว่าเขาชนะหรือทำลายอัตราต่อรอง

หากคุณเดิมพัน $50 เพื่อชนะ $10 โดยมีโอกาสชนะ 4 ต่อ 1 คุณจะได้รับความคาดหวังติดลบที่ $2 เพราะ โดยเฉลี่ยแล้ว คุณจะชนะรางวัล $10 สี่ครั้งและเสียเงิน $50 หนึ่งครั้ง ซึ่งแสดงว่าการเสียต่อการเดิมพันจะเป็น $10 แต่ถ้าคุณเดิมพัน $30 เพื่อชนะ $10 โดยมีอัตราต่อรองเท่ากันในการชนะ 4 ต่อ 1 ในกรณีนี้ คุณจะมีความคาดหวังเป็นบวกที่ $2 เพราะ คุณชนะอีกครั้งสี่เท่า $10 และเสียครั้งเดียว $30 ซึ่งก็คือ กำไรราคา 10 ดอลลาร์ ตัวอย่างเหล่านี้แสดงให้เห็นว่าการเดิมพันครั้งแรกนั้นไม่ดี และการเดิมพันครั้งที่สองนั้นดี

เสื่อ. ความคาดหวังเป็นศูนย์กลางของทุกสถานการณ์ในเกม เมื่อเจ้ามือรับแทงสนับสนุนให้แฟนฟุตบอลเดิมพัน 11 ดอลลาร์เพื่อรับรางวัล 10 ดอลลาร์ เขามีความคาดหวังเชิงบวกอยู่ที่ 50 เซ็นต์ทุกๆ 10 ดอลลาร์ หากคาสิโนจ่ายเงินเท่ากันจากพาสไลน์ ความคาดหวังเชิงบวกของคาสิโนจะอยู่ที่ประมาณ 1.40 ดอลลาร์ต่อทุกๆ 100 ดอลลาร์ เนื่องจาก เกมนี้ได้รับการออกแบบเพื่อให้ใครก็ตามที่เดิมพันในไลน์นี้จะสูญเสียโดยเฉลี่ย 50.7% และชนะ 49.3% ของเวลาทั้งหมด ไม่ต้องสงสัยเลยว่าความคาดหวังเชิงบวกเพียงเล็กน้อยที่ดูเหมือนจะนำผลกำไรมหาศาลมาสู่เจ้าของคาสิโนทั่วโลก ดังที่ Bob Stupak เจ้าของคาสิโน Vegas World กล่าวไว้ว่า “หนึ่งในพัน” เปอร์เซ็นต์ความน่าจะเป็นเชิงลบในระยะทางที่ยาวพอจะทำลายคนที่รวยที่สุดในโลก”

ความคาดหวังเมื่อเล่นโป๊กเกอร์

เกมโป๊กเกอร์เป็นตัวอย่างที่มีภาพประกอบและชัดเจนที่สุดจากมุมมองของการใช้ทฤษฎีและคุณสมบัติของคู่รักที่คาดหวัง

เสื่อ. มูลค่าที่คาดหวังในโป๊กเกอร์คือผลประโยชน์โดยเฉลี่ยจากการตัดสินใจครั้งใดครั้งหนึ่ง โดยมีเงื่อนไขว่าการตัดสินใจดังกล่าวสามารถพิจารณาได้ภายในกรอบของทฤษฎีตัวเลขจำนวนมากและระยะทางไกล เกมโป๊กเกอร์ที่ประสบความสำเร็จคือการยอมรับการเคลื่อนไหวโดยมีมูลค่าที่คาดหวังเป็นบวกเสมอ

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ความหมายทางคณิตศาสตร์ของคณิตศาสตร์ ความคาดหวังในการเล่นโป๊กเกอร์คือเรามักจะเจอตัวแปรสุ่มเมื่อทำการตัดสินใจ (เราไม่รู้แน่ชัดว่าฝ่ายตรงข้ามมีไพ่ใบไหนอยู่ในมือ ไพ่ใบใดที่จะมาในรอบต่อๆ ไป ซื้อขาย- เราต้องพิจารณาแต่ละคำตอบจากมุมมองของทฤษฎีจำนวนมาก ซึ่งระบุว่าเมื่อมีตัวอย่างจำนวนมากเพียงพอ ค่าเฉลี่ยของตัวแปรสุ่มจะมีแนวโน้มเป็นค่าที่คาดไว้

ในบรรดาสูตรเฉพาะสำหรับการคำนวณความคาดหวังของคู่ครอง สิ่งต่อไปนี้ใช้ได้กับโป๊กเกอร์มากที่สุด:

เมื่อเล่นโป๊กเกอร์รุกฆาต ความคาดหวังสามารถคำนวณได้ทั้งการเดิมพันและการโทร ในกรณีแรก ควรคำนึงถึงสัดส่วนการพับ ส่วนประการที่สองคืออัตราต่อรองของธนาคาร เมื่อประเมินเสื่อ ความคาดหวังของการเคลื่อนไหวใดการเคลื่อนไหวหนึ่ง ควรจำไว้ว่าการพับมักจะไม่มีความคาดหวังเสมอ ดังนั้นการทิ้งไพ่จะเป็นการตัดสินใจที่ให้ผลกำไรมากกว่าการเคลื่อนไหวเชิงลบใดๆ เสมอ

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ความคาดหวังจะบอกคุณถึงสิ่งที่คุณคาดหวัง (หรือการสูญเสีย) สำหรับทุกความเสี่ยงที่คุณได้รับ คาสิโนทำเงิน เงินเนื่องจากการรุกฆาตเป็นความคาดหวังจากทุกเกมที่มีการฝึกฝนในนั้นเพื่อประโยชน์ของคาสิโน ด้วยซีรีย์เกมที่ยาวเพียงพอ คุณสามารถคาดหวังได้ว่าลูกค้าจะสูญเสียเกมของเขาไป เงินเนื่องจาก “อัตราต่อรอง” อยู่ในความโปรดปรานของคาสิโน อย่างไรก็ตาม นักเก็งกำไรคาสิโนมืออาชีพจำกัดเกมของพวกเขาให้อยู่ในช่วงเวลาสั้น ๆ ซึ่งจะเป็นการเพิ่มโอกาสที่พวกเขาจะได้เปรียบ เช่นเดียวกับการลงทุน หากความคาดหวังของคุณเป็นไปในทางบวก คุณสามารถทำเงินได้มากขึ้นด้วยการเทรดหลายครั้งในเวลาอันสั้น ระยะเวลาเวลา. ความคาดหวังคือเปอร์เซ็นต์ของกำไรต่อการชนะคูณด้วยกำไรเฉลี่ย ลบความน่าจะเป็นที่จะสูญเสียคูณด้วยการสูญเสียโดยเฉลี่ย

โป๊กเกอร์ยังสามารถดูได้จากมุมมองของความคาดหวังในการรุกฆาต คุณอาจคิดว่าการเคลื่อนไหวบางอย่างมีกำไร แต่ในบางกรณี อาจไม่ดีที่สุดเพราะการเคลื่อนไหวอื่นทำกำไรได้มากกว่า สมมติว่าคุณตีเต็มบ้านในโป๊กเกอร์แบบจั่วไพ่ห้าใบ คู่ต่อสู้ของคุณทำการเดิมพัน คุณรู้ว่าถ้าคุณเพิ่มเดิมพัน เขาจะตอบสนอง ดังนั้นการเลี้ยงดูจึงเป็นกลยุทธ์ที่ดีที่สุด แต่ถ้าคุณเพิ่มเดิมพัน นักเก็งกำไรสองคนที่เหลือจะพับอย่างแน่นอน แต่ถ้าคุณโทรมาคุณก็มั่นใจเต็มที่ว่านักเก็งกำไรอีกสองคนหลังจากนั้นจะทำเช่นเดียวกัน เมื่อคุณเพิ่มเดิมพันคุณจะได้รับหนึ่งหน่วย และเมื่อคุณโทรหาคุณจะได้รับสองหน่วย ดังนั้นการโทรจะทำให้คุณได้รับความคาดหวังเชิงบวกที่สูงกว่าและจะเป็นกลยุทธ์ที่ดีที่สุด

เสื่อ. ความคาดหวังยังสามารถให้แนวคิดว่ากลยุทธ์โป๊กเกอร์แบบใดทำกำไรได้น้อยกว่าและกลยุทธ์ใดทำกำไรได้มากกว่า ตัวอย่างเช่น หากคุณเล่นมือใดมือหนึ่งและคุณคิดว่าการสูญเสียจะเฉลี่ย 75 เซ็นต์รวมแอนเต้ด้วย คุณควรเล่นมือนั้นเพราะว่า สิ่งนี้ดีกว่าการพับเมื่อ ante อยู่ที่ 1 ดอลลาร์

อื่น เหตุผลสำคัญเพื่อเข้าใจแก่นแท้ของเสื่อ ความคาดหวังคือมันให้ความรู้สึกสงบไม่ว่าคุณจะชนะการเดิมพันหรือไม่: หากคุณวางเดิมพันได้ดีหรือหมอบในเวลาที่เหมาะสม คุณจะรู้ว่าคุณได้รับหรือประหยัดเงินจำนวนหนึ่งซึ่งนักเก็งกำไรที่อ่อนแอกว่าไม่สามารถทำได้ บันทึก. การหมอบจะยากกว่ามากหากคุณอารมณ์เสียเพราะคู่ต่อสู้ดึงมือที่แข็งแกร่งกว่า ด้วยเหตุนี้ สิ่งที่คุณประหยัดได้จากการไม่เล่น แทนที่จะเดิมพัน จะถูกเพิ่มเข้าไปในเงินรางวัลของคุณต่อคืนหรือต่อเดือน

เพียงจำไว้ว่าหากคุณเปลี่ยนมือ คู่ต่อสู้จะโทรหาคุณ และดังที่คุณจะเห็นในบทความทฤษฎีบทพื้นฐานของโป๊กเกอร์ นี่เป็นเพียงหนึ่งในข้อดีของคุณ คุณควรจะมีความสุขเมื่อสิ่งนี้เกิดขึ้น คุณอาจเรียนรู้ที่จะสนุกกับการสูญเสียมือเพราะคุณรู้ว่านักเก็งกำไรคนอื่นๆ ในตำแหน่งของคุณจะสูญเสียมากกว่านั้นมาก

ตามที่กล่าวไว้ในตัวอย่างเกมหยอดเหรียญในตอนต้น อัตรากำไรรายชั่วโมงจะเชื่อมโยงกับความคาดหวังของเสื่อ และ แนวคิดนี้สำคัญอย่างยิ่งสำหรับนักเก็งกำไรมืออาชีพ เมื่อคุณไปเล่นโป๊กเกอร์ คุณควรประเมินในใจว่าคุณสามารถชนะได้มากแค่ไหนในการเล่นหนึ่งชั่วโมง ในกรณีส่วนใหญ่คุณจะต้องพึ่งพาสัญชาตญาณและประสบการณ์ของคุณ แต่คุณสามารถใช้คณิตศาสตร์ได้เช่นกัน ตัวอย่างเช่น คุณกำลังเล่น Draw Lowball และคุณเห็นผู้เล่นสามคนเดิมพัน $10 แล้วแลกไพ่สองใบ ซึ่งเป็นกลยุทธ์ที่แย่มาก คุณสามารถคิดได้ว่าทุกครั้งที่พวกเขาเดิมพัน $10 พวกเขาเสียเงินประมาณ $2 แต่ละคนทำสิ่งนี้แปดครั้งต่อชั่วโมง ซึ่งหมายความว่าทั้งสามคนเสียเงินประมาณ $48 ต่อชั่วโมง คุณเป็นหนึ่งในสี่นักเก็งกำไรที่เหลือ ซึ่งมีมูลค่าเท่ากัน ดังนั้นนักเก็งกำไรสี่คนนี้ (และคุณในนั้นด้วย) จะต้องแบ่งเงิน $48 โดยแต่ละคนทำกำไรได้ $12 ต่อชั่วโมง อัตราต่อรองรายชั่วโมงของคุณในกรณีนี้จะเท่ากับส่วนแบ่งของจำนวนเงินที่สูญเสียไปโดยนักเก็งกำไรที่ไม่ดีสามคนในหนึ่งชั่วโมง

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ในช่วงเวลาที่ยาวนาน เงินรางวัลรวมของนักเก็งกำไรคือผลรวมของความคาดหวังทางคณิตศาสตร์ของเขาในแต่ละมือ ยิ่งคุณเล่นหลายมือด้วยความคาดหวังเชิงบวก คุณก็จะยิ่งชนะมากขึ้น และในทางกลับกัน ยิ่งคุณเล่นด้วยความคาดหวังเชิงลบมากเท่าไร คุณก็ยิ่งสูญเสียมากขึ้นเท่านั้น ด้วยเหตุนี้ คุณควรเลือกเกมที่สามารถเพิ่มความคาดหวังเชิงบวกของคุณให้สูงสุด หรือลบล้างความคาดหวังเชิงลบของคุณ เพื่อให้คุณสามารถเพิ่มเงินรางวัลรายชั่วโมงได้สูงสุด

ความคาดหวังทางคณิตศาสตร์เชิงบวกในกลยุทธ์การเล่นเกม

หากคุณรู้วิธีนับไพ่ คุณสามารถได้เปรียบเหนือคาสิโน ตราบใดที่พวกเขาไม่สังเกตเห็นและโยนคุณออกไป คาสิโนชอบนักเก็งกำไรขี้เมาและทนการนับไพ่ไม่ได้ ข้อได้เปรียบจะทำให้คุณได้รับชัยชนะเมื่อเวลาผ่านไป จำนวนที่มากขึ้นครั้งกว่าจะสูญเสีย การบริหารจัดการที่ดีเงินทุนเมื่อใช้การคำนวณเสื่อรอสามารถช่วยให้คุณดึงกำไรมากขึ้นจากความได้เปรียบของคุณและลดการสูญเสีย ถ้าไม่มีข้อได้เปรียบ คุณก็บริจาคเงินให้การกุศลดีกว่า ในเกมในตลาดหลักทรัพย์ ระบบเกมจะมอบข้อได้เปรียบที่สร้างผลกำไรมากกว่าการขาดทุน ซึ่งก็คือความแตกต่าง ราคาและค่าคอมมิชชั่น ไม่มี การจัดการเงินจะไม่บันทึกระบบเกมที่ไม่ดี

ความคาดหวังเชิงบวกถูกกำหนดให้เป็นค่าที่มากกว่าศูนย์ ยิ่งตัวเลขนี้สูงเท่าไรก็ยิ่งแข็งแกร่งเท่านั้น ความคาดหวังทางสถิติ- หากค่าน้อยกว่าศูนย์ก็รุกฆาต ความคาดหวังก็จะเป็นลบเช่นกัน ยิ่งโมดูลมีขนาดใหญ่เท่าไร ค่าลบ, เหล่านั้น สถานการณ์ที่เลวร้ายยิ่ง- หากผลลัพธ์เป็นศูนย์ แสดงว่าการรอนั้นถึงจุดคุ้มทุน คุณสามารถชนะได้ก็ต่อเมื่อคุณมีความคาดหวังทางคณิตศาสตร์เชิงบวก และระบบการเล่นที่สมเหตุสมผล การเล่นโดยสัญชาตญาณนำไปสู่ความหายนะ

ความคาดหวังทางคณิตศาสตร์และ

ความคาดหวังรุกฆาตเป็นตัวบ่งชี้ทางสถิติที่เป็นที่ต้องการอย่างกว้างขวางและได้รับความนิยมเมื่อดำเนินการซื้อขายแลกเปลี่ยนทางการเงิน ตลาด- ประการแรก พารามิเตอร์นี้ใช้เพื่อวิเคราะห์ความสำเร็จของ ซื้อขาย- เดาได้ไม่ยากว่ามากขึ้น มูลค่าที่กำหนดยิ่งมีเหตุผลมากขึ้นในการพิจารณาการค้าที่กำลังศึกษาให้ประสบความสำเร็จ แน่นอนว่าการวิเคราะห์ งานเทรดเดอร์ไม่สามารถทำได้โดยใช้พารามิเตอร์นี้เท่านั้น อย่างไรก็ตามค่าที่คำนวณได้ร่วมกับวิธีการประเมินคุณภาพแบบอื่น งานสามารถปรับปรุงความแม่นยำของการวิเคราะห์ได้อย่างมาก

ความคาดหวังรุกฆาตมักถูกคำนวณในบริการติดตามบัญชีซื้อขาย ซึ่งช่วยให้คุณประเมินงานที่ทำกับเงินฝากได้อย่างรวดเร็ว ข้อยกเว้นรวมถึงกลยุทธ์ที่ใช้ "นั่งข้างนอก" การซื้อขายที่ไม่ได้ผลกำไร เทรดเดอร์โชคอาจมากับเขาระยะหนึ่ง ดังนั้น งานของเขาอาจไม่เสียหายเลย ในกรณีนี้ การคาดการณ์ทางคณิตศาสตร์เพียงอย่างเดียวจะไม่สามารถชี้นำได้ เนื่องจากความเสี่ยงที่ใช้ในงานจะไม่ถูกนำมาพิจารณา

ในการซื้อขาย ตลาดการรุกฆาตมักใช้เมื่อทำนายความสามารถในการทำกำไรของกลยุทธ์การซื้อขายใดๆ หรือเมื่อคาดการณ์รายได้ พ่อค้าจากข้อมูลทางสถิติจากครั้งก่อนของเขา การเสนอราคา.

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ในส่วนที่เกี่ยวข้องกับการจัดการเงิน สิ่งสำคัญมากคือต้องเข้าใจว่าไม่มีรูปแบบใดในการซื้อขายโดยมีความคาดหวังเชิงลบ การจัดการเงินซึ่งสามารถนำมาซึ่งผลกำไรสูงอย่างแน่นอน ถ้าจะเล่นต่อ ตลาดหลักทรัพย์ภายใต้เงื่อนไขเหล่านี้ ไม่ว่าจะด้วยวิธีใดก็ตาม การจัดการเงิน คุณจะสูญเสียบัญชีของคุณทั้งหมดไม่ว่าในตอนแรกจะมีขนาดใหญ่แค่ไหนก็ตาม

สัจพจน์นี้เป็นจริงไม่เพียงแต่สำหรับเกมหรือการเทรดที่มีความคาดหวังเชิงลบเท่านั้น แต่ยังเป็นจริงสำหรับเกมที่มีโอกาสเท่ากันอีกด้วย ดังนั้น ครั้งเดียวที่คุณมีโอกาสทำกำไรในระยะยาวคือการทำการซื้อขายโดยมีมูลค่าที่คาดหวังเป็นบวก

ความแตกต่างระหว่างความคาดหวังเชิงลบและความคาดหวังเชิงบวกคือความแตกต่างระหว่างชีวิตและความตาย ไม่สำคัญว่าความคาดหวังจะเป็นบวกหรือลบเพียงใด สิ่งสำคัญคือไม่ว่าจะเป็นบวกหรือลบ ดังนั้นก่อนที่จะพิจารณาประเด็นด้านการจัดการ เมืองหลวงคุณต้องค้นหาเกมที่มีความคาดหวังเชิงบวก

หากคุณไม่มีเกมดังกล่าว การจัดการเงินทั้งหมดในโลกจะไม่ช่วยคุณ ในทางกลับกัน หากคุณมีความคาดหวังเชิงบวก คุณสามารถเปลี่ยนมันให้เป็นฟังก์ชันการเติบโตแบบทวีคูณผ่านการจัดการเงินที่เหมาะสมได้ ความคาดหวังเชิงบวกจะน้อยแค่ไหนไม่สำคัญ! กล่าวอีกนัยหนึ่ง ไม่สำคัญว่าระบบการซื้อขายจะทำกำไรได้มากเพียงใดตามสัญญาเดียว หากคุณมีระบบที่ชนะรางวัล $10 ต่อสัญญาต่อการซื้อขาย (หลังจากค่าคอมมิชชั่นและสลิปเพจ) คุณสามารถใช้เทคนิคการจัดการได้ เมืองหลวงในลักษณะที่ทำให้ทำกำไรได้มากกว่าระบบที่แสดงกำไรเฉลี่ย $1,000 ต่อการเทรด (หลังจากค่าคอมมิชชั่นและสลิปเพจ)

สิ่งที่สำคัญไม่ใช่ว่าระบบจะทำกำไรได้แค่ไหน แต่สำคัญแค่ไหนที่ระบบสามารถพูดได้ว่าจะแสดงผลกำไรขั้นต่ำเป็นอย่างน้อยในอนาคต ดังนั้นการเตรียมการที่สำคัญที่สุดที่สามารถทำได้คือต้องแน่ใจว่าระบบจะแสดงค่าคาดหวังที่เป็นบวกในอนาคต

เพื่อให้มีค่าคาดหวังที่เป็นบวกในอนาคต สิ่งสำคัญมากคือการไม่จำกัดระดับความเป็นอิสระของระบบของคุณ ซึ่งสามารถทำได้ไม่เพียงแต่โดยการกำจัดหรือลดจำนวนพารามิเตอร์ที่จะปรับให้เหมาะสมเท่านั้น แต่ยังโดยการลดให้มากที่สุดเท่าที่เป็นไปได้ด้วย มากกว่ากฎของระบบ ทุกพารามิเตอร์ที่คุณเพิ่ม ทุกกฎที่คุณทำ ทุกการเปลี่ยนแปลงเล็กๆ น้อยๆ ที่คุณทำกับระบบจะลดจำนวนระดับความเป็นอิสระ เป็นการดีที่คุณจะต้องสร้างแบบที่ค่อนข้างดั้งเดิมและ ระบบที่เรียบง่ายซึ่งจะสร้างผลกำไรเล็กๆ น้อยๆ อย่างต่อเนื่องในเกือบทุกตลาด ขอย้ำอีกครั้ง สิ่งสำคัญคือคุณต้องเข้าใจว่าไม่สำคัญว่าระบบจะทำกำไรได้แค่ไหน ตราบใดที่ยังมีผลกำไร ที่คุณได้รับจากการซื้อขายจะได้รับผ่าน การจัดการที่มีประสิทธิภาพเงิน.

ความคาดหวังทางคณิตศาสตร์ (ค่าเฉลี่ยประชากร) คือ

ระบบการซื้อขายเป็นเพียงเครื่องมือที่ให้มูลค่าที่คาดหวังในเชิงบวกเพื่อให้คุณสามารถใช้การจัดการเงินได้ ระบบที่ทำงาน (แสดงผลกำไรขั้นต่ำเป็นอย่างน้อย) ในตลาดเดียวหรือไม่กี่ตลาด หรือมีกฎหรือพารามิเตอร์ที่แตกต่างกันสำหรับตลาดที่แตกต่างกัน มักจะไม่ทำงานแบบเรียลไทม์เป็นเวลานาน ปัญหาของเทรดเดอร์ที่เน้นทางเทคนิคส่วนใหญ่คือพวกเขาใช้เวลาและความพยายามมากเกินไปในการเพิ่มประสิทธิภาพ กฎที่แตกต่างกันและค่าพารามิเตอร์ของระบบการซื้อขาย สิ่งนี้ให้ผลลัพธ์ที่ตรงกันข้ามโดยสิ้นเชิง แทนที่จะสิ้นเปลืองพลังงานและ เวลาคอมพิวเตอร์เพื่อเพิ่มผลกำไรของระบบการซื้อขาย ทุ่มเทพลังงานของคุณเพื่อเพิ่มระดับความน่าเชื่อถือในการได้รับผลกำไรขั้นต่ำ

รู้ว่า การจัดการเงิน- มันเป็นเพียง เกมตัวเลขซึ่งต้องใช้ความคาดหวังเชิงบวก เทรดเดอร์สามารถหยุดค้นหา "จอกศักดิ์สิทธิ์" ของการซื้อขายหุ้นได้ แต่เขาสามารถเริ่มทดสอบวิธีการซื้อขายของเขา ค้นหาว่าวิธีนี้สมเหตุสมผลเพียงใด และให้ความคาดหวังเชิงบวกหรือไม่ วิธีการที่ถูกต้องการจัดการเงินที่นำไปใช้กับวิธีการซื้อขายใดๆ ก็ตาม แม้แต่วิธีการซื้อขายธรรมดาๆ ก็ตาม จะทำงานส่วนที่เหลือเอง

เพื่อให้เทรดเดอร์คนใดก็ตามประสบความสำเร็จในงานของเขา เขาจำเป็นต้องแก้ไขงานที่สำคัญที่สุดสามประการ: เพื่อให้แน่ใจว่าจำนวนธุรกรรมที่ประสบความสำเร็จมีมากกว่าข้อผิดพลาดและการคำนวณผิดที่หลีกเลี่ยงไม่ได้ ตั้งค่าระบบการซื้อขายของคุณเพื่อให้คุณมีโอกาสสร้างรายได้บ่อยที่สุด บรรลุผลลัพธ์เชิงบวกที่มั่นคงจากการดำเนินงานของคุณ

และสำหรับพวกเราที่ทำงานเทรดเดอร์ คู่ครองสามารถช่วยได้ดี ความคาดหวัง คำนี้เป็นหนึ่งในคำสำคัญในทฤษฎีความน่าจะเป็น ด้วยความช่วยเหลือนี้ คุณสามารถให้ค่าประมาณโดยเฉลี่ยได้บางส่วน ค่าสุ่ม- ความคาดหวังของตัวแปรสุ่มจะคล้ายกับจุดศูนย์ถ่วงหากคุณจินตนาการทุกอย่าง ความน่าจะเป็นที่เป็นไปได้จุดที่มีมวลต่างกัน

ในส่วนที่เกี่ยวข้องกับกลยุทธ์การซื้อขาย ความคาดหวังของกำไร (หรือขาดทุน) มักใช้ในการประเมินประสิทธิผล พารามิเตอร์นี้ถูกกำหนดให้เป็นผลรวมของผลิตภัณฑ์ของระดับกำไรและขาดทุนที่กำหนดและความน่าจะเป็นที่จะเกิดขึ้น ตัวอย่างเช่น กลยุทธ์การซื้อขายที่พัฒนาขึ้นถือว่า 37% ของการดำเนินการทั้งหมดจะสร้างผลกำไร และส่วนที่เหลือ - 63% - จะไม่สามารถทำกำไรได้ ขณะเดียวกันก็มีค่าเฉลี่ย รายได้จากการซื้อขายที่ประสบความสำเร็จจะอยู่ที่ 7 ดอลลาร์ และการสูญเสียโดยเฉลี่ยจะอยู่ที่ 1.4 ดอลลาร์ มาคำนวณคณิตศาสตร์กัน ความคาดหวังในการซื้อขายโดยใช้ระบบนี้:

มันหมายความว่าอะไร หมายเลขที่กำหนด- มันบอกว่าตามกฎของระบบนี้ โดยเฉลี่ยแล้วเราจะได้รับ $1,708 จากธุรกรรมที่ปิดแต่ละครั้ง เนื่องจากการประมาณประสิทธิภาพผลลัพธ์มีค่ามากกว่าศูนย์ จึงสามารถใช้ระบบดังกล่าวได้ งานจริง- จากการคำนวณการรุกฆาต หากความคาดหวังกลายเป็นลบแสดงว่ามีการสูญเสียโดยเฉลี่ยแล้วและสิ่งนี้จะนำไปสู่การทำลายล้าง

จำนวนกำไรต่อธุรกรรมสามารถแสดงเป็นได้ ขนาดสัมพัทธ์ในรูปของ % ตัวอย่างเช่น:

เปอร์เซ็นต์ของรายได้ต่อ 1 ธุรกรรมคือ 5%

เปอร์เซ็นต์ของการดำเนินการซื้อขายที่ประสบความสำเร็จคือ 62%;

เปอร์เซ็นต์การสูญเสียต่อ 1 การซื้อขาย - 3%;

เปอร์เซ็นต์ของการทำธุรกรรมที่ไม่สำเร็จคือ 38%

ในกรณีนี้รุกฆาต ความคาดหวังจะเป็น:

นั่นคือการค้าเฉลี่ยจะนำมาซึ่ง 1.96%

มีความเป็นไปได้ที่จะพัฒนาระบบที่แม้จะมีอิทธิพลเหนือการซื้อขายที่ไม่ได้ผลกำไร แต่ก็จะให้ผลลัพธ์ที่เป็นบวก เนื่องจาก MO>0

อย่างไรก็ตาม การรอเพียงอย่างเดียวไม่เพียงพอ เป็นเรื่องยากที่จะทำเงินหากระบบให้สัญญาณการซื้อขายน้อยมาก ในกรณีนี้จะเทียบได้กับดอกเบี้ยธนาคาร ปล่อยให้แต่ละการดำเนินการผลิตได้โดยเฉลี่ยเพียง 0.5 ดอลลาร์ แต่จะเกิดอะไรขึ้นหากระบบเกี่ยวข้องกับการดำเนินงาน 1,000 ครั้งต่อปี นี่จะเป็นจำนวนที่สำคัญมากในระยะเวลาอันสั้น มันตามมาจากสิ่งนี้อย่างมีเหตุผล จุดเด่นระบบการซื้อขายที่ดีถือได้ว่าเป็นช่วงระยะเวลาที่สั้นในการถือครองตำแหน่ง

แหล่งที่มาและลิงค์

dic.academic.ru - พจนานุกรมออนไลน์เชิงวิชาการ

mathematics.ru - เว็บไซต์การศึกษาด้านคณิตศาสตร์

nsu.ru - เว็บไซต์การศึกษาของ Novosibirsk State University

webmath.ru - พอร์ทัลการศึกษาสำหรับนักเรียน ผู้สมัคร และเด็กนักเรียน

exponenta.ru เว็บไซต์คณิตศาสตร์เพื่อการศึกษา

ru.tradimo.com - ฟรี โรงเรียนออนไลน์การซื้อขาย

crypto.hut2.ru - แหล่งข้อมูลสหสาขาวิชาชีพ

poker-wiki.ru - สารานุกรมโป๊กเกอร์ฟรี

sernam.ru - ห้องสมุดวิทยาศาสตร์สิ่งพิมพ์วิทยาศาสตร์ธรรมชาติที่เลือกสรร

reshim.su - เว็บไซต์ เราจะแก้ปัญหาการทดสอบรายวิชา

unfx.ru - ฟอเร็กซ์บน UNFX: การฝึกอบรม สัญญาณการซื้อขาย การจัดการความน่าเชื่อถือ

- — ความคาดหวังทางคณิตศาสตร์ หนึ่งในนั้น ลักษณะเชิงตัวเลขตัวแปรสุ่ม มักเรียกว่าค่าเฉลี่ยทางทฤษฎี สำหรับตัวแปรสุ่มแบบไม่ต่อเนื่อง X ทางคณิตศาสตร์... ... คู่มือนักแปลทางเทคนิค

ความคาดหวังทางคณิตศาสตร์- (ค่าที่คาดหวัง) ค่าเฉลี่ยของการแจกแจงตัวแปรทางเศรษฐกิจที่สามารถรับได้ ถ้า рt คือราคาของผลิตภัณฑ์ ณ เวลา t ความคาดหวังทางคณิตศาสตร์จะแสดงด้วย Ept เพื่อระบุช่วงเวลาที่จะ...... พจนานุกรมเศรษฐศาสตร์

ความคาดหวัง- ค่าเฉลี่ยของตัวแปรสุ่ม ความคาดหวังทางคณิตศาสตร์เป็นปริมาณที่กำหนด ค่าเฉลี่ยเลขคณิตของการตระหนักถึงตัวแปรสุ่มคือการประมาณค่าความคาดหวังทางคณิตศาสตร์ ค่าเฉลี่ยเลขคณิต...... คำศัพท์ที่เป็นทางการ - (ค่าเฉลี่ย) ของตัวแปรสุ่ม - ลักษณะตัวเลขของตัวแปรสุ่ม หากตัวแปรสุ่มถูกกำหนดบนปริภูมิความน่าจะเป็น (ดูทฤษฎีความน่าจะเป็น) ดังนั้น M. o MX (หรือ EX) ถูกกำหนดให้เป็นอินทิกรัล Lebesgue: โดยที่... สารานุกรมทางกายภาพ

ความคาดหวังทางคณิตศาสตร์- ตัวแปรสุ่มคือคุณลักษณะเชิงตัวเลข ถ้าตัวแปรสุ่ม X มีฟังก์ชันการกระจาย F(x) ดังนั้น M. o จะ: . หากการแจกแจง X ไม่ต่อเนื่องดังนั้น Mo: โดยที่ x1, x2, ... ค่าที่เป็นไปได้ของตัวแปรสุ่มแบบไม่ต่อเนื่อง X; พี1... สารานุกรมทางธรณีวิทยา

ความคาดหวังทางคณิตศาสตร์- ภาษาอังกฤษ มูลค่าที่คาดหวัง เยอรมัน คณิตศาสตร์เออร์วาร์ตุง. ค่าเฉลี่ยสุ่มหรือจุดศูนย์กลางการกระจายตัวของตัวแปรสุ่ม อันตินาซี. สารานุกรมสังคมวิทยา พ.ศ. 2552 ... สารานุกรมสังคมวิทยา

ความคาดหวัง- ดูเพิ่มเติมที่: ความคาดหวังทางคณิตศาสตร์แบบมีเงื่อนไข ความคาดหวังทางคณิตศาสตร์คือค่าเฉลี่ยของตัวแปรสุ่ม การแจกแจงความน่าจะเป็นของตัวแปรสุ่ม ได้รับการพิจารณาในทฤษฎีความน่าจะเป็น ในวรรณคดีอังกฤษและคณิตศาสตร์... ... Wikipedia

ความคาดหวัง- 1.14 ความคาดหวังทางคณิตศาสตร์ E (X) โดยที่ xi คือค่าของตัวแปรสุ่มแบบไม่ต่อเนื่อง พี = พี (X = xi); ความหนาแน่น f(x) ของตัวแปรสุ่มต่อเนื่อง * หากนิพจน์นี้มีอยู่ในความหมายของการลู่เข้าสัมบูรณ์ ที่มา... หนังสืออ้างอิงพจนานุกรมเกี่ยวกับเอกสารเชิงบรรทัดฐานและทางเทคนิค

เหมือนกัน คุกกี้สำหรับเว็บไซต์ที่ดีที่สุด Wenn Sie diese เว็บไซต์ของ weiterhin nutzen, กระตุ้น Sie dem zu. ตกลง

อดทนและอ่านข้อความนี้..

การเล่นเกมด้วยความคาดหวังเชิงบวกเป็นแนวคิดที่สำคัญสำหรับนักเก็งกำไรทุกคน มันเป็นแนวคิดเกี่ยวกับระบบแห่งศรัทธาที่ถูกสร้างขึ้น แต่แนวคิดนั้นไม่สามารถสร้างขึ้นจากศรัทธาได้ คาสิโนไม่ได้ดำเนินการด้วยความศรัทธา คาสิโนดำเนินการโดยการจัดการธุรกิจโดยใช้คณิตศาสตร์ล้วนๆ คาสิโนรู้ดีว่าในที่สุดกฎของรูเล็ตและลูกเต๋าก็จะมีผลเหนือกว่า ดังนั้นคาสิโนจึงไม่อนุญาตให้เกมหยุดลง คาสิโนไม่สนใจที่จะรอ แต่คาสิโนไม่หยุดและเล่นตลอดเวลา เพราะยิ่งคุณเล่นเกมที่มีความคาดหวังทางคณิตศาสตร์เชิงลบนานเท่าไหร่ ผู้จัดงานคาสิโนก็จะยิ่งมั่นใจว่าพวกเขาจะได้รับเงินของคุณมากขึ้นเท่านั้น

เทรดเดอร์จำเป็นต้องมีความเข้าใจเกี่ยวกับความคาดหวังทางคณิตศาสตร์ ขึ้นอยู่กับว่าใครมีข้อได้เปรียบทางคณิตศาสตร์ในเกม เรียกว่าข้อได้เปรียบของผู้เล่น - ความคาดหวังเชิงบวก หรือข้อได้เปรียบจากบ่อนการพนัน - ความคาดหวังเชิงลบ สมมติว่าเรากำลังเล่นหัวหรือก้อยกับคุณ ทั้งคุณและฉันไม่มีข้อได้เปรียบที่แต่ละคนมีโอกาสชนะ 50% แต่ถ้าเรานำเกมนี้ไปที่คาสิโนที่รับส่วนลด 10% ทุกการเดิมพัน คุณจะชนะเพียง 90 เซ็นต์สำหรับทุกๆ ดอลลาร์ที่คุณเสียไป ข้อดีของบ่อนการพนันนี้กลายเป็นความคาดหวังทางคณิตศาสตร์เชิงลบที่แข็งแกร่งสำหรับคุณในฐานะผู้เล่น และไม่มีระบบควบคุมเงินทุน ไม่มีกลยุทธ์ใดที่สามารถเอาชนะเกมที่มีความคาดหวังเชิงลบได้

ในเกมที่มีมูลค่าที่คาดหวังติดลบ ไม่มีแผนการจัดการเงิน (กลยุทธ์) ที่จะทำให้คุณเป็นผู้ชนะ

รูเล็ตถือเป็นสิ่งที่น่าสนใจผู้นำของเกมการพนันทั้งหลายขอถือเป็นพื้นฐาน ดังนั้น คาสิโน เสียงกรีดร้อง เสียง อารมณ์ และการแสดงที่หรูหรา แต่เราจะเน้นไปที่รูเล็ต ลองคำนวณความคาดหวังทางคณิตศาสตร์ในการเล่นรูเล็ตหากคุณเล่นเฉพาะสีแดงดำ (ในการซื้อขายจะยาวหรือสั้น) ดังนั้น วงล้อรูเล็ตจึงมีสนามเด็กเล่นเพียง 38 ช่อง - 36 หมายเลข (สีแดง 18 ช่องและสีดำ 18 ช่อง) และเลขศูนย์สองตัว (ลองใช้วงล้อที่มีเลขศูนย์สองตัวกัน) ดังนั้นความน่าจะเป็นที่จะชนะเมื่อเดิมพันสีแดงหรือสีดำจะอยู่ที่ประมาณ 0.45 (18/38) หากเดิมพันสำเร็จ เราจะเดิมพันเป็นสองเท่า และหากล้มเหลว เราจะสูญเสียทุกสิ่งที่เราเดิมพัน โอ้ ใช่ ถ้าเราได้ศูนย์ เราก็จะเสียเงินไปด้วย ดังนั้นเราจึงมีความคาดหวังทางคณิตศาสตร์เป็นลบ เกมนี้สามารถเรียกได้ว่าไม่ทำกำไรเนื่องจากมีศูนย์สองตัวอยู่ในสนามเด็กเล่น เมื่อพวกมันหลุดออกไป คาสิโนจะรับเดิมพันของเรา หนึ่งเซลล์คิดเป็นประมาณ 2.6% ของวงล้อรูเล็ต สองเซลล์มากกว่า 5% นี่คือเปอร์เซ็นต์ที่เจ้าของคาสิโนใส่ในกระเป๋าโดยเฉลี่ยจากการทำธุรกรรมแต่ละครั้ง ดังนั้นคาสิโนจึงค่อย ๆ สูบเงินออกจากลูกค้า สร้างรายได้ เป็นเวลาหลายสิบปี

แน่นอนว่าสำหรับคาสิโน เกมนี้มีความคาดหวังทางคณิตศาสตร์เชิงบวก เมื่อมีศูนย์สองตัว คาสิโนจะได้รับเงินของผู้เล่นเป็นยี่สิบกรณีจากทั้งหมด 38 กรณี และยิ่งเกมดำเนินต่อไปนานเท่าไร คาสิโนก็จะยิ่งได้รับกำไรมากขึ้นเท่านั้น

ความคาดหวังทางคณิตศาสตร์ของเกมการเงินคืออะไร? การเดิมพันในเครื่องมือทางการเงินมีคุณสมบัติภายนอกทั้งหมดของการพนัน; การกระจายรูเล็ตเป็นศูนย์ในองค์ประกอบความน่าจะเป็นจำนวนมาก - สเปรด, ค่าคอมมิชชั่นการแลกเปลี่ยน, ค่าคอมมิชชั่นนายหน้า, ค่าธรรมเนียมการสมัครสมาชิกสำหรับการใช้เทอร์มินัลการแลกเปลี่ยน, ค่าธรรมเนียมในการโอนเงินไปที่ บัญชีและภาษี 13% จากกำไรในอนาคตโดยรวมนั้นเป็นอะนาล็อกของรูเล็ตเป็นศูนย์ สิ่งนี้ทำให้มีเหตุผลในการพูดคุยเกี่ยวกับความคาดหวังทางคณิตศาสตร์เชิงลบและไม่เอื้ออำนวยในตอนแรกสำหรับผู้เล่น (เทรดเดอร์)

ฉันอยากให้คุณเข้าใจ - ไม่มีวิธีการจัดการเงิน ไม่มีกลยุทธ์ สามารถเปลี่ยนความคาดหวังเชิงลบให้เป็นบวกได้ นี่เป็นคำพูดที่ถูกต้องอย่างแน่นอน ไม่มีการพิสูจน์ทางคณิตศาสตร์สำหรับข้อความนี้ อย่างไรก็ตาม นี่ไม่ได้หมายความว่าสิ่งนี้จะเกิดขึ้นไม่ได้ แน่นอนว่าในการพนัน ผู้เข้าร่วมสามารถเข้าสู่การชนะ ความบังเอิญ และหยุดเล่นได้ ซึ่งผลที่ตามมาคือบุคคลดังกล่าวจะเป็นผู้ชนะ แต่เขาจะเลิกเล่นเกมนี้ไปอีกนานแค่ไหน...

ดังนั้นครั้งเดียวที่คุณมีโอกาสชนะในระยะยาวคือถ้าคุณเล่นโดยมีมูลค่าที่คาดหวังเป็นบวก- ฉันคิดว่าคุณมักจะสามารถชนะได้โดยใช้การเดิมพันเดียวกันหลายครั้งและต่อเมื่อไม่มีเท่านั้น อุปสรรคการดูดซึมด้านบน- นักพนันที่เริ่มต้นด้วยเงิน $100 จะหยุดเล่นหากบัญชีของเขาเพิ่มขึ้นเป็น $101 เป้าหมายบนนี้ ($101) เรียกว่าอุปสรรคการดูดซึม สมมติว่าผู้เล่นเดิมพัน 1 ดอลลาร์เสมอกับสีแดงของวงล้อรูเล็ต โดยที่ 18 แถบเป็นสีแดง 18 แถบเป็นสีดำ 2 แถบเป็นศูนย์ และเมื่อเป็นศูนย์ เงินจะเข้าคาสิโน ดังนั้น เกมนี้เล่นโดยมีความคาดหวังทางคณิตศาสตร์เชิงลบเล็กน้อย ผู้เล่นมีโอกาสที่ดีกว่าที่จะเห็นบัญชีของเขาไปถึง $101 และผู้เล่นหยุดเล่น มากกว่าที่จะเห็นบัญชีของเขากลายเป็นศูนย์และผู้เล่นไม่มีอะไรจะเล่น หากผู้เล่นเล่นรูเล็ตซ้ำแล้วซ้ำเล่า เขาจะกลายเป็นเหยื่อของความคาดหวังทางคณิตศาสตร์เชิงลบ หากคุณเล่นเกมดังกล่าวเพียงครั้งเดียว แน่นอนว่าหลักการของการล้มละลายที่หลีกเลี่ยงไม่ได้นั้นใช้ไม่ได้ หากคุณเล่นเกมนี้เพียงครั้งเดียว สมมติว่าพลังของการรุกฆาตเชิงลบ ความคาดหวังจะต่ำที่สุด ความแตกต่างระหว่างความคาดหวังเชิงลบและความคาดหวังเชิงบวกคือความแตกต่างระหว่างชีวิตและความตายของเงินฝากของคุณ

เมื่อคุณตระหนักว่าเกมมีค่าที่คาดหวังเป็นลบ ทางออกที่ดีที่สุดคือการไม่เดิมพัน จำไว้นะ ไม่มีกลยุทธ์การจัดการเงินที่สามารถเปลี่ยนเกมที่แพ้ให้กลายเป็นเกมที่ชนะได้- สมมติว่าคุณยังต้องเดิมพันในเกมที่มีความคาดหวังเชิงลบ ดังนั้น กลยุทธ์ที่ดีที่สุดน่าจะเป็น” กลยุทธ์ความกล้าหาญสูงสุด » - กล่าวอีกนัยหนึ่ง คุณต้องการเดิมพันให้น้อยที่สุดเท่าที่จะเป็นไปได้ (ซึ่งตรงกันข้ามกับเกมที่คาดหวังในเชิงบวก ซึ่งคุณควรเดิมพันให้บ่อยที่สุดเท่าที่จะทำได้ โดยไม่ควรออกจากเกมเลย) ดังนั้น ยิ่งคุณพยายามมากเท่าไร คุณจะยิ่งสูญเสียมากขึ้นเท่านั้นหากคุณมีความคาดหวังเชิงลบ ดังนั้น ด้วยความคาดหวังที่เป็นลบ จึงมีโอกาสแพ้น้อยลงเมื่อความยาวของเกมสั้นลง (นั่นคือ เมื่อจำนวนการทดลองเข้าใกล้ 1) หากคุณกำลังเล่นเกมที่คุณมีโอกาส 49% ที่จะชนะรางวัล 1 ดอลลาร์ และโอกาส 51% ที่จะเสียเงิน 1 ดอลลาร์ ทางออกที่ดีที่สุดของคุณคือการลองเล่นเพียงครั้งเดียวเท่านั้น ยิ่งคุณวางเดิมพันมากเท่าไร โอกาสที่คุณจะสูญเสียก็จะยิ่งมากขึ้นเท่านั้น (โดยมีความน่าจะเป็นที่จะสูญเสียความมั่นใจ 100% เมื่อเกมเข้าใกล้อนันต์ด้วยมูลค่าที่คาดหวังติดลบ)

ผู้จัดงานเกม คาสิโน จะไม่บอกเทรดเดอร์เกี่ยวกับความคาดหวังทางคณิตศาสตร์ “พวกเขา” จะบอกเทรดเดอร์เกี่ยวกับโอกาสที่จะชนะและค้นหา เหตุผลต่างๆเพื่อให้เทรดเดอร์วางเดิมพันได้ การฟังผู้จัดเกมและผู้คนจำนวนมากทั่วตลาดที่ได้รับค่าคอมมิชชั่นโดยไม่ต้องเสี่ยงเงิน เทรดเดอร์เชื่อว่าสำหรับเกมที่ประสบความสำเร็จเป็นสิ่งสำคัญในการวิเคราะห์แผนภูมิ ข่าวสาร วาดเส้นเกี่ยวกับวิทยาศาสตร์เทียมของเทคนิค วิเคราะห์และค้นหาช่วงเวลาที่เหมาะสมในการเปิดตำแหน่งและคาดว่าจะเพิ่มความน่าเชื่อถือของระบบของคุณ - กลยุทธ์ (ถ้าคุณมี) และเอาชนะตลาด แต่ความจริงก็คือ อย่างน้อย 97% ของคนที่พยายามคิดค้นระบบกลยุทธ์การซื้อขายก็แค่พยายามค้นหา สัญญาณอินพุตในอุดมคติ- สัญญาณอินพุตนี้ไม่มีกำลังกับความคาดหวังเชิงลบทางคณิตศาสตร์เริ่มต้น ในความเป็นจริง เทรดเดอร์มักจะรายงานว่าระบบของตนมีอัตราความน่าเชื่อถืออย่างน้อย 60% แต่ในขณะเดียวกัน พวกเขาก็สงสัยว่าทำไมพวกเขาถึงไม่ทำเงิน ในระยะยาว เทรดเดอร์ก็ขาดทุน! ทำความเข้าใจว่าแม้แต่ระบบที่มีเปอร์เซ็นต์การชนะสูงโดยมีความคาดหวังทางคณิตศาสตร์เป็นลบก็ยังเป็นหนทางไปไม่ถึง สิ่งที่ดีที่สุดที่เทรดเดอร์สามารถทำได้คือหยุดการชนะต่อเนื่องและไม่เข้าสู่ตลาดอีก

แบบนี้อีกครับ รายละเอียดที่น่าสนใจสมมติว่าคุณเริ่มเกมด้วยหนึ่งดอลลาร์ ชนะในการหมุนครั้งแรกและรับหนึ่งดอลลาร์ ในการหมุนครั้งถัดไป คุณเดิมพันจำนวนทั้งหมด ($2) แต่คราวนี้คุณแพ้และแพ้ คุณสูญเสียจำนวนเงินเริ่มต้น 1 ดอลลาร์และกำไร 1 ดอลลาร์ ความจริงก็คือหากคุณใช้บัญชี 100% คุณจะออกจากเกมทันทีที่คุณพบกับการสูญเสียซึ่งเป็นเหตุการณ์ที่หลีกเลี่ยงไม่ได้ มันต่อจากนี้ กฎที่สำคัญหากคุณเริ่มเกมในที่สุด ให้เล่นด้วยการเดิมพันเดิมและรับผลกำไรให้กับตัวคุณเอง อย่าเข้าสู่ตลาดด้วยการเดิมพันจำนวนมากเมื่อคณิตศาสตร์เป็นลบ

เทรดเดอร์ระยะสั้นมักพูดอยู่เสมอว่า: ฉันเป็นเดย์เทรดเดอร์ที่ประสบความสำเร็จ ฉันเข้าและออกจากตลาดหลายครั้งต่อวัน และฉันก็ทำเงินได้เกือบทุกวัน แต่ในหนึ่งวันเมื่อวานนี้ ฉันสูญเสียผลกำไรที่คุ้มค่าไปเกือบหนึ่งปี และฉันก็เสียใจมากกับเรื่องนี้ ข้อผิดพลาดดังกล่าวเกิดขึ้นจากการเปลี่ยนแปลงการเดิมพัน การตกหลุมพรางเลเวอเรจ และการซื้อขายตามอารมณ์ การเลือกรายการ การสร้างรายได้เป็นระยะเวลาหนึ่ง และการสูญเสียบัญชีในที่สุด นี่คือชะตากรรมของเทรดเดอร์ส่วนใหญ่ที่เล่นแต่สนามเป็นรุกฆาตเชิงลบ ความคาดหวัง

เทรดเดอร์จัดการกับตลาดอย่างไร? ความพยายามที่จะย้อนกลับความคาดหวังทางคณิตศาสตร์ที่เป็นลบนั้นเป็นการเดิมพันแบบเดียวกันใน “เหตุการณ์” ที่เหมือนกัน นี่เป็นตัวอย่างคลาสสิกของเกมแห่งโอกาสที่ผู้เข้าร่วมพยายามใช้ประโยชน์จากการสตรีค กรณีเดียวที่ทำให้พวกเขาแพ้ด้วยวิธีนี้คือเมื่อมีการโจมตีที่เหมือนกันหลายรายการติดต่อกันในซีรีส์ ซีรีส์ ยิ่งเล็กยิ่งดี - มีประสิทธิภาพมากกว่าการเล่นแบบตาบอด อย่างไรก็ตาม ซีรีส์ไม่ได้ให้ความคาดหวังทางคณิตศาสตร์เชิงบวก

คุณคงเคยได้ยินเกี่ยวกับ Martingale มาก่อน มันเป็นกลยุทธ์ซีรีส์ที่ได้รับการปรับปรุง ที่นี่ผู้เล่นเริ่มต้นด้วยการเดิมพันขั้นต่ำ โดยปกติคือ 1 ดอลลาร์ และหลังจากแพ้แต่ละครั้ง เขาจะเพิ่มเงินเดิมพันเป็นสองเท่า ตามทฤษฎีแล้ว เขาควรจะชนะไม่ช้าก็เร็ว จากนั้นจึงคืนทุกสิ่งที่เขาสูญเสียไปพร้อมเงินหนึ่งดอลลาร์ หลังจากนี้ เขาสามารถเดิมพันขั้นต่ำอีกครั้งและเริ่มต้นใหม่ได้ แนวคิดพื้นฐานของวิธี Martingale ขึ้นอยู่กับข้อเท็จจริงที่ว่าเมื่อจำนวนเงินที่เกิดจากการขาดทุนลดลง ความเป็นไปได้ในการชดเชยการขาดทุนจะเพิ่มขึ้นหรือยังคงเท่าเดิม นี่คือการจัดการเงินประเภทหนึ่งที่ได้รับความนิยมสำหรับนักพนัน ระบบการทวีคูณดูเหมือนเป็น win-win จนกว่าคุณจะตระหนักว่าการแพ้ติดต่อกันเป็นเวลานานจะทำลายผู้เล่นคนใดก็ตาม ไม่ว่าเขาจะรวยแค่ไหนก็ตาม ผู้เล่นที่เริ่มต้นด้วยเงิน 1 ดอลลาร์และแพ้ 46 ครั้งจะต้องวางเดิมพันครั้งที่ 47 ที่ 70 ล้านล้านดอลลาร์ซึ่งมีมูลค่ามากกว่ามูลค่าของโลกทั้งโลก (ประมาณ 50 ล้านล้าน) เป็นที่ชัดเจนว่าเร็วกว่านั้นมาก เขาจะหมดเงินหรือถูกจำกัดเงินฝากหรือคาสิโนของเขา ฉันเชื่อว่าระบบทวีคูณนั้นไร้ประโยชน์หากคุณมีความคาดหวังทางคณิตศาสตร์เชิงลบและมีความเสี่ยงเกินไปที่จะใช้ระบบนี้ด้วยเงินของคุณเอง

ในเกมที่ดำเนินไปอย่างไม่มีที่สิ้นสุด เกมที่มีความคาดหวังทางคณิตศาสตร์เชิงลบจะสิ้นหวัง แต่ด้วยจำนวนตอนที่จำกัดก็มีโอกาสที่จะได้รับชัยชนะ หรือคุณต้องมองหาเสื่อ เกมเชิงบวกที่กำไรที่เป็นไปได้จะมากกว่าการสูญเสียที่เป็นไปได้ต่อ 1 เดิมพัน

เทรดเดอร์ส่วนใหญ่เสียชีวิตจากหนึ่งในสองกระสุน: ความไม่รู้และอารมณ์ คนธรรมดาเล่นตามอำเภอใจ โดยเข้าไปยุ่งเกี่ยวกับธุรกรรมที่พวกเขาควรจะพลาด เนื่องจากความคาดหวังทางคณิตศาสตร์เชิงลบ หากพวกเขารอด เมื่อเรียนรู้แล้ว พวกเขาจะเริ่มพัฒนาระบบที่ชาญฉลาดยิ่งขึ้น จากนั้นด้วยความมั่นใจในตัวเองพวกเขาจึงยื่นหัวออกจากคูน้ำ - และตกอยู่ใต้กระสุนนัดที่สอง ด้วยความมั่นใจมากเกินไป พวกเขาเดิมพันมากเกินไปในการซื้อขายครั้งเดียวและต้องออกจากเกมหลังจากขาดทุนติดต่อกันเป็นระยะเวลาสั้นๆ อารมณ์มีผลกระทบโดยตรงมากที่สุดต่อผลลัพธ์ทางการเงินที่นักลงทุนได้รับ ในระดับที่มากขึ้นผู้เล่นจากการเก็งกำไรทางการเงิน และยิ่งพฤติกรรมของบุคคลมีอารมณ์มากเท่าใด ความเบี่ยงเบนของความคาดหวังทางคณิตศาสตร์ของผลลัพธ์ทางการเงินจากการซื้อขายของเขาจากความเป็นจริงก็จะยิ่งมีนัยสำคัญมากขึ้นเท่านั้น สำหรับเกมการพนันที่มีความคาดหวังทางคณิตศาสตร์เชิงลบ ผลลัพธ์ทางการเงินที่ได้รับภายใต้อิทธิพลของอารมณ์คือความตายของเงินฝาก

ตามกฎแล้ว เกมใดๆ ที่มีการชนะรางวัลเป็นตัวเงิน ไม่ว่าจะเป็นลอตเตอรี การเดิมพันในสนามแข่งและในเจ้ามือรับแทงม้า เครื่องสล็อต ฯลฯ ถือเป็นเกมที่มีความคาดหวังทางคณิตศาสตร์เชิงลบสำหรับผู้เล่น คาสิโนจัดเกมเหล่านี้ให้คุณด้วยเหตุผล ลักษณะเฉพาะของเทรดเดอร์ทั่วไปคือเขาไม่สามารถคำนวณสิ่งเล็กๆ น้อยๆ ทั้งหมดที่รอเขาอยู่ในอนาคตได้ ดังนั้นอนาคตของเกมของเขาจึงถูกกำหนดไว้ล่วงหน้า

ฉันต้องการให้คุณเข้าใจว่าการมีส่วนร่วมในเกมใด ๆ ที่มีความคาดหวังทางคณิตศาสตร์เชิงลบไม่สามารถถือเป็นแหล่งรายได้ที่มั่นคง

จะทำอย่างไร? ทุกคนตัดสินใจด้วยตัวเอง ฉันพบความคาดหวังเชิงบวกทางคณิตศาสตร์เกี่ยวกับตัวเลือกหุ้น แต่ถึงอย่างนั้น การเปลี่ยนแปลงกฎของเกมอย่างต่อเนื่องโดยโบรกเกอร์และการแลกเปลี่ยนทำให้รายได้สุดท้ายลดลงอย่างมาก รูเล็ตที่มีรอยเปื้อนเป็นศูนย์ในเรื่องสเปรด ค่าธรรมเนียม นายหน้าและสิ่งเล็กๆ น้อยๆ อื่น ๆ จะลดผลกำไรขั้นสุดท้ายลงอย่างมาก แต่ด้วยการใช้ตัวเลือกเท่านั้นที่คุณสามารถสร้างระบบรุกฆาต+ ใน "คาสิโนแห่งศตวรรษที่ 21" นี้

มองหาความคาดหวังเชิงบวกทางคณิตศาสตร์ไม่ว่าจะด้วยวิธีใดก็ตามที่จำเป็น!

ฉันคิดว่าอย่างนั้น กุญแจสำคัญในการสร้างรายได้ในตลาดการเงินคือการมีระบบที่มีความคาดหวังทางคณิตศาสตร์เชิงบวกสูง การใช้ระบบนี้เป็นสิ่งสำคัญอย่างยิ่งที่จะใช้ขนาดตำแหน่งที่กำหนดไว้ในตอนแรก ทำงานอย่างเคร่งครัดตามกฎและเล่นเกมต่อไป ซ้ำแล้วซ้ำอีกและนานที่สุดเท่าที่จะเป็นไปได้และรับเงินจากการต่อสู้กับการแสดงตลกของผู้จัดงาน “คาสิโน” นี้

ค่าแต่ละค่าจะถูกกำหนดโดยฟังก์ชันการแจกแจง นอกจากนี้เพื่อแก้ปัญหาในทางปฏิบัติก็เพียงพอที่จะทราบคุณลักษณะเชิงตัวเลขหลายประการซึ่งทำให้สามารถนำเสนอคุณลักษณะหลักของตัวแปรสุ่มในรูปแบบย่อได้

ปริมาณเหล่านี้ได้แก่ ความคาดหวังทางคณิตศาสตร์และ การกระจายตัว .

ความคาดหวัง— ค่าเฉลี่ยของตัวแปรสุ่มในทฤษฎีความน่าจะเป็น แสดงว่า.

มากที่สุด ด้วยวิธีง่ายๆความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่ม เอ็กซ์(ญ), ค้นหาวิธีการ บูรณาการเลเบสก์ที่เกี่ยวข้องกับการวัดความน่าจะเป็น ร ต้นฉบับ พื้นที่ความน่าจะเป็น

คุณยังสามารถค้นหาความคาดหวังทางคณิตศาสตร์ของค่าดังกล่าวได้ อินทิกรัลของเลอเบสก์จาก เอ็กซ์โดยการกระจายความน่าจะเป็น อาร์ เอ็กซ์ปริมาณ เอ็กซ์:

ชุดของค่าที่เป็นไปได้ทั้งหมดอยู่ที่ไหน เอ็กซ์.

ความคาดหวังทางคณิตศาสตร์ของฟังก์ชันจากตัวแปรสุ่ม เอ็กซ์พบได้จากการจำหน่าย อาร์ เอ็กซ์. ตัวอย่างเช่น, ถ้า เอ็กซ์- ตัวแปรสุ่มที่มีค่าเป็น และ ฉ(x)- ไม่คลุมเครือ ของโบเรลการทำงาน เอ็กซ์ , ที่:

ถ้า ฉ(x)- ฟังก์ชั่นการกระจาย เอ็กซ์จากนั้นสามารถแสดงความคาดหวังทางคณิตศาสตร์ได้ บูรณาการLebesgue - Stieltjes (หรือ Riemann - Stieltjes):

ในกรณีนี้คือบูรณาการได้ เอ็กซ์ในแง่ของ ( * ) สอดคล้องกับความจำกัดของอินทิกรัล

ในกรณีเฉพาะถ้า เอ็กซ์มีการแจกแจงแบบไม่ต่อเนื่องด้วยค่าที่เป็นไปได้ เอ็กซ์เค, เค=1, 2- และความน่าจะเป็นแล้ว

ถ้า เอ็กซ์มีอย่างแน่นอน การกระจายอย่างต่อเนื่องด้วยความหนาแน่นของความน่าจะเป็น พี(เอ็กซ์), ที่

ในกรณีนี้ การมีอยู่ของความคาดหวังทางคณิตศาสตร์จะเทียบเท่ากับการลู่เข้าสัมบูรณ์ของอนุกรมหรืออินทิกรัลที่สอดคล้องกัน

คุณสมบัติของความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่ม

• ความคาดหวังทางคณิตศาสตร์ของค่าคงที่จะเท่ากับค่านี้:

ค- คงที่;

• M=CM[X]

• ความคาดหวังทางคณิตศาสตร์ของผลรวมของค่าที่สุ่มมาจะเท่ากับผลรวมของความคาดหวังทางคณิตศาสตร์:

• ความคาดหวังทางคณิตศาสตร์ของผลิตภัณฑ์ของตัวแปรสุ่มอิสระ = ผลคูณของความคาดหวังทางคณิตศาสตร์:

ม=ม[X]+ม[ย]

ถ้า เอ็กซ์และ ยเป็นอิสระ.

หากซีรีส์มาบรรจบกัน:

อัลกอริทึมสำหรับการคำนวณความคาดหวังทางคณิตศาสตร์

คุณสมบัติของตัวแปรสุ่มแบบไม่ต่อเนื่อง: ค่าทั้งหมดสามารถกำหนดหมายเลขใหม่ได้ ตัวเลขธรรมชาติ- กำหนดค่าความน่าจะเป็นที่ไม่เป็นศูนย์ให้กับแต่ละค่า

1. คูณคู่ทีละคู่: x ฉันบน พี ฉัน.

2. เพิ่มสินค้าของแต่ละคู่ x ฉัน ฉัน.

ตัวอย่างเช่น, สำหรับ n = 4 :

ฟังก์ชันการกระจายของตัวแปรสุ่มแบบไม่ต่อเนื่องจะเพิ่มขึ้นอย่างกะทันหันที่จุดที่มีความน่าจะเป็นเป็นสัญญาณบวก

ตัวอย่าง:ค้นหาความคาดหวังทางคณิตศาสตร์โดยใช้สูตร

– จำนวนเด็กผู้ชายในจำนวนทารกแรกเกิด 10 คน

เป็นที่ชัดเจนอย่างยิ่งว่าไม่ทราบจำนวนนี้ล่วงหน้า และเด็ก 10 คนถัดไปที่เกิดอาจรวมถึง:

หรือเด็กผู้ชาย - หนึ่งเดียวเท่านั้นจากตัวเลือกที่แสดงไว้

และเพื่อรักษารูปร่างให้มีการพลศึกษาเล็กน้อย:

– ระยะกระโดดไกล (ในบางยูนิต).

แม้แต่ผู้เชี่ยวชาญด้านกีฬาก็ไม่สามารถคาดเดาได้ :)

อย่างไรก็ตาม สมมติฐานของคุณ?

2) ตัวแปรสุ่มต่อเนื่อง – ยอมรับ ทั้งหมดค่าตัวเลขจากช่วงจำกัดหรือช่วงอนันต์

บันทึก : วี วรรณกรรมการศึกษาตัวย่อยอดนิยม DSV และ NSV

ก่อนอื่น เรามาวิเคราะห์ตัวแปรสุ่มแบบไม่ต่อเนื่องกันก่อน จากนั้น - อย่างต่อเนื่อง.

กฎการกระจายของตัวแปรสุ่มแบบไม่ต่อเนื่อง

- นี้ การโต้ตอบระหว่างค่าที่เป็นไปได้ของปริมาณนี้และความน่าจะเป็น บ่อยครั้งที่กฎหมายเขียนไว้ในตาราง:

คำนี้ใช้ค่อนข้างบ่อย แถว การกระจายแต่ในบางสถานการณ์อาจฟังดูคลุมเครือ ดังนั้นฉันจะยึดติดกับ "กฎหมาย"

และตอนนี้ มาก จุดสำคัญ : เนื่องจากเป็นตัวแปรสุ่ม จำเป็นจะยอมรับ หนึ่งในค่านิยมจากนั้นเหตุการณ์ที่เกี่ยวข้องจะเกิดขึ้น เต็มกลุ่มและผลรวมของความน่าจะเป็นของการเกิดขึ้นมีค่าเท่ากับหนึ่ง:

หรือถ้าเขียนย่อ:

ตัวอย่างเช่น กฎการกระจายความน่าจะเป็นของแต้มที่ทอยได้ มุมมองถัดไป:

ไม่มีความคิดเห็น

คุณอาจรู้สึกว่าตัวแปรสุ่มแบบแยกสามารถรับเฉพาะค่าจำนวนเต็ม "ดี" เท่านั้น มาปัดเป่าภาพลวงตา - พวกมันสามารถเป็นอะไรก็ได้:

ตัวอย่างที่ 1

เกมบางเกมมีกฎการจำหน่ายที่ชนะดังต่อไปนี้:

...คุณคงฝันถึงงานแบบนี้มานานแล้ว :) ฉันจะบอกความลับกับคุณ - ฉันก็เหมือนกัน โดยเฉพาะหลังจากทำงานเสร็จแล้ว ทฤษฎีภาคสนาม.

สารละลาย: เนื่องจากตัวแปรสุ่มสามารถรับค่าได้เพียงค่าเดียวจากสามค่า เหตุการณ์จึงจะเกิดขึ้น เต็มกลุ่มซึ่งหมายความว่าผลรวมของความน่าจะเป็นมีค่าเท่ากับหนึ่ง:

การเปิดเผย "พรรคพวก":

– ดังนั้น ความน่าจะเป็นที่จะชนะหน่วยทั่วไปคือ 0.4

การควบคุม: นั่นคือสิ่งที่เราต้องทำให้แน่ใจ

คำตอบ:

ไม่ใช่เรื่องแปลกเมื่อคุณจำเป็นต้องร่างกฎหมายการจำหน่ายด้วยตัวเอง สำหรับสิ่งนี้พวกเขาใช้ คำจำกัดความคลาสสิกของความน่าจะเป็น, ทฤษฎีบทการคูณ/การบวกสำหรับความน่าจะเป็นของเหตุการณ์และชิปอื่นๆ เทอร์เวรา:

ตัวอย่างที่ 2

กล่องมี 50 ตั๋วลอตเตอรีในจำนวนนี้มีผู้ชนะ 12 คนและ 2 คนชนะรางวัลละ 1,000 รูเบิลและที่เหลือ - 100 รูเบิลต่อคน ร่างกฎหมายสำหรับการแจกแจงตัวแปรสุ่ม - ขนาดของเงินรางวัลหากมีการสุ่มตั๋วหนึ่งใบจากกล่อง

สารละลาย: อย่างที่คุณสังเกต ค่าของตัวแปรสุ่มมักจะถูกวางไว้ในนั้น ตามลำดับจากน้อยไปหามาก- ดังนั้นเราจึงเริ่มต้นด้วยเงินรางวัลที่น้อยที่สุดนั่นคือรูเบิล

มีตั๋วทั้งหมด 50 ใบ - 12 = 38 และตาม คำจำกัดความแบบคลาสสิก:
– ความน่าจะเป็นที่ตั๋วสุ่มจะเป็นผู้แพ้

ในกรณีอื่นๆ ทุกอย่างก็เรียบง่าย ความน่าจะเป็นที่จะชนะรูเบิลคือ:

ตรวจสอบ: – และนี่เป็นช่วงเวลาที่น่ายินดีอย่างยิ่งของงานดังกล่าว!

คำตอบ: กฎการกระจายเงินรางวัลที่ต้องการ:

ภารกิจต่อไปสำหรับ การตัดสินใจที่เป็นอิสระ:

ตัวอย่างที่ 3

ความน่าจะเป็นที่ผู้ยิงจะโดนเป้าหมายคือ ร่างกฎการกระจายสำหรับตัวแปรสุ่ม - จำนวนการเข้าชมหลังจาก 2 ช็อต

...ฉันรู้ว่าเธอคิดถึงเขา :) จำไว้นะ ทฤษฎีบทการคูณและการบวก- คำตอบและคำตอบอยู่ท้ายบทเรียน

กฎการกระจายอธิบายตัวแปรสุ่มอย่างสมบูรณ์ แต่ในทางปฏิบัติ อาจมีประโยชน์ (และบางครั้งก็มีประโยชน์มากกว่า) ที่รู้เพียงบางส่วนเท่านั้น ลักษณะเชิงตัวเลข .

ความคาดหวังของตัวแปรสุ่มแบบไม่ต่อเนื่อง

การพูด ในภาษาง่ายๆ, นี้ มูลค่าที่คาดหวังโดยเฉลี่ยเมื่อทำการทดสอบซ้ำหลายครั้ง ให้ตัวแปรสุ่มนำค่าที่มีความน่าจะเป็น ตามลำดับ จากนั้นความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่มนี้จะเท่ากับ ผลรวมของผลิตภัณฑ์ค่าทั้งหมดตามความน่าจะเป็นที่สอดคล้องกัน:

หรือยุบ:

ให้เราคำนวณความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่ม - จำนวนคะแนนที่กลิ้งบนลูกเต๋า:

ตอนนี้เรามาจำเกมสมมุติของเรา:

คำถามเกิดขึ้น: การเล่นเกมนี้มีกำไรหรือไม่? ...ใครมีความประทับใจบ้าง? ดังนั้นคุณไม่สามารถพูดว่า "ตรงไปตรงมา" ได้! แต่คำถามนี้สามารถตอบได้อย่างง่ายดายโดยการคำนวณความคาดหวังทางคณิตศาสตร์ โดยพื้นฐานแล้ว - ถัวเฉลี่ยถ่วงน้ำหนักตามความน่าจะเป็นที่จะชนะ:

ดังนั้นความคาดหวังทางคณิตศาสตร์ของเกมนี้ การสูญเสีย.

อย่าเชื่อความประทับใจของคุณ - เชื่อตัวเลข!

ใช่ ที่นี่คุณสามารถชนะ 10 หรือ 20-30 ครั้งติดต่อกัน แต่ในระยะยาว เราจะเผชิญกับความหายนะที่หลีกเลี่ยงไม่ได้ และฉันจะไม่แนะนำให้คุณเล่นเกมประเภทนี้ :) อาจจะเท่านั้น เพื่อความสนุกสนาน.

จากที่กล่าวมาทั้งหมด เป็นไปตามที่คาดหวังทางคณิตศาสตร์ไม่ใช่ค่าสุ่มอีกต่อไป

งานสร้างสรรค์สำหรับการวิจัยอิสระ:

ตัวอย่างที่ 4

Mr. X เล่นรูเล็ตยุโรปโดยใช้ระบบต่อไปนี้: เขาเดิมพัน 100 รูเบิลกับ "สีแดง" อย่างต่อเนื่อง ร่างกฎการกระจายของตัวแปรสุ่ม - เงินรางวัล คำนวณความคาดหวังทางคณิตศาสตร์ของการชนะและปัดเศษให้เป็น kopeck ที่ใกล้ที่สุด เท่าไหร่ โดยเฉลี่ยผู้เล่นเสียเงินเดิมพันทุก ๆ ร้อยหรือไม่?

อ้างอิง : ยูโรเปียนรูเล็ตประกอบด้วย 18 สีแดง 18 สีดำ และ 1 สีเขียว (“ศูนย์”) หากมีการเปิดตัว “สีแดง” ผู้เล่นจะได้รับเงินเดิมพันสองเท่า มิฉะนั้นจะตกเป็นรายได้ของคาสิโน

มีระบบรูเล็ตอื่นๆ อีกมากมายที่คุณสามารถสร้างตารางความน่าจะเป็นของคุณเองได้ แต่ในกรณีนี้คือเมื่อเราไม่ต้องการกฎการกระจายและตารางใดๆ เนื่องจากมีการกำหนดไว้แล้วว่าความคาดหวังทางคณิตศาสตร์ของผู้เล่นจะเหมือนกันทุกประการ สิ่งเดียวที่เปลี่ยนจากระบบหนึ่งไปอีกระบบหนึ่งคือ

ความคาดหวังทางคณิตศาสตร์ ความคาดหวังทางคณิตศาสตร์ตัวแปรสุ่มแบบไม่ต่อเนื่อง เอ็กซ์, เจ้าภาพ หมายเลขสุดท้ายค่านิยม เอ็กซ์ฉันด้วยความน่าจะเป็น รฉันจำนวนเงินเรียกว่า:

ความคาดหวังทางคณิตศาสตร์ตัวแปรสุ่มต่อเนื่อง เอ็กซ์เรียกว่าอินทิกรัลของผลคูณของค่าของมัน เอ็กซ์เรื่องความหนาแน่นของการแจกแจงความน่าจะเป็น ฉ(x):

(6ข)

อินทิกรัลไม่เหมาะสม (6 ข) ถือว่ามาบรรจบกันอย่างแน่นอน (ไม่อย่างนั้นก็จะบอกว่าเป็นความคาดหวังทางคณิตศาสตร์ ม(เอ็กซ์) ไม่มีอยู่) ความคาดหวังทางคณิตศาสตร์มีลักษณะเฉพาะ ค่าเฉลี่ยตัวแปรสุ่ม เอ็กซ์- มิติของมันเกิดขึ้นพร้อมกับมิติของตัวแปรสุ่ม

คุณสมบัติของความคาดหวังทางคณิตศาสตร์:

การกระจายตัว ความแปรปรวนตัวแปรสุ่ม เอ็กซ์หมายเลขนี้เรียกว่า:

ความแปรปรวนคือ ลักษณะการกระเจิงค่าตัวแปรสุ่ม เอ็กซ์เทียบกับมูลค่าเฉลี่ยของมัน ม(เอ็กซ์- มิติของความแปรปรวนเท่ากับมิติของตัวแปรสุ่มกำลังสอง จากคำจำกัดความของความแปรปรวน (8) และความคาดหวังทางคณิตศาสตร์ (5) สำหรับตัวแปรสุ่มแบบไม่ต่อเนื่อง และ (6) สำหรับตัวแปรสุ่มแบบต่อเนื่อง เราได้นิพจน์ที่คล้ายกันสำหรับความแปรปรวน:

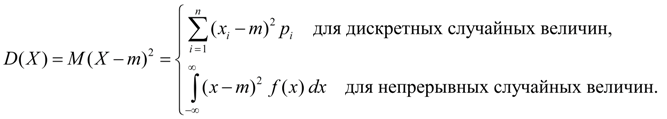(9)

ที่นี่ ม = ม(เอ็กซ์).

คุณสมบัติการกระจายตัว:

ส่วนเบี่ยงเบนมาตรฐาน:

(11)

เนื่องจากค่าเบี่ยงเบนมาตรฐานมีมิติเดียวกันกับตัวแปรสุ่ม จึงมักใช้เป็นหน่วยวัดการกระจายมากกว่าความแปรปรวน

ช่วงเวลาแห่งการแจกจ่าย แนวคิดเรื่องความคาดหวังและการกระจายตัวทางคณิตศาสตร์เป็นกรณีพิเศษมากกว่านั้น แนวคิดทั่วไปสำหรับคุณลักษณะเชิงตัวเลขของตัวแปรสุ่ม – ช่วงเวลาการกระจาย- โมเมนต์ของการแจกแจงของตัวแปรสุ่มถูกนำมาใช้เป็นความคาดหวังทางคณิตศาสตร์ของฟังก์ชันง่ายๆ ของตัวแปรสุ่ม ดังนั้นช่วงเวลาแห่งการสั่งซื้อ เคสัมพันธ์กับประเด็น เอ็กซ์ 0 เรียกว่าความคาดหวังทางคณิตศาสตร์ ม(เอ็กซ์–เอ็กซ์ 0 )เค- ช่วงเวลาเกี่ยวกับต้นกำเนิด เอ็กซ์= 0 ถูกเรียก ช่วงเวลาเริ่มต้น และถูกกำหนด:

(12)

ช่วงเวลาเริ่มต้นของลำดับแรกคือศูนย์กลางของการแจกแจงของตัวแปรสุ่มที่กำลังพิจารณา:

(13)

ช่วงเวลาเกี่ยวกับศูนย์กลางการกระจายสินค้า เอ็กซ์= มถูกเรียก จุดศูนย์กลางและถูกกำหนด:

(14)

จาก (7) ตามมาว่าโมเมนต์ศูนย์กลางอันดับหนึ่งจะเท่ากับศูนย์เสมอ:

โมเมนต์ศูนย์กลางไม่ได้ขึ้นอยู่กับที่มาของค่าของตัวแปรสุ่มเนื่องจากเมื่อเลื่อนด้วยค่าคงที่ กับศูนย์กลางการกระจายจะเปลี่ยนไปตามค่าเดียวกัน กับและการเบี่ยงเบนจากศูนย์กลางไม่เปลี่ยนแปลง: เอ็กซ์ – ม = (เอ็กซ์ – กับ) – (ม – กับ).
ตอนนี้ก็ชัดเจนว่า การกระจายตัว- นี้ ลำดับที่สอง ช่วงเวลากลาง:

ความไม่สมมาตร ช่วงเวลาสำคัญอันดับสาม:

(17)

ทำหน้าที่ในการประเมินผล ความไม่สมดุลในการกระจาย- ถ้าการกระจายตัวมีความสมมาตรเกี่ยวกับจุดนั้น เอ็กซ์= มจากนั้นโมเมนต์กลางลำดับที่สามจะเท่ากับศูนย์ (เหมือนกับโมเมนต์กลางทั้งหมดของคำสั่งคี่) ดังนั้น หากโมเมนต์ศูนย์กลางอันดับสามแตกต่างจากศูนย์ การกระจายตัวจะไม่สามารถสมมาตรได้ ขนาดของความไม่สมมาตรถูกประเมินโดยใช้สิ่งไร้มิติ ค่าสัมประสิทธิ์ความไม่สมดุล:

(18)

เครื่องหมายของค่าสัมประสิทธิ์ความไม่สมมาตร (18) บ่งบอกถึงความไม่สมมาตรด้านขวาหรือด้านซ้าย (รูปที่ 2)

ข้าว. 2. ประเภทของการกระจายไม่สมมาตร

ส่วนเกิน. ช่วงเวลาศูนย์กลางลำดับที่สี่:

(19)

ทำหน้าที่ประเมินสิ่งที่เรียกว่า ส่วนเกินซึ่งกำหนดระดับความชัน (ความแหลม) ของเส้นโค้งการกระจายใกล้กับจุดศูนย์กลางการกระจายสัมพันธ์กับเส้นโค้ง การกระจายตัวแบบปกติ- เนื่องจากการแจกแจงแบบปกติ ค่าที่ถือเป็นเคอร์โทซิสคือ:

(20)

ในรูป 3 แสดงตัวอย่างเส้นโค้งการกระจายตัวด้วย ความหมายที่แตกต่างกันส่วนเกิน. เพื่อการแจกแจงแบบปกติ อี= 0 เส้นโค้งที่มีจุดสูงสุดมากกว่าปกติจะมีความโด่งเป็นบวก ส่วนโค้งที่มียอดแบนมากกว่าจะมีความโด่งเป็นลบ

ข้าว. 3. เส้นโค้งการกระจายตัวด้วย องศาที่แตกต่างกันความเย็น (ส่วนเกิน)

ช่วงเวลาที่มีลำดับสูงกว่าในการใช้งานทางวิศวกรรม สถิติทางคณิตศาสตร์มักจะไม่ได้ใช้

แฟชั่น ไม่ต่อเนื่องตัวแปรสุ่มคือค่าที่เป็นไปได้มากที่สุด แฟชั่น อย่างต่อเนื่องตัวแปรสุ่มคือค่าที่ความหนาแน่นของความน่าจะเป็นสูงสุด (รูปที่ 2) หากเส้นโค้งการกระจายมีค่าสูงสุดหนึ่งเส้น การแจกแจงจะถูกเรียก ยูนิโมดัล- หากเส้นโค้งการกระจายมีค่าสูงสุดมากกว่าหนึ่งเส้น การแจกแจงจะถูกเรียก ต่อเนื่องหลายรูปแบบ- บางครั้งมีการแจกแจงที่มีเส้นโค้งมีค่าต่ำสุดมากกว่าค่าสูงสุด การแจกแจงดังกล่าวเรียกว่า ต่อต้านกิริยา- ในกรณีทั่วไป โหมดและความคาดหวังทางคณิตศาสตร์ของตัวแปรสุ่มไม่ตรงกัน ในกรณีพิเศษ สำหรับ เป็นกิริยาช่วย, เช่น. มีโหมดการแจกแจงแบบสมมาตรและมีความคาดหวังทางคณิตศาสตร์ โหมดหลังจะเกิดขึ้นพร้อมกับโหมดและศูนย์กลางของสมมาตรของการแจกแจง

ค่ามัธยฐาน ตัวแปรสุ่ม เอ็กซ์- นี่คือความหมายของมัน เอิ่ม.ซึ่งมีความเท่าเทียมกัน: กล่าวคือ มีความเป็นไปได้เท่ากันว่าตัวแปรสุ่ม เอ็กซ์จะน้อยหรือมากกว่านั้น เอิ่ม.- ทางเรขาคณิต ค่ามัธยฐานคือค่าขาดของจุดที่พื้นที่ใต้เส้นโค้งการกระจายแบ่งออกเป็นครึ่งหนึ่ง (รูปที่ 2) ในกรณีของการแจกแจงแบบโมดอลแบบสมมาตร ค่ามัธยฐาน โหมด และความคาดหวังทางคณิตศาสตร์จะเหมือนกัน