ค้นหาเมทริกซ์ผกผันกับเมทริกซ์ที่กำหนด a ค้นหาเมทริกซ์ผกผันออนไลน์

การหาเมทริกซ์ผกผัน- ปัญหาที่มักแก้ไขได้ด้วยสองวิธี:

วิธีการบวกพีชคณิตซึ่งต้องมีการค้นหาดีเทอร์มิแนนต์และการทรานสโพสเมทริกซ์
วิธีเกาส์เซียนในการกำจัดสิ่งที่ไม่รู้จัก ซึ่งต้องทำการแปลงเมทริกซ์เบื้องต้น (เพิ่มแถว คูณแถวด้วยจำนวนเดียวกัน ฯลฯ)

สำหรับผู้ที่สงสัยเป็นพิเศษ ยังมีวิธีอื่นๆ อีก เช่น วิธีแปลงเชิงเส้น ในบทนี้ เราจะวิเคราะห์วิธีการและอัลกอริธึมทั้งสามที่กล่าวถึงในการค้นหาเมทริกซ์ผกผันโดยใช้วิธีการเหล่านี้

เมทริกซ์ผกผัน กเรียกว่าเมทริกซ์ดังกล่าว

ก
. (1)

เมทริกซ์ผกผัน ซึ่งจำเป็นต้องค้นหาสำหรับเมทริกซ์จตุรัสที่กำหนด กเรียกว่าเมทริกซ์ดังกล่าว

ผลคูณของเมทริกซ์นั้น กทางด้านขวาคือเมทริกซ์เอกลักษณ์ เช่น
. (1)

เมทริกซ์เอกลักษณ์คือเมทริกซ์แนวทแยงซึ่งองค์ประกอบในแนวทแยงทั้งหมดมีค่าเท่ากับหนึ่ง

ทฤษฎีบท.สำหรับเมทริกซ์จตุรัสที่ไม่เป็นเอกพจน์ (ไม่เสื่อมและไม่เอกพจน์) ทุกเมทริกซ์ เราสามารถหาเมทริกซ์ผกผันได้เพียงเมทริกซ์เดียวเท่านั้น สำหรับเมทริกซ์จตุรัสพิเศษ (เสื่อมลง เอกพจน์) จะไม่มีเมทริกซ์ผกผัน

เรียกว่าเมทริกซ์จตุรัส ไม่พิเศษ(หรือ ไม่เสื่อม, ไม่ใช่เอกพจน์) ถ้าดีเทอร์มิแนนต์ไม่เป็นศูนย์ และ พิเศษ(หรือ เสื่อมโทรม, เอกพจน์) ถ้าดีเทอร์มิแนนต์เป็นศูนย์

ค่าผกผันของเมทริกซ์สามารถพบได้สำหรับเมทริกซ์จตุรัสเท่านั้น โดยปกติแล้ว เมทริกซ์ผกผันจะเป็นสี่เหลี่ยมจัตุรัสและอยู่ในลำดับเดียวกับเมทริกซ์ที่กำหนด เมทริกซ์ที่สามารถหาเมทริกซ์ผกผันได้เรียกว่าเมทริกซ์ผกผัน

สำหรับ เมทริกซ์ผกผัน มีความคล้ายคลึงที่เกี่ยวข้องกับค่าผกผันของตัวเลข สำหรับทุกหมายเลข กไม่เท่ากับศูนย์ก็มีจำนวนดังกล่าว ขว่างานนั้น กและ ขเท่ากับหนึ่ง: เกี่ยวกับ= 1 . ตัวเลข ขเรียกว่าค่าผกผันของจำนวน ข- ตัวอย่างเช่น สำหรับเลข 7 ส่วนกลับคือ 1/7 เนื่องจาก 7*1/7=1

การค้นหาเมทริกซ์ผกผันโดยใช้วิธีการบวกพีชคณิต (เมทริกซ์สัมพัทธ์)

สำหรับเมทริกซ์จตุรัสที่ไม่เป็นเอกพจน์ กส่วนผกผันคือเมทริกซ์

ดีเทอร์มิแนนต์ของเมทริกซ์อยู่ที่ไหน ก, a เป็นเมทริกซ์ที่เป็นพันธมิตรกับเมทริกซ์ ก.

เชื่อมโยงกับเมทริกซ์จตุรัส กคือเมทริกซ์ที่มีลำดับเดียวกัน องค์ประกอบซึ่งเป็นส่วนเสริมพีชคณิตขององค์ประกอบที่สอดคล้องกันของดีเทอร์มีแนนต์ของเมทริกซ์ที่ย้ายเทียบกับเมทริกซ์ A ดังนั้น ถ้า

ที่

และ

อัลกอริทึมในการค้นหาเมทริกซ์ผกผันโดยใช้วิธีการบวกพีชคณิต

1. ค้นหาดีเทอร์มิแนนต์ของเมทริกซ์นี้ ก- หากดีเทอร์มิแนนต์มีค่าเท่ากับศูนย์ การค้นหาเมทริกซ์ผกผันจะหยุดลง เนื่องจากเมทริกซ์เป็นเอกพจน์และไม่มีค่าผกผัน

2. ค้นหาเมทริกซ์ที่ถูกย้ายด้วยความเคารพ ก.

3. คำนวณองค์ประกอบของเมทริกซ์ยูเนียนเป็นการเสริมเชิงพีชคณิตของมาริทซ์ที่พบในขั้นตอนที่ 2

4. ใช้สูตร (2): คูณค่าผกผันของตัวกำหนดเมทริกซ์ กไปยังเมทริกซ์ยูเนียนที่พบในขั้นตอนที่ 4

5. ตรวจสอบผลลัพธ์ที่ได้ในขั้นตอนที่ 4 โดยการคูณเมทริกซ์นี้ กถึงเมทริกซ์ผกผัน ถ้าผลคูณของเมทริกซ์เหล่านี้เท่ากับเมทริกซ์เอกลักษณ์ ก็จะพบเมทริกซ์ผกผันได้ถูกต้อง มิฉะนั้น ให้เริ่มกระบวนการแก้ไขปัญหาอีกครั้ง

ตัวอย่างที่ 1สำหรับเมทริกซ์

ค้นหาเมทริกซ์ผกผัน

สารละลาย. ในการค้นหาเมทริกซ์ผกผัน คุณต้องค้นหาดีเทอร์มีแนนต์ของเมทริกซ์ ก- เราพบตามกฎของสามเหลี่ยม:

ดังนั้นเมทริกซ์ ก– ไม่เอกพจน์ (ไม่เสื่อม ไม่เอกพจน์) และมีการผกผันกับมัน

ลองหาเมทริกซ์ที่สัมพันธ์กับเมทริกซ์นี้กัน ก.

ลองหาเมทริกซ์ที่ย้ายเทียบกับเมทริกซ์กัน ก:

เราคำนวณองค์ประกอบของเมทริกซ์พันธมิตรเป็นการเสริมเชิงพีชคณิตของเมทริกซ์ที่ย้ายเทียบกับเมทริกซ์ ก:

ดังนั้นเมทริกซ์จึงสัมพันธ์กับเมทริกซ์ ก,มีรูปแบบ

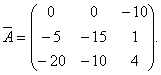
ความคิดเห็นลำดับที่คำนวณองค์ประกอบและเมทริกซ์ถูกย้ายอาจแตกต่างกัน ขั้นแรกคุณสามารถคำนวณการเสริมพีชคณิตของเมทริกซ์ได้ กแล้วย้ายเมทริกซ์ส่วนเติมเต็มพีชคณิต ผลลัพธ์ควรเป็นองค์ประกอบเดียวกันของเมทริกซ์ยูเนียน

การใช้สูตร (2) เราจะพบเมทริกซ์ผกผันกับเมทริกซ์ ก:

การค้นหาเมทริกซ์ผกผันโดยใช้วิธีการกำจัดแบบไม่ทราบค่าแบบเกาส์เซียน

ขั้นตอนแรกในการค้นหาเมทริกซ์ผกผันโดยใช้วิธีกำจัดแบบเกาส์เซียนคือการกำหนดให้กับเมทริกซ์ กเมทริกซ์ประจำตัวที่มีลำดับเดียวกัน โดยคั่นด้วยแถบแนวตั้ง เราจะได้เมทริกซ์คู่ ลองคูณทั้งสองข้างของเมทริกซ์นี้ด้วย แล้วเราจะได้

อัลกอริทึมในการค้นหาเมทริกซ์ผกผันโดยใช้วิธีกำจัดแบบไม่ทราบค่าแบบเกาส์เซียน

1. ไปที่เมทริกซ์ กกำหนดเมทริกซ์เอกลักษณ์ในลำดับเดียวกัน

2. แปลงผลลัพธ์ของเมทริกซ์คู่เพื่อให้ทางด้านซ้ายคุณจะได้เมทริกซ์หน่วย จากนั้นทางด้านขวา คุณจะได้เมทริกซ์ผกผันโดยอัตโนมัติ แทนที่จะเป็นเมทริกซ์เอกลักษณ์ เมทริกซ์ กทางด้านซ้ายจะถูกแปลงเป็นเมทริกซ์เอกลักษณ์โดยการแปลงเมทริกซ์เบื้องต้น

2. หากอยู่ในกระบวนการแปลงเมทริกซ์ กในเมทริกซ์เอกลักษณ์จะมีเพียงศูนย์ในแถวหรือคอลัมน์ใด ๆ จากนั้นดีเทอร์มิแนนต์ของเมทริกซ์จะเท่ากับศูนย์ และด้วยเหตุนี้เมทริกซ์ กจะเป็นเอกพจน์ และไม่มีเมทริกซ์ผกผัน ในกรณีนี้ การพิจารณาเพิ่มเติมของเมทริกซ์ผกผันจะหยุดลง

ตัวอย่างที่ 2สำหรับเมทริกซ์

ค้นหาเมทริกซ์ผกผัน

และเราจะแปลงมันเพื่อว่าทางด้านซ้ายเราจะได้เมทริกซ์เอกลักษณ์ เราเริ่มการเปลี่ยนแปลง

คูณแถวแรกของเมทริกซ์ด้านซ้ายและขวาด้วย (-3) แล้วบวกเข้ากับแถวที่สอง จากนั้นคูณแถวแรกด้วย (-4) แล้วบวกเข้ากับแถวที่สาม จากนั้นเราจะได้

เพื่อให้แน่ใจว่าไม่มีเศษส่วนในการแปลงครั้งต่อๆ ไป ให้เราสร้างหน่วยในแถวที่สองทางด้านซ้ายของเมทริกซ์คู่ก่อน เมื่อต้องการทำเช่นนี้ ให้คูณบรรทัดที่สองด้วย 2 แล้วลบบรรทัดที่สามจากนั้นเราจะได้

ลองเพิ่มบรรทัดแรกด้วยบรรทัดที่สอง จากนั้นคูณบรรทัดที่สองด้วย (-9) แล้วบวกกับบรรทัดที่สาม แล้วเราก็ได้

จากนั้นหารบรรทัดที่สามด้วย 8

คูณบรรทัดที่สามด้วย 2 แล้วบวกเข้ากับบรรทัดที่สอง ปรากฎว่า:

มาสลับบรรทัดที่สองและสามกัน แล้วในที่สุดเราก็จะได้:

เราจะเห็นว่าทางด้านซ้ายเรามีเมทริกซ์เอกลักษณ์ ดังนั้นทางด้านขวาเรามีเมทริกซ์ผกผัน ดังนั้น:

คุณสามารถตรวจสอบความถูกต้องของการคำนวณได้โดยการคูณเมทริกซ์ดั้งเดิมด้วยเมทริกซ์ผกผันที่พบ:

ผลลัพธ์ควรเป็นเมทริกซ์ผกผัน

ตัวอย่างที่ 3สำหรับเมทริกซ์

ค้นหาเมทริกซ์ผกผัน

สารละลาย. การรวบรวมเมทริกซ์คู่

และเราจะเปลี่ยนแปลงมัน

เราคูณบรรทัดแรกด้วย 3 และบรรทัดที่สองด้วย 2 แล้วลบออกจากบรรทัดที่สอง จากนั้นเราคูณบรรทัดแรกด้วย 5 และบรรทัดที่สามด้วย 2 แล้วลบออกจากบรรทัดที่สาม แล้วเราจะได้

เราคูณบรรทัดแรกด้วย 2 แล้วบวกเข้ากับบรรทัดที่สอง แล้วลบบรรทัดที่สองออกจากบรรทัดที่สาม จากนั้นเราจะได้

เราจะเห็นว่าในบรรทัดที่สามทางด้านซ้าย องค์ประกอบทั้งหมดมีค่าเท่ากับศูนย์ ดังนั้นเมทริกซ์จึงเป็นเอกพจน์และไม่มีเมทริกซ์ผกผัน เราหยุดการค้นหามาริทซ์ผกผันอีกต่อไป

วิธีการหาเมทริกซ์ผกผัน พิจารณาเมทริกซ์จตุรัส

ให้เราแสดงว่า Δ =det A.

เรียกว่าเมทริกซ์จตุรัส A ไม่เสื่อมโทรมหรือ ไม่พิเศษถ้าดีเทอร์มิแนนต์ไม่เป็นศูนย์ และ เสื่อมถอย,หรือ พิเศษ, ถ้าΔ = 0.

เมทริกซ์จัตุรัส B ใช้สำหรับเมทริกซ์จัตุรัส A ที่มีลำดับเดียวกัน หากผลคูณของเมทริกซ์คือ A B = B A = E โดยที่ E คือเมทริกซ์เอกลักษณ์ที่มีลำดับเดียวกันกับเมทริกซ์ A และ B

ทฤษฎีบท . เพื่อให้เมทริกซ์ A มีเมทริกซ์ผกผัน จำเป็นและเพียงพอที่ปัจจัยกำหนดของมันจะแตกต่างจากศูนย์

เมทริกซ์ผกผันของเมทริกซ์ A เขียนแทนด้วย A- 1 ดังนั้น B = A - 1 และคำนวณตามสูตร

, (1)

โดยที่ A i j เป็นส่วนเสริมพีชคณิตขององค์ประกอบ a i j ของเมทริกซ์ A..

การคำนวณ A -1 โดยใช้สูตร (1) สำหรับเมทริกซ์ระดับสูงนั้นต้องใช้แรงงานมาก ดังนั้นในทางปฏิบัติ จึงสะดวกที่จะหา A -1 โดยใช้วิธีการแปลงเบื้องต้น (ET) เมทริกซ์ A ที่ไม่ใช่เอกพจน์ใดๆ สามารถลดลงเป็นเมทริกซ์เอกลักษณ์ E ได้โดยใช้ ED ของคอลัมน์เท่านั้น (หรือเฉพาะแถว) ถ้า ED ที่ถูกทำให้สมบูรณ์เหนือเมทริกซ์ A ถูกนำไปใช้ในลำดับเดียวกันกับเมทริกซ์เอกลักษณ์ E แล้วผลลัพธ์ก็คือ เมทริกซ์ผกผัน สะดวกในการแสดง EP บนเมทริกซ์ A และ E พร้อมๆ กัน โดยเขียนเมทริกซ์ทั้งสองแบบเคียงข้างกันผ่านเส้นตรง โปรดทราบอีกครั้งว่าเมื่อค้นหารูปแบบมาตรฐานของเมทริกซ์ เพื่อที่จะค้นหา คุณสามารถใช้การแปลงแถวและคอลัมน์ได้ หากคุณต้องการค้นหาค่าผกผันของเมทริกซ์ คุณควรใช้เฉพาะแถวหรือคอลัมน์เท่านั้นในระหว่างขั้นตอนการแปลง

ตัวอย่าง 2.10- สำหรับเมทริกซ์ หา A -1 .

สารละลาย.อันดับแรก เราจะหาดีเทอร์มิแนนต์ของเมทริกซ์ A
ซึ่งหมายความว่ามีเมทริกซ์ผกผันอยู่ และเราสามารถค้นหาได้โดยใช้สูตร: โดยที่ A i j (i,j=1,2,3) คือการบวกพีชคณิตขององค์ประกอบ a i j ของเมทริกซ์ดั้งเดิม

ที่ไหน .

ตัวอย่าง 2.11- โดยใช้วิธีการแปลงเบื้องต้น หา A -1 สำหรับเมทริกซ์: A =

สารละลาย.เรากำหนดเมทริกซ์เอกลักษณ์ที่มีลำดับเดียวกันให้กับเมทริกซ์ดั้งเดิมทางด้านขวา: - เมื่อใช้การแปลงเบื้องต้นของคอลัมน์ เราจะลด "ครึ่ง" ด้านซ้ายให้เหลือเพียงค่าเอกลักษณ์หนึ่ง โดยดำเนินการแปลงเดียวกันทุกประการบนเมทริกซ์ด้านขวา
เมื่อต้องการทำเช่นนี้ ให้สลับคอลัมน์แรกและคอลัมน์ที่สอง: ~ - เราเพิ่มคอลัมน์แรกลงในคอลัมน์ที่สามและคอลัมน์ที่สอง - คอลัมน์แรกคูณด้วย -2: - จากคอลัมน์แรกเราลบคอลัมน์ที่สองเป็นสองเท่าและจากคอลัมน์ที่สาม - คอลัมน์ที่สองคูณด้วย 6 - เพิ่มคอลัมน์ที่สามลงในคอลัมน์แรกและคอลัมน์ที่สอง: - คูณคอลัมน์สุดท้ายด้วย -1: - เมทริกซ์จตุรัสที่ได้รับทางด้านขวาของแถบแนวตั้งคือเมทริกซ์ผกผันของเมทริกซ์ A ที่กำหนด ดังนั้น
.

ในส่วนแรก เรามาดูวิธีการค้นหาเมทริกซ์ผกผันโดยใช้การบวกพีชคณิต ในที่นี้เราจะอธิบายอีกวิธีหนึ่งในการค้นหาเมทริกซ์ผกผัน: โดยใช้การแปลงแบบเกาส์เซียนและเกาส์-จอร์แดน วิธีการค้นหาเมทริกซ์ผกผันนี้มักเรียกว่าวิธีการแปลงเบื้องต้น

วิธีการแปลงเบื้องต้น

หากต้องการใช้วิธีนี้ เมทริกซ์ $A$ และเมทริกซ์เอกลักษณ์ $E$ ที่กำหนดจะถูกเขียนลงในเมทริกซ์เดียว กล่าวคือ สร้างเมทริกซ์ของรูปแบบ $(A|E)$ (เมทริกซ์นี้เรียกอีกอย่างว่าส่วนขยาย) หลังจากนี้ ด้วยความช่วยเหลือของการแปลงเบื้องต้นที่ดำเนินการกับแถวของเมทริกซ์ขยาย จะรับประกันว่าเมทริกซ์ทางด้านซ้ายของเส้นจะกลายเป็นเอกลักษณ์ และเมทริกซ์ขยายจะอยู่ในรูปแบบ $\left(E| A^(- 1) \ขวา)$ การเปลี่ยนแปลงเบื้องต้นในสถานการณ์นี้รวมถึงการดำเนินการต่อไปนี้:

แทนที่สองบรรทัด
การคูณองค์ประกอบทั้งหมดของสตริงด้วยตัวเลขที่ไม่เท่ากับศูนย์
การเพิ่มองค์ประกอบที่สอดคล้องกันของอีกแถวหนึ่งลงในองค์ประกอบของแถวหนึ่งคูณด้วยปัจจัยใด ๆ

การแปลงเบื้องต้นเหล่านี้สามารถนำไปใช้ได้หลายวิธี โดยทั่วไปจะเลือกวิธีเกาส์เซียนหรือวิธีเกาส์-จอร์แดน โดยทั่วไป วิธีเกาส์และเกาส์-จอร์แดนมีไว้สำหรับแก้ระบบสมการพีชคณิตเชิงเส้น ไม่ใช่สำหรับการค้นหาเมทริกซ์ผกผัน วลี “การใช้วิธีเกาส์เซียนเพื่อค้นหาเมทริกซ์ผกผัน” ควรเข้าใจในที่นี้ว่า “การใช้การดำเนินการที่มีอยู่ในวิธีเกาส์เซียนเพื่อค้นหาเมทริกซ์ผกผัน”

การเรียงลำดับตัวอย่างต่อจากส่วนแรก ตัวอย่างจะอภิปรายถึงการใช้วิธีเกาส์ในการค้นหาเมทริกซ์ผกผัน และตัวอย่างอภิปรายเกี่ยวกับการใช้วิธีเกาส์-จอร์แดน ควรสังเกตว่าหากในระหว่างการแก้ปัญหาองค์ประกอบทั้งหมดของแถวหรือคอลัมน์ของเมทริกซ์ที่อยู่ก่อนบรรทัดจะถูกรีเซ็ตเป็นศูนย์แสดงว่าไม่มีเมทริกซ์ผกผัน

ตัวอย่างหมายเลข 5

ค้นหาเมทริกซ์ $A^(-1)$ ถ้า $A=\left(\begin(array) (ccc) 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end( อาร์เรย์) \right)$

ในตัวอย่างนี้ เมทริกซ์ผกผันจะพบได้โดยใช้วิธีเกาส์เซียน เมทริกซ์แบบขยาย ซึ่งโดยทั่วไปจะมีรูปแบบ $(A|E)$ ในตัวอย่างนี้จะอยู่ในรูปแบบต่อไปนี้: $ \left(\begin(array) (ccc|ccc) 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end(อาร์เรย์) \right)$

เป้าหมาย: ใช้การแปลงเบื้องต้น นำเมทริกซ์ขยายมาอยู่ในรูปแบบ $\left(E|A^(-1) \right)$ ให้เราใช้การดำเนินการเดียวกันกับที่ใช้ในการแก้ระบบสมการเชิงเส้นโดยใช้วิธีเกาส์ หากต้องการใช้วิธีเกาส์เซียน จะสะดวกเมื่อองค์ประกอบแรกของแถวแรกของเมทริกซ์แบบขยายเป็นองค์ประกอบเดียว เพื่อให้บรรลุเป้าหมายนี้ เราสลับแถวแรกและแถวที่สามของเมทริกซ์ที่ขยาย ซึ่งกลายเป็น: $ \left(\begin(array) (ccc|ccc) 1 & -1 & 3 & 0 & 0 & 1 \\ 2 & 5 & - 4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end(อาร์เรย์) \right)$

ตอนนี้เรามาดูวิธีแก้ปัญหากันดีกว่า วิธีเกาส์แบ่งออกเป็นสองขั้นตอน: ไปข้างหน้าและข้างหลัง (คำอธิบายโดยละเอียดของวิธีการแก้ระบบสมการนี้มีอยู่ในตัวอย่างของหัวข้อที่เกี่ยวข้อง) สองขั้นตอนเดียวกันนี้จะถูกนำไปใช้ในกระบวนการค้นหาเมทริกซ์ผกผัน

จังหวะตรง

ขั้นตอนแรก

เมื่อใช้บรรทัดแรก เราจะรีเซ็ตองค์ประกอบของคอลัมน์แรกที่อยู่ใต้บรรทัดแรก:

ฉันขอแสดงความคิดเห็นเล็กน้อยเกี่ยวกับการกระทำที่ทำ สัญกรณ์ $II-2\cdot I$ หมายความว่าองค์ประกอบที่สอดคล้องกันของแถวแรกซึ่งก่อนหน้านี้คูณด้วยสอง ถูกลบออกจากองค์ประกอบของแถวที่สอง การดำเนินการนี้สามารถเขียนแยกกันได้ดังนี้:

การดำเนินการ $III-7\cdot I$ ดำเนินการในลักษณะเดียวกันทุกประการ หากมีปัญหาในการดำเนินการเหล่านี้ ก็สามารถดำเนินการแยกกันได้ (คล้ายกับการดำเนินการ $II-2\cdot I$ ที่แสดงด้านบน) จากนั้นจึงสามารถป้อนผลลัพธ์ลงในเมทริกซ์ขยายได้

ขั้นตอนที่สอง

เมื่อใช้บรรทัดที่สอง เราจะรีเซ็ตองค์ประกอบของคอลัมน์ที่สองซึ่งอยู่ใต้บรรทัดที่สอง:

แบ่งบรรทัดที่สามด้วย 5:

การย้ายโดยตรงสิ้นสุดลงแล้ว องค์ประกอบทั้งหมดที่อยู่ใต้เส้นทแยงมุมหลักของเมทริกซ์จนถึงเส้นจะถูกรีเซ็ตเป็นศูนย์

จังหวะย้อนกลับ

ขั้นตอนแรก

เมื่อใช้บรรทัดที่สาม เราจะรีเซ็ตองค์ประกอบของคอลัมน์ที่สามซึ่งอยู่เหนือบรรทัดที่สาม:

ก่อนที่จะไปยังขั้นตอนถัดไป ให้หารบรรทัดที่สองด้วย $7$:

ขั้นตอนที่สอง

เมื่อใช้บรรทัดที่สอง เราจะรีเซ็ตองค์ประกอบของคอลัมน์ที่สองซึ่งอยู่เหนือบรรทัดที่สอง:

การแปลงเสร็จสมบูรณ์ พบเมทริกซ์ผกผันโดยใช้วิธีเกาส์เซียน: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \ \7/5 & -11/5 & -27/5 \end(อาร์เรย์) \right)$ การตรวจสอบ (หากจำเป็น) สามารถทำได้ในลักษณะเดียวกับตัวอย่างก่อนหน้านี้ หากคุณข้ามคำอธิบายทั้งหมด วิธีแก้ไขจะมีลักษณะดังนี้:

คำตอบ: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/ 5 & -27/5 \end(array) \right)$.

ตัวอย่างหมายเลข 6

ค้นหาเมทริกซ์ $A^(-1)$ ถ้า $A=\left(\begin(array) (cccc) -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & -4 & -3 \\ 1 & 4 & 0 & 6 \end(อาร์เรย์) \right)$

ในการค้นหาเมทริกซ์ผกผันในตัวอย่างนี้ เราจะใช้การดำเนินการเดียวกันกับที่ใช้ในการแก้ระบบสมการเชิงเส้นโดยใช้วิธีเกาส์เซียน มีคำอธิบายโดยละเอียด แต่ที่นี่เราจะจำกัดตัวเองอยู่เพียงความคิดเห็นสั้นๆ เท่านั้น ลองเขียนเมทริกซ์ขยาย: $\left(\begin(array) (cccc|cccc) -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \end(อาร์เรย์) \right)$ ลองสลับแถวแรกและแถวที่สี่ของเมทริกซ์นี้: $\left(\begin(array) (cccc|cccc) 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end(อาร์เรย์) \right)$

จังหวะตรง

การแปลงไปข้างหน้าเสร็จสมบูรณ์ องค์ประกอบทั้งหมดที่อยู่ใต้เส้นทแยงมุมหลักของเมทริกซ์ทางด้านซ้ายของเส้นจะถูกรีเซ็ตเป็นศูนย์

จังหวะย้อนกลับ

พบเมทริกซ์ผกผันโดยใช้วิธีเกาส์เซียน $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19 /8 & - 117/16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & - 9/4 \ end(อาร์เรย์)\right)$. หากจำเป็น เราจะดำเนินการตรวจสอบในลักษณะเดียวกับตัวอย่างที่ 2 และหมายเลข 3

คำตอบ: $A^(-1)=\left(\begin(อาร์เรย์) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49 /16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end(อาร์เรย์) \ ขวา)$.

ตัวอย่างหมายเลข 7

ค้นหาเมทริกซ์ $A^(-1)$ ถ้า $A=\left(\begin(array) (ccc) 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end( อาร์เรย์) \right)$

ในการค้นหาเมทริกซ์ผกผัน เราใช้คุณลักษณะการดำเนินการของวิธีเกาส์-จอร์แดน ความแตกต่างจากวิธีเกาส์ที่กล่าวถึงในตัวอย่างก่อนหน้านี้ ก็คือ การแก้ปัญหาจะดำเนินการในขั้นตอนเดียว ฉันขอเตือนคุณว่าวิธีเกาส์เซียนแบ่งออกเป็น 2 ขั้นตอน: การเคลื่อนไปข้างหน้า (“ เราสร้าง” เลขศูนย์ใต้เส้นทแยงมุมหลักของเมทริกซ์ไปยังเส้น) และการเคลื่อนที่แบบย้อนกลับ (เรารีเซ็ตองค์ประกอบเหนือเส้นทแยงมุมหลักของเมทริกซ์ ไปที่บรรทัด) ในการคำนวณเมทริกซ์ผกผันโดยใช้วิธีเกาส์-จอร์แดน ไม่จำเป็นต้องมีวิธีการแก้ปัญหาสองขั้นตอน ขั้นแรก เรามาสร้างเมทริกซ์แบบขยาย: $(A|E)$:

$$ (A|E)=\left(\begin(array) (ccc|ccc) 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & -2 &0 & 0 & 1 \end(array) \right) $$

ขั้นตอนแรก

มารีเซ็ตองค์ประกอบทั้งหมดของคอลัมน์แรกยกเว้นคอลัมน์เดียว ในคอลัมน์แรก องค์ประกอบทั้งหมดไม่เป็นศูนย์ ดังนั้นเราจึงสามารถเลือกองค์ประกอบใดก็ได้ ลองใช้ $(-4)$ เป็นตัวอย่าง:

องค์ประกอบที่เลือก $(-4)$ อยู่ในบรรทัดที่สาม ดังนั้นเราจึงใช้บรรทัดที่สามเพื่อรีเซ็ตองค์ประกอบที่เลือกของคอลัมน์แรก:

มาทำให้องค์ประกอบแรกของแถวที่สามเท่ากับหนึ่งกัน เมื่อต้องการทำเช่นนี้ ให้หารองค์ประกอบของแถวที่สามของเมทริกซ์ขยายด้วย $(-4)$:

ตอนนี้เรามาดำเนินการตั้งค่าองค์ประกอบที่สอดคล้องกันของคอลัมน์แรกเป็นศูนย์:

ในขั้นตอนต่อไป คุณจะไม่สามารถใช้บรรทัดที่สามได้อีกต่อไป เนื่องจากเราได้ใช้ไปแล้วในขั้นตอนแรก

ขั้นตอนที่สอง

ลองเลือกองค์ประกอบที่ไม่ใช่ศูนย์ของคอลัมน์ที่สองและรีเซ็ตองค์ประกอบอื่นๆ ทั้งหมดของคอลัมน์ที่สองให้เป็นศูนย์ เราสามารถเลือกองค์ประกอบใดองค์ประกอบหนึ่งจากสององค์ประกอบ: $\frac(11)(2)$ หรือ $\frac(39)(4)$ ไม่สามารถเลือกองค์ประกอบ $\left(-\frac(5)(4) \right)$ ได้ เนื่องจากองค์ประกอบนั้นอยู่ในบรรทัดที่สาม ซึ่งเราใช้ในขั้นตอนที่แล้ว ลองเลือกองค์ประกอบ $\frac(11)(2)$ ซึ่งอยู่ในบรรทัดแรก ตรวจสอบให้แน่ใจว่าแทนที่จะเป็น $\frac(11)(2)$ ในบรรทัดแรกจะมีหนึ่งรายการ:

ตอนนี้เรามารีเซ็ตองค์ประกอบที่เกี่ยวข้องของคอลัมน์ที่สอง:

บรรทัดแรกไม่สามารถใช้ในการสนทนาเพิ่มเติมได้

ขั้นตอนที่สาม

เราจำเป็นต้องรีเซ็ตองค์ประกอบทั้งหมดของคอลัมน์ที่สามยกเว้นคอลัมน์เดียว เราจำเป็นต้องเลือกองค์ประกอบที่ไม่ใช่ศูนย์ของคอลัมน์ที่สาม อย่างไรก็ตาม เราไม่สามารถรับ $\frac(6)(11)$ หรือ $\frac(13)(11)$ ได้ เนื่องจากองค์ประกอบเหล่านี้อยู่ในบรรทัดแรกและบรรทัดที่สามที่เราใช้ก่อนหน้านี้ ตัวเลือกมีขนาดเล็ก: เหลือเพียงองค์ประกอบ $\frac(2)(11)$ ซึ่งอยู่ในบรรทัดที่สอง ลองหารสมาชิกทั้งหมดของบรรทัดที่สองด้วย $\frac(2)(11)$:

ตอนนี้เรามารีเซ็ตองค์ประกอบที่เกี่ยวข้องของคอลัมน์ที่สาม:

การแปลงโดยใช้วิธีเกาส์-จอร์แดนเสร็จสมบูรณ์ สิ่งที่เหลืออยู่คือต้องแน่ใจว่าเมทริกซ์กลายเป็นหน่วยจนถึงเส้นตรง เมื่อต้องการทำเช่นนี้ คุณจะต้องเปลี่ยนลำดับของบรรทัด ก่อนอื่น เรามาสลับบรรทัดแรกและบรรทัดที่สามกัน:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \end(อาร์เรย์) \right) $$

ตอนนี้เรามาสลับบรรทัดที่สองและสาม:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & - 5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end(อาร์เรย์) \right) $$

ดังนั้น $A^(-1)=\left(\begin(array) (ccc) 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ - 39/4 & 11/2 & 19/4 \end(อาร์เรย์) \right)$ โดยธรรมชาติแล้วการแก้ปัญหาสามารถทำได้ในวิธีที่แตกต่างออกไปโดยเลือกองค์ประกอบที่อยู่บนเส้นทแยงมุมหลัก โดยปกติจะเป็นสิ่งที่พวกเขาทำ เพราะในกรณีนี้ เมื่อสิ้นสุดการแก้ปัญหา ไม่จำเป็นต้องสลับบรรทัด ฉันให้วิธีแก้ปัญหาก่อนหน้านี้เพื่อจุดประสงค์เดียวเท่านั้น: เพื่อแสดงให้เห็นว่าการเลือกบรรทัดในแต่ละขั้นตอนนั้นไม่สำคัญ หากคุณเลือกองค์ประกอบแนวทแยงในแต่ละขั้นตอน ผลลัพธ์จะมีลักษณะเช่นนี้

ขอเราให้เมทริกซ์จัตุรัสมา คุณต้องหาเมทริกซ์ผกผัน

วิธีแรก. ทฤษฎีบท 4.1 ของการดำรงอยู่และความเป็นเอกลักษณ์ของเมทริกซ์ผกผันระบุวิธีหนึ่งในการค้นหาเมทริกซ์ดังกล่าว

1. คำนวณดีเทอร์มิแนนต์ของเมทริกซ์นี้ หากไม่มีเมทริกซ์ผกผัน (เมทริกซ์เป็นเอกพจน์)

2. สร้างเมทริกซ์จากการเสริมพีชคณิตขององค์ประกอบเมทริกซ์

3. ย้ายเมทริกซ์เพื่อให้ได้เมทริกซ์ที่อยู่ติดกัน .

4. ค้นหาเมทริกซ์ผกผัน (4.1) โดยการหารองค์ประกอบทั้งหมดของเมทริกซ์ adjoint ด้วยดีเทอร์มิแนนต์

วิธีที่สอง. หากต้องการค้นหาเมทริกซ์ผกผัน คุณสามารถใช้การแปลงเบื้องต้นได้

1. สร้างบล็อกเมทริกซ์โดยกำหนดเมทริกซ์เอกลักษณ์ที่มีลำดับเดียวกันให้กับเมทริกซ์ที่กำหนด

2. ใช้การแปลงเบื้องต้นที่ดำเนินการกับแถวของเมทริกซ์ นำบล็อกด้านซ้ายไปสู่รูปแบบที่ง่ายที่สุด ในกรณีนี้เมทริกซ์บล็อกจะลดลงเป็นรูปแบบโดยที่เมทริกซ์จัตุรัสได้รับอันเป็นผลมาจากการแปลงจากเมทริกซ์เอกลักษณ์

3. ถ้า แล้วบล็อกจะเท่ากับค่าผกผันของเมทริกซ์ เช่น ถ้า แล้วเมทริกซ์จะไม่มีการผกผัน

ในความเป็นจริงด้วยความช่วยเหลือของการแปลงแถวเบื้องต้นของเมทริกซ์ทำให้สามารถลดบล็อกด้านซ้ายให้อยู่ในรูปแบบที่เรียบง่ายได้ (ดูรูปที่ 1.5) ในกรณีนี้เมทริกซ์บล็อกจะถูกแปลงเป็นรูปแบบโดยที่เมทริกซ์ระดับประถมศึกษามีความเท่าเทียมกัน หากเมทริกซ์ไม่เสื่อมตามวรรค 2 ของหมายเหตุ 3.3 รูปแบบที่เรียบง่ายจะสอดคล้องกับเมทริกซ์เอกลักษณ์ แล้วจากความเท่าเทียมกันก็เป็นไปตามนั้น หากเมทริกซ์เป็นเอกพจน์ รูปแบบที่เรียบง่ายของมันจะแตกต่างจากเมทริกซ์เอกลักษณ์ และเมทริกซ์จะไม่มีการผกผัน

11. สมการเมทริกซ์และคำตอบ รูปแบบเมทริกซ์ของการบันทึก SLAE วิธีเมทริกซ์ (วิธีเมทริกซ์ผกผัน) สำหรับการแก้ SLAE และเงื่อนไขสำหรับการนำไปประยุกต์ใช้

สมการเมทริกซ์คือสมการที่มีรูปแบบ: A*X=C; X*A=ค; A*X*B=C โดยที่ทราบเมทริกซ์ A, B, C, ไม่ทราบเมทริกซ์ X ถ้าเมทริกซ์ A และ B ไม่เสื่อมลง ผลเฉลยของเมทริกซ์ดั้งเดิมจะถูกเขียนในรูปแบบที่เหมาะสม: X = A - 1 * ค; X=ค*เอ -1 ; X=เอ -1 *ค*บี -1

รูปแบบเมทริกซ์ของระบบการเขียนของสมการพีชคณิตเชิงเส้น เมทริกซ์หลายตัวสามารถเชื่อมโยงกับ SLAE แต่ละรายการได้ นอกจากนี้ SLAE ยังสามารถเขียนได้ในรูปของสมการเมทริกซ์อีกด้วย สำหรับ SLAE (1) ให้พิจารณาเมทริกซ์ต่อไปนี้:เมทริกซ์ A เรียกว่า

เมทริกซ์ของระบบ - องค์ประกอบของเมทริกซ์นี้แสดงถึงค่าสัมประสิทธิ์ของ SLAE ที่กำหนดเรียกเมทริกซ์ A~

ระบบเมทริกซ์ขยาย - ได้มาจากการเพิ่มคอลัมน์ที่มีเงื่อนไขอิสระ b1,b2,...,bm ลงในเมทริกซ์ระบบ โดยปกติแล้วคอลัมน์นี้จะถูกคั่นด้วยเส้นแนวตั้งเพื่อความชัดเจนและเมทริกซ์คอลัมน์ X คือ เมทริกซ์ของสิ่งที่ไม่รู้.

การใช้สัญกรณ์ที่แนะนำข้างต้น SLAE (1) สามารถเขียนในรูปแบบของสมการเมทริกซ์: A⋅X=B

บันทึก

เมทริกซ์ที่เกี่ยวข้องกับระบบสามารถเขียนได้หลายวิธี ทุกอย่างขึ้นอยู่กับลำดับของตัวแปรและสมการของ SLAE ที่อยู่ระหว่างการพิจารณา แต่ไม่ว่าในกรณีใด ลำดับของสิ่งที่ไม่ทราบในแต่ละสมการของ SLAE ที่กำหนดจะต้องเหมือนกัน

วิธีเมทริกซ์เหมาะสำหรับการแก้ SLAE โดยจำนวนสมการเกิดขึ้นพร้อมกับจำนวนตัวแปรที่ไม่ทราบ และดีเทอร์มิแนนต์ของเมทริกซ์หลักของระบบแตกต่างจากศูนย์ หากระบบมีสมการมากกว่าสามสมการ การค้นหาเมทริกซ์ผกผันต้องใช้ความพยายามในการคำนวณอย่างมาก ดังนั้นในกรณีนี้ ขอแนะนำให้ใช้ วิธีเกาส์เซียน.

12. SLAE ที่เป็นเนื้อเดียวกัน เงื่อนไขสำหรับการมีอยู่ของโซลูชันที่ไม่เป็นศูนย์ คุณสมบัติของสารละลายบางส่วนของ SLAE ที่เป็นเนื้อเดียวกัน

สมการเชิงเส้นเรียกว่าเอกพันธ์ถ้าระยะอิสระเท่ากับศูนย์ และไม่เป็นเนื้อเดียวกัน ระบบที่ประกอบด้วยสมการเอกพันธ์เรียกว่าเอกพันธ์และมีรูปแบบทั่วไป:

13 แนวคิดเรื่องความเป็นอิสระเชิงเส้นและการพึ่งพาการแก้ปัญหาบางส่วนของ SLAE ที่เป็นเนื้อเดียวกัน ระบบการแก้ปัญหาขั้นพื้นฐาน (FSD) และความมุ่งมั่น การแสดงวิธีแก้ปัญหาทั่วไปของ SLAE ที่เป็นเนื้อเดียวกันผ่าน FSR

ระบบฟังก์ชั่น ย 1 (x ), ย 2 (x ), …, ย n (x ) เรียกว่า ขึ้นอยู่กับเชิงเส้นในช่วงเวลา ( ก , ข ) หากมีชุดของสัมประสิทธิ์คงที่ไม่เท่ากับศูนย์ในเวลาเดียวกัน ดังนั้นผลรวมเชิงเส้นของฟังก์ชันเหล่านี้จะเท่ากับศูนย์บน ( ก , ข ): สำหรับ . หากความเท่าเทียมกันสำหรับเป็นไปได้เพียงสำหรับ ระบบของฟังก์ชัน ย 1 (x ), ย 2 (x ), …, ย n (x ) เรียกว่า เป็นอิสระเชิงเส้นในช่วงเวลา ( ก , ข - กล่าวอีกนัยหนึ่งคือฟังก์ชัน ย 1 (x ), ย 2 (x ), …, ย n (x ) ขึ้นอยู่กับเชิงเส้นในช่วงเวลา ( ก , ข ) ถ้ามีค่าเท่ากับศูนย์บน ( ก , ข ) ผลรวมเชิงเส้นที่ไม่สำคัญ ฟังก์ชั่น ย 1 (x ),ย 2 (x ), …, ย n (x ) เป็นอิสระเชิงเส้นในช่วงเวลา ( ก , ข ) หากเพียงผลรวมเชิงเส้นเล็กน้อยเท่านั้นที่เท่ากับศูนย์บน ( ก , ข ).

ระบบการตัดสินใจขั้นพื้นฐาน (FSR) SLAE ที่เป็นเนื้อเดียวกันเป็นพื้นฐานของระบบคอลัมน์นี้

จำนวนองค์ประกอบใน FSR เท่ากับจำนวนสิ่งที่ไม่รู้จักของระบบ ลบด้วยอันดับของเมทริกซ์ระบบ คำตอบใดๆ ของระบบดั้งเดิมคือผลรวมเชิงเส้นของคำตอบของ FSR

ทฤษฎีบท

วิธีแก้ปัญหาทั่วไปของ SLAE ที่ไม่เป็นเนื้อเดียวกันจะเท่ากับผลรวมของวิธีแก้ปัญหาเฉพาะของ SLAE ที่ไม่เป็นเนื้อเดียวกันและวิธีแก้ปัญหาทั่วไปของ SLAE ที่เป็นเนื้อเดียวกันที่สอดคล้องกัน

1 . หากคอลัมน์ต่างๆ เป็นคำตอบของระบบสมการที่เป็นเนื้อเดียวกัน ผลรวมเชิงเส้นใดๆ ของคอลัมน์เหล่านั้นก็เป็นคำตอบของระบบสมการที่เป็นเนื้อเดียวกันด้วย

แท้จริงแล้วจากความเสมอภาคเป็นไปตามนั้น

เหล่านั้น. การรวมเชิงเส้นของสารละลายเป็นวิธีแก้ปัญหาของระบบที่เป็นเนื้อเดียวกัน

2. หากอันดับของเมทริกซ์ของระบบเอกพันธ์เท่ากับ แสดงว่าระบบจะมีคำตอบที่เป็นอิสระเชิงเส้น

แท้จริงแล้ว การใช้สูตร (5.13) สำหรับคำตอบทั่วไปของระบบที่เป็นเนื้อเดียวกัน เราจะพบคำตอบเฉพาะ โดยให้ตัวแปรอิสระดังต่อไปนี้ ชุดค่ามาตรฐาน (แต่ละครั้งสมมติว่าหนึ่งในตัวแปรอิสระเท่ากับหนึ่งและส่วนที่เหลือเท่ากับศูนย์):

ซึ่งเป็นอิสระเชิงเส้น ที่จริงแล้ว หากคุณสร้างเมทริกซ์จากคอลัมน์เหล่านี้ แถวสุดท้ายของเมทริกซ์จะก่อให้เกิดเมทริกซ์เอกลักษณ์ ดังนั้นผู้เยาว์ที่อยู่ในบรรทัดสุดท้ายจึงไม่เท่ากับศูนย์ (เท่ากับหนึ่ง) เช่น เป็นพื้นฐาน ดังนั้นอันดับของเมทริกซ์จะเท่ากัน ซึ่งหมายความว่าคอลัมน์ทั้งหมดของเมทริกซ์นี้มีความเป็นอิสระเชิงเส้น (ดูทฤษฎีบท 3.4)

คอลเลกชันของการแก้ปัญหาอิสระเชิงเส้นใด ๆ ของระบบที่เป็นเนื้อเดียวกันเรียกว่า ระบบพื้นฐาน (ชุด) ของการแก้ปัญหา .

14 รายย่อยของลำดับที่ รองพื้นฐาน อันดับของเมทริกซ์ การคำนวณอันดับของเมทริกซ์

ลำดับ k รองของเมทริกซ์ A คือดีเทอร์มีแนนต์ของเมทริกซ์ย่อยกำลังสองของลำดับ k

ในเมทริกซ์ A ที่มีขนาด m x n ลำดับรอง r จะถูกเรียกว่า พื้นฐาน หากไม่เป็นศูนย์ และลำดับรองที่สูงกว่าทั้งหมด (ถ้ามี) จะเท่ากับศูนย์

คอลัมน์และแถวของเมทริกซ์ A ที่จุดตัดที่มีฐานรองเรียกว่าคอลัมน์และแถวฐานของ A

ทฤษฎีบท 1 (อันดับของเมทริกซ์) สำหรับเมทริกซ์ใดๆ อันดับรองจะเท่ากับอันดับแถวและเท่ากับอันดับคอลัมน์

ทฤษฎีบท 2 (บนพื้นฐานรอง) คอลัมน์เมทริกซ์แต่ละคอลัมน์จะถูกแยกย่อยเป็นการรวมกันเชิงเส้นของคอลัมน์พื้นฐาน

อันดับของเมทริกซ์ (หรืออันดับรอง) คือลำดับของอันดับรองพื้นฐาน หรืออีกนัยหนึ่งคือลำดับที่ใหญ่ที่สุดซึ่งมีผู้รองที่ไม่ใช่ศูนย์อยู่ อันดับของเมทริกซ์ศูนย์ถือเป็น 0 ตามคำจำกัดความ

ให้เราสังเกตคุณสมบัติที่ชัดเจนสองประการของอันดับรอง

1) อันดับของเมทริกซ์จะไม่เปลี่ยนแปลงในระหว่างการขนย้าย เนื่องจากเมื่อเมทริกซ์ถูกย้าย เมทริกซ์ย่อยทั้งหมดจะถูกย้ายและผู้เยาว์จะไม่เปลี่ยนแปลง

2) ถ้า A' เป็นเมทริกซ์ย่อยของเมทริกซ์ A ดังนั้นอันดับของ A' จะไม่เกินอันดับของ A เนื่องจากรองที่ไม่เป็นศูนย์ซึ่งรวมอยู่ใน A' ก็รวมอยู่ใน A ด้วย

15. แนวคิดของเวกเตอร์เลขคณิตมิติ ความเท่าเทียมกันของเวกเตอร์ การดำเนินการกับเวกเตอร์ (บวก ลบ คูณด้วยตัวเลข คูณด้วยเมทริกซ์) ผลรวมเชิงเส้นของเวกเตอร์

สั่งสะสม nเรียกว่าจำนวนจริงหรือจำนวนเชิงซ้อน เวกเตอร์ n มิติ- ตัวเลขที่ถูกเรียกว่า พิกัดเวกเตอร์.

เวกเตอร์สองตัว (ไม่เป็นศูนย์) กและ ขจะเท่ากันหากได้รับการกำกับอย่างเท่าเทียมกันและมีโมดูลเดียวกัน เวกเตอร์ศูนย์ทั้งหมดถือว่าเท่ากัน ในกรณีอื่นทั้งหมด เวกเตอร์ไม่เท่ากัน

การบวกเวกเตอร์ การเพิ่มเวกเตอร์ทำได้ 2 วิธี: 1. กฎสี่เหลี่ยมด้านขนาน ในการเพิ่มเวกเตอร์ และเราวางจุดกำเนิดของทั้งสองไว้ที่จุดเดียวกัน เราสร้างเป็นสี่เหลี่ยมด้านขนานและจากจุดเดียวกันเราวาดเส้นทแยงมุมของสี่เหลี่ยมด้านขนาน นี่จะเป็นผลรวมของเวกเตอร์

2. วิธีที่สองในการบวกเวกเตอร์คือกฎสามเหลี่ยม ลองหาเวกเตอร์เดียวกันและ . เราจะเพิ่มจุดเริ่มต้นของวินาทีที่จุดสิ้นสุดของเวกเตอร์แรก ทีนี้มาเชื่อมโยงจุดเริ่มต้นของอันแรกและจุดสิ้นสุดของวินาทีกัน นี่คือผลรวมของเวกเตอร์ และ คุณสามารถเพิ่มเวกเตอร์ได้หลายตัวโดยใช้กฎเดียวกัน เราจัดเรียงพวกมันทีละอันแล้วเชื่อมต่อจุดเริ่มต้นของอันแรกกับจุดสิ้นสุดของอันสุดท้าย

การลบเวกเตอร์ เวกเตอร์มีทิศตรงข้ามกับเวกเตอร์ ความยาวของเวกเตอร์เท่ากัน ตอนนี้ก็ชัดเจนว่าการลบเวกเตอร์คืออะไร ผลต่างเวกเตอร์และเป็นผลรวมของเวกเตอร์กับเวกเตอร์

การคูณเวกเตอร์ด้วยตัวเลข

การคูณเวกเตอร์ด้วยตัวเลข k จะทำให้เกิดเวกเตอร์ที่มีความยาวเป็น k คูณด้วยความยาว มันเป็นทิศทางเดียวกับเวกเตอร์ถ้า k มากกว่าศูนย์ และทิศทางตรงข้ามถ้า k น้อยกว่าศูนย์

ผลคูณสเกลาร์ของเวกเตอร์คือผลคูณของความยาวของเวกเตอร์และโคไซน์ของมุมระหว่างเวกเตอร์เหล่านั้นหากเวกเตอร์ตั้งฉาก ผลคูณสเกลาร์ของพวกมันจะเป็นศูนย์ และนี่คือวิธีแสดงผลคูณสเกลาร์ผ่านพิกัดของเวกเตอร์ และ .

ผลรวมเชิงเส้นของเวกเตอร์

ผลรวมเชิงเส้นของเวกเตอร์ เรียกว่าเวกเตอร์

ที่ไหน - ค่าสัมประสิทธิ์การรวมเชิงเส้น ถ้า การรวมกันเรียกว่าเล็กน้อยหากไม่ใช่เรื่องเล็กน้อย

16 .ผลคูณสเกลาร์ของเวกเตอร์เลขคณิต ความยาวเวกเตอร์และมุมระหว่างเวกเตอร์ แนวคิดเรื่องความเป็นมุมฉากของเวกเตอร์

ผลคูณสเกลาร์ของเวกเตอร์ a และ b คือตัวเลข

ผลคูณสเกลาร์ใช้ในการคำนวณ: 1) การค้นหามุมระหว่างพวกเขา 2) การค้นหาเส้นโครงของเวกเตอร์ 3) การคำนวณความยาวของเวกเตอร์ 4) เงื่อนไขของความตั้งฉากของเวกเตอร์

ความยาวของส่วน AB เรียกว่าระยะห่างระหว่างจุด A และ B มุมระหว่างเวกเตอร์ A และ B เรียกว่ามุม α = (a, b), 0≤ α ≤P โดยคุณต้องหมุนเวกเตอร์ 1 ตัวเพื่อให้ทิศทางสอดคล้องกับเวกเตอร์อื่น โดยมีเงื่อนไขว่าต้นกำเนิดของพวกเขาตรงกัน

ออร์ทอม a คือเวกเตอร์ a ที่มีความยาวและทิศทางเป็นหน่วย

17. ระบบเวกเตอร์และผลรวมเชิงเส้นของมัน แนวคิดเรื่องการพึ่งพาเชิงเส้นและความเป็นอิสระของระบบเวกเตอร์ ทฤษฎีบทเกี่ยวกับเงื่อนไขที่จำเป็นและเพียงพอสำหรับการพึ่งพาเชิงเส้นของระบบเวกเตอร์

ระบบของเวกเตอร์ a1,a2,...,an เรียกว่าขึ้นอยู่กับเชิงเส้นถ้ามีตัวเลข แลมบ์ดา,เล2,...,แลม โดยที่อย่างน้อยหนึ่งในนั้นไม่เป็นศูนย์ และ แลมบ์ดา1+แลม2a2+...+แลแนน=0 . มิฉะนั้น ระบบจะเรียกว่าเป็นอิสระเชิงเส้น

เวกเตอร์ a1 และ a2 สองตัวเรียกว่า collinear ถ้าทิศทางของพวกมันเหมือนกันหรือตรงกันข้าม

เวกเตอร์ a1, a2 และ a3 สามตัวเรียกว่า coplanar ถ้าพวกมันขนานกับระนาบบางอัน

เกณฑ์ทางเรขาคณิตสำหรับการพึ่งพาเชิงเส้น:

a) ระบบ (a1,a2) จะขึ้นอยู่กับเชิงเส้นตรงก็ต่อเมื่อเวกเตอร์ a1 และ a2 เป็นเส้นตรงเท่านั้น

b) ระบบ (a1,a2,a3) จะขึ้นอยู่กับเชิงเส้นตรงก็ต่อเมื่อเวกเตอร์ a1,a2 และ a3 เป็นระนาบเดียวกัน

ทฤษฎีบท. (เงื่อนไขที่จำเป็นและเพียงพอสำหรับการพึ่งพาเชิงเส้น ระบบเวกเตอร์)

ระบบเวกเตอร์ เวกเตอร์ ช่องว่างเป็น เชิงเส้นขึ้นอยู่กับว่าเวกเตอร์ตัวใดตัวหนึ่งของระบบถูกแสดงเชิงเส้นตรงในรูปของเวกเตอร์ตัวอื่น เวกเตอร์ระบบนี้

ข้อพิสูจน์ 1. ระบบเวกเตอร์ในปริภูมิเวกเตอร์มีความเป็นอิสระเชิงเส้น ถ้าหากว่าไม่มีเวกเตอร์ของระบบใดถูกแสดงเป็นเส้นตรงในรูปของเวกเตอร์อื่นๆ ของระบบนี้2. ระบบเวกเตอร์ที่มีเวกเตอร์เป็นศูนย์หรือเวกเตอร์ที่เท่ากันสองตัวจะขึ้นอยู่กับเชิงเส้นตรง

สำหรับเมทริกซ์ A ที่ไม่ใช่เอกพจน์ใดๆ จะมีเมทริกซ์ A -1 ที่ไม่ซ้ำใครในลักษณะนั้น

A*A -1 =A -1 *A = E,

โดยที่ E คือเมทริกซ์เอกลักษณ์ของลำดับเดียวกันกับ A เมทริกซ์ A -1 เรียกว่าเมทริกซ์ผกผันของเมทริกซ์ A

ในกรณีที่มีคนลืม ในเมทริกซ์เอกลักษณ์ ยกเว้นเส้นทแยงมุมที่เต็มไปด้วยตำแหน่ง ตำแหน่งอื่นๆ ทั้งหมดจะเต็มไปด้วยศูนย์ ตัวอย่างของเมทริกซ์เอกลักษณ์:

การค้นหาเมทริกซ์ผกผันโดยใช้วิธีเมทริกซ์แบบแอดจอยท์

เมทริกซ์ผกผันถูกกำหนดโดยสูตร:

โดยที่ A ij - องค์ประกอบ a ij

เหล่านั้น. ในการคำนวณเมทริกซ์ผกผัน คุณต้องคำนวณดีเทอร์มิแนนต์ของเมทริกซ์นี้ จากนั้นหาการเสริมพีชคณิตสำหรับองค์ประกอบทั้งหมดแล้วสร้างเมทริกซ์ใหม่จากองค์ประกอบเหล่านั้น ต่อไปคุณจะต้องขนส่งเมทริกซ์นี้ และหารแต่ละองค์ประกอบของเมทริกซ์ใหม่ด้วยดีเทอร์มิแนนต์ของเมทริกซ์เดิม

ลองดูตัวอย่างบางส่วน

ค้นหา A -1 สำหรับเมทริกซ์

วิธีแก้ปัญหา ลองหา A -1 โดยใช้วิธีเมทริกซ์ที่อยู่ติดกัน เรามี det A = 2 ให้เราค้นหาการเสริมพีชคณิตขององค์ประกอบของเมทริกซ์ A ในกรณีนี้ การเสริมพีชคณิตขององค์ประกอบเมทริกซ์จะเป็นองค์ประกอบที่สอดคล้องกันของเมทริกซ์นั้นเอง โดยมีเครื่องหมายตามสูตร

เรามี A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2 เราสร้างเมทริกซ์ที่อยู่ติดกัน

เราขนส่งเมทริกซ์ A*:

เราค้นหาเมทริกซ์ผกผันโดยใช้สูตร:

เราได้รับ:

ใช้เมธอดเมทริกซ์ติด หา A -1 if

วิธีแก้ ก่อนอื่น เราคำนวณคำจำกัดความของเมทริกซ์นี้เพื่อตรวจสอบการมีอยู่ของเมทริกซ์ผกผัน เรามี

ที่นี่เราได้เพิ่มองค์ประกอบของแถวที่สามลงในองค์ประกอบของแถวที่สองซึ่งก่อนหน้านี้คูณด้วย (-1) แล้วขยายดีเทอร์มิแนนต์สำหรับแถวที่สอง เนื่องจากคำจำกัดความของเมทริกซ์นี้ไม่ใช่ศูนย์ จึงมีเมทริกซ์ผกผันอยู่ ในการสร้างเมทริกซ์ประชิด เราจะหาส่วนเสริมพีชคณิตขององค์ประกอบของเมทริกซ์นี้ เรามี

ตามสูตรครับ