การค้นหาอินทิกรัลไม่ จำกัด: จุดเริ่มต้น, ตัวอย่างของการแก้ปัญหา เครื่องคิดเลขออนไลน์ คำนวณอินทิกรัลไม่ จำกัด (แอนติเดริเวทีฟ)

การค้นหาอินทิกรัลไม่จำกัด (ชุดของแอนติเดริเวทีฟหรือ "แอนติเดริเวทีฟ") หมายถึงการสร้างฟังก์ชันขึ้นใหม่จากอนุพันธ์ที่ทราบของฟังก์ชันนี้ ชุดแอนติเดริเวทีฟที่ถูกเรียกคืน เอฟ(x) + กับ สำหรับฟังก์ชั่น ฉ(x) คำนึงถึงค่าคงที่การรวมเข้าด้วย ค- ขึ้นอยู่กับความเร็วของการเคลื่อนที่ของจุดวัสดุ (อนุพันธ์) กฎการเคลื่อนที่ของจุดนี้ (แอนติเดริเวทีฟ) สามารถคืนสภาพได้ ตามความเร่งของการเคลื่อนที่ของจุด - ความเร็วและกฎการเคลื่อนที่ อย่างที่คุณเห็น การบูรณาการเป็นพื้นที่กว้างสำหรับกิจกรรมของฟิสิกส์ของเชอร์ล็อก โฮล์มส์ และในทางเศรษฐศาสตร์ แนวคิดมากมายถูกนำเสนอผ่านฟังก์ชันและอนุพันธ์ ดังนั้น ตัวอย่างเช่น คุณสามารถเรียกคืนปริมาณของผลิตภัณฑ์ที่ผลิตในเวลาที่สอดคล้องกันโดยใช้ผลิตภาพแรงงาน ณ จุดหนึ่งของเวลา (อนุพันธ์)

การค้นหาอินทิกรัลไม่จำกัดต้องใช้สูตรอินทิกรัลพื้นฐานจำนวนไม่มาก แต่กระบวนการค้นหานั้นยากกว่าการใช้สูตรเหล่านี้เพียงอย่างเดียว ความซับซ้อนทั้งหมดไม่ได้เกี่ยวข้องกับการอินทิเกรต แต่เป็นการนำนิพจน์อินทิเกรตมาสู่รูปแบบที่ทำให้สามารถค้นหาอินทิกรัลไม่จำกัดโดยใช้สูตรพื้นฐานที่กล่าวมาข้างต้น ซึ่งหมายความว่าเพื่อเริ่มต้นการฝึกบูรณาการ คุณจะต้องเปิดใช้งานสิ่งที่คุณได้เรียนรู้มา โรงเรียนมัธยมปลายทักษะการเปลี่ยนแปลงการแสดงออก

เราจะเรียนรู้การหาอินทิกรัลโดยใช้ คุณสมบัติและตารางอินทิกรัลไม่ จำกัดจากบทเรียนเกี่ยวกับแนวคิดพื้นฐานของหัวข้อนี้ (เปิดในหน้าต่างใหม่)

มีหลายวิธีในการค้นหาอินทิกรัล วิธีการแทนที่ตัวแปรและ การบูรณาการโดยวิธีส่วนต่างๆ- ชุดสุภาพบุรุษบังคับสำหรับทุกคนที่สอบผ่านคณิตศาสตร์ระดับสูงได้สำเร็จ อย่างไรก็ตาม จะเป็นประโยชน์และน่าสนุกกว่าที่จะเริ่มเชี่ยวชาญการอินทิเกรตโดยใช้วิธีการขยาย โดยอิงตามทฤษฎีบทสองข้อต่อไปนี้เกี่ยวกับคุณสมบัติของอินทิกรัลไม่ จำกัด ซึ่งเราจะทำซ้ำที่นี่เพื่อความสะดวก

ทฤษฎีบท 3ตัวประกอบคงที่ในปริพันธ์สามารถนำออกจากเครื่องหมายของอินทิกรัลไม่ จำกัด ได้เช่น

ทฤษฎีบท 4อินทิกรัลไม่จำกัดของผลรวมพีชคณิต จำนวนจำกัดฟังก์ชั่นจะเท่ากัน ผลรวมพีชคณิตอินทิกรัลไม่จำกัดของฟังก์ชันเหล่านี้ เช่น

(2)

นอกจากนี้ กฎต่อไปนี้อาจมีประโยชน์ในการอินทิเกรต: หากการแสดงออกของปริพันธ์มีตัวประกอบคงที่ การแสดงออกของแอนติเดริเวทีฟจะถูกคูณด้วยค่าผกผันของตัวประกอบคงที่ นั่นคือ

(3)

เนื่องจากบทเรียนนี้เป็นบทเรียนเบื้องต้นในการแก้ปัญหาบูรณาการ จึงเป็นสิ่งสำคัญที่จะต้องทราบสองสิ่งที่มีอยู่แล้ว ระยะเริ่มแรกหรือหลังจากนั้นเล็กน้อยพวกเขาอาจทำให้คุณประหลาดใจ สิ่งที่น่าประหลาดใจก็คือการที่อินทิเกรตเป็นการดำเนินการผกผันของการหาอนุพันธ์ และอินทิกรัลไม่แน่นอนสามารถถูกเรียกว่า "แอนติเดริเวทีฟ" ได้อย่างถูกต้อง

สิ่งแรกที่คุณไม่ควรแปลกใจเมื่อทำการบูรณาการในตารางอินทิกรัล มีสูตรที่ไม่มีความคล้ายคลึงระหว่างสูตรตารางอนุพันธ์ - เหล่านี้เป็นสูตรต่อไปนี้:

อย่างไรก็ตาม คุณสามารถมั่นใจได้ว่าอนุพันธ์ของนิพจน์ทางด้านขวาของสูตรเหล่านี้ตรงกับปริพันธ์ที่สอดคล้องกัน

สิ่งที่สองที่ไม่น่าแปลกใจเมื่อบูรณาการ- แม้ว่าอนุพันธ์ของฟังก์ชันพื้นฐานใดๆ ก็เป็นฟังก์ชันพื้นฐานเช่นกัน อินทิกรัลไม่จำกัดของฟังก์ชันพื้นฐานบางฟังก์ชันไม่มีอีกต่อไป ฟังก์ชั่นเบื้องต้น - ตัวอย่างของอินทิกรัลดังกล่าวอาจเป็นดังต่อไปนี้:

ในการพัฒนาเทคนิคการรวมกลุ่ม ทักษะต่อไปนี้จะมีประโยชน์: การลดเศษส่วน การหารพหุนามในตัวเศษของเศษส่วนด้วยเอกพจน์ในตัวส่วน (เพื่อให้ได้ผลรวมของปริพันธ์ไม่จำกัด) การแปลงรากเป็นกำลัง การคูณเอกพจน์ด้วย a พหุนาม การยกกำลัง ทักษะเหล่านี้จำเป็นสำหรับการแปลงปริพันธ์ ซึ่งจะส่งผลให้ผลรวมของปริพันธ์ที่มีอยู่ในตารางปริพันธ์

การหาอินทิกรัลไม่ จำกัด เข้าด้วยกัน

ตัวอย่างที่ 1ค้นหาอินทิกรัลไม่ จำกัด

สารละลาย. เราเห็นพหุนามในตัวส่วนของปริพันธ์โดยที่ x กำลังสอง นี่เป็นสัญญาณที่เกือบจะแน่ใจว่าคุณสามารถใช้อินทิกรัลของตาราง 21 ได้ (โดยมีผลลัพธ์เป็นอาร์กแทนเจนต์) เรานำตัวประกอบที่สองออกจากตัวส่วน (มีคุณสมบัติดังกล่าวของอินทิกรัล - ตัวประกอบคงที่สามารถนำออกไปนอกเครื่องหมายของอินทิกรัลได้ ซึ่งกล่าวไว้ข้างต้นเป็นทฤษฎีบท 3) ผลลัพธ์ทั้งหมดนี้:

ตอนนี้ตัวส่วนคือผลรวมของกำลังสอง ซึ่งหมายความว่าเราสามารถใช้อินทิกรัลของตารางที่กล่าวถึงได้ ในที่สุดเราก็ได้คำตอบ:

ตัวอย่างที่ 2ค้นหาอินทิกรัลไม่ จำกัด

สารละลาย. เราใช้ทฤษฎีบท 3 อีกครั้ง - คุณสมบัติของอินทิกรัลโดยขึ้นอยู่กับปัจจัยคงที่ที่สามารถนำออกจากเครื่องหมายของอินทิกรัลได้:

เราใช้สูตร 7 จากตารางปริพันธ์ (ตัวแปรตามกำลัง) กับฟังก์ชันปริพันธ์:

เราลดเศษส่วนผลลัพธ์และได้คำตอบสุดท้าย:

ตัวอย่างที่ 3ค้นหาอินทิกรัลไม่ จำกัด

สารละลาย. เมื่อใช้ทฤษฎีบท 4 แรกและทฤษฎีบท 3 กับคุณสมบัติ เราจะพบว่าอินทิกรัลนี้เป็นผลรวมของอินทิกรัล 3 ตัว:

อินทิกรัลที่ได้รับทั้งสามแบบเป็นตาราง เราใช้สูตร (7) จากตารางอินทิกรัลสำหรับ n = 1/2, n= 2 และ n= 1/5 แล้ว

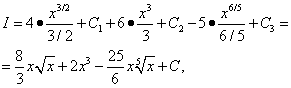
รวมค่าคงที่ตามอำเภอใจทั้งสามที่ถูกนำมาใช้เมื่อใด หาสามปริพันธ์ ดังนั้นในสถานการณ์ที่คล้ายคลึงกัน ควรแนะนำค่าคงที่การรวมตามอำเภอใจเพียงค่าเดียวเท่านั้น

ตัวอย่างที่ 4ค้นหาอินทิกรัลไม่ จำกัด

สารละลาย. เมื่อตัวส่วนของจำนวนเต็มมีเอกพจน์ เราสามารถหารตัวเศษด้วยเทอมของตัวส่วนทีละเทอม อินทิกรัลดั้งเดิมกลายเป็นผลรวมของอินทิกรัลสองตัว:

ในการใช้อินทิกรัลของตาราง เราจะแปลงรากเป็นกำลัง และนี่คือคำตอบสุดท้าย:

เรายังคงค้นหาอินทิกรัลไม่ จำกัด ด้วยกัน

ตัวอย่างที่ 7ค้นหาอินทิกรัลไม่ จำกัด

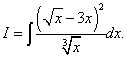
สารละลาย. หากเราแปลงปริพันธ์โดยการยกกำลังสองทวินามแล้วหารตัวเศษด้วยตัวส่วนแล้วอินทิกรัลดั้งเดิมจะกลายเป็นผลรวมของปริพันธ์สามตัว

ฟังก์ชัน F(x) เรียกว่าแอนติเดริเวทีฟสำหรับฟังก์ชัน f(x) ในช่วงเวลา (a; b) ถ้า f(x) สำหรับ x ทั้งหมด (a; b) ความเท่าเทียมกัน F (x) = f(x) 2

ทฤษฎีบท 1 ถ้า F(x) เป็นแอนติเดริเวทีฟสำหรับ f(x) บน (a; b) ดังนั้น F(x) + C โดยที่ C คือตัวเลข ก็เป็นแอนติเดริเวทีฟสำหรับ f(x) บน (a; ข) พิสูจน์: (F + C) = F + C = f + 0 = f 3

ขอให้เราพิสูจน์ทฤษฎีบทเสริมสองทฤษฎี: ถ้าฟังก์ชัน g(x) คงที่บน (a; b) แล้ว g (x) = 0 ถ้า g (x) = 0 สำหรับ x (a; b) ทั้งหมด แล้ว g( x) = C เปิด (a; b) 4

ทฤษฎีบท 2 ถ้า F(x) เป็นแอนติเดริเวทีฟสำหรับ f(x) บนช่วง (a; b) และ G(x) เป็นแอนติเดริเวทีฟอีกตัวหนึ่งสำหรับ f(x) บน (a; b) แล้ว G = F + C โดยที่ C คือตัวเลข 5

เซตของแอนติเดริเวทีฟทั้งหมดสำหรับฟังก์ชัน f(x) ในช่วงเวลา (a; b) เรียกว่าอินทิกรัลไม่จำกัด และเขียนแทนด้วยอินทิกรัล f(x)dx การคำนวณ dx ไม่ใช่ อินทิกรัลที่แน่นอนจาก ฟังก์ชันที่กำหนดเรียกว่าบูรณาการ 6

หากฟังก์ชัน f(x) มีความต่อเนื่อง และฟังก์ชัน (t) มีอนุพันธ์ต่อเนื่อง (t) สูตรจะคงไว้ดังนี้: f((t)) (t) dt = f(x) dx โดยที่ x = ( เสื้อ) 8

ให้ u(x) และ v(x) เป็นฟังก์ชันหาอนุพันธ์ได้ในช่วงเวลาหนึ่ง จากนั้น (uv) = u v + v u นี่หมายถึง (uv) dx = (u v + v u)dx = = u v dx + v u dx หรือ uv dx = uv – u v dx 10

นี่หมายถึงสูตรที่เรียกว่าอินทิเกรตตามส่วน สูตร: อินทิเกรตตามส่วน u(x)dv(x) = u(x) v(x) – v(x)du(x) 11

อินทิกรัลจำกัดหนึ่งของฟังก์ชันในช่วงเวลาหนึ่งคือขีดจำกัดที่ผลรวมอินทิกรัลมีแนวโน้มในระหว่างกระบวนการนี้ หากมีขีดจำกัด: 13

ตัวเลข a เรียกว่าขีดจำกัดล่างของอินทิเกรต และหมายเลข b เรียกว่าขีดจำกัดบนของอินทิเกรต ในรูปที่ 2 สี่เหลี่ยมคางหมูโค้งเน้นด้วยการแรเงา พื้นที่ S ของสี่เหลี่ยมคางหมูนี้ถูกกำหนดโดยสูตร 14

ปล่อยให้ฟังก์ชัน f(t) ถูกกำหนดและต่อเนื่องในช่วงเวลาหนึ่งที่มีจุด a จากนั้นแต่ละจำนวน x จากช่วงเวลานี้สามารถกำหนดตัวเลขได้ ดังนั้น จึงกำหนดฟังก์ชัน I(x) ในช่วงเวลาดังกล่าว ซึ่งเรียกว่าอินทิกรัลจำกัดขอบเขตพร้อมขีดจำกัดบนของตัวแปร 17

อนุพันธ์ของอินทิกรัลจำกัดจำนวนเทียบกับ ขีด จำกัด บนที่จุด x เท่ากับค่าของปริพันธ์ที่จุด x 18

ปล่อยให้ฟังก์ชัน y = f(x) ถูกกำหนดและต่อเนื่องกันในช่วงกึ่งอนันต์ (ที) dt

ซึ่งเมื่อคำนึงถึงสัญกรณ์ที่แนะนำแล้ว ถือเป็นข้อสันนิษฐานเบื้องต้น ทฤษฎีบทได้รับการพิสูจน์แล้ว

ตัวอย่าง.หา อินทิกรัลไม่ จำกัด
.

มาทำการเปลี่ยนกันเถอะ ที = บาป, dt = cosxdt.

ตัวอย่าง.

การทดแทน
เราได้รับ:

ด้านล่างนี้เราจะพิจารณาตัวอย่างอื่นๆ ของการใช้วิธีการทดแทนสำหรับฟังก์ชันประเภทต่างๆ

บูรณาการตามส่วนต่างๆ

วิธีการนี้ใช้สูตรอนุพันธ์ของผลิตภัณฑ์ที่รู้จักกันดี:

(ยูวี)=uv+vu

โดยที่ uиv คือฟังก์ชันบางส่วนของ x

ในรูปแบบดิฟเฟอเรนเชียล: d(uv) =udv+vdu

เมื่อบูรณาการ เราได้รับ:
และตามคุณสมบัติข้างต้นของอินทิกรัลไม่ จำกัด :

หรือ
;

เราได้รับสูตรสำหรับการอินทิเกรตตามส่วนต่างๆ ซึ่งช่วยให้เราสามารถค้นหาอินทิกรัลของฟังก์ชันพื้นฐานหลายๆ ฟังก์ชันได้

ตัวอย่าง.

อย่างที่คุณเห็น การใช้สูตรอินทิเกรตตามส่วนต่างๆ อย่างต่อเนื่องจะช่วยให้คุณสามารถค่อยๆ ลดความซับซ้อนของฟังก์ชันและนำอินทิกรัลมาไว้ในตารางได้

ตัวอย่าง.

จะเห็นได้ว่าจากการประยุกต์ใช้การรวมหลายส่วนซ้ำๆ กัน ทำให้ฟังก์ชันนี้ไม่สามารถทำให้เป็นรูปแบบตารางได้ง่ายขึ้น อย่างไรก็ตาม อินทิกรัลสุดท้ายที่ได้รับก็ไม่ต่างจากอินทิกรัลดั้งเดิม ดังนั้นเราจึงเลื่อนไปทางซ้ายของความเท่าเทียมกัน

ดังนั้นจึงพบอินทิกรัลโดยไม่ต้องใช้ตารางอินทิกรัลเลย

ก่อนที่จะพิจารณารายละเอียดวิธีการอินทิเกรตคลาสต่างๆ ของฟังก์ชัน เราจะให้ตัวอย่างเพิ่มเติมในการค้นหาอินทิกรัลไม่จำกัดโดยการลดให้เหลืออินทิกรัลแบบตาราง

ตัวอย่าง.

การบูรณาการเศษส่วนเบื้องต้น

คำนิยาม: ประถมศึกษาเศษส่วนสี่ประเภทต่อไปนี้เรียกว่า:

ฉัน.
ที่สาม

ครั้งที่สอง
IV.

ม,น– ตัวเลขธรรมชาติ(m2,n2) และ b 2 – 4ac<0.

อินทิกรัลสองประเภทแรกสามารถนำมาลงในตารางได้ง่ายๆ ด้วยการแทนที่ t=ax+b

ให้เราพิจารณาวิธีการอินทิเกรตเศษส่วนมูลฐานประเภท III

อินทิกรัลของเศษส่วนประเภท III สามารถแสดงเป็น:

ที่นี่ใน มุมมองทั่วไปการลดลงของอินทิกรัลเศษส่วนของประเภท III เหลือเพียงอินทิกรัลแบบตารางสองตัวจะแสดงขึ้น

ลองดูการประยุกต์ใช้สูตรข้างต้นโดยใช้ตัวอย่าง

ตัวอย่าง.

โดยทั่วไป ถ้าขวานตรีนาม 2 +bx+c มีนิพจน์ b 2 – 4ac>0 แสดงว่าเศษส่วนตามนิยามแล้วไม่ใช่เศษส่วนเบื้องต้น อย่างไรก็ตาม เศษส่วนดังกล่าวก็สามารถอินทิเกรตในลักษณะที่ระบุไว้ข้างต้นได้

ตัวอย่าง.

ให้เราพิจารณาวิธีการในการรวมเศษส่วนอย่างง่ายประเภท IV

ก่อนอื่น พิจารณากรณีพิเศษด้วย M = 0, N = 1

แล้วอินทิกรัลของฟอร์ม
สามารถแสดงในรูปแบบได้โดยการเลือกกำลังสองที่สมบูรณ์ในตัวส่วน
- เรามาทำการเปลี่ยนแปลงดังต่อไปนี้:

เราจะนำอินทิกรัลอันที่สองที่รวมอยู่ในความเท่าเทียมกันนี้ทีละส่วน

เรามาแสดงว่า:

สำหรับอินทิกรัลดั้งเดิมที่เราได้รับ:

สูตรผลลัพธ์เรียกว่า กำเริบหากคุณใช้มัน n-1 ครั้ง คุณจะได้อินทิกรัลของตาราง
.

ให้เรากลับไปสู่อินทิกรัลของเศษส่วนมูลฐานประเภท IV ในกรณีทั่วไป

ในผลลัพธ์ที่เท่าเทียมกัน อินทิกรัลแรกใช้การทดแทน ที = คุณ 2 + สลดเหลือเป็นตาราง และสูตรการเกิดซ้ำที่กล่าวถึงข้างต้นใช้กับอินทิกรัลตัวที่สอง

แม้ว่าการอินทิเกรตเศษส่วนมูลฐานประเภท IV จะมีความซับซ้อนอย่างเห็นได้ชัด แต่ในทางปฏิบัติ มันค่อนข้างง่ายที่จะใช้กับเศษส่วนที่มีดีกรีน้อย nและความแพร่หลายและลักษณะทั่วไปของแนวทางนี้ทำให้การนำวิธีนี้ไปใช้บนคอมพิวเตอร์เป็นเรื่องง่ายมาก

ตัวอย่าง:

การบูรณาการฟังก์ชันตรรกยะ

การบูรณาการเศษส่วนตรรกยะ

เพื่อที่จะรวมเศษส่วนที่เป็นตรรกยะ จำเป็นต้องแยกย่อยให้เป็นเศษส่วนมูลฐาน

ทฤษฎีบท: ถ้า
- เศษส่วนตรรกยะแท้ ซึ่งตัวส่วน P(x) แสดงเป็นผลคูณของตัวประกอบเชิงเส้นและกำลังสอง (โปรดทราบว่าพหุนามใดๆ ที่มีค่าสัมประสิทธิ์จำนวนจริงสามารถแสดงได้ในรูปแบบนี้: ป(x) = (x - ก)  …(x - ข)  (x 2 + พิกเซล + ถาม)  …(x 2 + รับ + ส)  ) จากนั้นเศษส่วนนี้สามารถแยกย่อยเป็นเศษส่วนเบื้องต้นได้ตามรูปแบบต่อไปนี้:

โดยที่ A i ,B i ,M i ,N i ,R i ,S i คือปริมาณคงที่

เมื่อรวมเศษส่วนตรรกยะ พวกมันจะใช้วิธีสลายเศษส่วนดั้งเดิมให้เป็นเศษส่วนเบื้องต้น เพื่อค้นหาปริมาณ A i , B i , M i , N i , R i , S i ที่เรียกว่า วิธีสัมประสิทธิ์ไม่แน่นอนสาระสำคัญก็คือเพื่อให้พหุนามสองตัวเท่ากัน จำเป็นและเพียงพอที่สัมประสิทธิ์ที่กำลังกำลัง x เท่ากันจะเท่ากัน

ลองพิจารณาการใช้วิธีนี้โดยใช้ตัวอย่างเฉพาะ

ตัวอย่าง.

เมื่อลดตัวส่วนร่วมและเท่ากับตัวเศษที่สอดคล้องกัน เราจะได้:

ตัวอย่าง.

เพราะ หากเศษส่วนไม่ถูกต้อง คุณต้องเลือกเศษส่วนทั้งหมดก่อน:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x– 7 3x 3 – 4x 2 – 17x+ 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x 3 + 8x 2 – 76x - 7

9x 3 – 12x 2 – 51x +18

20x 2 – 25x – 25

ลองแยกตัวประกอบของเศษส่วนที่ได้ออกมา. จะเห็นได้ว่าที่ x = 3 ตัวส่วนของเศษส่วนจะเปลี่ยนเป็นศูนย์ แล้ว:

3x 3 – 4x 2 – 17x+ 6x- 3

3x 3 – 9x 2 3x 2 + 5x- 2

ดังนั้น 3x 3 – 4x 2 – 17x+ 6 = (x– 3)(3x 2 + 5x– 2) = (x– 3)(x+ 2)(3x– 1) แล้ว:

เพื่อหลีกเลี่ยงการเปิดวงเล็บ การจัดกลุ่ม และการแก้ระบบสมการ (ซึ่งในบางกรณีอาจมีขนาดค่อนข้างใหญ่) เมื่อค้นหาสัมประสิทธิ์ที่ไม่แน่นอน ที่เรียกว่า วิธีค่าที่กำหนดเอง- สาระสำคัญของวิธีการนี้คือค่า x โดยพลการหลายค่า (ตามจำนวนสัมประสิทธิ์ที่ไม่ได้กำหนด) จะถูกแทนที่ในนิพจน์ข้างต้น เพื่อให้การคำนวณง่ายขึ้น เป็นเรื่องปกติที่จะใช้เป็นจุดค่าที่กำหนดเองซึ่งตัวส่วนของเศษส่วนเท่ากับศูนย์นั่นคือ ในกรณีของเรา – 3, -2, 1/3 เราได้รับ:

ในที่สุดเราก็ได้รับ:

ตัวอย่าง.

มาหาค่าสัมประสิทธิ์ที่ไม่ได้กำหนด:

จากนั้นค่าของอินทิกรัลที่กำหนด:

การบูรณาการตรีโกณมิติบางอย่าง

ฟังก์ชั่น

อินทิกรัลจาก ฟังก์ชันตรีโกณมิติสามารถมีได้มากมายนับไม่ถ้วน อินทิกรัลเหล่านี้ส่วนใหญ่ไม่สามารถคำนวณเชิงวิเคราะห์ได้เลย ลองมาพิจารณากันดู ประเภทหลักฟังก์ชั่นที่สามารถบูรณาการได้ตลอดเวลา

ส่วนประกอบของแบบฟอร์ม
.

โดยที่ R คือการกำหนดฟังก์ชันตรรกยะของตัวแปร sinx และ cosx

ปริพันธ์ประเภทนี้คำนวณโดยใช้การทดแทน
- การทดแทนนี้ช่วยให้คุณสามารถแปลงฟังก์ชันตรีโกณมิติเป็นฟังก์ชันตรรกยะได้

แล้ว

ดังนั้น:

การเปลี่ยนแปลงที่อธิบายไว้ข้างต้นเรียกว่า การทดแทนตรีโกณมิติสากล

ตัวอย่าง.

ข้อได้เปรียบที่ไม่อาจปฏิเสธได้ของการทดแทนนี้คือด้วยความช่วยเหลือคุณสามารถแปลงฟังก์ชันตรีโกณมิติให้เป็นฟังก์ชันตรรกยะและคำนวณอินทิกรัลที่เกี่ยวข้องได้เสมอ ข้อเสียรวมถึงความจริงที่ว่าการเปลี่ยนแปลงอาจส่งผลให้เกิดฟังก์ชันเชิงเหตุผลที่ค่อนข้างซับซ้อน ซึ่งการรวมเข้าด้วยกันจะต้องใช้เวลาและความพยายามอย่างมาก

อย่างไรก็ตาม หากเป็นไปไม่ได้ที่จะใช้การแทนที่ตัวแปรที่มีเหตุมีผลมากกว่านี้ วิธีการนี้เป็นวิธีเดียวที่ได้ผล

ตัวอย่าง.

ส่วนประกอบของแบบฟอร์ม
ถ้า

การทำงานรคอกซ์.

แม้จะมีความเป็นไปได้ในการคำนวณอินทิกรัลโดยใช้การทดแทนตรีโกณมิติสากล แต่ก็มีเหตุผลมากกว่าที่จะใช้การทดแทน ที = บาป.

การทำงาน
สามารถมี cosx ได้เฉพาะในกำลังเลขคู่เท่านั้น ดังนั้นจึงสามารถแปลงเป็นฟังก์ชันตรรกยะเทียบกับ sinx ได้

ตัวอย่าง.

โดยทั่วไป ในการใช้วิธีนี้ จำเป็นต้องมีค่าความคี่ของฟังก์ชันที่สัมพันธ์กับโคไซน์เท่านั้น และระดับของไซน์ที่รวมอยู่ในฟังก์ชันอาจเป็นค่าใดก็ได้ ทั้งจำนวนเต็มและเศษส่วน

ส่วนประกอบของแบบฟอร์ม
ถ้า

การทำงานรเป็นเรื่องแปลกเมื่อเทียบกับบาป.

โดยการเปรียบเทียบกับกรณีที่พิจารณาข้างต้นจะทำการทดแทน ที = คอกซ์.

ตัวอย่าง.

ส่วนประกอบของแบบฟอร์ม

การทำงานรค่อนข้างมากบาปและคอกซ์.

หากต้องการแปลงฟังก์ชัน R เป็นฟังก์ชันตรรกยะ ให้ใช้การทดแทน

เสื้อ = tgx

ตัวอย่าง.

อินทิกรัลของผลคูณของไซน์และโคไซน์

ข้อโต้แย้งต่างๆ

จะใช้หนึ่งในสามสูตรนี้ขึ้นอยู่กับประเภทของงาน:

ตัวอย่าง.

บางครั้งเมื่อรวมฟังก์ชันตรีโกณมิติ จะสะดวกในการใช้สูตรตรีโกณมิติที่รู้จักกันดีเพื่อลดลำดับของฟังก์ชัน

ตัวอย่าง.

บางครั้งมีการใช้เทคนิคที่ไม่ได้มาตรฐานบางอย่าง

ตัวอย่าง.

การบูรณาการฟังก์ชันที่ไม่ลงตัวบางประการ

ไม่ใช่ทุกคน ฟังก์ชั่นที่ไม่ลงตัวอาจมีอินทิกรัลแสดงโดยฟังก์ชันพื้นฐาน ในการค้นหาอินทิกรัลของฟังก์ชันไม่ลงตัว คุณควรใช้การทดแทนที่จะช่วยให้คุณสามารถแปลงฟังก์ชันให้เป็นฟังก์ชันตรรกยะ ซึ่งอินทิกรัลสามารถพบได้ดังที่ทราบกันดีอยู่แล้ว

เรามาดูเทคนิคบางอย่างในการรวมฟังก์ชันไม่มีเหตุผลประเภทต่างๆ กัน

ส่วนประกอบของแบบฟอร์ม
ที่ไหนn- จำนวนธรรมชาติ

การใช้การทดแทน
ฟังก์ชันถูกหาเหตุผลเข้าข้างตนเอง

ตัวอย่าง.

หากฟังก์ชันอตรรกยะรวมรากขององศาต่างๆ ไว้ด้วย ดังนั้นในฐานะตัวแปรใหม่ จึงมีเหตุผลที่จะหารากของดีกรีเท่ากับตัวคูณร่วมน้อยของดีกรีของรากที่รวมอยู่ในนิพจน์

ลองอธิบายเรื่องนี้ด้วยตัวอย่าง

ตัวอย่าง.

ปริพันธ์ของดิฟเฟอเรนเชียลทวินาม

คำนิยาม: ดิฟเฟอเรนเชียลทวินามเรียกว่าการแสดงออก

x ม (ก + บีเอ็กซ์ n ) พี ดีเอ็กซ์

ที่ไหน ม, n, และ พี– จำนวนตรรกยะ

ตามที่นักวิชาการ P.L. Chebyshev พิสูจน์แล้ว (1821-1894) อินทิกรัลของดิฟเฟอเรนเชียลทวินามสามารถแสดงในรูปของฟังก์ชันพื้นฐานได้เฉพาะในสามกรณีต่อไปนี้:

ถ้า รเป็นจำนวนเต็ม จากนั้นอินทิกรัลจะถูกหาเหตุผลเข้าข้างตนเองโดยใช้การทดแทน

โดยที่ ` เป็นตัวส่วนร่วม มและ n.

ก่อนหน้านี้ ด้วยฟังก์ชันที่กำหนดซึ่งชี้นำโดยสูตรและกฎเกณฑ์ต่างๆ เราจึงพบอนุพันธ์ของมัน อนุพันธ์มีประโยชน์หลายอย่าง: เป็นความเร็วของการเคลื่อนที่ (หรือโดยทั่วไปคือความเร็วของกระบวนการใด ๆ ); ความลาดชันแทนกราฟของฟังก์ชัน เมื่อใช้อนุพันธ์คุณสามารถตรวจสอบฟังก์ชันของความซ้ำซากจำเจและสุดขั้วได้ มันช่วยแก้ปัญหาการเพิ่มประสิทธิภาพ

แต่พร้อมกับปัญหาการหาความเร็วตามกฎการเคลื่อนที่ที่รู้จักก็มีเช่นกัน ปัญหาผกผัน- ปัญหาการฟื้นฟูกฎการเคลื่อนที่จากความเร็วที่ทราบ ลองพิจารณาหนึ่งในปัญหาเหล่านี้

ตัวอย่างที่ 1เคลื่อนที่เป็นเส้นตรง จุดวัสดุความเร็วของการเคลื่อนที่ ณ เวลา t จะได้จากสูตร v=gt ค้นหากฎการเคลื่อนที่
สารละลาย. ให้ s = s(t) เป็นกฎการเคลื่อนที่ที่ต้องการ เป็นที่ทราบกันว่า s"(t) = v(t) ซึ่งหมายความว่าในการแก้ปัญหาคุณต้องเลือกฟังก์ชัน s = s(t) ซึ่งเป็นอนุพันธ์ซึ่งเท่ากับ gt การเดาได้ไม่ยาก นั่น $s(t) = \frac(gt^ 2)(2)$
$s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t = gt$
คำตอบ: $s(t) = \frac(gt^2)(2) $

ให้เราทราบทันทีว่าตัวอย่างได้รับการแก้ไขอย่างถูกต้อง แต่ไม่สมบูรณ์ เราได้ $s(t) = \frac(gt^2)(2) $ ที่จริงแล้ว ปัญหามีวิธีแก้ไขมากมายนับไม่ถ้วน: ฟังก์ชันใดๆ ที่อยู่ในรูปแบบ $s(t) = \frac(gt^2)(2) + C$ โดยที่ C เป็นค่าคงที่ตามใจชอบ สามารถใช้เป็นกฎของ การเคลื่อนไหว เนื่องจาก $\left (\frac(gt^2)(2) +C \right)" = gt $

เพื่อให้ปัญหาเจาะจงมากขึ้น เราจำเป็นต้องแก้ไขสถานการณ์เริ่มต้น: ระบุพิกัดของจุดที่เคลื่อนที่ ณ จุดใดจุดหนึ่ง เช่น ที่ t = 0 ถ้า พูดว่า s(0) = s 0 แล้วจาก ความเท่าเทียมกัน s(t) = (gt 2)/2 + C เราได้: s(0) = 0 + C เช่น C = s 0 ตอนนี้กฎการเคลื่อนที่ถูกกำหนดไว้โดยเฉพาะ: s(t) = (gt 2)/2 + s 0

ในทางคณิตศาสตร์ การดำเนินการกลับกันถูกกำหนดไว้ ชื่อที่แตกต่างกันให้สร้างสัญลักษณ์พิเศษ เช่น กำลังสอง (x 2) และการแยกข้อมูล รากที่สอง($\sqrt(x) $), ไซน์ (sin x) และอาร์กไซน์ (อาร์คซิน x) ฯลฯ กระบวนการค้นหาอนุพันธ์ของฟังก์ชันที่กำหนดเรียกว่า ความแตกต่างและการดำเนินการผกผัน เช่น กระบวนการค้นหาฟังก์ชันจากอนุพันธ์ที่กำหนด ก็คือ บูรณาการ.

คำว่า "อนุพันธ์" นั้นสามารถอ้างเหตุผลได้ "ในชีวิตประจำวัน": ฟังก์ชัน y = f(x) "สร้าง" คุณลักษณะใหม่ย" = ฉ"(x) ฟังก์ชัน y = f(x) ทำหน้าที่เสมือนว่าเป็น "พาเรนต์" แต่นักคณิตศาสตร์ไม่เรียกฟังก์ชันนี้ว่า "พาเรนต์" หรือ "โปรดิวเซอร์" โดยธรรมชาติแล้ว พวกเขาบอกว่าฟังก์ชันนี้สัมพันธ์กับฟังก์ชัน y" = f"(x) รูปภาพหลักหรือดั้งเดิม

คำนิยาม.ฟังก์ชัน y = F(x) เรียกว่าแอนติเดริเวทีฟสำหรับฟังก์ชัน y = f(x) ในช่วง X ถ้าความเท่าเทียมกัน F"(x) = f(x) คงไว้สำหรับ $x \in X$

ในทางปฏิบัติ โดยทั่วไปแล้วช่วง X จะไม่ถูกระบุ แต่เป็นการบอกเป็นนัย (เป็นโดเมนธรรมชาติของคำจำกัดความของฟังก์ชัน)

ลองยกตัวอย่าง
1) ฟังก์ชัน y = x 2 เป็นแอนติเดริเวทีฟสำหรับฟังก์ชัน y = 2x เนื่องจากสำหรับ x ใดๆ ความเท่าเทียมกัน (x 2)" = 2x เป็นจริง
2) ฟังก์ชัน y = x 3 เป็นแอนติเดริเวทีฟสำหรับฟังก์ชัน y = 3x 2 เนื่องจากสำหรับ x ใดๆ ความเท่าเทียมกัน (x 3)" = 3x 2 เป็นจริง
3) ฟังก์ชัน y = sin(x) เป็นฟังก์ชันต้านอนุพันธ์ของฟังก์ชัน y = cos(x) เนื่องจากสำหรับ x ใดๆ ความเท่าเทียมกัน (sin(x))" = cos(x) เป็นจริง

เมื่อค้นหาแอนติเดริเวทีฟรวมถึงอนุพันธ์ ไม่เพียงแต่จะใช้สูตรเท่านั้น แต่ยังรวมถึงกฎบางอย่างด้วย เกี่ยวข้องโดยตรงกับกฎที่เกี่ยวข้องในการคำนวณอนุพันธ์

เรารู้ว่าอนุพันธ์ของผลรวมเท่ากับผลรวมของอนุพันธ์ของมัน กฎนี้สร้างกฎที่สอดคล้องกันสำหรับการค้นหาแอนติเดริเวทีฟ

กฎข้อที่ 1แอนติเดริเวทีฟของผลรวมเท่ากับผลรวมของแอนติเดริเวทีฟ

เรารู้ว่าตัวประกอบคงที่สามารถนำออกจากเครื่องหมายของอนุพันธ์ได้ กฎนี้สร้างกฎที่สอดคล้องกันสำหรับการค้นหาแอนติเดริเวทีฟ

กฎข้อที่ 2ถ้า F(x) เป็นแอนติเดริเวทีฟสำหรับ f(x) ดังนั้น kF(x) จะเป็นแอนติเดริเวทีฟสำหรับ kf(x)

ทฤษฎีบท 1ถ้า y = F(x) เป็นแอนติเดริเวทีฟของฟังก์ชัน y = f(x) แล้วแอนติเดริเวทีฟของฟังก์ชัน y = f(kx + m) จะเป็นฟังก์ชัน $y=\frac(1)(k)F (kx+m) $

ทฤษฎีบท 2ถ้า y = F(x) เป็นแอนติเดริเวทีฟสำหรับฟังก์ชัน y = f(x) บนช่วง X แล้วฟังก์ชัน y = f(x) จะมีแอนติเดริเวทีฟจำนวนอนันต์ และพวกมันทั้งหมดจะมีรูปแบบ y = F(x) + ซี

วิธีการบูรณาการ

วิธีการแทนที่ตัวแปร (วิธีการทดแทน)

วิธีการอินทิเกรตโดยการแทนที่เกี่ยวข้องกับการแนะนำตัวแปรอินทิเกรตใหม่ (นั่นคือ การแทนที่) ในกรณีนี้ อินทิกรัลที่กำหนดจะลดลงเป็นอินทิกรัลใหม่ ซึ่งเป็นแบบตารางหรือแบบลดได้ วิธีการทั่วไปไม่มีการเลือกการทดแทน ความสามารถในการกำหนดการเปลี่ยนตัวได้อย่างถูกต้องนั้นได้มาจากการฝึกฝน
ปล่อยให้จำเป็นต้องคำนวณอินทิกรัล $\textstyle \int F(x)dx $ มาทำการแทนค่า $x= \varphi(t) $ โดยที่ $\varphi(t) $ เป็นฟังก์ชันที่มีอนุพันธ์ต่อเนื่องกัน
จากนั้น $dx = \varphi " (t) \cdot dt $ และขึ้นอยู่กับคุณสมบัติไม่แปรเปลี่ยนของสูตรอินทิกรัลสำหรับอินทิกรัลไม่จำกัด เราจะได้สูตรอินทิกรัลโดยการแทนที่:
$\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt $

การรวมนิพจน์ในรูปแบบ $\textstyle \int \sin^n x \cos^m x dx $

ถ้า m เป็นเลขคี่ m > 0 จะสะดวกกว่าถ้าจะใช้แทน sin x = t
ถ้า n เป็นเลขคี่ n > 0 จะสะดวกกว่าถ้าจะใช้แทน cos x = t
ถ้า n และ m เป็นเลขคู่ จะสะดวกกว่าถ้าจะใช้แทน tg x = t

บูรณาการโดยส่วนต่างๆ

บูรณาการตามส่วนต่างๆ - ใช้สูตรต่อไปนี้เพื่อบูรณาการ:
$\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du $
หรือ:
$\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx $

ตารางอินทิกรัลไม่ จำกัด (แอนติเดริเวทีฟ) ของฟังก์ชันบางฟังก์ชัน

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +ค \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(อาร์คซิน) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch ) x +C $$

เป็นไปได้ไหมที่จะรวมฟังก์ชันไม่เชิงเส้นไว้ใต้เครื่องหมายดิฟเฟอเรนเชียล ใช่ ถ้าปริพันธ์เป็นผลคูณของสองปัจจัย ปัจจัยหนึ่งคือฟังก์ชันที่ซับซ้อนของปัจจัยบางตัว ฟังก์ชันไม่เชิงเส้นและตัวประกอบอีกตัวคืออนุพันธ์ของฟังก์ชันไม่เชิงเส้นนี้ ลองดูสิ่งที่พูดพร้อมตัวอย่าง

ค้นหาอินทิกรัลไม่ จำกัด

ตัวอย่างที่ 1- ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 วัน (x 2 + x + 2) =(x²+x+2) 6 : 6 + ซี

อินทิเกรตนี้แสดงถึงอะไร? งาน ฟังก์ชั่นพลังงานจาก (x 2 + x + 2) และตัวประกอบ (2x + 1) ซึ่งเท่ากับอนุพันธ์ของฐานของกำลัง: (x 2 + x + 2)" = 2x + 1

สิ่งนี้ทำให้เราใส่ (2x + 1) ไว้ใต้เครื่องหมายส่วนต่าง:

∫คุณ 5 ดู=คุณ 6 : 6+ C. (สูตร 1) )

การตรวจสอบ. (F (x)+ C)" =((x²+x+2) 6 : 6 + C)′=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =

=(x 2 + x + 2) 5 · (2x + 1) = (2x + 1)(x 2 + x + 2) 5 = f (x)

ตัวอย่างที่ 2∫(3x 2 – 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+ซี

และตัวอย่างนี้แตกต่างจากตัวอย่างที่ 1 อย่างไร ไม่มีอะไร! กำลังที่ห้าเดียวกันกับฐาน (x 3 – x 2 + 3x + 1) คูณด้วยตรีโกณมิติ (3x 2 – 2x + 3) ซึ่งเป็นอนุพันธ์ของฐานของกำลัง: (x 3 – x 2 + 3x + 1)" = 3x 2 – 2x + 3 เรานำฐานของดีกรีนี้มาไว้ใต้เครื่องหมายอนุพันธ์ ซึ่งค่าของปริพันธ์ไม่เปลี่ยนแปลง จากนั้นจึงใช้สูตรเดิม 1 () ปริพันธ์)

ตัวอย่างที่ 3

ที่นี่อนุพันธ์ของ (2x 3 – 3x) จะให้ (6x 2 – 3) และกับเรา

นั่นคือ (12x 2 – 6) นั่นคือ นิพจน์ใน 2 มากขึ้น ซึ่งหมายความว่าเราใส่ (2x 3 – 3x) ไว้ใต้เครื่องหมายดิฟเฟอเรนเชียล และใส่ตัวประกอบไว้หน้าอินทิกรัล 2 - ลองใช้สูตรกัน 2) (แผ่น ).

นี่คือสิ่งที่เกิดขึ้น:

มาตรวจสอบกันโดยคำนึงว่า:

ตัวอย่าง. ค้นหาอินทิกรัลไม่ จำกัด

1. ∫(6x+5) 3 dx เราจะตัดสินใจอย่างไร? กำลังดูแผ่นครับ และเราให้เหตุผลประมาณนี้ อินทิแกรนด์แสดงถึงดีกรี และเรามีสูตรสำหรับอินทิกรัลของดีกรี (สูตร 1) ) แต่ในนั้นก็เป็นพื้นฐานของปริญญา คุณและ ตัวแปรบูรณาการเดียวกัน คุณ

และเรามีตัวแปรอินทิเกรต เอ็กซ์และฐานของปริญญา (6x+5)- มาเปลี่ยนแปลงตัวแปรอินทิเกรตกัน: แทนที่จะเขียน dx เราเขียน d (6x+5) มีอะไรเปลี่ยนแปลงบ้าง? เนื่องจากสิ่งที่อยู่หลังเครื่องหมายดิฟเฟอเรนเชียล d ตามค่าเริ่มต้นแล้ว จะทำให้เกิดอนุพันธ์

แล้ว d (6x+5)=6dx เช่น เมื่อแทนที่ตัวแปร x ด้วยตัวแปร (6x+5) ฟังก์ชันปริพันธ์จะเพิ่มขึ้น 6 เท่า ดังนั้นเราจึงใส่ตัวประกอบ 1/6 ไว้หน้าเครื่องหมายอินทิกรัล อาร์กิวเมนต์เหล่านี้สามารถเขียนได้ดังนี้:

ดังนั้นเราจึงแก้ไขตัวอย่างนี้ด้วยการแนะนำตัวแปรใหม่ (ตัวแปร x ถูกแทนที่ด้วยตัวแปร 6x+5) คุณเขียนตัวแปรใหม่ (6x+5) ที่ไหน? ใต้เครื่องหมายส่วนต่าง นั่นเป็นเหตุผลว่าทำไม วิธีนี้การแนะนำตัวแปรใหม่มักเรียกว่า วิธี (หรือทาง ) โดยสรุป(ตัวแปรใหม่ ) ใต้เครื่องหมายส่วนต่าง.

ในตัวอย่างที่สอง อันดับแรกเราได้รับปริญญาด้วย ตัวบ่งชี้เชิงลบแล้ววางไว้ใต้เครื่องหมายอนุพันธ์ (7x-2) แล้วใช้สูตรอินทิกรัลดีกรี 1) (ปริพันธ์ ).

ลองดูวิธีแก้ปัญหาตัวอย่าง 3.

อินทิกรัลนำหน้าด้วยสัมประสิทธิ์ 1/5 ทำไม เนื่องจาก d (5x-2) = 5dx ดังนั้น โดยการแทนที่ฟังก์ชัน u = 5x-2 ใต้เครื่องหมายดิฟเฟอเรนเชียล เราจึงเพิ่มปริพันธ์ขึ้น 5 เท่า ดังนั้น เพื่อไม่ให้ค่าของนิพจน์นี้เปลี่ยนแปลง เราจึงได้ หารด้วย 5 คือ . คูณด้วย 1/5. ต่อมาก็ใช้สูตร 2) (ปริพันธ์) .

สูตรอินทิกรัลที่ง่ายที่สุดทั้งหมดจะมีลักษณะดังนี้:

∫f (x) dx=F (x)+Cและจะต้องได้รับความเท่าเทียมกัน:

(F (x)+C)"=ฉ (x)

สูตรอินทิเกรตสามารถหาได้โดยการกลับสูตรการหาอนุพันธ์ที่สอดคล้องกัน

จริงหรือ,

เลขชี้กำลัง nอาจเป็นเศษส่วน บ่อยครั้งคุณต้องหาอินทิกรัลไม่จำกัดของฟังก์ชัน y=√x ลองคำนวณอินทิกรัลของฟังก์ชัน f (x)=√x โดยใช้สูตร 1) .

ลองเขียนตัวอย่างนี้เป็นสูตร 2) .

เนื่องจาก (x+C)"=1 ดังนั้น ∫dx=x+C

3) ∫dx=x+C

แทนที่ 1/x² ด้วย x -2 เราจะคำนวณอินทิกรัลของ 1/x²

คุณสามารถได้รับคำตอบนี้โดยการติดต่อ สูตรดังความแตกต่าง:

ให้เราเขียนเหตุผลของเราในรูปแบบของสูตร 4).

เมื่อคูณทั้งสองด้านของผลลัพธ์ที่เท่ากันด้วย 2 เราจะได้สูตร 5).

มาหาอินทิกรัลของฟังก์ชันตรีโกณมิติหลักโดยรู้อนุพันธ์ของมัน: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. เราได้รับสูตรการรวม 6) — 9).

6) ∫cosxdx=บาปx+C;

7) ∫sinxdx=-cosx+C;

หลังจากศึกษาแบบสาธิตและ ฟังก์ชันลอการิทึมเรามาเพิ่มสูตรอีกสองสามสูตรกัน

คุณสมบัติพื้นฐานของอินทิกรัลไม่ จำกัด

ฉัน.อนุพันธ์ของอินทิกรัลไม่ จำกัด เท่ากับปริพันธ์ .

(∫f (x) dx)"=f (x)

ครั้งที่สองส่วนต่างของอินทิกรัลไม่ จำกัด เท่ากับปริพันธ์

d∫f (x) dx=f (x) dx

ที่สามอินทิกรัลไม่จำกัดของดิฟเฟอเรนเชียล (อนุพันธ์) ของฟังก์ชันบางฟังก์ชัน เท่ากับผลรวมฟังก์ชันนี้และค่าคงที่ตามอำเภอใจ C

∫dF (x)=F (x)+Cหรือ ∫F"(x) dx=F (x)+C

โปรดทราบ: ในคุณสมบัติ I, II และ III สัญญาณของดิฟเฟอเรนเชียลและอินทิกรัล (อินทิกรัลและดิฟเฟอเรนเชียล) จะ "กิน" ซึ่งกันและกัน!

IV.ตัวประกอบคงที่ของปริพันธ์สามารถนำออกจากเครื่องหมายปริพันธ์ได้

∫kf (x) dx=k ∫f (x) dx,ที่ไหน เค - คงที่, ไม่เท่ากับศูนย์

วี.อินทิกรัลของผลรวมพีชคณิตของฟังก์ชันจะเท่ากับผลรวมพีชคณิตของอินทิกรัลของฟังก์ชันเหล่านี้

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx

วี.ถ้า F (x) เป็นแอนติเดริเวทีฟของ f (x) และ เคและ ขเป็นค่าคงที่ และ เค≠0 จากนั้น (1/k)·F (kx+b) เป็นแอนติเดริเวทีฟสำหรับ f (kx+b) แท้จริงแล้วตามกฎการคำนวณอนุพันธ์ ฟังก์ชั่นที่ซับซ้อนเรามี:

คุณสามารถเขียน:

สำหรับการกระทำทางคณิตศาสตร์ทุกครั้งจะมีการกระทำที่ผกผัน สำหรับการกระทำของการสร้างความแตกต่าง (การค้นหาอนุพันธ์ของฟังก์ชัน) ยังมีการกระทำผกผัน - การบูรณาการ ด้วยการอินทิเกรต ฟังก์ชันจะถูกค้นพบ (สร้างใหม่) จากอนุพันธ์หรือดิฟเฟอเรนเชียลที่กำหนด ฟังก์ชันที่พบเรียกว่า แอนติเดริเวทีฟ.

คำนิยาม.ฟังก์ชันหาอนุพันธ์ ฉ(x)เรียกว่าแอนติเดริเวทีฟของฟังก์ชัน ฉ(x)ในช่วงเวลาที่กำหนด หากเป็นทั้งหมด เอ็กซ์จากช่วงนี้จะมีความเท่าเทียมกันดังต่อไปนี้: ฟ'(x)=ฉ (x).

ตัวอย่าง. ค้นหาแอนติเดริเวทีฟสำหรับฟังก์ชัน: 1) f (x)=2x; 2) ฉ(x)=3cos3x.

1) เนื่องจาก (x²)′=2x ดังนั้น ตามคำนิยามแล้ว ฟังก์ชัน F (x)=x² จะเป็นแอนติเดริเวทีฟของฟังก์ชัน f (x)=2x

2) (บาป3x)′=3คอส3x ถ้าเราแทน f (x)=3cos3x และ F (x)=sin3x ดังนั้น ตามนิยามของแอนติเดริเวทีฟ เราจะได้: F′(x)=f (x) และด้วยเหตุนี้ F (x)=sin3x คือ แอนติเดริเวทีฟสำหรับ f ( x)=3cos3x

โปรดทราบว่า (sin3x +5 )′= 3cos3xและ (sin3x -8,2 )′= 3cos3x, ... ในรูปแบบทั่วไปเราสามารถเขียนได้: (sin3x +ซี)′= 3cos3x, ที่ไหน กับ- ค่าคงที่บางส่วน ตัวอย่างเหล่านี้บ่งบอกถึงความคลุมเครือของการกระทำของการอินทิเกรต ตรงกันข้ามกับการกระทำของการหาอนุพันธ์ เมื่อฟังก์ชันหาอนุพันธ์ใดๆ มีอนุพันธ์เพียงตัวเดียว

คำนิยาม.ถ้าฟังก์ชั่น ฉ(x)คือแอนติเดริเวทีฟของฟังก์ชัน ฉ(x)ในช่วงระยะเวลาหนึ่ง เซตของแอนติเดริเวทีฟทั้งหมดของฟังก์ชันนี้จะมีรูปแบบ:

เอฟ(x)+ซีโดยที่ C คือจำนวนจริงใดๆ

เซตของแอนติเดริเวทีฟทั้งหมด F (x) + C ของฟังก์ชัน f (x) บนช่วงเวลาที่พิจารณาเรียกว่าอินทิกรัลไม่ จำกัด และเขียนแทนด้วยสัญลักษณ์ ∫ (เครื่องหมายอินทิกรัล) เขียนลงไป: ∫f (x) dx=F (x)+C.

การแสดงออก ∫f(x)dxอ่าน: “อินทิกรัล ef จาก x ถึง de x”

เอฟ(x)ดีเอ็กซ์- นิพจน์อินทิกรัล

ฉ(x)— ฟังก์ชันปริพันธ์

เอ็กซ์คือตัวแปรอินทิเกรต

ฉ(x)- แอนติเดริเวทีฟของฟังก์ชัน ฉ(x),

กับ- ค่าคงที่บางส่วน

ตอนนี้ตัวอย่างที่พิจารณาสามารถเขียนได้ดังนี้:

1) ∫ 2xdx=x²+C 2) ∫ 3cos3xdx=บาป3x+C

เครื่องหมาย d หมายถึงอะไร?

ง—เครื่องหมายดิฟเฟอเรนเชียล - มีวัตถุประสงค์สองประการ: ประการแรก เครื่องหมายนี้แยกอินทิแกรนด์ออกจากตัวแปรอินทิเกรต ประการที่สอง ทุกอย่างที่เกิดขึ้นหลังจากสัญลักษณ์นี้จะถูกสร้างความแตกต่างตามค่าเริ่มต้นและคูณด้วยปริพันธ์

ตัวอย่าง. ค้นหาอินทิกรัล: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) หลังไอคอนเฟืองท้าย งค่าใช้จ่าย เอ็กซ์เอ็กซ์, ก ร

∫ 2хрdx=рх²+С. เปรียบเทียบกับตัวอย่าง 1).

มาตรวจสอบกัน F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x)

4) หลังไอคอนเฟืองท้าย งค่าใช้จ่าย ร- ซึ่งหมายความว่าตัวแปรอินทิเกรต รและตัวคูณ เอ็กซ์ควรพิจารณาค่าคงที่บางอย่าง

∫ 2хрдр=р²х+С. เปรียบเทียบกับตัวอย่าง 1) และ 3).

มาตรวจสอบกัน F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p)

หน้า 1 จาก 1 1