การหาสมการของเส้นตรงจากจุดสองจุด สมการของเส้นที่ผ่านจุด สมการของเส้นที่ผ่านจุด 2 จุด มุมระหว่างเส้น 2 เส้น ความชันของเส้น
บทเรียนจากชุด “อัลกอริทึมทางเรขาคณิต”
สวัสดีผู้อ่านที่รัก!
วันนี้เราจะมาเริ่มเรียนรู้อัลกอริธึมที่เกี่ยวข้องกับเรขาคณิต ความจริงก็คือมีปัญหาโอลิมปิกในวิทยาการคอมพิวเตอร์ค่อนข้างมากที่เกี่ยวข้องกับเรขาคณิตเชิงคำนวณและการแก้ปัญหาดังกล่าวมักจะทำให้เกิดปัญหา
ตลอดบทเรียนหลายบท เราจะพิจารณางานย่อยเบื้องต้นจำนวนหนึ่งซึ่งเป็นพื้นฐานของการแก้ปัญหาส่วนใหญ่ในเรขาคณิตเชิงคำนวณ
ในบทเรียนนี้เราจะสร้างโปรแกรมสำหรับ การหาสมการของเส้นตรงผ่านมาให้ สองจุด- ในการแก้ปัญหาทางเรขาคณิต เราจำเป็นต้องมีความรู้เกี่ยวกับเรขาคณิตเชิงคำนวณบ้าง เราจะอุทิศส่วนหนึ่งของบทเรียนเพื่อทำความรู้จักกับพวกเขา
ข้อมูลเชิงลึกจากเรขาคณิตคำนวณ
เรขาคณิตเชิงคำนวณเป็นสาขาหนึ่งของวิทยาการคอมพิวเตอร์ที่ศึกษาอัลกอริทึมสำหรับการแก้ปัญหาทางเรขาคณิต
ข้อมูลเริ่มต้นสำหรับปัญหาดังกล่าวอาจเป็นชุดของจุดบนระนาบ ชุดของส่วน รูปหลายเหลี่ยม (ระบุตามรายการจุดยอดตามลำดับตามเข็มนาฬิกา) เป็นต้น
ผลลัพธ์อาจเป็นคำตอบสำหรับคำถามบางข้อ (เช่น จุดหนึ่งเป็นของเซ็กเมนต์หรือไม่ มี 2 ส่วนตัดกัน ...) หรือวัตถุทางเรขาคณิตบางอย่าง (เช่น รูปหลายเหลี่ยมนูนที่เล็กที่สุดที่เชื่อมต่อจุดที่กำหนด พื้นที่ของ รูปหลายเหลี่ยม ฯลฯ)
เราจะพิจารณาปัญหาของเรขาคณิตเชิงคำนวณเฉพาะบนระนาบและในระบบพิกัดคาร์ทีเซียนเท่านั้น
เวกเตอร์และพิกัด
ในการใช้วิธีการคำนวณเรขาคณิต จำเป็นต้องแปลภาพเรขาคณิตเป็นภาษาของตัวเลข เราจะสมมติว่าเครื่องบินมีระบบพิกัดคาร์ทีเซียน ซึ่งทิศทางการหมุนทวนเข็มนาฬิกาเรียกว่าค่าบวก
ตอนนี้วัตถุทางเรขาคณิตได้รับการแสดงออกเชิงวิเคราะห์ ดังนั้นเพื่อระบุจุดก็เพียงพอที่จะระบุพิกัดของมัน: คู่ของตัวเลข (x; y) ส่วนสามารถระบุได้โดยการระบุพิกัดของส่วนปลาย สามารถระบุเส้นตรงได้โดยการระบุพิกัดของคู่ของจุด
แต่เครื่องมือหลักของเราในการแก้ปัญหาคือเวกเตอร์ ฉันจึงขอจำข้อมูลบางอย่างเกี่ยวกับพวกเขา
เซ็กเมนต์ เอบีซึ่งมีประเด็น กถือเป็นจุดเริ่มต้น (จุดสมัคร) และจุด ใน– สิ้นสุด เรียกว่าเวกเตอร์ เอบีและแสดงด้วยอักษรตัวใดตัวหนึ่งหรือตัวพิมพ์เล็กตัวหนาเป็นต้น ก .
เพื่อแสดงความยาวของเวกเตอร์ (นั่นคือความยาวของส่วนที่เกี่ยวข้อง) เราจะใช้สัญลักษณ์มอดุลัส (เช่น )
เวกเตอร์ที่กำหนดเองจะมีพิกัดเท่ากับความแตกต่างระหว่างพิกัดที่สอดคล้องกันของจุดสิ้นสุดและจุดเริ่มต้น:
![]() ,
,
นี่คือประเด็น กและ บี
มีพิกัด ![]() ตามลำดับ
ตามลำดับ
สำหรับการคำนวณเราจะใช้แนวคิดนี้ มุมที่มุ่งเน้นนั่นคือมุมที่คำนึงถึงตำแหน่งสัมพัทธ์ของเวกเตอร์
มุมเชิงระหว่างเวกเตอร์ ก และ ข เป็นบวกถ้าการหมุนมาจากเวกเตอร์ ก เป็นเวกเตอร์ ข จะดำเนินการในทิศทางบวก (ทวนเข็มนาฬิกา) และเชิงลบในอีกกรณีหนึ่ง ดูรูปที่ 1a, รูปที่ 1b ว่ากันว่าเป็นเวกเตอร์คู่หนึ่ง ก และ ข มุ่งเน้นเชิงบวก (เชิงลบ)
ดังนั้นค่าของมุมเชิงจะขึ้นอยู่กับลำดับของเวกเตอร์ที่อยู่ในรายการและสามารถรับค่าในช่วงเวลาได้.
ปัญหาหลายประการในเรขาคณิตเชิงคำนวณใช้แนวคิดเกี่ยวกับผลคูณของเวกเตอร์ (เอียงหรือเทียม) ของเวกเตอร์
ผลคูณเวกเตอร์ของเวกเตอร์ a และ b คือผลคูณของความยาวของเวกเตอร์เหล่านี้กับไซน์ของมุมระหว่างเวกเตอร์เหล่านี้:
![]() .
.
ผลคูณไขว้ของเวกเตอร์ในพิกัด:
![]()
นิพจน์ทางด้านขวาเป็นตัวกำหนดลำดับที่สอง:

ต่างจากคำจำกัดความที่ให้ไว้ในเรขาคณิตวิเคราะห์ มันคือสเกลาร์
เครื่องหมายของผลิตภัณฑ์เวกเตอร์กำหนดตำแหน่งของเวกเตอร์ที่สัมพันธ์กัน:
ก และ ข มุ่งเน้นเชิงบวก
หากค่าเป็น แสดงว่าเวกเตอร์คู่หนึ่ง ก และ ข มุ่งเน้นเชิงลบ
ผลคูณไขว้ของเวกเตอร์ที่ไม่ใช่ศูนย์จะเป็นศูนย์ก็ต่อเมื่อพวกมันอยู่ในแนวเดียวกัน ( ![]() - ซึ่งหมายความว่าพวกมันอยู่บนเส้นเดียวกันหรือเส้นคู่ขนาน
- ซึ่งหมายความว่าพวกมันอยู่บนเส้นเดียวกันหรือเส้นคู่ขนาน
ลองดูปัญหาง่ายๆ สองสามข้อที่จำเป็นเมื่อแก้ไขปัญหาที่ซับซ้อนมากขึ้น
ลองหาสมการของเส้นตรงจากพิกัดสองจุดกัน
สมการของเส้นตรงที่ผ่านจุดสองจุดที่แตกต่างกันซึ่งระบุโดยพิกัด
ให้จุดที่ไม่ตรงกันสองจุดบนเส้นตรง: ด้วยพิกัด (x1; y1) และด้วยพิกัด (x2; y2) ดังนั้น เวกเตอร์ที่มีจุดเริ่มต้นที่จุดหนึ่งและจุดสิ้นสุดที่จุดหนึ่งจึงมีพิกัด (x2-x1, y2-y1) ถ้า P(x, y) เป็นจุดใดๆ บนเส้นตรงของเรา แล้วพิกัดของเวกเตอร์จะเท่ากับ (x-x1, y – y1)

การใช้ผลคูณเวกเตอร์ เงื่อนไขสำหรับความเป็นเส้นตรงของเวกเตอร์และสามารถเขียนได้ดังนี้
เหล่านั้น. (x-x1)(y2-y1)-(y-y1)(x2-x1)=0
(y2-y1)x + (x1-x2)y + x1(y1-y2) + y1(x2-x1) = 0
เราเขียนสมการสุดท้ายใหม่ดังนี้:
ขวาน + โดย + c = 0, (1)
ค = x1(y1-y2) + y1(x2-x1)
ดังนั้น เส้นตรงสามารถระบุได้ด้วยสมการในรูปแบบ (1)
ปัญหาที่ 1. ให้พิกัดของจุดสองจุด ค้นหาการเป็นตัวแทนในรูปแบบ ax + by + c = 0
ในบทเรียนนี้ เราได้เรียนรู้ข้อมูลบางอย่างเกี่ยวกับเรขาคณิตเชิงคำนวณ เราแก้ไขปัญหาการหาสมการของเส้นจากพิกัดของจุดสองจุด
ในบทต่อไป เราจะสร้างโปรแกรมเพื่อค้นหาจุดตัดของเส้นตรงสองเส้นที่กำหนดโดยสมการของเรา
ในบทความนี้ เราจะพิจารณาสมการทั่วไปของเส้นตรงบนระนาบ ขอให้เรายกตัวอย่างการสร้างสมการทั่วไปของเส้นตรงหากทราบจุดสองจุดของเส้นนี้ หรือหากทราบจุดหนึ่งและเวกเตอร์ปกติของเส้นนี้ ให้เรานำเสนอวิธีการแปลงสมการในรูปแบบทั่วไปเป็นรูปแบบมาตรฐานและพาราเมตริก
ให้ระบบพิกัดสี่เหลี่ยมคาร์ทีเซียนตามใจชอบ อ็อกซี่- พิจารณาดีกรีแรกหรือสมการเชิงเส้น:
| ขวาน+บาย+ซี=0, | (1) |
ที่ไหน ก, บี, ซี- ค่าคงที่บางตัว และองค์ประกอบอย่างน้อยหนึ่งองค์ประกอบ กและ บีแตกต่างจากศูนย์
เราจะแสดงว่าสมการเชิงเส้นบนระนาบกำหนดเส้นตรง ให้เราพิสูจน์ทฤษฎีบทต่อไปนี้
ทฤษฎีบท 1 ในระบบพิกัดสี่เหลี่ยมคาร์ทีเซียนตามอำเภอใจบนระนาบ เส้นตรงแต่ละเส้นสามารถระบุได้ด้วยสมการเชิงเส้น ในทางกลับกัน สมการเชิงเส้นแต่ละสมการ (1) ในระบบพิกัดสี่เหลี่ยมคาร์ทีเซียนใดๆ บนระนาบจะกำหนดเส้นตรง
การพิสูจน์. ก็เพียงพอที่จะพิสูจน์ได้ว่าเส้นตรง ลถูกกำหนดโดยสมการเชิงเส้นสำหรับระบบพิกัดสี่เหลี่ยมคาร์ทีเซียนระบบใดระบบหนึ่ง เนื่องจากจากนั้นจึงถูกกำหนดโดยสมการเชิงเส้นสำหรับตัวเลือกใดๆ ของระบบพิกัดสี่เหลี่ยมคาร์ทีเซียน
ให้เส้นตรงถูกกำหนดไว้บนเครื่องบิน ล- ให้เราเลือกระบบพิกัดเพื่อให้แกน วัวตรงกับเส้นตรง ลและแกน เฮ้ยตั้งฉากกับมัน แล้วสมการของเส้นตรง ลจะอยู่ในรูปแบบต่อไปนี้:
| ย=0. | (2) |
ทุกจุดในบรรทัด ลจะเป็นไปตามสมการเชิงเส้น (2) และจุดทั้งหมดที่อยู่นอกเส้นนี้จะไม่เป็นไปตามสมการ (2) ส่วนแรกของทฤษฎีบทได้รับการพิสูจน์แล้ว
ให้ระบบพิกัดสี่เหลี่ยมคาร์ทีเซียนและให้สมการเชิงเส้น (1) โดยมีองค์ประกอบอย่างน้อยหนึ่งองค์ประกอบ กและ บีแตกต่างจากศูนย์ ให้เราค้นหาตำแหน่งทางเรขาคณิตของจุดที่มีพิกัดเป็นไปตามสมการ (1) เนื่องจากมีค่าสัมประสิทธิ์อย่างน้อยหนึ่งค่า กและ บีแตกต่างจากศูนย์ ดังนั้นสมการ (1) จึงมีวิธีแก้ปัญหาอย่างน้อยหนึ่งวิธี ม(x 0 ,ย 0) (เช่น เมื่อ. ก≠0, จุด ม 0 (−ซี/เอ, 0) เป็นของจุดเรขาคณิตที่กำหนด) เมื่อแทนพิกัดเหล่านี้เป็น (1) เราจะได้ข้อมูลระบุตัวตน
| ขวาน 0 +โดย 0 +ค=0. | (3) |
ให้เราลบเอกลักษณ์ (3) จาก (1):
| ก(x−x 0)+บี(ย−ย 0)=0. | (4) |
แน่นอนว่าสมการ (4) เทียบเท่ากับสมการ (1) ดังนั้นจึงเพียงพอที่จะพิสูจน์ว่า (4) กำหนดเส้นบางเส้น
เนื่องจากเรากำลังพิจารณาระบบพิกัดสี่เหลี่ยมคาร์ทีเซียน มันจะตามมาจากความเท่าเทียมกัน (4) ว่าเวกเตอร์ที่มีส่วนประกอบ ( x−x 0 , ใช่แล้ว 0 ) ตั้งฉากกับเวกเตอร์ nมีพิกัด ( เอ บี}.
พิจารณาเส้นตรงบางเส้น ล,ผ่านจุด ม 0 (x 0 , ย 0) และตั้งฉากกับเวกเตอร์ n(รูปที่ 1) ปล่อยให้ประเด็น ม(x,y) อยู่ในบรรทัด ล- แล้วเวกเตอร์ที่มีพิกัด x−x 0 , ใช่แล้ว 0 ตั้งฉาก nและสมการ (4) เป็นไปตามสมการ (ผลคูณสเกลาร์ของเวกเตอร์ nและเท่ากับศูนย์) ในทางกลับกัน ถ้าชี้ ม(x,y) ไม่อยู่บนเส้น ลแล้วเวกเตอร์ที่มีพิกัด x−x 0 , ใช่แล้ว 0 ไม่เป็นมุมฉากกับเวกเตอร์ nและสมการ (4) ไม่เป็นที่พอใจ ทฤษฎีบทได้รับการพิสูจน์แล้ว
การพิสูจน์. เนื่องจากเส้น (5) และ (6) กำหนดเส้นเดียวกัน ดังนั้นเวกเตอร์ปกติ n 1 ={ก 1 ,บี 1) และ n 2 ={ก 2 ,บี 2) คอลลิเนียร์ เนื่องจากเวกเตอร์ n 1 ≠0, n 2 ≠0 แล้วก็มีตัวเลขดังกล่าว λ , อะไร n 2 =n 1 λ - จากที่นี่เรามี: ก 2 =ก 1 λ , บี 2 =บี 1 λ - มาพิสูจน์กัน ค 2 =ค 1 λ - แน่นอนว่าเส้นที่ตรงกันมีจุดร่วม ม 0 (x 0 , ย 0) การคูณสมการ (5) ด้วย λ และลบสมการ (6) จากนั้นเราจะได้:
เนื่องจากความเท่าเทียมกันสองรายการแรกจากนิพจน์ (7) เป็นที่พอใจแล้ว ค 1 λ −ค 2 = 0 เหล่านั้น. ค 2 =ค 1 λ - ข้อสังเกตได้รับการพิสูจน์แล้ว
โปรดทราบว่าสมการ (4) กำหนดสมการของเส้นตรงที่ผ่านจุด ม 0 (x 0 , ย 0) และมีเวกเตอร์ตั้งฉาก n={เอ บี- ดังนั้น หากทราบเวกเตอร์ปกติของเส้นตรงและจุดของเส้นนี้ ก็จะสามารถสร้างสมการทั่วไปของเส้นตรงได้โดยใช้สมการ (4)
ตัวอย่างที่ 1 เส้นตรงลากผ่านจุดหนึ่ง ม=(4,−1) และมีเวกเตอร์ปกติ n=(3, 5) สร้างสมการทั่วไปของเส้นตรง
สารละลาย. เรามี: x 0 =4, ย 0 =−1, ก=3, บี=5. ในการสร้างสมการทั่วไปของเส้นตรง เราจะแทนที่ค่าเหล่านี้เป็นสมการ (4):
คำตอบ:
เวกเตอร์นั้นขนานกับเส้นตรง ลและด้วยเหตุนี้ ตั้งฉากกับเวกเตอร์ตั้งฉากของเส้นตรง ล- ลองสร้างเวกเตอร์เส้นปกติกัน ลโดยคำนึงถึงผลคูณสเกลาร์ของเวกเตอร์ nและเท่ากับศูนย์ เราสามารถเขียนได้ เช่น n={1,−3}.
ในการสร้างสมการทั่วไปของเส้นตรง เราใช้สูตร (4) ให้เราแทนพิกัดของจุดลงใน (4) ม 1 (เรายังเอาพิกัดของจุดนั้นได้ด้วย ม 2) และเวกเตอร์ปกติ n:
การทดแทนพิกัดของจุดต่างๆ ม 1 และ ม 2 ใน (9) เรามั่นใจได้ว่าเส้นตรงที่กำหนดโดยสมการ (9) จะผ่านจุดเหล่านี้
คำตอบ:
ลบ (10) จาก (1):
เราได้รับสมการมาตรฐานของเส้นตรงแล้ว เวกเตอร์ ถาม={−บี, ก) คือเวกเตอร์ทิศทางของเส้นตรง (12)
ดู การแปลงแบบย้อนกลับ
ตัวอย่างที่ 3 เส้นตรงบนระนาบแสดงด้วยสมการทั่วไปต่อไปนี้:
ลองย้ายเทอมที่สองไปทางขวาแล้วหารทั้งสองข้างของสมการด้วย 2·5
สมการ Canonical ของเส้นในปริภูมิคือสมการที่กำหนดเส้นตรงที่ผ่านจุดที่กำหนดเส้นตรงไปยังเวกเตอร์ทิศทาง
ให้จุดและเวกเตอร์ทิศทางถูกกำหนดไว้ จุดใดจุดหนึ่งอยู่บนเส้น ลเฉพาะในกรณีที่เวกเตอร์และเป็นเส้นตรง กล่าวคือ เป็นไปตามเงื่อนไขสำหรับพวกมัน:
![]() .
.
สมการข้างต้นเป็นสมการมาตรฐานของเส้นตรง
ตัวเลข ม , nและ พีคือเส้นโครงของเวกเตอร์ทิศทางไปยังแกนพิกัด เนื่องจากเวกเตอร์ไม่เป็นศูนย์ จึงเป็นตัวเลขทั้งหมด ม , nและ พีไม่สามารถเท่ากับศูนย์พร้อมกันได้ แต่หนึ่งหรือสองคนอาจเป็นศูนย์ ตัวอย่างเช่น ในเรขาคณิตเชิงวิเคราะห์ อนุญาตให้ใช้รายการต่อไปนี้:
![]() ,
,
ซึ่งหมายความว่าเส้นโครงของเวกเตอร์บนแกน เฮ้ยและ ออนซ์มีค่าเท่ากับศูนย์ ดังนั้นทั้งเวกเตอร์และเส้นที่กำหนดโดยสมการบัญญัติจึงตั้งฉากกับแกน เฮ้ยและ ออนซ์เช่น เครื่องบิน คุณออซ .
ตัวอย่างที่ 1เขียนสมการของเส้นตรงในอวกาศที่ตั้งฉากกับระนาบ ![]() และผ่านจุดตัดของระนาบนี้กับแกน ออนซ์
.
และผ่านจุดตัดของระนาบนี้กับแกน ออนซ์
.
สารละลาย. ลองหาจุดตัดของระนาบนี้กับแกนกัน ออนซ์- เนื่องจากจุดใดๆ ที่วางอยู่บนแกน ออนซ์มีพิกัด แล้วสมมติในสมการที่กำหนดของระนาบ x = ย = 0 เราได้ 4 z- 8 = 0 หรือ z= 2 . ดังนั้นจุดตัดของระนาบนี้กับแกน ออนซ์มีพิกัด (0; 0; 2) . เนื่องจากเส้นที่ต้องการตั้งฉากกับระนาบ จึงขนานกับเวกเตอร์ปกติ ดังนั้นเวกเตอร์ทิศทางของเส้นตรงจึงสามารถเป็นเวกเตอร์ปกติได้ ![]() เครื่องบินที่ได้รับ
เครื่องบินที่ได้รับ
ทีนี้มาเขียนสมการที่ต้องการของเส้นตรงที่ผ่านจุดหนึ่งกัน ก= (0; 0; 2) ในทิศทางของเวกเตอร์:
![]()
สมการของเส้นตรงที่ผ่านจุดที่กำหนดสองจุด
เส้นตรงสามารถกำหนดได้ด้วยจุดสองจุดที่วางอยู่บนเส้นนั้น ![]() และ
และ ![]() ในกรณีนี้ เวกเตอร์ทิศทางของเส้นตรงสามารถเป็นเวกเตอร์ได้ จากนั้นสมการมาตรฐานของเส้นตรงจะเกิดขึ้น
ในกรณีนี้ เวกเตอร์ทิศทางของเส้นตรงสามารถเป็นเวกเตอร์ได้ จากนั้นสมการมาตรฐานของเส้นตรงจะเกิดขึ้น
![]() .
.
สมการข้างต้นกำหนดเส้นที่ผ่านจุดที่กำหนดสองจุด
ตัวอย่างที่ 2เขียนสมการของเส้นในปริภูมิที่ผ่านจุด และ
สารละลาย. ให้เราเขียนสมการเส้นตรงที่ต้องการในรูปแบบที่ให้ไว้ข้างต้นในการอ้างอิงทางทฤษฎี:
![]()
![]() .
.
เนื่องจาก ดังนั้นเส้นตรงที่ต้องการจึงตั้งฉากกับแกน เฮ้ย .
ตรงเหมือนเส้นตัดกันของระนาบ
เส้นตรงในอวกาศสามารถนิยามได้ว่าเป็นเส้นตัดกันของระนาบที่ไม่ขนานกัน 2 ระนาบ และนั่นคือ เซตของจุดที่เป็นไปตามระบบสมการเชิงเส้น 2 สมการ

สมการของระบบเรียกอีกอย่างว่าสมการทั่วไปของเส้นตรงในอวกาศ
ตัวอย่างที่ 3เขียนสมการมาตรฐานของเส้นตรงในปริภูมิที่กำหนดโดยสมการทั่วไป
![]()
สารละลาย. ในการเขียนสมการบัญญัติของเส้นตรงหรือสมการของเส้นตรงที่ผ่านจุดที่กำหนดสองจุด คุณจะต้องค้นหาพิกัดของจุดสองจุดใดๆ บนเส้นตรง พวกเขาสามารถเป็นจุดตัดกันของเส้นตรงกับระนาบพิกัดสองระนาบใดก็ได้ คุณออซและ xออซ .
จุดตัดของเส้นตรงและระนาบ คุณออซมีแอบซิสซา x= 0 . ดังนั้นหากสมมุติในระบบสมการนี้ x= 0 เราจะได้ระบบที่มีตัวแปรสองตัว:
![]()
การตัดสินใจของเธอ ย = 2 , z= 6 ร่วมกับ x= 0 กำหนดจุด ก(0; 2; 6) เส้นที่ต้องการ แล้วสมมติในระบบสมการที่กำหนด ย= 0 เราได้ระบบ
การตัดสินใจของเธอ x = -2 , z= 0 ร่วมกับ ย= 0 กำหนดจุด บี(-2; 0; 0) จุดตัดของเส้นตรงกับระนาบ xออซ .
ทีนี้ลองเขียนสมการของเส้นที่ผ่านจุดต่างๆ กัน ก(0; 2; 6) และ บี (-2; 0; 0) :
![]() ,
,
หรือหลังจากหารตัวส่วนด้วย -2:
![]() ,
,
คำนิยาม.เส้นตรงใดๆ บนระนาบสามารถระบุได้ด้วยสมการอันดับหนึ่ง
ขวาน + Wu + C = 0,
นอกจากนี้ค่าคงที่ A และ B ไม่เท่ากับศูนย์ในเวลาเดียวกัน สมการลำดับแรกนี้เรียกว่า สมการทั่วไปของเส้นตรงขึ้นอยู่กับค่าของค่าคงที่ A, B และ C อาจมีกรณีพิเศษต่อไปนี้:
C = 0, A ≠0, B ≠ 0 – เส้นตรงตัดผ่านจุดกำเนิด
A = 0, B ≠0, C ≠0 (By + C = 0) - เส้นตรงขนานกับแกน Ox
B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – เส้นตรงขนานกับแกน Oy
B = C = 0, A ≠0 – เส้นตรงเกิดขึ้นพร้อมกับแกน Oy
A = C = 0, B ≠0 – เส้นตรงเกิดขึ้นพร้อมกับแกน Ox
สมการของเส้นตรงสามารถแสดงได้ในรูปแบบต่างๆ ขึ้นอยู่กับเงื่อนไขเริ่มต้นที่กำหนด
สมการของเส้นตรงจากจุดและเวกเตอร์ปกติ
คำนิยาม.ในระบบพิกัดสี่เหลี่ยมคาร์ทีเซียน เวกเตอร์ที่มีส่วนประกอบ (A, B) จะตั้งฉากกับเส้นตรงที่กำหนดโดยสมการ Ax + By + C = 0
ตัวอย่าง- ค้นหาสมการของเส้นตรงที่ผ่านจุด A(1, 2) ซึ่งตั้งฉากกับ (3, -1)
สารละลาย- ด้วย A = 3 และ B = -1 ลองเขียนสมการของเส้นตรง: 3x – y + C = 0 ในการค้นหาสัมประสิทธิ์ C เราจะแทนที่พิกัดของจุด A ที่กำหนดลงในนิพจน์ผลลัพธ์ เราจะได้: 3 – 2 + C = 0 ดังนั้น C = -1 . ผลรวม: สมการที่ต้องการ: 3x – y – 1 = 0
สมการของเส้นตรงที่ผ่านจุดสองจุด
ให้จุดสองจุด M 1 (x 1, y 1, z 1) และ M 2 (x 2, y 2, z 2) ถูกกำหนดไว้ในอวกาศ จากนั้นสมการของเส้นตรงที่ผ่านจุดเหล่านี้คือ:

หากตัวส่วนใดๆ มีค่าเท่ากับศูนย์ ตัวเศษที่สอดคล้องกันควรตั้งค่าให้เท่ากับศูนย์ บนระนาบ สมการของเส้นที่เขียนด้านบนจะถูกทำให้ง่ายขึ้น:

ถ้า x 1 ≠ x 2 และ x = x 1 ถ้า x 1 = x 2
เรียกว่าเศษส่วน = k ความลาดชันโดยตรง.
ตัวอย่าง- ค้นหาสมการของเส้นตรงที่ผ่านจุด A(1, 2) และ B(3, 4)
สารละลาย.เมื่อใช้สูตรที่เขียนข้างต้น เราจะได้:

สมการของเส้นตรงจากจุดและความชัน
หากผลรวม Ax + Bu + C = 0 นำไปสู่รูปแบบ:

และกำหนด  จากนั้นจึงเรียกสมการผลลัพธ์ สมการของเส้นตรงกับความชันเค.
จากนั้นจึงเรียกสมการผลลัพธ์ สมการของเส้นตรงกับความชันเค.
สมการของเส้นตรงจากจุดและเวกเตอร์ทิศทาง
โดยการเปรียบเทียบกับจุดที่พิจารณาสมการของเส้นตรงผ่านเวกเตอร์ปกติ คุณสามารถป้อนคำจำกัดความของเส้นตรงผ่านจุดและเวกเตอร์ทิศทางของเส้นตรงได้
คำนิยาม.เวกเตอร์ที่ไม่ใช่ศูนย์แต่ละตัว (α 1, α 2) ส่วนประกอบที่ตรงตามเงื่อนไข A α 1 + B α 2 = 0 เรียกว่าเวกเตอร์กำกับของเส้น
ขวาน + Wu + C = 0
ตัวอย่าง. ค้นหาสมการของเส้นตรงที่มีเวกเตอร์ทิศทาง (1, -1) และผ่านจุด A(1, 2)
สารละลาย.เราจะค้นหาสมการของเส้นที่ต้องการในรูปแบบ: Ax + By + C = 0 ตามคำจำกัดความสัมประสิทธิ์จะต้องเป็นไปตามเงื่อนไข:
1 * A + (-1) * B = 0 เช่น ก = บี
จากนั้นสมการของเส้นตรงจะมีรูปแบบ: Ax + Ay + C = 0 หรือ x + y + C / A = 0 สำหรับ x = 1, y = 2 เราได้รับ C/ A = -3 เช่น สมการที่ต้องการ:
สมการของเส้นตรงในส่วนต่างๆ
หากในสมการทั่วไปของเส้นตรง Ах + Ву + С = 0 С≠0 จากนั้นหารด้วย –С เราจะได้:  หรือ
หรือ

ความหมายทางเรขาคณิตของค่าสัมประสิทธิ์ก็คือค่าสัมประสิทธิ์ กคือพิกัดจุดตัดของเส้นตรงกับแกนอ็อกซ์ และ ข– พิกัดจุดตัดของเส้นตรงกับแกนออย
ตัวอย่าง.จะได้สมการทั่วไปของเส้นตรง x – y + 1 = 0 ค้นหาสมการของเส้นตรงในส่วนนี้
C = 1, , ก = -1, ข = 1
สมการปกติของเส้นตรง
ถ้าทั้งสองข้างของสมการ Ax + By + C = 0 คูณด้วยตัวเลข  ซึ่งเรียกว่า ปัจจัยการทำให้เป็นมาตรฐานแล้วเราก็ได้
ซึ่งเรียกว่า ปัจจัยการทำให้เป็นมาตรฐานแล้วเราก็ได้
xcosφ + ysinφ - p = 0 –
สมการปกติของเส้นตรง ต้องเลือกเครื่องหมาย±ของปัจจัยการทำให้เป็นมาตรฐานเพื่อให้μ * C< 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
ตัวอย่าง- สมการทั่วไปของเส้นตรง 12x – 5y – 65 = 0 ถูกกำหนดไว้ จำเป็นต้องเขียนสมการประเภทต่างๆ สำหรับเส้นนี้
สมการของเส้นนี้ในส่วนต่างๆ: 
สมการของเส้นนี้ด้วยความชัน: (หารด้วย 5)

 - cos φ = 12/13; บาป φ= -5/13; พี = 5.
- cos φ = 12/13; บาป φ= -5/13; พี = 5.
ควรสังเกตว่าไม่ใช่ทุกเส้นตรงที่สามารถแสดงด้วยสมการในส่วนต่างๆ เช่น เส้นตรงที่ขนานกับแกนหรือผ่านจุดกำเนิดของพิกัด
ตัวอย่าง- เส้นตรงตัดส่วนบวกที่เท่ากันบนแกนพิกัด เขียนสมการของเส้นตรงถ้าพื้นที่ของสามเหลี่ยมที่เกิดจากส่วนเหล่านี้คือ 8 ซม. 2
สารละลาย.สมการของเส้นตรงมีรูปแบบ: , ab /2 = 8; ab=16; ก=4, ก=-4 ก = -4< 0 не подходит по условию задачи. Итого: или х + у – 4 = 0.
ตัวอย่าง- เขียนสมการของเส้นตรงที่ผ่านจุด A(-2, -3) และจุดกำเนิด
สารละลาย.
สมการของเส้นตรงคือ:  โดยที่ x 1 = y 1 = 0; x 2 = -2; ปี 2 = -3
โดยที่ x 1 = y 1 = 0; x 2 = -2; ปี 2 = -3
มุมระหว่างเส้นตรงบนเครื่องบิน
คำนิยาม.หากให้เส้นตรงสองเส้น y = k 1 x + b 1, y = k 2 x + b 2 มุมแหลมระหว่างเส้นเหล่านี้จะถูกกำหนดเป็น
 .
.
เส้นตรงสองเส้นขนานกันถ้า k 1 = k 2 เส้นตรงสองเส้นจะตั้งฉากกันถ้า k 1 = -1/ k 2
ทฤษฎีบท.เส้น Ax + Bу + C = 0 และ A 1 x + B 1 y + C 1 = 0 ขนานกันเมื่อสัมประสิทธิ์ A 1 = แลม A, B 1 = แลมบ์เป็นสัดส่วน ถ้า C 1 = แลมซีด้วย แสดงว่าเส้นตรง พิกัดของจุดตัดกันของเส้นตรงสองเส้นพบว่าเป็นวิธีแก้ระบบสมการของเส้นเหล่านี้
สมการของเส้นตรงที่ผ่านจุดที่กำหนดซึ่งตั้งฉากกับเส้นที่กำหนด
คำนิยาม.เส้นตรงที่ผ่านจุด M 1 (x 1, y 1) และตั้งฉากกับเส้นตรง y = kx + b แสดงด้วยสมการ:

ระยะทางจากจุดหนึ่งไปยังอีกบรรทัด
ทฤษฎีบท.หากกำหนดจุด M(x 0, y 0) ดังนั้นระยะทางถึงเส้น Ax + Bу + C = 0 จะถูกกำหนดเป็น
 .
.
การพิสูจน์.ให้จุด M 1 (x 1, y 1) เป็นฐานของจุดตั้งฉากที่ตกลงจากจุด M ไปยังเส้นตรงที่กำหนด จากนั้นระยะห่างระหว่างจุด M และ M 1:
![]() (1)
(1)
พิกัด x 1 และ y 1 สามารถพบได้โดยการแก้ระบบสมการ:

สมการที่สองของระบบคือสมการของเส้นที่ผ่านจุดที่กำหนด M 0 ซึ่งตั้งฉากกับเส้นที่กำหนด หากเราแปลงสมการแรกของระบบให้อยู่ในรูปแบบ:
A(x – x 0) + B(y – y 0) + ขวาน 0 + โดย 0 + C = 0,
จากนั้นเมื่อแก้ไขเราจะได้:

เมื่อแทนนิพจน์เหล่านี้เป็นสมการ (1) เราพบว่า:

ทฤษฎีบทได้รับการพิสูจน์แล้ว
ตัวอย่าง- กำหนดมุมระหว่างเส้น: y = -3 x + 7; y = 2 x + 1
เค 1 = -3; เค 2 = 2; ทีจีφ =  - φ= π /4.
- φ= π /4.
ตัวอย่าง- แสดงว่าเส้นตรง 3x – 5y + 7 = 0 และ 10x + 6y – 3 = 0 ตั้งฉากกัน
สารละลาย- เราพบว่า: k 1 = 3/5, k 2 = -5/3, k 1* k 2 = -1 ดังนั้น เส้นตรงทั้งสองจึงตั้งฉากกัน
ตัวอย่าง- ให้เป็นจุดยอดของสามเหลี่ยม A(0; 1), B (6; 5), C (12; -1) ค้นหาสมการของความสูงที่ดึงมาจากจุดยอด C
สารละลาย- เราพบสมการของด้าน AB:  - 4 x = 6 ปี – 6;
- 4 x = 6 ปี – 6;
2 x – 3 ปี + 3 = 0;
สมการความสูงที่ต้องการมีรูปแบบ: Ax + By + C = 0 หรือ y = kx + b เค = . แล้ว ย = . เพราะ ความสูงผ่านจุด C จากนั้นพิกัดจะเป็นไปตามสมการนี้:  จากโดยที่ b = 17. รวม: .
จากโดยที่ b = 17. รวม: . 
คำตอบ: 3 x + 2 y – 34 = 0
คุณสมบัติของเส้นตรงในเรขาคณิตแบบยุคลิด
เส้นตรงสามารถลากผ่านจุดใดก็ได้ไม่จำกัดจำนวน
จากจุดที่ไม่ตรงกันสองจุดใดๆ ก็สามารถลากเส้นตรงเส้นเดียวได้
เส้นตรงสองเส้นที่แยกออกจากกันในระนาบหนึ่งตัดกันที่จุดเดียวหรืออยู่
ขนาน (ต่อจากอันที่แล้ว)
ในพื้นที่สามมิติ มีสามตัวเลือกสำหรับตำแหน่งสัมพัทธ์ของเส้นสองเส้น:
- เส้นตัดกัน
- เส้นขนาน
- เส้นตรงตัดกัน
ตรง เส้น— เส้นโค้งพีชคณิตลำดับแรก: เส้นตรงในระบบพิกัดคาร์ทีเซียน
ได้รับบนระนาบโดยสมการระดับแรก (สมการเชิงเส้น)
สมการทั่วไปของเส้นตรง
คำนิยาม- เส้นตรงใดๆ บนระนาบสามารถระบุได้ด้วยสมการอันดับหนึ่ง
ขวาน + Wu + C = 0,
และคงที่ เอ, บีไม่เท่ากับศูนย์ในเวลาเดียวกัน สมการลำดับแรกนี้เรียกว่า ทั่วไป
สมการของเส้นตรงขึ้นอยู่กับค่าของค่าคงที่ เอ, บีและ กับกรณีพิเศษต่อไปนี้เป็นไปได้:
. ค = 0, ก ≠0, บี ≠ 0- เส้นตรงผ่านจุดกำเนิด
. A = 0, B ≠0, C ≠0 (โดย + C = 0)- เส้นตรงขนานกับแกน โอ้
. B = 0, A ≠0, C ≠ 0 (ขวาน + C = 0)- เส้นตรงขนานกับแกน โอ้
. B = C = 0, A ≠0- เส้นตรงเกิดขึ้นพร้อมกับแกน โอ้
. ก = ค = 0, บี ≠0- เส้นตรงเกิดขึ้นพร้อมกับแกน โอ้
สมการของเส้นตรงสามารถแสดงได้หลายรูปแบบขึ้นอยู่กับรูปแบบที่กำหนด
เงื่อนไขเริ่มต้น
สมการของเส้นตรงจากจุดและเวกเตอร์ปกติ
คำนิยาม- ในระบบพิกัดสี่เหลี่ยมคาร์ทีเซียน เวกเตอร์ที่มีส่วนประกอบ (A, B)
ตั้งฉากกับเส้นที่กำหนดโดยสมการ
ขวาน + Wu + C = 0
ตัวอย่าง- ค้นหาสมการของเส้นตรงที่ผ่านจุดหนึ่ง เอ(1, 2)ตั้งฉากกับเวกเตอร์ (3, -1).
สารละลาย- ด้วย A = 3 และ B = -1 ลองเขียนสมการของเส้นตรง: 3x - y + C = 0 เพื่อหาสัมประสิทธิ์ C
ลองแทนพิกัดของจุด A ลงในนิพจน์ผลลัพธ์ เราจะได้: 3 - 2 + C = 0
ค = -1 ผลรวม: สมการที่ต้องการ: 3x - y - 1 = 0
สมการของเส้นตรงที่ผ่านจุดสองจุด
ให้สองคะแนนในอวกาศ ม 1 (x 1 , ปี 1 , z 1)และ M2 (x 2, y 2, z 2),แล้ว สมการของเส้น,
ผ่านจุดเหล่านี้:
ถ้าตัวส่วนใดๆ เป็นศูนย์ ควรตั้งค่าตัวเศษที่สอดคล้องกันให้เท่ากับศูนย์ บน
ระนาบ สมการของเส้นตรงที่เขียนด้านบนจะถูกทำให้ง่ายขึ้น:

ถ้า x 1 ≠ x 2และ x = x 1, ถ้า x 1 = x 2 .
เศษส่วน = เคเรียกว่า ความลาดชัน โดยตรง.
ตัวอย่าง- ค้นหาสมการของเส้นตรงที่ผ่านจุด A(1, 2) และ B(3, 4)
สารละลาย- เมื่อใช้สูตรที่เขียนข้างต้น เราจะได้:

สมการเส้นตรงโดยใช้จุดและความชัน
ถ้าสมการทั่วไปของเส้นตรง ขวาน + Wu + C = 0นำไปสู่:

และกำหนด  จากนั้นจึงเรียกสมการผลลัพธ์
จากนั้นจึงเรียกสมการผลลัพธ์
สมการของเส้นตรงกับความชัน k
สมการของเส้นตรงจากจุดและเวกเตอร์ทิศทาง
โดยการเปรียบเทียบกับจุดที่พิจารณาสมการของเส้นตรงผ่านเวกเตอร์ปกติ คุณสามารถเข้าสู่งานได้
เส้นตรงที่ผ่านจุดหนึ่งและเวกเตอร์ทิศทางของเส้นตรง
คำนิยาม- เวกเตอร์ที่ไม่ใช่ศูนย์ทุกตัว (α 1 , α 2)ซึ่งมีส่วนประกอบตรงตามเงื่อนไข
เอเอ 1 + บีเอ 2 = 0เรียกว่า เวกเตอร์กำกับของเส้นตรง
ขวาน + Wu + C = 0
ตัวอย่าง- ค้นหาสมการของเส้นตรงที่มีเวกเตอร์ทิศทาง (1, -1) และผ่านจุด A(1, 2)
สารละลาย- เราจะค้นหาสมการของเส้นที่ต้องการในรูปแบบ: ขวาน + โดย + C = 0ตามคำนิยามที่ว่า
ค่าสัมประสิทธิ์ต้องเป็นไปตามเงื่อนไขต่อไปนี้:
1 * A + (-1) * B = 0 เช่น ก = บี
จากนั้นสมการของเส้นตรงจะมีรูปแบบ: ขวาน + Ay + C = 0,หรือ x + y + C / A = 0
ที่ x = 1, y = 2เราได้รับ ค/เอ = -3, เช่น. สมการที่ต้องการ:
x + y - 3 = 0
สมการของเส้นตรงในส่วนต่างๆ
หากในสมการทั่วไปของเส้นตรง Ах + Ву + С = 0 С≠0 จากนั้นหารด้วย -С เราจะได้:
 หรือที่ไหน
หรือที่ไหน

ความหมายทางเรขาคณิตของค่าสัมประสิทธิ์คือค่าสัมประสิทธิ์ a คือพิกัดของจุดตัดกัน
ตรงกับแกน โอ้,ก ข- พิกัดจุดตัดของเส้นกับแกน โอ้.
ตัวอย่าง- จะได้สมการทั่วไปของเส้นตรง x - y + 1 = 0ค้นหาสมการของเส้นนี้ในส่วนต่างๆ
C = 1, , ก = -1, ข = 1
สมการปกติของเส้นตรง
ถ้าสมการทั้งสองข้าง ขวาน + Wu + C = 0หารด้วยจำนวน  ซึ่งเรียกว่า
ซึ่งเรียกว่า
ปัจจัยการทำให้เป็นมาตรฐานแล้วเราก็ได้
xcosφ + ysinφ - p = 0 -สมการปกติของเส้นตรง.
ต้องเลือกเครื่องหมาย ± ของปัจจัยการทำให้เป็นมาตรฐาน μ*C< 0.
ร- ความยาวของเส้นตั้งฉากลดลงจากจุดกำเนิดถึงเส้นตรง
ก φ - มุมที่เกิดจากตั้งฉากกับทิศทางบวกของแกน โอ้.
ตัวอย่าง- จะได้สมการทั่วไปของเส้นตรง 12x - 5y - 65 = 0- จำเป็นต้องเขียนสมการประเภทต่างๆ
เส้นตรงนี้
สมการของเส้นนี้ในส่วนต่างๆ:

สมการของเส้นนี้กับความชัน: (หารด้วย 5)

สมการของเส้น:

cos φ = 12/13; บาป φ= -5/13; พี = 5.
ควรสังเกตว่าไม่ใช่ทุกเส้นตรงที่สามารถแสดงด้วยสมการในส่วนต่างๆ เช่น เส้นตรง
ขนานกับแกนหรือผ่านจุดกำเนิด
มุมระหว่างเส้นตรงบนเครื่องบิน
คำนิยาม- ถ้าให้สองบรรทัด y = k 1 x + b 1 , y = k 2 x + b 2ตามด้วยมุมแหลมระหว่างเส้นเหล่านี้
จะถูกกำหนดให้เป็น

เส้นตรงสองเส้นขนานกันถ้า เค 1 = เค 2- เส้นสองเส้นตั้งฉากกัน
ถ้า k 1 = -1/ k 2 .
ทฤษฎีบท.
โดยตรง ขวาน + Wu + C = 0และ A 1 x + B 1 ปี + C 1 = 0ขนานเมื่อสัมประสิทธิ์เป็นสัดส่วน
A 1 = แลมบ์ดา, B 1 = แลมบ์- ถ้ายัง ซ 1 = แลซแล้วเส้นก็ตรงกัน พิกัดจุดตัดของเส้นตรงสองเส้น
พบว่าเป็นวิธีแก้ระบบสมการของเส้นเหล่านี้
สมการของเส้นที่ผ่านจุดที่กำหนดซึ่งตั้งฉากกับเส้นที่กำหนด
คำนิยาม- เส้นที่ผ่านจุดหนึ่ง ม 1 (x 1, ย 1)และตั้งฉากกับเส้น y = kx + ข
แสดงโดยสมการ:

ระยะทางจากจุดถึงเส้น
ทฤษฎีบท- หากได้รับคะแนน M(x 0, y 0),แล้วระยะห่างถึงเส้นตรง ขวาน + Wu + C = 0กำหนดเป็น:

การพิสูจน์- ปล่อยให้ประเด็น ม 1 (x 1, ย 1)- ฐานของฉากตั้งฉากหลุดจากจุดหนึ่ง มสำหรับที่กำหนด
โดยตรง. แล้วระยะห่างระหว่างจุด มและ ม.1:
![]() (1)
(1)
พิกัด x1และ เวลา 1สามารถพบได้เป็นการแก้ระบบสมการ:

สมการที่สองของระบบคือสมการของเส้นตรงที่ผ่านจุดที่กำหนด M 0 ในแนวตั้งฉาก
ให้เส้นตรง หากเราแปลงสมการแรกของระบบให้อยู่ในรูปแบบ:
A(x - x 0) + B(y - y 0) + ขวาน 0 + โดย 0 + C = 0,
จากนั้นเมื่อแก้ไขเราจะได้:

เมื่อแทนนิพจน์เหล่านี้เป็นสมการ (1) เราพบว่า:

ทฤษฎีบทได้รับการพิสูจน์แล้ว
 สมการลอการิทึม
สมการลอการิทึม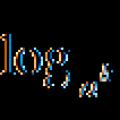 เทคนิคการแก้สมการลอการิทึม
เทคนิคการแก้สมการลอการิทึม การวิเคราะห์ตนเองของครูนักบำบัดการพูด
การวิเคราะห์ตนเองของครูนักบำบัดการพูด