พื้นที่ของรูปสามเหลี่ยมคือทฤษฎีบทพีทาโกรัส วิธีต่างๆ ในการพิสูจน์ทฤษฎีบทพีทาโกรัส: ตัวอย่าง คำอธิบาย และบทวิจารณ์
เมื่อคุณเริ่มเรียนรู้รากที่สองและวิธีแก้ปัญหา สมการอตรรกยะ(ความเท่าเทียมกันที่มีสิ่งที่ไม่รู้จักภายใต้เครื่องหมายราก) คุณอาจมีความคิดแรกเกี่ยวกับพวกเขา การใช้งานจริง. ความสามารถในการสกัด รากที่สองของตัวเลขก็จำเป็นสำหรับการแก้ปัญหาในการประยุกต์ใช้ทฤษฎีบทพีทาโกรัส ทฤษฎีบทนี้เกี่ยวข้องกับความยาวของด้านของสามเหลี่ยมมุมฉากใดๆ
ให้ความยาวของขาของรูปสามเหลี่ยมมุมฉาก (ด้านสองด้านที่มาบรรจบกันเป็นมุมฉาก) แทนด้วยตัวอักษร และ , และความยาวของด้านตรงข้ามมุมฉาก (ด้านที่ยาวที่สุดของสามเหลี่ยมตรงข้าม มุมฉาก) จะแสดงด้วยตัวอักษร จากนั้นความยาวที่เกี่ยวข้องสัมพันธ์กันด้วยความสัมพันธ์ต่อไปนี้:
สมการนี้ช่วยให้คุณหาความยาวของด้านของสามเหลี่ยมมุมฉากในกรณีที่ทราบความยาวของอีกสองด้านของมัน นอกจากนี้ยังช่วยให้คุณกำหนดได้ว่าสามเหลี่ยมที่พิจารณาเป็นสามเหลี่ยมมุมฉากหรือไม่ โดยมีเงื่อนไขว่าความยาวของทั้งหมด สามฝ่ายทราบล่วงหน้า
การแก้ปัญหาโดยใช้ทฤษฎีบทพีทาโกรัส
เพื่อรวมเนื้อหา เราจะแก้ปัญหาต่อไปนี้สำหรับการประยุกต์ใช้ทฤษฎีบทพีทาโกรัส

ให้:
- ความยาวของขาข้างหนึ่งคือ 48 ด้านตรงข้ามมุมฉากคือ 80
- ความยาวของขาคือ 84 ด้านตรงข้ามมุมฉากคือ 91
มาดูวิธีแก้ปัญหากัน:
ก) การแทนที่ข้อมูลลงในสมการข้างต้นให้ผลลัพธ์ดังต่อไปนี้:
48 2 + ข 2 = 80 2
2304 + ข 2 = 6400
ข 2 = 4096
ข= 64 หรือ ข = -64
เนื่องจากความยาวของด้านของสามเหลี่ยมไม่สามารถแสดงได้ จำนวนลบตัวเลือกที่สองจะถูกยกเลิกโดยอัตโนมัติ
ตอบรูปแรก: ข = 64.
b) ความยาวของขาของสามเหลี่ยมที่สองพบในลักษณะเดียวกัน:
84 2 + ข 2 = 91 2
7056 + ข 2 = 8281
ข 2 = 1225
ข= 35 หรือ ข = -35
เช่นเดียวกับในกรณีก่อนหน้านี้ การแก้ปัญหาเชิงลบจะถูกยกเลิก
ตอบภาพที่สอง: ข = 35

เราได้รับ:
- ความยาวของด้านที่เล็กกว่าของสามเหลี่ยมคือ 45 และ 55 ตามลำดับ และด้านที่ใหญ่กว่าคือ 75
- ความยาวของด้านที่เล็กกว่าของสามเหลี่ยมคือ 28 และ 45 ตามลำดับ และด้านที่ใหญ่กว่าคือ 53
เราแก้ปัญหา:
ก) จำเป็นต้องตรวจสอบว่าผลรวมของกำลังสองของความยาวของด้านที่เล็กกว่าของสามเหลี่ยมที่กำหนดนั้นเท่ากับกำลังสองของความยาวของด้านที่ใหญ่กว่าหรือไม่:
45 2 + 55 2 = 2025 + 3025 = 5050
ดังนั้น สามเหลี่ยมแรกจึงไม่ใช่สามเหลี่ยมมุมฉาก
b) มีการดำเนินการเดียวกัน:
28 2 + 45 2 = 784 + 2025 = 2809
ดังนั้น สามเหลี่ยมที่สองจึงเป็นสามเหลี่ยมมุมฉาก
อันดับแรก หาความยาว ส่วนที่ยาวที่สุดเกิดจากจุดที่มีพิกัด (-2, -3) และ (5, -2) สำหรับสิ่งนี้เราใช้ สูตรที่รู้จักเพื่อหาระยะห่างระหว่างจุดใน ระบบสี่เหลี่ยมพิกัด:
ในทำนองเดียวกัน เราพบความยาวของส่วนที่อยู่ระหว่างจุดที่มีพิกัด (-2, -3) และ (2, 1):
สุดท้าย เรากำหนดความยาวของส่วนระหว่างจุดที่มีพิกัด (2, 1) และ (5, -2):
เนื่องจากมีความเท่าเทียมกัน:
แล้วสามเหลี่ยมที่สอดคล้องกันก็คือสามเหลี่ยมมุมฉาก
ดังนั้นเราจึงสามารถกำหนดคำตอบของปัญหาได้ เนื่องจากผลรวมของกำลังสองของด้านที่มีความยาวน้อยที่สุด เท่ากับกำลังสองของด้านที่มี ยาวที่สุด, จุดคือจุดยอดของสามเหลี่ยมมุมฉาก
ฐาน (อยู่ในแนวนอนอย่างเคร่งครัด) วงกบ (อยู่ในแนวตั้งอย่างเคร่งครัด) และสายเคเบิล (ในแนวทแยงมุม) เป็นรูปสามเหลี่ยมมุมฉากตามลำดับ ทฤษฎีบทพีทาโกรัสสามารถใช้เพื่อค้นหาความยาวของสายเคเบิล:
ดังนั้นความยาวของสายเคเบิลจะอยู่ที่ประมาณ 3.6 เมตร
กำหนด: ระยะทางจากจุด R ถึงจุด P (ขาของสามเหลี่ยม) คือ 24 จากจุด R ถึงจุด Q (ด้านตรงข้ามมุมฉาก) - 26
ดังนั้นเราจึงช่วย Vitya แก้ปัญหา เนื่องจากด้านของสามเหลี่ยมที่แสดงในรูปควรจะเป็นสามเหลี่ยมมุมฉาก คุณสามารถใช้ทฤษฎีบทพีทาโกรัสเพื่อหาความยาวของด้านที่สามได้:
ดังนั้นความกว้างของบ่อคือ 10 เมตร
Sergey Valerievich
ทฤษฎีบทพีทาโกรัส
ทฤษฎีบทพีทาโกรัส- หนึ่งในทฤษฎีบทพื้นฐานของเรขาคณิตแบบยุคลิดที่สร้างความสัมพันธ์
ระหว่างด้านของสามเหลี่ยมมุมฉาก
เป็นที่เชื่อกันว่าได้รับการพิสูจน์โดยนักคณิตศาสตร์ชาวกรีก Pythagoras หลังจากที่ได้รับการตั้งชื่อ
สูตรทางเรขาคณิตของทฤษฎีบทพีทาโกรัส
ทฤษฎีบทเดิมถูกกำหนดไว้ดังนี้:
ในรูปสามเหลี่ยมมุมฉาก พื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างบนด้านตรงข้ามมุมฉากเท่ากับผลรวมของพื้นที่ของสี่เหลี่ยมจัตุรัส
สร้างขึ้นบนสายสวน
สูตรพีชคณิตของทฤษฎีบทพีทาโกรัส
ในรูปสามเหลี่ยมมุมฉาก กำลังสองของความยาวของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของความยาวของขา
นั่นคือ แทนความยาวของด้านตรงข้ามมุมฉากของสามเหลี่ยมผ่าน คและความยาวของขาผ่าน เอและ ข:
ทั้งสองสูตร ทฤษฎีบทพีทาโกรัสเทียบเท่ากัน แต่สูตรที่ 2 นั้นพื้นฐานกว่าก็ไม่
ต้องใช้แนวคิดของพื้นที่ นั่นคือ คำสั่งที่สองสามารถตรวจสอบได้โดยไม่รู้อะไรเกี่ยวกับพื้นที่และ
โดยการวัดเฉพาะความยาวของด้านของสามเหลี่ยมมุมฉาก
ทฤษฎีบทพีทาโกรัสผกผัน
หากกำลังสองของด้านหนึ่งของสามเหลี่ยมเท่ากับผลรวมของกำลังสองของอีกสองด้านที่เหลือ ดังนั้น
สามเหลี่ยมเป็นรูปสี่เหลี่ยมผืนผ้า
หรือกล่าวอีกนัยหนึ่ง:
สำหรับจำนวนบวกสามเท่าใดๆ เอ, ขและ ค, ดังนั้น
มีขาสามเหลี่ยมมุมฉาก เอและ ขและด้านตรงข้ามมุมฉาก ค.
ทฤษฎีบทพีทาโกรัสสำหรับสามเหลี่ยมหน้าจั่ว

ทฤษฎีบทพีทาโกรัสสำหรับรูปสามเหลี่ยมด้านเท่า

บทพิสูจน์ทฤษฎีบทพีทาโกรัส
ในขณะนี้ 367 ข้อพิสูจน์ของทฤษฎีบทนี้ได้รับการบันทึกไว้ในวรรณกรรมทางวิทยาศาสตร์ น่าจะเป็นทฤษฎีบท
พีทาโกรัสเป็นทฤษฎีบทเดียวที่มีข้อพิสูจน์มากมาย ความหลากหลายดังกล่าว
สามารถอธิบายได้ด้วยความสำคัญพื้นฐานของทฤษฎีบทสำหรับเรขาคณิตเท่านั้น
แน่นอน ตามแนวคิดแล้ว สิ่งเหล่านี้สามารถแบ่งออกเป็นชั้นเรียนจำนวนน้อยได้ ที่มีชื่อเสียงที่สุดของพวกเขา:
หลักฐานของ วิธีพื้นที่, สัจพจน์และ หลักฐานที่แปลกใหม่(ตัวอย่างเช่น,
โดยใช้ สมการเชิงอนุพันธ์).
1. พิสูจน์ทฤษฎีบทพีทาโกรัสในรูปสามเหลี่ยมที่คล้ายกัน
หลักฐานต่อไปนี้ของสูตรพีชคณิตเป็นข้อพิสูจน์ที่ง่ายที่สุด
จากสัจธรรมโดยตรง โดยเฉพาะอย่างยิ่งมันไม่ได้ใช้แนวคิดเรื่องพื้นที่ของร่าง
อนุญาต ABCมีสามเหลี่ยมมุมฉาก ค. ลองวาดความสูงจาก คและแสดงว่า
รากฐานของมันผ่าน ชม.
สามเหลี่ยม ACHคล้ายสามเหลี่ยม AB C สองมุม ในทำนองเดียวกัน สามเหลี่ยม CBHคล้ายกัน ABC.
โดยการแนะนำสัญกรณ์:

เราได้รับ:
![]() ,
,
ซึ่งตรงกับ -
พับแล้ว เอ 2 และ ข 2 เราได้รับ:
หรือซึ่งต้องพิสูจน์
2. พิสูจน์ทฤษฎีบทพีทาโกรัสโดยวิธีพื้นที่
หลักฐานต่อไปนี้แม้จะดูเรียบง่าย แต่ก็ไม่ง่ายเลย ทั้งหมด
ใช้คุณสมบัติของพื้นที่ ซึ่งการพิสูจน์นั้นซับซ้อนกว่าการพิสูจน์ทฤษฎีบทพีทาโกรัสนั่นเอง
- พิสูจน์ผ่านการเติมเต็ม
 จัดสี่สี่เหลี่ยมเท่ากัน
จัดสี่สี่เหลี่ยมเท่ากัน
สามเหลี่ยมตามภาพ
ด้านขวา.
สี่เหลี่ยมที่มีด้าน ค- สี่เหลี่ยม,
เนื่องจากผลรวมของมุมแหลมสองมุมคือ 90° และ
มุมที่พัฒนาแล้วคือ 180°
พื้นที่ของร่างทั้งหมดคือด้านหนึ่ง
พื้นที่สี่เหลี่ยมจัตุรัสที่มีด้าน ( a+b) และในทางกลับกัน ผลรวมของพื้นที่ สี่สามเหลี่ยมและ
![]()
![]()
คิวอีดี
3. พิสูจน์ทฤษฎีบทพีทาโกรัสด้วยวิธีการน้อยนิด

พิจารณาภาพวาดที่แสดงในรูปและ
มองการเปลี่ยนแปลงด้านข้างเอ, เราทำได้
เขียนความสัมพันธ์ต่อไปนี้สำหรับอนันต์
เล็ก เพิ่มด้านข้างกับและ เอ(ใช้ความเหมือน
สามเหลี่ยม):
โดยใช้วิธีการแยกตัวแปร เราพบว่า:
นิพจน์ทั่วไปสำหรับการเปลี่ยนด้านตรงข้ามมุมฉากในกรณีที่เพิ่มขึ้นของขาทั้งสองข้าง:
บูรณาการ สมการที่กำหนดและใช้เงื่อนไขเริ่มต้น เราได้รับ:
ดังนั้นเราจึงได้คำตอบที่ต้องการ:
เนื่องจากเห็นได้ง่าย การพึ่งพากำลังสองในสูตรสุดท้ายจึงปรากฏขึ้นเนื่องจากเส้นตรง
สัดส่วนระหว่างด้านของสามเหลี่ยมกับส่วนเพิ่ม ส่วนผลรวมนั้นสัมพันธ์กับส่วนอิสระ
ผลงานจากการเพิ่มขึ้นของขาที่แตกต่างกัน
สามารถหาข้อพิสูจน์ที่ง่ายกว่าได้หากเราคิดว่าขาข้างใดข้างหนึ่งไม่มีการเพิ่มขึ้น
(ใน กรณีนี้ขา ข). สำหรับค่าคงที่การรวมเราได้รับ:
(ตาม Papyrus 6619 ของพิพิธภัณฑ์เบอร์ลิน) ตามคำบอกเล่าของต้นเสียง ฮาร์พีดอนแนปต์ หรือ "ตัวปรับความตึงสาย" นั้นสร้างมุมฉากโดยใช้สามเหลี่ยมมุมฉากที่มีด้าน 3, 4 และ 5
ง่ายต่อการทำซ้ำวิธีการก่อสร้าง ลองเอาเชือกยาว 12 ม. มามัดด้วยแถบสีที่ระยะ 3 ม. จากปลายด้านหนึ่งและอีก 4 เมตรจากปลายอีกด้านหนึ่ง มุมฉากจะอยู่ระหว่างด้านที่ยาว 3 ถึง 4 เมตร อาจถูกค้านกับ Harpedonapts ว่าวิธีการก่อสร้างของพวกเขาจะซ้ำซาก ตัวอย่างเช่น ถ้าใช้สี่เหลี่ยมไม้ที่ช่างไม้ทั้งหมดใช้ อันที่จริงภาพวาดอียิปต์เป็นที่รู้จักซึ่งพบเครื่องมือดังกล่าว - ตัวอย่างเช่นภาพวาดที่แสดงถึงการประชุมเชิงปฏิบัติการช่างไม้
ค่อนข้างเป็นที่รู้จักมากขึ้นเกี่ยวกับทฤษฎีบทพีทาโกรัสในหมู่ชาวบาบิโลน ในข้อความหนึ่งย้อนหลังไปถึงสมัยของฮัมมูราบี นั่นคือ 2000 ปีก่อนคริสตกาล อี คำนวณโดยประมาณของด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉาก จากนี้เราสามารถสรุปได้ว่าในเมโสโปเตเมียพวกเขาสามารถคำนวณด้วยสามเหลี่ยมมุมฉากอย่างน้อยก็ในบางกรณี ในแง่หนึ่ง ในระดับความรู้ปัจจุบันของคณิตศาสตร์อียิปต์และบาบิโลน และในอีกด้านหนึ่ง จากการศึกษาเชิงวิพากษ์ของแหล่งข้อมูลกรีก Van der Waerden (นักคณิตศาสตร์ชาวดัตช์) สรุปว่ามีความเป็นไปได้สูงที่ ทฤษฎีบทสี่เหลี่ยมด้านตรงข้ามมุมฉากเป็นที่รู้จักในอินเดียเมื่อประมาณศตวรรษที่ 18 ก่อนคริสต์ศักราช อี
ประมาณ 400 ปีก่อนคริสตกาล e. ตาม Proclus เพลโตได้ให้วิธีการหาสามพีทาโกรัสรวมพีชคณิตและเรขาคณิต ประมาณ 300 ปีก่อนคริสตกาล อี องค์ประกอบของยุคลิดมีหลักฐานเชิงสัจพจน์ที่เก่าแก่ที่สุดของทฤษฎีบทพีทาโกรัส
ถ้อยคำ
สูตรทางเรขาคณิต:
ทฤษฎีบทเดิมถูกกำหนดไว้ดังนี้:
สูตรพีชคณิต:
นั่นคือ แสดงถึงความยาวของด้านตรงข้ามมุมฉากของสามเหลี่ยมทะลุ และความยาวของขาทะลุ และ:
ทั้งสองสูตรของทฤษฎีบทมีความเท่าเทียมกัน แต่สูตรที่สองเป็นพื้นฐานมากกว่า ไม่ต้องการแนวคิดของพื้นที่ นั่นคือ คำสั่งที่สองสามารถตรวจสอบได้โดยไม่รู้อะไรเลยเกี่ยวกับพื้นที่นั้น และโดยการวัดเฉพาะความยาวของด้านข้างของรูปสามเหลี่ยมมุมฉากเท่านั้น
ทฤษฎีบทพีทาโกรัสผกผัน:
หลักฐานของ
ในขณะนี้ 367 ข้อพิสูจน์ของทฤษฎีบทนี้ได้รับการบันทึกไว้ในวรรณกรรมทางวิทยาศาสตร์ อาจเป็นไปได้ว่าทฤษฎีบทพีทาโกรัสเป็นทฤษฎีบทเดียวที่มีการพิสูจน์จำนวนมาก ความหลากหลายดังกล่าวสามารถอธิบายได้ด้วยความสำคัญพื้นฐานของทฤษฎีบทสำหรับเรขาคณิตเท่านั้น
แน่นอน ตามแนวคิดแล้ว สิ่งเหล่านี้สามารถแบ่งออกเป็นชั้นเรียนจำนวนน้อยได้ ที่มีชื่อเสียงที่สุดของพวกเขา: พิสูจน์โดยวิธีพื้นที่, พิสูจน์จริงและแปลกใหม่ (เช่น การใช้สมการเชิงอนุพันธ์).
ผ่านรูปสามเหลี่ยมที่คล้ายกัน
หลักฐานต่อไปนี้ของสูตรพีชคณิตเป็นข้อพิสูจน์ที่ง่ายที่สุดที่สร้างขึ้นโดยตรงจากสัจพจน์ โดยเฉพาะอย่างยิ่งมันไม่ได้ใช้แนวคิดเรื่องพื้นที่

อนุญาต ABCมีสามเหลี่ยมมุมฉาก ค. ลองวาดความสูงจาก คและระบุฐานโดย ชม. สามเหลี่ยม ACHคล้ายสามเหลี่ยม ABCที่มุมสองมุม ในทำนองเดียวกัน สามเหลี่ยม CBHคล้ายกัน ABC. แนะนำสัญกรณ์
เราได้รับ
เทียบเท่าอะไร
เพิ่มเราได้รับ
ที่ต้องพิสูจน์หลักฐานพื้นที่
หลักฐานต่อไปนี้แม้จะดูเรียบง่าย แต่ก็ไม่ง่ายเลย พวกเขาทั้งหมดใช้คุณสมบัติของพื้นที่ซึ่งการพิสูจน์นั้นซับซ้อนกว่าการพิสูจน์ทฤษฎีบทพีทาโกรัสเอง
พิสูจน์ผ่านความเท่าเทียมกัน
- จัดเรียงสามเหลี่ยมมุมฉากเท่ากันสี่รูปดังแสดงในรูปที่ 1
- สี่เหลี่ยมที่มีด้าน คเป็นสี่เหลี่ยมจัตุรัสเพราะผลรวมของมุมแหลมสองมุมคือ 90° และมุมตรงคือ 180°
- พื้นที่ของรูปทั้งหมดเท่ากัน ด้านหนึ่ง กับพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้าน (a + b) และในทางกลับกัน ผลรวมของพื้นที่ของสามเหลี่ยมสี่รูปและพื้นที่ ของจตุรัสด้านใน
คิวอีดี
ข้อพิสูจน์ของยุคลิด
แนวความคิดในการพิสูจน์ของยุคลิดมีดังนี้: ลองพิสูจน์ว่าครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างบนด้านตรงข้ามมุมฉาก เท่ากับผลรวมของพื้นที่ครึ่งหนึ่งของสี่เหลี่ยมที่สร้างบนขา และจากนั้น พื้นที่ของ สี่เหลี่ยมขนาดใหญ่และสี่เหลี่ยมเล็กสองอันมีค่าเท่ากัน
พิจารณาภาพวาดทางด้านซ้าย เราสร้างสี่เหลี่ยมที่ด้านข้างของสามเหลี่ยมมุมฉากบนนั้นแล้วดึงรังสี s จากจุดยอดของมุมฉาก C ตั้งฉากกับด้านตรงข้ามมุมฉาก AB มันตัดสี่เหลี่ยม ABIK ที่สร้างบนด้านตรงข้ามมุมฉากออกเป็นสองสี่เหลี่ยม - BHJI และ HAKJ ตามลำดับ ปรากฎว่าพื้นที่ของสี่เหลี่ยมเหล่านี้เท่ากับพื้นที่ของสี่เหลี่ยมที่สร้างบนขาที่สอดคล้องกัน
ลองพิสูจน์ว่าพื้นที่ของสี่เหลี่ยมจัตุรัส DECA เท่ากับพื้นที่ของสี่เหลี่ยม AHJK ในการทำเช่นนี้เราใช้การสังเกตเสริม: พื้นที่ของรูปสามเหลี่ยมที่มีความสูงและฐานเท่ากันตามที่กำหนด สี่เหลี่ยมผืนผ้าเท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมที่กำหนด นี่เป็นผลมาจากการกำหนดพื้นที่ของรูปสามเหลี่ยมเป็นครึ่งหนึ่งของผลคูณของฐานและความสูง จากการสังเกตนี้จะตามมาว่าพื้นที่ของสามเหลี่ยม ACK เท่ากับพื้นที่ของสามเหลี่ยม AHK (ไม่แสดง) ซึ่งในทางกลับกันจะเท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมผืนผ้า AHJK
ให้เราพิสูจน์ว่าพื้นที่ของสามเหลี่ยม ACK นั้นเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยม DECA ด้วย สิ่งเดียวที่ต้องทำเพื่อสิ่งนี้คือการพิสูจน์ความเท่าเทียมกันของสามเหลี่ยม ACK และ BDA (เนื่องจากคุณสมบัติข้างต้นนั้น พื้นที่ของสามเหลี่ยม BDA เท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัส) ความเท่าเทียมกันนี้ชัดเจน: สามเหลี่ยมสองด้านเท่ากันและมุมระหว่างพวกเขา กล่าวคือ - AB=AK, AD=AC - ความเท่าเทียมกันของมุม CAK และ BAD นั้นง่ายต่อการพิสูจน์โดยวิธีการเคลื่อนไหว: ให้หมุนสามเหลี่ยม CAK 90 °ทวนเข็มนาฬิกา จะเห็นได้ว่าด้านที่สอดคล้องกันของสามเหลี่ยมทั้งสองที่พิจารณาจะตรงกัน (เนื่องจากมุมที่จุดยอดของสี่เหลี่ยมจัตุรัสคือ 90°)
อาร์กิวเมนต์เกี่ยวกับความเท่าเทียมกันของพื้นที่ของสี่เหลี่ยมจัตุรัส BCFG และสี่เหลี่ยม BHJI นั้นคล้ายคลึงกันโดยสิ้นเชิง
ดังนั้นเราจึงได้พิสูจน์แล้วว่าพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากเป็นผลรวมของพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างบนขา ความคิด หลักฐานนี้แสดงเพิ่มเติมด้วยภาพเคลื่อนไหวด้านบน
หลักฐานของ Leonardo da Vinci
องค์ประกอบหลักของการพิสูจน์คือความสมมาตรและการเคลื่อนไหว
พิจารณาภาพวาด ดังที่เห็นได้จากความสมมาตร ส่วนนั้นตัดสี่เหลี่ยมจัตุรัสออกเป็นสองส่วนที่เหมือนกัน (เนื่องจากสามเหลี่ยมและมีโครงสร้างเท่ากัน)
โดยใช้การหมุนทวนเข็มนาฬิกา 90 องศารอบจุด เราจะเห็นความเท่าเทียมกันของตัวเลขที่แรเงาและ
ตอนนี้เป็นที่ชัดเจนว่าพื้นที่ของรูปที่เราแรเงานั้นเท่ากับผลรวมของครึ่งหนึ่งของพื้นที่สี่เหลี่ยมเล็กๆ (สร้างบนขา) และพื้นที่ของสามเหลี่ยมเดิม ในทางกลับกัน มันเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัสขนาดใหญ่ (สร้างจากด้านตรงข้ามมุมฉาก) บวกกับพื้นที่ของสามเหลี่ยมเดิม ดังนั้น ผลรวมของพื้นที่สี่เหลี่ยมเล็ก ๆ ครึ่งหนึ่ง เท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมจัตุรัสใหญ่ ดังนั้น ผลรวมของพื้นที่ของสี่เหลี่ยมที่สร้างบนขา เท่ากับ พื้นที่ของสี่เหลี่ยมที่สร้าง บนด้านตรงข้ามมุมฉาก
พิสูจน์ด้วยวิธีการที่ไร้ขีดจำกัด
หลักฐานต่อไปนี้โดยใช้สมการเชิงอนุพันธ์มักจะนำมาประกอบกับที่รู้จักกันดี นักคณิตศาสตร์ชาวอังกฤษ Hardy ที่อาศัยอยู่ในครึ่งแรกของศตวรรษที่ 20
พิจารณาภาพวาดที่แสดงในรูปและสังเกตการเปลี่ยนแปลงด้านข้าง เอเราสามารถเขียนความสัมพันธ์ต่อไปนี้สำหรับการเพิ่มขึ้นทีละน้อย กับและ เอ(ใช้รูปสามเหลี่ยมที่คล้ายกัน):
โดยใช้วิธีการแยกตัวแปรเราพบว่า
นิพจน์ทั่วไปสำหรับการเปลี่ยนด้านตรงข้ามมุมฉากในกรณีที่เพิ่มขึ้นของขาทั้งสองข้าง
การรวมสมการนี้และการใช้เงื่อนไขเริ่มต้น เราได้รับ
เราจึงได้คำตอบที่ต้องการ
ดังที่เห็นได้ง่าย การพึ่งพากำลังสองในสูตรสุดท้ายปรากฏขึ้นเนื่องจากสัดส่วนเชิงเส้นตรงระหว่างด้านข้างของสามเหลี่ยมและการเพิ่มขึ้น ในขณะที่ผลรวมเกิดจากการมีส่วนร่วมอิสระจากการเพิ่มของขาต่างๆ
สามารถหาข้อพิสูจน์ที่ง่ายกว่านี้ได้หากเราคิดว่าขาข้างหนึ่งไม่มีส่วนเพิ่ม (ในกรณีนี้คือขา) จากนั้นสำหรับค่าคงที่การรวมเราได้รับ
รูปแบบและลักษณะทั่วไป
รูปทรงเรขาคณิตที่คล้ายกันทั้งสามด้าน
ลักษณะทั่วไปสำหรับ สามเหลี่ยมที่คล้ายกัน, พื้นที่ตัวเลขสีเขียว A + B = พื้นที่สีน้ำเงิน C
ทฤษฎีบทพีทาโกรัสโดยใช้สามเหลี่ยมมุมฉากที่คล้ายกัน
ภาพรวมของทฤษฎีบทพีทาโกรัสถูกสร้างขึ้นโดย Euclid ในงานของเขา จุดเริ่มต้น, ขยายพื้นที่สี่เหลี่ยมด้านข้างให้เป็นพื้นที่ที่คล้ายกัน รูปทรงเรขาคณิต :
หากเราสร้างรูปทรงเรขาคณิตที่คล้ายกัน (ดู เรขาคณิตแบบยุคลิด) ที่ด้านข้างของรูปสามเหลี่ยมมุมฉาก ผลรวมของตัวเลขที่เล็กกว่าสองรูปจะเท่ากับพื้นที่ของรูปที่ใหญ่กว่า
แนวคิดหลักของการวางนัยทั่วไปนี้คือพื้นที่ของรูปทรงเรขาคณิตดังกล่าวเป็นสัดส่วนกับกำลังสองของมิติเชิงเส้นใดๆ ของมัน และโดยเฉพาะอย่างยิ่ง กับกำลังสองของความยาวของด้านใดๆ ดังนั้น สำหรับตัวเลขที่ใกล้เคียงกันกับพื้นที่ อา, บีและ คสร้างบนด้านที่มีความยาว เอ, ขและ ค, เรามี:
แต่ตามทฤษฎีบทพีทาโกรัส เอ 2 + ข 2 = ค 2 แล้ว อา + บี = ค.
ในทางกลับกัน หากเราสามารถพิสูจน์ได้ว่า อา + บี = คสำหรับรูปทรงเรขาคณิตที่คล้ายกันสามรูปโดยไม่ใช้ทฤษฎีบทพีทาโกรัส เราก็สามารถพิสูจน์ทฤษฎีบทนั้นเองได้ โดยย้ายไปที่ ทิศทางย้อนกลับ. ตัวอย่างเช่น สามเหลี่ยมศูนย์กลางเริ่มต้นสามารถใช้เป็นรูปสามเหลี่ยมได้ คบนด้านตรงข้ามมุมฉาก และสามเหลี่ยมมุมฉากที่คล้ายกันสองรูป ( อาและ บี) สร้างขึ้นจากอีกสองด้านซึ่งเกิดขึ้นจากการหารสามเหลี่ยมกลางด้วยความสูง ผลรวมของพื้นที่เล็กสองแห่งของรูปสามเหลี่ยมนั้นย่อมเท่ากับพื้นที่ของสามเหลี่ยม ดังนั้น อา + บี = คและตามหลักฐานก่อนหน้าใน กลับลำดับ, เราได้ทฤษฎีบทพีทาโกรัส a 2 + b 2 = c 2
ทฤษฎีบทโคไซน์
ทฤษฎีบทพีทาโกรัสคือ กรณีพิเศษมากกว่า ทฤษฎีบททั่วไปโคไซน์ซึ่งสัมพันธ์กับความยาวของด้านในรูปสามเหลี่ยมโดยพลการ:
โดยที่ θ คือมุมระหว่างด้าน เอและ ข.
ถ้า θ เป็น 90 องศา แล้ว cos θ = 0 และสูตรถูกทำให้ง่ายขึ้นเป็นทฤษฎีบทพีทาโกรัสปกติ
สามเหลี่ยมตามอำเภอใจ
ไปยังมุมใดๆ ที่เลือกของรูปสามเหลี่ยมที่มีด้านต่างๆ ก, ข, คจารึกสามเหลี่ยมหน้าจั่วในลักษณะที่ มุมเท่ากันที่ฐานของมัน θ เท่ากับมุมที่เลือก สมมติว่ามุมที่เลือก θ อยู่ตรงข้ามกับด้านที่ระบุ ค. เป็นผลให้เราได้รูปสามเหลี่ยม ABD ที่มีมุม θ ซึ่งอยู่ตรงข้ามกับด้าน เอและงานปาร์ตี้ r. สามเหลี่ยมที่สองเกิดจากมุม θ ซึ่งอยู่ตรงข้ามกับด้าน ขและงานปาร์ตี้ กับยาว สตามที่แสดงในภาพ Thabit Ibn Qurra กล่าวว่าด้านในสามเหลี่ยมทั้งสามนี้มีความสัมพันธ์กันดังนี้:
เมื่อมุม θ เข้าใกล้ π/2 ฐาน สามเหลี่ยมหน้าจั่วลดลงและทั้งสองข้างเหลื่อมกันน้อยลง เมื่อ θ = π/2, ADB จะกลายเป็นสามเหลี่ยมมุมฉาก r + ส = คและเราจะได้ทฤษฎีบทพีทาโกรัสเริ่มต้น
ลองดูหนึ่งในอาร์กิวเมนต์ สามเหลี่ยม ABCมีมุมเท่ากับสามเหลี่ยม ABD แต่เรียงกลับกัน (สามเหลี่ยมสองรูปมีมุมร่วมที่จุดยอด B ทั้งสองมีมุม θ และมีมุมที่สามเหมือนกันด้วยผลรวมของมุมของสามเหลี่ยม) ดังนั้น ABC จึงคล้ายกับการสะท้อน ABD ของสามเหลี่ยม DBA ดังที่แสดง ในรูปด้านล่าง ให้เราเขียนความสัมพันธ์ระหว่าง ฝ่ายตรงข้ามและประชิดกับมุม θ
การสะท้อนของสามเหลี่ยมอีกรูปก็เช่นกัน
คูณเศษส่วนและเพิ่มอัตราส่วนทั้งสองนี้:
คิวอีดี
ลักษณะทั่วไปของรูปสามเหลี่ยมตามอำเภอใจผ่านสี่เหลี่ยมด้านขนาน
ลักษณะทั่วไปสำหรับ สามเหลี่ยมโดยพลการ,
พื้นที่สีเขียว พล็อต = พื้นที่สีฟ้า
หลักฐานวิทยานิพนธ์ว่าในรูปข้างบน
ลองทำการวางนัยทั่วไปเพิ่มเติมสำหรับรูปสามเหลี่ยมที่ไม่ใช่สี่เหลี่ยม โดยใช้สี่เหลี่ยมด้านขนานทั้งสามด้านแทนที่จะเป็นสี่เหลี่ยม (สี่เหลี่ยมเป็นกรณีพิเศษ) รูปบนแสดงว่า for สามเหลี่ยมแหลมพื้นที่ของสี่เหลี่ยมด้านขนานด้านยาวเท่ากับผลรวมของสี่เหลี่ยมด้านขนานของอีกสองด้าน โดยจะต้องสร้างสี่เหลี่ยมด้านขนานด้านยาวดังแสดงในรูป (ขนาดที่ทำเครื่องหมายด้วยลูกศรจะเหมือนกันและ กำหนดด้านของสี่เหลี่ยมด้านขนานล่าง) การแทนที่สี่เหลี่ยมจัตุรัสด้วยสี่เหลี่ยมด้านขนานนี้มีความคล้ายคลึงกับทฤษฎีบทพีทาโกรัสเริ่มต้นอย่างชัดเจน และเชื่อกันว่าได้รับการกำหนดสูตรโดย Pappus of Alexandria ใน 4 CE อี
รูปด้านล่างแสดงความคืบหน้าของการพิสูจน์ ลองดูที่ด้านซ้ายของสามเหลี่ยม สี่เหลี่ยมด้านขนานสีเขียวด้านซ้ายมีพื้นที่เท่ากับด้านซ้ายของสี่เหลี่ยมด้านขนานสีน้ำเงินเพราะมีฐานเท่ากัน ขและส่วนสูง ชม.. นอกจากนี้ กล่องสีเขียวด้านซ้ายจะมีพื้นที่เดียวกับกล่องสีเขียวด้านซ้ายในรูปบนเนื่องจากมี พื้นดินทั่วไป(บน ทางซ้ายมือสามเหลี่ยม) และความสูงรวมตั้งฉากกับด้านนั้นของสามเหลี่ยม การโต้เถียงกันทางด้านขวาของรูปสามเหลี่ยม เราพิสูจน์ว่าสี่เหลี่ยมด้านขนานล่างมีพื้นที่เท่ากับสี่เหลี่ยมด้านขนานสีเขียวสองรูป
ตัวเลขที่ซับซ้อน
ทฤษฎีบทพีทาโกรัสใช้เพื่อค้นหาระยะห่างระหว่างจุดสองจุดในระบบพิกัดคาร์ทีเซียน และทฤษฎีบทนี้เป็นจริงสำหรับพิกัดจริงทั้งหมด: ระยะทาง สระหว่างสองจุด ( ก, ข) และ ( ซีดี) เท่ากับ
ไม่มีปัญหากับสูตร ถ้านับจำนวนเชิงซ้อนเป็นเวกเตอร์ที่มีส่วนประกอบจริง x + ฉัน y = (x, y). . เช่น ระยะทาง สระหว่าง 0 + 1 ผมและ 1 + 0 ผมคำนวณเป็นโมดูลัสของเวกเตอร์ (0, 1) − (1, 0) = (−1, 1), หรือ
อย่างไรก็ตาม สำหรับการดำเนินการกับเวกเตอร์ที่มีพิกัดเชิงซ้อน จำเป็นต้องปรับปรุงสูตรพีทาโกรัสบางอย่าง ระยะห่างระหว่างจุดกับ ตัวเลขเชิงซ้อน (เอ, ข) และ ( ค, d); เอ, ข, ค, และ dล้วนซับซ้อน เรากำหนดโดยใช้ ค่าสัมบูรณ์. ระยะทาง สขึ้นอยู่กับความแตกต่างของเวกเตอร์ (เอ − ค, ข − d) ใน แบบฟอร์มต่อไปนี้: ปล่อยให้ความแตกต่าง เอ − ค = พี+ฉัน q, ที่ไหน พีคือส่วนที่แท้จริงของความแตกต่าง qเป็นส่วนจินตภาพ และ i = √(-1) ในทำนองเดียวกันให้ ข − d = r+ฉัน ส. แล้ว:
คอนจูเกตเชิงซ้อนของ . เช่น ระยะห่างระหว่างจุด (เอ, ข) = (0, 1) และ (ค, d) = (ผม, 0) คำนวณส่วนต่าง (เอ − ค, ข − d) = (−ผม, 1) และผลลัพธ์จะเป็น 0 หากไม่ได้ใช้คอนจูเกตที่ซับซ้อน ดังนั้นเมื่อใช้สูตรที่ปรับปรุงแล้วเราจะได้
โมดูลถูกกำหนดดังนี้:
Stereometry
ลักษณะทั่วไปที่สำคัญของทฤษฎีบทพีทาโกรัสสำหรับปริภูมิสามมิติคือทฤษฎีบทของเดอกัว ซึ่งตั้งชื่อตาม J.-P. de Gua: ถ้าจัตุรมุขมีมุมฉาก (เหมือนในลูกบาศก์) พื้นที่สี่เหลี่ยมจัตุรัสของใบหน้าที่อยู่ตรงข้ามมุมฉากจะเท่ากับผลรวมของสี่เหลี่ยมจัตุรัสของพื้นที่ของอีกสามหน้า ข้อสรุปนี้สามารถสรุปได้ว่า " น-มิติทฤษฎีบทพีทาโกรัส":
ทฤษฎีบทพีทาโกรัส พื้นที่สามมิติเชื่อม AD ในแนวทแยงกับสามด้าน
ลักษณะทั่วไปอื่น: ทฤษฎีบทพีทาโกรัสสามารถนำไปใช้กับ stereometry ในรูปแบบต่อไปนี้ พิจารณา ทรงลูกบาศก์ตามที่แสดงในภาพ ค้นหาความยาวของเส้นทแยงมุม BD โดยใช้ทฤษฎีบทพีทาโกรัส:
โดยที่ด้านทั้งสามเป็นสามเหลี่ยมมุมฉาก ใช้ BD แนวทแยงแนวนอนและขอบแนวตั้ง AB เพื่อค้นหาความยาวของ AD ในแนวทแยง อีกครั้งโดยใช้ทฤษฎีบทพีทาโกรัส:
หรือถ้าทุกอย่างเขียนด้วยสมการเดียว:
ผลลัพธ์นี้เป็นนิพจน์ 3 มิติสำหรับกำหนดขนาดของเวกเตอร์ วี(แนวทแยง AD) แสดงในรูปขององค์ประกอบตั้งฉาก ( วี k) (สามด้านตั้งฉากกัน):
สมการนี้สามารถมองได้ว่าเป็นลักษณะทั่วไปของทฤษฎีบทพีทาโกรัสสำหรับปริภูมิหลายมิติ อย่างไรก็ตาม ผลที่ได้จริง ๆ แล้วไม่มีอะไรมากไปกว่าการใช้ทฤษฎีบทพีทาโกรัสซ้ำๆ กับลำดับของสามเหลี่ยมมุมฉากในระนาบตั้งฉากต่อเนื่องกัน
ช่องว่างเวกเตอร์
ในกรณีของระบบเวกเตอร์มุมฉาก ความเท่าเทียมกันเกิดขึ้น ซึ่งเรียกอีกอย่างว่าทฤษฎีบทพีทาโกรัส:
ถ้า เป็นเส้นโครงของเวกเตอร์ลงบน แกนพิกัดดังนั้นสูตรนี้จึงเกิดขึ้นพร้อมกับระยะทางแบบยุคลิด - และหมายความว่าความยาวของเวกเตอร์เท่ากับราก ผลรวมสี่เหลี่ยมสี่เหลี่ยมของส่วนประกอบ
ความคล้ายคลึงของความเท่าเทียมกันในกรณีนี้ ระบบไม่มีที่สิ้นสุดเวกเตอร์เรียกว่าความเท่าเทียมกันของ Parseval
เรขาคณิตที่ไม่ใช่แบบยุคลิด
ทฤษฎีบทพีทาโกรัสได้มาจากสัจพจน์ของเรขาคณิตแบบยุคลิด และอันที่จริง ใช้ไม่ได้กับเรขาคณิตที่ไม่ใช่แบบยุคลิดในรูปแบบที่เขียนไว้ข้างต้น (นั่นคือ ทฤษฎีบทพีทาโกรัสกลายเป็นสิ่งที่เทียบเท่ากับสมมุติฐานของการขนานกันของยุคลิด) กล่าวอีกนัยหนึ่ง ในเรขาคณิตที่ไม่ใช่แบบยุคลิด อัตราส่วนระหว่างด้านของสามเหลี่ยมจะต้องอยู่ในรูปแบบที่แตกต่างจากทฤษฎีบทพีทาโกรัส . ตัวอย่างเช่น ในเรขาคณิตทรงกลม ทั้งสามด้านของสามเหลี่ยมมุมฉาก (พูดว่า เอ, ขและ ค) ที่ผูกออกแทนต์ (หนึ่งในแปด) ของทรงกลมหน่วยมีความยาว π/2 ซึ่งขัดแย้งกับทฤษฎีบทพีทาโกรัสเพราะ เอ 2 + ข 2 ≠ ค 2 .
พิจารณาที่นี่สองกรณีของเรขาคณิตที่ไม่ใช่แบบยุคลิด - เรขาคณิตทรงกลมและไฮเพอร์โบลิก ในทั้งสองกรณี สำหรับปริภูมิแบบยุคลิดสำหรับสามเหลี่ยมมุมฉาก ผลลัพธ์ที่แทนที่ทฤษฎีบทพีทาโกรัสตามมาจากทฤษฎีบทโคไซน์
อย่างไรก็ตาม ทฤษฎีบทพีทาโกรัสยังคงใช้ได้สำหรับเรขาคณิตไฮเปอร์โบลิกและรีลีปติก หากข้อกำหนดให้สามเหลี่ยมมีมุมฉากถูกแทนที่ด้วยเงื่อนไขที่ว่าผลรวมของมุมสองมุมของสามเหลี่ยมต้องเท่ากับมุมที่สาม กล่าวคือ อา+บี = ค. จากนั้นอัตราส่วนระหว่างด้านจะเป็นดังนี้: ผลรวมของพื้นที่วงกลมที่มีเส้นผ่านศูนย์กลาง เอและ ขเท่ากับพื้นที่ของวงกลมที่มีเส้นผ่านศูนย์กลาง ค.
เรขาคณิตทรงกลม
สำหรับสามเหลี่ยมมุมฉากใดๆ บนทรงกลมที่มีรัศมี R(เช่น ถ้ามุม γ ในสามเหลี่ยมเป็นมุมขวา) ที่มีด้าน เอ, ข, คความสัมพันธ์ระหว่างคู่สัญญาจะมีลักษณะดังนี้:
ความเท่าเทียมกันนี้สามารถหาได้เป็น เป็นกรณีพิเศษทฤษฎีบทโคไซน์ทรงกลมซึ่งใช้ได้กับรูปสามเหลี่ยมทรงกลมทั้งหมด:
โดยที่ cosh คือไฮเปอร์โบลิกโคไซน์ สูตรนี้เป็นกรณีพิเศษของทฤษฎีบทไฮเปอร์โบลิกโคไซน์ ซึ่งใช้ได้กับสามเหลี่ยมทั้งหมด:
โดยที่ γ คือมุมที่มีจุดยอดอยู่ตรงข้ามกับด้าน ค.
ที่ไหน g อิจเรียกว่าเมตริกเทนเซอร์ อาจเป็นฟังก์ชันตำแหน่ง พื้นที่โค้งดังกล่าวรวมถึงเรขาคณิตรีมันเนียน as ตัวอย่างทั่วไป. สูตรนี้ยังเหมาะสำหรับพื้นที่ยุคลิดเมื่อใช้พิกัดโค้ง ตัวอย่างเช่น สำหรับ พิกัดเชิงขั้ว:
ผลิตภัณฑ์เวกเตอร์
ทฤษฎีบทพีทาโกรัสเชื่อมโยงนิพจน์สองนิพจน์สำหรับขนาดของผลคูณเวกเตอร์ แนวทางหนึ่งในการกำหนดผลคูณต้องเป็นไปตามสมการ:
สูตรนี้ใช้ดอทโปรดัค ด้านขวาของสมการเรียกว่า ดีเทอร์มีแนนต์ของแกรม for เอและ ขซึ่งเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานที่เกิดจากเวกเตอร์สองตัวนี้ ตามข้อกำหนดนี้ เช่นเดียวกับข้อกำหนดที่ผลิตภัณฑ์เวกเตอร์ตั้งฉากกับส่วนประกอบ เอและ ขตามนั้น ยกเว้นกรณีเล็กน้อยของสเปซ 0 และ 1 มิติ ผลิตภัณฑ์เวกเตอร์ถูกกำหนดในสามมิติและเจ็ดเท่านั้น เราใช้นิยามของมุมใน น- พื้นที่มิติ:
คุณสมบัติของผลิตภัณฑ์เวกเตอร์นี้ให้ค่าในรูปแบบต่อไปนี้:
ผ่านพื้นฐาน เอกลักษณ์ตรีโกณมิติ Pythagoras เราได้รูปแบบการเขียนมูลค่าที่แตกต่างกัน:
วิธีอื่นในการกำหนดผลิตภัณฑ์ข้ามกลุ่มใช้นิพจน์สำหรับขนาด จากนั้น โต้เถียงกันในลำดับที่กลับกัน เราได้รับการเชื่อมต่อกับ ผลิตภัณฑ์สเกลาร์:
ดูสิ่งนี้ด้วย
หมายเหตุ
- หัวข้อประวัติศาสตร์: ทฤษฎีบทพีทาโกรัสในคณิตศาสตร์บาบิโลน
- ( , หน้า 351) หน้า 351
- ( , Vol I, p. 144)
- การอภิปราย ข้อเท็จจริงทางประวัติศาสตร์ให้ไว้ใน (, หน้า 351) หน้า 351
- เคิร์ต วอน ฟริตซ์ (เม.ย. 2488) "การค้นพบความไม่สมดุลของฮิปปาซัสของเมตาปอนทัม". พงศาวดารของคณิตศาสตร์ ชุดที่สอง(พงศาวดารของคณิตศาสตร์) 46 (2): 242–264.
- Lewis Carroll "เรื่องราวกับนอต", M. , Mir, 1985, p. 7
- Asger Aaboeตอนจากประวัติศาสตร์ตอนต้นของคณิตศาสตร์ - Mathematical Association of America, 1997. - P. 51. - ISBN 0883856131
- ข้อเสนอของพีทาโกรัสโดย Elisha Scott Loomis
- Euclid's องค์ประกอบ: Book VI, Proposition VI 31: "ในรูปสามเหลี่ยมมุมฉาก ตัวเลขที่ด้านลบมุมฉากจะเท่ากับตัวเลขที่คล้ายกันและอธิบายในทำนองเดียวกันที่ด้านข้างที่มีมุมฉาก"
- Lawrence S. Leff อ้างงาน. - ชุดการศึกษาของ Barron - หน้า 326 - ISBN 0764128922
- โฮเวิร์ด วิทลีย์ อีฟส์§4.8:...ลักษณะทั่วไปของทฤษฎีบทพีทาโกรัส // ช่วงเวลาที่ยิ่งใหญ่ในวิชาคณิตศาสตร์ (ก่อน 1650) - Mathematical Association of America, 1983. - P. 41. - ISBN 0883853108
- Tâbit ibn Qorra (ชื่อเต็ม Thabit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 AD) เป็นแพทย์ที่อาศัยอยู่ในแบกแดดที่เขียนเกี่ยวกับองค์ประกอบของยุคลิดอย่างกว้างขวาง และคนอื่น ๆวิชาคณิตศาสตร์
- อัยดิน ซายลี (มี.ค. 1960) "การสรุปทั่วไปของThâbit ibn Qurra ของทฤษฎีบทพีทาโกรัส" ไอซิส 51 (1): 35–37. ดอย:10.1086/348837.
- จูดิธ ดี. แซลลี่, พอล แซลลี่แบบฝึกหัด 2.10(ii) // งานที่อ้างถึง . - หน้า 62. - ISBN 0821844032
- ดูรายละเอียดการก่อสร้างได้ที่ จอร์จ เจนนิงส์รูปที่ 1.32: ทฤษฎีบทพีทาโกรัสทั่วไป // เรขาคณิตสมัยใหม่พร้อมการใช้งาน: มี 150 ตัวเลข . - ที่ 3 - สปริงเกอร์, 1997. - หน้า 23. - ISBN 038794222X
- Arlen Brown, Carl M. Pearcyสิ่งของ ค: บรรทัดฐานสำหรับพลการ น-tuple ... // บทนำสู่การวิเคราะห์ - สปริงเกอร์, 2538. - หน้า 124. - ISBN 0387943692ดูหน้า 47-50 ด้วย
- อัลเฟรด เกรย์, เอลซ่า แอบบีน่า, ไซม่อน ซาลามอนเรขาคณิตเชิงอนุพันธ์ที่ทันสมัยของเส้นโค้งและพื้นผิวด้วย Mathematica - ที่ 3 - CRC Press, 2006. - P. 194. - ISBN 1584884487
- Rajendra Bhatiaการวิเคราะห์เมทริกซ์ - สปริงเกอร์, 1997. - หน้า 21. - ISBN 0387948465
- Stephen W. Hawking อ้างงาน. - 2548. - หน้า 4. - ISBN 0762419229
- Eric W. Weisstein CRC สารานุกรมสั้นของคณิตศาสตร์ - ที่ 2 - 2546. - หน้า 2147. - ISBN 1584883472
- Alexander R. Pruss
ระดับเฉลี่ย
สามเหลี่ยมมุมฉาก. คู่มือภาพประกอบฉบับสมบูรณ์ (2019)
สามเหลี่ยมมุมฉาก. ระดับแรก
ในปัญหามุมฉากไม่จำเป็นเลย - มุมล่างซ้ายดังนั้นคุณต้องเรียนรู้วิธีจดจำสามเหลี่ยมมุมฉากในรูปแบบนี้

และในลักษณะนี้

และในลักษณะนี้ 
สามเหลี่ยมมุมฉากดีอย่างไร? ก็...ก่อนอื่นมีความพิเศษ ชื่อที่สวยงามสำหรับด้านข้างของเขา
ให้ความสนใจกับการวาดภาพ!

จำและอย่าสับสน: ขา - สองและด้านตรงข้ามมุมฉาก - เพียงหนึ่งเดียว(ตัวเดียว ไม่ซ้ำใคร และยาวที่สุด)!
เราคุยกันเรื่องชื่อแล้ว สิ่งที่สำคัญที่สุดคือทฤษฎีบทพีทาโกรัส
ทฤษฎีบทพีทาโกรัส
ทฤษฎีบทนี้เป็นกุญแจสำคัญในการแก้ปัญหามากมายเกี่ยวกับสามเหลี่ยมมุมฉาก พีทาโกรัสได้รับการพิสูจน์ในสมัยโบราณอย่างสมบูรณ์ และตั้งแต่นั้นมา ก็ได้นำประโยชน์มากมายมาสู่ผู้ที่รู้เรื่องนี้ และสิ่งที่ดีที่สุดเกี่ยวกับเธอคือเธอเป็นคนเรียบง่าย
ดังนั้น, ทฤษฎีบทพีทาโกรัส:
คุณจำเรื่องตลก: "กางเกงพีทาโกรัสเท่ากันทุกด้าน!"?
ลองวาดกางเกงพีทาโกรัสเหล่านี้แล้วมองดู 
มันดูเหมือนกางเกงขาสั้นจริงๆเหรอ? แล้วด้านไหนเท่ากัน? เรื่องตลกมาจากไหนและทำไม? และเรื่องตลกนี้เชื่อมโยงกับทฤษฎีบทพีทาโกรัสอย่างแม่นยำยิ่งขึ้นกับวิธีที่พีทาโกรัสกำหนดทฤษฎีบทของเขาเอง และท่านได้กำหนดไว้ดังนี้
"ซำ พื้นที่สี่เหลี่ยมสร้างขึ้นบนขาเท่ากับ พื้นที่สี่เหลี่ยมสร้างขึ้นบนด้านตรงข้ามมุมฉาก
ฟังดูไม่ต่างกันไปหน่อยเหรอ? ดังนั้น เมื่อพีทาโกรัสเขียนคำกล่าวของทฤษฎีบทของเขา ภาพดังกล่าวก็ปรากฎขึ้น

ในภาพนี้ ผลรวมของพื้นที่ของสี่เหลี่ยมจัตุรัสเล็ก ๆ เท่ากับพื้นที่ของสี่เหลี่ยมจัตุรัสใหญ่ และเพื่อให้เด็ก ๆ จดจำได้ดีขึ้นว่าผลรวมของสี่เหลี่ยมจัตุรัสของขานั้นเท่ากับกำลังสองของด้านตรงข้ามมุมฉาก มีคนที่มีไหวพริบประดิษฐ์มุกตลกนี้เกี่ยวกับกางเกงพีทาโกรัส
เหตุใดเราจึงกำหนดทฤษฎีบทพีทาโกรัส
พีทาโกรัสทนทุกข์และพูดคุยเกี่ยวกับสี่เหลี่ยมหรือไม่?
คุณเห็นไหมว่าในสมัยโบราณไม่มี ... พีชคณิต! ก็ไม่มีวี่แววเป็นต้น. ไม่มีจารึก คุณลองนึกดูสิว่าการที่นักเรียนโบราณที่น่าสงสารนั้นต้องจำทุกอย่างด้วยคำพูดนั้นแย่มากขนาดไหน?! และเราดีใจที่เรามีสูตรง่ายๆ ของทฤษฎีบทพีทาโกรัส มาทำซ้ำอีกครั้งเพื่อให้จำได้ดีขึ้น:
ตอนนี้ควรจะง่าย:
| กำลังสองของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของขา |
ได้มีการพูดถึงทฤษฎีบทที่สำคัญที่สุดเกี่ยวกับสามเหลี่ยมมุมฉากแล้ว หากคุณสงสัยว่ามันพิสูจน์ได้อย่างไร อ่านต่อ ระดับต่อไปทฤษฏีแล้วไปต่อ ... to ป่าที่มืด...ตรีโกณมิติ! สำหรับคำที่น่ากลัว ไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์
ไซน์ โคไซน์ แทนเจนต์ โคแทนเจนต์ในรูปสามเหลี่ยมมุมฉาก
อันที่จริงทุกอย่างไม่ได้น่ากลัวเลย แน่นอน คำจำกัดความ "ของจริง" ของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ควรได้รับการพิจารณาในบทความ แต่คุณไม่ต้องการจริงๆ ใช่ไหม เราสามารถชื่นชมยินดี: ในการแก้ปัญหาเกี่ยวกับสามเหลี่ยมมุมฉาก คุณสามารถกรอกข้อมูลง่ายๆ ต่อไปนี้:
ทำไมมันเกี่ยวกับมุม? มุมไหน? เพื่อให้เข้าใจสิ่งนี้ คุณจำเป็นต้องรู้ว่าข้อความที่ 1 - 4 นั้นเขียนด้วยคำพูดอย่างไร ดูเข้าใจและจำ!
1.
จริงๆแล้วดูเหมือนว่านี้:
แล้วมุมล่ะ? มีขาที่อยู่ตรงข้ามมุมนั่นคือขาตรงข้าม (สำหรับมุม) หรือไม่? มีแน่นอน! นี่คือสายสวน!
แต่แล้วมุมล่ะ? มองดูดีๆ. ขาไหนอยู่ติดกับมุม? แน่นอนว่าแมว ดังนั้น สำหรับมุม ขาอยู่ติดกัน และ
และตอนนี้ให้ความสนใจ! ดูสิ่งที่เราได้รับ:
ดูว่ามันยอดเยี่ยมแค่ไหน:
ทีนี้มาดูแทนเจนต์และโคแทนเจนต์กัน
ตอนนี้จะเขียนเป็นคำพูดได้อย่างไร? ขาเทียบกับมุมคืออะไร? ตรงข้ามแน่นอน - มัน "โกหก" ตรงข้ามกับมุม และสายสวน? ติดตรงหัวมุม. แล้วเราได้อะไร?
ดูว่าตัวเศษและตัวส่วนกลับกันอย่างไร?
และตอนนี้มุมและทำการแลกเปลี่ยน:
สรุป
มาเขียนสิ่งที่เราได้เรียนรู้โดยสังเขปกัน
 |
ทฤษฎีบทพีทาโกรัส: |
ทฤษฎีบทสามเหลี่ยมมุมฉากหลักคือทฤษฎีบทพีทาโกรัส
ทฤษฎีบทพีทาโกรัส
อ้อ คุณจำได้ดีว่าขาและด้านตรงข้ามมุมฉากคืออะไร? ถ้าไม่เช่นนั้นดูภาพ - รีเฟรชความรู้ของคุณ

เป็นไปได้ว่าคุณเคยใช้ทฤษฎีบทพีทาโกรัสมาหลายครั้งแล้ว แต่คุณเคยสงสัยไหมว่าทำไมทฤษฎีบทดังกล่าวถึงเป็นจริง คุณจะพิสูจน์ได้อย่างไร? มาทำเหมือนชาวกรีกโบราณกันเถอะ ลองวาดสี่เหลี่ยมที่มีด้าน

คุณเห็นว่าเราแบ่งด้านของมันออกเป็นส่วน ๆ ของความยาวได้อย่างไรและ!
ตอนนี้มาเชื่อมต่อจุดที่ทำเครื่องหมายไว้

อย่างไรก็ตามที่นี่เราสังเกตอย่างอื่น แต่คุณดูรูปตัวเองและคิดว่าทำไม
พื้นที่ของสี่เหลี่ยมขนาดใหญ่คืออะไร? ถูกต้อง, . แล้วพื้นที่ที่เล็กกว่าล่ะ? แน่นอน, . พื้นที่ทั้งหมดของมุมทั้งสี่ยังคงอยู่ ลองนึกภาพว่าเราเอาสองตัวมาพิงกันด้วยด้านตรงข้ามมุมฉาก เกิดอะไรขึ้น สองสี่เหลี่ยม ดังนั้นพื้นที่ของ "การตัด" จึงเท่ากัน
มารวมกันตอนนี้เลย
มาแปลงร่างกันเถอะ:
ดังนั้นเราจึงไปเยี่ยมชมพีทาโกรัส - เราพิสูจน์ทฤษฎีบทของเขาในสมัยโบราณ
สามเหลี่ยมมุมฉากกับตรีโกณมิติ
สำหรับสามเหลี่ยมมุมฉาก ความสัมพันธ์ต่อไปนี้ถือเป็น:

ไซนัส มุมแหลมเท่ากับอัตราส่วนของขาตรงข้ามกับด้านตรงข้ามมุมฉาก
โคไซน์ของมุมแหลมเท่ากับอัตราส่วนของขาที่อยู่ติดกันต่อด้านตรงข้ามมุมฉาก
แทนเจนต์ของมุมแหลมเท่ากับอัตราส่วนของขาตรงข้ามกับขาที่อยู่ติดกัน
โคแทนเจนต์ของมุมแหลมเท่ากับอัตราส่วนของขาที่อยู่ติดกันกับขาตรงข้าม
และอีกครั้ง ทั้งหมดนี้อยู่ในรูปของจาน:
มันสบายมาก!
เครื่องหมายความเท่าเทียมกันของสามเหลี่ยมมุมฉาก
I. สองขา

ครั้งที่สอง ตามขาและด้านตรงข้ามมุมฉาก

สาม. โดยด้านตรงข้ามมุมฉากและมุมแหลม

IV. ตามขาและมุมแหลม
ก) 
ข) 
ความสนใจ! นี่เป็นสิ่งสำคัญมากที่ขาจะ "สอดคล้อง" ตัวอย่างเช่น ถ้ามันเป็นแบบนี้:

แล้วสามเหลี่ยมก็ไม่เท่ากันแม้ว่าจะมีมุมแหลมเหมือนกันก็ตาม
จำเป็นต้อง ในรูปสามเหลี่ยมทั้งสองขาอยู่ติดกันหรือทั้งสอง - ตรงข้าม.
คุณเคยสังเกตไหมว่าเครื่องหมายความเท่าเทียมกันของสามเหลี่ยมมุมฉากแตกต่างจากเครื่องหมายปกติของความเท่าเทียมกันของรูปสามเหลี่ยมหรือไม่? ดูหัวข้อ "และให้ความสนใจกับความจริงที่ว่าสำหรับความเท่าเทียมกันของสามเหลี่ยม "ธรรมดา" คุณต้องมีความเท่าเทียมกันขององค์ประกอบทั้งสาม: สองด้านและมุมระหว่างพวกเขา สองมุมและด้านระหว่างพวกเขาหรือสามด้าน แต่เพื่อความเท่าเทียมกันของสามเหลี่ยมมุมฉาก มีเพียงสององค์ประกอบที่สอดคล้องกันเท่านั้นก็เพียงพอแล้ว มันเยี่ยมมากใช่มั้ย?
ประมาณสถานการณ์เดียวกันกับสัญญาณของความคล้ายคลึงกันของสามเหลี่ยมมุมฉาก
สัญญาณความคล้ายคลึงของสามเหลี่ยมมุมฉาก
I. มุมเฉียบพลัน

ครั้งที่สอง สองขา

สาม. ตามขาและด้านตรงข้ามมุมฉาก

ค่ามัธยฐานในรูปสามเหลี่ยมมุมฉาก
ทำไมถึงเป็นเช่นนั้น?
พิจารณาสี่เหลี่ยมทั้งหมดแทนที่จะเป็นสามเหลี่ยมมุมฉาก
ลองวาดเส้นทแยงมุมและพิจารณาจุด - จุดตัดของเส้นทแยงมุม คุณรู้อะไรเกี่ยวกับเส้นทแยงมุมของสี่เหลี่ยมผืนผ้าบ้าง?
และจากนี้ไปจะเป็นอย่างไร
มันเลยเกิดขึ้นว่า
- - ค่ามัธยฐาน:
จำข้อเท็จจริงนี้ไว้! ช่วยได้เยอะ!
สิ่งที่น่าประหลาดใจยิ่งกว่านั้นก็คือบทสนทนานั้นก็เป็นความจริงเช่นกัน
ได้อะไรที่ดีจากการที่ค่ามัธยฐานที่ลากไปยังด้านตรงข้ามมุมฉากเท่ากับครึ่งหนึ่งของด้านตรงข้ามมุมฉาก? มาดูรูปกันจ้า
มองดูดีๆ. เรามี: นั่นคือระยะทางจากจุดถึงจุดยอดทั้งสามของรูปสามเหลี่ยมกลับกลายเป็นว่าเท่ากัน แต่ในรูปสามเหลี่ยมมีจุดเดียว ระยะทางจากจุดยอดทั้งสามของสามเหลี่ยมนั้นเท่ากัน และนี่คือจุดศูนย์กลางของวงจรที่อธิบาย แล้วเกิดอะไรขึ้น?
เริ่มจาก "นอกจาก..." นี้ก่อน
ลองดูที่ไอ
แต่ในรูปสามเหลี่ยมที่คล้ายกันทุกมุมเท่ากัน!
เดียวกันสามารถพูดเกี่ยวกับและ
ทีนี้มาวาดกัน:
สามารถใช้อะไรได้บ้างจากความคล้ายคลึงกัน "สามประการ" นี้
ตัวอย่างเช่น - สองสูตรสำหรับความสูงของสามเหลี่ยมมุมฉาก
เราเขียนความสัมพันธ์ของฝ่ายที่เกี่ยวข้อง:

ในการหาความสูง เราแก้สัดส่วนแล้วได้ สูตรแรก "ความสูงในรูปสามเหลี่ยมมุมฉาก":
ลองใช้ความคล้ายคลึงกัน:

จะเกิดอะไรขึ้นตอนนี้?
อีกครั้งเราแก้สัดส่วนและรับสูตรที่สอง:
ทั้งสองสูตรนี้ต้องจำไว้ให้ดีและสูตรไหนสะดวกกว่ากัน มาเขียนมันลงไปอีกครั้ง
ทฤษฎีบทพีทาโกรัส:
ในรูปสามเหลี่ยมมุมฉาก สี่เหลี่ยมจัตุรัสของด้านตรงข้ามมุมฉากเท่ากับผลรวมของกำลังสองของขา:.

สัญญาณความเท่าเทียมกันของสามเหลี่ยมมุมฉาก:
- บนสองขา:
- ตามขาและด้านตรงข้ามมุมฉาก: หรือ
- ตามขาและมุมแหลมที่อยู่ติดกัน: หรือ
- ตามขาและมุมแหลมตรงข้าม: หรือ
- โดยด้านตรงข้ามมุมฉากและมุมแหลม: หรือ.
สัญญาณของความคล้ายคลึงกันของสามเหลี่ยมมุมฉาก:
- มุมคมหนึ่ง: หรือ
- จากสัดส่วนของขาทั้งสองข้าง:
- จากสัดส่วนของขาและด้านตรงข้ามมุมฉาก: หรือ
ไซน์ โคไซน์ แทนเจนต์ โคแทนเจนต์ในรูปสามเหลี่ยมมุมฉาก
- ไซน์ของมุมแหลมของสามเหลี่ยมมุมฉากคืออัตราส่วนของขาตรงข้ามกับด้านตรงข้ามมุมฉาก:
- โคไซน์ของมุมแหลมของสามเหลี่ยมมุมฉากคืออัตราส่วนของขาที่อยู่ติดกันต่อด้านตรงข้ามมุมฉาก:
- แทนเจนต์ของมุมแหลมของสามเหลี่ยมมุมฉากคืออัตราส่วนของขาตรงข้ามกับขาที่อยู่ติดกัน:
- โคแทนเจนต์ของมุมแหลมของสามเหลี่ยมมุมฉากคืออัตราส่วนของขาที่อยู่ติดกันกับด้านตรงข้าม:
ความสูงของสามเหลี่ยมมุมฉาก: หรือ
ในรูปสามเหลี่ยมมุมฉาก ค่ามัธยฐานที่ลากจากจุดยอดของมุมฉากเท่ากับครึ่งหนึ่งของด้านตรงข้ามมุมฉาก: .
พื้นที่ของสามเหลี่ยมมุมฉาก:
- ผ่านสายสวน:
 ในทำนองเดียวกัน สามเหลี่ยม CBH ก็คล้ายกับ ABC แนะนำสัญกรณ์
ในทำนองเดียวกัน สามเหลี่ยม CBH ก็คล้ายกับ ABC แนะนำสัญกรณ์  1. จัดเรียงสามเหลี่ยมมุมฉากเท่ากันสี่รูปตามที่แสดงในภาพ
1. จัดเรียงสามเหลี่ยมมุมฉากเท่ากันสี่รูปตามที่แสดงในภาพ 
 แนวความคิดในการพิสูจน์ของยุคลิดมีดังนี้: ลองพิสูจน์ว่าครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างบนด้านตรงข้ามมุมฉาก เท่ากับผลรวมของพื้นที่ครึ่งหนึ่งของสี่เหลี่ยมที่สร้างบนขา และจากนั้น พื้นที่ของ สี่เหลี่ยมขนาดใหญ่และสี่เหลี่ยมเล็กสองอันมีค่าเท่ากัน พิจารณาภาพวาดทางด้านซ้าย เราสร้างสี่เหลี่ยมที่ด้านข้างของสามเหลี่ยมมุมฉากบนนั้นแล้วดึงรังสี s จากจุดยอดของมุมฉาก C ตั้งฉากกับด้านตรงข้ามมุมฉาก AB มันตัดสี่เหลี่ยม ABIK ที่สร้างจากด้านตรงข้ามมุมฉากออกเป็นสองสี่เหลี่ยม - BHJI และ HAKJ ตามลำดับ ปรากฎว่าพื้นที่ของสี่เหลี่ยมเหล่านี้เท่ากับพื้นที่ของสี่เหลี่ยมที่สร้างบนขาที่สอดคล้องกัน ลองพิสูจน์ว่าพื้นที่ของสี่เหลี่ยมจัตุรัส DECA เท่ากับพื้นที่ของสี่เหลี่ยม AHJK ในการทำเช่นนี้เราใช้การสังเกตเสริม: พื้นที่ของรูปสามเหลี่ยมที่มีความสูงและฐานเท่ากันตามที่กำหนด สี่เหลี่ยมผืนผ้าเท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมที่กำหนด นี่เป็นผลมาจากการกำหนดพื้นที่ของรูปสามเหลี่ยมเป็นครึ่งหนึ่งของผลคูณของฐานและความสูง จากการสังเกตนี้จะตามมาว่าพื้นที่ของสามเหลี่ยม ACK เท่ากับพื้นที่ของสามเหลี่ยม AHK (ไม่แสดง) ซึ่งในทางกลับกันจะเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยม AHJK ให้เราพิสูจน์ว่าพื้นที่ของสามเหลี่ยม ACK นั้นเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยม DECA ด้วย สิ่งเดียวที่ต้องทำเพื่อสิ่งนี้คือการพิสูจน์ความเท่าเทียมกันของสามเหลี่ยม ACK และ BDA (เนื่องจากคุณสมบัติข้างต้นนั้น พื้นที่ของสามเหลี่ยม BDA เท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัส) ความเท่าเทียมกันนี้ชัดเจน สามเหลี่ยมสองด้านเท่ากันและมุมระหว่างพวกมัน กล่าวคือ - AB=AK,AD=AC - ความเท่าเทียมกันของมุม CAK และ BAD นั้นง่ายต่อการพิสูจน์โดยวิธีการเคลื่อนไหว: ลองหมุนสามเหลี่ยม CAK 90 °ทวนเข็มนาฬิกา จะเห็นได้ชัดเจนว่าด้านที่สอดคล้องกันของสามเหลี่ยมสองรูปที่พิจารณาจะ ตรงกัน (เนื่องจากมุมที่จุดยอดของสี่เหลี่ยมจัตุรัสคือ 90°) อาร์กิวเมนต์เกี่ยวกับความเท่าเทียมกันของพื้นที่ของสี่เหลี่ยมจัตุรัส BCFG และสี่เหลี่ยม BHJI นั้นคล้ายคลึงกันโดยสิ้นเชิง ดังนั้นเราจึงได้พิสูจน์แล้วว่าพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากเป็นผลรวมของพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างบนขา
แนวความคิดในการพิสูจน์ของยุคลิดมีดังนี้: ลองพิสูจน์ว่าครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างบนด้านตรงข้ามมุมฉาก เท่ากับผลรวมของพื้นที่ครึ่งหนึ่งของสี่เหลี่ยมที่สร้างบนขา และจากนั้น พื้นที่ของ สี่เหลี่ยมขนาดใหญ่และสี่เหลี่ยมเล็กสองอันมีค่าเท่ากัน พิจารณาภาพวาดทางด้านซ้าย เราสร้างสี่เหลี่ยมที่ด้านข้างของสามเหลี่ยมมุมฉากบนนั้นแล้วดึงรังสี s จากจุดยอดของมุมฉาก C ตั้งฉากกับด้านตรงข้ามมุมฉาก AB มันตัดสี่เหลี่ยม ABIK ที่สร้างจากด้านตรงข้ามมุมฉากออกเป็นสองสี่เหลี่ยม - BHJI และ HAKJ ตามลำดับ ปรากฎว่าพื้นที่ของสี่เหลี่ยมเหล่านี้เท่ากับพื้นที่ของสี่เหลี่ยมที่สร้างบนขาที่สอดคล้องกัน ลองพิสูจน์ว่าพื้นที่ของสี่เหลี่ยมจัตุรัส DECA เท่ากับพื้นที่ของสี่เหลี่ยม AHJK ในการทำเช่นนี้เราใช้การสังเกตเสริม: พื้นที่ของรูปสามเหลี่ยมที่มีความสูงและฐานเท่ากันตามที่กำหนด สี่เหลี่ยมผืนผ้าเท่ากับครึ่งหนึ่งของพื้นที่ของสี่เหลี่ยมที่กำหนด นี่เป็นผลมาจากการกำหนดพื้นที่ของรูปสามเหลี่ยมเป็นครึ่งหนึ่งของผลคูณของฐานและความสูง จากการสังเกตนี้จะตามมาว่าพื้นที่ของสามเหลี่ยม ACK เท่ากับพื้นที่ของสามเหลี่ยม AHK (ไม่แสดง) ซึ่งในทางกลับกันจะเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยม AHJK ให้เราพิสูจน์ว่าพื้นที่ของสามเหลี่ยม ACK นั้นเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยม DECA ด้วย สิ่งเดียวที่ต้องทำเพื่อสิ่งนี้คือการพิสูจน์ความเท่าเทียมกันของสามเหลี่ยม ACK และ BDA (เนื่องจากคุณสมบัติข้างต้นนั้น พื้นที่ของสามเหลี่ยม BDA เท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัส) ความเท่าเทียมกันนี้ชัดเจน สามเหลี่ยมสองด้านเท่ากันและมุมระหว่างพวกมัน กล่าวคือ - AB=AK,AD=AC - ความเท่าเทียมกันของมุม CAK และ BAD นั้นง่ายต่อการพิสูจน์โดยวิธีการเคลื่อนไหว: ลองหมุนสามเหลี่ยม CAK 90 °ทวนเข็มนาฬิกา จะเห็นได้ชัดเจนว่าด้านที่สอดคล้องกันของสามเหลี่ยมสองรูปที่พิจารณาจะ ตรงกัน (เนื่องจากมุมที่จุดยอดของสี่เหลี่ยมจัตุรัสคือ 90°) อาร์กิวเมนต์เกี่ยวกับความเท่าเทียมกันของพื้นที่ของสี่เหลี่ยมจัตุรัส BCFG และสี่เหลี่ยม BHJI นั้นคล้ายคลึงกันโดยสิ้นเชิง ดังนั้นเราจึงได้พิสูจน์แล้วว่าพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉากเป็นผลรวมของพื้นที่ของสี่เหลี่ยมจัตุรัสที่สร้างบนขา  พิจารณาภาพวาด ดังที่เห็นได้จากสมมาตร ส่วน CI ตัดสี่เหลี่ยม ABHJ ออกเป็นสองส่วนที่เหมือนกัน (เนื่องจากสามเหลี่ยม ABC และ JHI เท่ากันในการก่อสร้าง) โดยใช้การหมุนทวนเข็มนาฬิกา 90 องศา เราจะเห็นความเท่าเทียมกันของตัวเลขที่แรเงา CAJI และ GDAB ตอนนี้เป็นที่ชัดเจนว่าพื้นที่ของรูปที่เราแรเงานั้นเท่ากับผลรวมของครึ่งหนึ่งของพื้นที่สี่เหลี่ยมที่สร้างบนขาและพื้นที่ของสามเหลี่ยมเดิม ในทางกลับกัน มันเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉาก บวกกับพื้นที่ของสามเหลี่ยมเดิม ขั้นตอนสุดท้ายในการพิสูจน์จะถูกปล่อยให้ผู้อ่าน
พิจารณาภาพวาด ดังที่เห็นได้จากสมมาตร ส่วน CI ตัดสี่เหลี่ยม ABHJ ออกเป็นสองส่วนที่เหมือนกัน (เนื่องจากสามเหลี่ยม ABC และ JHI เท่ากันในการก่อสร้าง) โดยใช้การหมุนทวนเข็มนาฬิกา 90 องศา เราจะเห็นความเท่าเทียมกันของตัวเลขที่แรเงา CAJI และ GDAB ตอนนี้เป็นที่ชัดเจนว่าพื้นที่ของรูปที่เราแรเงานั้นเท่ากับผลรวมของครึ่งหนึ่งของพื้นที่สี่เหลี่ยมที่สร้างบนขาและพื้นที่ของสามเหลี่ยมเดิม ในทางกลับกัน มันเท่ากับครึ่งหนึ่งของพื้นที่สี่เหลี่ยมจัตุรัสที่สร้างขึ้นบนด้านตรงข้ามมุมฉาก บวกกับพื้นที่ของสามเหลี่ยมเดิม ขั้นตอนสุดท้ายในการพิสูจน์จะถูกปล่อยให้ผู้อ่าน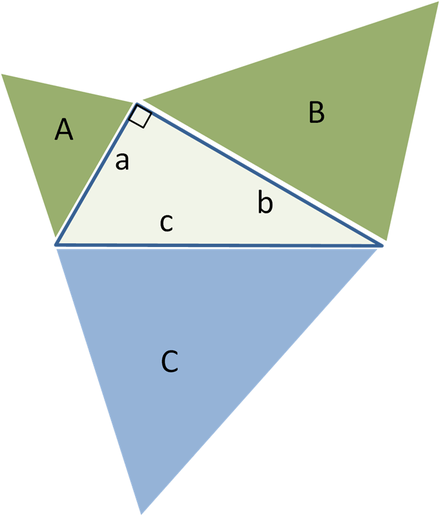




 ลุงวันยา พล็อตเรื่อง “ลุงอีวาน ทัศนคติต่ออาจารย์ของผู้อื่น
ลุงวันยา พล็อตเรื่อง “ลุงอีวาน ทัศนคติต่ออาจารย์ของผู้อื่น Tsakhes น้อยชื่อเล่น Zinnober
Tsakhes น้อยชื่อเล่น Zinnober Maikov, Apollon Nikolaevich - ชีวประวัติสั้น
Maikov, Apollon Nikolaevich - ชีวประวัติสั้น