แนวคิดของสูตรการปริพันธ์เชิงตัวเลข หนังสือเรียนเกี่ยวกับวิธีการทางคณิตศาสตร์ในภูมิศาสตร์
หน้า 1
ภาควิชาคณิตศาสตร์ชั้นสูง
เชิงนามธรรม:
เสร็จสิ้นโดย: Matveev F.I.
ตรวจสอบโดย: Burlova L.V.
อูลาน-อูเด.2002
1. วิธีการบูรณาการเชิงตัวเลข
2. ที่มาของสูตรซิมป์สัน
3.ภาพประกอบทางเรขาคณิต
4.การเลือกขั้นตอนการบูรณาการ
5.ตัวอย่าง
1. วิธีการบูรณาการเชิงตัวเลข
งาน การบูรณาการเชิงตัวเลขประกอบด้วยการคำนวณอินทิกรัล
 ผ่านชุดค่านิยมของปริพันธ์
ผ่านชุดค่านิยมของปริพันธ์  .
.
ปัญหาการรวมตัวเลขจะต้องได้รับการแก้ไขสำหรับฟังก์ชันที่ระบุในตาราง ซึ่งเป็นฟังก์ชันที่ไม่มีการอินทิกรัลเข้ามา ฟังก์ชั่นเบื้องต้นฯลฯ ลองพิจารณาเฉพาะฟังก์ชันของตัวแปรตัวเดียวเท่านั้น
แทนที่จะรวมฟังก์ชันที่ต้องอินทิเกรต เราจะรวมพหุนามการประมาณค่าเข้าด้วยกัน วิธีการที่ใช้การแทนที่จำนวนเต็มด้วยพหุนามการประมาณค่าทำให้สามารถประมาณความแม่นยำของผลลัพธ์โดยใช้พารามิเตอร์ของพหุนามหรือเลือกพารามิเตอร์เหล่านี้ตามความแม่นยำที่กำหนด
วิธีการเชิงตัวเลขสามารถจัดกลุ่มได้ตามเงื่อนไขตามวิธีการประมาณปริพันธ์
วิธีการของนิวตัน-โคตส์จะขึ้นอยู่กับการประมาณฟังก์ชัน  พหุนามของปริญญา
พหุนามของปริญญา  - อัลกอริธึมของคลาสนี้แตกต่างเฉพาะในระดับของพหุนามเท่านั้น ตามกฎแล้ว โหนดของพหุนามโดยประมาณนั้นมีความสัมพันธ์กันเท่ากัน
- อัลกอริธึมของคลาสนี้แตกต่างเฉพาะในระดับของพหุนามเท่านั้น ตามกฎแล้ว โหนดของพหุนามโดยประมาณนั้นมีความสัมพันธ์กันเท่ากัน
วิธีการรวม Spline ขึ้นอยู่กับการประมาณฟังก์ชัน  พหุนามแบบแยกเป็นชิ้นๆ
พหุนามแบบแยกเป็นชิ้นๆ
วิธีการที่มีความแม่นยำเชิงพีชคณิตสูงสุด (วิธีเกาส์เซียน) ใช้โหนดที่ไม่เท่ากันที่เลือกมาเป็นพิเศษซึ่งให้ข้อผิดพลาดในการรวมขั้นต่ำสำหรับจำนวนโหนดที่กำหนด (เลือก)
วิธีมอนติคาร์โลมักใช้ในการคำนวณอินทิกรัลหลายรายการ โดยเลือกโหนดแบบสุ่ม และคำตอบคือความน่าจะเป็น


 ข้อผิดพลาดทั้งหมด
ข้อผิดพลาดทั้งหมด
 ข้อผิดพลาดในการตัดทอน
ข้อผิดพลาดในการตัดทอน
ข้อผิดพลาดในการปัดเศษ

โดยไม่คำนึงถึงวิธีการที่เลือกในกระบวนการรวมตัวเลขจำเป็นต้องคำนวณค่าโดยประมาณของอินทิกรัลและประมาณค่าข้อผิดพลาด ข้อผิดพลาดจะลดลงเมื่อจำนวน n เพิ่มขึ้น
พาร์ทิชันส่วน  - อย่างไรก็ตาม สิ่งนี้จะเพิ่มข้อผิดพลาดในการปัดเศษ
- อย่างไรก็ตาม สิ่งนี้จะเพิ่มข้อผิดพลาดในการปัดเศษ
โดยการรวมค่าอินทิกรัลที่คำนวณจากส่วนบางส่วน
ข้อผิดพลาดในการตัดทอนขึ้นอยู่กับคุณสมบัติของปริพันธ์และความยาว  ส่วนบางส่วน
ส่วนบางส่วน
2. ที่มาของสูตรซิมป์สัน
ถ้าสำหรับแต่ละคู่ของเซ็กเมนต์  สร้างพหุนามระดับที่สอง จากนั้นอินทิเกรตและใช้คุณสมบัติของการบวกของอินทิกรัล เราจะได้สูตรของซิมป์สัน
สร้างพหุนามระดับที่สอง จากนั้นอินทิเกรตและใช้คุณสมบัติของการบวกของอินทิกรัล เราจะได้สูตรของซิมป์สัน
 พิจารณาฟังก์ชันปริพันธ์
พิจารณาฟังก์ชันปริพันธ์  บนส่วน
บนส่วน  - ขอให้เราแทนที่อินทิแกรนด์นี้ด้วยพหุนามการประมาณค่าลากรองจ์ของดีกรีที่สอง ซึ่งตรงกับ
- ขอให้เราแทนที่อินทิแกรนด์นี้ด้วยพหุนามการประมาณค่าลากรองจ์ของดีกรีที่สอง ซึ่งตรงกับ  ที่จุด:
ที่จุด:
มาบูรณาการกันเถอะ  :
:

สูตร:
และเรียกว่าสูตรของซิมป์สัน
ผลลัพธ์ที่ได้สำหรับอินทิกรัล  มูลค่าสอดคล้องกับพื้นที่ สี่เหลี่ยมคางหมูโค้งที่ถูกจำกัดด้วยแกน
มูลค่าสอดคล้องกับพื้นที่ สี่เหลี่ยมคางหมูโค้งที่ถูกจำกัดด้วยแกน  , ตรง
, ตรง  ,
,  และพาราโบลาที่ผ่านจุดต่างๆ
และพาราโบลาที่ผ่านจุดต่างๆ
ตอนนี้ให้เราประเมินข้อผิดพลาดในการรวมโดยใช้สูตรของซิมป์สัน เราจะถือว่า  บนส่วน
บนส่วน  มีอนุพันธ์ต่อเนื่องกัน
มีอนุพันธ์ต่อเนื่องกัน  - มาสร้างความแตกต่างกันเถอะ
- มาสร้างความแตกต่างกันเถอะ

ทฤษฎีบทค่าเฉลี่ยสามารถนำไปใช้กับอินทิกรัลทั้งสองแต่ละตัวได้แล้ว เนื่องจาก  อย่างต่อเนื่อง
อย่างต่อเนื่อง  และฟังก์ชันไม่เป็นลบในช่วงการรวมครั้งแรกและไม่เป็นเชิงบวกในช่วงที่สอง (นั่นคือ ฟังก์ชันจะไม่เปลี่ยนเครื่องหมายในแต่ละช่วงเวลาเหล่านี้) นั่นเป็นเหตุผล:
และฟังก์ชันไม่เป็นลบในช่วงการรวมครั้งแรกและไม่เป็นเชิงบวกในช่วงที่สอง (นั่นคือ ฟังก์ชันจะไม่เปลี่ยนเครื่องหมายในแต่ละช่วงเวลาเหล่านี้) นั่นเป็นเหตุผล:

(เราใช้ทฤษฎีบทค่าเฉลี่ยเพราะว่า  - ฟังก์ชั่นต่อเนื่อง;
- ฟังก์ชั่นต่อเนื่อง;  ).
).
การสร้างความแตกต่าง  สองครั้งแล้วใช้ทฤษฎีบทค่าเฉลี่ยที่เราได้รับ
สองครั้งแล้วใช้ทฤษฎีบทค่าเฉลี่ยที่เราได้รับ  การแสดงออกอื่น:
การแสดงออกอื่น:
 , ที่ไหน
, ที่ไหน 
จากการประมาณการทั้งสำหรับ  ตามมาด้วยว่าสูตรของซิมป์สันนั้นตรงกับพหุนามที่มีดีกรีไม่สูงกว่าสาม ลองเขียนสูตรของ Simpson ในรูปแบบ:
ตามมาด้วยว่าสูตรของซิมป์สันนั้นตรงกับพหุนามที่มีดีกรีไม่สูงกว่าสาม ลองเขียนสูตรของ Simpson ในรูปแบบ:
, .
.
ถ้าเป็นเซ็กเมนต์  บูรณาการมากเกินไปก็แบ่งออกเป็น
บูรณาการมากเกินไปก็แบ่งออกเป็น  ส่วนที่เท่ากัน(สมมติว่า
ส่วนที่เท่ากัน(สมมติว่า  ) จากนั้นไปยังแต่ละคู่ของส่วนที่อยู่ติดกัน
) จากนั้นไปยังแต่ละคู่ของส่วนที่อยู่ติดกัน  ,
,  ,...,
,..., ใช้สูตรของซิมป์สัน ได้แก่ :
ใช้สูตรของซิมป์สัน ได้แก่ :
ลองเขียนสูตรของซิมป์สันในรูปแบบทั่วไป:
(1)
 (2)
(2)
ข้อผิดพลาดของสูตรของซิมป์สัน - วิธีลำดับที่สี่:
 ,
,  (3)
(3)
เนื่องจากวิธีการของซิมป์สันทำให้เราได้ ความแม่นยำสูง, ถ้า  ไม่ใหญ่เกินไป มิฉะนั้นวิธีลำดับที่สองอาจให้ความแม่นยำมากกว่า
ไม่ใหญ่เกินไป มิฉะนั้นวิธีลำดับที่สองอาจให้ความแม่นยำมากกว่า
ตัวอย่างเช่น สำหรับฟังก์ชัน รูปร่างของสี่เหลี่ยมคางหมูที่  สำหรับ
สำหรับ  ให้ ผลลัพธ์ที่แน่นอน
ให้ ผลลัพธ์ที่แน่นอน  ในขณะที่เราใช้สูตรของซิมป์สันที่เราได้รับ
ในขณะที่เราใช้สูตรของซิมป์สันที่เราได้รับ 
3. ภาพประกอบทางเรขาคณิต


บนส่วน 
 ยาว 2h จะได้พาราโบลาลากผ่านจุด 3 จุด
ยาว 2h จะได้พาราโบลาลากผ่านจุด 3 จุด  ,
, - พื้นที่ใต้พาราโบลาที่อยู่ระหว่างแกน OX กับเส้นตรง
- พื้นที่ใต้พาราโบลาที่อยู่ระหว่างแกน OX กับเส้นตรง  , ยอมรับ เท่ากับอินทิกรัล
, ยอมรับ เท่ากับอินทิกรัล .
.
คุณลักษณะพิเศษของการใช้สูตรของซิมป์สันคือจำนวนพาร์ติชั่นของเซ็กเมนต์การรวมเป็นเลขคู่
หากจำนวนส่วนของพาร์ติชันเป็นเลขคี่ สำหรับสามส่วนแรก เราควรใช้สูตรโดยใช้พาราโบลาระดับที่สามที่ผ่านสี่จุดแรกเพื่อประมาณปริพันธ์
 (4)
(4)
นี่คือสูตรสามในแปดของซิมป์สัน
สำหรับส่วนของการรวมกลุ่มโดยพลการ  สูตร (4) สามารถ "ต่อ" ได้; ในกรณีนี้ จำนวนส่วนของบางส่วนจะต้องเป็นผลคูณของสาม (
สูตร (4) สามารถ "ต่อ" ได้; ในกรณีนี้ จำนวนส่วนของบางส่วนจะต้องเป็นผลคูณของสาม (  คะแนน)
คะแนน)
 , ม.=2,3,... (5)
, ม.=2,3,... (5)
 - ทั้งส่วน
- ทั้งส่วน
คุณสามารถรับสูตรของนิวตัน-โคตส์สำหรับลำดับที่สูงกว่าได้:
 (6)
(6)
 - จำนวนส่วนของพาร์ติชัน
- จำนวนส่วนของพาร์ติชัน
 - ระดับของพหุนามที่ใช้
- ระดับของพหุนามที่ใช้
 - อนุพันธ์
- อนุพันธ์  - ลำดับที่จุดหนึ่ง
- ลำดับที่จุดหนึ่ง  ;
;
 - ขั้นตอนการแบ่งพาร์ติชัน
- ขั้นตอนการแบ่งพาร์ติชัน
ตารางที่ 1 แสดงค่าสัมประสิทธิ์  - แต่ละบรรทัดสอดคล้องกับหนึ่งชุด
- แต่ละบรรทัดสอดคล้องกับหนึ่งชุด  ช่องว่าง
ช่องว่าง  โหนดเพื่อสร้างพหุนามดีกรี k เพื่อใช้โครงร่างนี้เพื่อ มากกว่าเซต (เช่น ด้วย k=2 และ n=6) คุณต้อง "ดำเนินการต่อ" สัมประสิทธิ์แล้วบวกเข้าด้วยกัน
โหนดเพื่อสร้างพหุนามดีกรี k เพื่อใช้โครงร่างนี้เพื่อ มากกว่าเซต (เช่น ด้วย k=2 และ n=6) คุณต้อง "ดำเนินการต่อ" สัมประสิทธิ์แล้วบวกเข้าด้วยกัน
ตารางที่ 1:
|
เค |
ค0 |
A0 |
ก1 |
ก2 |
ก3 |
ก4 |
ก5 |
ก6 | |
|
2 |
|
1 |
4 |
1 | |||||
|
1 |
4 |
1 | |||||||
|
1 |
4 |
1 | |||||||
|
1 |
4 |
2 |
2 |
4 |
1 |
|
อัลกอริธึมสำหรับการประมาณค่าความผิดพลาดของสูตรสี่เหลี่ยมคางหมูและซิมป์สันสามารถเขียนได้เป็น:  (7),
(7),
ที่ไหน  - ค่าสัมประสิทธิ์ขึ้นอยู่กับวิธีการอินทิเกรตและคุณสมบัติของปริพันธ์
- ค่าสัมประสิทธิ์ขึ้นอยู่กับวิธีการอินทิเกรตและคุณสมบัติของปริพันธ์
h - ขั้นตอนการบูรณาการ;
p - ลำดับวิธี
กฎของ Runge ใช้ในการคำนวณข้อผิดพลาดโดยการคำนวณอินทิกรัลสองครั้งด้วยขั้นตอน h และ kh
 (8)
(8)
(8) - การประมาณการหลัง แล้วไอสเปค.=  +โร (9),
+โร (9),  ค่ากลั่นของอินทิกรัล
ค่ากลั่นของอินทิกรัล  .
.
หากไม่ทราบลำดับของวิธีการ จำเป็นต้องคำนวณ I เพิ่มขึ้นเป็นครั้งที่สาม  นั่นคือ:
นั่นคือ:

จากระบบสามสมการ:

กับ ไม่ทราบ I,Aและ p เราได้รับ:
 (10)
(10)
จาก (10) ดังต่อไปนี้  (11)
(11)
ดังนั้น วิธีการคำนวณแบบคู่ ซึ่งใช้จำนวนครั้งที่ต้องการ ทำให้สามารถคำนวณอินทิกรัลด้วยระดับความแม่นยำที่กำหนดได้ จำนวนพาร์ติชั่นที่ต้องการจะถูกเลือกโดยอัตโนมัติ ในกรณีนี้ คุณสามารถใช้การเรียกหลายครั้งไปยังรูทีนย่อยของวิธีการรวมที่สอดคล้องกันโดยไม่ต้องเปลี่ยนอัลกอริทึมของวิธีการเหล่านี้ อย่างไรก็ตาม สำหรับวิธีการที่ใช้โหนดที่เกี่ยวข้องกันเท่ากัน คุณสามารถแก้ไขอัลกอริธึมและลดจำนวนการคำนวณอินทิแกรนด์ลงครึ่งหนึ่งได้โดยใช้ผลรวมอินทิกรัลที่สะสมระหว่างหลายพาร์ติชันก่อนหน้าของช่วงการรวม ค่าประมาณสองค่าของอินทิกรัล 
 และ
และ  คำนวณโดยใช้วิธีสี่เหลี่ยมคางหมูแบบมีขั้นตอน
คำนวณโดยใช้วิธีสี่เหลี่ยมคางหมูแบบมีขั้นตอน 
 และ
และ  มีความสัมพันธ์กันด้วยความสัมพันธ์:
มีความสัมพันธ์กันด้วยความสัมพันธ์:
ในทำนองเดียวกัน สำหรับอินทิกรัลที่คำนวณโดยใช้สูตรพร้อมขั้นตอน  และ
และ  ความสัมพันธ์ต่อไปนี้ถูกต้อง:
ความสัมพันธ์ต่อไปนี้ถูกต้อง:
 ,
,

 (13)
(13)

4. การเลือกขั้นตอนการบูรณาการ
เมื่อต้องการเลือกขั้นตอนการรวม คุณสามารถใช้นิพจน์ของเงื่อนไขส่วนที่เหลือได้ ยกตัวอย่างส่วนที่เหลือของสูตรของซิมป์สัน:
ถ้า 
 จากนั้น
จากนั้น 
 .
.
จากความถูกต้องที่กำหนด ของวิธีการบูรณาการ เราจะกำหนดขั้นตอนที่เหมาะสมจากความไม่เท่าเทียมกันครั้งล่าสุด  ,
,  .
.
อย่างไรก็ตามวิธีนี้ต้องมีการประเมิน  (ซึ่งในทางปฏิบัติก็ทำไม่ได้เสมอไป) ดังนั้นจึงใช้วิธีการอื่นในการประมาณค่าความแม่นยำซึ่งทำให้สามารถเลือกขั้นตอน h ที่ต้องการในระหว่างการคำนวณได้
(ซึ่งในทางปฏิบัติก็ทำไม่ได้เสมอไป) ดังนั้นจึงใช้วิธีการอื่นในการประมาณค่าความแม่นยำซึ่งทำให้สามารถเลือกขั้นตอน h ที่ต้องการในระหว่างการคำนวณได้
ลองดูหนึ่งในเทคนิคเหล่านี้ อนุญาต 
 ,
,
ที่ไหน  - ค่าประมาณของอินทิกรัลพร้อมสเต็ป
- ค่าประมาณของอินทิกรัลพร้อมสเต็ป  - มาลดขั้นตอนกันเถอะ
- มาลดขั้นตอนกันเถอะ  สองครั้ง ทำลายส่วนนี้
สองครั้ง ทำลายส่วนนี้  ออกเป็นสองส่วนเท่าๆ กัน
ออกเป็นสองส่วนเท่าๆ กัน  และ
และ  (
( ).
).
ให้เราสมมุติว่า  ไม่เปลี่ยนแปลงเร็วเกินไปดังนั้น
ไม่เปลี่ยนแปลงเร็วเกินไปดังนั้น  เกือบคงที่: . แล้ว
เกือบคงที่: . แล้ว  และ
และ  , ที่ไหน
, ที่ไหน  นั่นคือ
นั่นคือ  .
.
จากนี้เราสามารถสรุปได้ดังต่อไปนี้: ถ้า  นั่นคือถ้า
นั่นคือถ้า  ,
,  , ก
, ก  - ต้องการความแม่นยำแล้วจึงขั้น
- ต้องการความแม่นยำแล้วจึงขั้น  เหมาะสำหรับการคำนวณอินทิกรัลที่มีความแม่นยำเพียงพอ ถ้า
เหมาะสำหรับการคำนวณอินทิกรัลที่มีความแม่นยำเพียงพอ ถ้า  จากนั้นจึงทำการคำนวณซ้ำเป็นขั้นตอนแล้วจึงเปรียบเทียบ
จากนั้นจึงทำการคำนวณซ้ำเป็นขั้นตอนแล้วจึงเปรียบเทียบ  และ
และ  ฯลฯ กฎนี้เรียกว่ากฎของรุ่ง
ฯลฯ กฎนี้เรียกว่ากฎของรุ่ง
อย่างไรก็ตาม เมื่อใช้กฎของ Runge จำเป็นต้องคำนึงถึงขนาดของข้อผิดพลาดในการคำนวณด้วย: โดยลดลง  ข้อผิดพลาดแน่นอนการคำนวณการเพิ่มขึ้นของอินทิกรัล (การพึ่งพา
ข้อผิดพลาดแน่นอนการคำนวณการเพิ่มขึ้นของอินทิกรัล (การพึ่งพา  จาก
จาก  สัดส่วนผกผัน) และสำหรับขนาดเล็กเพียงพอ
สัดส่วนผกผัน) และสำหรับขนาดเล็กเพียงพอ  ข้อผิดพลาดของวิธีการอาจมากกว่านั้น ถ้าเกิน
ข้อผิดพลาดของวิธีการอาจมากกว่านั้น ถ้าเกิน  แล้วสำหรับ ขั้นตอนนี้ไม่สามารถใช้กฎของ Runge ได้และไม่สามารถบรรลุความแม่นยำตามที่ต้องการได้ ในกรณีเช่นนี้จำเป็นต้องเพิ่มมูลค่า
แล้วสำหรับ ขั้นตอนนี้ไม่สามารถใช้กฎของ Runge ได้และไม่สามารถบรรลุความแม่นยำตามที่ต้องการได้ ในกรณีเช่นนี้จำเป็นต้องเพิ่มมูลค่า  .
.
ในการได้มาซึ่งกฎของ Runge คุณจะต้องใช้สมมติฐานที่ว่า  - หากมีเพียงตารางค่า
- หากมีเพียงตารางค่า  จากนั้นตรวจสอบ
จากนั้นตรวจสอบ  “เพื่อความสม่ำเสมอ” สามารถทำได้โดยตรงจากตาราง การพัฒนาต่อไปของอัลกอริธึมข้างต้นช่วยให้เราสามารถก้าวไปสู่อัลกอริธึมแบบปรับตัวได้ โดยการเลือกขั้นตอนการรวมที่แตกต่างกัน ส่วนต่างๆส่วนของการรวมขึ้นอยู่กับคุณสมบัติ
“เพื่อความสม่ำเสมอ” สามารถทำได้โดยตรงจากตาราง การพัฒนาต่อไปของอัลกอริธึมข้างต้นช่วยให้เราสามารถก้าวไปสู่อัลกอริธึมแบบปรับตัวได้ โดยการเลือกขั้นตอนการรวมที่แตกต่างกัน ส่วนต่างๆส่วนของการรวมขึ้นอยู่กับคุณสมบัติ  จำนวนการคำนวณปริพันธ์จะลดลง
จำนวนการคำนวณปริพันธ์จะลดลง
อีกรูปแบบหนึ่งสำหรับการปรับแต่งค่าอินทิกรัลคือกระบวนการ Eithnen อินทิกรัลคำนวณเป็นขั้นตอน  , และ
, และ  - กำลังคำนวณค่า แล้ว
- กำลังคำนวณค่า แล้ว  (14).
(14).
การวัดความแม่นยำของวิธี Simpson คือ:
5. ตัวอย่าง
ตัวอย่างที่ 1คำนวณอินทิกรัล  ตามสูตรของซิมป์สัน ถ้า
ตามสูตรของซิมป์สัน ถ้า  มอบให้โดยโต๊ะ ประมาณการข้อผิดพลาด
มอบให้โดยโต๊ะ ประมาณการข้อผิดพลาด
ตารางที่ 3.
 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
 |
1 |
0.995 |
0.98 |
0.955 |
0.921 |
0.878 |
0.825 |
0.765 |
0.697 |
วิธีแก้ไข: คำนวณโดยใช้สูตร (1) ที่
 และ
และ  บูรณาการ
บูรณาการ ตามกฎของ Runge ที่เราได้รับ  เรายอมรับ.
เรายอมรับ.
ตัวอย่างที่ 2คำนวณอินทิกรัล
 .
.
วิธีแก้ปัญหา: เรามี  - ดังนั้น h=
- ดังนั้น h=  =0.1. ผลการคำนวณแสดงไว้ในตารางที่ 4
=0.1. ผลการคำนวณแสดงไว้ในตารางที่ 4
ตารางที่ 4.
การคำนวณอินทิกรัลโดยใช้สูตรซิมป์สัน
|
ฉัน |
 |
 |
 |
|
0 |
0 |
y0=1.00000 |
|
|
1 |
0.1 |
0,90909 | |
|
2 |
0.2 |
0,83333 |
|
|
3 |
0.3 |
0,76923 | |
|
4 |
0.4 |
0,71429 |
|
|
5 |
0.5 |
0,66667 | |
|
6 |
0.6 |
0,62500 |
|
|
7 |
0.7 |
0,58824 | |
|
8 |
0.8 |
0,55556 |
|
|
9 |
0,9 |
0,52632 | |
|
10 |
1,0 |
0.50000=yn |
|
|
|
3.45955(1) |
2.72818(2) |
จากการใช้สูตรของ Simpson เราจะได้:

มาคำนวณข้อผิดพลาดของผลลัพธ์ที่ได้รับ ข้อผิดพลาดทั้งหมด  ประกอบด้วยข้อผิดพลาดของการกระทำ
ประกอบด้วยข้อผิดพลาดของการกระทำ  และระยะเวลาที่เหลือ
และระยะเวลาที่เหลือ  - แน่นอน: -0.289687
- แน่นอน: -0.289687
4
2,35
-0,70271
-0,299026
2,4
-0,73739
-0,307246
2
2,45
-0,77023
-0,314380
2,5
-0,80114
-0,320465
4
2,55
-0,83005
-0,325510
2,6
-0,85689
-0,329573
2
2,65
-0,88158
-0,332672
2,7
-0,90407
-0,334841
4
2,75
-0,92430
-0,336109
3.
ให้เราแทนที่อินทิแกรนด์ที่อยู่ใน (2.50) ด้วยพหุนามการประมาณค่าลากรองจ์ของดีกรีศูนย์ที่ผ่านตรงกลางของเซ็กเมนต์ - จุด เอ็กซ์ = (ก + ข)/2(รูปที่ 2.5) พื้นที่ของสี่เหลี่ยมคางหมูโค้งสามารถถูกแทนที่ด้วยพื้นที่ของสี่เหลี่ยมเช่น
สูตร (2.52) เรียกว่า RECTANGLE FORMULA หรือ AVERAGE FORMULA ข้อผิดพลาดของมันคือ

การขยายฟังก์ชัน ฉ(x)เรียงกันเป็นแถวสัมพันธ์กับกึ่งกลางของปล้องมีรูปทรง
เราได้รับนิพจน์แทน (2.54) ลงใน (2.53)


ข้าว. 2.5
เมื่อคำนวณข้อผิดพลาดในการรวม ไม่เพียงแต่ส่วนแรกเท่านั้น แต่ยังรวมถึงส่วนที่สองของส่วนขยายที่ถูกทำลาย ซึ่งสัมพันธ์กับตัวเลือกแบบสมมาตรของโหนดการรวม และแม้ว่าโดยโครงสร้างแล้ว สูตรจะเป็นค่าพหุนามที่แน่นอนก็ตาม ลำดับศูนย์การเลือกโหนดการแก้ไขแบบสมมาตรทำให้สูตรมีความแม่นยำสำหรับฟังก์ชันเชิงเส้นใดๆ
ค่าของเทอมที่เหลือในสูตรสี่เหลี่ยมผืนผ้า (2.53) อาจมีค่ามาก เนื่องจากผลต่าง (6 - a) อาจมีค่าค่อนข้างมาก เพื่อเพิ่มความแม่นยำ เราขอแนะนำตาข่าย
ด้วยก้าวเล็กๆ ที่ค่อนข้างมาก สวัสดี=เจซี(- xt_ j และใช้สูตรสี่เหลี่ยมกับแต่ละขั้นตอนของตาราง จากนั้นเราจะได้สูตรทั่วไปสำหรับสี่เหลี่ยม
ด้วยมูลค่าของเทอมที่เหลือ
บนตารางที่มีขั้นสม่ำเสมอ สวัสดี «= เอ็กซ์ ( - xt _ j = สูตร const (2.56) เป็นแบบย่อและมีรูปแบบ
ค่าของเทอมที่เหลือคือการแทนที่ผลรวมใน (2.58) ด้วยอินทิกรัลที่เราได้รับ
เพื่อให้การประมาณระยะที่เหลือ (2.58) ถูกต้อง จำเป็นต้องมีอนุพันธ์อันดับสองต่อเนื่องกัน ถ้าเป็นอนุพันธ์อันดับสอง ฉ"x)- ต่อเนื่องเป็นชิ้น ๆ จึงเป็นไปได้ที่จะทำการประมาณค่าหลัก ๆ โดยการแทนที่เท่านั้น ฉ"(x)ค่าสูงสุดของมันอยู่ที่ [ก, 6]. จากนั้นถ้าเราแสดงว่า M 2 = สูงสุด | ฉ"(x)- [และส่วนที่เหลือ
ในกรณีที่มีฟังก์ชัน ฉ(x) จะได้รับในรูปแบบของตาราง โดยไม่ทราบค่าที่อยู่ตรงกลางของช่วงเวลา ค่านี้มักจะพบโดยการประมาณค่า ซึ่งทำให้ความแม่นยำของสูตรลดลง
ในกรณีของตาราง ฟังก์ชั่นที่ระบุสะดวกในการเลือกจุดเริ่มต้นและจุดสิ้นสุดของส่วนการรวมเป็นโหนดการแก้ไข เช่น แทนที่ฟังก์ชัน ฉ(x)พหุนามลากรองจ์ของดีกรี 1 เรามี

ข้าว. 2.6
ในกรณีนี้ ค่าของอินทิกรัล เท่ากับพื้นที่สี่เหลี่ยมคางหมูโค้งจะถูกแทนที่ด้วยพื้นที่ของสี่เหลี่ยมคางหมูโดยประมาณ (รูปที่ 2.6) ดังนั้นเราจึงได้

จำไว้ว่า x 0 = a, เอ็กซ์ ก = ข.สูตรนี้เรียกว่า TRAPEZIOUS FORMULA เมื่อใช้สูตรสี่เหลี่ยมคางหมูสำหรับ
ค่าประมาณของข้อผิดพลาดในการรวม เราคำนวณจาก J dx
สูตร (2.18) เรามี
ข้อผิดพลาดของสูตรสี่เหลี่ยมคางหมูเป็นสองเท่าของข้อผิดพลาดของสูตรสี่เหลี่ยม สิ่งนี้อธิบายได้จากข้อเท็จจริงที่ว่าการเลือกสี่เหลี่ยมในสูตรเป็นโหนดการแก้ไขโหนดแบบสมมาตรทำให้ความแม่นยำเพิ่มขึ้น
เพื่อปรับปรุงความแม่นยำของสูตร (2.61) เราแนะนำในส่วนนี้ [ก ข]ตาข่าย
เราได้รับการคำนวณค่าอินทิกรัลสำหรับแต่ละช่วงเวลาและรวมค่าเหล่านี้ ทั่วไปสูตรสี่เหลี่ยมคางหมู
ด้วยมูลค่าของเทอมที่เหลือ
สูตรเหล่านี้ถูกทำให้ง่ายขึ้นบนตารางโดยมีขั้นตอนคงที่ L = L (= เอ็กซ์จ- d:, t = const (i - 0, 1, - 1):
ให้เราแนะนำสัญกรณ์ ม2~ max |Гх^)1(а &] ในทางปฏิบัติ พวกเขาใช้การประมาณค่าหลักสำหรับมูลค่าของเทอมที่เหลือ
ดังนั้น สูตรสี่เหลี่ยมคางหมู (เช่น สูตรสี่เหลี่ยม) จึงมีความแม่นยำลำดับที่สองตามขั้นตอนของกริด และข้อผิดพลาดเชิงเส้นกำกับมีแนวโน้มที่จะเป็นศูนย์ที่ ชม.-» 0 ถึงภายในเงื่อนไขเพิ่มเติม ลำดับสูงเล็กน้อย.
เพื่อเพิ่มลำดับความแม่นยำของสูตรการรวมตัวเลข เราจะแทนที่ปริพันธ์ด้วยพาราโบลา - พหุนามการประมาณค่าลากรองจ์ในระดับที่สอง โดยเลือกปลายและตรงกลางของส่วนการรวมเป็นโหนดการแก้ไข: x 0 = ก, x x ~ (ก + ข)/ 2, x ก = ข(รูปที่ 2.7)
ในกรณีนี้ เราได้รับการรวมพหุนามการประมาณค่าสำหรับโหนดที่มีระยะห่างเท่ากัน

ข้าว. 2.7
ในกรณีนี้คือมูลค่าของเทอมที่เหลือ ร~ J D 2 (x) dx ประมาณโดยความสัมพันธ์โดยประมาณ° 
สูตร (2.67) เรียกว่า SIMPSON'S FORMULA สำหรับโหนดที่มีระยะห่างไม่เท่ากัน x 0, Xj, x 2 ค่า เอฟจำนวน 
เช่นเดียวกับในสองกรณีก่อนหน้านี้ เพื่อเพิ่มความแม่นยำของสูตร (2.67) เราจะแนะนำตารางที่มีขั้นตอนเล็กน้อยเพียงพอ เมื่อรวมค่าอินทิกรัลที่ได้รับจาก (2.67) สำหรับแต่ละช่วงเวลาเราจะได้สูตรซิมป์สันทั่วไป (พาราโบลา) ซึ่งบนตารางสม่ำเสมอจะมีรูปแบบ
และมูลค่าของเทอมที่เหลือคือ
ดังนั้นสูตรพาราโบลาจึงมีความแม่นยำลำดับที่สี่เมื่อเทียบกับขั้นตอนของกริด ให้เราแนะนำสัญกรณ์ ม.4= = สูงสุด |/ IV (x)| -
.
แล้ว .
เราจะใช้การประมาณค่าเชิงเส้นของปริพันธ์
ถ้าแทนที่จะเป็นเซ็กเมนต์ [-1; 1] ใช้โหนดที่เคลื่อนที่ได้ t1, t2 เป็นโหนดการแก้ไข จากนั้นคุณต้องเลือกค่าเหล่านี้เพื่อให้พื้นที่ของสี่เหลี่ยมคางหมูล้อมรอบด้วยเส้นตรงที่ผ่านจุด A1 (t1, φ(t1)) และ A2 (t2, φ(t2)) เท่ากับอินทิกรัลของพหุนามใดๆ ของค่าบางตัว ระดับสูงสุด.
สมมติว่านี่คือพหุนามของระดับที่สาม เราคำนวณ t1, t2 ซึ่งกลายเป็นเท่ากับ และ ต่างกันเฉพาะในการกำหนดหมายเลขของค่าเท่านั้น
ขั้นต่อไป เมื่อแบ่งส่วนการรวมออกเป็นส่วน n โดยใช้แนวคิดที่อธิบายไว้ข้างต้นกับแต่ละส่วน เราจะได้สูตร Gauss:
การเขียนโปรแกรมสูตรปริพันธ์เชิงตัวเลข
การแนะนำ
1. วิธีการรวมตัวเลข
2. สูตรการสร้างพื้นที่สี่เหลี่ยมจัตุรัส
3. การเลือกขั้นตอนการรวมระบบอัตโนมัติ
บทสรุป
บรรณานุกรม
การแนะนำ
วัตถุประสงค์ของเรียงความคือเพื่อศึกษาและ การวิเคราะห์เปรียบเทียบวิธีการรวมฟังก์ชันเชิงตัวเลข การใช้วิธีการเหล่านี้ในรูปแบบของโปรแกรมเครื่องในภาษา ระดับสูงและการแก้ปัญหาเชิงปฏิบัติของปัญหาการรวมตัวเลขบนคอมพิวเตอร์
เมื่อแก้ไขปัญหาทางวิศวกรรม มักจำเป็นต้องคำนวณค่าต่างๆ อินทิกรัลที่แน่นอนใจดี
. (1)หากฟังก์ชันต่อเนื่องในช่วงเวลา [ ก , ข] และแอนติเดริเวทีฟของมันสามารถนิยามได้ผ่าน ฟังก์ชั่นที่รู้จักดังนั้นอินทิกรัลดังกล่าวจะถูกคำนวณโดยใช้สูตรของนิวตัน–ไลบ์นิซ:
ใน ปัญหาทางวิศวกรรมแทบจะเป็นไปไม่ได้เลยที่จะได้ค่าอินทิกรัลในรูปแบบการวิเคราะห์ นอกจากนี้ฟังก์ชั่น ฉ (x) สามารถระบุได้ ตัวอย่างเช่น โดยตารางข้อมูลการทดลอง ดังนั้นในทางปฏิบัติ ในการคำนวณอินทิกรัลจำกัดเขตที่พวกเขาใช้ วิธีการพิเศษซึ่งขึ้นอยู่กับอุปกรณ์การแก้ไข
แนวคิดของวิธีการดังกล่าวมีดังนี้ แทนที่จะคำนวณอินทิกรัลโดยใช้สูตร (1) ให้คำนวณค่าของฟังก์ชันก่อน ฉ (x ฉัน) = ใช่แล้วในบางโหนด x ฉัน Î[ ก , ข- จากนั้นเลือกพหุนามการประมาณค่า ป (x) ผ่านจุดที่ได้รับ ( x ฉัน , ใช่แล้ว) ซึ่งใช้ในการคำนวณค่าโดยประมาณของอินทิกรัล (1):
เมื่อนำแนวทางนี้ไปใช้ สูตรการรวมเชิงตัวเลขจะใช้สิ่งต่อไปนี้ มุมมองทั่วไป:
ความหมายทางเรขาคณิตของการอินทิเกรตเชิงตัวเลขคือการคำนวณพื้นที่ของสี่เหลี่ยมคางหมูโค้งซึ่งจำกัดโดยกราฟของฟังก์ชัน ฉ (เอ็กซ์) แกน x และเส้นตรงสองเส้น x = กและ x = ขการคำนวณพื้นที่โดยประมาณจะนำไปสู่การปฏิเสธระยะที่เหลือในสูตรการสร้างพื้นที่สี่เหลี่ยมจัตุรัส รซึ่งระบุลักษณะข้อผิดพลาดของวิธีการซึ่งมีข้อผิดพลาดในการคำนวณซ้อนทับเพิ่มเติม
1. วิธีการอินทิเกรตเชิงตัวเลข
ใน การวิจัยประยุกต์บ่อยครั้งมีความจำเป็นต้องคำนวณค่าของอินทิกรัลจำกัดเขต
ดังที่คุณทราบจากหลักสูตรคณิตศาสตร์ อินทิกรัลไม่สามารถคำนวณเชิงวิเคราะห์ได้ในทุกกรณี และแม้กระทั่งในกรณีที่เป็นไปได้ที่จะค้นหารูปแบบการวิเคราะห์ของอินทิกรัลนี้ ขั้นตอนการคำนวณจะให้ผลลัพธ์โดยประมาณ ดังนั้นปัญหาค่าประมาณของอินทิกรัลนี้จึงเกิดขึ้น
สาระสำคัญของการคำนวณโดยประมาณอยู่ในการดำเนินการสองรายการ: 1. การเลือก จำนวนจำกัดแทนที่จะเป็น n; 2.ในการเลือกจุด
ในส่วนที่เกี่ยวข้องขึ้นอยู่กับทางเลือก
เราได้รับสูตรต่าง ๆ สำหรับการคำนวณอินทิกรัล: สูตรของสี่เหลี่ยมด้านซ้ายและขวา (5), (6)สูตรสี่เหลี่ยมคางหมู:
สูตรซิมป์สัน
b, a - จุดสิ้นสุดของส่วนที่อยู่ระหว่างการพิจารณา
เพื่อเปรียบเทียบผลการคำนวณกับสูตรการรวมตัวเลขข้างต้น เราคำนวณอินทิกรัลต่อไปนี้ใน 3 วิธี โดยแบ่งส่วนออกเป็น 6 ส่วนเท่า ๆ กัน: h=
ตามสูตรของสี่เหลี่ยมด้านซ้าย:
ตามสูตรสี่เหลี่ยมคางหมู:
ตามสูตรของซิมป์สัน:
และผลลัพธ์ที่ได้เชิงวิเคราะห์ก็เท่ากับ
=1ดังนั้นเราจึงสรุปได้ว่า วิธีการเชิงตัวเลขการบูรณาการโดยใช้สูตรของซิมป์สันมีความแม่นยำมากกว่า แต่นำมาใช้ใน กรณีทั่วไปเมื่อแบ่งส่วนออกเป็นช่วงเลขคู่
2. สูตรการสร้างพื้นที่สี่เหลี่ยมจัตุรัส
สูตรสี่เหลี่ยมเป็นสูตรการสร้างพื้นที่สี่เหลี่ยมจัตุรัสที่ง่ายที่สุด ให้เราแยกส่วนการรวม [ ก, ข] บน nความยาวส่วนที่เท่ากัน
- โปรดทราบว่าค่า ชม.เรียกว่าขั้นตอนการบูรณาการ ณ จุดแยก เอ็กซ์ 0 = ก ,เอ็กซ์ 1 =ก+ช , ..., x n = ขสังเกตคำสั่ง ย 0 ,ย 1 ,…,ใช่คดเคี้ยว ฉ (x), เช่น. มาคำนวณกัน ใช่ ฉัน = ฉ (x ฉัน), x i = a+ ih = x i -1 +ชม (ฉัน =- ในแต่ละส่วนของความยาว ชม.สร้างสี่เหลี่ยมผืนผ้าที่มีด้านข้าง ชม.และ ใช่แล้ว, ที่ไหน ฉัน =, เช่น. จากค่าลำดับที่คำนวณไว้ที่ปลายด้านซ้ายของเซ็กเมนต์ จากนั้นพื้นที่ของสี่เหลี่ยมคางหมูโค้งซึ่งกำหนดค่าของอินทิกรัล (1) สามารถแสดงโดยประมาณเป็นผลรวมของพื้นที่ของสี่เหลี่ยม (รูปที่ 1) จากที่นี่เราจะได้สูตรสำหรับสี่เหลี่ยม:. (3)
หากเมื่อคำนวณผลรวมอินทิกรัลเราจะรับค่าของฟังก์ชัน ฉ (x) ไม่ใช่ทางด้านซ้าย แต่อยู่ที่ปลายด้านขวาของส่วนที่มีความยาว ชม.ซึ่งแสดงไว้ในรูปที่. 1 ด้วยเส้นประ เราจะได้สูตรสี่เหลี่ยมเวอร์ชันที่สอง:
. (4)สูตรสี่เหลี่ยมเวอร์ชันที่สามสามารถรับได้โดยใช้ค่าฟังก์ชัน ฉ (x) คำนวณที่จุดกึ่งกลางของส่วนความยาวแต่ละส่วน ชม.(รูปที่ 2):
สูตร (3), (4) และ (4) เรียกว่าสูตรของสี่เหลี่ยมด้านซ้าย ด้านขวา และตรงกลาง ตามลำดับ
 |
สูตรซิมป์สันลองหารช่วงอินทิเกรตด้วย 2 กัน nความยาวส่วนที่เท่ากัน
เมื่อคำนวณบนคอมพิวเตอร์ สูตรต่อไปนี้จะสะดวกกว่า:

วิธีการของซิมป์สันเป็นหนึ่งในวิธีการรวมตัวเลขที่รู้จักและใช้กันอย่างแพร่หลาย โดยให้ค่าอินทิกรัลที่แม่นยำเมื่อรวมพหุนามจนถึงลำดับที่สาม
สูตรของนิวตันค่าประมาณของอินทิกรัลโดยใช้สูตรของนิวตันคำนวณได้ดังนี้:
โดยที่จำนวนส่วนของพาร์ติชั่นเป็นผลคูณของสามนั่นคือ คือ 3 n- เมื่อพัฒนาโปรแกรมคอมพิวเตอร์จะสะดวกกว่าถ้าใช้สูตรที่เทียบเท่า:

วิธีการของนิวตันให้ค่าที่แน่นอนของอินทิกรัลเมื่ออินทิเกรตพหุนามจนถึงลำดับที่สี่
3. การเลือกขั้นตอนการรวมระบบอัตโนมัติ
จากการคำนวณโดยใช้สูตร (3) - (8) จะได้ค่าประมาณของอินทิกรัลซึ่งอาจแตกต่างจากค่าที่แน่นอนในจำนวนหนึ่งเรียกว่าข้อผิดพลาดในการรวม ข้อผิดพลาดถูกกำหนดโดยสูตรส่วนที่เหลือ รแตกต่างกันสำหรับแต่ละวิธีการรวม หากจำเป็นต้องคำนวณค่าอินทิกรัลโดยมีข้อผิดพลาดไม่เกิน e ก็จำเป็นต้องเลือกขั้นตอนการอินทิกรัลดังกล่าว ชม.เพื่อให้เกิดความไม่เท่าเทียมกัน ร (ชม.) ปอนด์อี ในทางปฏิบัติ จะใช้การเลือกค่าอัตโนมัติ ชม.เพื่อให้แน่ใจว่าบรรลุผลสำเร็จของข้อผิดพลาดที่กำหนด ขั้นแรก ให้คำนวณค่าอินทิกรัล ฉัน (n) โดยแบ่งช่วงเวลาการรวมออกเป็น nส่วนต่างๆ จากนั้นจำนวนส่วนจะเพิ่มเป็นสองเท่าและคำนวณอินทิกรัล ฉัน (2n- กระบวนการคำนวณจะดำเนินต่อไปจนกว่าเงื่อนไขจะเป็นจริง
 ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ
ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ ความสัมพันธ์ระหว่างมนุษย์กับธรรมชาติ คำประสมที่มีสระเชื่อมกัน
คำประสมที่มีสระเชื่อมกัน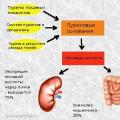 กรดยูริกในเลือด: บรรทัดฐานและการเบี่ยงเบน, เหตุใดจึงเพิ่มขึ้น, อาหารเพื่อลดกรด ผลิตภัณฑ์สุดท้ายของการเผาผลาญไนโตรเจนคือ
กรดยูริกในเลือด: บรรทัดฐานและการเบี่ยงเบน, เหตุใดจึงเพิ่มขึ้น, อาหารเพื่อลดกรด ผลิตภัณฑ์สุดท้ายของการเผาผลาญไนโตรเจนคือ