กฎบอกว่าถ้าฟังก์ชั่น ฉ(x) และ g(x) มีชุดเงื่อนไขดังต่อไปนี้:

แล้วมี . นอกจากนี้ ทฤษฎีบทนี้ยังเป็นจริงสำหรับฐานอื่นๆ (จะมีการพิสูจน์สำหรับฐานที่ระบุ)

เรื่องราว

วิธีการสำหรับการเปิดเผยความไม่แน่นอนประเภทนี้ได้รับการตีพิมพ์โดย Lopital ในงาน "Analysis of infinitesimals" ซึ่งตีพิมพ์ในปีดังกล่าว ในคำนำของงานนี้ Lopital ชี้ให้เห็นว่าเขาใช้การค้นพบของ Leibniz และพี่น้อง Bernoulli โดยไม่ลังเลใด ๆ และ "ไม่มีอะไรต่อต้านพวกเขาในการแสดงลิขสิทธิ์ของพวกเขาในสิ่งที่พวกเขาต้องการ" Johann Bernoulli อ้างสิทธิ์ในงานทั้งหมดของ L'Hospital และโดยเฉพาะอย่างยิ่งหลังจากที่ L'Hospital เสียชีวิต เขาได้ตีพิมพ์ผลงานภายใต้ชื่อที่น่าทึ่งว่า "การปรับปรุงวิธีการของฉันที่ตีพิมพ์ใน Infinitesimal Analysis สำหรับการกำหนดมูลค่าของเศษส่วน ตัวเศษ และตัวส่วน ซึ่งบางครั้งก็หายไป", .

การพิสูจน์

อัตราส่วนของอนันต์

ให้เราพิสูจน์ทฤษฎีบทสำหรับกรณีที่ลิมิตของฟังก์ชันมีค่าเท่ากับศูนย์ (ความไม่แน่นอนของรูปแบบที่เรียกว่า )

เนื่องจากเรากำลังดูหน้าที่ ฉและ gเฉพาะในกึ่งย่านที่เจาะด้านขวาของจุด เอเราสามารถกำหนดใหม่ได้อย่างต่อเนื่อง ณ จุดนี้: let ฉ(เอ) = g(เอ) = 0 . มากินกันเถอะ xจากกึ่งย่านที่อยู่ระหว่างการพิจารณาและใช้ทฤษฎีบท Cauchy กับกลุ่ม โดยทฤษฎีบทนี้ เราได้รับ:

,

แต่ ฉ(เอ) = g(เอ) = 0 นั่นเป็นเหตุผลที่ .

src="/pictures/wiki/files/56/85e2b8bb13d6fb1ddcf88e22a4bb6ef2.png" border="0"> สำหรับขีด จำกัด สิ้นสุดและ src="/pictures/wiki/files/101/e8b2f2b8861947c8728d4d1be40366d4.png" ใน fin="ity"> ,

ซึ่งเป็นคำจำกัดความของลิมิตอัตราส่วนของฟังก์ชัน

อัตราส่วนของขนาดใหญ่อนันต์

ให้เราพิสูจน์ทฤษฎีบทความไม่แน่นอนของแบบฟอร์ม

ให้สำหรับการเริ่มต้น ขีด จำกัด ของอัตราส่วนของอนุพันธ์มี จำกัด และเท่ากับ อา. จากนั้นในขณะที่พยายาม xถึง เอทางด้านขวา ความสัมพันธ์นี้สามารถเขียนเป็น อา+ α โดยที่ α - (1) ลองเขียนเงื่อนไขนี้:

.

มาแก้บน tจากส่วนและใช้ทฤษฎีบท Cauchy กับทั้งหมด xจากส่วน:

ซึ่งสามารถนำไปสู่ ชนิดต่อไป: .

สำหรับ x, ใกล้พอที่จะ เอ, นิพจน์มีความหมาย; ขีด จำกัด ของปัจจัยแรกของด้านขวามือ เท่ากับหนึ่ง(เพราะ ฉ(t) และ g(t) เป็นค่าคงที่ และ ฉ(x) และ g(x) มีแนวโน้มเป็นอนันต์). ดังนั้น ตัวประกอบนี้จึงเท่ากับ 1 + β โดยที่ β เป็นฟังก์ชันที่น้อยมากเช่น xถึง เอด้านขวา. เราเขียนคำจำกัดความของข้อเท็จจริงนี้โดยใช้ค่าเดียวกับในคำจำกัดความของ α :

.

เราพบว่าอัตราส่วนของฟังก์ชันสามารถแสดงได้ในรูปแบบ (1 + β)( อา+ α) และ . สำหรับตัวใดตัวหนึ่งสามารถหาได้ว่าโมดูลัสของความแตกต่างระหว่างอัตราส่วนของฟังก์ชันและ อาน้อยกว่า ซึ่งหมายความว่าขีดจำกัดของอัตราส่วนของฟังก์ชันจะเท่ากับ อา .

ถ้าถึงขีดจำกัด อาเป็นอนันต์ (สมมุติว่าเท่ากับบวกอนันต์) แล้ว

(x))(g"(x))>2M)" src="/pictures/wiki/files/101/e46c5113c49712376d1c357b5b202a65.png" border="0">

ในคำจำกัดความของ β เราจะใช้ ; ตัวประกอบแรกของด้านขวาจะมากกว่า 1/2 เมื่อ x, ใกล้พอที่จะ เอจากนั้น src="/pictures/wiki/files/50/2f7ced4a9b4b06f7b9085e982250dbcf.png" border="0">

สำหรับฐานอื่น ๆ หลักฐานจะคล้ายกับที่ให้มา

ตัวอย่าง

(เฉพาะในกรณีที่ตัวเศษและตัวส่วนทั้งสองมีแนวโน้มเป็น 0 ; หรือ ; หรือ .)

มูลนิธิวิกิมีเดีย 2010 .

ดูว่า "กฎ L'Hopital" ในพจนานุกรมอื่นๆ คืออะไร:

ชื่อที่ไม่ถูกต้องในอดีตสำหรับกฎพื้นฐานข้อใดข้อหนึ่งสำหรับการเปิดเผยความไม่แน่นอน L. p. ถูกค้นพบโดย I. Bernoulli และรายงานโดยเขาต่อ G. L'Hopital (ดู L'Hopital) ผู้ตีพิมพ์กฎนี้ในปี 1696 ดู นิพจน์ที่ไม่แน่นอน ... สารานุกรมแห่งสหภาพโซเวียตผู้ยิ่งใหญ่

การเปิดเผยความไม่แน่นอนของรูปแบบโดยการลดขีดจำกัดอัตราส่วนของฟังก์ชันเป็นขีดจำกัดอัตราส่วนอนุพันธ์ของฟังก์ชันที่พิจารณา ดังนั้น สำหรับกรณีที่เมื่อ ฟังก์ชั่นที่แท้จริง f และ g ถูกกำหนดไว้ในพื้นที่ใกล้เคียงทางขวามือที่เจาะทะลุของจุดตัวเลข ... ... สารานุกรมคณิตศาสตร์

กฎของโรงพยาบาล Bernoulli L'Hospital คือวิธีการหาขีดจำกัดของหน้าที่ ซึ่งเผยให้เห็นความไม่แน่นอนของรูปแบบ u ทฤษฎีบทที่อธิบายวิธีการระบุว่าภายใต้เงื่อนไขบางประการขีด จำกัด ของอัตราส่วนของฟังก์ชันจะเท่ากับขีด จำกัด ของอัตราส่วนของอนุพันธ์ ... ... Wikipedia

ในการวิเคราะห์ทางคณิตศาสตร์ กฎของโฮปิตาลคือวิธีการหาลิมิตของฟังก์ชัน โดยเปิดเผยความไม่แน่นอนของรูปแบบ 0 / 0 และ ทฤษฎีบทที่อธิบายวิธีการระบุว่าภายใต้เงื่อนไขบางประการขีด จำกัด ของอัตราส่วนของฟังก์ชันจะเท่ากับขีด จำกัด ... ... Wikipedia

ในการวิเคราะห์ทางคณิตศาสตร์ กฎของโฮปิตาลคือวิธีการหาลิมิตของฟังก์ชัน โดยเปิดเผยความไม่แน่นอนของรูปแบบ 0 / 0 และ ทฤษฎีบทที่อธิบายวิธีการระบุว่าภายใต้เงื่อนไขบางประการขีด จำกัด ของอัตราส่วนของฟังก์ชันจะเท่ากับขีด จำกัด ... ... Wikipedia

การพึ่งพาอาศัยของพิกัดตรงเวลาเมื่อเคลื่อนย้าย จุดวัสดุในเครื่องบิน

กำหนดความเร็วของโมดูล (

A. โมดูลัสของความเร็วของจุดวัสดุจากเวลาแสดงโดยสูตร:

ข. . โมดูลของการเร่งความเร็วของจุดวัสดุจากเวลาแสดงโดยสูตร:

สมการเหล่านี้อธิบายการเคลื่อนที่ของจุดวัสดุด้วยความเร่งคงที่

ดาวเทียมโคจรรอบโลกด้วยความสูง

ดาวเทียมที่เคลื่อนที่เป็นวงกลมอยู่ภายใต้แรงโน้มถ่วง

สูตรนี้สามารถลดความซับซ้อนได้ดังนี้ เกี่ยวกับน้ำหนักตัว

ทางนี้, ความเร็วสายดาวเทียมคือ

และความเร็วเชิงมุม

ลูกทั้งสองที่พิจารณาในปัญหาในรูปแบบระบบปิดและในกรณี ช็อกยางยืดทั้งโมเมนตัมของระบบและพลังงานกล (จลนศาสตร์) จะถูกอนุรักษ์ไว้ ให้เราเขียนกฎการอนุรักษ์ทั้งสอง (โดยคำนึงถึงความไม่สามารถเคลื่อนที่ของลูกที่สองก่อนกระทบ):

ดังนั้น ลูกบอลตกกระทบ (ลูกแรก) อันเป็นผลมาจากการกระแทกจึงลดความเร็วจาก 1.05 m/s เป็น 0.45 m/s แม้ว่าจะเคลื่อนที่ไปในทิศทางเดียวกันก็ตาม และลูกบอลที่หยุดนิ่ง (ลูกที่สอง) ก่อนหน้านี้ก็มีความเร็วเท่ากัน ไปที่ 1, 5 m/s และตอนนี้ทั้งสองลูกกำลังเคลื่อนที่เป็นเส้นตรงเดียวกันและไปในทิศทางเดียวกัน

เนื่องจากมวลของก๊าซในกระบอกสูบเปลี่ยนไปสถานะเริ่มต้นและสุดท้ายของก๊าซในกระบอกสูบจึงไม่สัมพันธ์กันโดยกฎหมาย Boyle-Mariotte หรือกฎ Charles หากก๊าซในกระบอกสูบเปลี่ยนแปลงโดยการปรับให้เท่ากัน สถานะเริ่มต้นและสุดท้ายของก๊าซในกระบอกสูบไม่สามารถสัมพันธ์กันโดยกฎหมาย Boyle-Mariotte แต่ละรัฐเขียนสมการ Mendeleev-Clapeyron

วิธีหาลิมิตของฟังก์ชันโดยไม่ใช้กฎลอปิทัล

รุ่นของระบบ:
7.47 (16.04.2018)

ข่าวทั่วไป:
13.04.2018, 10:33

คำถามสุดท้าย:
26.07.2018, 15:23

ตอบกลับล่าสุด:
27.07.2018, 13:48

ส่วน คณิตศาสตร์

ให้คำปรึกษาและแก้ปัญหาพีชคณิต เรขาคณิต วิเคราะห์ คณิตศาสตร์ไม่ต่อเนื่อง

ผู้เชี่ยวชาญที่ดีที่สุดในส่วนนี้

สวัสดี! ฉันมีปัญหากับคำถามนี้:

หาลิมิตของฟังก์ชันโดยไม่ต้องใช้กฎของโลปิตาล

lim (2x+3) [ ln (x+2) - ln x ] (ภายใต้ lim เขียนว่า "x มีแนวโน้มที่จะไม่มีที่สิ้นสุด")

มีตัวอย่างข้อจำกัดหลายอย่างในงานมอบหมาย แต่สิ่งนี้ทำให้งงงัน ฉันไม่รู้วิธีแก้ อาจใช้ขีด จำกัด ที่ยอดเยี่ยมที่สอง แต่อย่างไร (มีเพียงความคิดนี้เท่านั้นที่นึกถึง)?

ให้ฉันถามในคำถามเดียวกันว่าปัญหาดังกล่าวเกิดขึ้นหรือไม่ (หากเป็นเช่นนั้น ฉันจะโพสต์ในภายหลังเป็นคำถามที่ต้องเสียเงิน): ใช้สูตรเทย์เลอร์กับพจน์ที่เหลือในรูปแบบลากรองจ์กับฟังก์ชัน คำนวณ ค่าที่มีความแม่นยำ 0.001; ก = 0.29
ที่นี่ฉันไม่เข้าใจว่าฟังก์ชั่นอะไร? ไม่ได้ตั้งค่า (?) งานจะฟังเหมือนกับที่ฉันจดไว้ บางทีคุณสามารถใช้ฟังก์ชั่นนี้ได้ แต่อันไหน?

สถานะ: ปิดรับคำปรึกษา

สวัสดีอเล็กซานดริบ!
เป็นอันที่ 2 ที่ต้องใช้! ในการเริ่มต้น มาทำให้ง่ายขึ้น:
ลิม (2x+3) [ ln (x+2) - ln x ] = ลิม (2x+3) ln ((x+2)/x) = ลิม (2x+3) ln (1+2/x) = lim ln ((1+2/x)^(2x+3)) = lim ln ((1+2/x)^2x)+lim ln ((1+2/x)^3) [ขีดจำกัดที่สองคือ zero เนื่องจาก 2/x มีแนวโน้มที่จะเป็นศูนย์และ ln 1 = 0]
มาทำการเปลี่ยนแปลง y = x/2 จากนั้น lim ln ((1+2/x)^2x) = 4 lim ln ((1+1/y)^y) = 4 * ln e =4 คำตอบ: 4.

ต้องมีฟังก์ชั่นบางอย่าง

ส่งข้อความ
ผู้ดูแลสามารถ
เฉพาะสมาชิกของพอร์ทัล
เข้าสู่ระบบพอร์ทัล »
การลงทะเบียน "

กฎของโลปิตาล: ทฤษฎีและตัวอย่างของการแก้ปัญหา

กฎของโลปิตาลและการเปิดเผยความไม่แน่นอน

การเปิดเผยความไม่แน่นอนของแบบฟอร์ม 0/0 หรือ ∞/∞ และความไม่แน่นอนอื่นๆ ที่เกิดขึ้นเมื่อคำนวณขีดจำกัดอัตราส่วนของฟังก์ชันขนาดเล็กหรืออนันต์สองฟังก์ชันจะง่ายขึ้นอย่างมากโดยใช้กฎของ L'Hopital (จริงๆ แล้วคือกฎสองข้อและข้อคิดเห็นเกี่ยวกับพวกเขา ).

แก่นแท้ กฎของโรงพยาบาล L'Hospital คือในกรณีที่การคำนวณลิมิตอัตราส่วนของฟังก์ชันขนาดเล็กหรือใหญ่อนันต์สองตัวทำให้เกิดความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞ ขีดจำกัดของอัตราส่วนของสองฟังก์ชันสามารถแทนที่ด้วยขีดจำกัดของ อัตราส่วนของอนุพันธ์ของพวกมันและด้วยเหตุนี้จึงสามารถหาผลลัพธ์ได้

มาดูการกำหนดกฎของโลปิตาลกัน

กฎของ L'Hopital สำหรับกรณีของขีดจำกัดของค่าขนาดเล็กอนันต์สองค่า. ถ้าทำหน้าที่ ฉ(x) และ g(x เอ เอและในย่านนี้ g‘(x เอเท่ากันและเท่ากับศูนย์

(),

แล้วลิมิตของอัตราส่วนของฟังก์ชันเหล่านี้จะเท่ากับขีดจำกัดของอัตราส่วนของอนุพันธ์

().

กฎของโลปิตาลสำหรับกรณีการจำกัดปริมาณมากเป็นอนันต์ 2 รายการ. ถ้าทำหน้าที่ ฉ(x) และ g(x) มีความแตกต่างกันในบางพื้นที่ใกล้เคียงของจุด เอยกเว้นจุดที่เป็นไปได้ เอและในย่านนี้ g‘(x)≠0 และถ้าและถ้าลิมิตของฟังก์ชันเหล่านี้เป็น x มีแนวโน้มที่ค่าของฟังก์ชันที่จุด เอเท่ากันและเท่ากับอนันต์

(),

กล่าวอีกนัยหนึ่ง สำหรับความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞ ลิมิตของอัตราส่วนของฟังก์ชันสองฟังก์ชันจะเท่ากับขีดจำกัดของอัตราส่วนของอนุพันธ์ ถ้าตัวหลังมีอยู่ (จำกัดหรืออนันต์)

หมายเหตุ.

1. กฎของ L'Hopital ยังมีผลบังคับใช้เมื่อฟังก์ชันต่างๆ ฉ(x) และ g(x) ไม่ได้กำหนดไว้ที่ x = เอ.

2. ถ้าเมื่อคำนวณขีดจำกัดอัตราส่วนของอนุพันธ์ของฟังก์ชัน ฉ(x) และ g(x) เรากลับมาพบกับความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞ ดังนั้นกฎของ L'Hopital ควรใช้ซ้ำๆ (อย่างน้อยสองครั้ง)

3. กฎของ L'Hopital ยังใช้ได้เมื่ออาร์กิวเมนต์ของฟังก์ชัน (x) มีแนวโน้มว่าจะไม่ เลขสุดท้าย เอและถึงอนันต์ ( x → ∞).

ความไม่แน่นอนของประเภทอื่นสามารถลดลงเป็นความไม่แน่นอนของประเภท 0/0 และ ∞/∞ ได้เช่นกัน

การเปิดเผยความไม่แน่นอนของประเภท "ศูนย์หารด้วยศูนย์" และ "อนันต์หารด้วยอนันต์"

ตัวอย่าง 1

x=2 นำไปสู่ความไม่แน่นอนของรูปแบบ 0/0 ดังนั้นอนุพันธ์ของแต่ละฟังก์ชันจึงได้

ในตัวเศษ คำนวณอนุพันธ์ของพหุนาม และในตัวส่วน อนุพันธ์ของเชิงซ้อน ฟังก์ชันลอการิทึม. ก่อนเครื่องหมายเท่ากับสุดท้าย ขีดจำกัดปกติถูกคำนวณ แทนที่ deuce แทน x

ตัวอย่าง 2คำนวณขีด จำกัด ของอัตราส่วนของสองฟังก์ชันโดยใช้กฎของ L'Hospital:

ตัวอย่างที่ 3คำนวณขีด จำกัด ของอัตราส่วนของสองฟังก์ชันโดยใช้กฎของ L'Hospital:

วิธีการแก้. ทดแทนใน ฟังก์ชันที่กำหนดค่า x=0 นำไปสู่ความไม่แน่นอนของรูปแบบ 0/0 ดังนั้นเราจึงคำนวณอนุพันธ์ของฟังก์ชันในตัวเศษและส่วนและรับ:

ตัวอย่างที่ 4คำนวณ

วิธีการแก้. การแทนที่ค่าของ x เท่ากับบวกอนันต์ลงในฟังก์ชันที่กำหนดจะทำให้เกิดความไม่แน่นอนของรูปแบบ ∞/∞ ดังนั้นเราจึงใช้กฎของโลปิตาล:

ความคิดเห็น มาต่อกันที่ตัวอย่างที่ต้องใช้กฎ L'Hopital สองครั้ง นั่นคือ มาถึงจุดจำกัดอัตราส่วนของอนุพันธ์อันดับสอง เนื่องจากขีดจำกัดของอัตราส่วนของอนุพันธ์อันดับ 1 คือความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞

ตัวอย่างที่ 5คำนวณขีด จำกัด ของอัตราส่วนของสองฟังก์ชันโดยใช้กฎของ L'Hospital:

ในที่นี้กฎของโรงพยาบาลใช้สองครั้ง เนื่องจากทั้งขีดจำกัดของอัตราส่วนของฟังก์ชันและขีดจำกัดของอัตราส่วนของอนุพันธ์ทำให้เกิดความไม่แน่นอนของรูปแบบ ∞/∞

ตัวอย่างที่ 6คำนวณ

ในที่นี้กฎของโรงพยาบาลใช้สองครั้ง เนื่องจากทั้งขีดจำกัดของอัตราส่วนของฟังก์ชันและขีดจำกัดของอัตราส่วนของอนุพันธ์ทำให้เกิดความไม่แน่นอนของรูปแบบ 0/0

ตัวอย่าง 7คำนวณ

ในที่นี้กฎของ L'Hopital ถูกนำมาใช้สองครั้ง เนื่องจากทั้งลิมิตของอัตราส่วนของฟังก์ชันและขีดจำกัดของอัตราส่วนของอนุพันธ์ทำให้เกิดความไม่แน่นอนของรูปแบบก่อน - ∞/∞ และจากนั้นจึงมีความไม่แน่นอนของรูปแบบ 0/0

ตัวอย่างที่ 8คำนวณ

กฎของโรงพยาบาล L'Hospital ใช้สองครั้ง เนื่องจากทั้งขีดจำกัดของอัตราส่วนของฟังก์ชันและขีดจำกัดของอัตราส่วนของอนุพันธ์ทำให้เกิดความไม่แน่นอนของรูปแบบ ∞/∞ และจากนั้นจึงมีความไม่แน่นอนของรูปแบบ 0/0

ใช้กฎของโลปิตาลด้วยตัวเองแล้วดูวิธีแก้ปัญหา

ตัวอย่างที่ 9คำนวณ

เบาะแส. ที่นี่คุณต้องเติมการเปลี่ยนแปลงของนิพจน์ภายใต้เครื่องหมายจำกัดมากกว่าปกติเล็กน้อย

ตัวอย่าง 10คำนวณ

.

เบาะแส. ที่นี่กฎของโลปิตาลจะต้องใช้สามครั้ง

การเปิดเผยความไม่แน่นอนของแบบฟอร์ม "ศูนย์คูณด้วยอนันต์"

ตัวอย่างที่ 11คำนวณ

(ในที่นี้เราได้เปลี่ยนความไม่แน่นอนของรูปแบบ 0∙∞ เป็นรูปแบบ ∞/∞ ตั้งแต่

แล้วใช้กฎของโลปิตาล)

ตัวอย่างที่ 12คำนวณ

.

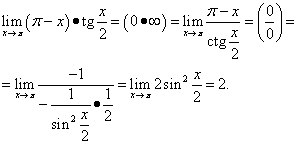
ตัวอย่างนี้ใช้เอกลักษณ์ตรีโกณมิติ

การเปิดเผยความไม่แน่นอนของประเภท "ศูนย์ต่อกำลังของศูนย์", "อนันต์ต่อกำลังของศูนย์" และ "หนึ่งต่อกำลังอนันต์"

ความไม่แน่นอนของแบบฟอร์ม หรือมักจะลดลงเป็นรูปแบบ 0/0 หรือ ∞/∞ โดยใช้ลอการิทึมของฟังก์ชันของแบบฟอร์ม

ในการคำนวณขีดจำกัดของนิพจน์ ควรใช้ เอกลักษณ์ลอการิทึมซึ่งเป็นกรณีพิเศษที่เป็นสมบัติของลอการิทึมด้วย .

การใช้เอกลักษณ์ลอการิทึมและคุณสมบัติความต่อเนื่องของฟังก์ชัน (เพื่อให้เกินเครื่องหมายขีด จำกัด ) ควรคำนวณขีด จำกัด ดังนี้:

แยกกัน ควรหาขีด จำกัด ของนิพจน์ในเลขชี้กำลังและ build อีในระดับที่พบ

ตัวอย่างที่ 13

.

.

ตัวอย่างที่ 14คำนวณโดยใช้กฎของโลปิตาล

.

.

ตัวอย่างที่ 15คำนวณโดยใช้กฎของโลปิตาล

คำนวณขีด จำกัด ของนิพจน์ในเลขชี้กำลัง

.

การเปิดเผยความไม่แน่นอนของรูปแบบ "อนันต์ลบอนันต์"

เหล่านี้เป็นกรณีที่การคำนวณขีด จำกัด ของความแตกต่างของฟังก์ชันนำไปสู่ความไม่แน่นอน "อนันต์ลบอนันต์": .

การคำนวณขีดจำกัดดังกล่าวตามกฎของโลปิตาลใน ปริทัศน์ดังนี้

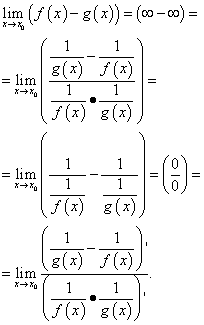
การเปลี่ยนแปลงเหล่านี้มักส่งผลให้ นิพจน์ที่ซับซ้อนดังนั้นจึงแนะนำให้ใช้การแปลงความแตกต่างของฟังก์ชันเป็นการลดเป็น ตัวส่วนร่วม, การคูณและหารด้วยจำนวนเดียวกัน, ใช้ อัตลักษณ์ตรีโกณมิติเป็นต้น

ตัวอย่างที่ 16คำนวณโดยใช้กฎของโลปิตาล

.

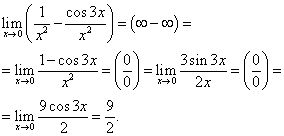
ตัวอย่างที่ 17คำนวณโดยใช้กฎของโลปิตาล

.

คำนวณขีดจำกัดโดยใช้กฎลอปิทัล

ความไม่แน่นอนยังไม่ต่อต้านการกลายเป็นหรือ:

กฎของโรงพยาบาล L'Hospital

เรายังคงพัฒนาหัวข้อนี้ต่อไป ซึ่ง Marquis Guillaume Francois de Lopital สมาชิกของ Paris Academy of Sciences ส่งมาให้เรา บทความนี้ได้รับการระบายสีที่ใช้งานได้จริงและในงานทั่วไปที่จำเป็น:

เพื่อไม่ให้หดตัว เราคำนวณขีดจำกัดของตัวบ่งชี้แยกกัน:

ปาปัวอีกคนยอมแพ้ก่อนออกสูตร ในกรณีนี้:

กฎของ L'Hopital เป็นวิธีที่ทรงพลังมากที่ช่วยให้คุณขจัดความไม่แน่นอนเหล่านี้ได้อย่างรวดเร็วและมีประสิทธิภาพ ไม่ใช่เรื่องบังเอิญที่มักพบในการรวบรวมปัญหา ในการทดสอบ การทดสอบ แสตมป์ที่มีเสถียรภาพ: "คำนวณขีด จำกัด โดยไม่ใช้กฎของโลปิตาล". อุทิศ ตัวหนาความต้องการเป็นไปได้ด้วย มีสติสัมปชัญญะมอบหมายและขีด จำกัด บทเรียนใด ๆ ขีดจำกัด ตัวอย่างโซลูชัน, ขีด จำกัด ที่โดดเด่น. จำกัดวิธีการแก้, ความเท่าเทียมกันที่โดดเด่นที่ซึ่งความไม่แน่นอนเกิดขึ้นจาก "ศูนย์ถึงศูนย์" หรือ "อนันต์ถึงอนันต์" แม้ว่างานจะได้รับการกำหนดไว้โดยสังเขป - "คำนวณขีด จำกัด" แต่ก็เข้าใจโดยปริยายว่าคุณจะใช้สิ่งที่คุณต้องการ แต่ไม่ใช่กฎของโรงพยาบาล L'Hospital

การเปลี่ยนแปลงยังคงดำเนินต่อไป ตอนนี้ความไม่แน่นอน "ศูนย์ถึงศูนย์" ได้ออกมาแล้ว โดยหลักการแล้ว คุณสามารถกำจัดโคไซน์โดยระบุว่ามันมีแนวโน้มที่จะเป็นหนึ่งเดียวกัน แต่กลยุทธ์ที่ชาญฉลาดคือการทำให้แน่ใจว่าไม่มีใครเข้าถึงจุดต่ำสุดของสิ่งใด ดังนั้นเราจึงใช้กฎ L'Hopital ทันทีตามเงื่อนไขของปัญหา:

งานที่คล้ายกันสำหรับโซลูชันอิสระ:

อย่างที่คุณเห็น ความแตกต่างของตัวเศษและตัวส่วนนำเราไปสู่คำตอบในครึ่งทาง: เราพบอนุพันธ์ง่าย ๆ สองตัว แทนที่ "สอง" ในนั้น และปรากฎว่าความไม่แน่นอนหายไปอย่างไร้ร่องรอย!

คำนวณขีดจำกัดของฟังก์ชันโดยใช้กฎของโลปิตาล

ในทางกลับกัน เพื่อนร่วมดื่มและสหายที่แปลกใหม่ก็ถูกดึงขึ้นสู่แสงสว่าง วิธีการแปลงนั้นเรียบง่ายและเป็นมาตรฐาน:

ตัวอย่างที่พิจารณาถูกทำลายและผ่าน ขีดจำกัดที่ยอดเยี่ยม กรณีคล้ายคลึงกันจะกล่าวถึงในตอนท้ายของบทความ ข้อจำกัดที่ซับซ้อน

ฉันจะจองทันทีว่ากฎจะได้รับในรูปแบบ "เชิงปฏิบัติ" ที่กระชับ และหากคุณต้องผ่านทฤษฎีนี้ ฉันแนะนำให้คุณเปิดตำราเรียนเพื่อการคำนวณที่เข้มงวดยิ่งขึ้น

6) บังคับ กฎข้อสุดท้ายข้อมูลไปยังพรมแดนที่ยอดเยี่ยมที่สอง

การเปิดเผยความไม่แน่นอนจะลดลงเหลือความไม่แน่นอนที่กล่าวถึงก่อนหน้านี้ ถ้า และ ที่ แล้วใช้การแปลง

อนันต์หรือศูนย์โดยศูนย์คือการประยุกต์ใช้กฎของโฮปิตาล: ขีด จำกัด ของอัตราส่วนสอง

ในกรณีของความไม่แน่นอนสามประการสุดท้าย จะต้องนำการแปลงไปใช้

5) มีความไม่แน่นอนของรูปแบบอนันต์ถึงอนันต์

ฟังก์ชันขนาดเล็กอนันต์หรือสองฟังก์ชันใหญ่อนันต์เท่ากับขีด จำกัด ของอัตราส่วนของอนุพันธ์

3) เมื่อพิจารณาถึงความไม่แน่นอน ให้ใช้กฎข้อที่แล้ว

การคำนวณขีดจำกัดตามกฎของโลปิตาล

วิธีที่มีประสิทธิภาพในการคำนวณขีดจำกัดของฟังก์ชันที่มีเอกพจน์ของประเภทอินฟินิตี้บน

วิธีการแก้. 1) โดยการแทนที่ เรากำหนดว่าเรามีความไม่แน่นอนของรูปแบบศูนย์คูณศูนย์ เพื่อกำจัด

อีกครั้งเราได้รับความไม่แน่นอนของแบบฟอร์มและนำกฎของโรงพยาบาลกลับมาใช้ใหม่

2) ในตัวอย่างก่อนหน้านี้ เรามีความไม่แน่นอน ตามกฎของโลปิตาล เราจะพบว่า

การใช้กฎของโลปิตาลแสดงให้เห็นถึงความเป็นไปได้ทั้งหมดในการเปิดเผยความไม่แน่นอน

ตัวเลขถูกเลือกในลักษณะที่ความเท่าเทียมกัน (1) เป็นที่พอใจและดังนั้น . ดังนั้น สำหรับฟังก์ชันบนช่วงเวลา

ในบริเวณใกล้เคียงของจุด x 0 นั่นคือ ใน (x 0 ,x) เงื่อนไขของทฤษฎีบท Cauchy เป็นที่พอใจสำหรับฟังก์ชัน f(x) และ g(x) ดังนั้นจึงมีจุด сО(x 0 , x) เช่นนั้น

กฎของโลปิตาล

อย่างไรก็ตาม สถานการณ์เป็นไปได้เมื่อฟังก์ชันจะมีปลายสุดที่จุด x 0 ในกรณีที่ไม่มีอนุพันธ์

ให้ฟังก์ชันหาอนุพันธ์ได้ n คูณในละแวกใกล้เคียงของจุด x 0 ลองหาพหุนามที่มีดีกรีไม่เกิน n-1 กัน จะได้ว่า

ให้ฟังก์ชัน f(x) และ g(x) มีความต่อเนื่องและหาอนุพันธ์ได้ในบางพื้นที่ใกล้เคียงของจุด x 0 ยกเว้นจุด x 0 เอง ยิ่งไปกว่านั้น อนุญาต, . จากนั้นหากมีขีดจำกัดของอัตราส่วนของอนุพันธ์ของฟังก์ชัน ก็มีขีดจำกัดของอัตราส่วนของฟังก์ชันเองและมีค่าเท่ากัน กล่าวคือ .

บทสรุป: ฟังก์ชันเลขชี้กำลัง(y=a n) เติบโตเร็วกว่ากฎกำลังเสมอ (y=x n)

ตัวอย่างการใช้สูตร Maclaurin เรากำหนดจำนวนพจน์ในการขยายฟังก์ชันในแง่ของ สูตรเพื่อคำนวณค่าด้วยความแม่นยำ 0.001 สำหรับ x ใดๆ จากช่วง [-1,1]

คำนิยาม:ฟังก์ชันนี้เรียกว่า ไม่ลดลง (ไม่เพิ่มขึ้น)ถึง (a;b) ถ้าสำหรับ x 1 ใด ๆ ที่โพสต์ในบทความที่เป็นประโยชน์

การหาลิมิตของฟังก์ชัน ณ จุดหนึ่งตามกฎของโลปิตาล

การหาขีดจำกัดของฟังก์ชันตามกฎของ L'Hopital เผยให้เห็นความไม่แน่นอนของรูปแบบ 0/0 และ ∞/∞

เครื่องคิดเลขด้านล่างหาขีดจำกัดของฟังก์ชันตามกฎของโรงพยาบาล (ผ่านอนุพันธ์ของตัวเศษและตัวส่วน) ดูคำอธิบายกฎด้านล่าง

ขีด จำกัด ของฟังก์ชัน ณ จุดหนึ่ง - กฎของโลปิตาล

การดำเนินการที่ถูกต้อง: + - / * ^ ค่าคงที่: pi ฟังก์ชั่น: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

กฎของโลปิตาล

หากตรงตามเงื่อนไขต่อไปนี้:

• ลิมิตของฟังก์ชัน f(x) และ g(x) มีค่าเท่ากันและเท่ากับศูนย์หรืออนันต์:
  หรือ;
• ฟังก์ชัน g(x) และ f(x) สามารถแยกความแตกต่างได้ในย่านที่มีการเจาะ a;
• อนุพันธ์ของฟังก์ชัน g(x) ไม่เท่ากับศูนย์ในย่านที่เจาะ a
• และมีข้อ จำกัด ในอัตราส่วนของอนุพันธ์ f(x) ต่ออนุพันธ์ g(x):

จากนั้นมีขีดจำกัดอัตราส่วนของฟังก์ชัน f(x) และ g(x):
,

และเท่ากับขีดจำกัดอัตราส่วนของอนุพันธ์ของฟังก์ชัน f(x) ต่ออนุพันธ์ของฟังก์ชัน g(x):

สูตรนี้อนุญาตให้ใช้ตัวเลข pi (pi) เลขชี้กำลัง (e) ตัวดำเนินการทางคณิตศาสตร์ต่อไปนี้

+ - ส่วนที่เพิ่มเข้าไป
— - การลบ
* - การคูณ
/ - แผนก
^ - การยกกำลัง

และคุณสมบัติดังต่อไปนี้:

sqrt - สแควร์รูท

ราก พี- องศาราก พีตัวอย่างเช่น root3(x) คือรูทคิวบ์

exp - e กำลังที่ระบุ

lb - ลอการิทึมฐาน 2

lg - ลอการิทึมฐาน 10

ln- ลอการิทึมธรรมชาติ(ขึ้นอยู่กับจ)

บันทึก พี- ลอการิทึมฐาน พีตัวอย่างเช่น log7(x) - ลอการิทึมฐาน 7

บาป - ไซน์

cos - โคไซน์

tg - แทนเจนต์

ctg - โคแทนเจนต์

วินาที - secant

cosec - cosecant

arcsin - arcsine

arccos - อาร์คโคไซน์

arctg - อาร์คแทนเจนต์

arcctg - อาร์คแทนเจนต์

arcsec - arcsecant

arccosec - arccosecant

versin - versinus

vercos - ครอบคลุม

ฮาเวอร์ซิน - ฮาเวอร์ซินัส

exsec - exsecant

excsc - excosecant

sh - ไฮเพอร์โบลิกไซน์

ch - ไฮเพอร์โบลิกโคไซน์

th - ไฮเพอร์โบลิกแทนเจนต์

cth - ไฮเพอร์โบลิกโคแทนเจนต์

sech - ไฮเปอร์โบลิกซีแคนต์

csch - ไฮเพอร์โบลิกโคซีแคนต์

เอบีเอส- ค่าสัมบูรณ์(โมดูล)

sgn - signum (เครื่องหมาย)

• เช่ารถ Gazelle หรือ Sable Van โดยไม่มีคนขับ Gazelle-Business คนขับ 1 คน + ผู้โดยสาร 2 คน ลำตัว : ยาว 3 ม. สูง 2 ม. บุษกา ปริมาตรของลูกบาศก์ 10.5. เครื่องยนต์: UMZ-4216 (เบนซิน), ยูโร-4, 106.8 […]
• รายละเอียดการชำระภาษีและเงินสมทบในปี 2560-2561 รายละเอียดการชำระภาษีในปี 2560-2561 เป็นส่วนหนึ่งของการชำระ กรอกคำสั่งชำระเงินให้ถูกต้อง […]
• ขั้นตอนการพิจารณาของสภาสหพันธ์ลูกบุญธรรม รัฐดูมา กฎหมายของรัฐบาลกลาง(มาตรา 103–110) บทความ 103. การยอมรับกฎหมายของรัฐบาลกลางเพื่อการพิจารณาโดย […]
• กฎหมายอาญา. ส่วนทั่วไป กฎแห่งกฎหมายอาญา กฎของกฎหมายอาญาคือกฎความประพฤติที่จัดตั้งขึ้นโดยรัฐที่ให้ผู้เข้าร่วม ประชาสัมพันธ์ […]
• ขนาดของบทลงโทษสำหรับความล่าช้าในการจำนองมี จำกัด ในวันที่ 24 กรกฎาคมกฎหมายจะมีผลบังคับใช้ที่จำกัดจำนวนเงินค่าปรับสำหรับการไม่ปฏิบัติตามหรือการปฏิบัติตามที่ไม่เหมาะสมของ […]
• การฆาตกรรมด้วยพฤติการณ์ที่รุนแรงขึ้น การลงโทษ ตามกฎหมายอาญาปัจจุบัน การฆาตกรรมธรรมดา (ตอนที่ 1 ของมาตรา 105 แห่งประมวลกฎหมายอาญาของสหพันธรัฐรัสเซีย) “มีโทษจำคุกสำหรับ […]

การเปิดเผยความไม่แน่นอนของแบบฟอร์ม 0/0 หรือ ∞/∞ และความไม่แน่นอนอื่นๆ ที่เกิดขึ้นในการคำนวณ ขีดจำกัดความสัมพันธ์ของหน้าที่เล็กหรือใหญ่สองอย่างนั้นง่ายมากด้วยความช่วยเหลือของกฎของโรงพยาบาล (อันที่จริงมีกฎและข้อสังเกตสองข้อเกี่ยวกับพวกเขา)

แก่นแท้ กฎของโรงพยาบาล L'Hospital คือในกรณีที่การคำนวณลิมิตอัตราส่วนของสองฟังก์ชันขนาดเล็กหรือใหญ่อนันต์ทำให้เกิดความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞ ขีดจำกัดของอัตราส่วนของสองฟังก์ชันสามารถแทนที่ด้วยขีดจำกัดของ อัตราส่วนของพวกเขา อนุพันธ์และได้ผลลัพธ์ที่แน่นอน

มาดูการกำหนดกฎของโลปิตาลกัน

กฎของ L'Hopital สำหรับกรณีของขีดจำกัดของค่าขนาดเล็กอนันต์สองค่า. ถ้าทำหน้าที่ ฉ(x) และ g(x เอเอและในย่านนี้ g"(x เอเท่ากันและเท่ากับศูนย์

().

กฎของโลปิตาลสำหรับกรณีการจำกัดปริมาณมากเป็นอนันต์ 2 รายการ. ถ้าทำหน้าที่ ฉ(x) และ g(x) มีความแตกต่างกันในบางพื้นที่ใกล้เคียงของจุด เอยกเว้นจุดที่เป็นไปได้ เอและในย่านนี้ g"(x)≠0 และถ้าและถ้าลิมิตของฟังก์ชันเหล่านี้เป็น x มีแนวโน้มที่ค่าของฟังก์ชันที่จุด เอเท่ากันและเท่ากับอนันต์

(),

แล้วลิมิตของอัตราส่วนของฟังก์ชันเหล่านี้จะเท่ากับขีดจำกัดของอัตราส่วนของอนุพันธ์

().

กล่าวอีกนัยหนึ่ง สำหรับความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞ ลิมิตของอัตราส่วนของฟังก์ชันสองฟังก์ชันจะเท่ากับขีดจำกัดของอัตราส่วนของอนุพันธ์ ถ้าตัวหลังมีอยู่ (จำกัดหรืออนันต์)

หมายเหตุ.

1. กฎของ L'Hopital ยังมีผลบังคับใช้เมื่อฟังก์ชันต่างๆ ฉ(x) และ g(x) ไม่ได้กำหนดไว้ที่ x = เอ.

2. ถ้าเมื่อคำนวณขีดจำกัดอัตราส่วนของอนุพันธ์ของฟังก์ชัน ฉ(x) และ g(x) เรากลับมาพบกับความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞ ดังนั้นกฎของ L'Hopital ควรใช้ซ้ำๆ (อย่างน้อยสองครั้ง)

3. กฎของ L'Hopital ยังใช้ได้เมื่ออาร์กิวเมนต์ของฟังก์ชัน (x) มีแนวโน้มเป็นจำนวนไม่จำกัด เอและถึงอนันต์ ( x → ∞).

ความไม่แน่นอนของประเภทอื่นสามารถลดลงเป็นความไม่แน่นอนของประเภท 0/0 และ ∞/∞ ได้เช่นกัน

การเปิดเผยความไม่แน่นอนของประเภท "ศูนย์หารด้วยศูนย์" และ "อนันต์หารด้วยอนันต์"

ตัวอย่าง 1

x=2 นำไปสู่ความไม่แน่นอนของรูปแบบ 0/0 ดังนั้นอนุพันธ์ของแต่ละฟังก์ชันจึงได้

ในตัวเศษ คำนวณอนุพันธ์ของพหุนามและในตัวส่วน - อนุพันธ์ของฟังก์ชันลอการิทึมเชิงซ้อน. ก่อนเครื่องหมายเท่ากับสุดท้าย ปกติ ขีดจำกัดแทน ดิวซ์ แทน x

ตัวอย่าง 2คำนวณขีด จำกัด ของอัตราส่วนของสองฟังก์ชันโดยใช้กฎของ L'Hospital:

วิธีการแก้. แทนที่ในฟังก์ชันค่าที่กำหนด x

ตัวอย่างที่ 3คำนวณขีด จำกัด ของอัตราส่วนของสองฟังก์ชันโดยใช้กฎของ L'Hospital:

วิธีการแก้. แทนที่ในฟังก์ชันค่าที่กำหนด x=0 นำไปสู่ความไม่แน่นอนของรูปแบบ 0/0 ดังนั้นเราจึงคำนวณอนุพันธ์ของฟังก์ชันในตัวเศษและส่วนและรับ:

ตัวอย่างที่ 4คำนวณ

วิธีการแก้. การแทนที่ค่าของ x เท่ากับบวกอนันต์ลงในฟังก์ชันที่กำหนดจะทำให้เกิดความไม่แน่นอนของรูปแบบ ∞/∞ ดังนั้นเราจึงใช้กฎของโลปิตาล:

ความคิดเห็น มาต่อกันที่ตัวอย่างที่ต้องใช้กฎ L'Hopital สองครั้ง นั่นคือ มาถึงจุดจำกัดอัตราส่วนของอนุพันธ์อันดับสอง เนื่องจากขีดจำกัดของอัตราส่วนของอนุพันธ์อันดับ 1 คือความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞/∞

ใช้กฎของโลปิตาลด้วยตัวเองแล้วดูวิธีแก้ปัญหา

การเปิดเผยความไม่แน่นอนของแบบฟอร์ม "ศูนย์คูณด้วยอนันต์"

ตัวอย่างที่ 12คำนวณ

.

วิธีการแก้. เราได้รับ

ตัวอย่างนี้ใช้เอกลักษณ์ตรีโกณมิติ

การเปิดเผยความไม่แน่นอนของประเภท "ศูนย์ต่อกำลังของศูนย์", "อนันต์ต่อกำลังของศูนย์" และ "หนึ่งต่อกำลังอนันต์"

ความไม่แน่นอนของแบบฟอร์ม หรือมักจะลดลงเป็นรูปแบบ 0/0 หรือ ∞/∞ โดยใช้ลอการิทึมของฟังก์ชันของแบบฟอร์ม

ในการคำนวณขีดจำกัดของนิพจน์ ควรใช้เอกลักษณ์ลอการิทึม ซึ่งเป็นกรณีพิเศษที่เป็นคุณสมบัติของลอการิทึม .

การใช้เอกลักษณ์ลอการิทึมและคุณสมบัติความต่อเนื่องของฟังก์ชัน (เพื่อให้เกินเครื่องหมายขีด จำกัด ) ควรคำนวณขีด จำกัด ดังนี้:

แยกกัน ควรหาขีด จำกัด ของนิพจน์ในเลขชี้กำลังและ build อีในระดับที่พบ

ตัวอย่างที่ 13

วิธีการแก้. เราได้รับ

.

.

ตัวอย่างที่ 14คำนวณโดยใช้กฎของโลปิตาล

วิธีการแก้. เราได้รับ

คำนวณขีด จำกัด ของนิพจน์ในเลขชี้กำลัง

.

.

ตัวอย่างที่ 15คำนวณโดยใช้กฎของโลปิตาล

นี้ เครื่องคำนวณทางคณิตศาสตร์ออนไลน์จะช่วยคุณได้หากจำเป็น คำนวณขีดจำกัดฟังก์ชัน. โปรแกรม ลิมิตโซลูชั่นไม่เพียงแต่ให้คำตอบของปัญหาเท่านั้น แต่ยังนำไปสู่ วิธีแก้ปัญหาโดยละเอียดพร้อมคำอธิบาย, เช่น. แสดงความคืบหน้าของการคำนวณขีดจำกัด

โปรแกรมนี้มีประโยชน์สำหรับนักเรียนมัธยมปลาย โรงเรียนการศึกษาทั่วไปในการเตรียมตัว ควบคุมงานและข้อสอบเมื่อทำการทดสอบความรู้ก่อนสอบผู้ปกครองต้องควบคุมการแก้ปัญหามากมายทางคณิตศาสตร์และพีชคณิต หรืออาจจะแพงเกินไปสำหรับคุณที่จะจ้างติวเตอร์หรือซื้อหนังสือเรียนเล่มใหม่? หรือคุณเพียงแค่ต้องการที่จะทำมันให้เสร็จโดยเร็วที่สุด? การบ้านคณิตศาสตร์หรือพีชคณิต? ในกรณีนี้ คุณสามารถใช้โปรแกรมของเราพร้อมวิธีแก้ไขปัญหาโดยละเอียดได้

ดังนั้นคุณสามารถดำเนินการ .ของคุณ การฝึกอบรมของตัวเองและ/หรืออบรม น้องชายหรือพี่น้องสตรีในขณะที่ระดับการศึกษาในสาขางานที่ได้รับการแก้ไขเพิ่มขึ้น

ป้อนนิพจน์ฟังก์ชัน

คำนวณขีดจำกัด

พบว่าไม่ได้โหลดสคริปต์บางตัวที่จำเป็นในการแก้ปัญหานี้ และโปรแกรมอาจไม่ทำงาน
คุณอาจเปิดใช้งาน AdBlock
ในกรณีนี้ ให้ปิดการใช้งานและรีเฟรชหน้า

คุณปิดการใช้งาน JavaScript ในเบราว์เซอร์ของคุณ
ต้องเปิดใช้งาน JavaScript เพื่อให้โซลูชันปรากฏขึ้น
นี่คือคำแนะนำเกี่ยวกับวิธีการเปิดใช้งาน JavaScript ในเบราว์เซอร์ของคุณ

เพราะ มีคนจำนวนมากที่ต้องการแก้ปัญหา คำขอของคุณอยู่ในคิว
หลังจากนั้นไม่กี่วินาที วิธีแก้ปัญหาจะปรากฏขึ้นด้านล่าง
กรุณารอ วินาที...

ถ้าคุณ สังเกตเห็นข้อผิดพลาดในการแก้ปัญหาจากนั้นคุณสามารถเขียนเกี่ยวกับเรื่องนี้ในแบบฟอร์มคำติชม
อย่าลืม ระบุว่างานใดคุณตัดสินใจอะไร เข้าไปในทุ่งนา.

เกม ปริศนา อีมูเลเตอร์ของเรา:

ทฤษฎีเล็กน้อย

ขีดจำกัดของฟังก์ชันที่ x-> x 0

ให้ฟังก์ชัน f(x) ถูกกำหนดในชุด X บางชุด และให้จุด \(x_0 \in X \) หรือ \(x_0 \notin X \)

ใช้ลำดับของจุดอื่นที่ไม่ใช่ x 0 จาก X:
x 1 , x 2 , x 3 , ..., xn , ... (1)
มาบรรจบกันเป็น x* ค่าฟังก์ชันที่จุดของลำดับนี้ยังก่อให้เกิดลำดับตัวเลข
f(x 1), f(x 2), f(x 3), ..., f(xn), ... (2)
และเราสามารถตั้งคำถามเกี่ยวกับการมีอยู่ของขีด จำกัด ของมันได้

คำนิยาม. จำนวน A เรียกว่าขีด จำกัด ของฟังก์ชัน f (x) ที่จุด x \u003d x 0 (หรือที่ x -> x 0) หากสำหรับลำดับใด ๆ (1) ของค่าของอาร์กิวเมนต์ x ที่บรรจบกันเป็น x 0 แตกต่างจาก x 0 ลำดับที่สอดคล้องกัน (2) ของฟังก์ชันค่ามาบรรจบกันเป็นตัวเลข A

$$ \lim_(x\to x_0)( f(x)) = A $$

ฟังก์ชัน f(x) สามารถมีขีดจำกัดได้เพียงจุดเดียวที่จุด x 0 สืบเนื่องมาจากลำดับ
(f(xn)) มีขีดจำกัดเดียวเท่านั้น

มีคำจำกัดความอื่นของลิมิตของฟังก์ชัน

คำนิยามจำนวน A เรียกว่าขีด จำกัด ของฟังก์ชัน f(x) ที่จุด x = x 0 ถ้าสำหรับตัวเลขใด ๆ \(\varepsilon > 0 \) มีตัวเลขอยู่ \(\delta > 0 \) เช่นนั้นสำหรับทั้งหมด \ (x \in X, \; x \neq x_0 \) ที่ตอบสนองความไม่เท่าเทียมกัน \(|x-x_0| การใช้สัญลักษณ์เชิงตรรกะ คำจำกัดความนี้สามารถเขียนได้เป็น
\(\forall \varepsilon > 0) (\exists \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| โปรดทราบว่าอสมการ \(x \neq x_0 , \; |x-x_0| คำจำกัดความแรกขึ้นอยู่กับแนวคิดของลิมิต ลำดับเลขซึ่งเป็นสาเหตุที่มักเรียกกันว่า "ภาษาลำดับ" คำจำกัดความที่สองเรียกว่าคำจำกัดความ "ภาษา \(\varepsilon - \delta \)"
คำจำกัดความทั้งสองนี้ของลิมิตของฟังก์ชันมีค่าเท่ากัน และคุณสามารถใช้คำจำกัดความใดก็ได้ แล้วแต่ว่าจะสะดวกกว่าสำหรับการแก้ปัญหาใดปัญหาหนึ่ง

โปรดทราบว่าคำจำกัดความของขีด จำกัด ของฟังก์ชัน "ในภาษาของลำดับ" เรียกอีกอย่างว่าคำจำกัดความของขีด จำกัด ของฟังก์ชันตาม Heine และคำจำกัดความของขีด จำกัด ของฟังก์ชัน "ในภาษา \(\varepsilon - \delta \)" เรียกอีกอย่างว่าคำจำกัดความของขีด จำกัด ของฟังก์ชันตาม Cauchy

จำกัดฟังก์ชันที่ x->x 0 - และที่ x->x 0 +

ต่อไปนี้ เราจะใช้แนวคิดของลิมิตด้านเดียวของฟังก์ชัน ซึ่งกำหนดไว้ดังนี้

คำนิยามจำนวน A เรียกว่าขีด จำกัด ขวา (ซ้าย) ของฟังก์ชัน f (x) ที่จุด x 0 หากลำดับใด ๆ (1) มาบรรจบกับ x 0 ซึ่งองค์ประกอบ x n มากกว่า (น้อยกว่า) x 0 ลำดับที่สอดคล้องกัน (2) บรรจบกับ A

ตามสัญลักษณ์เขียนดังนี้:
$$ \lim_(x \to x_0+) f(x) = A \; \left(\lim_(x \to x_0-) f(x) = A \right) $$

เราสามารถให้คำจำกัดความที่เทียบเท่ากับข้อจำกัดด้านเดียวของฟังก์ชัน "ในภาษา \(\varepsilon - \delta \)":

คำนิยามจำนวน A เรียกว่าขีด จำกัด ขวา (ซ้าย) ของฟังก์ชัน f(x) ที่จุด x 0 ถ้ามี \(\varepsilon > 0 \) ใด ๆ \(\delta > 0 \) เช่นนั้นสำหรับ x ทั้งหมดที่น่าพอใจ ความไม่เท่าเทียมกัน \(x_0 รายการสัญลักษณ์:

\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x, \; x_0

เราได้เริ่มจัดการกับข้อ จำกัด และแนวทางแก้ไขแล้ว มาไล่ตามร้อนกันต่อไปและจัดการกับข้อ จำกัด ตามกฎของโลปิตาล. นี้ กฎง่ายๆสามารถช่วยให้คุณหลุดพ้นจากกับดักที่ร้ายกาจและยากที่ครูชอบใช้ในตัวอย่างซอฟต์แวร์ควบคุม คณิตศาสตร์ชั้นสูงและการวิเคราะห์ทางคณิตศาสตร์ วิธีแก้ปัญหาตามกฎของ L'Hopital ทำได้ง่ายและรวดเร็ว สิ่งสำคัญคือต้องสามารถแยกแยะได้

L'Hopital's Rule: History and Definition

อันที่จริงนี่ไม่ใช่กฎของ L'Hopital แต่เป็นกฎ L'Hospital-Bernoulli. คิดค้นโดยนักคณิตศาสตร์ชาวสวิส Johann Bernoulliและภาษาฝรั่งเศส Guillaume Lopitalตีพิมพ์ครั้งแรกในตำราเล่มเล็กในสมัยอันรุ่งโรจน์ 1696 ปี. คุณลองนึกภาพว่าผู้คนต้องแก้ไขขีดจำกัดด้วยการเปิดเผยความไม่แน่นอนก่อนสิ่งนี้จะเกิดขึ้นได้อย่างไร พวกเราไม่.

ก่อนดำเนินการวิเคราะห์กฎ L'Hopital เราแนะนำให้อ่านบทความเบื้องต้นเกี่ยวกับและวิธีการแก้ไข บ่อยครั้งในงานมีถ้อยคำ: ค้นหาขีด จำกัด โดยไม่ต้องใช้กฎ L'Hopital คุณสามารถอ่านเกี่ยวกับเทคนิคต่างๆ ที่จะช่วยคุณได้ในบทความของเรา

หากคุณกำลังจัดการกับลิมิตของเศษส่วนของสองฟังก์ชัน ให้เตรียมพร้อม: อีกไม่นานคุณจะพบกับความไม่แน่นอนของรูปแบบ 0/0 หรืออินฟินิตี้/อินฟินิตี้ มันหมายความว่าอะไร? ในตัวเศษและตัวส่วน นิพจน์มักจะเป็นศูนย์หรืออนันต์ จะทำอย่างไรกับขีด จำกัด ดังกล่าวในแวบแรกนั้นไม่สามารถเข้าใจได้อย่างสมบูรณ์ อย่างไรก็ตาม หากคุณใช้กฎของโลปิตาลและคิดสักนิด ทุกอย่างก็เข้าที่

แต่มากำหนดกฎของโรงพยาบาล-เบอร์นูลลีกัน เพื่อให้แม่นยำที่สุด มันถูกแสดงโดยทฤษฎีบท กฎของโลปิตาล คำจำกัดความ:

ถ้าฟังก์ชันสองอย่างสามารถหาอนุพันธ์ได้ในย่านใกล้เคียงของจุด x=a หายไป ณ จุดนี้ และมีขีดจำกัดอัตราส่วนของอนุพันธ์ของฟังก์ชันเหล่านี้ ดังนั้นสำหรับ X ทะเยอทะยาน เอ มีการจำกัดอัตราส่วนของฟังก์ชันเอง ซึ่งเท่ากับขีดจำกัดอัตราส่วนของอนุพันธ์

มาเขียนสูตรกัน แล้วทุกอย่างจะง่ายขึ้นทันที กฎของโลปิตาล สูตร:

เนื่องจากเรามีความสนใจในด้านการปฏิบัติของปัญหา เราจะไม่นำเสนอข้อพิสูจน์ของทฤษฎีบทนี้ที่นี่ คุณจะต้องใช้คำพูดของเราหรือค้นหาในตำราแคลคูลัสใด ๆ และตรวจสอบให้แน่ใจว่าทฤษฎีบทนั้นถูกต้อง

อนึ่ง! สำหรับผู้อ่านของเราตอนนี้มีส่วนลด 10% สำหรับ

การเปิดเผยความไม่แน่นอนตามกฎของโลปิตาล

กฎของโรงพยาบาล L'Hospital ช่วยเปิดเผยความไม่แน่นอนอะไรบ้าง? ก่อนหน้านี้เราพูดถึงความไม่แน่นอนเป็นหลัก 0/0 . อย่างไรก็ตาม สิ่งนี้ยังห่างไกลจากความไม่แน่นอนเพียงอย่างเดียวที่สามารถพบได้ ความไม่แน่นอนประเภทอื่นๆ มีดังนี้

ลองพิจารณาการแปลงที่สามารถนำมาใช้เพื่อนำความไม่แน่นอนเหล่านี้มาสู่รูปแบบ 0/0 หรืออนันต์/อนันต์ หลังจากการเปลี่ยนแปลง จะสามารถใช้กฎ L'Hospital-Bernoulli และคลิกตัวอย่าง เช่น ถั่วได้

ความไม่แน่นอนของสายพันธุ์ อินฟินิตี้/อินฟินิตี้ ลดลงเป็นความไม่แน่นอนของรูปแบบ 0/0 การเปลี่ยนแปลงอย่างง่าย:

ให้มีผลคูณของสองฟังก์ชัน ฟังก์ชันแรกมีแนวโน้มเป็นศูนย์ และฟังก์ชันที่สองคืออนันต์ เราใช้การแปลงและผลคูณของศูนย์และอนันต์กลายเป็นความไม่แน่นอน 0/0 :

เพื่อหาขอบเขตด้วยความไม่แน่นอนของประเภท อินฟินิตี้ลบอินฟินิตี้ เราใช้การเปลี่ยนแปลงต่อไปนี้ซึ่งนำไปสู่ความไม่แน่นอน 0/0 :

ในการใช้กฎของโลปิตาล คุณต้องหาอนุพันธ์ได้ ด้านล่างเป็นตารางอนุพันธ์ ฟังก์ชั่นพื้นฐานซึ่งคุณสามารถใช้เมื่อแก้ตัวอย่าง รวมถึงกฎสำหรับการคำนวณอนุพันธ์ของฟังก์ชันที่ซับซ้อน:

ตอนนี้เรามาดูตัวอย่างกัน

ตัวอย่าง 1

ค้นหาขีด จำกัด ตามกฎของ L'Hospital:

ตัวอย่าง 2

คำนวณโดยใช้กฎของโลปิตาล:

จุดสำคัญ! หากมีขีดจำกัดของอนุพันธ์อันดับสองและอนุพันธ์ลำดับต่อมาของฟังก์ชันสำหรับ X ทะเยอทะยาน เอ ดังนั้นกฎของโลปิตาลจึงสามารถใช้ได้หลายครั้ง

มาหาขีดจำกัดกันเถอะ ( น – ตัวเลขธรรมชาติ). เมื่อต้องการทำเช่นนี้ ให้ใช้กฎของโรงพยาบาล L'Hospital น ครั้งหนึ่ง:

ขอให้โชคดีในการเรียนรู้ การวิเคราะห์ทางคณิตศาสตร์. และถ้าคุณต้องการหาขีด จำกัด โดยใช้กฎ L'Hopital ให้เขียนบทคัดย่อตามกฎ L'Hopital คำนวณราก สมการเชิงอนุพันธ์หรือแม้แต่คำนวณเทนเซอร์ความเฉื่อยของร่างกาย โปรดติดต่อผู้เขียนของเรา พวกเขายินดีที่จะช่วยคุณค้นหาความซับซ้อนของวิธีแก้ปัญหา