การแปลงฟูริเยร์โดยตรงช่วยให้คุณกำหนดได้ การแปลงฟูริเยร์

การแปลงฟูริเยร์เป็นตระกูลของวิธีการทางคณิตศาสตร์โดยพิจารณาจากการสลายตัวของฟังก์ชันต่อเนื่องดั้งเดิมของเวลาเป็นชุดของฟังก์ชันฮาร์มอนิกพื้นฐาน (ซึ่งเป็นฟังก์ชันไซน์) ที่มีความถี่ แอมพลิจูด และเฟสต่างกัน จะเห็นได้จากคำจำกัดความว่าแนวคิดหลักของการเปลี่ยนแปลงคือฟังก์ชันใด ๆ สามารถแสดงเป็นผลรวมของไซนัสที่ไม่มีที่สิ้นสุดซึ่งแต่ละอันจะมีลักษณะแอมพลิจูดความถี่และระยะเริ่มต้น

การแปลงฟูริเยร์เป็นผู้ก่อตั้งการวิเคราะห์สเปกตรัม การวิเคราะห์สเปกตรัมเป็นวิธีการประมวลผลสัญญาณที่ช่วยให้คุณกำหนดลักษณะเนื้อหาความถี่ของสัญญาณที่วัดได้ ขึ้นอยู่กับวิธีการแสดงสัญญาณ การแปลงฟูริเยร์ที่แตกต่างกันจะถูกใช้ การแปลงฟูริเยร์มีหลายประเภท:

– Continuous Fourier Transform (ในวรรณคดีอังกฤษ Continue Time Fourier Transform – CTFTหรือเรียกสั้นๆ ว่า FT);

– Discrete Fourier Transform (ในวรรณคดีอังกฤษ Discrete Fourier Transform – DFT);

– การแปลงฟูริเยร์อย่างรวดเร็ว (ในวรรณคดีอังกฤษ การแปลงฟูริเยร์อย่างรวดเร็ว – FFT).

การแปลงฟูริเยร์อย่างต่อเนื่อง

การแปลงฟูริเยร์เป็นเครื่องมือทางคณิตศาสตร์ที่ใช้ในสาขาวิทยาศาสตร์ต่างๆ ในบางกรณี สามารถใช้เป็นวิธีการแก้สมการที่ซับซ้อนซึ่งอธิบายกระบวนการไดนามิกที่เกิดขึ้นภายใต้อิทธิพลของพลังงานไฟฟ้า ความร้อน หรือพลังงานแสง ในกรณีอื่นๆ ช่วยให้คุณสามารถเน้นส่วนประกอบปกติในสัญญาณการสั่นที่ซับซ้อน เพื่อให้คุณสามารถตีความข้อสังเกตจากการทดลองในทางดาราศาสตร์ การแพทย์ และเคมีได้อย่างถูกต้อง การแปลงแบบต่อเนื่องเป็นการวางนัยทั่วไปของอนุกรมฟูริเยร์ โดยมีเงื่อนไขว่าคาบของฟังก์ชันขยายมีแนวโน้มเป็นอนันต์ ดังนั้น การแปลงฟูริเยร์แบบคลาสสิกจึงเกี่ยวข้องกับสเปกตรัมของสัญญาณที่ครอบคลุมช่วงการมีอยู่ของตัวแปรทั้งหมด

การเขียนการแปลงฟูริเยร์แบบต่อเนื่องมีหลายประเภท ซึ่งแตกต่างกันตามค่าสัมประสิทธิ์ที่อยู่หน้าอินทิกรัล (การเขียนสองรูปแบบ):

หรือ

โดยที่ และ เป็นภาพฟูริเยร์ของฟังก์ชันหรือสเปกตรัมความถี่ของฟังก์ชัน

- ความถี่วงกลม

ควรสังเกตว่าการบันทึกประเภทต่าง ๆ นั้นพบได้ในสาขาวิทยาศาสตร์และเทคโนโลยีต่างๆ ปัจจัยการทำให้เป็นมาตรฐานเป็นสิ่งจำเป็นสำหรับการปรับมาตราส่วนที่ถูกต้องของสัญญาณจากโดเมนความถี่ไปยังโดเมนเวลา ปัจจัยการทำให้เป็นมาตรฐานช่วยลดแอมพลิจูดของสัญญาณที่เอาต์พุตของการแปลงผกผันเพื่อให้ตรงกับแอมพลิจูดของสัญญาณดั้งเดิม ในวรรณคดีทางคณิตศาสตร์ การแปลงฟูริเยร์โดยตรงและแบบผกผันจะถูกคูณด้วยปัจจัย ในขณะที่ในฟิสิกส์ ส่วนใหญ่แล้ว ปัจจัยไม่ได้ถูกกำหนดไว้สำหรับการแปลงโดยตรง แต่ปัจจัยถูกกำหนดไว้สำหรับการกลับกัน หากเราคำนวณการแปลงฟูริเยร์โดยตรงของสัญญาณหนึ่งๆ ตามลำดับ จากนั้นจึงนำการแปลงฟูริเยร์ผกผัน ผลลัพธ์ของการแปลงฟูริเยร์ควรตรงกับสัญญาณดั้งเดิมอย่างสมบูรณ์

หากฟังก์ชันเป็นเลขคี่ในช่วงเวลา (−∞, +∞) การแปลงฟูริเยร์สามารถแสดงในรูปของฟังก์ชันไซน์ได้:

หากฟังก์ชันอยู่บนช่วง (−∞, +∞) การแปลงฟูริเยร์สามารถแสดงในรูปของฟังก์ชันโคไซน์ได้:

ดังนั้น การแปลงฟูริเยร์แบบต่อเนื่องช่วยให้เราสามารถแสดงฟังก์ชันที่ไม่ใช่คาบเป็นอินทิกรัลของฟังก์ชันที่แสดงค่าสัมประสิทธิ์ของอนุกรมฟูริเยร์สำหรับฟังก์ชันที่ไม่ใช่คาบแต่ละจุด

การแปลงฟูริเยร์สามารถย้อนกลับได้ กล่าวคือ หากภาพฟูริเยร์คำนวณจากฟังก์ชัน ฟังก์ชันดั้งเดิมก็สามารถกู้คืนจากอิมเมจฟูริเยร์ได้โดยไม่ซ้ำกัน การแปลงฟูริเยร์ผกผันเป็นที่เข้าใจกันว่าเป็นส่วนหนึ่งของรูปแบบ (การเขียนสองรูปแบบ):

หรือ

ภาพฟูริเยร์ของฟังก์ชันหรือสเปกตรัมความถี่ของฟังก์ชันอยู่ที่ไหน

- ความถี่วงกลม

หากฟังก์ชันเป็นเลขคี่ในช่วงเวลา (−∞, +∞) การแปลงฟูริเยร์ผกผันสามารถแสดงในรูปของฟังก์ชันไซน์ได้:

หากฟังก์ชันอยู่บนช่วง (−∞, +∞) การแปลงฟูริเยร์ผกผันสามารถแสดงในรูปของฟังก์ชันโคไซน์ได้:

ตัวอย่างเช่น พิจารณาฟังก์ชันต่อไปนี้ . กราฟของฟังก์ชันเลขชี้กำลังภายใต้การศึกษาแสดงไว้ด้านล่าง

เนื่องจากฟังก์ชันเป็นฟังก์ชันคู่ ดังนั้นการแปลงฟูริเยร์แบบต่อเนื่องจะถูกกำหนดดังนี้:

เป็นผลให้เราได้รับการเปลี่ยนแปลงในฟังก์ชันเลขชี้กำลังที่ศึกษาในช่วงเวลาความถี่ (ดูด้านล่าง)

การแปลงฟูริเยร์แบบต่อเนื่องมักใช้ในทฤษฎีเมื่อพิจารณาสัญญาณที่เปลี่ยนแปลงตามหน้าที่ที่กำหนด แต่ในทางปฏิบัติมักจะใช้การวัดที่เป็นข้อมูลที่ไม่ต่อเนื่อง ผลการวัดจะถูกบันทึกเป็นช่วงๆ ด้วยความถี่สุ่มตัวอย่าง เช่น 16000 Hz หรือ 22000 Hz อย่างไรก็ตาม ในกรณีทั่วไป การอ่านแบบไม่ต่อเนื่องอาจไปไม่เท่ากัน แต่สิ่งนี้จะทำให้เครื่องมือทางคณิตศาสตร์ของการวิเคราะห์ซับซ้อนขึ้น ดังนั้นจึงมักไม่ใช้ในทางปฏิบัติ

มีทฤษฎีบทที่สำคัญของ Kotelnikov (ในวรรณคดีต่างประเทศชื่อ "ทฤษฎีบท Nyquist-Shannon", "ทฤษฎีบทตัวอย่าง") ซึ่งระบุว่าสัญญาณคาบอะนาล็อกที่มีสเปกตรัม จำกัด (ความกว้าง จำกัด ) (0 ... fmax) สามารถเรียกคืนได้อย่างเฉพาะเจาะจงโดยไม่มีการบิดเบือนและความสูญเสียในการอ่านแบบไม่ต่อเนื่อง ซึ่งถ่ายด้วยความถี่ที่มากกว่าหรือเท่ากับสองเท่าของความถี่บนของสเปกตรัม - ความถี่สุ่มตัวอย่าง (fdisc >= 2*fmax) กล่าวอีกนัยหนึ่ง ที่อัตราการสุ่มตัวอย่าง 1,000 Hz สามารถกู้คืนสัญญาณที่มีความถี่สูงถึง 500 Hz จากสัญญาณคาบแอนะล็อกได้ ควรสังเกตว่าการแยกฟังก์ชันในเวลานำไปสู่การกำหนดช่วงเวลาของสเปกตรัมและการแยกความถี่ของสเปกตรัมในความถี่จะนำไปสู่การกำหนดช่วงเวลาของฟังก์ชัน

นี่เป็นหนึ่งในการแปลงฟูริเยร์ที่ใช้กันอย่างแพร่หลายในอัลกอริธึมการประมวลผลสัญญาณดิจิตอล

การแปลงฟูริเยร์แบบไม่ต่อเนื่องโดยตรงเชื่อมโยงฟังก์ชันเวลา ซึ่งกำหนดโดยจุดการวัด N ในช่วงเวลาที่กำหนด กับอีกฟังก์ชันหนึ่ง ซึ่งกำหนดไว้ในช่วงความถี่ ควรสังเกตว่ามีการระบุฟังก์ชันในช่วงเวลาโดยใช้ตัวอย่าง N และระบุฟังก์ชันบนโดเมนความถี่โดยใช้สเปกตรัม K-fold

k ˗ ดัชนีความถี่

ความถี่ของสัญญาณ kth ถูกกำหนดโดยนิพจน์

โดยที่ T คือช่วงเวลาที่รับข้อมูลเข้า

การแปลงแบบไม่ต่อเนื่องโดยตรงสามารถเขียนใหม่ในแง่ขององค์ประกอบจริงและองค์ประกอบจินตภาพ องค์ประกอบที่แท้จริงคืออาร์เรย์ที่มีค่าขององค์ประกอบโคไซน์และองค์ประกอบจินตภาพคืออาร์เรย์ที่มีค่าขององค์ประกอบไซน์

จากนิพจน์สุดท้าย จะเห็นได้ว่าการแปลงสลายสัญญาณเป็นองค์ประกอบไซน์ (ซึ่งเรียกว่าฮาร์โมนิก) ด้วยความถี่จากการแกว่งหนึ่งครั้งต่อคาบเป็น N การสั่นต่อคาบ

การแปลงฟูริเยร์แบบไม่ต่อเนื่องมีคุณสมบัติ เนื่องจากสามารถรับลำดับแบบไม่ต่อเนื่องได้จากผลรวมของฟังก์ชันที่มีองค์ประกอบต่างกันของสัญญาณฮาร์มอนิก กล่าวอีกนัยหนึ่ง ลำดับที่ไม่ต่อเนื่องจะถูกแบ่งออกเป็นตัวแปรฮาร์มอนิก - ไม่ชัดเจน ดังนั้น เมื่อขยายฟังก์ชันที่ไม่ต่อเนื่องโดยใช้การแปลงฟูริเยร์แบบไม่ต่อเนื่อง ส่วนประกอบความถี่สูงจะปรากฏในช่วงครึ่งหลังของสเปกตรัม ซึ่งไม่อยู่ในสัญญาณดั้งเดิม สเปกตรัมความถี่สูงนี้เป็นภาพสะท้อนของส่วนแรกของสเปกตรัม (ในแง่ของความถี่ เฟส และแอมพลิจูด) โดยปกติจะไม่พิจารณาช่วงครึ่งหลังของสเปกตรัม และแอมพลิจูดของสัญญาณในส่วนแรกของสเปกตรัมจะเพิ่มเป็นสองเท่า

ควรสังเกตว่าการขยายฟังก์ชันต่อเนื่องไม่ทำให้เกิดปรากฏการณ์สะท้อนกลับ เนื่องจากฟังก์ชันต่อเนื่องถูกแยกย่อยเป็นตัวแปรฮาร์มอนิกอย่างเฉพาะตัว

แอมพลิจูดของส่วนประกอบ DC คือค่าเฉลี่ยของฟังก์ชันในช่วงระยะเวลาที่เลือก และกำหนดได้ดังนี้:

แอมพลิจูดและเฟสของส่วนประกอบความถี่ของสัญญาณถูกกำหนดโดยความสัมพันธ์ต่อไปนี้:

ค่าแอมพลิจูดและเฟสที่ได้จะเรียกว่าสัญกรณ์ขั้ว เวกเตอร์สัญญาณที่ได้จะถูกกำหนดดังนี้:

พิจารณาอัลกอริธึมสำหรับการแปลงฟังก์ชันที่กำหนดอย่างไม่ต่อเนื่องในช่วงเวลาที่กำหนด (ในช่วงเวลาที่กำหนด) ด้วยจำนวนจุดเริ่มต้น

D spark การแปลงฟูริเยร์

ผลลัพธ์ของการแปลงทำให้เราได้รับค่าจริงและจินตภาพของฟังก์ชัน ซึ่งกำหนดไว้ที่ช่วงความถี่

การแปลงฟูริเยร์แบบแยกส่วนผกผันจะเชื่อมโยงฟังก์ชันความถี่ ซึ่งกำหนดโดยสเปกตรัม K-fold บนโดเมนความถี่ กับฟังก์ชันอื่น ซึ่งกำหนดไว้ในโดเมนเวลา

ยังไม่มีข้อความ ˗ จำนวนค่าสัญญาณที่วัดต่อช่วงเวลาตลอดจนความหลายหลากของสเปกตรัมความถี่

k ˗ ดัชนีความถี่

ดังที่ได้กล่าวไปแล้ว การแปลงฟูริเยร์แบบไม่ต่อเนื่องจะจับคู่จุด N ของสัญญาณแบบไม่ต่อเนื่องกับตัวอย่างสเปกตรัม N-complex ของสัญญาณ การคำนวณตัวอย่างสเปกตรัมต้องใช้การดำเนินการ N ของการคูณและการบวกที่ซับซ้อน ดังนั้น ความซับซ้อนในการคำนวณของอัลกอริธึมการแปลงฟูริเยร์แบบไม่ต่อเนื่องจึงเป็นกำลังสอง กล่าวอีกนัยหนึ่ง จำเป็นต้องมีการดำเนินการคูณและบวกที่ซับซ้อน

การแปลงฟูริเยร์ - การแปลงที่เปรียบเทียบฟังก์ชันของตัวแปรจริงบางตัว การดำเนินการนี้จะดำเนินการทุกครั้งที่เรารับรู้เสียงที่แตกต่างกัน หูทำ "การคำนวณ" อัตโนมัติซึ่งจิตสำนึกของเราสามารถดำเนินการได้หลังจากศึกษาส่วนที่เกี่ยวข้องของคณิตศาสตร์ที่สูงขึ้นเท่านั้น อวัยวะการได้ยินของมนุษย์สร้างการเปลี่ยนแปลงอันเป็นผลมาจากเสียง (การเคลื่อนที่แบบสั่นของอนุภาคตามเงื่อนไขในตัวกลางที่ยืดหยุ่นซึ่งแพร่กระจายในรูปคลื่นในตัวกลางที่เป็นของแข็ง ของเหลว หรือก๊าซ) ในรูปแบบของสเปกตรัมของค่าที่ต่อเนื่องกัน ​​ของระดับเสียงของโทนที่มีความสูงต่างกัน หลังจากนั้น สมองจะเปลี่ยนข้อมูลนี้เป็นเสียงที่ทุกคนคุ้นเคย

การแปลงฟูริเยร์ทางคณิตศาสตร์

การเปลี่ยนแปลงของคลื่นเสียงหรือกระบวนการแกว่งอื่นๆ (จากการแผ่รังสีแสงและกระแสน้ำในมหาสมุทรเป็นวัฏจักรของดาวฤกษ์หรือกิจกรรมของดวงอาทิตย์) สามารถทำได้โดยใช้วิธีการทางคณิตศาสตร์ ดังนั้น การใช้เทคนิคเหล่านี้ จึงเป็นไปได้ที่จะสลายฟังก์ชันโดยแสดงกระบวนการแกว่งเป็นชุดของส่วนประกอบไซน์ นั่นคือ เส้นโค้งคลื่นที่เปลี่ยนจากค่าต่ำสุดไปสูงสุด จากนั้นอีกครั้งเป็นค่าต่ำสุด เช่น คลื่นทะเล การแปลงฟูริเยร์ - การแปลงที่มีฟังก์ชันอธิบายเฟสหรือแอมพลิจูดของไซนัสอยด์แต่ละตัวที่สอดคล้องกับความถี่ที่แน่นอน เฟสเป็นจุดเริ่มต้นของเส้นโค้ง และแอมพลิจูดคือความสูง

การแปลงฟูริเยร์ (ตัวอย่างแสดงในรูปภาพ) เป็นเครื่องมือที่ทรงพลังมากซึ่งใช้ในด้านวิทยาศาสตร์ต่างๆ ในบางกรณี จะใช้เป็นวิธีแก้สมการที่ค่อนข้างซับซ้อนซึ่งอธิบายกระบวนการไดนามิกที่เกิดขึ้นภายใต้อิทธิพลของแสง ความร้อน หรือพลังงานไฟฟ้า ในกรณีอื่นๆ จะช่วยให้คุณกำหนดองค์ประกอบปกติในสัญญาณการสั่นที่ซับซ้อนได้ ซึ่งต้องขอบคุณการที่คุณจะสามารถตีความข้อสังเกตจากการทดลองต่างๆ ในด้านเคมี การแพทย์ และดาราศาสตร์ได้อย่างถูกต้อง

ประวัติอ้างอิง

บุคคลแรกที่ใช้วิธีนี้คือ Jean Baptiste Fourier นักคณิตศาสตร์ชาวฝรั่งเศส การเปลี่ยนแปลงซึ่งต่อมาตั้งชื่อตามเขา แต่เดิมใช้เพื่ออธิบายกลไกการนำความร้อน ฟูริเยร์ใช้เวลาทั้งชีวิตในวัยผู้ใหญ่ศึกษาคุณสมบัติของความร้อน เขามีส่วนร่วมอย่างมากในทฤษฎีทางคณิตศาสตร์ในการกำหนดรากของสมการพีชคณิต ฟูริเยร์เป็นศาสตราจารย์ด้านการวิเคราะห์ที่โรงเรียนโปลีเทคนิค เลขาธิการสถาบันอียิปต์วิทยา อยู่ในบริการของจักรพรรดิ ซึ่งเขาทำให้ตัวเองโดดเด่นในระหว่างการก่อสร้างถนนสู่ตูริน (ภายใต้การนำของเขา มีไข้มาลาเรียมากกว่า 80,000 ตารางกิโลเมตร หนองน้ำถูกระบายออก) อย่างไรก็ตาม กิจกรรมที่เข้มข้นทั้งหมดนี้ไม่ได้ป้องกันนักวิทยาศาสตร์จากการวิเคราะห์ทางคณิตศาสตร์ ในปี 1802 เขาได้รับสมการที่อธิบายการแพร่กระจายของความร้อนในของแข็ง ในปี ค.ศ. 1807 นักวิทยาศาสตร์ได้ค้นพบวิธีการแก้สมการนี้ซึ่งเรียกว่า "การแปลงฟูริเยร์"

การวิเคราะห์ค่าการนำความร้อน

นักวิทยาศาสตร์ใช้วิธีการทางคณิตศาสตร์เพื่ออธิบายกลไกการนำความร้อน ตัวอย่างที่สะดวกซึ่งไม่มีปัญหาในการคำนวณคือการแพร่กระจายของพลังงานความร้อนผ่านวงแหวนเหล็กซึ่งส่วนหนึ่งแช่อยู่ในกองไฟ เพื่อทำการทดลอง ฟูริเยร์ได้อุ่นส่วนหนึ่งของวงแหวนนี้ด้วยความร้อนแดงและฝังไว้ในทรายละเอียด หลังจากนั้นเขาทำการวัดอุณหภูมิที่ฝั่งตรงข้ามของมัน ในขั้นต้น การกระจายความร้อนไม่สม่ำเสมอ: ส่วนหนึ่งของวงแหวนเย็นและอีกส่วนหนึ่งร้อน และสามารถสังเกตการไล่ระดับอุณหภูมิที่คมชัดระหว่างโซนเหล่านี้ อย่างไรก็ตาม ในกระบวนการกระจายความร้อนทั่วทั้งพื้นผิวของโลหะ จะมีความสม่ำเสมอมากขึ้น ดังนั้นในไม่ช้า กระบวนการนี้ก็จะอยู่ในรูปของไซนัส ในตอนแรกกราฟจะเพิ่มขึ้นอย่างราบรื่นและลดลงอย่างราบรื่นตามกฎของการเปลี่ยนแปลงของฟังก์ชันโคไซน์หรือไซน์ คลื่นจะค่อยๆ ปรับระดับออก และด้วยเหตุนี้ อุณหภูมิจะเท่ากันทั่วทั้งพื้นผิวของวงแหวน

ผู้เขียนวิธีนี้แนะนำว่าการแจกแจงแบบผิดปกติช่วงแรกสามารถย่อยสลายเป็นชุดของไซนูซอยด์เบื้องต้นได้ แต่ละคนจะมีเฟสของตัวเอง (ตำแหน่งเริ่มต้น) และอุณหภูมิสูงสุดของตัวเอง นอกจากนี้ แต่ละองค์ประกอบดังกล่าวจะเปลี่ยนจากค่าต่ำสุดเป็นค่าสูงสุด และย้อนกลับเมื่อหมุนรอบวงแหวนเป็นจำนวนเต็มจำนวนครั้ง ส่วนประกอบที่มีคาบเดียวเรียกว่าฮาร์มอนิกพื้นฐาน และค่าที่มีคาบสองคาบขึ้นไปเรียกว่าที่สองเป็นต้น ดังนั้น ฟังก์ชันทางคณิตศาสตร์ที่อธิบายอุณหภูมิสูงสุด เฟส หรือตำแหน่งเรียกว่า การแปลงฟูริเยร์ของฟังก์ชันการกระจาย นักวิทยาศาสตร์ลดองค์ประกอบเดียวซึ่งยากต่อการอธิบายทางคณิตศาสตร์ ให้เป็นเครื่องมือที่ใช้งานง่าย - ชุดของโคไซน์และไซน์ ซึ่งร่วมกันให้การแจกแจงดั้งเดิม

สาระสำคัญของการวิเคราะห์

นักคณิตศาสตร์ได้ให้เหตุผลว่าการเพิ่มระยะเวลาขององค์ประกอบไซน์จะทำให้เกิดการสลายตัวอย่างรวดเร็วโดยใช้การวิเคราะห์นี้กับการเปลี่ยนแปลงของการแผ่กระจายความร้อนผ่านวัตถุแข็งที่มีรูปร่างเป็นวงแหวน เห็นได้ชัดเจนในฮาร์โมนิกพื้นฐานและฮาร์โมนิกที่สอง ในช่วงหลังอุณหภูมิถึงค่าสูงสุดและต่ำสุดสองครั้งในครั้งเดียวและในอดีตเพียงครั้งเดียวเท่านั้น ปรากฎว่าระยะทางที่ครอบคลุมโดยความร้อนในฮาร์มอนิกที่สองจะเป็นครึ่งหนึ่งของฮาร์มอนิกหลัก นอกจากนี้ การไล่ระดับสีในส่วนที่สองจะสูงชันเป็นสองเท่าของแบบแรก ดังนั้น เนื่องจากการไหลของความร้อนที่รุนแรงมากขึ้นเดินทางเป็นระยะทางสั้นเป็นสองเท่า ฮาร์มอนิกนี้จะสลายตัวเร็วกว่าฟังก์ชันพื้นฐานถึงสี่เท่าตามฟังก์ชันของเวลา ในอนาคต กระบวนการนี้จะเร็วยิ่งขึ้นไปอีก นักคณิตศาสตร์เชื่อว่าวิธีนี้ช่วยให้คุณสามารถคำนวณกระบวนการกระจายอุณหภูมิเริ่มต้นในช่วงเวลาหนึ่งได้

ท้าทายคนร่วมสมัย

อัลกอริธึมการแปลงฟูริเยร์กลายเป็นความท้าทายต่อพื้นฐานทางทฤษฎีของคณิตศาสตร์ในสมัยนั้น ในตอนต้นของศตวรรษที่สิบเก้า นักวิทยาศาสตร์ที่โดดเด่นที่สุด รวมทั้ง Lagrange, Laplace, Poisson, Legendre และ Biot ไม่ยอมรับคำกล่าวของเขาที่ว่าการกระจายอุณหภูมิเริ่มต้นถูกย่อยสลายเป็นส่วนประกอบในรูปแบบของฮาร์มอนิกพื้นฐานและความถี่ที่สูงขึ้น อย่างไรก็ตาม Academy of Sciences ไม่สามารถเพิกเฉยต่อผลลัพธ์ที่ได้รับจากนักคณิตศาสตร์และมอบรางวัลให้กับเขาสำหรับทฤษฎีกฎการนำความร้อนรวมถึงการเปรียบเทียบกับการทดลองทางกายภาพ ในแนวทางของฟูริเยร์ การคัดค้านหลักคือข้อเท็จจริงที่ว่าฟังก์ชันไม่ต่อเนื่องถูกแทนด้วยผลรวมของฟังก์ชันไซน์หลายหน้าที่ต่อเนื่องกัน ท้ายที่สุดพวกเขาอธิบายเส้นตรงและเส้นโค้งฉีกขาด ผู้ร่วมสมัยของนักวิทยาศาสตร์ไม่เคยพบกับสถานการณ์ที่คล้ายคลึงกัน เมื่ออธิบายฟังก์ชันที่ไม่ต่อเนื่องกันโดยใช้ฟังก์ชันต่อเนื่องร่วมกัน เช่น สมการกำลังสอง เส้นตรง ไซนัสหรือเลขชี้กำลัง ในกรณีที่นักคณิตศาสตร์พูดถูกในคำกล่าวของเขา ผลรวมของอนุกรมอนันต์ของฟังก์ชันตรีโกณมิติควรลดลงเป็นลำดับขั้นที่แน่นอน ในขณะนั้น ถ้อยแถลงดังกล่าวดูเหมือนไร้สาระ อย่างไรก็ตาม แม้จะมีข้อสงสัย นักวิจัยบางคน (เช่น Claude Navier, Sophie Germain) ได้ขยายขอบเขตของการวิจัยและนำสิ่งเหล่านี้ไปเหนือการวิเคราะห์การกระจายพลังงานความร้อน ในขณะเดียวกัน นักคณิตศาสตร์ยังคงวิตกกังวลกับคำถามที่ว่าผลรวมของฟังก์ชันไซน์หลายๆ อย่างสามารถลดลงเป็นการแสดงฟังก์ชันที่ไม่ต่อเนื่องได้อย่างแม่นยำหรือไม่

ประวัติศาสตร์ 200 ปี

ทฤษฎีนี้ได้พัฒนามาเป็นเวลากว่าสองศตวรรษ และในที่สุดมันก็ก่อตัวขึ้นในที่สุด ด้วยความช่วยเหลือ ฟังก์ชันเชิงพื้นที่หรือชั่วคราวจะแบ่งออกเป็นองค์ประกอบไซน์ซึ่งมีความถี่ เฟส และแอมพลิจูดของตัวเอง การแปลงนี้ได้มาโดยวิธีทางคณิตศาสตร์สองวิธีที่แตกต่างกัน ฟังก์ชันแรกจะใช้เมื่อฟังก์ชันเดิมเป็นแบบต่อเนื่อง และฟังก์ชันที่สองคือเมื่อแทนด้วยชุดของการเปลี่ยนแปลงแต่ละรายการที่ไม่ต่อเนื่อง หากนิพจน์ได้มาจากค่าที่กำหนดโดยช่วงที่ไม่ต่อเนื่องก็สามารถแบ่งออกเป็นนิพจน์ไซน์หลายตัวที่มีความถี่ไม่ต่อเนื่อง - จากต่ำสุดแล้วสองครั้งสามครั้งและอื่น ๆ ที่สูงกว่าค่าหลัก ผลรวมดังกล่าวเรียกว่าอนุกรมฟูริเยร์ ถ้านิพจน์เริ่มต้นได้รับค่าสำหรับจำนวนจริงแต่ละตัว ก็สามารถแยกย่อยออกเป็นหลายไซน์ของความถี่ที่เป็นไปได้ทั้งหมดได้ โดยทั่วไปเรียกว่าอินทิกรัลฟูริเยร์ และการแก้ปัญหาหมายถึงการแปลงอินทิกรัลของฟังก์ชัน ไม่ว่าจะได้การแปลงมาด้วยวิธีใด จะต้องระบุตัวเลขสองตัวสำหรับแต่ละความถี่: แอมพลิจูดและความถี่ ค่าเหล่านี้แสดงเป็นทฤษฎีเดียวของนิพจน์ของตัวแปรที่ซับซ้อนร่วมกับการแปลงฟูริเยร์ทำให้สามารถคำนวณในการออกแบบวงจรไฟฟ้าต่างๆ การวิเคราะห์การสั่นสะเทือนทางกล การศึกษา กลไกการแพร่กระจายคลื่นและอื่น ๆ

ฟูริเยร์แปลงร่างวันนี้

ทุกวันนี้ การศึกษากระบวนการนี้ส่วนใหญ่ลดลงไปจนถึงการค้นหาวิธีการที่มีประสิทธิภาพสำหรับการเปลี่ยนจากฟังก์ชันไปเป็นรูปแบบที่แปลงแล้ว และในทางกลับกัน โซลูชันนี้เรียกว่าการแปลงฟูริเยร์โดยตรงและแบบผกผัน มันหมายความว่าอะไร? ในการสร้างการแปลงฟูริเยร์โดยตรง เราสามารถใช้วิธีทางคณิตศาสตร์หรือวิธีวิเคราะห์ก็ได้ แม้ว่าจะมีปัญหาบางอย่างเกิดขึ้นเมื่อใช้พวกเขาในทางปฏิบัติ แต่ปริพันธ์ส่วนใหญ่ได้ถูกค้นพบและรวมอยู่ในหนังสืออ้างอิงทางคณิตศาสตร์แล้ว ด้วยความช่วยเหลือของวิธีการเชิงตัวเลข เราสามารถคำนวณนิพจน์ที่มีรูปแบบตามข้อมูลการทดลอง หรือฟังก์ชันที่อินทิกรัลไม่อยู่ในตารางและยากต่อการนำเสนอในรูปแบบการวิเคราะห์

ก่อนการถือกำเนิดของเทคโนโลยีคอมพิวเตอร์ การคำนวณการแปลงดังกล่าวเป็นเรื่องที่น่าเบื่อหน่าย พวกเขาต้องใช้การดำเนินการทางคณิตศาสตร์จำนวนมากด้วยตนเอง ซึ่งขึ้นอยู่กับจำนวนจุดที่อธิบายฟังก์ชันคลื่น เพื่ออำนวยความสะดวกในการคำนวณ วันนี้ มีโปรแกรมพิเศษที่ทำให้สามารถใช้โปรแกรมใหม่ได้ ดังนั้นในปี 1965 James Cooley และ John Tukey ได้สร้างซอฟต์แวร์ที่รู้จักกันในชื่อ "Fast Fourier Transform" ช่วยให้คุณประหยัดเวลาในการคำนวณโดยลดจำนวนการคูณในการวิเคราะห์เส้นโค้ง วิธีการแปลงฟูริเยร์แบบเร็วนั้นขึ้นอยู่กับการแบ่งเส้นโค้งออกเป็นค่าตัวอย่างที่สม่ำเสมอจำนวนมาก ดังนั้นจำนวนการคูณจะลดลงครึ่งหนึ่งด้วยจำนวนคะแนนที่ลดลงเช่นเดียวกัน

การใช้การแปลงฟูริเยร์

กระบวนการนี้ใช้ในสาขาวิทยาศาสตร์ต่างๆ: ในสาขาฟิสิกส์ การประมวลผลสัญญาณ combinatorics ทฤษฎีความน่าจะเป็น การเข้ารหัส สถิติ สมุทรศาสตร์ ทัศนศาสตร์ อะคูสติก เรขาคณิต และอื่นๆ ความเป็นไปได้ที่หลากหลายของแอปพลิเคชันจะขึ้นอยู่กับคุณลักษณะที่มีประโยชน์จำนวนหนึ่ง ซึ่งเรียกว่า "คุณสมบัติการแปลงฟูริเยร์" ลองพิจารณาพวกเขา

1. การแปลงของฟังก์ชันเป็นตัวดำเนินการเชิงเส้น และด้วยการทำให้เป็นมาตรฐานที่เหมาะสม จะรวมกันเป็นหนึ่งเดียว คุณสมบัตินี้เรียกว่าทฤษฎีบท Parseval หรือโดยทั่วไปแล้วทฤษฎีบท Plancherel หรือความเป็นคู่ของ Pontryagin

2. การเปลี่ยนแปลงสามารถย้อนกลับได้ นอกจากนี้ ผลลัพธ์ผกผันมีรูปแบบเกือบเหมือนกับในสารละลายโดยตรง

3. นิพจน์พื้นฐานไซน์เป็นฟังก์ชันที่แตกต่างกัน ซึ่งหมายความว่าการแสดงแทนดังกล่าวจะเปลี่ยนด้วยสัมประสิทธิ์คงที่เป็นพีชคณิตธรรมดา

4. ตามทฤษฎีบท "การบิด" กระบวนการนี้จะเปลี่ยนการดำเนินการที่ซับซ้อนเป็นการคูณเบื้องต้น

5. การแปลงฟูริเยร์แบบไม่ต่อเนื่องสามารถคำนวณได้อย่างรวดเร็วบนคอมพิวเตอร์โดยใช้วิธี "เร็ว"

ความหลากหลายของการแปลงฟูริเยร์

1. บ่อยที่สุด คำนี้ใช้เพื่อแสดงถึงการแปลงต่อเนื่องที่ให้นิพจน์ที่รวมกำลังสองเป็นกำลังสองเป็นผลรวมของนิพจน์เลขชี้กำลังที่ซับซ้อนด้วยความถี่เชิงมุมและแอมพลิจูดที่เฉพาะเจาะจง ประเภทนี้มีหลายรูปแบบ ซึ่งอาจแตกต่างกันในค่าสัมประสิทธิ์คงที่ วิธีการต่อเนื่องรวมถึงตารางการแปลงซึ่งสามารถพบได้ในหนังสืออ้างอิงทางคณิตศาสตร์ กรณีทั่วไปคือการแปลงเศษส่วน โดยกระบวนการที่กำหนดสามารถยกกำลังตามที่ต้องการได้

2. วิธีการต่อเนื่องเป็นลักษณะทั่วไปของเทคนิคเบื้องต้นของอนุกรมฟูริเยร์ ซึ่งกำหนดไว้สำหรับฟังก์ชันหรือนิพจน์ตามคาบต่างๆ ที่มีอยู่ในพื้นที่จำกัดและแสดงเป็นอนุกรมของไซนัส

3. การแปลงฟูริเยร์แบบไม่ต่อเนื่อง วิธีนี้ใช้ในเทคโนโลยีคอมพิวเตอร์สำหรับการคำนวณทางวิทยาศาสตร์และสำหรับการประมวลผลสัญญาณดิจิทัล ในการดำเนินการคำนวณประเภทนี้ จำเป็นต้องมีฟังก์ชันที่กำหนดจุดแต่ละจุด พื้นที่เป็นระยะหรือขอบเขตบนชุดที่ไม่ต่อเนื่องแทนที่จะเป็นอินทิกรัลฟูริเยร์แบบต่อเนื่อง การแปลงสัญญาณในกรณีนี้แสดงเป็นผลรวมของไซนัส ในเวลาเดียวกัน การใช้วิธีการ "เร็ว" ช่วยให้สามารถใช้วิธีแก้ปัญหาแบบแยกส่วนสำหรับปัญหาในทางปฏิบัติใดๆ

4. การแปลงฟูริเยร์แบบมีหน้าต่างเป็นรูปแบบทั่วไปของวิธีการแบบคลาสสิก ในทางตรงกันข้ามกับโซลูชันมาตรฐาน เมื่อใช้ ซึ่งครอบคลุมช่วงของการมีอยู่ของตัวแปรที่กำหนด เฉพาะการกระจายความถี่ท้องถิ่นที่น่าสนใจเป็นพิเศษ โดยมีเงื่อนไขว่าตัวแปรเดิม (เวลา) จะถูกรักษาไว้

5. การแปลงฟูริเยร์สองมิติ วิธีนี้ใช้เพื่อทำงานกับอาร์เรย์ข้อมูลสองมิติ ในกรณีนี้ การแปลงจะดำเนินการในทิศทางเดียวก่อน แล้วจึงในอีกทางหนึ่ง

บทสรุป

วันนี้วิธีการฟูริเยร์ได้รับการยึดมั่นอย่างแน่นหนาในด้านวิทยาศาสตร์ต่างๆ ตัวอย่างเช่น ในปี 1962 รูปทรงของเกลียวคู่ของ DNA ถูกค้นพบโดยใช้การวิเคราะห์แบบฟูริเยร์ร่วมกับรูปแบบหลังที่เน้นไปที่ผลึกของเส้นใย DNA ส่งผลให้ภาพที่ได้จากการเลี้ยวเบนของรังสีถูกบันทึกลงบนแผ่นฟิล์ม ภาพนี้ให้ข้อมูลเกี่ยวกับค่าของแอมพลิจูดเมื่อใช้การแปลงฟูริเยร์เป็นโครงสร้างผลึกที่กำหนด ข้อมูลเฟสได้มาจากการเปรียบเทียบแผนที่การเลี้ยวเบนของดีเอ็นเอกับแผนที่ที่ได้จากการวิเคราะห์โครงสร้างทางเคมีที่คล้ายคลึงกัน เป็นผลให้นักชีววิทยาได้ฟื้นฟูโครงสร้างผลึก - ฟังก์ชั่นดั้งเดิม

การแปลงฟูริเยร์มีบทบาทอย่างมากในการศึกษาอวกาศ ฟิสิกส์เซมิคอนดักเตอร์และพลาสมา อะคูสติกไมโครเวฟ สมุทรศาสตร์ เรดาร์ แผ่นดินไหววิทยา และการตรวจทางการแพทย์

การแปลงเหล่านี้เป็นฟังก์ชันเนื่องจากเปลี่ยนฟังก์ชันบางอย่างของตัวแปรเป็นฟังก์ชันที่ต่างไปจากเดิมอย่างสิ้นเชิงของตัวแปร และในทางกลับกัน

การแปลงฟูริเยร์มีรูปแบบดังนี้

สมการปริพันธ์ (4.34) เรียกว่าสมการตรง และสมการ (4.35) เรียกว่าการแปลงฟูริเยร์ผกผัน ชวเลขสำหรับสมการเหล่านี้

อินทิกรัลฟูริเยร์ (การแปลงฟูริเยร์โดยตรง) ช่วยให้คุณสามารถขยายฟังก์ชันที่ไม่ใช่คาบที่มีคุณสมบัติของการบูรณาการแบบสัมบูรณ์ภายในขอบเขตที่กำหนดเป็นอนุกรมฮาร์มอนิกที่ไม่มีที่สิ้นสุดที่สร้างสเปกตรัมความถี่ต่อเนื่องในช่วงตั้งแต่จนถึงช่วงความถี่ที่น้อยที่สุด ระหว่างฮาร์โมนิกที่อยู่ติดกัน (เช่น ในลิมิต

วิธีการแปลงฟูริเยร์ไม่เหมาะสมสำหรับเงื่อนไขเริ่มต้น (หรือขอบเขต) ที่ไม่เป็นศูนย์ วิธีนี้สามารถใช้ได้เฉพาะเมื่อฟังก์ชันที่ต้องการมีภาพฟูริเยร์ นั่นคือ สำหรับฟังก์ชันเวลาที่รวมเข้าด้วยกันอย่างสมบูรณ์ซึ่งตอบสนองความไม่เท่าเทียมกัน

ฟังก์ชันที่พบบ่อยที่สุดในทฤษฎีควบคุมคือฟังก์ชันหน่วยขั้นตอน (1.44) และผลิตภัณฑ์ของฟังก์ชันไซน์และฟังก์ชันหน่วย (1.51) การแปลงฟูริเยร์ใช้ไม่ได้กับฟังก์ชันเหล่านี้ เนื่องจากเงื่อนไข (4.38) ไม่เป็นที่พอใจ

ข้อบกพร่องเหล่านี้จำกัดการใช้วิธีการแปลงฟูริเยร์

ในการใช้อินทิกรัลฟูริเยร์ จำเป็นต้องเลือกฟังก์ชันที่ใกล้เคียงกับฟังก์ชันที่กำลังศึกษา เช่น ฟังก์ชันขั้นตอนที่ค่าจำกัด แต่ในขณะเดียวกันก็เป็นไปตามเงื่อนไข (4.38) ฟังก์ชันนี้หาได้จากการคูณ

ฟังก์ชันขั้นตอนโดยที่ c เป็นค่าบวกที่น้อยเพียงพอ ฟังก์ชันตัวช่วยที่ได้รับใหม่

ปล่อยให้ c มีค่าเป็นศูนย์และผ่านไปยังค่าลิมิต เราสามารถส่งผ่านจากฟังก์ชันเสริมไปยังฟังก์ชันหลักได้ นอกจากนี้ หากเราจำกัดตัวเองให้อยู่ในฟังก์ชันที่เท่ากับศูนย์เท่ากันสำหรับเงื่อนไข (4.38) จะถือเป็นคลาสขนาดใหญ่ ของฟังก์ชันและเราสามารถหาสเปกตรัมความถี่ของฟังก์ชันได้โดยใช้นิพจน์ (4.34) แต่เราแนะนำสัญกรณ์ใหม่ เนื่องจากตอนนี้ปริมาณนี้ยังขึ้นอยู่กับ c:

ใส่กับ find

สูตรนี้ตรงกับการแปลงลาปลาซโดยตรง (4.9)

ตามมาด้วยการแปลงฟูริเยร์ถือได้ว่าเป็นกรณีพิเศษของการแปลงลาปลาซ

วิธีการแปลงที่อธิบายข้างต้นช่วยให้เราสามารถสรุปได้ดังต่อไปนี้:

1) สมการจำนวนเต็มส่วนต่างถูกแทนที่ด้วยสมการพีชคณิต

2) การดำเนินการในการกำหนดค่าคงที่ของการรวมจะถูกตัดออกเนื่องจากเงื่อนไขเริ่มต้นถูกนำมาพิจารณาตั้งแต่เริ่มต้นเมื่อค้นหาภาพของค่าที่ต้องการ

3) การดำเนินการกำหนดรากของสมการลักษณะเฉพาะจะถูกรักษาไว้อย่างสมบูรณ์

วิธีที่สะดวกที่สุดในการแก้ปัญหาในทางปฏิบัติคือวิธีการแปลง Laplace ในรูปแบบดัดแปลงเล็กน้อย สามารถนำไปใช้กับการศึกษา ACS แบบไม่ต่อเนื่อง (ดูบทที่ 7)

พิจารณาการใช้วิธีการแปลงลาปลาซในการแก้สมการเชิงอนุพันธ์ของแบบฟอร์ม

เราแปลงสมการอนุพันธ์นี้โดยใช้การแปลงลาปลาซโดยตรง (4.9) และทฤษฎีบท 1 และ 2 ดังนั้นเราจึงได้สมการพีชคณิตที่เขียนขึ้นสำหรับรูปภาพ:

โดยที่เป็นผลรวมของเงื่อนไขทั้งหมดที่มีเงื่อนไขเริ่มต้น

จากนี้ไปจะเป็นภาพของฟังก์ชันที่ต้องการ

สำหรับเงื่อนไขเริ่มต้นเป็นศูนย์ นิพจน์ (4.41) และ (4.42) จะถูกทำให้ง่ายขึ้น:

เมื่อทราบรูปภาพของฟังก์ชันที่ต้องการแล้ว คุณจะค้นหาต้นฉบับได้ เช่น จากตารางรูปภาพ

หากภาพของค่าที่ต้องการเป็นเศษส่วนเชิงพีชคณิต พวกเขาพยายามเขียนเป็นผลรวมของเศษส่วนอย่างง่ายที่มีค่าสัมประสิทธิ์คงที่ การแปลงแบบย้อนกลับสำหรับเศษส่วนอย่างง่ายแต่ละส่วนสามารถหาได้จากตาราง และนิพจน์สุดท้ายของต้นฉบับจะแสดงเป็นผลรวมของค่าแต่ละค่าที่พบ คุณยังสามารถใช้ทฤษฎีบทการสลายตัวเพื่อกำหนดต้นฉบับได้

หากภาพ Laplace เป็นเศษส่วนเชิงพีชคณิตของรูปแบบ

พิจารณาคุณสมบัติพื้นฐานของการแปลงฟูริเยร์

ความเป็นลิเนียร์. พิจารณาหน้าที่และ
ด้วยสเปกตรัม
และ
:

(12)

จากนั้นสเปกตรัมของการรวมเชิงเส้นจะเป็น:

เวลาล่าช้า. เราคิดว่าสเปกตรัมเป็นที่รู้จัก
สัญญาณ

(14)

มาคำนวณสเปกตรัมของสัญญาณที่เปลี่ยนเวลากัน:
. แสดงถึงอาร์กิวเมนต์ฟังก์ชันของตัวแปรใหม่
, แล้ว
และ

เจอสัญญาณดีเลย์ไปซักพัก นำไปสู่การคูณของสเปกตรัมโดย
.

การเปลี่ยนแปลงมาตราส่วนเราคิดว่าสเปกตรัมเป็นที่รู้จัก
สัญญาณ
ผ่าน
แสดงสเปกตรัมของสัญญาณ
. เราแนะนำตัวแปรใหม่
, เราเปลี่ยนตัวแปรการรวม
.

(16)

คูณด้วย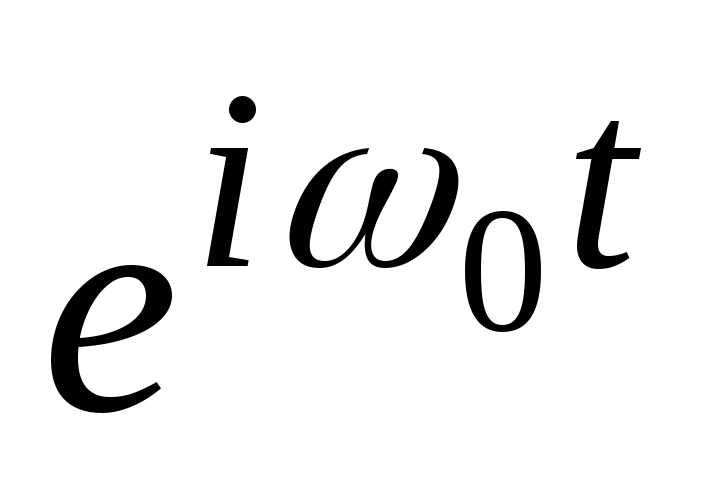
. ในกรณีก่อนหน้านี้ เราถือว่าสเปกตรัมเป็นที่รู้จัก
สัญญาณ
. จงหาสเปกตรัมของสัญญาณนี้ คูณด้วย
.

ดังนั้นการคูณสัญญาณด้วย
นำไปสู่การเปลี่ยนแปลงของสเปกตรัมโดย .

สเปกตรัมอนุพันธ์ในกรณีนี้ ประเด็นสำคัญคือการบูรณาการของฟังก์ชันอย่างสมบูรณ์ จากข้อเท็จจริงที่ว่าอินทิกรัลของโมดูลัสของฟังก์ชันต้องถูกจำกัดขอบเขต ตามนั้นที่อินฟินิตี้ฟังก์ชันจะต้องมีแนวโน้มเป็นศูนย์ อินทิกรัลของอนุพันธ์ของฟังก์ชันถูกนำมาเป็นส่วนๆ ผลลัพธ์ที่ไม่ใช่อินทิกรัลที่ได้จะเท่ากับศูนย์ เนื่องจากฟังก์ชันมีแนวโน้มที่จะเป็นศูนย์ที่อนันต์

(18)

สเปกตรัมของอินทิกรัลมาหาสเปกตรัมของสัญญาณกัน
. และเราจะถือว่า
นั่นคือสัญญาณไม่มีองค์ประกอบคงที่ ข้อกำหนดนี้จำเป็นเพื่อให้เงื่อนไขภายนอกอินทิกรัลเท่ากับศูนย์เมื่ออินทิกรัลถูกนำโดยส่วนต่างๆ

(19)

ทฤษฎีบทการบิดเป็นที่ทราบกันดีว่า
และ
ฟังก์ชั่นสเปกตรัม
และ
ตามลำดับ จำเป็นต้องแสดงสเปกตรัมการบิดงอ
ผ่าน
และ
. ในการทำเช่นนี้ ในอินทิกรัลฟูริเยร์ของการบิด ฟังก์ชันใดฟังก์ชันหนึ่งจะถูกแทนที่ด้วยตัวแปร
, จากนั้นเลขชี้กำลังจะถูกแทนที่
. ผลคูณของอินทิกรัลฟูริเยร์สองตัวจะเท่ากับผลคูณของอินทิกรัลฟูริเยร์สองตัว

(20)

การแปลงฟูริเยร์ของการบิดของสัญญาณสองสัญญาณให้ผลคูณของสเปกตรัมของสัญญาณเหล่านี้

การผลิตสัญญาณเป็นที่ทราบกันดีว่า
และ
เป็นสเปกตรัมของฟังก์ชัน
และ
ตามลำดับ จำเป็นต้องแสดงสเปกตรัมของผลิตภัณฑ์
ผ่านสเปกตรัม
และ
. ให้เราแทนอินทิกรัลฟูริเยร์แทนหนึ่งในสัญญาณ ตัวอย่างเช่น
นิพจน์ในแง่ของการแปลงฟูเรียร์ผกผันแล้วเปลี่ยนลำดับของการบูรณาการ

(21)

สเปกตรัมของผลิตภัณฑ์ของสัญญาณคือการบิดของสเปกตรัมของสัญญาณเหล่านี้

สเปกตรัมสัญญาณไม่ต่อเนื่อง

ควรให้ความสนใจเป็นพิเศษกับสัญญาณที่ไม่ต่อเนื่อง เนื่องจากสัญญาณดังกล่าวใช้ในการประมวลผลแบบดิจิทัล สัญญาณที่ไม่ต่อเนื่องซึ่งแตกต่างจากสัญญาณต่อเนื่องคือลำดับของตัวเลขที่สอดคล้องกับค่าของสัญญาณต่อเนื่องในบางจุดของเวลา สัญญาณที่ไม่ต่อเนื่องแบบมีเงื่อนไขถือได้ว่าเป็นสัญญาณต่อเนื่อง ซึ่งในบางครั้งจะใช้ค่าบางค่า และในบางครั้งจะเท่ากับศูนย์ เช่น ไม่ต่อเนื่อง
สามารถให้สัญญาณเป็นผลคูณของสัญญาณต่อเนื่อง
ตามลำดับของพัลส์สี่เหลี่ยมซ้ำเป็นระยะ
- จังหวะเวลา (รูปที่ 1)

ข้าว. 1. การแยกสัญญาณ

(22)

พัลส์สี่เหลี่ยมมีระยะเวลา , ระยะเวลาซ้ำ :

(23)

แอมพลิจูดของพัลส์ถูกเลือกเพื่อให้อินทิกรัลของพัลส์ตลอดคาบมีค่าเท่ากับ . ในกรณีนี้ พัลส์นาฬิกาจะไม่มีมิติ เราขยายลำดับของแรงกระตุ้นดังกล่าวเป็นอนุกรมตรีโกณมิติ:

(24)

เพื่อรับการอ่านสัญญาณทันที
จำเป็นต้องกำหนดระยะเวลาของพัลส์ให้เป็นศูนย์:
. เราเรียกว่าสัญญาณนาฬิกาในอุดมคติ ในกรณีนี้สัมประสิทธิ์การขยายตัว
ในอนุกรมฟูริเยร์ทั้งหมดจะเท่ากับ 1

(25)

รูปแบบเดียวกันนี้มีการขยายตัวในอนุกรมฟูริเยร์ของฟังก์ชัน:

(26)

สัมประสิทธิ์การขยายตัวเป็นอนุกรมตรีโกณมิติของสัญญาณนาฬิกา
:

(27)

จากนั้นสัญญาณที่ไม่ต่อเนื่องจะมีลักษณะดังนี้:

เมื่อคำนวณการแปลงฟูริเยร์ของสัญญาณแบบไม่ต่อเนื่อง เราจะสลับการดำเนินการของการรวมและการรวมกัน จากนั้นใช้คุณสมบัติ δ - ฟังก์ชั่น:

สเปกตรัมของสัญญาณไม่ต่อเนื่องเป็นฟังก์ชันคาบ พิจารณาเลขชี้กำลังในเทอมโรงแรม
เป็นหน้าที่ของความถี่ ช่วงเวลาการทำซ้ำคือ . ระยะเวลาการทำซ้ำที่ยาวที่สุดสำหรับเงื่อนไขที่มีตัวเลข
และนี่จะเป็นช่วงการทำซ้ำของสเปกตรัมทั้งหมด นั่นคือ สเปกตรัมของสัญญาณไม่ต่อเนื่องมีระยะเวลาการทำซ้ำเท่ากับความถี่ของการหาปริมาณ
.

มาโชว์กันอีกแล้ว
. เนื่องจากข้อเท็จจริงที่ว่า
เป็นผลผลิตของฟังก์ชัน
และ
, สเปกตรัมของสัญญาณไม่ต่อเนื่อง
คำนวณเป็นการบิดของสเปกตรัมของสัญญาณต่อเนื่อง
และสเปกตรัมของสัญญาณนาฬิกา
.

(30)

คำนวณ
ใช้ (25) เพราะ
ฟังก์ชั่นเป็นระยะสเปกตรัมของมันคือไม่ต่อเนื่อง

ดังนั้นการโน้มน้าวใจ (30)

จากนิพจน์ (32) ว่าสเปกตรัมของสัญญาณไม่ต่อเนื่องเป็นฟังก์ชันที่ทำซ้ำเป็นระยะ
.

ความจริงที่ว่าการเปลี่ยนแปลงเชิงคุณภาพเกิดขึ้นในสเปกตรัมของสัญญาณอันเป็นผลมาจากการสุ่มตัวอย่างแสดงให้เห็นว่าสัญญาณดั้งเดิมสามารถบิดเบือนได้เนื่องจากถูกกำหนดโดยสเปกตรัมอย่างสมบูรณ์ อย่างไรก็ตามในทางกลับกันการทำซ้ำเป็นระยะของสเปกตรัมเดียวกันในตัวเองไม่ได้แนะนำสิ่งใหม่ ๆ ในสเปกตรัมดังนั้นภายใต้เงื่อนไขบางประการการรู้ค่าสัญญาณในแต่ละจุดของเวลา คุณสามารถหาค่าของสัญญาณนี้ได้ ที่จุดอื่นใดในเวลา กล่าวคือ รับสัญญาณต่อเนื่องดั้งเดิม นี่คือความหมายของทฤษฎีบท Kotelnikov ซึ่งกำหนดเงื่อนไขในการเลือกความถี่ของการหาปริมาณตามความถี่สูงสุดในสเปกตรัมสัญญาณ

หากเงื่อนไขนี้ถูกละเมิด หลังจากการแปลงสัญญาณเป็นดิจิทัล สเปกตรัมที่ทำซ้ำเป็นระยะจะถูกซ้อนทับ (รูปที่ 2) สเปกตรัมที่เกิดจากโอเวอร์เลย์จะสอดคล้องกับสัญญาณอื่น

ข้าว. 2. สเปกตรัมคาบเกี่ยวกัน

ชุดนี้ยังสามารถเขียนเป็น:

(2),
โดยที่ แอมพลิจูดเชิงซ้อนที่ k

ความสัมพันธ์ระหว่างสัมประสิทธิ์ (1) และ (3) แสดงโดยสูตรต่อไปนี้:

โปรดทราบว่าการแสดงชุดฟูริเยร์ทั้งสามนี้เทียบเท่ากันโดยสิ้นเชิง บางครั้ง เมื่อทำงานกับอนุกรมฟูริเยร์ จะสะดวกกว่าที่จะใช้เลขชี้กำลังของอาร์กิวเมนต์จินตภาพแทนไซน์และโคไซน์ นั่นคือ การใช้การแปลงฟูริเยร์ในรูปแบบที่ซับซ้อน แต่สะดวกสำหรับเราที่จะใช้สูตร (1) โดยที่อนุกรมฟูริเยร์แสดงเป็นผลรวมของคลื่นโคไซน์ที่มีแอมพลิจูดและเฟสที่สอดคล้องกัน ไม่ว่าในกรณีใด มันไม่ถูกต้องที่จะบอกว่าผลลัพธ์ของการแปลงฟูริเยร์ของสัญญาณจริงจะเป็นแอมพลิจูดที่ซับซ้อนของฮาร์โมนิก ตามที่วิกิกล่าวไว้อย่างถูกต้อง "การแปลงฟูริเยร์ (?) เป็นการดำเนินการที่จับคู่ฟังก์ชันหนึ่งของตัวแปรจริงกับฟังก์ชันอื่น รวมทั้งของตัวแปรจริงด้วย"

ทั้งหมด:
พื้นฐานทางคณิตศาสตร์ของการวิเคราะห์สเปกตรัมของสัญญาณคือการแปลงฟูริเยร์

การแปลงฟูริเยร์ช่วยให้เราสามารถแสดงฟังก์ชันต่อเนื่อง f(x) (สัญญาณ) ที่กำหนดในส่วน (0, T) เป็นผลรวมของจำนวนอนันต์ (อนุกรมอนันต์) ของฟังก์ชันตรีโกณมิติ (ไซน์และ/หรือโคไซน์) ที่มีแอมพลิจูดที่แน่นอน และเฟส พิจารณาในส่วน (0, T) ด้วย ซีรีส์ดังกล่าวเรียกว่าอนุกรมฟูริเยร์

เราสังเกตบางประเด็นเพิ่มเติม ความเข้าใจซึ่งจำเป็นสำหรับการประยุกต์ใช้การแปลงฟูริเยร์เป็นการวิเคราะห์สัญญาณที่ถูกต้อง หากเราพิจารณาอนุกรมฟูริเยร์ (ผลรวมของไซนูซอยด์) บนแกน X ทั้งหมด เราจะเห็นว่านอกเซกเมนต์ (0, T) ฟังก์ชันที่แสดงโดยอนุกรมฟูริเยร์จะทำซ้ำฟังก์ชันของเราเป็นระยะ

ตัวอย่างเช่น ในกราฟในรูปที่ 7 ฟังก์ชันดั้งเดิมถูกกำหนดในส่วน (-T \ 2, + T \ 2) และอนุกรมฟูริเยร์แสดงถึงฟังก์ชันคาบที่กำหนดไว้บนแกน x ทั้งหมด

เนื่องจากไซนัสเป็นฟังก์ชันคาบตามลำดับ และผลรวมของไซนูซอยด์จะเป็นฟังก์ชันคาบ

fig.7 การแทนฟังก์ชันดั้งเดิมที่ไม่เป็นคาบโดยอนุกรมฟูริเยร์

ทางนี้:

ฟังก์ชันเดิมของเราเป็นแบบต่อเนื่อง ไม่มีคาบ โดยกำหนดช่วงบางช่วงของความยาว T
สเปกตรัมของฟังก์ชันนี้เป็นแบบไม่ต่อเนื่อง กล่าวคือ มันถูกนำเสนอเป็นชุดส่วนประกอบฮาร์มอนิกที่ไม่มีที่สิ้นสุด - ซีรีส์ฟูริเยร์
อันที่จริง ฟังก์ชันคาบบางอย่างถูกกำหนดโดยอนุกรมฟูริเยร์ ซึ่งตรงกับฟังก์ชันของเราในเซ็กเมนต์ (0, T) แต่ความเป็นคาบนี้ไม่จำเป็นสำหรับเรา

คาบของส่วนประกอบฮาร์มอนิกเป็นผลคูณของเซ็กเมนต์ (0, T) ซึ่งกำหนดฟังก์ชันดั้งเดิม f(x) กล่าวอีกนัยหนึ่ง ช่วงเวลาฮาร์มอนิกเป็นค่าทวีคูณของระยะเวลาของการวัดสัญญาณ ตัวอย่างเช่น คาบของฮาร์มอนิกแรกของอนุกรมฟูริเยร์เท่ากับช่วงเวลา T ซึ่งกำหนดฟังก์ชัน f(x) คาบของฮาร์มอนิกที่สองของอนุกรมฟูริเยร์เท่ากับช่วงเวลา T/2 และอื่นๆ (ดูรูปที่ 8)

fig.8 คาบ (ความถี่) ของส่วนประกอบฮาร์มอนิกของอนุกรมฟูริเยร์ (ที่นี่ T = 2?)

ดังนั้น ความถี่ของส่วนประกอบฮาร์มอนิกจึงเป็นทวีคูณของ 1/T นั่นคือความถี่ของส่วนประกอบฮาร์มอนิก Fk เท่ากับ Fk= k\T โดยที่ k มีตั้งแต่ 0 ถึง? ตัวอย่างเช่น k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (ที่ความถี่ศูนย์ - ส่วนประกอบคงที่)

ให้ฟังก์ชันเดิมของเราเป็นสัญญาณที่บันทึกไว้เป็นเวลา T=1 วินาที จากนั้นระยะเวลาของฮาร์มอนิกแรกจะเท่ากับระยะเวลาของสัญญาณของเรา T1=T=1 วินาทีและความถี่ของฮาร์มอนิกคือ 1 Hz ระยะเวลาของฮาร์โมนิกที่สองจะเท่ากับระยะเวลาของสัญญาณหารด้วย 2 (T2=T/2=0.5 วินาที) และความถี่คือ 2 Hz สำหรับฮาร์โมนิกที่สาม T3=T/3 วินาที และความถี่ 3 Hz และอื่นๆ.

ขั้นตอนระหว่างฮาร์โมนิกในกรณีนี้คือ 1 Hz

ดังนั้น สัญญาณที่มีระยะเวลา 1 วินาทีสามารถแบ่งออกเป็นส่วนประกอบฮาร์มอนิก (เพื่อให้ได้สเปกตรัม) ด้วยความละเอียดความถี่ 1 Hz
หากต้องการเพิ่มความละเอียด 2 เท่าเป็น 0.5 Hz จำเป็นต้องเพิ่มระยะเวลาในการวัด 2 เท่า - สูงสุด 2 วินาที สัญญาณที่มีระยะเวลา 10 วินาทีสามารถแบ่งออกเป็นส่วนประกอบฮาร์มอนิก (เพื่อให้ได้สเปกตรัม) ด้วยความละเอียดความถี่ 0.1 Hz ไม่มีวิธีอื่นในการเพิ่มความละเอียดความถี่

มีวิธีเพิ่มระยะเวลาของสัญญาณปลอมโดยการเพิ่มศูนย์ลงในอาร์เรย์ของตัวอย่าง แต่ไม่เพิ่มความละเอียดความถี่จริง

3. สัญญาณไม่ต่อเนื่องและการแปลงฟูริเยร์แบบไม่ต่อเนื่อง

ด้วยการพัฒนาเทคโนโลยีดิจิทัล วิธีการจัดเก็บข้อมูลการวัด (สัญญาณ) ก็เปลี่ยนไปเช่นกัน หากก่อนหน้านี้สามารถบันทึกสัญญาณลงในเครื่องบันทึกเทปและเก็บไว้ในเทปในรูปแบบแอนะล็อกได้ ตอนนี้สัญญาณจะถูกแปลงเป็นดิจิทัลและจัดเก็บไว้ในไฟล์ในหน่วยความจำของคอมพิวเตอร์เป็นชุดตัวเลข (นับ)

รูปแบบปกติสำหรับการวัดและแปลงสัญญาณเป็นดิจิทัลมีดังนี้

รูปที่ 9 แผนผังช่องวัด

สัญญาณจากทรานสดิวเซอร์การวัดมาถึง ADC ในช่วงเวลาหนึ่ง T ตัวอย่างสัญญาณ (ตัวอย่าง) ที่ได้รับในช่วงเวลา T จะถูกถ่ายโอนไปยังคอมพิวเตอร์และเก็บไว้ในหน่วยความจำ

fig.10 สัญญาณดิจิทัล - N การอ่านที่ได้รับในเวลา T

ข้อกำหนดสำหรับพารามิเตอร์การแปลงสัญญาณเป็นดิจิทัลมีอะไรบ้าง อุปกรณ์ที่แปลงสัญญาณแอนะล็อกอินพุตเป็นรหัสแบบไม่ต่อเนื่อง (สัญญาณดิจิทัล) เรียกว่าตัวแปลงแอนะล็อกเป็นดิจิทัล (ADC ตัวแปลงแอนะล็อกเป็นดิจิทัลภาษาอังกฤษ ADC) (วิกิ)

หนึ่งในพารามิเตอร์หลักของ ADC คืออัตราการสุ่มตัวอย่างสูงสุด (หรืออัตราการสุ่มตัวอย่าง อัตราตัวอย่างภาษาอังกฤษ) - ความถี่ของการสุ่มตัวอย่างสัญญาณอย่างต่อเนื่องในช่วงเวลาระหว่างการสุ่มตัวอย่าง วัดเป็นเฮิรตซ์ ((วิกิ))

ตามทฤษฎีบท Kotelnikov หากสัญญาณต่อเนื่องมีสเปกตรัมที่ จำกัด ด้วยความถี่ Fmax ก็สามารถกู้คืนได้อย่างสมบูรณ์และไม่ซ้ำกันจากตัวอย่างที่ไม่ต่อเนื่องซึ่งถ่ายในช่วงเวลา , เช่น. ด้วยความถี่ Fd ? 2*Fmax โดยที่ Fd - ความถี่สุ่มตัวอย่าง; Fmax - ความถี่สูงสุดของสเปกตรัมสัญญาณ กล่าวอีกนัยหนึ่งอัตราการสุ่มตัวอย่างสัญญาณ (อัตราการสุ่มตัวอย่าง ADC) ต้องมีความถี่สูงสุดของสัญญาณที่เราต้องการวัดอย่างน้อย 2 เท่า

และจะเกิดอะไรขึ้นถ้าเราอ่านค่าด้วยความถี่ต่ำกว่าที่กำหนดในทฤษฎีบท Kotelnikov

ในกรณีนี้ เอฟเฟกต์ของ "นามแฝง" (หรือที่เรียกว่าเอฟเฟกต์สโตรโบสโคปิก เอฟเฟกต์มัวเร) เกิดขึ้น ซึ่งสัญญาณความถี่สูงหลังจากการแปลงเป็นดิจิทัลกลายเป็นสัญญาณความถี่ต่ำที่ไม่มีอยู่จริง ในรูป 5 คลื่นไซน์สีแดงความถี่สูงเป็นสัญญาณจริง คลื่นไซน์สีน้ำเงินความถี่ต่ำเป็นสัญญาณจำลองที่เกิดจากข้อเท็จจริงที่ว่าสัญญาณความถี่สูงมากกว่าครึ่งช่วงเวลามีเวลาผ่านในช่วงเวลาสุ่มตัวอย่าง

ข้าว. 11. การปรากฏตัวของสัญญาณความถี่ต่ำเท็จเมื่ออัตราการสุ่มตัวอย่างไม่สูงพอ

เพื่อหลีกเลี่ยงผลกระทบของนามแฝง ตัวกรองป้องกันรอยหยักพิเศษจะถูกวางไว้ด้านหน้า ADC - LPF (ตัวกรองความถี่ต่ำผ่าน) ซึ่งส่งผ่านความถี่ที่ต่ำกว่าความถี่การสุ่มตัวอย่าง ADC ครึ่งหนึ่ง และตัดความถี่ที่สูงขึ้น

ในการคำนวณสเปกตรัมของสัญญาณจากตัวอย่างที่ไม่ต่อเนื่อง จะใช้การแปลงฟูริเยร์แบบไม่ต่อเนื่อง (DFT) เราสังเกตอีกครั้งว่าสเปกตรัมของสัญญาณแบบไม่ต่อเนื่องนั้น "ตามคำจำกัดความ" ที่จำกัดโดยความถี่ Fmax ซึ่งน้อยกว่าความถี่สุ่มตัวอย่าง Fd ดังนั้น สเปกตรัมของสัญญาณที่ไม่ต่อเนื่องสามารถแทนด้วยผลรวมของฮาร์โมนิกในจำนวนจำกัด ตรงกันข้ามกับผลรวมอนันต์สำหรับอนุกรมฟูริเยร์ของสัญญาณต่อเนื่อง ซึ่งสเปกตรัมของสัญญาณนั้นไม่จำกัด ตามทฤษฎีบท Kotelnikov ความถี่ฮาร์มอนิกสูงสุดจะต้องเป็นอย่างน้อยสองตัวอย่าง ดังนั้นจำนวนฮาร์มอนิกจะเท่ากับครึ่งหนึ่งของจำนวนตัวอย่างสัญญาณที่ไม่ต่อเนื่อง นั่นคือ หากมีตัวอย่าง N ตัวอย่าง จำนวนฮาร์โมนิกในสเปกตรัมจะเท่ากับ N/2

พิจารณาตอนนี้การแปลงฟูริเยร์แบบไม่ต่อเนื่อง (DFT)

เปรียบเทียบกับอนุกรมฟูริเยร์

เราเห็นว่ามันเกิดขึ้นพร้อมกัน ยกเว้นว่าเวลาใน DFT นั้นไม่ต่อเนื่องกัน และจำนวนฮาร์โมนิกถูกจำกัดที่ N/2 - ครึ่งหนึ่งของจำนวนตัวอย่าง

สูตร DFT เขียนด้วยตัวแปรจำนวนเต็มไร้มิติ k, s โดยที่ k คือตัวเลขของตัวอย่างสัญญาณ s คือตัวเลขขององค์ประกอบสเปกตรัม
ค่าของ s แสดงจำนวนการสั่นแบบเต็มของฮาร์มอนิกในช่วงเวลา T (ระยะเวลาของการวัดสัญญาณ) การแปลงฟูริเยร์แบบไม่ต่อเนื่องจะใช้เพื่อค้นหาแอมพลิจูดและเฟสของฮาร์โมนิกในเชิงตัวเลข เช่น "บนคอมพิวเตอร์"

กลับไปสู่ผลลัพธ์ที่ได้รับในตอนเริ่มต้น ดังที่ได้กล่าวไว้ข้างต้น เมื่อขยายฟังก์ชันที่ไม่เป็นคาบ (สัญญาณของเรา) เป็นอนุกรมฟูริเยร์ อนุกรมฟูริเยร์ที่เป็นผลลัพธ์จะสอดคล้องกับฟังก์ชันคาบที่มีคาบ T (รูปที่ 12)

fig.12 ฟังก์ชันธาตุ f(x) พร้อมคาบ Т0 พร้อมคาบการวัด Т>T0

ดังที่เห็นในรูปที่ 12 ฟังก์ชัน f(x) เป็นคาบที่มีคาบ Т0 อย่างไรก็ตาม เนื่องจากระยะเวลาของตัวอย่างการวัด T ไม่ตรงกับคาบของฟังก์ชัน T0 ฟังก์ชันที่ได้รับจากอนุกรมฟูริเยร์มีความไม่ต่อเนื่องที่จุด T ดังนั้น สเปกตรัมของฟังก์ชันนี้จะ มีฮาร์โมนิกความถี่สูงจำนวนมาก หากระยะเวลาของตัวอย่างการวัด T ใกล้เคียงกับคาบของฟังก์ชัน T0 ดังนั้นจะมีเพียงฮาร์มอนิกแรก (ไซนัสอยด์ที่มีคาบเท่ากับระยะเวลาตัวอย่าง) เท่านั้นที่จะปรากฏในสเปกตรัมที่ได้รับหลังจากการแปลงฟูริเยร์ เนื่องจากฟังก์ชัน f (x) เป็นไซนัส

กล่าวอีกนัยหนึ่ง โปรแกรม DFT "ไม่ทราบ" ว่าสัญญาณของเราคือ "ชิ้นส่วนของคลื่นไซน์" แต่พยายามแสดงฟังก์ชันคาบเป็นอนุกรมซึ่งมีช่องว่างเนื่องจากความไม่สอดคล้องกันของชิ้นส่วนแต่ละส่วน คลื่นไซน์

เป็นผลให้ฮาร์มอนิกปรากฏในสเปกตรัมซึ่งโดยรวมแล้วควรเป็นตัวแทนของรูปแบบของฟังก์ชันรวมถึงความไม่ต่อเนื่องนี้

ดังนั้น เพื่อให้ได้สเปกตรัมที่ "ถูกต้อง" ของสัญญาณ ซึ่งเป็นผลรวมของไซนัสหลายตัวที่มีคาบต่างๆ กัน จึงจำเป็นที่จำนวนเต็มของคาบของไซนัสแต่ละอันจะพอดีกับช่วงการวัดสัญญาณ ในทางปฏิบัติ สามารถปฏิบัติตามเงื่อนไขนี้ได้เป็นระยะเวลานานเพียงพอของการวัดสัญญาณ

รูปที่ 13 ตัวอย่างฟังก์ชันและสเปกตรัมของสัญญาณข้อผิดพลาดจลนศาสตร์ของกระปุกเกียร์

ด้วยระยะเวลาที่สั้นลง รูปภาพจะดู "แย่ลง":

รูปที่ 14 ตัวอย่างฟังก์ชันและสเปกตรัมของสัญญาณการสั่นสะเทือนของโรเตอร์

ในทางปฏิบัติ อาจเป็นเรื่องยากที่จะเข้าใจว่า "ส่วนประกอบที่แท้จริง" อยู่ที่ไหน และ "สิ่งประดิษฐ์" ที่เกิดจากการไม่คูณของคาบของส่วนประกอบและระยะเวลาของตัวอย่างสัญญาณหรือ "การกระโดดและการแตกหัก" ของ รูปคลื่น แน่นอน คำว่า "ส่วนประกอบที่แท้จริง" และ "สิ่งประดิษฐ์" ไม่ได้ถูกยกมาโดยเปล่าประโยชน์ การมีอยู่ของฮาร์โมนิกจำนวนมากบนกราฟสเปกตรัมไม่ได้หมายความว่าสัญญาณของเรา "ประกอบด้วย" พวกมันจริงๆ มันเหมือนกับคิดว่าเลข 7 "ประกอบด้วย" ของตัวเลข 3 และ 4 ตัวเลข 7 สามารถแสดงเป็นผลรวมของตัวเลข 3 และ 4 - ถูกต้อง

ดังนั้นสัญญาณของเรา ... หรือมากกว่านั้นไม่ใช่แม้แต่ "สัญญาณของเรา" แต่ฟังก์ชันเป็นระยะที่รวบรวมโดยการทำซ้ำสัญญาณของเรา (การสุ่มตัวอย่าง) สามารถแสดงเป็นผลรวมของฮาร์โมนิก (ไซนูซอยด์) ที่มีแอมพลิจูดและเฟสที่แน่นอน แต่ในหลายกรณีที่สำคัญสำหรับการปฏิบัติ (ดูรูปด้านบน) เป็นไปได้ที่จะเชื่อมโยงฮาร์โมนิกที่ได้รับในสเปกตรัมกับกระบวนการจริงที่มีลักษณะเป็นวัฏจักรและมีส่วนสำคัญต่อรูปร่างของสัญญาณ

ผลลัพธ์บางอย่าง

1. สัญญาณที่วัดได้จริง ระยะเวลา T วินาที แปลงเป็นดิจิทัลโดย ADC นั่นคือ แสดงด้วยชุดตัวอย่างแบบไม่ต่อเนื่อง (N ชิ้น) มีสเปกตรัมแบบไม่ต่อเนื่องกัน แทนด้วยชุดฮาร์โมนิก (N/2 ชิ้น) ).

2. สัญญาณจะแสดงด้วยชุดของค่าจริงและสเปกตรัมของสัญญาณจะแสดงด้วยชุดของค่าจริง ความถี่ฮาร์มอนิกเป็นบวก ความจริงที่ว่านักคณิตศาสตร์สะดวกกว่าในการแสดงสเปกตรัมในรูปแบบที่ซับซ้อนโดยใช้ความถี่เชิงลบไม่ได้หมายความว่า "ถูกต้อง" และ "ควรทำในลักษณะนี้เสมอ"

3. สัญญาณที่วัดในช่วงเวลา T ถูกกำหนดเฉพาะในช่วงเวลา T เกิดอะไรขึ้นก่อนที่เราจะเริ่มวัดสัญญาณและจะเกิดอะไรขึ้นหลังจากนั้น - สิ่งนี้ไม่เป็นที่รู้จักของวิทยาศาสตร์ และในกรณีของเรา - มันไม่น่าสนใจ DFT ของสัญญาณแบบจำกัดเวลาให้สเปกตรัม "ของจริง" ของมัน ในแง่ที่ว่าภายใต้เงื่อนไขบางประการ จะช่วยให้คุณสามารถคำนวณแอมพลิจูดและความถี่ของส่วนประกอบได้

วัสดุที่ใช้แล้วและวัสดุที่มีประโยชน์อื่นๆ