อันดับเมทริกซ์: คำจำกัดความ วิธีการค้นหา ตัวอย่าง วิธีแก้ไข การค้นหาอันดับของเมทริกซ์ อันดับของเมทริกซ์ 1123 5814 คืออะไร

เราจะพิจารณาการประยุกต์ใช้หัวข้อในทางปฏิบัติที่สำคัญด้วย: การศึกษาระบบสมการเชิงเส้นเพื่อความสม่ำเสมอ.

อันดับของเมทริกซ์คืออะไร?

บทตลกขบขันของบทความนี้มีความจริงจำนวนมาก เรามักจะเชื่อมโยงคำว่า "อันดับ" กับลำดับชั้นบางประเภท โดยส่วนใหญ่มักจะเกี่ยวข้องกับบันไดอาชีพ ยิ่งบุคคลมีความรู้ ประสบการณ์ ความสามารถ การเชื่อมต่อ ฯลฯ มากขึ้นเท่าใด – ยิ่งตำแหน่งและโอกาสของเขาสูงขึ้น ในแง่ของเยาวชน อันดับหมายถึงระดับทั่วไปของ "ความชัน"

และพี่น้องนักคณิตศาสตร์ของเราดำเนินชีวิตตามหลักการเดียวกัน สุ่มมาเดินเล่นสักหน่อย เมทริกซ์เป็นศูนย์:

ลองคิดดู, ถ้าอยู่ในเมทริกซ์ ศูนย์ทั้งหมดแล้วเราจะพูดถึงอันดับไหนล่ะ? ทุกคนคงคุ้นเคยกับสำนวนที่ไม่เป็นทางการว่า "total zero" ในสังคมเมทริกซ์ ทุกอย่างจะเหมือนกันทุกประการ:

อันดับของเมทริกซ์ศูนย์ขนาดใด ๆ เท่ากับศูนย์.

บันทึก : เมทริกซ์ศูนย์แสดงด้วยตัวอักษรกรีก "theta"

เพื่อให้เข้าใจอันดับของเมทริกซ์ได้ดีขึ้น ต่อไปฉันจะใช้สื่อช่วย เรขาคณิตเชิงวิเคราะห์- พิจารณาเป็นศูนย์ เวกเตอร์พื้นที่สามมิติของเราซึ่งไม่ได้กำหนดทิศทางเฉพาะและไม่มีประโยชน์ในการก่อสร้าง พื้นฐานความสัมพันธ์- จากมุมมองพีชคณิต พิกัดของเวกเตอร์นี้จะถูกเขียนลงไป เมทริกซ์“หนึ่งต่อสาม” และมีเหตุผล (ในความหมายทางเรขาคณิตที่ระบุ)สมมติว่าอันดับของเมทริกซ์นี้เป็นศูนย์

ตอนนี้เรามาดูบางส่วนกัน ไม่ใช่ศูนย์ เวกเตอร์คอลัมน์และ เวกเตอร์แถว:

แต่ละอินสแตนซ์มีองค์ประกอบที่ไม่เป็นศูนย์อย่างน้อยหนึ่งองค์ประกอบ และนั่นคือสิ่งที่!

อันดับของเวกเตอร์แถวที่ไม่ใช่ศูนย์ (เวกเตอร์คอลัมน์) จะเท่ากับ 1

และโดยทั่วไป - ถ้าอยู่ในเมทริกซ์ ขนาดที่กำหนดเองมีองค์ประกอบที่ไม่เป็นศูนย์อย่างน้อยหนึ่งองค์ประกอบ จากนั้นจะมีอันดับ ไม่น้อยหน่วย.

เวกเตอร์แถวพีชคณิตและเวกเตอร์คอลัมน์เป็นนามธรรมในระดับหนึ่ง ดังนั้นเรากลับมาที่การเชื่อมโยงทางเรขาคณิตอีกครั้ง ไม่เป็นศูนย์ เวกเตอร์กำหนดทิศทางในอวกาศได้ชัดเจนมาก และเหมาะสมกับการก่อสร้าง พื้นฐานดังนั้นอันดับของเมทริกซ์จะถือว่าเท่ากับหนึ่ง

ข้อมูลทางทฤษฎี : ในพีชคณิตเชิงเส้น เวกเตอร์เป็นองค์ประกอบของปริภูมิเวกเตอร์ (กำหนดผ่าน 8 สัจพจน์) ซึ่งโดยเฉพาะสามารถแทนแถวลำดับ (หรือคอลัมน์) ของจำนวนจริงด้วยการดำเนินการบวกและการคูณด้วยจำนวนจริงที่กำหนด สำหรับพวกเขา ข้อมูลรายละเอียดเพิ่มเติมเกี่ยวกับเวกเตอร์สามารถพบได้ในบทความ การแปลงเชิงเส้น.

ขึ้นอยู่กับเชิงเส้น(แสดงออกผ่านกันและกัน) จากมุมมองทางเรขาคณิต เส้นที่สองประกอบด้วยพิกัดของเวกเตอร์คอลลิเนียร์ ซึ่งไม่ได้ก้าวหน้าในเรื่องการก่อสร้างแต่อย่างใด พื้นฐานสามมิติอยู่ในความหมายนี้ฟุ่มเฟือย ดังนั้นอันดับของเมทริกซ์นี้จึงเท่ากับหนึ่งด้วย

ลองเขียนพิกัดของเวกเตอร์ลงในคอลัมน์ ( ย้ายเมทริกซ์):

มีการเปลี่ยนแปลงอะไรในแง่ของอันดับ? ไม่มีอะไร. คอลัมน์เป็นสัดส่วน ซึ่งหมายความว่าอันดับจะเท่ากับหนึ่ง โปรดทราบว่าทั้งสามบรรทัดนั้นเป็นสัดส่วนเช่นกัน สามารถระบุได้ด้วยพิกัด สามเวกเตอร์คอลลิเนียร์ของเครื่องบิน ซึ่ง เพียงหนึ่งเดียวมีประโยชน์สำหรับการสร้างพื้นฐาน "แบน" และนี่สอดคล้องกับความรู้สึกทางเรขาคณิตของอันดับโดยสิ้นเชิง

ข้อความสำคัญตามมาจากตัวอย่างข้างต้น:

อันดับของเมทริกซ์ในแถวจะเท่ากับอันดับของเมทริกซ์ในคอลัมน์- ฉันได้กล่าวถึงเรื่องนี้เล็กน้อยในบทเรียนเกี่ยวกับประสิทธิผล วิธีการคำนวณดีเทอร์มิแนนต์.

บันทึก : การพึ่งพาเชิงเส้นของแถวหมายถึงการพึ่งพาเชิงเส้นของคอลัมน์ (และในทางกลับกัน) แต่เพื่อประหยัดเวลาและไม่ติดเป็นนิสัย ฉันมักจะพูดถึงการพึ่งพาเชิงเส้นของสตริงเกือบทุกครั้ง

มาฝึกสัตว์เลี้ยงแสนรักของเรากันต่อ ลองเพิ่มพิกัดของเวกเตอร์คอลลิเนียร์อีกอันให้กับเมทริกซ์ในแถวที่สาม :

เขาช่วยเราสร้างพื้นฐานสามมิติหรือไม่? ไม่แน่นอน เวกเตอร์ทั้งสามเดินไปมาในเส้นทางเดียวกันและอันดับของเมทริกซ์เท่ากับหนึ่ง คุณสามารถใช้เวกเตอร์คอลลิเนียร์ได้มากเท่าที่คุณต้องการ เช่น 100 ใส่พิกัดของพวกมันลงในเมทริกซ์ "หนึ่งร้อยคูณสาม" และอันดับของตึกระฟ้าดังกล่าวจะยังคงเป็นหนึ่ง

มาทำความรู้จักกับเมทริกซ์ซึ่งเป็นแถวกันดีกว่า เป็นอิสระเชิงเส้น- เวกเตอร์ที่ไม่ใช่คอลลิเนียร์คู่หนึ่งเหมาะสำหรับการสร้างพื้นฐานสามมิติ อันดับของเมทริกซ์นี้คือสอง

เมทริกซ์มีอันดับเท่าไหร่? เส้นต่างๆ ดูเหมือนจะไม่เป็นสัดส่วน... ดังนั้น ตามทฤษฎีแล้ว มันเป็นสามเส้น อย่างไรก็ตามอันดับของเมทริกซ์นี้ก็เท่ากับสองเช่นกัน ฉันเพิ่มสองบรรทัดแรกแล้วเขียนผลลัพธ์ที่ด้านล่างสุด เช่น แสดงเป็นเส้นตรงบรรทัดที่สามถึงสองบรรทัดแรก ในเชิงเรขาคณิต แถวของเมทริกซ์สอดคล้องกับพิกัดของทั้งสาม เวกเตอร์โคพลานาร์และในสามคนนี้ก็ยังมีสหายที่ไม่ใช่คอลลิเนียร์อีกคู่หนึ่ง

อย่างที่คุณเห็น การพึ่งพาเชิงเส้นในเมทริกซ์ที่พิจารณานั้นไม่ชัดเจนและวันนี้เราจะได้เรียนรู้วิธีนำมันออกมาสู่ที่โล่ง

ฉันคิดว่าหลายคนคงเดาได้ว่าเมทริกซ์อันดับเท่าไหร่!

พิจารณาเมทริกซ์ที่มีแถว เป็นอิสระเชิงเส้น- แบบฟอร์มเวกเตอร์ พื้นฐานความสัมพันธ์และอันดับของเมทริกซ์นี้คือสาม

ดังที่คุณทราบ เวกเตอร์ที่สี่ ห้า และสิบใดๆ ของปริภูมิสามมิติจะถูกแสดงเป็นเส้นตรงในรูปของเวกเตอร์พื้นฐาน ดังนั้น หากคุณเพิ่มจำนวนแถวใดๆ ลงในเมทริกซ์ ก็จะได้อันดับของแถวนั้น จะยังคงเท่ากับสาม.

การให้เหตุผลที่คล้ายกันสามารถดำเนินการกับเมทริกซ์ที่มีขนาดใหญ่กว่าได้ (แน่นอนว่าไม่มีความหมายทางเรขาคณิต)

คำนิยาม : อันดับของเมทริกซ์คือจำนวนแถวอิสระเชิงเส้นสูงสุด- หรือ: อันดับของเมทริกซ์คือจำนวนคอลัมน์อิสระเชิงเส้นสูงสุด- ใช่แล้ว จำนวนของพวกเขาจะเท่ากันเสมอ

แนวทางปฏิบัติที่สำคัญยังเป็นไปตามข้างต้น: อันดับของเมทริกซ์ไม่เกินมิติขั้นต่ำ- ตัวอย่างเช่นในเมทริกซ์ สี่แถวและห้าคอลัมน์ มิติข้อมูลขั้นต่ำคือสี่ ดังนั้นอันดับของเมทริกซ์นี้จะไม่เกิน 4 อย่างแน่นอน

การกำหนด: ในทฤษฎีและการปฏิบัติของโลกไม่มีมาตรฐานที่เป็นที่ยอมรับโดยทั่วไปในการกำหนดอันดับของเมทริกซ์ บ่อยครั้งที่คุณจะพบ: - อย่างที่พวกเขาพูดกันชาวอังกฤษเขียนสิ่งหนึ่งเยอรมันอีกสิ่งหนึ่ง ดังนั้นจากเรื่องตลกที่โด่งดังเกี่ยวกับนรกของอเมริกาและรัสเซีย เรามาแสดงอันดับของเมทริกซ์ด้วยคำพื้นเมืองกัน ตัวอย่างเช่น: . และถ้าเมทริกซ์นั้น "ไม่มีชื่อ" ซึ่งมีจำนวนมากคุณก็สามารถเขียนได้ .

จะหาอันดับของเมทริกซ์โดยใช้ผู้เยาว์ได้อย่างไร?

หากคุณยายของเรามีคอลัมน์ที่ห้าในเมทริกซ์ของเธอ เราจะต้องคำนวณคอลัมน์รองลำดับที่ 4 อีกคอลัมน์หนึ่ง (“สีน้ำเงิน”, “ราสเบอร์รี่” + คอลัมน์ที่ 5)

บทสรุป: ลำดับสูงสุดของผู้เยาว์ที่ไม่เป็นศูนย์คือสาม ซึ่งหมายความว่า

บางทีอาจไม่ใช่ทุกคนที่เข้าใจวลีนี้อย่างสมบูรณ์: ผู้เยาว์ของลำดับที่ 4 มีค่าเท่ากับศูนย์ แต่ในบรรดาผู้เยาว์ของลำดับที่ 3 นั้นมีลำดับที่ไม่เป็นศูนย์ - ดังนั้นลำดับสูงสุด ไม่ใช่ศูนย์รายย่อยและเท่ากับสาม

คำถามเกิดขึ้นทำไมไม่คำนวณดีเทอร์มิแนนต์ทันที ประการแรกในงานส่วนใหญ่เมทริกซ์จะไม่เป็นสี่เหลี่ยมจัตุรัสและประการที่สองแม้ว่าคุณจะได้ค่าที่ไม่เป็นศูนย์ แต่งานก็มักจะถูกปฏิเสธเนื่องจากโดยปกติแล้วจะเกี่ยวข้องกับโซลูชัน "จากล่างขึ้นบน" มาตรฐาน และในตัวอย่างนี้ที่พิจารณา ค่าดีเทอร์มิแนนต์ของลำดับที่ 4 เป็นศูนย์ทำให้เราระบุได้ว่าอันดับของเมทริกซ์นั้นน้อยกว่าสี่เท่านั้น

ฉันต้องยอมรับว่าฉันพบปัญหาที่ฉันวิเคราะห์ตัวเองเพื่ออธิบายวิธีการผูกมัดผู้เยาว์ได้ดียิ่งขึ้น ในทางปฏิบัติจริง ทุกอย่างจะง่ายกว่า:

ตัวอย่างที่ 2

ค้นหาอันดับของเมทริกซ์โดยใช้วิธี Edge minors

คำตอบและคำตอบอยู่ท้ายบทเรียน

อัลกอริทึมทำงานเร็วที่สุดเมื่อใด ลองกลับไปสู่เมทริกซ์ขนาดสี่คูณสี่เหมือนเดิม. - แน่นอนว่าวิธีแก้ปัญหาจะสั้นที่สุดในกรณี “ดี” ผู้เยาว์มุม: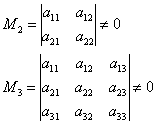

และถ้า แล้ว มิฉะนั้น –

ความคิดนี้ไม่ได้เป็นเพียงสมมุติฐานแต่อย่างใด - มีหลายตัวอย่างที่เรื่องทั้งหมดถูกจำกัดไว้เฉพาะผู้เยาว์เชิงมุมเท่านั้น

อย่างไรก็ตาม ในบางกรณี วิธีอื่นก็มีประสิทธิภาพและดีกว่า:

จะค้นหาอันดับของเมทริกซ์โดยใช้วิธี Gaussian ได้อย่างไร

ย่อหน้านี้มีไว้สำหรับผู้อ่านที่คุ้นเคยอยู่แล้ว วิธีเกาส์เซียนและพวกเขาก็ได้ลงมือทำไม่มากก็น้อย

จากมุมมองทางเทคนิค วิธีการนี้ไม่ใช่เรื่องใหม่:

1) ใช้การแปลงเบื้องต้น เราลดเมทริกซ์ให้อยู่ในรูปแบบขั้นตอน

2) อันดับของเมทริกซ์เท่ากับจำนวนแถว

เป็นที่ชัดเจนอย่างยิ่งว่า การใช้วิธีเกาส์เซียนจะไม่เปลี่ยนอันดับของเมทริกซ์และสาระสำคัญที่นี่ง่ายมาก: ตามอัลกอริทึมในระหว่างการแปลงเบื้องต้น แถวตามสัดส่วนที่ไม่จำเป็น (ขึ้นอยู่กับเชิงเส้น) ทั้งหมดจะถูกระบุและลบออก ส่งผลให้ "สารตกค้างแห้ง" - จำนวนสูงสุดของแถวอิสระเชิงเส้น

ลองแปลงเมทริกซ์เก่าที่คุ้นเคยด้วยพิกัดของเวกเตอร์คอลลิเนียร์สามตัว:

(1) บรรทัดแรกบวกกับบรรทัดที่สอง คูณด้วย –2 บรรทัดแรกถูกเพิ่มเข้าไปในบรรทัดที่สาม

(2) เส้นศูนย์จะถูกลบออก

ดังนั้นจึงเหลือบรรทัดเดียว ไม่จำเป็นต้องพูดว่า นี่เร็วกว่าการคำนวณผู้เยาว์ที่เป็นศูนย์เก้าคนในลำดับที่ 2 มาก จากนั้นจึงสรุปผลได้

ฉันเตือนคุณว่าในตัวเอง เมทริกซ์พีชคณิตไม่มีอะไรเปลี่ยนแปลงได้ และการเปลี่ยนแปลงจะดำเนินการเพื่อจุดประสงค์ในการกำหนดอันดับเท่านั้น! อย่างไรก็ตาม เรามาดูคำถามกันอีกครั้งว่าทำไมจะไม่ได้ล่ะ? เมทริกซ์แหล่งที่มา 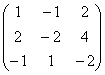นำข้อมูลที่แตกต่างโดยพื้นฐานจากข้อมูลของเมทริกซ์และแถว ในแบบจำลองทางคณิตศาสตร์บางแบบจำลอง (ไม่มีการกล่าวเกินจริง) ความแตกต่างในตัวเลขหนึ่งตัวอาจเป็นเรื่องของความเป็นและความตาย ...ฉันจำครูคณิตศาสตร์ระดับประถมศึกษาและมัธยมศึกษาที่ลดเกรดลง 1-2 คะแนนอย่างไร้ความปราณีเนื่องจากมีความคลาดเคลื่อนหรือเบี่ยงเบนไปจากอัลกอริทึมเพียงเล็กน้อย และเป็นเรื่องที่น่าผิดหวังอย่างยิ่งเมื่อแทนที่จะเป็น "A" ที่ดูเหมือนจะรับประกัน กลับกลายเป็นว่า "ดี" หรือแย่กว่านั้นอีก ความเข้าใจเกิดขึ้นในเวลาต่อมา - เราจะมอบดาวเทียม หัวรบนิวเคลียร์ และโรงไฟฟ้าให้กับมนุษย์ได้อย่างไร แต่ไม่ต้องกังวล ฉันไม่ได้ทำงานในพื้นที่เหล่านี้ =)

มาดูงานที่มีความหมายมากขึ้นกันดีกว่า โดยที่เราจะได้ทำความคุ้นเคยกับเทคนิคการคำนวณที่สำคัญ วิธีเกาส์:

ตัวอย่างที่ 3

ค้นหาอันดับของเมทริกซ์โดยใช้การแปลงเบื้องต้น

สารละลาย: ให้เมทริกซ์ "สี่คูณห้า" ซึ่งหมายความว่าอันดับของมันไม่เกิน 4 อย่างแน่นอน

ในคอลัมน์แรก ไม่มี 1 หรือ –1 ดังนั้น จำเป็นต้องดำเนินการเพิ่มเติมเพื่อให้ได้อย่างน้อยหนึ่งหน่วย ตลอดการมีอยู่ของไซต์ ฉันถูกถามคำถามซ้ำแล้วซ้ำเล่า: "เป็นไปได้หรือไม่ที่จะจัดเรียงคอลัมน์ใหม่ในระหว่างการแปลงเบื้องต้น" ที่นี่เราจัดเรียงคอลัมน์แรกและคอลัมน์ที่สองใหม่ และทุกอย่างเรียบร้อยดี! ในงานส่วนใหญ่ที่มีการใช้งาน วิธีเกาส์เซียนคอลัมน์สามารถจัดเรียงใหม่ได้อย่างแน่นอน แต่ไม่จำเป็น และประเด็นไม่ได้อยู่ที่ความสับสนกับตัวแปรที่เป็นไปได้ ประเด็นก็คือในหลักสูตรคลาสสิกของคณิตศาสตร์ระดับสูง การกระทำนี้ไม่ได้รับการพิจารณาแบบดั้งเดิม ดังนั้นการพยักหน้าดังกล่าวจะถูกมองว่าคดมาก (หรือแม้แต่ถูกบังคับให้ทำซ้ำทุกอย่าง)

ประเด็นที่สองเกี่ยวข้องกับตัวเลข เมื่อคุณตัดสินใจ การใช้หลักปฏิบัติต่อไปนี้จะเป็นประโยชน์: ถ้าเป็นไปได้ การแปลงเบื้องต้นควรลดจำนวนเมทริกซ์ลง- ท้ายที่สุดแล้ว มันง่ายกว่ามากในการทำงานกับ 1, 2, 3 มากกว่าเช่น 23, 45 และ 97 และการกระทำแรกนั้นไม่เพียงมุ่งเป้าไปที่การได้รับหนึ่งในคอลัมน์แรกเท่านั้น แต่ยังรวมถึงการกำจัดตัวเลขด้วย 7 และ 11.

ขั้นแรกให้แก้ปัญหาโดยสมบูรณ์ จากนั้นแสดงความคิดเห็น:

(1) บรรทัดแรกบวกกับบรรทัดที่สอง คูณด้วย –2 บรรทัดแรกบวกกับบรรทัดที่สาม คูณด้วย –3 และในฮีป: บรรทัดที่ 1 ถูกบวกเข้ากับบรรทัดที่ 4 คูณด้วย –1

(2) สามบรรทัดสุดท้ายเป็นสัดส่วน บรรทัดที่ 3 และ 4 ถูกลบออก บรรทัดที่สองถูกย้ายไปที่แรก

(3) บรรทัดแรกบวกกับบรรทัดที่สอง คูณด้วย –3

เมทริกซ์รีดิวซ์เป็นระดับขั้นมีสองแถว

คำตอบ:

ตอนนี้ถึงตาคุณแล้วที่จะต้องทรมานเมทริกซ์สี่คูณสี่:

ตัวอย่างที่ 4

ค้นหาอันดับของเมทริกซ์โดยใช้วิธีเกาส์เซียน

ฉันเตือนคุณว่า วิธีเกาส์เซียนไม่ได้หมายความถึงความเข้มงวดที่ชัดเจน และการตัดสินใจของคุณมักจะแตกต่างจากการตัดสินใจของฉัน ตัวอย่างงานโดยย่อในตอนท้ายของบทเรียน

ฉันควรใช้วิธีใดในการค้นหาอันดับของเมทริกซ์

ในทางปฏิบัติมักไม่ได้ระบุไว้เลยว่าควรใช้วิธีใดในการค้นหาอันดับ ในสถานการณ์เช่นนี้ควรวิเคราะห์เงื่อนไข - สำหรับเมทริกซ์บางตัวนั้นมีเหตุผลมากกว่าที่จะแก้ไขผ่านตัวรองในขณะที่สำหรับเมทริกซ์บางตัวจะทำกำไรได้มากกว่ามากหากใช้การแปลงเบื้องต้น:

ตัวอย่างที่ 5

ค้นหาอันดับของเมทริกซ์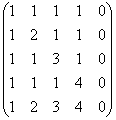

สารละลาย: วิธีแรกหายไปทันที =)

สูงกว่าเล็กน้อยฉันไม่แนะนำให้แตะคอลัมน์ของเมทริกซ์ แต่เมื่อมีคอลัมน์เป็นศูนย์หรือคอลัมน์ตามสัดส่วน/ตรงกันก็ยังคุ้มค่าที่จะตัดออก:

(1) คอลัมน์ที่ห้าเป็นศูนย์ ให้ลบออกจากเมทริกซ์ ดังนั้นอันดับของเมทริกซ์จึงไม่เกินสี่ บรรทัดแรกคูณด้วย –1 นี่เป็นคุณลักษณะเฉพาะอีกประการหนึ่งของวิธีเกาส์ ซึ่งเปลี่ยนการกระทำต่อไปนี้ให้เป็นการเดินที่น่ารื่นรมย์:

(2) ในทุกบรรทัด เริ่มจากบรรทัดที่สอง บรรทัดแรกจะถูกเพิ่ม

(3) บรรทัดแรกคูณด้วย –1 บรรทัดที่สามหารด้วย 2 บรรทัดที่สี่หารด้วย 3 บรรทัดที่สองบวกเข้ากับบรรทัดที่ห้าคูณด้วย –1

(4) บรรทัดที่สามบวกกับบรรทัดที่ห้าคูณด้วย –2

(5) สองบรรทัดสุดท้ายเป็นสัดส่วน ส่วนบรรทัดที่ห้าถูกลบออก

ผลลัพธ์คือ 4 บรรทัด

คำตอบ:

อาคารห้าชั้นมาตรฐานสำหรับการศึกษาอิสระ:

ตัวอย่างที่ 6

ค้นหาอันดับของเมทริกซ์

คำตอบสั้น ๆ และคำตอบในตอนท้ายของบทเรียน

ควรสังเกตว่าวลี "อันดับเมทริกซ์" ไม่ค่อยเห็นในทางปฏิบัติ และในปัญหาส่วนใหญ่คุณสามารถทำได้โดยไม่ต้องใช้เลย แต่มีงานหนึ่งที่แนวคิดที่เป็นปัญหาคือตัวละครหลัก และเราจะสรุปบทความด้วยการใช้งานจริงนี้:

จะศึกษาระบบสมการเชิงเส้นเพื่อความสม่ำเสมอได้อย่างไร?

บ่อยครั้งนอกเหนือจากการแก้ปัญหา ระบบสมการเชิงเส้นตามเงื่อนไขจะต้องตรวจสอบความเข้ากันได้ก่อนนั่นคือเพื่อพิสูจน์ว่ามีวิธีแก้ปัญหาใด ๆ อยู่เลย มีบทบาทสำคัญในการตรวจสอบดังกล่าว ทฤษฎีบทโครเนกเกอร์-คาเปลลีซึ่งฉันจะกำหนดในรูปแบบที่จำเป็น:

ถ้ายศ เมทริกซ์ระบบเท่ากับอันดับ ระบบเมทริกซ์ขยายแสดงว่าระบบมีความสอดคล้อง และหากตัวเลขนี้ตรงกับจำนวนที่ไม่ทราบ แสดงว่าโซลูชันนั้นไม่ซ้ำกัน

ดังนั้นเพื่อศึกษาความเข้ากันได้ของระบบจึงจำเป็นต้องตรวจสอบความเท่าเทียมกัน , ที่ไหน - เมทริกซ์ระบบ(จำคำศัพท์จากบทเรียน วิธีเกาส์), ก - เมทริกซ์ระบบขยาย(เช่น เมทริกซ์ที่มีค่าสัมประสิทธิ์ของตัวแปร + คอลัมน์ที่มีเงื่อนไขอิสระ)

บทความนี้จะกล่าวถึงแนวคิดเช่นอันดับของเมทริกซ์และแนวคิดเพิ่มเติมที่จำเป็น เราจะยกตัวอย่างและหลักฐานในการค้นหาอันดับของเมทริกซ์ และบอกคุณด้วยว่าเมทริกซ์รองคืออะไร และเหตุใดจึงมีความสำคัญมาก

เมทริกซ์ไมเนอร์

เพื่อทำความเข้าใจว่าอันดับของเมทริกซ์คืออะไร คุณต้องเข้าใจแนวคิดของเมทริกซ์รองก่อน

คำจำกัดความ 1

ส่วนน้อยเคลำดับที่ของเมทริกซ์ คือดีเทอร์มิแนนต์ของเมทริกซ์จตุรัสลำดับ k×k ซึ่งประกอบด้วยองค์ประกอบของเมทริกซ์ A ซึ่งอยู่ในแถว k และคอลัมน์ k ที่เลือกไว้ล่วงหน้า ในขณะที่ยังคงตำแหน่งขององค์ประกอบของเมทริกซ์ A ไว้

พูดง่ายๆ ก็คือ ถ้าในเมทริกซ์ A คุณลบแถว (p-k) และคอลัมน์ (n-k) และจากองค์ประกอบเหล่านั้นที่เหลืออยู่ ให้สร้างเมทริกซ์ โดยคงการจัดเรียงองค์ประกอบของเมทริกซ์ A ไว้ ดังนั้นดีเทอร์มิแนนต์ของเมทริกซ์ผลลัพธ์จะเป็น ลำดับ k รองของเมทริกซ์ A

จากตัวอย่างพบว่าตัวรองอันดับหนึ่งของเมทริกซ์ A คือองค์ประกอบเมทริกซ์ในตัวมันเอง

เราสามารถยกตัวอย่างผู้เยาว์ลำดับที่ 2 ได้หลายตัวอย่าง ลองเลือกสองแถวและสองคอลัมน์ ตัวอย่างเช่น แถวที่ 1 และ 2 คอลัมน์ที่ 3 และ 4

ด้วยการเลือกองค์ประกอบนี้ อันดับรองอันดับสองจะเป็น - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

อันดับรองอันดับ 2 อีกตัวหนึ่งของเมทริกซ์ A คือ 0 0 1 1 = 0

ให้เราจัดเตรียมภาพประกอบเกี่ยวกับการสร้างเมทริกซ์ A รองอันดับสอง:

ผู้เยาว์ลำดับที่ 3 ได้มาจากการขีดฆ่าคอลัมน์ที่สามของเมทริกซ์ A:

0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9

ภาพประกอบของวิธีการรับลำดับรองอันดับ 3 ของเมทริกซ์ A:

สำหรับเมทริกซ์ที่กำหนด ไม่มีรายย่อยที่สูงกว่าลำดับที่ 3 เพราะ

k ≤ m i n (p , n) = m i n (3 , 4) = 3

มีลำดับรอง k จำนวนเท่าใดสำหรับเมทริกซ์ A ของลำดับ p×n?

จำนวนผู้เยาว์คำนวณโดยใช้สูตรต่อไปนี้:

C p k × C n k โดยที่ e C p k = p ! เค! (ป-เค) ! และ C nk = n ! เค! (น-เค) ! - จำนวนชุดค่าผสมจาก p ถึง k จาก n ถึง k ตามลำดับ

หลังจากที่เราระบุได้ว่ารายย่อยของเมทริกซ์ A คืออะไรแล้ว เราก็จะสามารถกำหนดอันดับของเมทริกซ์ A ได้

อันดับเมทริกซ์: วิธีการค้นหา

คำจำกัดความ 2

อันดับเมทริกซ์ - ลำดับสูงสุดของเมทริกซ์ที่ไม่ใช่ศูนย์

การกำหนด 1

อันดับ (ก), Rg (A), รัง (A)

จากคำจำกัดความของอันดับของเมทริกซ์และอันดับรองของเมทริกซ์ จะเห็นได้ชัดว่าอันดับของเมทริกซ์ศูนย์เท่ากับศูนย์ และอันดับของเมทริกซ์ที่ไม่ใช่ศูนย์นั้นแตกต่างจากศูนย์

การค้นหาอันดับของเมทริกซ์ตามคำจำกัดความ

คำจำกัดความ 3

วิธีการแจกแจงผู้เยาว์ - วิธีการที่ใช้กำหนดอันดับของเมทริกซ์

อัลกอริทึมของการกระทำโดยใช้วิธีการแจกแจงผู้เยาว์ :

จำเป็นต้องค้นหาอันดับของเมทริกซ์ A ของลำดับ พี× n- หากมีองค์ประกอบที่ไม่เป็นศูนย์อย่างน้อยหนึ่งองค์ประกอบ อันดับของเมทริกซ์จะต้องมีอย่างน้อยเท่ากับหนึ่ง ( เพราะ มีลำดับรองอันดับ 1 ที่ไม่เท่ากับศูนย์).

ถัดมาคือการแจงนับผู้เยาว์ลำดับที่ 2 หากผู้เยาว์ลำดับที่ 2 ทั้งหมดมีค่าเท่ากับศูนย์ อันดับจะเท่ากับหนึ่ง หากมีอย่างน้อยหนึ่งรายที่ไม่เป็นศูนย์ในลำดับที่ 2 จำเป็นต้องดำเนินการต่อไปเพื่อแจกแจงผู้เยาว์ในลำดับที่ 3 และอันดับของเมทริกซ์ในกรณีนี้จะเท่ากับอย่างน้อยสอง

ลองทำแบบเดียวกันกับอันดับของลำดับที่ 3: ถ้าเมทริกซ์รองทั้งหมดมีค่าเท่ากับศูนย์ อันดับก็จะเท่ากับสอง หากมีอย่างน้อยหนึ่งผู้เยาว์ที่ไม่ใช่ศูนย์ในลำดับที่ 3 ดังนั้นอันดับของเมทริกซ์จะต้องมีอย่างน้อยสาม เป็นต้นโดยการเปรียบเทียบ

ตัวอย่างที่ 2

ค้นหาอันดับของเมทริกซ์:

ก = - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

เนื่องจากเมทริกซ์ไม่เป็นศูนย์ อันดับขั้นต่ำจึงเป็นหนึ่ง

อันดับ 2 รอง - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 ไม่ใช่ศูนย์ ตามมาด้วยอันดับของเมทริกซ์ A อย่างน้อยสอง

เราเรียงลำดับผู้เยาว์ลำดับที่ 3: C 3 3 × C 5 3 = 1 5! 3! (5 - 3) ! = 10 ชิ้น.

1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (- 1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 - (- 1) × 0 × 11 = 0

1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (- 1) × 0 × 3 = 0

1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

ผู้เยาว์ในลำดับที่ 3 มีค่าเท่ากับศูนย์ ดังนั้นอันดับของเมทริกซ์คือ 2

คำตอบ : อันดับ (A) = 2.

การค้นหาอันดับของเมทริกซ์โดยใช้วิธี Bordering minors

คำจำกัดความ 3

วิธีย่อยที่มีขอบเขต - วิธีการที่ช่วยให้ได้ผลลัพธ์โดยใช้การคำนวณน้อยลง

ขอบรอง - M รองลงมา (k + 1) ของลำดับที่ 3 ของเมทริกซ์ A ซึ่งล้อมรอบ M รองของลำดับ k ของเมทริกซ์ A หากเมทริกซ์ที่สอดคล้องกับรอง M o k “มี” เมทริกซ์ที่สอดคล้องกับ ไมเนอร์ เอ็ม.

พูดง่ายๆ ก็คือ เมทริกซ์ที่สอดคล้องกับ M รองที่มีขอบนั้นได้มาจากเมทริกซ์ที่สอดคล้องกับ M รองที่มีขอบ M ok โดยการลบองค์ประกอบของหนึ่งแถวและหนึ่งคอลัมน์

ตัวอย่างที่ 3

ค้นหาอันดับของเมทริกซ์:

ก = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

ในการค้นหาอันดับ เราใช้ลำดับที่ 2 รอง M = 2 - 1 4 1

เราเขียนผู้เยาว์ที่มีพรมแดนติดกันทั้งหมด:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

เพื่อพิสูจน์วิธีการกำหนดขอบเขตผู้เยาว์ เรานำเสนอทฤษฎีบท ซึ่งสูตรดังกล่าวไม่จำเป็นต้องมีการพิสูจน์

ทฤษฎีบท 1

หากผู้เยาว์ทุกรายที่อยู่ในลำดับ k รองของเมทริกซ์ A ของลำดับ p คูณ n เท่ากับศูนย์ ดังนั้น ลำดับรองทั้งหมด (k+1) ของเมทริกซ์ A จะเท่ากับศูนย์

อัลกอริทึมของการกระทำ :

ในการค้นหาอันดับของเมทริกซ์ ไม่จำเป็นต้องผ่านตัวรองทั้งหมด เพียงแค่ดูที่เส้นขอบ

หากผู้เยาว์ที่มีขอบเท่ากับศูนย์ อันดับของเมทริกซ์จะเป็นศูนย์ หากมีผู้เยาว์อย่างน้อยหนึ่งรายที่ไม่เท่ากับศูนย์ เราจะพิจารณาผู้เยาว์ที่มีขอบเขต

หากทั้งหมดเป็นศูนย์ อันดับ (A) จะเป็นสอง หากมีผู้เยาว์ที่มีพรมแดนติดกันอย่างน้อยหนึ่งราย เราจะดำเนินการพิจารณาผู้เยาว์ที่มีพรมแดนติดกัน และเช่นเดียวกัน

ตัวอย่างที่ 4

ค้นหาอันดับของเมทริกซ์โดยใช้วิธี Edge minors

ก = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

วิธีแก้ปัญหา?

เนื่องจากองค์ประกอบ 11 ของเมทริกซ์ A ไม่เท่ากับศูนย์ เราจึงหาค่ารองของลำดับที่ 1 มาเริ่มมองหาผู้เยาว์ที่มีขอบเขตแตกต่างจากศูนย์:

2 1 4 2 = 2 × 2 - 1 × 4 = 0 2 0 4 1 = 2 × 1 - 0 × 4 = 2

เราพบขอบเขตรองของลำดับที่ 2 ซึ่งไม่เท่ากับศูนย์ 2 0 4 1

แจกแจงผู้เยาว์ที่มีพรมแดนติดกัน - (มี (4 - 2) × (5 - 2) = 6 ชิ้น)

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

คำตอบ : อันดับ(A) = 2.

การค้นหาอันดับของเมทริกซ์โดยใช้วิธีเกาส์เซียน (โดยใช้การแปลงเบื้องต้น)

จำไว้ว่าการแปลงเบื้องต้นคืออะไร

การเปลี่ยนแปลงเบื้องต้น:

โดยการจัดเรียงแถว (คอลัมน์) ของเมทริกซ์ใหม่
โดยการคูณองค์ประกอบทั้งหมดของแถว (คอลัมน์) ของเมทริกซ์ด้วยตัวเลขที่ไม่ใช่ศูนย์โดยพลการ k

โดยการเพิ่มองค์ประกอบของแถว (คอลัมน์) ใด ๆ ที่สอดคล้องกับแถวอื่น (คอลัมน์) ของเมทริกซ์ซึ่งคูณด้วยตัวเลขที่กำหนดเอง k

คำจำกัดความที่ 5

การค้นหาอันดับของเมทริกซ์โดยใช้วิธีเกาส์เซียน - วิธีการที่อยู่บนพื้นฐานของทฤษฎีการสมมูลของเมทริกซ์: ถ้าเมทริกซ์ B ได้มาจากเมทริกซ์ A โดยใช้การแปลงเบื้องต้นในจำนวนจำกัด ดังนั้น อันดับ(A) = อันดับ(B)

ความถูกต้องของคำสั่งนี้ตามมาจากคำจำกัดความของเมทริกซ์:

ถ้าแถวหรือคอลัมน์ของเมทริกซ์ถูกจัดเรียงใหม่ ดีเทอร์มิแนนต์ของเมทริกซ์จะเปลี่ยนเครื่องหมาย ถ้ามันเท่ากับศูนย์ เมื่อจัดเรียงแถวหรือคอลัมน์ใหม่ ก็ยังคงเท่ากับศูนย์
ในกรณีที่คูณองค์ประกอบทั้งหมดของแถว (คอลัมน์) ของเมทริกซ์ด้วยตัวเลขที่กำหนดเอง k ที่ไม่เท่ากับศูนย์ ตัวดีเทอร์มิแนนต์ของเมทริกซ์ผลลัพธ์จะเท่ากับดีเทอร์มิแนนต์ของเมทริกซ์ดั้งเดิมซึ่งคูณด้วย เค;

ในกรณีที่เพิ่มองค์ประกอบของแถวหรือคอลัมน์หนึ่งของเมทริกซ์องค์ประกอบที่สอดคล้องกันของแถวหรือคอลัมน์อื่นซึ่งคูณด้วยตัวเลข k จะไม่เปลี่ยนดีเทอร์มิแนนต์

สาระสำคัญของวิธีการเปลี่ยนแปลงเบื้องต้น : ลดเมทริกซ์ที่ต้องค้นหาอันดับให้เป็นสี่เหลี่ยมคางหมูโดยใช้การแปลงเบื้องต้น

เพื่ออะไร?

อันดับของเมทริกซ์ประเภทนี้ค่อนข้างหาง่าย เท่ากับจำนวนบรรทัดที่มีองค์ประกอบที่ไม่เป็นศูนย์อย่างน้อยหนึ่งองค์ประกอบ และเนื่องจากอันดับไม่เปลี่ยนแปลงเมื่อทำการแปลงเบื้องต้น นี่จึงเป็นอันดับของเมทริกซ์

เรามาอธิบายกระบวนการนี้กัน:

สำหรับเมทริกซ์สี่เหลี่ยม A ของลำดับ p x n จำนวนแถวที่มากกว่าจำนวนคอลัมน์:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k

สำหรับเมทริกซ์สี่เหลี่ยม A ของลำดับ p คูณ n จำนวนแถวที่น้อยกว่าจำนวนคอลัมน์:

A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b p p + 1 ⋯ b p n , R a n k (A) = p

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0

สำหรับเมทริกซ์จตุรัส A ตามลำดับ n โดย n:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k , k< n

ตัวอย่างที่ 5

ค้นหาอันดับของเมทริกซ์ A โดยใช้การแปลงเบื้องต้น:

ก = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11

วิธีแก้ปัญหา?

เนื่องจากองค์ประกอบ a 11 แตกต่างจากศูนย์ จึงจำเป็นต้องคูณองค์ประกอบของแถวแรกของเมทริกซ์ A ด้วย 1 a 11 = 1 2:

ก = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

เราเพิ่มองค์ประกอบที่สอดคล้องกันของบรรทัดที่ 1 ให้กับองค์ประกอบของบรรทัดที่ 2 ซึ่งคูณด้วย (-3) ในองค์ประกอบของบรรทัดที่ 3 เราเพิ่มองค์ประกอบของบรรทัดที่ 1 ซึ่งคูณด้วย (-1):

~ ก (1) = 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ ก (2) = = 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

องค์ประกอบ a 22 (2) ไม่ใช่ศูนย์ ดังนั้นเราจึงคูณองค์ประกอบของแถวที่ 2 ของเมทริกซ์ A ด้วย A (2) ด้วย 1 a 22 (2) = - 2 3:

ก (3) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0

ในองค์ประกอบของแถวที่ 3 ของเมทริกซ์ผลลัพธ์เราจะเพิ่มองค์ประกอบที่สอดคล้องกันของแถวที่ 2 ซึ่งคูณด้วย 3 2
ถึงองค์ประกอบของบรรทัดที่ 4 - องค์ประกอบของบรรทัดที่ 2 ซึ่งคูณด้วย 9 2;
ถึงองค์ประกอบของแถวที่ 5 - องค์ประกอบของแถวที่ 2 ซึ่งคูณด้วย 3 2

องค์ประกอบแถวทั้งหมดเป็นศูนย์ ดังนั้น เมื่อใช้การแปลงเบื้องต้น เราจึงนำเมทริกซ์มาเป็นรูปแบบสี่เหลี่ยมคางหมู ซึ่งจะเห็นได้ว่า R an k (A (4)) = 2 ตามมาว่าอันดับของเมทริกซ์ดั้งเดิมก็เท่ากับสองด้วย

ความคิดเห็น

หากคุณทำการแปลงเบื้องต้นจะไม่อนุญาตให้ใช้ค่าโดยประมาณ!

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter

ในแต่ละเมทริกซ์ สามารถเชื่อมโยงสองอันดับได้: อันดับแถว (อันดับของระบบแถว) และอันดับคอลัมน์ (อันดับของระบบคอลัมน์)

ทฤษฎีบท

อันดับแถวของเมทริกซ์เท่ากับอันดับคอลัมน์

อันดับเมทริกซ์

คำนิยาม

อันดับเมทริกซ์$A$ คืออันดับของระบบแถวหรือคอลัมน์

แสดงโดย $\operatorname(rang) A$

ในทางปฏิบัติเพื่อค้นหาอันดับของเมทริกซ์จะใช้คำสั่งต่อไปนี้: อันดับของเมทริกซ์เท่ากับจำนวนแถวที่ไม่ใช่ศูนย์หลังจากลดเมทริกซ์ให้อยู่ในรูปแบบระดับระดับ

การแปลงเบื้องต้นในแถว (คอลัมน์) ของเมทริกซ์จะไม่เปลี่ยนอันดับ

อันดับของเมทริกซ์ขั้นตอนเท่ากับจำนวนแถวที่ไม่ใช่ศูนย์

ตัวอย่าง

ออกกำลังกาย.ค้นหาอันดับของเมทริกซ์ $ A=\left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & ( 7) \ \ (10) & (18) & (40) & (17) \\ (1) & (7) & (17) & (3)\end(อาร์เรย์)\right) $

สารละลาย.เมื่อใช้การแปลงเบื้องต้นในแถว เราจะลดเมทริกซ์ $A$ ให้อยู่ในรูปแบบระดับขั้น เมื่อต้องการทำเช่นนี้ ให้ลบสองตัวที่สองออกจากบรรทัดที่สามก่อน:

$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \\ (2) & (2) & (4) & (3) \\ (1) & (7) & (17) & (3)\end(อาร์เรย์)\right) $$

จากบรรทัดที่สองเราลบบรรทัดที่สี่คูณด้วย 4 จากสาม - สองในสี่:

$$ A \sim \left(\begin(array)(rrrr)(0) & (4) & (10) & (1) \\ (0) & (-20) & (-50) & (-5 ) \\ (0) & (-12) & (-30) & (-3) \\ (1) & (7) & (17) & (3)\end(อาร์เรย์)\right) $$

เราเพิ่มห้ารายการแรกในบรรทัดที่สอง และสามรายการที่สามเข้ากับบรรทัดที่สาม:

$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(อาร์เรย์)\right) $$

สลับบรรทัดแรกและบรรทัดที่สอง:

$$ A \sim \left(\begin(อาร์เรย์)(cccc)(0) & (0) & (0) & (0) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\end(อาร์เรย์)\right) $$

$$ A \sim \left(\begin(array)(cccc)(1) & (7) & (17) & (3) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0)\end(array)\right) \ลูกศรขวา \ชื่อตัวดำเนินการ(rang) A=2 $$

คำตอบ.$ ชื่อผู้ดำเนินการ (รัง) A=2 $

วิธีการกั้นพรมแดนผู้เยาว์

อีกวิธีหนึ่งในการค้นหาอันดับของเมทริกซ์นั้นขึ้นอยู่กับทฤษฎีบทนี้ - วิธีการขอบเล็กน้อย- สาระสำคัญของวิธีนี้คือการค้นหาผู้เยาว์ โดยเริ่มจากคำสั่งซื้อที่ต่ำกว่าและย้ายไปยังคำสั่งซื้อที่สูงกว่า หากค่ารองของลำดับ $n$th ไม่เท่ากับศูนย์ และค่ารองทั้งหมดของลำดับ $n+1$th เท่ากับศูนย์ ดังนั้นอันดับของเมทริกซ์จะเท่ากับ $n$

ตัวอย่าง

ออกกำลังกาย.ค้นหาอันดับของเมทริกซ์ $ A=\left(\begin(array)(rrrr)(1) & (2) & (-1) & (-2) \\ (2) & (4) & (3) & (0 ) \\ (-1) & (-2) & (6) & (6)\end(array)\right) $ โดยใช้วิธีการตัดขอบเล็กน้อย

สารละลาย.ลำดับรองขั้นต่ำคือลำดับรองของลำดับแรก ซึ่งเท่ากับองค์ประกอบของเมทริกซ์ $A$ ลองพิจารณาตัวอย่าง ตัวรอง $ M_(1)=1 \neq 0 $ อยู่ในแถวแรกและคอลัมน์แรก เราล้อมมันด้วยความช่วยเหลือของแถวที่สองและคอลัมน์ที่สอง เราจะได้ $ M_(2)^(1)=\left| ตัวรอง \begin(array)(ll)(1) & (2) \\ (2) & (4)\end(array)\right|=0 $ ; ลองพิจารณาลำดับที่สองรองอีกอัน โดยเราจะล้อม $M_1$ รองด้วยความช่วยเหลือของแถวที่สองและคอลัมน์ที่สาม จากนั้นเราก็จะได้ $ M_(2)^(2)=\left| \begin(array)(rr)(1) & (-1) \\ (2) & (3)\end(array)\right|=5 \neq 0 $ นั่นคืออันดับของเมทริกซ์คือ ไม่น้อยกว่าสอง ต่อไป เราจะพิจารณาผู้เยาว์ลำดับที่สามที่ล้อมรอบผู้เยาว์ $ M_(2)^(2) $ มีผู้เยาว์สองคน: การรวมกันของแถวที่สามกับคอลัมน์ที่สองหรือคอลัมน์ที่สี่ มาคำนวณรายย่อยเหล่านี้กัน

§3 อันดับเมทริกซ์

การกำหนดอันดับของเมทริกซ์

สตริงที่ขึ้นต่อเชิงเส้น

การแปลงเมทริกซ์เบื้องต้น

เมทริกซ์ที่เท่ากัน

อัลกอริทึมสำหรับการค้นหาอันดับของเมทริกซ์โดยใช้การแปลงเบื้องต้น

§4 ปัจจัยกำหนดลำดับที่หนึ่ง สอง และสาม

ปัจจัยกำหนดลำดับที่หนึ่ง

ปัจจัยกำหนดลำดับที่สอง

ปัจจัยกำหนดลำดับที่สาม

กฎซาร์รัส

§5 การคำนวณปัจจัยกำหนดคำสั่งซื้อจำนวนมาก

ส่วนเสริมพีชคณิต

ทฤษฎีบทของลาปลาซ

ตัวกำหนดเมทริกซ์สามเหลี่ยม

แอปพลิเคชัน. แนวคิดของปัจจัยกำหนด n-ลำดับที่โดยทั่วไป

§ 3 อันดับเมทริกซ์

เมทริกซ์แต่ละตัวมีลักษณะเป็นจำนวนหนึ่งซึ่งมีความสำคัญเมื่อแก้ระบบสมการเชิงเส้น เบอร์นี้มีชื่อว่า อันดับเมทริกซ์.

อันดับเมทริกซ์เท่ากับจำนวนแถวอิสระเชิงเส้น (คอลัมน์) ซึ่งแถวอื่นๆ (คอลัมน์) อื่นๆ ทั้งหมดจะแสดงเป็นเส้นตรง

เรียกแถว (คอลัมน์) ของเมทริกซ์ ขึ้นอยู่กับเชิงเส้นถ้าองค์ประกอบที่สอดคล้องกันนั้นเป็นสัดส่วน

กล่าวอีกนัยหนึ่ง องค์ประกอบของแถวที่ขึ้นต่อกันเชิงเส้นเส้นหนึ่งจะเท่ากับองค์ประกอบของอีกแถวหนึ่ง คูณด้วยจำนวนเดียวกัน ตัวอย่างเช่น แถวที่ 1 และ 2 ของเมทริกซ์ กจะขึ้นอยู่กับเชิงเส้นตรง ถ้า โดยที่ (แล คือตัวเลขจำนวนหนึ่ง)

ตัวอย่าง- ค้นหาอันดับของเมทริกซ์

สารละลาย.

บรรทัดที่สองจะได้มาจากบรรทัดแรกหากองค์ประกอบคูณด้วย -3 บรรทัดที่สามจะได้มาจากบรรทัดแรกหากองค์ประกอบคูณด้วย 0 และบรรทัดที่สี่ไม่สามารถแสดงผ่านบรรทัดแรกได้ ปรากฎว่าเมทริกซ์มีสองแถวที่เป็นอิสระเชิงเส้น เพราะ แถวที่หนึ่งและสี่ไม่เป็นสัดส่วน ดังนั้นอันดับของเมทริกซ์คือ 2

อันดับเมทริกซ์ กแสดงโดย อันดับ Aหรือ ร(ก).

จากคำจำกัดความของอันดับเมทริกซ์จะเป็นดังนี้:

1. อันดับของเมทริกซ์ไม่เกินขนาดที่เล็กที่สุดนั่นคือ สำหรับเมทริกซ์ เช้า × n .

2. อันดับของเมทริกซ์จะเป็นศูนย์ก็ต่อเมื่อเป็นเมทริกซ์ศูนย์เท่านั้น

ในกรณีทั่วไป การกำหนดอันดับของเมทริกซ์นั้นต้องใช้แรงงานค่อนข้างมาก เพื่ออำนวยความสะดวกในงานนี้จึงมีการใช้การแปลงที่รักษาอันดับของเมทริกซ์ซึ่งเรียกว่า การเปลี่ยนแปลงเบื้องต้น:

1) ละทิ้งแถวศูนย์ (คอลัมน์)

2) การคูณองค์ประกอบทั้งหมดของแถว (คอลัมน์) ด้วยตัวเลขอื่นที่ไม่ใช่ศูนย์

3) การเปลี่ยนลำดับของแถว (คอลัมน์)

4) การเพิ่มองค์ประกอบของหนึ่งแถว (คอลัมน์) องค์ประกอบที่เกี่ยวข้องของอีกแถวหนึ่ง (คอลัมน์) คูณด้วยตัวเลขใด ๆ

5) การขนย้ายเมทริกซ์

เมทริกซ์ทั้งสองเรียกว่า เทียบเท่าถ้าได้สิ่งหนึ่งจากอีกสิ่งหนึ่งโดยใช้การแปลงเบื้องต้นในจำนวนจำกัด

ความเท่าเทียมกันของเมทริกซ์ระบุด้วยเครื่องหมาย “~” (เทียบเท่า)

เมื่อใช้การแปลงเบื้องต้น เมทริกซ์ใด ๆ ก็สามารถลดลงเป็นรูปแบบสามเหลี่ยมได้ จากนั้นการคำนวณอันดับก็ไม่ใช่เรื่องยาก

กระบวนการคำนวณอันดับของเมทริกซ์โดยใช้การแปลงเบื้องต้นลองดูตัวอย่าง

ตัวอย่าง- ค้นหาอันดับของเมทริกซ์

เอ =

สารละลาย.

หน้าที่ของเราคือนำเมทริกซ์มาสู่รูปสามเหลี่ยม เช่น ใช้การแปลงเบื้องต้น ตรวจสอบให้แน่ใจว่ามีเพียงศูนย์ที่ต่ำกว่าเส้นทแยงมุมหลักในเมทริกซ์

1. พิจารณาบรรทัดแรก ถ้าธาตุ ก 11 = 0 ดังนั้นเมื่อจัดเรียงแถวหรือคอลัมน์ใหม่เรารับรองว่า ก 11 ¹ 0 ในตัวอย่างของเรา เรามาสลับกัน เช่น แถวแรกและแถวที่สองของเมทริกซ์:

เอ =

ตอนนี้องค์ประกอบ ก 11 ¹ 0. ด้วยการคูณแถวแรกด้วยตัวเลขที่เหมาะสมแล้วบวกกับแถวอื่น เราจะตรวจสอบให้แน่ใจว่าองค์ประกอบทั้งหมดของคอลัมน์แรก (ยกเว้น ก 11) เท่ากับศูนย์

2. พิจารณาบรรทัดที่สอง ถ้าธาตุ ก 22 = 0 ดังนั้นเมื่อจัดเรียงแถวหรือคอลัมน์ใหม่ เรารับรองว่า ก 22 ¹ 0. ถ้าเป็นองค์ประกอบ ก 22 ¹ 0 (และเรามี ก 22 = –1 ¹ 0) จากนั้นโดยการคูณแถวที่สองด้วยตัวเลขที่เหมาะสมแล้วบวกกับแถวอื่นๆ เราจะตรวจสอบให้แน่ใจว่าองค์ประกอบทั้งหมดของคอลัมน์ที่สอง (ยกเว้น ก 22) เท่ากับศูนย์

3. หากกระบวนการแปลงส่งผลให้แถว (คอลัมน์) ประกอบด้วยศูนย์ทั้งหมด ให้ละทิ้งแถวเหล่านั้น ในตัวอย่างของเรา เราจะละทิ้งบรรทัดที่ 3 และ 4:

เมทริกซ์สุดท้ายมีรูปแบบขั้นบันไดและประกอบด้วยสองแถว พวกมันมีความเป็นอิสระเชิงเส้น ดังนั้นอันดับของเมทริกซ์คือ 2

§ 4 ปัจจัยกำหนดลำดับที่หนึ่ง สอง และสาม

ในบรรดาเมทริกซ์ที่หลากหลาย เมทริกซ์จัตุรัสจะมีความโดดเด่นแยกกัน เมทริกซ์ประเภทนี้ดีเพราะ:

1. เมทริกซ์หน่วยเป็นรูปสี่เหลี่ยมจัตุรัส

2. คุณสามารถคูณและเพิ่มเมทริกซ์จตุรัสที่มีลำดับเดียวกันได้ ซึ่งส่งผลให้ได้เมทริกซ์ที่มีลำดับเดียวกัน

3. เมทริกซ์จัตุรัสสามารถยกกำลังได้

นอกจากนี้ เฉพาะเมทริกซ์จัตุรัสเท่านั้นที่สามารถคำนวณดีเทอร์มิแนนต์ได้

ดีเทอร์มิแนนต์เมทริกซ์เป็นตัวเลขพิเศษที่คำนวณตามกฎเกณฑ์บางประการ ดีเทอร์มิแนนต์เมทริกซ์ กแสดงโดย:

หรือวงเล็บเหลี่ยม: ,

หรือด้วยอักษรกรีกตัวพิมพ์ใหญ่ เดลต้า: Δ( ก),

หรือสัญลักษณ์ “ดีเทอร์มิแนนต์” : det ( ก).

ตัวกำหนดเมทริกซ์ลำดับที่หนึ่ง ก= (ก 11) หรือ ปัจจัยกำหนดลำดับที่หนึ่งเป็นตัวเลขเท่ากับองค์ประกอบเมทริกซ์:

Δ 1 = =ก 11

ตัวกำหนดเมทริกซ์ลำดับที่สอง หรือ ปัจจัยกำหนดลำดับที่สอง

ตัวอย่าง:

ตัวกำหนดเมทริกซ์ลำดับที่สาม หรือ ปัจจัยกำหนดลำดับที่สามคือตัวเลขที่คำนวณโดยสูตร:

สามารถคำนวณปัจจัยกำหนดลำดับที่สามได้โดยใช้ กฎของซาร์รัส .

กฎซาร์รัส- ไปที่ตัวกำหนดลำดับที่สามทางด้านขวาให้ลงนามในสองคอลัมน์แรกและมีเครื่องหมายบวก (+) นำผลรวมของผลิตภัณฑ์ของสามองค์ประกอบที่อยู่บนเส้นทแยงมุมหลักของดีเทอร์มิแนนต์และบน "เส้นตรง" ขนานกับหลัก เส้นทแยงมุมที่มีเครื่องหมายลบ (-) นำผลรวมของผลิตภัณฑ์ขององค์ประกอบที่อยู่บนเส้นทแยงมุมที่สองและบน "เส้นตรง" ขนานไปกับมัน

ตัวอย่าง:

สังเกตได้ง่ายว่าจำนวนคำศัพท์ในดีเทอร์มิแนนต์เพิ่มขึ้นตามลำดับ โดยทั่วไปในปัจจัยกำหนด nลำดับที่ 2 จำนวนพจน์คือ 1·2·3·…· n = n!.

ตรวจสอบกัน: สำหรับ Δ 1 จำนวนเทอมคือ 1! = 1,

สำหรับ Δ 2 จำนวนเทอมคือ 2! = 1 2 = 2,

สำหรับ Δ 3 จำนวนเทอมคือ 3! = 1·2·3 = 6.

ตามมาว่าสำหรับตัวกำหนดลำดับที่ 4 จำนวนเทอมคือ 4! = 1·2·3·4 = 24 ซึ่งหมายความว่าการคำนวณปัจจัยกำหนดดังกล่าวต้องใช้แรงงานค่อนข้างมาก ไม่ต้องพูดถึงปัจจัยกำหนดลำดับที่สูงกว่าด้วย เมื่อคำนึงถึงสิ่งนี้ พวกเขาพยายามลดการคำนวณปัจจัยกำหนดของคำสั่งซื้อจำนวนมากให้เป็นการคำนวณปัจจัยกำหนดของลำดับที่สองหรือสาม

§ 5 การคำนวณปัจจัยกำหนดคำสั่งซื้อจำนวนมาก

ให้เราแนะนำแนวคิดหลายประการ

ให้เมทริกซ์จตุรัสมา หนึ่ง-ลำดับที่:

ก=

ส่วนน้อย มองค์ประกอบ ij ก ij เรียกว่าดีเทอร์มิแนนต์ ( n– 1)ลำดับที่ได้มาจากเมทริกซ์ กโดยการขีดฆ่าออก ฉัน-บรรทัดที่ และ เจคอลัมน์ที่

ยกตัวอย่างธาตุรอง กเมทริกซ์ลำดับที่สาม 12 ตัวจะเป็น:

ส่วนเสริมพีชคณิต กองค์ประกอบ ij ก ij เป็นผู้เยาว์ มีเครื่องหมาย (−1) ฉัน + เจ:

กไอจ = (−1) ฉัน + เจเอ็มฉัน

กล่าวอีกนัยหนึ่ง กไอ = มฉันถ้า ฉัน+เจเลขคู่

กไอจ = − มฉันถ้า ฉัน+เจเลขคี่

ตัวอย่าง- ค้นหาการเสริมพีชคณิตขององค์ประกอบของแถวที่สองของเมทริกซ์

สารละลาย.

การใช้การบวกพีชคณิตทำให้สามารถคำนวณปัจจัยกำหนดลำดับขนาดใหญ่ได้โดยอิงตามทฤษฎีบทของลาปลาซ

ทฤษฎีบทของลาปลาซ ดีเทอร์มิแนนต์ของเมทริกซ์จตุรัสเท่ากับผลรวมของผลิตภัณฑ์ขององค์ประกอบของแถว (คอลัมน์) ใด ๆ และการเสริมพีชคณิต:

– การขยายตัวตามแถวที่ i

( – การขยายตัวในคอลัมน์ j)

ตัวอย่าง- คำนวณดีเทอร์มิแนนต์ของเมทริกซ์ ขยายไปตามแถวแรก

สารละลาย.

ดังนั้น ปัจจัยกำหนดลำดับใดๆ จึงสามารถลดลงเหลือเพียงการคำนวณปัจจัยกำหนดลำดับที่ต่ำกว่าหลายตัวได้ เห็นได้ชัดว่าสำหรับการสลายตัวจะสะดวกในการเลือกแถวหรือคอลัมน์ที่มีศูนย์มากที่สุดเท่าที่จะเป็นไปได้

ลองดูอีกตัวอย่างหนึ่ง

ตัวอย่าง- คำนวณดีเทอร์มิแนนต์ของเมทริกซ์รูปสามเหลี่ยม

สารละลาย.

เข้าใจแล้ว ดีเทอร์มิแนนต์ของเมทริกซ์สามเหลี่ยมเท่ากับผลคูณขององค์ประกอบของเส้นทแยงมุมหลัก .

การได้มาที่สำคัญนี้ทำให้ง่ายต่อการคำนวณดีเทอร์มีแนนต์ของเมทริกซ์สามเหลี่ยมใดๆ ทั้งหมดนี้มีประโยชน์มากกว่า เนื่องจากถ้าจำเป็น ตัวกำหนดใดๆ ก็สามารถถูกลดทอนให้อยู่ในรูปสามเหลี่ยมได้ ในกรณีนี้ มีการใช้คุณสมบัติบางอย่างของดีเทอร์มิแนนต์

แอปพลิเคชัน

แนวคิดของปัจจัยกำหนด n-ลำดับที่โดยทั่วไป

โดยทั่วไป เป็นไปได้ที่จะให้คำจำกัดความที่เข้มงวดสำหรับดีเทอร์มิแนนต์ของเมทริกซ์ n-สั่งซื้อ แต่สำหรับสิ่งนี้จำเป็นต้องแนะนำแนวคิดหลายประการ

การจัดเรียงใหม่หมายเลข 1, 2, ..., nการจัดเรียงตัวเลขเหล่านี้ตามลำดับใด ๆ เรียกว่า ในพีชคณิตเบื้องต้นมีการพิสูจน์แล้วว่าจำนวนการเรียงสับเปลี่ยนทั้งหมดที่สามารถเกิดขึ้นได้ nตัวเลขเท่ากับ 12...n = n- ตัวอย่างเช่นจากสามหมายเลข 1, 2, 3 คุณสามารถสร้าง 3 ได้! = 6 การเรียงสับเปลี่ยน: 123, 132, 312, 321, 231, 213

พวกเขาบอกว่าในการเรียงสับเปลี่ยนตัวเลขนี้ ฉันและ เจแต่งหน้า การผกผัน(เลอะเทอะ) ถ้า ฉัน> เจ, แต่ ฉันมาก่อนหน้านี้ในการเรียงสับเปลี่ยนนี้ เจนั่นคือถ้าจำนวนที่มากกว่าอยู่ทางด้านซ้ายของจำนวนที่น้อยกว่า

การเรียงสับเปลี่ยนเรียกว่า สม่ำเสมอ(หรือ แปลก) ถ้ามีจำนวนการผกผันเป็นคู่ (คี่)

การดำเนินการที่หนึ่งผ่านจากการเรียงสับเปลี่ยนที่หนึ่งไปยังอีกที่ประกอบด้วยสิ่งเดียวกัน nเรียกว่าตัวเลข การทดแทน nระดับที่.

การทดแทนที่แปลงการเรียงสับเปลี่ยนหนึ่งไปเป็นอีกวิธีหนึ่งจะเขียนเป็นสองบรรทัดในวงเล็บทั่วไปและตัวเลขที่อยู่ในตำแหน่งเดียวกันในการเรียงสับเปลี่ยนที่กำลังพิจารณาเรียกว่าสอดคล้องกันและเขียนไว้ด้านล่างอีกอัน เช่น สัญลักษณ์

หมายถึงการแทนที่โดยที่ 3 ไปที่ 4, 1 ไปที่ 2, 2 ไปที่ 1, 4 ไปที่ 3 การแทนที่เรียกว่าคู่ (หรือคี่) ถ้าจำนวนการกลับรายการทั้งหมดในทั้งสองแถวของการแทนที่เป็นเลขคู่ (คี่ ). การทดแทนใดๆ n- เลขยกกำลังเขียนได้เป็น

เหล่านั้น. โดยมีตัวเลขธรรมชาติอยู่บรรทัดบนสุด

ให้เราได้รับเมทริกซ์กำลังสองตามลำดับ n

ให้เราพิจารณาผลิตภัณฑ์ที่เป็นไปได้ทั้งหมดตาม nองค์ประกอบของเมทริกซ์นี้ ซึ่งนำมาเพียงรายการเดียวจากแต่ละแถวและแต่ละคอลัมน์ เช่น ผลงานในรูปแบบ:

ดัชนีอยู่ที่ไหน ถาม 1 , ถาม 2 ,..., qnทำการเรียงสับเปลี่ยนตัวเลข
1, 2,..., n- จำนวนผลิตภัณฑ์ดังกล่าวเท่ากับจำนวนการเรียงสับเปลี่ยนที่แตกต่างกัน nตัวละครเช่น เท่ากับ n- เครื่องหมายการทำงาน เท่ากับ (–1) ถาม, ที่ไหน ถาม– จำนวนการผกผันในการเรียงสับเปลี่ยนดัชนีที่สองขององค์ประกอบ

ปัจจัยกำหนด n-ลำดับที่คือผลรวมพีชคณิตของผลิตภัณฑ์ที่เป็นไปได้ทั้งหมดเทียบกับ nองค์ประกอบเมทริกซ์ที่นำมาหนึ่งรายการเท่านั้นจากแต่ละแถวและแต่ละคอลัมน์เช่น ผลงานในรูปแบบ: - ในกรณีนี้คือสัญลักษณ์ของผลิตภัณฑ์ เท่ากับ (–1) ถาม, ที่ไหน ถาม– จำนวนการผกผันในการเรียงสับเปลี่ยนดัชนีที่สองขององค์ประกอบ

พีชคณิตเชิงเส้น

พิจารณาเมทริกซ์ A ที่มีขนาด

ก=
ให้เราเลือก k แถวและ k คอลัมน์ (
).

คำนิยาม 26:ส่วนน้อยลำดับที่ k ของเมทริกซ์ A คือดีเทอร์มิแนนต์ของเมทริกซ์จตุรัสที่ได้จากเมทริกซ์ที่กำหนดโดยการเลือกมัน

krows และ kcolumns

คำนิยาม 27:อันดับของเมทริกซ์เรียกว่าลำดับที่ใหญ่ที่สุดที่ไม่ใช่ศูนย์ของผู้เยาว์ r(A)

คำนิยาม 28:ผู้เยาว์ซึ่งมีลำดับตรงกับยศเรียกว่า ผู้เยาว์ขั้นพื้นฐาน.

คำแถลง:

1. อันดับแสดงเป็นจำนวนเต็ม (
)

2.ร=0,
เมื่อ A เป็นศูนย์

การแปลงเบื้องต้นของเมทริกซ์

การแปลงเมทริกซ์เบื้องต้นมีดังต่อไปนี้:

1) การคูณองค์ประกอบทั้งหมดของแถว (คอลัมน์) ของเมทริกซ์ด้วยจำนวนเดียวกัน

2) การเพิ่มองค์ประกอบของแถว (คอลัมน์) ของเมทริกซ์องค์ประกอบที่เกี่ยวข้องของแถวอื่น (คอลัมน์) คูณด้วยจำนวนเดียวกันลงในองค์ประกอบของแถวใด ๆ (คอลัมน์)

3) การจัดเรียงแถว (คอลัมน์) ของเมทริกซ์ใหม่

4) ละทิ้งแถวศูนย์ (คอลัมน์)

5) แทนที่แถวเมทริกซ์ด้วยคอลัมน์ที่เกี่ยวข้อง

คำนิยาม 29:เมทริกซ์ที่เกิดจากกันและกันภายใต้การแปลงเบื้องต้นเรียกว่าเมทริกซ์ที่เท่ากันและเขียนแทนด้วย “~”

คุณสมบัติหลักของเมทริกซ์ที่เทียบเท่า: อันดับของเมทริกซ์ที่เท่ากันจะเท่ากัน

ตัวอย่างที่ 18:คำนวณ r(A)

สารละลาย:คูณบรรทัดแรกทีละขั้นตอนด้วย (-4)(-2)

(-7) จากนั้นเพิ่มบรรทัดที่สอง สาม และสี่ตามลำดับ

สลับบรรทัดที่สองและสี่
คูณบรรทัดที่สองด้วย (-2) แล้วบวกเข้ากับบรรทัดที่สี่ มาเพิ่มบรรทัดที่สองและสามกัน

มาเพิ่มบรรทัดที่สามและสี่กัน

~
ลบเส้นศูนย์

~
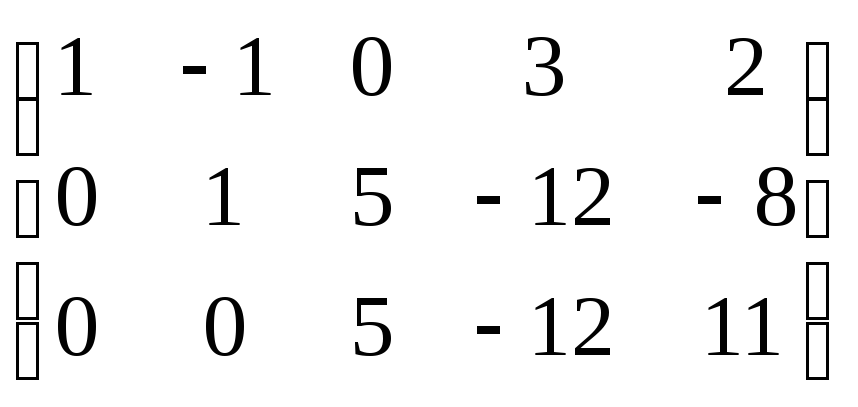r(A)=3
ตำแหน่งของเมทริกซ์ดั้งเดิม

เท่ากับสาม

คำนิยาม 30:ลองเรียกเมทริกซ์ A ทีละขั้นตอนหากองค์ประกอบทั้งหมดของเส้นทแยงมุมหลัก 0 และองค์ประกอบใต้เส้นทแยงมุมหลักจะเป็นศูนย์

เสนอ:

1) อันดับของเมทริกซ์ขั้นตอนเท่ากับจำนวนแถว

2) เมทริกซ์ใดๆ สามารถถูกรีดิวซ์เป็นรูปแบบระดับชั้นได้โดยใช้การแปลงเบื้องต้น

ตัวอย่างที่ 19:เมทริกซ์มีค่าเท่าใด
มีอันดับเท่ากับหนึ่งเหรอ?

สารละลาย:อันดับจะเท่ากับหนึ่งถ้าดีเทอร์มิแนนต์ลำดับที่สองเท่ากับศูนย์ เช่น

§6 ระบบสมการเชิงเส้นรูปแบบทั่วไป

ดูระบบ
---(9) เรียกว่าระบบรูปทั่วไป

คำนิยาม 31:ทั้งสองระบบจะเรียกว่าเท่ากันถ้าแต่ละคำตอบของระบบแรกเป็นคำตอบของระบบที่สองและในทางกลับกัน

ในระบบ (1) เมทริกซ์ A=
เราเรียกมันว่าเมทริกซ์หลักของระบบ และ =
ระบบเมทริกซ์ขยาย

ทฤษฎีบท.โครเนกเกอร์-คาเปลลี

เพื่อให้ระบบ (9) เข้ากันได้ มีความจำเป็นและเพียงพอที่อันดับของเมทริกซ์หลักของระบบจะเท่ากับอันดับของเมทริกซ์ขยาย กล่าวคือ r(A)=r( )

ทฤษฎีบท 1หากอันดับของเมทริกซ์ของระบบร่วมเท่ากับจำนวนไม่ทราบ แสดงว่าระบบมีวิธีแก้ปัญหาเฉพาะ

ทฤษฎีบท 2หากอันดับของเมทริกซ์ของระบบข้อต่อน้อยกว่าจำนวนที่ไม่ทราบ ระบบก็จะมีคำตอบจำนวนอนันต์

กฎสำหรับการแก้ระบบสมการเชิงเส้นตามอำเภอใจ:

1) ค้นหาอันดับของเมทริกซ์หลักและเมทริกซ์ขยายของระบบ ถ้า
แล้วระบบเข้ากันไม่ได้

2) ถ้า
=r แสดงว่าระบบมีความสม่ำเสมอ ค้นหาคำสั่งย่อยพื้นฐานของคำสั่ง r

เราจะเรียกผู้เยาว์ขั้นพื้นฐานว่าผู้เยาว์โดยพิจารณาจากอันดับของเมทริกซ์

ค่าไม่ทราบซึ่งมีสัมประสิทธิ์รวมอยู่ในค่ารองพื้นฐานเรียกว่า เงินต้น (พื้นฐาน) และจะทิ้งไว้ทางซ้าย ในขณะที่ค่าไม่ทราบที่เหลือจะเรียกว่าว่างและโอนไปทางด้านขวาของสมการ

3) ค้นหาสำนวนของสิ่งที่ไม่รู้จักหลักโดยใช้สิ่งที่ฟรี ได้รับวิธีแก้ปัญหาทั่วไปของระบบตัวอย่างที่ 20: