การแบ่งระนาบพิกัดออกเป็นสี่ส่วน ระนาบพิกัด: มันคืออะไร? จะทำเครื่องหมายจุดและสร้างตัวเลขบนระนาบพิกัดได้อย่างไร? ตัวอย่างของระนาบพิกัด
นี้ เครื่องคิดเลขคณิตศาสตร์ออนไลน์จะช่วยคุณได้ แก้สมการหรืออสมการด้วยโมดูลัส- โปรแกรมสำหรับ การแก้สมการและอสมการด้วยมอดูลิไม่เพียงแต่ให้คำตอบต่อปัญหาเท่านั้น แต่ยังนำไปสู่อีกด้วย วิธีแก้ปัญหาโดยละเอียดพร้อมคำอธิบาย, เช่น. แสดงกระบวนการรับผลลัพธ์
โปรแกรมนี้อาจเป็นประโยชน์สำหรับนักเรียนมัธยมปลาย โรงเรียนมัธยมศึกษาในการเตรียมตัวสำหรับ การทดสอบและการสอบเมื่อทดสอบความรู้ก่อนการสอบ Unified State เพื่อให้ผู้ปกครองได้ควบคุมการแก้ปัญหาต่างๆในวิชาคณิตศาสตร์และพีชคณิต หรืออาจจะแพงเกินไปสำหรับคุณที่จะจ้างครูสอนพิเศษหรือซื้อตำราเรียนใหม่ หรือคุณเพียงต้องการที่จะทำให้มันเสร็จโดยเร็วที่สุด?การบ้าน
ในวิชาคณิตศาสตร์หรือพีชคณิต? ในกรณีนี้ คุณสามารถใช้โปรแกรมของเราพร้อมวิธีแก้ปัญหาโดยละเอียดได้ ด้วยวิธีนี้คุณสามารถใช้จ่ายของคุณการฝึกอบรมของตัวเอง และ/หรือฝึกอบรมพวกเขาน้องชาย
หรือน้องสาวในขณะที่ระดับการศึกษาในด้านปัญหาที่กำลังแก้ไขเพิ่มขึ้น|x|
x^2 + 2|x-1| -6 = 0
แก้สมการหรืออสมการ
พบว่าไม่ได้โหลดสคริปต์บางตัวที่จำเป็นในการแก้ปัญหานี้ และโปรแกรมอาจไม่ทำงาน
ในกรณีนี้ ให้ปิดการใช้งานและรีเฟรชเพจ
JavaScript ถูกปิดใช้งานในเบราว์เซอร์ของคุณ
เพื่อให้วิธีแก้ปัญหาปรากฏขึ้น คุณต้องเปิดใช้งาน JavaScript
ต่อไปนี้เป็นคำแนะนำเกี่ยวกับวิธีเปิดใช้งาน JavaScript ในเบราว์เซอร์ของคุณ
เพราะ มีคนจำนวนมากยินดีแก้ไขปัญหา คำขอของคุณอยู่ในคิวแล้ว ภายในไม่กี่วินาทีวิธีแก้ปัญหาจะปรากฏขึ้นด้านล่าง
โปรดรอ วินาที...ถ้าคุณ
สังเกตเห็นข้อผิดพลาดในการแก้ปัญหา จากนั้นคุณสามารถเขียนเกี่ยวกับเรื่องนี้ในแบบฟอร์มคำติชมอย่าลืม ระบุว่างานใด.
คุณตัดสินใจว่าอะไร
เข้าไปในทุ่งนา
เกม ปริศนา อีมูเลเตอร์ของเรา:
ในหลักสูตรพีชคณิตขั้นพื้นฐานของโรงเรียน คุณอาจพบกับสมการและอสมการที่ง่ายที่สุดด้วยโมดูลัส ในการแก้ปัญหาเหล่านี้ คุณสามารถใช้วิธีเรขาคณิตโดยยึดตามข้อเท็จจริงที่ว่า \(|x-a| \) คือระยะห่างบนเส้นจำนวนระหว่างจุด x และ a: \(|x-a| = \rho (x;\; a) \) ตัวอย่างเช่น ในการแก้สมการ \(|x-3|=2\) คุณต้องหาจุดบนเส้นจำนวนที่อยู่ห่างจากจุดที่ 3 ที่ระยะ 2 โดยมีจุดดังกล่าวสองจุด: \(x_1=1 \) และ \(x_2=5\)
![]()
การแก้อสมการ \(|2x+7| ![]()
แต่วิธีหลักในการแก้สมการและอสมการด้วยโมดูลัสนั้นเกี่ยวข้องกับสิ่งที่เรียกว่า "การเปิดเผยของโมดูลัสตามคำจำกัดความ":
ถ้า \(a \geq 0 \) ดังนั้น \(|a|=a \);
ถ้า \(a ตามกฎแล้ว สมการ (อสมการ) ที่มีมอดูลิลดลงเหลือเพียงเซตของสมการ (อสมการ) ที่ไม่มีเครื่องหมายโมดูลัส
นอกเหนือจากคำจำกัดความข้างต้นแล้ว ยังมีการใช้ข้อความต่อไปนี้:
1) ถ้า \(c > 0\) ดังนั้นสมการ \(|f(x)|=c \) จะเทียบเท่ากับเซตของสมการ: \(\left[\begin(array)(l) f(x )=c \\ f(x)=-c \end(อาร์เรย์)\right
2) ถ้า \(c > 0 \) แล้วความไม่เท่าเทียมกัน \(|f(x)| 3) ถ้า \(c \geq 0 \) แล้วความไม่เท่าเทียมกัน \(|f(x)| > c \) คือ เทียบเท่ากับเซตของอสมการ : \(\left[\begin(array)(l) f(x) c \end(array)\right. \)
4) ถ้าทั้งสองด้านมีความไม่เท่ากัน \(f(x) ตัวอย่าง 1. แก้สมการ \(x^2 +2|x-1| -6 = 0\)
ถ้า \(x-1 \geq 0\) แล้ว \(|x-1| = x-1\) และ สมการที่กำหนดใช้แบบฟอร์ม
\(x^2 +2(x-1) -6 = 0 \ลูกศรขวา x^2 +2x -8 = 0 \)
ถ้า \(x-1 \(x^2 -2(x-1) -6 = 0 \ลูกศรขวา x^2 -2x -4 = 0 \)
ดังนั้นควรพิจารณาสมการที่กำหนดแยกกันในแต่ละกรณีที่ระบุ
1) ให้ \(x-1 \geq 0 \) เช่น \(x\geq 1\) จากสมการ \(x^2 +2x -8 = 0\) เราพบว่า \(x_1=2, \; x_2=-4\)
เงื่อนไข \(x \geq 1 \) เป็นไปตามค่า \(x_1=2\) เท่านั้น
2) ให้ \(x-1 ตอบ: \(2; \;\; 1-\sqrt(5) \)
ตัวอย่าง 2. แก้สมการ \(|x^2-6x+7| = \frac(5x-9)(3)\)วิธีแรก
(การขยายโมดูลตามคำจำกัดความ)
การให้เหตุผลตามตัวอย่างที่ 1 เราได้ข้อสรุปว่าสมการที่กำหนดจะต้องพิจารณาแยกกันหากตรงตามเงื่อนไขสองข้อ: \(x^2-6x+7 \geq 0 \) หรือ \(x^2-6x+7 1) ถ้า \(x^2-6x+7 \geq 0 \) ดังนั้น \(|x^2-6x+7| = x^2-6x+7 \) และสมการที่ให้มาจะอยู่ในรูปแบบ \(x ^2 -6x+7 = \frac(5x-9)(3) \ลูกศรขวา 3x^2-23x+30=0 \) ตัดสินใจเรื่องนี้แล้วสมการกำลังสอง
เราได้รับ: \(x_1=6, \; x_2=\frac(5)(3) \) มาดูกันว่าค่า \(x_1=6\) ตรงตามเงื่อนไข \(x^2-6x+7 \geq 0\) หรือไม่ เมื่อต้องการทำเช่นนี้ ให้แทนที่ค่าที่ระบุลงใน- เราได้รับ: \(6^2-6 \cdot 6+7 \geq 0 \) เช่น \(7 \geq 0 \) คืออสมการที่แท้จริง
ซึ่งหมายความว่า \(x_1=6\) คือรากของสมการที่กำหนด
มาดูกันว่าค่า \(x_2=\frac(5)(3)\) ตรงตามเงื่อนไข \(x^2-6x+7 \geq 0\) หรือไม่ เมื่อต้องการทำเช่นนี้ ให้แทนที่ค่าที่ระบุลงในอสมการกำลังสอง เราได้รับ: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \) เช่น \(\frac(25)(9) -3 \geq 0 \) เป็นอสมการที่ไม่ถูกต้อง ซึ่งหมายความว่า \(x_2=\frac(5)(3)\) ไม่ใช่รากของสมการที่กำหนด
2) ถ้า \(x^2-6x+7 Value \(x_3=3\) ตรงตามเงื่อนไข \(x^2-6x+7 Value \(x_4=\frac(4)(3) \) ไม่ตรงตามเงื่อนไข เงื่อนไข \ (x^2-6x+7 ดังนั้น สมการที่ให้มามีสองราก: \(x=6, \; x=3 \)วิธีที่สอง.
ถ้าสมการ \(|f(x)| = h(x) \) ถูกกำหนดไว้ ดังนั้นด้วย \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(อาร์เรย์)\right \) สมการทั้งสองนี้ได้รับการแก้ไขข้างต้น (โดยใช้วิธีแรกในการแก้สมการที่กำหนด) รากของสมการมีดังนี้: \(6,\; \frac(5)(3),\; 3,\; \frac(4 )(3)\) เงื่อนไข \(\frac(5x-9)(3) \geq 0 \) จากสิ่งเหล่านี้สี่ค่า
พอใจเพียงสอง: 6 และ 3 ซึ่งหมายความว่าสมการที่กำหนดมีสองราก: \(x=6, \; x=3\)วิธีที่สาม
(กราฟิก)
1) มาสร้างกราฟของฟังก์ชัน \(y = |x^2-6x+7| \) กัน ก่อนอื่น เรามาสร้างพาราโบลา \(y = x^2-6x+7\) กันก่อน
เรามี \(x^2-6x+7 = (x-3)^2-2 \) กราฟของฟังก์ชัน \(y = (x-3)^2-2\) สามารถหาได้จากกราฟของฟังก์ชัน \(y = x^2 \) โดยเลื่อนไปทางขวา 3 หน่วยมาตราส่วน (ตาม แกน x) และลดลง 2 หน่วย (ตามแกน y) เส้นตรง x=3 คือแกนของพาราโบลาที่เราสนใจ เป็นจุดควบคุมสำหรับการวางแผนที่แม่นยำยิ่งขึ้น สะดวกในการใช้จุด (3; -2) - จุดยอดของพาราโบลา จุด (0; 7) และจุด (6; 7) สมมาตรกับจุดนั้นสัมพันธ์กับแกนของพาราโบลา .หากต้องการสร้างกราฟของฟังก์ชัน \(y = |x^2-6x+7| \) คุณต้องปล่อยส่วนต่างๆ ของพาราโบลาที่สร้างขึ้นซึ่งไม่ต่ำกว่าแกน x ไว้ไม่เปลี่ยนแปลง และสะท้อนส่วนนั้นของ พาราโบลาที่อยู่ต่ำกว่าแกน x สัมพันธ์กับแกน x

สิ่งสำคัญคือจุด x = 1.8 ของจุดตัดของเส้นตรงกับแกน abscissa จะอยู่ทางด้านขวาของจุดตัดด้านซ้ายของพาราโบลากับแกน abscissa - นี่คือจุด \(x=3-\ sqrt(2) \) (เนื่องจาก \(3-\sqrt(2 ) 3) เมื่อพิจารณาจากรูปวาด กราฟจะตัดกันที่จุดสองจุด - A(3; 2) และ B(6; 7) โดยแทนที่จุดขาดของสิ่งเหล่านี้ คะแนน x = 3 และ x = 6 ในสมการที่กำหนด เราเชื่อว่าในทั้งสองกรณี ในอีกค่าหนึ่ง จะได้ความเท่าเทียมกันของตัวเลขที่ถูกต้อง ซึ่งหมายความว่าสมมติฐานของเราได้รับการยืนยัน - สมการมีสองราก: x = 3 และ x = 6 คำตอบ: 3;
ความคิดเห็น. วิธีกราฟิกเพื่อความสง่างามทั้งหมดจึงไม่น่าเชื่อถือมากนัก ในตัวอย่างที่พิจารณา มันได้ผลเพียงเพราะว่ารากของสมการเป็นจำนวนเต็ม
ตัวอย่าง 3. แก้สมการ \(|2x-4|+|x+3| = 8\)
ตัวอย่าง 2. แก้สมการ \(|x^2-6x+7| = \frac(5x-9)(3)\)
นิพจน์ 2x–4 กลายเป็น 0 ที่จุด x = 2 และนิพจน์ x + 3 กลายเป็น 0 ที่จุด x = –3 สองจุดนี้แบ่งเส้นจำนวนออกเป็นสามช่วง: \(x
![]()
พิจารณาช่วงแรก: \((-\infty; \; -3) \)
ถ้า x พิจารณาช่วงที่สอง: \([-3; \; 2) \)
ถ้า \(-3 \leq x พิจารณาช่วงที่สาม: \(
อื่น ข้อเท็จจริงที่สำคัญ: โมดูลัสไม่เคยเป็นลบ- ไม่ว่าเราจะหาจำนวนใดก็ตาม ไม่ว่าจะเป็นค่าบวกหรือค่าลบ โมดูลัสของค่านั้นจะกลายเป็นค่าบวกเสมอ (หรือในกรณีที่รุนแรง ค่าศูนย์) นั่นคือสาเหตุที่โมดูลัสมักถูกเรียกว่าค่าสัมบูรณ์ของตัวเลข
นอกจากนี้ ถ้าเรารวมคำจำกัดความของโมดูลัสสำหรับจำนวนบวกและลบ เราจะได้คำจำกัดความสากลของโมดูลัสสำหรับตัวเลขทั้งหมด กล่าวคือ: โมดูลัสของตัวเลขจะเท่ากับตัวเลขนี้เอง ถ้าตัวเลขเป็นบวก (หรือศูนย์) หรือเท่ากับ หมายเลขตรงข้ามถ้าจำนวนเป็นลบ คุณสามารถเขียนสิ่งนี้เป็นสูตรได้:
นอกจากนี้ยังมีโมดูลัสเป็นศูนย์ แต่จะเท่ากับศูนย์เสมอ นอกจากนี้ยังเป็นศูนย์ เอกพจน์ซึ่งไม่มีสิ่งที่ตรงกันข้าม
ดังนั้น หากเราพิจารณาฟังก์ชัน $y=\left| x \right|$ แล้วลองวาดกราฟ คุณจะได้สิ่งนี้:
กราฟโมดูลัสและตัวอย่างการแก้สมการ
จากภาพนี้ จะเห็นได้ชัดทันทีว่า $\left| -m \right|=\ซ้าย| m \right|$ และกราฟโมดูลัสไม่เคยต่ำกว่าแกน x แต่นั่นไม่ใช่ทั้งหมด เส้นสีแดงทำเครื่องหมายเส้นตรง $y=a$ ซึ่งหากบวก $a$ จะทำให้เรามีรากสองตัวพร้อมกัน: $((x)_(1))$ และ $((x) _(2)) $ แต่เราจะพูดถึงเรื่องนั้นในภายหลัง :)
นอกเหนือจากคำจำกัดความพีชคณิตล้วนๆ แล้ว ยังมีคำจำกัดความทางเรขาคณิตอีกด้วย สมมติว่ามีจุดสองจุดบนเส้นจำนวน: $((x)_(1))$ และ $((x)_(2))$ ในกรณีนี้ นิพจน์ $\left| ((x)_(1))-((x)_(2)) \right|$ เป็นเพียงระยะห่างระหว่างจุดที่ระบุ หรือถ้าคุณต้องการความยาวของส่วนที่เชื่อมต่อจุดเหล่านี้:
 โมดูลัสคือระยะห่างระหว่างจุดบนเส้นจำนวน
โมดูลัสคือระยะห่างระหว่างจุดบนเส้นจำนวน คำจำกัดความนี้ยังบอกเป็นนัยว่าโมดูลัสไม่เป็นลบเสมอ แต่พอมีคำจำกัดความและทฤษฎี - มาดูสมการจริงกันดีกว่า :)
สูตรพื้นฐาน
โอเค เราได้แยกคำจำกัดความออกแล้ว แต่นั่นไม่ได้ทำให้มันง่ายขึ้นเลย จะแก้สมการที่มีโมดูลนี้ได้อย่างไร?
ใจเย็นๆ ใจเย็นๆ นะ เริ่มจากสิ่งที่ง่ายที่สุดกันก่อน พิจารณาบางสิ่งเช่นนี้:
\[\ซ้าย| x\ขวา|=3\]
ดังนั้นโมดูลัสของ $x$ เท่ากับ 3 $x$ จะเท่ากับเท่าใด? เมื่อดูจากคำจำกัดความแล้ว เราค่อนข้างพอใจกับ $x=3$ จริงหรือ:
\[\ซ้าย| 3\ขวา|=3\]
มีเลขอื่นอีกไหม? แคปดูเหมือนจะบอกเป็นนัยว่ามี ตัวอย่างเช่น $x=-3$ ก็เท่ากับ $\left| -3 \right|=3$ เช่น เป็นไปตามความเท่าเทียมกันที่ต้องการ
แล้วบางทีถ้าเราค้นหาแล้วคิดว่าเราจะเจอตัวเลขมากขึ้นล่ะ? แต่แยกมันออก: ตัวเลขมากขึ้นเลขที่ สมการ $\left| x \right|=3$ มีเพียงสองราก: $x=3$ และ $x=-3$
ตอนนี้เรามาทำให้งานซับซ้อนขึ้นเล็กน้อย ปล่อยให้ฟังก์ชัน $f\left(x \right)$ อยู่ใต้เครื่องหมายโมดูลัสแทนตัวแปร $x$ และใส่ตัวเลข $a$ แทนที่ตัวเลขสามตัวทางด้านขวา เราได้รับสมการ:
\[\ซ้าย| f\left(x \right) \right|=a\]
แล้วเราจะแก้ปัญหานี้ได้อย่างไร? ฉันขอเตือนคุณว่า $f\left(x \right)$ เป็นฟังก์ชันที่กำหนดเอง ส่วน $a$ คือตัวเลขใดๆ เหล่านั้น. อะไรก็ได้! ตัวอย่างเช่น:
\[\ซ้าย| 2x+1 \ขวา|=5\]
\[\ซ้าย| 10x-5 \ขวา|=-65\]
มาดูสมการที่สองกันดีกว่า คุณสามารถพูดเกี่ยวกับเขาได้ทันที: เขาไม่มีราก ทำไม ถูกต้อง: เพราะมันต้องการให้โมดูลัสเท่ากับ จำนวนลบซึ่งไม่เคยเกิดขึ้น เนื่องจากเรารู้อยู่แล้วว่าโมดูลัสจะเป็นจำนวนบวกเสมอ หรือในกรณีที่รุนแรง จะเป็นศูนย์
แต่ด้วยสมการแรก ทุกอย่างจะสนุกยิ่งขึ้น มีสองตัวเลือก: มีนิพจน์เชิงบวกอยู่ใต้เครื่องหมายโมดูลัส แล้วตามด้วย $\left| 2x+1 \right|=2x+1$ หรือนิพจน์นี้ยังคงเป็นลบ จากนั้น $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$ ในกรณีแรก สมการของเราจะถูกเขียนใหม่ดังนี้:
\[\ซ้าย| 2x+1 \right|=5\ลูกศรขวา 2x+1=5\]
และทันใดนั้นปรากฎว่านิพจน์ย่อย $2x+1$ นั้นเป็นบวกจริงๆ - มันเท่ากับเลข 5 นั่นคือ เราสามารถแก้สมการนี้ได้อย่างปลอดภัย - รากที่ได้จะเป็นคำตอบส่วนหนึ่ง:
ผู้ที่ไม่ไว้วางใจเป็นพิเศษสามารถลองแทนที่รากที่พบลงในสมการดั้งเดิมและตรวจสอบให้แน่ใจว่าโมดูลัสนั้นอยู่จริง จำนวนบวก.
ตอนนี้เรามาดูกรณีของนิพจน์ submodular เชิงลบ:
\[\left\( \begin(align)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end(align) \right.\Rightarrow -2x-1=5 \ลูกศรขวา 2x+1=-5\]
อ๊ะ! ทุกอย่างชัดเจนอีกครั้ง: เราถือว่า $2x+1 \lt 0$ และด้วยเหตุนี้เราจึงได้ $2x+1=-5$ - จริงๆ แล้วนิพจน์นี้มีค่าน้อยกว่าศูนย์ เราแก้สมการผลลัพธ์ในขณะที่รู้อยู่แล้วว่ารูทที่พบจะเหมาะกับเรา:
โดยรวมแล้ว เราได้รับสองคำตอบอีกครั้ง: $x=2$ และ $x=3$ ใช่ จำนวนการคำนวณมากกว่าสมการง่ายๆ $\left| เล็กน้อย x \right|=3$ แต่ไม่มีการเปลี่ยนแปลงโดยพื้นฐาน บางทีอาจมีอัลกอริธึมสากลบางประเภท?
ใช่ มีอัลกอริธึมดังกล่าวอยู่ และตอนนี้เราจะวิเคราะห์มัน
กำจัดเครื่องหมายมอดุลัส
ให้เราได้รับสมการ $\left| f\left(x \right) \right|=a$, และ $a\ge 0$ (มิฉะนั้น อย่างที่เรารู้อยู่แล้วว่าไม่มีราก) จากนั้น คุณสามารถกำจัดเครื่องหมายมอดุลัสได้โดยใช้กฎต่อไปนี้:
\[\ซ้าย| f\left(x \right) \right|=a\ลูกศรขวา f\left(x \right)=\pm a\]
ดังนั้นสมการของเราที่มีโมดูลัสจึงแยกออกเป็นสองส่วน แต่ไม่มีโมดูลัส นั่นคือทั้งหมดที่เทคโนโลยีเป็น! ลองแก้สมการสองสามข้อกัน เริ่มจากสิ่งนี้กันก่อน
\[\ซ้าย| 5x+4 \right|=10\ลูกศรขวา 5x+4=\pm 10\]
ลองพิจารณาแยกกันเมื่อมีเครื่องหมายบวกสิบทางด้านขวา และแยกกันเมื่อมีเครื่องหมายลบ เรามี:
\[\begin(align)& 5x+4=10\ลูกศรขวา 5x=6\ลูกศรขวา x=\frac(6)(5)=1,2; \\& 5x+4=-10\ลูกศรขวา 5x=-14\ลูกศรขวา x=-\frac(14)(5)=-2.8. \\\end(จัดแนว)\]
แค่นั้นแหละ! เรามีสองราก: $x=1.2$ และ $x=-2.8$ โซลูชันทั้งหมดใช้เวลาสองบรรทัดอย่างแท้จริง
โอเค ไม่ต้องสงสัย มาดูอะไรที่จริงจังกว่านี้กันหน่อย:
\[\ซ้าย| 7-5x\ขวา|=13\]
เราเปิดโมดูลอีกครั้งด้วยเครื่องหมายบวกและลบ:
\[\begin(align)& 7-5x=13\ลูกศรขวา -5x=6\ลูกศรขวา x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\ลูกศรขวา -5x=-20\ลูกศรขวา x=4 \\\end(จัดแนว)\]
สองสามบรรทัดอีกครั้ง - และคำตอบก็พร้อมแล้ว! อย่างที่ฉันบอกไปแล้วว่าโมดูลไม่มีอะไรซับซ้อน คุณเพียงแค่ต้องจำกฎสองสามข้อ ดังนั้นเราจึงเดินหน้าต่อไปและเริ่มต้นด้วยงานที่ซับซ้อนมากขึ้นอย่างแท้จริง
กรณีของตัวแปรทางขวามือ
พิจารณาสมการนี้:
\[\ซ้าย| 3x-2 \ขวา|=2x\]
สมการนี้แตกต่างโดยพื้นฐานจากสมการก่อนหน้าทั้งหมด ยังไง? และความจริงที่ว่าทางด้านขวาของเครื่องหมายเท่ากับคือนิพจน์ $2x$ - และเราไม่สามารถรู้ล่วงหน้าได้ว่าเป็นค่าบวกหรือค่าลบ
จะทำอย่างไรในกรณีนี้? ก่อนอื่น เราต้องเข้าใจสักครั้ง ถ้าด้านขวาของสมการกลายเป็นลบ สมการก็จะไม่มีราก- เรารู้แล้วว่าโมดูลไม่สามารถเท่ากับจำนวนลบได้
และประการที่สอง หากส่วนที่ถูกต้องยังคงเป็นค่าบวก (หรือเท่ากับศูนย์) คุณสามารถดำเนินการได้เหมือนเดิมทุกประการ เพียงเปิดโมดูลแยกกันด้วยเครื่องหมายบวกและแยกจากกันด้วยเครื่องหมายลบ
ดังนั้นเราจึงกำหนดกฎเกณฑ์สำหรับ ฟังก์ชั่นที่กำหนดเอง$f\left(x \right)$ และ $g\left(x \right)$ :
\[\ซ้าย| f\left(x \right) \right|=g\left(x \right)\ลูกศรขวา \left\( \begin(align)& f\left(x \right)=\pm g\left(x \right ), \\& g\left(x \right)\ge 0. \\\end(align) \right.\]
สัมพันธ์กับสมการของเราเราได้รับ:
\[\ซ้าย| 3x-2 \right|=2x\ลูกศรขวา \left\( \begin(align)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(align) \right.\]
เราจะจัดการกับข้อกำหนด $2x\ge 0$ บ้าง ในท้ายที่สุด เราสามารถแทนที่รากที่เราได้รับจากสมการแรกอย่างโง่เขลา และตรวจสอบว่าความไม่เท่าเทียมกันยังคงอยู่หรือไม่
เรามาแก้สมการกัน:
\[\begin(align)& 3x-2=2\ลูกศรขวา 3x=4\ลูกศรขวา x=\frac(4)(3); \\& 3x-2=-2\ลูกศรขวา 3x=0\ลูกศรขวา x=0 \\\end(จัดแนว)\]
แล้ว รากสองตัวนี้อันไหนเป็นไปตามข้อกำหนด $2x\ge 0$? ใช่ทั้งคู่! ดังนั้น คำตอบจะเป็นตัวเลขสองตัว: $x=(4)/(3)\;$ และ $x=0$ นั่นคือวิธีแก้ปัญหา :)
สงสัยว่านักเรียนบางคนเริ่มเบื่อแล้วเหรอ? เรามาดูสมการที่ซับซ้อนกว่านี้กันดีกว่า:
\[\ซ้าย| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]
แม้ว่ามันจะดูชั่วร้าย แต่จริงๆ แล้ว มันยังคงเป็นสมการเดียวกันของรูปแบบ “โมดูลัสเท่ากับฟังก์ชัน”:
\[\ซ้าย| f\left(x \right) \right|=g\left(x \right)\]
และได้รับการแก้ไขในลักษณะเดียวกันทุกประการ:
\[\ซ้าย| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\ลูกศรขวา \left\( \begin(align)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \right), \\& x-((x )^(3))\ge 0 \\\end(align) \right.\]
เราจะจัดการกับความไม่เท่าเทียมกันในภายหลัง - มันชั่วร้ายเกินไป (อันที่จริงมันง่าย แต่เราจะไม่แก้ไข) ในตอนนี้ ควรจัดการกับสมการผลลัพธ์จะดีกว่า ลองพิจารณากรณีแรก - นี่คือตอนที่โมดูลถูกขยายด้วยเครื่องหมายบวก:
\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]
ไม่ใช่เรื่องง่ายที่คุณจะต้องรวบรวมทุกอย่างจากทางซ้าย นำสิ่งที่คล้ายกันมาและดูว่าเกิดอะไรขึ้น และนี่คือสิ่งที่เกิดขึ้น:
\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\end(จัดแนว)\]
เรานำตัวประกอบร่วม $((x)^(2))$ ออกจากวงเล็บแล้วได้สมการง่ายๆ:
\[((x)^(2))\left(2x-3 \right)=0\ลูกศรขวา \left[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\end(align) \right.\]
\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1.5.\]
ที่นี่เราใช้ ทรัพย์สินที่สำคัญผลิตภัณฑ์ เพื่อประโยชน์ในการแยกตัวประกอบพหุนามดั้งเดิม: ผลคูณจะเท่ากับศูนย์เมื่อตัวประกอบอย่างน้อยหนึ่งตัวเท่ากับศูนย์
ทีนี้มาจัดการกับสมการที่สองในลักษณะเดียวกันทุกประการซึ่งได้มาจากการขยายโมดูลด้วยเครื่องหมายลบ:
\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\left(-3x+2 \right)=0 \\\end(จัดแนว)\]
เช่นเดียวกัน: ผลคูณจะเท่ากับศูนย์เมื่อตัวประกอบอย่างน้อยหนึ่งตัวมีค่าเท่ากับศูนย์ เรามี:
\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(align) \right.\]
เรามีสามราก: $x=0$, $x=1.5$ และ $x=(2)/(3)\;$ แล้วชุดนี้ชุดไหนจะตอบโจทย์สุดท้าย? ในการดำเนินการนี้ โปรดจำไว้ว่าเรามีข้อจำกัดเพิ่มเติมในรูปแบบของความไม่เท่าเทียมกัน:
จะคำนึงถึงข้อกำหนดนี้อย่างไร? ลองแทนที่รากที่พบและตรวจสอบว่า $x$ เหล่านี้มีค่าอสมการหรือไม่ เรามี:
\[\begin(align)& x=0\ลูกศรขวา x-((x)^(3))=0-0=0\ge 0; \\& x=1.5\ลูกศรขวา x-((x)^(3))=1.5-((1.5)^(3)) \lt 0; \\& x=\frac(2)(3)\ลูกศรขวา x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\end(จัดแนว)\]
ดังนั้นรูต $x=1.5$ จึงไม่เหมาะกับเรา และในการตอบสนองจะมีเพียงสองรากเท่านั้น:
\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]
อย่างที่คุณเห็นแม้ในกรณีนี้ไม่มีอะไรซับซ้อน - สมการกับโมดูลจะได้รับการแก้ไขโดยใช้อัลกอริทึมเสมอ คุณเพียงแค่ต้องมีความเข้าใจที่ดีเกี่ยวกับพหุนามและอสมการ ดังนั้นเราจึงก้าวไปสู่งานที่ซับซ้อนมากขึ้น - จะไม่ใช่หนึ่งโมดูลอีกต่อไป แต่มีสองโมดูล
สมการที่มีสองโมดูล
จนถึงตอนนี้เราได้ศึกษาเพียงส่วนใหญ่เท่านั้น สมการง่ายๆ— มีหนึ่งโมดูลและอย่างอื่น เราส่ง "อย่างอื่น" นี้ไปยังอีกส่วนหนึ่งของความไม่เท่าเทียมกัน ห่างจากโมดูล เพื่อว่าสุดท้ายแล้วทุกอย่างจะถูกลดขนาดให้อยู่ในสมการในรูปแบบ $\left| f\left(x \right) \right|=g\left(x \right)$ หรือง่ายกว่านั้น $\left| f\left(x \right) \right|=a$.
แต่ โรงเรียนอนุบาลสิ้นสุดแล้ว - ถึงเวลาพิจารณาบางสิ่งที่จริงจังกว่านี้แล้ว เริ่มต้นด้วยสมการดังนี้:
\[\ซ้าย| f\left(x \right) \right|=\left| g\left(x \right) \right|\]
นี่คือสมการของรูปแบบ "โมดูลัส เท่ากับโมดูลัส- โดยพื้นฐานแล้ว จุดสำคัญคือการไม่มีข้อกำหนดและปัจจัยอื่นๆ: มีเพียงโมดูลเดียวทางด้านซ้าย อีกหนึ่งโมดูลทางด้านขวา - และไม่มีอะไรเพิ่มเติม
ตอนนี้บางคนอาจคิดว่าสมการดังกล่าวแก้ได้ยากกว่าที่เราศึกษามาจนถึงตอนนี้ แต่เปล่าเลย สมการเหล่านี้แก้ได้ง่ายกว่าด้วยซ้ำ นี่คือสูตร:
\[\ซ้าย| f\left(x \right) \right|=\left| g\left(x \right) \right|\ลูกศรขวา f\left(x \right)=\pm g\left(x \right)\]
ทั้งหมด! เราเพียงแค่เปรียบเทียบนิพจน์ submodular โดยการใส่เครื่องหมายบวกหรือลบไว้ข้างหน้าหนึ่งในนั้น จากนั้นเราก็แก้สมการสองผลลัพธ์ - และรากก็พร้อม! ไม่มี ข้อ จำกัด เพิ่มเติม, ไม่มีความไม่เท่าเทียมกัน ฯลฯ มันง่ายมาก
มาลองแก้ไขปัญหานี้กัน:
\[\ซ้าย| 2x+3 \right|=\ซ้าย| 2x-7 \ขวา|\]
ชั้นประถม วัตสัน! การขยายโมดูล:
\[\ซ้าย| 2x+3 \right|=\ซ้าย| 2x-7 \right|\ลูกศรขวา 2x+3=\pm \left(2x-7 \right)\]
พิจารณาแต่ละกรณีแยกกัน:
\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\ซ้าย(2x-7 \right)\ลูกศรขวา 2x+3=-2x+7 \\\end(จัดแนว)\]
สมการแรกไม่มีราก เพราะเมื่อไหร่ที่ $3=-7$? $x$ มีค่าเท่าไหร่? “$x$ คืออะไร? คุณเมาหรือเปล่า? ไม่มี $x$ เลย” คุณพูด และคุณจะพูดถูก เราได้รับความเท่าเทียมกันซึ่งไม่ได้ขึ้นอยู่กับตัวแปร $x$ และในขณะเดียวกัน ความเท่าเทียมกันเองก็ไม่ถูกต้อง นั่นเป็นสาเหตุที่ไม่มีราก :)
ด้วยสมการที่สอง ทุกอย่างจะน่าสนใจขึ้นอีกเล็กน้อย แต่ก็ง่ายมากเช่นกัน:
อย่างที่คุณเห็น ทุกอย่างได้รับการแก้ไขอย่างแท้จริงในสองสามบรรทัด - เราไม่ได้คาดหวังสิ่งอื่นใดจากสมการเชิงเส้น :)
ด้วยเหตุนี้ คำตอบสุดท้ายคือ: $x=1$
แล้วยังไงล่ะ? ยาก? ไม่แน่นอน เรามาลองอย่างอื่นกันดีกว่า:
\[\ซ้าย| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\]
อีกครั้งที่เรามีสมการในรูปแบบ $\left| f\left(x \right) \right|=\left| g\left(x \right) \right|$. ดังนั้นเราจึงเขียนมันใหม่ทันทีโดยเผยให้เห็นเครื่องหมายโมดูลัส:
\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]
บางทีตอนนี้อาจมีคนถามว่า:“ เฮ้เรื่องไร้สาระอะไร? เหตุใด “บวก-ลบ” จึงปรากฏบนนิพจน์ทางขวาและไม่ปรากฏทางด้านซ้าย” ใจเย็นๆ ฉันจะอธิบายทุกอย่างตอนนี้ ในทางที่ดีเราควรเขียนสมการของเราใหม่ดังนี้:
จากนั้นคุณจะต้องเปิดวงเล็บ ย้ายพจน์ทั้งหมดไปไว้ด้านหนึ่งของเครื่องหมายเท่ากับ (เนื่องจากสมการเห็นได้ชัดว่าจะเป็นกำลังสองในทั้งสองกรณี) จากนั้นจึงหาราก แต่คุณต้องยอมรับ: เมื่อ "บวกหรือลบ" ปรากฏก่อนคำศัพท์สามคำ (โดยเฉพาะอย่างยิ่งเมื่อมีคำใดคำหนึ่งเหล่านี้ นิพจน์กำลังสอง) วิธีนี้ดูซับซ้อนกว่าสถานการณ์ที่ "บวกหรือลบ" ปรากฏเฉพาะหน้าคำสองคำเท่านั้น
แต่ไม่มีอะไรขัดขวางเราจากการเขียนสมการดั้งเดิมใหม่ดังนี้:
\[\ซ้าย| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\ลูกศรขวา \left| ((x)^(2))-3x+2 \right|=\left| x-1 \ขวา|\]
เกิดอะไรขึ้น ไม่มีอะไรพิเศษ: พวกเขาเพิ่งเปลี่ยนอันซ้ายและ ด้านขวาในบางสถานที่ สิ่งเล็กๆ น้อยๆ ที่จะทำให้ชีวิตเราง่ายขึ้นนิดหน่อยในที่สุด :)
โดยทั่วไป เราจะแก้สมการนี้ โดยพิจารณาตัวเลือกที่มีเครื่องหมายบวกและเครื่องหมายลบ:
\[\begin(align)& ((x)^(2))-3x+2=x-1\ลูกศรขวา ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\ลูกศรขวา ((x)^(2))-2x+1=0 \\\end(จัดแนว)\]
สมการแรกมีราก $x=3$ และ $x=1$ โดยทั่วไปอันที่สองจะเป็นกำลังสองที่แน่นอน:
\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]
ดังนั้นจึงมีเพียงรากเดียวเท่านั้น: $x=1$ แต่เราได้รับรากนี้มาก่อนหน้านี้แล้ว ดังนั้นคำตอบสุดท้ายจึงมีเพียงตัวเลขสองตัวเท่านั้น:
\[((x)_(1))=3;\quad ((x)_(2))=1.\]
ภารกิจสำเร็จแล้ว! คุณสามารถนำพายจากชั้นวางมากินได้ มี 2 อันครับ ของคุณคืออันกลางครับ :)
หมายเหตุสำคัญ- การปรากฏตัวของรากที่เหมือนกันสำหรับ ตัวเลือกที่แตกต่างกันการขยายตัวของโมดูลัสหมายความว่าพหุนามดั้งเดิมถูกแยกตัวประกอบ และในบรรดาปัจจัยเหล่านี้ ก็จำเป็นต้องมีปัจจัยร่วมด้วย จริงหรือ:
\[\begin(align)& \left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|; \\& \ซ้าย| x-1 \right|=\left| \left(x-1 \right)\left(x-2 \right) \right| \\\end(จัดแนว)\]
หนึ่งในคุณสมบัติของโมดูล: $\left| a\cdot b \right|=\left| \right|\cdot \left| b \right|$ (เช่น โมดูลัสของผลิตภัณฑ์ เท่ากับสินค้าโมดูล) ดังนั้นสมการดั้งเดิมสามารถเขียนใหม่ได้ดังนี้:
\[\ซ้าย| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \ขวา|\]
อย่างที่คุณเห็น เรามีปัจจัยร่วมจริงๆ ตอนนี้ หากคุณรวบรวมโมดูลทั้งหมดไว้ที่ด้านเดียว คุณสามารถนำปัจจัยนี้ออกจากวงเล็บได้:
\[\begin(align)& \left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \ขวา|; \\& \ซ้าย| x-1 \ขวา|-\ซ้าย| x-1 \right|\cdot \left| x-2 \ขวา|=0; \\& \ซ้าย| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0 \\\end(จัดแนว)\]
ทีนี้ จำไว้ว่าผลคูณเท่ากับศูนย์เมื่อปัจจัยอย่างน้อยหนึ่งตัวเท่ากับศูนย์:
\[\left[ \begin(align)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\end(align) \right.\]
ดังนั้น สมการดั้งเดิมที่มีสองโมดูลจึงลดลงเหลือสมการที่ง่ายที่สุดสองสมการที่เราพูดถึงในตอนต้นของบทเรียน สมการดังกล่าวสามารถแก้ไขได้ในสองสามบรรทัด :)
หมายเหตุนี้อาจดูซับซ้อนโดยไม่จำเป็นและไม่สามารถนำไปใช้ในทางปฏิบัติได้ อย่างไรก็ตาม ในความเป็นจริงคุณอาจพบเจออะไรอีกมากมาย งานที่ซับซ้อนกว่าที่เราจะวิเคราะห์ในวันนี้ ในนั้นโมดูลสามารถรวมกับพหุนามได้ รากเลขคณิต, ลอการิทึม ฯลฯ และในสถานการณ์เช่นนี้ ความสามารถในการลดระดับโดยรวมของสมการโดยการนำบางอย่างออกจากวงเล็บจะมีประโยชน์มาก :)
ตอนนี้ผมอยากจะวิเคราะห์สมการอื่น ซึ่งเมื่อมองแวบแรกอาจดูบ้าไปแล้ว นักเรียนหลายคนติดขัดกับสิ่งนี้ แม้แต่ผู้ที่คิดว่าตนเองมีความเข้าใจในโมดูลต่างๆ เป็นอย่างดี
อย่างไรก็ตาม สมการนี้แก้ได้ง่ายกว่าที่เราดูก่อนหน้านี้ และถ้าคุณเข้าใจว่าทำไม คุณก็จะได้เคล็ดลับอีกอย่างหนึ่ง วิธีแก้ปัญหาอย่างรวดเร็วสมการกับโมดูล
ดังนั้นสมการคือ:
\[\ซ้าย| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\]
ไม่ นี่ไม่ใช่การพิมพ์ผิด แต่เป็นข้อดีระหว่างโมดูลต่างๆ และเราต้องค้นหาว่า $x$ ผลรวมของสองโมดูลเท่ากับศูนย์อย่างไร :)
ว่าแต่มีปัญหาอะไรมั้ย? แต่ปัญหาคือแต่ละโมดูลเป็นจำนวนบวก หรือในกรณีที่รุนแรง จะเป็นศูนย์ จะเกิดอะไรขึ้นถ้าคุณบวกเลขบวกสองตัว? เห็นได้ชัดว่าเป็นจำนวนบวกอีกครั้ง:
\[\begin(align)& 5+7=12 \gt 0; \\& 0.004+0.0001=0.0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(align)\]
บรรทัดสุดท้ายอาจทำให้คุณมีแนวคิด: ครั้งเดียวที่ผลรวมของโมดูลเป็นศูนย์คือถ้าแต่ละโมดูลเป็นศูนย์:
\[\ซ้าย| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\ลูกศรขวา \left\( \begin(align)& \left| x-((x)^(3)) \right|=0, \\& \left|. ((x)^(2))+x-2 \right|=0.
และเมื่อใดที่โมดูลจะเท่ากับศูนย์? ในกรณีเดียวเท่านั้น - เมื่อนิพจน์ submodular เท่ากับศูนย์:
\[((x)^(2))+x-2=0\ลูกศรขวา \left(x+2 \right)\left(x-1 \right)=0\ลูกศรขวา \left[ \begin(align)& x=-2 \\& x=1 \\\end(align) \right.\]
ดังนั้นเราจึงมีสามจุดที่โมดูลแรกถูกรีเซ็ตเป็นศูนย์: 0, 1 และ −1; เช่นเดียวกับจุดสองจุดที่โมดูลที่สองถูกรีเซ็ตเป็นศูนย์: −2 และ 1 อย่างไรก็ตาม เราจำเป็นต้องรีเซ็ตทั้งสองโมดูลให้เป็นศูนย์ในเวลาเดียวกัน ดังนั้นในบรรดาตัวเลขที่พบ เราจำเป็นต้องเลือกจำนวนที่รวมอยู่ใน ทั้งสองชุด แน่นอนว่ามีเพียงหมายเลขเดียวเท่านั้น: $x=1$ - นี่จะเป็นคำตอบสุดท้าย
วิธีการแตกแยก
เราได้ครอบคลุมปัญหาต่างๆ ไปแล้วและเรียนรู้เทคนิคมากมาย คุณคิดว่านั่นคือทั้งหมดหรือไม่? แต่ไม่! ตอนนี้เราจะมาดูเทคนิคสุดท้าย - และในขณะเดียวกันก็สำคัญที่สุด เราจะพูดถึงการแยกสมการด้วยโมดูลัส เราจะพูดถึงเรื่องอะไร? ลองย้อนกลับไปดูสมการง่ายๆ บ้าง ตัวอย่างเช่น:
\[\ซ้าย| 3x-5 \ขวา|=5-3x\]
โดยหลักการแล้ว เรารู้วิธีแก้สมการดังกล่าวแล้ว เนื่องจากเป็นรูปแบบมาตรฐานของรูปแบบ $\left| f\left(x \right) \right|=g\left(x \right)$. แต่ลองพิจารณาสมการนี้จากมุมที่ต่างออกไปเล็กน้อย ถ้าให้เจาะจงกว่านี้ ให้พิจารณานิพจน์ใต้เครื่องหมายโมดูลัส ฉันขอเตือนคุณว่าโมดูลัสของจำนวนใดๆ สามารถเท่ากับจำนวนนั้นเอง หรืออาจตรงกันข้ามกับจำนวนนี้ก็ได้:
\[\ซ้าย| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(align) \right.\]
ที่จริงแล้ว ความคลุมเครือนี้คือปัญหาทั้งหมด เนื่องจากตัวเลขภายใต้โมดูลัสเปลี่ยนแปลง (ขึ้นอยู่กับตัวแปร) เราจึงไม่ชัดเจนสำหรับเราว่าเป็นค่าบวกหรือค่าลบ
แต่ถ้าคุณต้องการให้ตัวเลขนี้เป็นค่าบวกในตอนแรกล่ะ? ตัวอย่างเช่น กำหนดให้ $3x-5 \gt 0$ - ในกรณีนี้ เรารับประกันได้ว่าจะได้จำนวนบวกภายใต้เครื่องหมายโมดูลัส และเราสามารถกำจัดโมดูลัสนี้ออกไปได้อย่างสมบูรณ์:
ดังนั้นสมการของเราจะกลายเป็นสมการเชิงเส้นซึ่งสามารถแก้ไขได้ง่าย:
จริงอยู่ ความคิดทั้งหมดนี้สมเหตุสมผลภายใต้เงื่อนไข $3x-5 \gt 0$ เท่านั้น - เราเองก็แนะนำข้อกำหนดนี้เพื่อที่จะเปิดเผยโมดูลอย่างไม่คลุมเครือ ดังนั้น ลองแทนที่ $x=\frac(5)(3)$ ที่พบไปในเงื่อนไขนี้แล้วตรวจสอบ:
ปรากฎว่าเมื่อไร. ค่าที่ระบุ$x$ ไม่เป็นไปตามข้อกำหนดของเรา เนื่องจาก นิพจน์กลายเป็นศูนย์ แต่เราต้องการให้เคร่งครัด มากกว่าศูนย์- เศร้า :(
แต่ไม่เป็นไร! ท้ายที่สุดแล้ว ยังมีอีกตัวเลือกหนึ่ง $3x-5 \lt 0$ ยิ่งกว่านั้น: ยังมีกรณี $3x-5=0$ - จะต้องพิจารณาเรื่องนี้ด้วย ไม่เช่นนั้นวิธีแก้ปัญหาจะไม่สมบูรณ์ ดังนั้น ลองพิจารณากรณี $3x-5 \lt 0$:
แน่นอนว่าโมดูลจะเปิดขึ้นโดยมีเครื่องหมายลบ แต่แล้วสถานการณ์แปลก ๆ ก็เกิดขึ้น: ทั้งทางด้านซ้ายและทางขวาในสมการดั้งเดิมนิพจน์เดียวกันจะโดดเด่น:
ฉันสงสัยว่า $x$ นิพจน์ $5-3x$ จะเท่ากับนิพจน์ $5-3x$ เท่าใด แม้แต่ Captain Obviousness ก็ยังสำลักน้ำลายจากสมการดังกล่าว แต่เรารู้ว่าสมการนี้คืออัตลักษณ์ กล่าวคือ มันเป็นจริงสำหรับค่าใดๆ ของตัวแปร!
ซึ่งหมายความว่า $x$ ใดๆ จะเหมาะกับเรา อย่างไรก็ตาม เรามีข้อจำกัด:
กล่าวอีกนัยหนึ่ง คำตอบจะไม่ใช่ตัวเลขตัวเดียว แต่เป็นช่วงทั้งหมด:
สุดท้ายนี้ ยังมีอีกกรณีหนึ่งที่ต้องพิจารณา: $3x-5=0$ ทุกอย่างเป็นเรื่องง่ายที่นี่: ภายใต้โมดูลัสจะมีศูนย์และโมดูลัสของศูนย์ก็เท่ากับศูนย์ด้วย (ซึ่งตามมาจากคำจำกัดความโดยตรง):
แต่แล้วสมการดั้งเดิม $\left| 3x-5 \right|=5-3x$ จะถูกเขียนใหม่ดังนี้:
เราได้รับรากนี้แล้วเมื่อเราพิจารณากรณีของ $3x-5 \gt 0$ ยิ่งไปกว่านั้น รูทนี้เป็นวิธีแก้สมการ $3x-5=0$ - นี่คือข้อจำกัดที่เราแนะนำในการรีเซ็ตโมดูล :)
ดังนั้น นอกจากช่วงเวลาแล้ว เรายังพอใจกับจำนวนที่อยู่ท้ายสุดของช่วงเวลานี้ด้วย:
 การรวมรากในสมการโมดูโล
การรวมรากในสมการโมดูโล คำตอบสุดท้ายทั้งหมด: $x\in \left(-\infty ;\frac(5)(3) \right]$ มันไม่ธรรมดาเลยที่จะเห็นเรื่องไร้สาระในคำตอบของสมการที่ค่อนข้างง่าย (โดยพื้นฐานแล้วเป็นเส้นตรง) พร้อมโมดูลัส จริงเหรอ? ทำความคุ้นเคยกับมันแล้ว: ความยากของโมดูลคือคำตอบในสมการดังกล่าวไม่สามารถคาดเดาได้อย่างสมบูรณ์
สิ่งอื่นที่สำคัญกว่ามาก: เราเพิ่งวิเคราะห์อัลกอริธึมสากลสำหรับการแก้สมการด้วยโมดูลัส! และอัลกอริทึมนี้ประกอบด้วยขั้นตอนต่อไปนี้:
- ปรับแต่ละโมดูลัสในสมการให้เป็นศูนย์ เราได้สมการหลายสมการ
- แก้สมการทั้งหมดนี้และทำเครื่องหมายรากบนเส้นจำนวน เป็นผลให้เส้นตรงจะถูกแบ่งออกเป็นหลายช่วง โดยแต่ละโมดูลทั้งหมดจะถูกเปิดเผยไม่ซ้ำกัน
- แก้สมการดั้งเดิมสำหรับแต่ละช่วงเวลาแล้วรวมคำตอบของคุณ
แค่นั้นแหละ! เหลือเพียงคำถามเดียว: จะทำอย่างไรกับรากที่ได้รับในขั้นตอนที่ 1? สมมติว่าเรามีสองราก: $x=1$ และ $x=5$ พวกเขาจะแบ่งเส้นจำนวนออกเป็น 3 ส่วน:
 การแบ่งเส้นจำนวนออกเป็นระยะโดยใช้จุด
การแบ่งเส้นจำนวนออกเป็นระยะโดยใช้จุด แล้วมีช่วงไหนบ้าง? เห็นได้ชัดว่ามีสามคน:
- อันซ้ายสุด: $x \lt 1$ — หน่วยนั้นไม่รวมอยู่ในช่วงเวลา;
- ส่วนกลาง: $1\le x \lt 5$ - ในที่นี้อันหนึ่งจะรวมไว้ในช่วงเวลา แต่จะไม่รวมห้าอัน
- ขวาสุด: $x\ge 5$ - ห้ารวมอยู่ที่นี่เท่านั้น!
ฉันคิดว่าคุณเข้าใจรูปแบบแล้ว แต่ละช่วงจะรวมปลายด้านซ้ายและไม่รวมด้านขวา
เมื่อดูเผินๆ รายการดังกล่าวอาจดูไม่สะดวก ไร้เหตุผล และโดยทั่วไปแล้วเป็นเรื่องบ้าบอ แต่เชื่อฉันเถอะ: หลังจากฝึกฝนเล็กน้อยแล้วคุณจะพบว่าแนวทางนี้น่าเชื่อถือที่สุดและไม่รบกวนการเปิดโมดูลอย่างชัดเจน ควรใช้รูปแบบดังกล่าวมากกว่าคิดทุกครั้ง: ให้ปลายซ้าย/ขวากับช่วงเวลาปัจจุบันหรือ "โยน" ลงในช่วงเวลาถัดไป
 สมการลอการิทึม
สมการลอการิทึม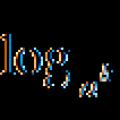 เทคนิคการแก้สมการลอการิทึม
เทคนิคการแก้สมการลอการิทึม การวิเคราะห์ตนเองของครูนักบำบัดการพูด
การวิเคราะห์ตนเองของครูนักบำบัดการพูด