การสลายจำนวนให้เป็นปัจจัยเฉพาะ วิธีการ และตัวอย่างการสลาย รับการแยกตามรูปแบบบัญญัติของจำนวนให้เป็นตัวประกอบเฉพาะ

การบรรยาย 14 กระบวนการสุ่ม การขยายตัวของกระบวนการสุ่มที่เป็นที่ยอมรับ การสลายตัวของสเปกตรัมเครื่องเขียน กระบวนการสุ่ม. บทบรรยาย 14
กระบวนการสุ่ม
การขยายตัวของกระบวนการสุ่มที่ยอมรับได้
การสลายตัวทางสเปกตรัมของการสุ่มแบบคงที่
กระบวนการ. กระบวนการสุ่มกับอิสระ
ส่วน กระบวนการมาร์คอฟและห่วงโซ่มาร์คอฟ
กระบวนการสุ่มปกติ เป็นระยะ
กระบวนการสุ่มแบบไม่คงที่
(อัคห์เมตอฟ เอส.เค.)

การสลายตัวที่เป็นที่ยอมรับของกระบวนการสุ่ม

SP X(t) อะไรก็ได้ นำเสนอใน
รูปแบบของการขยายตัวเช่น เป็นผลรวม
กระบวนการเบื้องต้น:
Vk- ตัวแปรสุ่ม
φk(t) เป็นฟังก์ชันที่ไม่สุ่ม (ไซน์ซอยด์ เลขชี้กำลัง เลขยกกำลัง
ฟังก์ชั่น ฯลฯ)
กรณีพิเศษของการสลายตัวคือ Canonical
การสลายตัว
SP X(t) มีแบบฟอร์ม
mx(t) = M – ความคาดหวังทางคณิตศาสตร์ของ SP X(t)
V1, V2…Vk – SW ที่ไม่สัมพันธ์กันและอยู่กึ่งกลาง
D1, D2 …Dk- SW การกระจายตัว V1, V2…Vk
φk(t) เป็นฟังก์ชันที่ไม่สุ่มของอาร์กิวเมนต์ t
ตัวแปรสุ่ม V1, V2…Vk เรียกว่าสัมประสิทธิ์ของบัญญัติ
การสลายตัว
และฟังก์ชันไม่สุ่ม φ1(t), φ2(t) φk(t) - ฟังก์ชันพิกัด
การสลายตัวตามบัญญัติ

ลักษณะสำคัญของ SP ที่กำหนดโดยการขยายแบบบัญญัติ

M – ความคาดหวังทางคณิตศาสตร์ของ SP X(t)
Kx(t,t’) – ฟังก์ชันสหสัมพันธ์เอสพีเอ็กซ์(เสื้อ)
การแสดงออก
- การขยายความสัมพันธ์ที่เป็นที่ยอมรับ
ฟังก์ชั่น
ถ้า t=t' ให้เป็นไปตามข้อแรก
คุณสมบัติของฟังก์ชันสหสัมพันธ์
การแสดงออก
ดีเค(เสื้อ) -
การกระจายตัว
การขยายตัวตามรูปแบบบัญญัติของความแปรปรวนของ SP X(t)

การสลายตัวทางสเปกตรัมของ SP ที่อยู่นิ่ง

กิจการร่วมค้าเครื่องเขียนสามารถ แสดงโดยการสลายตัวตามบัญญัติ
Vk และ Uk เป็น SW ที่ไม่มีความสัมพันธ์กันและอยู่กึ่งกลางด้วยการกระจายตัว
D=D=ดค
ω - ค่าที่ไม่สุ่ม (ความถี่)
ในกรณีนี้ การขยายตัวตามรูปแบบบัญญัติของฟังก์ชันสหสัมพันธ์
ถูกกำหนดโดยนิพจน์
เป็นตัวแทน
เป็นที่ยอมรับ
การสลายตัว
กิจการร่วมค้า
เอ็กซ์(เสื้อ)
เรียกว่า
การสลายตัวทางสเปกตรัมของ SP และ
แสดงเป็น
Θk - เฟส การสั่นแบบฮาร์มอนิกกิจการร่วมค้าเครื่องเขียนระดับประถมศึกษา
ซึ่งเป็น SW กระจายอย่างสม่ำเสมอในช่วงเวลา (0, 2π);
Zk - SW ซึ่งเป็นแอมพลิจูดของการสั่นของฮาร์มอนิก
กิจการร่วมค้าเครื่องเขียนระดับประถมศึกษา

การสลายตัวทางสเปกตรัมของ SP ที่อยู่นิ่ง (2)

ตัวแปรสุ่ม Θk และ Zk นั้นขึ้นอยู่กับและตัวแปรต่อไปนี้ถือเป็นจริงสำหรับพวกเขา:
Vk = Zk cos Θk
อุค = Zk บาป Θk
กิจการร่วมค้าเครื่องเขียนสามารถ แสดงเป็นผลรวมของฮาร์มอนิก
การสั่นด้วยแอมพลิจูดแบบสุ่ม Zk และเฟสสุ่ม Θk เปิด
ความถี่ที่ไม่สุ่มต่างกัน ωk
ฟังก์ชันสหสัมพันธ์ของ SP X(t) ที่อยู่นิ่งจะเป็นเลขคู่
หน้าที่ของอาร์กิวเมนต์คือ kx(τ) = kx(-τ) ดังนั้นจึงอยู่ในช่วง (-T,
T) สามารถขยายได้ในอนุกรมฟูเรียร์ในฮาร์มอนิกคู่ (โคไซน์):
ความแปรปรวนของค่าคงที่ SP X(t) เท่ากับ
ผลรวม
ความแปรปรวน
ทั้งหมด
ฮาร์มอนิก
ของเขา
การสลายตัวของสเปกตรัม
การพึ่งพา Dk = f(wk) เรียกว่าสเปกตรัมที่ไม่ต่อเนื่องของความแปรปรวน หรือ
สเปกตรัมที่ไม่ต่อเนื่องของ SP ที่อยู่กับที่

การสลายตัวทางสเปกตรัมของ SP ที่อยู่นิ่ง (3)

ที่ ∆ω
→ 0 จะมีการเปลี่ยนแปลงเป็นสเปกตรัมต่อเนื่อง
Sx(ω) - ความหนาแน่นสเปกตรัม
ดังนั้นฟังก์ชันสหสัมพันธ์และความหนาแน่นของสเปกตรัม
มีความสัมพันธ์กันโดยการแปลงฟูริเยร์โคไซน์ ดังนั้นสเปกตรัม
ความหนาแน่นของกิจการร่วมค้าที่อยู่กับที่สามารถเป็นได้ แสดงออกมาทางความสัมพันธ์
ฟังก์ชันตามสูตร

กระบวนการสุ่มที่มีส่วนอิสระ

ในทางอุทกวิทยาถือว่าอนุกรมนั้นสอดคล้องกับแบบจำลองของการสุ่ม
ค่าถ้าไม่มีความสัมพันธ์อย่างมีนัยสำคัญระหว่างสมาชิกของชุดนี้
สำหรับกะใด ๆ τ
กระบวนการสุ่มที่มีส่วนอิสระเป็น SP ซึ่ง
สำหรับ t และ t'
มx(t) = มx
Dx(t) = Dx
Kx(t,t’) = kx(τ) = (Dx สำหรับ τ = 0 และ 0 สำหรับ τ ≠ 0)
กระบวนการดังกล่าวเป็นแบบคงที่และเป็นไปตามหลักสรีรศาสตร์
คุณสมบัติ
สำหรับกระบวนการดังกล่าว ลักษณะของกฎการกระจายหนึ่งมิติ
สามารถประมาณได้ทั้งสำหรับส่วนใด ๆ และสำหรับส่วนใด ๆ (ก็เพียงพอแล้ว
อย่างต่อเนื่อง) การนำไปปฏิบัติ
กระบวนการดังกล่าวไม่มีความสัมพันธ์ระหว่างสมาชิกภายในแต่อย่างใด
การนำไปใช้งาน
การยอมรับแบบจำลองดังกล่าวจึงสันนิษฐานว่ามีปริมาณทางอุทกวิทยาจำนวนหนึ่ง
แสดงถึงการดำเนินการอย่างหนึ่งของการร่วมทุน
บางครั้งเรียกว่ากระบวนการสุ่มที่มีส่วนที่เป็นอิสระ
"เสียงสีขาว" โดยเปรียบเทียบกับแสงสีขาว

กระบวนการมาร์คอฟและห่วงโซ่มาร์คอฟ

กระบวนการสุ่ม
เรียกว่ามาร์คอฟถ้ามี
ช่วงเวลา t ความน่าจะเป็นของแต่ละสถานะของระบบในอนาคต
(สำหรับ t > t0) ขึ้นอยู่กับสถานะของมันในปัจจุบันเท่านั้น (สำหรับ t = t0) และไม่
ขึ้นอยู่กับสถานะในอดีต (ที่ t< t0)
ห่วงโซ่มาร์คอฟหรือง่าย ห่วงโซ่มาร์คอฟเรียกว่า
กระบวนการมาร์คอฟด้วยสถานะที่ไม่ต่อเนื่องและเวลาที่ไม่ต่อเนื่อง
Markov SP ได้รับการอธิบายอย่างสมบูรณ์โดยกฎหมายสองมิติ
การกระจาย. ถ้า กระบวนการของมาร์คอฟอยู่นิ่งและ
ตามหลักสรีรศาสตร์แล้วสามารถประมาณลักษณะของมันได้
การนำไปใช้งาน
ห่วงโซ่ที่ ความน่าจะเป็นแบบมีเงื่อนไขรัฐในอนาคตขึ้นอยู่กับ
จากสถานะในหลายขั้นตอนก่อนหน้านี้ เรียกว่าซับซ้อน
ห่วงโซ่มาร์คอฟ

กระบวนการสุ่มแบบปกติ (เกาส์เซียน)

กระบวนการสุ่มแบบปกติ (เกาส์เซียน) X(t) เรียกว่า
SP ซึ่งในทุกส่วนของ SW X(ti) มีลักษณะปกติ
การกระจาย
SP ที่ไม่คงที่เป็นระยะ
เมื่อเรียนรายปี รายเดือน รายวัน ฯลฯ กระบวนการโดยปกติ
มีภายในประจำปี ฯลฯ ความผันผวน ในกรณีนี้ เช่น
แบบจำลองทางคณิตศาสตร์ คุณสามารถใช้แบบจำลองเป็นระยะๆ
กระบวนการสุ่มแบบไม่คงที่ (PNSP)
กระบวนการสุ่มกล่าวกันว่าเป็นระยะไม่คงที่ถ้า
ลักษณะความน่าจะเป็นของมันจะไม่แปรเปลี่ยนตามการเปลี่ยนแปลง
จำนวนบวก T ตัวอย่างเช่น มีขั้นตอนที่ไม่ต่อเนื่องในหนึ่งเดือน
ค่าคงที่ต้องคงไว้ที่กะ 12, 24, 36 เป็นต้น

บทความนี้ให้คำตอบสำหรับคำถามเกี่ยวกับการแยกตัวประกอบของตัวเลขในแผ่นงาน พิจารณา ความคิดทั่วไปเกี่ยวกับการย่อยสลายพร้อมตัวอย่าง มาวิเคราะห์กัน รูปแบบบัญญัติการขยายตัวและอัลกอริทึมของมัน วิธีการทางเลือกทั้งหมดจะพิจารณาโดยใช้เครื่องหมายของการหารและตารางการคูณ

Yandex.RTB R-A-339285-1

การแยกจำนวนออกเป็นตัวประกอบเฉพาะหมายความว่าอย่างไร

ลองวิเคราะห์แนวคิด ปัจจัยสำคัญ. เป็นที่ทราบกันว่าตัวประกอบเฉพาะทุกตัวเป็นจำนวนเฉพาะ ในผลคูณของรูปแบบ 2 7 7 23 เรามีตัวประกอบเฉพาะ 4 ตัวในรูปแบบ 2 , 7 , 7 , 23 .

แฟคตอริ่งเกี่ยวข้องกับการแสดงเป็นผลิตภัณฑ์ของจำนวนเฉพาะ หากคุณต้องการแยกย่อยหมายเลข 30 เราจะได้ 2, 3, 5 รายการจะอยู่ในรูปแบบ 30 = 2 3 5 . เป็นไปได้ที่ตัวคูณสามารถทำซ้ำได้ ตัวเลขเช่น 144 มี 144 = 2 2 2 2 3 3

ไม่ใช่ตัวเลขทั้งหมดที่จะสลายตัว จำนวนที่มากกว่า 1 และเป็นจำนวนเต็มสามารถแยกตัวประกอบได้ จำนวนเฉพาะหารด้วย 1 และตัวมันเองเมื่อแยกย่อย ดังนั้นจึงเป็นไปไม่ได้ที่จะแสดงจำนวนเหล่านี้เป็นผลคูณ

เมื่อ z อ้างถึงจำนวนเต็ม มันจะแสดงเป็นผลคูณของ a และ b โดยที่ z หารด้วย a และ b จำนวนประกอบจะถูกแยกย่อยเป็นปัจจัยเฉพาะโดยใช้ทฤษฎีบทพื้นฐานของเลขคณิต ถ้าจำนวนมากกว่า 1 ดังนั้นการแยกตัวประกอบ p 1 , p 2 , … , p n ใช้รูปแบบ a = p 1 , p 2 , … , p n . จะถือว่าการสลายตัวเป็นตัวแปรเดียว

การสลายตัวตามรูปแบบบัญญัติของจำนวนให้เป็นตัวประกอบเฉพาะ

ปัจจัยต่างๆ สามารถเกิดขึ้นซ้ำได้ในระหว่างการสลายตัว พวกเขาเขียนอย่างกะทัดรัดโดยใช้ปริญญา ถ้าเมื่อแยกย่อยจำนวน a เรามีตัวประกอบ p 1 ซึ่งเกิดขึ้น s 1 ครั้งและต่อไป p n - s n ครั้ง ดังนั้นการสลายตัวจึงเป็นรูปเป็นร่าง a=p 1 s 1 a = p 1 s 1 p 2 s 2 … p n s n. รายการนี้เรียกว่าการสลายตัวตามรูปแบบบัญญัติของจำนวนให้เป็นปัจจัยเฉพาะ

เมื่อแยกย่อยหมายเลข 609840 เราจะได้ 609 840 = 2 2 2 2 3 3 5 7 11 11 รูปแบบบัญญัติของมันจะเป็น 609 840 = 2 4 3 2 5 7 11 2 . เมื่อใช้การขยายตามรูปแบบบัญญัติ คุณจะหาตัวหารทั้งหมดของตัวเลขและจำนวนได้

คุณต้องมีความเข้าใจเกี่ยวกับจำนวนเฉพาะและจำนวนประกอบจึงจะแยกตัวประกอบได้อย่างถูกต้อง ประเด็นคือการได้จำนวนตัวหารติดต่อกันในรูปแบบ p 1 , p 2 , … , p n ตัวเลข ก , a 1 , a 2 , … , a n - 1สิ่งนี้ทำให้สามารถรับได้ ก = หน้า 1 และ 1โดยที่ a 1 \u003d a: p 1, a \u003d p 1 a 1 \u003d p 1 p 2 a 2 โดยที่ a 2 \u003d a 1: p 2, ..., a \u003d p 1 p 2 . .. ... p n a n ที่ไหน n = a n - 1: p n. เมื่อได้รับ n = 1แล้วความเท่าเทียมกัน a = p 1 p 2 … p nเราได้รับการสลายตัวที่จำเป็นของจำนวน a เป็นปัจจัยสำคัญ สังเกตว่า หน้า 1 ≤ หน้า 2 ≤ หน้า 3 ≤ … ≤ หน้า.

เพื่อหาสิ่งที่เล็กที่สุด ตัวหารร่วมกันคุณต้องใช้ตารางจำนวนเฉพาะ ทำได้โดยใช้ตัวอย่างการหาตัวหารเฉพาะที่น้อยที่สุดของจำนวน z เมื่อนำจำนวนเฉพาะ 2, 3, 5, 11 และอื่นๆ มาหารด้วยจำนวน z เนื่องจาก z ไม่ใช่ จำนวนเฉพาะโปรดทราบว่าตัวหารเฉพาะที่น้อยที่สุดจะต้องไม่มากกว่า z จะเห็นได้ว่าไม่มีตัวหารของ z ดังนั้นจึงชัดเจนว่า z เป็นจำนวนเฉพาะ

ตัวอย่างที่ 1

พิจารณาตัวอย่างหมายเลข 87 เมื่อหารด้วย 2 เราจะได้ 87: 2 \u003d 43 โดยเหลือเศษ 1 2 เป็นตัวหารไม่ได้ ต้องหารทั้งหมด เมื่อหารด้วย 3 จะได้ 87:3 = 29 ดังนั้นข้อสรุป - 3 เป็นตัวหารเฉพาะที่น้อยที่สุดของจำนวน 87

เมื่อแยกย่อยเป็นปัจจัยเฉพาะ จำเป็นต้องใช้ตารางของจำนวนเฉพาะ โดยที่ a เมื่อแยกย่อย 95 ควรใช้ประมาณ 10 ไพรม์ และเมื่อแยกย่อย 846653 ควรใช้ประมาณ 1,000

พิจารณาอัลกอริทึมการแยกตัวประกอบเฉพาะ:

• การหาตัวประกอบที่น้อยที่สุดด้วยตัวหาร p 1 ของจำนวน กตามสูตร a 1 \u003d a: p 1 เมื่อ 1 \u003d 1 แล้ว a เป็นจำนวนเฉพาะและรวมอยู่ในการแยกตัวประกอบเมื่อไม่เท่ากับ 1 ดังนั้น a \u003d p 1 a 1 และปฏิบัติตามจนถึงจุดต่อไปนี้
• การหาตัวหารเฉพาะ p 2 ของ a 1 โดยการแจกแจงลำดับของจำนวนเฉพาะ โดยใช้ a 2 = a 1: p 2 , เมื่อ 2 = 1 , จากนั้นการขยายตัวจะอยู่ในรูปแบบ a = p 1 p 2 , เมื่อ a 2 \u003d 1 แล้ว a \u003d p 1 p 2 a 2 , และเราเปลี่ยนไปสู่ขั้นตอนต่อไป
• วนซ้ำจำนวนเฉพาะและหาตัวหารเฉพาะ หน้า 3ตัวเลข 2ตามสูตร a 3 \u003d a 2: p 3 เมื่อ a 3 \u003d 1 , แล้วเราจะได้ a = p 1 p 2 p 3 , เมื่อไม่เท่ากับ 1 แล้ว a = p 1 p 2 p 3 a 3 และดำเนินการขั้นตอนต่อไป
• หาตัวหารสำคัญ พี เอ็นตัวเลข น - 1โดยการแจกแจงจำนวนเฉพาะด้วย พี n - 1เช่นเดียวกับ n = a n - 1: p nโดยที่ a n = 1 ขั้นตอนถือเป็นที่สิ้นสุด ผลที่ได้คือ a = p 1 p 2 … p n .

ผลลัพธ์ของอัลกอริทึมถูกเขียนในรูปแบบของตารางที่มีปัจจัยที่แยกย่อยพร้อมแถบแนวตั้งตามลำดับในคอลัมน์ พิจารณารูปด้านล่าง

อัลกอริทึมที่เป็นผลลัพธ์สามารถนำไปใช้ได้โดยการแยกย่อยตัวเลขให้เป็นปัจจัยเฉพาะ

เมื่อแยกตัวประกอบเป็นปัจจัยสำคัญ ควรปฏิบัติตามอัลกอริทึมพื้นฐาน

ตัวอย่างที่ 2

แยกเลข 78 ออกเป็นตัวประกอบเฉพาะ

การตัดสินใจ

ในการหาตัวหารเฉพาะที่น้อยที่สุด จำเป็นต้องแจกแจงจำนวนเฉพาะทั้งหมดใน 78 นั่นคือ 78:2 = 39 การหารที่ไม่มีเศษ ดังนั้นนี่คือตัวหารหลักตัวแรก ซึ่งเราแสดงว่าเป็น p 1 เราได้ a 1 = a: p 1 = 78: 2 = 39 เรามาถึงความเท่าเทียมกันของรูปแบบ a = p 1 a 1 , โดยที่ 78 = 2 39 . จากนั้น a 1 = 39 นั่นคือคุณควรไปที่ขั้นตอนถัดไป

เรามาโฟกัสกันที่การหาตัวหารสำคัญกัน พี 2ตัวเลข 1 = 39. คุณควรเรียงลำดับจำนวนเฉพาะ นั่นคือ 39:2 = 19 (เหลือ 1) เนื่องจากการหารมีเศษเหลือ 2 จึงไม่ใช่ตัวหาร เมื่อเลือกหมายเลข 3 เราจะได้ 39:3 = 13 ซึ่งหมายความว่า p 2 = 3 เป็นตัวหารเฉพาะที่น้อยที่สุดของ 39 โดย a 2 = a 1: p 2 = 39: 3 = 13 เราได้รับแบบฟอร์มที่เท่าเทียมกัน ก = พี 1 พี 2 2ในรูปแบบ 78 = 2 3 13 . เรามีว่า a 2 = 13 ไม่เท่ากับ 1 เราควรไปต่อ

ตัวหารเฉพาะที่น้อยที่สุดของจำนวน a 2 = 13 หาได้จากการแจกแจงตัวเลข โดยเริ่มจาก 3 เราได้ 13: 3 = 4 (ส่วนที่เหลือ 1) นี่แสดงว่า 13 หารด้วย 5, 7, 11 ไม่ได้เพราะ 13: 5 = 2 (ส่วนที่เหลือ 3), 13: 7 = 1 (ส่วนที่เหลือ 6) และ 13: 11 = 1 (ส่วนที่เหลือ 2) จะเห็นได้ว่า 13 เป็นจำนวนเฉพาะ สูตรมีลักษณะดังนี้: a 3 \u003d a 2: p 3 \u003d 13:13 \u003d 1 เราได้ 3 = 1 ซึ่งหมายถึงจุดสิ้นสุดของอัลกอริทึม ตอนนี้ตัวประกอบเขียนเป็น 78 = 2 3 13 (a = p 1 p 2 p 3) .

ตอบ: 78 = 2 3 13 .

ตัวอย่างที่ 3

แยกย่อยหมายเลข 83,006 ให้เป็นตัวประกอบเฉพาะ

การตัดสินใจ

ขั้นตอนแรกเกี่ยวข้องกับการแยกตัวประกอบ หน้า 1 = 2และ ก 1 \u003d ก: หน้า 1 \u003d 83 006: 2 \u003d 41 503โดยที่ 83 006 = 2 41 503 .

ขั้นตอนที่สองถือว่า 2 , 3 และ 5 ไม่ใช่ตัวหารเฉพาะสำหรับ 1 = 41503 แต่ 7 เป็นตัวหารเฉพาะเนื่องจาก 41503: 7 = 5929 เราได้รับสิ่งนั้น p 2 \u003d 7, a 2 \u003d a 1: p 2 \u003d 41 503: 7 \u003d 5 929 แน่นอน 83 006 = 2 7 5 929 .

การหาตัวหารเฉพาะที่น้อยที่สุด p 4 ของจำนวน a 3 = 847 คือ 7 จะเห็นได้ว่า a 4 \u003d a 3: p 4 \u003d 847: 7 \u003d 121 ดังนั้น 83 006 \u003d 2 7 7 7 121

ในการหาตัวหารเฉพาะของจำนวน a 4 = 121 เราใช้เลข 11 นั่นคือ p 5 = 11 จากนั้นเราจะได้รับการแสดงออกของแบบฟอร์ม 5 \u003d 4: p 5 \u003d 121: 11 \u003d 11, และ 83 006 = 2 7 7 7 11 11 .

สำหรับเบอร์ 5 = 11ตัวเลข p6 = 11เป็นตัวหารเฉพาะที่น้อยที่สุด ดังนั้น a 6 \u003d a 5: p 6 \u003d 11:11 \u003d 1 แล้ว 6 = 1 สิ่งนี้บ่งชี้การสิ้นสุดของอัลกอริทึม ตัวคูณจะเขียนเป็น 83006 = 2 7 7 7 11 11 .

สัญกรณ์มาตรฐานของคำตอบจะอยู่ในรูปแบบ 83 006 = 2 7 3 11 2

ตอบ: 83 006 = 2 7 7 7 11 11 = 2 7 3 11 2 .

ตัวอย่างที่ 4

แยกตัวประกอบของจำนวน 897 924 289

การตัดสินใจ

ในการหาตัวประกอบเฉพาะตัวแรก ให้วนซ้ำจำนวนเฉพาะโดยเริ่มจาก 2 เลขท้ายเลขออกตรงกับเลข 937 จากนั้น p 1 = 937, a 1 = a: p 1 = 897 924 289: 937 = 958 297 และ 897 924 289 = 937 958 297

ขั้นตอนที่สองของอัลกอริทึมคือการแจกแจงจำนวนเฉพาะที่น้อยลง นั่นคือเราเริ่มต้นด้วยหมายเลข 937 เลข 967 ถือเป็นจำนวนเฉพาะเพราะเป็นตัวหารเฉพาะของจำนวน a 1 = 958 297 จากที่นี่เราจะได้ว่า p 2 \u003d 967 จากนั้น a 2 \u003d a 1: p 1 \u003d 958 297: 967 \u003d 991 และ 897 924 289 \u003d 937 967 991

ขั้นตอนที่สามบอกว่า 991 เป็นจำนวนเฉพาะ เนื่องจากไม่มีตัวหารเฉพาะที่น้อยกว่าหรือเท่ากับ 991 ค่าโดยประมาณของนิพจน์รากคือ 991< 40 2 . Иначе запишем как 991 < 40 2 . จากนี้จะเห็นได้ว่า p 3 \u003d 991 และ a 3 \u003d a 2: p 3 \u003d 991: 991 \u003d 1 เราได้การสลายตัวของหมายเลข 897 924 289 เป็นตัวประกอบเฉพาะ จะได้เป็น 897 924 289 \u003d 937 967 991

ตอบ: 897 924 289 = 937 967 991 .

การใช้การทดสอบการหารสำหรับการแยกตัวประกอบเฉพาะ

ในการแยกจำนวนออกเป็นปัจจัยเฉพาะ คุณต้องทำตามอัลกอริทึม เมื่อมีจำนวนน้อยอนุญาตให้ใช้สูตรคูณและเครื่องหมายหารได้ ลองดูตัวอย่างนี้

ตัวอย่างที่ 5

หากจำเป็นต้องแยกตัวประกอบเป็น 10 ตารางจะแสดง: 2 5 \u003d 10 เลขผลลัพธ์ 2 และ 5 เป็นตัวประกอบเฉพาะสำหรับเลข 10

ตัวอย่างที่ 6

หากจำเป็นต้องแยกย่อยหมายเลข 48 ตารางจะแสดง: 48 \u003d 6 8 แต่ 6 และ 8 ไม่ใช่ตัวประกอบเฉพาะ เนื่องจากสามารถแยกย่อยได้เป็น 6 = 2 3 และ 8 = 2 4 แล้ว การสลายตัวที่สมบูรณ์จากที่นี่จะกลายเป็น 48 = 6 8 = 2 3 2 4 . สัญกรณ์บัญญัติจะอยู่ในรูปแบบ 48 = 2 4 3 .

ตัวอย่างที่ 7

เมื่อแยกย่อยหมายเลข 3400 คุณสามารถใช้สัญลักษณ์ของการหารได้ ที่ กรณีนี้สัญญาณของการหารด้วย 10 และ 100 ลงตัว จากที่นี่เราจะได้ 3400 \u003d 34 100 โดยที่ 100 สามารถหารด้วย 10 นั่นคือเขียนเป็น 100 \u003d 10 10 ซึ่งหมายความว่า 3400 \u003d 34 10 10 จากสัญลักษณ์ของการหารเราจะได้ว่า 3400 = 34 10 10 = 2 17 2 5 2 5 . ปัจจัยทั้งหมดเป็นเรื่องง่าย การขยายตัวตามรูปแบบบัญญัติใช้รูปแบบ 3400 = 2 3 5 2 17.

เมื่อเราพบตัวประกอบเฉพาะ จำเป็นต้องใช้เครื่องหมายของการหารและตารางการคูณ หากคุณแทนจำนวน 75 เป็นผลคูณของปัจจัย คุณต้องคำนึงถึงกฎการหารด้วย 5 ลงตัว เราได้ 75 = 5 15 และ 15 = 3 5 นั่นคือ การสลายตัวที่ต้องการเป็นตัวอย่างของรูปแบบผลิตภัณฑ์ 75 = 5 · 3 · 5 .

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดเน้นข้อความนั้นแล้วกด Ctrl+Enter

ตัวแปรสุ่ม V ถูกเรียก เป็นศูนย์กลาง ถ้าความคาดหวังทางคณิตศาสตร์เท่ากับ 0 กระบวนการสุ่มระดับประถมศึกษาที่มีศูนย์กลางเป็นผลคูณของตัวแปรสุ่มที่มีศูนย์กลาง V และฟังก์ชันที่ไม่ใช่การสุ่ม φ(t):X(t)=Vφ(t) กระบวนการสุ่มแบบมีศูนย์กลางระดับประถมศึกษามีลักษณะดังต่อไปนี้:

การแสดงออกของแบบฟอร์ม
โดยที่ φ เค ( ที ), เค =1;2;…-ฟังก์ชันไม่สุ่ม; , เค =1;2;… - ตัวแปรสุ่มที่อยู่กึ่งกลางที่ไม่มีความสัมพันธ์กัน เรียกว่าการขยายแบบบัญญัติของกระบวนการสุ่มเอ็กซ์ ( ที ) ในขณะที่ตัวแปรสุ่ม เรียกว่าค่าสัมประสิทธิ์ของการขยายตัวตามรูปแบบบัญญัติ ในขณะที่ฟังก์ชันที่ไม่สุ่ม φ เค ( ที ) - ประสานงานฟังก์ชั่นของการขยายตัวตามบัญญัติ

พิจารณาลักษณะของกระบวนการสุ่ม

เนื่องจากตามสภาพ
แล้ว

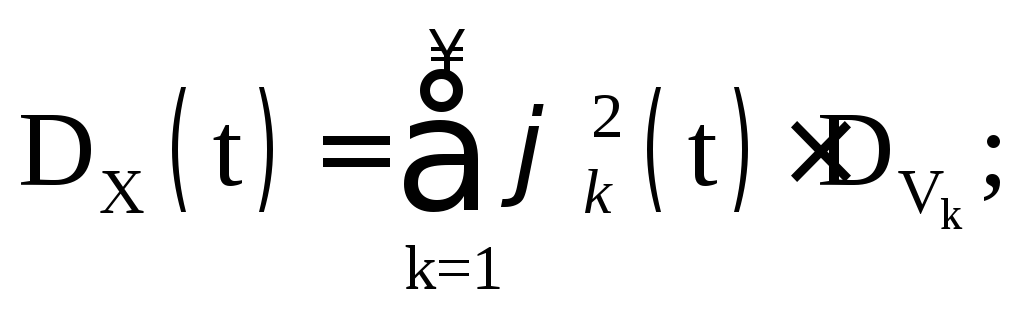
เห็นได้ชัดว่ามีกระบวนการสุ่มแบบเดียวกัน ชนิดต่างๆการขยายตามรูปแบบบัญญัติขึ้นอยู่กับตัวเลือกของฟังก์ชันพิกัด ยิ่งไปกว่านั้น แม้จะมีตัวเลือกของฟังก์ชันพิกัด การกระจายของตัวแปรสุ่ม V k ก็มีความเด็ดขาด ในทางปฏิบัติ จากผลการทดลอง จะได้ค่าประมาณสำหรับความคาดหวังทางคณิตศาสตร์และฟังก์ชันสหสัมพันธ์:
. หลังจากการย่อยสลาย
ในอนุกรมฟูริเยร์คู่ในฟังก์ชันพิกัด φ ถึง (t):

รับค่าของความแปรปรวน
ตัวแปรสุ่ม V k .

4.2. แนวคิดของฟังก์ชันทั่วไป ฟังก์ชันไดแรคเดลต้า การเป็นตัวแทนแบบบัญญัติของกระบวนการสุ่ม

ฟังก์ชั่นทั่วไป เรียกว่าลิมิตของลำดับของฟังก์ชันต่อเนื่องตระกูลหนึ่งพารามิเตอร์

ฟังก์ชันไดแรคเดลต้า
- เป็นฟังก์ชันทั่วไปที่เป็นผลมาจากการผ่านไปยังขีดจำกัดที่
ในครอบครัวของฟังก์ชั่น

ในบรรดาคุณสมบัติ คุณสมบัติหมายเหตุต่อไปนี้:

2.

3. ถ้า f(t)- ฟังก์ชันต่อเนื่อง, แล้ว

กระบวนการสุ่ม X( ที ) ซึ่งฟังก์ชันสหสัมพันธ์มีรูปแบบที่เรียกว่า "เสียงสีขาว" ที่ไม่หยุดนิ่ง ถ้า ว ( ที 1 )= ว - คอสต์ แล้ว X( ที ) - "เสียงสีขาว" นิ่ง

จากคำจำกัดความต่อไปนี้ไม่มีส่วนตัดขวางของ "เสียงสีขาว" ที่สัมพันธ์กันแม้ปิดโดยพลการ นิพจน์ W(t) เรียกว่า ความเข้มของสัญญาณรบกวนสีขาว

การเป็นตัวแทนแบบบัญญัติของกระบวนการสุ่ม X( ที ) เรียกว่าการแสดงออกของรูปแบบ
ที่ไหน
- ฟังก์ชั่นกึ่งกลางแบบสุ่ม
- ฟังก์ชันที่ไม่ใช่การสุ่มของอาร์กิวเมนต์ต่อเนื่อง

ฟังก์ชันความสัมพันธ์ของกระบวนการสุ่มดังกล่าวมีรูปแบบ:

มันสามารถแสดงให้เห็นว่ามีฟังก์ชั่นที่ไม่สุ่ม G(λ) เช่นนั้น

โดยที่ G(λ 1) คือความหนาแน่นของการกระจายตัว δ(x) - ฟังก์ชันไดแรคเดลต้า เราได้รับ

ดังนั้น ความแปรปรวนของกระบวนการสุ่ม X(t):

.

4.3. การแปลงเชิงเส้นและไม่เชิงเส้นของกระบวนการสุ่ม

พิจารณาปัญหาต่อไปนี้: อินพุตของระบบ (อุปกรณ์, ตัวแปลง) S มาพร้อมกับ "สัญญาณอินพุต" ซึ่งมีลักษณะของกระบวนการสุ่ม X(t) ระบบจะแปลงเป็น "สัญญาณออก" Y(t):

.

อย่างเป็นทางการ การแปลงกระบวนการสุ่ม X(t) เป็น Y(t) สามารถอธิบายได้โดยใช้สิ่งที่เรียกว่าตัวดำเนินการระบบ A t:

Y(t)=ก t (X(t)).

ดัชนี t บ่งชี้ว่าตัวดำเนินการนี้ทำการแปลงตามเวลา สูตรต่อไปนี้ของปัญหาการเปลี่ยนแปลงของกระบวนการสุ่มเป็นไปได้

กฎของการกระจายเป็นที่รู้จักหรือ ลักษณะทั่วไปกระบวนการสุ่ม X(t) ที่อินพุตไปยังระบบ S ผู้ดำเนินการจะได้รับ A t ของระบบ S ซึ่งจำเป็นต้องกำหนดกฎการกระจายหรือลักษณะทั่วไปของกระบวนการสุ่ม Y(t) ที่เอาต์พุตของระบบ S

กฎการกระจาย (ลักษณะทั่วไป) ของกระบวนการสุ่ม X(t) และข้อกำหนดสำหรับกระบวนการสุ่ม Y(t) เป็นที่ทราบกันดี จำเป็นต้องกำหนดรูปแบบของตัวดำเนินการ A t ของระบบ S ที่ตอบสนองความต้องการที่กำหนด kY(t) ได้ดีที่สุด

กฎของการกระจาย (ลักษณะทั่วไป) ของกระบวนการสุ่ม Y(t) เป็นที่รู้จักและให้ตัวดำเนินการ A t ของระบบ S จำเป็นต้องกำหนดกฎการกระจายหรือลักษณะทั่วไปของกระบวนการสุ่ม X(t)

พี รินยาตา การจำแนกประเภทต่อไปตัวดำเนินการ A t ของระบบ S:

ตัวดำเนินการระบบ

Linear Lไม่เชิงเส้นN

เชิงเส้นที่เป็นเนื้อเดียวกัน L 0 เชิงเส้นที่ไม่เป็นเนื้อเดียวกัน L n

พิจารณาผลกระทบของระบบเอกพันธ์เชิงเส้น

L n (...) \u003d L 0 (...) + φ (t)

ในกระบวนการสุ่ม X(t) ที่มีการขยายตัวแบบบัญญัติต่อไปนี้:

.

เราได้รับ:

เราแนะนำสัญกรณ์

จากนั้นการสลายตัวตามรูปแบบบัญญัติของ Y(t) จะอยู่ในรูปแบบ:

.

ความคาดหวังทางคณิตศาสตร์ของกระบวนการสุ่ม Y(t):

ฟังก์ชันสหสัมพันธ์ของกระบวนการสุ่ม Y(t):

เพราะเหตุนี้,

ในอีกด้านหนึ่ง

การกระจายตัวของกระบวนการสุ่ม Y(t):

โดยสรุปในส่วนนี้ เราทราบว่าตัวดำเนินการของการสร้างความแตกต่างและการบูรณาการของกระบวนการสุ่มนั้นเป็นเนื้อเดียวกันเชิงเส้น

2. พิจารณาการแปลงกำลังสอง:

Y(t)=(X(t)) 2 ,

V k -ตัวแปรสุ่มที่มีการกระจายสมมาตรประมาณศูนย์ ทั้งสี่คนมีความเป็นอิสระร่วมกัน แล้ว

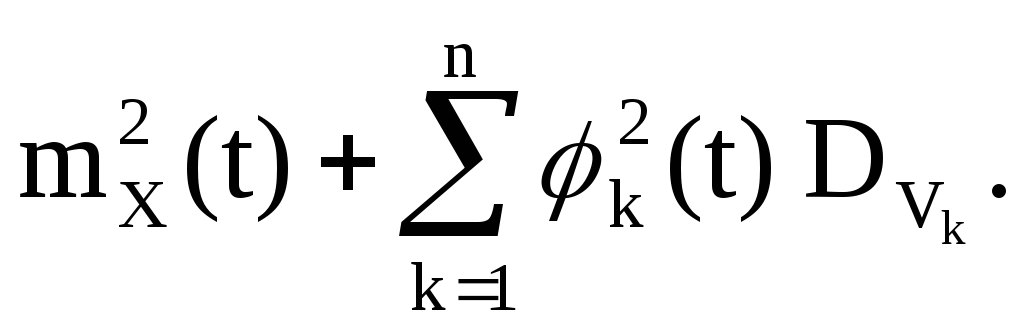
เราแนะนำฟังก์ชันที่ไม่สุ่ม

และตัวแปรสุ่ม

จากนั้นกระบวนการสุ่ม Y(t) จะอยู่ในรูปแบบ

ได้รับการสลายตัวแบบบัญญัติของกระบวนการสุ่ม Y(t) ฟังก์ชันสหสัมพันธ์ Y(t):

สูตรที่ให้ไว้ จำนวนธรรมชาติ n (n > 1). รับการสลายตัวตามรูปแบบบัญญัติเป็นปัจจัยเฉพาะ นั่นคือ แสดงให้เห็นว่าเป็นผลคูณของปัจจัยเฉพาะ ในกรณีนี้อนุญาตให้ระบุปัจจัย 1 ในการสลายตัว ตัวอย่างเช่น 264 = 2 * 2 * 2 * 3 * 11 (อนุญาตให้โปรแกรมให้คำตอบ 264 = 1 * 2 * 2 * 2*3*11).

การตัดสินใจ. งานนี้มีทางออกที่ค่อนข้างดี

จาก ทฤษฎีบทพื้นฐานของเลขคณิตเป็นที่ทราบกันว่าสำหรับจำนวนธรรมชาติใดๆ ที่มากกว่า 1 จะมีการแยกตัวตามรูปแบบบัญญัติออกเป็นปัจจัยเฉพาะ และการสลายตัวนี้จะมีลักษณะเฉพาะขึ้นอยู่กับลำดับของปัจจัย ตัวอย่างเช่น 12 = 2 * 2 * 2 และ 12 = 3 * 2 * 2 เป็นการขยายเดียวกัน

พิจารณารูปแบบบัญญัติของตัวเลขใดๆ บน ตัวอย่างเฉพาะ. ตัวอย่างเช่น 264 = 2 * 2 * 2 * 3 * 11 โครงสร้างนี้เปิดเผยได้อย่างไร เพื่อตอบคำถามนี้ ให้เราระลึกถึง หลักสูตรของโรงเรียนกฎพีชคณิตสำหรับการหาร monomials โดยจินตนาการว่าตัวเลขในการสลายตัวตามบัญญัติเป็นตัวแปร อย่างที่คุณทราบ หากคุณแบ่งนิพจน์เป็นตัวแปรในระดับหนึ่งที่มีอยู่ในนิพจน์นี้ในระดับเดียวกัน นิพจน์นั้นจะถูกลบในบันทึก

นั่นคือถ้าเราหาร 264 ด้วย 2 ผีสางหนึ่งตัวจะหายไปในการขยายตามรูปแบบบัญญัติ จากนั้นเราตรวจสอบได้ว่าผลหารที่ได้นั้นหารด้วย 2 ลงตัวอีกครั้งหรือไม่ คำตอบคือได้ แต่การหารครั้งที่สามจะให้เศษ จากนั้นคุณต้องคำนึงถึงจำนวนธรรมชาติ 3 ต่อไปนี้ - ผลหารจะถูกแบ่งออกเป็นหนึ่งครั้ง เป็นผลให้ผ่านเส้นจำนวนในทิศทางที่เป็นบวกเราจะไปถึงหมายเลข 11 และหลังจากหารด้วย 11 นมีค่าเท่ากับ 1 ซึ่งจะระบุถึงความจำเป็นในการสิ้นสุดขั้นตอน

เหตุใดด้วย "การลบ" ของปัจจัยที่พบเช่นนี้ เราจึงไม่สามารถหารด้วยจำนวนประกอบได้ อันที่จริง ทุกอย่างเรียบง่ายที่นี่ - จำนวนประกอบใดๆ เป็นผลคูณของตัวประกอบเฉพาะที่น้อยกว่า เป็นผลให้ปรากฎว่าเราจะลบออกจาก นตัวประกอบทั้งหมดของจำนวนประกอบใดๆ จนกว่าเราจะมาถึงตัวมันเองในห่วงโซ่ของการหาร ตัวอย่างเช่นด้วยการทำซ้ำดังกล่าว นจะไม่ถูกหารด้วย 4 เนื่องจาก "ระหว่างทาง" เราจะขีดฆ่าหมายเลขนี้ นปัจจัยทั้งหมดเป็นสองเท่า

อัลกอริทึมในภาษาธรรมชาติ:

1) การป้อนข้อมูล น;

2) การกำหนดตัวแปร หน้าหมายเลข 2;

3) เอาต์พุตตัวเลข นเครื่องหมายเท่ากับและหน่วยสำหรับตกแต่งการสลายตัว

4) เรียกใช้ลูปโดยมีเงื่อนไขล่วงหน้า น< > 1 . ในวง:

1. ถ้า มม็อดพี = 0จากนั้นแสดงเครื่องหมายคูณและตัวแปร p จากนั้นหาร นบน หน้ามิฉะนั้นให้เพิ่มมูลค่า ผมโดย 1;

1. โปรแกรม PrimeFactors;
2. n, p: คำ;
3. เริ่ม
4. พี:= 2;
5. อ่าน (n);
6. เขียน (n, '=1');
7. ในขณะที่ n<>1 เริ่มกันเลย
8. ถ้า (n mod p) = 0 ให้เริ่ม
9. เขียน ('*', p);
10. n:= n div พี
11. อย่างอื่นเริ่มต้น
12. อิงค์(พี)