การขยายตัวในซีรีส์ Taylor อนุกรมกำลัง การบรรจบกัน การขยายฟังก์ชันเป็นอนุกรมกำลัง

ในบรรดาอนุกรมการทำงาน ตำแหน่งที่สำคัญที่สุดถูกครอบครองโดยอนุกรมพลังงาน

อนุกรมกำลังเรียกว่าอนุกรม

ซึ่งมีสมาชิกเป็นฟังก์ชันเลขยกกำลังที่จัดเรียงด้วยเลขยกกำลังที่ไม่เป็นลบเพิ่มขึ้น x, ก ค0 , ค 1 , ค 2 , คน เป็นค่าคงที่ ตัวเลข ค1 , ค 2 , คน - ค่าสัมประสิทธิ์ของสมาชิกชุด ค0 - สมาชิกฟรี เงื่อนไขของอนุกรมกำลังถูกกำหนดไว้ในเส้นจำนวนทั้งหมด

มาทำความรู้จักกับแนวคิด บริเวณที่บรรจบกันของอนุกรมกำลัง นี่คือชุดของค่าตัวแปร xซึ่งซีรีส์มาบรรจบกัน อนุกรมกำลังมีขอบเขตของการบรรจบกันที่ค่อนข้างง่าย สำหรับค่าจริงของตัวแปร xพื้นที่บรรจบกันประกอบด้วยจุดเดียวหรือเป็นช่วงที่แน่นอน (ช่วงของการบรรจบกัน) หรือเกิดขึ้นพร้อมกับแกนทั้งหมด วัว .

เมื่อแทนค่าในอนุกรมกำลัง x= 0 คุณจะได้ชุดตัวเลข

ค0 +0+0+...+0+... ,

ซึ่งมาบรรจบกัน

ดังนั้น เมื่อ x= 0 ลู่เข้าอนุกรมกำลังใด ๆ ดังนั้น พื้นที่บรรจบกัน ไม่สามารถเป็นเซตว่างได้ โครงสร้างของขอบเขตการบรรจบกันของอนุกรมกำลังทั้งหมดจะเหมือนกัน สามารถสร้างได้โดยใช้ทฤษฎีบทต่อไปนี้

ทฤษฎีบทที่ 1 (ทฤษฎีบทของอาเบล). ถ้าอนุกรมกำลังมาบรรจบกันที่ค่าใดค่าหนึ่ง x = x 0 ซึ่งแตกต่างจากศูนย์ จากนั้นจึงมาบรรจบกัน และยิ่งไปกว่านั้น สำหรับค่าทั้งหมด |x| < |x 0 | . โปรดทราบ: ทั้งค่าเริ่มต้น "x เป็นศูนย์" และค่าใดๆ ของ "x" ที่เปรียบเทียบกับค่าเริ่มต้นจะถูกนำมาโมดูโล - โดยไม่คำนึงถึงเครื่องหมาย

ผลที่ตามมา ถ้า ความแตกต่างของอนุกรมพลังงาน ด้วยค่าบางอย่าง x = x 1 จากนั้นจะแยกออกสำหรับค่าทั้งหมด |x| > |x 1 | .

ตามที่เราทราบก่อนหน้านี้ อนุกรมกำลังใดๆ รวมกันเป็นค่า x= 0 มีอนุกรมกำลังที่ลู่เข้าเฉพาะสำหรับ x= 0 และแยกสำหรับค่าอื่นๆ เอ็กซ์. หากไม่รวมกรณีนี้ในการพิจารณา เราถือว่าอนุกรมกำลังลู่เข้าที่บางค่า x = x 0 แตกต่างจากศูนย์ จากนั้น ตามทฤษฎีบทของอาเบล มันจะลู่เข้าทุกจุดของช่วงเวลา ]-| x0 |, |x 0 |[ (ช่วงเวลา, ขอบเขตด้านซ้ายและขวาซึ่งเป็นค่าของ x, ที่อนุกรมกำลังมาบรรจบกัน, ถ่ายตามลำดับด้วยเครื่องหมายลบและเครื่องหมายบวก), สมมาตรเกี่ยวกับจุดกำเนิด

ถ้าอนุกรมกำลังเบี่ยงเบนที่ค่าใดค่าหนึ่ง x = x 1 จากนั้น ตามผลสรุปของทฤษฎีบทของอาเบล มันยังแยกออกจากทุกจุดที่อยู่นอกส่วน [-| x1 |, |x 1 |] . ตามนั้นสำหรับอนุกรมกำลังใดๆ จะมีช่วง สมมาตรตามจุดกำเนิด เรียกว่า ช่วงการบรรจบกัน ในแต่ละจุดที่อนุกรมมาบรรจบกัน อาจบรรจบกันที่ขอบเขต หรืออาจแตกต่างกัน และไม่จำเป็นต้องพร้อมกัน แต่นอกเซ็กเมนต์ อนุกรมจะแยกออกจากกัน ตัวเลข รเรียกว่ารัศมีการบรรจบกันของอนุกรมกำลัง

ในกรณีพิเศษ ช่วงการบรรจบกันของอนุกรมกำลัง เสื่อมถึงจุดหนึ่งได้ (แล้วอนุกรมมาบรรจบกันเฉพาะสำหรับ x= 0 และสันนิษฐานว่า ร= 0) หรือแทนเส้นจำนวนทั้งหมด (จากนั้นอนุกรมจะลู่เข้าที่ทุกจุดของเส้นจำนวน และถือว่า )

ดังนั้น คำจำกัดความของขอบเขตของการบรรจบกันของอนุกรมกำลังจึงเป็นการกำหนดขอบเขตของมัน รัศมีของการบรรจบกัน รและการศึกษาการลู่เข้าของอนุกรมบนขอบเขตของช่วงลู่เข้า (สำหรับ )

ทฤษฎีบท 2หากค่าสัมประสิทธิ์ทั้งหมดของอนุกรมกำลังเริ่มต้นจากค่าใดค่าหนึ่งไม่ใช่ศูนย์ ดังนั้นรัศมีของการบรรจบกันจะเท่ากับขีด จำกัด ที่อัตราส่วนของค่าสัมบูรณ์ของค่าสัมประสิทธิ์ของสมาชิกทั่วไปต่อไปนี้ของอนุกรม เช่น

ตัวอย่างที่ 1 หาขอบเขตของการบรรจบกันของอนุกรมกำลัง

การตัดสินใจ. ที่นี่

ใช้สูตร (28) เราพบรัศมีของการบรรจบกันของอนุกรมนี้:

ให้เราศึกษาการบรรจบกันของอนุกรมเมื่อสิ้นสุดช่วงเวลาของการบรรจบกัน . ตัวอย่างที่ 13 แสดงว่าอนุกรมนี้ลู่เข้าหากัน x= 1 และเบี่ยงที่ x= -1. ดังนั้น พื้นที่บรรจบกันคือ ครึ่งช่วง

ตัวอย่างที่ 2 ค้นหาขอบเขตของการบรรจบกันของอนุกรมกำลัง

การตัดสินใจ. ค่าสัมประสิทธิ์ของอนุกรมเป็นบวก และ

ให้เราหาขีดจำกัดของอัตราส่วนนี้ เช่น รัศมีการบรรจบกันของอนุกรมกำลัง:

เราตรวจสอบการบรรจบกันของอนุกรมเมื่อสิ้นสุดช่วงเวลา การทดแทนค่า x= -1/5 และ x= 1/5 ในซีรีส์นี้ให้:

ชุดแรกมาบรรจบกัน (ดูตัวอย่างที่ 5) แต่จากนั้นโดยอาศัยทฤษฎีบทของย่อหน้า "การบรรจบกันสัมบูรณ์" ชุดที่สองก็บรรจบกันและขอบเขตของการบรรจบกันคือส่วน

ตัวอย่างที่ 3 หาขอบเขตของการบรรจบกันของอนุกรมกำลัง

การตัดสินใจ. ที่นี่

ใช้สูตร (28) เราพบรัศมีของการบรรจบกันของอนุกรม:

ให้เราศึกษาการบรรจบกันของอนุกรมสำหรับค่า . แทนที่พวกเขาในซีรีส์นี้ตามลำดับที่เราได้รับ

อนุกรมทั้งสองต่างกันเนื่องจากเงื่อนไขการลู่เข้าที่จำเป็นไม่เป็นที่พอใจ ดังนั้น ที่ปลายทั้งสองข้างของช่วงการบรรจบกัน อนุกรมนี้จะแยกออก และขอบเขตของการลู่เข้าคือช่วง

ตัวอย่างที่ 5 หาขอบเขตของการบรรจบกันของอนุกรมกำลัง

การตัดสินใจ. เราพบความสัมพันธ์ ที่ไหน และ :

ตามสูตร (28) รัศมีของการบรรจบกันของอนุกรมนี้

,

นั่นคืออนุกรมจะมาบรรจบกันก็ต่อเมื่อ x= 0 และแตกต่างสำหรับค่าอื่นๆ เอ็กซ์.

ตัวอย่างแสดงให้เห็นว่าอนุกรมทำงานแตกต่างกันเมื่อสิ้นสุดช่วงคอนเวอร์เจนซ์ ในตัวอย่างที่ 1 อนุกรมลู่เข้าที่ปลายด้านหนึ่งของช่วงการลู่เข้าและแยกออกที่ปลายอีกด้านหนึ่ง ในตัวอย่างที่ 2 อนุกรมลู่เข้าที่ปลายทั้งสอง ในตัวอย่างที่ 3 อนุกรมลู่ออกที่ปลายทั้งสอง

สูตรสำหรับรัศมีการบรรจบกันของอนุกรมกำลังได้ภายใต้สมมติฐานที่ว่าค่าสัมประสิทธิ์ทั้งหมดของพจน์ของอนุกรมที่เริ่มต้นจากบางส่วนไม่ใช่ศูนย์ ดังนั้น อนุญาตให้ใช้สูตร (28) ในกรณีเหล่านี้เท่านั้น หากเงื่อนไขนี้ถูกละเมิด ควรใช้รัศมีของการบรรจบกันของอนุกรมกำลัง สัญลักษณ์ของ d'Alembertหรือโดยการเปลี่ยนแปลงตัวแปร โดยการแปลงอนุกรมเป็นรูปแบบที่ตรงตามเงื่อนไขที่กำหนด

ตัวอย่างที่ 6 ค้นหาช่วงเวลาของการลู่เข้าของอนุกรมกำลัง

การตัดสินใจ. ชุดนี้ไม่มีคำที่มีองศาคี่ เอ็กซ์. ดังนั้นเราจึงเปลี่ยนชุดโดยการตั้งค่า จากนั้นเราจะได้รับซีรีส์

สามารถใช้สูตร (28) เพื่อหารัศมีการบรรจบกันได้ เนื่องจาก , และ , จากนั้นรัศมีของการบรรจบกันของอนุกรมนี้

จากความเท่าเทียมกันที่เราได้รับ ดังนั้น อนุกรมนี้จึงมาบรรจบกับช่วงเวลา

ผลรวมอนุกรมกำลัง ความแตกต่างและการรวมของอนุกรมกำลัง

ให้ชุดพลังงาน

รัศมีของการบรรจบกัน ร> 0 เช่น อนุกรมนี้มาบรรจบกับช่วงเวลา

แล้วละค่า เอ็กซ์จากช่วงเวลาของการบรรจบกันสอดคล้องกับผลรวมของอนุกรม ดังนั้นผลรวมของอนุกรมกำลังจึงเป็นฟังก์ชันของ เอ็กซ์ในช่วงของการบรรจบกัน แสดงว่ามันผ่าน ฉ(x) เราสามารถเขียนความเท่าเทียมกันได้

เข้าใจในแง่ที่ว่าผลรวมของอนุกรมในแต่ละจุด เอ็กซ์จากช่วงเวลาของการลู่เข้าเท่ากับค่าของฟังก์ชัน ฉ(x) ณ จุดนี้. ในความหมายเดียวกัน เราจะบอกว่าอนุกรมกำลัง (29) ลู่เข้าหาฟังก์ชัน ฉ(x) ในช่วงของการลู่เข้า

นอกช่วงเวลาของการบรรจบกัน ความเสมอภาค (30) ไม่มีความหมาย

ตัวอย่างที่ 7หาผลรวมของอนุกรมกำลัง

การตัดสินใจ. นี่คืออนุกรมเรขาคณิต ก= 1 และ ถาม= x. ดังนั้นผลรวมของมันคือฟังก์ชัน . อนุกรมลู่เข้า if และเป็นระยะลู่เข้า ดังนั้นความเท่าเทียมกัน

ใช้ได้กับค่าเท่านั้น แม้ว่าฟังก์ชัน กำหนดไว้สำหรับค่าทั้งหมด เอ็กซ์, นอกจากนี้ เอ็กซ์= 1.

สามารถแสดงว่าผลรวมของอนุกรมกำลัง ฉ(x) มีความต่อเนื่องและหาอนุพันธ์ได้บนช่วงใดๆ ภายในช่วงของการลู่เข้า โดยเฉพาะอย่างยิ่ง ณ จุดใดๆ ของช่วงการลู่เข้าของอนุกรม

ให้เรานำเสนอทฤษฎีบทเกี่ยวกับการหาอนุพันธ์แบบเทอมต่อเทอมและการอินทิเกรตของอนุกรมกำลัง

ทฤษฎีบท 1.อนุกรมกำลัง (30) ในช่วงของการลู่เข้าสามารถแยกความแตกต่างของพจน์ต่อพจน์ได้โดยไม่จำกัดจำนวนครั้ง และอนุกรมกำลังที่ได้จะมีรัศมีการบรรจบกันเท่ากับอนุกรมเดิม และผลรวมของอนุกรมกำลังตามลำดับเท่ากับ

ทฤษฎีบท 2อนุกรมกำลัง (30) สามารถรวมเทอมต่อเทอมได้ไม่จำกัดจำนวนครั้งภายในช่วงตั้งแต่ 0 ถึง เอ็กซ์, ถ้า , และอนุกรมกำลังผลลัพธ์มีรัศมีการบรรจบกันเท่ากับอนุกรมเดิม และผลรวมตามลำดับเท่ากับ

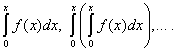
การขยายฟังก์ชันเป็นอนุกรมกำลัง

ให้ฟังก์ชั่น ฉ(x) ซึ่งจะขยายเป็นอนุกรมกำลัง เช่น เป็นตัวแทนในรูปแบบ (30):

ปัญหาคือการกำหนดค่าสัมประสิทธิ์ แถว (30) ในการทำเช่นนี้ การแยกความแตกต่างของความเท่าเทียมกัน (30) ทีละคำ เราพบตามลำดับ:

……………………………………………….. (31)

สมมติว่าเท่ากัน (30) และ (31) เอ็กซ์= 0 เราพบว่า

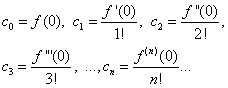
เราได้รับนิพจน์ที่พบแทนความเท่าเทียมกัน (30)

(32)

ให้เราค้นหาการขยายอนุกรม Maclaurin ของฟังก์ชันพื้นฐานบางอย่าง

ตัวอย่างที่ 8ขยายฟังก์ชันในชุด Maclaurin

การตัดสินใจ. อนุพันธ์ของฟังก์ชันนี้เหมือนกับฟังก์ชันเอง:

ดังนั้น เมื่อ เอ็กซ์= 0 เรามี

การแทนที่ค่าเหล่านี้เป็นสูตร (32) เราได้รับการขยายที่ต้องการ:

(33)

อนุกรมนี้บรรจบกันบนเส้นจำนวนทั้งหมด (รัศมีการบรรจบกันคือ )

ถ้าฟังก์ชั่น ฉ(x)มีบางช่วงเวลาที่มีจุด ก, อนุพันธ์ของคำสั่งซื้อทั้งหมด จากนั้นจึงสามารถใช้สูตร Taylor ได้:

ที่ไหน ร.น- สิ่งที่เรียกว่าเทอมที่เหลือหรือส่วนที่เหลือของซีรีส์ สามารถประมาณได้โดยใช้สูตรลากรองจ์:

โดยที่ตัวเลข x อยู่ระหว่าง เอ็กซ์และ ก.

หากมีค่าบางอย่าง x r n®0 ที่ น®¥ จากนั้นในขีดจำกัด สูตร Taylor สำหรับค่านี้จะเปลี่ยนเป็นสูตรที่บรรจบกัน ชุดเทย์เลอร์:

ดังนั้นฟังก์ชัน ฉ(x)สามารถขยายเป็นซีรี่ส์ Taylor ได้ ณ จุดที่พิจารณา เอ็กซ์, ถ้า:

1) มีอนุพันธ์ของคำสั่งทั้งหมด;

2) อนุกรมที่สร้างขึ้นมาบรรจบกันที่จุดนี้

ที่ ก= 0 เราได้รับซีรีส์ที่เรียกว่า ใกล้แมคลอริน:

ตัวอย่างที่ 1 ฉ(x)= 2x.

การตัดสินใจ. ให้เราหาค่าของฟังก์ชันและอนุพันธ์ได้ที่ เอ็กซ์=0

ฉ(x) = 2x, ฉ( 0) = 2 0 =1;

ฉ ¢ (x) = 2x ln2, ฉ ( 0) = 2 0 ln2=ln2;

ฉ ¢ ¢ (x) = 2xลน 2 2, ฉ ¢ ¢ ( 0) = 2 0 บันทึก 2 2= บันทึก 2 2;

ฉ(น)(x) = 2xล น 2, ฉ(น)( 0) = 2 0 ล น 2=ลน น 2.

แทนค่าที่ได้รับของอนุพันธ์ลงในสูตรอนุกรมเทย์เลอร์ เราได้รับ:

รัศมีการบรรจบกันของอนุกรมนี้เท่ากับอนันต์ ดังนั้นการขยายนี้จึงใช้ได้สำหรับ -¥<x<+¥.

ตัวอย่างที่ 2 เอ็กซ์+4) สำหรับฟังก์ชัน ฉ(x)=อี x.

การตัดสินใจ. การหาอนุพันธ์ของฟังก์ชัน e xและคุณค่าของพวกเขาที่จุด เอ็กซ์=-4.

ฉ(x)= อี x, ฉ(-4) = อี -4 ;

ฉ ¢ (x)= อี x, ฉ (-4) = อี -4 ;

ฉ ¢ ¢ (x)= อี x, ฉ ¢ ¢ (-4) = อี -4 ;

ฉ(น)(x)= อี x, ฉ(น)( -4) = อี -4 .

ดังนั้นอนุกรมของฟังก์ชัน Taylor ที่ต้องการจึงมีรูปแบบดังนี้

การสลายตัวนี้ยังใช้ได้สำหรับ -¥<x<+¥.

ตัวอย่างที่ 3 . ขยายฟังก์ชัน ฉ(x)=ลน xในชุดตามองศา ( X- 1),

(เช่นในซีรี่ส์ Taylor ในบริเวณใกล้เคียงกับจุดนั้น เอ็กซ์=1).

การตัดสินใจ. เราพบอนุพันธ์ของฟังก์ชันนี้

แทนค่าเหล่านี้ลงในสูตรเราจะได้ชุด Taylor ที่ต้องการ:

ด้วยความช่วยเหลือของการทดสอบของ d'Alembert เราสามารถตรวจสอบได้ว่าอนุกรมลู่เข้าเมื่อใด

½ X- 1½<1. Действительно,

อนุกรมลู่เข้าหากันถ้า ½ X- 1½<1, т.е. при 0<x<2. При เอ็กซ์=2 เราได้รับอนุกรมทางเลือกที่ตรงตามเงื่อนไขของการทดสอบไลบ์นิซ ที่ เอ็กซ์=0 ไม่ได้กำหนดฟังก์ชัน ดังนั้น ขอบเขตของการบรรจบกันของอนุกรมเทย์เลอร์คือช่วงครึ่งเปิด (0;2]

ให้เรานำเสนอส่วนขยายที่ได้รับด้วยวิธีนี้ในซีรีส์ Maclaurin (กล่าวคือ ในบริเวณใกล้เคียงของจุด เอ็กซ์=0) สำหรับฟังก์ชันพื้นฐานบางอย่าง:

(2) ,

(3) ,

(การขยายตัวครั้งสุดท้ายเรียกว่า อนุกรมทวินาม)

ตัวอย่างที่ 4 . ขยายฟังก์ชันเป็นอนุกรมกำลัง

การตัดสินใจ. ในการสลายตัว (1) เราแทนที่ เอ็กซ์บน - เอ็กซ์ 2 เราได้รับ:

ตัวอย่างที่ 5 . ขยายฟังก์ชันในชุด Maclaurin

การตัดสินใจ. เรามี

โดยใช้สูตร (4) เราสามารถเขียน:

แทนที่ เอ็กซ์ลงในสูตร -X, เราได้รับ:

จากที่นี่เราพบ:

เราได้รับการขยายวงเล็บจัดเรียงเงื่อนไขของชุดใหม่และลดคำศัพท์ที่คล้ายกัน

ซีรีส์นี้มาบรรจบกันในช่วงเวลา

(-1;1) เนื่องจากได้มาจากสองชุด ซึ่งแต่ละชุดมาบรรจบกันในช่วงเวลานี้

ความคิดเห็น .

นอกจากนี้ยังสามารถใช้สูตร (1)-(5) เพื่อขยายฟังก์ชันที่สอดคล้องกันในอนุกรม Taylor เช่น สำหรับการขยายฟังก์ชันที่เป็นจำนวนเต็มบวก ( ฮา). ในการทำเช่นนี้จำเป็นต้องทำการแปลงที่เหมือนกันในฟังก์ชันที่กำหนดเพื่อให้ได้ฟังก์ชันใดฟังก์ชันหนึ่ง (1) - (5) ซึ่งแทนที่จะเป็น เอ็กซ์ค่าใช้จ่าย k( ฮา) m โดยที่ k เป็นจำนวนคงที่ m เป็นจำนวนเต็มบวก การเปลี่ยนตัวแปรมักจะสะดวก ที=ฮาและขยายฟังก์ชันผลลัพธ์ที่เกี่ยวกับ t ในอนุกรม Maclaurin

วิธีนี้แสดงทฤษฎีบทเกี่ยวกับลักษณะเฉพาะของการขยายตัวของฟังก์ชันในอนุกรมกำลัง สาระสำคัญของทฤษฎีบทนี้คือ ในบริเวณใกล้เคียงกับจุดเดียวกัน ไม่สามารถรับชุดกำลังสองชุดที่แตกต่างกันซึ่งจะมาบรรจบกันเป็นฟังก์ชันเดียวกันได้ ไม่ว่าจะขยายด้วยวิธีใด

ตัวอย่างที่ 6 . ขยายฟังก์ชันในชุด Taylor ในบริเวณใกล้เคียงของจุด เอ็กซ์=3.

การตัดสินใจ. ปัญหานี้สามารถแก้ไขได้เช่นเดิมโดยใช้คำจำกัดความของอนุกรม Taylor ซึ่งจำเป็นต้องค้นหาอนุพันธ์ของฟังก์ชันและค่าของมันที่ เอ็กซ์=3. อย่างไรก็ตาม การใช้การสลายตัวที่มีอยู่จะง่ายกว่า (5):

อนุกรมผลลัพธ์บรรจบกันที่ หรือ -3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

ตัวอย่างที่ 7 . เขียนอนุกรมเทย์เลอร์ในอำนาจ ( เอ็กซ์-1) คุณสมบัติ .

การตัดสินใจ.

ซีรีส์มาบรรจบที่ หรือ 2< x 5 ปอนด์

จะใส่สูตรทางคณิตศาสตร์บนเว็บไซต์ได้อย่างไร?

หากคุณต้องการเพิ่มสูตรทางคณิตศาสตร์หนึ่งหรือสองสูตรลงในหน้าเว็บ วิธีที่ง่ายที่สุดในการทำเช่นนี้คือดังที่อธิบายไว้ในบทความ: สูตรทางคณิตศาสตร์สามารถแทรกลงในไซต์ได้อย่างง่ายดายในรูปแบบของรูปภาพที่ Wolfram Alpha สร้างขึ้นโดยอัตโนมัติ นอกจากความเรียบง่ายแล้ว วิธีการสากลนี้จะช่วยปรับปรุงการมองเห็นไซต์ในเครื่องมือค้นหา มันทำงานมานานแล้ว (และฉันคิดว่ามันจะใช้ได้ตลอดไป) แต่มันล้าสมัยทางศีลธรรม

หากคุณใช้สูตรทางคณิตศาสตร์บนเว็บไซต์ของคุณเป็นประจำ ฉันขอแนะนำให้คุณใช้ MathJax ซึ่งเป็นไลบรารี JavaScript พิเศษที่แสดงสัญลักษณ์ทางคณิตศาสตร์ในเว็บเบราว์เซอร์โดยใช้มาร์กอัป MathML, LaTeX หรือ ASCIIMathML

มีสองวิธีในการเริ่มใช้ MathJax: (1) ใช้โค้ดง่ายๆ คุณสามารถเชื่อมต่อสคริปต์ MathJax กับไซต์ของคุณได้อย่างรวดเร็ว ซึ่งจะถูกโหลดโดยอัตโนมัติจากเซิร์ฟเวอร์ระยะไกลในเวลาที่เหมาะสม (รายชื่อเซิร์ฟเวอร์) (2) อัปโหลดสคริปต์ MathJax จากเซิร์ฟเวอร์ระยะไกลไปยังเซิร์ฟเวอร์ของคุณและเชื่อมต่อกับทุกหน้าในไซต์ของคุณ วิธีที่สองมีความซับซ้อนและใช้เวลานานกว่า และจะช่วยให้คุณสามารถโหลดหน้าเว็บของไซต์ของคุณได้เร็วขึ้น และหากเซิร์ฟเวอร์หลัก MathJax ไม่สามารถใช้งานได้ชั่วคราวด้วยเหตุผลบางประการ การดำเนินการนี้จะไม่ส่งผลกระทบต่อไซต์ของคุณแต่อย่างใด แม้จะมีข้อดีเหล่านี้ ฉันเลือกวิธีแรกเนื่องจากง่ายกว่า เร็วกว่า และไม่ต้องใช้ทักษะด้านเทคนิค ทำตามตัวอย่างของฉัน และภายใน 5 นาที คุณจะสามารถใช้คุณลักษณะทั้งหมดของ MathJax บนไซต์ของคุณได้

คุณสามารถเชื่อมต่อสคริปต์ไลบรารี MathJax จากเซิร์ฟเวอร์ระยะไกลโดยใช้ตัวเลือกโค้ดสองตัวที่นำมาจากเว็บไซต์หลัก MathJax หรือจากหน้าเอกสาร:

หนึ่งในตัวเลือกโค้ดเหล่านี้จำเป็นต้องคัดลอกและวางลงในโค้ดของหน้าเว็บของคุณ โดยควรอยู่ระหว่างแท็ก และหรือหลังแท็ก . ตามตัวเลือกแรก MathJax โหลดเร็วขึ้นและทำให้หน้าช้าลง แต่ตัวเลือกที่สองจะติดตามและโหลด MathJax เวอร์ชันล่าสุดโดยอัตโนมัติ หากคุณใส่รหัสแรก จะต้องมีการอัปเดตเป็นระยะ หากคุณวางโค้ดที่สอง หน้าเว็บจะโหลดช้าลง แต่คุณไม่จำเป็นต้องตรวจสอบการอัปเดตของ MathJax อย่างต่อเนื่อง

วิธีที่ง่ายที่สุดในการเชื่อมต่อ MathJax คือใน Blogger หรือ WordPress: ในแผงควบคุมของไซต์ ให้เพิ่มวิดเจ็ตที่ออกแบบมาเพื่อแทรกโค้ด JavaScript ของบุคคลที่สาม คัดลอกเวอร์ชันแรกหรือเวอร์ชันที่สองของโค้ดโหลดด้านบน และวางวิดเจ็ตให้ใกล้กับ จุดเริ่มต้นของเทมเพลต (อย่างไรก็ตาม สิ่งนี้ไม่จำเป็นเลย เนื่องจากสคริปต์ MathJax ถูกโหลดแบบอะซิงโครนัส) นั่นคือทั้งหมด ตอนนี้เรียนรู้ไวยากรณ์มาร์กอัปของ MathML, LaTeX และ ASCIIMathML และคุณก็พร้อมที่จะฝังสูตรทางคณิตศาสตร์ลงในหน้าเว็บของคุณแล้ว

แฟร็กทัลใดๆ ถูกสร้างขึ้นตามกฎบางอย่าง ซึ่งใช้อย่างต่อเนื่องโดยไม่จำกัดจำนวนครั้ง แต่ละครั้งเรียกว่าการวนซ้ำ

ขั้นตอนวิธีวนซ้ำสำหรับการสร้างฟองน้ำ Menger นั้นค่อนข้างง่าย: ลูกบาศก์เดิมที่มีด้าน 1 ถูกแบ่งด้วยระนาบที่ขนานกับใบหน้าออกเป็น 27 ลูกบาศก์เท่าๆ กัน หนึ่งลูกบาศก์กลางและ 6 ลูกบาศก์ที่อยู่ติดกับใบหน้าจะถูกลบออกจากมัน กลายเป็นชุดที่ประกอบด้วยลูกบาศก์ขนาดเล็กที่เหลืออีก 20 ลูก ทำเช่นเดียวกันกับแต่ละลูกบาศก์เหล่านี้ เราจะได้ชุดที่ประกอบด้วยลูกบาศก์ขนาดเล็กกว่า 400 ลูก ดำเนินขั้นตอนนี้ไปเรื่อย ๆ เราจะได้ฟองน้ำ Menger

"ค้นหาการขยายตัวของ Maclaurin ของ f(x)"- นี่คือสิ่งที่งานในคณิตศาสตร์ระดับสูงฟังดูเหมือนซึ่งนักเรียนบางคนสามารถทำได้ในขณะที่คนอื่นไม่สามารถรับมือกับตัวอย่างได้ มีหลายวิธีในการขยายอนุกรมของพลัง ในที่นี้เราจะให้วิธีการขยายฟังก์ชันในอนุกรมของ Maclaurin เมื่อพัฒนาฟังก์ชันในอนุกรม คุณต้องเก่งเรื่องการคำนวณอนุพันธ์

ตัวอย่าง 4.7 ขยายฟังก์ชันเป็นอนุกรมกำลัง x

การคำนวณ: เราทำการขยายฟังก์ชันตามสูตร Maclaurin ขั้นแรก เราขยายส่วนของฟังก์ชันเป็นชุด

สุดท้าย เราคูณการขยายตัวด้วยตัวเศษ
เทอมแรกคือค่าของฟังก์ชันที่ศูนย์ f (0) = 1/3
ค้นหาอนุพันธ์ของฟังก์ชันลำดับที่หนึ่งและสูงกว่า f (x) และค่าของอนุพันธ์เหล่านี้ที่จุด x=0




นอกจากนี้ ด้วยรูปแบบของการเปลี่ยนค่าของอนุพันธ์เป็น 0 เราจึงเขียนสูตรสำหรับอนุพันธ์อันดับ n

ดังนั้นเราจึงเป็นตัวแทนของส่วนเสริมในชุด Maclaurin

เราคูณด้วยตัวเศษและได้การขยายฟังก์ชันตามที่ต้องการในอนุกรมกำลัง x

อย่างที่คุณเห็นไม่มีอะไรซับซ้อนที่นี่
ประเด็นสำคัญทั้งหมดขึ้นอยู่กับความสามารถในการคำนวณอนุพันธ์และสรุปมูลค่าของอนุพันธ์ของคำสั่งซื้อขายที่สูงขึ้นได้อย่างรวดเร็วที่ศูนย์ ตัวอย่างต่อไปนี้จะช่วยให้คุณเรียนรู้วิธีขยายฟังก์ชันเป็นชุดได้อย่างรวดเร็ว

ตัวอย่าง 4.10 จงหาส่วนขยายของฟังก์ชัน Maclaurin

การคำนวณ: อย่างที่คุณเดาได้ เราจะขยายโคไซน์ในตัวเศษเป็นชุด ในการทำเช่นนี้ คุณสามารถใช้สูตรสำหรับค่าที่น้อยมาก หรือคุณสามารถรับการขยายตัวของโคไซน์ในรูปของอนุพันธ์ เป็นผลให้เรามาถึงชุดต่อไปในพลังของ x

อย่างที่คุณเห็น เรามีการคำนวณขั้นต่ำและการนำเสนอแบบย่อของส่วนขยายซีรีส์

ตัวอย่าง 4.16 ขยายฟังก์ชันเป็นอนุกรมกำลัง x:
7/(12-x-x^2)
การคำนวณ: ในตัวอย่างประเภทนี้ จำเป็นต้องขยายเศษส่วนผ่านผลรวมของเศษส่วนอย่างง่าย
วิธีการทำเช่นนี้เราจะไม่แสดงตอนนี้ แต่ด้วยความช่วยเหลือของสัมประสิทธิ์ไม่แน่นอนเราจะได้ผลรวมของเศษส่วนอดีต
ต่อไป เราเขียนตัวส่วนในรูปแบบเลขยกกำลัง

มันยังคงขยายเงื่อนไขโดยใช้สูตร Maclaurin เมื่อรวมพจน์ที่มีกำลังเท่ากันของ "x" เราเขียนสูตรสำหรับพจน์ทั่วไปของการขยายฟังก์ชันในชุดข้อมูล



ส่วนสุดท้ายของการเปลี่ยนไปใช้ซีรีส์ในตอนเริ่มต้นเป็นเรื่องยากที่จะนำไปใช้ เนื่องจากเป็นการยากที่จะรวมสูตรสำหรับดัชนีที่จับคู่และไม่จับคู่ (ยกกำลัง) แต่ด้วยการฝึกฝน คุณจะทำได้ดีขึ้น

ตัวอย่าง 4.18 จงหาส่วนขยายของฟังก์ชัน Maclaurin

การคำนวณ: ค้นหาอนุพันธ์ของฟังก์ชันนี้:

เราขยายฟังก์ชันเป็นชุดโดยใช้หนึ่งในสูตรของ McLaren:

เราสรุปคำศัพท์ของซีรีส์ทีละคำโดยพิจารณาจากพื้นฐานที่ว่าทั้งคู่ตรงกันทุกประการ โดยการอินทิเกรตอนุกรมทั้งเทอมทีละเทอม เราได้รับการขยายของฟังก์ชันเป็นอนุกรมกำลัง x

ระหว่างสองบรรทัดสุดท้ายของการสลายตัว มีการเปลี่ยนแปลงซึ่งในตอนเริ่มต้นจะใช้เวลามาก การทำให้สูตรเป็นอนุกรมโดยทั่วไปไม่ใช่เรื่องง่ายสำหรับทุกคน ดังนั้นอย่ากังวลว่าจะไม่ได้สูตรที่ดีและกะทัดรัด

ตัวอย่าง 4.28 ค้นหาส่วนขยายของฟังก์ชัน Maclaurin:

เราเขียนลอการิทึมดังนี้

ใช้สูตร Maclaurin เพื่อขยายลอการิทึมของฟังก์ชันในอนุกรมกำลัง x

การพับครั้งสุดท้ายนั้นซับซ้อนในตอนแรก แต่เมื่อสลับตัวอักษรคุณจะได้สิ่งที่คล้ายกันเสมอ บทเรียนเบื้องต้นในหัวข้อการจัดตารางการทำงานในแถวเสร็จสมบูรณ์ แผนการสลายตัวอื่นๆ ที่น่าสนใจไม่แพ้กันจะกล่าวถึงในรายละเอียดในเนื้อหาต่อไปนี้

การแยกย่อยของฟังก์ชันในชุดของ Taylor, Maclaurin และ Laurent บนไซต์เพื่อฝึกทักษะการปฏิบัติ การขยายฟังก์ชันแบบอนุกรมนี้ช่วยให้นักคณิตศาสตร์มีแนวคิดในการประมาณค่าโดยประมาณของฟังก์ชัน ณ จุดใดจุดหนึ่งในขอบเขตของคำจำกัดความ การคำนวณค่าฟังก์ชันดังกล่าวทำได้ง่ายกว่ามาก เมื่อเทียบกับการใช้ตาราง Bredis ซึ่งล้าสมัยในยุคของการคำนวณ การขยายฟังก์ชันเป็นอนุกรมเทย์เลอร์หมายถึงการคำนวณค่าสัมประสิทธิ์ที่อยู่หน้าฟังก์ชันเชิงเส้นของอนุกรมนี้และเขียนในรูปแบบที่ถูกต้อง นักเรียนสับสนระหว่างสองซีรีส์นี้ โดยไม่เข้าใจว่าอะไรคือกรณีทั่วไปและอะไรคือกรณีพิเศษของสอง เราเตือนคุณทุกครั้งว่าอนุกรม Maclaurin เป็นกรณีพิเศษของอนุกรม Taylor นั่นคือเป็นอนุกรม Taylor แต่ ณ จุด x = 0 บันทึกย่อทั้งหมดของการขยายฟังก์ชันที่รู้จัก เช่น e ^x, Sin(x), Cos(x) และอื่นๆ นี่คือส่วนขยายในอนุกรม Taylor แต่ที่จุด 0 สำหรับการโต้แย้ง สำหรับฟังก์ชันของอาร์กิวเมนต์ที่ซับซ้อน อนุกรม Laurent เป็นปัญหาที่พบบ่อยที่สุดใน TFKT เนื่องจากเป็นอนุกรมอนันต์ที่มีสองด้าน เป็นผลรวมของสองแถว เราขอแนะนำให้คุณดูตัวอย่างการสลายตัวโดยตรงบนเว็บไซต์ การทำเช่นนี้ทำได้ง่ายมากโดยคลิกที่ "ตัวอย่าง" ด้วยตัวเลขใดก็ได้ จากนั้นคลิกปุ่ม "โซลูชัน" มันคือการขยายฟังก์ชันออกเป็นอนุกรมที่มีการเชื่อมโยงอนุกรมหลัก ซึ่งจำกัดฟังก์ชันดั้งเดิมในขอบเขตที่กำหนดตามแกนพิกัด หากตัวแปรเป็นของขอบเขต abscissa การวิเคราะห์เวกเตอร์นำมาเปรียบเทียบกับวินัยที่น่าสนใจอื่น ๆ ในวิชาคณิตศาสตร์ เนื่องจากต้องมีการตรวจสอบคำศัพท์แต่ละคำ จึงต้องใช้เวลามากในการดำเนินการ อนุกรมของเทย์เลอร์ใด ๆ สามารถเชื่อมโยงกับอนุกรม Maclaurin ได้โดยการแทนที่ x0 ด้วยศูนย์ แต่สำหรับอนุกรม Maclaurin การแสดงย้อนกลับของอนุกรม Taylor บางครั้งไม่ชัดเจน ไม่ว่าจะไม่จำเป็นต้องทำในรูปแบบที่บริสุทธิ์ แต่ก็น่าสนใจสำหรับการพัฒนาตนเองโดยทั่วไป อนุกรม Laurent แต่ละชุดสอดคล้องกับอนุกรมกำลังอนันต์สองด้านในเลขยกกำลังของ z-a หรืออีกนัยหนึ่งคืออนุกรมของ Taylor ประเภทเดียวกัน แต่แตกต่างกันเล็กน้อยในการคำนวณค่าสัมประสิทธิ์ เราจะพูดถึงขอบเขตของการบรรจบกันของซีรี่ส์ Laurent ในภายหลัง หลังจากการคำนวณทางทฤษฎีหลายครั้ง เช่นเดียวกับในศตวรรษที่ผ่านมา การขยายฟังก์ชันทีละขั้นเป็นอนุกรมแทบจะไม่สามารถทำได้โดยการลดเงื่อนไขให้เหลือส่วนร่วมเท่านั้น เนื่องจากฟังก์ชันในตัวส่วนไม่เป็นเชิงเส้น การคำนวณค่าการทำงานโดยประมาณจำเป็นต้องมีการกำหนดปัญหา ลองนึกถึงข้อเท็จจริงที่ว่าเมื่ออาร์กิวเมนต์ของอนุกรมเทย์เลอร์เป็นตัวแปรเชิงเส้น การขยายตัวจะเกิดขึ้นในหลายขั้นตอน แต่เป็นภาพที่แตกต่างอย่างสิ้นเชิง เมื่อฟังก์ชันเชิงซ้อนหรือไม่เป็นเชิงเส้นทำหน้าที่เป็นอาร์กิวเมนต์ของฟังก์ชันที่ขยาย กระบวนการแสดงฟังก์ชันดังกล่าวในอนุกรมกำลังนั้นชัดเจน เพราะด้วยวิธีดังกล่าว มันง่ายที่จะคำนวณ แม้ว่าจะเป็นค่าประมาณ แต่ค่าที่จุดใดๆ มีผลต่อการคำนวณต่อไป นอกจากนี้ยังใช้กับซีรี่ส์ Maclaurin เมื่อจำเป็นต้องคำนวณฟังก์ชันที่จุดศูนย์ อย่างไรก็ตาม ซีรีส์ Laurent เองก็แสดงด้วยการขยายระนาบด้วยหน่วยจินตภาพ นอกจากนี้ไม่ประสบความสำเร็จจะเป็นทางออกที่ถูกต้องของปัญหาในกระบวนการโดยรวม ในวิชาคณิตศาสตร์ วิธีนี้ไม่เป็นที่ทราบแน่ชัด แต่มีอยู่จริง เป็นผลให้คุณสามารถหาข้อสรุปของเซตย่อยที่เรียกว่า pointwise และในการขยายฟังก์ชันในอนุกรม คุณต้องใช้วิธีการที่รู้จักสำหรับกระบวนการนี้ เช่น การประยุกต์ใช้ทฤษฎีอนุพันธ์ เป็นอีกครั้งที่เราเชื่อมั่นในความถูกต้องของครูผู้ตั้งสมมติฐานเกี่ยวกับผลลัพธ์ของการคำนวณหลังการคำนวณ โปรดทราบว่าชุดเทย์เลอร์ซึ่งได้รับตามหลักคณิตศาสตร์ทั้งหมดมีอยู่และถูกกำหนดไว้ในแกนตัวเลขทั้งหมดอย่างไรก็ตามผู้ใช้บริการเว็บไซต์ที่รักอย่าลืมรูปแบบของฟังก์ชันดั้งเดิมเพราะอาจกลายเป็น ในขั้นต้นจำเป็นต้องตั้งค่าโดเมนของฟังก์ชันนั่นคือเขียนและแยกออกจากการพิจารณาเพิ่มเติมจุดที่ฟังก์ชันไม่ได้กำหนดไว้ในโดเมนของจำนวนจริง การพูดเช่นนี้จะแสดงให้เห็นถึงความรวดเร็วในการแก้ปัญหาของคุณ การสร้างอนุกรม Maclaurin ที่มีค่าอาร์กิวเมนต์เป็นศูนย์จะไม่มีข้อยกเว้นสำหรับสิ่งที่ได้กล่าวไปแล้ว ในขณะเดียวกันก็ไม่มีใครยกเลิกกระบวนการค้นหาโดเมนของนิยามของฟังก์ชัน และคุณต้องเข้าใกล้การกระทำทางคณิตศาสตร์นี้อย่างจริงจัง หากชุด Laurent มีส่วนหลักพารามิเตอร์ "a" จะเรียกว่าจุดเอกพจน์ที่แยกได้และชุด Laurent จะขยายในวงแหวน - นี่คือจุดตัดของพื้นที่บรรจบกันของส่วนต่าง ๆ ซึ่งสอดคล้องกัน ทฤษฎีบทจะตามมา แต่ไม่ใช่ทุกอย่างจะยากอย่างที่คิดสำหรับนักเรียนที่ไม่มีประสบการณ์ เมื่อศึกษาเฉพาะอนุกรมของ Taylor แล้ว เราสามารถเข้าใจอนุกรมของ Laurent ได้อย่างง่ายดาย ซึ่งเป็นกรณีทั่วไปสำหรับการขยายช่องว่างของตัวเลข การขยายฟังก์ชันเป็นอนุกรมสามารถทำได้ที่จุดในโดเมนของฟังก์ชันเท่านั้น เราควรคำนึงถึงคุณสมบัติของฟังก์ชันดังกล่าว ตัวอย่างเช่น ช่วงเวลาหรือความแตกต่างที่ไม่สิ้นสุด นอกจากนี้ เรายังแนะนำให้คุณใช้ตารางส่วนขยายสำเร็จรูปในอนุกรมของฟังก์ชันเบื้องต้นของอนุกรม Taylor เนื่องจากฟังก์ชันหนึ่งสามารถแสดงด้วยอนุกรมกำลังที่แตกต่างกันได้มากถึงหลายสิบชุด ซึ่งสามารถดูได้จากการใช้เครื่องคิดเลขออนไลน์ของเรา ซีรี่ส์ออนไลน์ของ Maclaurin นั้นง่ายกว่าที่เคยเพื่อตรวจสอบว่าคุณใช้บริการเว็บไซต์ที่ไม่ซ้ำใครหรือไม่ คุณเพียงแค่ป้อนฟังก์ชันที่เขียนถูกต้อง แล้วคุณจะได้รับคำตอบที่นำเสนอในเวลาไม่กี่วินาที รับประกันความถูกต้องและอยู่ในรูปแบบมาตรฐานที่เป็นลายลักษณ์อักษร . คุณสามารถเขียนผลลัพธ์ใหม่ได้ทันทีในสำเนาที่สะอาดเพื่อส่งให้กับครู จะเป็นการถูกต้องที่จะพิจารณาการวิเคราะห์ของฟังก์ชันภายใต้การพิจารณาในวงแหวนก่อน แล้วจึงระบุอย่างชัดเจนว่าสามารถขยายได้ในอนุกรม Laurent ในวงแหวนดังกล่าวทั้งหมด ประเด็นสำคัญคืออย่าละสายตาจากสมาชิกของซีรีส์ Laurent ที่มีดีกรีเป็นลบ ให้ความสำคัญกับเรื่องนี้มากที่สุด ใช้ทฤษฎีบทของ Laurent ในการขยายฟังก์ชันเป็นอนุกรมในเลขยกกำลัง