การวาดเส้นแบ่งครึ่งตั้งฉาก เส้นแบ่งครึ่งตั้งฉาก
ในบทเรียนที่แล้ว เราดูคุณสมบัติของเส้นแบ่งครึ่งของมุม ทั้งที่อยู่ในรูปสามเหลี่ยมและอิสระ รูปสามเหลี่ยมประกอบด้วยมุมสามมุมและแต่ละมุมจะคงคุณสมบัติที่พิจารณาของเส้นแบ่งครึ่งไว้
ทฤษฎีบท:
เส้นแบ่งครึ่ง AA 1, BB 1, СС 1 ของสามเหลี่ยมตัดกันที่จุดหนึ่ง O (รูปที่ 1)

ข้าว. 1. ภาพประกอบสำหรับทฤษฎีบท
การพิสูจน์:
ก่อนอื่นให้เราพิจารณาเส้นแบ่งครึ่ง BB 1 และ CC 1 สองตัวก่อน พวกมันตัดกัน มีจุดตัด O อยู่ เพื่อพิสูจน์สิ่งนี้ ให้เราสมมติสิ่งที่ตรงกันข้าม: อย่าให้เส้นแบ่งครึ่งที่กำหนดมาตัดกัน ซึ่งในกรณีนี้พวกมันจะขนานกัน เส้นตรง BC คือเส้นตัดขวาง และผลรวมของมุมเท่ากับ ![]() ซึ่งขัดแย้งกับความจริงที่ว่าผลรวมของมุมในสามเหลี่ยมทั้งหมดคือ
ซึ่งขัดแย้งกับความจริงที่ว่าผลรวมของมุมในสามเหลี่ยมทั้งหมดคือ
ดังนั้น จุด O ของจุดตัดของเส้นแบ่งครึ่งสองตัวจึงมีอยู่ พิจารณาคุณสมบัติของมัน:
จุด O อยู่บนเส้นแบ่งครึ่งของมุม ซึ่งหมายความว่ามีระยะห่างจากด้าน BA และ BC เท่ากัน ถ้า OK ตั้งฉากกับ BC, OL ตั้งฉากกับ BA ดังนั้นความยาวของตั้งฉากเหล่านี้จะเท่ากัน - นอกจากนี้ จุด O ตั้งอยู่บนเส้นแบ่งครึ่งของมุม และมีระยะห่างเท่ากันจากด้าน CB และ CA โดยที่ OM และ OK ตั้งฉากเท่ากัน
เราได้รับความเท่าเทียมกันดังต่อไปนี้:
![]() กล่าวคือ เส้นตั้งฉากทั้งสามเส้นที่ตกลงจากจุด O ไปยังด้านข้างของรูปสามเหลี่ยมจะเท่ากัน
กล่าวคือ เส้นตั้งฉากทั้งสามเส้นที่ตกลงจากจุด O ไปยังด้านข้างของรูปสามเหลี่ยมจะเท่ากัน
เราสนใจในความเท่าเทียมกันของเส้นตั้งฉาก OL และ OM ความเท่าเทียมกันนี้บอกว่าจุด O มีระยะห่างจากด้านข้างของมุมเท่ากัน และตามมาด้วยว่าจุด O อยู่บนเส้นแบ่งครึ่ง AA 1
ดังนั้นเราจึงพิสูจน์ได้ว่าเส้นแบ่งครึ่งทั้งสามของสามเหลี่ยมตัดกันที่จุดหนึ่ง
นอกจากนี้ รูปสามเหลี่ยมยังประกอบด้วยสามส่วน ซึ่งหมายความว่าเราควรพิจารณาคุณสมบัติของแต่ละส่วนด้วย
กำหนดให้เซ็กเมนต์ AB ส่วนใดๆ มีจุดกึ่งกลาง และสามารถลากเส้นตั้งฉากผ่านมันได้ - แสดงว่ามันเป็น p ดังนั้น p คือเส้นแบ่งครึ่งตั้งฉาก

ข้าว. 2. ภาพประกอบสำหรับทฤษฎีบท
จุดใดๆ ที่วางอยู่บนเส้นแบ่งครึ่งตั้งฉากจะมีระยะห่างจากปลายของส่วนนั้นเท่ากัน
พิสูจน์สิ่งนั้น (รูปที่ 2)
การพิสูจน์:
พิจารณารูปสามเหลี่ยมและ พวกมันเป็นรูปสี่เหลี่ยมผืนผ้าและเท่ากัน เพราะมีขา OM เหมือนกัน และขา AO และ OB เท่ากันตามเงื่อนไข ดังนั้นเราจึงมีสามเหลี่ยมมุมฉากสองอัน ซึ่งเท่ากันในสองขา ตามมาว่าด้านตรงข้ามมุมฉากของสามเหลี่ยมก็เท่ากันเช่นกัน นั่นคือสิ่งที่ต้องพิสูจน์
ทฤษฎีบทสนทนาเป็นจริง
แต่ละจุดที่ห่างจากปลายส่วนนั้นเท่ากันจะอยู่บนเส้นแบ่งครึ่งตั้งฉากกับส่วนนี้
เมื่อพิจารณาจากส่วน AB, เส้นแบ่งครึ่งตั้งฉาก p และจุด M ซึ่งอยู่ห่างจากปลายของส่วนนั้นเท่ากัน พิสูจน์ว่าจุด M อยู่บนเส้นแบ่งครึ่งตั้งฉากกับส่วนนั้น (รูปที่ 3)

ข้าว. 3. ภาพประกอบสำหรับทฤษฎีบท
การพิสูจน์:
พิจารณารูปสามเหลี่ยม เป็นหน้าจั่วตามเงื่อนไข พิจารณาค่ามัธยฐานของรูปสามเหลี่ยม โดยจุด O คือจุดกึ่งกลางของฐาน AB, OM คือค่ามัธยฐาน ตามคุณสมบัติของสามเหลี่ยมหน้าจั่ว ค่ามัธยฐานที่ลากไปที่ฐานนั้นเป็นทั้งระดับความสูงและเส้นแบ่งครึ่ง เป็นไปตามนั้น. แต่เส้นตรง p ก็ตั้งฉากกับ AB เช่นกัน เรารู้ว่าที่จุด O คุณสามารถวาดเส้นตั้งฉากกับส่วน AB ได้ ซึ่งหมายความว่าเส้น OM และ p ตรงกัน หลังจากนั้นจุด M อยู่ในเส้นตรง p ซึ่งเป็นสิ่งที่เราจำเป็นต้องพิสูจน์
ทฤษฎีบททางตรงและทางกลับสามารถสรุปได้
จุดจะอยู่บนเส้นแบ่งครึ่งตั้งฉากของเซ็กเมนต์ก็ต่อเมื่อจุดนั้นอยู่ห่างจากปลายของเซกเมนต์นี้เท่ากัน
ให้เราทำซ้ำว่ามีสามส่วนในรูปสามเหลี่ยมและคุณสมบัติของเส้นแบ่งครึ่งตั้งฉากใช้กับแต่ละส่วน
ทฤษฎีบท:
เส้นแบ่งครึ่งตั้งฉากของสามเหลี่ยมตัดกันที่จุดหนึ่ง
สามเหลี่ยมจะได้รับ ตั้งฉากกับด้านข้าง: P 1 ไปยังด้าน BC, P 2 ไปยังด้าน AC, P 3 ไปยังด้าน AB
พิสูจน์ว่าเส้นตั้งฉาก P 1, P 2 และ P 3 ตัดกันที่จุด O (รูปที่ 4)

ข้าว. 4. ภาพประกอบสำหรับทฤษฎีบท
การพิสูจน์:
ลองพิจารณาเส้นแบ่งครึ่งตั้งฉากสองตัว P 2 และ P 3 ซึ่งพวกมันตัดกันและมีจุดตัด O อยู่ ลองพิสูจน์ข้อเท็จจริงนี้โดยขัดแย้งกัน - ให้ตั้งฉาก P 2 และ P 3 ขนานกัน จากนั้นมุมจะกลับกัน ซึ่งขัดแย้งกับข้อเท็จจริงที่ว่าผลรวมของมุมทั้งสามของรูปสามเหลี่ยมคือ มีจุด O ของจุดตัดของเส้นแบ่งครึ่งตั้งฉากสองในสามเส้น คุณสมบัติของจุด O: อยู่บนเส้นแบ่งครึ่งตั้งฉากกับด้าน AB ซึ่งหมายความว่ามีระยะห่างจากปลายส่วน AB เท่ากัน: นอกจากนี้ยังอยู่บนเส้นแบ่งครึ่งตั้งฉากกับด้าน AC ซึ่งหมายความว่า เราได้รับความเท่าเทียมกันดังต่อไปนี้
อภิธานศัพท์เงื่อนไข planimetry- รวบรวมคำจำกัดความของคำศัพท์จาก planimetry ไว้ที่นี่ การอ้างอิงคำศัพท์ในอภิธานศัพท์นี้ (ในหน้านี้) เป็นแบบตัวเอียง # A B C D E E E F G H I K L M N O P R S ... วิกิพีเดีย
จุดคอลลิเนียร์
การแข่งขันโดยตรง- รวบรวมคำจำกัดความของคำศัพท์จาก planimetry ไว้ที่นี่ การอ้างอิงคำศัพท์ในอภิธานศัพท์นี้ (ในหน้านี้) เป็นแบบตัวเอียง # A B C D E E F G H I J K L M N O P R S T U V ... วิกิพีเดีย
วงเวียนอพอลโลเนีย- รวบรวมคำจำกัดความของคำศัพท์จาก planimetry ไว้ที่นี่ การอ้างอิงคำศัพท์ในอภิธานศัพท์นี้ (ในหน้านี้) เป็นแบบตัวเอียง # A B C D E E F G H I J K L M N O P R S T U V ... วิกิพีเดีย
การเปลี่ยนแปลงเครื่องบิน- รวบรวมคำจำกัดความของคำศัพท์จาก planimetry ไว้ที่นี่ การอ้างอิงคำศัพท์ในอภิธานศัพท์นี้ (ในหน้านี้) เป็นแบบตัวเอียง # A B C D E E F G H I J K L M N O P R S T U V ... วิกิพีเดีย
เซเวียนา- รวบรวมคำจำกัดความของคำศัพท์จาก planimetry ไว้ที่นี่ การอ้างอิงคำศัพท์ในอภิธานศัพท์นี้ (ในหน้านี้) เป็นแบบตัวเอียง # A B C D E E F G H I J K L M N O P R S T U V ... วิกิพีเดีย
อภิธานศัพท์ของ planimetry- หน้านี้เป็นอภิธานศัพท์ ดูเพิ่มเติมที่บทความหลัก: Planimetry คำจำกัดความของคำศัพท์จาก planimetry ถูกรวบรวมไว้ที่นี่ ลิงก์ไปยังคำศัพท์ในพจนานุกรมนี้ (ในหน้านี้) เป็นตัวเอียง... Wikipedia
ปัญหาของอพอลโลเนียส- งานของ Apollonius คือการสร้างวงกลมแทนเจนต์ให้กับวงกลมสามวงที่กำหนดโดยใช้เข็มทิศและไม้บรรทัด ตามตำนาน ปัญหาดังกล่าวถูกกำหนดโดย Apollonius แห่ง Perga ประมาณ 220 ปีก่อนคริสตกาล จ. ในหนังสือ “สัมผัส” ที่หายไป…วิกิพีเดีย
ปัญหาของอพอลโลเนียส- ปัญหาของ Apollonius คือการสร้างวงกลมแทนเจนต์ให้กับวงกลมที่กำหนดสามวงโดยใช้เข็มทิศและไม้บรรทัด ตามตำนาน ปัญหาดังกล่าวถูกกำหนดโดย Apollonius แห่ง Perga ประมาณ 220 ปีก่อนคริสตกาล จ. ในหนังสือ “สัมผัส” ที่สูญหายไปแต่ถูก... ... วิกิพีเดีย
แผนภาพโวโรน้อย- ชุดจุดสุ่มบนระนาบ แผนภาพโวโรนอยของชุดจุด S ที่มีขอบเขตจำกัดบนเครื่องบินแสดงถึงฉากกั้นของเครื่องบินในลักษณะที่ ... วิกิพีเดีย
คุณสมบัติ
โดยที่ตัวห้อยหมายถึงด้านที่วาดเส้นตั้งฉาก คือพื้นที่ของสามเหลี่ยมและสันนิษฐานว่าด้านต่างๆ สัมพันธ์กันด้วยอสมการ และ กล่าวอีกนัยหนึ่ง เส้นแบ่งครึ่งตั้งฉากที่เล็กที่สุดของรูปสามเหลี่ยมจะอยู่ในส่วนตรงกลางเขียนบทวิจารณ์เกี่ยวกับบทความ "เส้นแบ่งครึ่งตั้งฉาก"
หมายเหตุ
ข้อความที่ตัดตอนมาซึ่งแสดงลักษณะของเส้นแบ่งครึ่งตั้งฉาก
Kutuzov หยุดเคี้ยวแล้วจ้องมอง Wolzogen ด้วยความประหลาดใจราวกับไม่เข้าใจสิ่งที่กำลังพูดกับเขา Wolzogen สังเกตเห็นความตื่นเต้นของ des alten Herrn [สุภาพบุรุษชรา (ชาวเยอรมัน)] กล่าวด้วยรอยยิ้ม:- ฉันไม่คิดว่าตัวเองมีสิทธิ์ที่จะซ่อนสิ่งที่ฉันเห็นจากการเป็นเจ้านายของคุณ... กองทหารอยู่ในความยุ่งเหยิงโดยสิ้นเชิง...
-คุณเคยเห็นมันไหม? เห็นมั้ย?.. – คูทูซอฟตะโกน ขมวดคิ้ว ลุกขึ้นอย่างรวดเร็วและบุกโจมตีโวลโซเกน “คุณเป็นยังไงบ้าง... คุณกล้าดียังไง!” เขาตะโกน ทำท่าทางคุกคามด้วยการจับมือและสำลัก - คุณกล้าดียังไงมาพูดแบบนี้กับฉัน? คุณไม่รู้อะไรเลย บอกนายพลบาร์เคลย์จากฉันว่าข้อมูลของเขาไม่ถูกต้อง และผู้บัญชาการทหารสูงสุดของฉันรู้แนวทางการต่อสู้ที่แท้จริงดีกว่าเขา
Wolzogen ต้องการคัดค้าน แต่ Kutuzov ขัดจังหวะเขา
- ศัตรูถูกขับไล่ทางด้านซ้ายและพ่ายแพ้ทางด้านขวา ถ้าท่านไม่เห็นดีนัก ท่านก็อย่าปล่อยให้ตัวเองพูดในสิ่งที่ท่านไม่รู้ กรุณาไปหานายพลบาร์เคลย์และบอกเขาในวันรุ่งขึ้นว่าฉันมีความตั้งใจที่จะโจมตีศัตรู” คูทูซอฟพูดอย่างเคร่งขรึม ทุกคนเงียบ และสิ่งที่สามารถได้ยินได้ก็มีเพียงเสียงหายใจเฮือกของนายพลเฒ่าเท่านั้น “พวกเขาถูกขับไล่ไปทุกที่ ซึ่งฉันขอขอบคุณพระเจ้าและกองทัพที่กล้าหาญของเรา” ศัตรูพ่ายแพ้แล้วและพรุ่งนี้เราจะขับไล่เขาออกจากดินแดนศักดิ์สิทธิ์ของรัสเซีย” คูทูซอฟกล่าวพร้อมกับข้ามตัวเอง และจู่ๆ ก็สะอื้นจากน้ำตาที่ไหลออกมา Wolzogen ยักไหล่และเม้มริมฝีปาก เดินออกไปด้านข้างอย่างเงียบๆ โดยสงสัยว่า uber diese Eingenommenheit des alten Herrn [ในความกดขี่ของสุภาพบุรุษเฒ่าคนนี้ (เยอรมัน)]
“ ใช่แล้ว เขาอยู่นี่แล้ว ฮีโร่ของฉัน” คูทูซอฟพูดกับนายพลผมดำรูปร่างอ้วนท้วนซึ่งกำลังเข้ามาในเนินดินในขณะนั้น Raevsky ซึ่งใช้เวลาทั้งวันที่จุดหลักของสนาม Borodino
Raevsky รายงานว่ากองทหารอยู่ในที่ของตนอย่างมั่นคงและฝรั่งเศสไม่กล้าโจมตีอีกต่อไป หลังจากฟังเขาแล้ว Kutuzov พูดเป็นภาษาฝรั่งเศส:
– Vous ne pensez donc pas comme lesautres que nous sommes obliges de nous retirer? [แล้วคุณไม่คิดว่าเราควรถอยเหมือนคนอื่นๆ เหรอ?]
ในบทเรียนที่แล้ว เราดูคุณสมบัติของเส้นแบ่งครึ่งของมุม ทั้งที่อยู่ในรูปสามเหลี่ยมและอิสระ รูปสามเหลี่ยมประกอบด้วยมุมสามมุมและแต่ละมุมจะคงคุณสมบัติที่พิจารณาของเส้นแบ่งครึ่งไว้
ทฤษฎีบท:
เส้นแบ่งครึ่ง AA 1, BB 1, СС 1 ของสามเหลี่ยมตัดกันที่จุดหนึ่ง O (รูปที่ 1)

ข้าว. 1. ภาพประกอบสำหรับทฤษฎีบท
การพิสูจน์:
ก่อนอื่นให้เราพิจารณาเส้นแบ่งครึ่ง BB 1 และ CC 1 สองตัวก่อน พวกมันตัดกัน มีจุดตัด O อยู่ เพื่อพิสูจน์สิ่งนี้ ให้เราสมมติสิ่งที่ตรงกันข้าม: อย่าให้เส้นแบ่งครึ่งที่กำหนดมาตัดกัน ซึ่งในกรณีนี้พวกมันจะขนานกัน เส้นตรง BC คือเส้นตัดขวาง และผลรวมของมุมเท่ากับ ![]() ซึ่งขัดแย้งกับความจริงที่ว่าผลรวมของมุมในสามเหลี่ยมทั้งหมดคือ
ซึ่งขัดแย้งกับความจริงที่ว่าผลรวมของมุมในสามเหลี่ยมทั้งหมดคือ
ดังนั้น จุด O ของจุดตัดของเส้นแบ่งครึ่งสองตัวจึงมีอยู่ พิจารณาคุณสมบัติของมัน:
จุด O อยู่บนเส้นแบ่งครึ่งของมุม ซึ่งหมายความว่ามีระยะห่างจากด้าน BA และ BC เท่ากัน ถ้า OK ตั้งฉากกับ BC, OL ตั้งฉากกับ BA ดังนั้นความยาวของตั้งฉากเหล่านี้จะเท่ากัน - นอกจากนี้ จุด O ตั้งอยู่บนเส้นแบ่งครึ่งของมุม และมีระยะห่างเท่ากันจากด้าน CB และ CA โดยที่ OM และ OK ตั้งฉากเท่ากัน
เราได้รับความเท่าเทียมกันดังต่อไปนี้:
![]() กล่าวคือ เส้นตั้งฉากทั้งสามเส้นที่ตกลงจากจุด O ไปยังด้านข้างของรูปสามเหลี่ยมจะเท่ากัน
กล่าวคือ เส้นตั้งฉากทั้งสามเส้นที่ตกลงจากจุด O ไปยังด้านข้างของรูปสามเหลี่ยมจะเท่ากัน
เราสนใจในความเท่าเทียมกันของเส้นตั้งฉาก OL และ OM ความเท่าเทียมกันนี้บอกว่าจุด O มีระยะห่างจากด้านข้างของมุมเท่ากัน และตามมาด้วยว่าจุด O อยู่บนเส้นแบ่งครึ่ง AA 1
ดังนั้นเราจึงพิสูจน์ได้ว่าเส้นแบ่งครึ่งทั้งสามของสามเหลี่ยมตัดกันที่จุดหนึ่ง
นอกจากนี้ รูปสามเหลี่ยมยังประกอบด้วยสามส่วน ซึ่งหมายความว่าเราควรพิจารณาคุณสมบัติของแต่ละส่วนด้วย
กำหนดให้เซ็กเมนต์ AB ส่วนใดๆ มีจุดกึ่งกลาง และสามารถลากเส้นตั้งฉากผ่านมันได้ - แสดงว่ามันเป็น p ดังนั้น p คือเส้นแบ่งครึ่งตั้งฉาก

ข้าว. 2. ภาพประกอบสำหรับทฤษฎีบท
จุดใดๆ ที่วางอยู่บนเส้นแบ่งครึ่งตั้งฉากจะมีระยะห่างจากปลายของส่วนนั้นเท่ากัน
พิสูจน์สิ่งนั้น (รูปที่ 2)
การพิสูจน์:
พิจารณารูปสามเหลี่ยมและ พวกมันเป็นรูปสี่เหลี่ยมผืนผ้าและเท่ากัน เพราะมีขา OM เหมือนกัน และขา AO และ OB เท่ากันตามเงื่อนไข ดังนั้นเราจึงมีสามเหลี่ยมมุมฉากสองอัน ซึ่งเท่ากันในสองขา ตามมาว่าด้านตรงข้ามมุมฉากของสามเหลี่ยมก็เท่ากันเช่นกัน นั่นคือสิ่งที่ต้องพิสูจน์
ทฤษฎีบทสนทนาเป็นจริง
แต่ละจุดที่ห่างจากปลายส่วนนั้นเท่ากันจะอยู่บนเส้นแบ่งครึ่งตั้งฉากกับส่วนนี้
เมื่อพิจารณาจากส่วน AB, เส้นแบ่งครึ่งตั้งฉาก p และจุด M ซึ่งอยู่ห่างจากปลายของส่วนนั้นเท่ากัน พิสูจน์ว่าจุด M อยู่บนเส้นแบ่งครึ่งตั้งฉากกับส่วนนั้น (รูปที่ 3)

ข้าว. 3. ภาพประกอบสำหรับทฤษฎีบท
การพิสูจน์:
พิจารณารูปสามเหลี่ยม เป็นหน้าจั่วตามเงื่อนไข พิจารณาค่ามัธยฐานของรูปสามเหลี่ยม โดยจุด O คือจุดกึ่งกลางของฐาน AB, OM คือค่ามัธยฐาน ตามคุณสมบัติของสามเหลี่ยมหน้าจั่ว ค่ามัธยฐานที่ลากไปที่ฐานนั้นเป็นทั้งระดับความสูงและเส้นแบ่งครึ่ง เป็นไปตามนั้น. แต่เส้นตรง p ก็ตั้งฉากกับ AB เช่นกัน เรารู้ว่าที่จุด O คุณสามารถวาดเส้นตั้งฉากกับส่วน AB ได้ ซึ่งหมายความว่าเส้น OM และ p ตรงกัน หลังจากนั้นจุด M อยู่ในเส้นตรง p ซึ่งเป็นสิ่งที่เราจำเป็นต้องพิสูจน์
ทฤษฎีบททางตรงและทางกลับสามารถสรุปได้
จุดจะอยู่บนเส้นแบ่งครึ่งตั้งฉากของเซ็กเมนต์ก็ต่อเมื่อจุดนั้นอยู่ห่างจากปลายของเซกเมนต์นี้เท่ากัน
ให้เราทำซ้ำว่ามีสามส่วนในรูปสามเหลี่ยมและคุณสมบัติของเส้นแบ่งครึ่งตั้งฉากใช้กับแต่ละส่วน
ทฤษฎีบท:
เส้นแบ่งครึ่งตั้งฉากของสามเหลี่ยมตัดกันที่จุดหนึ่ง
สามเหลี่ยมจะได้รับ ตั้งฉากกับด้านข้าง: P 1 ไปยังด้าน BC, P 2 ไปยังด้าน AC, P 3 ไปยังด้าน AB
พิสูจน์ว่าเส้นตั้งฉาก P 1, P 2 และ P 3 ตัดกันที่จุด O (รูปที่ 4)

ข้าว. 4. ภาพประกอบสำหรับทฤษฎีบท
การพิสูจน์:
ลองพิจารณาเส้นแบ่งครึ่งตั้งฉากสองตัว P 2 และ P 3 ซึ่งพวกมันตัดกันและมีจุดตัด O อยู่ ลองพิสูจน์ข้อเท็จจริงนี้โดยขัดแย้งกัน - ให้ตั้งฉาก P 2 และ P 3 ขนานกัน จากนั้นมุมจะกลับกัน ซึ่งขัดแย้งกับข้อเท็จจริงที่ว่าผลรวมของมุมทั้งสามของรูปสามเหลี่ยมคือ มีจุด O ของจุดตัดของเส้นแบ่งครึ่งตั้งฉากสองในสามเส้น คุณสมบัติของจุด O: อยู่บนเส้นแบ่งครึ่งตั้งฉากกับด้าน AB ซึ่งหมายความว่ามีระยะห่างจากปลายส่วน AB เท่ากัน: นอกจากนี้ยังอยู่บนเส้นแบ่งครึ่งตั้งฉากกับด้าน AC ซึ่งหมายความว่า เราได้รับความเท่าเทียมกันดังต่อไปนี้
 สมการลอการิทึม
สมการลอการิทึม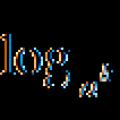 เทคนิคการแก้สมการลอการิทึม
เทคนิคการแก้สมการลอการิทึม การวิเคราะห์ตนเองของครูนักบำบัดการพูด
การวิเคราะห์ตนเองของครูนักบำบัดการพูด