Y 5x 1 แผนภูมิ การแปลงกราฟด้วยโมดูล

บ่อยครั้งสามารถระบุได้ คุณสมบัติที่สำคัญการเคลื่อนที่ของระบบเครื่องกลโดยไม่ต้องใช้การบูรณาการของระบบสมการเชิงอนุพันธ์ของการเคลื่อนที่ สิ่งนี้สามารถทำได้โดยการประยุกต์ใช้ทฤษฎีบททั่วไปของพลศาสตร์

5.1. แนวคิดพื้นฐานและคำจำกัดความ

แรงภายนอกและภายในแรงใดๆ ที่กระทำต่อจุดหนึ่งในระบบกลไกนั้นจำเป็นต้องเป็นแรงแอคทีฟหรือปฏิกิริยาคัปปลิ้ง แรงทั้งชุดที่กระทำต่อจุดของระบบสามารถแบ่งออกเป็นสองประเภทที่แตกต่างกัน: แรงภายนอกและแรงภายใน (ดัชนี e และ i - จาก คำภาษาละตินภายนอก - ภายนอกและภายใน - ภายใน) แรงภายนอกคือแรงที่กระทำต่อจุดของระบบจากจุดและวัตถุที่ไม่เป็นส่วนหนึ่งของระบบที่อยู่ระหว่างการพิจารณา พลังแห่งปฏิสัมพันธ์ระหว่างจุดและส่วนต่างๆ ของระบบที่กำลังพิจารณาเรียกว่าภายใน

แผนกนี้ขึ้นอยู่กับจุดวัสดุและเนื้อหาที่ผู้วิจัยรวมไว้ในระบบเครื่องกลที่อยู่ระหว่างการพิจารณา หากคุณขยายองค์ประกอบของระบบโดยรวมจุดและวัตถุเพิ่มเติม แรงบางอย่างที่อยู่ภายนอกสำหรับระบบก่อนหน้านี้สามารถกลายเป็นภายในสำหรับระบบที่ขยายได้

คุณสมบัติ กองกำลังภายใน. เนื่องจากแรงเหล่านี้เป็นแรงปฏิสัมพันธ์ระหว่างส่วนต่าง ๆ ของระบบ พวกมันจึงเข้าสู่ระบบแรงภายในที่สมบูรณ์ในรูปแบบ "สอง" ซึ่งจัดระเบียบตามสัจพจน์การกระทำ-ปฏิกิริยา แต่ละ “สอง” ดังกล่าวมีจุดแข็ง

เวกเตอร์หลักและช่วงเวลาหลักเกี่ยวกับจุดศูนย์กลางโดยพลการมีค่าเท่ากับศูนย์ เนื่องจากระบบกำลังภายในที่สมบูรณ์ประกอบด้วย "สอง" เท่านั้น

1) เวกเตอร์หลักของระบบแรงภายในคือศูนย์

2) ช่วงเวลาหลักของระบบกองกำลังภายในที่สัมพันธ์กับ จุดใดก็ได้เท่ากับศูนย์

มวลของระบบเรียกว่า ผลรวมทางคณิตศาสตร์มวลของจุดและวัตถุทั้งหมดที่สร้างระบบ:

ศูนย์กลางของมวล(จุดศูนย์กลางความเฉื่อย) ของระบบกลไกเรียกว่า จุดเรขาคณิต C เวกเตอร์รัศมีและพิกัดที่กำหนดโดยสูตร

เวกเตอร์รัศมีและพิกัดของจุดที่สร้างระบบอยู่ที่ไหน

สำหรับ แข็งซึ่งตั้งอยู่ในสนามแรงโน้มถ่วงที่สม่ำเสมอ ตำแหน่งของจุดศูนย์กลางมวลและจุดศูนย์ถ่วงตรงกัน ในกรณีอื่นๆ จุดเหล่านี้เป็นจุดทางเรขาคณิตที่แตกต่างกัน

กันด้วย ระบบเฉื่อยการอ้างอิงมักจะพิจารณาพร้อมกันถึงระบบอ้างอิงที่ไม่เฉื่อยซึ่งเคลื่อนที่ในการแปล แกนพิกัดของมัน (แกนเคอนิก) ถูกเลือกเพื่อให้จุดกำเนิด C เกิดขึ้นพร้อมกับจุดศูนย์กลางมวลของระบบกลไกอย่างต่อเนื่อง ตามคำนิยาม จุดศูนย์กลางมวลอยู่กับที่ในแกนโคนิกและอยู่ที่จุดกำเนิดของพิกัด

โมเมนต์ความเฉื่อยของระบบสัมพันธ์กับแกนเรียกว่า ปริมาณสเกลาร์ เท่ากับผลรวมผลคูณของมวล mk ของทุกจุดของระบบด้วยกำลังสองของระยะทางถึงแกน:

หากระบบกลไกเป็นแบบแข็ง หากต้องการหา 12 คุณสามารถใช้สูตรได้

ความหนาแน่นปริมาตรที่ร่างกายครอบครองอยู่ที่ไหน

การบรรยายครั้งที่ 3 ทฤษฎีบททั่วไปลำโพง

พลศาสตร์ของระบบจุดวัสดุเป็นส่วนสำคัญ กลศาสตร์เชิงทฤษฎี- ในที่นี้เราจะพิจารณาปัญหาเกี่ยวกับการเคลื่อนที่ของระบบกลไกเป็นหลัก (ระบบจุดวัสดุ) ด้วยจำนวนองศาอิสระที่จำกัด ซึ่งเป็นจำนวนพารามิเตอร์อิสระสูงสุดที่กำหนดตำแหน่งของระบบ ภารกิจหลักพลศาสตร์ของระบบ - การศึกษากฎการเคลื่อนที่ของวัตถุแข็งเกร็งและระบบกลไก

วิธีที่ง่ายที่สุดในการศึกษาการเคลื่อนที่ของระบบประกอบด้วย เอ็นประเด็นสำคัญ พิจารณาถึงความเคลื่อนไหวของแต่ละจุดของระบบ ในกรณีนี้ แรงทั้งหมดที่กระทำต่อแต่ละจุดของระบบ รวมถึงแรงปฏิสัมพันธ์ระหว่างจุดต่างๆ จะต้องได้รับการพิจารณาด้วย

เมื่อพิจารณาความเร่งของแต่ละจุดตามกฎข้อที่สองของนิวตัน (1.2) เราจะได้กฎการเคลื่อนที่เชิงอนุพันธ์สเกลาร์สามข้อของลำดับที่สองสำหรับแต่ละจุด นั่นคือ 3 เอ็น กฎการเคลื่อนที่แบบดิฟเฟอเรนเชียลของทั้งระบบ

เพื่อค้นหาสมการการเคลื่อนที่ของระบบเครื่องกลโดยพิจารณาจากแรงที่กำหนดและ เงื่อนไขเริ่มต้นสำหรับแต่ละจุดของระบบที่ได้รับ กฎหมายที่แตกต่างจำเป็นต้องบูรณาการ ปัญหานี้เป็นเรื่องยากแม้ในกรณีที่มีจุดวัตถุสองจุดซึ่งเคลื่อนที่ภายใต้อิทธิพลของแรงปฏิสัมพันธ์ตามกฎแรงดึงดูดสากล (ปัญหาสองจุด) และยากมากในกรณีที่มีจุดโต้ตอบสามจุด (ปัญหาสามจุด) ).

ดังนั้นจึงจำเป็นต้องค้นหาวิธีการแก้ปัญหาที่จะนำไปสู่สมการที่แก้ได้และให้แนวคิดเกี่ยวกับการเคลื่อนที่ของระบบเครื่องกล ทฤษฎีบททั่วไปของพลศาสตร์ซึ่งเป็นผลมาจากกฎการเคลื่อนที่แบบดิฟเฟอเรนเชียลช่วยให้เราหลีกเลี่ยงความซับซ้อนที่เกิดขึ้นระหว่างการรวมกลุ่มและรับผลลัพธ์ที่จำเป็น

3. 1. หมายเหตุทั่วไป

เราจะนับคะแนนของระบบกลไกด้วยดัชนี ฉัน, เจ, เคฯลฯ ซึ่งวิ่งผ่านค่าทั้งหมด 1, 2, 3… เอ็น, ที่ไหน เอ็น – จำนวนคะแนนของระบบ ปริมาณทางกายภาพเกี่ยวข้องกับ เคจุดที่ถูกกำหนดโดยดัชนีเดียวกันกับจุด ตัวอย่างเช่น แสดงเวกเตอร์รัศมีและความเร็ว ตามลำดับ เคจุดที่

แต่ละจุดของระบบถูกกระทำโดยแรงจากสองจุดกำเนิด: ประการแรก แรงที่มีแหล่งกำเนิดอยู่นอกระบบ เรียกว่า ภายนอกกองกำลังและกำหนด; ประการที่สอง กองกำลังจากจุดอื่นของระบบที่กำหนด เรียกว่า ภายในกองกำลังและกำหนด. แรงภายในเป็นไปตามกฎข้อที่สามของนิวตัน ให้เราพิจารณาคุณสมบัติที่ง่ายที่สุดของแรงภายในที่กระทำต่อระบบกลไกทั้งหมดในทุกสถานะ

คุณสมบัติแรก ผลรวมทางเรขาคณิตของแรงภายในทั้งหมดของระบบ (เวกเตอร์หลักของแรงภายใน) เท่ากับศูนย์.

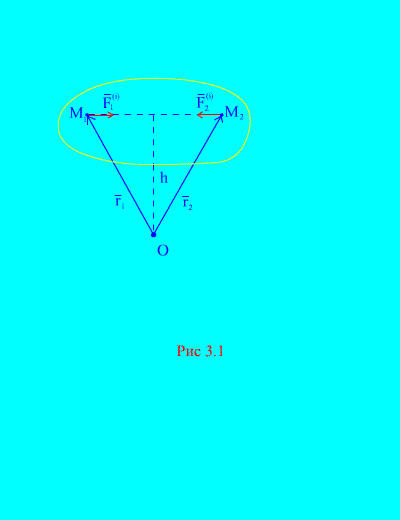
แน่นอนถ้าเราพิจารณาจุดสองจุดใด ๆ ของระบบตามอำเภอใจเช่น และ (รูปที่ 3.1)แล้วสำหรับพวกเขา , เพราะ แรงกระทำและแรงปฏิกิริยาจะมีขนาดเท่ากันเสมอ โดยกระทำไปตามแนวการกระทำหนึ่งเส้นในทิศทางตรงกันข้าม ซึ่งเชื่อมต่อจุดโต้ตอบกัน เวกเตอร์หลักของแรงภายในประกอบด้วยแรงคู่ของจุดที่มีปฏิสัมพันธ์กัน

(3.1)

คุณสมบัติที่สอง ผลรวมทางเรขาคณิตของโมเมนต์ของแรงภายในทั้งหมดที่สัมพันธ์กับจุดใดๆ ในอวกาศจะเท่ากับศูนย์.

ให้เราพิจารณาระบบโมเมนต์ของแรงและสัมพันธ์กับจุดนั้น เกี่ยวกับ(รูปที่ 3.1)- จาก (รูปที่ 3.1)- มันชัดเจนว่า

,

เพราะ แรงทั้งสองมีแขนเท่ากันและมีทิศทางตรงกันข้ามของโมเมนต์เวกเตอร์ ประเด็นหลักแรงภายในสัมพันธ์กับจุดหนึ่ง เกี่ยวกับประกอบด้วยผลรวมเวกเตอร์ของนิพจน์ดังกล่าว และมีค่าเท่ากับศูนย์ เพราะฉะนั้น,

ให้แรงภายนอกและภายในกระทำต่อระบบทางกลประกอบด้วย เอ็นคะแนน (รูปที่ 3.2)- หากมีการใช้ผลลัพธ์กับแต่ละจุดของระบบ กองกำลังภายนอกและผลลัพธ์ของพลังภายในทั้งหมดแล้วสำหรับสิ่งใดสิ่งหนึ่ง เค-คะแนนของระบบสามารถประกอบได้ สมการเชิงอนุพันธ์การเคลื่อนไหว ก็จะมีสมการดังกล่าวทั้งหมด เอ็น:

และในการฉายภาพบนแกนพิกัดคงที่ 3 เอ็น:

(3.4)

สมการเวกเตอร์ (3.3) หรือสมการสเกลาร์ที่เทียบเท่า (3.4) แสดงถึงกฎการเคลื่อนที่ของจุดวัสดุทั้งระบบ หากจุดทั้งหมดเคลื่อนที่ขนานกับระนาบเดียวหรือเส้นตรงเส้นเดียว จำนวนสมการ (3.4) ในกรณีแรกจะเป็น 2 เอ็นในครั้งที่สอง เอ็น.

ตัวอย่างที่ 1มวลสองตัวเชื่อมต่อถึงกันด้วยสายเคเบิลที่ขยายไม่ได้ซึ่งโยนข้ามบล็อก (รูปที่ 3.3)- การละเลยแรงเสียดทานตลอดจนมวลของบล็อกและสายเคเบิลจะกำหนดกฎการเคลื่อนที่ของโหลดและความตึงของสายเคเบิล

สารละลาย- ระบบประกอบด้วยวัสดุสองชิ้น (เชื่อมต่อกันด้วยสายเคเบิลที่ขยายไม่ได้) ซึ่งเคลื่อนที่ขนานไปกับแกนเดียวกัน เอ็กซ์ให้เราเขียนกฎการเคลื่อนที่แบบดิฟเฟอเรนเชียลลงในเส้นโครงบนแกน เอ็กซ์สำหรับทุกคน

ปล่อยให้น้ำหนักที่เหมาะสมลดลงด้วยความเร่ง แล้วน้ำหนักซ้ายจะเพิ่มขึ้นตามความเร่ง เราปลดปล่อยจิตใจจากการเชื่อมต่อ (สายเคเบิล) และแทนที่ด้วยปฏิกิริยาและ (รูปที่ 3.3)- เมื่อพิจารณาว่าวัตถุเป็นอิสระ ให้เราวาดกฎการเคลื่อนที่แบบดิฟเฟอเรนเชียลขึ้นมาบนแกน เอ็กซ์(หมายถึงความตึงของเกลียวเป็นแรงภายใน และน้ำหนักของโหลดอยู่ภายนอก):

เนื่องจากและ (ร่างกายเชื่อมต่อกันด้วยสายเคเบิลที่ขยายไม่ได้) เราจึงได้

การแก้สมการเหล่านี้สำหรับการเร่งความเร็วและความตึงของสายเคเบิล ตเราได้รับ

.

โปรดทราบว่าความตึงของสายเคเบิลไม่เท่ากับแรงโน้มถ่วงของโหลดที่สอดคล้องกัน

3. 2. ทฤษฎีบทการเคลื่อนที่ของจุดศูนย์กลางมวล

เป็นที่ทราบกันว่าร่างกายที่แข็งแกร่งและระบบกลไกในเครื่องบินสามารถเคลื่อนที่ได้ค่อนข้างซับซ้อน ทฤษฎีบทแรกเกี่ยวกับการเคลื่อนที่ของวัตถุและระบบกลไกสามารถหาได้ดังนี้: โยน k.-l วัตถุที่ประกอบด้วยวัตถุแข็งจำนวนมากยึดติดกัน เห็นได้ชัดว่าเขาจะบินในพาราโบลา สิ่งนี้ถูกเปิดเผยเมื่อศึกษาความเคลื่อนไหวของจุดนั้น อย่างไรก็ตาม ตอนนี้วัตถุนั้นไม่ใช่จุด มันจะหมุนและแกว่งไปมาระหว่างที่บินไปรอบๆ จุดศูนย์กลางที่มีประสิทธิภาพซึ่งเคลื่อนที่เป็นรูปพาราโบลา ทฤษฎีบทการเคลื่อนที่ครั้งแรก วิชาที่ซับซ้อนกล่าวว่าจุดศูนย์กลางที่มีประสิทธิภาพจุดหนึ่งคือจุดศูนย์กลางมวลของวัตถุที่กำลังเคลื่อนที่ จุดศูนย์กลางมวลไม่จำเป็นต้องอยู่ที่ตัววัตถุเอง แต่อาจอยู่ที่ไหนสักแห่งด้านนอกก็ได้

ทฤษฎีบท. จุดศูนย์กลางมวลของระบบกลไกเคลื่อนที่เหมือนกับจุดวัสดุที่มีมวล มวลเท่ากันระบบทั้งหมดที่ใช้แรงภายนอกทั้งหมดที่กระทำต่อระบบ

เพื่อพิสูจน์ทฤษฎีบท เราจะเขียนกฎการเคลื่อนที่เชิงอนุพันธ์ (3.3) ใหม่ลงใน แบบฟอร์มต่อไปนี้:

(3.5)

ที่ไหน เอ็น – จำนวนคะแนนของระบบ

มาบวกสมการเข้าด้วยกันทีละเทอม:

(ก)

ตำแหน่งจุดศูนย์กลางมวลของระบบกลไกสัมพันธ์กับระบบพิกัดที่เลือกถูกกำหนดโดยสูตร (2.1): ที่ไหน ม– มวลของระบบ จากนั้นด้านซ้ายของความเท่าเทียมกัน (a) จะถูกเขียน

ผลรวมแรกทางด้านขวาของความเท่าเทียมกัน (a) เท่ากับเวกเตอร์หลักของแรงภายนอก และผลรวมสุดท้ายเมื่อพิจารณาจากคุณสมบัติของแรงภายใน เท่ากับศูนย์ จากนั้นความเท่าเทียมกัน (a) โดยคำนึงถึง (b) จะถูกเขียนใหม่

, (3.6)

เหล่านั้น. ผลคูณของมวลของระบบและความเร่งของจุดศูนย์กลางมวลเท่ากับ ผลรวมทางเรขาคณิตแรงภายนอกทั้งหมดที่กระทำต่อระบบ

จากสมการ (3.6) พบว่าแรงภายในไม่ส่งผลโดยตรงต่อการเคลื่อนที่ของจุดศูนย์กลางมวล อย่างไรก็ตาม ในบางกรณีสิ่งเหล่านี้เป็นสาเหตุของการปรากฏตัวของแรงภายนอกที่ใช้กับระบบ ดังนั้นแรงภายในที่ขับเคลื่อนล้อขับเคลื่อนของรถให้หมุนทำให้เกิดแรงยึดเกาะภายนอกที่นำไปใช้กับขอบล้อเพื่อกระทำกับล้อนั้น

ตัวอย่างที่ 2กลไกที่อยู่ในระนาบแนวตั้งได้รับการติดตั้งบนระนาบเรียบแนวนอนและติดกับกลไกนั้นด้วยแถบที่ยึดกับพื้นผิวอย่างแน่นหนา ถึงและ ล (รูปที่ 3.4).

รัศมีดิสก์ 1 รไม่นิ่ง ดิสก์ 2 มวล มและรัศมี ร ติดอยู่กับข้อเหวี่ยงความยาว ร+ รตรงจุด ค 2- ข้อเหวี่ยงหมุนคงที่

ความเร็วเชิงมุม ใน ช่วงเวลาเริ่มต้นข้อเหวี่ยงอยู่ในตำแหน่งแนวนอนด้านขวา หากละเลยมวลของข้อเหวี่ยง ให้กำหนดแรงในแนวนอนและแนวตั้งสูงสุดที่กระทำต่อคานถ้า มวลรวมเตียงและล้อ 1 เท่ากัน ม.พิจารณาพฤติกรรมของกลไกด้วยในกรณีที่ไม่มีบาร์

สารละลาย- ระบบประกอบด้วยสองมวล ( เอ็น=2 ): แก้ไขดิสก์ 1 พร้อมเฟรมและดิสก์แบบเคลื่อนย้ายได้ 2 กำหนดทิศทางแกน ที่ผ่านจุดศูนย์ถ่วงของดิสก์ที่อยู่นิ่งในแนวตั้งขึ้นไปบนแกน เอ็กซ์– ตามแนวระนาบแนวนอน

ให้เราเขียนทฤษฎีบทเกี่ยวกับการเคลื่อนที่ของจุดศูนย์กลางมวล (3.6) ในรูปแบบพิกัด

แรงภายนอกของระบบนี้คือ: น้ำหนักของเฟรมและดิสก์คงที่ - มก, น้ำหนักดิสก์เคลื่อนที่ – มก, - ปฏิกิริยาแนวนอนรวมของสลักเกลียว - ปฏิกิริยารวมปกติของระนาบ เพราะฉะนั้น,

จากนั้นกฎการเคลื่อนที่ (b) จะถูกเขียนใหม่

ลองคำนวณพิกัดของจุดศูนย์กลางมวลของระบบกลไก:

- (ช)

ดังที่เห็นได้จาก (รูปที่ 3.4), , , (มุมข้อเหวี่ยง) - แทนนิพจน์เหล่านี้เป็น (d) และคำนวณอนุพันธ์อันดับสองตามเวลา ทีจาก , , เราเข้าใจแล้ว

(ง)

เมื่อแทน (c) และ (e) ลงใน (b) เราจะพบ

แรงกดแนวนอนที่กระทำบนแท่งจะยิ่งใหญ่ที่สุดและ ค่าที่น้อยที่สุด, เมื่อไร เพราะ = 1 ตามนั้น กล่าวคือ

กลไกกดดันอยู่ ระนาบแนวนอนมีค่ามากที่สุดและน้อยที่สุดเมื่อใด บาป ตามนั้น กล่าวคือ

ในความเป็นจริง ปัญหาแรกของพลศาสตร์ได้รับการแก้ไขแล้ว: ตามสมการการเคลื่อนที่ที่ทราบของจุดศูนย์กลางมวลของระบบ (d) แรงที่เกี่ยวข้องกับการเคลื่อนไหวจะถูกฟื้นฟู

ในกรณีที่ไม่มีบาร์ เคและ ล (รูปที่ 3.4)กลไกอาจเริ่มเด้งเหนือระนาบแนวนอน สิ่งนี้จะเกิดขึ้นเมื่อเช่น เมื่อ เป็นไปตามที่ความเร็วเชิงมุมของการหมุนของข้อเหวี่ยงที่กลไกกระเด้งจะต้องเป็นไปตามความเท่าเทียมกัน

.

3. 3. กฎการอนุรักษ์การเคลื่อนที่ของจุดศูนย์กลางมวล

หากเวกเตอร์หลักของแรงภายนอกที่กระทำต่อระบบมีค่าเท่ากับศูนย์ เช่น จากนั้นจาก(3.6)ตามมาด้วยความเร่งของจุดศูนย์กลางมวลเป็นศูนย์ ดังนั้น ความเร็วของจุดศูนย์กลางมวลจึงมีขนาดและทิศทางคงที่ โดยเฉพาะอย่างยิ่ง หากจุดศูนย์กลางมวลหยุดนิ่ง ณ จุดเริ่มแรก จุดศูนย์กลางมวลก็จะหยุดนิ่งตลอดเวลาโดยที่เวกเตอร์หลักของแรงภายนอกมีค่าเท่ากับศูนย์

ผลที่ตามมาหลายประการมาจากทฤษฎีบทนี้

· แรงภายในเพียงอย่างเดียวไม่สามารถเปลี่ยนลักษณะของการเคลื่อนที่ของจุดศูนย์กลางมวลของระบบได้

· ถ้าเวกเตอร์หลักของแรงภายนอกที่กระทำต่อระบบเป็นศูนย์ ศูนย์กลางของมวลก็จะอยู่นิ่งหรือเคลื่อนที่สม่ำเสมอและเป็นเส้นตรง

· ถ้าเส้นโครงของเวกเตอร์หลักของแรงภายนอกของระบบบนแกนคงที่บางแกนมีค่าเท่ากับศูนย์ ดังนั้นเส้นโครงของความเร็วของจุดศูนย์กลางมวลของระบบบนแกนนี้จะไม่เปลี่ยนแปลง

· แรงคู่หนึ่งที่กระทำกับวัตถุที่แข็งเกร็งไม่สามารถเปลี่ยนการเคลื่อนที่ของจุดศูนย์กลางมวลได้ (ทำได้เพียงทำให้วัตถุหมุนรอบจุดศูนย์กลางมวลเท่านั้น)

ลองพิจารณาตัวอย่างที่แสดงให้เห็นกฎการอนุรักษ์การเคลื่อนที่ของจุดศูนย์กลางมวล

ตัวอย่างที่ 3มวลสองก้อนเชื่อมต่อกันด้วยด้ายที่ขยายไม่ได้ซึ่งโยนผ่านบล็อก (รูปที่ 3.5), จับจ้องไปที่ลิ่มที่มีมวล ม.ลิ่มวางอยู่บนระนาบแนวนอนเรียบ ในตอนแรกระบบได้หยุดนิ่ง ค้นหาการกระจัดของลิ่มตามแนวระนาบเมื่อโหลดแรกถูกลดระดับความสูงลง เอ็น.ละเลยมวลของบล็อกและด้าย

สารละลาย.แรงภายนอกที่กระทำต่อลิ่มพร้อมกับโหลดคือแรงโน้มถ่วง และ มกและยัง ปฏิกิริยาปกติพื้นผิวแนวนอนเรียบ N ดังนั้น

เนื่องจากในช่วงแรกๆ ระบบหยุดนิ่ง เรามี

ขอให้เราคำนวณพิกัดของจุดศูนย์กลางมวลของระบบ ณ ขณะนี้ ที 1 เมื่อน้ำหนักบรรทุกมาก กจะลงมาสู่ที่สูง ชม.

ในขณะนี้:

,

ที่ไหน , , เอ็กซ์– ตามลำดับ พิกัดของจุดศูนย์กลางมวลของโหลดที่ชั่งน้ำหนัก g, g และการชั่งน้ำหนักลิ่ม มก.

สมมติว่าลิ่มในขณะนั้นเคลื่อนที่ไปในทิศทางบวกของแกน วัวตามจำนวนเงิน ลถ้าน้ำหนักของภาระลดลงจนถึงความสูง เอ็น.จากนั้นสักครู่

เพราะ โหลดพร้อมกับลิ่มจะเคลื่อนไป ลไปทางขวาและภาระจะเคลื่อนขึ้นตามลิ่ม เนื่องจาก แล้วหลังจากการคำนวณเราจึงได้

.

3.4. ปริมาณการเคลื่อนไหวของระบบ

3.4.1. การคำนวณโมเมนตัมของระบบ

ปริมาณการเคลื่อนที่ของจุดวัสดุเรียกว่าปริมาณเวกเตอร์ เท่ากับสินค้ามวลของจุดด้วยเวกเตอร์ความเร็ว

หน่วยวัดโมเมนตัม -

โมเมนตัมของระบบกลไกคือผลรวมเวกเตอร์ของโมเมนตัมของแต่ละจุดของระบบ เช่น

ที่ไหน เอ็น – จำนวนคะแนนของระบบ

โมเมนตัมของระบบเครื่องกลสามารถแสดงเป็นมวลของระบบได้ มและความเร็วของจุดศูนย์กลางมวล จริงหรือ,

เหล่านั้น. โมเมนตัมของระบบเท่ากับผลคูณของมวลของระบบทั้งหมดและความเร็วของจุดศูนย์กลางมวลทิศทางก็เหมือนกับทิศทาง (รูปที่ 3.6)

ในการฉายภาพบนแกนสี่เหลี่ยมที่เรามี

โดยที่ , คือการคาดคะเนความเร็วของจุดศูนย์กลางมวลของระบบ

ที่นี่ ม– มวลของระบบเครื่องกล ไม่เปลี่ยนแปลงเมื่อระบบเคลื่อนที่

ผลลัพธ์เหล่านี้สะดวกเป็นพิเศษเมื่อคำนวณปริมาณการเคลื่อนที่ของวัตถุแข็งเกร็ง

จากสูตร (3.7) เห็นได้ชัดว่าหากระบบกลไกเคลื่อนที่ในลักษณะที่จุดศูนย์กลางมวลยังคงอยู่กับที่ โมเมนตัมของระบบจะยังคงเท่ากับศูนย์

3.4.2. แรงกระตุ้นเบื้องต้นและเต็มกำลัง

การกระทำของแรงบนจุดวัตถุในช่วงเวลาหนึ่ง dtสามารถระบุได้ด้วยแรงกระตุ้นเบื้องต้น แรงกระตุ้นรวมในช่วงเวลาหนึ่ง ที, หรือแรงกระตุ้นที่กำหนดโดยสูตร

หรือในการฉายภาพบนพิกัดแกน

(3.8ก)

หน่วยของแรงกระตุ้นคือ

3.4.3. ทฤษฎีบทเกี่ยวกับการเปลี่ยนแปลงโมเมนตัมของระบบ

ปล่อยให้แรงภายนอกและภายในถูกนำไปใช้กับจุดต่างๆ ของระบบ จากนั้นสำหรับแต่ละจุดของระบบ เราสามารถใช้กฎการเคลื่อนที่แบบดิฟเฟอเรนเชียล (3.3) ได้ โดยคำนึงไว้เสมอ :

.

เมื่อรวมทุกจุดของระบบแล้วเราได้รับ

โดยคุณสมบัติของกองกำลังภายในและตามคำจำกัดความ เรามี

(3.9)

คูณทั้งสองข้างของสมการนี้ด้วย dtเราได้ทฤษฎีบทเกี่ยวกับการเปลี่ยนแปลงโมเมนตัมใน รูปแบบที่แตกต่าง:

, (3.10)

เหล่านั้น. โมเมนตัมเชิงอนุพันธ์ของระบบเชิงกลเท่ากับผลรวมเวกเตอร์ของแรงกระตุ้นเบื้องต้นของแรงภายนอกทั้งหมดที่กระทำต่อจุดของระบบกลไก

การคำนวณอินทิกรัลของทั้งสองข้าง (3.10) ในช่วงเวลาตั้งแต่ 0 ถึง ที, เราได้ทฤษฎีบทในรูปแบบจำกัดหรืออินทิกรัล

(3.11)

ในการฉายภาพบนแกนพิกัดเราจะได้

การเปลี่ยนแปลงโมเมนตัมของระบบกลไกเมื่อเวลาผ่านไปทีเท่ากับผลรวมเวกเตอร์ของแรงกระตุ้นภายนอกทั้งหมดที่กระทำต่อจุดของระบบกลไกในช่วงเวลาเดียวกัน

ตัวอย่างที่ 4โหลดน้ำหนัก ม ลงไปที่ เครื่องบินเอียงจากการสงบนิ่งภายใต้อิทธิพลของพลัง เอฟ, สัดส่วนกับเวลา: ที่ไหน (รูปที่ 3.7)- ร่างกายจะได้ความเร็วเท่าใดหลังจากนั้น ที วินาทีหลังจากเริ่มการเคลื่อนที่ หากค่าสัมประสิทธิ์แรงเสียดทานของการเลื่อนของโหลดบนระนาบเอียงเท่ากับ ฉ.

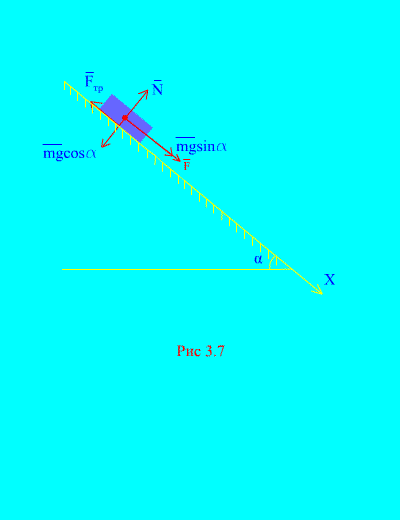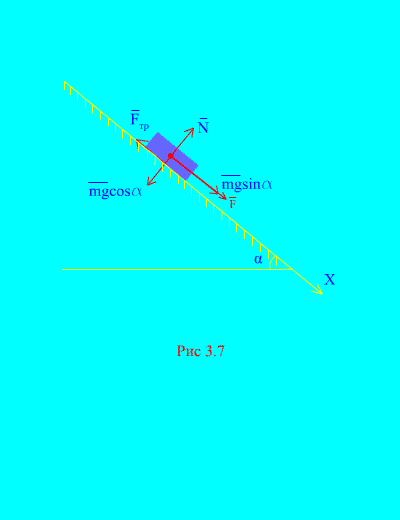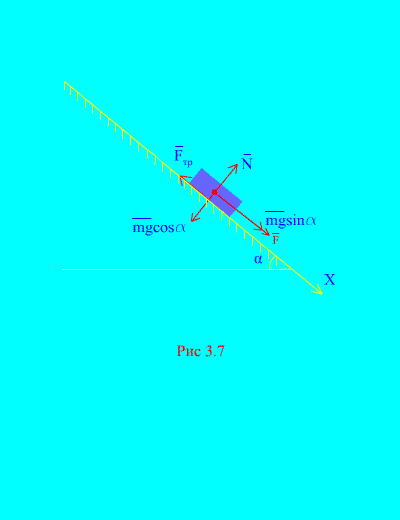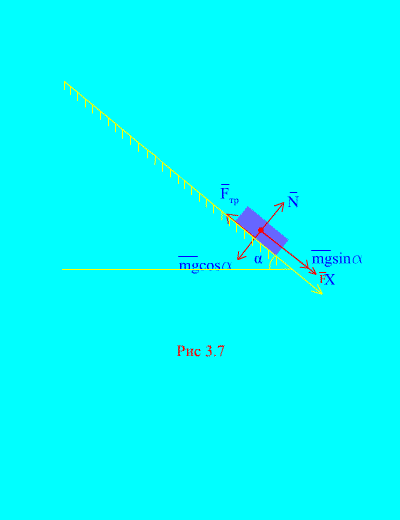
สารละลาย.ให้เราพรรณนาถึงแรงที่ใช้กับโหลด: มก – แรงโน้มถ่วงโหลด เอ็นคือ ปฏิกิริยาปกติของระนาบ คือ แรงเสียดทานแบบเลื่อนของโหลดบนระนาบ และ ทิศทางของแรงทั้งหมดจะแสดงใน (รูปที่ 3.7).

ลองกำหนดทิศทางของแกนดู เอ็กซ์ตามแนวระนาบเอียงลง ให้เราเขียนทฤษฎีบทเกี่ยวกับการเปลี่ยนแปลงของโมเมนตัม (3.11) ในการฉายภาพบนแกน เอ็กซ์:

(ก)

ตามเงื่อนไขเพราะว่า ในช่วงเวลาเริ่มต้นโหลดจะนิ่งอยู่ ผลรวมของเส้นโครงของแรงกระตุ้นของแรงทั้งหมดบนแกน x เท่ากับ

เพราะฉะนั้น,

,

.

3.4.4. กฎการอนุรักษ์โมเมนตัม

กฎการอนุรักษ์ได้รับเป็นกรณีพิเศษของทฤษฎีบทเกี่ยวกับการเปลี่ยนแปลงโมเมนตัม เป็นไปได้สองกรณีพิเศษ

· หากผลรวมเวกเตอร์ของแรงภายนอกทั้งหมดที่ใช้กับระบบมีค่าเท่ากับศูนย์ นั่นคือ จากนั้นจากทฤษฎีบทมันจะเป็นดังนี้ (3.9) , อะไร ,

เหล่านั้น. ถ้าเวกเตอร์หลักของแรงภายนอกของระบบเป็นศูนย์ ปริมาณการเคลื่อนที่ของระบบจะคงที่ทั้งขนาดและทิศทาง

· หากการฉายภาพเวกเตอร์หลักของแรงภายนอกบนแกนพิกัดใด ๆ เท่ากับศูนย์ เช่น Ox เช่น จากนั้นเส้นโครงของโมเมนตัมบนแกนนี้จะเป็นค่าคงที่

ลองพิจารณาตัวอย่างการใช้กฎการอนุรักษ์โมเมนตัม

ตัวอย่างที่ 5ลูกตุ้มขีปนาวุธคือวัตถุที่มีมวลแขวนอยู่บนเส้นด้ายยาว (รูปที่ 3.8).

กระสุนมวล เคลื่อนที่ด้วยความเร็ว วีไปกระทบกายที่นิ่งติดอยู่ในนั้นกายก็เบี่ยงไป ถ้าร่างกายลอยขึ้นไปจะมีความเร็วของกระสุนเป็นเท่าใด ชม. ?

สารละลาย.ปล่อยให้ร่างกายที่กระสุนติดอยู่ได้รับความเร็ว จากนั้นเราสามารถเขียนกฎการอนุรักษ์โมเมนตัมระหว่างปฏิสัมพันธ์ของวัตถุทั้งสองได้ .

ความเร็วสามารถคำนวณได้โดยใช้กฎหมายอนุรักษ์ พลังงานกล - แล้ว . ส่งผลให้เราพบว่า

.

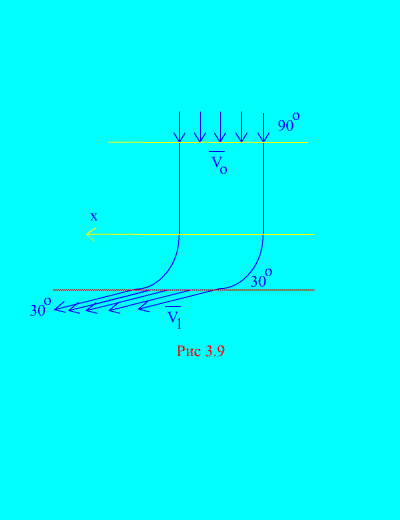
ตัวอย่างที่ 6- น้ำเข้าสู่ช่องทางนิ่ง (รูปที่ 3.9)หน้าตัดแปรผันด้วยความเร็วที่มุมถึงแนวนอน สี่เหลี่ยม ภาพตัดขวางช่องทางที่ทางเข้า; ความเร็วน้ำที่ทางออกจากช่องทำมุมกับขอบฟ้า

กำหนดองค์ประกอบแนวนอนของปฏิกิริยาที่น้ำมีต่อผนังช่อง ความหนาแน่นของน้ำ .

สารละลาย.เราจะพิจารณาองค์ประกอบแนวนอนของปฏิกิริยาที่กระทำโดยผนังช่องน้ำ แรงนี้มีขนาดเท่ากันและตรงกันข้ามกับแรงที่ต้องการ เรามีตาม (3.11a)

- (ก)

เราคำนวณมวลของปริมาตรของของเหลวที่เข้าสู่ช่องในช่วงเวลา t:

เรียกค่า rAV 0 มวลที่สอง - มวลของของเหลวที่ไหลผ่านส่วนใดส่วนหนึ่งของท่อต่อหน่วยเวลา

ปริมาณน้ำออกจากคลองในเวลาเดียวกัน ความเร็วเริ่มต้นและความเร็วสุดท้ายถูกกำหนดไว้ในเงื่อนไข

มาคำนวณกัน ด้านขวาความเท่าเทียมกัน (a) ซึ่งกำหนดผลรวมของเส้นโครงบนแกนนอนของแรงภายนอกที่ใช้กับระบบ (น้ำ) แรงในแนวนอนเพียงอย่างเดียวคือองค์ประกอบในแนวนอนของปฏิกิริยาผนังที่เป็นผลลัพธ์ อาร์เอ็กซ์- แรงนี้จะคงที่ในระหว่างการเคลื่อนที่ของน้ำอย่างสม่ำเสมอ นั่นเป็นเหตุผล

- (วี)

เมื่อแทน (b) และ (c) ไปเป็น (a) เราจะได้

3.5. โมเมนต์จลนศาสตร์ระบบ

3.5.1. โมเมนตัมหลักของระบบ

อนุญาต เป็นเวกเตอร์รัศมีของจุดที่มีมวลของระบบสัมพันธ์กับจุด A ที่เรียกว่าจุดศูนย์กลาง (รูปที่ 3.10).

โมเมนตัมของโมเมนตัม (โมเมนตัมจลน์) ของจุด สัมพันธ์กับศูนย์กลาง Aเรียกว่าเวกเตอร์ , กำหนดโดยสูตร

. (3.12)

ในกรณีนี้คือเวกเตอร์ ตั้งฉากกับระนาบที่ผ่านจุดศูนย์กลาง กและเวกเตอร์ .

โมเมนตัมของโมเมนตัม (โมเมนตัมจลน์) ของจุดที่สัมพันธ์กับแกนเรียกว่าการฉายภาพบนแกนนี้ของโมเมนตัมของจุดที่สัมพันธ์กับจุดศูนย์กลางที่เลือกบนแกนนี้

โมเมนตัมหลักของโมเมนตัม (โมเมนต์จลน์) ของระบบสัมพันธ์กับศูนย์กลาง Aเรียกว่าปริมาณ

(3.13)

โมเมนตัมหลักของโมเมนตัม (โมเมนต์จลน์) ของระบบสัมพันธ์กับแกนเรียกว่าการฉายภาพบนแกนนี้ของโมเมนตัมหลักของโมเมนตัมของระบบเทียบกับค่าใดๆ ที่เลือกไว้บนแกนนี้ แกนกลาง

3.5.2. โมเมนต์จลน์ของวัตถุแข็งเกร็งที่กำลังหมุนรอบแกนการหมุน

เข้ากันได้ จุดคงที่ เกี่ยวกับร่างกายนอนอยู่บนแกนหมุน เกี่ยวกับzโดยมีที่มาของระบบพิกัด โอ้โหzแกนที่จะหมุนไปพร้อมกับลำตัว (รูปที่ 3.11)- อนุญาต เป็นเวกเตอร์รัศมีของจุดของร่างกายสัมพันธ์กับที่มาของพิกัด; การฉายภาพบนแกนจะแสดงด้วย , , . การฉายภาพเวกเตอร์ ความเร็วเชิงมุมวัตถุบนแกนเดียวกันเราแสดงว่า 0, 0, ()

1. ฟังก์ชันเชิงเส้นแบบเศษส่วนและกราฟ

ฟังก์ชันที่อยู่ในรูปแบบ y = P(x) / Q(x) โดยที่ P(x) และ Q(x) เป็นพหุนาม เรียกว่า ฟังก์ชันตรรกยะเศษส่วน

ด้วยแนวคิด จำนวนตรรกยะคุณอาจจะรู้จักกันอยู่แล้ว เช่นเดียวกัน ฟังก์ชันตรรกยะ เป็นฟังก์ชันที่สามารถแสดงเป็นผลหารของพหุนามสองตัวได้

ถ้าฟังก์ชันตรรกยะเศษส่วนเป็นผลหารของสอง ฟังก์ชันเชิงเส้น– พหุนามของดีกรีแรก เช่น ฟังก์ชั่นของแบบฟอร์ม

y = (ax + b) / (cx + d) จากนั้นเรียกว่าเศษส่วนเชิงเส้น

โปรดทราบว่าในฟังก์ชัน y = (ax + b) / (cx + d), c ≠ 0 (ไม่เช่นนั้นฟังก์ชันจะกลายเป็นเส้นตรง y = ax/d + b/d) และ a/c ≠ b/d (มิฉะนั้น ฟังก์ชันคงที่) ฟังก์ชันเชิงเส้นแบบเศษส่วนถูกกำหนดไว้สำหรับทุกคน ตัวเลขจริงยกเว้น x = -d/c กราฟของฟังก์ชันเชิงเส้นแบบเศษส่วนไม่มีรูปร่างแตกต่างจากกราฟ y = 1/x ที่คุณทราบ เส้นโค้งที่เป็นกราฟของฟังก์ชัน y = 1/x เรียกว่า อติพจน์- ด้วยการเพิ่ม x อย่างไม่จำกัด ค่าสัมบูรณ์ฟังก์ชัน y = 1/x ลดลงอย่างไม่มีกำหนดในค่าสัมบูรณ์ และกิ่งทั้งสองของกราฟเข้าใกล้แกน x โดยกิ่งด้านขวาเข้าใกล้จากด้านบน และกิ่งด้านซ้ายจากด้านล่าง เส้นตรงที่เรียกว่ากิ่งก้านของแนวทางไฮเปอร์โบลา เส้นกำกับ.

ตัวอย่างที่ 1

y = (2x + 1) / (x – 3)

สารละลาย.

ลองเลือกทั้งส่วน: (2x + 1) / (x – 3) = 2 + 7/(x – 3)

ตอนนี้เห็นได้ง่ายว่ากราฟของฟังก์ชันนี้ได้มาจากกราฟของฟังก์ชัน y = 1/x โดยการแปลงต่อไปนี้: เลื่อนไป 3 ส่วนหน่วยไปทางขวา ยืดไปตามแกน Oy 7 ครั้ง และเลื่อนไป 2 ส่วนของหน่วยขึ้นไป

เศษส่วนใดๆ y = (ax + b) / (cx + d) สามารถเขียนได้ในลักษณะเดียวกัน โดยเน้นที่ "ทั้งส่วน" ดังนั้น กราฟของฟังก์ชันเชิงเส้นแบบเศษส่วนทั้งหมดจึงเป็นไฮเปอร์โบลา ซึ่งมีการเลื่อนในลักษณะต่างๆ กัน แกนประสานงานและทอดยาวไปตามแกนออย

เพื่อสร้างกราฟแบบใดก็ได้ ฟังก์ชันเชิงเส้นเศษส่วนไม่จำเป็นต้องแปลงเศษส่วนที่กำหนดฟังก์ชันนี้เลย เนื่องจากเรารู้ว่ากราฟเป็นไฮเปอร์โบลา จึงเพียงพอที่จะหาเส้นตรงที่กิ่งก้านของกราฟเข้าใกล้ นั่นคือเส้นกำกับของไฮเปอร์โบลา x = -d/c และ y = a/c

ตัวอย่างที่ 2

ค้นหาเส้นกำกับของกราฟของฟังก์ชัน y = (3x + 5)/(2x + 2)

สารละลาย.

ไม่ได้กำหนดฟังก์ชันไว้ที่ x = -1 ซึ่งหมายความว่าเส้นตรง x = -1 ทำหน้าที่เป็นเส้นกำกับแนวตั้ง ในการค้นหาเส้นกำกับแนวนอน เรามาดูกันว่าค่าของฟังก์ชัน y(x) เข้าใกล้ค่าใดเมื่ออาร์กิวเมนต์ x เพิ่มขึ้นเป็นค่าสัมบูรณ์

เมื่อต้องการทำเช่นนี้ ให้หารทั้งเศษและส่วนของเศษส่วนด้วย x:

y = (3 + 5/x) / (2 + 2/x)

เมื่อ x → ∞ เศษส่วนจะมีแนวโน้มเป็น 3/2 วิธี, เส้นกำกับแนวนอน– นี่คือเส้นตรง y = 3/2

ตัวอย่างที่ 3

สร้างกราฟฟังก์ชัน y = (2x + 1)/(x + 1)

สารละลาย.

เรามาเลือก “ทั้งหมด” ของเศษส่วนกัน:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

2 – 1/(x + 1)

ตอนนี้เห็นได้ง่ายว่ากราฟของฟังก์ชันนี้ได้มาจากกราฟของฟังก์ชัน y = 1/x โดยการแปลงต่อไปนี้: การเลื่อนไปทางซ้าย 1 หน่วย การแสดงแบบสมมาตรเทียบกับ Ox และการเปลี่ยนแปลงโดย แบ่งหน่วย 2 หน่วยขึ้นไปตามแกน Oy

โดเมน D(y) = (-∞; -1)ᴗ(-1; +∞)

ช่วงของค่า E(y) = (-∞; 2)ᴗ(2; +∞)

จุดตัดด้วยแกน: c Oy: (0; 1); ค อ็อกซ์: (-1/2; 0) ฟังก์ชันจะเพิ่มขึ้นในแต่ละช่วงของโดเมนคำจำกัดความ

คำตอบ: รูปที่ 1

2. ฟังก์ชันตรรกยะเศษส่วน

พิจารณาฟังก์ชันตรรกยะเศษส่วนในรูปแบบ y = P(x) / Q(x) โดยที่ P(x) และ Q(x) เป็นพหุนามที่มีดีกรีสูงกว่าค่าแรก

ตัวอย่างของฟังก์ชันตรรกยะดังกล่าว:

y = (x 3 – 5x + 6) / (x 7 – 6) หรือ y = (x – 2) 2 (x + 1) / (x 2 + 3)

หากฟังก์ชัน y = P(x) / Q(x) แทนค่าผลหารของพหุนามสองตัวที่มีดีกรีสูงกว่าฟังก์ชันแรก ตามกฎแล้วกราฟของมันจะซับซ้อนกว่า และบางครั้งอาจเป็นเรื่องยากที่จะสร้างมันให้แม่นยำ พร้อมรายละเอียดทั้งหมด อย่างไรก็ตาม การใช้เทคนิคก็มักจะเพียงพอแล้ว หัวข้อที่คล้ายกันซึ่งเราได้พบกันข้างต้นแล้ว

ให้เศษส่วนเป็นเศษส่วนแท้ (n< m). Известно, что любую несократимую เศษส่วนตรรกยะสามารถเป็นตัวแทนและในลักษณะเฉพาะเป็นผลรวมได้ จำนวนจำกัดเศษส่วนเบื้องต้น ซึ่งมีรูปแบบที่กำหนดโดยการแยกตัวส่วนของเศษส่วน Q(x) เป็นผลคูณของตัวประกอบจริง:

P(x)/Q(x) = A 1 /(x – K 1) m1 + A 2 /(x – K 1) m1-1 + … + A m1 /(x – K 1) + …+

L 1 /(x – K s) ms + L 2 /(x – K s) ms-1 + … + L ms /(x – K s) + …+

+ (B 1 x + C 1) / (x 2 +p 1 x + q 1) m1 + … + (B m1 x + C m1) / (x 2 +p 1 x + q 1) + …+

+ (ม. 1 x + N 1) / (x 2 +p เสื้อ x + q เสื้อ) m1 + … + (ม. ม.1 x + N ม.1) / (x 2 +พี เสื้อ x + q เสื้อ)

แน่นอนว่ากราฟของฟังก์ชันเศษส่วนเชิงตรรกศาสตร์สามารถหาได้จากผลรวมของกราฟของเศษส่วนเบื้องต้น

การพล็อตกราฟของฟังก์ชันตรรกยะเศษส่วน

ลองพิจารณาหลายวิธีในการสร้างกราฟของฟังก์ชันตรรกยะเศษส่วน

ตัวอย่างที่ 4

วาดกราฟของฟังก์ชัน y = 1/x 2

สารละลาย.

เราใช้กราฟของฟังก์ชัน y = x 2 เพื่อสร้างกราฟที่มี y = 1/x 2 และใช้เทคนิค "หาร" กราฟ

โดเมน D(y) = (-∞; 0)ᴗ(0; +∞)

ช่วงของค่า E(y) = (0; +∞)

ไม่มีจุดตัดกับแกน ฟังก์ชันเป็นคู่ เพิ่มขึ้นสำหรับ x ทั้งหมดจากช่วงเวลา (-∞; 0) ลดลงสำหรับ x จาก 0 ถึง +∞

คำตอบ: รูปที่ 2

ตัวอย่างที่ 5

สร้างกราฟฟังก์ชัน y = (x 2 – 4x + 3) / (9 – 3x)

สารละลาย.

โดเมน D(y) = (-∞; 3)ᴗ(3; +∞)

y = (x 2 – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/ 3 + 1/3.

ในที่นี้เราใช้เทคนิคการแยกตัวประกอบ การลดลง และการลดลงเป็นฟังก์ชันเชิงเส้น

คำตอบ: รูปที่ 3

ตัวอย่างที่ 6

สร้างกราฟฟังก์ชัน y = (x 2 – 1)/(x 2 + 1)

สารละลาย.

ขอบเขตของคำจำกัดความคือ D(y) = R เนื่องจากฟังก์ชันเป็นเลขคู่ กราฟจึงมีความสมมาตรเกี่ยวกับพิกัด ก่อนที่จะสร้างกราฟ มาแปลงนิพจน์อีกครั้งโดยเน้นส่วนทั้งหมด:

y = (x 2 – 1)/(x 2 + 1) = 1 – 2/(x 2 + 1)

โปรดทราบว่าการแยกส่วนจำนวนเต็มออกจากสูตรของฟังก์ชันเศษส่วนเป็นเหตุผลหลักในการสร้างกราฟ

ถ้า x → ±∞ ดังนั้น y → 1 เช่น เส้นตรง y = 1 เป็นเส้นกำกับแนวนอน

คำตอบ: รูปที่ 4

ตัวอย่างที่ 7

ลองพิจารณาฟังก์ชัน y = x/(x 2 + 1) แล้วลองค้นหาค่าที่ใหญ่ที่สุดอย่างแม่นยำ เช่น มากที่สุด จุดสูงสุดครึ่งขวาของกราฟ การสร้างกราฟนี้อย่างถูกต้องแม่นยำ ความรู้ในปัจจุบันยังไม่เพียงพอ แน่นอนว่าเส้นโค้งของเราไม่สามารถ "ขึ้น" สูงมากได้เพราะว่า ตัวส่วนเริ่ม "แซง" ตัวเศษอย่างรวดเร็ว ลองดูว่าค่าของฟังก์ชันจะเท่ากับ 1 ได้หรือไม่ เมื่อต้องการทำสิ่งนี้ เราต้องแก้สมการ x 2 + 1 = x, x 2 – x + 1 = 0 สมการนี้ไม่มีรากจริง ซึ่งหมายความว่าสมมติฐานของเราไม่ถูกต้อง ให้พบมากที่สุด คุ้มค่ามากฟังก์ชัน คุณต้องหาว่าสมการ A = x/(x 2 + 1) มีค่าเท่าใดจึงจะมีคำตอบ ลองแทนที่สมการดั้งเดิมด้วยสมการกำลังสอง: Аx 2 – x + А = 0 สมการนี้มีคำตอบเมื่อ 1 – 4А 2 ≥ 0 จากที่นี่ เราจะพบ มูลค่าสูงสุดก = 1/2

คำตอบ: รูปที่ 5, สูงสุด y(x) = ½

ยังมีคำถามอยู่ใช่ไหม? ไม่รู้วิธีสร้างกราฟฟังก์ชันใช่ไหม?
หากต้องการความช่วยเหลือจากครูสอนพิเศษ ให้ลงทะเบียน
บทเรียนแรกฟรี!

เว็บไซต์ เมื่อคัดลอกเนื้อหาทั้งหมดหรือบางส่วน จำเป็นต้องมีลิงก์ไปยังแหล่งที่มา

การสร้างกราฟของฟังก์ชันที่มีโมดูลมักจะทำให้เกิดปัญหาอย่างมากสำหรับเด็กนักเรียน อย่างไรก็ตามทุกอย่างก็ไม่ได้เลวร้ายนัก ก็เพียงพอแล้วที่จะจดจำอัลกอริธึมสองสามตัวในการแก้ปัญหาดังกล่าวและคุณสามารถสร้างกราฟได้อย่างง่ายดายแม้จะดูเหมือนมากที่สุดก็ตาม ฟังก์ชั่นที่ซับซ้อน- เรามาดูกันว่าอัลกอริธึมเหล่านี้คืออะไร

1. เขียนกราฟของฟังก์ชัน y = |f(x)|

โปรดทราบว่าชุดของค่าฟังก์ชัน y = |f(x)| : y ≥ 0 ดังนั้น กราฟของฟังก์ชันดังกล่าวจึงอยู่ในระนาบครึ่งบนเสมอ

การพล็อตกราฟของฟังก์ชัน y = |f(x)| ประกอบด้วยสี่ขั้นตอนง่ายๆ ดังต่อไปนี้

1) สร้างกราฟของฟังก์ชัน y = f(x) อย่างระมัดระวังและรอบคอบ

2) ปล่อยจุดทั้งหมดบนกราฟที่อยู่เหนือหรือบนแกน 0x ไว้ไม่เปลี่ยนแปลง

3) แสดงส่วนของกราฟที่อยู่ต่ำกว่าแกน 0x อย่างสมมาตรสัมพันธ์กับแกน 0x

ตัวอย่างที่ 1 วาดกราฟของฟังก์ชัน y = |x 2 – 4x + 3|

1) เราสร้างกราฟของฟังก์ชัน y = x 2 – 4x + 3 แน่นอนว่ากราฟของฟังก์ชันนี้คือพาราโบลา ลองหาพิกัดของทุกจุดตัดของพาราโบลากับแกนพิกัดและพิกัดของจุดยอดของพาราโบลากัน

x 2 – 4x + 3 = 0

x 1 = 3, x 2 = 1

ดังนั้น พาราโบลาจะตัดแกน 0x ที่จุด (3, 0) และ (1, 0)

ปี = 0 2 – 4 0 + 3 = 3

ดังนั้น พาราโบลาจะตัดแกน 0y ที่จุด (0, 3)

พิกัดจุดยอดพาราโบลา:

x ใน = -(-4/2) = 2, y ใน = 2 2 – 4 2 + 3 = -1

ดังนั้น จุด (2, -1) คือจุดยอดของพาราโบลานี้

วาดพาราโบลาโดยใช้ข้อมูลที่ได้รับ (รูปที่ 1)

2) ส่วนของกราฟที่อยู่ต่ำกว่าแกน 0x จะแสดงแบบสมมาตรสัมพันธ์กับแกน 0x

3) เราได้กราฟของฟังก์ชันดั้งเดิม ( ข้าว. 2, แสดงเป็นเส้นประ)

2. การสร้างกราฟฟังก์ชัน y = f(|x|)

โปรดทราบว่าฟังก์ชันที่อยู่ในรูปแบบ y = f(|x|) จะเป็นคู่:

y(-x) = f(|-x|) = f(|x|) = y(x) ซึ่งหมายความว่ากราฟของฟังก์ชันดังกล่าวมีความสมมาตรเกี่ยวกับแกน 0y

การสร้างกราฟของฟังก์ชัน y = f(|x|) ประกอบด้วยลำดับการกระทำอย่างง่ายดังต่อไปนี้

1) สร้างกราฟฟังก์ชัน y = f(x)

2) ปล่อยส่วนของกราฟซึ่งมี x ≥ 0 ซึ่งก็คือส่วนของกราฟที่อยู่ในระนาบครึ่งขวา

3) แสดงส่วนของกราฟที่ระบุในจุด (2) แบบสมมาตรกับแกน 0y

4) เป็นกราฟสุดท้าย ให้เลือกการรวมกันของเส้นโค้งที่ได้รับในจุด (2) และ (3)

ตัวอย่างที่ 2 วาดกราฟของฟังก์ชัน y = x 2 – 4 · |x| + 3

เนื่องจาก x 2 = |x| 2 จากนั้นฟังก์ชันดั้งเดิมสามารถเขียนใหม่ได้ในรูปแบบต่อไปนี้: y = |x| 2 – 4 · |x| + 3. ตอนนี้เราสามารถใช้อัลกอริธึมที่เสนอข้างต้นได้แล้ว

1) เราสร้างกราฟของฟังก์ชัน y = x 2 – 4 x + 3 อย่างระมัดระวังและรอบคอบ (ดูเพิ่มเติม ข้าว. 1).

2) เราปล่อยให้ส่วนของกราฟมี x ≥ 0 ซึ่งก็คือส่วนของกราฟที่อยู่ในระนาบครึ่งขวา

3) แสดงด้านขวาของกราฟอย่างสมมาตรกับแกน 0y

(รูปที่ 3).

ตัวอย่างที่ 3 วาดกราฟของฟังก์ชัน y = log 2 |x|

เราใช้รูปแบบที่ให้ไว้ข้างต้น

1) สร้างกราฟของฟังก์ชัน y = log 2 x (รูปที่ 4).

3. การพล็อตฟังก์ชัน y = |f(|x|)|

โปรดทราบว่าฟังก์ชันที่อยู่ในรูปแบบ y = |f(|x|)| ก็ยังเท่ากัน แท้จริงแล้ว y(-x) = y = |f(|-x|)| = y = |ฉ(|x|)| = y(x) ดังนั้น กราฟของพวกมันจึงสมมาตรรอบแกน 0y ชุดค่าของฟังก์ชันดังกล่าว: y ≥ 0 ซึ่งหมายความว่ากราฟของฟังก์ชันดังกล่าวจะอยู่ในระนาบครึ่งบนทั้งหมด

ในการพล็อตฟังก์ชัน y = |f(|x|)| คุณต้อง:

1) สร้างกราฟของฟังก์ชัน y = f(|x|) อย่างระมัดระวัง

2) ปล่อยส่วนของกราฟที่อยู่เหนือหรือบนแกน 0x ไว้ไม่เปลี่ยนแปลง

3) แสดงส่วนของกราฟที่อยู่ด้านล่างแกน 0x แบบสมมาตรสัมพันธ์กับแกน 0x

4) เป็นกราฟสุดท้าย ให้เลือกการรวมกันของเส้นโค้งที่ได้รับในจุด (2) และ (3)

ตัวอย่างที่ 4 วาดกราฟของฟังก์ชัน y = |-x 2 + 2|x| – 1|.

1) โปรดทราบว่า x 2 = |x| 2. ซึ่งหมายความว่าแทนที่จะเป็นฟังก์ชันเดิม y = -x 2 + 2|x| – 1

คุณสามารถใช้ฟังก์ชัน y = -|x| 2 + 2|x| – 1 เนื่องจากกราฟตรงกัน

เราสร้างกราฟ y = -|x| 2 + 2|x| – 1. สำหรับสิ่งนี้ เราใช้อัลกอริทึม 2

ก) สร้างกราฟฟังก์ชัน y = -x 2 + 2x – 1 (รูปที่ 6).

b) เราปล่อยให้ส่วนของกราฟที่อยู่ในครึ่งระนาบด้านขวา

c) เราแสดงส่วนผลลัพธ์ของกราฟแบบสมมาตรกับแกน 0y

d) กราฟผลลัพธ์จะแสดงเป็นเส้นประในรูป (รูปที่ 7).

2) ไม่มีจุดที่อยู่เหนือแกน 0x เราปล่อยให้จุดบนแกน 0x ไม่เปลี่ยนแปลง

3) ส่วนของกราฟที่อยู่ด้านล่างแกน 0x จะแสดงแบบสมมาตรสัมพันธ์กับ 0x

4) กราฟผลลัพธ์จะแสดงในรูปด้วยเส้นประ (รูปที่ 8).

ตัวอย่างที่ 5 สร้างกราฟฟังก์ชัน y = |(2|x| – 4) / (|x| + 3)|

1) ก่อนอื่นคุณต้องพล็อตฟังก์ชัน y = (2|x| – 4) / (|x| + 3) เมื่อต้องการทำเช่นนี้ เรากลับไปที่อัลกอริทึม 2

a) พลอตฟังก์ชัน y = (2x – 4) / (x + 3) อย่างระมัดระวัง (รูปที่ 9).

โปรดทราบว่า ฟังก์ชั่นนี้เป็นเศษส่วนเชิงเส้นและกราฟของมันคือไฮเปอร์โบลา ในการพล็อตเส้นโค้ง คุณต้องหาเส้นกำกับของกราฟก่อน แนวนอน – y = 2/1 (อัตราส่วนของสัมประสิทธิ์ของ x ในตัวเศษและส่วนของเศษส่วน), แนวตั้ง – x = -3

2) เราจะปล่อยให้ส่วนของกราฟที่อยู่เหนือแกน 0x หรือบนนั้นไม่เปลี่ยนแปลง

3) ส่วนของกราฟที่อยู่ด้านล่างแกน 0x จะแสดงแบบสมมาตรสัมพันธ์กับ 0x

4) กราฟสุดท้ายจะแสดงในรูป (รูปที่ 11).

เว็บไซต์ เมื่อคัดลอกเนื้อหาทั้งหมดหรือบางส่วน จำเป็นต้องมีลิงก์ไปยังแหล่งที่มา