Як визначити, чому дорівнює межа. Межа послідовності та функції
Сьогодні розглянемо добірку нових завдань на знаходження межі у точці. Почнемо з простих прикладів на підстановку значення, найчастіше розглядають у 11 класі шкільної програми з математики.
Далі зупинимося та проаналізуємо межі з невизначеностями, методи розкриття невизначеностей, застосуванням першої та другої важливих меж та їх наслідків.
Наведені приклади повністю не охоплять всієї теми, але багато питань внесуть ясність.
Знайти межу функції у точці:
Приклад 46. Межа функції у точці визначаємо підстановкою
Оскільки знаменник дробу не перетворюється на нуль, то таке завдання під силу вирішити кожному випускнику школи.
Приклад 47. Маємо частку поліномів, крім того знаменник не містить особливості (не дорівнює нулю).
Ще одне завдання фактично за 11 клас.
Приклад 48. Методом підстановки визначаємо межу функції
З умови випливає, що межа функції дорівнює двом, якщо змінна прагне нескінченності.
Приклад 49. Пряма підстановка x=2 показує, що межа в точці має особливість (0/0). Це означає, як і чисельник і знаменник приховано містять (x-2) .
Виконуємо розкладання поліномів на прості множники, а потім скорочуємо дріб на вказаний множник (x-2).
Межу дробу, що залишиться, знаходимо методом підстановки.
Приклад 50. Межа функції у точці має особливість типу (0/0).
Позбавляємося різниці коренів методом множення на суму коренів (сполучений вираз), полином розкладаємо.
Далі, спростивши функцію, знаходимо значення межі в одиниці.

Приклад 51. Розглянемо завдання складні межі.
До цього часу ірраціональності позбавлялися методом множення на сполучене вираз.
Тут же, у знаменнику, маємо корінь кубічний, тому потрібно використовувати формулу різниці кубів.
Решта інших змін повторюються від умови до умови.
Поліном розкладаємо на прості множники,
далі скорочуємо на множник, який вносить особливість (0)
і підстановкою x=-3 знаходимо межу функції у точці 
Приклад 52. Особливість виду (0/0) розкриваємо за допомогою першої чудової межі та її наслідків.
Спочатку різницю синусів розпишемо згідно з тригонометричною формулою
sin(7x)-sin(3x)=2sin(2x)cos(5x).
Далі чисельник і знаменник дробу доповнюємо виразами, які необхідні виділення важливих меж.
Переходимо до добутку меж та оцінюємо вкладення кожного множника.

Тут використали першу чудову межу:
та наслідки з нього ![]()
![]()
де a та b – довільні числа.
Приклад 53. Щоб розкрити невизначеність при змінній, що прагне до нуля, використовуємо другу чудову межу.
Щоб виділити експоненту, наводимо показник до 2-ї чудової межі, а все інше, що залишиться в граничному переході, дасть ступінь експоненти. 
Тут використали слідство з другої чудової межі: 
Обчислити межу функції у точці:
Приклад 54. Потрібно визначити межу функції у точці. Проста підстановка значення показує, що маємо поділ нулів.
Для її розкриття розкладемо на прості множники поліноми та виконаємо скорочення на множник, який вносить особливість (х+2).
Проте чисельник далі містить (x+2) , але це означає, що з x=-2 межа дорівнює нулю. 
Приклад 55. Маємо дробову функцію – у чисельнику різниця коренів, у знаменнику – поленом.
Пряма підстановка дає особливість виду (0/0).
Змінна прагне мінус одиниці, а це означає, що слід шукати і позбавлятися особливості виду (x+1) .
Для цього позбавляємось ірраціональності множенням на суму коренів, а квадратичну функцію розкладаємо на прості множники.
Після всіх скорочень методом підстановки визначаємо межу функції у точці 
Приклад 56. На вигляд підлімітної функції можна помилково укласти, що потрібно застосувати першу межу, але обчислення показали, що все набагато простіше.
Спочатку розпишемо суму синусів у знаменнику sin(2x)+sin(6x)=2sin(4x)*cos(2x).
Далі розписуємо tg(2x) і синус подвійного кута sin(4x)=2sin(2x)cos (2x).
Синуси спрощуємо і методом підстановки обчислюємо межу дробу 
Приклад 57. Завдання на вміння використовувати другу чудову межу:
суть полягає в тому, що слід виділити ту частину, що дає експоненту.
Решта, що залишиться у показнику в граничному переході, дасть ступінь експоненти. 
У цьому розбір завдань межі функцій і послідовностей не закінчується.
В даний час підготовлено більше 150 готових відповідейдо меж функцій, тому вивчайте та ділитеся посиланнями на матеріали з однокласниками.
Визначення 1. Нехай Е- Безліч безліч. Якщо будь-яка околиця містить точки множини Е, відмінні від точки а, то аназивається граничною точкою множини Е.
Визначення 2. (Генріх Гейне (1821-1881)). Нехай функція  визначена на безлічі Хі
визначена на безлічі Хі  Аназивається межею
функції
Аназивається межею
функції  у точці
у точці  (або при
(або при  якщо для будь-якої послідовності значень аргументу
якщо для будь-якої послідовності значень аргументу  , що сходить до
, що сходить до 
 , відповідна послідовність значень функції сходить до А. Пишуть:
, відповідна послідовність значень функції сходить до А. Пишуть:  .
.
Приклади. 1) Функція  має межу, рівну з, у будь-якій точці числової прямої.
має межу, рівну з, у будь-якій точці числової прямої.
Дійсно, для будь-якої точки  та будь-якої послідовності значень аргументу
та будь-якої послідовності значень аргументу  , що сходить до
, що сходить до  і що складається з чисел, відмінних від
і що складається з чисел, відмінних від  , відповідна послідовність значень функції має вигляд
, відповідна послідовність значень функції має вигляд  , а ми знаємо, що ця послідовність сходиться до з. Тому
, а ми знаємо, що ця послідовність сходиться до з. Тому  .
.
2) Для функції 
 .
.
Це очевидно, тому що якщо  , то й
, то й  .
.
3) Функція Діріхле  не має межі в жодній точці.
не має межі в жодній точці.
Справді, нехай  і
і  , причому все
, причому все  - Раціональні числа. Тоді
- Раціональні числа. Тоді  для всіх nтому
для всіх nтому  . Якщо ж
. Якщо ж  і все
і все  - ірраціональні числа, то
- ірраціональні числа, то  для всіх nтому
для всіх nтому  . Ми бачимо, що умови визначення 2 не виконуються, тому
. Ми бачимо, що умови визначення 2 не виконуються, тому  немає.
немає.
4)
 .
.
Справді, візьмемо довільну послідовність  , що сходить до
, що сходить до
числу 2. Тоді . Що й потрібно було довести.
Визначення 3. (Коші (1789-1857)). Нехай функція  визначена на безлічі Хі
визначена на безлічі Хі  - Гранична точка цієї множини. Число Аназивається межею
функції
- Гранична точка цієї множини. Число Аназивається межею
функції  у точці
у точці  (або при
(або при  , якщо для будь-кого
, якщо для будь-кого  знайдеться
знайдеться  , таке, що для всіх значень аргументу х, що задовольняють нерівності
, таке, що для всіх значень аргументу х, що задовольняють нерівності
 ,
,
справедлива нерівність
 .
.
Пишуть:  .
.
Визначення Коші можна дати і за допомогою околиць, якщо помітити, що :
нехай функція  визначена на безлічі Хі
визначена на безлічі Хі  - Гранична точка цієї множини. Число Аназивається межею
функції
- Гранична точка цієї множини. Число Аназивається межею
функції  у точці
у точці  якщо для будь-якої
якщо для будь-якої  -околиці точки А
-околиці точки А  знайдеться проколота
знайдеться проколота  - околиця точки
- околиця точки 
 ,така, що
,така, що  .
.
Це визначення корисно проілюструвати малюнком.
приклад 5. .
.
Справді, візьмемо  довільно та знайдемо
довільно та знайдемо  , таке, що для всіх х, що задовольняють нерівності
, таке, що для всіх х, що задовольняють нерівності  виконується нерівність
виконується нерівність  . Остання нерівність рівнозначна нерівності
. Остання нерівність рівнозначна нерівності  тому бачимо, що достатньо взяти
тому бачимо, що достатньо взяти  . Твердження доведене.
. Твердження доведене.
Справедлива
Теорема 1. Визначення межі функції по Гейні та Коші еквівалентні.
Доказ. 1) Нехай  по Коші. Доведемо, що це число є межею і за Гейне.
по Коші. Доведемо, що це число є межею і за Гейне.
Візьмемо  довільно. Відповідно до визначення 3 існує
довільно. Відповідно до визначення 3 існує  , таке, що для всіх
, таке, що для всіх  виконується нерівність
виконується нерівність  . Нехай
. Нехай  - довільна послідовність така, що
- довільна послідовність така, що  при
при  . Тоді існує номер Nтакий, що для всіх
. Тоді існує номер Nтакий, що для всіх  виконується нерівність
виконується нерівність  тому
тому  для всіх
для всіх  , тобто.
, тобто. 
 по Гейні.
по Гейні.
2) Нехай тепер  по Гейні. Доведемо, що
по Гейні. Доведемо, що  і по Коші.
і по Коші.
Припустимо неприємне, тобто. що  по Коші. Тоді існує
по Коші. Тоді існує  таке, що для будь-кого
таке, що для будь-кого  знайдеться
знайдеться  ,
, і
і  . Розглянемо послідовність
. Розглянемо послідовність  . Для вказаного
. Для вказаного  та будь-якого nіснує
та будь-якого nіснує 
 і
і  . Це означає, що
. Це означає, що  хоча
хоча  , тобто. число Ане є межею
, тобто. число Ане є межею  у точці
у точці  по Гейні. Набули протиріччя, яке і доводить твердження. Теорему доведено.
по Гейні. Набули протиріччя, яке і доводить твердження. Теорему доведено.
Теорема 2 (про єдиність межі). Якщо існує межа функції у точці  , То він єдиний.
, То він єдиний.
Доказ. Якщо межа визначена по Гейне, його єдиність випливає з єдиності межі послідовності. Якщо межа визначена по Коші, його єдиність випливає з еквівалентності визначень межі по Коші і за Гейне. Теорему доведено.
Аналогічно критерію Коші для послідовностей має місце критерій Коші існування межі функції. Перш ніж його сформулювати, дамо
Визначення 4. Кажуть, що функція  задовольняє умові Коші у точці
задовольняє умові Коші у точці  , якщо для будь-кого
, якщо для будь-кого  існує
існує 
 , таких, що
, таких, що  і
і  , виконується нерівність
, виконується нерівність  .
.
Теорема 3 (критерій Коші існування межі). Для того, щоб функція  мала в точці
мала в точці  кінцева межа, необхідно і достатньо, щоб у цій точці функція задовольняла умові Коші.
кінцева межа, необхідно і достатньо, щоб у цій точці функція задовольняла умові Коші.
Доказ.Необхідність. Нехай  . Потрібно довести, що
. Потрібно довести, що  задовольняє у точці
задовольняє у точці  умові Коші.
умові Коші.
Візьмемо  довільно і покладемо
довільно і покладемо  . За визначенням межі для
. За визначенням межі для  існує
існує  , таке, що для будь-яких значень
, таке, що для будь-яких значень  , що задовольняють нерівності
, що задовольняють нерівності  і
і  , виконуються нерівності
, виконуються нерівності  і
і  . Тоді
. Тоді
Необхідність доведена.
Достатність. Нехай функція  задовольняє у точці
задовольняє у точці  умові Коші. Потрібно довести, що вона має в точці
умові Коші. Потрібно довести, що вона має в точці  кінцева межа.
кінцева межа.
Візьмемо  довільно. За визначенням 4 знайдеться
довільно. За визначенням 4 знайдеться  , таке, що з нерівностей
, таке, що з нерівностей  ,
, слід, що
слід, що  – це дано.
– це дано.
Покажемо спочатку, що для будь-якої послідовності  , що сходить до
, що сходить до  , послідовність
, послідовність  значень функції сходиться. Справді, якщо
значень функції сходиться. Справді, якщо  , то, з визначення межі послідовності, для заданого
, то, з визначення межі послідовності, для заданого  знайдеться номер N, такий, що для будь-яких
знайдеться номер N, такий, що для будь-яких 
 і
і  . Оскільки
. Оскільки  у точці
у точці  задовольняє умові Коші, маємо
задовольняє умові Коші, маємо  . Тоді за критерієм Коші для послідовностей послідовність
. Тоді за критерієм Коші для послідовностей послідовність  сходиться. Покажемо, що всі такі послідовності
сходиться. Покажемо, що всі такі послідовності  сходяться до однієї й тієї ж межі. Припустимо неприємне, тобто. що є послідовності
сходяться до однієї й тієї ж межі. Припустимо неприємне, тобто. що є послідовності  і
і  ,
, ,
, , такі, що. Розглянемо послідовність. Ясно, що вона сходить до
, такі, що. Розглянемо послідовність. Ясно, що вона сходить до  тому по доведеному вище послідовність сходиться, що неможливо, тому що підпослідовності
тому по доведеному вище послідовність сходиться, що неможливо, тому що підпослідовності  і
і  мають різні межі
мають різні межі  і
і  . Отримана суперечність показує, що
. Отримана суперечність показує, що  =
= . Тому за визначенням Гейне функція має у точці
. Тому за визначенням Гейне функція має у точці  кінцева межа. Достатність, отже і теорема, доведено.
кінцева межа. Достатність, отже і теорема, доведено.
Розглянемо функцію %%f(x)%%, визначену принаймні в деякому проколотом околиці %%\stackrel(\circ)(\text(U))(a)%% точки %%a \in \overline( \mathbb(R))%% розширеної числової прямої.
Поняття межі по Коші
Число %%A \in \mathbb(R)%% називають межею функції%%f(x)%% у точці %%a \in \mathbb(R)%% (або при %%x%%, що прагне до %%a \in \mathbb(R)%%), якщо, яке б не було позитивне число %%\varepsilon%%, знайдеться позитивне число %%\delta%%, таке, що для всіх точок проколотою %%\delta%%-околиці точки %%a%% значення функції належать %%varepsilon %%-околиці точки %%A%%, або
$$ A = \lim\limits_(x \to a)(f(x)) \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel(\circ)(\text (U))_\delta(a) \Rightarrow f(x) \in \text(U)_\varepsilon (A) \big) $$
Це визначення називається визначенням мовою %%varepsilon%% і %%delta%%, запропоноване французьким математиком Огюстеном Коші і використовується з початку XIX століття по теперішній час, оскільки має необхідну математичну строгість і точність.
Комбінуючи різні околиці точки %%a%% виду %%\stackrel(\circ)(\text(U))_\delta(a), \text(U)_\delta (\infty), \text(U) _\delta (-\infty), \text(U)_\delta (+\infty), \text(U)_\delta^+ (a), \text(U)_\delta^- (a) %% з околицями %%\text(U)_\varepsilon (A), \text(U)_\varepsilon (\infty), \text(U)_\varepsilon (+\infty), \text(U) _\varepsilon (-\infty)%%, отримаємо 24 визначення межі по Коші.
Геометричний зміст
Геометричний зміст межі функції
З'ясуємо, у чому полягає геометричний зміст межі функції у точці. Побудуємо графік функції %%y = f(x)%% і відзначимо на ньому точки %%x = a%% та %%y = A%%.
Межа функції %%y = f(x)%% у точці %%x \to a%% існує і дорівнює A, якщо для будь-якої %%\varepsilon%%-околиці точки %%A%% можна вказати таку %%\ delta%%-околиця точки %%a%%, що для будь-якого %%x%% з цієї %%\delta%%-околиці значення %%f(x)%% буде знаходитися в %%varepsilon%%-околиці точки %%A%%.
Зазначимо, що за визначенням межі функції по Коші для існування межі при %%x \to a%% не важливо, яке значення набуває функція в самій точці %%a%%. Можна навести приклади, коли функція не визначена при %%x = a%% або приймає значення, відмінне від %%A%%. Проте межа може дорівнювати %%A%%.
Визначення межі за Гейном
Елемент %%A \in \overline(\mathbb(R))%% називається межею функції %%f(x)%% при %% x \to a, a \in \overline(\mathbb(R))%% , якщо для будь-якої послідовності %%(x_n\) \to a%% з області визначення, послідовність відповідних значень %%\big\(f(x_n)\big\)%% прагне %%A%%.
Визначення межі по Гейне зручно використовувати, коли виникають сумніви щодо існування межі функції у цій точці. Якщо можна побудувати хоча б одну послідовність %%(x_n)%% з межею в точці %%a%% таку, що послідовність %%big(f(x_n)big)%% не має межі, то можна зробити висновок про те, що функція %%f(x)%% не має межі у цій точці. Якщо для двох різнихпослідовностей %%(x"_n\)%% і %%\(x""_n\)%%, що мають однаковиймежа %%a%%, послідовності %%big(f(x"_n)\big\)%% і %%big(f(x""_n)\big\)%% мають різнімежі, то цьому випадку також немає межа функції %%f(x)%%.
приклад
Нехай %%f(x) = \sin(1/x)%%. Перевіримо, чи існує межа цієї функції у точці %%a = 0%%.
Виберемо спочатку послідовність, що сходить до цієї точки, $$ \(x_n\) = \left\(\frac((-1)^n)(n\pi)\right\). $$
Ясно, що %% x_n \ne 0~\forall~n \in \mathbb(N)%% і %%\lim (x_n) = 0%%. Тоді %%f(x_n) = \sin(\left((-1)^n n\pi\right)) \equiv 0%% і %%\lim\big\(f(x_n)\big\) = 0 %%.
Потім візьмемо послідовність, що сходить до тієї ж точки $$ x"_n = \left\( \frac(2)((4n + 1)\pi) \right\), $$
для якої %%\lim(x"_n) = +0%%, %%f(x"_n) = \sin(\big((4n + 1)\pi/2\big)) \equiv 1%% і %%\lim\big\(f(x"_n)\big\) = 1%%. Аналогічно для послідовності $$ x""_n = \left\(-\frac(2)((4n + 1) \pi) \right\), $$
також сходить до точки %%x = 0%%, %%limbig(f(x""_n)big) = -1%%.
Усі три послідовності дали різні результати, що суперечить умові визначення Гейне, тобто. дана функція не має межі в точці %%x = 0%%.
Теорема
Визначення межі по Коші та по Гейні еквівалентні.
Межі завдають всім студентам, які вивчають математику, чимало клопоту. Щоб вирішити межу, часом доводиться застосовувати масу хитрощів і вибирати з багатьох способів розв'язання саме той, який підійде для конкретного прикладу.
У цій статті ми не допоможемо вам зрозуміти межі своїх можливостей чи осягнути межі контролю, але постараємося відповісти на запитання: як зрозуміти межі у вищій математиці? Розуміння приходить з досвідом, тому зараз наведемо кілька докладних прикладів вирішення меж з поясненнями.
Поняття межі математики
Перше питання: що це взагалі за межу та межу чого? Можна говорити про межі числових послідовностей та функцій. Нас цікавить поняття межі функції, оскільки саме з ними найчастіше стикаються студенти. Але спочатку - загальне визначення межі:
Припустимо, є певна змінна величина. Якщо ця величина у процесі зміни необмежено наближається до певного числа a , то a - Межа цієї величини.
Для певної в інтервалі функції f(x)=y межею називається таке число A , якого прагне функція при х , що прагне до певної точки а . Крапка а належить інтервалу, у якому визначено функція.
Звучить громіздко, але записується дуже просто:
Lim- від англійської limit- Межа.
Існує також геометричне пояснення визначення межі, але тут ми не лізтимемо в теорію, оскільки нас більше цікавить практична, ніж теоретична сторона питання. Коли ми говоримо, що х прагне якогось значення, це означає, що змінна не приймає значення числа, але нескінченно близько до нього наближається.
Наведемо конкретний приклад. Завдання – знайти межу.

Щоб вирішити такий приклад, підставимо значення x=3 у функцію. Отримаємо:

До речі, якщо Вас цікавлять читайте окрему статтю на цю тему.
У прикладах х може прагнути будь-якого значення. Це може бути будь-яке число чи нескінченність. Ось приклад, коли х прагне нескінченності:

Інтуїтивно зрозуміло, що чим більше число у знаменнику, тим менше значення прийматиме функція. Так, за необмеженого зростання х значення 1/х буде зменшуватись і наближатися до нуля.
Як бачимо, щоб вирішити межу, потрібно просто підставити на функцію значення, якого прагнути х . Однак це найпростіший випадок. Часто перебування межі негаразд очевидне. У межах зустрічаються невизначеності типу 0/0 або нескінченність/нескінченність . Що робити у таких випадках? Вдаватися до хитрощів!

Невизначеності в межах
Невизначеність виду нескінченність/нескінченність
Нехай є межа:

Якщо спробуємо у функцію підставити нескінченність, то отримаємо нескінченність як і чисельнику, і у знаменнику. Взагалі варто сказати, що у вирішенні таких невизначеностей є певний елемент мистецтва: треба помітити, як можна перетворити функцію в такий спосіб, щоб невизначеність пішла. У нашому випадку розділимо чисельник і знаменник на х у старшому ступені. Що вийде?

З уже розглянутого вище прикладу ми знаємо, що члени, які містять у знаменнику х, прагнутимуть нуля. Тоді рішення межі:

Для розкриття невизначеностей типу нескінченність/нескінченністьділимо чисельник і знаменник на хнайвищою мірою.

До речі! Для наших читачів зараз діє знижка 10% на
Ще один вид невизначеностей: 0/0

Як завжди, підстановка у функцію значення х=-1 дає 0 у чисельнику та знаменнику. Подивіться трохи уважніше і Ви помітите, що у чисельнику у нас квадратне рівняння. Знайдемо коріння та запишемо:

Скоротимо та отримаємо:

Отже, якщо ви стикаєтеся з невизначеністю типу 0/0 - Розкладайте чисельник і знаменник на множники.
Щоб Вам було простіше вирішувати приклади, наведемо таблицю за межами деяких функцій:

Правило Лопіталя в межах
Ще один потужний спосіб дозволяє усунути невизначеності обох типів. У чому полягає суть методу?
Якщо межі є невизначеність, беремо похідну від чисельника і знаменника до того часу, поки невизначеність не зникне.
Наочно правило Лопіталя виглядає так:

Важливий момент : межа, в якій замість чисельника та знаменника стоять похідні від чисельника та знаменника, має існувати.
А тепер – реальний приклад:

В наявності типова невизначеність 0/0 . Візьмемо похідні від чисельника та знаменника:

Вуаля, невизначеність усунена швидко та елегантно.
Сподіваємося, що Ви зможете з користю застосувати цю інформацію на практиці та знайти відповідь на питання "як вирішувати межі у вищій математиці". Якщо потрібно визначити межу послідовності або межу функції в точці, а часу на цю роботу немає від слова «зовсім», зверніться до професійного студентського сервісу за швидким і докладним рішенням.
Сьогодні на уроці ми розберемо суворе визначення послідовностіі суворе визначення межі функції, а також навчимося вирішувати відповідні завдання теоретичного характеру. Стаття призначена, перш за все, для студентів 1-го курсу природничо-технічних спеціальностей, які почали вивчати теорію математичного аналізу, і зіткнулися з труднощами в плані розуміння цього розділу вищої математики. Крім того, матеріал цілком доступний і учням старших класів.
За роки існування сайту я отримав недобрий десяток листів приблизно такого змісту: "Погано розумію математичний аналіз, що робити?", "Зовсім не розумію матан, думаю кинути навчання" і т.п. Саме матан часто проріджує студентську групу після першої ж сесії. Чому так справи? Тому що предмет неймовірно складний? Зовсім ні! Теорія математичного аналізу не така важка, скільки своєрідна. І її потрібно прийняти і полюбити такою, якою вона є =)
Почнемо з найважчого випадку. Перше та головне – не треба кидати навчання. Зрозумійте правильно, кинути, воно завжди встигнеться;-) Безумовно, якщо через рік-два від обраної спеціальності нудитиме, тоді так – слід задуматися (А не пороти гарячку!)про зміну діяльності. Але поки що варто продовжити. І, будь ласка, забудьте фразу «Нічого не розумію» – так не буває, щоб ЗОВСІМ нічого не розуміти.
Що робити, якщо з теорією погано? Це, до речі, стосується як математичного аналізу. Якщо з теорією погано, то спочатку потрібно СЕРЙОЗНО налягти на практику. При цьому вирішуються одразу два стратегічні завдання:
- По-перше, значна частка теоретичних знань з'явилася завдяки практиці. І тому багато людей розуміють теорію через… – вірно! Ні-ні, ви не про те подумали =)
– І, по-друге, практичні навички з великою ймовірністю «витягнуть» вас на іспиті, навіть якщо… але не будемо так налаштовуватися! Все реально і все реально підняти в досить короткі терміни. Математичний аналіз – це мій улюблений розділ вищої математики, і тому я просто не міг не простягнути вам ноги руку допомоги:
На початку 1-го семестру зазвичай проходять межі послідовностей та межі функцій. Чи не розумієте, що це таке і не знаєте, як їх вирішувати? Почніть зі статті Межі функцій, у якій «на пальцях» розглянуто саме поняття та розібрано найпростіші приклади. Далі опрацюйте інші уроки на тему, у тому числі урок про межах послідовностей, На якому я фактично вже сформулював суворе визначення.
Які значки, крім знаків нерівностей і модуля, ви знаєте?
- Довга вертикальна палиця читається так: "таке, що", "така, що", "такий, що" або "такі, що", у нашому випадку, очевидно, йдеться про номер – тому «такий, що»;
– для всіх «ен», більших за ;
– знак модуля означає відстань, тобто. цей запис повідомляє нам про те, що відстань між значеннями менша за епсілон.
Ну як, вбивчо складно? =)
Після освоєння практики чекаю на вас у наступному параграфі:
І справді, трохи поміркуємо – як сформулювати суворе визначення послідовності? …Перше, що спадає на думку у світлі практичного заняття: «межа послідовності – це число, якого нескінченно близько наближаються члени послідовності».
Добре, розпишемо послідовність :
Неважко вловити, що підпослідовність ![]() нескінченно близько наближаються до –1, а члени з парними номерами
нескінченно близько наближаються до –1, а члени з парними номерами ![]() - До «одиниці».
- До «одиниці».
А може бути межі дві? Але тоді чому якась послідовність їх не може мати десять чи двадцять? Так можна зайти далеко. У зв'язку з цим логічно вважати, що якщо у послідовності існує межа, то вона єдина.
Примітка : у послідовності немає межі, проте з неї можна виділити дві підпослідовності (див. вище), у кожної з яких існує своя межа.
Таким чином, висловлене вище визначення виявляється неспроможним. Так, воно працює для випадків на кшталт (Чим я не зовсім коректно користувався у спрощених поясненнях практичних прикладів), Але тепер нам необхідно знайти суворе визначення.
Спроба друга: «межа послідовності - це число, до якого наближаються ВСІ члени послідовності, за винятком, хіба що їх кінцевогокількості». Це вже ближче до істини, але все одно не зовсім точно. Так, наприклад, у послідовності ![]() половина членів зовсім не наближається до нуля - вони йому просто рівні =) До речі, «мигалка» взагалі приймає два фіксованих значення.
половина членів зовсім не наближається до нуля - вони йому просто рівні =) До речі, «мигалка» взагалі приймає два фіксованих значення.
Формулювання неважко уточнити, але тоді виникає інше питання: як записати визначення у математичних знаках? Науковий світ довго бився над цією проблемою, доки ситуацію не вирішив відомий маестроякий, по суті, і оформив класичний матаналіз у всій його строгості. Коші запропонував оперувати околицями чим значно просунув теорію.
Розглянемо деяку точку та її довільну-околиця:
Значення «епсілон» завжди позитивне, і, більше того, ми маємо право вибрати його самостійно. Припустимо, що в околиці знаходиться безліч членів (Не обов'язково все)деякої послідовності. Як записати той факт, що, наприклад, десятий член потрапив в околицю? Нехай він знаходиться у правій її частині. Тоді відстань між точками і повинна бути меншою за «епсілон»: . Однак якщо «ікс десяте» розташоване ліворуч від точки «а», то різниця буде негативна, і тому до неї потрібно додати знак модуля: .
Визначення: число називається межею послідовності, якщо для будь-якоїйого околиці (заздалегідь обраною)існує натуральний номер - ТАКИЙ, що ВСЕчлени послідовності з більшими номерами виявляться всередині околиці:
Або коротше: якщо
Іншими словами, яке б мале значення «епсілон» ми не взяли, рано чи пізно «нескінченний хвіст» послідовності ПОВНІСТТЮ опиниться в цій околиці.
Так, наприклад, "нескінченний хвіст" послідовності ПОВНІСТТЮ зайде в будь-яку скільки завгодно малу - околицю точки. Таким чином, це значення є межею послідовності визначення. Нагадую, що послідовність, межа якої дорівнює нулю, називають нескінченно малою.
Слід зазначити, що з послідовності не можна сказати «нескінченний хвіст зайде» – члени з непарними номерами за фактом дорівнюють нулю і «нікуди не заходять» =) Саме тому у визначенні використано дієслово «виявляться». І, зрозуміло, члени такої послідовності, як також «нікуди не йдуть». До речі, перевірте, чи буде її числом межею.
Тепер покажемо, що послідовність не має межі. Розглянемо, наприклад, околицю точки. Цілком зрозуміло, що немає такого номера, після якого всі члени опиняться в даній околиці – непарні члени завжди «вискакуватимуть» до «мінус одиниці». З аналогічної причини немає межі й у точці.
Закріпимо матеріал практикою:
Приклад 1
Довести, що межа послідовності дорівнює нулю. Вказати номер, після якого, всі члени послідовності гарантовано виявляться всередині будь-якої скільки завгодно малої околиці точки.
Примітка : у багатьох послідовностей шуканий натуральний номер залежить від значення - звідси і позначення.
Рішення: розглянемо довільну чи знайдетьсяномер – такий, що ВСІ члени з більшими номерами виявляться всередині цієї околиці:
Щоб показати існування шуканого номера, виразимо через.
Так як за будь-якого значення «ен» , то знак модуля можна прибрати:
Використовуємо «шкільні» дії з нерівностями, які я повторював під час уроків Лінійні нерівностіі Область визначення функції. При цьому важливою обставиною є те, що «епсілон» та «ен» позитивні:
Оскільки зліва йдеться про натуральні номери, а права частина в загальному випадку дробова, то її потрібно округлити:
Примітка : іноді для перестрахування праворуч додають одиницю, але насправді це надмірність. Умовно кажучи, якщо і ми послабимо результат округленням у менший бік, то найближчий відповідний номер («трійка») все одно задовольнятиме початкову нерівність.
А тепер дивимося на нерівність та згадуємо, що спочатку ми розглядали довільну-околиця, тобто. «епсілон» може бути рівним будь-комупозитивного числа.
Висновок: для будь-якої малої -околиці точки знайшлося значення ![]()
![]() . Таким чином, число є межею послідовності визначення. Що й потрібно було довести.
. Таким чином, число є межею послідовності визначення. Що й потрібно було довести.
До речі, з отриманого результату ![]() добре проглядається природна закономірність: що менше -околиця – то більше вписувалося номер , після якого ВСІ члени послідовності опиняться у цій околиці. Але яким би малим не було «епсілон» – усередині завжди буде «нескінченний хвіст», а зовні – хай навіть велике, проте кінцевеЧисло членів.
добре проглядається природна закономірність: що менше -околиця – то більше вписувалося номер , після якого ВСІ члени послідовності опиняться у цій околиці. Але яким би малим не було «епсілон» – усередині завжди буде «нескінченний хвіст», а зовні – хай навіть велике, проте кінцевеЧисло членів.
Як враження? =) Згоден, що дивно. Але ж суворо!Будь ласка, перечитайте та осмисліть все ще раз.
Розглянемо аналогічний приклад та познайомимося з іншими технічними прийомами:
Приклад 2
![]()
Рішення: за визначенням послідовності потрібно довести, що (Промовляємо вголос!).
Розглянемо довільну-околиця точки і перевіримо, чи існуєнатуральний номер – такий, що для всіх великих номерів виконано нерівність: 
Щоб показати існування такого, потрібно висловити "ен" через "епсілон". Спрощуємо вираз під знаком модуля: 
Модуль знищує знак "мінус": ![]()
Знаменник позитивний за будь-якого «ен», отже, палиці можна прибрати:
Перетасування: 
Тепер треба б витягти квадратний корінь, але проблема полягає в тому, що при деяких «епсілон» права частина буде негативною. Щоб уникнути цієї неприємності посилимонерівність модулем: ![]()
Чому можна так зробити? Якщо, умовно кажучи, виявиться, що , то буде виконано і умова . Модуль може тільки збільшитиномер, що розшукується, і це нас теж влаштує! Грубо кажучи, якщо підходить сотий, то підійде і двохсот! Відповідно до визначення, потрібно показати сам факт існування номера(хоча якогось), після якого всі члени послідовності опиняться в околиці. До речі, саме тому нам не страшне фінальне округлення правої частини в більшу сторону.
Вилучаємо корінь: 
І округляємо результат: 
Висновок: т.к. значення «епсілон» вибиралося довільно, то для будь-якої скільки завгодно малої околиці точки знайшлося значення  , таке, що для всіх великих номерів виконано нерівність
, таке, що для всіх великих номерів виконано нерівність  . Таким чином,
. Таким чином, ![]() за визначенням. Що й потрібно було довести.
за визначенням. Що й потрібно було довести.
Раджу особливоРозібратися у посиленні та ослабленні нерівностей – це типові та дуже поширені прийоми математичного аналізу. Єдине, слід стежити за коректністю тієї чи іншої дії. Так, наприклад, нерівність ![]() ні в якому разі не можна послаблювати, віднімаючи, скажімо, одиницю:
ні в якому разі не можна послаблювати, віднімаючи, скажімо, одиницю: ![]()
Знову ж умовно: якщо номер точно підійде, попередній може вже й не підійти.
Наступний приклад для самостійного вирішення:
Приклад 3
Використовуючи визначення послідовності, довести, що ![]()
Коротке рішення та відповідь наприкінці уроку.
Якщо послідовність нескінченно великато визначення межі формулюється схожим чином: точка називається межею послідовності, якщо для будь-якого, скільки завгодно великогочисла існує номер , такий, що для всіх більших номерів буде виконано нерівність . Число називають околицею точки «плюс нескінченність»:
Іншими словами, яке б велике значення ми не взяли, «нескінченний хвіст» послідовності обов'язково зайде в околицю точки, залишивши зліва лише кінцеве число членів.
Черговий приклад:
І скорочений запис: якщо
Для випадку запишіть визначення самостійно. Правильна версія наприкінці уроку.
Після того, як ви набили руку на практичних прикладах і розібралися з визначенням межі послідовності, можна звернутися до літератури з математичного аналізу та/або свого зошита з лекціями. Рекомендую закачати 1-й том Бохана (простіше – для заочників)та Фіхтенгольця (Детальніше і докладніше). З інших авторів раджу Піскунова, курс якого орієнтований на технічні вузи.
Спробуйте сумлінно вивчити теореми, що стосуються межі послідовності, їх доказів, наслідків. Спочатку теорія може здаватися "каламутною", але це нормально - просто потрібно звикнути. І багато хто навіть увійдуть у смак!
Суворе визначення межі функції
Почнемо з того самого – як сформулювати це поняття? Словесне визначення межі функції формулюється значно простіше: «число є межею функції , якщо при «ікс», що прагне (І зліва, і праворуч), відповідні значення функції прагнуть до » (Див. креслення). Все начебто нормально, але словами словами, сенс змістом, значок значком, а строгих математичних позначень замало. І в другому параграфі ми познайомимося із двома підходами до вирішення цього питання.
Нехай функція визначена на деякому проміжку, за винятком, можливо, точки . У навчальній літературі вважають, що функція там невизначено: 
Такий вибір наголошує суть межі функції: «ікс» нескінченно близьконаближається до , і відповідні значення функції – нескінченно близькодо. Іншими словами, поняття межі має на увазі не «точний захід» у крапки, а саме нескінченно близьке наближення, при цьому не важливо – чи визначено функцію в точці чи ні.
Перше визначення межі функції, що не дивно, формулюється за допомогою двох послідовностей. По-перше, поняття споріднені, і, по-друге, межі функцій зазвичай вивчають після меж послідовностей.
Розглянемо послідовність ![]() точок (на кресленні відсутні), що належать проміжку та відмінних від, яка сходитьсядо. Тоді відповідні значення функції також утворюють числову послідовність, члени якої розташовуються на осі ординат.
точок (на кресленні відсутні), що належать проміжку та відмінних від, яка сходитьсядо. Тоді відповідні значення функції також утворюють числову послідовність, члени якої розташовуються на осі ординат.
Межа функції по Гейні для будь-якоїпослідовності точок ![]() (належних та відмінних від ), яка сходить до точки , відповідна послідовність значень функції сходить до .
(належних та відмінних від ), яка сходить до точки , відповідна послідовність значень функції сходить до .
Едуард Гейне – німецький математик. …І не треба тут нічого такого думати, гей у Європі лише один – це Гей-Люссак =)
Друге визначення межі спорудив… так-так, ви маєте рацію. Але спочатку розберемося у його конструкції. Розглянемо довільну околицю точки («чорна» околиця). За мотивами попереднього параграфа запис означає, що деяке значенняФункція знаходиться всередині «епсілон»-околиці.
Тепер знайдемо -околиця, яка відповідає заданій -околиці (подумки проводимо чорні пунктирні лінії зліва направо і потім зверху донизу). Зверніть увагу, що значення вибирається по довжині меншого відрізка, у разі – по довжині більш короткого лівого відрізка. Більш того, «малинову» -окраїну точки можна навіть зменшити, оскільки в наступному визначенні важливий сам факт існуванняцієї околиці. І, аналогічно, запис означає, що деяке значення знаходиться всередині «дельта»-околиці.
Межа функції по Коші: число називається межею функції у точці , якщо для будь-якої заздалегідь обраноюоколиці (як завгодно малої), існує-околиця точки, ТАКА, що: ЯК ТІЛЬКИ значення (належні)входять у цю околицю: (червоні стрілки)- ТАК ВІДРАЗУ відповідні значення функції гарантовано зайдуть в околицю: (сині стрілки).
Повинен попередити, що з метою більшої зрозумілості я трохи симпровізував, тому не зловживайте =)
Короткий запис: якщо
У чому суть визначення? Образно кажучи, нескінченно зменшуючи околиця, ми «супроводжуємо» значення функції до своєї межі, не залишаючи їм альтернативи наближатися кудись ще. Досить незвично, але знову ж таки суворо! Щоб як слід перейнятися ідеєю, перечитайте формулювання ще раз.
! Увага: якщо вам потрібно сформулювати тільки визначення по Гейніабо тільки визначення по Коші, будь ласка, не забувайте про суттєвомупопередньому коментарі: "Розглянемо функцію , яка визначена на деякому проміжку за винятком, можливо, точки". Я позначив це одного разу на самому початку і щоразу не повторював.
Відповідно до відповідної теореми математичного аналізу, визначення по Гейні та Коші еквівалентні, проте найбільш відомий другий варіант (ще б пак!), який також називають «кордон на мові»:
Приклад 4
Використовуючи визначення межі, довести, що ![]()
Рішення: функція визначена на всій числовій прямій крім точки. Використовуючи визначення , доведемо існування межі у цій точці.
Примітка : величина «дельта»-околиці залежить від «епсілон», звідси і позначення
Розглянемо довільну-околиця. Завдання полягає в тому, щоб за цим значенням перевірити, чи існує-околиця, ТАКА, що з нерівності ![]() слідує нерівність
слідує нерівність  .
.
Припускаючи, що , перетворимо останню нерівність: ![]() (розклали квадратний тричлен)
(розклали квадратний тричлен)

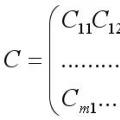 Позначення елементів матриці
Позначення елементів матриці Метод крамаря розв'язання систем лінійних рівнянь
Метод крамаря розв'язання систем лінійних рівнянь Війна в ліжках - Це фейк чи правда
Війна в ліжках - Це фейк чи правда