Площа трикутника теорема піфагору. Різні способи доказу теореми Піфагора: приклади, опис та відгуки
Коли ви тільки починали вивчати квадратне коріння та способи вирішення ірраціональних рівнянь(рівностей, що містять невідому під знаком кореня), ви, ймовірно, отримали перше уявлення про їх практичному використанні. Вміння отримувати квадратний коріньз чисел також необхідно вирішення завдань застосування теореми Піфагора. Ця теорема пов'язує довжини сторін будь-якого прямокутного трикутника.
Нехай довжини катетів прямокутного трикутника (тих двох сторін, які сходяться під прямим кутом) будуть позначені літерами і , а довжина гіпотенузи (найдовшої сторони трикутника, розташованої навпроти прямого кута) буде позначена літерою . Тоді відповідні довжини пов'язані наступним співвідношенням:
Дане рівняння дозволяє знайти довжину сторони прямокутного трикутника у тому випадку, коли відома довжина двох інших сторін. Крім того, воно дозволяє визначити, чи є трикутник, що розглядається, прямокутним, за умови, що довжини всіх трьох сторіннаперед відомі.
Розв'язання задач з використанням теореми Піфагора
Для закріплення матеріалу вирішимо такі завдання застосування теореми Піфагора.

Отже, дано:
- Довжина одного з катетів дорівнює 48, гіпотенузи - 80.
- Довжина катета дорівнює 84, гіпотенузи - 91.
Приступимо до вирішення:
a) Підстановка даних у наведене вище рівняння дає такі результати:
48 2 + b 2 = 80 2
2304 + b 2 = 6400
b 2 = 4096
b= 64 або b = -64
Оскільки довжина сторони трикутника не може бути виражена негативним числом, другий варіант автоматично відкидається.
Відповідь до першого малюнку: b = 64.
b) Довжина катета другого трикутника знаходиться тим самим способом:
84 2 + b 2 = 91 2
7056 + b 2 = 8281
b 2 = 1225
b= 35 або b = -35
Як і попередньому випадку, негативне рішення відкидається.
Відповідь до другого малюнку: b = 35

Нам дано:
- Довжини менших сторін трикутника дорівнюють 45 і 55 відповідно, більшій – 75.
- Довжини менших сторін трикутника дорівнюють 28 і 45 відповідно, більшій – 53.
Вирішуємо завдання:
a) Необхідно перевірити, чи дорівнює сума квадратів довжин менших сторін даного трикутника квадрату довжини більшої:
45 2 + 55 2 = 2025 + 3025 = 5050
Отже, перший трикутник не прямокутний.
b) Виконується та сама операція:
28 2 + 45 2 = 784 + 2025 = 2809
Отже, другий трикутник прямокутний.
Спочатку знайдемо довжину найбільшого відрізка, утвореного точками з координатами (-2, -3) та (5, -2). Для цього використовуємо відому формулудля знаходження відстані між точками в прямокутної системикоординат:
Аналогічно знаходимо довжину відрізка, укладеного між точками з координатами (-2, -3) та (2, 1):
Нарешті, визначаємо довжину відрізка між точками з координатами (2, 1) та (5, -2):
Оскільки має місце рівність:
то відповідний трикутник прямокутний.
Таким чином, можна сформулювати відповідь до завдання: оскільки сума квадратів сторін з найменшою довжиною дорівнює квадрату сторони найбільшою довжиноюкрапки є вершинами прямокутного трикутника.
Основа (розташована строго горизонтально), косяк (розташований строго вертикально) і трос (протягнутий по діагоналі) формують прямокутний трикутник, відповідно, для знаходження довжини троса може використовуватися теорема Піфагора:
Таким чином, довжина троса складатиме приблизно 3,6 метра.
Дано: відстань від точки R до точки P (катет трикутника) дорівнює 24, від точки R до точки Q (гіпотенуза) – 26.
Отже, допомагаємо Віте вирішити завдання. Оскільки сторони трикутника, зображеного на малюнку, імовірно утворюють прямокутний трикутник, для знаходження довжини третьої сторони можна використовувати теорему Піфагора:
Отже, ширина ставка становить 10 метрів.
Сергій Валерійович
теорема Піфагора
теорема Піфагора- Одна з основних теорем евклідової геометрії, що встановлює співвідношення
між сторонами прямокутного трикутника.
Вважається, що доведено грецьким математиком Піфагором, на честь якого названо.
Геометричне формулювання теореми Піфагора.
Спочатку теорема була сформульована наступним чином:
У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів,
побудованих на катетах.
Алгебраїчне формулювання теореми Піфагора.
У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.
Тобто, позначивши довжину гіпотенузи трикутника через c, а довжини катетів через aі b:
Обидві формулювання теореми Піфагораеквівалентні, але друге формулювання більш елементарне, воно не
потребує поняття площі. Тобто друге твердження можна перевірити, нічого не знаючи про площу та
вимірявши тільки довжини сторін прямокутного трикутника.
Зворотний теорема Піфагора.
Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, то
трикутник прямокутний.
Або, іншими словами:
Для будь-якої трійки позитивних чисел a, bі c, такий, що
існує прямокутний трикутник із катетами aі bта гіпотенузою c.
Теорема Піфагора для рівнобедреного трикутника.

Теорема Піфагор для рівностороннього трикутника.

Докази теореми Піфагора.
На даний момент у науковій літературі зафіксовано 367 доказів цієї теореми. Ймовірно, теорема
Піфагора є єдиною теоремою з настільки значним числом доказів. Таке різноманіття
можна пояснити лише фундаментальним значенням теореми для геометрії.
Зрозуміло, концептуально їх можна розбити на малу кількість класів. Найвідоміші з них:
докази методом площ, аксіоматичніі екзотичні докази(наприклад,
за допомогою диференціальних рівнянь).
1. Доказ теореми Піфагора через трикутники.
Наступний доказ алгебраїчного формулювання - найпростіший з доказів, що будуються
безпосередньо з аксіом. Зокрема воно не використовує поняття площі фігури.
Нехай ABCє прямокутний трикутник із прямим кутом C. Проведемо висоту з Cі позначимо
її заснування через H.
Трикутник ACHподібний до трикутника ABЗ двома кутами. Аналогічно трикутник CBHподібний ABC.
Ввівши позначення:

отримуємо:
![]() ,
,
що відповідає -
Склавши a 2 та b 2, отримуємо:
або , що потрібно було довести.
2. Підтвердження теореми Піфагора шляхом площ.
Нижче наведені докази, незважаючи на їхню простоту, зовсім не такі прості. Всі вони
використовують властивості площі, докази яких складніші за доказ самої теореми Піфагора.
- Доказ через рівнодоповнюваність.
 Розташуємо чотири рівні прямокутні
Розташуємо чотири рівні прямокутні
трикутника так, як показано на малюнку
праворуч.
Чотирикутник зі сторонами c- Квадратом,
оскільки сума двох гострих кутів 90°, а
розгорнутий кут - 180 °.
Площа всієї фігури дорівнює, з одного боку,
площі квадрата зі стороною ( a+b), а з іншого боку, сумі площ чотирьох трикутниківі
![]()
![]()
Що і потрібно було довести.
3. Доказ теореми Піфагора методом нескінченно малих.

Розглядаючи креслення, показане на малюнку, і
спостерігаючи зміну сторониa, ми можемо
записати наступне співвідношення для нескінченно
малих прирощень сторінзі a(використовуючи подобу
трикутників):
Використовуючи метод поділу змінних, знаходимо:
Більш загальний вираз зміни гіпотенузи у разі прирощень обох катетів:
Інтегруючи дане рівняннята використовуючи початкові умови, отримуємо:
Таким чином, ми приходимо до бажаної відповіді:
Як неважко бачити, квадратична залежність у остаточній формулі з'являється завдяки лінійній
пропорційності між сторонами трикутника та прирощеннями, тоді як сума пов'язана з незалежними
вкладами від збільшення різних катетів.
Простіший доказ можна отримати, якщо вважати, що один з катетів не відчуває збільшення
(у даному випадкукатет b). Тоді для константи інтегрування отримаємо:
(згідно з папірусом 6619 Берлінського музею). На думку Кантора, гарпедонапти, або натягувачі мотузок, будували прямі кути за допомогою прямокутних трикутників зі сторонами 3, 4 і 5.
Дуже легко можна відтворити їхній спосіб побудови. Візьмемо мотузку довжиною в 12 м і прив'яжемо до неї кольоровою смужкою на відстані 3 м від одного кінця і 4 метри від іншого. Прямий кут виявиться ув'язненим між сторонами завдовжки 3 і 4 метри. Гарпедонаптам можна було б заперечити, що їхній спосіб побудови стає зайвим, якщо скористатися, наприклад, дерев'яним косинцем, що застосовується всіма теслярами. І справді, відомі єгипетські малюнки, у яких зустрічається такий інструмент, - наприклад, малюнки, що зображують столярну майстерню.
Дещо більше відомо про теорему Піфагора у вавилонян. В одному тексті, що відноситься до часу Хаммурапі, тобто до 2000 до н. е. наводиться наближене обчислення гіпотенузи прямокутного трикутника. Звідси можна дійти невтішного висновку, що у Дворіччя вміли робити обчислення з прямокутними трикутниками, по крайнього заходу у деяких випадках. Грунтуючись, з одного боку, на сьогоднішньому рівні знань про єгипетську та вавілонську математику, а з іншого - на критичному вивченні грецьких джерел, Ван-дер-Варден (голландський математик) зробив висновок про велику ймовірність того, що теорема про квадрат гіпотенузи була відома в Індії близько XVIII століття до зв. е.
Приблизно 400 р. до зв. е., згідно з Проклом, Платон дав метод знаходження піфагорових трійок, що поєднує алгебру та геометрію. Приблизно 300 р. до зв. е. у «Початках» Евкліда з'явився найстаріший аксіоматичний доказ теореми Піфагора.
Формулювання
Геометричне формулювання:
Спочатку теорема була сформульована наступним чином:
Алгебраїчне формулювання:
Тобто, позначивши довжину гіпотенузи трикутника через , а довжини катетів через і :
Обидві формулювання теореми еквівалентні, але друге формулювання більш елементарне, вона вимагає поняття площі . Тобто друге твердження можна перевірити, нічого не знаючи про площу та вимірявши лише довжини сторін прямокутного трикутника.
Зворотня теорема Піфагора:
Докази
На даний момент у науковій літературі зафіксовано 367 доказів цієї теореми. Ймовірно, теорема Піфагора є єдиною теоремою з настільки значним числом доказів. Таке різноманіття можна пояснити лише фундаментальним значенням теореми для геометрії.
Зрозуміло, концептуально їх можна розбити на малу кількість класів. Найвідоміші з них: докази методом площ, аксіоматичні та екзотичні докази (наприклад, за допомогою диференціальних рівнянь).
Через подібні трикутники
Наступний доказ алгебраїчної формулювання - найпростіший з доказів, що будуються безпосередньо з аксіом. Зокрема, воно не використовує поняття площі фігури.

Нехай ABCє прямокутний трикутник із прямим кутом C. Проведемо висоту з Cі позначимо її основу через H. Трикутник ACHподібний до трикутника ABCпо двох кутах. Аналогічно трикутник CBHподібний ABC. Ввівши позначення
отримуємо
Що еквівалентно
Склавши, отримуємо
, що і потрібно було довестиДокази методом площ
Нижче наведені докази, незважаючи на їхню простоту, зовсім не такі прості. Всі вони використовують властивості площі, докази яких складніші за доказ самої теореми Піфагора.
Доказ через рівнодоповнюваність
- Розташуємо чотири рівні прямокутні трикутники так, як показано на малюнку 1.
- Чотирикутник зі сторонами cє квадратом, оскільки сума двох гострих кутів 90 °, а розгорнутий кут - 180 °.
- Площа всієї фігури дорівнює, з одного боку, площі квадрата зі стороною (a+b), з другого боку, сумі площ чотирьох трикутників і площі внутрішнього квадрата.
Що і потрібно було довести.
Доказ Евкліда
Ідея доказу Евкліда полягає в наступному: спробуємо довести, що половина площі квадрата, побудованого на гіпотенузі, дорівнює сумі половин площ квадратів, побудованих на катетах, а тоді площі великого і двох малих квадратів рівні.
Розглянемо креслення зліва. На ньому ми побудували квадрати на сторонах прямокутного трикутника і провели з вершини прямого кута С промінь перпендикулярно до гіпотенузи AB, він розсікає квадрат ABIK, побудований на гіпотенузі, на два прямокутники - BHJI і HAKJ відповідно. Виявляється, що площі даних прямокутників точно рівні площам квадратів, побудованих на відповідних катетах.
Спробуємо довести, що площа квадрата DECA дорівнює площі прямокутника AHJK Для цього скористаємося допоміжним спостереженням: Площа трикутника з тією самою висотою та основою, що й даний прямокутник дорівнює половині площі заданого прямокутника. Це наслідок визначення площі трикутника як половини добутку основи висоту. З цього спостереження випливає, що площа трикутника ACK дорівнює площі трикутника AHK (не зображеного на малюнку), яка, у свою чергу, дорівнює половині площі прямокутника AHJK.
Доведемо тепер, що площа трикутника ACK також дорівнює половині площі квадрата DECA. Єдине, що необхідно для цього зробити, - це довести рівність трикутників ACK і BDA (оскільки площа трикутника BDA дорівнює половині площі квадрата за вказаною вище властивістю). Рівність ця очевидна: трикутники рівні з обох боків і розі між ними. Саме - AB=AK, AD=AC - рівність кутів CAK і BAD легко довести методом руху: повернемо трикутник CAK на 90° проти годинникової стрілки, тоді очевидно, що відповідні сторони двох трикутників, що розглядаються, співпадуть (через кут при вершині квадрата - 90 °).
Міркування про рівність площ квадрата BCFG і прямокутника BHJI абсолютно аналогічне.
Тим самим було доведено, що площа квадрата, побудованого на гіпотенузі, складається з площ квадратів, побудованих на катетах. Ідея цього доказудодатково проілюстровано за допомогою анімації, розташованої вище.
Доказ Леонардо да Вінчі
Головні елементи доказу – симетрія та рух.
Розглянемо креслення, як видно з симетрії, відрізок розсікає квадрат на дві однакові частини (оскільки трикутники і рівні по побудові).
Користуючись поворотом на 90 градусів проти годинникової стрілки навколо крапки, ми вбачаємо рівність заштрихованих фігур і.
Тепер ясно, що площа заштрихованої нами фігури дорівнює сумі половин площ маленьких квадратів (побудованих на катетах) та площі вихідного трикутника. З іншого боку, вона дорівнює половині площі великого квадрата (побудованого на гіпотенузі) плюс площа вихідного трикутника. Таким чином, половина суми площ маленьких квадратів дорівнює половині площі великого квадрата, а отже сума площ квадратів, побудованих на катетах, дорівнює площі квадрата, побудованого на гіпотенузі.
Доказ методом нескінченно малих
Наступний доказ за допомогою диференціальних рівнянь часто приписують відомому англійському математикуХарді, який жив у першій половині XX століття.
Розглядаючи креслення, показане на малюнку, і спостерігаючи зміну сторони a, ми можемо записати наступне співвідношення для нескінченно малих прирощень сторін зі a(використовуючи подобу трикутників):
Користуючись методом поділу змінних, знаходимо
Більше загальний вираз зміни гіпотенузи у разі прирощень обох катетов
Інтегруючи дане рівняння та використовуючи початкові умови, отримуємо
Таким чином, ми приходимо до бажаної відповіді
Як неважко бачити, квадратична залежність у остаточній формулі з'являється завдяки лінійній пропорційності між сторонами трикутника та прирощеннями, тоді як сума пов'язана з незалежними вкладами від прирощення різних катетів.
Простіший доказ можна отримати, якщо вважати, що один з катетів не відчуває збільшення (в даному випадку катет). Тоді для константи інтегрування отримаємо
Варіації та узагальнення
Подібні геометричні фігури на трьох сторонах
Узагальнення для подібних трикутників, площа зелених фігур A + B = площі синій C
Теорема Піфагора з використанням подібних прямокутних трикутників
Узагальнення теореми Піфагора зробив Евклід у своїй роботі Початок, розширивши площі квадратів на сторонах до подібних площ геометричних фігур :
Якщо побудувати подібні геометричні фігури (див. Евклідова геометрія) на сторонах прямокутного трикутника, тоді сума двох менших фігур дорівнюватиме площі більшої фігури.
Головна ідея цього узагальнення полягає в тому, що площа подібної геометричної фігури є пропорційною квадрату будь-якого свого лінійного розміру і зокрема квадрату довжини будь-якої сторони. Отже, для подібних фігур із майданами A, Bі Cпобудованих на сторонах із довжиною a, bі c, маємо:
Але, за теоремою Піфагора, a 2 + b 2 = c 2 , тоді A + B = C.
І навпаки, якщо ми зможемо довести, що A + B = Cдля трьох подібних геометричних фігур без використання теореми Піфагора, тоді ми зможемо довести саму теорему, рухаючись у зворотному напрямку. Наприклад, стартовий центральний трикутник може бути повторно використаний як трикутник Cна гіпотенузі, і два подібні прямокутні трикутники ( Aі B), побудовані на двох інших сторонах, які утворюються в результаті розподілу центрального трикутника його заввишки. Сума двох менших площ трикутників тоді, очевидно, дорівнює площі третього, таким чином A + B = Cі, виконуючи попереднє доказування в зворотному порядку, Отримаємо теорему Піфагора a 2 + b 2 = c 2 .
Теорема косінусів
Теорема Піфагора – це окремий випадокбільше загальної теоремикосінусів, яка пов'язує довжини сторін у довільному трикутнику:
де θ - кут між сторонами aі b.
Якщо θ дорівнює 90 градусів, тоді cos θ = 0 і формула спрощується до нормальної теореми Піфагора.
Довільний трикутник
У будь-який вибраний кут довільного трикутника зі сторонами a, b, cвпишемо рівнобедрений трикутник таким чином, щоб рівні кутипри його основі θ дорівнювали обраному кутку. Припустимо, що вибраний кут θ розташований навпроти сторони, позначеної c. В результаті ми отримали трикутник ABD з кутом θ, що розташований навпроти сторони aі сторони r. Другий трикутник утворюється кутом θ, що розташований навпроти сторони bі сторони здовжиною s, як показано на малюнку. Сабіт Ібн Курра стверджував, що сторони у цих трьох трикутниках пов'язані таким чином:
Коли кут θ наближається до π/2, основа рівнобедреного трикутниказменшується і дві сторони r і s перекривають один одного все менше і менше. Коли θ = π/2, ADB перетворюється на прямокутний трикутник, r + s = cі одержуємо початкову теорему Піфагора.
Розглянемо один із аргументів. Трикутник ABCмає такі ж кути, як і трикутник ABD, але у зворотному порядку. (Два трикутники мають загальний кут при вершині B, обидва мають кут θ і мають однаковий третій кут, за сумою кутів трикутника) Відповідно, ABC - подібний до відображення ABD трикутника DBA, як показано на нижньому малюнку. Запишемо співвідношення між протилежними сторонамиі прилеглими до кута θ,
Так само відображення іншого трикутника,
Перемножимо дроби і додамо ці два співвідношення:
що і потрібно було довести.
Узагальнення для довільних трикутників через паралелограми
Узагальнення для довільних трикутників,
площа зеленого ділянки = площісинього
Доказ тези, що на малюнку вище
Зробимо подальше узагальнення для непрямокутних трикутників, використовуючи паралелограми на трьох сторонах замість квадратів. (квадрати - окремий випадок.) Верхній малюнок демонструє, що для гострокутного трикутникаплоща паралелограма на довгій стороні дорівнює сумі паралелограмів на двох інших сторонах, за умови, що паралелограм на довгій стороні побудований, як зображено на малюнку (розміри, позначені стрілками, однакові та визначають сторони нижнього паралелограма). Ця заміна квадратів паралелограмами має чітку схожість із початковою теоремою Піфагора, вважається, що її сформулював Папп Олександрійський у 4 р. н. е.
Нижній малюнок показує перебіг доказу. Подивимося на ліву сторону трикутника. Лівий зелений паралелограм має таку ж площу, як ліва частина синього паралелограма, тому що вони мають таку ж основу bта висоту h. Крім того, лівий зелений паралелограм має таку ж площу, як лівий зелений паралелограм на верхньому малюнку, тому що вони мають загальна основа(верхня ліва сторонатрикутника) та загальну висоту, перпендикулярну до цієї сторони трикутника. Аналогічно міркуючи праворуч трикутника доведемо, що нижній паралелограм має таку ж площу, як у двох зелених паралелограмів.
Комплексні числа
Теорему Піфагора використовують, щоб знайти відстань між двома точками в декартовій координатній системі і ця теорема справедлива для всіх істинних координат: відстань sміж двома точками ( a, b) та ( c, d) одно
Не виникає проблем із формулою, якщо до комплексних чисел ставитися як до векторів із дійсними компонентами x + i y = (x, y). . Наприклад, відстань sміж 0 + 1 iта 1 + 0 iрозраховуємо як модуль вектора (0, 1) − (1, 0) = (−1, 1), або
Проте, для операцій із векторами з комплексними координатами необхідно провести певне вдосконалення формули Піфагора. Відстань між точками з комплексними числами (a, b) та ( c, d); a, b, c, і dвсі комплексні, сформулюємо використовуючи абсолютні величини. Відстань sзаснований на векторній різниці (a − c, b − d) в наступному вигляді: нехай різниця a − c = p+ i q, де p- дійсна частина різниці, q- уявна частина, і i = √(−1). Аналогічно, хай b − d = r+ i s. Тоді:
де - це комплексне сполучене число для . Наприклад, відстань між точками (a, b) = (0, 1) і (c, d) = (i, 0) , розрахуємо різницею (a − c, b − d) = (−i, 1) і в результаті ми отримали б 0, якби не були використані комплексні пов'язані. Отже, використовуючи вдосконалену формулу, отримаємо
Модуль визначено так:
Стереометрія
Значним узагальненням теореми Піфагора для тривимірного простору є теорема де Гуа, названа на честь Ж.-П. де Гуа: якщо тетраедр має прямий кут (як у кубі), тоді квадрат площі грані, що лежить навпроти прямого кута, дорівнює сумі квадратів площ інших трьох граней. Цей висновок може бути узагальнено як « n-мірна теорема Піфагора»:
Теорема Піфагора в тривимірному просторізв'язує діагональ AD із трьома сторонами.
Інше узагальнення: Теорема Піфагора може бути використана для стереометрії в наступному вигляді. Розглянемо прямокутний паралелепіпед, як показано на малюнку. Знайдемо довжину діагоналі BD за теоремою Піфагора:
де три сторони утворюють прямокутний трикутник. Використовуємо горизонтальну діагональ BD та вертикальне ребро AB, щоб знайти довжину діагоналі AD, для цього знову використовуємо теорему Піфагора:
або, якщо все записати одним рівнянням:
Цей результат - це тривимірне вираз визначення величини вектора v(Діагональ AD), вираженого через його перпендикулярні складові ( v k) (три взаємно перпендикулярні сторони):
Це рівняння можна як узагальнення теореми Піфагора для багатовимірного простору. Проте, результат насправді не що інше, як неодноразове застосування теореми Піфагора до послідовності прямокутних трикутників в послідовно перпендикулярних площинах.
Векторний простір
У разі ортогональної системи векторів має місце рівність, яку теж називають теоремою Піфагора:
Якщо - це векторні проекції на координатні осі, то ця формула збігається з відстанню Евкліда - і означає, що довжина вектора дорівнює кореню квадратної сумиквадратів його компонентів.
Аналог цієї рівності у разі нескінченної системивекторів має назву рівності Парсеваля.
Неєвклідова геометрія
Теорема Піфагора виводиться з аксіом геометрії евклідової і, фактично, не дійсна для неевклідової геометрії, в тому вигляді, в якому записана вище. (Тобто теорема Піфагора виявляється своєрідним еквівалентом постулату Евкліда про паралельність) Іншими словами, у неевклідовій геометрії співвідношення між сторонами трикутника обов'язково буде у формі, відмінної від теореми Піфагора. Наприклад, у сферичній геометрії всі три сторони прямокутного трикутника (скажімо a, bі c), які обмежують собою октант (восьму частину) одиничної сфери, мають довжину π/2, що суперечить теоремі Піфагора, тому що a 2 + b 2 ≠ c 2 .
Розглянемо тут два випадки неевклідової геометрії – сферична та гіперболічна геометрія; в обох випадках, як і для евклідового простору для прямокутних трикутників, результат, який замінює теорему Піфагора, випливає з теореми косінусів.
Однак, теорема Піфагора залишається справедливою для гіперболічної та еліптичної геометрії, якщо вимогу про прямокутність трикутника замінити умовою, що сума двох кутів трикутника має дорівнювати третьому, скажімо A+B = C. Тоді співвідношення між сторонами виглядає так: сума площ кіл з діаметрами aі bдорівнює площі кола з діаметром c.
Сферична геометрія
Для будь-якого прямокутного трикутника на сфері радіусом R(наприклад, якщо кут γ у трикутнику прямий) зі сторонами a, b, cспіввідношення між сторонами матиме такий вигляд:
Ця рівність може бути виведена як особливий випадоксферичної теореми косінусів, яке справедливе для всіх сферичних трикутників:
де cosh – це гіперболічний косинус. Ця формула є окремим випадком гіперболічної теореми косінусів, яка справедлива для всіх трикутників:
де γ - це кут, вершина якого протилежна стороні c.
де g ijназивається метричним тензором. Він може бути функцією позиції. Такі криволінійні простори включають Ріманову геометрію як загальний приклад. Це формулювання також підходить для Евклідова простору при застосуванні криволінійних координат. Наприклад, для полярних координат:
Векторний витвір
Теорема Піфагора пов'язує два вирази величини векторного твору. Один із підходів до визначення векторного твору вимагає, щоб він задовольняв рівняння:
у цій формулі використовується скалярний твір. Права сторона рівняння називається детермінант Грама для aі bщо дорівнює площі паралелограма, утвореного цими двома векторами. Виходячи з цієї вимоги, а також вимоги про перпендикулярність векторного твору до його складових aі bслід, що, крім виняткових випадків з 0- і 1-мерного простору, векторне твір визначено лише у трьох і семи вимірах. Використовуємо визначення кута в n-мірному просторі:
ця властивість векторного твору дає його величину в такому вигляді:
Через фундаментальне тригонометрична тотожністьПіфагора отримуємо іншу форму запису його величини:
Альтернативний підхід до визначення векторного твору використовує вираз його величини. Тоді, розмірковуючи у зворотному порядку, отримуємо зв'язок зі скалярним твором:
Див. також
Примітки
- History topic: Pythagoras's theorem in Babylonian математики
- ( , С. 351) С. 351
- ( , Vol I, p. 144)
- Обговорення історичних фактівнаведено в ( , С. 351) С. 351
- Kurt Von Fritz (Apr., 1945). "Дисcovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics, Second Series(Annals of Mathematics) 46 (2): 242–264.
- Льюїс Керрол, "Історія з вузликами", М., Світ, 1985, с. 7
- Asger Aaboe Episodes from the early history of mathematics . - Mathematical Association of America, 1997. - P. 51. - ISBN 0883856131
- Pythagorean Proposition Elisha Scott Loomis
- Euclid’s Elements: Book VI, Proposition VI 31: «У правій-залицяючій ланцюжку фігури на стороні підтримують праву янгу є еквівалентною для подібних і подібних позначених зображень на сторінках, розташованих в правій янглі.»
- Lawrence S. Leff cited work. - Barron"s Educational Series. - P. 326. - ISBN 0764128922
- Howard Whitley Eves§4.8:...generalization of Pythagorean theorem // Great moments in mathematics (before 1650) . - Mathematical Association of America, 1983. - P. 41. - ISBN 0883853108
- Tâbit ibn Qorra (full name Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 AD) був фізичним життям у Багдаді, який простіше на Euclid's Elements and otherматематичні предмети.
- Aydin Sayili (Mar. 1960). «Thabit ibn Qurra» з Generalization of the Pythagorean Theorem». Isis 51 (1): 35-37. DOI: 10.1086/348837.
- Judith D. Sally, Paul Sally Exercise 2.10 (ii) // Cited work. – P. 62. – ISBN 0821844032
- Для details of such a construction, viz George Jennings Figure 1.32: Generalized Pythagorean theorem // Modern geometry with applications: with 150 figures . - 3rd. - Springer, 1997. - P. 23. - ISBN 038794222X
- Arlen Brown, Carl M. Pearcy Item C: Norm for an arbitrary n-tuple ... / / An introduction to analysis. - Springer, 1995. - P. 124. - ISBN 0387943692 See also pages 47-50.
- Alfred Gray, Elsa Abbena, Simon Salamon Modern differential geometry curves and surfaces with Mathematica . - 3rd. – CRC Press, 2006. – P. 194. – ISBN 1584884487
- Rajendra Bhatia Matrix analysis. - Springer, 1997. - P. 21. - ISBN 0387948465
- Stephen W. Hawking cited work. – 2005. – P. 4. – ISBN 0762419229
- Eric W. Weisstein CRC concise encyclopedia of mathematics. - 2nd. – 2003. – P. 2147. – ISBN 1584883472
- Alexander R. Pruss
Середній рівень
Прямокутний трикутник. Повний ілюстрований гід (2019)
ПРЯМОКУТНИЙ ТРИКУТНИК. ПОЧАТКОВИЙ РІВЕНЬ.
У задачах прямий кут зовсім не обов'язково - лівий нижній, так що тобі потрібно навчитися впізнавати прямокутний трикутник і в такому вигляді,

і в такому,

і в такому 
Що ж хорошого є у прямокутному трикутнику? Ну..., по-перше, є спеціальні красиві назвидля його сторін.
Увага на малюнок!

Запам'ятай і не плутай: катетів – два, а гіпотенуза – всього одна(Єдина, неповторна і найдовша)!
Ну ось назви обговорили, тепер найважливіше: Теорема Піфагора.
Теорема Піфагора.
Ця теорема - ключик до вирішення багатьох завдань за участю прямокутного трикутника. Її довів Піфагор у зовсім незапам'ятні часи, і з того часу вона принесла багато користі тим, хто її знає. А найкраще в ній те, що вона проста.
Отже, Теорема Піфагора:
Пам'ятаєш жарт: «Піфагорові штани на всі боки рівні!»?
Давай намалюємо ці піфагорові штани і подивимося на них. 
Щоправда, схоже на якісь шорти? Ну і на які сторони, і де вона рівні? Чому і звідки виник жарт? А жарт цей пов'язаний саме з теоремою Піфагора, точніше з тим, як сам Піфагор формулював свою теорему. А формулював він її так:
«Сума площ квадратів, побудованих на катетах, дорівнює площі квадрата, побудованого на гіпотенузі»
Щоправда, трохи по-іншому звучить? І ось, коли Піфагор намалював твердження своєї теореми, якраз і вийшла така картинка.

На цьому малюнку сума площ маленьких квадратів дорівнює площі великого квадрата. А щоб діти краще запам'ятовували, що сума квадратів катетів дорівнює квадрату гіпотенузи, хтось дотепний і вигадав цей жарт про Піфагорові штани.
Чому ж ми зараз формулюємо теорему Піфагора
А Піфагор мучився і міркував про майдани?
Розумієш, у давнину не було… алгебри! Не було жодних позначень і таке інше. Не було написів. Уявляєш, як бідним древнім учням було жахливо запам'ятовувати все словами??! А ми можемо радіти, що ми маємо просте формулювання теореми Піфагора. Давай її ще раз повторимо, щоб краще запам'ятати:
Тепер уже має бути легко:
| Квадрат гіпотенузи дорівнює сумі квадратів катетів. |
Ну ось, найголовнішу теорему про прямокутний трикутник обговорили. Якщо тобі цікаво, як вона доводиться, читай наступні рівнітеорії, а зараз підемо далі ... в темний ліс… тригонометрії! До жахливих слів синус, косинус, тангенс та котангенс.
Синус, косинус, тангенс, котангенс у прямокутному трикутнику.
Насправді все зовсім не таке страшно. Звичайно, «справжнє» визначення синуса, косинуса, тангенсу та котангенсу потрібно дивитися у статті. Але дуже не хочеться, правда? Можемо порадувати: для вирішення задач прямокутного трикутника можна просто заповнити наступні прості речі:
А чому все тільки про кут? Де ж кут? Щоб у цьому розібратися, треба зазначити, як твердження 1 - 4 записуються словами. Дивись, розумій та запам'ятай!
1.
Взагалі звучить це так:
А що ж кут? Чи є катет, який знаходиться навпроти кута, тобто катет, що протилежить (для кута)? Звісно є! Це катет!
А як же кут? Подивись уважно. Який катет прилягає до кутка? Звісно ж, катет. Значить, для кута катет – прилеглий, та
А тепер, увага! Подивися, що в нас вийшло:
Бачиш, як чудово:
Тепер перейдемо до тангенсу та котангенсу.
Як це тепер записати словами? Катет яким є по відношенню до кута? Протилежним, звісно – він «лежать» навпроти кута. А катет? Прилягає до кутку. Виходить, що в нас вийшло?
Бачиш, чисельник та знаменник помінялися місцями?
І тепер знову кути і здійснили обмін:
Резюме
Давайте коротко запишемо все, що ми дізналися.
 |
Теорема Піфагора: |
Головна теорема про прямокутний трикутник - теорема Піфагора.
теорема Піфагора
До речі, чи добре ти пам'ятаєш, що таке катети та гіпотенуза? Якщо не дуже, то дивись на малюнок – освіжай знання

Цілком можливо, що ти вже багато разів використовував теорему Піфагора, а ось чи ти замислювався, чому ж вірна така теорема. Як би її довести? А давай вчинимо, як давні греки. Намалюємо квадрат зі стороною.

Бачиш, як хитро ми поділили його сторони на відрізки довжин і!
А тепер з'єднаємо зазначені точки

Тут ми, щоправда, ще дещо відзначили, але ти сам подивися на малюнок і подумай, чому так.
Чому дорівнює площа більшого квадрата? Правильно, . А площа меншого? Звісно, . Залишилася сумарна площа чотирьох куточків. Уяви, що ми взяли їх по два і притулили один до одного гіпотенузами. Що вийшло? Два прямокутники. Отже, площа «обрізків» дорівнює.
Давай тепер зберемо все разом.
Перетворюємо:
Ось і побували ми Піфагором – довели його теорему давнім способом.
Прямокутний трикутник та тригонометрія
Для прямокутного трикутника виконуються такі співвідношення:

Сінус гострого кутадорівнює відношенню протилежного катета до гіпотенузи
Косинус гострого кута дорівнює відношенню прилеглого катета до гіпотенузи.
Тангенс гострого кута дорівнює відношенню протилежного катета до прилеглого катета.
Котангенс гострого кута дорівнює відношенню прилеглого катета до протилежного катета.
І ще раз все це у вигляді таблички:
Це дуже зручно!
Ознаки рівності прямокутних трикутників
I. За двома катетами

ІІ. По катету та гіпотенузі

ІІІ. По гіпотенузі та гострому куту

IV. По катету та гострому куту
a) 
b) 
Увага! Тут дуже важливо, щоб катети були «відповідні». Наприклад, якщо буде так:

То ТРИКУТНИКИ НЕ РІВНІ, незважаючи на те, що мають один однаковий гострий кут.
Потрібно, щоб в обох трикутниках катет був прилеглим, або в обох - протилежним.
Ти помітив чим відрізняються ознаки рівності прямокутних трикутників від звичайних ознак рівності трикутників? Заглянь у тему « і зверни увагу те що, що з рівності « рядових » трикутників потрібна рівність трьох їх елементів: дві сторони і кут з-поміж них, два кута і сторона з-поміж них чи три стороны. А ось для рівності прямокутних трикутників достатньо лише двох відповідних елементів. Здорово, правда?
Приблизно така сама ситуація і з ознаками подоби прямокутних трикутників.
Ознаки подоби прямокутних трикутників
I. По гострому кутку

ІІ. За двома катетами

ІІІ. По катету та гіпотенузі

Медіана у прямокутному трикутнику
Чому це так?
Розглянемо замість прямокутного трикутника цілий прямокутник.
Проведемо діагональ і розглянемо точку – точку перетину діагоналей. Що відомо про діагоналі прямокутника?
І що з цього випливає?
Ось і вийшло, що
- - медіана:
Запам'ятай цей факт! Дуже допомагає!
А що ще дивовижніше, так це те, що вірне і зворотне твердження.
Що ж хорошого можна отримати з того, що медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи? А давай подивимося на картинку
Подивись уважно. У нас є: тобто відстані від точки до всіх трьох вершин трикутника виявилися рівними. Але в трикутнику є всього одна точка, відстані від якої про всі три вершини трикутника рівні, і це - ЦЕНТР ОПИСАНОГО ОКРУЖЕННЯ. Виходить, що вийшло?
Ось давай ми почнемо з цього «крім того...».
Подивимося на в.
Але у подібних трикутників усі кути рівні!
Те саме можна сказати і про і
А тепер намалюємо це разом:
Яку ж користь можна отримати з цієї «троїстої» подоби.
Ну наприклад - дві формули для висоти прямокутного трикутника.
Запишемо відносини відповідних сторін:

Для знаходження висоти вирішуємо пропорцію та отримуємо першу формулу "Висота у прямокутному трикутнику":
Отже, застосуємо подібність: .

Що тепер вийде?
Знову вирішуємо пропорцію і отримуємо другу формулу:
Обидві ці формули потрібно дуже добре пам'ятати та застосовувати ту, яку зручніше. Запишемо їх ще раз
Теорема Піфагора:
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів: .

Ознаки рівності прямокутних трикутників:
- по двох катетах:
- по катету та гіпотенузі: або
- по катету та прилеглому гострому кутку: або
- по катету та протилежному гострому куту: або
- з гіпотенузи та гострого кута: або.
Ознаки подоби прямокутних трикутників:
- одному гострому кутку: або
- із пропорційності двох катетів:
- з пропорційності катета та гіпотенузи: або.
Синус, косинус, тангенс, котангенс у прямокутному трикутнику
- Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до гіпотенузи:
- Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи:
- Тангенсом гострого кута прямокутного трикутника називається відношення протилежного катета до прилеглого:
- Котангенсом гострого кута прямокутного трикутника називається відношення прилеглого катета до протилежного: .
Висота прямокутного трикутника: або.
У прямокутному трикутнику медіана, проведена з вершини прямого кута, дорівнює половині гіпотенузи: .
Площа прямокутного трикутника:
- через катети:
 Аналогічно, трикутник CBH подібний до ABC. Ввівши позначення
Аналогічно, трикутник CBH подібний до ABC. Ввівши позначення  1. Розташуємо чотири рівні прямокутні трикутники так, як показано на малюнку.
1. Розташуємо чотири рівні прямокутні трикутники так, як показано на малюнку. 
 Ідея доказу Евкліда полягає в наступному: спробуємо довести, що половина площі квадрата, побудованого на гіпотенузі, дорівнює сумі половин площ квадратів, побудованих на катетах, а тоді площі великого і двох малих квадратів рівні. Розглянемо креслення зліва. На ньому ми побудували квадрати на сторонах прямокутного трикутника і провели з вершини прямого кута С промінь перпендикулярно до гіпотенузи AB, він розсікає квадрат ABIK, побудований на гіпотенузі, на два прямокутники - BHJI і HAKJ відповідно. Виявляється, що площі даних прямокутників точно рівні площам квадратів, побудованих на відповідних катетах. Спробуємо довести, що площа квадрата DECA дорівнює площі прямокутника AHJK Для цього скористаємося допоміжним спостереженням: Площа трикутника з тією самою висотою та основою, що й даний прямокутник дорівнює половині площі заданого прямокутника. Це наслідок визначення площі трикутника як половини добутку основи висоту. З цього спостереження випливає, що площа трикутника ACK дорівнює площі трикутника AHK (не зображеного на малюнку), яка, у свою чергу, дорівнює половині площі прямокутника AHJK. Доведемо тепер, що площа трикутника ACK також дорівнює половині площі квадрата DECA. Єдине, що необхідно для цього зробити, - це довести рівність трикутників ACK і BDA (оскільки площа трикутника BDA дорівнює половині площі квадрата за вказаною вище властивістю). Рівність це очевидно, трикутники рівні з обох боків та кутку між ними. Саме - AB=AK,AD=AC - рівність кутів CAK і BAD легко довести методом руху: повернемо трикутник CAK на 90° проти годинникової стрілки, тоді очевидно, що відповідні сторони двох трикутників, що розглядаються, збігатимуться (через кут при вершині квадрата - 90 °). Міркування про рівність площ квадрата BCFG і прямокутника BHJI абсолютно аналогічне. Тим самим було доведено, що площа квадрата, побудованого на гіпотенузі, складається з площ квадратів, побудованих на катетах.
Ідея доказу Евкліда полягає в наступному: спробуємо довести, що половина площі квадрата, побудованого на гіпотенузі, дорівнює сумі половин площ квадратів, побудованих на катетах, а тоді площі великого і двох малих квадратів рівні. Розглянемо креслення зліва. На ньому ми побудували квадрати на сторонах прямокутного трикутника і провели з вершини прямого кута С промінь перпендикулярно до гіпотенузи AB, він розсікає квадрат ABIK, побудований на гіпотенузі, на два прямокутники - BHJI і HAKJ відповідно. Виявляється, що площі даних прямокутників точно рівні площам квадратів, побудованих на відповідних катетах. Спробуємо довести, що площа квадрата DECA дорівнює площі прямокутника AHJK Для цього скористаємося допоміжним спостереженням: Площа трикутника з тією самою висотою та основою, що й даний прямокутник дорівнює половині площі заданого прямокутника. Це наслідок визначення площі трикутника як половини добутку основи висоту. З цього спостереження випливає, що площа трикутника ACK дорівнює площі трикутника AHK (не зображеного на малюнку), яка, у свою чергу, дорівнює половині площі прямокутника AHJK. Доведемо тепер, що площа трикутника ACK також дорівнює половині площі квадрата DECA. Єдине, що необхідно для цього зробити, - це довести рівність трикутників ACK і BDA (оскільки площа трикутника BDA дорівнює половині площі квадрата за вказаною вище властивістю). Рівність це очевидно, трикутники рівні з обох боків та кутку між ними. Саме - AB=AK,AD=AC - рівність кутів CAK і BAD легко довести методом руху: повернемо трикутник CAK на 90° проти годинникової стрілки, тоді очевидно, що відповідні сторони двох трикутників, що розглядаються, збігатимуться (через кут при вершині квадрата - 90 °). Міркування про рівність площ квадрата BCFG і прямокутника BHJI абсолютно аналогічне. Тим самим було доведено, що площа квадрата, побудованого на гіпотенузі, складається з площ квадратів, побудованих на катетах.  Розглянемо креслення, як видно з симетрії, відрізок CI розсікає квадрат ABHJ на дві однакові частини (оскільки трикутники ABC і JHI рівні по побудові). Користуючись поворотом на 90 градусів проти годинникової стрілки, ми вбачаємо рівність заштрихованих фігур CAJI та GDAB. Тепер ясно, що площа заштрихованої нами фігури дорівнює сумі половин площ квадратів, побудованих на катетах, та площі вихідного трикутника. З іншого боку, вона дорівнює половині площі квадрата, побудованого на гіпотенузі плюс площа вихідного трикутника. Останній крок у доказі надається читачеві.
Розглянемо креслення, як видно з симетрії, відрізок CI розсікає квадрат ABHJ на дві однакові частини (оскільки трикутники ABC і JHI рівні по побудові). Користуючись поворотом на 90 градусів проти годинникової стрілки, ми вбачаємо рівність заштрихованих фігур CAJI та GDAB. Тепер ясно, що площа заштрихованої нами фігури дорівнює сумі половин площ квадратів, побудованих на катетах, та площі вихідного трикутника. З іншого боку, вона дорівнює половині площі квадрата, побудованого на гіпотенузі плюс площа вихідного трикутника. Останній крок у доказі надається читачеві.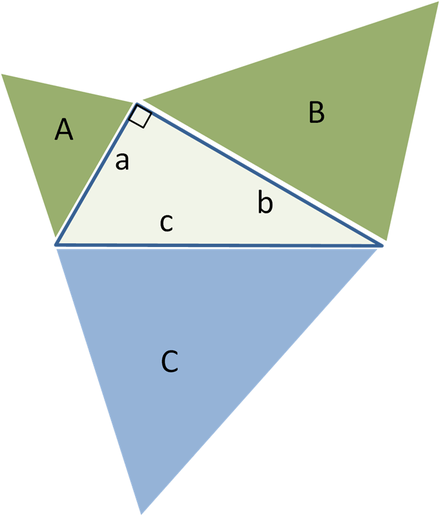




 Ораторське мистецтво як прообраз публіцистики
Ораторське мистецтво як прообраз публіцистики Цитати про Наполеона - dslinkov — LiveJournal
Цитати про Наполеона - dslinkov — LiveJournal Мені помста Людина на бульдозері зруйнувала місто
Мені помста Людина на бульдозері зруйнувала місто