Maclaurin mở rộng trực tuyến. Mở rộng Taylor

Học sinh giỏi toán cao hơn cần lưu ý rằng tổng của một số chuỗi lũy thừa thuộc khoảng đồng quy của chuỗi đã cho là một hàm phân biệt liên tục và không giới hạn số lần. Câu hỏi đặt ra: liệu có thể khẳng định rằng một hàm tùy ý đã cho f (x) là tổng của một chuỗi lũy thừa nào đó không? Tức là với điều kiện nào thì hàm số f (x) có thể được biểu diễn bằng một chuỗi lũy thừa? Tầm quan trọng của câu hỏi này nằm ở chỗ có thể thay thế gần đúng hàm f (x) bằng tổng của một vài số hạng đầu tiên của chuỗi lũy thừa, tức là bằng một đa thức. Việc thay thế một hàm bằng một biểu thức khá đơn giản - một đa thức - như vậy cũng thuận tiện khi giải một số bài toán, cụ thể là: khi giải tích phân, khi tính toán, v.v.

Người ta chứng minh rằng đối với một số hàm f (x), trong đó các đạo hàm lên đến bậc (n + 1), bao gồm cả bậc cuối cùng, có thể được tính, trong lân cận (α - R; x 0 + R) của một số điểm x = α công thức:

Công thức này được đặt theo tên của nhà khoa học nổi tiếng Brook Taylor. Loạt thu được từ phần trước được gọi là loạt Maclaurin:

Quy tắc giúp nó có thể mở rộng trong chuỗi Maclaurin:

1. Xác định phái sinh của các lệnh thứ nhất, thứ hai, thứ ba….
2. Tính đạo hàm tại x = 0.
3. Viết chuỗi Maclaurin cho hàm này, sau đó xác định khoảng thời gian hội tụ của nó.
4. Xác định khoảng (-R; R), trong đó phần còn lại của công thức Maclaurin

R n (x) -> 0 với n -> vô cùng. Nếu tồn tại một hàm f (x) trong nó phải trùng với tổng của chuỗi Maclaurin.

Bây giờ hãy xem xét loạt Maclaurin cho các chức năng riêng lẻ.

1. Vì vậy, đầu tiên sẽ là f (x) = e x. Tất nhiên, theo các đặc điểm của nó, một hàm như vậy có các đạo hàm của các bậc rất khác nhau và f (k) (x) \ u003d e x, trong đó k bằng mọi thứ Hãy thay x \ u003d 0. Ta nhận được f (k) (0) \ u003d e 0 \ u003d 1, k \ u003d 1.2 ... Dựa trên những điều đã nói ở trên, chuỗi e x sẽ như sau:

2. Chuỗi Maclaurin cho hàm f (x) = sin x. Hãy làm rõ ngay rằng hàm cho tất cả các ẩn số sẽ có đạo hàm, ngoài f "(x) \ u003d cos x \ u003d sin (x + n / 2), f" "(x) \ u003d -sin x \ u003d sin (x + 2 * n / 2) ..., f (k) (x) = sin (x + k * n / 2), trong đó k bằng bất kỳ số tự nhiên nào. chuỗi cho f (x) = sin x sẽ giống như sau:

3. Bây giờ chúng ta hãy thử xét hàm f (x) = cos x. Nó có các đạo hàm có thứ tự tùy ý với mọi ẩn số, và | f (k) (x) | = | cos (x + k * n / 2) |<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Vì vậy, chúng tôi đã liệt kê các hàm quan trọng nhất có thể được mở rộng trong chuỗi Maclaurin, nhưng chúng được bổ sung bởi chuỗi Taylor cho một số hàm. Bây giờ chúng tôi sẽ liệt kê chúng. Cũng cần lưu ý rằng chuỗi Taylor và Maclaurin là một phần quan trọng của thực hành giải chuỗi trong toán học cao hơn. Vì vậy, chuỗi Taylor.

1. Đầu tiên sẽ là một hàng cho f-ii f (x) = ln (1 + x). Như trong các ví dụ trước, với f (x) = ln (1 + x), chúng ta có thể thêm một chuỗi bằng cách sử dụng dạng tổng quát của chuỗi Maclaurin. tuy nhiên, đối với chức năng này, chuỗi Maclaurin có thể được lấy đơn giản hơn nhiều. Sau khi tích phân một chuỗi hình học nhất định, chúng ta nhận được một chuỗi cho f (x) = ln (1 + x) của một mẫu như vậy:

2. Và phần thứ hai, sẽ là phần cuối cùng trong bài viết của chúng tôi, sẽ là một chuỗi cho f (x) \ u003d arctg x. Với x thuộc khoảng [-1; 1] thì khai triển có giá trị:

Đó là tất cả. Trong bài báo này, chuỗi Taylor và Maclaurin được sử dụng nhiều nhất trong toán học bậc cao, đặc biệt là ở các trường đại học kinh tế và kỹ thuật, đã được xem xét.

Làm thế nào để chèn các công thức toán học trên trang web?

Nếu bạn cần thêm một hoặc hai công thức toán học vào trang web, thì cách dễ nhất để thực hiện việc này như được mô tả trong bài viết: các công thức toán học dễ dàng được chèn vào trang web dưới dạng hình ảnh mà Wolfram Alpha tự động tạo ra. Ngoài sự đơn giản, phương pháp phổ quát này sẽ giúp cải thiện khả năng hiển thị của trang web trong các công cụ tìm kiếm. Nó đã hoạt động trong một thời gian dài (và tôi nghĩ rằng nó sẽ hoạt động mãi mãi), nhưng nó đã lỗi thời về mặt đạo đức.

Nếu bạn thường xuyên sử dụng các công thức toán học trên trang web của mình, thì tôi khuyên bạn nên sử dụng MathJax, một thư viện JavaScript đặc biệt hiển thị ký hiệu toán học trong trình duyệt web sử dụng đánh dấu MathML, LaTeX hoặc ASCIIMathML.

Có hai cách để bắt đầu sử dụng MathJax: (1) sử dụng mã đơn giản, bạn có thể nhanh chóng kết nối tập lệnh MathJax với trang web của mình, tập lệnh này sẽ được tự động tải từ máy chủ từ xa vào đúng thời điểm (danh sách các máy chủ); (2) tải tập lệnh MathJax từ máy chủ từ xa lên máy chủ của bạn và kết nối nó với tất cả các trang trên trang web của bạn. Phương pháp thứ hai phức tạp hơn và tốn thời gian hơn và sẽ cho phép bạn tăng tốc tải các trang trên trang web của mình và nếu máy chủ MathJax mẹ tạm thời không khả dụng vì lý do nào đó, điều này sẽ không ảnh hưởng đến trang web của bạn theo bất kỳ cách nào. Mặc dù có những ưu điểm này, tôi đã chọn phương pháp đầu tiên, vì nó đơn giản hơn, nhanh hơn và không đòi hỏi kỹ năng kỹ thuật. Hãy làm theo ví dụ của tôi, và trong vòng 5 phút, bạn sẽ có thể sử dụng tất cả các tính năng của MathJax trên trang web của mình.

Bạn có thể kết nối tập lệnh thư viện MathJax từ một máy chủ từ xa bằng hai tùy chọn mã được lấy từ trang web MathJax chính hoặc từ trang tài liệu:

Một trong những tùy chọn mã này cần được sao chép và dán vào mã của trang web của bạn, tốt nhất là giữa các thẻ và hoặc ngay sau thẻ . Theo tùy chọn đầu tiên, MathJax tải nhanh hơn và làm chậm trang ít hơn. Nhưng tùy chọn thứ hai sẽ tự động theo dõi và tải các phiên bản mới nhất của MathJax. Nếu bạn chèn mã đầu tiên, thì nó sẽ cần được cập nhật định kỳ. Nếu bạn dán mã thứ hai, thì các trang sẽ tải chậm hơn, nhưng bạn sẽ không cần phải liên tục theo dõi các bản cập nhật MathJax.

Cách dễ nhất để kết nối MathJax là trong Blogger hoặc WordPress: trong bảng điều khiển của trang web, thêm tiện ích con được thiết kế để chèn mã JavaScript của bên thứ ba, sao chép phiên bản đầu tiên hoặc thứ hai của mã tải ở trên vào đó và đặt tiện ích con gần hơn phần đầu của mẫu (nhân tiện, điều này không cần thiết, vì tập lệnh MathJax được tải không đồng bộ). Đó là tất cả. Bây giờ, hãy học cú pháp đánh dấu MathML, LaTeX và ASCIIMathML và bạn đã sẵn sàng để nhúng các công thức toán học vào các trang web của mình.

Fractal nào cũng được xây dựng theo một quy tắc nhất định, được áp dụng nhất quán không giới hạn số lần. Mỗi lần như vậy được gọi là một lần lặp.

Thuật toán lặp lại để xây dựng một miếng bọt biển Menger khá đơn giản: hình lập phương ban đầu có cạnh 1 được chia bởi các mặt phẳng song song với các mặt của nó thành 27 hình lập phương bằng nhau. Một khối trung tâm và 6 khối liền kề với nó dọc theo các mặt được loại bỏ khỏi nó. Nó chỉ ra một tập hợp bao gồm 20 hình khối nhỏ hơn còn lại. Làm tương tự với mỗi hình lập phương này, ta được một tập hợp gồm 400 hình lập phương nhỏ hơn. Tiếp tục quá trình này vô thời hạn, chúng ta nhận được miếng bọt biển Menger.

Trong số các chuỗi chức năng, vị trí quan trọng nhất được chiếm bởi các chuỗi quyền lực.

Chuỗi lũy thừa được gọi là chuỗi

các thành viên của nó là các hàm lũy thừa được sắp xếp theo lũy thừa số nguyên không âm tăng dần x, một c0 , c 1 , c 2 , c N là các giá trị không đổi. Con số c1 , c 2 , c N - hệ số của các thành viên trong chuỗi, c0 - thành viên miễn phí. Các số hạng của chuỗi lũy thừa được xác định trên toàn bộ dãy số.

Hãy làm quen với khái niệm vùng hội tụ của chuỗi lũy thừa. Đây là tập hợp các giá trị biến x mà chuỗi hội tụ. Chuỗi lũy thừa có một vùng hội tụ khá đơn giản. Đối với các giá trị thực của một biến x vùng hội tụ bao gồm một điểm duy nhất hoặc là một khoảng nhất định (khoảng hội tụ), hoặc trùng với toàn bộ trục Con bò .

Khi thay thế trong một chuỗi lũy thừa, các giá trị x= 0 bạn nhận được một chuỗi số

c0 +0+0+...+0+... ,

cái nào hội tụ.

Do đó, khi x= 0 hội tụ bất kỳ chuỗi lũy thừa nào và do đó, khu vực hội tụ của nó không thể là một tập hợp trống. Cấu trúc của vùng hội tụ của tất cả các chuỗi lũy thừa là như nhau. Nó có thể được thiết lập bằng cách sử dụng định lý sau.

Định lý 1 (Định lý Abel). Nếu chuỗi lũy thừa hội tụ ở một giá trị nào đó x = x 0 , khác 0, thì nó hội tụ, và hơn nữa, hoàn toàn, đối với tất cả các giá trị |x| < |x 0 | . Xin lưu ý: cả giá trị bắt đầu "x bằng không" và bất kỳ giá trị nào của "x" được so sánh với giá trị bắt đầu đều được tính theo modulo - không tính đến dấu hiệu.

Hậu quả. Nếu một phân kỳ loạt điện ở một số giá trị x = x 1 , sau đó nó phân kỳ cho tất cả các giá trị |x| > |x 1 | .

Như chúng ta đã tìm hiểu trước đó, bất kỳ chuỗi lũy thừa nào đều hội tụ cho giá trị x= 0. Có chuỗi lũy thừa chỉ hội tụ cho x= 0 và phân kỳ cho các giá trị khác X. Loại trừ trường hợp này khỏi việc xem xét, chúng tôi giả định rằng chuỗi lũy thừa hội tụ tại một số giá trị x = x 0 , khác 0. Khi đó, theo định lý Abel, nó hội tụ tại mọi điểm trong khoảng] - | x0 |, |x 0 |[ (khoảng, ranh giới bên trái và bên phải của chúng là các giá trị của x, tại đó chuỗi lũy thừa hội tụ, lấy tương ứng với một dấu trừ và với một dấu cộng), đối xứng về gốc.

Nếu chuỗi công suất phân kỳ ở một số giá trị x = x 1 , sau đó, dựa trên hệ quả của định lý Abel, nó cũng phân kỳ tại tất cả các điểm bên ngoài đoạn [- | x1 |, |x 1 |] . Theo đó, đối với bất kỳ chuỗi lũy thừa nào, có một khoảng, đối xứng với gốc, được gọi là khoảng hội tụ , tại mỗi điểm mà chuỗi hội tụ, có thể hội tụ tại các ranh giới, hoặc có thể phân kỳ, và không nhất thiết đồng thời, nhưng bên ngoài phân đoạn, chuỗi phân kỳ. Con số Rđược gọi là bán kính hội tụ của chuỗi lũy thừa.

Trong những trường hợp đặc biệt khoảng thời gian hội tụ chuỗi công suất có thể suy biến đến một điểm (khi đó chuỗi chỉ hội tụ cho x= 0 và giả định rằng R= 0) hoặc đại diện cho toàn bộ trục số (khi đó chuỗi số hội tụ tại tất cả các điểm của trục số và giả sử như vậy).

Do đó, định nghĩa vùng hội tụ của một chuỗi lũy thừa là xác định bán kính hội tụ R và nghiên cứu về sự hội tụ của chuỗi trên các ranh giới của khoảng hội tụ (cho).

Định lý 2. Nếu tất cả các hệ số của một chuỗi lũy thừa, bắt đầu từ một chuỗi nào đó, là khác không, thì bán kính hội tụ của nó bằng giới hạn theo tỷ lệ giữa các giá trị tuyệt đối của hệ số của các thành viên chung sau của chuỗi, tức là

Ví dụ 1. Tìm miền hội tụ của một chuỗi lũy thừa

Dung dịch. Nơi đây

Sử dụng công thức (28), chúng tôi tìm thấy bán kính hội tụ của chuỗi này:

Chúng ta hãy nghiên cứu sự hội tụ của chuỗi tại các điểm cuối của khoảng hội tụ. Ví dụ 13 cho thấy rằng chuỗi này hội tụ cho x= 1 và phân kỳ ở x= -1. Do đó, vùng hội tụ là nửa khoảng.

Ví dụ 2. Tìm miền hội tụ của một chuỗi lũy thừa

Dung dịch. Các hệ số của chuỗi là số dương, và

Hãy để chúng tôi tìm giới hạn của tỷ lệ này, tức là bán kính hội tụ chuỗi công suất:

Chúng tôi khảo sát sự hội tụ của chuỗi ở các điểm cuối của khoảng. Thay thế giá trị x= -1/5 và x= 1/5 trong chuỗi này cho:

Đầu tiên của chuỗi này hội tụ (xem ví dụ 5). Nhưng sau đó, theo định lý của đoạn "Hội tụ tuyệt đối", chuỗi thứ hai cũng hội tụ, và vùng hội tụ của nó là đoạn

Ví dụ 3. Tìm miền hội tụ của một chuỗi lũy thừa

Dung dịch. Nơi đây

Sử dụng công thức (28), chúng tôi tìm thấy bán kính hội tụ của chuỗi:

Chúng ta hãy nghiên cứu sự hội tụ của chuỗi cho các giá trị. Thay thế chúng trong loạt bài này, tương ứng, chúng ta nhận được

Cả hai chuỗi phân kỳ vì điều kiện hội tụ cần thiết không được thỏa mãn (các số hạng chung của chúng không có xu hướng bằng 0 tại). Vì vậy, ở cả hai đầu của khoảng hội tụ, chuỗi này phân kỳ và vùng hội tụ của nó là khoảng.

Ví dụ 5. Tìm miền hội tụ của một chuỗi lũy thừa

Dung dịch. Chúng tôi tìm thấy mối liên hệ, ở đâu và :

Theo công thức (28), bán kính hội tụ của chuỗi này

,

nghĩa là, chuỗi chỉ hội tụ khi x= 0 và phân kỳ cho các giá trị khác X.

Các ví dụ cho thấy rằng chuỗi hoạt động khác nhau ở các đầu của khoảng hội tụ. Trong ví dụ 1, chuỗi hội tụ ở một đầu của khoảng hội tụ và phân kỳ ở điểm kia, trong ví dụ 2, chuỗi hội tụ ở cả hai đầu, trong ví dụ 3, chuỗi hội tụ ở cả hai đầu.

Công thức về bán kính hội tụ của một chuỗi lũy thừa thu được theo giả thiết rằng tất cả các hệ số của các số hạng của chuỗi, bắt đầu từ một số, là khác không. Do đó, chỉ cho phép áp dụng công thức (28) trong những trường hợp này. Nếu điều kiện này bị vi phạm, thì bán kính hội tụ của chuỗi lũy thừa nên được tìm kiếm bằng cách sử dụng dấu hiệu của d'Alembert hoặc, bằng cách thay đổi một biến, bằng cách biến đổi chuỗi thành dạng thỏa mãn điều kiện đã chỉ định.

Ví dụ 6. Tìm khoảng hội tụ của một chuỗi lũy thừa

Dung dịch. Loạt bài này không chứa các thuật ngữ có độ lẻ X. Do đó, chúng tôi biến đổi chuỗi bằng cách thiết lập. Sau đó, chúng tôi nhận được loạt

công thức (28) có thể được sử dụng để tìm bán kính hội tụ của nó. Kể từ, và, khi đó bán kính hội tụ của chuỗi này

Do đó, từ đẳng thức chúng ta thu được, chuỗi này hội tụ trên khoảng.

Tổng chuỗi lũy thừa. Sự khác biệt và tích hợp của chuỗi nguồn

Hãy để cho một chuỗi quyền lực

bán kính hội tụ R> 0, tức là chuỗi này hội tụ trên khoảng.

Sau đó, mỗi giá trị X từ khoảng hội tụ tương ứng với một số tổng của chuỗi. Do đó, tổng của chuỗi lũy thừa là một hàm của X trên khoảng hội tụ. Biểu thị nó qua f(x), chúng ta có thể viết đẳng thức

hiểu nó theo nghĩa là tổng của chuỗi tại mỗi điểm X từ khoảng đồng biến bằng giá trị của hàm số f(x) tại thời điểm này. Theo nghĩa tương tự, chúng ta sẽ nói rằng chuỗi lũy thừa (29) hội tụ đến hàm f(x) trên khoảng hội tụ.

Bên ngoài khoảng hội tụ, đẳng thức (30) không có ý nghĩa gì.

Ví dụ 7 Tìm tổng của chuỗi lũy thừa

Dung dịch. Đây là một loạt hình học một= 1 và q= x. Do đó, tổng của nó là một hàm . Chuỗi hội tụ nếu, và là khoảng hội tụ của nó. Do đó, bình đẳng

chỉ hợp lệ cho các giá trị, mặc dù hàm được xác định cho tất cả các giá trị X, Ngoài ra X= 1.

Có thể chứng minh rằng tổng của chuỗi lũy thừa f(x) là liên tục và có thể phân biệt trên bất kỳ khoảng nào trong khoảng hội tụ, cụ thể là tại bất kỳ điểm nào của khoảng hội tụ của chuỗi.

Chúng ta hãy trình bày các định lý về sự phân biệt theo kỳ và tích phân của chuỗi lũy thừa.

Định lý 1. Chuỗi lũy thừa (30) trong khoảng thời gian hội tụ của nó có thể được phân biệt theo số hạng với số lần không giới hạn và chuỗi lũy thừa thu được có cùng bán kính hội tụ như chuỗi ban đầu và tổng của chúng tương ứng bằng.

Định lý 2. Chuỗi lũy thừa (30) có thể được tích hợp theo thời hạn không giới hạn số lần trong phạm vi từ 0 đến X, nếu, và chuỗi lũy thừa thu được có cùng bán kính hội tụ như chuỗi ban đầu, và tổng của chúng tương ứng bằng

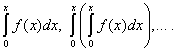
Mở rộng các chức năng thành chuỗi công suất

Hãy để chức năng f(x), sẽ được mở rộng thành một chuỗi lũy thừa, tức là biểu diễn dưới dạng (30):

Vấn đề là xác định các hệ số hàng (30). Để làm được điều này, phân biệt đẳng thức (30) theo thuật ngữ, chúng tôi tuần tự tìm:

……………………………………………….. (31)

Giả sử bằng nhau (30) và (31) X= 0, chúng tôi tìm thấy

Thay các biểu thức tìm được vào đẳng thức (30), chúng ta thu được

(32)

Hãy để chúng tôi tìm sự mở rộng chuỗi Maclaurin của một số hàm cơ bản.

Ví dụ 8 Mở rộng chức năng trong chuỗi Maclaurin

Dung dịch. Các đạo hàm của hàm này giống như chính hàm:

Do đó, khi X= 0 chúng tôi có

Thay các giá trị này vào công thức (32), chúng ta sẽ có được sự mở rộng mong muốn:

(33)

Chuỗi này hội tụ trên toàn bộ trục số (bán kính hội tụ của nó là).

Nếu hàm f (x) có đạo hàm tất cả các bậc trên một khoảng nào đó chứa điểm a, thì công thức Taylor có thể được áp dụng cho nó:
,
ở đâu rn- cái gọi là số hạng còn lại hoặc phần còn lại của chuỗi, nó có thể được ước tính bằng công thức Lagrange:
, trong đó số x nằm giữa x và a.

f (x) =

tại điểm x 0 = Số phần tử hàng 3 4 5 6 7

Sử dụng khai triển các hàm cơ bản e x, cos (x), sin (x), ln (1 + x), (1 + x) m

Quy tắc nhập hàm:

Nếu vì một số giá trị X rn→ 0 lúc N→ ∞, thì trong giới hạn, công thức Taylor biến giá trị này thành giá trị hội tụ Chuỗi Taylor:
,
Do đó, hàm f (x) có thể được khai triển thành một chuỗi Taylor tại điểm x đang xét nếu:
1) nó có các dẫn xuất của tất cả các lệnh;
2) chuỗi đã xây dựng hội tụ tại điểm này.

Đối với a = 0, chúng tôi nhận được một chuỗi có tên là gần Maclaurin:
,
Mở rộng các hàm đơn giản nhất (cơ bản) trong chuỗi Maclaurin:
hàm số mũ
, R = ∞
Hàm lượng giác
, R = ∞
, R = ∞
, (-π / 2< x < π/2), R=π/2
Hàm actgx không mở rộng theo lũy thừa của x, bởi vì ctg0 = ∞
Hàm hyperbolic


Hàm lôgarit
, -1
Chuỗi nhị thức
.

Ví dụ 1. Mở rộng hàm thành một chuỗi lũy thừa f (x) = 2x.
Dung dịch. Hãy để chúng tôi tìm các giá trị của hàm và các đạo hàm của nó tại X=0
f (x) = 2x, f ( 0) = 2 0 =1;
f "(x) = 2x ln2, f "( 0) = 2 0 ln2 = ln2;
f "" (x) = 2x Năm 2 2, f "" ( 0) = 2 0 log 2 2 = log 2 2;
…
f (n) (x) = 2x ln N 2, f (n) ( 0) = 2 0 ln N 2 = ln N 2.
Thay các giá trị thu được của các đạo hàm vào công thức chuỗi Taylor, ta được:

Bán kính hội tụ của chuỗi này bằng vô cùng, do đó, sự mở rộng này có giá trị -∞<x<+∞.

Ví dụ # 2. Viết chuỗi Taylor theo lũy thừa ( X+4) cho chức năng f (x) = e x.
Dung dịch. Tìm các đạo hàm của hàm e x và giá trị của chúng tại điểm X=-4.
f (x)= e x, f (-4) = e -4 ;
f "(x)= e x, f "(-4) = e -4 ;
f "" (x)= e x, f "" (-4) = e -4 ;
…
f (n) (x)= e x, f (n) ( -4) = e -4 .
Do đó, chuỗi Taylor mong muốn của hàm có dạng:

Mở rộng này cũng hợp lệ cho -∞<x<+∞.

Ví dụ # 3. Mở rộng chức năng f (x)= ln x trong một chuỗi theo độ ( X- 1),
(tức là trong một chuỗi Taylor ở vùng lân cận của điểm X=1).
Dung dịch. Chúng tôi tìm các đạo hàm của hàm này.
f (x) = lnx,,,

f (1) = ln1 = 0, f "(1) = 1, f" "(1) = - 1, f" "" (1) = 1 * 2, ..., f (n) = (- 1) n-1 (n-1)!
Thay các giá trị này vào công thức, chúng ta nhận được chuỗi Taylor mong muốn:

Với sự trợ giúp của thử nghiệm d'Alembert, người ta có thể xác minh rằng chuỗi hội tụ ở ½x-1½<1 . Действительно,

Chuỗi hội tụ nếu ½ X- 1½<1, т.е. при 0<x<2. При X= 2 chúng ta thu được một chuỗi xen kẽ thỏa mãn các điều kiện của thử nghiệm Leibniz. Với x = 0, hàm không xác định. Như vậy, vùng hội tụ của chuỗi Taylor là khoảng nửa mở (0; 2].

Ví dụ # 4. Mở rộng hàm trong một chuỗi lũy thừa.
Dung dịch. Trong phép phân tích (1), chúng ta thay x bằng -x 2, chúng ta nhận được:
, -∞

Ví dụ số 5. Mở rộng hàm trong chuỗi Maclaurin.
Dung dịch. Chúng ta có
Sử dụng công thức (4), chúng ta có thể viết:

thay x trong công thức -x, ta được:

Từ đây ta tìm được: ln (1 + x) -ln (1-x) = -
Mở rộng dấu ngoặc, sắp xếp lại các điều khoản của chuỗi và giảm các điều khoản tương tự, chúng tôi nhận được
. Chuỗi này hội tụ trong khoảng (-1; 1) vì nó có được từ hai chuỗi, mỗi chuỗi hội tụ trong khoảng này.

Bình luận .
Công thức (1) - (5) cũng có thể được sử dụng để mở rộng các hàm tương ứng trong chuỗi Taylor, tức là để khai triển các hàm theo lũy thừa số nguyên dương ( Hà). Để làm được điều này, cần phải thực hiện các phép biến đổi giống hệt như vậy trên một hàm đã cho để có được một trong các hàm (1) - (5), trong đó thay vì X chi phí k ( Hà) m, với k là một số không đổi, m là một số nguyên dương. Thường thuận tiện để thay đổi biến t=Hà và mở rộng hàm kết quả đối với t trong chuỗi Maclaurin.

Phương pháp này dựa trên định lý về tính duy nhất của khai triển một hàm trong một chuỗi lũy thừa. Bản chất của định lý này là trong vùng lân cận của cùng một điểm, không thể thu được hai chuỗi lũy thừa khác nhau sẽ hội tụ về cùng một hàm, bất kể việc khai triển của nó được thực hiện như thế nào.

Ví dụ số 5a. Mở rộng hàm trong một chuỗi Maclaurin, chỉ ra vùng hội tụ.
Dung dịch. Đầu tiên chúng ta tìm 1-x-6x 2 = (1-3x) (1 + 2x) ,.
đến tiểu học:

Phân số 3 / (1-3x) có thể được xem như là tổng của một cấp tiến hình học giảm vô hạn có mẫu số là 3x nếu | 3x |< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

với miền hội tụ | x |< 1/3.

Ví dụ số 6. Khai triển hàm theo chuỗi Taylor trong vùng lân cận của điểm x = 3.
Dung dịch. Vấn đề này có thể được giải quyết, như trước đây, bằng cách sử dụng định nghĩa của chuỗi Taylor, mà cần phải tìm các đạo hàm của các hàm và giá trị của chúng tại X= 3. Tuy nhiên, sẽ dễ dàng hơn khi sử dụng phân tích hiện có (5):
=
Chuỗi kết quả hội tụ tại hoặc -3

Ví dụ số 7. Viết chuỗi Taylor theo lũy thừa (x -1) của hàm ln (x + 2).
Dung dịch.


Chuỗi hội tụ tại, hoặc -2< x < 5.

Ví dụ số 8. Khai triển hàm f (x) = sin (πx / 4) theo chuỗi Taylor xung quanh điểm x = 2.
Dung dịch. Hãy thực hiện thay thế t = x-2:

Sử dụng khai triển (3), trong đó chúng ta thay π / 4 t cho x, chúng ta nhận được:

Chuỗi kết quả hội tụ đến hàm đã cho tại -∞< π / 4 t<+∞, т.е. при (-∞Bằng cách này,
, (-∞

Tính toán gần đúng sử dụng chuỗi lũy thừa

Chuỗi lũy thừa được sử dụng rộng rãi trong các phép tính gần đúng. Với sự trợ giúp của họ, với độ chính xác nhất định, bạn có thể tính giá trị của nghiệm nguyên, hàm lượng giác, logarit của số, tích phân xác định. Chuỗi cũng được sử dụng trong tích phân của các phương trình vi phân.
Hãy xem xét sự mở rộng của hàm trong một chuỗi lũy thừa:

Để tính giá trị gần đúng của một hàm tại một điểm đã cho X, thuộc khu vực hội tụ của chuỗi được chỉ định, chuỗi đầu tiên N các thành viên ( N là một số hữu hạn), và các số hạng còn lại bị loại bỏ:

Để ước tính sai số của giá trị gần đúng thu được, cần ước lượng phần dư r n (x) bị loại bỏ. Đối với điều này, các phương pháp sau được sử dụng:

• nếu chuỗi kết quả là ký tự xen kẽ, thì thuộc tính sau sẽ được sử dụng: đối với một chuỗi xen kẽ thỏa mãn các điều kiện Leibniz, giá trị tuyệt đối của phần còn lại của chuỗi không vượt quá số hạng bị loại bỏ đầu tiên.
• nếu chuỗi đã cho có dấu không đổi, thì chuỗi bao gồm các số hạng bị loại bỏ được so sánh với một cấp tiến hình học giảm vô hạn.
• trong trường hợp chung, để ước tính phần còn lại của chuỗi Taylor, bạn có thể sử dụng công thức Lagrange: a x ).

Ví dụ 1. Tính ln (3) trong phạm vi 0,01.
Dung dịch. Hãy sử dụng phép phân rã, trong đó x = 1/2 (xem ví dụ 5 trong chủ đề trước):

Hãy kiểm tra xem chúng ta có thể loại bỏ phần còn lại sau ba số hạng đầu tiên của khai triển hay không, đối với điều này, chúng tôi đánh giá nó bằng cách sử dụng tổng của một tiến trình hình học giảm vô hạn:

Vì vậy, chúng tôi có thể loại bỏ phần còn lại này và nhận được

Ví dụ # 2. Tính chính xác đến 0,0001.
Dung dịch. Hãy sử dụng chuỗi nhị thức. Vì 5 3 là khối số nguyên gần nhất với 130, nên biểu diễn số 130 là 130 = 5 3 +5.



vì số hạng thứ tư của chuỗi xen kẽ dấu hiệu thu được thỏa mãn phép thử Leibniz đã nhỏ hơn độ chính xác cần thiết:
, vì vậy nó và các điều khoản sau nó có thể bị loại bỏ.
Nhiều tích phân xác định hoặc không đúng thực tế cần thiết không thể được tính bằng công thức Newton-Leibniz, bởi vì ứng dụng của nó liên quan đến việc tìm một đạo hàm, thường không có biểu thức trong các hàm cơ bản. Cũng có thể xảy ra rằng việc tìm kiếm một chất chống chất diệt khuẩn là có thể, nhưng tốn nhiều công sức một cách không cần thiết. Tuy nhiên, nếu tích phân được mở rộng thành một chuỗi lũy thừa và các giới hạn tích phân thuộc khoảng hội tụ của chuỗi này, thì có thể tính gần đúng tích phân với độ chính xác định trước.

Ví dụ # 3. Tính tích phân ∫ 0 1 4 sin (x) x để trong khoảng 10 -5.
Dung dịch. Tích phân không xác định tương ứng không thể được biểu diễn trong các hàm cơ bản, tức là là một "tích phân bất khả thi". Không thể áp dụng công thức Newton-Leibniz ở đây. Hãy để chúng tôi tính tích phân gần đúng.
Phân chia thuật ngữ theo thuật ngữ trong chuỗi cho tội lỗi x trên x, chúng tôi nhận được:

Tích hợp số hạng của chuỗi này theo số hạng (điều này là có thể, vì các giới hạn của tích phân thuộc khoảng hội tụ của chuỗi này), chúng ta thu được:

Vì chuỗi kết quả thỏa mãn các điều kiện của Leibniz và nó đủ để lấy tổng của hai số hạng đầu tiên để có được giá trị mong muốn với độ chính xác cho trước.
Do đó, chúng tôi thấy
.

Ví dụ # 4. Tính tích phân ∫ 0 1 4 e x 2 trong phạm vi 0,001.
Dung dịch.
. Hãy kiểm tra xem chúng ta có thể loại bỏ phần còn lại sau số hạng thứ hai của chuỗi kết quả hay không.
0,0001<0.001. Следовательно, .

Trong lý thuyết về chuỗi hàm, phần dành cho việc mở rộng một hàm thành một chuỗi chiếm một vị trí trung tâm.

Do đó, bài toán được đặt ra: đối với một hàm cho trước nó được yêu cầu để tìm một chuỗi công suất như vậy

hội tụ trên một khoảng nào đó và tổng của nó bằng
, những thứ kia.

= ..

Nhiệm vụ này được gọi là vấn đề khai triển một hàm thành một chuỗi lũy thừa.

Điều kiện cần thiết để khai triển một hàm thành một chuỗi lũy thừa là khả năng phân biệt của nó với số lần vô hạn - điều này xuất phát từ các tính chất của chuỗi lũy thừa hội tụ. Điều kiện này được thỏa mãn, như một quy luật, đối với các hàm cơ bản trong miền định nghĩa của chúng.

Vì vậy, giả sử rằng hàm
có các dẫn xuất của bất kỳ đơn đặt hàng nào. Nó có thể được mở rộng thành một chuỗi lũy thừa, nếu có, làm thế nào để tìm thấy chuỗi này? Phần thứ hai của vấn đề dễ giải quyết hơn, vì vậy hãy bắt đầu với nó.

Giả sử rằng hàm
có thể được biểu diễn dưới dạng tổng của một chuỗi lũy thừa hội tụ trong một khoảng có chứa một điểm X 0 :

= .. (*)

ở đâu một 0 ,một 1 ,một 2 ,...,một P ,... - hệ số không chắc chắn (chưa).

Hãy để chúng tôi đặt giá trị bằng (*) x = x 0 , sau đó chúng tôi nhận được

.

Chúng tôi phân biệt số hạng của chuỗi lũy thừa (*) theo thuật ngữ

= ..

và đặt ở đây x = x 0 , chúng tôi nhận được

.

Với sự khác biệt tiếp theo, chúng tôi nhận được loạt

= ..

giả định x = x 0 , chúng tôi nhận được
, ở đâu
.

Sau P- sự khác biệt gấp đôi chúng tôi nhận được

Giả sử trong bình đẳng cuối cùng x = x 0 , chúng tôi nhận được
, ở đâu

Vì vậy, các hệ số được tìm thấy

,
,
, …,
,….,

thay thế hàng nào thành một hàng (*), chúng ta nhận được

Chuỗi kết quả được gọi là gần taylor cho chức năng
.

Vì vậy, chúng tôi đã thiết lập rằng nếu hàm có thể được mở rộng thành một chuỗi lũy thừa theo lũy thừa (x - x 0 ), thì khai triển này là duy nhất và chuỗi kết quả nhất thiết phải là chuỗi Taylor.

Lưu ý rằng chuỗi Taylor có thể thu được đối với bất kỳ hàm nào có đạo hàm theo bậc bất kỳ tại điểm x = x 0 . Nhưng điều này không có nghĩa là một dấu bằng có thể được đặt giữa hàm và chuỗi kết quả, tức là rằng tổng của chuỗi bằng hàm ban đầu. Thứ nhất, một đẳng thức như vậy chỉ có ý nghĩa trong vùng hội tụ và chuỗi Taylor thu được cho hàm có thể phân kỳ, và thứ hai, nếu chuỗi Taylor hội tụ, thì tổng của nó có thể không trùng với hàm ban đầu.

3.2. Điều kiện đủ để khai triển một hàm thành một chuỗi Taylor

Hãy để chúng tôi xây dựng một tuyên bố với sự trợ giúp của vấn đề đã nêu sẽ được giải quyết.

Nếu chức năng
trong một số vùng lân cận của điểm x 0 có các dẫn xuất lên đến (N+ 1) -th order bao gồm, sau đó trong vùng lân cận này, chúng tôi cócông thức Taylor

ở đâuR N (X)- số hạng dư của công thức Taylor - có dạng (dạng Lagrange)

ở đâu dấu chấmξ nằm giữa x và x 0 .

Lưu ý rằng có sự khác biệt giữa chuỗi Taylor và công thức Taylor: công thức Taylor là một tổng hữu hạn, tức là P - số cố định.

Nhớ lại rằng tổng của chuỗi S(x) có thể được định nghĩa là giới hạn của chuỗi hàm của các tổng từng phần S P (x) tại một số khoảng thời gian X:

.

Theo đó, để mở rộng một hàm thành một chuỗi Taylor có nghĩa là tìm một chuỗi sao cho bất kỳ XX

Chúng tôi viết công thức Taylor dưới dạng

thông báo rằng
xác định lỗi chúng tôi nhận được, thay thế chức năng f(x) đa thức S N (x).

Nếu một
, sau đó
,những thứ kia. hàm mở rộng thành một chuỗi Taylor. Ngược lại, nếu
, sau đó
.

Như vậy, chúng tôi đã chứng minh tiêu chí cho việc khai triển một hàm thành một chuỗi Taylor.

Để trong một khoảng thời gian nào đó, hàmf(x) mở rộng trong một chuỗi Taylor, điều đó là cần thiết và đủ trong khoảng này
, ở đâuR N (x) là phần còn lại của chuỗi Taylor.

Với sự trợ giúp của tiêu chí đã xây dựng, người ta có thể đạt được hợp lýđiều kiện để khai triển một hàm thành một chuỗi Taylor.

Nếu trongmột số vùng lân cận của điểm x 0 các giá trị tuyệt đối của tất cả các đạo hàm của một hàm được giới hạn bởi cùng một số M≥ 0, tức là

, to trong vùng lân cận này, hàm mở rộng thành một chuỗi Taylor.

Từ trên nó sau thuật toánmở rộng chức năng f(x) trong một chuỗi Taylor trong vùng lân cận của điểm X 0 :

1. Tìm các hàm đạo hàm f(x):

f (x), f ’(x), f” (x), f ’” (x), f (N) (x),…

2. Ta tính giá trị của hàm số và các giá trị của các đạo hàm của nó tại điểm X 0

f (x 0 ), f '(x 0 ), f ”(x 0 ), f ’” (x 0 ), f (N) (x 0 ),…

3. Chúng tôi chính thức viết chuỗi Taylor và tìm vùng hội tụ của chuỗi lũy thừa.

4. Chúng tôi kiểm tra việc đáp ứng các điều kiện đủ, tức là thiết lập cho cái nào X từ vùng hội tụ, phần còn lại R N (x) có xu hướng bằng không lúc
hoặc
.

Việc mở rộng các hàm trong một chuỗi Taylor theo thuật toán này được gọi là khai triển của một hàm trong chuỗi Taylor theo định nghĩa hoặc phân hủy trực tiếp.