Phương trình Schrödinger đứng yên được viết cho. Phương trình sóng Schrödinger
Giới thiệu
Được biết, quá trình cơ học lượng tử là một trong những điều khó hiểu nhất. Đây không phải là quá nhiều về cái mới và "bất thường" bộ máy toán học trước hết là do khó hiểu được tính cách mạng, từ quan điểm của vật lý cổ điển, những ý tưởng làm cơ sở cho cơ học lượng tử và sự phức tạp của việc diễn giải các kết quả.
Hầu hết dạy học Qua cơ lượng tử phần trình bày của tài liệu, như một quy luật, dựa trên việc phân tích nghiệm của các phương trình Schrödinger cố định. Tuy nhiên, cách tiếp cận cố định không cho phép so sánh trực tiếp kết quả giải một bài toán cơ học lượng tử với các kết quả cổ điển tương tự. Ngoài ra, nhiều quá trình được nghiên cứu trong quá trình cơ học lượng tử (chẳng hạn như sự di chuyển của một hạt qua hàng rào thế năng, sự phân rã của trạng thái gần như dừng, v.v.) về nguyên tắc là không dừng trong tự nhiên và do đó, có thể chỉ được hiểu một cách đầy đủ trên cơ sở các nghiệm của phương trình bất động Schrödinger. Vì số lượng bài toán có thể giải bằng phương pháp phân tích là ít nên việc sử dụng máy tính trong quá trình nghiên cứu cơ học lượng tử đặc biệt phù hợp.
phương trình Schrödinger và ý nghĩa vật lý quyết định của mình
Phương trình sóng Schrödinger
Một trong những phương trình cơ bản của cơ học lượng tử là phương trình Schrödinger, nó xác định sự thay đổi trạng thái của các hệ lượng tử theo thời gian. Nó được viết dưới dạng
trong đó H là Hamiltonian của hệ thống, trùng với toán tử năng lượng nếu nó không phụ thuộc vào thời gian. Loại toán tử được xác định bởi các thuộc tính của hệ thống. Đối với chuyển động phi tương đối tính của hạt có khối lượng trong trường thế U(r), toán tử là số thực và được biểu diễn bằng tổng các toán tử của động năng và thế năng của hạt
Nếu hạt chuyển động trong trường điện từ, thì toán tử Hamilton sẽ phức tạp.
Mặc dù phương trình (1.1) là phương trình bậc nhất theo thời gian nhưng do đơn vị ảo nên nó cũng có nghiệm tuần hoàn. Do đó, phương trình Schrödinger (1.1) thường được gọi là phương trình sóng Schrödinger, và nghiệm của nó được gọi là hàm sóng phụ thuộc thời gian. Phương trình (1.1) cho hình thức đã biết toán tử H cho phép bạn xác định giá trị của hàm sóng tại bất kỳ thời điểm nào sau đó, nếu giá trị này được biết trong khoảnh khắc ban đầu thời gian. Như vậy, phương trình sóng Schrödinger thể hiện nguyên lý nhân quả trong cơ học lượng tử.
Phương trình sóng Schrödinger có thể thu được dựa trên những cân nhắc chính thức sau đây. Trong cơ học cổ điển, người ta biết rằng nếu năng lượng được cho dưới dạng hàm của tọa độ và động lượng
sau đó chuyển sang phương trình Hamilton-Jacobi cổ điển cho hàm tác dụng S
có thể thu được từ (1.3) bằng phép biến đổi chính thức
Tương tự, phương trình (1.1) nhận được từ (1.3) khi chuyển từ (1.3) về phương trình toán tử bằng một phép biến đổi chính thức
nếu (1.3) không chứa các tích của tọa độ và xung lượng, hoặc chứa các tích của chúng mà sau khi chuyển cho các toán tử (1.4) sẽ giao hoán với nhau. Cân bằng sau phép biến đổi này kết quả của hành động trên hàm của các toán tử bên phải và bên trái của đẳng thức toán tử kết quả, chúng tôi đi đến phương trình sóng(1.1). Tuy nhiên, người ta không nên coi những phép biến đổi hình thức này là dẫn xuất của phương trình Schrödinger. Phương trình Schrödinger là sự tổng quát hóa dữ liệu thực nghiệm. Nó không bắt nguồn từ cơ học lượng tử, cũng như các phương trình Maxwell không bắt nguồn từ điện động lực học, nguyên lý ảnh hưởng ít nhất(hay phương trình Newton) trong cơ học cổ điển.
Dễ dàng chứng minh rằng phương trình (1.1) thỏa mãn đối với hàm sóng
miêu tả phong trào tự do các hạt với giá trị nhất định thúc đẩy. TRONG trường hợp chung tính hợp lệ của phương trình (1.1) được chứng minh bằng sự đồng ý với kinh nghiệm của tất cả các kết luận thu được với sự trợ giúp của phương trình này.
Hãy chứng minh rằng phương trình (1.1) hàm ý đẳng thức quan trọng
chỉ ra việc duy trì sự chuẩn hóa của hàm sóng theo thời gian. Chúng ta hãy nhân (1.1) ở bên trái với hàm * và nhân phương trình phức liên hợp với (1.1) với hàm và trừ phương trình thứ hai khỏi phương trình thứ nhất thu được; sau đó chúng tôi tìm thấy
Tích phân hệ thức này trên tất cả các giá trị của các biến và có xét đến tính tự liên kết của toán tử, ta thu được (1.5).
Nếu chúng ta thay thế biểu thức rõ ràng của toán tử Hamilton (1.2) cho chuyển động của một hạt trong trường thế vào quan hệ (1.6), thì chúng ta sẽ đi đến phương trình vi phân(phương trình liên tục)
ở đâu là mật độ xác suất và vectơ
có thể gọi là véc tơ mật độ dòng xác suất.
Hàm sóng phức luôn có thể được biểu diễn dưới dạng
ở đâu và -- hàm thực thời gian và tọa độ. Vậy mật độ xác suất
và mật độ dòng xác suất
Từ (1.9) suy ra j = 0 với mọi hàm mà hàm Φ không phụ thuộc vào tọa độ. Đặc biệt, j= 0 cho tất cả các hàm thực.
Các nghiệm của phương trình Schrödinger (1.1) thường được biểu diễn bằng các hàm phức. Sử dụng các chức năng phức tạp là rất thuận tiện, mặc dù không cần thiết. thay vì một chức năng phức tạp trạng thái của hệ thống có thể được mô tả bởi hai hàm thực và thỏa mãn hai phương trình liên quan. Ví dụ, nếu toán tử H là thực, thì thay hàm vào (1.1) và tách phần thực và phần ảo, ta thu được hệ hai phương trình
trong trường hợp này, mật độ xác suất và mật độ dòng xác suất có dạng
Các hàm sóng trong biểu diễn động lượng.
Biến đổi Fourier của hàm sóng đặc trưng cho sự phân bố động lượng ở trạng thái lượng tử. Cần phải rút ra một phương trình tích phân với phép biến đổi Fourier của thế năng là hạt nhân.
Giải pháp. Có hai mối quan hệ nghịch biến lẫn nhau giữa các chức năng và .
Nếu quan hệ (2.1) được sử dụng làm định nghĩa và một phép toán được áp dụng cho nó, thì, có tính đến định nghĩa của hàm 3 chiều,
kết quả là, dễ thấy, ta thu được hệ thức nghịch đảo (2.2). Các cân nhắc tương tự được sử dụng dưới đây trong dẫn xuất của quan hệ (2.8).
sau đó đối với hình ảnh Fourier của tiềm năng chúng ta có
Giả sử rằng tính năng mới thỏa mãn phương trình Schrödinger
Thay ở đây thay và lần lượt các biểu thức (2.1) và (2.3), ta được
TRONG tích phân kép chúng ta chuyển từ tích phân theo biến sang tích phân theo biến, và sau đó chúng ta lại biểu thị biến mới này bằng . Tích phân trên biến mất ở bất kỳ giá trị nào chỉ khi tích phân chính nó bằng 0, nhưng sau đó
Đây là phương trình tích phân mong muốn với phép biến đổi Fourier của thế năng là hạt nhân. Tất nhiên, phương trình tích phân (2.6) chỉ có thể thu được với điều kiện tồn tại biến đổi Fourier của thế (2.4); đối với điều này, ví dụ, tiềm năng phải giảm trên khoảng cách lớn, ít nhất là, ở đâu.
Cần lưu ý rằng từ điều kiện chuẩn hóa
bình đẳng sau
Điều này có thể được chỉ ra bằng cách thay biểu thức (2.1) cho hàm vào (2.7):
Nếu ở đây ta thực hiện tích phân trên trước thì sẽ dễ dàng thu được quan hệ (2.8).
Từ cách giải thích thống kê về sóng de Broglie (xem § và hệ thức bất định Heisenberg (xem § 215), theo đó phương trình chuyển động trong cơ học lượng tử, mô tả chuyển động của các vi hạt theo nhiều cách khác nhau trường lực, phải có một phương trình mà từ đó quan sát bằng thực nghiệm tính chất sóng vật rất nhỏ.
Phương trình chính phải là một phương trình cho hàm sóng, vì chính điều này, hay chính xác hơn, đại lượng |Ф|2, xác định xác suất hạt tồn tại tại thời điểm t trong khối lượng dv, trong vùng có tọa độ và X+ dx, y+dy,
z và Vì phương trình mong muốn phải tính đến tính chất sóng của các hạt nên nó phải là phương trình sóng, giống như một phương trình mô tả sóng điện từ. phương trình cơ bản cơ học lượng tử phi tương đối tínhđược xây dựng vào năm 1926 bởi E. Schrödinger. Phương trình Schrödinger, giống như tất cả các phương trình cơ bản của vật lý (ví dụ, phương trình Newton trong cơ học cổ điển và phương trình Maxwell cho điện từ trường), không bắt nguồn, nhưng được mặc định. Tính đúng đắn của phương trình này được xác nhận bằng sự đồng ý với kinh nghiệm về các kết quả thu được với sự trợ giúp của nó, do đó, mang lại cho nó đặc tính của một quy luật tự nhiên. phương trình
 Schrödinger có dạng
Schrödinger có dạng
|
đơn vị tưởng tượng, y,z,t) -
Hàm thế năng của một hạt trong trường lực mà nó chuyển động; z,t) - mong muốn hàm sóng
Phương trình đúng cho bất kỳ hạt nào (có spin bằng 0; xem § 225) chuyển động với tốc độ nhỏ (so với tốc độ ánh sáng), tức là với tốc độ v Với. Nó được bổ sung bởi các điều kiện áp đặt cho hàm sóng: 1) hàm sóng phải hữu hạn, có một giá trị và liên tục (xem § 216);
2) dẫn xuất -, -, -, phải-
dx làm
chúng tôi được liên tục; 3) hàm |Ф|2 phải có thể tích phân; điều kiện này trong các trường hợp đơn giản nhất giảm xuống
Điều kiện chuẩn hóa (216.3).
Để đi đến phương trình Schrödinger, chúng ta xét một hạt chuyển động tự do, mà theo de Broglie, là liên kết Để đơn giản, chúng ta xét trường hợp một chiều. Phương trình của sóng phẳng truyền dọc theo một trục X, có dạng (xem § 154) t) = A cos - hoặc trong ký hiệu phức tạp t)- Do đó, sóng phẳng de Broglie có dạng
![]() (217.2)
(217.2)
(có tính đến điều đó - = -). trong lượng tử thứ
Số mũ được lấy với dấu “-”, vì chỉ |Ф|2 có ý nghĩa vật lý, điều này không có ý nghĩa. Sau đó
 |
Sử dụng mối quan hệ giữa năng lượng e và động lượng = --) và thay thế
![]() biểu thức (217.3), ta thu được phương trình vi phân
biểu thức (217.3), ta thu được phương trình vi phân
trùng với phương trình cho trường hợp U- O (chúng tôi coi là một hạt miễn phí).
Nếu một hạt chuyển động trong một trường lực được đặc trưng bởi thế năng bạn, Cái đó Tổng năng lượng eđược tạo thành từ động năng và thế năng. Thực hiện suy luận tương tự và sử dụng mối quan hệ giữa ("cho
trường hợp = EU), chúng ta đi đến một phương trình vi phân trùng với (217.1).
Lý luận trên không nên được coi là đạo hàm của phương trình Schrödinger. Họ chỉ giải thích làm thế nào để đạt được phương trình này. Bằng chứng về tính đúng đắn của phương trình Schrödinger là sự phù hợp với kinh nghiệm của các kết luận mà nó dẫn đến.
Phương trình (217.1) là phương trình tổng quát Schrödinger. Ông cũng được gọi là phương trình Schrödinger phụ thuộc thời gian. Cho nhieu hiện tượng vật lý xảy ra trong thế giới vi mô, phương trình (217.1) có thể được đơn giản hóa bằng cách loại bỏ sự phụ thuộc thời gian, nói cách khác, để tìm phương trình Schrödinger cho trạng thái đứng yên- các trạng thái có giá trị năng lượng cố định.Điều này có thể xảy ra nếu trường lực trong đó hạt chuyển động đứng yên, tức là hàm U=z) không phụ thuộc rõ ràng vào thời gian và có ý nghĩa thế năng.
TRONG trường hợp này nghiệm của phương trình Schrödinger có thể được biểu diễn dưới dạng tích của hai hàm, một trong số đó là hàm chỉ tọa độ, hàm kia chỉ là hàm của thời gian và sự phụ thuộc vào thời gian được thể hiện
được nhân với e" = e, do đó
![]() (217.4)
(217.4)
Ở đâu e là năng lượng toàn phần của hạt, không đổi trong trường hợp trường đứng yên. Thay (217.4) vào (217.1), ta được

Từ đó, sau khi chia cho ước chung e của các phép biến hình tương ứng
 ing, chúng tôi đi đến một phương trình xác định chức năng
ing, chúng tôi đi đến một phương trình xác định chức năng
phương trình tương đương-
Khái niệm của Schrödinger về trạng thái dừng. Phương trình này bao gồm tổng năng lượng như một tham số e vật rất nhỏ. Trong lý thuyết về phương trình vi phân, người ta chứng minh rằng các phương trình đó có vô số nghiệm, trong đó bởi vìáp đặt các điều kiện biên chọn các giải pháp có tính chất vật lý
Đối với phương trình Schrödinger, các điều kiện như vậy là điều kiện cho tính đều đặn của hàm sóng: các hàm sóng phải hữu hạn, có một giá trị và liên tục cùng với các đạo hàm bậc nhất của chúng.
Như vậy chỉ những nghiệm biểu diễn bởi hàm chính quy mới có ý nghĩa vật lý thực sự, còn nghiệm chính quy không xảy ra với bất kỳ giá trị nào của tham số E, nhưng chỉ đối với một tập hợp nhất định của chúng, điển hình cho vấn đề này. Những cái này giá trị năng lượng được gọi là sở hữu. Các giải pháp tương ứng với các giá trị riêng năng lượng được gọi là chức năng riêng. giá trị bản địa e có thể hình thành như tiếp diễn, Và chuỗi rời rạc. TRONG Đầu tiên trường hợp họ nói về tiếp diễn, hoặc liên tục, quang phổ, trong lần thứ hai - quang phổ rời rạc.
§ 218. Nguyên lý nhân quả trong cơ học lượng tử
Từ mối quan hệ không chắc chắn, người ta thường kết luận rằng
nguyên lý nhân quả đối với các hiện tượng xảy ra trong thế giới vi quan. Trong trường hợp này, chúng dựa trên những cân nhắc sau đây. Trong cơ học cổ điển, theo nguyên lý nhân quả - nguyên lý tất định luận cổ điển, Qua trạng thái đã biết của hệ thống tại một thời điểm nào đó (nó hoàn toàn được xác định bởi các giá trị tọa độ và động lượng của tất cả các hạt của hệ thống) và các lực tác dụng lên nó, bạn hoàn toàn có thể thiết lập chính xác trạng thái của nó tại bất kỳ thời điểm nào tiếp theo chốc lát. Kể từ đây, vật lý cổ điển dựa trên sự hiểu biết về quan hệ nhân quả như sau: trạng thái của một hệ cơ học tại thời điểm ban đầu với quy luật tương tác hạt đã biết là nguyên nhân và trạng thái của nó tại thời điểm sau là kết quả.
Mặt khác, các vật thể vi mô không thể có cả tọa độ nhất định và hình chiếu động lượng tương ứng nhất định [chúng được cho bởi hệ thức bất định; do đó, người ta kết luận rằng tại thời điểm ban đầu, trạng thái của hệ không được xác định chính xác . Nếu trạng thái của hệ thống không chắc chắn tại thời điểm ban đầu, thì các trạng thái tiếp theo không thể dự đoán được, tức là nguyên tắc nhân quả bị vi phạm.
Tuy nhiên, không có sự vi phạm nguyên tắc nhân quả liên quan đến các vật thể vi mô, vì trong cơ học lượng tử, khái niệm trạng thái của một vật thể vi mô có một ý nghĩa hoàn toàn khác so với trong cơ học cổ điển. Trong cơ học lượng tử, trạng thái của một vi vật thể hoàn toàn được xác định bởi hàm sóng, môđun bình phương của nó
2 đặt mật độ xác suất tìm thấy một hạt tại một điểm có tọa độ XYZ.
Đổi lại, hàm sóng thỏa mãn phương trình
Schrödinger chứa đạo hàm bậc nhất của hàm Ф theo thời gian. Điều này cũng có nghĩa là việc gán một hàm (trong một thời điểm xác định giá trị của nó ở những thời điểm tiếp theo. Do đó, trong cơ học lượng tử trạng thái ban đầu có một nguyên nhân, và trạng thái của F tại một thời điểm tiếp theo là một hệ quả. Đây là dạng của nguyên lý nhân quả trong cơ học lượng tử, tức là việc gán hàm xác định trước các giá trị của nó cho bất kỳ khoảnh khắc nào tiếp theo. Do đó, trạng thái của một hệ vi hạt, được định nghĩa trong cơ học lượng tử, rõ ràng là tiếp nối từ trạng thái trước đó, theo yêu cầu của nguyên lý nhân quả.
§219. Chuyển động hạt tự do
hạt tự do - hạt chuyển động khi không có trường ngoài. Vì vật tự do (để nó chuyển động dọc theo trục X) lực không tác dụng thì thế năng của hạt U(x) = const và nó có thể được lấy bằng không. Khi đó năng lượng toàn phần của hạt trùng với động năng của nó. Trong trường hợp này, phương trình Schrödinger (217.5) cho trạng thái dừng có dạng
![]() (219.1)
(219.1)
Bằng cách thay thế trực tiếp, người ta có thể xác minh rằng một nghiệm cụ thể của phương trình (219.1) là hàm - Ở đâu một = const và ĐẾN= const, với giá trị riêng năng lượng
Hàm = = chỉ biểu thị phần tọa độ của hàm sóng Do đó, hàm sóng phụ thuộc vào thời gian, theo (217.4),

(219.3) là sóng de Broglie đơn sắc phẳng [xem. (217.2)].
Từ biểu thức (219.2) suy ra sự phụ thuộc của năng lượng vào động lượng
![]()
hóa ra là phổ biến đối với các hạt phi tương đối tính. Do đó, năng lượng của một hạt tự do có thể lấy bất kỳ giá trị(vì số sóng ĐẾN có thể nhận bất kỳ giá trị dương nào), tức là năng lượng phạm vi hạt tự do là tiếp diễn.
Như vậy, một hạt lượng tử tự do được mô tả bằng một sóng de Broglie đơn sắc phẳng. Điều này tương ứng với mật độ xác suất không phụ thuộc vào thời gian của việc phát hiện một hạt tại một điểm nhất định trong không gian
tức là, tất cả các vị trí của một hạt tự do trong không gian đều có thể xác định được.
§ 220. Một hạt trong "giếng thế" hình chữ nhật một chiều có độ cao vô hạn
"bức tường"
Hãy chi tiêu phân tích định tính nghiệm của phương trình Schrödinger
 Cơm. 299
Cơm. 299
 (220.4)
(220.4)
so với hạt V một "giếng tiềm năng" hình chữ nhật một chiều với các "bức tường" cao vô hạn. Một "hố" như vậy được mô tả năng lượng tiềm năng dạng (để đơn giản ta giả sử rằng hạt chuyển động dọc theo trục X)

chiều rộng của "hố" ở đâu? MỘT năng lượng được đo từ đáy của nó (Hình 299).
Phương trình Schrödinger (217.5) cho trạng thái dừng trong trường hợp bài toán một chiều có thể được viết là
![]()
![]() Theo điều kiện của bài toán (các “bức tường” cao vô hạn), hạt không xuyên qua ngoài “hố”, vì vậy xác suất phát hiện ra nó (và do đó, hàm sóng) bên ngoài “hố” bằng không . Tại ranh giới của "hố" (tại X- 0 và x = hàm sóng liên tục cũng phải triệt tiêu. Do đó, điều kiện biên trong trường hợp này có dạng
Theo điều kiện của bài toán (các “bức tường” cao vô hạn), hạt không xuyên qua ngoài “hố”, vì vậy xác suất phát hiện ra nó (và do đó, hàm sóng) bên ngoài “hố” bằng không . Tại ranh giới của "hố" (tại X- 0 và x = hàm sóng liên tục cũng phải triệt tiêu. Do đó, điều kiện biên trong trường hợp này có dạng
Trong "hố" (0 X phương trình Schrödinger (220.1) rút gọn thành phương trình
| |
|||
Nghiệm tổng quát của phương trình vi phân (220.3):
Vì (220,2) = 0 nên TRONG= 0.
![]() (220.5)
(220.5)
Điều kiện (220,2) = 0 chỉ thỏa mãn khi P- số nguyên, tức là cần thiết
 Từ biểu thức (220.4) và (220.6) suy ra
Từ biểu thức (220.4) và (220.6) suy ra
I E. phương trình đứng yên Schrödinger, mô tả chuyển động của một hạt trong một “giếng thế năng” với những “bức tường” cao vô hạn, chỉ thỏa mãn đối với các giá trị riêng phụ thuộc vào một số nguyên P. Do đó, năng lượng hạt trong
"giếng tiềm năng" với "bức tường" cao vô hạn chỉ mất các giá trị rời rạc nhất định, những thứ kia. được lượng tử hóa.
Các giá trị năng lượng đã lượng tử hóa được gọi là mức năng lượng, và số P, xác định mức năng lượng hạt được gọi là số lượng tử chính. Do đó, một vi hạt trong một “giếng thế năng” với “những bức tường” cao vô hạn chỉ có thể ở một mức năng lượng nhất định, hay như người ta nói, một hạt ở trong một lượng tử.
Thay thế vào (220,5) giá trị ĐẾN từ (220,6), tìm của chúng tađặc trưng:
| |
hằng tích phân MỘT chúng tôi tìm thấy từ điều kiện chuẩn hóa (216.3), trong trường hợp này có thể được viết dưới dạng

TRONG kết quả của bán hội nhập
MỘT - MỘT các chức năng riêng sẽ trông như thế nào

tôi rafiki chức năng riêng(220.8) tương ứng với các mức
năng lượng (220,7) tại n=1,2, 3 được thể hiện trong hình. 300, MỘT. Trên hình. 300, b mật độ xác suất phát hiện một hạt ở các khoảng cách khác nhau từ “các bức tường” của giếng được hiển thị, bằng =
Vì n= 1, 2 và 3. Từ hình vẽ, ví dụ, ở trạng thái lượng tử với P= 2 hạt không thể ở giữa “hố”, trong khi nó có thể ở bên trái và bên trái của nó. bộ phận bên phải. Hành vi này của một hạt chỉ ra rằng các khái niệm về quỹ đạo của hạt trong cơ học lượng tử là không thể giải thích được. Từ biểu thức (220.7) suy ra khoảng năng lượng giữa hai
Các mức lân cận bằng
 |
Ví dụ, đối với một điện tử có kích thước giếng - 10 "1 m (miễn phí điện

Ngai vàng bằng kim loại) 10 J
Nghĩa là, các mức năng lượng có khoảng cách gần nhau đến mức trên thực tế, quang phổ có thể được coi là liên tục. Nếu kích thước của giếng tương xứng với nguyên tử m), thì đối với một electron J eV, tức là thu được các giá trị năng lượng rời rạc một cách rõ ràng (phổ vạch).
Do đó, việc áp dụng phương trình Schrödinger cho một hạt trong “giếng thế” với độ cao vô hạn
“bức tường” dẫn đến các giá trị năng lượng được lượng tử hóa, trong khi cơ học cổ điển không áp đặt bất kỳ hạn chế nào đối với năng lượng của hạt này.
Bên cạnh đó,
Việc xem xét vấn đề này dẫn đến kết luận rằng một hạt "trong giếng thế" với "cao vô hạn" những bức tường» không thể ít năng lượng hơn
Tối thiểu, bằng [xem. (220.7)].
Sự hiện diện của năng lượng tối thiểu khác không không phải là ngẫu nhiên và xuất phát từ hệ thức bất định. tọa độ không chắc chắn Ồ các hạt trong một "hố" rộng À = Khi đó, theo hệ thức bất định, xung lượng không thể có một giá trị chính xác, trong trường hợp này là 0. Động lượng không chắc chắn
Sự lan truyền các giá trị như vậy
động lượng tương ứng động năng
![]()
Tất cả các cấp độ khác (n > 1) có năng lượng vượt quá giá trị tối thiểu này.
Từ công thức (220.9) và (220.7) suy ra rằng đối với số lượng tử lớn
tức là các cấp độ lân cận có khoảng cách gần nhau: càng gần, càng có nhiều P. Nếu như P rất lớn, thì chúng ta có thể nói về một chuỗi các mức thực tế liên tục và tính năng đặc trưng của các quá trình lượng tử - tính rời rạc - được làm mịn. Kết quả này là một trường hợp đặc biệt nguyên lý tương ứng Bohr (1923), theo đó các định luật cơ học lượng tử nên giá trị lớn Số lượng tử tuân theo các định luật vật lý cổ điển.
Hơn Giải thích chung về nguyên tắc tương ứng: bất kỳ lý thuyết mới, tổng quát hơn, là sự phát triển của lý thuyết cổ điển, không bác bỏ nó hoàn toàn, nhưng bao gồm lý thuyết cổ điển, chỉ ra các giới hạn của ứng dụng của nó và trong một số trường hợp hạn chế nhất định lý thuyết mớiđi đến cái cũ. Vì vậy, các công thức của động học và động lực học lý thuyết đặc biệt thuyết tương đối đi qua tại v c thành các công thức của cơ học Newton. Ví dụ, mặc dù giả thuyết da Broglie thuộc tính làn sóng mới tính chất cho tất cả các vật thể, nhưng trong những trường hợp khi chúng ta đang xử lý các vật thể vĩ mô, tính chất sóng của chúng có thể bị bỏ qua, tức là áp dụng cơ học Newton cổ điển.
§ 221. Sự đi qua của một hạt qua hàng rào thế năng.
hiệu ứng đường hầm
 rào cản tiềm năng đơn giản nhất hình chữ nhật(Hình. đối với một chiều (dọc theo trục chuyển động của hạt). Đối với hàng rào thế năng hình chữ nhật có chiều cao bằng chiều rộng l, chúng ta có thể viết
rào cản tiềm năng đơn giản nhất hình chữ nhật(Hình. đối với một chiều (dọc theo trục chuyển động của hạt). Đối với hàng rào thế năng hình chữ nhật có chiều cao bằng chiều rộng l, chúng ta có thể viết
Trong các điều kiện đã cho của bài toán, một hạt cổ điển, có năng lượng E, hoặc vượt qua rào cản không bị cản trở (với E > U), hoặc phản ánh từ nó (khi e< U) sẽ chuyển đến mặt trái, I E. nó không thể xuyên qua hàng rào. Đối với một vi hạt, ngay cả ở E > U, có sẵn xuất sắc từ 0 xác suất hạt sẽ bị phản xạ khỏi rào cản và sẽ chuyển động theo hướng ngược lại. Tại e cũng có một xác suất khác không là hạt sẽ ở trong vùng x> những thứ kia. xuyên qua hàng rào. Những kết luận có vẻ nghịch lý như vậy suy ra trực tiếp từ nghiệm của phương trình Schrödinger, được mô tả
 412
412
trong đó mô tả chuyển động của một vi hạt trong các điều kiện của một vấn đề nhất định.
 Phương trình (217.5) cho các trạng thái dừng đối với từng hình đã chọn. 301, MỘT khu vực có
Phương trình (217.5) cho các trạng thái dừng đối với từng hình đã chọn. 301, MỘT khu vực có
(đối với khu vực
(đối với diện tích
Giải pháp chung các phương trình vi phân này:
Giải pháp (221.3) cũng chứa các sóng (sau khi nhân với hệ số thời gian) truyền theo cả hai hướng. Tuy nhiên, trong khu vực 3 chỉ có một làn sóng vượt qua rào cản và truyền từ trái sang phải. Do đó, hệ số trong công thức (221.3) nên được lấy bằng không.
Trong khu vực 2
quyết định phụ thuộc vào quan hệ E>U hoặc e
(đối với diện tích
(đối với vùng 2);
Nghĩa q và 0, ta thu được nghiệm của phương trình Schrödinger cho ba miền có dạng sau:
(đối với diện tích 3).
TRONGđặc biệt, đối với khu vực 1 hàm sóng tổng, theo (217.4), sẽ có dạng
 |
Trong biểu thức này, số hạng đầu tiên là sóng phẳng loại (219.3) truyền theo chiều dương của trục X(tương ứng với hạt chuyển động về phía rào cản) và sóng thứ hai - sóng truyền theo hướng ngược lại, tức là phản xạ từ rào cản (tương ứng với hạt chuyển động từ rào cản sang trái).
(đối với diện tích 3).
 Trong khu vực 2
hàm không còn tương ứng với sóng phẳng lan truyền theo cả hai hướng, vì số mũ của số mũ không phải là ảo, mà là thực. Có thể chỉ ra rằng đối với trường hợp cụ thể của hàng rào cao và rộng, khi 1,
Trong khu vực 2
hàm không còn tương ứng với sóng phẳng lan truyền theo cả hai hướng, vì số mũ của số mũ không phải là ảo, mà là thực. Có thể chỉ ra rằng đối với trường hợp cụ thể của hàng rào cao và rộng, khi 1,
Bản chất định tính của các chức năng và được minh họa trong Hình. 301, từ đó nó theo làn sóng
Hàm này cũng không bằng 0 bên trong hàng rào, nhưng trong khu vực 3, nếu rào cản không rộng lắm, nó sẽ lại có dạng sóng de Broglie với cùng động lượng, tức là có cùng tần số, nhưng có biên độ nhỏ hơn. Do đó, chúng tôi thấy rằng hạt có xác suất khác không khi đi qua một rào thế có chiều rộng hữu hạn.
Do đó, cơ học lượng tử dẫn đến một hiện tượng lượng tử cụ thể mới về cơ bản, được gọi là hiệu ứng đường hầm, kết quả là vật thể vi mô có thể "vượt qua" hàng rào tiềm năng. về mặt Giải pháp chung của các phương trình cho một rào thế hình chữ nhật mang lại (giả sử rằng hệ số trong suốt nhỏ so với đơn vị)
đâu là một yếu tố không đổi có thể được đánh đồng với một; U- chiều cao rào cản tiềm năng; E - năng lượng hạt; là chiều rộng của hàng rào.
Từ biểu thức (221.7) suy ra D phụ thuộc nhiều vào khối lượng t các hạt, chiều rộng / rào cản và từ (U- rào cản càng rộng thì khả năng một hạt đi qua nó càng ít.
Đối với một hàng rào thế năng có hình dạng tùy ý (Hình 302) thỏa mãn các điều kiện của cái gọi là xấp xỉ bán cổ điển(một hình dạng khá trơn tru của đường cong), chúng ta có
| |
Ở đâu U=U(x).
Theo quan điểm cổ điển, sự đi qua của một hạt qua một hàng rào tiềm năng tại e không thể được, vì hạt đang ở trong miền chắn sẽ phải có động năng âm. Hiệu ứng đường hầm là một hiệu ứng lượng tử cụ thể.
Việc một hạt đi qua một vùng mà theo các định luật cơ học cổ điển, nó không thể xuyên qua, có thể được giải thích bằng hệ thức bất định. Động lượng không chắc chắn ar trên phân khúc à = là Ar > -. Liên kết với sự lây lan này trong các giá trị của động lượng, động năng
 302
302
Năng lượng của Séc có thể được
đủ để hoàn thành
hóa ra năng lượng của hạt lớn hơn thế năng.
Nền tảng của lý thuyết về nút giao đường hầm đã được đặt ra trong các tác phẩm của L.I.
Đường hầm xuyên qua một rào cản tiềm năng là cơ sở của nhiều hiện tượng trong vật lý chất rắn (ví dụ: hiện tượng trong lớp tiếp xúc ở giao diện giữa hai chất bán dẫn), vật lý nguyên tử và hạt nhân (ví dụ: phân rã, phản ứng nhiệt hạch).
§ 222. Dao động điều hòa tuyến tính
Trong cơ học lượng tử
Dao động điều hòa tuyến tính- một hệ thống thực hiện chuyển động một chiều dưới tác dụng của lực gần như đàn hồi là một mô hình được sử dụng trong nhiều vấn đề của lý thuyết cổ điển và lượng tử (xem § 142). Con lắc lò xo, vật lý và toán học là những ví dụ về dao động điều hòa cổ điển.
Thế năng của một dao động điều hòa [xem. (141,5)] là
Đâu là tần số tự nhiên của bộ dao động; T - khối lượng hạt.
Sự phụ thuộc (222.1) có dạng parabol (Hình 303), tức là "Giếng tiềm năng" trong trường hợp này là parabol.
Biên độ của các dao động nhỏ của một dao động cổ điển được xác định bằng năng lượng toàn phần của nó e(xem hình 17).
Dinger, có tính đến biểu thức (222.1) cho thế năng. Khi đó các trạng thái dừng của bộ dao động lượng tử được xác định bởi phương trình Schrödinger có dạng
![]() = 0, (222.2)
= 0, (222.2)
Ở đâu E - năng lượng toàn phần của dao động. Trong lý thuyết phương trình vi phân
Người ta chứng minh rằng phương trình (222.2) chỉ được giải đối với các giá trị riêng năng lượng
![]() (222.3)
(222.3)
Công thức (222.3) cho thấy năng lượng của một dao động lượng tử có thể
chỉ có giá trị rời rạc, I E. được lượng tử hóa. Năng lượng được giới hạn từ bên dưới bởi một giá trị khác không, như đối với một “hố” hình chữ nhật với “những bức tường” cao vô hạn (xem § 220), bởi một giá trị năng lượng tối thiểu = Su-
sự tồn tại của một năng lượng tối thiểu - nó được gọi là năng lượng điểm không - là điển hình cho các hệ lượng tử và là hệ quả trực tiếp của hệ thức bất định.
Sự hiện diện của các dao động bằng không có nghĩa là hạt không thể ở đáy của “giếng thế năng” (bất kể hình dạng của giếng). Thật vậy, "rơi xuống đáy hố" gắn liền với sự biến mất của động lượng của hạt, đồng thời, sự không chắc chắn của nó. Khi đó độ bất định của tọa độ trở nên lớn tùy ý, do đó mâu thuẫn với sự có mặt của hạt trong
"lỗ hổng tiềm năng".
Kết luận về sự hiện diện năng lượng của các dao động tại điểm không của một bộ dao động lượng tử mâu thuẫn với kết luận của lý thuyết cổ điển, theo đó năng lượng nhỏ nhất mà một bộ dao động có thể có bằng không (tương ứng với một hạt đang đứng yên ở vị trí cân bằng) . Ví dụ, theo kết luận của vật lý cổ điển tại t= 0, năng lượng của chuyển động dao động của các nguyên tử của tinh thể sẽ biến mất. Do đó, sự tán xạ ánh sáng do dao động của các nguyên tử cũng sẽ biến mất. Tuy nhiên, thí nghiệm cho thấy cường độ tán xạ ánh sáng khi nhiệt độ giảm không bằng 0 mà có xu hướng tiến tới một giá trị giới hạn nhất định, chứng tỏ rằng tại t 0 dao động của các nguyên tử trong tinh thể không ngừng. Đây là một xác nhận về sự hiện diện của dao động bằng không.

Từ công thức (222.3) cũng suy ra rằng các mức năng lượng của một dao động điều hòa tuyến tính nằm ở những khoảng cách bằng nhau (xem Hình 303), cụ thể là khoảng cách giữa các mức năng lượng liền kề bằng và giá trị năng lượng cực tiểu. =
Một giải pháp nghiêm ngặt cho vấn đề bộ dao động lượng tử dẫn đến một sự khác biệt đáng kể khác so với giải pháp cổ điển.
Dạng phương trình sóng của một hệ vật lý được xác định bởi Hamiltonian của nó, do đó, có ý nghĩa cơ bản trong toàn bộ bộ máy toán học của cơ học lượng tử.
Dạng Hamilton của một hạt tự do đã được thiết lập bởi các yêu cầu chung liên quan đến tính đồng nhất và đẳng hướng của không gian và nguyên lý tương đối của Galileo. Trong cơ học cổ điển, những yêu cầu này dẫn đến sự phụ thuộc bậc hai của năng lượng của hạt vào động lượng của nó: trong đó hằng số được gọi là khối lượng của hạt (xem I, § 4). Trong cơ học lượng tử, các yêu cầu giống nhau dẫn đến cùng một mối quan hệ đối với các giá trị riêng của năng lượng và động lượng - các đại lượng bảo toàn (đối với hạt tự do) có thể đo được đồng thời.
Nhưng để mối quan hệ giữ cho tất cả các giá trị riêng của năng lượng và động lượng, nó cũng phải có giá trị đối với các toán tử của chúng:
![]()
Thay (15.2) vào đây, ta thu được Hamiltonian của hạt chuyển động tự do ở dạng
![]()
toán tử Laplace ở đâu.
Hamiltonian của một hệ gồm các hạt không tương tác bằng tổng các Hamiltonian của mỗi hạt:
![]()
trong đó chỉ số a đánh số các hạt; là toán tử Laplace, trong đó sự phân biệt được thực hiện đối với tọa độ của hạt.
Trong cơ học cổ điển (phi tương đối tính), tương tác của các hạt được mô tả bằng một thuật ngữ cộng trong hàm Hamilton - thế năng tương tác, là một hàm của tọa độ hạt.
Bằng cách thêm chức năng tương tự vào Hamiltonian của hệ thống, tương tác của các hạt trong cơ học lượng tử cũng được mô tả:
![]()
thuật ngữ đầu tiên có thể được coi là toán tử động năng và thuật ngữ thứ hai là toán tử thế năng. Đặc biệt, Hamiltonian cho một hạt trong trường bên ngoài là
trong đó U(x, y, z) là thế năng của hạt trong trường ngoài.
Việc thay các biểu thức (17.2)-(17.5) vào phương trình tổng quát (8.1) sẽ cho các phương trình sóng của các hệ tương ứng. Chúng tôi viết ở đây phương trình sóng cho một hạt trong một trường bên ngoài
Phương trình (10.2), xác định trạng thái dừng, có dạng
Phương trình (17.6) và (17.7) được Schrödinger thiết lập năm 1926 và được gọi là phương trình Schrödinger.
Đối với hạt tự do, phương trình (17.7) có dạng
![]()
Phương trình này có các nghiệm hữu hạn trong toàn bộ không gian đối với bất kỳ giá trị dương nào của năng lượng E. Đối với các trạng thái có hướng chuyển động nhất định, các nghiệm này là hàm riêng của toán tử động lượng và . Các hàm sóng tổng (phụ thuộc vào thời gian) của các trạng thái đứng yên như vậy có dạng
![]() (17,9)
(17,9)
Mỗi hàm như vậy - sóng phẳng - mô tả trạng thái trong đó hạt có năng lượng E và động lượng nhất định. Tần số của sóng này là và vectơ sóng ứng với bước sóng của nó được gọi là bước sóng de Broglie của hạt.
Do đó, phổ năng lượng của một hạt chuyển động tự do hóa ra là liên tục, kéo dài từ 0 đến Mỗi giá trị riêng này (ngoại trừ chỉ có giá trị là suy biến và sự suy biến là bội số vô hạn. Thật vậy, đối với mỗi giá trị khác không của E tương ứng với một tập hợp vô hạn các hàm riêng (17, 9), khác nhau về hướng vectơ cho cùng một giá trị tuyệt đối.
Chúng ta hãy theo dõi quá trình chuyển đổi giới hạn sang cơ học cổ điển xảy ra như thế nào trong phương trình Schrödinger, xét cho đơn giản chỉ một hạt trong trường ngoài. Thay thế vào phương trình Schrödinger (17.6) biểu thức giới hạn (6.1) của hàm sóng, chúng ta thu được, sau khi đạo hàm,
Phương trình này có các số hạng thuần thực và thuần ảo (nhớ lại rằng S và a là số thực); đánh đồng cả hai riêng biệt với 0, chúng tôi thu được hai phương trình:

Bỏ qua số hạng chứa trong phương trình đầu tiên, chúng ta thu được
![]() (17,10)
(17,10)
tức là, đúng như vậy, phương trình Hamilton-Jacobi cổ điển cho tác dụng của hạt S. Nhân tiện, chúng ta thấy rằng đối với , cơ học cổ điển có giá trị cho đến các giá trị của thứ tự đầu tiên (chứ không phải 0) cho đến và bao gồm.
Phương trình thứ hai thu được sau khi nhân với 2a có thể được viết lại dưới dạng
![]()
Phương trình này có một ý nghĩa vật lý rõ ràng: có mật độ xác suất tìm thấy một hạt ở nơi này hay nơi khác trong không gian, có vận tốc cổ điển v của hạt. Do đó, phương trình (17.11) không là gì ngoài một phương trình liên tục chỉ ra rằng mật độ xác suất "di chuyển" theo các định luật của cơ học cổ điển với vận tốc cổ điển v tại mỗi điểm.
Nhiệm vụ
Tìm quy luật biến đổi của hàm sóng dưới phép biến đổi Galilê.
Giải pháp. Chúng ta hãy thực hiện một phép biến đổi trên hàm sóng của chuyển động tự do của một hạt (sóng phẳng). Vì bất kỳ hàm nào cũng có thể được mở rộng dưới dạng sóng phẳng, nên luật biến đổi cũng sẽ được tìm thấy cho một hàm sóng tùy ý.
Sóng phẳng trong hệ quy chiếu K và K" (K" chuyển động tương đối so với K với tốc độ V):
và động lượng và năng lượng của hạt trong cả hai hệ thống có liên quan với nhau bằng các công thức
(xem I, § 8), Thay các biểu thức này vào, chúng ta có được
Ở dạng này, công thức này không còn chứa các đại lượng đặc trưng cho chuyển động tự do của hạt và thiết lập định luật chung mong muốn cho sự biến đổi hàm sóng của trạng thái tùy ý của hạt. Đối với một hệ thống các hạt, số mũ trong (1) phải bao gồm tổng trên các hạt.
Phương trình Schrödinger tổng quát. Phương trình Schrödinger cho trạng thái đứng yên
Diễn giải thống kê về sóng de Broglie (xem § 216) và hệ thức bất định Heisenberg (xem 5 215) dẫn đến kết luận rằng phương trình chuyển động trong cơ học lượng tử, mô tả chuyển động của các vi hạt trong các trường lực khác nhau, phải là một phương trình từ mà các vật quan sát được trải nghiệm các tính chất sóng của các hạt. Phương trình cơ bản phải là phương trình cho hàm sóng Ψ (x, y, z, t), vì nó chính xác là điều này, hay chính xác hơn là đại lượng |Ψ| 2 , xác định xác suất để hạt ở lại tại thời điểm t trong thể tích dV, nghĩa là, trong vùng có tọa độ x và x+dx, y và y+dy, z và z+dz. Vì phương trình mong muốn phải xét đến tính chất sóng của các hạt nên nó phải là một phương trình sóng, tương tự như phương trình mô tả sóng điện từ.
Phương trình cơ bản của cơ học lượng tử phi tương đối tính được E. Schrödinger xây dựng vào năm 1926. Phương trình Schrödinger, giống như tất cả các phương trình cơ bản của vật lý học (ví dụ, phương trình Newton trong cơ học cổ điển và phương trình Maxwell cho trường điện từ), không được suy ra, mà được mặc định. Tính đúng đắn của phương trình này được xác nhận bằng sự đồng thuận với kinh nghiệm về các kết quả thu được với sự trợ giúp của nó, do đó, mang lại cho nó đặc tính của một quy luật tự nhiên. Phương trình Schrödinger có dạng
trong đó h=h/(2π), m là khối lượng của hạt, ∆ là toán tử Laplace (  ),
),
i - đơn vị ảo, U (x, y, z, t) - hàm thế năng của một hạt trong trường lực mà nó chuyển động, Ψ (x, y, z, t ) - hàm sóng mong muốn của hạt.
Phương trình (217.1) đúng cho bất kỳ hạt nào (có spin bằng 0; xem § 225) chuyển động với tốc độ nhỏ (so với tốc độ ánh sáng), tức là với tốc độ υ<<с. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной (см. § 216); 2) производные

phải liên tục; 3) hàm |Ψ| 2 phải tích hợp được; điều kiện này trong các trường hợp đơn giản nhất rút gọn thành điều kiện chuẩn hóa xác suất (216.3).
Để đi đến phương trình Schrödinger, chúng ta hãy xét một hạt chuyển động tự do, mà theo ý tưởng của de Broglie, hạt này có liên hệ với một sóng phẳng. Để đơn giản, ta xét trường hợp một chiều. Phương trình của sóng phẳng truyền dọc theo trục x là (xem § 154)
Hoặc trong ký hiệu phức tạp ![]() . Do đó, sóng phẳng de Broglie có dạng
. Do đó, sóng phẳng de Broglie có dạng
![]() (217.2)
(217.2)
(có tính đến ω = E/h, k=p/h). Trong cơ học lượng tử, số mũ được lấy với dấu trừ, nhưng chỉ vì |Ψ| 2 , thì điều này (xem (217.2)) là không cần thiết. Sau đó
 ,
,
 ; (217.3)
; (217.3)
Sử dụng mối quan hệ giữa năng lượng E và động lượng p (E = p 2 /(2m)) và thay các biểu thức (217.3), chúng ta thu được phương trình vi phân

trùng với phương trình (217.1) đối với trường hợp U = 0 (ta coi là hạt tự do).
Nếu một hạt chuyển động trong một trường lực đặc trưng bởi thế năng U, thì năng lượng toàn phần E là tổng của động năng và thế năng. Thực hiện suy luận tương tự bằng cách sử dụng mối quan hệ giữa E và p (trong trường hợp này, p 2 / (2m) = E - U), chúng ta quay về một phương trình vi phân trùng với (217.1).
Lập luận trên không nên được coi là dẫn xuất của phương trình Schrödinger. Họ chỉ giải thích làm thế nào để đạt được phương trình này. Bằng chứng về tính đúng đắn của phương trình Schrödinger là sự phù hợp với kinh nghiệm của các kết luận mà nó dẫn đến.
Phương trình (217.1) là phương trình Schrödinger tổng quát. Nó còn được gọi là phương trình Schrödinger phụ thuộc thời gian. Đối với nhiều hiện tượng vật lý xảy ra trong thế giới vi mô, phương trình (217.1) có thể được đơn giản hóa bằng cách loại bỏ sự phụ thuộc của Ψ vào thời gian, hay nói cách khác là tìm phương trình Schrödinger cho trạng thái dừng - trạng thái có giá trị năng lượng cố định. Điều này có thể xảy ra nếu trường lực trong đó hạt chuyển động đứng yên, nghĩa là hàm U = U(x, y, z ) không phụ thuộc rõ ràng vào thời gian và có ý nghĩa thế năng. Trong trường hợp này, nghiệm của phương trình Schrödinger có thể được biểu diễn dưới dạng tích của hai hàm, một trong số đó là hàm chỉ tọa độ, hàm kia chỉ là hàm của thời gian và sự phụ thuộc vào thời gian được biểu thị bằng hệ số
![]() ,
,
nơi E - năng lượng toàn phần của hạt, không đổi trong trường hợp trường đứng yên. Thay (217.4) vào (217.1), ta được
từ đó, sau khi chia cho nhân tử chung e – i(E/ h)t và các phép biến đổi tương ứng, ta đi đến phương trình xác định hàm ψ:
![]() (217.5)
(217.5)
Phương trình (217.5) được gọi là phương trình Schrödinger cho trạng thái dừng.
Phương trình này bao gồm tổng năng lượng E của hạt như một tham số. Trong lý thuyết về phương trình vi phân, người ta chứng minh rằng các phương trình như vậy có vô số nghiệm, từ đó các nghiệm có ý nghĩa vật lý được chọn bằng cách áp đặt các điều kiện biên. Đối với phương trình Schrödinger, những điều kiện như vậy là điều kiện về tính đều đặn của các hàm sóng: các hàm sóng phải hữu hạn, có một giá trị và liên tục cùng với các đạo hàm bậc nhất của chúng. Như vậy, chỉ những nghiệm được biểu diễn bởi hàm chính quy ψ . Nhưng các giải pháp thông thường không diễn ra đối với bất kỳ giá trị nào của tham số E, mà chỉ đối với một tập hợp nhất định của chúng, đặc trưng của vấn đề đã cho. Các giá trị năng lượng này được gọi là nội tại. Các giải pháp tương ứng với các giá trị riêng năng lượng được gọi là hàm riêng. Các giá trị riêng E có thể tạo thành một chuỗi liên tục hoặc rời rạc. Trong trường hợp thứ nhất, người ta nói về một quang phổ liên tục, hoặc liên tục, trong trường hợp thứ hai, nói về một quang phổ rời rạc.
1. Giới thiệu
Thuyết lượng tử ra đời vào năm 1900, khi Max Planck đề xuất một kết luận lý thuyết về mối quan hệ giữa nhiệt độ của một vật thể và bức xạ phát ra từ vật thể này - một kết luận mà trong một thời gian dài đã lảng tránh các nhà khoa học khác. các bộ dao động phát ra bức xạ, nhưng đồng thời, ông tin rằng năng lượng của các bộ dao động (và do đó, bức xạ do chúng phát ra) tồn tại dưới dạng các phần nhỏ rời rạc, mà Einstein gọi là lượng tử. Năng lượng của mỗi lượng tử tỷ lệ với tần số bức xạ. Mặc dù công thức của Planck được ngưỡng mộ rộng rãi, nhưng các giả định mà ông đưa ra vẫn không thể hiểu được, vì chúng mâu thuẫn với vật lý cổ điển.
Năm 1905, Einstein sử dụng lý thuyết lượng tử để giải thích một số khía cạnh của hiệu ứng quang điện - sự phát xạ của các electron từ bề mặt kim loại tiếp xúc với bức xạ cực tím. Trên đường đi, Einstein lưu ý một điều dường như nghịch lý: ánh sáng, vốn đã được biết đến trong hai thế kỷ là truyền đi theo sóng liên tục, trong một số trường hợp nhất định có thể hành xử giống như một dòng hạt.
Khoảng tám năm sau, Niels Bohr mở rộng lý thuyết lượng tử sang nguyên tử và giải thích tần số của sóng phát ra từ các nguyên tử bị kích thích trong ngọn lửa hoặc trong điện tích. Ernest Rutherford đã chỉ ra rằng khối lượng của một nguyên tử gần như hoàn toàn tập trung ở hạt nhân trung tâm mang điện tích dương và được bao quanh bởi những khoảng cách tương đối lớn bởi các electron mang điện tích âm, do đó toàn bộ nguyên tử là trung hòa về điện. Bohr đề xuất rằng các electron chỉ có thể ở trong một số quỹ đạo rời rạc nhất định tương ứng với các mức năng lượng khác nhau và "sự nhảy vọt" của một electron từ quỹ đạo này sang quỹ đạo khác, với năng lượng thấp hơn, đi kèm với sự phát xạ của một photon, có năng lượng bằng nhau. đến sự chênh lệch năng lượng giữa hai quỹ đạo. Theo lý thuyết của Planck, tần số tỷ lệ thuận với năng lượng của photon. Do đó, mô hình nguyên tử Bohr đã thiết lập mối liên hệ giữa các vạch quang phổ khác nhau đặc trưng của một chất phát ra bức xạ và cấu trúc nguyên tử. Mặc dù đạt được thành công ban đầu, nhưng mô hình nguyên tử của Bohr sớm cần phải sửa đổi để loại bỏ sự khác biệt giữa lý thuyết và thực nghiệm. Ngoài ra, lý thuyết lượng tử ở giai đoạn đó vẫn chưa cung cấp một quy trình hệ thống để giải nhiều bài toán lượng tử.
Một đặc điểm cơ bản mới của thuyết lượng tử xuất hiện vào năm 1924, khi de Broglie đưa ra một giả thuyết cấp tiến về bản chất sóng của vật chất: nếu sóng điện từ, chẳng hạn như ánh sáng, đôi khi hành xử giống như các hạt (như Einstein đã chỉ ra), thì các hạt, chẳng hạn như một electron, trong những trường hợp nhất định, có thể hoạt động giống như sóng. Trong công thức của de Broglie, tần số tương ứng với một hạt có liên quan đến năng lượng của nó, như trong trường hợp của một photon (một hạt ánh sáng), nhưng biểu thức toán học của de Broglie là một mối quan hệ tương đương giữa bước sóng, khối lượng của hạt và vận tốc (động lượng). Sự tồn tại của sóng điện tử đã được chứng minh bằng thực nghiệm vào năm 1927 bởi Clinton Davisson và Lester Germer ở Hoa Kỳ và bởi John Paget Thomson ở Anh.
Bị ấn tượng bởi những bình luận của Einstein về những ý tưởng của de Broglie, Schrödinger đã cố gắng áp dụng mô tả sóng của các electron để xây dựng một lý thuyết lượng tử nhất quán, không liên quan đến mô hình nguyên tử không đầy đủ của Bohr. Theo một nghĩa nào đó, ông có ý định đưa lý thuyết lượng tử đến gần hơn với vật lý cổ điển, vốn đã tích lũy nhiều ví dụ về mô tả toán học của sóng. Nỗ lực đầu tiên do Schrödinger thực hiện năm 1925 đã thất bại.
Vận tốc của các electron trong lý thuyết II của Schrödinger gần bằng tốc độ ánh sáng, đòi hỏi phải đưa vào đó thuyết tương đối đặc biệt của Einstein và tính đến sự gia tăng đáng kể về khối lượng của electron mà nó dự đoán với vận tốc rất cao.
Một trong những lý do khiến Schrödinger thất bại là ông đã không tính đến sự có mặt của một tính chất cụ thể của electron, ngày nay được gọi là spin (sự quay của một electron quanh trục của chính nó, giống như một đỉnh), mà vào thời điểm đó ít được biết đến.
Nỗ lực tiếp theo được Schrödinger thực hiện vào năm 1926. Lần này, vận tốc electron được ông chọn nhỏ đến mức nhu cầu liên quan đến thuyết tương đối tự nó biến mất.
Nỗ lực thứ hai đã thành công rực rỡ với sự dẫn xuất của phương trình sóng Schrödinger, phương trình đưa ra một mô tả toán học của vật chất theo hàm sóng. Schrödinger gọi lý thuyết của ông là cơ học sóng. Các nghiệm của phương trình sóng phù hợp với các quan sát thực nghiệm và có ảnh hưởng sâu sắc đến sự phát triển tiếp theo của thuyết lượng tử.
Trước đó không lâu, Werner Heisenberg, Max Born và Pascual Jordan đã công bố một phiên bản khác của lý thuyết lượng tử, được gọi là cơ học ma trận, mô tả các hiện tượng lượng tử bằng cách sử dụng các bảng quan sát. Các bảng này là các tập hợp toán học được sắp xếp theo một cách nhất định, được gọi là ma trận, trên đó, theo các quy tắc đã biết, có thể thực hiện các phép toán khác nhau. Cơ học ma trận cũng cho phép đạt được sự thống nhất với dữ liệu thực nghiệm quan sát được, nhưng không giống như cơ học sóng, nó không chứa bất kỳ tham chiếu cụ thể nào đến tọa độ không gian hoặc thời gian. Heisenberg đặc biệt nhấn mạnh vào việc từ bỏ mọi mô hình hoặc biểu diễn trực quan đơn giản để chỉ ủng hộ những thuộc tính có thể được xác định từ thực nghiệm.
Schrödinger đã chỉ ra rằng cơ học sóng và cơ học ma trận là tương đương nhau về mặt toán học. Hiện được gọi chung là cơ học lượng tử, hai lý thuyết này đã cung cấp cơ sở chung đã được chờ đợi từ lâu để mô tả các hiện tượng lượng tử. Nhiều nhà vật lý thích cơ học sóng hơn, bởi vì bộ máy toán học của nó quen thuộc hơn với họ và các khái niệm của nó có vẻ "vật lý" hơn; hoạt động trên ma trận là cồng kềnh hơn.
Chức năng Ψ. Chuẩn hóa xác suất.
Việc phát hiện ra tính chất sóng của các vi hạt chỉ ra rằng cơ học cổ điển không thể đưa ra một mô tả chính xác về hành vi của các hạt đó. Cần phải tạo ra cơ học của các vi hạt, cơ học này cũng sẽ tính đến các đặc tính sóng của chúng. Cơ học mới do Schrödinger, Heisenberg, Dirac và những người khác tạo ra được gọi là cơ học sóng hay cơ học lượng tử.
Sóng phẳng De Broglie
(1)là một dạng sóng rất đặc biệt tương ứng với chuyển động tự do đều của hạt theo một hướng nhất định và với một xung lượng nhất định. Nhưng một hạt, ngay cả trong không gian tự do và đặc biệt là trong trường lực, có thể thực hiện các chuyển động khác được mô tả bởi các hàm sóng phức tạp hơn. Trong những trường hợp này, một mô tả đầy đủ về trạng thái của một hạt trong cơ học lượng tử không được đưa ra bởi sóng phẳng de Broglie, mà bởi một số hàm phức tạp hơn
phụ thuộc vào tọa độ và thời gian. Nó được gọi là hàm sóng. Trong trường hợp cụ thể chuyển động tự do của hạt, hàm sóng chuyển thành sóng phẳng de Broglie (1). Bản thân hàm sóng được giới thiệu như một ký hiệu phụ trợ nào đó và không phải là một trong những đại lượng có thể quan sát trực tiếp. Nhưng kiến thức của nó làm cho nó có thể dự đoán thống kê các giá trị của đại lượng thu được bằng thực nghiệm và do đó có ý nghĩa vật lý thực sự.Thông qua hàm sóng, xác suất tương đối của việc phát hiện một hạt ở các vị trí khác nhau trong không gian được xác định. Ở giai đoạn này, khi chỉ thảo luận về các tỷ lệ xác suất, hàm sóng về cơ bản được xác định theo một hệ số không đổi tùy ý. Nếu tại tất cả các điểm trong không gian, hàm sóng được nhân với cùng một hằng số (nói chung là số phức) khác 0, thì sẽ thu được một hàm sóng mới mô tả chính xác trạng thái đó. Thật vô nghĩa khi nói rằng Ψ bằng không tại mọi điểm trong không gian, bởi vì một "hàm sóng" như vậy không bao giờ cho phép người ta kết luận về xác suất tương đối của việc tìm thấy một hạt ở những nơi khác nhau trong không gian. Nhưng sự không chắc chắn trong định nghĩa của Ψ có thể được thu hẹp đáng kể bằng cách chuyển từ xác suất tương đối sang xác suất tuyệt đối. Chúng ta hãy quản lý thừa số bất định trong hàm Ψ sao cho giá trị |Ψ|2dV cho xác suất tuyệt đối tìm thấy hạt trong phần tử thể tích không gian dV. Khi đó |Ψ|2 = Ψ*Ψ (Ψ* là liên hợp phức của Ψ) sẽ có ý nghĩa về mật độ xác suất nên có khi cố gắng phát hiện một hạt trong không gian. Trong trường hợp này, Ψ vẫn sẽ được xác định theo một hệ số phức không đổi tùy ý, tuy nhiên, mô đun của nó bằng một. Với định nghĩa này, điều kiện chuẩn hóa phải được thỏa mãn:
(2)trong đó tích phân được lấy trên toàn bộ không gian vô hạn. Điều đó có nghĩa là trong mọi không gian, hạt sẽ được phát hiện một cách chắc chắn. Nếu lấy tích phân của |Ψ|2 trên một thể tích V1 nào đó, ta tính xác suất tìm thấy hạt trong không gian của thể tích V1.
Chuẩn hóa (2) có thể không thực hiện được nếu tích phân (2) phân kỳ. Ví dụ, đây sẽ là trường hợp trong trường hợp sóng phẳng de Broglie, khi xác suất phát hiện ra một hạt là như nhau tại mọi điểm trong không gian. Nhưng những trường hợp như vậy nên được coi là sự lý tưởng hóa của một tình huống thực tế trong đó hạt không đi đến vô tận mà buộc phải ở trong một vùng không gian giới hạn. Sau đó bình thường hóa không khó.
Vì vậy, ý nghĩa vật lý trực tiếp không được liên kết với chính hàm Ψ, mà với mô đun Ψ*Ψ của nó. Vậy tại sao trong lý thuyết lượng tử, chúng hoạt động với các hàm sóng Ψ, mà không trực tiếp với các đại lượng quan sát được bằng thực nghiệm Ψ*Ψ? Điều này là cần thiết để giải thích các tính chất sóng của vật chất - giao thoa và nhiễu xạ. Ở đây, tình huống hoàn toàn giống như trong bất kỳ lý thuyết sóng nào. Nó (ít nhất là trong phép tính gần đúng tuyến tính) chấp nhận tính hợp lệ của nguyên lý chồng chất của chính các trường sóng chứ không phải cường độ của chúng, và do đó đạt được sự đưa vào lý thuyết về các hiện tượng giao thoa và nhiễu xạ sóng. Vì vậy, trong cơ học lượng tử, nguyên lý chồng chất của các hàm sóng được coi là một trong những định đề chính, bao gồm những điều sau đây.
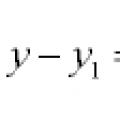 Phương trình đường thẳng và đường cong trong mặt phẳng
Phương trình đường thẳng và đường cong trong mặt phẳng Phương trình thuần nhất tổng quát Phương trình thuần nhất tổng quát cấp 2
Phương trình thuần nhất tổng quát Phương trình thuần nhất tổng quát cấp 2 Nhờ dấu phẩy Do thực tế là trong họ
Nhờ dấu phẩy Do thực tế là trong họ