Структура общих решений линейных однородных дифференциальных уравнений. Структура общего решения лнду
Для линейного неоднородного дифференциального уравнения n- го порядка
y (n ) + a 1(x ) y (n- 1) + ... + an- 1 (x ) y " + an (x ) y = f(x) ,
где y
= y
(x
) - неизвестная функция, a
1(x
), a
2(x
), ..., an-
1(x
), an
(x
), f
(x
) - известные, непрерывные, справедливо
:
1) если y
1(x
) и y
2(x
) - два решения неоднородного уравнения, то функция
y
(x
) = y
1(x
) - y
2(x
) - решение соответствующего однородного уравнения;
2) если y
1(x
) решение неоднородного уравнения, а y
2(x
) - решение соответствующего однородного уравнения, то функция
y
(x
) = y
1(x
) + y
2(x
) - решение неоднородного уравнения;
3) если y
1(x
), y
2(x
), ..., yn
(x
) - n
линейно независимых решений однородного уравнения, а yч
(x
) - произвольное решение неоднородного уравнения,
то для любых начальных значений
x
0, y
0, y
0,1, ..., y
0,n-
1
Выражение
y
(x
)= c
1 y
1(x
) + c
2 y
2(x
) + ... + cn yn
(x
) + yч
(x
)
называется общим решением
линейного неоднородного дифференциального уравнения n
-го порядка.
Для отыскания частных решений неоднородных дифференциальных уравнений с постоянными коэффициентами с правыми частями вида:
Pk
(x
)exp(ax
)cos(bx
) + Qm
(x
)exp(ax
)sin(bx
),
где Pk
(x
), Qm
(x
) - многочлены степени k
и m
соответственно, существует простой алгоритм построения частного решения, называемый методом подбора
.
Метод подбора, или метод неопределенных коэффициентов, состоит в следующем.
Искомое решение уравнения записывается в виде:
(Pr
(x
)exp(ax
)cos(bx
) + Qr
(x
)exp(ax
)sin(bx
))xs
,
где Pr
(x
), Qr
(x
) - многочлены степени r
= max(k
, m
) с неизвестными
коэффициентами
pr
, pr-
1, ..., p
1, p
0, qr
, qr-
1, ..., q
1, q
0.
Таким образом, для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует
найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения l
1, l
2, ... , ln
, записать фундаментальную систему решений y
1(x
), y
2(x
), ..., yn
(x
));
найти любое частное решение неоднородного уравнения yч
(x
);
записать выражение для общего решения
y
(x
)= c
1 y
1(x
) + c
2 y
2(x
) + ... + cn yn
(x
) + yч
(x
);
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами с правой частью специального вида. Метод неопределенных коэффициентов.
Дифференциальное уравнение вида (1)
где , f - известная функция, называется линейнымдифференциальным уравнением n - го порядка с постоянными коэффициентами. Если , то уравнение (1) называется однородным, в противном случае - неоднородным.
Для линейных неоднородных уравнений с постоянными коэффициентами и с правой частью специального вида, а именно состоящей из сумм и произведений функций , частное решение можно искать методом неопределенных коэффициентов. Вид частного решения зависит от корней характеристического уравнения. Ниже представлена таблица видов частных решений линейного неоднородного уравнения с правой частью специального вида.
Комплексная плоскость. Модуль и аргумент комплексного числа. Главное значение аргумента. Геометрический смысл
Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Два комплексных числа a+ bi и a – bi называются сопряжёнными комплексными числами.
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью.

Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль. __
Аргумент комплексного числа - это угол между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan = b / a .
Д У высших порядков
Как мы уже говорили, дифференциальные уравнения могут содержать производные различных порядков.
Такие дифференциальные уравнения имеют решения, которые содержат столько произвольных постоянных интегрирования → каков порядок дифференциального уравнения, т.е. для дифференциального уравнения 2го порядка произвольных постоянных будет две С1 и С2 , для 3го →С1 ,С2 , и С3 , и т.д.
Таким образом, общим решением (общим интегралом) такого дифференциального уравнения будет функция
![]() .
.
Для получения частного решения, таких дифференциальных уравнений, необходимо задать столько начальных условий, каков порядок дифференциального уравнения, или сколько произвольных постоянных получено в общем решении.
Д У в полных дифференциалах. Интегрирующий множитель
Дифференциальное уравнение вида называется дифференциальным уравнением в полных диффернциалах, если его левая часть является полным дифференциалом некоторой гладкой функции , т.е. если ![]() ,
, ![]() . Необходимое и достаточное условие для существования такой функции имеет вид:
. Необходимое и достаточное условие для существования такой функции имеет вид: 
Чтобы решить дифференциальное уравнение в полных дифференциалах необходимо найти функцию . Тогда общее решение дифференциального уравнения можно записать в виде для произвольной постоянной С.
Интегрирующим множителем для дифференциального уравнения
называется такая функция , после умножения на которую дифференциальное уравнение превращается в уравнение в полных дифференциалах. Если функции M и N в уравнении имеют непрерывные частные производные и не обращаются в ноль одновременно, то интегрирующий множитель существует. Однако, общего метода для его отыскания не существует.
Структура общего решения ЛНДУ
Рассмотрим линейное неоднородное дифференциальное уравнение
+ (x) + ... + (x)y" + (x)y = f(x).
− какова бы ни была начальная точка (x0, y0, ) , x0∈ , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функция y = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y "(x0) ,..., (x0) = .
Справедливо следующее утверждение (теорема о структуре общего решения линейного неоднородного уравнения).
Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке , а функции y1(x), y2(x),..., yn(x) образуют систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид
y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) + ... + Cn yn(x) + y*(x),
где C1,...,Cn - произвольные постоянные, y*(x) - частное решение неоднородного уравнения.
ЛНДУ 2-ого порядка
Линейные неоднородные дифференциальные уравнения второго порядка.
Уравнение вида y" + py" + qy = f(x), где р и q - вещественные числа, f(x) - непрерывная функция, называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами.
Общее решение уравнения представляет собой сумму частного решения неоднородного уравнения н общего решения соответствующего однородного уравнения. Нахождение общего решения однородного уравнения изучено. Для нахождения частного решения воспользуемся методом неопределенных коэффициентов, не содержащим процесса интегрирования.
Рассмотрим различные виды правых частей уравнения y" + py" + qy = f(x).
1) Правая часть имеет вид F(x) = Pn(x), где Pn(х) – многочлен степени n. Тогда частное решение у можно искать в виде, где Qn (x) – многочлен той же степени, что и Pn (х), а r – число корней характеристического уравнения, равных нулю.
Пример. Найти общее решение уравнения у" – 2у" + у = x+1.
Решение: Общее решение соответствующего однородного уравнения имеет вид У = ех (C1 + C2x) . Так как ни один из корней характеристического уравнения k2 – 2k + 1 = 0 не равен нулю (k1 = k2 = 1), то частное решение ищем в виде, где А и В – неизвестные коэффициенты. Дифференцируя дважды и подставляя, " и " в данное уравнение, найдем –2А + Ах + В = х + 1.
Приравнивая коэффициенты при одинаковых степенях х в обеих частях равенства: А = 1, –2А + В = 1, – находим А = 1, В = 3. Итак, частное решение данного уравнения имеет вид = х + 3, а его общее решение у = еx (С1 + C2x) + х + З.
2) Правая часть имеет вид f(x) = eax Pn(x), где Рn (х) – многочлен степени n. Тогда частное решение следует искать в виде, где Qn(x) – многочлен той же степени, что и Рn (х), а r - число корней характеристического уравнения, равных а. Если а = 0, то f(х) = Рn (х), т. е. имеет место случай 1.
ЛОДУ с постоянными коэфф.
Рассмотрим дифференциальное уравнение
где – вещественные постоянные.
Для нахождения общего решения уравнения (8) поступаем так. Составляем характеристическое уравнение для уравнения (8): (9)
Пусть - корни уравнения (9), причем среди них могут быть и кратные. Возможны следующие случаи:
а) - вещественные и различные. Общим решением однородного уравнения будет ;
б) корни характеристического уравнения вещественные, но среди них есть кратные, т.е. , тогда общее решение будет
в) если корни характеристического уравнения комплексные (k=a±bi), то общее решение имеет вид .
Структура общ. решения ЛОДУ 2-ого порядка
Рассмотрим на линейное однородное дифференциальное уравнение
+ (x) + ... + (x)y" + (x)y = 0.
Общим решением этого уравнения на отрезке называется функция y = Φ(x, C1,..., Cn), зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим условиям:
− при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn) является решением уравнения на ;
− какова бы ни была начальная точка (x0, y0, ) , x0∈ , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функция y = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y "(x0) = y1,0 ,..., (x0) = .
Знание фундаментальной системы решений уравнения дает возможность построить общее решение этого уравнения. Напомним определение общего решения дифференциального уравненияп -го порядка
Функция
 ,
определенная в некоторой области
изменения переменных
,
определенная в некоторой области
изменения переменных ,
в каждой точке которой имеет место
существование и единственность решения
задачи Коши, и имеющая непрерывные
частные производные пох
до порядка п
включительно, называется общим решением
уравнения (15) в указанной области, если:
,
в каждой точке которой имеет место
существование и единственность решения
задачи Коши, и имеющая непрерывные
частные производные пох
до порядка п
включительно, называется общим решением
уравнения (15) в указанной области, если:
система уравнений

разрешима в
указанной области относительно
произвольных постоянных
 ,
так что
,
так что
 (16)
(16)
2. функция
 является решением уравнения (15) при всех
значениях произвольных постоянных
является решением уравнения (15) при всех
значениях произвольных постоянных ,
выраженных формулами (16), когда точка
,
выраженных формулами (16), когда точка принадлежит рассматриваемой области.
принадлежит рассматриваемой области.
Теорема 1. (о
структуре общего решения линейного
однородного дифференциального уравнения)
.
Если функции
 ,
, ,
…,
,
…, образуют фундаментальную систему
решений однородного линейного уравненияп
-го
порядка
образуют фундаментальную систему
решений однородного линейного уравненияп
-го
порядка
 в интервале
в интервале ,
т.е. в интервале непрерывности коэффициентов,
то функция
,
т.е. в интервале непрерывности коэффициентов,
то функция является общим решением этого уравнения
в областиD
:
является общим решением этого уравнения
в областиD
:
 ,
, ,
, .
.
Доказательство.
В каждой точке указанной области имеет
место существование и единственность
решения задачи Коши. Покажем теперь,
что функция
 удовлетворяет определению общего
решения уравненияп
-го
порядка.
удовлетворяет определению общего
решения уравненияп
-го
порядка.
система уравнений

разрешима в области
D
относительно произвольных постоянных
 так как определитель этой системы
является определителем Вронского для
фундаментальной системы решений (12) и
следовательно, отличен от нуля.
так как определитель этой системы
является определителем Вронского для
фундаментальной системы решений (12) и
следовательно, отличен от нуля.
2. Функция
 по свойству решений однородного линейного
уравнения является решением уравнения
по свойству решений однородного линейного
уравнения является решением уравнения при всех значениях произвольных
постоянных
при всех значениях произвольных
постоянных .
.
Поэтому функция
 является общим решением уравнения
является общим решением уравнения в областиD
.
Теорема доказана.
в областиD
.
Теорема доказана.
Пример.
 .
.
Решениями этого
уравнения, очевидно являются функции
 ,
, .
Эти решения образуют фундаментальную
систему решений, так как
.
Эти решения образуют фундаментальную
систему решений, так как
 .
.
Поэтому общим решением исходного уравнения является функция .
Структура общего решения неоднородного линейного уравнения п-го порядка.
Рассмотрим неоднородное линейное уравнение п -го порядка
Покажем, что, как и в случае линейного неоднородного уравнения первого порядка, интегрирование уравнения (1) сводится к интегрированию однородного уравнения, если известно одно частное решение неоднородного уравнения (1).
Пусть
 - частное решение уравнения (1), т.е.
- частное решение уравнения (1), т.е.
 ,
,
 . (2)
. (2)
Положим
 ,
гдеz
– новая неизвестная функция от х
.
Тогда уравнение (1) примет вид
,
гдеz
– новая неизвестная функция от х
.
Тогда уравнение (1) примет вид
 или
или
 ,
,
откуда в силу тождества (2) получаем
 . (3)
. (3)
Это есть однородное линейное уравнение, левая часть которого та же, что и рассматриваемого неоднородного уравнения (1). Т.е. мы получили однородное уравнение, соответствующее данному неоднородному уравнению (1).
 ,
,
 ,
…,
,
…, ,
,
есть фундаментальная система решений однородного уравнения (3). Тогда все решения этого уравнения содержатся в формуле его общего решения, т.е.
 .
.
Подставим это
значение z
в формулу
 ,
получим
,
получим
 .
.
Полученная функция является общим решением уравнения (1) в области D .
Таким образом, мы показали, что общее решение линейного неоднородного уравнения (1) равно сумме какого-нибудь частного решения этого уравнения и общего решения соответствующего однородного линейного уравнения.
Пример. Найти общее решение уравнения
 .
.
Решение. Имеем, частное решение данного неоднородного линейного уравнения имеет вид
 .
.
Общее решение
соответствующего однородного уравнения
 ,
как мы уже показали ранее, имеет вид
,
как мы уже показали ранее, имеет вид
Следовательно,
общее решение исходного уравнения:
 .
.
Во многих случаях задача нахождения частного решения неоднородного уравнения облегчается, если воспользоваться следующим свойством:
Теорема. Если в уравнении (1) правая часть имеет вид

и известно, что

 ,
а
,
а - частное решение уравнения
- частное решение уравнения ,
то сумма этих частных решений
,
то сумма этих частных решений +
+ будет частным решением уравнения (1).
будет частным решением уравнения (1).
Доказательство.
Действительно, так как по условию
 есть частное решение уравнения
есть частное решение уравнения ,
а
,
а - частное решение уравнения
- частное решение уравнения ,
то
,
то
 ,
,
 .
.
т.е.
 +
+ является частным решением уравнения
(1).
является частным решением уравнения
(1).
 Воля: функции, понятие, основные признаки
Воля: функции, понятие, основные признаки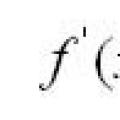 Геометрический и механический смысл производной
Геометрический и механический смысл производной Свойства степеней при сложении
Свойства степеней при сложении