Угол между векторами определение. Записи с меткой "найти косинус угла между векторами"
По вашим просьбам!
1. Исключите иррациональность в знаменателе:
3. Решите показательное уравнение:

4. Решить неравенство:
Арифметический квадратный корень существует только из неотрицательного числа и всегда выражается неотрицательным числом , поэтому, данное неравенство будет верным для всех х , удовлетворяющих условию: 2-х≥0. Отсюда получаем: х≤2. Записываем ответ в виде числового промежутка: (-∞; 2].
5. Решить неравенство: 7 x > -1.
По определению: показательной называют функцию вида y = a x , где а >0, a≠1, x — любое число. Областью значений показательной функции служит множество всех положительных чисел , так как положительное число в любой степени будет положительным. Вот поэтому 7 x >0 при любом х, и тем более 7 x > -1 , т.е. неравенство верно при всех х ∈ (-∞; +∞).
6. Преобразовать в произведение:
![]()
Применим формулу суммы синусов: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
8. Известно, что f(x) = -15х+3. При каких значениях х, f(x)=0?
Подставим вместо f(x) число 0 и решаем уравнение:
15х+3=0 ⇒ -15х=-3 ⇒ х=3:15 ⇒ х = 1/5.
11 . В первом и втором сплавах медь и цинк находятся в соотношении 5:2 и 3:4. Сколько каждого сплава нужно взять, чтобы получить 28 кг нового сплава с равным содержанием меди и цинка.
Понимаем, что в новом сплаве будет 14 кг меди и 14 кг цинка. Подобные задачи решаются все одинаково: составляют уравнение, в левой и правой частях которого одно и то же количество вещества (возьмем медь), записанное по-разному (исходят из конкретного условия задачи). У нас 14 кг меди в новом сплаве будет составлено из меди обоих данных сплавов. Пусть масса первого сплава х кг, тогда масса второго сплава равна (28-х )кг. В первом сплаве 5 частей меди и 2 части цинка, следовательно меди будет (5/7) от х кг. Чтобы найти дробь от числа нужно эту дробь умножить на данное число. Во втором сплаве 3 части меди и 4 части цинка, т.е. меди содержится (3/7) от (28-х) кг. Итак:

12. Решите уравнение: log 2 8 x = -1.
По определению логарифма:
8 х = 2 -1 ⇒ 2 3х = 2 -1 ⇒ 3х = -1 ⇒ х = -1/3.
15. Найдите производную функции f(x) = -ln cosx 2 .

20. Найти значение выражения:
Модуль числа может выражаться только неотрицательным числом. Если под знаком модуля находится отрицательное выражение, то при раскрытии модульных скобок все слагаемые записывают с противоположными знаками.
22. Решите систему неравенств:
Вначале решаем каждое неравенство по отдельности.

Обратите внимание, что наименьшим общим периодом для данных функций будет 2π, поэтому и слева и справа приписали 2πn . Ответ С).
23. Найдите площадь фигуры, ограниченной графиком функции y=3-|x-3| и прямой у=0.
График данной функции будет состоять из двух полупрямых, выходящих из одной точки. Запишем уравнения прямых. При x≥3 мы раскрываем модульные скобки и получаем: y=3-x+3 ⇒ y=6-x. При x<3 получаем функцию: y=3+x-3 ⇒ y=x .
 Треугольник, ограниченный графиком функции и отрезком оси Ох — фигура, площадь которой нужно найти. Конечно, обойдемся здесь без интегралов. Найдем площадь треугольника как половину произведения его основания на высоту, проведенную к этому основанию. Основание у нас равно 6 единичным отрезкам, а высота, проведенная к этому основанию равна 3 единичным отрезкам. Площадь будет равна 9 кв. ед.
Треугольник, ограниченный графиком функции и отрезком оси Ох — фигура, площадь которой нужно найти. Конечно, обойдемся здесь без интегралов. Найдем площадь треугольника как половину произведения его основания на высоту, проведенную к этому основанию. Основание у нас равно 6 единичным отрезкам, а высота, проведенная к этому основанию равна 3 единичным отрезкам. Площадь будет равна 9 кв. ед.
24. Найдите косинус угла А треугольника с вершинами в точках А(1; 4), В(-2; 3), С(4; 2).
Чтобы найти координаты вектора, заданного координатами его концов нужно из координат конца вычесть координаты начала.
Угол А образуют векторы:

25. В коробке лежат 23 шара: красные, белые и черные. Белых шаров в 11 раз больше, чем красных. Сколько черных шаров?
Пусть в коробке лежит х красных шаров. Тогда белых 11х шаров.
Красных и белых х+11х=12х шаров. Следовательно, черных шаров 23-12х. Так как это целое число шаров, то возможно лишь значение х=1 . Получается: 1 красный шар, 11 белых шаров и 11 черных шаров.
Угол между двумя векторами , :
Если угол между двумя векторами острый, то их скалярное произведение положительно; если угол между векторами тупой, то скалярное произведение этих векторов отрицательно. Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы ортогональны.
Задание. Найти угол между векторами и
Решение. Косинус искомого угла

![]()
16. Вычисление угла между прямыми, прямой и плоскостью
Угол между прямой и плоскостью , пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость.
Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми: самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.

Угол между перпендикулярными прямой и плоскостью считают равным , а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным .
§ 69. Вычисление угла между прямыми.
Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости (§ 32). Обозначим через φ величину угла между прямыми l 1 и l 2 , а через ψ - величину угла между направляющими векторами а и b этих прямых.

Тогда, если
ψ 90° (рис. 206,6), то φ = 180° - ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (1) § 20 имеем
![]()
следовательно, ![]()
Пусть прямые заданы своими каноническими уравнениями
Тогда угол φ между прямыми определяется с помощью формулы
Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).
17. Параллельные прямые, Теоремы о параллельных прямых
Определение. Две прямые на плоскости называются параллельными , если они не имеют общих точек.

Две прямые в трехмерном пространстве называются параллельными , если они лежат в одной плоскости и не имеют общих точек.

Угол между двумя векторами.
Из определения скалярного произведения:
 .
.
Условие ортогональности двух векторов :
Условие коллинеарности двух векторов:
![]() .
.
Следует из определения 5 - . Действительно, из определения произведения вектора на число, следует . Поэтому, исходя из правила равенства векторов, запишем , , , откуда вытекает ![]() . Но вектор , получившийся в результате умножения вектора на число , коллинеарен вектору .
. Но вектор , получившийся в результате умножения вектора на число , коллинеарен вектору .
Проекция вектора на вектор:
 .
.
Пример 4 . Даны точки , , , .
Найти скалярное произведение .
Решение . найдем по формуле скалярного произведения векторов, заданных своими координатами. Поскольку
, ![]() ,
,
Пример 5. Даны точки , , , .
Найти проекцию .
Решение . Поскольку
, ![]() ,
,
На основании формулы проекции, имеем
 .
.
Пример 6. Даны точки , , , .
Найти угол между векторами и .
Решение . Заметим, что вектора
, ![]() ,
,
не являются коллинеарными, поскольку не пропорциональны их координаты:
![]() .
.
Эти вектора не являются также перпендикулярными, так как их скалярное произведение .
Найдем ,
Угол ![]() найдем из формулы:
найдем из формулы:
 .
.
Пример 7.
Определить при каких вектора и ![]() коллинеарны.
коллинеарны.
Решение
. В случае коллинеарности, соответствующие координаты векторов ![]() и должны быть пропорциональны, то есть:
и должны быть пропорциональны, то есть:
![]() .
.
Отсюда и .
Пример 8
. Определить, при каком значении вектора ![]() и
и ![]() перпендикулярны.
перпендикулярны.
Решение
. Вектора ![]() и перпендикулярны, если их скалярное произведение равно нулю. Из этого условия получаем: . Стало быть, .
и перпендикулярны, если их скалярное произведение равно нулю. Из этого условия получаем: . Стало быть, .
Пример 9
. Найти ![]() , если , , .
, если , , .
Решение . В силу свойств скалярного произведения, имеем:
Пример 10 . Найдите угол между векторами и , где и - единичные векторы и угол между векторами и равен 120о.
Решение
. Имеем:  , ,
, ,
Окончательно имеем: ![]() .
.
5.б. Векторное произведение .
Определение 21 .Векторным произведением вектора на вектор называется вектор , или , определяемый следующими тремя условиями:
1) Модуль вектора равен , где - угол между векторами и , т.е. ![]() .
.
Отсюда следует, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах и как на сторонах.
2) Вектор перпендикулярен к каждому из векторов и ( ; ), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах и .
3) Вектор направлен так, что если смотреть из его конца, то кратчайший поворот от вектора к вектору был бы против часовой стрелки (векторы , , образуют правую тройку).
Как вычислить углы между векторами?
При изучении геометрии немало вопросов возникает по теме векторов. Особенные трудности обучающийся испытывает при необходимости найти углы между векторами.
Основные термины
Перед тем как рассматривать углы между векторами, необходимо ознакомиться с определением вектора и понятием угла между векторами.

Вектором называют отрезок, имеющий направление, то есть отрезок, для которого определено его начало и конец.
Углом между двумя векторами на плоскости, имеющих общее начало, называют меньший из углов, на величину которого требуется переместить один из векторов вокруг общей точки, до положения, когда их направления совпадут.
Формула для решения
Поняв, что собой представляет вектор и как определяется его угол, можно вычислить угол между векторами. Формула решения для этого достаточно проста, и результатом её применения будет значение косинуса угла. Согласно определению, он равен частному скалярного произведения векторов и произведения их длин.
Скалярное произведение векторов считается как сумма помноженных друг на друга соответствующих координат векторов-сомножителей. Длина вектора, или его модуль, вычисляется как квадратный корень из суммы квадратов его координат.
Получив значение косинуса угла, вычислить величину самого угла можно с помощью калькулятора или воспользовавшись тригонометрической таблицей.
Пример
После того как вы разберетесь с тем, как вычислить угол между векторами, решение соответствующей задачи станет простым и понятным. В качестве примера стоит рассмотреть несложную задачу о нахождении величины угла.

Первым делом удобнее будет вычислить необходимые для решения значения длин векторов и их скалярного произведения. Воспользовавшись описанием, представленным выше, получим:

Подставив полученные значения в формулу, вычислим значение косинуса искомого угла:

Это число не является одним из пяти распространённых значений косинуса, поэтому для получения величины угла, придётся воспользоваться калькулятором или тригонометрической таблицей Брадиса. Но перед тем, как получить угол между векторами, формула может быть упрощена, чтобы избавиться от лишнего отрицательного знака:

Итоговый ответ для сохранения точности можно оставить в таком виде, а можно вычислить значение угла в градусах. По таблице Брадиса его величина составит примерно 116 градусов и 70 минут, а калькулятор покажет значение 116,57 градуса.
Вычисление угла в n-мерном пространстве
При рассмотрении двух векторов в трёхмерном пространстве, понять, о каком угле идёт речь гораздо сложнее, если они не лежат в одной плоскости. Для упрощения восприятия можно начертить два пересекающихся отрезка, которые образуют наименьший угол между ними, он и будет искомым. Несмотря на наличие третьей координаты в векторе, процесс того, как вычисляются углы между векторами, не изменится. Вычислите скалярное произведение и модули векторов, арккосинус их частного и будет являться ответом на данную задачу.
В геометрии нередко встречаются задачи и с пространствами, имеющими больше трёх измерений. Но и для них алгоритм нахождения ответа выглядит аналогично.
Разница между 0 и 180 градусами
Одна из распространённых ошибок при написании ответа на задачу, рассчитанную на то чтобы вычислить угол между векторами, - решение записать, что векторы параллельны, то есть искомый угол получился равен 0 или 180 градусам. Этот ответ является неверным.
Получив по итогам решения значение угла 0 градусов, правильным ответом будет обозначение векторов как сонаправленных, то есть у векторов будет совпадать направление. В случае получения 180 градусов векторы будут носить характер противоположно направленных.
Специфические векторы
Найдя углы между векторами, можно встретить один из особых типов, помимо описанных выше сонаправленных и противоположно направленных.
- Несколько векторов параллельных одной плоскости называются компланарными.
- Векторы, одинаковые по длине и направлению, называются равными.
- Векторы, лежащие на одной прямой, независимо от направления, именуются коллинеарными.
- Если длина вектора равна нулю, то есть его начало и конец совпадают, то его называют нулевым, а если единице, то единичным.
Как найти угол между векторами?
помогите пожалуйста! формулу знаю, а вычислить не получается ((
вектор a (8; 10; 4) вектор b (5; -20; -10)
Александр титов
Угол между векторами, заданными своими координатами, находится по стандартному алгоритму. Сначала нужно найти скалярное произведение векторов a и b: (a, b) = x1x2 + y1y2 + z1z2. Подставляем сюда координаты данных векторов и считаем:
(a,b) = 8*5 + 10*(-20) = 4*(-10) = 40 - 200 - 40 = -200.
Далее определяем длины каждого из векторов. Длина или модуль вектора - это корень квадратный из суммы квадратов его координат:
|a| = корень из (x1^2 + y1^2 + z1^2) = корень из (8^2 + 10^2 + 4^2) = корень из (64 + 100 + 16) = корень из 180 = 6 корней из 5
|b| = корень из (x2^2 + y2^2 + z2^2) = корень из (5^2 + (-20)^2 + (-10)^2) = корень из (25 + 400 + 100) = корень из 525 = 5 корней из 21.
Перемножаем эти длины. Получаем 30 корней из 105.
И наконец, делим скалярное произведение векторов на произведение длин этих векторов. Получаем, -200/(30 корней из 105) или
- (4 корня из 105) / 63. Это - косинус угла между векторами. А сам угол равен арккосинусу из этого числа
ф = arccos(-4 корня из 105) / 63.
Если я всё правильно посчитал.
Как вычислить синус угла между векторами по координатам векторов
Михаил ткачев
Умножаем эти вектора. Их скалярное произведение равно произведению длин этих векторов на косинус угла между ними.
Угол нам неизвестен, зато известны координаты.
Математически запишем это так.
Пусть, даны вектора a{x1;y1} и b{x2;y2}
Тогда
A*b=|a|*|b|*cosA
CosA=a*b/|a|*|b|
Рассуждаем.
a*b-скалярное произведение векторов, равно сумме произведений соответствующих координат координат этих векторов, т. е. равно x1*x2+y1*y2
|a|*|b|-произведение длин векторов, равно √((x1)^2+(y1)^2)*√((x2)^2+(y2)^2).
Значит, косинус угла между векторами равен:
CosA=(x1*x2+y1*y2)/√((x1)^2+(y1)^2)*√((x2)^2+(y2)^2)
Зная косинус угла, можем вычислить и его синус. Рассуждаем, как это сделать:
Если косинус угла положительный, значит это угол лежит в 1 или 4 четверти, значит его синус либо положительный, либо отрицательный. Но т. к. угол между векторами-меньше или равен 180 градусов, то его синус - положительный. Аналогично рассуждаем, если косинус - отрицательный.
SinA=√(1-cos^2A)=√(1-((x1*x2+y1*y2)/√((x1)^2+(y1)^2)*√((x2)^2+(y2)^2))^2)
Вот так)))) удачи разобраться)))
Дмитрий левищев
То, что напрямую синус нельзя - это неправда.
Кроме формулы:
(a,b)=|a|*|b|*cos A
Есть ещё и такая:
||=|a|*|b|*sin A
То есть вместо скалярного произведения можно взять модуль векторного произведения.
При изучении геометрии немало вопросов возникает по теме векторов. Особенные трудности обучающийся испытывает при необходимости найти углы между векторами.
Основные термины
Перед тем как рассматривать углы между векторами, необходимо ознакомиться с определением вектора и понятием угла между векторами.
Вектором называют отрезок, имеющий направление, то есть отрезок, для которого определено его начало и конец.
Углом между двумя векторами на плоскости, имеющих общее начало, называют меньший из углов, на величину которого требуется переместить один из векторов вокруг общей точки, до положения, когда их направления совпадут.
Формула для решения
Поняв, что собой представляет вектор и как определяется его угол, можно вычислить угол между векторами. Формула решения для этого достаточно проста, и результатом её применения будет значение косинуса угла. Согласно определению, он равен частному скалярного произведения векторов и произведения их длин.
Скалярное произведение векторов считается как сумма помноженных друг на друга соответствующих координат векторов-сомножителей. Длина вектора, или его модуль, вычисляется как квадратный корень из суммы квадратов его координат.
Получив значение косинуса угла, вычислить величину самого угла можно с помощью калькулятора или воспользовавшись тригонометрической таблицей.
Пример
После того как вы разберетесь с тем, как вычислить угол между векторами, решение соответствующей задачи станет простым и понятным. В качестве примера стоит рассмотреть несложную задачу о нахождении величины угла.

Первым делом удобнее будет вычислить необходимые для решения значения длин векторов и их скалярного произведения. Воспользовавшись описанием, представленным выше, получим:

Подставив полученные значения в формулу, вычислим значение косинуса искомого угла:

Это число не является одним из пяти распространённых значений косинуса, поэтому для получения величины угла, придётся воспользоваться калькулятором или тригонометрической таблицей Брадиса. Но перед тем, как получить угол между векторами, формула может быть упрощена, чтобы избавиться от лишнего отрицательного знака:

Итоговый ответ для сохранения точности можно оставить в таком виде, а можно вычислить значение угла в градусах. По таблице Брадиса его величина составит примерно 116 градусов и 70 минут, а калькулятор покажет значение 116,57 градуса.
Вычисление угла в n-мерном пространстве
При рассмотрении двух векторов в трёхмерном пространстве, понять, о каком угле идёт речь гораздо сложнее, если они не лежат в одной плоскости. Для упрощения восприятия можно начертить два пересекающихся отрезка, которые образуют наименьший угол между ними, он и будет искомым. Несмотря на наличие третьей координаты в векторе, процесс того, как вычисляются углы между векторами, не изменится. Вычислите скалярное произведение и модули векторов, арккосинус их частного и будет являться ответом на данную задачу.
В геометрии нередко встречаются задачи и с пространствами, имеющими больше трёх измерений. Но и для них алгоритм нахождения ответа выглядит аналогично.
Разница между 0 и 180 градусами
Одна из распространённых ошибок при написании ответа на задачу, рассчитанную на то чтобы вычислить угол между векторами, - решение записать, что векторы параллельны, то есть искомый угол получился равен 0 или 180 градусам. Этот ответ является неверным.
Получив по итогам решения значение угла 0 градусов, правильным ответом будет обозначение векторов как сонаправленных, то есть у векторов будет совпадать направление. В случае получения 180 градусов векторы будут носить характер противоположно направленных.
Специфические векторы
Найдя углы между векторами, можно встретить один из особых типов, помимо описанных выше сонаправленных и противоположно направленных.
- Несколько векторов параллельных одной плоскости называются компланарными.
- Векторы, одинаковые по длине и направлению, называются равными.
- Векторы, лежащие на одной прямой, независимо от направления, именуются коллинеарными.
- Если длина вектора равна нулю, то есть его начало и конец совпадают, то его называют нулевым, а если единице, то единичным.
Инструкция
Пусть на плоскости заданы два ненулевых вектора, отложенные от одной точки: вектор A с координатами (x1, y1) B с координатами (x2, y2). Угол между ними обозначен как θ. Чтобы найти градусную меру угла θ необходимо воспользоваться определением скалярного произведения.
Скалярным произведением двух ненулевых называется число, равное произведению длин этих векторов на косинус угла между ними, то есть (A,B)=|A|*|B|*cos(θ). Теперь нужно выразить из данной косинус угла: cos(θ)=(A,B)/(|A|*|B|).
Скалярное произведение можно найти также по формуле (A,B)=x1*x2+y1*y2, так как произведение двух ненулевых векторов равно сумме произведений соответствующих этих векторов. Если скалярное произведение ненулевых векторов равно нулю, то векторы являются перпендикулярными (угол между ними равен 90 градусов) и дальнейшие вычисления можно не производить. Если скалярное произведение двух векторов положительно, то угол между этими векторами острый, а если отрицательно, то угол тупой.
Теперь посчитайте длины векторов A и B по формулам: |A|=√(x1²+y1²), |B|=√(x2²+y2²). Длина вектора вычисляется как квадратный корень из суммы квадратов его координат.
Найденные значения скалярного произведения и длин векторов подставьте в полученную в шаге 2 формулу для угла, то есть cos(θ)=(x1*x2+y1*y2)/(√(x1²+y1²)+√(x2²+y2²)). Теперь, зная значение , чтобы найти градусную меру угла между векторами нужно воспользоваться таблицей Брадиса или взять из этого : θ=arccos(cos(θ)).
Если векторы A и B заданы в трехмерном пространстве и имеют координаты (x1, y1, z1) и (x2, y2, z2) соответственно, то при нахождении косинуса угла добавляется еще одна координата. В этом случае косинус : cos(θ)=(x1*x2+y1*y2+z1*z2)/(√(x1²+y1²+z1²)+√(x2²+y2²+z2²)).
Полезный совет
Если два вектора отложены не от одной точки, то для нахождения угла между ними параллельным переносом нужно совместить начала этих векторов.
Угол между двумя векторами не может быть больше 180 градусов.
Источники:
- как вычислить угол между векторами
- Угол между прямой и плоскостью
Для решения многих задач, как прикладных, так и теоретических, в физике и линейной алгебре необходимо вычислять угол между векторами. Эта простая на первый взгляд задача способна доставить множество трудностей, если вы четко не усвоите сущность скалярного произведения и какая величина появляется в результате этого произведения.
Инструкция
Угол между векторами в векторном линейном пространстве – минимальный угол при , на который достигается сонаправленность векторов. Осуществляется одного из векторов вокруг его начальной точки. Из определения становится очевидно, что значение угла не может превышать 180 градусов (cм. к шагу).
При этом совершенно справедливо предполагается, что в линейном пространстве при осуществлении параллельного переноса векторов угол между ними не меняется. Поэтому для аналитического расчета угла пространственная ориентация векторов не имеет значения.
Результат скалярного произведения – число, иначе скаляр. Запомните (это важно знать), чтобы не допустить в дальнейших расчетах ошибок. Формула скалярного произведения, расположенных на плоскости либо в пространстве векторов, имеет вид (см. рисунок к шагу).
Если вектора располагаются в пространстве, то расчет производите аналогичным способом. Единственным будет появление слагаемого в делимом - это слагаемое за аппликату, т.е. третью компоненту вектора. Соответственно, при вычислении модуля векторов компоненту z также необходимо учесть, тогда для векторов, расположенных в пространстве, последнее выражение преобразуется следующим образом (см. рисунок 6 к шагу).
Вектор - это отрезок с заданным направлением. Угол между векторами имеет физическое значение, например при нахождении длины проекции вектора на ось.

Инструкция
Угол между двумя ненулевыми векторами с помощью вычисления скалярного произведения. По определению произведение равно произведению длин на угла между ними. С другой стороны, скалярное произведение для двух векторов a с координатами (x1; y1) и b с координатами (x2; y2) вычисляется : ab = x1x2 + y1y2. Из этих двух способов скалярного произведения легко угол между векторами.
Найдите длины или модули векторов. Для наших векторов a и b: |a| = (x1² + y1²)^1/2, |b| = (x2² + y2²)^1/2.
Найдите скалярное произведение векторов, перемножив их координаты попарно: ab = x1x2 + y1y2. Из определения скалярного произведения ab = |a|*|b|*cos α, где α - угол между векторами. Тогда получим, что x1x2 + y1y2 = |a|*|b|*cos α. Тогда cos α = (x1x2 + y1y2)/(|a|*|b|) = (x1x2 + y1y2)/((x1² + y1²)(x2² + y2²))^1/2.
Найдите угол α с помощью таблиц Брадиса.
Видео по теме
Обратите внимание
Скалярное произведение - это скалярная характеристика длин векторов и угла между ними.
Плоскость – одно их исходных понятий в геометрии. Плоскостью называется поверхность, для которой верно утверждение - любая прямая, соединяющая две ее точки, целиком принадлежит этой поверхности. Плоскости принято обозначать греческими буквами α, β, γ и т.д. Две плоскости всегда пересекаются по прямой линии, которая принадлежит обеим плоскостям.

Инструкция
Рассмотрим полуплоскости α и β образованные при пересечении . Угол, образованный прямой a и двумя полуплоскостями α и β двугранным углом. При этом полуплоскости образующие двугранный угол гранями, прямая a по которой пересекаются плоскости называется ребром двугранного угла.

Двугранный угол, как и плоский угол, в градусах. Чтобы двугранный угол необходимо на его грани выбрать произвольную точку O. В обеих через точку O проводятся два луча a. Образованный угол AOB называется линейным углом двугранного угла a.
Итак, пусть задан вектор V = (а, b, с) и плоскость А x + В y + C z = 0, где А, В и C – координаты нормали N. Тогда косинус угла α между векторами V и N равен:сos α = (а А + b В + с C)/(√(а² + b² + с²) √(А² + В² + C²)).
Чтобы вычислить величину угла в градусах или радианах, нужно от получившегося выражения рассчитать функцию, обратную к косинусу, т.е. арккосинус:α = аrссos ((а А + b В + с C)/(√(а² + b² + с²) √(А² + В² + C²))).
Пример: найдите угол между вектором (5, -3, 8) и плоскостью , заданной общим уравнением 2 x – 5 y + 3 z = 0.Решение: выпишите координаты нормального вектора плоскости N = (2, -5, 3). Подставьте все известные значения в приведенную формулу:сos α = (10 + 15 + 24)/√3724 ≈ 0,8 → α = 36,87°.
Видео по теме
Составьте равенство и вычлените из него косинус. По одной формуле скалярное произведение векторов равно их длинам, перемноженным друг на дружку и на косинус угла , а по другой - сумме произведений координат вдоль каждой из осей. Приравняв обе формулы можно сделать вывод, что косинус угла должен быть равен отношению суммы произведений координат к произведению длин векторов.
Запишите полученное равенство. Для этого надо обозначить обоих векторов. Допустим, они даны в трехмерной декартовой системе и их начальные точки в координатной сетки. Направление и величина первого вектора будет задана точкой (X₁,Y₁,Z₁), второго - (X₂,Y₂,Z₂), а угол обозначьте буквой γ. Тогда длины каждого из векторов можно , например, по теореме Пифагора для , образуемых их проекциями на каждую из координатных осей: √(X₁² + Y₁² + Z₁²) и √(X₂² + Y₂² + Z₂²). Подставьте эти выражения в сформулированную на предыдущем шаге формулу и вы получите равенство: cos(γ) = (X₁*X₂ + Y₁*Y₂ + Z₁*Z₂) / (√(X₁² + Y₁² + Z₁²) * √(X₂² + Y₂² + Z₂²)).
Используйте тот факт, что сумма возведенных в квадрат синуса и косинуса от угла одной величины всегда дает единицу. Значит, возведя полученное на предыдущем шаге для косинуса в квадрат и отняв от единицы, а затем
 Воля: функции, понятие, основные признаки
Воля: функции, понятие, основные признаки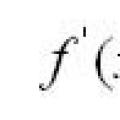 Геометрический и механический смысл производной
Геометрический и механический смысл производной Свойства степеней при сложении
Свойства степеней при сложении