اللوغاريتمات: الأمثلة والحلول. اللوغاريتم - الخصائص والصيغ والرسم البياني الخصائص الأساسية للوغاريتمات
\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)
دعونا نشرح ذلك بشكل أكثر بساطة. على سبيل المثال، \(\log_(2)(8)\) تساوي القدرة التي يجب رفع \(2\) إليها للحصول على \(8\). ومن هذا يتضح أن \(\log_(2)(8)=3\).
|
أمثلة: |
\(\log_(5)(25)=2\) |
لأن \(5^(2)=25\) |
||
|
\(\log_(3)(81)=4\) |
لأن \(3^(4)=81\) |
|||
|
\(\log_(2)\)\(\frac(1)(32)\) \(=-5\) |
لأن \(2^(-5)=\)\(\frac(1)(32)\) |
الوسيطة وقاعدة اللوغاريتم
أي لوغاريتم لديه "التشريح" التالي:
عادة ما تتم كتابة وسيطة اللوغاريتم عند مستواه، ويتم كتابة القاعدة بخط منخفض أقرب إلى علامة اللوغاريتم. وهذا الإدخال يقرأ على النحو التالي: "لوغاريتم خمسة وعشرين للأساس خمسة".
كيفية حساب اللوغاريتم؟
لحساب اللوغاريتم، عليك الإجابة على السؤال: إلى أي قوة يجب رفع القاعدة للحصول على الوسيطة؟
على سبيل المثال، احسب اللوغاريتم: أ) \(\log_(4)(16)\) ب) \(\log_(3)\)\(\frac(1)(3)\) ج) \(\log_(\ sqrt (5))(1)\) د) \(\log_(\sqrt(7))(\sqrt(7))\) ه) \(\log_(3)(\sqrt(3))\)
أ) إلى أي أس يجب رفع \(4\) للحصول على \(16\)؟ ومن الواضح أن الثاني. لهذا السبب:
\(\log_(4)(16)=2\)
\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)
ج) إلى أي قوة يجب رفع \(\sqrt(5)\) للحصول على \(1\)؟ ما هي القوة التي تجعل أي رقم واحد؟ صفر بالطبع!
\(\log_(\sqrt(5))(1)=0\)
د) إلى أي قوة يجب رفع \(\sqrt(7)\) للحصول على \(\sqrt(7)\)؟ أولًا، أي عدد أس الأول يساوي نفسه.
\(\log_(\sqrt(7))(\sqrt(7))=1\)
e) إلى أي قوة يجب رفع \(3\) للحصول على \(\sqrt(3)\)؟ نعلم أن هذه قوة كسرية، مما يعني أن الجذر التربيعي هو قوة \(\frac(1)(2)\) .
\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)
مثال : حساب اللوغاريتم \(\log_(4\sqrt(2))(8)\)
حل :
|
\(\log_(4\sqrt(2))(8)=x\) |
نحن بحاجة إلى إيجاد قيمة اللوغاريتم، لنشير إليها بـ x. الآن دعونا نستخدم تعريف اللوغاريتم: |
|
|
\((4\sqrt(2))^(x)=8\) |
ما الذي يربط \(4\sqrt(2)\) و\(8\)؟ اثنان، لأن كلا الرقمين يمكن تمثيلهما برقمين: |
|
|
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\) |
على اليسار نستخدم خصائص الدرجة: \(a^(m)\cdot a^(n)=a^(m+n)\) و \((a^(m))^(n)= أ^(م\كدوت ن)\) |
|
|
\(2^(\frac(5)(2)x)=2^(3)\) |
القواعد متساوية، ننتقل إلى المساواة في المؤشرات |
|
|
\(\frac(5x)(2)\) \(=3\) |
|
اضرب طرفي المعادلة في \(\frac(2)(5)\) |
|
|
الجذر الناتج هو قيمة اللوغاريتم |
إجابة : \(\log_(4\sqrt(2))(8)=1,2\)
لماذا تم اختراع اللوغاريتم؟
لفهم ذلك، دعونا نحل المعادلة: \(3^(x)=9\). فقط قم بمطابقة \(x\) لتفعيل المساواة. بالطبع \(x=2\).
الآن قم بحل المعادلة: \(3^(x)=8\).ما قيمة x؟ هذا هو بيت القصيد.
سيقول الأذكى: "X أقل بقليل من اثنين". كيف بالضبط لكتابة هذا الرقم؟ للإجابة على هذا السؤال، تم اختراع اللوغاريتم. وبفضله يمكن كتابة الإجابة هنا بالشكل \(x=\log_(3)(8)\).
أريد التأكيد على أن \(\log_(3)(8)\)، مثل أي لوغاريتم هو مجرد رقم. نعم، يبدو غير عادي، لكنه قصير. لأننا إذا أردنا كتابتها على شكل عدد عشري فستبدو هكذا: \(1.892789260714.....\)
مثال : حل المعادلة \(4^(5x-4)=10\)
حل :
|
\(4^(5x-4)=10\) |
لا يمكن إحضار \(4^(5x-4)\) و \(10\) إلى نفس القاعدة. هذا يعني أنه لا يمكنك الاستغناء عن اللوغاريتم. دعونا نستخدم تعريف اللوغاريتم: |
|
|
\(\log_(4)(10)=5x-4\) |
دعونا نقلب المعادلة بحيث تكون X على اليسار |
|
|
\(5x-4=\log_(4)(10)\) |
قبلنا. لننتقل \(4\) إلى اليمين. ولا تخف من اللوغاريتم، تعامل معه كرقم عادي. |
|
|
\(5x=\log_(4)(10)+4\) |
قسمة المعادلة على 5 |
|
|
\(x=\)\(\frac(\log_(4)(10)+4)(5)\) |
|
هذا هو جذرنا. نعم، يبدو الأمر غير عادي، لكنهم لم يختاروا الإجابة. |
إجابة : \(\frac(\log_(4)(10)+4)(5)\)
اللوغاريتمات العشرية والطبيعية
كما هو مذكور في تعريف اللوغاريتم، يمكن أن تكون قاعدته أي رقم موجب باستثناء واحد \((a>0, a\neq1)\). ومن بين جميع القواعد المحتملة، هناك أساسان يتكرران كثيرًا لدرجة أنه تم اختراع تدوين قصير خاص للوغاريتمات الخاصة بهما:
اللوغاريتم الطبيعي: لوغاريتم قاعدته رقم أويلر \(\e\) (يساوي \(2.7182818…\)) تقريباً، ويكتب اللوغاريتم بالشكل \(\ln(a)\).
إنه، \(\ln(a)\) هو نفسه \(\log_(e)(a)\)
اللوغاريتم العشري: يتم كتابة اللوغاريتم الذي أساسه 10 \(\lg(a)\).
إنه، \(\lg(a)\) هو نفس \(\log_(10)(a)\)، حيث \(a\) هو رقم ما.
الهوية اللوغاريتمية الأساسية
اللوغاريتمات لها العديد من الخصائص. إحداها تسمى "الهوية اللوغاريتمية الأساسية" وتبدو كما يلي:
| \(a^(\log_(a)(c))=c\) |
هذه الخاصية تتبع مباشرة من التعريف. دعونا نرى بالضبط كيف جاءت هذه الصيغة.
دعونا نتذكر ملاحظة قصيرة لتعريف اللوغاريتم:
إذا \(a^(b)=c\)، ثم \(\log_(a)(c)=b\)
أي أن \(b\) هو نفسه \(\log_(a)(c)\). بعد ذلك يمكننا كتابة \(\log_(a)(c)\) بدلاً من \(b\) في الصيغة \(a^(b)=c\). اتضح \(a^(\log_(a)(c))=c\) - الهوية اللوغاريتمية الرئيسية.
يمكنك العثور على خصائص أخرى للوغاريتمات. بمساعدتهم، يمكنك تبسيط وحساب قيم التعبيرات باللوغاريتمات، والتي يصعب حسابها مباشرة.
مثال : أوجد قيمة التعبير \(36^(\log_(6)(5))\)
حل :
إجابة : \(25\)
كيفية كتابة رقم على شكل لوغاريتم؟
كما ذكر أعلاه، أي لوغاريتم هو مجرد رقم. والعكس صحيح أيضًا: يمكن كتابة أي رقم على شكل لوغاريتم. على سبيل المثال، نحن نعلم أن \(\log_(2)(4)\) يساوي اثنين. ثم بدلاً من اثنين يمكنك كتابة \(\log_(2)(4)\).
لكن \(\log_(3)(9)\) يساوي أيضًا \(2\)، مما يعني أنه يمكننا أيضًا كتابة \(2=\log_(3)(9)\) . وبالمثل مع \(\log_(5)(25)\)، ومع \(\log_(9)(81)\)، وما إلى ذلك. وهذا هو، اتضح
\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ سجل_(7)(49)...\)
ومن ثم، إذا أردنا، يمكننا كتابة اثنين على هيئة لوغاريتم مع أي أساس في أي مكان (سواء كان ذلك في معادلة، أو في تعبير، أو في متباينة) - فنحن ببساطة نكتب الأساس تربيعًا كوسيطة.
الأمر نفسه ينطبق على الثلاثي - يمكن كتابته كـ \(\log_(2)(8)\)، أو كـ \(\log_(3)(27)\)، أو كـ \(\log_(4)( 64) \)... هنا نكتب القاعدة في المكعب كوسيطة:
\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ سجل_(7)(343)...\)
ومع أربعة:
\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ سجل_(7)(2401)...\)
ومع ناقص واحد:
\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1 )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)
ومع الثلث:
\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)
يمكن تمثيل أي رقم \(a\) على هيئة لوغاريتم ذو الأساس \(b\): \(a=\log_(b)(b^(a))\)
مثال : ابحث عن معنى التعبير \(\frac(\log_(2)(14))(1+\log_(2)(7))\)
حل :
إجابة : \(1\)
اللوغاريتمات، مثل أي أرقام، يمكن جمعها وطرحها وتحويلها بكل الطرق. ولكن بما أن اللوغاريتمات ليست أرقامًا عادية تمامًا، فهناك قواعد تسمى هنا الخصائص الرئيسية.
تحتاج بالتأكيد إلى معرفة هذه القواعد - بدونها، لا يمكن حل أي مشكلة لوغاريتمية خطيرة. بالإضافة إلى ذلك، هناك عدد قليل جدًا منهم - يمكنك تعلم كل شيء في يوم واحد. اذا هيا بنا نبدأ.
جمع وطرح اللوغاريتمات
فكر في لوغاريتمين لهما نفس الأساس: السجل أ سوسجل أ ذ. ومن ثم يمكن إضافتها وطرحها، و:
- سجل أ س+ سجل أ ذ=log أ (س · ذ);
- سجل أ س- سجل أ ذ=log أ (س : ذ).
إذن، مجموع اللوغاريتمات يساوي لوغاريتم حاصل الضرب، والفرق يساوي لوغاريتم حاصل القسمة. يرجى ملاحظة: النقطة الأساسية هنا هي أسباب متطابقة. إذا كانت الأسباب مختلفة، فهذه القواعد لا تعمل!
ستساعدك هذه الصيغ في حساب التعبير اللوغاريتمي حتى في حالة عدم أخذ أجزائه الفردية في الاعتبار (راجع الدرس "ما هو اللوغاريتم"). ألقِ نظرة على الأمثلة وانظر:
سجل 6 4 + سجل 6 9.
بما أن اللوغاريتمات لها نفس الأساس، فإننا نستخدم صيغة الجمع:
سجل 6 4 + سجل 6 9 = سجل 6 (4 9) = سجل 6 36 = 2.
مهمة. أوجد قيمة التعبير: log 2 48 − log 2 3.
القواعد هي نفسها، نستخدم صيغة الفرق:
سجل 2 48 - سجل 2 3 = سجل 2 (48: 3) = سجل 2 16 = 4.
مهمة. أوجد قيمة التعبير: log 3 135 − log 3 5.
مرة أخرى القواعد هي نفسها، لذلك لدينا:
سجل 3 135 - سجل 3 5 = سجل 3 (135: 5) = سجل 3 27 = 3.
كما ترون، تتكون التعبيرات الأصلية من لوغاريتمات "سيئة"، والتي لا يتم حسابها بشكل منفصل. ولكن بعد التحويلات يتم الحصول على أرقام طبيعية تماما. وتستند العديد من الاختبارات على هذه الحقيقة. نعم، يتم تقديم التعبيرات الشبيهة بالاختبار بكل جدية (أحيانًا بدون أي تغييرات تقريبًا) في امتحان الدولة الموحدة.
استخراج الأس من اللوغاريتم
الآن دعونا نعقد المهمة قليلاً. ماذا لو كانت قاعدة أو وسيطة اللوغاريتم قوة؟ ومن ثم يمكن إخراج أس هذه الدرجة من إشارة اللوغاريتم وفق القواعد التالية:
ومن السهل أن نرى أن القاعدة الأخيرة تتبع القاعدة الأولى والثانية. ولكن من الأفضل أن تتذكرها على أي حال - ففي بعض الحالات سوف تقلل بشكل كبير من حجم العمليات الحسابية.
بالطبع، كل هذه القواعد تكون منطقية إذا تمت ملاحظة ODZ للوغاريتم: أ > 0, أ ≠ 1, س> 0. وشيء آخر: تعلم كيفية تطبيق جميع الصيغ ليس فقط من اليسار إلى اليمين، ولكن أيضًا بالعكس، أي. يمكنك إدخال الأرقام قبل تسجيل اللوغاريتم في اللوغاريتم نفسه. وهذا هو المطلوب في أغلب الأحيان.
مهمة. أوجد قيمة التعبير: log 7 49 6 .
دعونا نتخلص من الدرجة في الوسيطة باستخدام الصيغة الأولى:
سجل 7 49 6 = 6 سجل 7 49 = 6 2 = 12
مهمة. ابحث عن معنى العبارة:
[تعليق على الصورة]
لاحظ أن المقام يحتوي على لوغاريتم، قاعدته ووسيطه عبارة عن قوى دقيقة: 16 = 2 4 ; 49 = 7 2. لدينا:
 [تعليق على الصورة]
[تعليق على الصورة] أعتقد أن المثال الأخير يتطلب بعض التوضيح. أين ذهبت اللوغاريتمات؟ حتى اللحظة الأخيرة نحن نعمل فقط مع القاسم. لقد قدمنا أساس ووسيطة اللوغاريتم الموجود هناك في شكل قوى وأزلنا الأسس - لقد حصلنا على كسر "من ثلاثة طوابق".
الآن دعونا نلقي نظرة على الكسر الرئيسي. يحتوي البسط والمقام على نفس الرقم: log 2 7. بما أن log 2 7 ≠ 0، يمكننا تبسيط الكسر - سيبقى 2/4 في المقام. ووفقا للقواعد الحسابية، يمكن نقل الأربعة إلى البسط، وهذا ما تم. وكانت النتيجة الجواب: 2.
الانتقال إلى أساس جديد
عند الحديث عن قواعد جمع وطرح اللوغاريتمات، أكدت على وجه التحديد أنها تعمل فقط مع نفس القواعد. وماذا لو كانت الأسباب مختلفة؟ ماذا لو لم تكن صلاحيات محددة لنفس العدد؟
تأتي صيغ الانتقال إلى أساس جديد للإنقاذ. دعونا صياغتها في شكل نظرية:
دع سجل اللوغاريتم يعطى أ س. ثم لأي رقم جمثل ذلك ج> 0 و ج≠ 1، المساواة صحيحة:
[تعليق على الصورة]
على وجه الخصوص، إذا وضعنا ج = س، نحن نحصل:
[تعليق على الصورة]
ويترتب على الصيغة الثانية أنه يمكن تبديل أساس ووسيطة اللوغاريتم، ولكن في هذه الحالة يتم "قلب" التعبير بأكمله، أي. يظهر اللوغاريتم في المقام.
نادرًا ما توجد هذه الصيغ في التعبيرات العددية العادية. من الممكن تقييم مدى ملاءمتها فقط عند حل المعادلات اللوغاريتمية والمتباينات.
ولكن هناك مشاكل لا يمكن حلها على الإطلاق إلا بالانتقال إلى أساس جديد. دعونا نلقي نظرة على اثنين من هذه:
مهمة. أوجد قيمة التعبير: سجل 5 16 سجل 2 25.
لاحظ أن وسيطات كلا اللوغاريتمات تحتوي على قوى دقيقة. لنأخذ المؤشرات: log 5 16 = log 5 2 4 = 4log 5 2; سجل 2 25 = سجل 2 5 2 = 2سجل 2 5;
الآن دعونا "نعكس" اللوغاريتم الثاني:
[تعليق على الصورة]وبما أن حاصل الضرب لا يتغير عند إعادة ترتيب العوامل، فقد ضربنا أربعة في اثنين بهدوء، ثم تعاملنا مع اللوغاريتمات.
مهمة. أوجد قيمة التعبير: log 9 100 lg 3.
أساس ووسيطة اللوغاريتم الأول هما القوى الدقيقة. دعنا نكتب هذا ونتخلص من المؤشرات:
[تعليق على الصورة]الآن دعونا نتخلص من اللوغاريتم العشري بالانتقال إلى قاعدة جديدة:
[تعليق على الصورة]الهوية اللوغاريتمية الأساسية
في كثير من الأحيان، في عملية الحل، من الضروري تمثيل رقم على هيئة لوغاريتم لقاعدة معينة. في هذه الحالة، سوف تساعدنا الصيغ التالية:
في الحالة الأولى العدد نيصبح مؤشرا على درجة الوقوف في الحجة. رقم نيمكن أن تكون أي شيء على الإطلاق، لأنها مجرد قيمة لوغاريتمية.
الصيغة الثانية هي في الواقع تعريف معاد صياغته. وهذا ما يطلق عليه: الهوية اللوغاريتمية الأساسية.
في الواقع، ماذا سيحدث إذا كان العدد برفع إلى هذه القوة أن العدد بلهذه القوة يعطي الرقم أ؟ هذا صحيح: تحصل على نفس الرقم أ. اقرأ هذه الفقرة بعناية مرة أخرى - كثير من الناس عالقون فيها.
مثل صيغ الانتقال إلى قاعدة جديدة، تكون الهوية اللوغاريتمية الأساسية في بعض الأحيان هي الحل الوحيد الممكن.
مهمة. ابحث عن معنى العبارة:
[تعليق على الصورة]
لاحظ أن log 25 64 = log 5 8 - ببساطة أخذ المربع من قاعدة اللوغاريتم ووسيطه. مع الأخذ بعين الاعتبار قواعد ضرب القوى ذات الأساس نفسه، نحصل على:
[تعليق على الصورة]إذا كان أي شخص لا يعرف، كانت هذه مهمة حقيقية من امتحان الدولة الموحدة :)
الوحدة اللوغاريتمية والصفر اللوغاريتمي
في الختام، سأقدم هويتين يصعب وصفهما بالخصائص - بل هما نتيجة لتعريف اللوغاريتم. إنهم يظهرون باستمرار في المشاكل، ومن المدهش أنهم يخلقون مشاكل حتى للطلاب "المتقدمين".
- سجل أ أ= 1 هي وحدة لوغاريتمية. تذكر مرة واحدة وإلى الأبد: اللوغاريتم لأي قاعدة أمن هذه القاعدة ذاتها يساوي واحدًا.
- سجل أ 1 = 0 هو صفر لوغاريتمي. قاعدة أيمكن أن يكون أي شيء، ولكن إذا كانت الوسيطة تحتوي على واحد، فإن اللوغاريتم يساوي صفرًا! لأن أ 0 = 1 هو نتيجة مباشرة للتعريف.
هذا كل الخصائص. تأكد من ممارسة وضعها موضع التنفيذ! قم بتنزيل ورقة الغش في بداية الدرس وطباعتها وحل المشكلات.
يتبع من تعريفه. وهكذا لوغاريتم الرقم بمرتكز على أيتم تعريفه على أنه الأس الذي يجب رفع الرقم إليه أللحصول على الرقم ب(اللوغاريتم موجود فقط للأرقام الموجبة).
ويترتب على هذه الصيغة أن الحساب س = سجل ب، يعادل حل المعادلة أ س = ب.على سبيل المثال، سجل 2 8 = 3لأن 8 = 2 3 . صياغة اللوغاريتم تجعل من الممكن تبرير ذلك إذا ب=أ ج، ثم لوغاريتم الرقم بمرتكز على أيساوي مع. ومن الواضح أيضًا أن موضوع اللوغاريتمات يرتبط ارتباطًا وثيقًا بموضوع قوى العدد.
مع اللوغاريتمات، كما هو الحال مع أي أرقام، يمكنك القيام بذلك عمليات الجمع والطرحوالتحول بكل الطرق الممكنة. ولكن نظرًا لحقيقة أن اللوغاريتمات ليست أرقامًا عادية تمامًا، فإن قواعدها الخاصة تنطبق هنا، والتي تسمى الخصائص الرئيسية.
جمع وطرح اللوغاريتمات.
لنأخذ لوغاريتمين لهما نفس الأساس: سجل xو سجل ذ. ومن الممكن بعد ذلك إجراء عمليات الجمع والطرح:
سجل x+ سجل y= سجل a (x·y);
سجل س - سجل ص = سجل أ (س: ص).
سجل أ(س 1 . س 2 . س 3 ... س ك) = سجل x 1 + سجل x 2 + سجل x 3 + ... + سجل × ك.
من نظرية حاصل اللوغاريتميمكن الحصول على خاصية أخرى للوغاريتم. ومن المعروف أن السجل أ 1=0، لذلك
سجل أ 1 /ب=log أ 1 - السجل أ ب= - سجل أ ب.
وهذا يعني أن هناك مساواة:
سجل أ 1 / ب = - سجل أ ب.
لوغاريتمات رقمين متبادلينلنفس السبب سوف تختلف عن بعضها البعض فقط من خلال الإشارة. لذا:
سجل 3 9= - سجل 3 1 / 9 ; سجل 5 1/125 = - سجل 5 125.
نواصل دراسة اللوغاريتمات. في هذا المقال سنتحدث عنه حساب اللوغاريتمات، وتسمى هذه العملية اللوغاريتم. أولاً سوف نفهم حساب اللوغاريتمات حسب التعريف. بعد ذلك، دعونا نلقي نظرة على كيفية العثور على قيم اللوغاريتمات باستخدام خصائصها. بعد ذلك سنركز على حساب اللوغاريتمات من خلال القيم المحددة في البداية للوغاريتمات الأخرى. وأخيرًا، دعونا نتعلم كيفية استخدام جداول اللوغاريتمات. يتم تزويد النظرية بأكملها بأمثلة مع حلول مفصلة.
التنقل في الصفحة.
حساب اللوغاريتمات حسب التعريف
في أبسط الحالات، من الممكن تنفيذ الأمر بسرعة وسهولة إيجاد اللوغاريتم حسب التعريف. دعونا نلقي نظرة فاحصة على كيفية حدوث هذه العملية.
جوهرها هو تمثيل الرقم ب في النموذج ج، والذي، من خلال تعريف اللوغاريتم، الرقم ج هو قيمة اللوغاريتم. وهذا يعني، حسب التعريف، أن سلسلة المساواة التالية تتوافق مع إيجاد اللوغاريتم: log a b=log a a c =c.
لذا، فإن حساب اللوغاريتم حسب التعريف يتلخص في العثور على رقم c بحيث يكون a c = b، والرقم c نفسه هو القيمة المطلوبة للوغاريتم.
مع الأخذ في الاعتبار المعلومات الواردة في الفقرات السابقة، عندما يتم إعطاء الرقم الموجود أسفل علامة اللوغاريتم بواسطة قوة معينة لقاعدة اللوغاريتم، يمكنك الإشارة على الفور إلى ما يساويه اللوغاريتم - فهو يساوي الأس. دعونا نعرض الحلول بالأمثلة.
مثال.
ابحث عن السجل 2 2 −3 واحسب أيضًا اللوغاريتم الطبيعي للرقم e 5,3.
حل.
يتيح لنا تعريف اللوغاريتم أن نقول على الفور أن السجل 2 2 −3 =−3. في الواقع، الرقم الموجود تحت علامة اللوغاريتم يساوي الأساس 2 أس −3.
وبالمثل نجد اللوغاريتم الثاني: lne 5.3 =5.3.
إجابة:
سجل 2 2 −3 =−3 و lne 5,3 =5,3.
إذا لم يتم تحديد الرقم b تحت علامة اللوغاريتم كقوة لقاعدة اللوغاريتم، فأنت بحاجة إلى النظر بعناية لمعرفة ما إذا كان من الممكن التوصل إلى تمثيل للرقم b في النموذج a c . غالبًا ما يكون هذا التمثيل واضحًا تمامًا، خاصة عندما يكون الرقم الموجود تحت علامة اللوغاريتم مساويًا للأساس أس 1، أو 2، أو 3، ...
مثال.
احسب اللوغاريتمات log 5 25 و .
حل.
من السهل أن ترى أن 25=5 2، وهذا يسمح لك بحساب اللوغاريتم الأول: log 5 25=log 5 5 2 =2.
دعنا ننتقل إلى حساب اللوغاريتم الثاني. يمكن تمثيل الرقم كقوة 7:  (انظر إذا لزم الأمر). لذلك،
(انظر إذا لزم الأمر). لذلك،  .
.
لنعد كتابة اللوغاريتم الثالث بالشكل التالي. الآن يمكنك أن ترى ذلك  ، ومنه نستنتج ذلك
، ومنه نستنتج ذلك  . لذلك، من خلال تعريف اللوغاريتم
. لذلك، من خلال تعريف اللوغاريتم  .
.
باختصار يمكن كتابة الحل كالتالي: .
إجابة:
سجل 5 25=2 , ![]() و
و  .
.
عندما يكون هناك عدد طبيعي كبير بما فيه الكفاية تحت علامة اللوغاريتم، فلن يضر تحليله إلى عوامل أولية. غالبًا ما يساعد على تمثيل هذا الرقم كقوة لقاعدة اللوغاريتم، وبالتالي حساب هذا اللوغاريتم حسب التعريف.
مثال.
أوجد قيمة اللوغاريتم.
حل.
تسمح لك بعض خصائص اللوغاريتمات بتحديد قيمة اللوغاريتمات على الفور. تتضمن هذه الخصائص خاصية لوغاريتم واحد وخاصية لوغاريتم رقم يساوي الأساس: log 1 1=log a a 0 =0 وlog a=log a 1 =1. أي أنه عندما يكون هناك رقم 1 أو رقم يساوي أساس اللوغاريتم تحت علامة اللوغاريتم، فإن اللوغاريتمات في هذه الحالات تساوي 0 و1 على التوالي.
مثال.
ما هي اللوغاريتمات وlog10 يساوي؟
حل.
منذ ذلك الحين يتبع من تعريف اللوغاريتم ![]() .
.
في المثال الثاني، يتطابق الرقم 10 تحت علامة اللوغاريتم مع قاعدته، وبالتالي فإن اللوغاريتم العشري للعشرة يساوي واحدًا، أي lg10=lg10 1 =1.
إجابة:
و إل جي10=1 .
لاحظ أن حساب اللوغاريتمات حسب التعريف (الذي ناقشناه في الفقرة السابقة) يعني استخدام سجل المساواة a a p =p، وهو أحد خصائص اللوغاريتمات.
من الناحية العملية، عندما يتم تمثيل رقم تحت علامة اللوغاريتم وقاعدة اللوغاريتم بسهولة كقوة لرقم معين، فمن الملائم جدًا استخدام الصيغة  وهو ما يتوافق مع إحدى خصائص اللوغاريتمات. دعونا نلقي نظرة على مثال لإيجاد لوغاريتم يوضح استخدام هذه الصيغة.
وهو ما يتوافق مع إحدى خصائص اللوغاريتمات. دعونا نلقي نظرة على مثال لإيجاد لوغاريتم يوضح استخدام هذه الصيغة.
مثال.
احسب اللوغاريتم.
حل.
إجابة:
![]() .
.
تُستخدم أيضًا خصائص اللوغاريتمات غير المذكورة أعلاه في العمليات الحسابية، لكننا سنتحدث عن ذلك في الفقرات التالية.
إيجاد اللوغاريتمات من خلال اللوغاريتمات المعروفة الأخرى
تستمر المعلومات الواردة في هذه الفقرة في موضوع استخدام خصائص اللوغاريتمات عند حسابها. لكن الاختلاف الرئيسي هنا هو أن خصائص اللوغاريتمات تُستخدم للتعبير عن اللوغاريتم الأصلي بدلالة لوغاريتم آخر تكون قيمته معروفة. دعونا نعطي مثالا للتوضيح. لنفترض أننا نعرف ذلك log 2 3≈1.584963، ثم يمكننا إيجاد، على سبيل المثال، log 2 6 عن طريق إجراء تحويل بسيط باستخدام خصائص اللوغاريتم: سجل 2 6=سجل 2 (2 3)=سجل 2 2+سجل 2 3≈ 1+1,584963=2,584963 .
في المثال أعلاه، كان يكفينا استخدام خاصية لوغاريتم المنتج. ومع ذلك، في كثير من الأحيان يكون من الضروري استخدام ترسانة أوسع من خصائص اللوغاريتمات لحساب اللوغاريتم الأصلي من خلال تلك المحددة.
مثال.
احسب لوغاريتم 27 للأساس 60 إذا كنت تعلم أن log 60 2=a وlog 60 5=b.
حل.
لذلك نحن بحاجة إلى العثور على سجل 60 27 . من السهل أن نرى أن 27 = 3 3 ، واللوغاريتم الأصلي، بسبب خاصية لوغاريتم الأس، يمكن إعادة كتابته بالشكل 3·log 60 3 .
الآن دعونا نرى كيفية التعبير عن السجل 60 3 بدلالة اللوغاريتمات المعروفة. خاصية لوغاريتم الرقم الذي يساوي الأساس تسمح لنا بكتابة سجل المساواة 60 60=1. ومن ناحية أخرى، سجل 60 60=log60(2 2 3 5)= سجل 60 2 2 +سجل 60 3+سجل 60 5= 2·سجل 60 2+سجل 60 3+سجل 60 5 . هكذا، 2 سجل 60 2+سجل 60 3+سجل 60 5=1. لذلك، سجل 60 3=1−2·سجل 60 2−سجل 60 5=1−2·أ−ب.
أخيرًا، نحسب اللوغاريتم الأصلي: log 60 27=3 log 60 3= 3·(1−2·a−b)=3−6·a−3·b.
إجابة:
سجل 60 27=3·(1−2·a−b)=3−6·a−3·b.
بشكل منفصل، تجدر الإشارة إلى معنى صيغة الانتقال إلى قاعدة لوغاريتم النموذج الجديدة  . يتيح لك الانتقال من اللوغاريتمات ذات الأساس إلى اللوغاريتمات ذات الأساس المحدد والتي تكون قيمها معروفة أو من الممكن العثور عليها. عادة، من اللوغاريتم الأصلي، باستخدام صيغة الانتقال، ينتقلون إلى اللوغاريتمات في إحدى القواعد 2 أو e أو 10، حيث توجد لهذه القواعد جداول لوغاريتمية تسمح بحساب قيمها بدرجة معينة من دقة. وفي الفقرة التالية سوف نبين كيف يتم ذلك.
. يتيح لك الانتقال من اللوغاريتمات ذات الأساس إلى اللوغاريتمات ذات الأساس المحدد والتي تكون قيمها معروفة أو من الممكن العثور عليها. عادة، من اللوغاريتم الأصلي، باستخدام صيغة الانتقال، ينتقلون إلى اللوغاريتمات في إحدى القواعد 2 أو e أو 10، حيث توجد لهذه القواعد جداول لوغاريتمية تسمح بحساب قيمها بدرجة معينة من دقة. وفي الفقرة التالية سوف نبين كيف يتم ذلك.
الجداول اللوغاريتمية واستخداماتها
يمكن استخدام الحساب التقريبي لقيم اللوغاريتم جداول اللوغاريتم. جدول اللوغاريتم الأساسي 2 الأكثر استخدامًا، وجدول اللوغاريتم الطبيعي، وجدول اللوغاريتم العشري. عند العمل في نظام الأرقام العشرية، من المناسب استخدام جدول اللوغاريتمات على أساس العشرة. بمساعدتها سوف نتعلم كيفية العثور على قيم اللوغاريتمات.





يتيح لك الجدول المعروض العثور على قيم اللوغاريتمات العشرية للأرقام من 1000 إلى 9999 (مع ثلاث منازل عشرية) بدقة تصل إلى جزء من عشرة آلاف. سنقوم بتحليل مبدأ إيجاد قيمة اللوغاريتم باستخدام جدول اللوغاريتمات العشرية باستخدام مثال محدد - الأمر أكثر وضوحًا بهذه الطريقة. لنجد log1.256.
في العمود الأيسر من جدول اللوغاريتمات العشرية نجد أول رقمين من الرقم 1.256، أي نجد 1.2 (هذا الرقم محاط بدائرة باللون الأزرق من أجل الوضوح). تم العثور على الرقم الثالث من الرقم 1.256 (الرقم 5) في السطر الأول أو الأخير على يسار الخط المزدوج (هذا الرقم محاط بدائرة باللون الأحمر). الرقم الرابع من الرقم الأصلي 1.256 (الرقم 6) موجود في السطر الأول أو الأخير على يمين الخط المزدوج (هذا الرقم محاط بدائرة بخط أخضر). الآن نجد الأرقام في خلايا جدول اللوغاريتم عند تقاطع الصف المحدد والأعمدة المحددة (يتم تمييز هذه الأرقام باللون البرتقالي). مجموع الأرقام المحددة يعطي القيمة المطلوبة للوغاريتم العشري بدقة حتى المنزلة العشرية الرابعة، أي، سجل1.236≈0.0969+0.0021=0.0990.
هل من الممكن باستخدام الجدول أعلاه إيجاد قيم اللوغاريتمات العشرية للأعداد التي تحتوي على أكثر من ثلاثة أرقام بعد العلامة العشرية، وكذلك تلك التي تتجاوز النطاق من 1 إلى 9.999؟ نعم يمكنك ذلك. دعونا نظهر كيف يتم ذلك مع مثال.
دعونا نحسب lg102.76332. أولا تحتاج إلى الكتابة الرقم في النموذج القياسي: 102.76332=1.0276332·10 2. بعد ذلك، ينبغي تقريب الجزء العشري إلى المنزلة العشرية الثالثة، لدينا 1.0276332 10 2 ≈1.028 10 2، في حين أن اللوغاريتم العشري الأصلي يساوي تقريبًا لوغاريتم الرقم الناتج، أي أننا نأخذ log102.76332≈lg1.028·10 2. الآن نطبق خصائص اللوغاريتم: lg1.028·10 2 =lg1.028+lg10 2 =lg1.028+2. وأخيرا نجد قيمة اللوغاريتم lg1.028 من جدول اللوغاريتمات العشرية lg1.028≈0.0086+0.0034=0.012. ونتيجة لذلك، تبدو عملية حساب اللوغاريتم برمتها كما يلي: log102.76332=log1.0276332 10 2 ≈lg1.028 10 2 = log1.028+lg10 2 =log1.028+2≈0.012+2=2.012.
في الختام، تجدر الإشارة إلى أنه باستخدام جدول اللوغاريتمات العشرية، يمكنك حساب القيمة التقريبية لأي لوغاريتم. للقيام بذلك، يكفي استخدام صيغة الانتقال للانتقال إلى اللوغاريتمات العشرية، والعثور على قيمها في الجدول، وإجراء العمليات الحسابية المتبقية.
على سبيل المثال، دعونا نحسب السجل 2 3 . وفقا لصيغة الانتقال إلى قاعدة جديدة للوغاريتم، لدينا . من جدول اللوغاريتمات العشرية نجد log3≈0.4771 و log2≈0.3010. هكذا، .
فهرس.
- Kolmogorov A.N.، Abramov A.M.، Dudnitsyn Yu.P. وغيرها الجبر وبدايات التحليل: كتاب مدرسي للصفوف 10 - 11 بمؤسسات التعليم العام.
- جوسيف ف.أ.، موردكوفيتش أ.ج. الرياضيات (دليل للملتحقين بالمدارس الفنية).
يتم إعطاء الخصائص الأساسية للوغاريتم، الرسم البياني اللوغاريتمي، مجال التعريف، مجموعة القيم، الصيغ الأساسية، الزيادة والتناقص. يعتبر العثور على مشتق اللوغاريتم. بالإضافة إلى توسيع سلسلة القوى وتمثيلها باستخدام الأعداد المركبة.
محتوىالمجال، مجموعة من القيم، متزايدة، متناقصة
اللوغاريتم هو دالة رتيبة، لذلك ليس لديها القيم القصوى. يتم عرض الخصائص الرئيسية للوغاريتم في الجدول.
| اِختِصاص | 0 < x < + ∞ | 0 < x < + ∞ |
| مدى من القيم | - ∞ < y < + ∞ | - ∞ < y < + ∞ |
| روتيني | يزيد رتابة | يتناقص رتابة |
| أصفار، ص = 0 | س = 1 | س = 1 |
| نقاط التقاطع مع المحور الإحداثي x = 0 | لا | لا |
| + ∞ | - ∞ | |
| - ∞ | + ∞ |
القيم الخاصة
يسمى اللوغاريتم للأساس 10 اللوغاريتم العشريويرمز لها على النحو التالي:
اللوغاريتم للقاعدة همُسَمًّى اللوغاريتم الطبيعي:
الصيغ الأساسية للوغاريتمات
خصائص اللوغاريتم الناشئة عن تعريف الدالة العكسية:
الخاصية الرئيسية للوغاريتمات وعواقبها
صيغة استبدال القاعدة
اللوغاريتم هو العملية الرياضية لأخذ اللوغاريتم. عند أخذ اللوغاريتمات، يتم تحويل منتجات العوامل إلى مجموع المصطلحات.
التقوية هي العملية الرياضية العكسية للوغاريتم. أثناء التقوية، يتم رفع قاعدة معينة إلى درجة التعبير التي يتم تنفيذ التقوية عليها. في هذه الحالة، يتم تحويل مجموع المصطلحات إلى منتجات العوامل.
إثبات الصيغ الأساسية للوغاريتمات
تتبع الصيغ المتعلقة باللوغاريتمات صيغ الدوال الأسية ومن تعريف الدالة العكسية.
النظر في خاصية الدالة الأسية
.
ثم
.
دعونا نطبق خاصية الدالة الأسية
:
.
دعونا نثبت صيغة الاستبدال الأساسية.
;
.
بافتراض ج = ب، لدينا:
وظيفة عكسية
معكوس اللوغاريتم للأساس a هو دالة أسية ذات الأس a.
اذا ثم
اذا ثم
مشتق من اللوغاريتم
مشتق من لوغاريتم المعامل x:
.
مشتق من الترتيب ن:
.
اشتقاق الصيغ > > >
للعثور على مشتقة اللوغاريتم، يجب اختزاله إلى الأساس ه.
;
.
أساسي
يتم حساب تكامل اللوغاريتم عن طريق التكامل بالأجزاء: .
لذا،
التعبيرات باستخدام الأعداد المركبة
خذ بعين الاعتبار دالة الأعداد المركبة ض:
.
دعونا نعبر عن عدد مركب ضعبر الوحدة النمطية صوالحجة φ
:
.
ثم باستخدام خصائص اللوغاريتم نحصل على:
.
أو
ومع ذلك الحجة φ
لم يتم تعريفها بشكل فريد. إذا وضعت
، حيث n عدد صحيح،
ثم سيكون نفس الرقم لمختلف ن.
ولذلك، فإن اللوغاريتم، كدالة لمتغير معقد، ليس دالة ذات قيمة واحدة.
توسيع سلسلة الطاقة
عندما يحدث التوسع:
مراجع:
في. برونشتاين، ك.أ. سيمنديايف، دليل الرياضيات للمهندسين وطلاب الجامعات، "لان"، 2009.
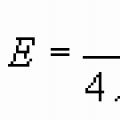 نظرية أوستروجرادسكي-غاوس
نظرية أوستروجرادسكي-غاوس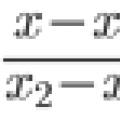 كيف تتعلم حل المشاكل في الهندسة التحليلية؟
كيف تتعلم حل المشاكل في الهندسة التحليلية؟ معنى كلمة تجاري معنى كلمة تجاري
معنى كلمة تجاري معنى كلمة تجاري