أوجد قيمة الاحتمال. يسقط الشك ، أو كيف تجد الاحتمال
كفئة وجودية تعكس مقياس إمكانية ظهور أي كيان في أي ظروف. على عكس التفسيرات الرياضية والمنطقية لهذا المفهوم ، لا تربط V. الأنطولوجية نفسها بضرورة التعبير الكمي. يتم الكشف عن قيمة V. في سياق فهم الحتمية وطبيعة التنمية بشكل عام.
تعريف رائع
تعريف غير كامل ↓
احتمالا
مفهوم يميز الكميات. مقياس لإمكانية ظهور حدث معين في وقت معين. شروط. في علمي المعرفة هناك ثلاثة تفسيرات للمفهوم الخامس للمفهوم الكلاسيكي ، والتي نشأت من الرياضيات. تحليل المقامرة والذي تم تطويره بشكل كامل من قبل B. Pascal و J. Bernoulli و P. Laplace ، يعتبر V. نسبة عدد الحالات المؤاتية إلى العدد الإجمالي للجميع على قدم المساواة. على سبيل المثال ، عند رمي نرد يحتوي على 6 جوانب ، يمكن توقع أن يأتي كل جانب بـ V يساوي 1/6 ، حيث لا يتمتع أي جانب بمزايا على الآخر. يؤخذ هذا التناسق في نتائج التجربة في الاعتبار بشكل خاص عند تنظيم الألعاب ، ولكنه نادر نسبيًا في دراسة الأحداث الموضوعية في العلم والممارسة. كلاسيك أفسح تفسير V. المجال للإحصائية. مفاهيم V. ، في جوهرها صالحة. مراقبة ظهور حدث معين خلال المدة. تجربة في ظل ظروف ثابتة بدقة. تؤكد الممارسة أنه كلما حدث حدث في كثير من الأحيان ، زادت درجة الاحتمال الموضوعي لوقوعه ، أو V. لذلك ، الإحصاء. يعتمد تفسير V. على مفهوم المتعلقات. الترددات ، يمكن تحديد القطع تجريبيا. خامسا النظرية. المفهوم لا يتطابق أبدًا مع تكرار محدد تجريبيًا ، ومع ذلك ، من نواح كثيرة. من الناحية العملية يختلف قليلاً عن الأقارب. تم العثور على التردد نتيجة للمدة. الملاحظات. العديد من الإحصائيين يعتبرون V. إشارة "مزدوجة". التردد ، يتم تحديد الحافة بالإحصائية. دراسة نتائج الملاحظة
أو التجارب. كان تعريف V. أقل واقعية كما يتعلق بالحد. ترددات الأحداث الجماعية ، أو التجمعات ، التي اقترحها R.Mises. كتطوير إضافي لنهج التردد لـ V. ، تم طرح تفسير ميول أو نزوع لـ V. (K. Popper ، J. Hecking ، M. Bunge ، T. Setl). وفقًا لهذا التفسير ، يميز V. خاصية توليد الظروف ، على سبيل المثال. تجربة. التثبيت ، للحصول على سلسلة من الأحداث العشوائية الضخمة. هذا هو الموقف الذي يؤدي إلى المادية التصرفات ، أو الميول ، يمكن التحقق من V. to-rykh عن طريق النسبي. الترددات.
الإحصاء يهيمن تفسير V. المعرفة ، لأنها تعكس المحدد. طبيعة الأنماط المتأصلة في الظواهر الجماعية ذات الطبيعة العشوائية. في العديد من الفيزيائية والبيولوجية والاقتصادية والديموغرافية والعمليات الاجتماعية الأخرى ، فمن الضروري أن تأخذ في الاعتبار عمل العديد من العوامل العشوائية ، تتميز الجاودار بتردد ثابت. تحديد هذا التردد المستقر والكميات. تقييمه بمساعدة V. يجعل من الممكن الكشف عن الضرورة ، والتي تشق طريقها من خلال العمل التراكمي للعديد من الحوادث. هذا هو المكان الذي يجد فيه ديالكتيك تحول الصدفة إلى ضرورة تجلياته (انظر ف.إنجلز ، في كتاب: ك. ماركس وإف.إنجلز ، سوتش ، المجلد 20 ، ص 535-36).
يميز الاستدلال المنطقي أو الاستقرائي العلاقة بين المقدمات واستنتاج الاستدلال غير التوضيحي ، وعلى وجه الخصوص ، الاستقرائي. على عكس الاستنتاج ، فإن مقدمات الاستقراء لا تضمن حقيقة الاستنتاج ، ولكنها تجعلها أكثر أو أقل منطقية. يمكن أحيانًا تقدير هذه المصداقية ، مع فرضيات مصاغة بدقة ، بمساعدة V. غالبًا ما يتم تحديد قيمة V. المفاهيم (أكبر من أو أقل من أو يساوي) وأحيانًا بطريقة رقمية. منطق غالبًا ما يستخدم التفسير لتحليل الاستدلال الاستقرائي وبناء أنظمة مختلفة من المنطق الاحتمالي (آر.كارناب ، آر جيفري). في الدلالي مفاهيم منطقية. غالبًا ما يتم تعريف V. على أنها درجة تأكيد بيان واحد من قبل الآخرين (على سبيل المثال ، فرضية بياناتها التجريبية).
فيما يتعلق بتطوير نظريات صنع القرار والألعاب ، فإن ما يسمى ب. التفسير الشخصي لـ V. على الرغم من أن V. في نفس الوقت تعبر عن درجة الإيمان بالموضوع ووقوع حدث معين ، يجب اختيار V. نفسها بطريقة تُرضي البديهيات الخاصة بحساب V. لذلك ، ف مع مثل هذا التفسير لا يعبر عن درجة الذاتية بقدر ما يعبر عن الإيمان العقلاني. وبالتالي ، فإن القرارات المتخذة على أساس هذه V. ستكون عقلانية ، لأنها لا تأخذ في الاعتبار الحالة النفسية. خصائص وميول الموضوع.
من المعرفية ر. الفرق بين الإحصاء المنطقي. والتفسيرات الشخصية لـ V. تكمن في حقيقة أنه إذا كان الأول يميز الخصائص الموضوعية وعلاقات الظواهر الجماعية ذات الطبيعة العشوائية ، فإن الأخيرين يحللان سمات الذات ، المدركة. الأنشطة البشرية في ظل ظروف عدم اليقين.
احتمالا
من أهم مفاهيم العلم تميز الرؤية النظامية الخاصة للعالم وهيكله وتطوره وإدراكه. يتم الكشف عن خصوصية النظرة الاحتمالية للعالم من خلال إدراج مفاهيم الصدفة والاستقلالية والتسلسل الهرمي (أفكار المستويات في البنية وتحديد الأنظمة) بين المفاهيم الأساسية للوجود.
نشأت الأفكار حول الاحتمالية في العصور القديمة وكانت مرتبطة بخصائص معرفتنا ، بينما تم التعرف على وجود المعرفة الاحتمالية ، والتي تختلف عن المعرفة الموثوقة والمعرفة الزائفة. يرتبط تأثير فكرة الاحتمال على التفكير العلمي ، على تطوير المعرفة ارتباطًا مباشرًا بتطوير نظرية الاحتمال كنظام رياضي. يعود أصل عقيدة الاحتمالات الرياضية إلى القرن السابع عشر ، عندما سمح تطور جوهر المفاهيم. الخصائص الكمية (العددية) والتعبير عن فكرة احتمالية.
تطبيقات الاحتمالية المكثفة لتنمية المعرفة تقع في الطابق الثاني. 19- الدور الأول. القرن ال 20 دخلت الاحتمالية في هياكل العلوم الأساسية للطبيعة مثل الفيزياء الإحصائية الكلاسيكية ، وعلم الوراثة ، ونظرية الكم ، وعلم التحكم الآلي (نظرية المعلومات). وفقًا لذلك ، يجسد الاحتمال تلك المرحلة في تطور العلم ، والذي يُعرَّف الآن على أنه علم غير كلاسيكي. للكشف عن الحداثة وخصائص طريقة التفكير الاحتمالية ، من الضروري الانطلاق من تحليل موضوع نظرية الاحتمالات وأسس تطبيقاتها العديدة. تُعرَّف نظرية الاحتمالات عادةً بأنها تخصص رياضي يدرس قوانين الظواهر العشوائية الجماعية في ظل ظروف معينة. تعني العشوائية أنه في إطار الطابع الجماعي ، لا يعتمد وجود كل ظاهرة أولية على وجود ظواهر أخرى ولا يتحدد بها. في الوقت نفسه ، فإن الطبيعة الجماعية للظواهر لها بنية مستقرة ، وتحتوي على بعض الانتظام. تنقسم ظاهرة الكتلة بشكل صارم إلى أنظمة فرعية ، والعدد النسبي للظواهر الأولية في كل نظام فرعي (التردد النسبي) مستقر للغاية. يقارن هذا الاستقرار مع الاحتمال. تتميز الظاهرة الجماعية ككل بتوزيع الاحتمالات ، أي تخصيص النظم الفرعية والاحتمالات المقابلة لها. لغة نظرية الاحتمالات هي لغة التوزيعات الاحتمالية. وفقًا لذلك ، يتم تعريف نظرية الاحتمالية على أنها العلم المجرد للعمل مع التوزيعات.
أدت الاحتمالية في العلم إلى أفكار حول الانتظام الإحصائي والأنظمة الإحصائية. هذه الأخيرة عبارة عن أنظمة مكونة من كيانات مستقلة أو شبه مستقلة ، ويتميز هيكلها بتوزيعات احتمالية. ولكن كيف يمكن تكوين أنظمة من كيانات مستقلة؟ عادة ما يُفترض أنه من أجل تكوين أنظمة ذات خصائص متكاملة ، من الضروري أن توجد بين عناصرها روابط مستقرة بدرجة كافية تعزز الأنظمة. يتم توفير استقرار الأنظمة الإحصائية من خلال وجود الظروف الخارجية ، والبيئة الخارجية ، والقوى الخارجية بدلاً من القوى الداخلية. إن تعريف الاحتمال ذاته يعتمد دائمًا على تحديد الشروط لتشكيل ظاهرة الكتلة الأولية. فكرة أخرى مهمة تميز النموذج الاحتمالي هي فكرة التسلسل الهرمي (التبعية). تعبر هذه الفكرة عن العلاقة بين خصائص العناصر الفردية والخصائص المتكاملة للأنظمة: فالأخيرة ، كما كانت ، مبنية على الأول.
تكمن أهمية الأساليب الاحتمالية في الإدراك في حقيقة أنها تسمح لنا باستكشاف أنماط بنية وسلوك الكائنات والأنظمة التي لها بنية هرمية "ثنائية المستوى" والتعبير عنها نظريًا.
يعتمد تحليل طبيعة الاحتمال على تواترها وتفسيرها الإحصائي. في الوقت نفسه ، لفترة طويلة جدًا ، سيطر هذا الفهم للاحتمالية على العلم ، والذي كان يسمى الاحتمال المنطقي أو الاستقرائي. يهتم الاحتمال المنطقي بالأسئلة المتعلقة بصحة حكم فردي منفصل في ظل ظروف معينة. هل من الممكن تقييم درجة التأكيد (الموثوقية ، الحقيقة) للاستنتاج الاستقرائي (الاستنتاج الافتراضي) في شكل كمي؟ في سياق تشكيل نظرية الاحتمال ، تمت مناقشة مثل هذه الأسئلة مرارًا وتكرارًا ، وبدأوا في الحديث عن درجات تأكيد الاستنتاجات الافتراضية. يتم تحديد مقياس الاحتمال هذا من خلال المعلومات المتوفرة لدى شخص معين ، وتجربته ، ووجهات نظره حول العالم والعقلية النفسية. في جميع هذه الحالات ، لا يكون حجم الاحتمال قابلاً للقياسات الصارمة ويقع عمليًا خارج اختصاص نظرية الاحتمالات كنظام رياضي ثابت.
تم إنشاء تفسير موضوعي وتكرار للاحتمالية في العلوم بصعوبة كبيرة. في البداية ، تأثر فهم طبيعة الاحتمال بشدة بتلك الآراء الفلسفية والمنهجية التي كانت من سمات العلوم الكلاسيكية. تاريخياً ، حدث تشكيل الطرق الاحتمالية في الفيزياء تحت التأثير الحاسم لأفكار الميكانيكا: تم التعامل مع الأنظمة الإحصائية ببساطة على أنها ميكانيكية. نظرًا لأن المشكلات المقابلة لم يتم حلها بالطرق الصارمة للميكانيكا ، فقد نشأت تصريحات مفادها أن اللجوء إلى الأساليب الاحتمالية والانتظام الإحصائي هو نتيجة عدم اكتمال معرفتنا. في تاريخ تطور الفيزياء الإحصائية الكلاسيكية ، بذلت محاولات عديدة لإثباتها على أساس الميكانيكا الكلاسيكية ، لكنها فشلت جميعًا. أساس الاحتمال هو أنه يعبر عن سمات بنية فئة معينة من الأنظمة ، بخلاف أنظمة الميكانيكا: تتميز حالة عناصر هذه الأنظمة بعدم الاستقرار وطبيعة التفاعلات الخاصة (غير القابلة للاختزال إلى الميكانيكا). .
يؤدي دخول الاحتمالية إلى الإدراك إلى إنكار مفهوم الحتمية الصارمة ، إلى إنكار النموذج الأساسي للوجود والإدراك الذي تم تطويره في عملية تكوين العلم الكلاسيكي. النماذج الأساسية التي تمثلها النظريات الإحصائية ذات طبيعة مختلفة وأكثر عمومية: فهي تتضمن أفكار العشوائية والاستقلالية. ترتبط فكرة الاحتمال بالكشف عن الديناميكيات الداخلية للأشياء والأنظمة ، والتي لا يمكن تحديدها بالكامل من خلال الظروف والظروف الخارجية.
لقد كشف مفهوم الرؤية الاحتمالية للعالم ، القائمة على الإقصاء المطلق للأفكار حول الاستقلال (كما كان من قبل ، نموذج التحديد الصارم) ، عن حدوده ، والتي تؤثر بشدة على انتقال العلم الحديث إلى الأساليب التحليلية لدراسة معقدة. الأنظمة والأسس الفيزيائية والرياضية لظواهر التنظيم الذاتي.
تعريف رائع
تعريف غير كامل ↓
دعونا لا نفكر في النبيلة لفترة طويلة - لنبدأ على الفور بتعريف.
مخطط برنولي هو عندما يتم إجراء تجارب مستقلة من نفس النوع ، قد يظهر في كل منها حدث يهمنا ، ويعرف احتمال هذا الحدث P (A) \ u003d p. مطلوب لتحديد احتمال وقوع الحدث A بالضبط k مرة خلال n من التجارب.
المهام التي يتم حلها وفقًا لنظام برنولي متنوعة للغاية: من المهام البسيطة (مثل "العثور على احتمال أن يصوب مطلق النار مرة واحدة من أصل 10") إلى المهام الشديدة جدًا (على سبيل المثال ، مهام النسب المئوية أو أوراق اللعب) . في الواقع ، غالبًا ما يستخدم هذا المخطط لحل المشكلات المتعلقة بمراقبة جودة المنتج وموثوقية الآليات المختلفة ، والتي يجب معرفة جميع خصائصها قبل بدء العمل.
دعنا نعود إلى التعريف. نظرًا لأننا نتحدث عن تجارب مستقلة ، وفي كل تجربة ، فإن احتمالية الحدث A هي نفسها ، فهناك نتيجتان فقط ممكنتان:
- A هو حدوث الحدث A مع الاحتمال p ؛
- "ليس A" - لم يظهر الحدث A ، والذي يحدث مع الاحتمال q = 1 - p.
إن أهم شرط بدونه يفقد مخطط برنولي معناه هو الثبات. بغض النظر عن عدد التجارب التي نجريها ، فنحن مهتمون بنفس الحدث أ الذي يحدث بنفس الاحتمال ص.
بالمناسبة ، لا يمكن اختزال كل المشكلات في نظرية الاحتمالات إلى ظروف ثابتة. أي مدرس مختص في الرياضيات العليا سيخبرك بهذا. حتى الشيء البسيط مثل انتقاء الكرات الملونة من الصندوق لا يعد تجربة ذات ظروف ثابتة. أخذوا كرة أخرى - تغيرت نسبة الألوان في الصندوق. لذلك ، تغيرت الاحتمالات أيضًا.
إذا كانت الظروف ثابتة ، فيمكن للمرء أن يحدد بدقة احتمالية وقوع الحدث A بالضبط k مرة من n ممكن. نصوغ هذه الحقيقة في شكل نظرية:
نظرية برنولي. اجعل احتمال حدوث الحدث A في كل تجربة ثابتًا ويساوي p. ثم يتم حساب احتمال ظهور الحدث A بالضبط في n من التجارب المستقلة بواسطة الصيغة:
حيث C n k هو عدد التوليفات ، q = 1 - p.
هذه الصيغة تسمى صيغة برنولي. من المثير للاهتمام أن نلاحظ أن المشاكل أدناه قد تم حلها بالكامل دون استخدام هذه الصيغة. على سبيل المثال ، يمكنك تطبيق صيغ جمع الاحتمالات. ومع ذلك ، فإن مقدار الحساب سيكون ببساطة غير واقعي.
مهمة. احتمال إنتاج منتج معيب على الجهاز هو 0.2. أوجد احتمال أن يكون k بالضبط بدون عيوب في دفعة من عشرة أجزاء منتجة على آلة معينة. حل المسألة من أجل k = 0 ، 1 ، 10.
حسب الشرط ، نحن مهتمون بالحدث A لإصدار منتجات بدون عيوب ، والذي يحدث في كل مرة مع احتمال p = 1 - 0.2 = 0.8. نحتاج إلى تحديد احتمال وقوع هذا الحدث ك مرة. الحدث أ يعارض الحدث "ليس أ" ، أي إنتاج منتج معيب.
وهكذا ، لدينا: n = 10 ؛ ع = 0.8 ؛ ف = 0.2.
لذلك ، نجد احتمال أن تكون جميع الأجزاء في الدفعة معيبة (ك = 0) ، وأن جزءًا واحدًا فقط معيب (ك = 1) ، وأنه لا توجد أجزاء معيبة على الإطلاق (ك = 10):

مهمة. تم رمي العملة 6 مرات. من المحتمل بنفس القدر فقدان شعار النبالة وذيول. أوجد احتمال أن:
- شعار النبالة يسقط ثلاث مرات ؛
- شعار النبالة سوف يسقط مرة واحدة ؛
- سيظهر شعار النبالة مرتين على الأقل.
لذلك ، نحن مهتمون بالحدث "أ" عندما يسقط شعار النبالة. احتمالية حدوث هذا الحدث هي p = 0.5. يتم مواجهة الحدث A بالحدث "ليس A" ، عندما يظهر ذيول ، والذي يحدث مع الاحتمال q = 1 - 0.5 = 0.5. من الضروري تحديد احتمال سقوط شعار النبالة k مرة.
وهكذا ، لدينا: n = 6 ؛ ع = 0.5 ؛ ف = 0.5.
دعونا نحدد احتمال سقوط شعار النبالة ثلاث مرات ، أي ك = 3:
لنحدد الآن احتمال سقوط شعار النبالة مرة واحدة فقط ، أي ك = 1:
يبقى تحديد ما هو احتمال سقوط شعار النبالة مرتين على الأقل. العقبة الرئيسية هي عبارة "لا أقل". اتضح أن أي k يناسبنا ، باستثناء 0 و 1 ، أي تحتاج إلى إيجاد قيمة المجموع X \ u003d P 6 (2) + P 6 (3) + ... + P 6 (6).
لاحظ أن هذا المبلغ يساوي أيضًا (1 - P 6 (0) - P 6 (1)) ، أي من بين جميع الخيارات الممكنة ، يكفي "قطع" تلك الخيارات عندما سقط شعار النبالة مرة واحدة (ك = 1) أو لم يسقط على الإطلاق (ك = 0). بما أن P 6 (1) نعلم بالفعل ، يبقى إيجاد P 6 (0):

مهمة. يبلغ احتمال أن يكون التلفزيون به عيوبًا خفية هو 0.2. استقبل المستودع 20 جهاز تلفزيون. ما هو الحدث الأكثر احتمالًا: وجود جهازي تلفزيون بهما عيوب خفية في هذه الدفعة أو الثلاثة؟
حدث الاهتمام A هو وجود عيب كامن. إجمالي أجهزة التلفزيون n = 20 ، احتمال وجود عيب خفي p = 0.2. وفقًا لذلك ، فإن احتمال الحصول على جهاز تلفزيون بدون عيب خفي هو q = 1 - 0.2 = 0.8.
نحصل على شروط البداية لنظام برنولي: n = 20 ؛ ع = 0.2 ؛ ف = 0.8.
لنجد احتمال الحصول على جهازي تلفاز "معيبين" (k = 2) وثلاثة (k = 3):
\ [\ start (array) (l) (P_ (20)) \ left (2 \ right) = C_ (20) ^ 2 (p ^ 2) (q ^ (18)) = \ frac ((20}{{2!18!}} \cdot {0,2^2} \cdot {0,8^{18}} \approx 0,137\\{P_{20}}\left(3 \right) = C_{20}^3{p^3}{q^{17}} = \frac{{20!}}{{3!17!}} \cdot {0,2^3} \cdot {0,8^{17}} \approx 0,41\end{array}\]!}
من الواضح ، P 20 (3)> P 20 (2) ، أي من المرجح أن تحصل ثلاثة أجهزة تلفزيون بها عيوب خفية على جهازي تلفزيون فقط من هذا القبيل. علاوة على ذلك ، فإن الاختلاف ليس ضعيفًا.
ملاحظة صغيرة حول العوامل. يشعر الكثير من الناس بشعور غامض بعدم الراحة عندما يرون الإدخال "0"! (اقرأ "صفر عاملي"). إذن ، 0! = 1 بالتعريف.
ص. س. والاحتمال الأكبر في المهمة الأخيرة هو الحصول على أربعة أجهزة تلفزيون بها عيوب خفية. قم بالحسابات وانظر بنفسك.
هل تريد أن تعرف ما هي الفرص الحسابية لنجاح رهانك؟ ثم لدينا خبران جيدان لك. أولاً: لحساب المباح ، لا تحتاج إلى إجراء حسابات معقدة وقضاء الكثير من الوقت. يكفي استخدام الصيغ البسيطة ، والتي ستستغرق دقيقتين للعمل بها. ثانيًا ، بعد قراءة هذا المقال ، ستتمكن بسهولة من حساب احتمالية اجتياز أي من تداولاتك.
لتحديد صلاحية المباح بشكل صحيح ، تحتاج إلى اتخاذ ثلاث خطوات:
- حساب النسبة المئوية لاحتمالية نتيجة الحدث وفقًا لمكتب المراهنات ؛
- احسب الاحتمال من البيانات الإحصائية بنفسك ؛
- اكتشف قيمة الرهان في ضوء كلا الاحتمالين.
دعونا نفكر بالتفصيل في كل خطوة من الخطوات ، ليس فقط باستخدام الصيغ ، ولكن أيضًا باستخدام الأمثلة.
مرور سريع
حساب الاحتمالية المضمنة في احتمالات الرهان
الخطوة الأولى هي معرفة الاحتمالية التي يقيمها صانع المراهنات لفرص نتيجة معينة. بعد كل شيء ، من الواضح أن وكلاء المراهنات لا يراهنون على احتمالات من هذا القبيل. لهذا نستخدم الصيغة التالية:
صب= (1 / ك) * 100٪ ،
حيث P B هو احتمال النتيجة وفقًا لمكتب المراهنات ؛
ك - احتمالات المراهنات على النتيجة.

لنفترض أن الاحتمالات هي 4 لفوز أرسنال اللندني في مبارزة ضد بايرن ، وهذا يعني أن احتمالية فوزه من قبل كولومبيا البريطانية تعتبر (1/4) * 100٪ = 25٪. أو ديوكوفيتش يلعب ضد الجنوب. مضاعف انتصار نوفاك 1.2 ، فرصه تساوي (1 / 1.2) * 100٪ = 83٪.
هذه هي الطريقة التي يقيّم بها صانع المراهنات نفسه فرص النجاح لكل لاعب وفريق. بعد الانتهاء من الخطوة الأولى ، ننتقل إلى الثانية.
حساب احتمال وقوع حدث من قبل اللاعب
النقطة الثانية في خطتنا هي تقييمنا لاحتمال وقوع الحدث. نظرًا لأنه لا يمكننا أن نأخذ في الاعتبار حسابيًا مثل هذه المعلمات مثل التحفيز ونبرة اللعبة ، فسنستخدم نموذجًا مبسطًا ونستخدم فقط إحصائيات الاجتماعات السابقة. لحساب الاحتمال الإحصائي لنتيجة ما ، نستخدم الصيغة:
صو\ u003d (UM / M) * 100٪ ،
أينصو- احتمالية وقوع الحدث حسب اللاعب ؛
UM - عدد المباريات الناجحة التي حدث فيها مثل هذا الحدث ؛
M هو العدد الإجمالي للمباريات.

لتوضيح الأمر ، دعنا نعطي أمثلة. خاض آندي موراي ورافائيل نادال 14 مباراة. في 6 منها ، تم تسجيل إجمالي أقل من 21 مباراة ، في 8 - أكثر من المجموع. من الضروري معرفة احتمال أن يتم لعب المباراة التالية بإجمالي أكثر: (8/14) * 100 = 57٪. لعب فالنسيا 74 مباراة على ملعب ميستايا ضد أتلتيكو ، حيث سجل 29 انتصارا. احتمال فوز فالنسيا: (29/74) * 100٪ = 39٪.
وكلنا نعرف هذا فقط بفضل إحصائيات الألعاب السابقة! بطبيعة الحال ، لا يمكن حساب مثل هذا الاحتمال لبعض الفريق أو اللاعب الجديد ، لذا فإن استراتيجية الرهان هذه مناسبة فقط للمباريات التي لا يلتقي فيها الخصوم للمرة الأولى. الآن نحن نعرف كيفية تحديد الرهان والاحتمالات الخاصة بالنتائج ، ولدينا كل المعرفة للانتقال إلى الخطوة الأخيرة.
تحديد قيمة الرهان
ترتبط قيمة (قابلية التقييم) للرهان وقابلية المرور ارتباطًا مباشرًا: كلما ارتفع التقييم ، زادت فرصة التمرير. يتم حساب القيمة على النحو التالي:
الخامس =صو* K-100٪ ،
حيث V هي القيمة ؛
P I - احتمال نتيجة وفقًا للأفضل ؛
ك - احتمالات المراهنات على النتيجة.
لنفترض أننا نريد المراهنة على ميلان للفوز بالمباراة ضد روما وقد حسبنا أن احتمال فوز الحمر والسود هو 45٪. تقدم لنا شركة المراهنات معامل 2.5 لهذه النتيجة. هل مثل هذا الرهان سيكون ذا قيمة؟ نجري الحسابات: V \ u003d 45٪ * 2.5-100٪ \ u003d 12.5٪. رائع ، لدينا رهان قيم وفرص جيدة للنجاح.
لنأخذ حالة أخرى. ماريا شارابوفا تلعب ضد بيترا كفيتوفا. نريد عقد صفقة تفوز ماريا ، والتي ، وفقًا لحساباتنا ، لديها احتمال 60٪. تقدم المراهنات مضاعفًا قدره 1.5 لهذه النتيجة. حدد القيمة: V = 60٪ * 1.5-100 = -10٪. كما ترى ، هذا الرهان ليس له قيمة ويجب الامتناع عنه.

في البداية ، كونها مجرد مجموعة من المعلومات والملاحظات التجريبية للعبة النرد ، أصبحت نظرية الاحتمالية علمًا قويًا. كان فيرما وباسكال أول من أعطاها إطارًا رياضيًا.
من تأملات في الأبدية إلى نظرية الاحتمال
يُعرف شخصان تدين لهما نظرية الاحتمالية بالعديد من الصيغ الأساسية ، وهما بليز باسكال وتوماس بايز ، باسم الأشخاص المتدينين بشدة ، وكان الأخير قسيسًا مشيخيًا. على ما يبدو ، فإن رغبة هذين العالمين في إثبات مغالطة الرأي حول ثروة معينة ، ومنح الحظ السعيد لمفضلاتها ، أعطت قوة دافعة للبحث في هذا المجال. بعد كل شيء ، في الواقع ، أي لعبة حظ ، مع انتصاراتها وخسائرها ، هي مجرد سيمفونية من المبادئ الرياضية.
بفضل إثارة Chevalier de Mere ، الذي كان بنفس القدر لاعبًا وشخصًا لم يكن غير مبالٍ بالعلم ، اضطر باسكال إلى إيجاد طريقة لحساب الاحتمال. كان De Mere مهتمًا بهذا السؤال: "كم مرة تحتاج إلى رمي نردتين في أزواج حتى يتجاوز احتمال الحصول على 12 نقطة 50٪؟". السؤال الثاني الذي أثار اهتمام الرجل المحترم للغاية: "كيف يقسم الرهان بين المشاركين في اللعبة غير المنتهية؟" بالطبع ، نجح باسكال في الإجابة على كلا السؤالين عن دي مير ، الذي أصبح البادئ غير المتعمد لتطوير نظرية الاحتمال. من المثير للاهتمام أن شخصية دي مير بقيت معروفة في هذا المجال ، وليس في الأدب.
في السابق ، لم يقم أي عالم رياضيات بمحاولة حساب احتمالات الأحداث ، حيث كان يُعتقد أن هذا كان مجرد حل للتخمين. قدم بليز باسكال أول تعريف لاحتمال وقوع حدث وأظهر أن هذا رقم محدد يمكن تبريره رياضيًا. أصبحت نظرية الاحتمالات أساس الإحصاء وتستخدم على نطاق واسع في العلوم الحديثة.
ما هي العشوائية
إذا أخذنا في الاعتبار اختبارًا يمكن تكراره لعدد غير محدود من المرات ، فيمكننا تحديد حدث عشوائي. هذه إحدى النتائج المحتملة للتجربة.
الخبرة هي تنفيذ إجراءات محددة في ظروف ثابتة.

لكي تكون قادرًا على العمل مع نتائج التجربة ، عادةً ما يتم الإشارة إلى الأحداث بالحروف A ، B ، C ، D ، E ...
احتمال وقوع حدث عشوائي
لتكون قادرًا على المضي قدمًا في الجزء الرياضي من الاحتمال ، من الضروري تحديد جميع مكوناته.
احتمال وقوع حدث هو مقياس رقمي لإمكانية حدوث حدث ما (أ أو ب) نتيجة للتجربة. يُشار إلى الاحتمال على أنه P (A) أو P (B).
نظرية الاحتمالية هي:
- موثوقالحدث مضمون حدوثه كنتيجة للتجربة Р (Ω) = 1 ؛
- مستحيللا يمكن أن يحدث الحدث أبدًا Р (Ø) = 0 ؛
- عشوائييقع الحدث بين مؤكد ومستحيل ، أي أن احتمال حدوثه ممكن ، لكنه غير مضمون (احتمال وقوع حدث عشوائي يكون دائمًا في حدود 0≤P (A) ≤1).
العلاقات بين الأحداث
يتم أخذ كل من الحدث ومجموع الأحداث A + B في الاعتبار عندما يتم حساب الحدث في تنفيذ أحد المكونات على الأقل ، A أو B ، أو كليهما - A و B.
فيما يتعلق ببعضها البعض ، يمكن أن تكون الأحداث:
- ممكن بنفس القدر.
- متناسق.
- غير متوافق.
- العكس (يستبعد أحدهما الآخر).
- متكل.
إذا كان من الممكن حدوث حدثين باحتمالية متساوية ، فعندئذٍ ممكن بالتساوي.
إذا كان وقوع الحدث A لا يلغي احتمال وقوع الحدث B ، فعندئذٍ هم متناسق.
إذا لم يحدث الحدثان A و B في نفس الوقت في نفس التجربة ، فسيتم استدعاؤهما غير متوافق. يُعد إلقاء عملة معدنية مثالاً جيدًا على ذلك: فالذيول التي تظهر لا تظهر بشكل تلقائي.

يتكون احتمال مجموع هذه الأحداث غير المتوافقة من مجموع احتمالات كل حدث من الأحداث:
ل (أ + ب) = ف (أ) + ف (ب)
إذا كان وقوع حدث ما يجعل حدوث حدث آخر أمرًا مستحيلًا ، فيُدعى العكس. ثم يتم تعيين أحدهما على أنه A ، والآخر - Ā (يُقرأ على أنه "ليس A"). يعني حدوث الحدث A أن Ā لم يحدث. يشكل هذان الحدثان مجموعة كاملة بمجموع احتمالات يساوي 1.

الأحداث التابعة لها تأثير متبادل ، مما يقلل أو يزيد من احتمال الآخر.
العلاقات بين الأحداث. أمثلة
من الأسهل بكثير فهم مبادئ نظرية الاحتمالية ومجموعة الأحداث باستخدام الأمثلة.
التجربة التي سيتم تنفيذها هي سحب الكرات من الصندوق ، وتكون نتيجة كل تجربة نتيجة أولية.
الحدث هو أحد النتائج المحتملة للتجربة - كرة حمراء ، كرة زرقاء ، كرة برقم ستة ، إلخ.
رقم الاختبار 1. هناك 6 كرات ، ثلاث منها زرقاء بأرقام فردية ، والثلاث الأخرى حمراء بأرقام زوجية.

رقم الاختبار 2. هناك 6 كرات زرقاء بأرقام من واحد إلى ستة.

بناءً على هذا المثال ، يمكننا تسمية المجموعات:
- حدث موثوق.بالإسبانية رقم 2 ، حدث "الحصول على الكرة الزرقاء" يمكن الاعتماد عليه ، لأن احتمال حدوثه هو 1 ، حيث أن جميع الكرات زرقاء ولا يمكن تفويتها. في حين أن حدث "الحصول على الكرة بالرقم 1" يكون عشوائيًا.
- حدث مستحيل.بالإسبانية رقم 1 مع الكرات الزرقاء والحمراء ، فإن حدث "الحصول على الكرة الأرجواني" مستحيل ، لأن احتمال حدوثه هو صفر.
- أحداث مماثلة.بالإسبانية رقم 1 ، الأحداث "الحصول على الكرة بالرقم 2" و "الحصول على الكرة بالرقم 3" متساوية الاحتمال ، والأحداث "الحصول على الكرة برقم زوجي" و "الحصول على الكرة بالرقم 2 "احتمالات مختلفة.
- أحداث متوافقة.الحصول على ستة في عملية رمي النرد مرتين على التوالي أحداث متوافقة.
- أحداث غير متوافقة.في نفس الاسبانية لا يمكن الجمع بين الحدثين رقم 1 "الحصول على الكرة الحمراء" و "الحصول على الكرة برقم فردي" في نفس التجربة.
- أحداث معاكسة.ولعل أبرز مثال على ذلك هو رمي العملات المعدنية ، حيث يكون رسم الرؤوس هو نفسه عدم رسم ذيول ، ومجموع احتمالاته دائمًا هو 1 (مجموعة كاملة).
- الأحداث التابعة. لذلك ، باللغة الإسبانية رقم 1 ، يمكنك أن تضع لنفسك هدف استخراج كرة حمراء مرتين على التوالي. يؤثر استخراجه أو عدم استخراجه في المرة الأولى على احتمال استخراجه للمرة الثانية.

يمكن ملاحظة أن الحدث الأول يؤثر بشكل كبير على احتمال الثاني (40٪ و 60٪).
صيغة احتمالية الحدث
يحدث الانتقال من الكهانة إلى البيانات الدقيقة عن طريق نقل الموضوع إلى المستوى الرياضي. وهذا يعني أن الأحكام المتعلقة بحدث عشوائي مثل "الاحتمالية العالية" أو "الحد الأدنى من الاحتمال" يمكن ترجمتها إلى بيانات رقمية محددة. يجوز بالفعل تقييم هذه المواد ومقارنتها وإدخالها في حسابات أكثر تعقيدًا.
من وجهة نظر الحساب ، فإن تعريف احتمال حدث ما هو نسبة عدد النتائج الإيجابية الأولية إلى عدد جميع النتائج المحتملة للتجربة فيما يتعلق بحدث معين. يُشار إلى الاحتمال بواسطة P (A) ، حيث P تعني كلمة "probability" ، والتي تُترجم من الفرنسية إلى "probability".
إذن ، صيغة احتمال وقوع حدث هي:
حيث m هو عدد النتائج المفضلة للحدث A ، n هو مجموع كل النتائج الممكنة لهذه التجربة. دائمًا ما يكون احتمال وقوع حدث ما بين 0 و 1:
0 ≤ الفوسفور (أ) ≤ 1.
حساب احتمال وقوع حدث. مثال
لنأخذ الإسبانية. رقم 1 مع الكرات الموصوفة سابقاً: 3 كرات زرقاء بأرقام 1/3/5 و 3 كرات حمراء بأرقام 2/4/6.

بناءً على هذا الاختبار ، يمكن النظر في عدة مهام مختلفة:
- أ- قطرة الكرة الحمراء. هناك ثلاث كرات حمراء ، وهناك 6 متغيرات في المجموع ، وهذا هو أبسط مثال ، حيث يكون احتمال وقوع حدث هو P (A) = 3/6 = 0.5.
- ب - إسقاط رقم زوجي. هناك 3 (2،4،6) أرقام زوجية في المجموع ، والعدد الإجمالي للخيارات العددية الممكنة هو 6. احتمال هذا الحدث هو P (B) = 3/6 = 0.5.
- C - خسارة رقم أكبر من 2. هناك 4 خيارات من هذا القبيل (3،4،5،6) من العدد الإجمالي للنتائج المحتملة 6. احتمال الحدث C هو P (C) = 4/6 = 0.67.
كما يتضح من الحسابات ، يكون للحدث C احتمالية أعلى ، نظرًا لأن عدد النتائج الإيجابية المحتملة أعلى منه في A و B.
أحداث غير متوافقة
لا يمكن أن تظهر مثل هذه الأحداث في نفس الوقت في نفس التجربة. كما في الاسبانية رقم 1 ، من المستحيل الحصول على كرة زرقاء وحمراء في نفس الوقت. أي يمكنك الحصول على كرة زرقاء أو حمراء. بالطريقة نفسها ، لا يمكن أن يظهر الرقم الفردي والزوجي في النرد في نفس الوقت.
يعتبر احتمال حدثين بمثابة احتمال لمجموعهما أو حاصل ضربهما. يعتبر مجموع هذه الأحداث A + B حدثًا يتكون من ظهور حدث A أو B ، وحاصل AB الخاص بهم - في ظهور كليهما. على سبيل المثال ، ظهور اثنين من الستات مرة واحدة على وجوه نردتين في رمية واحدة.

مجموع الأحداث المتعددة هو حدث يشير إلى حدوث واحد منها على الأقل. نتاج العديد من الأحداث هو حدوثها جميعًا بشكل مشترك.
في نظرية الاحتمالات ، كقاعدة عامة ، يشير استخدام الاتحاد "و" إلى المجموع أو الاتحاد "أو" - الضرب. ستساعدك الصيغ مع الأمثلة على فهم منطق الجمع والضرب في نظرية الاحتمالات.
احتمال مجموع الأحداث غير المتوافقة
إذا تم أخذ احتمال الأحداث غير المتوافقة في الاعتبار ، فإن احتمال مجموع الأحداث يساوي مجموع احتمالاتها:
ل (أ + ب) = ف (أ) + ف (ب)
على سبيل المثال: نحسب احتمال ذلك باللغة الإسبانية. رقم 1 مع الكرات الزرقاء والحمراء سوف يسقط رقمًا بين 1 و 4. لن نحسب في إجراء واحد ، ولكن من خلال مجموع احتمالات المكونات الأولية. لذلك ، في مثل هذه التجربة هناك 6 كرات فقط أو 6 من جميع النتائج الممكنة. الأرقام التي تحقق الشرط هي 2 و 3. احتمال الحصول على الرقم 2 هو 1/6 ، واحتمال الرقم 3 هو أيضًا 1/6. احتمال الحصول على رقم بين 1 و 4 هو:
احتمال مجموع الأحداث غير المتوافقة لمجموعة كاملة هو 1.
لذا ، إذا قمنا في التجربة باستخدام مكعب بجمع احتمالات الحصول على جميع الأرقام ، فنتيجة لذلك نحصل على واحد.
وينطبق هذا أيضًا على الأحداث المعاكسة ، على سبيل المثال ، في تجربة عملة معدنية ، حيث يكون أحد جانبيها هو الحدث A ، والآخر هو الحدث المعاكس Ā ، كما هو معروف ،
Р (А) + Р (Ā) = 1
احتمال إنتاج أحداث غير متوافقة
يتم استخدام مضاعفة الاحتمالات عند النظر في حدوث حدثين غير متوافقين أو أكثر في ملاحظة واحدة. احتمال ظهور الحدثين A و B فيه في نفس الوقت يساوي ناتج احتمالاتهما ، أو:
الفوسفور (أ * ب) = ف (أ) * ف (ب)
على سبيل المثال ، احتمال أن في رقم 1 نتيجة محاولتين ، ستظهر كرة زرقاء مرتين ، تساوي
أي أن احتمال وقوع حدث عندما ، نتيجة محاولتين لاستخراج الكرات ، سيتم استخراج الكرات الزرقاء فقط ، هو 25٪. من السهل جدًا إجراء تجارب عملية على هذه المشكلة ومعرفة ما إذا كان هذا هو الحال بالفعل.
الأحداث المشتركة
تعتبر الأحداث مشتركة عندما يتزامن ظهور أحدهما مع ظهور الآخر. على الرغم من حقيقة أنها مشتركة ، يتم النظر في احتمال وقوع أحداث مستقلة. على سبيل المثال ، يمكن أن يعطي رمي نردتين نتيجة عندما يسقط الرقم 6 على كليهما. على الرغم من أن الأحداث تزامنت وظهرت في نفس الوقت ، إلا أنها مستقلة عن بعضها البعض - يمكن أن تسقط ستة واحدة فقط ، بينما لا يوجد للنرد الثاني التأثير عليه.

يعتبر احتمال الأحداث المشتركة بمثابة احتمال لمجموعها.
احتمال مجموع الأحداث المشتركة. مثال
إن احتمال مجموع الأحداث A و B ، والمشتركين فيما يتعلق ببعضهما البعض ، يساوي مجموع احتمالات الحدث مطروحًا منه احتمال منتجهم (أي التنفيذ المشترك):
مفصل R. (A + B) \ u003d P (A) + P (B) - P (AB)
افترض أن احتمال إصابة الهدف برصاصة واحدة هو 0.4. ثم حدث أ - إصابة الهدف في المحاولة الأولى ، ب - في المحاولة الثانية. هذه الأحداث مشتركة ، لأنه من الممكن إصابة الهدف من اللقطة الأولى ومن اللقطة الثانية. لكن الأحداث لا تتوقف. ما هو احتمالية إصابة الهدف برقطتين (واحدة على الأقل)؟ حسب الصيغة:
0,4+0,4-0,4*0,4=0,64
والجواب على السؤال: "احتمال إصابة الهدف بضربتين 64٪".
يمكن أيضًا تطبيق هذه الصيغة الخاصة باحتمالية وقوع حدث ما على الأحداث غير المتوافقة ، حيث يكون احتمال الحدوث المشترك لحدث P (AB) = 0. وهذا يعني أن احتمال مجموع الأحداث غير المتوافقة يمكن اعتباره حالة خاصة من الصيغة المقترحة.
هندسة الاحتمالية من أجل الوضوح
ومن المثير للاهتمام ، أن احتمال مجموع الأحداث المشتركة يمكن تمثيله كمنطقتين أ و ب يتقاطعان مع بعضهما البعض. كما ترى من الصورة ، فإن مساحة اتحادهم تساوي المساحة الكلية مطروحًا منها مساحة تقاطعهم. هذا التفسير الهندسي يجعل الصيغة التي تبدو غير منطقية أكثر قابلية للفهم. لاحظ أن الحلول الهندسية ليست غير شائعة في نظرية الاحتمالات.

يعد تعريف احتمال مجموع مجموعة (أكثر من اثنين) من الأحداث المشتركة مرهقًا إلى حد ما. لحسابها ، تحتاج إلى استخدام الصيغ المتوفرة لهذه الحالات.
الأحداث التابعة
يتم استدعاء الأحداث التابعة إذا كان حدوث أحدها (أ) يؤثر على احتمال حدوث الآخر (ب). علاوة على ذلك ، يتم أخذ تأثير حدوث كل من الحدث A وعدم حدوثه في الاعتبار. على الرغم من أن الأحداث تسمى تابعة حسب التعريف ، إلا أن واحدًا منها فقط يعتمد على (B). تم الإشارة إلى الاحتمال المعتاد على أنه P (B) أو احتمال وقوع أحداث مستقلة. في حالة المعالين ، يتم تقديم مفهوم جديد - الاحتمال الشرطي P A (B) ، وهو احتمال الحدث التابع B بشرط وقوع الحدث A (الفرضية) ، والذي يعتمد عليه.
لكن الحدث A عشوائي أيضًا ، لذا فإن له أيضًا احتمالًا يجب ويمكن أخذه في الاعتبار في الحسابات. سيوضح المثال التالي كيفية التعامل مع الأحداث التابعة والفرضية.
مثال لحساب احتمالية الأحداث التابعة
من الأمثلة الجيدة لحساب الأحداث التابعة مجموعة أوراق اللعب القياسية.

في مثال مجموعة الأوراق المكونة من 36 بطاقة ، ضع في اعتبارك الأحداث التابعة. من الضروري تحديد احتمال أن تكون البطاقة الثانية المسحوبة من سطح السفينة بدلة ماسية ، إذا كانت البطاقة الأولى المسحوبة هي:
- دف صغير.
- حلة أخرى.
من الواضح أن احتمال الحدث الثاني B يعتمد على الأول A. لذا ، إذا كان الخيار الأول صحيحًا ، وهو بطاقة واحدة (35) و 1 ماسة (8) أقل في المجموعة ، فإن احتمال الحدث B:
الفوسفور أ (ب) = 8/35 = 0.23
إذا كان الخيار الثاني صحيحًا ، فهناك 35 بطاقة في المجموعة ، ولا يزال إجمالي عدد الدفوف (9) محفوظًا ، فإن احتمال الحدث التالي هو B:
الفوسفور أ (ب) = 9/35 = 0.26.
يمكن ملاحظة أنه إذا كان الحدث A مشروطًا بحقيقة أن البطاقة الأولى عبارة عن ماسة ، فإن احتمال الحدث B يتناقص والعكس صحيح.
مضاعفة الأحداث التابعة
بناءً على الفصل السابق ، نقبل الحدث الأول (أ) كحقيقة ، لكن في جوهره ، له طابع عشوائي. احتمال حدوث هذا الحدث ، أي استخراج الدف من مجموعة أوراق اللعب ، يساوي:
الفوسفور (أ) = 9/36 = 1/4
نظرًا لأن النظرية لا توجد في حد ذاتها ، ولكن يتم استدعاؤها لخدمة أغراض عملية ، فمن الإنصاف ملاحظة أنه غالبًا ما تكون هناك حاجة إلى احتمال إنتاج أحداث تابعة.
وفقًا للنظرية حول ناتج احتمالات الأحداث التابعة ، فإن احتمال حدوث أحداث مرتبطة بشكل مشترك A و B يساوي احتمال حدث واحد A ، مضروبًا في الاحتمال الشرطي للحدث B (اعتمادًا على A):
ف (أ ب) \ u003d ف (أ) * ف أ (ب)
ثم في المثال الذي يحتوي على سطح السفينة ، فإن احتمال سحب ورقتين ببدلة من الماس هو:
9/36 * 8/35 = 0.0571 أو 5.7٪
واحتمال الاستخراج ليس الماس في البداية ثم الماس يساوي:
27/36 * 9/35 = 0.19 أو 19٪
يمكن ملاحظة أن احتمال حدوث الحدث B أكبر ، بشرط أن يتم رسم بطاقة من نوع آخر غير الماسة أولاً. هذه النتيجة منطقية ومفهومة تمامًا.
إجمالي احتمال وقوع حدث
عندما تصبح مشكلة الاحتمالات الشرطية متعددة الأوجه ، لا يمكن حسابها بالطرق التقليدية. عندما يكون هناك أكثر من فرضيتين ، وهما A1 ، A2 ، ... ، A n ، .. تشكل مجموعة كاملة من الأحداث تحت الشرط:
- P (A i)> 0 ، i = 1،2 ، ...
- A i ∩ A j = Ø، i ≠ j.
- Σ ل أ ل = Ω.
إذن ، صيغة الاحتمال الإجمالي للحدث B مع مجموعة كاملة من الأحداث العشوائية A1 ، A2 ، ... ، A n هي:

نظرة إلى المستقبل
يعد احتمال وقوع حدث عشوائي أمرًا ضروريًا في العديد من مجالات العلوم: الاقتصاد القياسي والإحصاء والفيزياء وما إلى ذلك. نظرًا لأن بعض العمليات لا يمكن وصفها بشكل حتمي ، نظرًا لأنها احتمالية بحد ذاتها ، هناك حاجة إلى طرق عمل خاصة. يمكن استخدام احتمالية نظرية الحدث في أي مجال تقني كطريقة لتحديد احتمال حدوث خطأ أو عطل.
يمكن القول أنه من خلال التعرف على الاحتمال ، فإننا بطريقة ما نتخذ خطوة نظرية في المستقبل ، بالنظر إليها من خلال منظور الصيغ.
في مدونته ، ترجمة المحاضرة التالية لدورة "مبادئ توازن اللعبة" لمصمم الألعاب جان شرايبر ، الذي عمل في مشاريع مثل Marvel Trading Card Game و Playboy: the Mansion.
حتى اليوم ، كان كل ما تحدثنا عنه تقريبًا حتميًا ، وفي الأسبوع الماضي ألقينا نظرة فاحصة على الميكانيكا المتعدية ، وقمنا بتقسيمها بأكبر قدر ممكن من التفاصيل التي يمكنني شرحها. لكن حتى الآن ، لم ننتبه للجوانب الأخرى للعديد من الألعاب ، وهي اللحظات غير الحتمية - وبعبارة أخرى ، العشوائية.
فهم طبيعة العشوائية مهم جدًا لمصممي الألعاب. نقوم بإنشاء أنظمة تؤثر على تجربة المستخدم في لعبة معينة ، لذلك نحتاج إلى معرفة كيفية عمل هذه الأنظمة. إذا كانت هناك عشوائية في النظام ، فنحن بحاجة إلى فهم طبيعة هذه العشوائية ومعرفة كيفية تغييرها من أجل الحصول على النتائج التي نحتاجها.
حجر النرد
لنبدأ بشيء بسيط - النرد المتداول. عندما يفكر معظم الناس في النرد ، فإنهم يفكرون في نرد من ستة جوانب يُعرف باسم d6. لكن معظم اللاعبين رأوا العديد من النردات الأخرى: رباعي الجوانب (d4) ، ثمانية جوانب (d8) ، اثني عشر جانبًا (d12) ، عشرين جانبًا (d20). إذا كنت مهووسًا حقيقيًا ، فقد يكون لديك 30 أو 100 حبة نرد في مكان ما.
إذا لم تكن معتادًا على هذا المصطلح ، فإن d تعني النرد ، والرقم الذي يليه هو عدد الوجوه. إذا كان الرقم قبل d ، فإنه يشير إلى عدد النرد عند الرمي. على سبيل المثال ، في لعبة Monopoly ، تقوم بتدوير 2d6.
لذلك ، في هذه الحالة ، فإن عبارة "النرد" هي تسمية تقليدية. هناك عدد كبير من مولدات الأرقام العشوائية الأخرى التي لا تشبه الأشكال البلاستيكية ، ولكنها تؤدي نفس الوظيفة - فهي تولد عددًا عشوائيًا من 1 إلى n. يمكن أيضًا تمثيل العملة العادية على شكل يموت ثنائي السطوح d2.
رأيت تصميمين لنرد من سبعة جوانب: أحدهما بدا مثل حجر النرد ، والثاني بدا أشبه بقلم رصاص خشبي من سبعة جوانب. دريدل رباعي السطوح ، المعروف أيضًا باسم تيتوتوم ، هو نظير لعظم رباعي السطوح. لوحة اللعبة التي تحتوي على سهم دوار في Chutes & Ladders ، حيث يمكن أن تكون النتيجة من 1 إلى 6 ، تتوافق مع نرد سداسي الجوانب.
يمكن لمولد الأرقام العشوائية في الكمبيوتر إنشاء أي رقم من 1 إلى 19 إذا أعطى المصمم مثل هذا الأمر ، على الرغم من أن الكمبيوتر لا يحتوي على نرد من 19 جانبًا (بشكل عام ، سأتحدث أكثر عن احتمال الحصول على أرقام على الكمبيوتر الأسبوع المقبل). تبدو كل هذه العناصر مختلفة ، لكنها في الواقع متكافئة: لديك فرصة متساوية لكل من النتائج المحتملة العديدة.
للنرد بعض الخصائص المثيرة للاهتمام التي نحتاج إلى معرفتها. أولاً ، احتمال الحصول على أي من الوجوه هو نفسه (أفترض أنك ترمي نردًا هندسيًا منتظمًا). إذا كنت تريد معرفة متوسط قيمة اللفة (المعروفة باسم التوقع الرياضي لمن هم مغرمون بنظرية الاحتمالات) ، فقم بجمع القيم على جميع الحواف وقسم هذا الرقم على عدد الحواف.
مجموع قيم جميع الوجوه لنرد قياسي سداسي الجوانب هو 1 + 2 + 3 + 4 + 5 + 6 = 21. قسّم 21 على عدد الوجوه واحصل على متوسط قيمة اللف: 21 / 6 = 3.5. هذه حالة خاصة لأننا نفترض أن جميع النتائج متساوية في الاحتمال.
ماذا لو كان لديك نرد خاص؟ على سبيل المثال ، رأيت لعبة ذات نرد سداسي مع ملصقات خاصة على الوجوه: 1 ، 1 ، 1 ، 2 ، 2 ، 3 ، لذا فهي تتصرف مثل نرد غريب ثلاثي الجوانب ، والذي من المرجح أن يتدحرج رقم 1 من 2 ، ومن المرجح أن تتدحرج 2 بدلاً من 3. ما هو متوسط قيمة التدحرج لهذا النرد؟ لذا ، 1 + 1 + 1 + 2 + 2 + 3 = 10 ، اقسم على 6 - تحصل على 5/3 ، أو حوالي 1.66. لذلك إذا كان لديك نرد خاص وقام اللاعبون برمي ثلاثة أحجار نرد ثم جمعوا النتائج ، فأنت تعلم أن مجموعهم سيكون حوالي 5 ، ويمكنك موازنة اللعبة بناءً على هذا الافتراض.
النرد والاستقلال
كما قلت سابقًا ، ننطلق من افتراض أن تسرب كل وجه هو احتمال متساوٍ. لا يهم عدد أحجار النرد التي تدحرجها هنا. كل لفة من النرد مستقلة ، مما يعني أن اللفات السابقة لا تؤثر على نتائج اللفات اللاحقة. مع وجود عدد كافٍ من التجارب ، لا بد أن تلاحظ سلسلة من الأرقام - على سبيل المثال ، تتدحرج في الغالب قيمًا أعلى أو أقل - أو ميزات أخرى ، لكن هذا لا يعني أن النرد "ساخن" أو "بارد". سنتحدث عن هذا لاحقًا.
إذا رميت نردًا قياسيًا سداسي الجوانب وظهر الرقم 6 مرتين على التوالي ، فإن احتمال أن تكون نتيجة اللف التالي ستكون 6 هو أيضًا 1/6. ". في الوقت نفسه ، لا ينخفض الاحتمال: من الخطأ القول بأن الرقم 6 قد سقط بالفعل مرتين على التوالي ، مما يعني أن وجهًا آخر يجب أن يسقط الآن.
بالطبع ، إذا رميت نردًا عشرين مرة وظهر الرقم 6 في كل مرة ، فإن فرصة ظهور الرقم 6 في المرة الحادية والعشرين تكون عالية جدًا: قد يكون لديك نرد خاطئ. ولكن إذا كان القالب صحيحًا ، فإن احتمال الحصول على كل وجه هو نفسه ، بغض النظر عن نتائج اللفات الأخرى. يمكنك أيضًا أن تتخيل أننا نغير الزهر في كل مرة: إذا دحرج الرقم 6 مرتين على التوالي ، فقم بإزالة الزهر "الساخن" من اللعبة واستبداله بآخر جديد. أنا آسف إذا كان أي منكم على علم بهذا بالفعل ، لكنني كنت بحاجة لتوضيح ذلك قبل الانتقال.
كيفية جعل النرد يتدحرج بشكل عشوائي
لنتحدث عن كيفية الحصول على نتائج مختلفة على نرد مختلف. إذا رميت النرد مرة واحدة فقط أو عدة مرات ، ستشعر اللعبة بمزيد من العشوائية عندما يكون للنرد حواف أكثر. كلما دحرجت النرد في كثير من الأحيان وكلما زاد عدد النرد ، كلما اقتربت النتائج من المتوسط.
على سبيل المثال ، في حالة 1d6 + 4 (أي ، إذا رميت نردًا قياسيًا من ستة جوانب مرة واحدة وأضفت 4 إلى النتيجة) ، فسيكون المتوسط عددًا بين 5 و 10. إذا قمت بلف 5d2 ، فإن المتوسط سيكون أيضًا رقمًا بين 5 و 10. نتيجة التدحرج 5d2 ستكون في الغالب الأرقام 7 و 8 ، وغالبًا ما تكون القيم الأخرى. نفس السلسلة ، حتى نفس القيمة المتوسطة (7.5 في كلتا الحالتين) ، لكن طبيعة العشوائية مختلفة.
انتظر دقيقة. ألم أقل فقط أن النرد لا "يسخن" أو "يبرد"؟ والآن أقول: إذا دحرجت الكثير من أحجار النرد ، فإن نتائج القوائم تكون أقرب إلى متوسط القيمة. لماذا؟
دعني أشرح. إذا رميت نردًا واحدًا ، فإن احتمال ظهور كل وجه هو نفسه. هذا يعني أنك إذا رميت الكثير من أحجار النرد بمرور الوقت ، فسيظهر كل وجه بنفس عدد المرات تقريبًا. كلما رمي المزيد من النرد ، كلما اقتربت النتيجة الإجمالية من المتوسط.
هذا ليس لأن الرقم الذي تم تدويره "يتسبب" في ظهور رقم آخر لم يتم تدويره بعد. لأن خطًا صغيرًا من دحرجة الرقم 6 (أو 20 ، أو أيًا كان) لن تحدث فرقًا كبيرًا في النهاية إذا دحرجت النرد عشرة آلاف مرة أخرى وهو في الغالب المتوسط. الآن سيكون لديك عدد قليل من الأعداد الكبيرة ، وبعد ذلك عدد قليل من الأرقام الصغيرة - وبمرور الوقت ستقترب من القيمة المتوسطة.
هذا ليس لأن اللفات السابقة تؤثر على النرد (بشكل جدي ، الزهر مصنوع من البلاستيك ، وليس لديه العقل للتفكير ، "أوه ، لقد مر وقت طويل منذ ظهور الرقم 2") ، ولكن لأنه يحدث عادةً مع الكثير من القوائم. لعب النرد.
لذلك من السهل جدًا حساب لفة عشوائية واحدة لنرد - على الأقل حساب متوسط قيمة اللفة. هناك أيضًا طرق لحساب "مدى عشوائية" شيء ما والقول إن نتائج لفة 1d6 + 4 ستكون "أكثر عشوائية" من 5d2. بالنسبة إلى 5d2 ، سيتم توزيع النتائج الملتفة بشكل متساوٍ. للقيام بذلك ، تحتاج إلى حساب الانحراف المعياري: فكلما كانت القيمة أكبر ، كانت النتائج أكثر عشوائية. لا أرغب في إجراء الكثير من العمليات الحسابية اليوم ، سأشرح هذا الموضوع لاحقًا.
الشيء الوحيد الذي سأطلبه منك أن تتذكره ، كقاعدة عامة ، كلما قل عدد النرد الذي رميت به ، كلما كانت عشوائية. وكلما زاد عدد جوانب القالب ، زادت العشوائية ، نظرًا لوجود المزيد من الخيارات الممكنة للقيمة.
كيفية حساب الاحتمالية باستخدام العد
قد تتساءل: كيف يمكننا حساب الاحتمال الدقيق لظهور نتيجة معينة؟ في الواقع ، هذا مهم جدًا للعديد من الألعاب: إذا رميت النرد في البداية ، فمن المحتمل أن تكون هناك بعض النتائج المثلى. الإجابة هي: نحتاج إلى حساب قيمتين. أولاً ، العدد الإجمالي للنتائج عند رمي النرد ، وثانيًا ، عدد النتائج الإيجابية. بقسمة القيمة الثانية على الأولى ، تحصل على الاحتمال المطلوب. للحصول على نسبة مئوية ، اضرب الناتج في 100.
أمثلة
هنا مثال بسيط جدا. أنت تريد دحرجة 4 أو أعلى ورمي نرد ذي ستة جوانب مرة واحدة. الحد الأقصى لعدد النتائج هو 6 (1 ، 2 ، 3 ، 4 ، 5 ، 6). من بين هذه ، 3 نتائج (4 ، 5 ، 6) مواتية. لذلك ، لحساب الاحتمال ، نقسم 3 على 6 ونحصل على 0.5 أو 50٪.
هذا مثال أكثر تعقيدًا بعض الشيء. تريد أن تأتي لفة 2d6 برقم زوجي. الحد الأقصى لعدد النتائج هو 36 (6 خيارات لكل نرد ، لا يؤثر أحد النردات على الآخر ، لذلك نضرب 6 في 6 ونحصل على 36). تكمن صعوبة هذا النوع من الأسئلة في سهولة العد مرتين. على سبيل المثال ، في لفة 2d6 ، هناك نتيجتان محتملتان لـ 3: 1 + 2 و 2 + 1. يبدوان متشابهين ، لكن الاختلاف هو الرقم الذي يظهر على حجر النرد الأول وأيهما على الثاني.
يمكنك أيضًا أن تتخيل أن الزهر له ألوان مختلفة: على سبيل المثال ، في هذه الحالة ، يكون أحد الزهر أحمر والآخر أزرق. ثم احسب عدد التكرارات المحتملة لرقم زوجي:
- 2 (1+1);
- 4 (1+3);
- 4 (2+2);
- 4 (3+1);
- 6 (1+5);
- 6 (2+4);
- 6 (3+3);
- 6 (4+2);
- 6 (5+1);
- 8 (2+6);
- 8 (3+5);
- 8 (4+4);
- 8 (5+3);
- 8 (6+2);
- 10 (4+6);
- 10 (5+5);
- 10 (6+4);
- 12 (6+6).
اتضح أن هناك 18 خيارًا للحصول على نتيجة إيجابية من أصل 36 - كما في الحالة السابقة ، يكون الاحتمال 0.5 أو 50٪. ربما غير متوقع ، لكنه دقيق تمامًا.
محاكاة مونت كارلو
ماذا لو كان لديك الكثير من النرد لهذا الحساب؟ على سبيل المثال ، تريد أن تعرف ما هو احتمال ظهور إجمالي 15 أو أكثر على لفة 8d6. هناك عدد كبير من النتائج المختلفة لثمانية أحجار نرد ، وسيستغرق عدها يدويًا وقتًا طويلاً - حتى لو تمكنا من إيجاد حل جيد لتجميع سلسلة مختلفة من لفات النرد.
في هذه الحالة ، أسهل طريقة هي عدم العد يدويًا ، ولكن باستخدام الكمبيوتر. هناك طريقتان لحساب الاحتمال على جهاز الكمبيوتر. يمكن أن تحصل الطريقة الأولى على الإجابة الدقيقة ، ولكنها تتضمن القليل من البرمجة أو البرمجة النصية. سينظر الكمبيوتر في كل احتمال ، ويقيم ويحسب العدد الإجمالي للتكرارات وعدد التكرارات التي تطابق النتيجة المرجوة ، ثم يقدم الإجابات. قد تبدو شفرتك كما يلي:
إذا لم تكن مبرمجًا وتريد إجابة تقريبية بدلاً من إجابة دقيقة ، فيمكنك محاكاة هذا الموقف في Excel ، حيث تقوم بتدوير 8d6 عدة آلاف من المرات والحصول على الإجابة. للفة 1d6 في Excel ، استخدم الصيغة = FLOOR (RAND () * 6) +1.
هناك اسم للموقف عندما لا تعرف الإجابة وحاول عدة مرات - محاكاة مونت كارلو. يعد هذا حلاً رائعًا للرجوع إليه عندما يكون من الصعب للغاية حساب الاحتمال. الشيء العظيم هو أنه في هذه الحالة ، لسنا بحاجة إلى فهم كيفية عمل الرياضيات ، ونعلم أن الإجابة ستكون "جيدة جدًا" لأنه ، كما نعلم بالفعل ، كلما زاد عدد اللفات ، كلما اقتربت النتيجة من متوسط القيمة.
كيفية الجمع بين التجارب المستقلة
إذا سألت عن تجارب متعددة متكررة ولكن مستقلة ، فلن تؤثر نتيجة لفة واحدة على نتيجة القوائم الأخرى. هناك تفسير آخر أبسط لهذا الموقف.
كيف نميز بين الشيء التابع والمستقل؟ من حيث المبدأ ، إذا كان بإمكانك عزل كل لفة (أو سلسلة من اللفات) لقالب كحدث منفصل ، فسيكون ذلك مستقلاً. على سبيل المثال ، نرمي 8d6 ونريد أن نرمي ما مجموعه 15. لا يمكن تقسيم هذا الحدث إلى عدة لفات مستقلة من النرد. للحصول على النتيجة ، تقوم بحساب مجموع كل القيم ، وبالتالي فإن النتيجة المتدحرجة على قالب واحد تؤثر على النتائج التي يجب أن تتدحرج على الآخرين.
إليك مثال على القوائم المستقلة: أنت تلعب لعبة النرد وتدحرج نردًا سداسي الجوانب عدة مرات. يجب أن يتدحرج أول لفة على 2 أو أعلى لكي تبقى في اللعبة. للفة الثانية - 3 أو أعلى. الثالث يتطلب 4 أو أكثر ، والرابع يتطلب 5 أو أكثر ، والخامس يتطلب 6. إذا نجحت جميع القوائم الخمس ، فإنك تفوز. في هذه الحالة ، كل رميات مستقلة. نعم ، إذا فشلت إحدى الرولات ، فسيؤثر ذلك على نتيجة اللعبة بأكملها ، لكن لفة واحدة لا تؤثر على الأخرى. على سبيل المثال ، إذا كانت رمية النرد الثانية جيدة جدًا ، فهذا لا يعني أن القوائم التالية ستكون بنفس الجودة. لذلك ، يمكننا النظر في احتمال كل لفة من النرد على حدة.
إذا كانت لديك احتمالات مستقلة وتريد أن تعرف ما هو احتمال وقوع جميع الأحداث ، فأنت تحدد كل احتمالية فردية وتضربها. طريقة أخرى: إذا استخدمت علامة العطف "و" لوصف عدة شروط (على سبيل المثال ، ما هو احتمال وقوع حدث عشوائي وبعض الأحداث العشوائية المستقلة الأخرى؟) - احسب الاحتمالات الفردية واضربها.
لا يهم ما تعتقده - لا تلخص الاحتمالات المستقلة أبدًا. هذا خطأ شائع. لفهم سبب خطأ هذا ، تخيل موقفًا تقوم فيه برمي عملة معدنية وتريد أن تعرف ما هو احتمال الحصول على الوجه مرتين على التوالي. احتمال السقوط من كل جانب هو 50٪. إذا جمعت هذين الاحتمالين ، فستحصل على فرصة 100٪ للحصول على صورة الوجه ، لكننا نعلم أن هذا ليس صحيحًا ، لأنه قد يظهر ذيلان متتاليان. إذا قمت بضرب الاحتمالين بدلاً من ذلك ، فستحصل على 50٪ * 50٪ = 25٪ - وهي الإجابة الصحيحة لحساب احتمال الحصول على الوجه مرتين على التوالي.
مثال
لنعد إلى لعبة النرد سداسية الجوانب ، حيث تحتاج أولاً إلى رمي رقم أكبر من 2 ، ثم أكثر من 3 - وهكذا حتى 6. ما هي فرص ذلك في سلسلة معينة من خمس لفات ، كل ستكون النتائج مواتية؟
كما ذكرنا سابقًا ، هذه تجارب مستقلة ، لذلك نحسب الاحتمالية لكل لفة فردية ، ثم نضربها. احتمال أن تكون نتيجة القرعة الأولى مواتية هو 5/6. الثاني - 4/6. الثالث - 3/6. الرابع - 2/6 ، الخامس - 1/6. نضرب كل النتائج ببعضنا البعض ونحصل على حوالي 1.5٪. الانتصارات في هذه اللعبة نادرة جدًا ، لذا إذا أضفت هذا العنصر إلى لعبتك ، فستحتاج إلى الفوز بالجائزة الكبرى.
النفي
إليك تلميح آخر مفيد: في بعض الأحيان يكون من الصعب حساب احتمالية وقوع حدث ما ، ولكن من الأسهل تحديد فرص عدم وقوع حدث ما. على سبيل المثال ، افترض أن لدينا لعبة أخرى: تدحرجت 6d6 وتفوز إذا رميت 6 مرة واحدة على الأقل ، ما هو احتمال الفوز؟
في هذه الحالة ، هناك العديد من الخيارات التي يجب مراعاتها. من الممكن أن يسقط رقم واحد 6 ، أي أن الرقم 6 سيسقط على أحد النرد ، والأرقام من 1 إلى 5 ستسقط على الآخرين ، ثم هناك 6 خيارات لأي من النردات أ 6. يمكنك الحصول على الرقم 6 على عظمتين من حجر النرد ، أو ثلاثة ، أو حتى أكثر ، وفي كل مرة ستحتاج إلى إجراء عملية حسابية منفصلة ، لذلك من السهل الخلط هنا.
لكن دعونا ننظر إلى المشكلة من الجانب الآخر. ستخسر إذا لم يلقي أي من النرد الرقم 6. في هذه الحالة ، لدينا 6 تجارب مستقلة. احتمالية أن يلقي كل حجر رقمًا بخلاف الرقم 6 هو 5/6. اضربهم - واحصل على حوالي 33٪. وبالتالي ، فإن احتمال الخسارة هو واحد من كل ثلاثة. لذلك ، فإن احتمال الفوز هو 67٪ (أو اثنين إلى ثلاثة).
من هذا المثال ، من الواضح أنك إذا كنت تحسب احتمال عدم حدوث حدث ما ، فأنت بحاجة إلى طرح النتيجة من 100٪. إذا كان احتمال الفوز 67٪ ، فإن احتمال الخسارة هو 100٪ ناقص 67٪ ، أو 33٪ ، والعكس صحيح. إذا كان من الصعب حساب احتمال واحد ، ولكن من السهل حساب العكس ، احسب العكس ، ثم اطرح هذا الرقم من 100٪.
ربط الشروط لاختبار مستقل واحد
لقد قلت قبل قليل أنه لا يجب عليك جمع الاحتمالات في التجارب المستقلة. هل هناك حالات يمكن فيها جمع الاحتمالات؟ نعم ، في حالة معينة.
إذا كنت ترغب في حساب احتمالية وجود عدة نتائج إيجابية غير ذات صلة في نفس التجربة ، فقم بجمع احتمالات كل نتيجة مواتية. على سبيل المثال ، فإن احتمال التدحرج 4 أو 5 أو 6 على 1d6 يساوي مجموع احتمالية التدحرج 4 ، واحتمال التدحرج 5 ، واحتمال التدحرج 6. يمكن تمثيل هذا الموقف على النحو التالي: إذا استخدم أداة الربط "أو" في سؤال حول الاحتمال (على سبيل المثال ، ما هو احتمال نتيجة واحدة أو أخرى لحدث عشوائي واحد؟) - احسب الاحتمالات الفردية ولخصها.
يرجى ملاحظة: عندما تقوم بحساب جميع النتائج المحتملة للعبة ، يجب أن يكون مجموع احتمالات حدوثها مساويًا لـ 100٪ ، وإلا تم إجراء الحساب بشكل غير صحيح. هذه طريقة جيدة لمضاعفة التحقق من حساباتك. على سبيل المثال ، قمت بتحليل احتمال الحصول على كل المجموعات في البوكر. إذا جمعت جميع النتائج التي تحصل عليها ، فيجب أن تحصل على 100٪ بالضبط (أو على الأقل قيمة قريبة جدًا من 100٪: إذا كنت تستخدم آلة حاسبة ، فقد يكون هناك خطأ بسيط في التقريب ، ولكن إذا كنت تضيف الأرقام الدقيقة باليد ، يجب أن يتم جمعها جميعًا.). إذا لم يتم جمع المبلغ ، فمن المرجح أنك لم تأخذ في الاعتبار بعض المجموعات أو قمت بحساب احتمالات بعض المجموعات بشكل غير صحيح ، وتحتاج الحسابات إلى إعادة التحقق.
احتمالات غير متكافئة
حتى الآن ، افترضنا أن كل وجه من وجوه النرد يسقط بنفس التردد ، لأن هذه هي الطريقة التي يعمل بها النرد. لكن في بعض الأحيان قد تواجه موقفًا تكون فيه النتائج المختلفة ممكنة ولديهم فرص مختلفة للسقوط.
على سبيل المثال ، في إحدى الإضافات إلى لعبة الورق Nuclear War ، يوجد ملعب به سهم يحدد نتيجة إطلاق الصاروخ. في أغلب الأحيان ، يتسبب في ضرر عادي ، أكثر أو أقل ، ولكن في بعض الأحيان يتضاعف الضرر أو يتضاعف ثلاث مرات ، أو ينفجر الصاروخ على منصة الإطلاق ويضر بك ، أو يحدث بعض الأحداث الأخرى. على عكس لوحة الأسهم في Chutes & Ladders أو A Game of Life ، فإن نتائج اللوحة في الحرب النووية ليست محتملة بنفس القدر. تكون بعض أقسام الملعب أكبر ويتوقف السهم عليها كثيرًا ، في حين أن الأقسام الأخرى صغيرة جدًا ونادرًا ما يتوقف السهم عليها.
لذلك ، للوهلة الأولى ، تبدو العظام شيئًا كالتالي: 1 ، 1 ، 1 ، 2 ، 2 ، 3 - لقد تحدثنا عنها بالفعل ، إنها شيء مثل 1d3 مرجح. لذلك ، نحتاج إلى تقسيم كل هذه الأقسام إلى أجزاء متساوية ، وإيجاد أصغر وحدة قياس ، المقسوم عليه ، حيث يكون كل شيء مضاعفًا ، ثم تمثيل الموقف بالصيغة d522 (أو غيره) ، حيث تكون مجموعة النرد الوجوه ستمثل نفس الموقف ، ولكن مع المزيد من النتائج. هذه إحدى طرق حل المشكلة ، وهي مجدية تقنيًا ، ولكن هناك خيار أسهل.
دعنا نعود إلى حجر النرد القياسي سداسي الجوانب. قلنا أنه لحساب متوسط قيمة لفة للنرد العادي ، تحتاج إلى جمع قيم جميع الوجوه وتقسيمها على عدد الوجوه ، ولكن كيف يتم الحساب بالضبط؟ يمكنك التعبير عنها بشكل مختلف. بالنسبة لحجر نرد سداسي الجوانب ، فإن احتمال ظهور كل وجه هو 1/6 بالضبط. نقوم الآن بضرب نتيجة كل وجه في احتمال هذه النتيجة (في هذه الحالة 1/6 لكل وجه) ثم نجمع القيم الناتجة. إذن ، جمع (1 * 1/6) + (2 * 1/6) + (3 * 1/6) + (4 * 1/6) + (5 * 1/6) + (6 * 1/6) ، نحصل على نفس النتيجة (3.5) كما في الحساب أعلاه. في الواقع ، نحسب هذا في كل مرة: نضرب كل نتيجة في احتمال تلك النتيجة.
هل يمكننا إجراء نفس الحساب للسهم الموجود على لوحة اللعبة في الحرب النووية؟ بالطبع نستطيع. وإذا جمعنا جميع النتائج ، نحصل على متوسط القيمة. كل ما نحتاج إلى القيام به هو حساب احتمال كل نتيجة للسهم على أرض الملعب وضربها في قيمة النتيجة.
مثال آخر
تعد الطريقة المذكورة لحساب المتوسط مناسبة أيضًا إذا كانت النتائج متساوية في الاحتمال ولكن لها مزايا مختلفة - على سبيل المثال ، إذا دحرجت نردًا وربحت أكثر على بعض الوجوه أكثر من غيرها. على سبيل المثال ، لنأخذ لعبة تحدث في كازينو: تضع رهانًا وتقوم برمي 2d6. إذا ظهرت ثلاثة أرقام منخفضة القيمة (2 ، 3 ، 4) أو أربعة أرقام عالية القيمة (9 ، 10 ، 11 ، 12) ، فستربح مبلغًا يساوي رهانك. الأرقام ذات أدنى وأعلى قيمة خاصة: إذا ظهرت 2 أو 12 ، فستربح ضعف رهانك. إذا ظهر أي رقم آخر (5 ، 6 ، 7 ، 8) ، ستخسر رهانك. هذه لعبة بسيطة جدا. لكن ما هو احتمال الفوز؟
لنبدأ بإحصاء عدد المرات التي يمكنك الفوز فيها. الحد الأقصى لعدد النتائج في لفة 2d6 هو 36. ما هو عدد النتائج المفضلة؟
- هناك خيار واحد من شأنه أن يلف 2 ، وخيار واحد سيحمل 12.
- هناك خياران للخيارين 3 و 2 لـ 11.
- هناك 3 خيارات لـ 4 و 3 خيارات لـ 10.
- هناك 4 خيارات من شأنها أن تتدحرج 9.
بتلخيص جميع الخيارات ، نحصل على 16 نتيجة إيجابية من أصل 36. وبالتالي ، في ظل الظروف العادية ، ستربح 16 مرة من أصل 36 مرة محتملة - احتمال الفوز أقل بقليل من 50٪.
لكن مرتين من هؤلاء الستة عشر ستفوز مرتين - إنه مثل الفوز مرتين. إذا لعبت هذه اللعبة 36 مرة ، وراهنت بدولار واحد في كل مرة ، وظهرت كل نتيجة ممكنة مرة واحدة ، فستربح ما مجموعه 18 دولارًا (في الواقع تربح 16 مرة ، لكن اثنتان منها تعتبران فوزين). إذا لعبت 36 مرة وربحت 18 دولارًا ، ألا يعني ذلك أن الاحتمالات متساوية؟
خذ وقتك. إذا قمت بحساب عدد المرات التي يمكن أن تخسر فيها ، فستحصل على 20 وليس 18. إذا لعبت 36 مرة ، وراهنت بدولار واحد في كل مرة ، فستربح ما مجموعه 18 دولارًا عند انتهاء كل الاحتمالات. لكنك ستخسر ما مجموعه 20 دولارًا على جميع النتائج السيئة العشرين. نتيجة لذلك ، ستكون متأخرًا قليلاً: ستخسر ما متوسطه 2 دولارًا صافيًا لكل 36 لعبة (يمكنك أيضًا أن تقول أنك تخسر 1/18 دولارًا في المتوسط في اليوم). الآن ترى مدى سهولة ارتكاب خطأ في هذه الحالة وحساب الاحتمال بشكل غير صحيح.
التقليب
حتى الآن ، افترضنا أن الترتيب الذي يتم به إلقاء الأرقام لا يهم عند رمي النرد. لفة 2 + 4 هي نفسها لفة 4 + 2. في معظم الحالات ، نحسب عدد النتائج المفضلة يدويًا ، ولكن في بعض الأحيان تكون هذه الطريقة غير عملية ومن الأفضل استخدام صيغة رياضية.
مثال على هذا الموقف هو من لعبة النرد Farkle. لكل جولة جديدة ، تقوم بتدوير 6d6. إذا كنت محظوظًا وظهرت جميع النتائج المحتملة من 1-2-3-4-5-6 (مباشرة) ، فستحصل على مكافأة كبيرة. ما هو احتمال حدوث ذلك؟ في هذه الحالة ، هناك العديد من الخيارات لفقدان هذه المجموعة.
الحل هو كما يلي: على أحد النرد (وفقط على واحد) يجب أن يسقط الرقم 1. كم عدد الخيارات للرقم 1 الذي يسقط على نرد واحد؟ هناك 6 خيارات ، حيث يوجد 6 نرد ، والرقم 1 يمكن أن يقع على أي منها ، وبناءً عليه ، خذ نردًا واحدًا وضعه جانبًا. الآن يجب أن يقع الرقم 2. على أحد أحجار النرد المتبقية ، وهناك 5 خيارات لذلك. خذ نردًا آخر وضعه جانبًا. ثم 4 من النرد المتبقي قد يهبط على 3 ، 3 من النرد المتبقي قد يهبط على 4 ، و 2 من النرد المتبقي قد يهبط على 5. نتيجة لذلك ، يتبقى لك نرد واحد ، عليه الرقم 6 يجب أن يسقط (في الحالة الأخيرة ، النرد هناك عظم واحد فقط ، وليس هناك خيار).
من أجل حساب عدد النتائج المفضلة لتكوين تركيبة مباشرة ، نقوم بضرب جميع الخيارات المستقلة المختلفة: 6 × 5 × 4 × 3 × 2 × 1 = 720 - يبدو أن هناك عددًا كبيرًا من الخيارات لـ هذا المزيج يأتي.
لحساب احتمال الحصول على توليفة مستقيمة ، علينا قسمة 720 على عدد كل النتائج الممكنة لتدحرج 6d6. ما هو عدد كل النتائج الممكنة؟ يمكن لكل قالب دحرجة 6 وجوه ، لذلك نضرب 6 × 6 × 6 × 6 × 6 × 6 = 46656 (عدد أكبر بكثير من الرقم السابق). نقسم 720 على 46656 ونحصل على احتمال يساوي حوالي 1.5٪. إذا كنت تصمم هذه اللعبة ، فسيكون من المفيد لك معرفة ذلك حتى تتمكن من إنشاء نظام تسجيل مناسب. الآن نحن نفهم لماذا تحصل في Farkle على مثل هذه المكافأة الكبيرة إذا وصلت إلى تركيبة مستقيمة: هذا الموقف نادر جدًا.
النتيجة مثيرة للاهتمام أيضًا لسبب آخر. يوضح المثال مدى ندرة حدوث النتيجة المقابلة للاحتمال في فترة قصيرة. بالطبع ، إذا دحرجنا عدة آلاف من النرد ، فستظهر جوانب مختلفة من النرد كثيرًا. ولكن عندما نرمي ستة أحجار نرد فقط ، لم يحدث أن يظهر كل نرد. يتضح أنه من الحماقة أن نتوقع أن يسقط الآن وجه لم يكن كذلك بعد ، لأننا "لم نتخلى عن الرقم 6 لفترة طويلة". انظر ، مولد الأرقام العشوائية معطل.
يقودنا هذا إلى الاعتقاد الخاطئ الشائع بأن جميع النتائج تأتي بنفس المعدل خلال فترة زمنية قصيرة. إذا رمي النرد عدة مرات ، فلن يكون تكرار كل وجه هو نفسه.
إذا سبق لك أن عملت في لعبة عبر الإنترنت مع نوع من مولد الأرقام العشوائية من قبل ، فمن المرجح أنك واجهت موقفًا يكتب فيه أحد اللاعبين للدعم الفني بشكوى من أن مولد الأرقام العشوائية لا يعرض أرقامًا عشوائية. لقد توصل إلى هذا الاستنتاج لأنه قتل 4 وحوش على التوالي وحصل على 4 نفس المكافآت بالضبط ، ويجب أن تنخفض هذه المكافآت بنسبة 10 ٪ فقط من الوقت ، لذلك من الواضح أن هذا لن يحدث أبدًا تقريبًا.
أنت تفعل الرياضيات. الاحتمال هو 1/10 * 1/10 * 1/10 * 1/10 ، أي أن نتيجة واحدة من أصل 10 آلاف حالة نادرة إلى حد ما. هذا ما يحاول اللاعب إخبارك به. هل هناك مشكلة في هذه الحالة؟
كل شيء يعتمد على الظروف. كم عدد اللاعبين على الخادم الخاص بك الآن؟ لنفترض أن لديك لعبة شائعة إلى حد ما ، ويلعبها كل يوم 100000 شخص. كم عدد اللاعبين الذين سيقتلون أربعة وحوش على التوالي؟ ربما كل شيء ، عدة مرات في اليوم ، لكن دعنا نفترض أن نصفهم يتداولون فقط عناصر مختلفة في المزادات ، أو يتحدثون على خوادم RP ، أو يقومون بأنشطة ألعاب أخرى - لذا فإن نصفهم فقط يصطادون الوحوش. ما هو احتمال حصول شخص ما على نفس المكافأة؟ في هذه الحالة ، يمكنك توقع حدوث ذلك عدة مرات على الأقل في اليوم.
بالمناسبة ، لهذا السبب يبدو أن شخصًا ما يفوز باليانصيب كل بضعة أسابيع ، حتى لو لم يكن هذا الشخص هو أنت أو شخص تعرفه. إذا لعب عدد كافٍ من الناس بانتظام ، فمن المحتمل أن يكون هناك شخص محظوظ واحد على الأقل في مكان ما. ولكن إذا لعبت اليانصيب بنفسك ، فمن غير المرجح أن تفوز ، فمن المرجح أن تتم دعوتك للعمل في Infinity Ward.
الخرائط والإدمان
لقد ناقشنا أحداثًا مستقلة ، مثل إلقاء النرد ، والآن نعرف العديد من الأدوات القوية لتحليل العشوائية في العديد من الألعاب. يكون حساب الاحتمال أكثر تعقيدًا بعض الشيء عندما يتعلق الأمر بسحب البطاقات من المجموعة ، لأن كل بطاقة نخرجها تؤثر على البطاقات المتبقية في المجموعة.
إذا كان لديك مجموعة أوراق قياسية تتكون من 52 بطاقة ، فأنت ترسم 10 قلوب منها وتريد معرفة احتمالية أن تكون البطاقة التالية هي نفس النوع - فقد تغير الاحتمال عن البطاقة الأصلية لأنك قمت بالفعل بإزالة بطاقة قلب واحدة من البطاقة. ظهر السفينة. كل بطاقة تقوم بإزالتها تغير احتمالية ظهور البطاقة التالية في المجموعة. في هذه الحالة ، يؤثر الحدث السابق على التالي ، لذلك نسمي هذا الاحتمال بالتوقف.
لاحظ أنه عندما أقول "بطاقات" أعني أي ميكانيكي لعبة يحتوي على مجموعة من الكائنات وتقوم بإزالة أحد الكائنات دون استبداله. تشبه "مجموعة أوراق اللعب" في هذه الحالة حقيبة من الرقائق التي تخرج منها شريحة واحدة ، أو جرة يتم إخراج الكرات الملونة منها (لم أشاهد مطلقًا ألعابًا بها جرة يتم أخذ الكرات الملونة منها للخروج ، ولكن معلمي نظرية الاحتمالات على ما لسبب ما ، هذا المثال هو المفضل).
خصائص التبعية
أود أن أوضح أنه عندما يتعلق الأمر بالبطاقات ، أفترض أنك ترسم البطاقات وتنظر إليها وتزيلها من المجموعة. كل من هذه الإجراءات هي خاصية مهمة. إذا كان لدي مجموعة من ستة بطاقات ، على سبيل المثال ، مرقمة من 1 إلى 6 ، فسأقوم بخلطها ورسم بطاقة واحدة ، ثم خلط جميع البطاقات الستة مرة أخرى - سيكون هذا مشابهًا لدحرجة نرد من ستة جوانب ، لأن نتيجة واحدة لا تفعل ذلك تؤثر هنا على التالي. وإذا قمت برسم بطاقات ولم أستبدلها ، فعند رسم بطاقة واحدة ، سأزيد احتمالية أن أرسم بطاقة بالرقم 6. في المرة القادمة التي أقوم فيها برسم بطاقة. سيزداد الاحتمال حتى أقوم في النهاية برسم هذه البطاقة أو خلط المجموعة.
حقيقة أننا ننظر إلى البطاقات مهمة أيضًا. إذا أخرجت بطاقة من المجموعة ولم أنظر إليها ، فلن يكون لدي معلومات إضافية وفي الحقيقة لن يتغير الاحتمال. قد يبدو هذا غير منطقي. كيف يمكن ببساطة قلب بطاقة بطريقة سحرية تغيير الاحتمالات؟ لكن هذا ممكن لأنه يمكنك فقط حساب احتمالية العناصر غير المعروفة بناءً على ما تعرفه.
على سبيل المثال ، إذا قمت بخلط مجموعة أوراق قياسية ، وكشفت عن 51 بطاقة ولم يكن أي منها ملكة النوادي ، فيمكنك التأكد بنسبة 100٪ من أن البطاقة المتبقية هي ملكة النوادي. إذا قمت بخلط مجموعة أوراق قياسية وسحبت 51 بطاقة دون النظر إليها ، فإن احتمال أن تكون البطاقة المتبقية هي ملكة النوادي لا يزال 1/52. عند فتح كل بطاقة ، تحصل على مزيد من المعلومات.
يتبع حساب احتمالية الأحداث التابعة نفس مبادئ الأحداث المستقلة ، باستثناء أنها أكثر تعقيدًا بعض الشيء ، حيث تتغير الاحتمالات عندما تكشف عن البطاقات. وبالتالي ، تحتاج إلى ضرب العديد من القيم المختلفة ، بدلاً من ضرب نفس القيمة. في الواقع ، هذا يعني أننا بحاجة إلى جمع كل العمليات الحسابية التي أجريناها في مجموعة واحدة.
مثال
يمكنك خلط مجموعة قياسية مكونة من 52 بطاقة ورسم ورقتين. ما هو احتمال أن تخرج زوجًا؟ هناك عدة طرق لحساب هذا الاحتمال ، ولكن ربما يكون أبسطها كما يلي: ما هو احتمال أنك بعد أن سحبت بطاقة واحدة لن تتمكن من رسم زوج؟ هذا الاحتمال هو صفر ، لذلك لا يهم حقًا البطاقة الأولى التي ترسمها ، طالما أنها تطابق الثانية. لا يهم البطاقة التي نرسمها أولاً ، لا يزال لدينا فرصة لرسم زوج. لذلك ، فإن احتمال إخراج زوج بعد إخراج البطاقة الأولى هو 100٪.
ما هو احتمال تطابق البطاقة الثانية مع الأولى؟ هناك 51 بطاقة متبقية في المجموعة ، و 3 منها تطابق البطاقة الأولى (في الواقع ستكون 4 من 52 ، لكنك قمت بالفعل بإزالة إحدى البطاقات المطابقة عندما سحبت البطاقة الأولى) ، لذا فإن الاحتمال هو 1 / 17. لذا في المرة القادمة التي يلعب فيها الرجل المقابل لك على الطاولة لعبة تكساس هولدم ، قال ، "رائع ، زوج آخر؟ أنا محظوظ اليوم "، ستعرف أنه مخادع بدرجة عالية من الاحتمال.
ماذا لو أضفنا مهرجين ، إذن لدينا 54 بطاقة في المجموعة ، ونريد أن نعرف ما هو احتمال سحب زوج؟ يمكن أن تكون البطاقة الأولى جوكر ، وبعد ذلك سيكون هناك بطاقة واحدة فقط في المجموعة تتطابق ، وليس ثلاثة. كيف تجد الاحتمال في هذه الحالة؟ نقسم الاحتمالات ونضرب كل احتمال.
قد تكون بطاقتنا الأولى جوكر أو بطاقة أخرى. احتمال رسم جوكر هو 2/54 ، واحتمال سحب بطاقة أخرى هو 52/54. إذا كانت البطاقة الأولى جوكر (2/54) ، فإن احتمال تطابق البطاقة الثانية مع الأولى هو 1/53. نضرب القيم (يمكننا ضربها لأنهما حدثان منفصلان ونريد حدوث كلا الحدثين) ونحصل على 1/1431 - أقل من عُشر بالمائة.
إذا قمت برسم بطاقة أخرى أولاً (52/54) ، فإن احتمال مطابقة البطاقة الثانية هو 3/53. نضرب القيم ونحصل على 78/1431 (أكثر بقليل من 5.5٪). ماذا نفعل بهاتين النتيجتين؟ لا يتقاطعان ، ونريد معرفة احتمالية كل منهما ، لذلك نلخص القيم. حصلنا على النتيجة النهائية 79/1431 (لا تزال حوالي 5.5٪).
إذا أردنا التأكد من دقة الإجابة ، فيمكننا حساب احتمال جميع النتائج المحتملة الأخرى: رسم الجوكر وعدم مطابقة البطاقة الثانية ، أو رسم بطاقة أخرى وعدم مطابقة البطاقة الثانية. بتلخيص هذه الاحتمالات واحتمال الفوز ، سنحصل بالضبط على 100٪. لن أعطي الرياضيات هنا ، لكن يمكنك تجربة الرياضيات للتحقق مرة أخرى.
مفارقة مونتي هول
يقودنا هذا إلى مفارقة معروفة جيدًا غالبًا ما تربك الكثيرين ، وهي مفارقة مونتي هول. تمت تسمية المفارقة على اسم مضيف البرنامج التلفزيوني Let's Make a Deal. بالنسبة لأولئك الذين لم يشاهدوا هذا العرض التلفزيوني من قبل ، سأقول إنه كان عكس برنامج The Price Is Right.
في The Price Is Right ، المضيف (الذي استضافه سابقًا Bob Barker ، والآن Drew Carey؟ Nevermind) هو صديقك. يريدك أن تفوز بالمال أو بجوائز رائعة. يحاول أن يمنحك كل فرصة للفوز ، طالما يمكنك تخمين القيمة الفعلية للعناصر التي ترعاها.
تصرف مونتي هول بشكل مختلف. كان مثل التوأم الشرير لبوب باركر. كان هدفه أن يجعلك تبدو مثل أحمق في التلفزيون الوطني. إذا كنت في العرض ، فقد كان خصمك ، ولعبت ضده وكانت الاحتمالات لصالحه. ربما أكون قاسيًا للغاية ، لكن بالنظر إلى عرض من المرجح أن تدخل فيه إذا كنت ترتدي زيًا سخيفًا ، فهذا بالضبط ما أتيت إليه.
من أشهر الميمات في العرض: هناك ثلاثة أبواب أمامك ، باب رقم 1 ، باب رقم 2 ، باب رقم 3. يمكنك اختيار باب واحد مجانًا. وخلف أحدهم جائزة رائعة - على سبيل المثال ، سيارة جديدة. لا توجد جوائز خلف البابين الآخرين ، كلاهما ليس له قيمة. من المفترض أن يذلوك ، لذا فإن خلفهم ليس مجرد شيء ، بل شيء غبي ، على سبيل المثال ، عنزة أو أنبوب ضخم من معجون الأسنان - أي شيء سوى سيارة جديدة.
اخترت أحد الأبواب ، مونتي على وشك فتحه لإعلامك إذا فزت أم لا ... لكن انتظر. قبل أن نعرف ، دعنا نلقي نظرة على أحد تلك الأبواب التي لم تخترها. يعرف مونتي أي باب خلف الجائزة ، ويمكنه دائمًا فتح باب ليس خلفه جائزة. ”هل تختار الباب رقم 3؟ ثم دعونا نفتح الباب رقم 1 لنظهر أنه لا توجد جائزة وراءه ". والآن ، بدافع الكرم ، يقدم لك فرصة استبدال الباب المختار رقم 3 بما هو خلف الباب رقم 2.
في هذه المرحلة ، يطرح سؤال الاحتمال: هل تزيد هذه الفرصة من احتمالية الفوز ، أم تخفضه ، أم تظل دون تغيير؟ كيف تفكر؟
الإجابة الصحيحة: القدرة على اختيار باب آخر تزيد من فرصة الفوز من 1/3 إلى 2/3. هذا غير منطقي. إذا لم تكن قد واجهت هذه المفارقة من قبل ، فعلى الأرجح أنك تفكر: انتظر ، كيف الحال: بفتح باب واحد ، قمنا بتغيير الاحتمال بطريقة سحرية؟ كما رأينا في مثال الخرائط ، هذا بالضبط ما يحدث عندما نحصل على مزيد من المعلومات. من الواضح ، عندما تختار لأول مرة ، فإن احتمال الفوز هو 1/3. عندما يفتح أحد الأبواب ، فإنه لا يغير من احتمالية الفوز للخيار الأول على الإطلاق: لا يزال الاحتمال 1/3. لكن احتمال أن يكون الباب الآخر صحيحًا هو الآن 2/3.
لنلق نظرة على هذا المثال من الجانب الآخر. اخترت الباب. احتمال الفوز هو 1/3. أقترح عليك تغيير البابين الآخرين ، وهو ما يفعله مونتي هول. بالطبع ، يفتح أحد الأبواب ليبين أنه لا توجد جائزة خلفه ، لكن يمكنه دائمًا القيام بذلك ، لذلك لا يغير أي شيء حقًا. بالطبع ، سترغب في اختيار باب مختلف.
إذا كنت لا تفهم السؤال تمامًا وتحتاج إلى شرح أكثر إقناعًا ، فانقر فوق هذا الرابط للانتقال إلى تطبيق Flash صغير رائع يتيح لك استكشاف هذا التناقض بمزيد من التفاصيل. يمكنك البدء بحوالي 10 أبواب ثم الانتقال تدريجيًا إلى لعبة بثلاثة أبواب. هناك أيضًا جهاز محاكاة حيث يمكنك اللعب بأي عدد من الأبواب من 3 إلى 50 أو تشغيل عدة آلاف من المحاكاة ومعرفة عدد المرات التي ستفوز فيها إذا لعبت.
اختر أحد الأبواب الثلاثة - احتمال الفوز هو 1/3. الآن لديك استراتيجيتان: تغيير الخيار بعد فتح الباب الخطأ أم لا. إذا لم تقم بتغيير اختيارك ، فسيظل الاحتمال 1/3 ، لأن الاختيار يكون في المرحلة الأولى فقط ، ويجب أن تخمن على الفور. إذا قمت بالتغيير ، فيمكنك الفوز إذا اخترت أولاً الباب الخطأ (ثم يفتحون بابًا خاطئًا آخر ، ويبقى الباب الصحيح - تغيير القرار ، أنت فقط تأخذه). احتمال اختيار الباب الخطأ في البداية هو 2/3 - لذا اتضح أنه بتغيير قرارك ، فإنك تضاعف احتمال الفوز.
ملاحظة من مدرس الرياضيات العليا والمتخصص في توازن اللعبة مكسيم سولداتوف - بالطبع ، لم يكن لدى شريبر ذلك ، ولكن بدونها يصعب فهم هذا التحول السحري
إعادة النظر في مفارقة مونتي هول
بالنسبة للعرض نفسه ، حتى لو لم يكن خصوم مونتي هول جيدًا في الرياضيات ، فقد كان جيدًا فيه. إليك ما فعله لتغيير اللعبة قليلاً. إذا اخترت الباب الذي كانت الجائزة خلفه ، مع احتمال 1/3 ، فقد عرض عليك دائمًا خيار اختيار باب آخر. تختار سيارة ثم تستبدلها بالماعز وتبدو غبيًا جدًا - وهذا بالضبط ما تحتاجه ، لأن هول نوع من الرجل الشرير.
ولكن إذا اخترت بابًا ليس به جائزة ، فسيعرض عليك بابًا مختلفًا نصف الوقت فقط ، أو سيُظهر لك عنزة جديدة فقط وستغادر المسرح. دعنا نحلل هذه اللعبة الجديدة حيث يمكن لمونتي هول أن يقرر ما إذا كان سيقدم لك فرصة اختيار باب آخر أم لا.
لنفترض أنه يتبع هذه الخوارزمية: إذا اخترت بابًا به جائزة ، فإنه يعرض عليك دائمًا فرصة اختيار باب آخر ، وإلا فمن المرجح أن يعرض عليك اختيار باب آخر أو منحك عنزة. ما هو احتمال فوزك؟
في أحد الخيارات الثلاثة ، تختار على الفور الباب الذي توجد خلفه الجائزة ، ويدعوك المضيف لاختيار آخر.
من بين الخيارين المتبقيين من أصل ثلاثة (تختار مبدئيًا الباب بدون جائزة) ، في نصف الحالات سيقدم لك المضيف تغيير قرارك ، وفي النصف الآخر لن يفعل ذلك.
نصف 2/3 هو 1/3 ، أي أنه في حالة واحدة من أصل ثلاثة ستحصل على عنزة ، وفي حالة واحدة من أصل ثلاثة ستختار الباب الخطأ وسيقدم لك المضيف اختيار باب آخر ، وفي في حالة واحدة من بين ثلاثة ، ستختار الباب الصحيح ، لكنه يعرض آخر مرة أخرى.
إذا عرض الميسر اختيار باب آخر ، فنحن نعلم بالفعل أن إحدى الحالات الثلاث عندما أعطانا عنزة ونغادرها لم تحدث. هذه معلومات مفيدة: تعني أن فرصنا في الفوز قد تغيرت. حالتان من الحالات الثلاث التي يكون لدينا فيها خيار: في إحدى الحالات ، يعني ذلك أننا خمّننا بشكل صحيح ، وفي الحالة الأخرى ، خمننا بشكل غير صحيح ، لذلك إذا عرض علينا خيار على الإطلاق ، فإن احتمال فوزنا هو 1 / 2 ، ولا يهم رياضيًا ما إذا كنت ستلتزم باختيارك أو تختار بابًا آخر.
مثل البوكر ، إنها لعبة نفسية وليست رياضية. لماذا عرض عليك مونتي الاختيار؟ هل يعتقد أنك غبي لا يعرف أن اختيار باب آخر هو القرار "الصحيح" وسوف يتمسك باختياره بعناد (بعد كل شيء ، يكون الوضع أكثر تعقيدًا من الناحية النفسية عندما تختار سيارة ثم تفقدها) ؟
أم أنه ، الذي يقرر أنك ذكي ويختار بابًا آخر ، يمنحك هذه الفرصة ، لأنه يعلم أنك خمنت في البداية بشكل صحيح وسقطت على الخطاف؟ أو ربما يكون لطيفًا بشكل غير معهود ويدفعك لفعل شيء مفيد لك ، لأنه لم يقدم سيارات لفترة طويلة ويقول المنتجون إن الجمهور يشعر بالملل ، وسيكون من الأفضل منح جائزة كبيرة قريبًا بحيث هل انخفضت التصنيفات؟
وهكذا ، تمكن مونتي في بعض الأحيان من تقديم خيار ، بينما يظل الاحتمال الإجمالي للفوز يساوي 1/3. تذكر أن احتمال خسارتك على الفور هو 1/3. هناك احتمال 1/3 أن تخمن على الفور ، و 50٪ من تلك المرات ستفوز (1/3 × 1/2 = 1/6).
احتمال أن تخمن خاطئًا في البداية ، ولكن لديك فرصة لاختيار باب آخر هو 1/3 ، وفي نصف هذه الحالات ستربح (أيضًا 1/6). أضف احتمالين مستقلين للفوز وستحصل على احتمال 1/3 ، لذلك لا يهم إذا بقيت على اختيارك أو اخترت بابًا آخر - فإن إجمالي احتمال فوزك طوال اللعبة هو 1/3.
لا يصبح الاحتمال أكبر مما كان عليه في الموقف عندما خمنت الباب وأظهر لك المضيف ببساطة ما هو خلفه ، دون عرض اختيار آخر. الهدف من الاقتراح ليس تغيير الاحتمالية ، ولكن لجعل عملية صنع القرار أكثر متعة لمشاهدة التلفزيون.
بالمناسبة ، هذا هو أحد الأسباب التي تجعل البوكر مثيرًا للاهتمام: في معظم التنسيقات بين الجولات ، عندما يتم عمل الرهانات (على سبيل المثال ، التقليب والانعطاف والنهر في Texas Hold'em) ، يتم الكشف عن البطاقات تدريجياً ، وإذا كانت لديك فرصة واحدة للفوز في بداية اللعبة ، فبعد كل جولة مراهنة ، عندما يتم فتح المزيد من البطاقات ، يتغير هذا الاحتمال.
مفارقة الصبي والفتاة
يقودنا هذا إلى مفارقة أخرى معروفة تميل إلى إرباك الجميع ، وهي مفارقة الصبي والفتاة. الشيء الوحيد الذي أكتب عنه اليوم ليس له علاقة مباشرة بالألعاب (على الرغم من أنني أعتقد أنني يجب أن أدفعك لإنشاء آليات لعب مناسبة). هذا أكثر من مجرد لغز ، لكنه مثير للاهتمام ، ومن أجل حله ، عليك أن تفهم الاحتمال الشرطي الذي تحدثنا عنه أعلاه.
المهمة: لدي صديقة لطفلين ، واحدة منهم على الأقل فتاة. ما هو احتمال أن تكون الطفلة الثانية فتاة أيضًا؟ لنفترض أنه في أي عائلة تكون فرص إنجاب فتاة وصبي هي 50/50 ، وهذا ينطبق على كل طفل.
في الواقع ، يمتلك بعض الرجال عددًا أكبر من الحيوانات المنوية التي تحتوي على كروموسوم X أو كروموسوم Y في السائل المنوي ، لذلك تختلف الاحتمالات قليلاً. إذا كنت تعلم أن أحد الأطفال هو فتاة ، فإن فرصة إنجاب فتاة أخرى تكون أعلى قليلاً ، وهناك حالات أخرى ، مثل الخنوثة. لكن لحل هذه المشكلة ، لن نأخذ ذلك في الحسبان ونفترض أن ولادة طفل هي حدث مستقل وأن ولادة صبي وفتاة متساوية في الاحتمال.
نظرًا لأننا نتحدث عن فرصة 1/2 ، فإننا نتوقع حدسيًا أن تكون الإجابة 1/2 أو 1/4 ، أو مضاعفات أخرى لاثنين في المقام. لكن الجواب هو 1/3. لماذا؟
تكمن الصعوبة في هذه الحالة في أن المعلومات التي لدينا تقلل من عدد الاحتمالات. لنفترض أن الوالدين معجبان بشارع سمسم وبغض النظر عن جنس الأبناء الذين يطلق عليهم اسم "أ" و "ب" في ظل الظروف العادية ، هناك أربعة احتمالات متساوية في الاحتمال: "أ" و "ب" ولدان ، و "أ" و "ب" فتاتان ، و "أ". فتى و B فتاة ، و A فتاة و B صبي. نظرًا لأننا نعلم أن طفلاً واحدًا على الأقل هو فتاة ، يمكننا استبعاد احتمال أن يكون "أ" و "ب" صبيان. لذلك يتبقى لدينا ثلاثة احتمالات - لا تزال متساوية في الاحتمال. إذا كانت جميع الاحتمالات متساوية في الاحتمال وكان هناك ثلاثة منها ، فإن احتمال كل منها هو 1/3. فقط في واحد من هذه الخيارات الثلاثة يوجد كل من الفتيات الصغيرات ، لذا فإن الإجابة هي 1/3.
ومرة أخرى حول التناقض بين صبي وفتاة
يصبح حل المشكلة غير منطقي أكثر. تخيل أن صديقي لديه طفلان أحدهما فتاة ولدت يوم الثلاثاء. لنفترض أنه في ظل الظروف العادية ، من المرجح بشكل متساوٍ أن يولد الطفل في كل يوم من أيام الأسبوع السبعة. ما هو احتمال أن تكون الطفلة الثانية فتاة أيضًا؟
قد تعتقد أن الإجابة ستظل 1/3: ماذا يعني الثلاثاء؟ لكن في هذه الحالة ، يخذلنا الحدس. الجواب هو 13/27 ، وهو ليس فقط بديهيًا ، ولكنه غريب جدًا. ما هو الأمر في هذه الحالة؟
في الواقع ، يغير الثلاثاء الاحتمال لأننا لا نعرف أي طفل ولد يوم الثلاثاء ، أو ربما كلاهما ولد يوم الثلاثاء. في هذه الحالة ، نستخدم نفس المنطق: نحسب كل التوليفات الممكنة عندما يكون طفل واحد على الأقل فتاة ولدت يوم الثلاثاء. كما في المثال السابق ، افترض أن الأطفال سموا أ و ب. تبدو المجموعات على النحو التالي:
- A هي فتاة ولدت يوم الثلاثاء ، و B صبي (في هذه الحالة ، هناك 7 احتمالات ، واحدة لكل يوم من أيام الأسبوع يمكن أن يولد فيه الصبي).
- ب- البنت التي ولدت يوم الثلاثاء أ- ولد (ايضا 7 احتمالات).
- أ هي فتاة ولدت يوم الثلاثاء ، ب هي فتاة ولدت في يوم مختلف من الأسبوع (6 احتمالات).
- ب- البنت التي ولدت يوم الثلاثاء أ- البنت التي لم تولد يوم الثلاثاء (ايضا 6 احتمالات).
- A و B فتاتان ولدتا يوم الثلاثاء (احتمال واحد ، عليك الانتباه إلى هذا حتى لا تحسب مرتين).
نلخصها ونحصل على 27 مجموعة مختلفة متساوية من ولادة الأطفال وأيام مع احتمال واحد على الأقل لولادة فتاة يوم الثلاثاء. من بين هؤلاء ، هناك 13 احتمالًا عند ولادة فتاتين. يبدو أيضًا غير منطقي تمامًا - يبدو أن هذه المهمة تم اختراعها فقط لإحداث صداع. إذا كنت لا تزال في حيرة من أمرك ، فإن موقع الويب الخاص بمنظر اللعبة Jesper Juhl لديه شرح جيد لهذا الأمر.
إذا كنت تعمل حاليًا على لعبة
إذا كانت هناك عشوائية في اللعبة التي تصممها ، فهذه فرصة رائعة لتحليلها. حدد أي عنصر تريد تحليله. اسأل نفسك أولاً ما الذي تتوقعه من احتمال وجود عنصر معين في سياق اللعبة.
على سبيل المثال ، إذا كنت تصنع لعبة تقمص أدوار وتفكر في مدى احتمالية فوز اللاعب على وحش في معركة ، اسأل نفسك عن نسبة الفوز التي تشعر أنها مناسبة لك. عادة ، في حالة ألعاب تقمص الأدوار على وحدة التحكم ، يشعر اللاعبون بالاستياء الشديد عندما يخسرون ، لذلك من الأفضل أن يخسروا بشكل غير متكرر - 10٪ من الوقت أو أقل. إذا كنت من مصممي ألعاب تقمص الأدوار ، فمن المحتمل أنك تعرف أفضل مني ، ولكن يجب أن تكون لديك فكرة أساسية عما يجب أن يكون عليه الاحتمال.
ثم اسأل نفسك ما إذا كانت احتمالاتك تعتمد (كما هو الحال مع البطاقات) أو مستقلة (كما هو الحال مع النرد). ناقش كل النتائج المحتملة واحتمالاتها. تأكد من أن مجموع كل الاحتمالات هو 100٪. وبالطبع قارن نتائجك بتوقعاتك. هل من الممكن دحرجة النرد أو رسم البطاقات كما تريد ، أو من الواضح أن القيم بحاجة إلى تعديل. وبالطبع ، إذا وجدت عيوبًا ، يمكنك استخدام نفس الحسابات لتحديد مقدار ما تحتاجه لتغيير القيم.
العمل في المنزل
سيساعدك "الواجب المنزلي" هذا الأسبوع على صقل مهارات الاحتمالات لديك. فيما يلي لعبتي نرد ولعبة بطاقة يجب عليك تحليلها باستخدام الاحتمالات ، بالإضافة إلى ميكانيكي لعبة غريب قمت بتطويره مرة واحدة وستختبر طريقة مونت كارلو عليه.
اللعبة رقم 1 - عظام التنين
هذه لعبة نرد توصلت إليها أنا وزملائي ذات مرة (بفضل Jeb Havens و Jesse King) - إنها تهب عمداً عقول الناس باحتمالاتها. هذه لعبة كازينو بسيطة تسمى "Dragon Dice" وهي عبارة عن مسابقة نرد قمار بين اللاعب والمنشأة.
يتم إعطاؤك يموت 1d6 منتظم. الهدف من اللعبة هو دحرجة رقم أعلى من رقم المنزل. حصل توم على 1d6 غير قياسي - مثل وجهك ، ولكن على وجه واحد بدلاً من وجه واحد - صورة تنين (وبالتالي ، فإن الكازينو لديه نرد تنين-2-3-4-5-6). إذا حصلت المؤسسة على تنين ، فإنها تفوز تلقائيًا ، وتخسر. إذا حصل كلاهما على نفس الرقم ، فسيتم تعادلاً وتدحرج النرد مرة أخرى. الشخص الذي يلقي أكبر عدد يفوز.
بالطبع ، كل شيء ليس في صالح اللاعب تمامًا ، لأن الكازينو يتمتع بميزة في شكل وجه التنين. ولكن هل هو حقا كذلك؟ هذا ما عليك حسابه. لكن تحقق أولاً من حدسك.
لنفترض أن الفوز هو 2 إلى 1. لذا إذا فزت ، ستحافظ على رهانك وتحصل على ضعف المبلغ. على سبيل المثال ، إذا راهنت بمبلغ 1 دولار وفزت ، فستحتفظ بهذا الدولار وتحصل على 2 دولار أخرى في الأعلى ، ليصبح المجموع 3 دولارات. إذا خسرت ، فإنك تخسر رهانك فقط. هل تلعب؟ هل تشعر بشكل بديهي أن الاحتمال أكبر من 2 إلى 1 ، أم أنك ما زلت تعتقد أنه أقل؟ بمعنى آخر ، في المتوسط أكثر من 3 ألعاب ، هل تتوقع الفوز أكثر من مرة ، أو أقل ، أو مرة واحدة؟
بمجرد الانتهاء من الحدس الخاص بك ، قم بتطبيق الرياضيات. لا يوجد سوى 36 موضعًا ممكنًا لكلا النرد ، لذا يمكنك بسهولة عدهم جميعًا. إذا لم تكن متأكدًا من عرض 2 إلى 1 هذا ، ففكر في هذا: لنفترض أنك لعبت اللعبة 36 مرة (راهنت 1 دولار في كل مرة). مقابل كل فوز تحصل على 2 دولار ، مقابل كل خسارة تخسر دولارًا واحدًا ، ولا يغير السحب أي شيء. احسب كل مكاسبك وخسائرك المحتملة وقرر ما إذا كنت ستخسر بعض الدولارات أو ستكسب. ثم اسأل نفسك عن مدى صواب حدسك. ثم أدرك كم أنا الشرير.
ونعم ، إذا كنت قد فكرت بالفعل في هذا السؤال - لقد أربكتك عمدًا عن طريق تشويه الآليات الحقيقية لألعاب النرد ، لكنني متأكد من أنه يمكنك التغلب على هذه العقبة بمجرد التفكير الجيد. حاول حل هذه المشكلة بنفسك.
اللعبة رقم 2 - لفة الحظ
هذه لعبة نرد تسمى Roll of Luck (أيضًا Birdcage لأنه في بعض الأحيان لا يتم دحرجة النرد ولكن يتم وضعها في قفص سلكي كبير ، يشبه قفص البنغو). اللعبة بسيطة ، وتتلخص بشكل أساسي في هذا: الرهان ، لنقل ، 1 دولار على رقم بين 1 و 6. ثم تقوم برمي 3d6. لكل نرد يصل إلى رقمك ، تحصل على دولار واحد (واحتفظ برهانك الأصلي). إذا لم يصل رقمك إلى أي حجر نرد ، فإن الكازينو يحصل على دولارك ولن تحصل على شيء. لذلك إذا راهنت على 1 وحصلت على 1 على الوجه ثلاث مرات ، فستحصل على 3 دولارات.
حدسيًا ، يبدو أن الفرص متساوية في هذه اللعبة. كل نرد هو فرصة للفوز 1 من 6 ، لذا فإن فرصتك في الفوز هي 3 إلى 6 على ثلاث لفات. ومع ذلك ، تذكر ، بالطبع ، أنك تقوم بتكديس ثلاث نرد منفصلة ولا يُسمح لك بالإضافة إلا إذا أردنا ذلك. نتحدث عن مجموعات فائزة منفصلة من نفس الزهر. شيء سوف تحتاج لمضاعفته.
بمجرد أن تقوم بحساب جميع النتائج المحتملة (ربما يكون القيام بها في Excel أسهل من القيام بها يدويًا ، فهناك 216 منها) ، لا تزال اللعبة تبدو زوجية للوهلة الأولى. في الواقع ، لا يزال من المرجح أن يفوز الكازينو - فكم أكثر؟ على وجه الخصوص ، ما مقدار الأموال التي تتوقع أن تخسرها في المتوسط في كل جولة لعبة؟
كل ما عليك فعله هو جمع المكاسب والخسائر لجميع النتائج البالغ عددها 216 ثم القسمة على 216 ، والتي يجب أن تكون سهلة للغاية. ولكن كما ترى ، هناك بعض المزالق التي يمكنك الوقوع فيها ، ولهذا السبب أقول إنه إذا كنت تعتقد أن هناك فرصة للفوز في هذه اللعبة ، فقد أساءت فهمها.
لعبة # 3 - 5 بطاقات عشيق
إذا كنت قد استعدت بالفعل للألعاب السابقة ، فلنتحقق مما نعرفه عن الاحتمال الشرطي باستخدام لعبة الورق هذه كمثال. لنتخيل لعبة البوكر بمجموعة من 52 ورقة. لنتخيل أيضًا 5 بطاقات ، حيث يحصل كل لاعب على 5 بطاقات فقط. لا يمكنك تجاهل بطاقة ، أو رسم بطاقة جديدة ، أو مجموعة أوراق مشتركة - ستحصل على 5 بطاقات فقط.
التدفق الملكي هو 10-J-Q-K-A في يد واحدة ، ليصبح المجموع أربعة ، لذلك هناك أربع طرق ممكنة للحصول على تدفق ملكي. احسب احتمال حصولك على إحدى هذه المجموعات.
لدي شيء واحد أحذرك منه: تذكر أنه يمكنك رسم هذه البطاقات الخمس بأي ترتيب. هذا يعني أنه في البداية يمكنك رسم الآس ، أو عشرة ، لا يهم. لذلك عند إجراء حساباتك ، ضع في اعتبارك أن هناك بالفعل أكثر من أربع طرق للحصول على تدفق ملكي ، بافتراض أن البطاقات قد تم توزيعها بالترتيب.
اللعبة رقم 4 - صندوق اليانصيب
لن يكون حل المهمة الرابعة بهذه السهولة باستخدام الأساليب التي تحدثنا عنها اليوم ، ولكن يمكنك بسهولة محاكاة الموقف باستخدام البرمجة أو Excel. في مثال هذه المشكلة يمكنك عمل طريقة مونت كارلو.
لقد ذكرت سابقًا لعبة Chron X التي عملت عليها ذات مرة ، وكانت هناك بطاقة واحدة مثيرة جدًا للاهتمام - يانصيب صندوق النقد الدولي. وإليك طريقة عملها: لقد استخدمتها في لعبة. بعد انتهاء الجولة ، تمت إعادة توزيع البطاقات ، وكان هناك احتمال بنسبة 10٪ أن البطاقة ستكون خارج اللعب وأن اللاعب العشوائي سيحصل على 5 من كل نوع من الموارد التي تحتوي على رمز مميز على تلك البطاقة. تم تشغيل بطاقة بدون رمز واحد ، ولكن في كل مرة تظل فيها قيد التشغيل في بداية الجولة التالية ، تتلقى رمزًا واحدًا.
لذلك كانت هناك فرصة بنسبة 10٪ أن تلعبها ، وتنتهي الجولة ، وستترك البطاقة تلعب ، ولن يحصل أحد على أي شيء. إذا لم يحدث ذلك (مع فرصة 90٪) ، فهناك فرصة 10٪ (9٪ في الواقع ، بما أن 10٪ من 90٪) ستترك اللعبة في الجولة التالية وسيحصل شخص ما على 5 موارد. إذا غادرت البطاقة اللعبة بعد جولة واحدة (10٪ من 81٪ متوفرة ، وبالتالي فإن الاحتمال هو 8.1٪) ، سيحصل شخص ما على 10 وحدات ، وجولة أخرى - 15 ، و 20 أخرى ، وهكذا. سؤال: ما هي القيمة المتوقعة لعدد الموارد التي ستحصل عليها من هذه البطاقة عندما تغادر اللعبة أخيرًا؟
سنحاول عادةً حل هذه المسألة بحساب احتمالية كل نتيجة وضربها في عدد كل النتائج. هناك احتمال 10٪ أن تحصل على 0 (0.1 * 0 = 0). 9٪ أنك ستتلقى 5 وحدات من الموارد (9٪ * 5 = 0.45 موارد). 8.1٪ مما تحصل عليه هو 10 (8.1٪ * 10 = 0.81 من الموارد - بشكل عام ، القيمة المتوقعة). وما إلى ذلك وهلم جرا. ثم نلخص كل شيء.
والآن أصبحت المشكلة واضحة بالنسبة لك: هناك دائمًا احتمال ألا تغادر البطاقة اللعبة ، ويمكن أن تبقى في اللعبة إلى الأبد ، لعدد لا حصر له من الجولات ، لذلك لا توجد طريقة لحساب أي احتمالية. الأساليب التي تعلمناها اليوم لا تسمح لنا بحساب العودية اللانهائية ، لذلك سيتعين علينا إنشاءها بشكل مصطنع.
إذا كنت جيدًا بما يكفي في البرمجة ، فاكتب برنامجًا يحاكي هذه البطاقة. يجب أن يكون لديك حلقة زمنية تجعل المتغير يصل إلى الموضع الأولي للصفر ، ويظهر رقمًا عشوائيًا ، وباحتمال 10٪ يخرج المتغير من الحلقة. وإلا فإنه يضيف 5 إلى المتغير وتتكرر الحلقة. عندما تخرج أخيرًا من الحلقة ، قم بزيادة العدد الإجمالي للتشغيل التجريبي بمقدار 1 وإجمالي عدد الموارد (حسب مقدار يعتمد على مكان توقف المتغير). ثم أعد تعيين المتغير وابدأ من جديد.
قم بتشغيل البرنامج عدة آلاف من المرات. في النهاية ، قسّم إجمالي الموارد على العدد الإجمالي للتشغيل - ستكون هذه هي القيمة المتوقعة لطريقة مونت كارلو. قم بتشغيل البرنامج عدة مرات للتأكد من أن الأرقام التي تحصل عليها هي نفسها تقريبًا. إذا كان الحيز لا يزال كبيرًا ، فقم بزيادة عدد التكرارات في الحلقة الخارجية حتى تبدأ في الحصول على المطابقات. يمكنك التأكد من أن الأرقام التي ستنتهي بها ستكون صحيحة تقريبًا.
إذا كنت جديدًا في البرمجة (حتى لو كنت كذلك) ، فإليك بعض التمارين لاختبار مهاراتك في Excel. إذا كنت مصمم ألعاب ، فلن تكون هذه المهارات غير ضرورية أبدًا.
الآن ستكون وظائف if و rand مفيدة جدًا لك. لا يتطلب Rand قيمًا ، فهو ينتج فقط عددًا عشريًا عشوائيًا بين 0 و 1. وعادةً ما نجمعه مع الكلمة والإيجابيات والسلبيات لمحاكاة لفة النرد ، والتي ذكرتها سابقًا. ومع ذلك ، في هذه الحالة ، نترك فرصة بنسبة 10٪ أن البطاقة ستغادر اللعبة ، لذلك يمكننا فقط التحقق مما إذا كان الراند أقل من 0.1 ولا داعي للقلق بشأنه بعد الآن.
إذا كان لديه ثلاث قيم. بالترتيب ، الشرط إما صحيحًا أم لا ، ثم القيمة التي يتم إرجاعها إذا كان الشرط صحيحًا ، والقيمة التي يتم إرجاعها إذا كان الشرط خاطئًا. لذا فإن الوظيفة التالية سترجع 5٪ من الوقت ، و 0 الأخرى 90٪ من الوقت: = إذا (RAND ()<0.1,5,0) .
هناك عدة طرق لتعيين هذا الأمر ، لكنني سأستخدم هذه الصيغة للخلية التي تمثل الجولة الأولى ، دعنا نقول إنها الخلية A1: = إذا (RAND ()<0.1,0,-1) .
أستخدم هنا متغيرًا سالبًا يعني "هذه البطاقة لم تغادر اللعبة ولم تقدم أي موارد بعد". لذلك إذا انتهت الجولة الأولى وكانت البطاقة خارج اللعب ، فإن A1 تكون 0 ؛ وإلا فهو -1.
بالنسبة للخلية التالية التي تمثل الجولة الثانية: = IF (A1> -1، A1، IF (RAND ()<0.1,5,-1)) . لذلك إذا انتهت الجولة الأولى وغادرت البطاقة اللعبة على الفور ، فإن A1 هي 0 (عدد الموارد) وستقوم هذه الخلية ببساطة بنسخ هذه القيمة. خلاف ذلك ، A1 هي -1 (البطاقة لم تغادر اللعبة بعد) ، وتستمر هذه الخلية في التحرك بشكل عشوائي: 10٪ من الوقت ستعيد 5 وحدات من الموارد ، وبقية الوقت ستظل قيمتها - 1. إذا طبقنا هذه الصيغة على خلايا إضافية ، فسنحصل على جولات إضافية ، وأي خلية تنتهي بها ، ستحصل على النتيجة النهائية (أو -1 إذا لم تغادر البطاقة اللعبة بعد كل الجولات التي لعبتها).
خذ هذا الصف من الخلايا ، وهو الجولة الوحيدة التي تحتوي على هذه البطاقة ، وانسخ والصق بضع مئات (أو آلاف) من الصفوف. قد لا نتمكن من إجراء اختبار لا نهائي لبرنامج Excel (يوجد عدد محدود من الخلايا في الجدول) ، ولكن على الأقل يمكننا تغطية معظم الحالات. ثم حدد خلية واحدة حيث ستضع متوسط نتائج جميع الجولات - يرجى من Excel توفير وظيفة المتوسط () لهذا الغرض.
في Windows ، يمكنك على الأقل الضغط على F9 لإعادة حساب جميع الأرقام العشوائية. كما كان من قبل ، قم بذلك عدة مرات واعرف ما إذا كنت تحصل على نفس القيم. إذا كان الحيز كبيرًا جدًا ، فقم بمضاعفة عدد الدورات وحاول مرة أخرى.
مشاكل لم تحل
إذا حصلت على درجة علمية في نظرية الاحتمالات وتبدو المشكلات المذكورة أعلاه سهلة للغاية بالنسبة لك - فهناك مشكلتان كنت أخدش رأسي بهما منذ سنوات ، لكن ، للأسف ، لست جيدًا في الرياضيات لحلها.
المشكلة رقم 1 التي لم يتم حلها: يانصيب صندوق النقد الدولي
المشكلة الأولى التي لم يتم حلها هي الواجب المنزلي السابق. يمكنني بسهولة استخدام طريقة مونت كارلو (باستخدام C ++ أو Excel) وتأكد من الإجابة على السؤال "كم عدد الموارد التي سيتلقاها اللاعب" ، لكنني لا أعرف بالضبط كيفية تقديم إجابة دقيقة يمكن إثباتها رياضيًا (هذا هو سلسلة لانهائية).
المشكلة رقم 2 التي لم يتم حلها: تسلسل الشكل
هذه المهمة (تتجاوز أيضًا المهام التي تم حلها في هذه المدونة) تم إلقاؤها من قبل لاعب مألوف منذ أكثر من عشر سنوات. أثناء لعب البلاك جاك في فيجاس ، لاحظ ميزة واحدة مثيرة للاهتمام: رسم بطاقات من حذاء ذي 8 طوابق ، ورأى عشر قطع متتالية (قطعة أو بطاقة وجه هي 10 ، جوكر ، كينغ أو كوين ، لذلك هناك 16 في المجموع. مجموعة قياسية من 52 بطاقة أو 128 في حذاء من 416 بطاقة).
ما هو احتمال أن يحتوي هذا الحذاء على سلسلة واحدة على الأقل من عشر قطع أو أكثر؟ لنفترض أنه تم خلطهم بأمانة ، بترتيب عشوائي. أو ، إذا كنت تفضل ذلك ، ما هو احتمال عدم وجود تسلسل من عشرة أشكال أو أكثر في أي مكان؟
يمكننا تبسيط المهمة. هنا تسلسل من 416 جزء. كل جزء هو 0 أو 1. هناك 128 آحاد و 288 صفراً منتشرة بشكل عشوائي في جميع أنحاء التسلسل. كم عدد الطرق المتاحة لدمج 128 بشكل عشوائي مع 288 صفرًا ، وكم مرة سيكون هناك مجموعة واحدة على الأقل من عشرة أو أكثر بهذه الطرق؟
في كل مرة أبدأ فيها حل هذه المشكلة ، بدا الأمر سهلاً وواضحًا بالنسبة لي ، ولكن بمجرد أن أتعمق في التفاصيل ، انهار فجأة وبدا ببساطة مستحيلاً.
لذا لا تتسرع في توضيح الإجابة: اجلس ، فكر جيدًا ، ادرس الظروف ، حاول إدخال أرقام حقيقية ، لأن جميع الأشخاص الذين تحدثت معهم حول هذه المشكلة (بما في ذلك العديد من طلاب الدراسات العليا العاملين في هذا المجال) تفاعلوا كثيرًا. بالطريقة نفسها: "الأمر واضح تمامًا ... أوه لا ، انتظر ، ليس واضحًا على الإطلاق." هذا هو الحال عندما لا يكون لدي طريقة لحساب جميع الخيارات. بالطبع ، يمكنني أن أجبر المشكلة من خلال خوارزمية حاسوبية ، لكن سيكون من المثير للاهتمام اكتشاف الطريقة الرياضية لحلها.
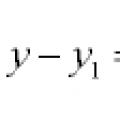 معادلات الخطوط والمنحنيات في المستوى
معادلات الخطوط والمنحنيات في المستوى معادلة متجانسة معممة معادلات متجانسة معممة من الدرجة الثانية
معادلة متجانسة معممة معادلات متجانسة معممة من الدرجة الثانية بفضل الفاصلة يرجع ذلك إلى حقيقة أن في
بفضل الفاصلة يرجع ذلك إلى حقيقة أن في