ج 8 30 معادلات منطقية كسرية. المعادلات الكسرية المنطقية
خصوصيتك مهمة بالنسبة لنا. لهذا السبب ، قمنا بتطوير سياسة الخصوصية التي تصف كيفية استخدامنا لمعلوماتك وتخزينها. يرجى قراءة سياسة الخصوصية الخاصة بنا وإعلامنا إذا كان لديك أي أسئلة.
جمع واستخدام المعلومات الشخصية
تشير المعلومات الشخصية إلى البيانات التي يمكن استخدامها لتحديد أو الاتصال بشخص معين.
قد يُطلب منك تقديم معلوماتك الشخصية في أي وقت عند الاتصال بنا.
فيما يلي بعض الأمثلة على أنواع المعلومات الشخصية التي قد نجمعها وكيف يمكننا استخدام هذه المعلومات.
ما هي المعلومات الشخصية التي نجمعها:
- عندما تقدم طلبًا على الموقع ، فقد نجمع معلومات مختلفة ، بما في ذلك اسمك ورقم هاتفك وعنوان بريدك الإلكتروني وما إلى ذلك.
كيف نستخدم المعلومات الشخصية الخاصة بك:
- تسمح لنا المعلومات الشخصية التي نجمعها بالاتصال بك وإبلاغك بالعروض الفريدة والعروض الترويجية وغيرها من الأحداث والأحداث القادمة.
- من وقت لآخر ، قد نستخدم معلوماتك الشخصية لإرسال إخطارات ورسائل مهمة إليك.
- يجوز لنا أيضًا استخدام المعلومات الشخصية لأغراض داخلية ، مثل إجراء عمليات التدقيق وتحليل البيانات والأبحاث المختلفة من أجل تحسين الخدمات التي نقدمها وتزويدك بالتوصيات المتعلقة بخدماتنا.
- إذا دخلت في سحب على جائزة أو مسابقة أو حافز مماثل ، فقد نستخدم المعلومات التي تقدمها لإدارة هذه البرامج.
الإفصاح للغير
نحن لا نكشف عن المعلومات التي نتلقاها منك لأطراف ثالثة.
استثناءات:
- في حالة الضرورة - وفقًا للقانون والنظام القضائي و / أو الإجراءات القانونية و / أو بناءً على طلبات عامة أو طلبات من هيئات الدولة في أراضي الاتحاد الروسي - الكشف عن معلوماتك الشخصية. قد نكشف أيضًا عن معلومات عنك إذا قررنا أن هذا الكشف ضروري أو مناسب للأمن أو إنفاذ القانون أو لأسباب أخرى تتعلق بالمصلحة العامة.
- في حالة إعادة التنظيم أو الدمج أو البيع ، يجوز لنا نقل المعلومات الشخصية التي نجمعها إلى الجهة الأخرى التي تخلف الطرف الثالث.
حماية المعلومات الشخصية
نحن نتخذ الاحتياطات - بما في ذلك الإدارية والفنية والمادية - لحماية معلوماتك الشخصية من الضياع والسرقة وسوء الاستخدام ، وكذلك من الوصول غير المصرح به والكشف والتعديل والتدمير.
الحفاظ على خصوصيتك على مستوى الشركة
للتأكد من أن معلوماتك الشخصية آمنة ، فإننا ننقل ممارسات الخصوصية والأمان لموظفينا ونطبق ممارسات الخصوصية بصرامة.
قدمنا المعادلة أعلاه في الفقرة 7. أولاً ، نتذكر ما هو التعبير المنطقي. هذا تعبير جبري مكون من أرقام والمتغير x باستخدام عمليات الجمع والطرح والضرب والقسمة والأس مع الأس الطبيعي.
إذا كانت r (x) تعبيرًا منطقيًا ، فإن المعادلة r (x) = 0 تسمى معادلة منطقية.
ومع ذلك ، في الممارسة العملية ، من الأنسب استخدام تفسير أوسع إلى حد ما لمصطلح "المعادلة المنطقية": هذه معادلة من الشكل h (x) = q (x) ، حيث h (x) و q (x) هي تعابير عقلانية.
حتى الآن ، لم نتمكن من حل أي معادلة عقلانية ، ولكن فقط واحدة تم اختزالها إلى معادلة خط مستقيم. الآن إمكانياتنا أكبر بكثير: سنكون قادرين على حل معادلة منطقية ، لا تختصر فقط إلى الخطية
mu ، ولكن أيضًا للمعادلة التربيعية.
تذكر كيف حللنا المعادلات المنطقية في وقت سابق وحاول صياغة خوارزمية الحل.
مثال 1حل المعادلة
حل. نعيد كتابة المعادلة بالصورة
في هذه الحالة ، كالعادة ، نستخدم حقيقة أن المساواة A \ u003d B و A - B \ u003d 0 تعبر عن نفس العلاقة بين A و B. وهذا سمح لنا بنقل المصطلح إلى الجانب الأيسر من المعادلة باستخدام علامة المعاكس.
لنقم بإجراء تحويلات على الجانب الأيسر من المعادلة. لدينا

أذكر شروط المساواة كسورصفر: إذا ، وفقط إذا ، تم استيفاء علاقتين في وقت واحد:
1) بسط الكسر هو صفر (أ = 0) ؛ 2) مقام الكسر يختلف عن الصفر).
نحصل على يساوي صفرًا في بسط الكسر على الجانب الأيسر من المعادلة (1)

يبقى التحقق من استيفاء الشرط الثاني المذكور أعلاه. النسبة تعني المعادلة (1) ذلك. القيم x 1 = 2 و x 2 = 0.6 تفي بالعلاقات المشار إليها وبالتالي فهي بمثابة جذور المعادلة (1) ، وفي نفس الوقت جذور المعادلة المعطاة.
1) دعنا نحول المعادلة إلى الشكل
![]()
2) لنقم بإجراء تحويلات الجانب الأيسر من هذه المعادلة:

(تغيرت في نفس الوقت العلامات الموجودة في البسط و
الكسور).
وهكذا ، تأخذ المعادلة الشكل
![]()
3) حل المعادلة x 2-6x + 8 = 0. أوجد

4) للقيم التي تم العثور عليها ، تحقق من الشرط ![]() . الرقم 4 يلبي هذا الشرط ، لكن الرقم 2 لا. إذن ، 4 هو جذر المعادلة المعطاة ، و 2 هو جذر خارجي.
. الرقم 4 يلبي هذا الشرط ، لكن الرقم 2 لا. إذن ، 4 هو جذر المعادلة المعطاة ، و 2 هو جذر خارجي.
الجواب: 4.
2. حل المعادلات المنطقية بإدخال متغير جديد
طريقة إدخال متغير جديد مألوفة لك ، لقد استخدمناها أكثر من مرة. دعونا نوضح بأمثلة كيف يتم استخدامه في حل المعادلات المنطقية.
مثال 3حل المعادلة x 4 + x 2-20 = 0.
حل. نقدم متغيرًا جديدًا y \ u003d x 2. بما أن x 4 \ u003d (x 2) 2 \ u003d y 2 ، فيمكن إعادة كتابة المعادلة المعطاة بالشكل
ص 2 + ص - 20 = 0.
هذه معادلة من الدرجة الثانية ، سنجد جذورها باستخدام المعلومة الصيغ؛ نحصل على y 1 = 4 ، y 2 = - 5.
لكن y \ u003d x 2 ، مما يعني أنه تم تقليل المشكلة إلى حل معادلتين:
س 2 = 4 ؛ × 2 \ u003d -5.
من المعادلة الأولى نجد أن المعادلة الثانية ليس لها جذور.
إجابة: .
تسمى المعادلة ذات الشكل ax 4 + bx 2 + c \ u003d 0 معادلة biquadratic ("ثنائية" - اثنان ، أي ، كما كانت ، معادلة "مربعتان"). كانت المعادلة التي تم حلها للتو ذات طبيعة ثنائية. يتم حل أي معادلة ثنائية بنفس الطريقة التي يتم بها حل المعادلة من المثال 3: يتم إدخال متغير جديد y \ u003d x 2 ، ويتم حل المعادلة التربيعية الناتجة فيما يتعلق بالمتغير y ، ثم يتم إرجاعها إلى المتغير x.
مثال 4حل المعادلة
![]()
حل. لاحظ أن نفس التعبير x 2 + 3x يظهر مرتين هنا. ومن ثم ، فمن المنطقي إدخال متغير جديد y = x 2 + Zx. سيسمح لنا ذلك بإعادة كتابة المعادلة بصيغة أبسط وأكثر إمتاعًا (وهو في الواقع الغرض من إدخال صيغة جديدة عامل- والتسجيل أسهل
، وتصبح بنية المعادلة أكثر وضوحًا):
![]()
والآن سنستخدم الخوارزمية لحل المعادلة الكسرية.
1) دعنا ننقل كل شروط المعادلة إلى جزء واحد:
![]() = 0
= 0
2) لنحول الجانب الأيسر من المعادلة

لذلك ، قمنا بتحويل المعادلة المعطاة إلى الصورة

3) من المعادلة - 7y 2 + 29y -4 = 0 وجدنا (لقد حللنا بالفعل عددًا كبيرًا من المعادلات التربيعية ، لذلك ربما لا يستحق دائمًا إعطاء حسابات مفصلة في الكتاب المدرسي).
4) دعنا نتحقق من الجذور التي تم العثور عليها باستخدام الشرط 5 (ص - 3) (ص + 1). كلا الجذور تفي بهذا الشرط.
لذلك ، تم حل المعادلة التربيعية للمتغير الجديد y: ![]()
نظرًا لأن y \ u003d x 2 + Zx ، و y ، كما أنشأنا ، تأخذ قيمتين: 4 و - لا يزال يتعين علينا حل معادلتين: x 2 + Zx \ u003d 4 ؛ × 2 + Zx \ u003d. جذور المعادلة الأولى هي الأرقام 1 و - 4 ، وجذور المعادلة الثانية هي الأرقام

في الأمثلة المدروسة ، كانت طريقة إدخال متغير جديد ، كما يحب علماء الرياضيات أن يقولوا ، مناسبة للموقف ، أي أنها تتوافق معها بشكل جيد. لماذا؟ نعم ، لأنه تم العثور على نفس التعبير بوضوح في سجل المعادلة عدة مرات وكان من المعقول تعيين هذا التعبير بحرف جديد. ولكن هذا ليس هو الحال دائمًا ، ففي بعض الأحيان "يظهر" متغير جديد فقط في عملية التحولات. هذا بالضبط ما سيحدث في المثال التالي.
مثال 5حل المعادلة
x (x-1) (x-2) (x-3) = 24.
حل. لدينا
س (س - 3) \ u003d × 2 - 3 س ؛
(x - 1) (x - 2) \ u003d x 2-3x + 2.
لذلك يمكن إعادة كتابة المعادلة على النحو التالي
(س 2-3 س) (س 2 + 3 س + 2) = 24
الآن "ظهر" متغير جديد: y = x 2 - Zx.
بمساعدتها ، يمكن إعادة كتابة المعادلة بالصيغة y (y + 2) \ u003d 24 ثم y 2 + 2y - 24 \ u003d 0. جذور هذه المعادلة هي الأرقام 4 و -6.
بالعودة إلى المتغير الأصلي x ، نحصل على معادلتين x 2 - Zx \ u003d 4 و x 2 - Zx \ u003d - 6. من المعادلة الأولى نجد x 1 \ u003d 4 ، x 2 \ u003d - 1 ؛ المعادلة الثانية ليس لها جذور.
الجواب: 4 ، - 1.
ببساطة ، هذه معادلات يوجد فيها واحد على الأقل به متغير في المقام.
على سبيل المثال:
\ (\ فارك (9 س ^ 2-1) (3 س) \) \ (= 0 \)
\ (\ frac (1) (2x) + \ frac (x) (x + 1) = \ frac (1) (2) \)
\ (\ فارك (6) (س + 1) = \ فارك (س ^ 2-5 س) (س + 1) \)
مثال لاالمعادلات المنطقية الكسرية:
\ (\ فارك (9x ^ 2-1) (3) \) \ (= 0 \)
\ (\ frac (x) (2) \) \ (+ 8x ^ 2 = 6 \)
كيف يتم حل المعادلات المنطقية الكسرية؟
الشيء الرئيسي الذي يجب تذكره حول المعادلات المنطقية الكسرية هو أنك تحتاج إلى الكتابة فيها. وبعد العثور على الجذور ، تأكد من التحقق من قبولها. خلاف ذلك ، قد تظهر جذور دخيلة ، وسيعتبر الحل الكامل غير صحيح.
خوارزمية لحل المعادلة المنطقية الكسرية:
اكتب و "حل" ODZ.
اضرب كل حد في المعادلة بمقام مشترك واختزل الكسور الناتجة. ستختفي القواسم.
اكتب المعادلة دون فتح الأقواس.
حل المعادلة الناتجة.
تحقق من الجذور التي تم العثور عليها باستخدام ODZ.
اكتب استجابةً الجذور التي اجتازت الاختبار في الخطوة 7.
لا تحفظ الخوارزمية ، 3-5 معادلات محلولة - وسوف يتم تذكرها من تلقاء نفسها.
مثال . حل المعادلة المنطقية الكسرية \ (\ frac (x) (x-2) - \ frac (7) (x + 2) = \ frac (8) (x ^ 2-4) \)
حل:
إجابة: \(3\).
مثال . أوجد جذور المعادلة المنطقية الكسرية \ (= 0 \)
حل:
|
\ (\ frac (x) (x + 2) + \ frac (x + 1) (x + 5) - \ frac (7-x) (x ^ 2 + 7x + 10) \)\(=0\) ODZ: \ (س + 2 ≠ 0⇔x ≠ -2 \) |
نكتب و "نحل" ODZ. وسّع \ (x ^ 2 + 7x + 10 \) في الصيغة: \ (ax ^ 2 + bx + c = a (x-x_1) (x-x_2) \). |
|
|
\ (\ frac (x) (x + 2) + \ frac (x + 1) (x + 5) - \ frac (7-x) ((x + 2) (x + 5)) \)\(=0\) |
من الواضح أن المقام المشترك للكسور: \ ((x + 2) (x + 5) \). نضرب المعادلة بأكملها بها. |
|
|
\ (\ فارك (س (س + 2) (س + 5)) (س + 2) + \ فارك ((س + 1) (س + 2) (س + 5)) (س + 5) - \) |
نحن نختصر الكسور |
|
|
\ (س (س + 5) + (س + 1) (س + 2) -7 + س = 0 \) |
فتح الأقواس |
|
|
\ (س ^ 2 + 5 س + س ^ 2 + 3 س + 2-7 + س = 0 \) |
|
نعطي شروط مماثلة |
|
\ (2x ^ 2 + 9x-5 = 0 \) |
|
إيجاد جذور المعادلة |
|
\ (x_1 = -5 ؛ \) \ (x_2 = \ frac (1) (2). \) |
|
أحد الجذور لا يتناسب مع ODZ ، لذا رداً على ذلك نكتب الجذر الثاني فقط. |
إجابة: \ (\ فارك (1) (2) \).
نواصل الحديث عن حل المعادلات. في هذه المقالة ، سوف نركز على المعادلات المنطقيةومبادئ حل المعادلات المنطقية بمتغير واحد. أولاً ، دعنا نتعرف على نوع المعادلات التي تسمى عقلانية ، ونعطي تعريفًا لعدد صحيح من المعادلات المنطقية والكسرية ، ونعطي أمثلة. علاوة على ذلك ، سوف نحصل على خوارزميات لحل المعادلات المنطقية ، وبالطبع سننظر في حلول الأمثلة النموذجية مع جميع التفسيرات اللازمة.
التنقل في الصفحة.
بناءً على التعريفات الصوتية ، نقدم العديد من الأمثلة على المعادلات المنطقية. على سبيل المثال ، x = 1 ، 2 x − 12 x 2 y z 3 = 0 ، كلها معادلات منطقية.
من الأمثلة الموضحة ، يمكن ملاحظة أن المعادلات المنطقية ، وكذلك المعادلات من الأنواع الأخرى ، يمكن أن تكون إما بمتغير واحد ، أو بمتغيرين ، أو ثلاثة ، إلخ. المتغيرات. في الفقرات التالية سنتحدث عن حل المعادلات المنطقية في متغير واحد. حل المعادلات ذات المتغيرينوعددهم الكبير يستحق اهتماما خاصا.
بالإضافة إلى قسمة المعادلات المنطقية على عدد المتغيرات غير المعروفة ، يتم تقسيمها أيضًا إلى عدد صحيح وكسر. دعونا نعطي التعاريف المقابلة.
تعريف.
تسمى المعادلة المنطقية جميع، إذا كان كلا الجزأين الأيمن والأيسر عبارة عن تعبيرات منطقية عددية.
تعريف.
إذا كان أحد أجزاء المعادلة المنطقية على الأقل عبارة عن تعبير كسري ، فسيتم استدعاء هذه المعادلة عقلاني كسور(أو عقلاني كسري).
من الواضح أن المعادلات الصحيحة لا تحتوي على قسمة على متغير ؛ على العكس من ذلك ، تحتوي المعادلات المنطقية الكسرية بالضرورة على القسمة على متغير (أو متغير في المقام). إذن 3 س + 2 = 0 و (س + ص) (3 × 2 −1) + س = ص + 0.5هي معادلات عقلانية كاملة ، وكلا أجزائها عبارة عن تعبيرات عدد صحيح. A و x: (5 x 3 + y 2) = 3: (x − 1): 5 أمثلة على المعادلات المنطقية الكسرية.
في ختام هذه الفقرة ، دعونا ننتبه إلى حقيقة أن المعادلات الخطية والمعادلات التربيعية المعروفة في هذه اللحظة هي معادلات منطقية كاملة.
حل المعادلات الصحيحة
أحد الأساليب الرئيسية لحل المعادلات بأكملها هو تقليلها إلى ما يعادلها المعادلات الجبرية. يمكن القيام بذلك دائمًا عن طريق إجراء التحويلات المكافئة التالية للمعادلة:
- أولاً ، يتم نقل التعبير من الجانب الأيمن من معادلة العدد الصحيح الأصلي إلى الجانب الأيسر مع الإشارة المعاكسة للحصول على الصفر على الجانب الأيمن ؛
- بعد ذلك ، على الجانب الأيسر من المعادلة ، النموذج القياسي الناتج.
والنتيجة هي معادلة جبرية تعادل المعادلة الكاملة الأصلية. لذلك في أبسط الحالات ، يتم تقليل حل المعادلات بأكملها إلى حل المعادلات الخطية أو التربيعية ، وفي الحالة العامة - إلى حل معادلة جبرية من الدرجة n. من أجل الوضوح ، دعنا نحلل حل المثال.
مثال.
أوجد جذور المعادلة بأكملها 3 (x + 1) (x − 3) = x (2 x − 1) −3.
حل.
دعونا نختزل حل هذه المعادلة بأكملها إلى حل معادلة جبرية مكافئة. للقيام بذلك ، أولاً ، ننقل التعبير من الجانب الأيمن إلى اليسار ، ونتيجة لذلك نصل إلى المعادلة 3 (x + 1) (x − 3) −x (2 x − 1) + 3 = 0. وثانياً ، نقوم بتحويل التعبير الذي تم تكوينه على الجانب الأيسر إلى كثير حدود للصيغة القياسية عن طريق القيام بما يلزم: 3 (x + 1) (x − 3) −x (2 x − 1) + 3 = (3 س + 3) (س − 3) −2 س 2 + س + 3 = 3 x 2 −9 x + 3 x − 9−2 x 2 + x + 3 = x 2 −5 x − 6. وبالتالي ، يتم تقليل حل المعادلة الصحيحة الأصلية إلى حل المعادلة التربيعية x 2 −5 · x − 6 = 0.
احسب مميزها د = (- 5) 2 4 1 (6) = 25 + 24 = 49، إنها موجبة ، مما يعني أن للمعادلة جذران حقيقيان ، نجدهما في صيغة جذور المعادلة التربيعية:
للتأكد تمامًا ، دعنا نفعل التحقق من الجذور الموجودة للمعادلة. أولاً ، نتحقق من الجذر 6 ، ونعوضه بدلاً من المتغير x في معادلة العدد الصحيح الأصلية: 3 (6 + 1) (6−3) = 6 (2 6−1) −3أي 63 = 63. هذه معادلة عددية صحيحة ، لذا فإن x = 6 هو بالفعل جذر المعادلة. الآن نتحقق من الجذر −1 ، لدينا 3 (1 + 1) (−1−3) = (- 1) (2 (−1) −1) −3، من أين ، 0 = 0. بالنسبة إلى x = −1 ، تحولت المعادلة الأصلية أيضًا إلى مساواة عددية حقيقية ، وبالتالي ، فإن x = −1 هو أيضًا جذر المعادلة.
إجابة:
6 , −1 .
وهنا تجدر الإشارة أيضًا إلى أن مصطلح "قوة معادلة كاملة" يرتبط بتمثيل معادلة كاملة في شكل معادلة جبرية. نعطي التعريف المقابل:
تعريف.
درجة المعادلة بأكملهانسمي درجة المعادلة الجبرية المكافئة لها.
وفقًا لهذا التعريف ، فإن المعادلة الكاملة من المثال السابق لها الدرجة الثانية.
في هذا يمكن أن ينتهي المرء بحل المعادلات المنطقية بأكملها ، إن لم يكن لواحد ولكن ... كما هو معروف ، فإن حل المعادلات الجبرية ذات الدرجة الأعلى من الثانية يرتبط بصعوبات كبيرة ، وبالنسبة للمعادلات ذات الدرجة الأعلى من الرابعة ، لا توجد صيغ عامة للجذور على الإطلاق. لذلك ، لحل المعادلات الكاملة للدرجات الثالثة والرابعة والعالية ، غالبًا ما يتعين على المرء اللجوء إلى طرق حل أخرى.
في مثل هذه الحالات ، في بعض الأحيان النهج لحل المعادلات المنطقية بأكملها على أساس طريقة التحليل. في الوقت نفسه ، يتم اتباع الخوارزمية التالية:
- يسعون أولاً إلى الحصول على صفر في الجانب الأيمن من المعادلة ، لذلك ينقلون التعبير من الجانب الأيمن للمعادلة بأكملها إلى اليسار ؛
- بعد ذلك ، يتم تقديم التعبير الناتج على الجانب الأيسر كمنتج لعدة عوامل ، مما يسمح لك بالانتقال إلى مجموعة من عدة معادلات أبسط.
تتطلب الخوارزمية المذكورة أعلاه لحل المعادلة بأكملها من خلال التحليل إلى العوامل شرحًا مفصلاً باستخدام مثال.
مثال.
حل المعادلة بأكملها (س 2 −1) (س 2 10 س + 13) = 2 × (× 2 × 10 × + 13).
حل.
أولاً ، كالعادة ، ننقل التعبير من الجانب الأيمن إلى الجانب الأيسر من المعادلة ، ولا ننسى تغيير الإشارة ، نحصل على (× 2 -1) (× 2 × 10 × + 13) - 2 × (× 2 10 × + 13) = 0. من الواضح تمامًا هنا أنه لا يُنصح بتحويل الجانب الأيسر من المعادلة الناتجة إلى كثير حدود للصيغة القياسية ، لأن هذا سيعطي معادلة جبرية من الدرجة الرابعة من النموذج x 4 −12 x 3 +32 x 2 16 x − 13 = 0الذي يكون حله صعبًا.
من ناحية أخرى ، من الواضح أن x 2 −10 · x + 13 يمكن العثور عليها على الجانب الأيسر من المعادلة الناتجة ، وبالتالي تمثيلها كمنتج. لدينا (س 2 −10 س + 13) (س 2 −2 س − 1) = 0. المعادلة الناتجة تعادل المعادلة الكاملة الأصلية ، ويمكن استبدالها بدورها بمجموعة من معادلتين من الدرجة الثانية x 2 −10 · x + 13 = 0 و x 2 2 · x − 1 = 0. العثور على جذورهم باستخدام صيغ الجذر المعروفة من خلال المميز ليس بالأمر الصعب ، فالجذور متساوية. هم الجذور المرغوبة للمعادلة الأصلية.
إجابة:
إنه مفيد أيضًا في حل المعادلات المنطقية بأكملها. طريقة لإدخال متغير جديد. في بعض الحالات ، يسمح للمرء بالمرور إلى المعادلات التي تكون درجتها أقل من درجة معادلة العدد الصحيح الأصلي.
مثال.
أوجد الجذور الحقيقية لمعادلة عقلانية (س 2 +3 س + 1) 2 + 10 = 2 (س 2 +3 س − 4).
حل.
إن اختزال هذه المعادلة المنطقية بالكامل إلى معادلة جبرية ، بعبارة ملطفة ، ليس فكرة جيدة جدًا ، لأننا في هذه الحالة سنصل إلى الحاجة إلى حل معادلة من الدرجة الرابعة ليس لها جذور منطقية. لذلك ، سيتعين عليك البحث عن حل آخر.
من السهل أن ترى هنا أنه يمكنك إدخال متغير جديد y واستبدال التعبير x 2 +3 x به. يقودنا هذا الاستبدال إلى المعادلة الكاملة (y + 1) 2 + 10 = −2 (y − 4) ، والتي بعد نقل التعبير −2 (y − 4) إلى الجانب الأيسر والتحويل اللاحق للتعبير المتكون هناك ، تصغر المعادلة y 2 +4 y + 3 = 0. من السهل العثور على جذور هذه المعادلة y = −1 و y = −3 ، على سبيل المثال ، يمكن إيجادها استنادًا إلى نظرية معكوس نظرية فييتا.
الآن دعنا ننتقل إلى الجزء الثاني من طريقة إدخال متغير جديد ، أي إجراء تعويض عكسي. بعد إجراء الاستبدال العكسي ، نحصل على معادلتين x 2 +3 x = −1 و x 2 +3 x = −3 ، والتي يمكن إعادة كتابتها كـ x 2 +3 x + 1 = 0 و x 2 +3 x + 3 = 0. وفقًا لصيغة جذور المعادلة التربيعية ، نجد جذور المعادلة الأولى. والمعادلة التربيعية الثانية ليس لها جذور حقيقية ، لأن مميزها سالب (D = 3 2 −4 3 = 9−12 = −3).
إجابة:
بشكل عام ، عندما نتعامل مع معادلات كاملة ذات درجات عالية ، يجب أن نكون دائمًا مستعدين للبحث عن طريقة غير قياسية أو تقنية مصطنعة لحلها.
حل المعادلات الكسرية الكسرية
أولاً ، سيكون من المفيد فهم كيفية حل المعادلات المنطقية الكسرية للصيغة ، حيث p (x) و q (x) عبارة عن تعبيرات عدد صحيح منطقي. وبعد ذلك سنوضح كيفية اختزال حل المعادلات الكسرية الكسرية المتبقية في حل المعادلات بالصيغة المشار إليها.
تعتمد إحدى طرق حل المعادلة على البيان التالي: الكسر العددي u / v ، حيث v هو رقم غير صفري (وإلا سنواجهه ، وهو غير محدد) ، يساوي صفرًا إذا وفقط إذا بسطها يساوي صفرًا ، إذن ، إذا وفقط إذا كانت u = 0. بموجب هذا البيان ، يتم تقليل حل المعادلة إلى تحقيق شرطين ص (س) = 0 و ف (س) ≠ 0.
هذا الاستنتاج يتفق مع ما يلي خوارزمية لحل معادلة منطقية كسور. لحل المعادلة المنطقية الكسرية للصيغة
- حل المعادلة المنطقية الكاملة ص (س) = 0 ؛
- وتحقق مما إذا كان الشرط q (x) ≠ 0 مستوفيًا لكل جذر تم العثور عليه ، بينما
- إذا كان هذا صحيحًا ، فإن هذا الجذر هو جذر المعادلة الأصلية ؛
- إذا لم يكن كذلك ، فإن هذا الجذر غريب ، أي أنه ليس جذر المعادلة الأصلية.
دعنا نحلل مثالاً على استخدام الخوارزمية الصوتية عند حل المعادلة المنطقية الكسرية.
مثال.
أوجد جذور المعادلة.
حل.
هذه معادلة كسرية في الصورة ، حيث p (x) = 3 x − 2، q (x) = 5 x 2 −2 = 0.
وفقًا لخوارزمية حل المعادلات الكسرية من هذا النوع ، نحتاج أولاً إلى حل المعادلة 3 · x − 2 = 0. هذه معادلة خطية جذرها x = 2/3.
يبقى التحقق من هذا الجذر ، أي للتحقق مما إذا كان يفي بالشرط 5 × 2 −2 ≠ 0. نعوض بالرقم 2/3 بدلاً من x في التعبير 5 x 2 −2 ، نحصل عليه. تم استيفاء الشرط ، لذا فإن x = 2/3 هو جذر المعادلة الأصلية.
إجابة:
2/3 .
يمكن الاقتراب من حل المعادلة المنطقية الكسرية من موضع مختلف قليلاً. هذه المعادلة تعادل المعادلة بأكملها ص (س) = 0 على المتغير س للمعادلة الأصلية. هذا هو ، يمكنك متابعة هذا خوارزمية لحل معادلة منطقية كسور :
- حل المعادلة ص (س) = 0 ؛
- أوجد متغير ODZ x ؛
- خذ الجذور التي تنتمي إلى منطقة القيم المقبولة - فهي الجذور المرغوبة للمعادلة المنطقية الكسرية الأصلية.
على سبيل المثال ، لنحل معادلة كسرية منطقية باستخدام هذه الخوارزمية.
مثال.
حل المعادلة.
حل.
أولاً ، نحل المعادلة التربيعية x 2 −2 · x − 11 = 0. يمكن حساب جذوره باستخدام صيغة الجذر لمعامل حتى ثاني ، لدينا د 1 = (- 1) 2 1 (11) = 12، و .
ثانيًا ، نجد ODZ للمتغير x للمعادلة الأصلية. يتكون من جميع الأرقام التي x 2 +3 x ≠ 0 ، والتي هي نفسها x (x + 3) ≠ 0 ، حيث x ≠ 0 ، x ≠ −3.
يبقى التحقق مما إذا كانت الجذور التي تم العثور عليها في الخطوة الأولى مدرجة في ODZ. بالطبع نعم. لذلك ، فإن المعادلة الكسرية الكسرية لها جذرين.
إجابة:
لاحظ أن هذا النهج أكثر ربحية من الأسلوب الأول إذا كان من السهل العثور على ODZ ، ويكون مفيدًا بشكل خاص إذا كانت جذور المعادلة p (x) = 0 غير منطقية ، على سبيل المثال ، أو عقلانية ، ولكن مع كبير إلى حد ما البسط و / أو المقام ، على سبيل المثال ، 127/1101 و -31 / 59. ويرجع ذلك إلى حقيقة أنه في مثل هذه الحالات ، سيتطلب التحقق من الشرط q (x) ≠ 0 جهودًا حسابية كبيرة ، ومن الأسهل استبعاد الجذور الخارجية من ODZ.
في حالات أخرى ، عند حل المعادلة ، خاصةً عندما تكون جذور المعادلة ص (س) = 0 أعدادًا صحيحة ، فمن الأفضل استخدام أول الخوارزميات المذكورة أعلاه. أي أنه من المستحسن إيجاد جذور المعادلة بأكملها على الفور ص (س) = 0 ، ثم التحقق مما إذا كان الشرط q (س) ≠ 0 مستوفى لهم ، وعدم إيجاد ODZ ، ثم حل المعادلة p (x) = 0 في ODZ هذا. ويرجع ذلك إلى حقيقة أنه في مثل هذه الحالات يكون من الأسهل عادةً إجراء فحص بدلاً من العثور على ODZ.
ضع في اعتبارك حل مثالين لتوضيح الفروق الدقيقة المنصوص عليها.
مثال.
أوجد جذور المعادلة.
حل.
أولًا نجد جذور المعادلة بأكملها (2 x − 1) (x − 6) (x 2 −5 x + 14) (x + 1) = 0، مجمعة باستخدام بسط الكسر. الجانب الأيسر من هذه المعادلة منتج ، والجانب الأيمن صفر ، لذلك ، وفقًا لطريقة حل المعادلات من خلال التحليل إلى عوامل ، فإن هذه المعادلة تعادل مجموعة المعادلات الأربع 2 x − 1 = 0 ، x − 6 = 0 ، س 2 −5 س + 14 = 0 ، س + 1 = 0. ثلاث من هذه المعادلات خطية وواحدة تربيعية ، يمكننا حلها. من المعادلة الأولى نجد x = 1/2 ، من الثانية - x = 6 ، من الثالثة - x = 7 ، x = −2 ، من الرابعة - x = −1.
مع العثور على الجذور ، من السهل جدًا التحقق منها لمعرفة ما إذا كان مقام الكسر الموجود على الجانب الأيسر من المعادلة الأصلية لا يختفي ، وليس من السهل تحديد ODZ ، حيث سيتعين حل ذلك معادلة جبرية من الدرجة الخامسة. لذلك ، سوف نرفض العثور على ODZ لصالح فحص الجذور. للقيام بذلك ، نعوض بهم بدورهم بدلاً من المتغير x في التعبير × 5 15 × 4 +57 × 3 13 × 2 +26 × + 112، التي تم الحصول عليها بعد الاستبدال ، ومقارنتها بالصفر: (1/2) 5 15 (1/2) 4 + 57 (1/2) 3 13 (1/2) 2 +26 (1/2) + 112 = 1/32−15/16+57/8−13/4+13+112=
122+1/32≠0
;
6 5 −15 6 4 +57 6 3 13 6 2 +26 6 + 112 = 448≠0
;
7 5 −15 7 4 +57 7 3 13 7 2 +26 7 + 112 = 0;
(−2) 5 15 (2) 4 +57 (2) 3 −13 (−2) 2 + 26 (−2) + 112 = −720 ≠ 0 ؛
(1) 5 −15 (1) 4 +57 (1) 3 −13 (−1) 2 + 26 · (1) + 112 = 0.
وبالتالي ، فإن 1/2 و 6 و 2 هي الجذور المرغوبة للمعادلة المنطقية الكسرية الأصلية ، و 7 و -1 هي جذور دخيلة.
إجابة:
1/2 , 6 , −2 .
مثال.
أوجد جذور معادلة كسرية منطقية.
حل.
أولًا نجد جذور المعادلة (5x2 −7x − 1) (x 2) = 0. هذه المعادلة تكافئ مجموعة من معادلتين: المربع 5 · x 2 −7 · x − 1 = 0 والخطي x − 2 = 0. وفقًا لصيغة جذور المعادلة التربيعية ، نجد جذرين ، ومن المعادلة الثانية لدينا x = 2.
التحقق مما إذا كان المقام لا يتلاشى عند القيم التي تم العثور عليها لـ x هو أمر غير سار إلى حد ما. وتحديد نطاق القيم المقبولة للمتغير x في المعادلة الأصلية أمر بسيط للغاية. لذلك ، سوف نعمل من خلال ODZ.
في حالتنا ، يتكون ODZ للمتغير x للمعادلة المنطقية الكسرية الأصلية من جميع الأرقام ، باستثناء تلك التي يتم استيفاء شرطها x 2 + 5 · x − 14 = 0. جذور هذه المعادلة التربيعية هي x = −7 و x = 2 ، والتي نستنتج منها حول ODZ: إنها تتكون من كل x هكذا.
يبقى التحقق مما إذا كانت الجذور الموجودة و x = 2 تنتمي إلى منطقة القيم المقبولة. الجذور - تنتمي ، لذلك ، فهي جذور المعادلة الأصلية ، و x = 2 لا تنتمي ، لذلك فهي جذر دخيل.
إجابة:
سيكون من المفيد أيضًا التركيز بشكل منفصل على الحالات التي تحتوي فيها المعادلة المنطقية الكسرية للنموذج على رقم في البسط ، أي عندما يتم تمثيل p (x) ببعض الأرقام. حيث
- إذا كان هذا الرقم مختلفًا عن الصفر ، فإن المعادلة ليس لها جذور ، لأن الكسر هو صفر إذا وفقط إذا كان البسط هو صفر ؛
- إذا كان هذا الرقم صفرًا ، فإن جذر المعادلة هو أي رقم من ODZ.
مثال.
حل.
نظرًا لوجود رقم غير صفري في بسط الكسر في الجانب الأيسر من المعادلة ، فلا يمكن أن تساوي قيمة x صفرًا. لذلك ، هذه المعادلة ليس لها جذور.
إجابة:
لا جذور.
مثال.
حل المعادلة.
حل.
بسط الكسر على الجانب الأيسر من هذه المعادلة المنطقية الكسرية هو صفر ، لذا فإن قيمة هذا الكسر تساوي صفرًا لأي x يكون منطقيًا له. بمعنى آخر ، حل هذه المعادلة هو أي قيمة لـ x من DPV لهذا المتغير.
يبقى تحديد هذا النطاق من القيم المقبولة. يتضمن كل هذه القيم x التي x 4 +5 x 3 0. حلول المعادلة x 4 +5 x 3 \ u003d 0 هي 0 و −5 ، لأن هذه المعادلة تعادل المعادلة x 3 (x + 5) \ u003d 0 ، وهي بدورها تعادل المجموعة من معادلتين x 3 \ u003d 0 و x + 5 = 0 ، حيث تظهر هذه الجذور. لذلك ، فإن النطاق المطلوب للقيم المقبولة هو أي x ، باستثناء x = 0 و x = −5.
وبالتالي ، فإن المعادلة الكسرية لها عدد لا نهائي من الحلول ، وهي عبارة عن أي أرقام باستثناء صفر وسالب خمسة.
إجابة:
أخيرًا ، حان الوقت للحديث عن حل المعادلات المنطقية الكسرية التعسفية. يمكن كتابتها كـ r (x) = s (x) ، حيث r (x) و s (x) تعبيران منطقيان ، وواحد منهما على الأقل كسري. بالنظر إلى المستقبل ، نقول إن حلهم يقتصر على حل المعادلات بالصيغة المألوفة لدينا بالفعل.
من المعروف أن نقل مصطلح من جزء من المعادلة إلى آخر بعلامة معاكسة يؤدي إلى معادلة مكافئة ، وبالتالي فإن المعادلة r (x) = s (x) تعادل المعادلة r (x) −s (س) = 0.
نعلم أيضًا أن أيًا يمكن أن يكون مساويًا لهذا المقدار. وبالتالي ، يمكننا دائمًا تحويل التعبير المنطقي على الجانب الأيسر من المعادلة r (x) −s (x) = 0 إلى كسر منطقي متساوٍ من النموذج.
لذلك ننتقل من المعادلة المنطقية الكسرية الأصلية r (x) = s (x) إلى المعادلة ، وحلها ، كما اكتشفنا أعلاه ، ينخفض إلى حل المعادلة p (x) = 0.
ولكن من الضروري هنا مراعاة حقيقة أنه عند استبدال r (x) −s (x) = 0 بـ ، ثم بـ p (x) = 0 ، قد يتوسع نطاق القيم المسموح بها للمتغير x .
لذلك ، قد لا تكون المعادلة الأصلية r (x) = s (x) والمعادلة p (x) = 0 ، التي توصلنا إليها ، متكافئة ، ومن خلال حل المعادلة p (x) = 0 ، يمكننا الحصول على الجذور ستكون جذورًا دخيلة للمعادلة الأصلية r (x) = s (x). من الممكن تحديد الجذور الدخيلة وعدم تضمينها في الإجابة ، إما عن طريق التحقق أو التحقق من انتمائها إلى ODZ للمعادلة الأصلية.
نلخص هذه المعلومات في خوارزمية لحل المعادلة المنطقية الكسرية r (x) = s (x). لحل المعادلة المنطقية الكسرية r (x) = s (x) ، يجب على المرء
- احصل على صفر على اليمين بتحريك التعبير من الجانب الأيمن بالإشارة المعاكسة.
- نفذ الإجراءات باستخدام الكسور ومتعددة الحدود على الجانب الأيسر من المعادلة ، وبالتالي تحويلها إلى كسر منطقي من الصورة.
- حل المعادلة ص (س) = 0.
- تحديد واستبعاد الجذور الدخيلة ، والذي يتم عن طريق استبدالها في المعادلة الأصلية أو عن طريق التحقق من انتمائها إلى ODZ للمعادلة الأصلية.
لمزيد من الوضوح ، سوف نعرض السلسلة الكاملة لحل المعادلات المنطقية الكسرية:
.
دعنا ننتقل إلى حلول العديد من الأمثلة مع شرح مفصل للحل من أجل توضيح كتلة المعلومات المحددة.
مثال.
حل معادلة كسرية منطقية.
حل.
سوف نتصرف وفقًا لخوارزمية الحل التي تم الحصول عليها للتو. وننقل أولاً الحدود من الجانب الأيمن للمعادلة إلى الطرف الأيسر ، ونتيجة لذلك نمرر إلى المعادلة.
في الخطوة الثانية ، علينا تحويل التعبير المنطقي الكسري الموجود على الجانب الأيسر من المعادلة الناتجة إلى صورة كسر. للقيام بذلك ، نجري اختزال الكسور النسبية إلى مقام مشترك وتبسيط التعبير الناتج:. لذلك نصل إلى المعادلة.
في الخطوة التالية ، علينا حل المعادلة −2 · x − 1 = 0. أوجد x = −1 / 2.
يبقى أن نتحقق مما إذا كان الرقم الموجود −1/2 هو جذر خارجي للمعادلة الأصلية. للقيام بذلك ، يمكنك التحقق أو العثور على متغير ODZ x الخاص بالمعادلة الأصلية. دعونا نوضح كلا النهجين.
لنبدأ بالشيك. نعوض بالرقم −1/2 بدلاً من المتغير x في المعادلة الأصلية ، ونحصل على نفس الرقم −1 = −1. يعطي الاستبدال المساواة العددية الصحيحة ، لذلك ، x = −1 / 2 هو جذر المعادلة الأصلية.
سنعرض الآن كيف يتم تنفيذ الخطوة الأخيرة من الخوارزمية من خلال ODZ. نطاق القيم المقبولة للمعادلة الأصلية هو مجموعة جميع الأرقام باستثناء 1 و 0 (عندما تكون x = −1 و x = 0 ، تختفي مقامات الكسور). الجذر x = −1 / 2 الموجود في الخطوة السابقة ينتمي إلى ODZ ، لذلك ، x = −1 / 2 هو جذر المعادلة الأصلية.
إجابة:
−1/2 .
لنفكر في مثال آخر.
مثال.
أوجد جذور المعادلة.
حل.
نحتاج إلى حل معادلة كسرية منطقية ، فلنستعرض جميع خطوات الخوارزمية.
أولاً ، ننقل المصطلح من الجانب الأيمن إلى اليسار ، نحصل عليه.
ثانيًا ، نقوم بتحويل التعبير المكون على الجانب الأيسر:. نتيجة لذلك ، نصل إلى المعادلة x = 0.
جذره واضح - إنه صفر.
في الخطوة الرابعة ، يبقى معرفة ما إذا كان الجذر الموجود ليس خارجيًا للمعادلة المنطقية الكسرية الأصلية. عندما يتم استبداله في المعادلة الأصلية ، يتم الحصول على التعبير. من الواضح أنه لا معنى له ، لأنه يحتوي على قسمة على صفر. من هنا نستنتج أن 0 هو جذر دخيل. لذلك ، فإن المعادلة الأصلية ليس لها جذور.
7 ، الأمر الذي يؤدي إلى المعادلة. من هذا يمكننا أن نستنتج أن المقدار الموجود في مقام الطرف الأيسر يجب أن يساوي من الطرف الأيمن ، أي. الآن نطرح من كلا الجزأين من الثلاثي:. عن طريق القياس ، من أين ، وأبعد.
يظهر الفحص أن كلا الجذور التي تم العثور عليها هي جذور المعادلة المنطقية الكسرية الأصلية.
إجابة:
فهرس.
- الجبر:كتاب مدرسي لمدة 8 خلايا. تعليم عام المؤسسات / [Yu. ن. ماكاريشيف ، إن جي مينديوك ، ك. آي. نيشكوف ، إس ب. سوفوروفا] ؛ إد. S. A. Telyakovsky. - الطبعة ال 16. - م: التربية والتعليم 2008. - 271 ص. : مريض. - ردمك 978-5-09-019243-9.
- مردكوفيتش أ.الجبر. الصف 8. الساعة 2 بعد الظهر الجزء 1. كتاب مدرسي لطلاب المؤسسات التعليمية / أ. ج. مردكوفيتش. - الطبعة الحادية عشرة ، ممحاة. - م: Mnemozina، 2009. - 215 ص: م. ردمك 978-5-346-01155-2.
- الجبر:الصف التاسع: كتاب مدرسي. للتعليم العام المؤسسات / [Yu. ن. ماكاريشيف ، إن جي مينديوك ، ك. آي. نيشكوف ، إس ب. سوفوروفا] ؛ إد. S. A. Telyakovsky. - الطبعة ال 16. - م: التربية 2009. - 271 ص. : مريض. - ردمك 978-5-09-021134-5.
التعبير الصحيح هو تعبير رياضي يتكون من أرقام ومتغيرات حرفية باستخدام عمليات الجمع والطرح والضرب. تتضمن الأعداد الصحيحة أيضًا التعبيرات التي تتضمن القسمة على عدد ما بخلاف الصفر.
مفهوم التعبير المنطقي الكسري
التعبير الكسري هو تعبير رياضي يحتوي أيضًا ، بالإضافة إلى عمليات الجمع والطرح والضرب التي يتم إجراؤها باستخدام الأرقام والمتغيرات الحرفية ، وكذلك القسمة على رقم لا يساوي الصفر ، على تقسيم إلى تعبيرات ذات متغيرات حرفية.
التعابير العقلانية كلها تعبيرات عدد صحيح وكسور. المعادلات المنطقية هي المعادلات التي يمثل جانبها الأيمن والأيسر تعبيرات منطقية. إذا كانت الأجزاء اليمنى واليسرى في المعادلة المنطقية عبارة عن تعبيرات عدد صحيح ، فإن هذه المعادلة المنطقية تسمى عددًا صحيحًا.
إذا كانت الأجزاء اليسرى أو اليمنى في المعادلة المنطقية عبارة عن تعبيرات كسرية ، فإن هذه المعادلة المنطقية تسمى كسور.
أمثلة على التعبيرات المنطقية الكسرية
1.x-3 / x = -6 * x + 19
2. (x-4) / (2 * x + 5) = (x + 7) / (x-2)
3. (x-3) / (x-5) + 1 / x = (x + 5) / (x * (x-5))
مخطط لحل المعادلة المنطقية الكسرية
1. أوجد المقام المشترك لجميع الكسور التي يتم تضمينها في المعادلة.
2. اضرب طرفي المعادلة بالمقام المشترك.
3. حل المعادلة الناتجة.
4. افحص الجذور واستبعد الجذور التي تحول المقام المشترك إلى صفر.
نظرًا لأننا نحل المعادلات المنطقية الكسرية ، فسيكون هناك متغيرات في مقامات الكسور. إذن ، سيكونان في قاسم مشترك. وفي الفقرة الثانية من الخوارزمية ، نضرب في قاسم مشترك ، ثم تظهر الجذور الخارجية. عندما يكون المقام المشترك مساويًا للصفر ، ما يعني أن الضرب به سيكون بلا معنى. لذلك ، في النهاية ، تأكد من التحقق من الجذور التي تم الحصول عليها.
فكر في مثال:
حل معادلة كسرية منطقية: (x-3) / (x-5) + 1 / x = (x + 5) / (x * (x-5)).
سوف نلتزم بالمخطط العام: نجد أولاً المقام المشترك لجميع الكسور. نحصل على x * (x-5).
اضرب كل كسر بمقام مشترك واكتب المعادلة الكاملة الناتجة.
(x-3) / (x-5) * (x * (x-5)) = x * (x + 3) ؛
1 / x * (x * (x-5)) = (x-5) ؛
(x + 5) / (x * (x-5)) * (x * (x-5)) = (x + 5) ؛
س * (س + 3) + (س -5) = (س + 5) ؛
لنبسط المعادلة الناتجة. نحن نحصل:
س ^ 2 + 3 * س + س -5 - س - 5 = 0 ؛
س ^ 2 + 3 * س 10 = 0 ؛
حصلنا على معادلة بسيطة من الدرجة الثانية. نحلها بأي من الطرق المعروفة ، نحصل على الجذور x = -2 و x = 5.
الآن نتحقق من الحلول التي تم الحصول عليها:
نعوض بالعددين -2 و 5 في المقام المشترك. عند x = -2 ، لا يختفي المقام المشترك x * (x-5) ، -2 * (- 2-5) = 14. إذن ، سيكون الرقم -2 هو جذر المعادلة المنطقية الكسرية الأصلية.
عند x = 5 ، يصبح المقام المشترك x * (x-5) صفرًا. لذلك ، هذا الرقم ليس جذر المعادلة المنطقية الكسرية الأصلية ، حيث سيكون هناك قسمة على صفر.
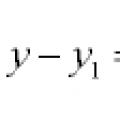 معادلات الخطوط والمنحنيات في المستوى
معادلات الخطوط والمنحنيات في المستوى معادلة متجانسة معممة معادلات متجانسة معممة من الدرجة الثانية
معادلة متجانسة معممة معادلات متجانسة معممة من الدرجة الثانية بفضل الفاصلة يرجع ذلك إلى حقيقة أن في
بفضل الفاصلة يرجع ذلك إلى حقيقة أن في