С това видео започвам дълга поредица от уроци по производни. Този урок се състои от няколко части.

Първо ще ви кажа какво изобщо представляват производните и как да ги броим, но не на изискан академичен език, а по начина, по който аз самият го разбирам и как го обяснявам на студентите си. На второ място ще разгледаме най-простото правило за решаване на задачи, в които ще търсим производни на суми, производни на разлики и производни степенна функция.

Ще разгледаме по-сложни комбинирани примери, от които по-специално ще научите, че подобни задачи, включващи корени и дори дроби, могат да бъдат решени с помощта на формулата за производна на степенна функция. Освен това, разбира се, ще има много проблеми и примери за решения за повечето различни ниватрудности.

Като цяло, първоначално щях да запиша кратко 5-минутно видео, но можете да видите как се получи. Така че стига с текстовете - нека да се заемем с работата.

Какво е дериват?

И така, да започнем отдалече. Преди много години, когато дърветата бяха по-зелени и животът беше по-забавен, математиците мислеха за това: помислете за проста функция, дефинирана от нейната графика, наречете я $y=f\left(x \right)$. Разбира се, графиката не съществува сама по себе си, така че трябва да начертаете осите $x$, както и оста $y$. Сега нека изберем всяка точка от тази графика, абсолютно всяка. Нека наречем абсцисата $((x)_(1))$, ординатата, както може би се досещате, ще бъде $f\left(((x)_(1)) \right)$.

Нека разгледаме друга точка на същата графика. Няма значение кой, важното е да се различава от оригиналния. Отново има абциса, нека я наречем $((x)_(2))$, а също и ордината - $f\left(((x)_(2)) \right)$.

И така, имаме две точки: те имат различни абциси и следователно, различни значенияфункции, въпреки че последното не е задължително. Но това, което е наистина важно, е, че знаем от курса по планиметрия: през две точки можете да начертаете права линия и освен това само една. Така че нека го изпълним.

Сега нека начертаем права линия през първия от тях, успоредна на абсцисната ос. Получаваме правоъгълен триъгълник. Нека го наречем $ABC$, прав ъгъл $C$. Този триъгълник има едно много интересно свойство: факт е, че ъгълът $\alpha $ всъщност, равен на ъгъл, под която правата $AB$ се пресича с продължението на абсцисната ос. Преценете сами:

1. правата $AC$ е успоредна на оста $Ox$ по построение,
2. линия $AB$ пресича $AC$ под $\alpha $,
3. следователно $AB$ пресича $Ox$ под същия $\alpha $.

Какво можем да кажем за $\text( )\!\!\alpha\!\!\text( )$? Нищо конкретно, освен че в триъгълника $ABC$ отношението на катет $BC$ към катет $AC$ е равно на тангенса на същия този ъгъл. Така че нека го запишем:

Разбира се, $AC$ влиза в такъв случайлесен за изчисляване:

По същия начин за $BC$:

С други думи, можем да напишем следното:

\[\operatorname(tg)\text( )\!\!\alpha\!\!\text( )=\frac(f\left(((x)_(2)) \right)-f\left( ((x)_(1)) \right))(((x)_(2))-((x)_(1)))\]

Сега, след като изчистихме всичко това, нека се върнем към нашата графика и да я разгледаме нова точка$B$. Нека изтрием старите стойности и вземем $B$ някъде по-близо до $((x)_(1))$. Нека отново означим неговата абциса с $((x)_(2))$, а ординатата му с $f\left(((x)_(2)) \right)$.

Нека погледнем отново нашия малък триъгълник $ABC$ и $\text( )\!\!\alpha\!\!\text( )$ вътре в него. Съвсем очевидно е, че това ще бъде съвсем различен ъгъл, тангентата също ще бъде различна, тъй като дължините на отсечките $AC$ и $BC$ са се променили значително, но формулата за тангенса на ъгъла не се е променила изобщо - това все още е връзката между промяна във функцията и промяна в аргумента.

И накрая, продължаваме да приближаваме $B$ към първоначалната точка $A$, в резултат на което триъгълникът ще стане още по-малък и правата линия, съдържаща сегмента $AB$, ще изглежда все повече и повече като допирателна към графиката на функцията.

В резултат на това, ако продължим да приближаваме точките една до друга, т.е. намалим разстоянието до нула, тогава правата $AB$ наистина ще се превърне в допирателна към графиката в дадена точка и $\text( )\ !\!\alpha\!\ !\text( )$ ще се трансформира от елемент на правилен триъгълник в ъгъла между допирателната към графиката и положителната посока на оста $Ox$.

И тук плавно преминаваме към дефиницията на $f$, а именно, производната на функция в точката $((x)_(1))$ е тангенса на ъгъла $\alpha $ между допирателната към графика в точката $((x)_( 1))$ и положителната посока на оста $Ox$:

\[(f)"\left(((x)_(1)) \right)=\operatorname(tg)\text( )\!\!\alpha\!\!\text( )\]

Връщайки се към нашата графика, трябва да се отбележи, че всяка точка от графиката може да бъде избрана като $((x)_(1))$. Например, със същия успех бихме могли да премахнем щриха в точката, показана на фигурата.

Нека наречем ъгъла между допирателната и положителната посока на оста $\beta$. Съответно $f$ в $((x)_(2))$ ще бъде равно на тангенса на този ъгъл $\beta $.

\[(f)"\left(((x)_(2)) \right)=tg\text( )\!\!\beta\!\!\text( )\]

Всяка точка на графиката ще има своя собствена допирателна и, следователно, собствена стойност на функцията. Във всеки от тези случаи, в допълнение към точката, в която търсим производната на разликата или сумата, или производната на степенна функция, е необходимо да вземем друга точка, разположена на известно разстояние от нея, и след това да насочи тази точка към първоначалната и, разбира се, разберете как в процеса Такова движение ще промени тангенса на ъгъла на наклон.

Производна на степенна функция

За жалост, подобно определениеИзобщо не сме доволни. Всички тези формули, снимки, ъгли не ни дават ни най-малка представа за това как да изчислим реалната производна в реални проблеми. Затова нека се отклоним малко от формалната дефиниция и да разгледаме по-ефективни формули и техники, с които вече можете да решавате реални проблеми.

Нека започнем с най-простите конструкции, а именно функции от формата $y=((x)^(n))$, т.е. мощностни функции. В този случай можем да напишем следното: $(y)"=n\cdot ((x)^(n-1))$. С други думи, степента, която е в експонентата, е показана в предния множител, а самият показател се намалява с единица. Например:

\[\begin(align)& y=((x)^(2)) \\& (y)"=2\cdot ((x)^(2-1))=2x \\\end(align) \]

Ето още един вариант:

\[\begin(align)& y=((x)^(1)) \\& (y)"=((\left(x \right))^(\prime ))=1\cdot ((x )^(0))=1\cdot 1=1 \\& ((\left(x \right))^(\prime ))=1 \\\end(align)\]

Използвайки тези прости правила, нека се опитаме да премахнем докосването на следните примери:

Така получаваме:

\[((\left(((x)^(6)) \right))^(\prime ))=6\cdot ((x)^(5))=6((x)^(5)) \]

Сега нека решим втория израз:

\[\begin(align)& f\left(x \right)=((x)^(100)) \\& ((\left(((x)^(100)) \right))^(\ просто ))=100\cdot ((x)^(99))=100((x)^(99)) \\\end(align)\]

Разбира се, това бяха много прости задачи. Реалните проблеми обаче са по-сложни и не се ограничават само до степени на функция.

И така, правило №1 - ако една функция е представена под формата на другите две, то производната на тази сума е равна на сумата от производните:

\[((\left(f+g \right))^(\prime ))=(f)"+(g)"\]

По същия начин, производната на разликата на две функции е равна на разликата на производните:

\[((\left(f-g \right))^(\prime ))=(f)"-(g)"\]

\[((\left(((x)^(2))+x \right))^(\prime ))=((\left(((x)^(2)) \right))^(\ просто ))+((\left(x \right))^(\prime ))=2x+1\]

Освен това има още един важно правило: ако някое $f$ е предшествано от константа $c$, по която тази функция се умножава, тогава $f$ на цялата тази конструкция се изчислява, както следва:

\[((\left(c\cdot f \right))^(\prime ))=c\cdot (f)"\]

\[((\left(3((x)^(3)) \right))^(\prime ))=3((\left(((x)^(3)) \right))^(\ просто ))=3\cdot 3((x)^(2))=9((x)^(2))\]

И накрая, още едно много важно правило: в задачите често има отделен член, който изобщо не съдържа $x$. Например, можем да наблюдаваме това в нашите изрази днес. Производната на константа, т.е. число, което не зависи по никакъв начин от $x$, винаги е равна на нула и няма никакво значение на какво е равна константата $c$:

\[((\left(c \right))^(\prime ))=0\]

Примерно решение:

\[((\left(1001 \right))^(\prime ))=((\left(\frac(1)(1000) \right))^(\prime ))=0\]

Отново ключови точки:

1. Производната на сумата от две функции винаги е равна на сумата на производните: $((\left(f+g \right))^(\prime ))=(f)"+(g)"$;
2. По подобни причини производната на разликата на две функции е равна на разликата на две производни: $((\left(f-g \right))^(\prime ))=(f)"-(g)"$;
3. Ако функцията има постоянен фактор, тогава тази константа може да бъде извадена като знак за производна: $((\left(c\cdot f \right))^(\prime ))=c\cdot (f)"$;
4. Ако цялата функция е константа, тогава нейната производна винаги е нула: $((\left(c \right))^(\prime ))=0$.

Нека да видим как работи всичко реални примери. Така:

Записваме:

\[\begin(align)& ((\left(((x)^(5))-3((x)^(2))+7 \right))^(\prime ))=((\left (((x)^(5)) \right))^(\prime ))-((\left(3((x)^(2)) \right))^(\prime ))+(7) "= \\& =5((x)^(4))-3((\left(((x)^(2)) \right))^(\prime ))+0=5((x) ^(4))-6x \\\край (подравняване)\]

В този пример виждаме както производната на сумата, така и производната на разликата. Общо производната е равна на $5((x)^(4))-6x$.

Да преминем към втората функция:

Нека запишем решението:

\[\begin(align)& ((\left(3((x)^(2))-2x+2 \right))^(\prime ))=((\left(3((x)^( 2)) \right))^(\prime ))-((\left(2x \right))^(\prime ))+(2)"= \\& =3((\left(((x) ^(2)) \right))^(\prime ))-2(x)"+0=3\cdot 2x-2\cdot 1=6x-2 \\\end(align)\]

Тук намерихме отговора.

Нека да преминем към третата функция - тя е по-сериозна:

\[\begin(align)& ((\left(2((x)^(3))-3((x)^(2))+\frac(1)(2)x-5 \right)) ^(\prime ))=((\left(2((x)^(3)) \right))^(\prime ))-((\left(3((x)^(2)) \right ))^(\prime ))+((\left(\frac(1)(2)x \right))^(\prime ))-(5)"= \\& =2((\left(( (x)^(3)) \right))^(\prime ))-3((\left(((x)^(2)) \right))^(\prime ))+\frac(1) (2)\cdot (x)"=2\cdot 3((x)^(2))-3\cdot 2x+\frac(1)(2)\cdot 1=6((x)^(2)) -6x+\frac(1)(2) \\\end(align)\]

Намерихме отговора.

Да преминем към последния израз - най-сложният и най-дълъг:

И така, ние считаме:

\[\begin(align)& ((\left(6((x)^(7))-14((x)^(3))+4x+5 \right))^(\prime ))=( (\left(6((x)^(7)) \right))^(\prime ))-((\left(14((x)^(3)) \right))^(\prime )) +((\left(4x \right))^(\prime ))+(5)"= \\& =6\cdot 7\cdot ((x)^(6))-14\cdot 3((x )^(2))+4\cdot 1+0=42((x)^(6))-42((x)^(2))+4 \\\end(align)\]

Но решението не свършва дотук, защото от нас се иска не просто да премахнем щрих, но и да изчислим стойността му в конкретна точка, така че заместваме −1 вместо $x$ в израза:

\[(y)"\left(-1 \right)=42\cdot 1-42\cdot 1+4=4\]

Нека отидем по-далеч и да преминем към още по-сложни и интересни примери. Факт е, че формулата за решаване на степенната производна $((\left(((x)^(n)) \right))^(\prime ))=n\cdot ((x)^(n-1) )$ има още по-широк обхват, отколкото обикновено се смята. С негова помощ можете да решавате примери с дроби, корени и т.н. Това ще направим сега.

Като начало, нека отново запишем формулата, която ще ни помогне да намерим производната на степенна функция:

А сега внимание: досега разглеждахме само $n$ цели числа, обаче нищо не ни пречи да разглеждаме дроби и дори отрицателни числа. Например можем да напишем следното:

\[\begin(align)& \sqrt(x)=((x)^(\frac(1)(2))) \\& ((\left(\sqrt(x) \right))^(\ prime ))=((\left(((x)^(\frac(1)(2))) \right))^(\prime ))=\frac(1)(2)\cdot ((x) ^(-\frac(1)(2)))=\frac(1)(2)\cdot \frac(1)(\sqrt(x))=\frac(1)(2\sqrt(x)) \\\край (подравняване)\]

Нищо сложно, така че нека видим как тази формула ще ни помогне, когато решаваме повече сложни задачи. И така, пример:

Нека запишем решението:

\[\begin(align)& \left(\sqrt(x)+\sqrt(x)+\sqrt(x) \right)=((\left(\sqrt(x) \right))^(\prime ))+((\left(\sqrt(x) \right))^(\prime ))+((\left(\sqrt(x) \right))^(\prime )) \\& ((\ ляво(\sqrt(x) \right))^(\prime ))=\frac(1)(2\sqrt(x)) \\& ((\left(\sqrt(x) \right))^( \prime ))=((\left(((x)^(\frac(1)(3))) \right))^(\prime ))=\frac(1)(3)\cdot ((x )^(-\frac(2)(3)))=\frac(1)(3)\cdot \frac(1)(\sqrt(((x)^(2)))) \\& (( \left(\sqrt(x) \right))^(\prime ))=((\left(((x)^(\frac(1)(4))) \right))^(\prime )) =\frac(1)(4)((x)^(-\frac(3)(4)))=\frac(1)(4)\cdot \frac(1)(\sqrt(((x) ^(3)))) \\\end(align)\]

Нека се върнем към нашия пример и напишем:

\[(y)"=\frac(1)(2\sqrt(x))+\frac(1)(3\sqrt(((x)^(2))))+\frac(1)(4 \sqrt(((x)^(3))))\]

Това е толкова трудно решение.

Да преминем към втория пример - има само два термина, но всеки от тях съдържа както класическа степен, така и корени.

Сега ще научим как да намерим производната на степенна функция, която освен това съдържа корена:

\[\begin(align)& ((\left(((x)^(3))\sqrt(((x)^(2)))+((x)^(7))\sqrt(x) \right))^(\prime ))=((\left(((x)^(3))\cdot \sqrt(((x)^(2))) \right))^(\prime )) =((\left(((x)^(3))\cdot ((x)^(\frac(2)(3))) \right))^(\prime ))= \\& =(( \left(((x)^(3+\frac(2)(3))) \right))^(\prime ))=((\left(((x)^(\frac(11)(3 ))) \right))^(\prime ))=\frac(11)(3)\cdot ((x)^(\frac(8)(3)))=\frac(11)(3)\ cdot ((x)^(2\frac(2)(3)))=\frac(11)(3)\cdot ((x)^(2))\cdot \sqrt(((x)^(2 ))) \\& ((\left(((x)^(7))\cdot \sqrt(x) \right))^(\prime ))=((\left(((x)^(7 ))\cdot ((x)^(\frac(1)(3))) \right))^(\prime ))=((\left(((x)^(7\frac(1)(3) ))) \right))^(\prime ))=7\frac(1)(3)\cdot ((x)^(6\frac(1)(3)))=\frac(22)(3 )\cdot ((x)^(6))\cdot \sqrt(x) \\\end(align)\]

И двата члена са изчислени, остава само да напишем крайния отговор:

\[(y)"=\frac(11)(3)\cdot ((x)^(2))\cdot \sqrt(((x)^(2)))+\frac(22)(3) \cdot ((x)^(6))\cdot \sqrt(x)\]

Намерихме отговора.

Производна на дроб чрез степенна функция

Но възможностите на формулата за решаване на производната на степенна функция не свършват дотук. Факт е, че с негова помощ можете да изчислявате не само примери с корени, но и с дроби. Именно това е рядката възможност, която значително опростява решаването на подобни примери, но често се пренебрегва не само от учениците, но и от учителите.

И така, сега ще се опитаме да комбинираме две формули наведнъж. От една страна, класическата производна на степенна функция

\[((\left(((x)^(n)) \right))^(\prime ))=n\cdot ((x)^(n-1))\]

От друга страна, знаем, че израз от формата $\frac(1)(((x)^(n)))$ може да бъде представен като $((x)^(-n))$. следователно

\[\left(\frac(1)(((x)^(n))) \right)"=((\left(((x)^(-n)) \right))^(\prime ) )=-n\cdot ((x)^(-n-1))=-\frac(n)(((x)^(n+1)))\]

\[((\left(\frac(1)(x) \right))^(\prime ))=\left(((x)^(-1)) \right)=-1\cdot ((x )^(-2))=-\frac(1)(((x)^(2)))\]

По този начин, производни прости дроби, където числителят е константа, а знаменателят е степен, също се изчисляват с помощта на класическа формула. Нека да видим как работи това на практика.

И така, първата функция:

\[((\left(\frac(1)(((x)^(2))) \right))^(\prime ))=((\left(((x)^(-2)) \ дясно))^(\prime ))=-2\cdot ((x)^(-3))=-\frac(2)(((x)^(3)))\]

Първият пример е решен, нека преминем към втория:

\[\begin(align)& ((\left(\frac(7)(4((x)^(4)))-\frac(2)(3((x)^(3)))+\ frac(5)(2)((x)^(2))+2((x)^(3))-3((x)^(4)) \right))^(\prime ))= \ \& =((\left(\frac(7)(4((x)^(4))) \right))^(\prime ))-((\left(\frac(2)(3(( x)^(3))) \right))^(\prime ))+((\left(2((x)^(3)) \right))^(\prime ))-((\left( 3((x)^(4)) \right))^(\prime )) \\& ((\left(\frac(7)(4((x)^(4))) \right))^ (\prime ))=\frac(7)(4)((\left(\frac(1)(((x)^(4))) \right))^(\prime ))=\frac(7 )(4)\cdot ((\left(((x)^(-4)) \right))^(\prime ))=\frac(7)(4)\cdot \left(-4 \right) \cdot ((x)^(-5))=\frac(-7)(((x)^(5))) \\& ((\left(\frac(2)(3((x)^ (3))) \right))^(\prime ))=\frac(2)(3)\cdot ((\left(\frac(1)(((x)^(3))) \right) )^(\prime ))=\frac(2)(3)\cdot ((\left(((x)^(-3)) \right))^(\prime ))=\frac(2)( 3)\cdot \left(-3 \right)\cdot ((x)^(-4))=\frac(-2)(((x)^(4))) \\& ((\left( \frac(5)(2)((x)^(2)) \right))^(\prime ))=\frac(5)(2)\cdot 2x=5x \\& ((\left(2) ((x)^(3)) \right))^(\prime ))=2\cdot 3((x)^(2))=6((x)^(2)) \\& ((\ ляво(3((x)^(4)) \right))^(\prime ))=3\cdot 4((x)^(3))=12((x)^(3)) \\\ край (подравняване)\]...

Сега събираме всички тези термини в една формула:

\[(y)"=-\frac(7)(((x)^(5)))+\frac(2)(((x)^(4)))+5x+6((x)^ (2))-12((x)^(3))\]

Получихме отговор.

Въпреки това, преди да продължа, бих искал да насоча вниманието ви към формата на писане на самите оригинални изрази: в първия израз написахме $f\left(x \right)=...$, във втория: $y =...$ Много ученици се губят, когато видят различни формизаписи. Каква е разликата между $f\left(x \right)$ и $y$? Наистина нищо. Това са просто различни записи с едно и също значение. Просто когато кажем $f\left(x \right)$, тогава ние говорим за, на първо място, за функция, а когато говорим за $y$, най-често имаме предвид графиката на функция. В противен случай това е едно и също нещо, т.е. производната и в двата случая се счита за една и съща.

Комплексни задачи с производни

В заключение бих искал да разгледам няколко сложни комбинирани задачи, които използват всичко, което разгледахме днес. Те съдържат корени, дроби и суми. Тези примери обаче ще бъдат сложни само в днешния видео урок, защото наистина сложни производни функции ще ви очакват напред.

И така, финалната част на днешния видео урок, състоящ се от две комбинирани задачи. Да започнем с първия от тях:

\[\begin(align)& ((\left(((x)^(3))-\frac(1)(((x)^(3)))+\sqrt(x) \right))^ (\prime ))=((\left(((x)^(3)) \right))^(\prime ))-((\left(\frac(1)(((x)^(3) )) \right))^(\prime ))+\left(\sqrt(x) \right) \\& ((\left(((x)^(3)) \right))^(\prime ) )=3((x)^(2)) \\& ((\left(\frac(1)(((x)^(3))) \right))^(\prime ))=((\ ляво(((x)^(-3)) \right))^(\prime ))=-3\cdot ((x)^(-4))=-\frac(3)(((x)^ (4))) \\& ((\left(\sqrt(x) \right))^(\prime ))=((\left(((x)^(\frac(1)(3))) \right))^(\prime ))=\frac(1)(3)\cdot \frac(1)(((x)^(\frac(2)(3))))=\frac(1) (3\sqrt(((x)^(2)))) \\\end(align)\]

Производната на функцията е равна на:

\[(y)"=3((x)^(2))-\frac(3)(((x)^(4)))+\frac(1)(3\sqrt(((x)^ (2))))\]

Първият пример е решен. Нека разгледаме втория проблем:

Във втория пример процедираме по подобен начин:

\[((\left(-\frac(2)(((x)^(4)))+\sqrt(x)+\frac(4)(x\sqrt(((x)^(3)) )) \right))^(\prime ))=((\left(-\frac(2)(((x)^(4))) \right))^(\prime ))+((\left (\sqrt(x) \right))^(\prime ))+((\left(\frac(4)(x\cdot \sqrt(((x)^(3)))) \right))^ (\prime ))\]

Нека изчислим всеки член поотделно:

\[\begin(align)& ((\left(-\frac(2)(((x)^(4))) \right))^(\prime ))=-2\cdot ((\left( ((x)^(-4)) \right))^(\prime ))=-2\cdot \left(-4 \right)\cdot ((x)^(-5))=\frac(8 )(((x)^(5))) \\& ((\left(\sqrt(x) \right))^(\prime ))=((\left(((x)^(\frac( 1)(4))) \right))^(\prime ))=\frac(1)(4)\cdot ((x)^(-\frac(3)(4)))=\frac(1 )(4\cdot ((x)^(\frac(3)(4))))=\frac(1)(4\sqrt(((x)^(3)))) \\& ((\ ляво(\frac(4)(x\cdot \sqrt(((x)^(3)))) \right))^(\prime ))=((\left(\frac(4)(x\cdot) ((x)^(\frac(3)(4)))) \right))^(\prime ))=((\left(\frac(4)(((x)^(1\frac(3) )(4)))) \right))^(\prime ))=4\cdot ((\left(((x)^(-1\frac(3)(4))) \right))^( \prime ))= \\& =4\cdot \left(-1\frac(3)(4) \right)\cdot ((x)^(-2\frac(3)(4)))=4 \cdot \left(-\frac(7)(4) \right)\cdot \frac(1)(((x)^(2\frac(3)(4))))=\frac(-7) (((x)^(2))\cdot ((x)^(\frac(3)(4))))=-\frac(7)(((x)^(2))\cdot \sqrt (((x)^(3)))) \\\end(align)\]

Всички условия са изчислени. Сега се връщаме към първоначалната формула и събираме и трите члена заедно. Получаваме, че крайният отговор ще бъде така:

\[(y)"=\frac(8)(((x)^(5)))+\frac(1)(4\sqrt(((x)^(3))))-\frac(7 )(((x)^(2))\cdot \sqrt(((x)^(3))))\]

И това е всичко. Това беше първият ни урок. В следващите уроци ще разгледаме по-сложни конструкции и също така ще разберем защо са необходими производни на първо място.

Производно изчисляване- един от най важни операции V диференциално смятане. По-долу има таблица за намиране на производни прости функции. | Повече ▼ сложни правиладиференциация, вижте други уроци:

• Таблица с производни на експоненциални и логаритмични функции

Използвайте дадените формули като референтни стойности. Те ще ви помогнат да решите диференциални уравненияи задачи. На снимката, в таблицата с производни на прости функции, има „мамски лист“ на основните случаи на намиране на производна във форма, която е разбираема за използване, до него има обяснения за всеки случай.

Производни на прости функции

1. Производната на число е нула
с´ = 0
Пример:
5´ = 0

Обяснение:
Производната показва скоростта, с която се променя стойността на функция, когато нейният аргумент се промени. Тъй като числото не се променя по никакъв начин при никакви условия, скоростта на промяната му винаги е нула.

2. Производна на променливаравно на едно
x´ = 1

Обяснение:
С всяко увеличение на аргумент (x) с единица, стойността на функцията (резултатът от изчисленията) се увеличава със същото количество. По този начин скоростта на промяна на стойността на функцията y = x е точно равна на скоростта на промяна на стойността на аргумента.

3. Производната на променлива и фактор е равна на този фактор
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Обяснение:
В този случай всеки път, когато аргументът на функцията се промени ( х) неговата стойност (y) нараства в сведнъж. По този начин скоростта на промяна на стойността на функцията по отношение на скоростта на промяна на аргумента е точно равна на стойността с.

Откъдето следва, че
(cx + b)" = c
тоест диференциалът на линейната функция y=kx+b е равен на наклоннаклон на правата (k).

4. Производна по модул на променливаравно на частното на тази променлива спрямо нейния модул
|x|"= x / |x| при условие, че x ≠ 0
Обяснение:
Тъй като производната на променлива (вижте формула 2) е равна на единица, производната на модула се различава само по това, че стойността на скоростта на промяна на функцията се променя на противоположната при пресичане на началната точка (опитайте да начертаете графика на функцията y = |x| и вижте сами каква е стойността и връща израза x / |x|< 0 оно равно (-1), а когда x >0 - едно. Тоест, когато отрицателни стойностипроменлива x, при всяко увеличаване на аргумента стойността на функцията намалява с точно същата стойност, а за положителните, напротив, се увеличава, но с точно същата стойност.

5. Производна на променлива на степенравно на произведението на число на тази степен и променлива на степен, намалена с единица
(x c)"= cx c-1, при условие че x c и cx c-1 са дефинирани и c ≠ 0
Пример:
(x 2)" = 2x
(x 3)" = 3x 2
За запомняне на формулата:
Преместете степента на променливата надолу като фактор и след това намалете самата степен с единица. Например, за x 2 - двете бяха пред x и тогава намалената мощност (2-1 = 1) просто ни даде 2x. Същото се случи и с x 3 - „преместваме“ тройката надолу, намаляваме я с единица и вместо куб имаме квадрат, тоест 3x 2. Малко "ненаучно", но много лесно за запомняне.

6.Производна на дроб 1/x
(1/x)" = - 1 / x 2
Пример:
Тъй като една дроб може да бъде представена като повдигане на отрицателна степен
(1/x)" = (x -1)", тогава можете да приложите формулата от правило 5 от таблицата с производни
(x -1)" = -1x -2 = - 1 / x 2

7. Производна на дроб с променлива с произволна степенв знаменателя
(1 / x c)" = - c / x c+1
Пример:
(1 / x 2)" = - 2 / x 3

8. Производна на корена(производно на променлива под квадратен корен)
(√x)" = 1 / (2√x)или 1/2 x -1/2
Пример:
(√x)" = (x 1/2)" означава, че можете да приложите формулата от правило 5
(x 1/2)" = 1/2 x -1/2 = 1 / (2√x)

9. Производна на променлива под корена на произволна степен
(n √x)" = 1 / (n n √x n-1)

Операцията за намиране на производната се нарича диференциране.

В резултат на решаването на задачи за намиране на производни на най-простите (и не много прости) функции чрез дефиниране на производната като граница на съотношението на увеличението към увеличението на аргумента, се появи таблица с производни и точно определени правила за диференциране . Първите, които работят в областта на намирането на производни, са Исак Нютон (1643-1727) и Готфрид Вилхелм Лайбниц (1646-1716).

Следователно, в наше време, за да намерите производната на която и да е функция, не е необходимо да изчислявате горепосочената граница на съотношението на увеличението на функцията към увеличението на аргумента, а трябва само да използвате таблицата на производни и правилата за диференциране. Следният алгоритъм е подходящ за намиране на производната.

За намиране на производната, имате нужда от израз под главния знак разделят прости функции на компонентии определя какви действия (продукт, сбор, частно)тези функции са свързани. Допълнителни производни елементарни функциинамираме в таблицата с производните, а формулите за производните на произведението, сумата и частното са в правилата за диференциране. Таблицата за производни и правилата за диференциране са дадени след първите два примера.

Пример 1.Намерете производната на функция

Решение. От правилата за диференциране откриваме, че производната на сума от функции е сумата от производните на функциите, т.е.

От таблицата на производните откриваме, че производната на "х" е равна на единица, а производната на синус е равна на косинус. Ние заместваме тези стойности в сумата от производните и намираме производната, изисквана от условието на проблема:

Пример 2.Намерете производната на функция

Решение. Ние диференцираме като производна на сума, в която вторият член има постоянен фактор, той може да бъде изваден от знака на производната:

Ако все пак възникнат въпроси за това откъде идва нещо, те обикновено се изясняват след запознаване с таблицата на производните и най-простите правила за диференциране. В момента преминаваме към тях.

Таблица с производни на прости функции

1. Производна на константа (число). Всяко число (1, 2, 5, 200...), което е в израза на функцията. Винаги равно на нула. Това е много важно да запомните, тъй като се изисква много често
2. Производна на независимата променлива. Най-често "Х". Винаги равно на едно. Това също е важно да запомните за дълго време
3. Производна на степен. Когато решавате задачи, трябва да преобразувате неквадратни корени в степени.
4. Производна на променлива на степен -1
5. Производна на квадратен корен
6. Производна на синус
7. Производна на косинус
8. Производна на тангенс
9. Производна на котангенс
10. Производна на арксинус
11. Производна на аркосинус
12. Производна на арктангенс
13. Производна на аркотангенс
14. Производна на натурален логаритъм
15. Производна на логаритмична функция
16. Производна на показателя
17. Производна експоненциална функция

Правила за диференциране

1. Производна на сбор или разлика
2. Производна на продукта
2а. Производна на израз, умножен по постоянен множител
3. Производна на частното
4. Производна на сложна функция

Правило 1.Ако функциите

са диференцируеми в дадена точка, тогава функциите са диференцируеми в същата точка

и

тези. производната на алгебричната сума от функции е равна на алгебрична сумапроизводни на тези функции.

Последица. Ако две диференцируеми функции се различават с постоянен член, тогава техните производни са равни, т.е.

Правило 2.Ако функциите

са диференцируеми в дадена точка, тогава техният продукт е диференцируем в същата точка

и

тези. Производната на произведението на две функции е равна на сумата от произведенията на всяка от тези функции и производната на другата.

Следствие 1. Постоянният фактор може да бъде изваден от знака на производната:

Следствие 2. Производната на произведението на няколко диференцируеми функции е равна на сумата от произведенията на производната на всеки фактор и всички останали.

Например за три множителя:

Правило 3.Ако функциите

диференцируеми в даден момент И , тогава в тази точка тяхното частно също е диференцируемоu/v и

тези. производната на частното на две функции е равна на дроб, чийто числител е разликата между произведенията на знаменателя и производната на числителя и числителя и производната на знаменателя, а знаменателят е квадратът на бившият числител.

Къде да търсите неща на други страници

При намиране на производната на произведение и частно в реални задачи винаги е необходимо да се прилагат няколко правила за диференциране наведнъж, така че в статията има повече примери за тези производни"Производна на произведение и частно на функции".

Коментирайте.Не трябва да бъркате константа (т.е. число) като член в сума и като постоянен фактор! При член производната му е равна на нула, а при постоянен множител се изважда от знака на производните. Това типична грешка, което се случва на начална фазаучат производни, но тъй като решават няколко примера от една и две части, средният ученик вече не прави тази грешка.

И ако, когато диференцирате продукт или коефициент, имате член u"v, в който u- число, например 2 или 5, тоест константа, тогава производната на това число ще бъде равна на нула и следователно целият термин ще бъде равен на нула (този случай е разгледан в пример 10).

Друга често срещана грешка е механичното решаване на производната на сложна функция като производна на проста функция. Ето защо производна на сложна функцияе посветена отделна статия. Но първо ще се научим да намираме производни на прости функции.

По пътя не можете да правите без трансформиране на изрази. За да направите това, може да се наложи да отворите ръководството в нови прозорци. Действия със сили и корениИ Действия с дроби .

Ако търсите решения за производни на дроби със степени и корени, т.е. когато функцията изглежда като , след това следвайте урока „Производна на суми от дроби със степени и корени.“

Ако имате задача като , тогава ще вземете урока „Производни на прости тригонометрични функции“.

Примери стъпка по стъпка - как да намерим производната

Пример 3.Намерете производната на функция

Решение. Дефинираме частите на израза на функцията: целият израз представлява продукт, а неговите множители са суми, във втория от които един от членовете съдържа постоянен множител. Прилагаме правилото за диференциране на продукта: производната на произведението на две функции е равна на сумата от произведенията на всяка от тези функции по производната на другата:

След това прилагаме правилото за диференциране на сумата: производната на алгебрична сума от функции е равна на алгебричната сума на производните на тези функции. В нашия случай във всеки сбор вторият член има знак минус. Във всяка сума виждаме както независима променлива, чиято производна е равна на единица, така и константа (число), чиято производна е равна на нула. И така, "X" се превръща в едно, а минус 5 се превръща в нула. Във втория израз "x" се умножава по 2, така че ние умножаваме две по същата единица като производната на "x". Получаваме следните стойностипроизводни:

Заместваме намерените производни в сумата от продуктите и получаваме производната на цялата функция, изисквана от условието на проблема:

Пример 4.Намерете производната на функция

Решение. От нас се изисква да намерим производната на частното. Прилагаме формулата за диференциране на частното: производната на частното на две функции е равна на дроб, чийто числител е разликата между произведенията на знаменателя и производната на числителя и числителя и производната на знаменател, а знаменателят е квадрат на предишния числител. Получаваме:

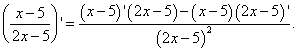
Вече намерихме производната на множителите в числителя в пример 2. Нека също така не забравяме, че произведението, което е вторият множител в числителя в настоящия пример, се приема със знак минус:

Ако търсите решения на задачи, в които трябва да намерите производната на функция, където има непрекъсната купчина корени и степени, като например , тогава добре дошли в класа "Производна на суми от дроби със степени и корени" .

Ако трябва да научите повече за производните на синуси, косинуси, тангенс и други тригонометрични функции, тоест когато функцията изглежда така , тогава урок за вас "Производни на прости тригонометрични функции" .

Пример 5.Намерете производната на функция

Решение. В тази функция виждаме продукт, един от факторите на който е Корен квадратенот независимата променлива, чиято производна видяхме в таблицата с производни. Според правилото за диференциране на продукта и таблична стойностпроизводна на корен квадратен получаваме:

Пример 6.Намерете производната на функция

Решение. В тази функция виждаме частно, чийто дивидент е корен квадратен от независимата променлива. Използвайки правилото за диференциране на частните, което повторихме и приложихме в пример 4, и табличната стойност на производната на квадратния корен, получаваме:

За да се отървете от дроб в числителя, умножете числителя и знаменателя по .

На което анализирахме най-простите производни, а също така се запознахме с правилата за диференциране и някои технически методинамиране на производни. Така че, ако не сте много добри с производните на функции или някои точки в тази статия не са напълно ясни, тогава първо прочетете горния урок. Моля, задайте сериозно настроение - материалът не е прост, но все пак ще се опитам да го представя просто и ясно.

На практика трябва да се справяте с производната на сложна функция много често, дори бих казал, почти винаги, когато ви дават задачи да намирате производни.

Разглеждаме таблицата на правилото (№ 5) за разграничаване на сложна функция:

Нека да го разберем. Първо, нека обърнем внимание на влизането. Тук имаме две функции - и , като функцията, образно казано, е вложена във функцията . Функция от този тип (когато една функция е вложена в друга) се нарича сложна функция.

Ще извикам функцията външна функция, и функцията – вътрешна (или вложена) функция.

! Тези определения не са теоретични и не трябва да присъстват в окончателния дизайн на задачите. Използвам неофициални изрази „външна функция“, „вътрешна“ функция само за да ви улесня при разбирането на материала.

За да изясните ситуацията, помислете за:

Пример 1

Намерете производната на функция

Под синуса имаме не само буквата „X“, а цял израз, така че намирането на производната веднага от таблицата няма да работи. Също така забелязваме, че тук е невъзможно да се приложат първите четири правила, изглежда има разлика, но факт е, че синусът не може да бъде „разкъсан на парчета“:

IN в този примерВече интуитивно става ясно от моите обяснения, че функцията е сложна функция, а полиномът е вътрешна функция (вграждане) и е външна функция.

Първа стъпкатова, което трябва да направите, когато намирате производната на сложна функция, е да разбере коя функция е вътрешна и коя е външна.

Кога прости примериИзглежда ясно, че под синуса е вграден полином. Но какво ще стане, ако всичко не е очевидно? Как точно да определим коя функция е външна и коя вътрешна? За да направите това, предлагам да използвате следната техника, която може да се направи наум или на чернова.

Нека си представим, че трябва да изчислим стойността на израза при на калкулатор (вместо единица може да има произволно число).

Какво ще изчислим първо? Преди всичкоще трябва да извършите следното действие: , следователно полиномът ще бъде вътрешна функция:

Второще трябва да се намери, така че синус – ще бъде външна функция:

След като ние ПРОДАДЕНОс вътрешни и външни функции е време да приложите правилото за диференциране на сложни функции .

Да започнем да решаваме. От урока Как да намерим производната?ние помним, че дизайнът на решение за всяка производна винаги започва така - затваряме израза в скоби и поставяме черта горе вдясно:

Първонамираме производната на външната функция (синус), погледнете таблицата с производни на елементарни функции и забележете, че . Всички таблични формули са приложими и ако „x“ се замени със сложен израз, в такъв случай:

Моля, имайте предвид, че вътрешната функция не се е променило, не го пипаме.

Е, това е съвсем очевидно

Резултатът от прилагането на формулата в окончателния си вид изглежда така:

Константният фактор обикновено се поставя в началото на израза:

Ако има някакво недоразумение, запишете решението на хартия и прочетете отново обясненията.

Пример 2

Намерете производната на функция

Пример 3

Намерете производната на функция

Както винаги, ние записваме:

Нека разберем къде имаме външна функция и къде имаме вътрешна. За да направим това, ние се опитваме (мислено или в чернова) да изчислим стойността на израза при . Какво трябва да направите първо? Първо, трябва да изчислите на какво е равна основата: следователно полиномът е вътрешната функция:

И едва тогава се извършва степенуването, следователно степенната функция е външна функция:

Според формулата , първо трябва да намерите производната на външната функция, в този случай степента. Търси се в таблицата необходимата формула: . Пак повтаряме: всяка таблична формула е валидна не само за „X“, но и за сложен израз. По този начин резултатът от прилагането на правилото за диференциране на сложна функция следващия:

Отново подчертавам, че когато вземем производната на външната функция, нашата вътрешна функция не се променя:

Сега всичко, което остава, е да се намери много проста производна на вътрешната функция и да се промени малко резултата:

Пример 4

Намерете производната на функция

Това е пример за независимо решение(отговор в края на урока).

За да консолидирам вашето разбиране за производната на сложна функция, ще дам пример без коментари, опитайте се да го разберете сами, помислете къде е външната и къде вътрешната функция, защо задачите се решават по този начин?

Пример 5

а) Намерете производната на функцията

б) Намерете производната на функцията

Пример 6

Намерете производната на функция

Тук имаме корен и за да разграничим корена, той трябва да бъде представен като степен. Така първо привеждаме функцията във формата, подходяща за диференциране:

Анализирайки функцията, стигаме до извода, че сумата от трите члена е вътрешна функция, а повдигането на степен е външна функция. Прилагаме правилото за диференциране на сложни функции :

Отново представяме степента като радикал (корен), а за производната на вътрешната функция прилагаме просто правило за диференциране на сумата:

Готов. Можете също да дадете израза в скоби на общ знаменатели запишете всичко като една дроб. Красиво е, разбира се, но когато получите тромави дълги производни, е по-добре да не правите това (лесно е да се объркате, да направите ненужна грешка и ще бъде неудобно за учителя да проверява).

Пример 7

Намерете производната на функция

Това е пример, който можете да решите сами (отговорете в края на урока).

Интересно е да се отбележи, че понякога вместо правилото за диференциране на сложна функция можете да използвате правилото за диференциране на частно , но такова решение ще изглежда като необичайно извращение. Ето типичен пример:

Пример 8

Намерете производната на функция

Тук можете да използвате правилото за диференциране на частното , но е много по-изгодно да се намери производната чрез правилото за диференциране на сложна функция:

Подготвяме функцията за диференциране - преместваме минуса от знака за производна и повдигаме косинуса в числителя:

Косинусът е вътрешна функция, степенуването е външна функция.
Нека използваме нашето правило :

Намираме производната на вътрешната функция и нулираме косинуса обратно надолу:

Готов. В разглеждания пример е важно да не се объркате в знаците. Между другото, опитайте се да го решите с помощта на правилото , отговорите трябва да съвпадат.

Пример 9

Намерете производната на функция

Това е пример, който можете да решите сами (отговорете в края на урока).

Досега разглеждахме случаи, в които имахме само едно влагане в сложна функция. В практическите задачи често можете да намерите производни, където, подобно на кукли, една в друга, 3 или дори 4-5 функции са вложени наведнъж.

Пример 10

Намерете производната на функция

Нека разберем прикачените файлове на тази функция. Нека се опитаме да изчислим израза, като използваме експерименталната стойност. Как ще разчитаме на калкулатор?

Първо трябва да намерите , което означава, че арксинусът е най-дълбокото вграждане:

След това този арксинус от едно трябва да бъде повдигнат на квадрат:

И накрая, повдигаме седем на степен:

Тоест в този пример имаме три различни функциии две вграждания, като най-вътрешната функция е арксинусът, а най-външната функция е експоненциалната функция.

Да започнем да решаваме

Според правилото Първо трябва да вземете производната на външната функция. Разглеждаме таблицата с производни и намираме производната на експоненциалната функция: Единствената разлика е, че вместо “x” имаме сложен израз, което не отрича валидността на тази формула. И така, резултатът от прилагането на правилото за диференциране на сложна функция следващия.

Първо ниво

Производна на функция. Изчерпателно ръководство (2019)

Нека си представим прав път, минаващ през хълмиста местност. Тоест върви нагоре и надолу, но не завива надясно или наляво. Ако оста е насочена хоризонтално по протежение на пътя и вертикално, тогава линията на пътя ще бъде много подобна на графиката на някаква непрекъсната функция:

Оста е определено ниво на нулева надморска височина; в живота ние използваме морското ниво като него.

Докато се движим напред по такъв път, ние също се движим нагоре или надолу. Можем също да кажем: когато аргументът се промени (движение по абсцисната ос), стойността на функцията се променя (движение по ординатната ос). Сега нека помислим как да определим „стръмността“ на нашия път? Каква стойност може да бъде това? Много е просто: колко се променя височината, когато се движите напред определено разстояние. Наистина, на различни участъци от пътя, движейки се напред (по оста x) с един километър, ще се издигаме или падаме с различни количестваметра спрямо морското равнище (по ординатната ос).

Нека обозначим напредъка (прочетете „делта x“).

Гръцката буква (делта) обикновено се използва в математиката като префикс, означаващ "промяна". Тоест - това е промяна в количеството, - промяна; тогава какво е? Точно така, промяна в големината.

Важно: изразът е едно цяло, една променлива. Никога не отделяйте "делта" от "х" или друга буква! Това е, например,.

И така, ние се придвижихме напред, хоризонтално, с. Ако сравним линията на пътя с графиката на функцията, тогава как ще означим издигането? Разбира се,. Тоест, докато вървим напред, се издигаме по-високо.

Стойността е лесна за изчисляване: ако в началото сме били на височина и след преместване сме се озовали на височина, тогава. Ако крайната точка е по-ниска от началната, тя ще бъде отрицателна - това означава, че не се изкачваме, а слизаме.

Да се ​​върнем към "стръмнина": това е стойност, която показва колко (стръмно) се увеличава височината, когато се движите напред с една единица разстояние:

Да приемем, че на някакъв участък от пътя, при движение напред с километър, пътят се издига с километър. Тогава наклонът на това място е равен. И ако пътят, докато се движи напред с m, падна с km? Тогава наклонът е равен.

Сега нека погледнем върха на един хълм. Ако вземете началото на участъка на половин километър преди върха и края на половин километър след него, можете да видите, че височината е почти същата.

Тоест, според нашата логика се оказва, че наклонът тук е почти равен на нула, което явно не е вярно. Само на разстояние от километри много може да се промени. По-малките площи трябва да се обмислят за по-адекватни и точна оценкастръмност. Например, ако измервате промяната във височината, докато се движите с един метър, резултатът ще бъде много по-точен. Но дори тази точност може да не ни е достатъчна - в крайна сметка, ако има стълб по средата на пътя, можем просто да го подминем. Какво разстояние да изберем тогава? сантиметър? Милиметър? По-малко е по-добре!

IN Истински животИзмерването на разстояния до най-близкия милиметър е повече от достатъчно. Но математиците винаги се стремят към съвършенство. Следователно концепцията е измислена безкрайно малък, тоест абсолютната стойност е по-малка от всяко число, което можем да назовем. Например, казвате: една трилионна! Колко по-малко? И разделяте това число на - и ще бъде още по-малко. И така нататък. Ако искаме да напишем, че дадено количество е безкрайно малко, пишем така: (четем „х клони към нула“). Много е важно да се разбере че това число не е нула!Но много близо до него. Това означава, че можете да разделите по него.

Концепцията, противоположна на безкрайно малкото, е безкрайно голямо (). Вероятно вече сте го срещали, когато сте работили върху неравенства: това число е по модул по-голямо от всяко число, за което можете да се сетите. Ако излезете с възможно най-голямото число, просто го умножете по две и ще получите още по-голямо число. И още безкрайност освен товакакво ще се случи. Всъщност безкрайно голямото и безкрайно малкото са обратни едно на друго, тоест at, и обратно: at.

Сега да се върнем на нашия път. Идеално изчисленият наклон е наклонът, изчислен за безкрайно малък сегмент от пътя, тоест:

Отбелязвам, че при безкрайно малко преместване промяната във височината също ще бъде безкрайно малка. Но нека ви напомня, че безкрайно малко не означава равно на нула. Ако разделите безкрайно малки числа едно на друго, можете да получите съвсем обикновено число, например . Тоест една малка стойност може да бъде точно пъти по-голяма от друга.

За какво е всичко това? Пътят, стръмнината... Не ходим на автомобилно рали, но учим математика. И в математиката всичко е абсолютно същото, само се нарича по различен начин.

Понятие за производна

Производната на функция е отношението на нарастването на функцията към нарастването на аргумента за безкрайно малко увеличение на аргумента.

Постепеннов математиката те наричат ​​промяна. Извиква се степента, до която аргументът () се променя, докато се движи по оста увеличение на аргументаи се обозначава Колко се е променила функцията (височината) при движение напред по оста с разстояние се нарича увеличение на функциятаи е обозначен.

И така, производната на функция е съотношението към кога. Производната означаваме със същата буква като функцията, само че с просто число горе вдясно: или просто. И така, нека напишем формулата за производна, използвайки тези обозначения:

Както и в аналогията с пътя, тук при нарастване на функцията производната е положителна, а при намаляване е отрицателна.

Може ли производната да е равна на нула? Със сигурност. Например, ако се движим по равен хоризонтален път, стръмността е нула. И това е вярно, височината изобщо не се променя. Същото с производната: производна постоянна функция(константи) е равно на нула:

тъй като увеличението на такава функция е равно на нула за всяка.

Нека си спомним примера на върха на хълма. Оказа се, че е възможно да се подредят краищата на сегмента различни страниотгоре, така че височината в краищата да е еднаква, т.е. сегментът да е успореден на оста:

Но големите сегменти са знак за неточно измерване. Ще повдигнем нашия сегмент нагоре успоредно на себе си, след което дължината му ще намалее.

В крайна сметка, когато сме безкрайно близо до върха, дължината на сегмента ще стане безкрайно малка. Но в същото време тя остава успоредна на оста, тоест разликата във височините в нейните краища е равна на нула (не клони към, но е равна). Така че производното

Това може да се разбере по следния начин: когато стоим на самия връх, едно малко изместване наляво или надясно променя височината ни незначително.

Има и чисто алгебрично обяснение: вляво от върха функцията нараства, а вдясно намалява. Както разбрахме по-рано, когато една функция расте, производната е положителна, а когато намалява, тя е отрицателна. Но се променя плавно, без скокове (тъй като пътят никъде не променя рязко наклона си). Следователно между отрицателни и положителни стойностиопределено трябва да има. То ще бъде там, където функцията нито нараства, нито намалява - в точката на върха.

Същото важи и за дъното (областта, където функцията отляво намалява, а отдясно се увеличава):

Още малко за увеличенията.

Така че променяме аргумента на величина. Променяме от каква стойност? В какво се превърна (аргументът) сега? Можем да изберем всяка точка и сега ще танцуваме от нея.

Помислете за точка с координата. Стойността на функцията в него е равна. След това правим същото увеличение: увеличаваме координатата с. Сега какво? равен аргумент? Много лесно: . Каква е стойността на функцията сега? Където отива аргументът, отива и функцията: . Какво ще кажете за увеличаване на функцията? Нищо ново: това все още е сумата, с която функцията се е променила:

Практикувайте намирането на увеличения:

1. Намерете увеличението на функцията в точка, когато увеличението на аргумента е равно на.
2. Същото важи и за функцията в точка.

Решения:

IN различни точкипри едно и също увеличение на аргумента увеличението на функцията ще бъде различно. Това означава, че производната във всяка точка е различна (обсъдихме това в самото начало - стръмността на пътя е различна в различните точки). Следователно, когато пишем производна, трябва да посочим в кой момент:

Силова функция.

Степенна функция е функция, при която аргументът е до известна степен (логичен, нали?).

Нещо повече - във всякаква степен: .

Най-простият случай- това е, когато показателят:

Нека намерим производната му в точка. Нека си припомним дефиницията на производна:

Така аргументът се променя от на. Колко е нарастването на функцията?

Увеличението е това. Но функция във всяка точка е равна на своя аргумент. Ето защо:

Производната е равна на:

Производната на е равна на:

б) Сега помислете квадратична функция (): .

Сега нека си припомним това. Това означава, че стойността на увеличението може да бъде пренебрегната, тъй като е безкрайно малка и следователно незначителна на фона на другия член:

И така, измислихме друго правило:

в) Продължаваме логическия ред: .

Този израз може да бъде опростен по различни начини: отворете първата скоба, като използвате формулата за съкратено умножение на куба на сбора, или разложете на множители целия израз, като използвате формулата за разликата на кубовете. Опитайте се да го направите сами, като използвате някой от предложените методи.

И така, получих следното:

И отново нека си припомним това. Това означава, че можем да пренебрегнем всички термини, съдържащи:

Получаваме: .

г) Подобни правила могат да бъдат получени за големи мощности:

д) Оказва се, че това правило може да се обобщи за степенна функция с произволен показател, дори не цяло число:

(2)

Правилото може да се формулира с думите: „степента се изнася напред като коефициент и след това се намалява с .“

Ще докажем това правило по-късно (почти в самия край). Сега нека да разгледаме няколко примера. Намерете производната на функциите:

1. (по два начина: чрез формула и чрез определението за производна - чрез изчисляване на приращението на функцията);

1. . Вярвате или не, това е мощностна функция. Ако имате въпроси като „Как е това? Къде е дипломата?“, помнете темата „“!
   Да, да, коренът също е степен, само дробна: .
   Това означава, че нашият квадратен корен е просто степен с показател:
   .
   Търсим производната, използвайки наскоро научената формула:

   Ако в този момент пак стане неясно повторете темата “”!!! (относно степен с отрицателен показател)

2. . Сега степента:

   А сега през дефиницията (забравили ли сте още?):
   ;
   .
   Сега, както обикновено, пренебрегваме термина, съдържащ:
   .

3. . Комбинация от предишни случаи: .

Тригонометрични функции.

Тук ще използваме един факт от висшата математика:

С израз.

Ще научите доказателството през първата година на института (и за да стигнете до там, трябва да издържите добре Единния държавен изпит). Сега просто ще го покажа графично:

Виждаме, че когато функцията не съществува - точката от графиката се изрязва. Но колкото по-близо до стойността, толкова по-близо е функцията до това.

Освен това можете да проверите това правило с помощта на калкулатор. Да, да, не се срамувайте, вземете калкулатор, все още не сме на Единния държавен изпит.

И така, нека опитаме: ;

Не забравяйте да превключите калкулатора си в режим на радиани!

и т.н. Виждаме, че колкото по-малък е, толкова по-близо е стойността на отношението до.

а) Разгледайте функцията. Както обикновено, нека намерим нарастването му:

Нека превърнем разликата на синусите в произведение. За целта използваме формулата (запомнете темата „”): .

Сега производното:

Да направим замяна: . Тогава за безкрайно малко също е безкрайно малко: . Изразът за приема формата:

И сега си спомняме това с израза. И също така, какво ще стане, ако едно безкрайно малко количество може да бъде пренебрегнато в сумата (тоест at).

И така, получаваме следното правило: производната на синуса е равна на косинуса:

Това са основни („таблични“) производни. Ето ги в един списък:

По-късно ще добавим още няколко към тях, но тези са най-важните, тъй като се използват най-често.

практика:

1. Намерете производната на функцията в точка;
2. Намерете производната на функцията.

Решения:

1. Първо, нека намерим производната в общ изгледи след това заменете стойността му:
   ;
   .
2. Тук имаме нещо подобно на степенна функция. Нека се опитаме да я доведем
   нормален изглед:
   .
   Страхотно, сега можете да използвате формулата:
   .
   .
3. . Еееееее….. Какво е това????

Добре, прав си, все още не знаем как да намерим такива производни. Тук имаме комбинация от няколко вида функции. За да работите с тях, трябва да научите още няколко правила:

Експонента и натурален логаритъм.

В математиката има функция, чиято производна за всяка стойност е равна на стойността на самата функция в същото време. Нарича се „експонента“ и е експоненциална функция

Основата на тази функция е константа - тя е безкрайна десетичен знак, тоест ирационално число (като). Нарича се „число на Ойлер“, поради което се обозначава с буква.

И така, правилото:

Много лесен за запомняне.

Е, нека не отиваме далеч, нека го разгледаме веднага обратна функция. Коя функция е обратна на експоненциалната функция? Логаритъм:

В нашия случай основата е числото:

Такъв логаритъм (т.е. логаритъм с основа) се нарича „естествен“ и ние използваме специална нотация за него: пишем вместо това.

На какво е равно? Разбира се, .

Производната на естествения логаритъм също е много проста:

Примери:

1. Намерете производната на функцията.
2. Каква е производната на функцията?

Отговори: Изложител и натурален логаритъм- функциите са уникално прости по отношение на производни. Експоненциалните и логаритмичните функции с всяка друга основа ще имат различна производна, която ще анализираме по-късно, след това нека да преминем през правилатадиференциация.

Правила за диференциране

Правила на какво? Отново нов срок, отново?!...

Диференциацияе процесът на намиране на производната.

Това е всичко. Как иначе можете да наречете този процес с една дума? Не производна... Математиците наричат ​​диференциала същото нарастване на функция при. Този термин идва от латинския differentia - разлика. Тук.

Когато извличаме всички тези правила, ще използваме две функции, например и. Ще ни трябват и формули за техните увеличения:

Има общо 5 правила.

Константата се изважда от знака за производна.

Ако - някои постоянно число(константа), тогава.

Очевидно това правило работи и за разликата: .

Нека го докажем. Нека бъде или по-просто.

Примери.

Намерете производните на функциите:

1. в точка;
2. в точка;
3. в точка;
4. в точката.

Решения:

1. (производната е една и съща във всички точки, тъй като това линейна функция, помня?);

Производно на продукта

Тук всичко е подобно: да влезем нова функцияи намерете увеличението му:

Производна:

Примери:

1. Намерете производните на функциите и;
2. Намерете производната на функцията в точка.

Решения:

Производна на експоненциална функция

Сега знанията ви са достатъчни, за да научите как да намирате производната на всяка експоненциална функция, а не само на експоненти (забравили ли сте вече какво е това?).

И така, къде е някакво число.

Вече знаем производната на функцията, така че нека се опитаме да намалим нашата функция до нова основа:

За това ще използваме просто правило: . Тогава:

Е, проработи. Сега се опитайте да намерите производната и не забравяйте, че тази функция е сложна.

Се случи?

Ето, проверете сами:

Формулата се оказа много подобна на производната на експонента: както беше, остава същата, само се появи фактор, който е просто число, но не и променлива.

Примери:
Намерете производните на функциите:

Отговори:

Това е просто число, което не може да се изчисли без калкулатор, тоест не може да се запише повече в проста форма. Затова го оставяме в този вид в отговора.

Производна на логаритмична функция

Тук е подобно: вече знаете производната на естествения логаритъм:

Следователно, за да намерите произволен логаритъм с различна основа, например:

Трябва да намалим този логаритъм до основата. Как се променя основата на логаритъм? Надявам се, че помните тази формула:

Само сега вместо това ще напишем:

Знаменателят е просто константа (постоянно число, без променлива). Производната се получава много просто:

Производни на експоненциална и логаритмични функциипочти никога не се появяват в Единния държавен изпит, но няма да навреди да ги знаете.

Производна на сложна функция.

Какво е "сложна функция"? Не, това не е логаритъм и не е арктангенс. Тези функции могат да бъдат трудни за разбиране (въпреки че ако намирате логаритъма за труден, прочетете темата „Логаритми“ и ще се оправите), но от математическа гледна точка думата „комплексен“ не означава „труден“.

Представете си малка конвейерна лента: двама души седят и извършват някакви действия с някакви предмети. Например, първият увива шоколадово блокче в обвивка, а вторият го завързва с панделка. Резултатът е съставен обект: шоколадово блокче, увито и завързано с панделка. За да изядете блокче шоколад, трябва да направите обратните стъпки обратен ред.

Нека създадем подобен математически конвейер: първо ще намерим косинуса на число и след това ще повдигнем на квадрат полученото число. И така, получаваме число (шоколад), аз намирам неговия косинус (обвивка) и след това вие повдигате на квадрат полученото (завързвате го с панделка). Какво стана? функция. Това е пример за сложна функция: когато, за да намерим нейната стойност, извършваме първото действие директно с променливата и след това второ действие с това, което е резултат от първото.

Можем лесно да направим същите стъпки в обратен ред: първо го повдигате на квадрат, а аз след това търся косинуса на полученото число: . Лесно е да се досетите, че резултатът почти винаги ще бъде различен. Важна характеристикасложни функции: когато редът на действията се промени, функцията се променя.

С други думи, сложна функция е функция, чийто аргумент е друга функция: .

За първия пример,.

Втори пример: (същото нещо). .

Действието, което извършваме последно, ще бъде извикано "външна" функция, а първо извършеното действие - съотв "вътрешна" функция(това са неофициални имена, използвам ги само за да обясня материала на прост език).

Опитайте се да определите сами коя функция е външна и коя вътрешна:

Отговори:Разделянето на вътрешни и външни функции е много подобно на промяната на променливи: например във функция

1. Какво действие ще извършим първо? Първо, нека изчислим синуса и едва след това го кубираме. Това означава, че това е вътрешна функция, но външна.
   И първоначалната функция е тяхната композиция: .
2. Вътрешен: ; външен: .
   Преглед: .
3. Вътрешен: ; външен: .
   Преглед: .
4. Вътрешен: ; външен: .
   Преглед: .
5. Вътрешен: ; външен: .
   Преглед: .

Променяме променливи и получаваме функция.

Е, сега ще извлечем нашето шоколадово блокче и ще потърсим производната. Процедурата винаги е обратна: първо търсим производната на външната функция, след това умножаваме резултата по производната на вътрешната функция. Във връзка с оригиналния пример изглежда така:

Друг пример:

И така, нека най-накрая формулираме официалното правило:

Алгоритъм за намиране на производната на сложна функция:

Изглежда просто, нали?

Нека проверим с примери:

Решения:

1) Вътрешен: ;

Външен: ;

2) Вътрешен: ;

(Само не се опитвайте да го отрежете досега! Нищо не излиза изпод косинуса, помните ли?)

3) Вътрешен: ;

Външен: ;

Веднага става ясно, че това е сложна функция на три нива: в крайна сметка това вече е сложна функция сама по себе си и ние също извличаме корена от нея, тоест извършваме третото действие (поставяме шоколада в обвивка и с панделка в куфарчето). Но няма причина да се страхувате: ние все пак ще „разопаковаме“ тази функция в същия ред, както обикновено: от края.

Тоест, първо диференцираме корена, след това косинуса и едва след това израза в скоби. И след това умножаваме всичко.

В такива случаи е удобно действията да се номерират. Тоест нека си представим това, което знаем. В какъв ред ще извършим действия за изчисляване на стойността на този израз? Да разгледаме един пример:

Колкото по-късно се извърши действието, толкова по-„външна“ ще бъде съответната функция. Последователността на действията е същата като преди:

Тук гнезденето обикновено е 4-степенно. Да определим хода на действие.

1. Радикален израз. .

2. Корен. .

3. Синус. .

4. Квадрат. .

5. Събираме всичко заедно:

ПРОИЗВОДНО. НАКРАТКО ЗА ГЛАВНОТО

Производна на функция- отношението на нарастването на функцията към увеличението на аргумента за безкрайно малко увеличение на аргумента:

Основни производни:

Правила за диференциация:

Константата се изважда от знака за производна:

Производна на сумата:

Производно на продукта:

Производна на коефициента:

Производна на сложна функция:

Алгоритъм за намиране на производната на сложна функция:

1. Дефинираме „вътрешната“ функция и намираме нейната производна.
2. Дефинираме „външната“ функция и намираме нейната производна.
3. Умножаваме резултатите от първа и втора точка.