Koja su osnovna svojstva neodređenog integrala. Najjednostavnija svojstva integrala
U ovom članku ćemo navesti glavna svojstva određenog integrala. Većina ovih svojstava dokazana je na osnovu koncepta definitivnog integrala Riemann i Darboux.
Izračunavanje definitivnog integrala se vrlo često vrši korištenjem prvih pet svojstava, pa ćemo se na njih pozvati kada bude potrebno. Preostala svojstva određenog integrala uglavnom se koriste za procjenu različitih izraza.
Prije nego krenemo dalje osnovna svojstva određenog integrala, složimo se da a ne prelazi b.
Za funkciju y = f(x) definiranu na x = a, jednakost je tačna.
Odnosno, vrijednost određenog integrala sa istim granicama integracije jednaka je nuli. Ovo svojstvo je posledica definicije Riemanovog integrala, jer je u ovom slučaju svaki integralni zbir za bilo koju particiju intervala i bilo koji izbor tačaka jednak nuli, pošto je, prema tome, granica integralnih suma nula.
Za funkciju integrabilnu na intervalu,  .
.
Drugim riječima, kada se gornja i donja granica integracije mijenjaju, vrijednost određenog integrala se mijenja u suprotno. Ovo svojstvo određenog integrala također proizlazi iz koncepta Riemanovog integrala, samo numeriranje podjele segmenta treba početi od tačke x = b.
 za funkcije integrabilne na intervalu y = f(x) i y = g(x) .
za funkcije integrabilne na intervalu y = f(x) i y = g(x) .
Dokaz.
Zapišimo integralni zbir funkcije ![]() za datu particiju segmenta i dati izbor tačaka:
za datu particiju segmenta i dati izbor tačaka: 
gdje su i integralni zbroji funkcija y = f(x) i y = g(x) za datu particiju segmenta, respektivno.
Ići do granice u ![]() dobijamo da je, po definiciji Riemanovog integrala, ekvivalentno iskazu svojstva koje se dokazuje.
dobijamo da je, po definiciji Riemanovog integrala, ekvivalentno iskazu svojstva koje se dokazuje.
Konstantni faktor se može izvaditi iz predznaka određenog integrala. To jest, za funkciju y = f(x) integrabilnu na intervalu i proizvoljan broj k, vrijedi sljedeća jednakost:  .
.
Dokaz ovog svojstva definitivnog integrala je apsolutno sličan prethodnom: 
Neka je funkcija y = f(x) integrabilna na intervalu X, i ![]() i onda
i onda  .
.
Ovo svojstvo vrijedi i za , i ili .
Dokaz se može izvesti na osnovu prethodnih svojstava određenog integrala.
Ako je funkcija integrabilna na intervalu, onda je integrabilna na bilo kojem internom intervalu.
Dokaz se zasniva na svojstvu Darbouxovih suma: ako se postojećoj particiji segmenta dodaju nove točke, tada se donja Darbouxova suma neće smanjiti, a gornja se neće povećati.
Ako je funkcija y = f(x) integrabilna na intervalu i za bilo koju vrijednost argumenta, onda  .
.
Ovo svojstvo je dokazano kroz definiciju Riemanovog integrala: bilo koji integralni zbir za bilo koji izbor tačaka podjele segmenta i tačaka u će biti nenegativan (nije pozitivan).
Posljedica.
Za funkcije y = f(x) i y = g(x) integrabilne na intervalu vrijede sljedeće nejednakosti: 
Ova izjava znači da je integracija nejednakosti dozvoljena. Koristićemo ovaj zaključak da dokažemo sljedeća svojstva.
Neka je funkcija y = f(x) integrabilna na intervalu , tada vrijedi nejednakost  .
.
Dokaz.
Očigledno je da ![]() . U prethodnom svojstvu smo saznali da se nejednakost može integrirati pojam po član, dakle, istina je
. U prethodnom svojstvu smo saznali da se nejednakost može integrirati pojam po član, dakle, istina je  . Ova dvostruka nejednakost se može zapisati kao
. Ova dvostruka nejednakost se može zapisati kao  .
.
Neka su funkcije y = f(x) i y = g(x) integrabilne na intervalu i za bilo koju vrijednost argumenta , tada  , Gdje
, Gdje ![]() I
I ![]() .
.
Dokaz se izvodi na sličan način. Kako su m i M najmanja i najveća vrijednost funkcije y = f(x) na segmentu, tada ![]() . Množenjem dvostruke nejednakosti nenegativnom funkcijom y = g(x) dolazimo do sljedeće dvostruke nejednakosti. Integrirajući ga na interval , dolazimo do tvrdnje koja se dokazuje.
. Množenjem dvostruke nejednakosti nenegativnom funkcijom y = g(x) dolazimo do sljedeće dvostruke nejednakosti. Integrirajući ga na interval , dolazimo do tvrdnje koja se dokazuje.
U diferencijalnom računu problem je riješen: pod ovom funkcijom ƒ(x) naći njen izvod(ili diferencijal). Integralni račun rješava inverzni problem: pronađite funkciju F(x), znajući njen izvod F"(x)=ƒ(x) (ili diferencijal). Tražena funkcija F(x) naziva se antiderivatom funkcije ƒ(x) ).
Poziva se funkcija F(x). antiderivativ funkcija ƒ(x) na intervalu (a; b), ako je za bilo koje x ê (a; b) jednakost
F " (x)=ƒ(x) (ili dF(x)=ƒ(x)dx).
Na primjer, antiderivat funkcije y = x 2, x ê R, je funkcija, jer
![]()
Očigledno, sve funkcije će također biti antiderivate

gdje je C konstanta, jer
Teorema 29. 1. Ako je funkcija F(x) antiderivat funkcije ƒ(x) na (a;b), tada je skup svih antiderivata za ƒ(x) dan formulom F(x)+ C, gdje je C konstantan broj.
▲ Funkcija F(x)+C je antiderivat od ƒ(x).
Zaista, (F(x)+C) " =F " (x)=ƒ(x).
Neka je F(h) neki drugi antiderivat funkcije ƒ(x), različit od F(x), tj. F "(x)=ƒ(h). Tada za bilo koje x ê (a; b) imamo
A to znači (vidi Korolar 25.1) da
gdje je C konstantan broj. Dakle, F(x)=F(x)+S.▼
Poziva se skup svih antiderivativnih funkcija F(x)+S za ƒ(x). neodređeni integral funkcije ƒ(x) i označava se simbolom ∫ ƒ(x) dx.
Dakle, po definiciji 
∫ ƒ(x)dx= F(x)+C.
Ovdje se poziva ƒ(x). integrand funkcija, ƒ(x)dx — integrand izraz, X - integracijska varijabla, ∫ -znak neodređenog integrala.
Operacija pronalaženja neodređenog integrala funkcije naziva se integriranjem ove funkcije.
Geometrijski gledano, neodređeni integral je porodica „paralelnih“ krivih y=F(x)+C (svaka numerička vrednost C odgovara specifičnoj krivoj porodice) (vidi sliku 166). Graf svakog antiderivata (kriva) se zove integralna kriva.
Da li svaka funkcija ima neodređeni integral?
Postoji teorema koja kaže da “svaka funkcija kontinuirana na (a;b) ima antiderivativ na ovom intervalu,” i, posljedično, neodređeni integral.
Zapazimo niz svojstava neodređenog integrala koja proizlaze iz njegove definicije.
1. Diferencijal neodređenog integrala jednak je integrandu, a derivacija neodređenog integrala jednaka je integrandu:
d(∫ ƒ(x)dx)=ƒ(x)dh, (∫ ƒ(x)dx) " =ƒ(x).
Zaista, d(∫ ƒ(x) dx)=d(F(x)+C)=dF(x)+d(C)=F " (x) dx =ƒ(x) dx
(∫ ƒ (x) dx) " =(F(x)+C)"=F"(x)+0 =ƒ (x).
Zahvaljujući ovoj osobini, ispravnost integracije se provjerava diferencijacijom. Na primjer, jednakost
∫(3x 2 + 4) dx=h z +4h+S
tačno, pošto (x 3 +4x+C)"=3x 2 +4.
2. Neodređeni integral diferencijala određene funkcije jednak je zbiru ove funkcije i proizvoljne konstante:
∫dF(x)= F(x)+C.
stvarno,
3. Konstantni faktor se može izvaditi iz predznaka integrala:
α ≠ 0 je konstanta.
stvarno,
(stavite C 1 / a = C.)
4. Neodređeni integral algebarskog zbira konačnog broja kontinuiranih funkcija jednak je algebarskom zbiru integrala sabiraka funkcija:
Neka je F"(x)=ƒ(x) i G"(x)=g(x). Onda

gdje je C 1 ±C 2 =C.
5. (Invarijantnost formule integracije).
Ako ![]() , gdje je u=φ(x) proizvoljna funkcija s kontinuiranim izvodom.
, gdje je u=φ(x) proizvoljna funkcija s kontinuiranim izvodom.
▲ Neka je x nezavisna varijabla, ƒ(x) kontinuirana funkcija i F(x) njen antiderivat. Onda
![]()
Postavimo sada u=φ(x), gdje je φ(x) kontinuirano diferencibilna funkcija. Razmotrimo kompleksnu funkciju F(u)=F(φ(x)). Zbog invarijantnosti oblika prvog diferencijala funkcije (vidi str. 160), imamo
Odavde▼
Dakle, formula za neodređeni integral ostaje važeća bez obzira da li je varijabla integracije nezavisna varijabla ili bilo koja njena funkcija koja ima kontinuirani izvod.
Dakle, iz formule ![]() zamjenom x sa u (u=φ(x)) dobijamo
zamjenom x sa u (u=φ(x)) dobijamo ![]()
posebno,

Primjer 29.1. Pronađite integral ![]()
![]()
![]()
gdje je C=C1+C 2 +C 3 +C 4.
Primjer 29.2. Pronađite integralno rješenje:
![]()
![]()
- 29.3. Tabela osnovnih neodređenih integrala
Koristeći činjenicu da je integracija inverzno djelovanje diferencijacije, može se dobiti tabela osnovnih integrala invertiranjem odgovarajućih formula diferencijalnog računa (tabela diferencijala) i korištenjem svojstava neodređenog integrala.
Na primjer, jer
d(sin u)=cos u . du
Izvođenje većeg broja formula u tabeli će biti dato prilikom razmatranja osnovnih metoda integracije.
Integrali u tabeli ispod nazivaju se tabelarni. Treba ih znati napamet. U integralnom računu ne postoje jednostavna i univerzalna pravila za pronalaženje antiderivata elementarnih funkcija, kao u diferencijalnom računu. Metode za pronalaženje antiderivata (tj. integracija funkcije) svode se na indiciranje tehnika koje dovode dati (traženi) integral u tabelarni. Stoga je neophodno poznavati tablične integrale i znati ih prepoznati.
Imajte na umu da u tabeli osnovnih integrala varijabla integracije može označavati i nezavisnu varijablu i funkciju nezavisne varijable (prema svojstvu invarijantnosti formule integracije).
Ispravnost donjih formula može se provjeriti uzimanjem diferencijala na desnoj strani, koji će biti jednak integrandu na lijevoj strani formule.
Dokažimo, na primjer, valjanost formule 2. Funkcija 1/u je definirana i kontinuirana za sve vrijednosti od i osim nule.
Ako je u > 0, onda je ln|u|=lnu ![]() Zbog toga
Zbog toga
Ako u<0, то ln|u|=ln(-u). Но![]() Sredstva
Sredstva
Dakle, formula 2 je tačna. Slično, provjerimo formulu 15:
Tabela glavnih integrala


Prijatelji! Pozivamo vas na diskusiju. Ako imate svoje mišljenje, pišite nam u komentarima.
Ova svojstva se koriste za izvođenje transformacija integrala kako bi se on sveo na jedan od elementarnih integrala i dalje izračunavanje.
1. Derivat neodređenog integrala jednak je integrandu:
2. Diferencijal neodređenog integrala jednak je integrandu:
3. Neodređeni integral diferencijala određene funkcije jednak je zbiru ove funkcije i proizvoljne konstante:
4. Konstantni faktor se može izvaditi iz predznaka integrala:
Štaviše, a ≠ 0
5. Integral zbira (razlike) jednak je zbiru (razlici) integrala:
6. Nekretnina je kombinacija svojstava 4 i 5:
Štaviše, a ≠ 0 ˄ b ≠ 0
7. Svojstvo invarijantnosti neodređenog integrala:
Ako onda
8. Nekretnina:
Ako onda
U stvari, ovo svojstvo je poseban slučaj integracije pomoću metode promjene promjenljive, o čemu se detaljnije govori u sljedećem odjeljku.
Pogledajmo primjer:
Prvo smo primijenili svojstvo 5, zatim svojstvo 4, zatim smo koristili tabelu antiderivata i dobili rezultat.
Algoritam našeg online integralnog kalkulatora podržava sva gore navedena svojstva i lako će pronaći detaljno rješenje za vaš integral.
Antiderivativni i neodređeni integral.
Antiderivat funkcije f(x) na intervalu (a; b) je funkcija F(x) takva da jednakost vrijedi za bilo koji x iz datog intervala.
Ako uzmemo u obzir činjenicu da je izvod konstante C jednak nuli, onda je jednakost tačna ![]() . Dakle, funkcija f(x) ima skup antiderivata F(x)+C, za proizvoljnu konstantu C, a ti se antiderivati međusobno razlikuju za proizvoljnu konstantnu vrijednost.
. Dakle, funkcija f(x) ima skup antiderivata F(x)+C, za proizvoljnu konstantu C, a ti se antiderivati međusobno razlikuju za proizvoljnu konstantnu vrijednost.
Cijeli skup antiderivata funkcije f(x) naziva se neodređenim integralom ove funkcije i označava se ![]() .
.
Izraz se naziva integrand, a f(x) se naziva integrand. Integrand predstavlja diferencijal funkcije f(x).
Radnja pronalaženja nepoznate funkcije s obzirom na njen diferencijal naziva se neodređenom integracijom, jer rezultat integracije nije jedna funkcija F(x), već skup njenih antiderivata F(x)+C.
Tablični integrali

Najjednostavnija svojstva integrala
1. Derivat rezultata integracije jednak je integrandu.
![]()
2. Neodređeni integral diferencijala funkcije jednak je zbiru same funkcije i proizvoljne konstante.
3. Koeficijent se može izvaditi iz predznaka neodređenog integrala.
![]()
4. Neodređeni integral zbira/razlike funkcija jednak je zbiru/razlici neodređenih integrala funkcija.
Za pojašnjenje date su međujednakosti prvog i drugog svojstva neodređenog integrala.
Da bismo dokazali treće i četvrto svojstvo, dovoljno je pronaći izvode desnih strana jednakosti:

Ove derivacije su jednake integrandima, što je dokaz zbog prvog svojstva. Također se koristi u posljednjim prijelazima.
Dakle, problem integracije je inverzan problemu diferencijacije i postoji vrlo bliska veza između ovih problema:
prvo svojstvo omogućava provjeru integracije. Za provjeru ispravnosti izvršene integracije dovoljno je izračunati derivaciju dobivenog rezultata. Ako se funkcija dobijena kao rezultat diferencijacije pokaže da je jednaka integrandu, to će značiti da je integracija obavljena ispravno;
drugo svojstvo neodređenog integrala omogućava da se pronađe njegov antiderivat iz poznatog diferencijala funkcije. Direktno izračunavanje neodređenih integrala zasniva se na ovoj osobini.
1.4. Invarijantnost integracionih oblika.
Invarijantna integracija je vrsta integracije za funkcije čiji su argumenti elementi grupe ili tačke homogenog prostora (svaka tačka u takvom prostoru može se preneti na drugu datom akcijom grupe).
funkcija f(x) se svodi na izračunavanje integrala diferencijalnog oblika f.w, gdje je
Eksplicitna formula za r(x) je data u nastavku. Uslov ugovora ima formu ![]() .
.
ovdje Tg označava operator pomaka na X koristeći gOG: Tgf(x)=f(g-1x). Neka je X=G topologija, grupa koja djeluje na sebe pomacima ulijevo. Ja i. postoji ako i samo ako je G lokalno kompaktan (posebno, na beskonačno-dimenzionalnim grupama I.I. ne postoji). Za podskup od I. i. karakteristična funkcija cA (jednaka 1 na A i 0 izvan A) specificira lijevu Xaar mjeru m(A). Definirajuće svojstvo ove mjere je njena invarijantnost prema lijevom pomaku: m(g-1A)=m(A) za sve gOG. Leva Haarova mera na grupi je jednoznačno definisana do pozitivnog skalarnog faktora. Ako je Haarova mjera m poznata, onda je I. i. funkcija f je data formulom ![]() . Prava Haarova mera ima slična svojstva. Postoji kontinuirani homomorfizam (karta koja čuva svojstvo grupe) DG grupe G u grupnu (u odnosu na množenje) poziciju. brojevi za koje
. Prava Haarova mera ima slična svojstva. Postoji kontinuirani homomorfizam (karta koja čuva svojstvo grupe) DG grupe G u grupnu (u odnosu na množenje) poziciju. brojevi za koje
gdje su dmr i dmi desna i lijeva Haar mjera. Poziva se funkcija DG(g). modul grupe G. Ako je , tada se zove grupa G. unimodularno; u ovom slučaju desna i lijeva Haar mjera se poklapaju. Kompaktne, polujednostavne i nilpotentne (posebno komutativne) grupe su unimodularne. Ako je G n-dimenzionalna Lijeva grupa i q1,...,qn je baza u prostoru lijevo nepromjenjivih 1-forma na G, tada je lijeva Haarova mjera na G data n-formom. U lokalnim koordinatama za izračun
oblika qi, možete koristiti bilo koju matričnu realizaciju grupe G: matrica 1-forma g-1dg je lijevo nepromjenjiva, a njen koeficijent. su lijevo invarijantni skalarni 1-oblici iz kojih se bira tražena baza. Na primjer, kompletna matrična grupa GL(n, R) je unimodularna i Haarova mjera na njoj je data oblikom. Neka ![]() X=G/H je homogen prostor za koji je lokalno kompaktna grupa G transformaciona grupa, a zatvorena podgrupa H stabilizator određene tačke. Da bi i.i. postojao na X, potrebno je i dovoljno da za sve hOH vrijedi jednakost DG(h)=DH(h). To je posebno tačno u slučaju kada je H kompaktan ili polujednostavan. Kompletna teorija I. i. ne postoji na beskonačno-dimenzionalnim mnogostrukostima.
X=G/H je homogen prostor za koji je lokalno kompaktna grupa G transformaciona grupa, a zatvorena podgrupa H stabilizator određene tačke. Da bi i.i. postojao na X, potrebno je i dovoljno da za sve hOH vrijedi jednakost DG(h)=DH(h). To je posebno tačno u slučaju kada je H kompaktan ili polujednostavan. Kompletna teorija I. i. ne postoji na beskonačno-dimenzionalnim mnogostrukostima.
Zamjena varijabli.

Glavni zadatak diferencijalnog računa je pronaći izvod f'(x) ili diferencijal df=f'(x)dx funkcije f(x). U integralnom računu riješen je inverzni problem. Prema datoj funkciji f(x) morate pronaći takvu funkciju F(x),Šta F'(x)=f(x) ili dF(x)=F'(x)dx=f(x)dx.
dakle, glavni zadatak integralnog računa je obnova funkcije F(x) po poznatom izvodu (diferencijalu) ove funkcije. Integralni račun ima brojne primjene u geometriji, mehanici, fizici i tehnologiji. Daje opću metodu za pronalaženje površina, zapremina, centara gravitacije, itd.
Definicija. FunkcijaF(x), , naziva se antiderivatom funkcijef(x) na skupu X ako je diferencibilan za bilo koji iF'(x)=f(x) ilidF(x)=f(x)dx.
Teorema. Bilo koja neprekidna linija na intervalu [a;b] funkcijaf(x) ima antiderivat na ovom segmentuF(x).
Teorema. AkoF 1 (x) iF 2 (x) – dva različita antiderivata iste funkcijef(x) na skupu x, tada se međusobno razlikuju po konstantnom članu, tj.F 2 (x)=F 1x)+C, gdje je C konstanta.
- Neodređeni integral, njegova svojstva.
Definicija. TotalnostF(x)+Od svih antiderivativnih funkcijaf(x) na skupu X naziva se neodređenim integralom i označava se:
- (1)U formuli (1) f(x)dx pozvao integrand izraz,f(x) – funkcija integranda, x – integraciona varijabla, A C – integraciona konstanta.
Razmotrimo svojstva neodređenog integrala koja proizlaze iz njegove definicije.
1. Derivat neodređenog integrala jednak je integrandu, diferencijal neodređenog integrala jednak je integrandu:
i .2. Neodređeni integral diferencijala određene funkcije jednak je zbroju ove funkcije i proizvoljne konstante:
3. Konstantni faktor a (a≠0) može se uzeti kao predznak neodređenog integrala:
4. Neodređeni integral algebarskog zbira konačnog broja funkcija jednak je algebarskom zbiru integrala ovih funkcija:
5. AkoF(x) – antiderivat funkcijef(x), onda:
6 (invarijantnost integracijskih formula). Bilo koja integracijska formula zadržava svoj oblik ako se varijabla integracije zamijeni bilo kojom diferencijabilnom funkcijom ove varijable:
Gdjeu je diferencijabilna funkcija.
- Tabela neodređenih integrala.
Hajde da damo osnovna pravila za integraciju funkcija.
Hajde da damo tabela osnovnih neodređenih integrala.(Imajte na umu da je ovdje, kao iu diferencijalnom računu, slovo u može se označiti kao nezavisna varijabla (u=x), i funkcija nezavisne varijable (u=u(x)).)
(n≠-1). (a >0, a≠1). (a≠0). (a≠0). (|u| > |a|).(|u|< |a|).
Integrali 1 – 17 se nazivaju tabelarni.
Neke od navedenih formula u tablici integrala, koje nemaju analogiju u tabeli derivacija, provjeravaju se diferenciranjem njihovih desnih strana.
- Promjena varijable i integracija po dijelovima u neodređenom integralu.
Integracija zamjenom (zamjena varijable). Neka je potrebno izračunati integral
, što nije tabelarno. Suština metode zamjene je da je u integralu varijabla X zamijeniti promjenljivom t prema formuli x=φ(t), gdje dx=φ’(t)dt.Teorema. Neka funkcijax=φ(t) je definiran i diferencibilan na određenom skupu T i neka je X skup vrijednosti ove funkcije na kojem je funkcija definiranaf(x). Tada ako je na skupu X funkcijaf(
 Sfera, lopta, segment i sektor
Sfera, lopta, segment i sektor Specijalnost "Sestrinstvo" (diploma)
Specijalnost "Sestrinstvo" (diploma)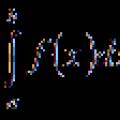 Najjednostavnija svojstva integrala
Najjednostavnija svojstva integrala