Κάθετες και παρακείμενες γωνίες και οι ιδιότητές τους. Γωνία

ΚΕΦΑΛΑΙΟ Ι.

ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ.

§έντεκα. ΠΑΡΑΚΕΙΜΕΝΕΣ ΚΑΙ ΚΑΘΕΤΕΣ ΓΩΝΙΕΣ.

1. Παρακείμενες γωνίες.

Αν επεκτείνουμε την πλευρά οποιασδήποτε γωνίας πέρα από την κορυφή της, έχουμε δύο γωνίες (Εικ. 72): / Και ο ήλιος και / SVD, στην οποία η μία πλευρά BC είναι κοινή, και οι άλλες δύο A και BD σχηματίζουν μια ευθεία γραμμή.

Δύο γωνίες στις οποίες η μία πλευρά είναι κοινή και οι άλλες δύο σχηματίζουν ευθεία ονομάζονται γειτονικές γωνίες.

Οι γειτονικές γωνίες μπορούν επίσης να ληφθούν με αυτόν τον τρόπο: αν σχεδιάσουμε μια ακτίνα από κάποιο σημείο μιας ευθείας (όχι σε μια δεδομένη γραμμή), θα λάβουμε γειτονικές γωνίες.
Για παράδειγμα, / ADF και / FDВ - γειτονικές γωνίες (Εικ. 73).

Οι παρακείμενες γωνίες μπορούν να έχουν μεγάλη ποικιλία θέσεων (Εικ. 74).

Οι γειτονικές γωνίες αθροίζονται σε μια ευθεία γωνία, έτσι umma των δύο παρακείμενες γωνίεςίσο με 2ρε.

Ως εκ τούτου, μια ορθή γωνία μπορεί να οριστεί ως μια γωνία ίση με τη γειτονική γωνία της.

Γνωρίζοντας το μέγεθος μιας από τις γειτονικές γωνίες, μπορούμε να βρούμε το μέγεθος της άλλης γωνίας που βρίσκεται δίπλα της.

Για παράδειγμα, εάν μία από τις διπλανές γωνίες είναι 3/5 ρε, τότε η δεύτερη γωνία θα είναι ίση με:

2ρε- 3 / 5 ρε= l 2 / 5 ρε.

2. Κάθετες γωνίες.

Αν επεκτείνουμε τις πλευρές της γωνίας πέρα από την κορυφή της, παίρνουμε κάθετες γωνίες. Στο σχέδιο 75, οι γωνίες EOF και AOC είναι κάθετες. Οι γωνίες AOE και COF είναι επίσης κάθετες.

Δύο γωνίες ονομάζονται κάθετες αν οι πλευρές της μιας γωνίας είναι συνεχείς των πλευρών της άλλης γωνίας.

Αφήνω / 1 = 7 / 8 ρε(Εικόνα 76). Δίπλα σε αυτό / 2 θα ισούται με 2 ρε- 7 / 8 ρε, δηλαδή 1 1/8 ρε.

Με τον ίδιο τρόπο μπορείτε να υπολογίσετε με τι ισούνται / 3 και / 4.
/ 3 = 2ρε - 1 1 / 8 ρε = 7 / 8 ρε; / 4 = 2ρε - 7 / 8 ρε = 1 1 / 8 ρε(Εικόνα 77).

Το βλέπουμε αυτό / 1 = / 3 και / 2 = / 4.

Μπορείτε να λύσετε πολλά περισσότερα από τα ίδια προβλήματα και κάθε φορά θα έχετε το ίδιο αποτέλεσμα: οι κάθετες γωνίες είναι ίσες μεταξύ τους.

Ωστόσο, για να βεβαιωθείτε ότι οι κατακόρυφες γωνίες είναι πάντα ίσες μεταξύ τους, δεν αρκεί να θεωρήσετε μεμονωμένες αριθμητικά παραδείγματα, δεδομένου ότι τα συμπεράσματα που συνάγονται με βάση συγκεκριμένα παραδείγματα μπορεί μερικές φορές να είναι λανθασμένα.

Είναι απαραίτητο να επαληθευτεί η εγκυρότητα των ιδιοτήτων των κατακόρυφων γωνιών με συλλογισμό, με απόδειξη.

Η απόδειξη μπορεί να πραγματοποιηθεί ως εξής (Εικ. 78):

/ α+/ ντο = 2ρε;
/ β+/ ντο = 2ρε;

(αφού το άθροισμα των διπλανών γωνιών είναι 2 ρε).

/ α+/ ντο = / β+/ ντο

(αφού και η αριστερή πλευρά αυτής της ισότητας είναι ίση με 2 ρε, και η δεξιά πλευρά του είναι επίσης ίση με 2 ρε).

Αυτή η ισότητα περιλαμβάνει την ίδια γωνία Με.

Αν είμαστε από ίσες αξίεςαφαιρέστε ίσα, τότε θα παραμείνει ίσο. Το αποτέλεσμα θα είναι: / ένα = / σι, δηλαδή οι κατακόρυφες γωνίες είναι ίσες μεταξύ τους.

Κατά την εξέταση του θέματος των κατακόρυφων γωνιών, αρχικά εξηγήσαμε ποιες γωνίες ονομάζονται κάθετες, δηλ. ορισμόςκάθετες γωνίες.

Στη συνέχεια κάναμε μια κρίση (δήλωση) για την ισότητα των κατακόρυφων γωνιών και πειστήκαμε για την εγκυρότητα αυτής της κρίσης μέσω της απόδειξης. Τέτοιες κρίσεις, η εγκυρότητα των οποίων πρέπει να αποδειχθεί, καλούνται θεωρήματα. Έτσι, σε αυτή την ενότητα δώσαμε έναν ορισμό των κατακόρυφων γωνιών, καθώς και αναφέραμε και αποδείξαμε ένα θεώρημα για τις ιδιότητές τους.

Στο μέλλον, κατά τη μελέτη της γεωμετρίας, θα πρέπει συνεχώς να συναντάμε ορισμούς και αποδείξεις θεωρημάτων.

3. Το άθροισμα των γωνιών που έχουν κοινή κορυφή.

Στο σχέδιο 79 / 1, / 2, / 3 και / Τα 4 βρίσκονται στη μία πλευρά μιας γραμμής και έχουν μια κοινή κορυφή σε αυτή τη γραμμή. Συνολικά, αυτές οι γωνίες αποτελούν μια ευθεία γωνία, δηλ.
/ 1+ / 2+/ 3+ / 4 = 2ρε.

Στο σχέδιο 80 / 1, / 2, / 3, / 4 και / 5 έχουν κοινή κορυφή. Το άθροισμα αυτών των γωνιών είναι πλήρης γωνία, δηλ. / 1 + / 2 + / 3 + / 4 + / 5 = 4ρε.

Γυμνάσια.

1. Μία από τις διπλανές γωνίες είναι 0,72 ρε.Να υπολογίσετε τη γωνία που σχηματίζουν οι διχοτόμοι αυτών των διπλανών γωνιών.

2. Να αποδείξετε ότι οι διχοτόμοι δύο γειτονικών γωνιών σχηματίζουν ορθή γωνία.

3. Να αποδείξετε ότι αν δύο γωνίες είναι ίσες, τότε και οι διπλανές τους γωνίες είναι ίσες.

4. Πόσα ζεύγη γειτονικών γωνιών υπάρχουν στο σχέδιο 81;

5. Μπορεί ένα ζεύγος γειτονικών γωνιών να αποτελείται από δύο οξείες γωνίες; από δύο αμβλείες γωνίες; από ορθές και αμβλείες γωνίες; από ορθή και οξεία γωνία;

6. Αν μία από τις διπλανές γωνίες είναι ορθή, τότε τι μπορεί να ειπωθεί για το μέγεθος της γωνίας που γειτνιάζει με αυτήν;

7. Αν στη τομή δύο ευθειών η μία γωνία είναι ορθή, τότε τι μπορεί να λεχθεί για το μέγεθος των άλλων τριών γωνιών;

με θέμα: Παρακείμενες και κάθετες γωνίες, οι ιδιότητές τους.

(3 μαθήματα)

Ως αποτέλεσμα της μελέτης του θέματος που χρειάζεστε:

ΕΧΩ ΤΗΝ ΔΥΝΑΤΟΤΗΤΑ ΝΑ:

Έννοιες: παρακείμενες και κάθετες γωνίες, κάθετες γραμμές

Διακρίνετε τις γειτονικές και τις κατακόρυφες γωνίες

Θεωρήματα παρακείμενης και κατακόρυφης γωνίας

Λύστε προβλήματα χρησιμοποιώντας τις ιδιότητες γειτονικών και κάθετων γωνιών

Ιδιότητες παρακείμενων και κάθετων γωνιών

Κατασκευάστε γειτονικές και κάθετες γωνίες κάθετες σε ευθείες γραμμές

ΒΙΒΛΙΟΓΡΑΦΙΑ:

1. Γεωμετρία. 7η τάξη. Zh. Kaydasov, G. Dosmagambetova, V. Abdiev. Αλμάτι «Μεκτέπ». 2012

2. Γεωμετρία. 7η τάξη. K.O.Bukubaeva, A.T. Μιράζοβα. Αλμάτι"Αταμούρα" 2012

3. Γεωμετρία. 7η τάξη. Μεθοδικό εγχειρίδιο. Κ.Ο.Μπουκουμπάεβα. Αλμάτι"Αταμούρα" 2012

4. Γεωμετρία. 7η τάξη. Διδακτικό υλικό. A.N. Shynybekov. Αλμάτι"Αταμούρα" 2012

5. Γεωμετρία. 7η τάξη. Συλλογή εργασιών και ασκήσεων. K.O Bukubaeva, A.T. Αλμάτι"Αταμούρα" 2012

Θυμηθείτε ότι πρέπει να εργαστείτε σύμφωνα με τον αλγόριθμο!

Μην ξεχάσετε να ελέγξετε, κάντε σημειώσεις στα περιθώρια,

Παρακαλώ μην αφήνετε καμία ερώτηση που έχετε αναπάντητη.

Να είστε αντικειμενικοί κατά την αμοιβαία επαλήθευση, θα βοηθήσει τόσο εσάς όσο και το άτομο

ποιον ελέγχεις;

ΣΟΥ ΕΥΧΟΜΑΙ ΕΠΙΤΥΧΙΑ!

ΕΡΓΟ Νο. 1.

Διαβάστε τον ορισμό και μάθετε (2β):

Ορισμός. Οι γωνίες στις οποίες η μία πλευρά είναι κοινή και οι άλλες δύο πλευρές πρόσθετες ακτίνες ονομάζονται γειτονικές.

2) Μάθετε και γράψτε το θεώρημα στο τετράδιό σας: (2β)

Το άθροισμα των διπλανών γωνιών είναι 180.

Δεδομένος:

∠ ΑΝΜ και∠ DOV – δεδομένα γειτονικές γωνίες

OD - κοινή πλευρά

Αποδεικνύω:

∠ AOD +∠ DOV = 180

Απόδειξη:

Με βάση το αξίωμαIII 4:

∠ AOD +∠ DOV =∠ AOB.

∠ AOB - επεκτάθηκε. Ως εκ τούτου,

∠ AOD +∠ DOV = 180

Το θεώρημα είναι αποδεδειγμένο.

3) Από το θεώρημα προκύπτει: (2β)

1) Αν δύο γωνίες είναι ίσες, τότε οι γειτονικές τους γωνίες είναι ίσες.

2) αν οι διπλανές γωνίες είναι ίσες, τότε μέτρο βαθμούκαθένα από αυτά είναι ίσο με 90°.

Θυμάμαι!

Μια γωνία ίση με 90° ονομάζεται ορθή γωνία.

Μια γωνία μικρότερη από 90° ονομάζεται οξεία γωνία.

Ονομάζεται γωνία μεγαλύτερη από 90° και μικρότερη από 180° αμβλεία γωνία.

Ορθή γωνία Οξεία γωνία Αμβλεία γωνία

Αφού το άθροισμα των παρακείμενων γωνιών είναι 180°, τότε

1) μια γωνία δίπλα σε μια ορθή γωνία, ευθεία.

2) η γωνία δίπλα στην οξεία γωνία είναι αμβλεία.

3) μια γωνία δίπλα σε μια αμβλεία γωνία είναι οξεία.

4) Εξετάστε ένα δείγμα διαλύματοςadachi:

α) Δεδομένα:∠ ηκΚαι∠ kl- δίπλα∠ ηκπερισσότερο∠ klστους 50°.

Εύρημα:∠ ηκΚαι∠ kl.

Λύση: Αφήστε∠ kl= x, λοιπόν∠ ηκ= x + 50°. Με την ιδιότητα του αθροίσματος των παρακείμενων γωνιών∠ kl + ∠ ηκ= 180°.

x + x + 50° = 180°;

2x = 180° - 50°;

2x = 130°;

x = 65°.

∠ kl= 65°;∠ ηκ= 65°+ 50° = 115°.

Απάντηση: 115° και 65°.

β) Αφήστε∠ kl= x, λοιπόν∠ ηκ= 3x

x + 3x = 180°; 4x = 180°; x = 45°;∠ kl= 45°;∠ hk= 135°.

Απάντηση: 135° και 45°.

5) Εργασία με τον προσδιορισμό παρακείμενων γωνιών: (2 β)

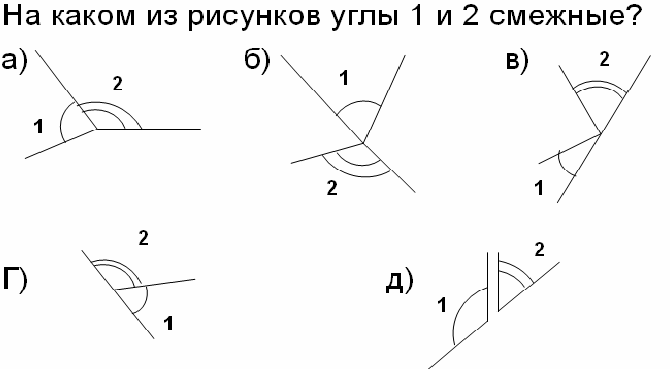
6) Βρείτε λάθη στους ορισμούς: (2β)

Επιτυχής δοκιμή #1

Εργασία Νο. 2

1) Κατασκευάστε 2 γειτονικές γωνίες έτσι ώστε η κοινή τους πλευρά να διέρχεται από το σημείο C και η πλευρά μιας από τις γωνίες να συμπίπτει με την ακτίνα ΑΒ (2b).

2). Πρακτική δουλειάνα ανακαλύψετε τις ιδιότητες των παρακείμενων γωνιών: (5β)

Πρόοδος

1. Κατασκευάστε μια γωνίαδιπλανή γωνίαΕΝΑ , ΑνΕΝΑ : κοφτερό, ίσιο, αμβλύ.

2. Μετρήστε τις γωνίες.

3. Εισαγάγετε τα δεδομένα μέτρησης στον πίνακα.

4. Να βρείτε τη σχέση μεταξύ των γωνιώνΕΝΑ Και.

5. Να βγάλετε συμπέρασμα για την ιδιότητα των διπλανών γωνιών.

Επιτυχής δοκιμή #2

Εργασία Νο. 3

Σχεδιάστε το μη διογκωμένο∠ AOB και ονομάστε τις ακτίνες που είναι οι πλευρές αυτής της γωνίας.

Σχεδιάστε την ακτίνα O, η οποία είναι συνέχεια της ακτίνας OA, και την ακτίνα OD, η οποία είναι συνέχεια της ακτίνας OB.

Γράψε στο τετράδιό σου: γωνίες∠ AOB και∠ Τα SOD ονομάζονται κάθετα. (3β)

Μάθετε και γράψτε στο τετράδιό σας: (4β)

Ορισμός: Οι γωνίες στις οποίες οι πλευρές του ενός είναι συμπληρωματικές ακτίνες του άλλου ονομάζονταικάθετες γωνίες.

< 1 και<2, <3 и <4 κάθετες γωνίες

ΑκτίνεςΤΟΥΚαιΟ Ο.Α. , O.C.ΚαιΟ Ο.Ε.είναι συμπληρωματικές ακτίνες κατά ζεύγη.

Θεώρημα: Οι κάθετες γωνίες είναι ίσες.

Απόδειξη.

Κάθετες γωνίες σχηματίζονται όταν τέμνονται δύο ευθείες γραμμές. Έστω ευθείες α καισιτέμνονται στο σημείο Ο.∠ 1 και∠ 2 – κάθετες γωνίες.

∠ AOC-expanded, που σημαίνει∠ AOC = 180°. Ωστόσο∠ 1+ ∠ 2= ∠ AOC, δηλ.

∠ 3+ ∠ 1= 180°, από εδώ έχουμε:

∠ 1= 180 - ∠ 3. (1)

Το έχουμε και αυτό∠ DOV = 180°, από εδώ∠ 2+ ∠ 3= 180°, ή∠ 2= 180°- ∠ 3. (2)

Αφού στις ισότητες (1) και (2) τα ευθύγραμμα μέρη είναι ίσα, τότε∠ 1= ∠ 2.

Το θεώρημα είναι αποδεδειγμένο.

5). Εργασία με τον προσδιορισμό κάθετων γωνιών: (2β)

6) Βρείτε το σφάλμα στον ορισμό: (2β).

Επιτυχής δοκιμή #3

Εργασία Νο. 4

1) Πρακτική εργασία για την ανακάλυψη των ιδιοτήτων των κατακόρυφων γωνιών: (5β)

Πρόοδος:

1. Κατασκευάστε τη γωνία β κατακόρυφη γωνίαα , Ανα :

κοφτερό, ίσιο, αμβλύ.

2.Μετρήστε τις γωνίες.

3. Εισαγάγετε τα δεδομένα μέτρησης στον πίνακα

4. Να βρείτε τη σχέση των γωνιών α και β.

5. Εξάγετε συμπέρασμα για τις ιδιότητες των κατακόρυφων γωνιών.

2) Απόδειξη των ιδιοτήτων γειτονικών και κατακόρυφων γωνιών. (3β)

2) Εξετάστε ένα δείγμα διαλύματοςadachi.

Εργο. Οι ευθείες ΑΒ και CD τέμνονται στο σημείο Ο έτσι ώστε∠ AOD = 35°. Βρείτε τις γωνίες AOC και BOC.

Λύση:

1) Οι γωνίες AOD και AOS είναι γειτονικές, επομένως∠ BOC= 180° - 35° = 145°.

2) Οι γωνίες AOC και BOC είναι επίσης γειτονικές, επομένως∠ BOC= 180° - 145° = 35°.

Που σημαίνει,∠ BOC = ∠ AOD = 35°, και αυτές οι γωνίες είναι κάθετες. Ερώτηση: Είναι αλήθεια ότι όλες οι κατακόρυφες γωνίες είναι ίσες;

3) Επίλυση προβλημάτων σε ολοκληρωμένα σχέδια: (3β)

1. Να βρείτε τις γωνίες AOB, AOD, COD.

3) Βρείτε γωνίες BOC, FOA.: (3β)

3. Βρείτε διπλανές και κάθετες γωνίες στο σχήμα. Να είναι γνωστές οι τιμές των δύο γωνιών που σημειώνονται στο σχέδιο, 28; και 90;. Είναι δυνατόν να βρεθούν οι τιμές των υπόλοιπων γωνιών χωρίς να πραγματοποιηθούν μετρήσεις (2b)

Επιτυχία δοκιμής αριθμός 4

Εργασία Νο. 5

Δοκιμάστε τις γνώσεις σας συμπληρώνονταςΔοκιμαστική εργασία Νο. 1

Εργασία Νο. 6

1) Αποδείξτε μόνοι σας τις ιδιότητες των κατακόρυφων γωνιών και γράψτε αυτές τις αποδείξεις στο τετράδιό σας. (3β)

Οι μαθητές ανεξάρτητα, χρησιμοποιώντας τις ιδιότητες κάθετης και παρακείμενης γωνίας, πρέπει να αιτιολογήσουν το γεγονός ότι εάν, όταν τέμνονται δύο ευθείες, μία από τις γωνίες που προκύπτουν είναι ευθεία γραμμή, τότε και οι υπόλοιπες γωνίες είναι ορθές.

2) Λύστε δύο προβλήματα για να διαλέξετε:

1.Τα μέτρα μοιρών των παρακείμενων γωνιών είναι σε αναλογία 7:2. Βρείτε αυτές τις γωνίες (2β)

2. Μία από τις γωνίες που σχηματίζονται όταν τέμνονται δύο ευθείες είναι 11 φορές μικρότερη από την άλλη.

3. Να βρείτε διπλανές γωνίες αν η διαφορά τους και το άθροισμά τους είναι 2:9.

Εργασία Νο. 7

Μπράβο! Μπορείτε να προχωρήσετε στη δοκιμή Νο. 2.

Δοκιμαστική εργασία Νο. 1.

Αποφασίστε να επιλέξετε οποιαδήποτε από τις επιλογές (10β)

Επιλογή 1

<1 и <2,

<3 и <2,

ΣΟΛ)<1 и <3. Какие это углы?

Σχετίζεται με

ε) Σχεδιάστε (με το μάτι) γωνία 30° και< αλφάβητο, δίπλα στο δεδομένο

στ) Ποιες γωνίες ονομάζονται κάθετες;

Δύο γωνίες ονομάζονται κάθετες αν είναι ίσες.

ζ) Από το σημείο Α να σχεδιάσετε δύο ευθείες κάθετες στην ευθείαΕΝΑ

Μπορείτε να σχεδιάσετε μόνο μία ευθεία γραμμή.

Επιλογή 2

1. Ο μαθητής, απαντώντας στις ερωτήσεις του δασκάλου, έδωσε τις κατάλληλες απαντήσεις. Ελέγξτε αν είναι σωστές σημειώνοντας τις λέξεις «ΝΑΙ», «ΟΧΙ», «ΔΕΝ ΞΕΡΩ» στην τρίτη στήλη. Εάν «ΟΧΙ», γράψτε εκεί τη σωστή απάντηση ή προσθέστε αυτή που λείπει.

<1 и <4,

<2 и <4

ΡΕ)<1 и < 3 смежные?

Οχι. Είναι κάθετες

Ε) Ποιες ευθείες ονομάζονται κάθετες;

Δύο ευθείες ονομάζονται κάθετες αν τέμνονται κάθετες

Ζ) Σχεδιάστε κάθετες γωνίες ώστε οι πλευρές τους να είναι κάθετες σε ευθείες γραμμές.

2. Ονομάστε τις κατακόρυφες γωνίες σε αυτό το σχήμα.

Σύνολο: 10 βαθμοί

"5" -10 βαθμοί.

"4" -8-9 βαθμοί.

«3» -5-7 πόντοι.

Δοκιμαστική εργασία Νο 2.

Αποφασίστε να επιλέξετε οποιαδήποτε επιλογή

Επιλογή Ι

Να βρείτε διπλανές γωνίες αν η διαφορά τους και το άθροισμά τους είναι σε αναλογία 2:9. (4β)

Να βρείτε όλες τις γωνίες που σχηματίζονται από την τομή δύο ευθειών εάν η μία από αυτές είναι 240° μικρότερη από το άθροισμα των άλλων δύο (6β).

Επιλογή II

1) Βρείτε τις γειτονικές γωνίες αν η διαφορά τους και το άθροισμά τους είναι στην αναλογία 5:8(4b)

2) Να βρείτε όλες τις μη ανεπτυγμένες γωνίες που σχηματίζονται στη τομή δύο ευθειών, αν η μία από αυτές είναι 60° μεγαλύτερη από το άθροισμα των άλλων δύο (6β).

Σύνολο: 10 βαθμοί

"5" -10 βαθμοί.

"4" -8-9 βαθμοί.

«3» -5-7 πόντοι.

Δύο γωνίες ονομάζονται γειτονικές αν έχουν μια κοινή πλευρά και οι άλλες πλευρές αυτών των γωνιών είναι συμπληρωματικές ακτίνες. Στο Σχήμα 20, οι γωνίες AOB και BOC είναι γειτονικές.

Το άθροισμα των παρακείμενων γωνιών είναι 180°

Θεώρημα 1. Το άθροισμα των διπλανών γωνιών είναι 180°.

Απόδειξη. Η δοκός OB (βλ. Εικ. 1) διέρχεται μεταξύ των πλευρών της ξεδιπλωμένης γωνίας. Να γιατί ∠ AOB + ∠ BOS = 180°.

Από το Θεώρημα 1 προκύπτει ότι αν δύο γωνίες είναι ίσες, τότε οι γειτονικές τους γωνίες είναι ίσες.

Οι κάθετες γωνίες είναι ίσες

Δύο γωνίες ονομάζονται κάθετες αν οι πλευρές της μιας γωνίας είναι συμπληρωματικές ακτίνες των πλευρών της άλλης. Οι γωνίες AOB και COD, BOD και AOC, που σχηματίζονται στη διασταύρωση δύο ευθειών, είναι κάθετες (Εικ. 2).

Θεώρημα 2. Οι κάθετες γωνίες είναι ίσες.

Απόδειξη. Ας εξετάσουμε τις κατακόρυφες γωνίες AOB και COD (βλ. Εικ. 2). Η γωνία BOD είναι δίπλα σε καθεμία από τις γωνίες AOB και COD. Με το θεώρημα 1 ∠ AOB + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Από αυτό συμπεραίνουμε ότι ∠ AOB = ∠ COD.

Συμπέρασμα 1. Μια γωνία δίπλα σε μια ορθή γωνία είναι μια ορθή γωνία.

Ας εξετάσουμε δύο τεμνόμενες ευθείες AC και BD (Εικ. 3). Σχηματίζουν τέσσερις γωνίες. Εάν μία από αυτές είναι ευθεία (η γωνία 1 στο Σχ. 3), τότε οι υπόλοιπες γωνίες είναι επίσης ορθές (οι γωνίες 1 και 2, 1 και 4 γειτονεύουν, οι γωνίες 1 και 3 είναι κάθετες). Σε αυτή την περίπτωση, λένε ότι αυτές οι ευθείες τέμνονται κάθετες και ονομάζονται κάθετες (ή αμοιβαία κάθετες). Η καθετότητα των ευθειών AC και BD συμβολίζεται ως εξής: AC ⊥ BD.

Κάθετη διχοτόμος σε ένα τμήμα είναι μια ευθεία κάθετη σε αυτό το τμήμα και διέρχεται από το μέσο του.

AN - κάθετη σε μια γραμμή

Θεωρήστε μια ευθεία γραμμή α και ένα σημείο Α που δεν βρίσκεται πάνω της (Εικ. 4). Ας συνδέσουμε το σημείο Α με ένα τμήμα στο σημείο Η με ευθεία α. Το τμήμα AN ονομάζεται κάθετο που σύρεται από το σημείο Α στην ευθεία a εάν οι ευθείες AN και a είναι κάθετες. Το σημείο Η ονομάζεται βάση της κάθετης.

Τετράγωνο σχεδίασης

Το παρακάτω θεώρημα είναι αληθές.

Θεώρημα 3. Από οποιοδήποτε σημείο που δεν βρίσκεται σε μια ευθεία, είναι δυνατό να σχεδιάσουμε μια κάθετο σε αυτήν την ευθεία, και, επιπλέον, μόνο μία.

Για να σχεδιάσετε μια κάθετη από ένα σημείο σε μια ευθεία γραμμή σε ένα σχέδιο, χρησιμοποιήστε ένα τετράγωνο σχεδίου (Εικ. 5).

Σχόλιο. Η διατύπωση του θεωρήματος συνήθως αποτελείται από δύο μέρη. Ένα μέρος μιλάει για αυτό που δίνεται. Αυτό το μέρος ονομάζεται συνθήκη του θεωρήματος. Το άλλο μέρος μιλάει για το τι πρέπει να αποδειχθεί. Αυτό το μέρος ονομάζεται συμπέρασμα του θεωρήματος. Για παράδειγμα, η συνθήκη του Θεωρήματος 2 είναι ότι οι γωνίες είναι κάθετες. συμπέρασμα - αυτές οι γωνίες είναι ίσες.

Οποιοδήποτε θεώρημα μπορεί να εκφραστεί λεπτομερώς με λέξεις έτσι ώστε η κατάστασή του να αρχίζει με τη λέξη «αν» και το συμπέρασμα του με τη λέξη «τότε». Για παράδειγμα, το Θεώρημα 2 μπορεί να διατυπωθεί αναλυτικά ως εξής: «Αν δύο γωνίες είναι κάθετες, τότε είναι ίσες».

Παράδειγμα 1.Μία από τις παρακείμενες γωνίες είναι 44°. Με τι ισούται το άλλο;

Λύση. Ας συμβολίσουμε το μέτρο της μοίρας μιας άλλης γωνίας με x, τότε σύμφωνα με το Θεώρημα 1.
44° + x = 180°.
Λύνοντας την εξίσωση που προκύπτει, βρίσκουμε ότι x = 136°. Επομένως, η άλλη γωνία είναι 136°.

Παράδειγμα 2.Έστω η γωνία COD στο Σχήμα 21 45°. Ποιες είναι οι γωνίες AOB και AOC;

Λύση. Οι γωνίες COD και AOB είναι κάθετες, επομένως, σύμφωνα με το Θεώρημα 1.2 είναι ίσες, δηλαδή ∠ AOB = 45°. Η γωνία AOC είναι δίπλα στη γωνία COD, που σημαίνει σύμφωνα με το Θεώρημα 1.
∠ AOC = 180° - ∠ COD = 180° - 45° = 135°.

Παράδειγμα 3.Βρείτε τις γειτονικές γωνίες αν η μία από αυτές είναι 3 φορές μεγαλύτερη από την άλλη.

Λύση. Ας συμβολίσουμε το μέτρο της μοίρας της μικρότερης γωνίας με x. Τότε το μέτρο μοίρας της μεγαλύτερης γωνίας θα είναι 3x. Εφόσον το άθροισμα των παρακείμενων γωνιών είναι ίσο με 180° (Θεώρημα 1), τότε x + 3x = 180°, από όπου x = 45°.
Αυτό σημαίνει ότι οι γειτονικές γωνίες είναι 45° και 135°.

Παράδειγμα 4.Το άθροισμα δύο κάθετων γωνιών είναι 100°. Βρείτε το μέγεθος καθεμιάς από τις τέσσερις γωνίες.

Λύση. Έστω οι συνθήκες του προβλήματος να αντιστοιχούν στο Σχήμα 2. Οι κατακόρυφες γωνίες COD προς AOB είναι ίσες (Θεώρημα 2), που σημαίνει ότι τα μέτρα βαθμού τους είναι επίσης ίσα. Επομένως, ∠ COD = ∠ AOB = 50° (το άθροισμά τους σύμφωνα με την συνθήκη είναι 100°). Η γωνία BOD (επίσης γωνία AOC) γειτνιάζει με τη γωνία COD, και επομένως, από το Θεώρημα 1
∠ BOD = ∠ AOC = 180° - 50° = 130°.

Σε αυτό το μάθημα θα εξετάσουμε και θα κατανοήσουμε την έννοια των παρακείμενων γωνιών. Ας εξετάσουμε ένα θεώρημα που τους αφορά. Ας εισαγάγουμε την έννοια των «κάθετων γωνιών». Ας δούμε μερικά υποστηρικτικά στοιχεία σχετικά με αυτές τις γωνίες. Στη συνέχεια, διατυπώνουμε και αποδεικνύουμε δύο συμπεράσματα σχετικά με τη γωνία μεταξύ των διχοτόμων των κατακόρυφων γωνιών. Στο τέλος του μαθήματος θα εξετάσουμε αρκετά προβλήματα σχετικά με αυτό το θέμα.

Ας ξεκινήσουμε το μάθημά μας με την έννοια των «γειτονικών γωνιών». Το σχήμα 1 δείχνει την ανεπτυγμένη γωνία ∠AOC και την ακτίνα OB, που χωρίζει αυτή τη γωνία σε 2 γωνίες.

Ρύζι. 1. Γωνία ∠AOC

Ας εξετάσουμε τις γωνίες ∠AOB και ∠BOC. Είναι προφανές ότι έχουν μια κοινή πλευρά VO και οι πλευρές AO και OS είναι απέναντι. Οι ακτίνες OA και OS αλληλοσυμπληρώνονται, πράγμα που σημαίνει ότι βρίσκονται στην ίδια ευθεία γραμμή. Οι γωνίες ∠AOB και ∠BOC είναι γειτονικές.

Ορισμός: Εάν δύο γωνίες έχουν κοινή πλευρά και οι άλλες δύο πλευρές είναι συμπληρωματικές, τότε αυτές οι γωνίες ονομάζονται γειτονικός.

Θεώρημα 1: Το άθροισμα των διπλανών γωνιών είναι 180 o.

Ρύζι. 2. Σχέδιο για το Θεώρημα 1

∠MOL + ∠LON = 180 ο. Αυτή η δήλωση είναι αληθής, αφού η ακτίνα OL διαιρεί την ξεδιπλωμένη γωνία ∠MON σε δύο γειτονικές γωνίες. Δηλαδή, δεν γνωρίζουμε τα μέτρα μοιρών καμίας από τις γειτονικές γωνίες, αλλά γνωρίζουμε μόνο το άθροισμά τους - 180 μοίρες.

Θεωρήστε την τομή δύο ευθειών. Το σχήμα δείχνει την τομή δύο ευθειών στο σημείο Ο.

Ρύζι. 3. Κάθετες γωνίες ∠ВОА και ∠СOD

Ορισμός: Αν οι πλευρές μιας γωνίας είναι συνέχεια της δεύτερης γωνίας, τότε τέτοιες γωνίες ονομάζονται κάθετες. Γι' αυτό το σχήμα δείχνει δύο ζεύγη κατακόρυφων γωνιών: ∠AOB και ∠COD, καθώς και ∠AOD και ∠BOC.

Θεώρημα 2: Οι κάθετες γωνίες είναι ίσες.

Ας χρησιμοποιήσουμε το Σχήμα 3. Θεωρήστε τη γωνία περιστροφής ∠AOC. ∠AOB = ∠AOC - ∠BOC = 180 o - β. Ας εξετάσουμε την περιστρεφόμενη γωνία ∠BOD. ∠COD = ∠BОD - ∠BOC = 180 o - β.

Από αυτές τις σκέψεις συμπεραίνουμε ότι ∠AOB = ∠COD = α. Ομοίως, ∠AOD = ∠BOS = β.

Συμπέρασμα 1: Η γωνία μεταξύ των διχοτόμων γειτονικών γωνιών είναι 90°.

Ρύζι. 4. Σχέδιο για το συμπέρασμα 1

Εφόσον το OL είναι η διχοτόμος της γωνίας ∠BOA, τότε η γωνία ∠LOB = , παρόμοια με ∠BOA = . ∠LOK = ∠LOB + ∠BOK = + = . Το άθροισμα των γωνιών α + β είναι ίσο με 180°, αφού αυτές οι γωνίες είναι γειτονικές.

Συμπέρασμα 2: Η γωνία μεταξύ των διχοτόμων των κατακόρυφων γωνιών είναι ίση με 180°.

Ρύζι. 5. Σχέδιο για το συμπέρασμα 2

Το KO είναι η διχοτόμος ∠AOB, το LO είναι η διχοτόμος ∠COD. Προφανώς, ∠KOL = ∠KOB + ∠BOC + ∠COL = ο. Το άθροισμα των γωνιών α + β είναι ίσο με 180°, αφού αυτές οι γωνίες είναι γειτονικές.

Ας δούμε μερικές εργασίες:

Βρείτε τη γωνία δίπλα στο ∠AOC αν ∠AOC = 111 o.

Ας κάνουμε ένα σχέδιο για την εργασία:

Ρύζι. 6. Σχέδιο για παράδειγμα 1

Εφόσον ∠AOC = β και ∠COD = α είναι γειτονικές γωνίες, τότε α + β = 180 o. Δηλαδή 111 ο + β = 180 ο.

Αυτό σημαίνει β = 69 ο.

Αυτός ο τύπος προβλήματος εκμεταλλεύεται το θεώρημα του αθροίσματος γειτονικών γωνιών.

Μία από τις διπλανές γωνίες είναι ορθή, ποια είναι η άλλη γωνία (οξεία, αμβλεία ή ορθή);

Αν μία από τις γωνίες είναι ορθή και το άθροισμα των δύο γωνιών είναι 180°, τότε και η άλλη γωνία είναι ορθή. Αυτό το πρόβλημα ελέγχει τη γνώση σχετικά με το άθροισμα των παρακείμενων γωνιών.

Είναι αλήθεια ότι αν οι διπλανές γωνίες είναι ίσες, τότε είναι ορθές;

Ας κάνουμε μια εξίσωση: α + β = 180 ο, αλλά αφού α = β, τότε β + β = 180 ο, που σημαίνει β = 90 ο.

Απάντηση: Ναι, η δήλωση είναι αλήθεια.

Δίνονται δύο ίσες γωνίες. Είναι αλήθεια ότι οι γωνίες που γειτνιάζουν με αυτές θα είναι επίσης ίσες;

Ρύζι. 7. Σχέδιο για παράδειγμα 4

Αν δύο γωνίες είναι ίσες με α, τότε οι αντίστοιχες γειτονικές τους γωνίες θα είναι 180 o - α. Δηλαδή θα είναι ίσοι μεταξύ τους.

Απάντηση: Η δήλωση είναι σωστή.

Alexandrov A.D., Werner A.L., Ryzhik V.I. και άλλα Γεωμετρία 7. - Μ.: Εκπαίδευση.
Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. και άλλα Γεωμετρία 7. 5η έκδ. - Μ.: Διαφωτισμός.
\Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Γεωμετρία 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, επιμέλεια V.A. Sadovnichigo. - Μ.: Εκπαίδευση, 2010.

Μέτρηση τμημάτων ().
Γενικό μάθημα γεωμετρίας στην 7η τάξη ().
Ευθεία γραμμή, τμήμα ().

Νο. 13, 14. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Γεωμετρία 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, επιμέλεια V.A. Sadovnichigo. - Μ.: Εκπαίδευση, 2010.
Βρείτε δύο γειτονικές γωνίες αν η μία είναι 4 φορές η άλλη.
Δεδομένης της γωνίας. Κατασκευάστε γειτονικές και κάθετες γωνίες για αυτό. Πόσες τέτοιες γωνίες μπορούν να κατασκευαστούν;
* Σε ποια περίπτωση λαμβάνονται περισσότερα ζεύγη κάθετων γωνιών: όταν τρεις ευθείες τέμνονται σε ένα σημείο ή σε τρία σημεία;

1. Παρακείμενες γωνίες.

Αν επεκτείνουμε την πλευρά οποιασδήποτε γωνίας πέρα από την κορυφή της, έχουμε δύο γωνίες (Εικ. 72): ∠ABC και ∠CBD, στις οποίες η μία πλευρά BC είναι κοινή και οι άλλες δύο, AB και BD, σχηματίζουν μια ευθεία γραμμή.

Για παράδειγμα, οι ∠ADF και ∠FDB είναι γειτονικές γωνίες (Εικ. 73).

Οι παρακείμενες γωνίες μπορούν να έχουν μεγάλη ποικιλία θέσεων (Εικ. 74).

Οι γειτονικές γωνίες αθροίζονται σε μια ευθεία γωνία, έτσι το άθροισμα δύο γειτονικών γωνιών είναι 180°

Ως εκ τούτου, μια ορθή γωνία μπορεί να οριστεί ως μια γωνία ίση με τη γειτονική γωνία της.

Για παράδειγμα, εάν μία από τις γειτονικές γωνίες είναι 54°, τότε η δεύτερη γωνία θα είναι ίση με:

180° - 54° = l26°.

2. Κάθετες γωνίες.

Αν επεκτείνουμε τις πλευρές της γωνίας πέρα από την κορυφή της, έχουμε κατακόρυφες γωνίες. Στο Σχήμα 75, οι γωνίες EOF και AOC είναι κάθετες. Οι γωνίες AOE και COF είναι επίσης κάθετες.

Δύο γωνίες ονομάζονται κάθετες αν οι πλευρές της μιας γωνίας είναι συνεχείς των πλευρών της άλλης γωνίας.

Έστω ∠1 = \(\frac(7)(8)\) ⋅ 90°(Εικ. 76). ∠2 δίπλα σε αυτό θα είναι ίσο με 180° - \(\frac(7)(8)\) ⋅ 90°, δηλαδή 1\(\frac(1)(8)\) ⋅ 90°.

Με τον ίδιο τρόπο, μπορείτε να υπολογίσετε με τι ίσον ∠3 και ∠4.

∠3 = 180° - 1\(\frac(1)(8)\) ⋅ 90° = \(\frac(7)(8)\) ⋅ 90°;

∠4 = 180° - \(\frac(7)(8)\) ⋅ 90° = 1\(\frac(1)(8)\) ⋅ 90° (Εικ. 77).

Βλέπουμε ότι ∠1 = ∠3 και ∠2 = ∠4.

Ωστόσο, για να βεβαιωθείτε ότι οι κατακόρυφες γωνίες είναι πάντα ίσες μεταξύ τους, δεν αρκεί να εξετάσουμε μεμονωμένα αριθμητικά παραδείγματα, καθώς τα συμπεράσματα που προκύπτουν από συγκεκριμένα παραδείγματα μπορεί μερικές φορές να είναι λανθασμένα.

Είναι απαραίτητο να επαληθευτεί η εγκυρότητα των ιδιοτήτων των κατακόρυφων γωνιών με απόδειξη.

Η απόδειξη μπορεί να πραγματοποιηθεί ως εξής (Εικ. 78):

∠α+∠ντο= 180°;

∠β+∠ντο= 180°;

(αφού το άθροισμα των παρακείμενων γωνιών είναι 180°).

∠α+∠ντο = ∠β+∠ντο

(καθώς η αριστερή πλευρά αυτής της ισότητας είναι ίση με 180°, και η δεξιά πλευρά της είναι επίσης ίση με 180°).

Αυτή η ισότητα περιλαμβάνει την ίδια γωνία Με.

Αν αφαιρέσουμε ίσα ποσά από ίσες ποσότητες, τότε θα παραμείνουν ίσα ποσά. Το αποτέλεσμα θα είναι: ∠ένα = ∠σι, δηλαδή οι κατακόρυφες γωνίες είναι ίσες μεταξύ τους.

3. Το άθροισμα των γωνιών που έχουν κοινή κορυφή.

Στο σχέδιο 79, τα ∠1, ∠2, ∠3 και ∠4 βρίσκονται στη μία πλευρά μιας ευθείας και έχουν κοινή κορυφή σε αυτήν την ευθεία. Συνολικά, αυτές οι γωνίες αποτελούν μια ευθεία γωνία, δηλ.

∠1 + ∠2 + ∠3 + ∠4 = 180°.

Στο σχήμα 80, οι ∠1, ∠2, ∠3, ∠4 και ∠5 έχουν κοινή κορυφή. Αυτές οι γωνίες αθροίζονται σε μια πλήρη γωνία, δηλαδή ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.

Άλλα υλικά