Линейные разностные уравнения с постоянными коэффициентами. Дифференциальные уравнения для "чайников"

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х) , которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Приведем пример:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все "игреки", а в другой – "иксы":

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию , обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему "Как решать дифференциальные уравнения":

Рассмотрим разностное уравнение n-го порядка

y(k) = F(k) (92)

Как и для дифференциальных уравнений, решение всегда опре­деляется для уравнений первого порядка и в общем случае не может быть найдено для уравнений более высокого порядка.

Вспомогательное решение.

Рассмотрим однородной уравнение первого порядка

a 1 (k)y(k+1) + a 0 (k)y(k) = 0, (93)

где a 0 (k)≠0 и a 1 (k)≠0. Его можно переписать в виде

y(k+1) = a(k)y(k). (94)

при k=0,1,2...

у(1)=а(0)у(0),

у(2)=а(1)а(0)у(0)

у(3)=а(2)а(1)а(0)у(0)

или, в общем случае,

так что общее решение уравнения (94) равно

Нижний предел произведения произволен, так как любое фик­сированное число множителей а(0), а(1), и а(2), ... можно объединить с произвольной постоянной С.

Решение однородного уравнения выше первого порядка в общем случае не выражается в виде элементарных функций, так как процедура, основанная на уравнениях (81) и (82), при зависящих от k коэффициентах перестает быть справедливой. Если известны все, кроме одного, независимые решения уравнения, то можно определить и ос­тавшееся решение. Как и для дифференциальных уравнений, в ряде отдель­ных случаев удается получить, решение в явном виде. Уравнение вида

a n f(k + n)y(k + n) + ... + a 1 f (k + 1)y(k + 1) + a n f(k)y(k) = 0,

где коэффициенты а i - постоянные величины, путем подстановки z(k)=f(k)y(k) сводится к разностному уравнению с постоянными коэффициентами. Проце­дура отчасти сходна с используемой для дифференциального уравнения Эй­лера, но замене в данном случае подлежит зависимая (а не независимая) пе­ременная. Этот метод широко используется при решении уравнений с пе­ременными коэффициентами.

Дифференциальные уравнения систем автоматического регулирования. Методика составления дифференциальных уравнений систем автоматического регулирования.

Общие замечания.

Системы автоматического регулирования разнообразны по своему назначению и конструктивному исполнению. Поведение САР может описываться обыкновенными дифференциальными уравнениями в частных производных, разностными уравнениями и т.д.

Любая САР представляет совокупность отдельных взаимодействующих друг с другом элементов, соединенных между собой связями. Первым этапом при составлении дифференциальных уравнений САР является разделение системы на отдельные элементы и составление дифференциальных уравнений этих элементов. Уравнения элементов и уравнения связей между отдельными элементами описывают процесс в системе регулирования, т.е. изменение по времени всех координат системы. Зная уравнения элементов и уравнения связей, можно составить структурную схему САР.

Структурная схема САР характеризует геометрию системы, т.е. показывает, из каких элементов состоит САР и как эти элементы связаны между собой. Состояние САР, а также каждого входящего в нее элемента характеризуется некоторым числом независимых переменных. Этими переменными могут быть как электрические величины (ток, напряжение, и т.д.), так и механические (скорость, угол поворота, перемещение и т.д.). Обычно, чтобы характеризовать состояние системы или ее элемента, выбирают одну обобщенную координату на входе системы или элемента (g(t)) и одну – на выходе (x(t)). В ряде случаев такое представление невозможно, так как система или ее элемент могут иметь несколько входных и выходных величин. В многомерных системах можно рассматривать векторные входную и выходную величины с размерностями, совпадающими соответственно с числом входных и выходных величин САР.

Составление и линеаризация дифференциальных уравнений элементов систем.

При составлении дифференциальных уравнений САР основной задачей является составление дифференциальных уравнений отдельных элементов системы. Уравнение отдельных элементов составляются на основе тех физических законов, которые характеризуют поведение элемента.

При составлении дифференциальных уравнений элементов САР следует стремиться возможно точнее описать поведение данного элемента. Однако сложность получаемых при этом уравнений затрудняет исследование свойств их решений. Поэтому при составлении дифференциальных уравнений необходимо стремиться к разумному компромиссу между возможно более полным описанием поведения элемента и возможностью обозрения и исследования полученных уравнений.

Если динамика элемента описывается линейным дифференциальным уравнением, то этот элемент называется линейным , если дифференциальное уравнение не линейно, то элемент называется нелинейным .

Для упрощения анализа, когда это возможно, приближенно заменяют нелинейные дифференциальные уравнения такими линейными уравнениями, решение которых с достаточной степенью точности совпадают с решениями нелинейных уравнений. Этот процесс замены нелинейного дифференциального уравнения линейным называется линеаризацией .

Если дифференциальное уравнение элемента нелинейно из-за нелинейности его статической характеристики, то линеаризация уравнения сводится к замене нелинейной характеристики элемента x =φ(g ) некоторой линейной функцией x = ag + b . Аналитически эта замена производится с помощью разложения в ряд Тейлора функции x =φ(g ) в окрестности точки, соответствующей установившемуся состоянию и отбрасывания всех членов содержащих отклонение ∆g входной величины элемента в степени выше первой. Геометрически это означает замену кривой x =φ(g ) касательной, проведенной к кривой в точке (x 0 , g 0), соответствующей установившемуся состоянию работы элемента (рис. 29). В других случаях линеаризация производится путем проведения секущей, мало отклоняющейся от функции x =φ(g ) в требуемом диапазоне изменения входной величины элемента.

Наряду с линеаризуемыми характеристиками имеются такие характеристики, которые не поддаются такой линеаризации. К ним относятся, например, характеристики, не разлагаемые в ряд Тейлора в окрестности точки установившегося состояния. Такие характеристики будем называть существенно нелинейными .

Рассмотрим процесс линеаризации нелинейного уравнения элемента с помощью ряда Тейлора. Пусть поведение элемента описывается нелинейным дифференциальным уравнением

F(x n , x ’ , x, g) = 0 (1). Тогда установившееся состояние элемента характеризуется уравнением F(0, 0, x, g) = 0 (2). пусть g 0 и х 0 – значения установившегося состояния. Тогда координаты g и х можно записать в виде x = x 0 + ∆x, g = g 0 + ∆g, где ∆g и ∆x – отклонение координат g и х от установившегося состояния. Уравнение (1) в отклонениях имеет вид:

F(∆x ’’ , ∆x ’ , x 0 + ∆x, g 0 + ∆g) = 0 (3).

Разложим левую часть уравнения (3) в ряд Тейлора относительно точки установившегося состояния (0, 0, x 0 , g 0):

Частные производные в левой части уравнения (4) представляют собой некоторые числа, величины которых зависят от вида функции F(x ’’ , x ’ , x, g) и значений координат x 0 и g 0 .

Считая отклонения ∆g, ∆x от установившегося состояния, а также их производные по времени малыми и пологая, что функция F(x ’’ , x ’ , x, g) достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в уравнении (4) все члены, которые содержат отклонения ∆g и ∆x, а также их производные в степени выше первой. Полученное уравнение (5) является линейным дифференциальным уравнением с постоянными коэффициентами,,,и представляет собой результат линеаризации уравнения (1).

Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x ’’ , x ’ , x, g) в окрестности точки, соответствующей установившемуся состоянию.

Процесс линеаризации уравнения (1) может быть геометрически интерпретирован следующим образом. В пространстве переменных x ’’ , x ’ , x, g уравнение (1) задает некоторую поверхность. Переход от уравнения (1) к линейному уравнению (5) означает замену поверхности некоторой касательной плоскостью, проведенной к поверхности в точке, соответствующей установившемуся состоянию. Естественно, что ошибка при такой замене тем меньше, чем меньше отличаются друг от друга точки поверхности и точки плоскости. Это справедливо лишь в некоторой малой окрестности установившегося состояния.

Понятие управляемости и наблюдаемости.

Процесс или объект принято называть полностью управляемым, если он может быть переведен из некоторого состояния х(t 0) в желаемое состояние равновесия х(t 1) за конечный интервал времени t 1 – t 0 . Другими словами, процесс является полностью управляемым, если существует управляющее воздействие m(t), определенное на конечном интервале времени t 0 ≤ t ≤ t 1 , которое переводит процесс из начального состояния х(t 0) в желаемое состояние равновесия х(t 1) за время t 1 – t 0 .

Необходимые и достаточные условия полной управляемости для случая дискретных систем можно сформулировать следующим образом.

Линейный дискретный процесс n-го порядка является полностью управляемым тогда и только тогда, когда векторы

s 1 = φ(-T)h(T),

s 2 = φ(-T)h(T),

s n = φ(-T)h(T)

линейно независимы.

Эти векторы возникают в связи со следующими преобразованиями.

(t) = Ax(t) + d m(t),

в котором m(t) – единственное управляющее воздействие. Случай единственного управляющего воздействия рассматривается ради упрощения интерпретации получаемых выражений. Уравнение переходных состояний процесса имеет вид

где φ(Т) – матрица перехода процесса и
.

Понятию управляемости можно дать еще и другое толкование, способствующее лучшему его пониманию. Пусть линейный многомерный процесс описывается векторным дифференциальным уравнением (t) = Ax(t) + D m(t), где х – n-мерный вектор состояния;

m – r-мерный вектор, представляющий управляющие воздействия;

А – квадратичная матрица коэффициентов n-го порядка;

D – матрица управления размера n×r.

Матрица А может быть приведена к диагональной форме

,

где λ i – собственные значения матрицы А линейного процесса, которые предполагаются все различными.

Применяя подстановку x=Tz, уравнение запишем в канонической форме

(t) = Λz(t) + ∆ m(t),

где
. Векторz будем называть каноническим вектором состояния.

Процесс, описываемый уравнением (t) = Ax(t) + D m(t), является управляемым, если матрица ∆ не содержит строк, все элементы которых равны нулю; координаты, соответствующие ненулевым строкам ∆, считаются управляемыми.

Пример:

Вывести дифференциальное уравнение центробежного маятника, который применяется в качестве чувствительного элемента в некоторых САР. Схема маятника изображена на рисунке. Входной величиной является угловая скорость ω, а выходной величиной – перемещение х платформы. При увеличении скорости вращения шары под действием центробежной силы расходятся и перемещают платформу. На платформу воздействует также сила упругости пружины, силы демпфирования и силы инерции.

Введем обозначения: с – коэффициент жесткости пружины; k – коэффициент вязкого трения; m – масса шара; М – масса частей, участвующих в поступательном движении вдоль оси ОХ; ω – угловая скорость вала; f 0 – сила предварительного поджатия пружины.

Для составления дифференциального уравнения центробежного маятника используем уравнение Лагранжа второго рода:
(I = 1, 2,…, n) (*). В качестве обобщенной координаты x i выберем выходную координату – перемещение платформы х. Найдем выражение для кинетической энергии Т, потенциальной энергии П и диссипативной функции R центробежного маятника. Из рисунка видно, что

ρ = r + l sin α, x = 2a(1 – cos α).

Кинетическая энергия системы Т = Т 1 + Т 2 + Т 3 , где Т 1 – кинетическая энергия во вращательном движении вокруг оси ОХ; Т 2 – кинетическая энергия шаров во вращательном движении вокруг точек А и А’; Т 3 – кинетическая энергия масс в поступательном движении вдоль оси ОХ. Имеем:

,

,
. (*1)

Потенциальная энергия маятника П = П 1 + П 2 + П 3 , где П 1 – потенциальная энергия масс, движущихся параллельно оси ОХ; П 2 – потенциальная энергия; П 3 – потенциальная энергия пружины. Для рассматриваемого случая имеем:

,
,
. (*2)

Найдем обобщенную диссипативную силу Q R . Благодаря наличию демпфера сила сухого трения мала по сравнению с силой вязкого трения и ею можно пренебречь. Согласно формуле
будем иметь

. (*3)

Вычислим значение отдельных слагаемых, входящих в уравнение Лагранжа (*):

,

,

.

Подставим полученные выражения в уравнение Лагранжа второго рода (*), тогда

Введем следующее обозначения:

,
,

; (*5)

. (*6)

С учетом принятых обозначений уравнение центробежного маятника запишется в виде

Уравнение (*7) представляет собой нелинейное дифференциальное уравнение. Состояние равновесия (х 0 , ω 0) является решением уравнения

Рассмотрим малые колебания маятника относительно состояния равновесия

х = х 0 + ∆х, ω = ω 0 + ∆ω. (*9)

Разложим функции f 1 (x), f 2 (x), f 3 (x, ω) в ряд Тейлора в окрестности состояния равновесия (х 0 , ω 0).

где функции F 1 (∆x), F 2 (∆x), F 3 (∆x, ∆ω) имеют более высокий порядок малости по сравнению с ∆x и ∆ω. Учитывая, что x’ = ∆x’ и x” = ∆x”, и принимая во внимание выражения (*8), (*9), (*10), уравнение (*7) можно переписать в виде

где функция

имеет более высокий порядок малости по сравнению с
. Отбрасывая функцию
, получим линеаризованное уравнение колебаний маятника относительно состояния равновесия (х 0 , ω 0)

, (*11)

,

(*12)

.

Системы, у которых входная и выходная последовательности и связаны линейным разностным уравнением с постоянными коэффициентами, образуют подмножество класса линейных систем с постоянными параметрами. Описание ЛПП-систем разностными уравнениями очень важно, так как оно часто позволяет найти эффективные способы построения таких систем. Более того, по разностному уравнению можно определить многие характеристики рассматриваемой системы, включая собственные частоты и их кратность, порядок системы, частоты, соответствующие нулевому коэффициенту передачи, и т. д.

В самом общем случае линейное разностное уравнение -го порядка с постоянными коэффициентами, относящееся к физически реализуемой системе, имеет вид

(2.18)

где коэффициенты и описывают конкретную систему, причем . Каким именно образом порядок системы характеризует математические свойства разностного уравнения, будет показано ниже. Уравнение (2.18) записано в виде, удобном для решения методом прямой подстановки. Имея набор начальных условий [например, , для ] и входную последовательность , по формуле (2.18) можно непосредственно вычислить выходную последовательность для . Например, разностное уравнение

(2.19)

с начальным условием и можно решить подстановкой, что дает

Хотя решение разностных уравнений прямой подстановкой и целесообразно в некоторых случаях, значительно полезнее получить решение уравнения в явном виде. Методы нахождения таких решений подробно освещены в литературе по разностным Уравнениям, и здесь будет дан лишь краткий обзор. Основная идея сводится к получению двух решений разностного уравнения: однородного и частного. Однородное решение получается путем подстановки нулей вместо всех членов, содержащих элементы входной последовательности , и определения отклика при нулевой входной последовательности. Именно этот класс решений описывает основные свойства заданной системы. Частное решение получают, подбирая вид последовательности на выходе при заданной входной последовательности . Для определения произвольных постоянных однородного решения используются начальные условия. В качестве примера решим этим методом уравнение (2.19). Однородное уравнение имеет вид

(2.20)

Известно, что характеристическими решениями однородных уравнений, соответствующих линейным разностным уравнениям с постоянными коэффициентами, являются решения вида .Поэтому, подставив в уравнение (2.20) вместо , получим

(2.21)

Частное решение, соответствующее входной последовательности , попробуем найти в виде

(2.22)

Из уравнения (2.19) получаем

Поскольку коэффициенты при равных степенях должны совпадать, B,СиDдолжны быть равны

(2.24)

Таким образом, общее решение имеет вид

(2.25)

Коэффициент определяется из начального условия , откуда и

(2.26)

Выборочная проверка решения (2.26) при показывает полное его совпадение с приведенным выше прямым решением. Очевидное преимущество решения (2.26) состоит в том, что оно позволяет весьма просто определить для любого конкретного .

Фиг. 2.7. Схема реализации простого разностного уравнения первого порядка.

Важное значение разностных уравнений состоит в том, что они непосредственно определяют способ построения цифровой системы. Так, разностное уравнение первого порядка самого общего вида

можно реализовать с помощью схемы, изображенной на фиг. 2.7. Блок «задержка» осуществляет задержку на один отсчет. Рассмотренная форма построения системы, в которой для входной и выходной последовательностей используются раздельные элементы задержки, называется прямой формой 1. Ниже мы обсудим различные методы построения этой и других цифровых систем.

Разностное уравнение второго порядка самого общего вида

Фиг. 2.8. Схема реализации разностного уравнения второго порядка.

может быть реализовано с помощью схемы, приведенной на фиг. 2.8. В этой схеме для входной и выходной последовательностей также используются раздельные элементы задержки.

Из последующего изложения материалов этой главы станет ясно, что системы первого и второго порядка могут быть использованы при реализации систем более высокого порядка, так как последние могут быть представлены в виде последовательно или параллельно соединенных систем первого и второго порядка.

Р а з н о с т н ы м у р а в н е н и е м наз. уравнение вида

где - искомая и F - заданная функции. Замена в (2) конечных разностей их выражениями через значения искомой функции согласно (1) приводит к уравнению вида

Если , т. е. уравнение (3) действительно содержит как , так и , то уравне-вие (3) наз. р а з н о с т н ы м у р а в н е н и е м m-го п о р я д к а, или д и ф ф е р е н ц и а л ь н о-р а з н о с т н ы м у р а в н е н и е м.

(6)

где - произвольные постоянные.

3) Общее решение неоднородного Р. у. (4) представляется в виде суммы какого-либо частного его решения и общего решения однородного Р. у. (5).

Частное решение неоднородного уравнения (5) можно построить, исходя из общего решения (6) однородного уравнения, путем применения метода вариации произвольных постоянных (см., напр., ). В случае Р. у. с постоянными коэффициентами

можно непосредственно найти тлинейно независимых частных решений. Для этого рассматривается харак-теристич. уравнение

и ищутся его корни . Если все корни простые, то функции

образуют линейно независимую систему решений уравнения (7). В случае, когда - корень кратности r, линейно независимыми являются решения

Если коэффициенты а 0 , a 1 , . . ., а т действительные и уравнение (8) имеет комплексный корень, напр. простой корень , то вместо комплексных решений выделяют два линейно независимых действительных решения

Пусть имеется Р. у. 2-го порядка с постоянными действительными коэффициентами

(9) Характеристич. уравнение

имеет корни

Общее решение уравнения (9) в случае удобно записывать в виде

(10)

где с 1 и с 2 - произвольные постоянные. Если и - комплексно сопряженные корни:

то другое представление общего решения имеет вид

В случае кратного корня общее решение может быть получено предельным переходом из (10) или (11). Оно имеет вид

Как и в случае уравнений произвольного порядка, для Р. у. 2-го порядка можно рассматривать задачу Коши или различные краевые задачи. Напр., для задачи Коши

Решение обыкновенных линейных разностных уравнений

с постоянными коэффициентами

Связь выхода и входа линейной дискретной системы может быть описана обыкновенным линейным разностным уравнением с постоянными коэффициентами

,

где y[ n] - выходной сигнал в момент n ,

x[ n] - входной сигнал в момент n ,

a i , b k – постоянные коэффициенты.

Для решения таких уравнений могут использоваться два метода

• Прямой метод,
• Метод Z – преобразования.

Вначале рассмотрим решение линейного разностного уравнения с помощью прямого метода.

Общее решение неоднородного (с отличной от нуля правой частью) линейного разностного уравнения равно сумме общего решения линейного однородного разностного уравнения и частного решения неоднородного уравнения

Общее решение однородного разностного уравнения (zero- input response ) y h [ n]

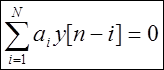
определяется в виде

.

Подставляя это решение в однородное уравнение, получаем

Такой полином называют характеристическим полиномом системы. Он имеет N корней . Корни могут быть действительными или комплексными и некоторые корни - совпадающими (кратными).

Если корни являются действительными и разными, то решение однородного уравнения имеет вид

где коэффициенты

Если некоторый корень, например, λ 1 имеет кратность m , то соответствующий ему член решения приобретает форму

Если все коэффициенты однородного уравнения и соответственно характеристического многочлена действительны, то два члена решения, соответствующие простым комплексно сопряженным корням можно представить (записать) в виде , при этом коэффициенты A, B определяются по начальным условиям.

Вид частного решения y p [ n] уравнения зависит от правой части (входного сигнала) и определяется согласно нижеприведенной таблице

Таблица 1. Вид частного решения для различного характера правой части

Входной сигнал x[n]	Частное решение y p [n]
A (константа)

Решение линейного разностного уравнения методом Z – преобразования заключается в применении Z – преобразования к уравнению с использованием свойств линейности и временного сдвига. В результате получается линейное алгебраическое уравнение относительно Z - изображения искомой функции. Обратное Z – преобразование дает искомое решение во временной области. Для получения обратного Z – преобразования чаще всего используется разложение рационального выражения на простые (элементарные) дроби, так как обратное преобразование от отдельной элементарной дроби имеет простой вид.

Заметим, что для перехода во временную область могут использоваться и другие методы вычисления обратного Z – преобразования.

Пример . Определим отклик (выходной сигнал) системы, описываемой линейным разностным уравнением , на входной сигнал

Решение .

1. Прямой метод решения уравнения.

Однородное уравнение . Его характеристический полином .

Корни полинома .

Решение однородного уравнения .

Поскольку,то частное решение определяем в виде .

Подставляем его в уравнение

Для нахождения константы К примем n = 2 . Тогда

Или , К=2,33

Отсюда частное решение и общее решение разностного уравнения (1)

Найдем константы С 1 и С 2 . Для этого положим n = 0 , тогда из исходного разностного уравнения получаем . Для данного уравнения

Поэтому . Из выражения (1)

Следовательно,

.

Из выражения (1) для n = 1 имеем .
Получаем следующие два уравнения для С 1 и С 2

.

Решение этой системы дает следующие значения: С 1 =0,486 и С 2 = -0,816.

Следовательно, общее решение данного уравнения

2. Решение методом Z – преобразования.

Возьмем Z – преобразование от исходного разностного уравнения , учитывая свойство (теорему) временного сдвига . Получаем