Mengapakah formula Poisson dipanggil formula fenomena jarang berlaku. Formula pengedaran dan Poisson
kebarangkalian p = 0.7 . Cari nombor paling berkemungkinan m 0 orang yang akan datang ke mesyuarat itu dan kebarangkalian yang sepadan P n (m 0 ) .
Penyelesaian. Oleh kerana P 50 (m 0 )= C 50 m 0 (0.7)m 0 (0.3)50 − m 0 , masalahnya ialah untuk mencari integer bukan negatif m 0 ≤ 50 yang memaksimumkan fungsi P 50 (m 0 ) . Kami melihat di atas bahawa nombor sedemikian diberikan oleh formula (6.4). DALAM
P 50 (35)= C 50 35 (0.7)35 (0.3)15 ≈ 0.123.
6.4. Formula Poisson
Formula (6.1) dan (6.3) memberikan kebarangkalian tepat yang dikaitkan dengan skema percubaan Bernoulli bebas. Walau bagaimanapun, pengiraan menggunakan formula ini, terutamanya apabila nilai yang besar n dan m adalah sangat sukar. Adalah menarik minat praktikal untuk mendapatkan formula anggaran yang agak mudah untuk mengira kebarangkalian yang sepadan. Pertama formula yang serupa dibiakkan pada tahun 1837 ahli matematik Perancis dan ahli fizik Simon Poisson (1781–1840). Di bawah ialah rumusan keputusan Poisson.
Pertimbangkan skim Bernoulli bagi percubaan bebas di mana bilangan percubaan n adalah "agak besar", kebarangkalian "kejayaan" p adalah "agak kecil", dan hasil darab λ= np ialah "tidak kecil mahupun besar"41. Di bawah keadaan ini, formula
Ini adalah anggaran Poisson yang terkenal untuk taburan binomial. Bukti formula (6.6) akan diberikan dalam lampiran bahagian ini.
41 Maksud tepat istilah yang dipetik akan diterangkan di bawah, khususnya dalam § 6e.
Fungsi di sebelah kanan formula (6.6) dipanggil
Pengagihan Poisson:
Dengan tatatanda ini, p(k, λ) akan menjadi ungkapan anggaran untuk kebarangkalian b(k;n, λn) apabila n "cukup besar".
Sebelum membincangkan formula (6.6), kami membentangkan sangat contoh ilustrasi kegunaannya.
Nilai taburan binomial dan nilai taburan Poisson pada n = 100, p = 0.01, λ= 1 dibentangkan dalam Jadual. 6.2. Seperti yang kita dapat lihat, ketepatan formula anggaran agak tinggi.
Semakin besar n, semakin tinggi ketepatan formula Poisson. Ini digambarkan oleh contoh berikut. Mari kita hitung kebarangkalian p k bahawa dalam masyarakat 500 orang tepat k orang dilahirkan pada hari tertentu dalam setahun. Jika 500 orang ini dipilih secara rawak, maka skema Bernoulli boleh digunakan daripada n = 500 percubaan dengan kebarangkalian "berjaya" p = 1365. Pengiraan mengikut formula tepat (6.1) dan formula anggaran (6.6) pada λ= 500365≈ 1.3699 dibentangkan dalam Jadual. 6.3. Seperti yang kita dapat lihat, ralat hanya di tempat perpuluhan keempat, yang agak boleh diterima untuk latihan.
Jadual 6.2 |
|||
b(k; 100, 1.100) | p(k; 1) |
||
Jadual 6.3.
b(k; 500.1/365) | p(k, λ) | |||
Pertimbangkan contoh tipikal berikut untuk menggunakan formula |
||||
Poisson. | ||||
Hendaklah diketahui bahawa kebarangkalian "kegagalan" dalam pengendalian pertukaran telefon bagi setiap panggilan ialah 0.002. Menerima 1000 panggilan. Tentukan kebarangkalian bahawa 7 "kegagalan" akan berlaku dalam kes ini.
Penyelesaian. Adalah wajar untuk menganggap bahawa dalam keadaan biasa panggilan yang tiba di pertukaran telefon adalah bebas antara satu sama lain. Kami akan mempertimbangkan "kejayaan" dalam ujian - panggilan - kegagalan pertukaran telefon. Kebarangkalian kegagalan (p = 0.002) boleh dianggap sebagai nilai "cukup kecil", dan bilangan panggilan (n = 1000) adalah "cukup besar". Oleh itu, kita berada dalam keadaan teorem Poisson. Untuk parameter λ, kami memperoleh nilai
Sekarang mari kita bincangkan had kebolehgunaan formula Poisson. Pada
Apabila menggunakan sebarang formula anggaran, persoalan tentang had kebolehgunaannya timbul secara semula jadi. Dalam berbuat demikian, kita menghadapi dua aspek masalah. Pertama, adalah wajar untuk bertanya dalam keadaan sebenar apakah undang-undang Poisson boleh digunakan? Pengalaman menunjukkan bahawa taburan Poisson yang mudah mempunyai kebolehgunaan yang agak universal. Secara umum, dari sudut aplikasi, teorem matematik adalah baik dan buruk dalam erti kata berikut: teorem yang baik terus beroperasi walaupun syaratnya dilanggar, dan teorem yang buruk serta-merta berhenti menjadi benar jika syarat untuk terbitannya dilanggar. . Teorem Poisson (6.6) adalah baik dan juga cemerlang dalam pengertian ini. Iaitu, undang-undang Poisson terus beroperasi walaupun syarat-syarat skim Bernoulli dilanggar (iaitu, seseorang boleh menganggap kebarangkalian kejayaan yang berubah-ubah dan juga pergantungan yang tidak terlalu kuat terhadap keputusan percubaan individu)42. Seseorang juga boleh berhujah bahawa pengedaran Poisson mempunyai kebolehgunaan yang agak universal. Ini mesti difahami dalam erti kata bahawa jika data eksperimen menunjukkan bahawa hukum Poisson tidak terpakai, manakala, menurut akal, ia perlu beroperasi, adalah lebih wajar untuk mempersoalkan kestabilan statistik data kami daripada mencari beberapa undang-undang pengedaran lain. Dengan kata lain, Taburan Poisson ialah rumusan matematik yang sangat berjaya bagi salah satu undang-undang alam sejagat (dalam kebolehgunaan teori kebarangkalian).
Kedua, persoalan timbul tentang susunan magnitud parameter tersebut yang termasuk dalam formula Poisson, dan yang mana di atas kami menggunakan istilah samar "agak besar", "agak kecil", "tidak kecil dan besar". Sekali lagi, amalan menggunakan formula (6.6) memberikan jawapan yang menjelaskan. Ternyata formula Poisson cukup tepat untuk permohonan praktikal jika bilangan percubaan n mempunyai susunan
42 Sememangnya, ciri pengedaran Poisson ini tidak seharusnya disalahgunakan. Sebagai contoh, undang-undang Poisson jelas dilanggar dalam situasi di mana keputusan ujian individu sangat bergantung.
beberapa puluh (sebaik-baiknya ratusan), dan nilai parameter λ = np terletak dalam julat dari 0 hingga 10.
Untuk menggambarkan penggunaan formula Poisson, pertimbangkan contoh lain.
Perlu diketahui bahawa 10,000 kismis bergantung pada membakar 1000 roti kismis manis. Ia diperlukan untuk mencari taburan bilangan kismis dalam beberapa roti yang dipilih secara rawak.
Penyelesaian. Kami membentuk urutan ujian bebas seperti berikut. Akan ada n = 10,000 percubaan secara keseluruhan (mengikut bilangan kismis), iaitu: nombor percubaan k ialah kita menentukan sama ada kita mendapat kismis nombor k ke dalam bun yang dipilih secara rawak43. Kemudian, oleh kerana terdapat 1000 roti kesemuanya, kebarangkalian bahawa kismis ke-k masuk ke dalam bun kami ialah p = 1/1000 (dengan mengandaikan adunan sebati semasa menyediakan roti). Kami kini menggunakan taburan Poisson dengan parameter λ= np = 10000 11000= 10. Kami mendapat:
P 10000 (k )≈ p (k ,10)= 10 k e − 10 .
Khususnya, kebarangkalian bahawa kita akan mendapat roti tanpa kismis sama sekali (k = 0) adalah sama dengan e − 10 ≈ 0.5 10 − 4 . Bilangan kismis yang paling berkemungkinan ialah, mengikut formula (6.4), bersamaan dengan 10. Kebarangkalian yang sepadan
P 10000(10) ≈ 10 10 e − 10 ≈ 0.125 . 10!
Contoh dengan roti dan kismis, walaupun perkataan biasa, sangat watak umum. Jadi, bukannya kismis dalam roti, anda boleh bercakap, sebagai contoh, tentang bilangan bakteria dalam setitik air yang diambil dari baldi yang dicampur dengan baik. Contoh yang lain. Mari kita anggap atom bahan radioaktif pereputan secara bebas antara satu sama lain, dan semasa selang masa tertentu, pereputan atom tertentu berlaku dengan
43 Ambil perhatian bahawa pembelian roti di kedai boleh dilihat sebagai pilihan rawak.
Biarkan eksperimen dijalankan ujian berulang mengikut skema Bernoulli dan bilangan percubaan adalah besar, kebarangkalian berlakunya peristiwa yang diperhatikan dalam satu percubaan adalah kecil, dan parameternya adalah nilai tetap. Kemudian untuk kebarangkalian - kebarangkalian bahawa peristiwa dalam ujian akan muncul sekali, hubungannya adalah benar
 . (3.1)
. (3.1)
Apabila mengira kebarangkalian dalam eksperimen rawak sedemikian, anda boleh menggunakan formula anggaran
 , (3.2)
, (3.2)
yang dipanggil Formula Poisson, dan nombornya ialah parameter Poisson.
Tugasan 3.1. Kebarangkalian perkahwinan dalam pembuatan produk tertentu ialah 0.008. Cari kebarangkalian bahawa semasa pemeriksaan akan terdapat tidak lebih daripada dua item yang rosak di antara 500 item.
Penyelesaian: memandangkan kebarangkalian adalah kecil dan bilangan percubaan adalah besar, kita boleh menggunakan formula Poisson dengan parameter . Kebarangkalian yang diingini ialah kebarangkalian jumlah tiga peristiwa: terdapat dua produk yang rosak, satu atau tiada. sebab tu
Definisi 3.1
Aliran peristiwa ialah urutan peristiwa yang berlaku pada masa rawak.
Sebagai contoh, aliran acara akan menjadi panggilan tiba di PBX, isyarat semasa sesi radio, mesej tiba di pelayan, dsb.
Definisi 3.2
Aliran peristiwa dipanggil Poisson(paling mudah) jika ada sifat-sifat berikut:
1. Harta pegun, iaitu kadar aliran- malar.
2. sifat biasa, mereka. berlakunya dua atau lebih peristiwa dalam selang yang kecil boleh dikatakan mustahil.
3. Harta tiada kesan, mereka. kebarangkalian berlakunya peristiwa dalam tempoh masa tidak bergantung pada berapa banyak peristiwa telah muncul dalam mana-mana segmen lain.
Jika kita nyatakan - kebarangkalian berlakunya peristiwa aliran Poisson dengan keamatan dari semasa ke semasa , maka formula itu sah:
 . (3.3)
. (3.3)
Tugasan 3.2. Sebuah syarikat insurans melayani 10,000 pelanggan. Kebarangkalian bahawa pelanggan akan menghubungi syarikat dalam masa satu hari ialah 0.0003. Apakah kebarangkalian bahawa 4 pelanggan akan menghubunginya dalam masa dua hari?
Penyelesaian: Keamatan aliran pelanggan dalam satu hari adalah sama dengan
Oleh itu,  .
.
Menyelesaikan masalah 3.1 dan 3.2 dalam persekitaran Mathcad ditunjukkan dalam rajah. 3.

Tugasan 3.3. Kebarangkalian kegagalan pembaca turnstile kereta bawah tanah dalam masa sejam adalah kecil. Cari kebarangkalian ini jika kebarangkalian akan berlaku sekurang-kurangnya satu kegagalan dalam 8 jam ialah 0.98, dan jika diketahui purata 1000 orang melalui pintu putar sejam?
Penyelesaian: Menurut formula (1.3) dan (3.3) dengan , kebarangkalian bahawa terdapat sekurang-kurangnya satu kegagalan dalam masa 8 jam adalah sama dengan:
Menggunakan arahan simbolik, dan kemudian kebarangkalian yang diingini ditentukan.
Pertimbangkan persamaan
Di mana fungsi ditakrifkan pada .
Persamaan ini mentakrifkan perambatan gelombang perjalanan dalam medium homogen berdimensi n dengan kelajuan a pada titik masa t > 0 .
Agar penyelesaian menjadi jelas, adalah perlu untuk menentukan keadaan awal. Keadaan awal menentukan keadaan ruang (atau, seperti yang mereka katakan, "gangguan awal") pada satu ketika dalam masa t = 0 :

Kemudian formula Kirchhoff umum memberikan penyelesaian kepada masalah ini.
Kirchhoff sendiri menganggap hanya kes tiga dimensi.
Idea untuk mendapatkan penyelesaian
Terbitan ringkas penyelesaian kepada masalah utama menggunakan transformasi Fourier. Formula Kirchhoff umum mempunyai pandangan seterusnya:
 .
.
Jika persamaan gelombang mengandungi bahagian kanan f, istilah akan muncul di sebelah kanan formula:

Akibat Fizikal

Bahagian hadapan gelombang yang mendahului dan mengekori daripada gangguan yang dilokalkan di angkasa lepas bertindak ke atas pemerhati untuk tempoh masa yang terhad
Biar masuk detik awal masa t= 0 pada beberapa padat M terdapat gangguan setempat ( dan/atau ). Jika kita berada pada satu ketika, maka, seperti yang dapat dilihat dari formula (kawasan integrasi), kita akan merasakan gangguan itu selepas masa ![]() .
.
Di luar selang masa di mana ![]() , fungsi u(x 0 , t) adalah sama dengan sifar.
, fungsi u(x 0 , t) adalah sama dengan sifar.
Oleh itu, gangguan awal, disetempatkan di ruang angkasa, menyebabkan pada setiap titik dalam ruang tindakan yang disetempatkan dalam masa, iaitu, gangguan merambat dalam bentuk gelombang dengan bahagian hadapan dan belakang, yang menyatakan prinsip Huygens). Di dalam pesawat, prinsip ini dilanggar. Justifikasi untuk ini ialah hakikat bahawa pembawa gangguan, yang padat dalam , tidak lagi padat dalam , tetapi akan membentuk silinder tak terhingga, dan, akibatnya, gangguan akan tidak terhad dalam masa (y gelombang silinder hujung belakang hilang).
Formula Poisson-Parseval
Penyelesaian Persamaan Ayunan Membran
dengan syarat awal
diberikan oleh formula:
tex" alt=" +\frac(\partial)(\partial t)\frac(1)(2\pi a)\iint\limits_(rFormula D "Alamber
Penyelesaian satu dimensi persamaan gelombang
dengan syarat awal
mempunyai bentuk

Ke kawasan II ciri datang dari satu keluarga sahaja
Apabila menggunakan formula d "Alembert, ia harus diambil kira bahawa kadangkala penyelesaian mungkin tidak unik di seluruh kawasan yang sedang dipertimbangkan. Penyelesaian persamaan gelombang diwakili sebagai hasil tambah dua fungsi: u(x,t) = f(x + at) + g(x − at)
, iaitu ditentukan oleh dua keluarga ciri: . Contoh yang ditunjukkan dalam rajah di sebelah kanan menggambarkan persamaan gelombang untuk rentetan separa tak terhingga, dan keadaan awal di dalamnya hanya diberikan pada garis hijau x≥0. Ia boleh dilihat di kawasan itu saya kedua-dua ξ-ciri dan η-ciri datang, manakala di rantau ini II hanya ada ξ-ciri. Iaitu, di kawasan itu II Formula D'Alembert tidak berfungsi.
Aplikasi formula
DALAM Pandangan umum formula Kirchhoff agak rumit, dan oleh itu penyelesaian masalah fizik matematik menggunakannya biasanya sukar. Walau bagaimanapun, seseorang boleh menggunakan kelinearan persamaan gelombang ![]() dengan keadaan awal dan cari penyelesaian dalam bentuk hasil tambah tiga fungsi: u(x,t) = A(x,t) + B(x,t) + C(x,t)
yang memuaskan syarat berikut:
dengan keadaan awal dan cari penyelesaian dalam bentuk hasil tambah tiga fungsi: u(x,t) = A(x,t) + B(x,t) + C(x,t)
yang memuaskan syarat berikut:
Dengan sendirinya, operasi sedemikian tidak memudahkan penggunaan formula Kirchhoff, tetapi untuk beberapa masalah adalah mungkin untuk memilih penyelesaian, atau mengurangkan masalah multidimensi kepada satu dimensi dengan menukar pembolehubah. Sebagai contoh, biarkan ![]() . Kemudian, membuat penggantian ξ = x + 3y − 2z
, persamaan untuk masalah "C" akan berbentuk:
. Kemudian, membuat penggantian ξ = x + 3y − 2z
, persamaan untuk masalah "C" akan berbentuk:
Oleh itu, kita sampai kepada persamaan satu dimensi, yang bermaksud kita boleh menggunakan formula d "Alembert:
Kerana pariti keadaan awal, penyelesaian akan mengekalkan penampilannya di seluruh kawasan t > 0 .
kesusasteraan
Mikhailov V.P., Mikhailova T.V., Shabunin M.I. Koleksi tugas biasa kursus Persamaan fizik matematik. - M.: MIPT, 2007. - ISBN 5-7417-0206-6
Pautan
Yayasan Wikimedia. 2010 .
Lihat apakah "Formula Poisson" dalam kamus lain:
Formula Kirchhoff ialah ungkapan analitikal untuk menyelesaikan persamaan pembezaan separa hiperbolik (yang dipanggil "persamaan gelombang") dalam segala-galanya ruang tiga dimensi. Dengan kaedah keturunan (iaitu, dengan mengurangkan dimensi) daripadanya anda boleh ... ... Wikipedia
Formula Kirchhoff ialah ungkapan analitikal untuk menyelesaikan persamaan pembezaan separa hiperbolik (yang dipanggil "persamaan gelombang") di seluruh ruang. Dengan kaedah penurunan (iaitu, dengan mengurangkan dimensi), seseorang boleh mendapatkan penyelesaian dua dimensi daripadanya ... ... Wikipedia
Formula yang mewakili perpaduan. klasik penyelesaian u(x, t) masalah Koshi untuk persamaan gelombang dalam ruang-masa tiga dimensi, (di mana c ialah kelajuan perambatan isyarat) jika data awal f(x), p(x), masing-masing adalah tiga kali dan dua kali ... ... Ensiklopedia Fizikal
Formula untuk mengira jumlah siri bentuk Jika penjelmaan Fourier (agak berbeza daripada biasa, dinormalkan) bagi fungsi F (x), maka (m dan n ialah integer). Ini ialah P. f. Dengan.; dia mungkin…… Ensiklopedia Soviet yang Hebat
Formula P. f. Dengan. memegang jika, sebagai contoh, fungsi g(x) boleh disepadukan secara mutlak pada selang, mempunyai variasi sempadan, dan P.f. Dengan. juga ditulis sebagai di mana ai dan b adalah mana-mana dua nombor positif, memenuhi syarat ab=2p, dan c(u).is… … Ensiklopedia Matematik
1) Sama seperti kamiran Poisson 2) Formula yang memberikan perwakilan kamiran bagi penyelesaian masalah Cauchy untuk persamaan gelombang dalam ruang: dan mempunyai bentuk (1) di mana nilai purata fungsi j pada sfera Duduk dalam ruang (x, y, z) jejari di Dengan… … Ensiklopedia Matematik
Taburan terbahagi tak terhingga dalam teori kebarangkalian ialah taburan pembolehubah rawak supaya ia boleh diwakili sebagai bilangan arbitrari istilah bebas yang diagihkan sama rata. Isi 1 Definisi 2 ... ... Wikipedia
Di mana λ adalah sama dengan purata bilangan kejadian kejadian dalam yang sama ujian bebas, iaitu λ = n × p, di mana p ialah kebarangkalian kejadian dalam satu percubaan, e = 2.71828 .
Siri pengedaran hukum Poisson mempunyai bentuk:
Tugasan perkhidmatan. Kalkulator dalam talian digunakan untuk membina taburan Poisson dan mengira semua ciri siri: jangkaan matematik, varians dan sisihan piawai. Laporan dengan keputusan itu disediakan dalam format Word. Dalam kes apabila n adalah besar, dan λ = p n > 10, formula Poisson memberikan anggaran yang sangat kasar dan teorem Moivre-Laplace tempatan dan integral digunakan untuk mengira P n (m).
Ciri berangka pembolehubah rawak X
Jangkaan matematik taburan PoissonM[X] = λ
Varian taburan Poisson
D[X] = λ
Contoh #1. Benih mengandungi 0.1% rumpai. Apakah kebarangkalian untuk mencari 5 biji rumpai dalam pemilihan rawak 2000 biji?
Penyelesaian.
Kebarangkalian p adalah kecil, dan nombor n adalah besar. np = 2 P(5) = λ 5 e -5 /5! = 0.03609
Nilai yang dijangkakan: M[X] = λ = 2
Penyerakan: D[X] = λ = 2
Contoh #2. Terdapat 0.4% biji rumpai di antara biji rai. Lukiskan hukum taburan bilangan rumpai dengan pemilihan rawak sebanyak 5000 biji. Cari nilai yang dijangkakan dan varians pembolehubah rawak ini.
Penyelesaian. Jangkaan: M[X] = λ = 0.004*5000 = 20. Varians: D[X] = λ = 20
Undang-undang pengedaran:
| X | 0 | 1 | 2 | … | m | … |
| P | e-20 | 20e-20 | 200e-20 | … | 20 meter -20 / meter! | … |
Contoh #3. Di pertukaran telefon, sambungan yang salah berlaku dengan kebarangkalian 1/200. Cari kebarangkalian bahawa antara 200 sambungan akan ada:
a) betul-betul satu sambungan yang salah;
b) kurang daripada tiga sambungan yang salah;
c) lebih daripada dua sambungan yang salah.
Penyelesaian. Mengikut keadaan masalah, kebarangkalian sesuatu peristiwa adalah kecil, jadi kita menggunakan formula Poisson (15).
a) Diberi: n = 200, p = 1/200, k = 1. Cari P 200 (1).
Kita mendapatkan: ![]() . Kemudian P 200 (1) ≈ e -1 ≈ 0.3679.
. Kemudian P 200 (1) ≈ e -1 ≈ 0.3679.
b) Diberi: n = 200, p = 1/200, k< 3. Найдем P 200 (k < 3).
Kami mempunyai: a = 1. 
c) Diberi: n = 200, p = 1/200, k > 2. Cari P 200 (k > 2).
Masalah ini boleh diselesaikan dengan lebih mudah: cari kebarangkalian peristiwa bertentangan, kerana dalam kes ini adalah perlu untuk mengira istilah yang lebih sedikit. Mengambil kira kes sebelum ini, kita ada
Pertimbangkan kes di mana n cukup besar dan p cukup kecil; kita letak np = a, dengan a ialah beberapa nombor. Dalam kes ini, kebarangkalian yang dikehendaki ditentukan oleh formula Poisson:

Kebarangkalian berlakunya peristiwa k dalam masa tempoh t juga boleh didapati menggunakan formula Poisson:
di mana λ ialah keamatan aliran peristiwa, iaitu purata bilangan peristiwa yang muncul setiap unit masa.
Contoh #4. Kebarangkalian bahawa sesuatu bahagian itu rosak ialah 0.005. 400 bahagian diperiksa. Nyatakan formula untuk mengira kebarangkalian bahawa lebih daripada 3 bahagian rosak.
Contoh nombor 5. Kebarangkalian kemunculan bahagian yang rosak apabila ia pengeluaran besar-besaran adalah sama dengan p. tentukan kebarangkalian bahawa kumpulan N bahagian mengandungi a) tepat tiga bahagian; b) tidak lebih daripada tiga bahagian yang rosak.
p=0.001; N=4500
Penyelesaian.
Kebarangkalian p adalah kecil, dan nombor n adalah besar. np = 4.5< 10. Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон.
Pembolehubah rawak X mempunyai julat (0,1,2,...,m). Kebarangkalian nilai ini boleh didapati dengan formula:
Mari cari siri pengedaran X.
Di sini λ = np = 4500*0.001 = 4.5
P(0) = e - λ = e -4.5 = 0.01111
P(1) = λe -λ = 4.5e -4.5 = 0.04999 
Maka kebarangkalian bahawa sekumpulan bahagian N mengandungi tepat tiga bahagian adalah sama dengan: ![]()
Maka kebarangkalian bahawa sekumpulan bahagian N mengandungi tidak lebih daripada tiga bahagian yang rosak ialah:
P(x<3) = P(0) + P(1) + P(2) = 0,01111 + 0,04999 + 0,1125 = 0,1736
Contoh nombor 6. Pertukaran telefon automatik menerima, secara purata, N panggilan sejam. Tentukan kebarangkalian bahawa dalam minit tertentu dia akan menerima: a) tepat dua panggilan; b) lebih daripada dua panggilan.
N = 18
Penyelesaian.
Dalam satu minit, ATS menerima purata λ = 18/60 min. = 0.3
Dengan mengandaikan bahawa nombor rawak X panggilan diterima di PBX dalam satu minit,
mematuhi undang-undang Poisson, dengan formula kita dapati kebarangkalian yang diperlukan
Mari cari siri pengedaran X.
Di sini λ = 0.3
P(0) = e - λ = e -0.3 = 0.7408
P(1) = λe -λ = 0.3e -0.3 = 0.2222 ![]()
Kebarangkalian bahawa dia akan menerima tepat dua panggilan dalam satu minit adalah:
P(2) = 0.03334
Kebarangkalian bahawa dia akan menerima lebih daripada dua panggilan dalam satu minit adalah:
P(x>2) = 1 - 0.7408 - 0.2222 - 0.03334 = 0.00366
Contoh nombor 7. Kami menganggap dua elemen yang berfungsi secara bebas antara satu sama lain. Tempoh masa hidup mempunyai taburan eksponen dengan parameter λ1 = 0.02 untuk elemen pertama dan λ2 = 0.05 untuk elemen kedua. Cari kebarangkalian bahawa dalam 10 jam: a) kedua-dua elemen akan berfungsi dengan sempurna; b) hanya Kebarangkalian bahawa elemen #1 tidak akan gagal dalam 10 jam:
Penyelesaian.
P 1 (0) \u003d e -λ1 * t \u003d e -0.02 * 10 \u003d 0.8187
Kebarangkalian bahawa elemen #2 tidak akan gagal dalam 10 jam ialah:
P 2 (0) \u003d e -λ2 * t \u003d e -0.05 * 10 \u003d 0.6065
a) kedua-dua elemen akan berfungsi dengan sempurna;
P(2) = P 1 (0)*P 2 (0) = 0.8187*0.6065 = 0.4966
b) hanya satu elemen sahaja yang akan gagal.
P(1) = P 1 (0)*(1-P 2 (0)) + (1-P 1 (0))*P 2 (0) = 0.8187*(1-0.6065) + (1-0.8187) *0.6065 = 0.4321
Contoh nombor 7. Pengeluaran memberikan 1% daripada perkahwinan. Apakah kebarangkalian bahawa daripada 1100 produk yang diambil untuk penyelidikan, tidak lebih daripada 17 akan ditolak?
Catatan: memandangkan di sini n*p =1100*0.01=11 > 10, perlu digunakan
Dalam banyak masalah praktikal, seseorang perlu berurusan dengan pembolehubah rawak yang diedarkan mengikut undang-undang pelik, yang dipanggil undang-undang Poisson.
Pertimbangkan pembolehubah rawak tak selanjar , yang boleh mengambil hanya integer, nilai bukan negatif:
dan urutan nilai ini secara teorinya tidak terhad.
Pembolehubah rawak dikatakan diedarkan mengikut hukum Poisson jika kebarangkalian ia berlaku nilai tertentu, dinyatakan oleh formula
di mana a ialah beberapa nilai positif, dipanggil parameter hukum Poisson.
Siri taburan pembolehubah rawak, diedarkan mengikut hukum Poisson, mempunyai bentuk:

Pertama sekali, mari kita pastikan bahawa urutan kebarangkalian yang diberikan oleh formula (5.9.1) boleh menjadi siri taburan, i.e. bahawa jumlah semua kebarangkalian adalah sama dengan satu. Kami ada:

 .
.
Pada rajah. 5.9.1 menunjukkan poligon taburan pembolehubah rawak yang diedarkan mengikut hukum Poisson, sepadan dengan makna yang berbeza parameter . Jadual 8 lampiran menyenaraikan nilai untuk pelbagai .

Mari kita tentukan ciri utama - jangkaan dan varians matematik - pembolehubah rawak yang diedarkan mengikut undang-undang Poisson. Mengikut definisi jangkaan matematik
 .
.
Sebutan pertama jumlah (bersamaan dengan ) adalah sama dengan sifar, oleh itu, penjumlahan boleh dimulakan dari :
Mari kita nyatakan; Kemudian
 . (5.9.2)
. (5.9.2)
Oleh itu, parameter adalah tidak lebih daripada jangkaan matematik pembolehubah rawak.
Untuk menentukan serakan, kita mula-mula mencari momen awal kedua kuantiti:

Mengikut yang telah terbukti sebelum ini

selain itu,

Oleh itu, serakan pembolehubah rawak yang diedarkan mengikut hukum Poisson adalah sama dengan jangkaan matematiknya.
Sifat taburan Poisson ini sering digunakan dalam amalan untuk memutuskan sama ada hipotesis bahawa pembolehubah rawak diedarkan mengikut hukum Poisson adalah munasabah. Untuk melakukan ini, tentukan daripada pengalaman ciri statistik - jangkaan dan varians matematik - pembolehubah rawak. Sekiranya nilai mereka hampir, maka ini boleh berfungsi sebagai hujah yang memihak kepada hipotesis pengedaran Poisson; perbezaan ketara dalam ciri-ciri ini, sebaliknya, membuktikan terhadap hipotesis.
Untuk pembolehubah rawak yang diedarkan mengikut hukum Poisson, mari tentukan kebarangkalian bahawa ia akan mengambil nilai tidak kurang daripada yang diberikan. Mari kita nyatakan kebarangkalian ini:
Jelas sekali, kebarangkalian boleh dikira sebagai jumlah

Walau bagaimanapun, adalah lebih mudah untuk menentukannya daripada kebarangkalian peristiwa yang bertentangan:
 (5.9.4)
(5.9.4)
Khususnya, kebarangkalian bahawa nilai akan diambil nilai positif, dinyatakan oleh formula
![]() (5.9.5)
(5.9.5)
Kami telah menyebut bahawa banyak tugas praktikal membawa kepada pengedaran Poisson. Pertimbangkan salah satu daripada tugas biasa sebegitu rupa.

Biarkan mata diedarkan secara rawak pada paksi-x Lembu (Rajah 5.9.2). Andaikan bahawa taburan rawak mata memenuhi syarat berikut:
1. Kebarangkalian untuk memukul bilangan mata tertentu pada segmen bergantung hanya pada panjang segmen ini, tetapi tidak bergantung pada kedudukannya pada paksi-x. Dalam erti kata lain, titik diedarkan pada paksi-x dengan ketumpatan purata yang sama. Mari kita nyatakan ketumpatan ini (iaitu jangkaan matematik bilangan mata seunit panjang) sebagai .
2. Titik diedarkan pada paksi-x secara bebas antara satu sama lain, i.e. kebarangkalian untuk memukul satu atau satu lagi bilangan mata segmen yang diberikan tidak bergantung pada berapa banyak daripada mereka jatuh pada mana-mana segmen lain yang tidak bertindih dengannya.
3. Kebarangkalian untuk memukul kawasan kecil dua atau lebih mata adalah diabaikan berbanding dengan kebarangkalian memukul satu mata (keadaan ini bermakna kemustahilan praktikal kebetulan dua atau lebih mata).
Mari kita pilih segmen panjang tertentu pada paksi absis dan pertimbangkan pembolehubah rawak diskret - bilangan mata yang jatuh pada segmen ini. Kemungkinan nilai kuantiti akan
Oleh kerana mata jatuh pada segmen secara bebas antara satu sama lain, secara teorinya mungkin terdapat sejumlah besar secara sewenang-wenangnya, i.e. siri (5.9.6) berterusan selama-lamanya.
Mari kita buktikan bahawa pembolehubah rawak mempunyai hukum taburan Poisson. Untuk melakukan ini, kami mengira kebarangkalian bahawa betul-betul mata jatuh pada segmen.
Mari kita selesaikan terlebih dahulu tugas yang mudah. Pertimbangkan bahagian kecil pada paksi Lembu dan hitung kebarangkalian bahawa sekurang-kurangnya satu titik akan jatuh pada bahagian ini. Kami akan berhujah seperti berikut. Jangkaan matematik bilangan mata yang jatuh pada bahagian ini jelas sama (kerana terdapat mata secara purata per unit panjang). Mengikut syarat 3, untuk segmen kecil, kemungkinan dua atau lebih mata jatuh padanya boleh diabaikan. Oleh itu, jangkaan matematik bilangan mata yang jatuh pada bahagian akan lebih kurang sama dengan kebarangkalian satu mata jatuh padanya (atau, yang bersamaan dalam keadaan kami, sekurang-kurangnya satu).
Oleh itu, sehingga sangat kecil susunan yang lebih tinggi, apabila kita boleh mempertimbangkan kebarangkalian bahawa satu (sekurang-kurangnya satu) mata akan jatuh pada tapak bersamaan dengan , dan kebarangkalian bahawa tiada satu pun akan jatuh sama dengan .
Mari kita gunakan ini untuk mengira kebarangkalian mencapai mata tepat pada segmen. Bahagikan segmen kepada bahagian yang sama panjang . Marilah kita bersetuju untuk memanggil segmen asas "kosong" jika ia tidak mengandungi satu titik, dan "diduduki" jika sekurang-kurangnya satu telah jatuh ke dalamnya. Mengikut perkara di atas, kebarangkalian bahawa segmen itu akan "diduduki" adalah lebih kurang sama dengan; kebarangkalian bahawa ia akan menjadi "kosong" ialah . Oleh kerana, mengikut syarat 2, hits mata dalam segmen tidak bertindih adalah bebas, maka segmen n kami boleh dianggap sebagai "eksperimen" bebas, yang mana setiap segmen boleh "diduduki" dengan kebarangkalian . Cari kebarangkalian bahawa antara segmen itu akan ada betul-betul "sibuk". Mengikut teorem pengulangan, kebarangkalian ini adalah sama dengan

atau, menandakan
 (5.9.7)
(5.9.7)
Untuk cukup besar, kebarangkalian ini adalah lebih kurang sama dengan kebarangkalian bahawa betul-betul mata jatuh pada segmen, kerana dua atau lebih mata jatuh pada segmen mempunyai kebarangkalian yang boleh diabaikan. Untuk mencari nilai tepat , perlu dalam ungkapan (5.9.7) untuk pergi ke had di :
 (5.9.8)
(5.9.8)
Mari kita ubah ungkapan di bawah tanda had:
 (5.9.9)
(5.9.9)
Pecahan pertama dan penyebut pecahan terakhir dalam ungkapan (5.9.9) pada jelas cenderung kepada perpaduan. Ungkapan tidak bergantung kepada. Pengangka bagi pecahan terakhir boleh ditukar seperti berikut:
 (5.9.10)
(5.9.10)
Bila dan ungkapan (5.9.10) cenderung kepada . Oleh itu, telah dibuktikan bahawa kebarangkalian tepat titik jatuh ke dalam segmen dinyatakan oleh formula
di mana , iaitu kuantiti X diedarkan mengikut hukum Poisson dengan parameter .
Ambil perhatian bahawa maksud nilai ialah purata bilangan mata bagi setiap segmen .
Magnitud (kebarangkalian bahawa X akan positif) dalam kes ini menyatakan kebarangkalian bahawa sekurang-kurangnya satu mata akan jatuh pada segmen:
Oleh itu, kita telah melihat bahawa taburan Poisson berlaku di mana beberapa titik (atau elemen lain) menduduki kedudukan rawak secara bebas antara satu sama lain, dan bilangan titik ini yang jatuh ke dalam beberapa kawasan dikira. Dalam kes kami, "kawasan" sedemikian ialah segmen pada paksi-x. Walau bagaimanapun, kesimpulan kami boleh diperluaskan dengan mudah kepada kes pengagihan titik dalam satah (medan rata rawak titik) dan dalam ruang (medan spatial titik rawak). Adalah mudah untuk membuktikan bahawa jika syarat berikut dipenuhi:
1) mata diedarkan secara statistik seragam di lapangan dengan ketumpatan purata;
2) mata jatuh ke kawasan tidak bertindih secara bebas;
3) mata muncul secara tunggal, dan bukan berpasangan, tiga kali ganda, dsb., maka bilangan mata yang jatuh ke mana-mana kawasan (rata atau ruang) diagihkan mengikut undang-undang Poisson:
di manakah purata bilangan mata yang jatuh ke dalam kawasan tersebut .
Untuk kes rata
di manakah kawasan wilayah itu; untuk spatial
di manakah isipadu rantau itu.
Ambil perhatian bahawa untuk taburan Poisson bilangan titik yang jatuh ke dalam segmen atau rantau, keadaan ketumpatan malar () tidak penting. Jika dua syarat lain dipenuhi, maka hukum Poisson masih berlaku, hanya parameter a di dalamnya memperoleh ungkapan yang berbeza: ternyata tidak pendaraban mudah ketumpatan pada panjang, luas atau isipadu rantau, tetapi dengan menyepadukan ketumpatan berubah-ubah ke atas segmen, kawasan atau isipadu. (Untuk lebih lanjut tentang ini, lihat n° 19.4)
Kehadiran titik rawak yang bertaburan pada garis, pada satah atau pada isipadu bukanlah satu-satunya keadaan di mana taburan Poisson berlaku. Sebagai contoh, seseorang boleh membuktikan bahawa hukum Poisson mengehadkan untuk taburan binomial:
![]() , (5.9.12)
, (5.9.12)
jika kita secara serentak mengarahkan bilangan eksperimen kepada infiniti, dan kebarangkalian kepada sifar, dan hasil darabnya kekal malar:
Sesungguhnya, sifat mengehadkan taburan binomial ini boleh ditulis sebagai:
![]() . (5.9.14)
. (5.9.14)
Tetapi dari syarat (5.9.13) ia mengikutinya
Menggantikan (5.9.15) kepada (5.9.14), kita memperoleh kesamaan
 , (5.9.16)
, (5.9.16)
yang baru dibuktikan oleh kami di lain kesempatan.
Sifat mengehadkan undang-undang binomial ini sering digunakan dalam amalan. Katakan ia dihasilkan sejumlah besar eksperimen bebas, di mana setiap kejadian mempunyai kebarangkalian yang sangat kecil. Kemudian, untuk mengira kebarangkalian sesuatu peristiwa akan berlaku tepat sekali, anda boleh menggunakan formula anggaran:
![]() , (5.9.17)
, (5.9.17)
di manakah parameter undang-undang Poisson itu, yang lebih kurang menggantikan taburan binomial.
Daripada sifat undang-undang Poisson ini - untuk menyatakan taburan binomial dengan sejumlah besar eksperimen dan kebarangkalian kecil sesuatu peristiwa - muncul namanya, sering digunakan dalam buku teks statistik: undang-undang kejadian yang jarang berlaku.
Mari kita lihat beberapa contoh yang berkaitan dengan pengedaran Poisson dari pelbagai bidang amalan.
Contoh 1: Pertukaran telefon automatik menerima panggilan dengan purata kepadatan panggilan setiap jam. Dengan mengandaikan bahawa bilangan panggilan dalam mana-mana tempoh masa diedarkan mengikut undang-undang Poisson, cari kebarangkalian bahawa tepat tiga panggilan akan tiba di stesen dalam masa dua minit.
Penyelesaian. Purata bilangan panggilan setiap dua minit ialah:
persegi Untuk mencapai sasaran, sekurang-kurangnya satu serpihan cukup untuk memukulnya. Cari kebarangkalian mengenai sasaran untuk kedudukan tertentu bagi titik ketakselanjaran.
Penyelesaian. . Menggunakan formula (5.9.4), kita dapati kebarangkalian untuk memukul sekurang-kurangnya satu serpihan:
(Untuk mengira nilai fungsi eksponen gunakan jadual 2 dalam lampiran).
Contoh 7 Ketumpatan purata mikrob patogen dalam satu meter padu udara ialah 100. 2 meter padu diambil untuk sampel. dm udara. Cari kebarangkalian bahawa sekurang-kurangnya satu mikrob akan ditemui di dalamnya.
Penyelesaian. Menerima hipotesis taburan Poisson bagi bilangan mikrob dalam isipadu, kita dapati:
Contoh 8. 50 tembakan bebas dilepaskan pada beberapa sasaran. Kebarangkalian untuk terkena sasaran dengan satu pukulan ialah 0.04. Mengambil kesempatan mengehadkan harta benda taburan binomial (formula (5.9.17)), cari lebih kurang kebarangkalian sasaran akan terkena: tiada peluru, satu peluru, dua peluru.
Penyelesaian. Kami ada. Menurut jadual 8 aplikasi, kita dapati kebarangkalian.
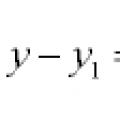 Persamaan garis dan lengkung dalam satah
Persamaan garis dan lengkung dalam satah Persamaan homogen umum Persamaan homogen umum tertib kedua
Persamaan homogen umum Persamaan homogen umum tertib kedua Terima kasih kepada koma Kerana fakta bahawa dalam mereka
Terima kasih kepada koma Kerana fakta bahawa dalam mereka