Tall sammenlignbare modulo 7. Sammenligning modulo et naturlig tall
Sammenligning med en ukjent x ser ut som
Hvor . Hvis en n ikke delelig med m, det er det som heter grad sammenligninger.
Ved avgjørelse sammenligning er et hvilket som helst heltall x 0 , for hvilket
Hvis X 0 tilfredsstiller sammenligningen, så, i henhold til egenskapen til 9 sammenligninger, er alle heltall sammenlignbare med x 0 modulo m. Derfor er alle sammenligningsløsninger som tilhører samme restklasse modulo T, vil vi vurdere det som én løsning. Dermed har sammenligningen like mange løsninger som det er elementer i det komplette systemet av rester som tilfredsstiller den.
Sammenligninger hvis løsningssett faller sammen kalles tilsvarende.
2.2.1 Sammenligninger av første grad
Første grads sammenligning med en ukjent X ser ut som
![]() (2.2)
(2.2)
Teorem 2.4. For at en sammenligning skal ha minst én løsning, er det nødvendig og tilstrekkelig at antallet b delt på GCD( en, m).
Bevis. Først beviser vi nødvendigheten. La d
=
GCD( en,
m)
Og X 0
- sammenligningsløsning. Deretter ![]() , altså forskjellen Åh 0
−
b
delt på T. Så det er et slikt heltall q,
Hva Åh 0
−
b
=
qm.
Herfra b= ah 0
−
qm.
Og siden d,
som en felles divisor, deler tall EN Og T, så deles minuend og subtrahend med d,
og derfor b
delt på d.
, altså forskjellen Åh 0
−
b
delt på T. Så det er et slikt heltall q,
Hva Åh 0
−
b
=
qm.
Herfra b= ah 0
−
qm.
Og siden d,
som en felles divisor, deler tall EN Og T, så deles minuend og subtrahend med d,
og derfor b
delt på d.
La oss nå bevise tilstrekkeligheten. La d- største felles deler av tall EN Og T, Og b delt på d. Da, ved definisjonen av delbarhet, eksisterer det følgende heltall en 1 , b 1 ,T 1 , Hva .
Ved å bruke den utvidede euklidiske algoritmen finner vi en lineær representasjon av tallet 1 = gcd( en 1 , m 1 ):
![]()
for noen x 0 , y 0 . La oss multiplisere begge sider av den siste likheten med b 1 d:
eller, hva er det samme,
,
det vil si, og er løsningen på sammenligningen. □
Eksempel 2.10. Sammenligning 9 X= 6 (mod 12) har en løsning siden gcd(9, 12) = 3 og 6 er delelig med 3. □
Eksempel 2.11. Sammenligning 6x= 9 (mod 12) har ingen løsninger, siden gcd(6, 12) = 6, og 9 ikke er delelig med 6. □
Teorem 2.5. La sammenligning (2.2) være løsbar og d = GCD( en, m). Da består settet med sammenligningsløsninger (2.2) av d modulo restklasser T, nemlig hvis X 0 - en av løsningene, så er alle andre løsninger
Bevis. La X 0
- sammenligningsløsning (2.2), altså ![]() Og ,
.
Så det er noe slikt q, Hva Åh 0
−
b
=
qm.
Nå erstatter inn i den siste likestillingen i stedet for X 0
en vilkårlig løsning av formen, hvor vi får uttrykket
Og ,
.
Så det er noe slikt q, Hva Åh 0
−
b
=
qm.
Nå erstatter inn i den siste likestillingen i stedet for X 0
en vilkårlig løsning av formen, hvor vi får uttrykket
, delelig med m. □
Eksempel 2.12. Sammenligning 9 X=6 (mod 12) har nøyaktig tre løsninger, siden gcd(9, 12)=3. Disse løsningene: X 0 = 2, x 0 + 4 = 6, X 0 + 2∙4=10.□
Eksempel 2.13. Sammenligning 11 X=2 (mod 15) har en unik løsning X 0 = 7, siden GCD(11,15)=1,□
Vi viser deg hvordan du løser førstegradssammenlikninger. Uten tap av generalitet, vil vi anta at GCD( en, t) = 1. Deretter kan løsningen til sammenligning (2.2) søkes, for eksempel ved hjelp av den euklidiske algoritmen. Faktisk, ved å bruke den utvidede euklidiske algoritmen, representerer vi tallet 1 som en lineær kombinasjon av tall en Og T:
La oss multiplisere begge sider av denne likheten med b, vi får: b = abq + mrb, hvor abq - b = - mrb, det er en ∙ (bq) = b(mod m) Og bq- sammenligningsløsning (2.2).
En annen løsning er å bruke Eulers teorem. Igjen tror vi at GCD(a, T)= 1. Vi bruker Eulers teorem: ![]() . Multipliser begge sider av sammenligningen med b:
. Multipliser begge sider av sammenligningen med b:
![]() .
Omskriver det siste uttrykket som
.
Omskriver det siste uttrykket som  , får vi som er en løsning på sammenligning (2.2).
, får vi som er en løsning på sammenligning (2.2).
La nå GCD( en, m) = d>1. Deretter en = entd, m = mtd, hvor GCD( EN 1 , m 1) = 1. I tillegg er det nødvendig b = b 1 d, for at sammenligningen skal kunne løses. Hvis X 0 - sammenligningsløsning EN 1 x = b 1 (mod m 1), og den eneste, siden GCD( EN 1 , m 1) = 1, da X 0 vil være løsningen og sammenligningen EN 1 xd = db 1 (mod m 1), altså den opprinnelige sammenligningen (2.2). Hvile d- 1 løsninger er funnet av teorem 2.5.
Matematisk prosjekt om emnet
"Sammenligninger modulo"
Zaripova Aisylu
Sovetsky-distriktet i Kazan
MBOU "Videregående skole nr. 166", 7a klasse
Vitenskapelig veileder: Antonova N.A.
Innholdsfortegnelse
Innledning__________________________________________________________3
Hva er sammenligninger______________________________________________________4
Konseptet med sammenligninger modulo__________________________4
Historien om fremveksten av begrepet sammenligninger modulo_____4
Egenskaper ved sammenligninger_________________________________________4
Den enkleste bruken av modulo-sammenligninger er å bestemme delbarheten til tall____________________6
Én sammenligningsoppgave__________________________________________8
Bruk av modulo-sammenligninger i faglige aktiviteter_________________________________________________9
Bruke sammenligninger på problemløsning______________________________6
Konklusjon_________________________________________________10
Liste over brukt litteratur_______________________________________11
Introduksjon.
Emne: Modulo sammenligninger.
Problem: Mange studenter står overfor problemer når de forbereder seg til olympiader, hvor løsningen er basert på kunnskap om rester fra å dele heltall med et naturlig tall. Vi var interessert i denne typen problemer og mulige metoder for å løse dem. Det viser seg at de kan løses ved hjelp av modulo-sammenligninger.
Mål: Finn ut essensen av modulo-sammenligninger, hovedmetodene for å jobbe med modulo-sammenligninger.
Mål: finne teoretisk materiale om dette emnet, vurdere problemer som løses ved hjelp av modulo-sammenligninger, vise de vanligste metodene for å løse slike problemer, trekke konklusjoner.
Studieobjekt: tallteori.
Forskningsemne: teori om modulo-sammenligninger.
Arbeidet er knyttet til teoretisk forskning og kan brukes som forberedelse til matematikk-olympiade. Innholdet avslører de grunnleggende konseptene for modulo-sammenligninger og deres hovedegenskaper, og gir eksempler på å løse problemer om dette emnet.
Jeg . Hva er sammenligninger?
Konseptet med modulo-sammenligninger.
Tallene og sies å være sammenlignbare i modul hvis de er delbare med, med andre ord, a og b har de samme restene når de divideres med.
Betegnelse
Eksempler:
12 og 32 er sammenlignbare modulo 5, siden 12 når deles på 5 har en rest på 2 og 32 når de deles på 2 har en rest på 2. Det er skrevet12 ;
101 og 17 er sammenlignbare modulo 21;
Historien om fremveksten av begrepet modulo-sammenligninger.
Teorien om delbarhet ble i stor grad skapt av Euler. Definisjonen av sammenligning ble formulert i boken av K.F. Gauss "Arithmetic Studies". Dette verket, skrevet på latin, begynte å bli trykt i 1797, men boken ble utgitt først i 1801 på grunn av det faktum at trykkeprosessen på den tiden var ekstremt arbeidskrevende og langvarig. Den første delen av Gauss bok heter: "Om sammenligning av tall." Det var Gauss som foreslo symbolikken til modulo-sammenligninger som har blitt etablert i matematikk.
Egenskaper ved sammenligninger.
Hvis
Bevis:
Hvis vi legger den andre til den første likheten, får vi
er summen av to heltall, er derfor et heltall, derfor.
Hvis vi trekker den andre fra den første likheten, får vi
dette er forskjellen på to heltall, noe som betyr at det derfor er et heltall.
Tenk på uttrykket:
Dette er forskjellen mellom produkter av heltall, noe som betyr at det derfor er et heltall.
Dette er en konsekvens av sammenligningens tredje egenskap.
Q.E.D.
5) Hvis.
Bevis: La oss finne summen av disse to uttrykkene:
er summen av to heltall, derfor er det et heltall, derfor .
Q.E.D.
6) Hvis er et heltall, da
Bevis: , hvors– et heltall, multipliser denne likheten med, vi får: . Siden er et produkt av heltall, er det det som måtte bevises.
7) Hvis
Bevis: begrunnelsen er lik eiendomsbeviset 6.
8) Hvis - coprimtall altså
Bevis: , dividere dette uttrykket med, får vi: - coprimtall, som betyr at de er delbare med et heltall, dvs. =. Og dette betyr at det som måtte bevises.
II . Bruke sammenligninger på problemløsning.
2.1. Den enkleste bruken av modulo-sammenligninger er å bestemme delbarheten til tall.
Eksempel. Finn resten av 2 2009 klokken 7.
Løsning: Tenk på potensene til 2:
hever sammenligningen til potensen 668 og multipliserer med, får vi:.
Svar: 4.
Eksempel. Bevis at 7+7 2 +7 3 +…+7 4 n er delelig med 100 for enhvernfra et sett med heltall.
Løsning: Vurder sammenligninger
etc. Den sykliske naturen til rester forklares av reglene for å multiplisere tall i en kolonne. Legger vi sammen de fire første sammenligningene, får vi:
Dette betyr at dette beløpet deles på 100 uten rest. På samme måte, ved å legge til følgende sammenligninger om fire, får vi at hver slik sum er delelig med 100 uten en rest. Dette betyr at hele summen består av 4nledd er delelig med 100 uten en rest. Q.E.D.
Eksempel. Bestem hvilken verdinuttrykket er delelig med 19 uten en rest.
Løsning: .
La oss multiplisere denne sammenligningen med 20. Vi får.
La oss legge sammen sammenligningene, da. . Dermed er høyresiden av sammenligningen alltid delelig med 19 for et hvilket som helst naturlig talln, som betyr at det opprinnelige uttrykket er delelig med 19 med naturlign.
Svar n – et hvilket som helst naturlig tall.
Eksempel. Hvilket siffer slutter tallet på?
Løsning. For å løse dette problemet vil vi bare overvåke det siste sifferet. Tenk på potensene til tallet 14:
Du kan legge merke til at hvis eksponenten er oddetall, ender verdien av graden på 4, og hvis eksponenten er partall, ender den på 6. Da ender den på 6, dvs. er et partall. Så det ender i 6.
Svar 6.
2.2. En sammenligningsoppgave.
Artikkelen til N. Vilenkin "Sammenligninger og klasser av rester" presenterer et problem som ble løst av den berømte engelske fysikeren Dirac i løpet av studietiden.
Det er også en kort løsning på dette problemet ved å bruke modulo-sammenligninger. Men vi møtte en rekke lignende problemer. For eksempel.
En forbipasserende fant en haug med epler nær et tre som en ape satt på. Etter å ha telt dem, innså han at hvis 1 eple blir gitt til apen, vil antallet gjenværende epler deles inn i n uten et spor. Etter å ha gitt det ekstra eplet til apen, tok han 1/ n gjenværende epler og venstre. Senere nærmet neste forbipasserende haugen, så neste osv. Hver påfølgende forbipasserende, etter å ha telt eplene, la merke til at antallet deres ble delt med n gir resten 1, og etter å ha gitt det ekstra eplet til apen, tok han 1 for seg selv n de resterende eplene og gikk videre. Etter at den siste gikk, n den forbipasserende ble antallet epler som var igjen i haugen delt på n uten et spor. Hvor mange epler var det i haugen først?
Ved å utføre samme resonnement som Dirac, fikk vi en generell formel for å løse en klasse med lignende problemer: , hvorn- naturlig tall.
2.3. Anvendelse av modulsammenlikninger i faglige aktiviteter.
Sammenligningsteori brukes på kodingsteori, så alle som velger et yrke relatert til datamaskiner vil studere, og eventuelt anvende sammenligninger i sin faglige virksomhet. For eksempel brukes en rekke tallteoretiske konsepter, inkludert modulo-sammenligninger, for å utvikle krypteringsalgoritmer for offentlig nøkkel.
Konklusjon.
Arbeidet skisserer de grunnleggende begrepene og egenskapene til modulo-sammenlikninger og illustrerer bruken av modulo-sammenligninger med eksempler. Materialet kan brukes som forberedelse til olympiader i matematikk og Unified State Exam.
Den gitte referanselisten tillater, om nødvendig, å vurdere noen mer komplekse aspekter ved teorien om modulo-sammenligninger og dens anvendelser.
Liste over brukt litteratur.
Alfutova N.B. Algebra og tallteori./N.B.Alfutova, A.V.Ustinov. M.:MCNMO, 2002, 466 s.
Bukhshtab A.A. Tallteori. /A.A.Bukhshtab. M.: Utdanning, 1960.
Vilenkin N. Sammenligninger og klasser av rester./N. Vilenkin.//Quantum. – 1978.- 10.
Fedorova N.E. Studie av algebra og matematisk analyse. Karakter 10.http:// www. prosv. ru/ e-bøker/ Fedorova_ Algebra_10 kl/1/ xht
ru. wikipedia. org/ wiki/Comparison_modulo.
Definisjon 1. Hvis to tall er 1) en Og b når delt på s gi den samme resten r, da kalles slike tall equiremainder eller sammenlignbar i modul s.
Uttalelse 1. La s et positivt tall. Deretter hvert tall en alltid og dessuten på den eneste måten kan representeres i skjemaet
Men disse tallene kan fås ved å stille inn r lik 0, 1, 2,..., s−1. Derfor sp+r=a vil få alle mulige heltallsverdier.
La oss vise at denne representasjonen er unik. La oss late som det s kan representeres på to måter a=sp+r Og a=s 1 s+r 1 . Deretter
| (2) |
Fordi r 1 aksepterer et av tallene 0,1, ..., s−1, deretter den absolutte verdien r 1 −r mindre s. Men av (2) følger det at r 1 −r flere s. Derfor r 1 =r Og s 1 =s.
Antall r kalt minus tall en modulo s(med andre ord, tallet r kalt resten av et nummer en på s).
Uttalelse 2. Hvis to tall en Og b sammenlignbar i modul s, Det a−b delt på s.
Egentlig. Hvis to tall en Og b sammenlignbar i modul s, så når delt på s ha den samme resten s. Deretter
delt på s, fordi høyre side av ligning (3) er delt med s.
Uttalelse 3. Hvis forskjellen på to tall er delelig med s, da er disse tallene sammenlignbare i modul s.
Bevis. La oss betegne med r Og r 1 divisjon resten en Og b på s. Deretter
Eksempler 25≡39 (mod 7), −18≡14 (mod 4).
Fra det første eksemplet følger det at 25 når deles på 7 gir den samme resten som 39. Faktisk, 25 = 3·7+4 (resten 4). 39=3·7+4 (resten 4). Når du vurderer det andre eksemplet, må du ta i betraktning at resten må være et ikke-negativt tall mindre enn modulen (dvs. 4). Da kan vi skrive: −18=−5·4+2 (rest 2), 14=3·4+2 (rest 2). Derfor vil −18 når deles på 4 etterlater en rest av 2, og 14 når de divideres med 4 gir en rest av 2.
Egenskaper til modulo-sammenligninger
Eiendom 1. For alle en Og s Alltid
det er ikke alltid en sammenligning
Hvor λ er den største felles deleren av tall m Og s.
Bevis. La λ største felles deler av tall m Og s. Deretter
Fordi m(a−b) delt på k, Det
Derfor
Og m er en av divisorene til tallet s, Det
Hvor h=pqs.
Merk at vi kan tillate sammenligninger basert på negative moduler, dvs. sammenligning a≡b mod( s) betyr i dette tilfellet at forskjellen a−b delt på s. Alle egenskapene til sammenligninger forblir i kraft for negative moduler.
En førstegrads sammenligning med en ukjent har formen:
f(x) 0 (mod m); f(X) = Åh + og n. (1)
Løs sammenligning- betyr å finne alle verdiene av x som tilfredsstiller den. To sammenligninger som tilfredsstiller de samme verdiene av x kalles tilsvarende.
Hvis sammenligning (1) er tilfredsstilt av noen x = x 1, deretter (ifølge 49) alle tall sammenlignbare med x 1, modulo m: x x 1 (mod m). Hele denne klassen av tall anses å være én løsning. Med en slik avtale kan følgende konklusjon trekkes.
66.C Justering (1) vil ha like mange løsninger som antall rester av hele systemet som tilfredsstiller det.
Eksempel. Sammenligning
6x– 4 0 (mod 8)
Blant tallene 0, 1,2, 3, 4, 5, 6, 7, tilfredsstiller to tall hele systemet av rester modulo 8: X= 2 og X= 6. Derfor har denne sammenligningen to løsninger:
x 2 (mod 8), X 6 (mod 8).
Sammenligning av første grad ved å flytte frileddet (med motsatt fortegn) til høyre side kan reduseres til formen
øks b(mod m). (2)
Tenk på en sammenligning som tilfredsstiller betingelsen ( EN, m) = 1.
Ifølge 66 har vår sammenligning like mange løsninger som det er rester av hele systemet som tilfredsstiller det. Men når x går gjennom hele systemet av modulo-rester T, At Åh går gjennom hele systemet med fradrag (av 60). Derfor for én og bare én verdi X, hentet fra hele systemet, Åh vil kunne sammenlignes med b. Så,
67. Når (a, m) = 1 sammenligningsaks b(mod m)har én løsning.
La nå ( en, m) = d> 1. Så, for at sammenligning (2) skal ha løsninger, er det nødvendig (av 55) at b delt på d, ellers er sammenligning (2) umulig for et heltall x . Forutsatt derfor b multipler d, la oss sette en = en 1 d, b = b 1 d, m = m 1 d. Da vil sammenligning (2) tilsvare dette (forkortet til d): en 1 x b 1 (mod m), der allerede ( EN 1 , m 1) = 1, og derfor vil den ha én løsning modulo m 1 . La X 1 - den minste ikke-negative resten av denne løsningen modulo m 1 , da er alle tall x , danner denne løsningen finnes i skjemaet
x x 1 (mod m 1). (3)
Modulo m, tall (3) danner ikke én løsning, men flere, nøyaktig like mange løsninger som det er tall (3) i serien 0, 1, 2, ..., m – 1 minst ikke-negative modulo-rester m. Men følgende tall (3) vil falle her:
x 1 , x 1 + m 1 , x 1 + 2m 1 , ..., x 1 + (d – 1) m 1 ,
de. Total d tall (3); derfor har sammenligning (2). d beslutninger.
Vi får teoremet:
68. La (a, m) = d. Sammenligning ax b ( mod m) er umulig hvis b ikke er delelig med d. Når b er et multiplum av d, har sammenligningen d-løsninger.
69. En metode for å løse sammenligninger av første grad, basert på teorien om fortsatte brøker:
Utvider relasjonen til en fortsatt brøkdel m:a,

og ser på de to siste samsvarende brøkene:

i henhold til egenskapene til fortsatte fraksjoner (i henhold til 30 ) vi har

Så sammenligningen har en løsning
å finne, som er nok til å beregne Pn– 1 i henhold til metoden spesifisert i 30.
Eksempel. La oss løse sammenligningen
111x= 75 (mod 321). (4)
Her (111, 321) = 3, og 75 er et multiplum av 3. Derfor har sammenligningen tre løsninger.
Ved å dele begge sider av sammenligningen og modulen med 3, får vi sammenligningen
37x= 25 (mod 107), (5)
som vi først må løse. Vi har
| q | |||||
| P 3 |

Så i dette tilfellet n = 4, P n – 1 = 26, b= 25, og vi har en løsning til sammenligning (5) i skjemaet
x–26 ∙ 25 99 (mod 107).
Derfor presenteres løsningene til sammenligning (4) som følger:
X 99; 99 + 107; 99 + 2 ∙ 107 (mod 321),
Xº99; 206; 313 (mod 321).
Beregning av det inverse elementet ved en gitt modulo
70.Hvis tallene er heltall en Og n er coprime, så er det et tall en', som tilfredsstiller sammenligningen a ∙ a′ ≡ 1 (mod n). Antall en' kalt multiplikativ invers av en modulo n og notasjonen som brukes for det er en- 1 (mod n).
Beregningen av gjensidige størrelser modulo en viss verdi kan utføres ved å løse en sammenligning av første grad med en ukjent, der x nummer akseptert en'.
For å finne en sammenligningsløsning
a∙x≡ 1(mod m),
Hvor ( er)= 1,
du kan bruke Euclid-algoritmen (69) eller Fermat-Euler-teoremet, som sier at hvis ( er) = 1, da
en φ( m) ≡ 1(mod m).
x ≡ en φ( m)–1 (mod m).
Grupper og deres eiendommer
Grupper er en av de taksonomiske klassene som brukes til å klassifisere matematiske strukturer med felles karakteristiske egenskaper. Grupper har to komponenter: en haug med (G) Og operasjoner() definert på dette settet.
Begrepene sett, element og medlemskap er de grunnleggende udefinerte begrepene i moderne matematikk. Ethvert sett er definert av elementene som er inkludert i det (som i sin tur også kan være sett). Dermed sier vi at et sett er definert eller gitt hvis vi for et element kan fortelle om det tilhører dette settet eller ikke.
For to sett A, B poster B EN, B EN, B∩ EN, B EN, B \ EN, EN × B henholdsvis mener det B er en delmengde av settet EN(dvs. ethvert element fra B er også inneholdt i EN, for eksempel er settet med naturlige tall inneholdt i settet med reelle tall; dessuten alltid EN EN), B er en riktig delmengde av settet EN(de. B EN Og B ≠ EN), skjæringspunktet mellom mange B Og EN(dvs. alle slike elementer som ligger samtidig i EN, og i B, for eksempel, skjæringspunktet mellom heltall og positive reelle tall er settet av naturlige tall), foreningen av sett B Og EN(dvs. et sett som består av elementer som enten ligger i EN, enten i B), sett forskjell B Og EN(dvs. settet med elementer som ligger i B, men ikke ligge i EN), kartesisk produkt av sett EN Og B(dvs. et sett med par av skjemaet ( en, b), Hvor en EN, b B). Via | EN| kraften til settet er alltid angitt EN, dvs. antall elementer i settet EN.
En operasjon er en regel i henhold til hvilke to elementer i et sett G(en Og b) er matchet med det tredje elementet fra G: a b.
Mange elementer G med en operasjon kalles gruppe, hvis følgende betingelser er oppfylt.
Ved n gir de de samme restene.
Ekvivalente formuleringer: a og b sammenlignbar i modul n hvis deres forskjell en - b er delelig med n, eller hvis a kan representeres som en = b + kn , Hvor k- noe heltall. For eksempel: 32 og -10 er sammenlignbare modulo 7, siden
Utsagnet "a og b er sammenlignbare modulo n" er skrevet som:
Modulo likhetsegenskaper
Modulo sammenligningsrelasjonen har egenskapene
Hvilke som helst to heltall en Og b sammenlignbar modulo 1.
For tallene en Og b var sammenlignbare i modul n, er det nødvendig og tilstrekkelig at deres forskjell er delelig med n.
Hvis tallene og er parvis sammenlignbare i modul n, deretter deres summer og , samt produktene og er også sammenlignbare i modul n.
Hvis tallene en Og b sammenlignbar i modul n, deretter gradene deres en k Og b k er også sammenlignbare i modul n under enhver naturlig k.
Hvis tallene en Og b sammenlignbar i modul n, Og n delt på m, Det en Og b sammenlignbar i modul m.
For tallene en Og b var sammenlignbare i modul n, presentert i form av sin kanoniske dekomponering i enkle faktorer s Jeg
nødvendig og tilstrekkelig til
Sammenligningsrelasjonen er en ekvivalensrelasjon og har mange av egenskapene til vanlige likheter. For eksempel kan de legges til og multipliseres: if
Sammenligninger kan imidlertid generelt sett ikke deles på hverandre eller med andre tall. Eksempel: , men reduseres med 2, får vi en feilaktig sammenligning: . Forkortelsesreglene for sammenligninger er som følger.
Du kan heller ikke utføre operasjoner på sammenligninger hvis modulene deres ikke stemmer overens.
Andre eiendommer:
Beslektede definisjoner
Fradragsklasser
Settet med alle tall som kan sammenlignes med en modulo n kalt fradragsklasse en modulo n , og er vanligvis betegnet [ en] n eller . Dermed er sammenligningen ekvivalent med likheten mellom restklasser [en] n = [b] n .
Siden modulo sammenligning n er en ekvivalensrelasjon på settet med heltall, så er restklassene modulo n representere ekvivalensklasser; deres antall er likt n. Settet med alle restklasser modulo n betegnet med eller.
Operasjonene med addisjon og multiplikasjon ved å indusere tilsvarende operasjoner på settet:
[en] n + [b] n = [en + b] nMed hensyn til disse operasjonene er settet en endelig ring, og hvis n enkelt - begrenset felt.
Fradragssystemer
Restsystemet lar deg utføre aritmetiske operasjoner på et begrenset sett med tall uten å gå utover grensene. Fullt system med fradrag modulo n er ethvert sett med n heltall som er uforlignelige modulo n. Vanligvis blir de minste ikke-negative restene tatt som et komplett system av rester modulo n
0,1,...,n − 1eller de absolutt minste fradragene som består av tall
,ved oddetall n og tall
i tilfelle jevn n .
Løse sammenligninger
Sammenligninger av første grad
I tallteori, kryptografi og andre vitenskapsfelt oppstår ofte problemet med å finne løsninger på førstegradssammenlikninger av formen:
Å løse en slik sammenligning begynner med å beregne gcd (a, m)=d. I dette tilfellet er 2 tilfeller mulig:
- Hvis b ikke et multiplum d, så har sammenligningen ingen løsninger.
- Hvis b flere d, så har sammenligningen en unik løsning modulo m / d, eller, hva er det samme, d modulo løsninger m. I dette tilfellet, som et resultat av å redusere den opprinnelige sammenligningen med d sammenligningen er:
Hvor en 1 = en / d , b 1 = b / d Og m 1 = m / d er heltall, og en 1 og m 1 er relativt gode. Derfor nummeret en 1 kan inverteres modulo m 1, det vil si finne et slikt tall c, det (med andre ord, ). Nå er løsningen funnet ved å multiplisere den resulterende sammenligningen med c:
Praktisk beregning av verdi c kan implementeres på forskjellige måter: ved hjelp av Eulers teorem, Euklids algoritme, teorien om fortsatte brøker (se algoritme), etc. Spesielt Eulers teorem lar deg skrive ned verdien c som:
Eksempel
Til sammenligning har vi d= 2, så modulo 22 har sammenligningen to løsninger. La oss erstatte 26 med 4, som kan sammenlignes med modulo 22, og deretter redusere alle 3 tallene med 2:
Siden 2 er coprime til modulo 11, kan vi redusere venstre og høyre side med 2. Som et resultat får vi én løsning modulo 11: , tilsvarende to løsninger modulo 22:.
Sammenligninger av andre grad
Å løse sammenligninger av andre grad kommer ned til å finne ut om et gitt tall er en kvadratisk rest (ved å bruke den kvadratiske resiprositetsloven) og deretter beregne kvadratroten modulo.
Historie
Den kinesiske restsetningen, kjent i mange århundrer, sier (i moderne matematisk språk) at restringen modulo produktet av flere coprimtall er
 Se hva "Legion (nummer)" er i andre ordbøker
Se hva "Legion (nummer)" er i andre ordbøker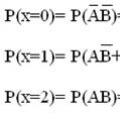 Eksempler på å løse problemer om emnet "Tilfeldige variabler"
Eksempler på å løse problemer om emnet "Tilfeldige variabler" Jeg leser diktet "Frost, rød nese" av Nekrasov
Jeg leser diktet "Frost, rød nese" av Nekrasov