Arealet av en trekant er Pythagoras setning. Ulike måter å bevise Pythagoras teorem: eksempler, beskrivelse og anmeldelser
Når du først begynte å lære kvadratrøtter og hvordan du løser irrasjonelle ligninger(likheter som inneholder det ukjente under rottegnet), har du sannsynligvis fått den første ideen om dem praktisk bruk. Evnen til å trekke ut Kvadratrot av tall er også nødvendig for å løse problemer med anvendelsen av Pythagoras teoremet. Denne teoremet relaterer lengden på sidene til en rettvinklet trekant.
La lengdene på bena i en rettvinklet trekant (de to sidene som konvergerer i rette vinkler) angis med bokstavene og , og lengden på hypotenusen (den lengste siden av trekanten overfor rett vinkel) vil bli merket med bokstaven . Da er de tilsvarende lengdene relatert til følgende relasjon:
Denne ligningen lar deg finne lengden på en side av en rettvinklet trekant i tilfelle lengden på de to andre sidene er kjent. I tillegg lar den deg bestemme om den betraktede trekanten er en rettvinklet trekant, forutsatt at lengdene på alle tre sider kjent på forhånd.
Løse problemer ved hjelp av Pythagoras teorem
For å konsolidere materialet, vil vi løse følgende problemer for anvendelsen av Pythagoras teorem.

Så gitt:
- Lengden på ett av bena er 48, hypotenusen er 80.
- Lengden på benet er 84, hypotenusen er 91.
La oss komme til løsningen:
a) Å erstatte dataene i ligningen ovenfor gir følgende resultater:
48 2 + b 2 = 80 2
2304 + b 2 = 6400
b 2 = 4096
b= 64 eller b = -64
Siden lengden på en side av en trekant ikke kan uttrykkes negativt tall, forkastes det andre alternativet automatisk.
Svar på det første bildet: b = 64.
b) Lengden på benet til den andre trekanten finnes på samme måte:
84 2 + b 2 = 91 2
7056 + b 2 = 8281
b 2 = 1225
b= 35 eller b = -35
Som i forrige tilfelle blir den negative løsningen forkastet.
Svar på det andre bildet: b = 35

Vi får:
- Lengdene på de mindre sidene av trekanten er henholdsvis 45 og 55, og de større er 75.
- Lengdene på de mindre sidene av trekanten er henholdsvis 28 og 45, og de større er 53.
Vi løser problemet:
a) Det er nødvendig å sjekke om summen av kvadratene av lengdene til de mindre sidene i en gitt trekant er lik kvadratet av lengden til den større:
45 2 + 55 2 = 2025 + 3025 = 5050
Derfor er den første trekanten ikke en rettvinklet.
b) Den samme operasjonen utføres:
28 2 + 45 2 = 784 + 2025 = 2809
Derfor er den andre trekanten en rettvinklet trekant.
Først finner vi lengden lengste segmentet, dannet av punkter med koordinater (-2, -3) og (5, -2). Til dette bruker vi kjent formel for å finne avstanden mellom punkter i rektangulært system koordinater:
På samme måte finner vi lengden på segmentet innelukket mellom punktene med koordinater (-2, -3) og (2, 1):
Til slutt bestemmer vi lengden på segmentet mellom punkter med koordinater (2, 1) og (5, -2):
Siden det er en likhet:
da er den tilsvarende trekanten en rettvinklet trekant.
Dermed kan vi formulere svaret på problemet: siden summen av kvadratene av sidene med den minste lengden er lik kvadratet på siden med største lengde, punktene er toppunktene i en rettvinklet trekant.
Basen (plassert strengt horisontalt), jamben (plassert strengt vertikalt) og kabelen (strukket diagonalt) danner henholdsvis en rettvinklet trekant, Pythagoras teoremet kan brukes til å finne lengden på kabelen:
Dermed vil lengden på kabelen være cirka 3,6 meter.
Gitt: avstanden fra punkt R til punkt P (benet til trekanten) er 24, fra punkt R til punkt Q (hypotenuse) - 26.
Så vi hjelper Vitya med å løse problemet. Siden sidene av trekanten vist i figuren er ment å danne en rettvinklet trekant, kan du bruke Pythagoras teoremet til å finne lengden på den tredje siden:
Så bredden på dammen er 10 meter.
Sergey Valerievich
Pythagoras teorem
Pythagoras teorem- en av de grunnleggende teoremene i euklidisk geometri, som etablerer sammenhengen
mellom sidene i en rettvinklet trekant.
Det antas at det ble bevist av den greske matematikeren Pythagoras, som det er oppkalt etter.
Geometrisk formulering av Pythagoras teorem.
Teoremet ble opprinnelig formulert som følger:
I en rettvinklet trekant er arealet av kvadratet bygget på hypotenusen lik summen av arealene til kvadratene,
bygget på katetre.
Algebraisk formulering av Pythagoras teorem.
I en rettvinklet trekant er kvadratet av lengden på hypotenusen lik summen av kvadratene av lengdene på bena.
Det vil si, angir lengden på hypotenusen til trekanten gjennom c, og lengdene på beina gjennom en Og b:
Begge formuleringene pythagoras teoremer er likeverdige, men den andre formuleringen er mer elementær, det gjør den ikke
krever områdebegrepet. Det vil si at den andre påstanden kan verifiseres uten å vite noe om området og
ved å måle bare lengdene på sidene i en rettvinklet trekant.
Den inverse Pythagoras teorem.
Hvis kvadratet på en side av en trekant er lik summen av kvadratene på de to andre sidene, da
trekanten er rektangulær.
Eller med andre ord:
For alle trippel positive tall en, b Og c, slik at
det er en rettvinklet trekant med ben en Og b og hypotenusen c.
Pythagoras teorem for en likebenet trekant.

Pythagoras teorem for en likesidet trekant.

Bevis for Pythagoras teorem.
For øyeblikket er 367 bevis på denne teoremet registrert i vitenskapelig litteratur. Sannsynligvis teoremet
Pythagoras er det eneste teoremet med et så imponerende antall bevis. Slikt mangfold
kan bare forklares med den grunnleggende betydningen av teoremet for geometri.
Selvfølgelig, konseptuelt, kan alle deles inn i et lite antall klasser. Den mest kjente av dem:
bevis arealmetode, aksiomatisk Og eksotiske bevis(For eksempel,
ved bruk av differensiallikninger).
1. Bevis for Pythagoras teorem i form av lignende trekanter.
Følgende bevis på den algebraiske formuleringen er det enkleste av bevisene som er konstruert
direkte fra aksiomene. Spesielt bruker den ikke konseptet med området til en figur.
La ABC det er en rettvinklet trekant C. La oss tegne en høyde fra C og betegne
sitt grunnlag gjennom H.
Triangel ACH ligner på en trekant AB C på to hjørner. Likeledes trekanten CBH lignende ABC.
Ved å introdusere notasjonen:

vi får:
![]() ,
,
som passer -
Etter å ha brettet seg en 2 og b 2 får vi:
eller , som skulle bevises.
2. Bevis for Pythagoras teorem ved arealmetoden.
Følgende bevis, til tross for deres tilsynelatende enkelhet, er ikke så enkle i det hele tatt. Alle sammen
bruk egenskapene til området, beviset på det er mer komplisert enn beviset for selve Pythagoras teoremet.
- Bevis gjennom ekvikomplementering.
 Ordne fire like rektangulære
Ordne fire like rektangulære
trekant som vist på bildet
til høyre.
Firkant med sider c- torget,
siden summen av to spisse vinkler er 90°, og
den utviklede vinkelen er 180°.
Arealet til hele figuren er på den ene siden,
arealet av en firkant med side ( a+b), og på den annen side summen av arealene fire trekanter Og
![]()
![]()
Q.E.D.
3. Bevis for Pythagoras teorem ved infinitesimal-metoden.

Tatt i betraktning tegningen vist på figuren, og
ser siden endre segen, vi kan
skriv følgende relasjon for uendelig
liten sideøkningerMed Og en(ved å bruke likhet
trekanter):
Ved å bruke metoden for separasjon av variabler finner vi:
Et mer generelt uttrykk for å endre hypotenusen i tilfelle av økninger av begge ben:
Integrering gitt ligning og ved å bruke startbetingelsene får vi:
Dermed kommer vi til ønsket svar:
Som det er lett å se, vises den kvadratiske avhengigheten i den endelige formelen på grunn av det lineære
proporsjonalitet mellom sidene i trekanten og inkrementene, mens summen er relatert til den uavhengige
bidrag fra økningen av forskjellige ben.
Et enklere bevis kan fås hvis vi antar at et av bena ikke opplever en økning
(V denne saken bein b). Så for integrasjonskonstanten får vi:
(ifølge Papyrus 6619 fra Berlin Museum). I følge Cantor bygde harpedonapts, eller "strengstrammere", rette vinkler ved å bruke rette trekanter med sidene 3, 4 og 5.
Det er veldig enkelt å reprodusere deres konstruksjonsmetode. La oss ta et 12 m langt tau og binde det til det langs en farget stripe i en avstand på 3 m fra den ene enden og 4 meter fra den andre. En rett vinkel vil være innelukket mellom sider som er 3 og 4 meter lange. Det kan innvendes mot Harpedonaptene at deres konstruksjonsmetode blir overflødig hvis for eksempel treplassen som brukes av alle snekkere, brukes. Faktisk er egyptiske tegninger kjent der et slikt verktøy finnes - for eksempel tegninger som viser et snekkerverksted.
Noe mer er kjent om Pythagoras teorem blant babylonerne. I en tekst som dateres tilbake til Hammurabis tid, det vil si til 2000 f.Kr. e. , gis en omtrentlig beregning av hypotenusen til en rettvinklet trekant. Av dette kan vi konkludere med at de i Mesopotamia var i stand til å utføre beregninger med rettvinklede trekanter, i det minste i noen tilfeller. Basert på den ene siden på det nåværende kunnskapsnivået i egyptisk og babylonsk matematikk, og på den andre siden på en kritisk studie av greske kilder, konkluderte van der Waerden (en nederlandsk matematiker) at det var stor sannsynlighet for at hypotenus kvadratsetningen var kjent i India allerede rundt 1700-tallet f.Kr. e.
Rundt 400 f.Kr. e., ifølge Proclus, ga Platon en metode for å finne pythagoras trippel, ved å kombinere algebra og geometri. Rundt 300 f.Kr. e. Euklids elementer inneholder det eldste aksiomatiske beviset for Pythagoras teoremet.
Ordlyd
Geometrisk formulering:
Teoremet ble opprinnelig formulert som følger:
Algebraisk formulering:
Det vil si, angir lengden på hypotenusen til trekanten gjennom, og lengden på bena gjennom og:
Begge formuleringene av teoremet er ekvivalente, men den andre formuleringen er mer elementær, den krever ikke arealbegrepet. Det vil si at det andre utsagnet kan verifiseres uten å vite noe om arealet og ved å måle bare lengdene på sidene i en rettvinklet trekant.
Invers Pythagoras teorem:
Bevis
For øyeblikket er 367 bevis på denne teoremet registrert i vitenskapelig litteratur. Sannsynligvis er Pythagoras teorem den eneste teoremet med et så imponerende antall bevis. En slik variasjon kan bare forklares med den grunnleggende betydningen av teoremet for geometri.
Selvfølgelig, konseptuelt, kan alle deles inn i et lite antall klasser. De mest kjente av dem: bevis etter områdemetoden, aksiomatiske og eksotiske bevis (for eksempel ved bruk av differensialligninger).
Gjennom lignende trekanter
Følgende bevis på den algebraiske formuleringen er det enkleste av bevisene bygget direkte fra aksiomene. Spesielt bruker den ikke begrepet figurareal.

La ABC det er en rettvinklet trekant C. La oss tegne en høyde fra C og angi basen med H. Triangel ACH ligner på en trekant ABC i to hjørner. Likeledes trekanten CBH lignende ABC. Vi introduserer notasjonen
vi får
Hva er ekvivalent
Legger til, får vi
, som skulle bevisesOmrådebevis
Følgende bevis, til tross for deres tilsynelatende enkelhet, er ikke så enkle i det hele tatt. Alle bruker egenskapene til området, beviset på det er mer komplisert enn beviset for selve Pythagoras teorem.
Bevis via ekvivalens
- Ordne fire like rette trekanter som vist i figur 1.
- Firkant med sider c er et kvadrat fordi summen av to spisse vinkler er 90° og den rette vinkelen er 180°.
- Arealet til hele figuren er på den ene siden lik arealet av en firkant med en side (a + b), og på den annen side summen av arealene til fire trekanter og arealet av den indre firkanten.
Q.E.D.
Euklids bevis
Ideen til Euklids bevis er som følger: la oss prøve å bevise at halve arealet av kvadratet bygget på hypotenusen er lik summen av de halve arealene av kvadratene bygget på bena, og deretter arealene til de store og to små rutene er like.
Tenk på tegningen til venstre. Vi bygget firkanter på sidene av en rettvinklet trekant på den og tegnet en stråle s fra toppunktet til rett vinkel C vinkelrett på hypotenusen AB, den kutter kvadratet ABIK, bygget på hypotenusen, i to rektangler - BHJI og HAKJ , henholdsvis. Det viser seg at arealene til disse rektanglene er nøyaktig lik arealene til firkantene bygget på de tilsvarende bena.
La oss prøve å bevise at arealet av kvadratet DECA er lik arealet av rektangelet AHJK For å gjøre dette bruker vi en hjelpeobservasjon: Arealet av en trekant med samme høyde og base som den gitte rektangel er lik halve arealet av det gitte rektangelet. Dette er en konsekvens av å definere arealet av en trekant som halvparten av produktet av basen og høyden. Fra denne observasjonen følger det at arealet av trekanten ACK er lik arealet av trekanten AHK (ikke vist), som igjen er lik halve arealet av rektangelet AHJK.
La oss nå bevise at arealet av trekanten ACK også er lik halvparten av arealet av kvadratet DECA. Det eneste som må gjøres for dette er å bevise likheten mellom trekantene ACK og BDA (siden arealet av trekanten BDA er lik halvparten av kvadratets areal med egenskapen ovenfor). Denne likheten er åpenbar: trekanter er like i to sider og vinkelen mellom dem. Nemlig - AB=AK, AD=AC - likheten mellom vinklene CAK og BAD er lett å bevise med bevegelsesmetoden: la oss rotere trekanten CAK 90° mot klokken, da er det åpenbart at de tilsvarende sidene til de to betraktede trekantene vil falle sammen (på grunn av det faktum at vinkelen ved toppen av kvadratet er 90°).
Argumentet om likheten mellom arealene til kvadratet BCFG og rektangelet BHJI er fullstendig analogt.
Dermed har vi bevist at arealet av kvadratet bygget på hypotenusen er summen av arealene til kvadratene bygget på bena. Idé dette beviset ytterligere illustrert med animasjonen ovenfor.
Bevis for Leonardo da Vinci
Hovedelementene i beviset er symmetri og bevegelse.
Tenk på tegningen, som kan sees fra symmetrien, kutter segmentet kvadratet i to identiske deler (siden trekantene og er like i konstruksjon).
Ved å bruke en rotasjon mot klokken på 90 grader rundt punktet ser vi likheten mellom de skraverte figurene og .
Nå er det klart at arealet av figuren vi har skyggelagt er lik summen av halvparten av arealene til små firkanter (bygget på bena) og arealet til den opprinnelige trekanten. På den annen side er det lik halvparten av arealet av den store firkanten (bygget på hypotenusen) pluss arealet av den opprinnelige trekanten. Dermed er halve summen av arealene til de små firkantene lik halve arealet av den store firkanten, og derfor er summen av arealene til rutene bygget på bena lik arealet av kvadratet som er bygget på hypotenusen.
Bevis med den uendelige metoden
Følgende bevis ved hjelp av differensialligninger tilskrives ofte det velkjente Engelsk matematiker Hardy, som levde i første halvdel av 1900-tallet.
Tatt i betraktning tegningen vist på figuren og observerer endringen i siden en, kan vi skrive følgende relasjon for infinitesimale sideinkrementer Med Og en(bruker lignende trekanter):
Ved å bruke metoden for separasjon av variabler finner vi
Et mer generelt uttrykk for å endre hypotenusen ved økninger av begge ben
Ved å integrere denne ligningen og bruke startbetingelsene får vi
Dermed kommer vi frem til ønsket svar
Som det er lett å se, vises den kvadratiske avhengigheten i den endelige formelen på grunn av den lineære proporsjonaliteten mellom sidene i trekanten og inkrementene, mens summen skyldes de uavhengige bidragene fra inkrementet til forskjellige ben.
Et enklere bevis kan fås hvis vi antar at et av bena ikke opplever en økning (i dette tilfellet benet). Så for integreringskonstanten får vi
Variasjoner og generaliseringer
Lignende geometriske former på tre sider
Generalisering for lignende trekanter, arealet av grønne figurer A + B = arealet av blått C
Pythagoras teorem som bruker lignende rette trekanter
En generalisering av Pythagoras teorem ble gjort av Euklid i hans arbeid Begynnelser, utvide arealene av rutene på sidene til områdene av lignende geometriske former :
Hvis vi konstruerer lignende geometriske figurer (se euklidisk geometri) på sidene av en rettvinklet trekant, vil summen av de to mindre figurene være lik arealet til den større figuren.
Hovedideen med denne generaliseringen er at arealet til en slik geometrisk figur er proporsjonal med kvadratet til en hvilken som helst av dens lineære dimensjoner, og spesielt kvadratet på lengden på en side. Derfor, for lignende tall med områder EN, B Og C bygget på sider med lengde en, b Og c, vi har:
Men ifølge Pythagoras teorem, en 2 + b 2 = c 2, da EN + B = C.
Omvendt, hvis vi kan bevise det EN + B = C for tre lignende geometriske figurer uten å bruke Pythagoras teoremet, så kan vi bevise selve teoremet ved å gå til motsatt retning. For eksempel kan startsentertrekanten gjenbrukes som en trekant C på hypotenusen, og to like rette trekanter ( EN Og B) bygget på de to andre sidene, som er dannet som et resultat av å dele den sentrale trekanten med høyden. Summen av de to mindre områdene av trekantene er da åpenbart lik arealet til den tredje, altså EN + B = C og, etter de tidligere bevisene i omvendt rekkefølge, får vi Pythagoras teorem a 2 + b 2 = c 2 .
Cosinus teorem
Pythagoras teorem er spesielt tilfelle mer generell teorem cosinus, som relaterer lengden på sidene i en vilkårlig trekant:
hvor θ er vinkelen mellom sidene en Og b.
Hvis θ er 90 grader, vil cos θ = 0 og formelen er forenklet til den vanlige Pythagoras teorem.
Vilkårlig trekant
Til et hvilket som helst valgt hjørne av en vilkårlig trekant med sider a, b, c skriv inn en likebenet trekant på en slik måte at like vinkler ved basen var θ lik den valgte vinkelen. La oss anta at den valgte vinkelen θ er plassert på motsatt side av den angitte siden c. Som et resultat fikk vi en trekant ABD med vinkel θ, som er plassert motsatt siden en og fester r. Den andre trekanten dannes av vinkelen θ, som er motsatt siden b og fester Med lang s, som vist på bildet. Thabit Ibn Qurra uttalte at sidene i disse tre trekantene er relatert som følger:
Når vinkelen θ nærmer seg π/2, vil basen likebent trekant avtar, og de to sidene r og s overlapper hverandre mindre og mindre. Når θ = π/2, blir ADB til en rettvinklet trekant, r + s = c og vi får den innledende Pythagoras teorem.
La oss se på ett av argumentene. Trekant ABC har samme vinkler som trekant ABD, men i omvendt rekkefølge. (De to trekantene har en felles vinkel ved toppunktet B, begge har vinkelen θ, og har også den samme tredje vinkelen, med summen av vinklene til trekanten) Følgelig er ABC lik refleksjon ABD av trekanten DBA, som vist i den nedre figuren. La oss skrive sammenhengen mellom motsatte sider og ved siden av vinkelen θ,
Det samme er refleksjonen av en annen trekant,
Multipliser brøkene og legg til disse to forholdstallene:
Q.E.D.
Generalisering for vilkårlige trekanter via parallellogrammer
Generalisering for vilkårlige trekanter,
område med grønt tomt = areal blå
Bevis på oppgaven som i figuren over
La oss gjøre en ytterligere generalisering for ikke-rektangulære trekanter, ved å bruke parallellogrammer på tre sider i stedet for kvadrater. (firkanter er et spesialtilfelle.) Den øverste figuren viser at for spiss trekant arealet av parallellogrammet på langsiden er lik summen av parallellogrammene på de to andre sidene, forutsatt at parallellogrammet på langsiden er bygget som vist på figuren (dimensjonene markert med piler er de samme og bestemme sidene til det nedre parallellogrammet). Denne erstatningen av kvadrater med parallellogrammer har en klar likhet med den opprinnelige Pythagoras teorem og antas å ha blitt formulert av Pappus av Alexandria i 4 e.Kr. e.
Den nederste figuren viser fremdriften av beviset. La oss se på venstre side av trekanten. Det venstre grønne parallellogrammet har samme areal som venstre side av det blå parallellogrammet fordi de har samme base b og høyde h. Dessuten har den venstre grønne boksen samme område som den venstre grønne boksen i det øverste bildet fordi de har felles plattform(øverste venstre side trekant) og den totale høyden vinkelrett på den siden av trekanten. Ved å argumentere på samme måte for høyre side av trekanten, beviser vi at det nedre parallellogrammet har samme areal som de to grønne parallellogrammene.
Komplekse tall
Pythagoras teorem brukes til å finne avstanden mellom to punkter i et kartesisk koordinatsystem, og denne teoremet gjelder for alle sanne koordinater: avstand s mellom to punkter ( a, b) Og ( c, d) er lik
Det er ingen problemer med formelen hvis komplekse tall behandles som vektorer med reelle komponenter x + jeg y = (x, y). . For eksempel avstanden s mellom 0 + 1 Jeg og 1 + 0 Jeg beregne som vektormodul (0, 1) − (1, 0) = (−1, 1), eller
For operasjoner med vektorer med komplekse koordinater er det imidlertid nødvendig å gjøre en viss forbedring av den pythagoriske formelen. Avstand mellom punkter med komplekse tall (en, b) Og ( c, d); en, b, c, Og d er alle komplekse, formulerer vi vha absolutte verdier. Avstand s basert på vektorforskjell (en − c, b − d) V følgende skjema: la forskjellen en − c = s+ i q, Hvor s er den virkelige delen av forskjellen, q er den imaginære delen, og i = √(−1). Likeledes, la b − d = r+i s. Deretter:
hvor er det komplekse konjugatet av . For eksempel avstanden mellom punktene (en, b) = (0, 1) Og (c, d) = (Jeg, 0) , beregne forskjellen (en − c, b − d) = (−Jeg, 1) og resultatet ville være 0 hvis komplekse konjugater ikke ble brukt. Derfor, ved å bruke den forbedrede formelen, får vi
Modulen er definert slik:
Stereometri
En betydelig generalisering av Pythagoras teorem for tredimensjonalt rom er de Guas teorem, oppkalt etter J.-P. de Gua: hvis et tetraeder har en rett vinkel (som i en terning), så er kvadratet av arealet av ansiktet motsatt den rette vinkelen lik summen av kvadratene av arealene til de tre andre flatene. Denne konklusjonen kan oppsummeres som " n-dimensjonal Pythagoras teorem":
Pythagoras sin teorem tredimensjonalt rom forbinder diagonalen AD med tre sider.
En annen generalisering: Pythagoras teorem kan brukes på stereometri i følgende form. Ta i betraktning kuboid, som vist på bildet. Finn lengden på diagonalen BD ved å bruke Pythagoras setning:
hvor tre sider danner en rettvinklet trekant. Bruk den horisontale diagonalen BD og den vertikale kanten AB for å finne lengden på diagonalen AD, igjen ved å bruke Pythagoras teorem:
eller, hvis alt er skrevet i en ligning:
Dette resultatet er et 3D-uttrykk for å bestemme størrelsen på vektoren v(diagonal AD) uttrykt i form av dens vinkelrette komponenter ( v k) (tre gjensidig vinkelrette sider):
Denne ligningen kan sees på som en generalisering av Pythagoras teorem for et flerdimensjonalt rom. Imidlertid er resultatet faktisk ikke noe mer enn den gjentatte anvendelsen av Pythagoras teorem på en sekvens av rette trekanter i suksessivt vinkelrette plan.
vektorrom
Når det gjelder et ortogonalt system av vektorer, skjer det en likhet, som også kalles Pythagoras teorem:
If er projeksjonen av vektoren på koordinatakser, så faller denne formelen sammen med den euklidiske avstanden - og betyr at lengden på vektoren er lik roten kvadratsum kvadrater av dens komponenter.
En analog av denne likestillingen i saken endeløst system vektorer kalles Parsevals likhet.
Ikke-euklidisk geometri
Pythagoras teoremet er avledet fra aksiomene til euklidisk geometri og er faktisk ikke gyldig for ikke-euklidisk geometri, i den formen den er skrevet ovenfor. (Det vil si at Pythagoras teorem viser seg å være en slags ekvivalent med Euklids postulat om parallellisme) Med andre ord, i ikke-euklidisk geometri vil forholdet mellom sidene i trekanten nødvendigvis være i en annen form enn Pythagoras teoremet . For eksempel, i sfærisk geometri, alle tre sidene av en rettvinklet trekant (si en, b Og c) som binder oktanten (en åttendedel) av enhetssfæren har lengden π/2, noe som motsier Pythagoras teorem fordi en 2 + b 2 ≠ c 2 .
Tenk her to tilfeller av ikke-euklidisk geometri - sfærisk og hyperbolsk geometri; i begge tilfeller, som for det euklidiske rommet for rettvinklede trekanter, følger resultatet som erstatter Pythagoras teorem av cosinussetningen.
Imidlertid forblir Pythagoras teoremet gyldig for hyperbolsk og elliptisk geometri hvis kravet om at trekanten er rettvinklet erstattes av betingelsen om at summen av to vinkler i trekanten må være lik den tredje, for eksempel EN+B = C. Da ser forholdet mellom sidene slik ut: summen av arealene av sirkler med diametre en Og b lik arealet av en sirkel med diameter c.
sfærisk geometri
For enhver rettvinklet trekant på en kule med radius R(for eksempel hvis vinkelen γ i trekanten er rett) med sider en, b, c forholdet mellom partene vil se slik ut:
Denne likheten kan utledes som et spesielt tilfelle sfærisk cosinus-teorem, som er gyldig for alle sfæriske trekanter:
der cosh er den hyperbolske cosinus. Denne formelen er et spesialtilfelle av hyperbolsk cosinus-teoremet, som er gyldig for alle trekanter:
hvor γ er vinkelen hvis toppunkt er motsatt siden c.
Hvor g ij kalles den metriske tensoren. Det kan være en posisjonsfunksjon. Slike krumlinjede rom inkluderer Riemannsk geometri som generelt eksempel. Denne formuleringen er også egnet for euklidisk rom ved bruk av krumlinjede koordinater. For eksempel for polare koordinater:
vektor produkt
Pythagoras teorem forbinder to uttrykk for størrelsen på et vektorprodukt. En tilnærming til å definere et kryssprodukt krever at det tilfredsstiller ligningen:
denne formelen bruker punktproduktet. Høyre side av ligningen kalles Grams determinant for en Og b, som er lik arealet av parallellogrammet dannet av disse to vektorene. Basert på dette kravet, samt kravet om at vektorproduktet skal være vinkelrett på dets komponenter en Og b det følger at, bortsett fra de trivielle tilfellene av 0- og 1-dimensjonalt rom, er vektorproduktet bare definert i tre og syv dimensjoner. Vi bruker definisjonen av vinkelen i n-dimensjonalt rom:
denne egenskapen til vektorproduktet gir sin verdi i følgende form:
Gjennom det grunnleggende trigonometrisk identitet Pythagoras, vi får en annen form for å skrive verdien:
En alternativ tilnærming til å definere et kryssprodukt bruker et uttrykk for størrelsen. Så, argumenterende i omvendt rekkefølge, får vi en sammenheng med skalært produkt:
se også
Notater
- Historietema: Pythagoras sin teorem i babylonsk matematikk
- ( , s. 351) s. 351
- ( , bind I, s. 144)
- Diskusjon historiske fakta gitt i (, s. 351) s. 351
- Kurt Von Fritz (apr., 1945). "Oppdagelsen av incommensurability av Hippasus of Metapontum". The Annals of Mathematics, andre serie(Annals of Mathematics) 46 (2): 242–264.
- Lewis Carroll, "The story with knots", M., Mir, 1985, s. 7
- Asger Aaboe Episoder fra matematikkens tidlige historie. - Mathematical Association of America, 1997. - S. 51. - ISBN 0883856131
- Pythagoras forslag av Elisha Scott Loomis
- Euklids Elementer: Bok VI, påstand VI 31: "I rettvinklede trekanter er figuren på siden som undertrykker den rette vinkelen lik de lignende og lignende beskrevne figurene på sidene som inneholder den rette vinkelen."
- Lawrence S. Leff siterte verk. - Barron's Educational Series. - S. 326. - ISBN 0764128922
- Howard Whitley Eves§4.8:...generalisering av Pythagoras teorem // Store øyeblikk i matematikk (før 1650) . - Mathematical Association of America, 1983. - S. 41. - ISBN 0883853108
- Tâbit ibn Qorra (fullt navn Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 e.Kr.) var en lege bosatt i Bagdad som skrev mye om Euklids elementer og andre matematiske fag.
- Aydin Sayili (mars 1960). "Thâbit ibn Qurras generalisering av Pythagoras teorem". Isis 51 (1): 35–37. DOI:10.1086/348837.
- Judith D. Sally, Paul Sally Oppgave 2.10(ii) // Sitert arbeid . - S. 62. - ISBN 0821844032
- For detaljer om en slik konstruksjon, se George Jennings Figur 1.32: Den generaliserte Pythagoras teorem // Moderne geometri med anvendelser: med 150 figurer . - 3. - Springer, 1997. - S. 23. - ISBN 038794222X
- Arlen Brown, Carl M. Pearcy punkt C: Norm for en vilkårlig n-tuple ... // En introduksjon til analyse . - Springer, 1995. - S. 124. - ISBN 0387943692 Se også side 47-50.
- Alfred Gray, Elsa Abbena, Simon Salamon Moderne differensialgeometri av kurver og overflater med Mathematica. - 3. - CRC Press, 2006. - S. 194. - ISBN 1584884487
- Rajendra Bhatia matriseanalyse. - Springer, 1997. - S. 21. - ISBN 0387948465
- Stephen W. Hawking siterte verk. - 2005. - S. 4. - ISBN 0762419229
- Eric W. Weisstein CRC kortfattet leksikon for matematikk. - 2. - 2003. - S. 2147. - ISBN 1584883472
- Alexander R. Pruss
Gjennomsnittlig nivå
Høyre trekant. Komplett illustrert veiledning (2019)
HØYRE TREKANT. FØRSTE NIVÅ.
I problemer er en rett vinkel ikke nødvendig i det hele tatt - den nedre venstre, så du må lære å gjenkjenne en rettvinklet trekant i denne formen,

og i slikt

og i slikt 
Hva er bra med en rettvinklet trekant? Vel... for det første er det spesielle vakre navn for hans sider.
Oppmerksomhet på tegningen!

Husk og ikke forveksle: ben - to, og hypotenusen - bare en(den eneste, unike og lengste)!
Vel, vi diskuterte navnene, nå det viktigste: Pythagoras teorem.
Pythagoras teorem.
Denne teoremet er nøkkelen til å løse mange problemer som involverer en rettvinklet trekant. Det ble bevist av Pythagoras i helt uminnelige tider, og siden da har det brakt mange fordeler for de som kjenner det. Og det beste med henne er at hun er enkel.
Så, Pythagoras teorem:
Husker du vitsen: «Pythagorean-bukser er like på alle kanter!»?
La oss tegne disse veldig pytagoreiske buksene og se på dem. 
Ser det virkelig ut som en shorts? Vel, på hvilke sider og hvor er de like? Hvorfor og hvor kom vitsen fra? Og denne vitsen henger nettopp sammen med Pythagoras teorem, mer presist med måten Pythagoras selv formulerte teoremet på. Og han formulerte det slik:
"Sum område av firkanter, bygget på bena, er lik kvadratisk areal bygget på hypotenusen.
Høres det ikke litt annerledes ut, gjør det ikke? Og så, da Pythagoras tegnet utsagnet om teoremet sitt, viste det seg nettopp et slikt bilde.

På dette bildet er summen av arealene til de små firkantene lik arealet til den store firkanten. Og for at barna bedre skal huske at summen av kvadratene på bena er lik kvadratet på hypotenusen, fant noen vittig opp denne vitsen om pytagoreiske bukser.
Hvorfor formulerer vi Pythagoras teorem nå?
Led Pythagoras og snakket om firkanter?
Du skjønner, i antikken var det ingen ... algebra! Det var ingen tegn og så videre. Det var ingen inskripsjoner. Kan du forestille deg hvor forferdelig det var for de stakkars eldgamle studentene å lære alt utenat med ord??! Og vi kan være glade for at vi har en enkel formulering av Pythagoras teorem. La oss gjenta det igjen for bedre å huske:
Nå skal det være enkelt:
| Kvadraten på hypotenusen er lik summen av kvadratene på bena. |
Vel, det viktigste teoremet om en rettvinklet trekant ble diskutert. Hvis du lurer på hvordan det er bevist, les videre. neste nivåer teori, og la oss nå gå videre ... til mørk skog... trigonometri! Til de forferdelige ordene sinus, cosinus, tangent og cotangens.
Sinus, cosinus, tangens, cotangens i en rettvinklet trekant.
Faktisk er ikke alt så skummelt i det hele tatt. Selvfølgelig bør den "virkelige" definisjonen av sinus, cosinus, tangens og cotangens ses på i artikkelen. Men du vil virkelig ikke, gjør du? Vi kan glede oss: for å løse problemer om en rettvinklet trekant, kan du bare fylle ut følgende enkle ting:
Hvorfor handler det om hjørnet? Hvor er hjørnet? For å forstå dette må du vite hvordan påstandene 1 - 4 er skrevet med ord. Se, forstå og husk!
1.
Det høres faktisk slik ut:
Hva med vinkelen? Er det et ben som er motsatt hjørnet, det vil si det motsatte benet (for hjørnet)? Selvfølgelig har! Dette er en katet!
Men hva med vinkelen? Se nærmere. Hvilket ben er ved siden av hjørnet? Selvfølgelig, katten. Så, for vinkelen, er benet tilstøtende, og
Og nå, oppmerksomhet! Se hva vi har:
Se hvor flott det er:
La oss nå gå videre til tangent og cotangens.
Hvordan sette ord på det nå? Hva er beinet i forhold til hjørnet? Motsatt, selvfølgelig - den "ligger" overfor hjørnet. Og kateten? I tilknytning til hjørnet. Så hva fikk vi?
Ser du hvordan telleren og nevneren er reversert?
Og nå igjen hjørnene og byttet:
Sammendrag
La oss kort skrive ned hva vi har lært.
 |
Pythagoras teorem: |
Den viktigste rettvinklede trekantsatsen er Pythagoras teorem.
Pythagoras teorem
Husker du forresten godt hva bena og hypotenusen er? Hvis ikke, så se på bildet - oppdater kunnskapen din

Det er mulig du allerede har brukt Pythagoras teorem mange ganger, men har du noen gang lurt på hvorfor en slik teorem er sann. Hvordan vil du bevise det? La oss gjøre som de gamle grekerne. La oss tegne en firkant med en side.

Du ser hvor snedig vi delte sidene inn i segmenter av lengder og!
La oss nå koble sammen de merkede punktene

Her noterte vi imidlertid noe annet, men du selv ser på bildet og tenker på hvorfor.
Hva er arealet av den større firkanten? Ikke sant, . Hva med det mindre området? Gjerne,. Det totale arealet av de fire hjørnene gjenstår. Tenk deg at vi tok to av dem og lente oss mot hverandre med hypotenuser. Hva skjedde? To rektangler. Så arealet av "borekaks" er likt.
La oss sette alt sammen nå.
La oss transformere:
Så vi besøkte Pythagoras - vi beviste teoremet hans på en eldgammel måte.
Rettvinklet trekant og trigonometri
For en rettvinklet trekant gjelder følgende relasjoner:

Sinus spiss vinkel lik forholdet mellom det motsatte benet og hypotenusen
Cosinus til en spiss vinkel er lik forholdet mellom det tilstøtende benet og hypotenusen.
Tangensen til en spiss vinkel er lik forholdet mellom det motsatte benet og det tilstøtende benet.
Kotangensen til en spiss vinkel er lik forholdet mellom det tilstøtende benet og det motsatte benet.
Og nok en gang, alt dette i form av en tallerken:
Det er veldig behagelig!
Tegn på likhet av rette trekanter
I. På to ben

II. Ved ben og hypotenus

III. Ved hypotenus og spiss vinkel

IV. Langs benet og spiss vinkel
en) 
b) 
Merk følgende! Her er det veldig viktig at bena er "korresponderende". For eksempel, hvis det går slik:

DA ER IKKE TREKANTENE LIKE, til tross for at de har en identisk spiss vinkel.
Trenger å i begge trekanter var benet ved siden av hverandre, eller i begge - motsatt.
Har du lagt merke til hvordan likhetstegnene til rette trekanter skiller seg fra de vanlige likhetstegnene til trekanter? Se på emnet "og vær oppmerksom på det faktum at for likheten mellom "vanlige" trekanter trenger du likheten mellom de tre elementene: to sider og en vinkel mellom dem, to vinkler og en side mellom dem, eller tre sider. Men for likestilling av rettvinklede trekanter er bare to tilsvarende elementer nok. Det er flott, ikke sant?
Omtrent samme situasjon med tegn på likhet av rette trekanter.
Tegn på likhet med rette trekanter
I. Akutt hjørne

II. På to bein

III. Ved ben og hypotenus

Median i en rettvinklet trekant
Hvorfor er det slik?
Tenk på et helt rektangel i stedet for en rettvinklet trekant.
La oss tegne en diagonal og vurdere et punkt - skjæringspunktet mellom diagonalene. Hva vet du om diagonalene til et rektangel?
Og hva følger av dette?
Så det skjedde
- - median:
Husk dette faktum! Hjelper mye!
Det som er enda mer overraskende er at det motsatte også er sant.
Hva kan man få ut av det faktum at medianen trukket til hypotenusen er lik halve hypotenusen? La oss se på bildet
Se nærmere. Vi har: , det vil si at avstandene fra punktet til alle tre hjørnene i trekanten viste seg å være like. Men i en trekant er det bare ett punkt, avstandene som omtrent alle tre toppunktene i trekanten er like fra, og dette er SENTERET AV SIRKUMET beskrevet. Så hva skjedde?
Så la oss starte med dette "foruten...".
La oss se på i.
Men i like trekanter er alle vinkler like!
Det samme kan sies om og
La oss nå tegne det sammen:
Hvilken nytte kan trekkes fra denne "trippel" likheten.
Vel, for eksempel - to formler for høyden til en rettvinklet trekant.
Vi skriver forholdet til de tilsvarende partene:

For å finne høyden løser vi proporsjonen og får første formel "Høyde i en rettvinklet trekant":
Så la oss bruke likheten: .

Hva vil skje nå?
Igjen løser vi proporsjonen og får den andre formelen:
Begge disse formlene må huskes veldig godt og den som er mer praktisk å bruke. La oss skrive dem ned igjen.
Pythagoras teorem:
I en rettvinklet trekant er kvadratet på hypotenusen lik summen av kvadratene til bena:.

Tegn på likhet i rette trekanter:
- på to ben:
- langs benet og hypotenusen: eller
- langs benet og den tilstøtende spisse vinkelen: eller
- langs benet og motsatt spiss vinkel: eller
- ved hypotenuse og spiss vinkel: eller.
Tegn på likhet med rette trekanter:
- ett skarpt hjørne: eller
- fra proporsjonaliteten til de to benene:
- fra proporsjonaliteten til benet og hypotenusen: eller.
Sinus, cosinus, tangens, cotangens i en rettvinklet trekant
- Sinusen til en spiss vinkel i en rettvinklet trekant er forholdet mellom det motsatte benet og hypotenusen:
- Cosinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom det tilstøtende benet og hypotenusen:
- Tangensen til en spiss vinkel i en rettvinklet trekant er forholdet mellom det motsatte benet og det tilstøtende:
- Kotangensen til en spiss vinkel i en rettvinklet trekant er forholdet mellom det tilstøtende benet og det motsatte:.
Høyde på en rettvinklet trekant: eller.
I en rettvinklet trekant er medianen trukket fra toppunktet til den rette vinkelen lik halve hypotenusen: .
Arealet av en rettvinklet trekant:
- gjennom katetrene:
 På samme måte ligner trekant CBH på ABC. Vi introduserer notasjonen
På samme måte ligner trekant CBH på ABC. Vi introduserer notasjonen  1. Ordne fire like rette trekanter som vist på figuren.
1. Ordne fire like rette trekanter som vist på figuren. 
 Ideen til Euklids bevis er som følger: la oss prøve å bevise at halve arealet av kvadratet bygget på hypotenusen er lik summen av de halve arealene av kvadratene bygget på bena, og deretter arealene til de store og to små rutene er like. Tenk på tegningen til venstre. Vi bygget firkanter på sidene av en rettvinklet trekant på den og tegnet en stråle s fra toppunktet til rett vinkel C vinkelrett på hypotenusen AB, den kutter kvadratet ABIK, bygget på hypotenusen, i to rektangler - BHJI og HAKJ , henholdsvis. Det viser seg at arealene til disse rektanglene er nøyaktig lik arealene til firkantene bygget på de tilsvarende bena. La oss prøve å bevise at arealet av kvadratet DECA er lik arealet av rektangelet AHJK For å gjøre dette bruker vi en hjelpeobservasjon: Arealet av en trekant med samme høyde og base som den gitte rektangel er lik halve arealet av det gitte rektangelet. Dette er en konsekvens av å definere arealet av en trekant som halvparten av produktet av basen og høyden. Fra denne observasjonen følger det at arealet av trekanten ACK er lik arealet av trekanten AHK (ikke vist), som igjen er lik halve arealet av rektangelet AHJK. La oss nå bevise at arealet av trekanten ACK også er lik halvparten av arealet av kvadratet DECA. Det eneste som må gjøres for dette er å bevise likheten mellom trekantene ACK og BDA (siden arealet av trekanten BDA er lik halvparten av kvadratets areal med egenskapen ovenfor). Denne likheten er åpenbar, trekantene er like i to sider og vinkelen mellom dem. Nemlig - AB=AK,AD=AC - likheten mellom vinklene CAK og BAD er lett å bevise med bevegelsesmetoden: la oss rotere trekanten CAK 90° mot klokken, da er det åpenbart at de tilsvarende sidene til de to trekantene som vurderes vil sammenfaller (på grunn av det faktum at vinkelen ved toppen av kvadratet er 90°). Argumentet om likheten mellom arealene til kvadratet BCFG og rektangelet BHJI er fullstendig analogt. Dermed har vi bevist at arealet av kvadratet bygget på hypotenusen er summen av arealene til kvadratene bygget på bena.
Ideen til Euklids bevis er som følger: la oss prøve å bevise at halve arealet av kvadratet bygget på hypotenusen er lik summen av de halve arealene av kvadratene bygget på bena, og deretter arealene til de store og to små rutene er like. Tenk på tegningen til venstre. Vi bygget firkanter på sidene av en rettvinklet trekant på den og tegnet en stråle s fra toppunktet til rett vinkel C vinkelrett på hypotenusen AB, den kutter kvadratet ABIK, bygget på hypotenusen, i to rektangler - BHJI og HAKJ , henholdsvis. Det viser seg at arealene til disse rektanglene er nøyaktig lik arealene til firkantene bygget på de tilsvarende bena. La oss prøve å bevise at arealet av kvadratet DECA er lik arealet av rektangelet AHJK For å gjøre dette bruker vi en hjelpeobservasjon: Arealet av en trekant med samme høyde og base som den gitte rektangel er lik halve arealet av det gitte rektangelet. Dette er en konsekvens av å definere arealet av en trekant som halvparten av produktet av basen og høyden. Fra denne observasjonen følger det at arealet av trekanten ACK er lik arealet av trekanten AHK (ikke vist), som igjen er lik halve arealet av rektangelet AHJK. La oss nå bevise at arealet av trekanten ACK også er lik halvparten av arealet av kvadratet DECA. Det eneste som må gjøres for dette er å bevise likheten mellom trekantene ACK og BDA (siden arealet av trekanten BDA er lik halvparten av kvadratets areal med egenskapen ovenfor). Denne likheten er åpenbar, trekantene er like i to sider og vinkelen mellom dem. Nemlig - AB=AK,AD=AC - likheten mellom vinklene CAK og BAD er lett å bevise med bevegelsesmetoden: la oss rotere trekanten CAK 90° mot klokken, da er det åpenbart at de tilsvarende sidene til de to trekantene som vurderes vil sammenfaller (på grunn av det faktum at vinkelen ved toppen av kvadratet er 90°). Argumentet om likheten mellom arealene til kvadratet BCFG og rektangelet BHJI er fullstendig analogt. Dermed har vi bevist at arealet av kvadratet bygget på hypotenusen er summen av arealene til kvadratene bygget på bena.  Tenk på tegningen, som man kan se av symmetrien, segmentet CI kutter kvadratet ABHJ i to identiske deler (siden trekantene ABC og JHI er like i konstruksjon). Ved å bruke en 90 graders rotasjon mot klokken ser vi likheten mellom de skraverte figurene CAJI og GDAB. Nå er det klart at arealet av figuren som er skyggelagt av oss, er lik summen av halvparten av arealene til rutene bygget på bena og arealet til den opprinnelige trekanten. På den annen side er det lik halve arealet av kvadratet bygget på hypotenusen, pluss arealet av den opprinnelige trekanten. Det siste trinnet i beviset overlates til leseren.
Tenk på tegningen, som man kan se av symmetrien, segmentet CI kutter kvadratet ABHJ i to identiske deler (siden trekantene ABC og JHI er like i konstruksjon). Ved å bruke en 90 graders rotasjon mot klokken ser vi likheten mellom de skraverte figurene CAJI og GDAB. Nå er det klart at arealet av figuren som er skyggelagt av oss, er lik summen av halvparten av arealene til rutene bygget på bena og arealet til den opprinnelige trekanten. På den annen side er det lik halve arealet av kvadratet bygget på hypotenusen, pluss arealet av den opprinnelige trekanten. Det siste trinnet i beviset overlates til leseren.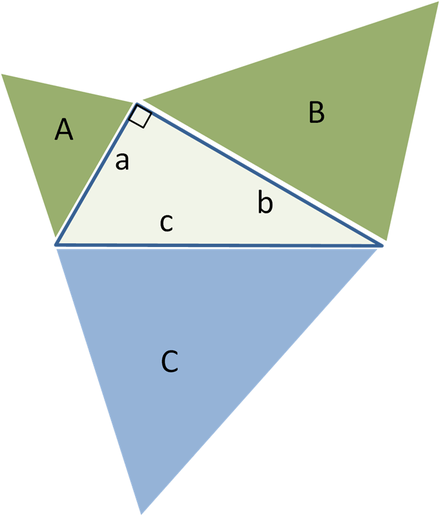




 Hvorfor gråter en person uten grunn
Hvorfor gråter en person uten grunn Generelle data om lengden på veiene i den russiske føderasjonen Trans-Siberian Highway, Russland
Generelle data om lengden på veiene i den russiske føderasjonen Trans-Siberian Highway, Russland Hvordan beregne volumet av en boks?
Hvordan beregne volumet av en boks?