Den direkte Fourier-transformasjonen lar deg bestemme. Fourier-transformasjon

Fourier-transformasjon er en familie av matematiske metoder basert på dekomponering av den opprinnelige kontinuerlige funksjonen av tid til et sett med grunnleggende harmoniske funksjoner (som er sinusformede funksjoner) med forskjellig frekvens, amplitude og fase. Det kan sees fra definisjonen at hovedideen med transformasjonen er at enhver funksjon kan representeres som en uendelig sum av sinusoider, som hver vil være preget av sin amplitude, frekvens og startfase.

Fourier-transformasjonen er grunnleggeren spektral analyse. Spektralanalyse er en signalbehandlingsmetode som lar deg karakterisere frekvensinnholdet i det målte signalet. Avhengig av hvordan signalet er representert, brukes forskjellige Fourier-transformasjoner. Det finnes flere typer Fourier-transformasjoner:

– Continuous Fourier Transform (i engelsk litteratur Continue Time Fourier Transform – CTFT eller kort sagt, FT);

– Discrete Fourier Transform (i engelsk litteratur Discrete Fourier Transform – DFT);

– Fast Fourier transform (i engelsk litteratur Fast Fourier transform – FFT).

Kontinuerlig Fourier-transformasjon

Fourier-transformasjonen er et matematisk verktøy som brukes i ulike vitenskapelige felt. I noen tilfeller kan det brukes som en løsning komplekse ligninger beskriver dynamiske prosesser som skjer under påvirkning av elektrisk, termisk eller lysenergi. I andre tilfeller lar den deg fremheve de vanlige komponentene i et komplekst oscillerende signal, slik at du kan tolke riktig eksperimentelle observasjoner innen astronomi, medisin og kjemi. En kontinuerlig transformasjon er faktisk en generalisering av Fourier-rekker, forutsatt at perioden med den utvidede funksjonen har en tendens til uendelig. Dermed omhandler den klassiske Fourier-transformen spekteret til signalet tatt over hele området for eksistensen av variabelen.

Det er flere typer skriving av den kontinuerlige Fourier-transformasjonen, som skiller seg fra hverandre ved verdien av koeffisienten foran integralet (to former for skriving):

eller

hvor og er Fourier-bildet av funksjonen eller frekvensspekteret til funksjonen;

- sirkulær frekvens.

Det er verdt å merke seg at forskjellige typer poster finnes i ulike felt vitenskap og teknologi. Normaliseringsfaktoren er nødvendig for riktig skalering av signalet fra frekvensdomenet til tidsdomenet. Normaliseringsfaktoren reduserer amplituden til signalet ved utgangen av den inverse transformasjonen slik at den samsvarer med amplituden til det opprinnelige signalet. I den matematiske litteraturen multipliseres de direkte og inverse Fourier-transformasjonene med faktoren, mens i fysikk som oftest ikke er faktoren satt for den direkte transformasjonen, men faktoren er satt for den motsatte. Hvis vi suksessivt beregner direkte konvertering Fourier av et eller annet signal, og etter å ha tatt den inverse Fourier-transformasjonen, må resultatet av den inverse transformasjonen være fullstendig sammenfallende med det opprinnelige signalet.

Hvis funksjonen er oddetall i intervallet (−∞, +∞), kan Fourier-transformasjonen representeres i form av sinusfunksjonen:

Hvis funksjonen er jevn på intervallet (−∞, +∞), kan Fourier-transformasjonen representeres i form av cosinusfunksjonen:

Dermed lar den kontinuerlige Fourier-transformen oss representere ikke periodisk funksjon som et integral av en funksjon som ved hvert av dens punkter representerer koeffisienten til Fourier-serien for en ikke-periodisk funksjon.

Fourier-transformasjonen er reversibel, det vil si at hvis Fourier-bildet ble beregnet fra funksjonen, kan den opprinnelige funksjonen gjenopprettes unikt fra Fourier-bildet. Den inverse Fourier-transformasjonen forstås som en integral av formen (to former for skriving):

eller

hvor er Fourier-bildet av funksjonen eller frekvensspekteret til funksjonen;

- sirkulær frekvens.

Hvis funksjonen er oddetall i intervallet (−∞, +∞), kan den inverse Fourier-transformasjonen representeres i form av sinusfunksjonen:

Hvis funksjonen er jevn på intervallet (−∞, +∞), kan den inverse Fourier-transformasjonen representeres i form av cosinusfunksjonen:

Tenk på følgende funksjon som et eksempel . Grafen for eksponentialfunksjonen som studeres er presentert nedenfor.

Fordi funksjonen er jevn funksjon, vil den kontinuerlige Fourier-transformasjonen bli definert som følger:

Som et resultat oppnådde vi avhengigheten av endringen i den studerte eksponentialfunksjonen på frekvensintervallet (se nedenfor).

Den kontinuerlige Fourier-transformen brukes vanligvis i teorien når man vurderer signaler som endres i samsvar med gitte funksjoner, men i praksis omhandler de vanligvis målinger som er diskrete data. Måleresultatene registreres med jevne mellomrom med en viss samplingsfrekvens, for eksempel 16000 Hz eller 22000 Hz. Imidlertid, i generell sak diskrete avlesninger kan gå ujevnt, men dette kompliserer matematisk apparat analyse, så det brukes vanligvis ikke i praksis.

Det er et viktig teorem fra Kotelnikov (i utenlandsk litteratur er det navnet "Nyquist-Shannon-teorem", "sample-teorem"), som sier at et analogt periodisk signal med et begrenset (begrenset i bredde) spektrum (0 ... fmax) kan gjenopprettes unikt uten forvrengninger og tap i deres diskrete avlesninger, tatt med en frekvens større enn eller lik to ganger øvre frekvens av spekteret - samplingsfrekvens (fdisc >= 2*fmax). Med andre ord, ved en samplingshastighet på 1000 Hz, kan et signal med en frekvens på opptil 500 Hz gjenvinnes fra et analogt periodisk signal. Det skal bemerkes at diskretisering av en funksjon i tid fører til periodisering av spekteret, og diskretisering av spekteret i frekvens fører til periodisering av funksjonen.

Dette er en av Fourier-transformasjonene som er mye brukt i digitale signalbehandlingsalgoritmer.

Den direkte diskrete Fourier-transformasjonen assosierer en tidsfunksjon , som er definert av N-målepunkter på et gitt tidsintervall, med en annen funksjon , som er definert på et frekvensintervall. Det skal bemerkes at funksjonen på tidsintervallet er spesifisert ved bruk av N-prøver, og funksjonen på frekvensdomenet er spesifisert ved bruk av K-fold spekteret.

k ˗ frekvensindeks.

Frekvensen til det kth signalet bestemmes av uttrykket

hvor T er tidsperioden som inndataene ble tatt.

Den direkte diskrete transformasjonen kan omskrives når det gjelder de virkelige og imaginære komponentene. Den virkelige komponenten er en matrise som inneholder verdiene til cosinuskomponentene, og den imaginære komponenten er en matrise som inneholder verdiene til sinuskomponentene.

Fra de siste uttrykkene kan man se at transformasjonen dekomponerer signalet til sinusformede komponenter (som kalles harmoniske) med frekvenser fra en svingning per periode til N svingninger per periode.

Den diskrete Fourier-transformen har en singularitet fordi diskret sekvens kan oppnås ved summen av funksjoner med ulik sammensetning av det harmoniske signalet. Med andre ord, en diskret sekvens dekomponeres i harmoniske variabler – tvetydig. Derfor, når du utvider en diskret funksjon ved å bruke en diskret Fourier-transformasjon, vises høyfrekvente komponenter i andre halvdel av spekteret, som ikke var i det opprinnelige signalet. Dette høyfrekvente spekteret er et speilbilde av den første delen av spekteret (når det gjelder frekvens, fase og amplitude). Vanligvis vurderes ikke den andre halvdelen av spekteret, og signalamplitudene til den første delen av spekteret dobles.

Det skal bemerkes at utvidelsen av en kontinuerlig funksjon ikke fører til utseendet til en speileffekt, siden en kontinuerlig funksjon er unikt dekomponert til harmoniske variabler.

Amplituden til DC-komponenten er gjennomsnittsverdien av funksjonen over en valgt tidsperiode og bestemmes som følger:

Amplitudene og fasene til signalets frekvenskomponenter bestemmes av følgende forhold:

De resulterende amplitude- og faseverdiene kalles polar notasjon. Den resulterende signalvektoren vil bli definert som følger:

Vurder transformasjonsalgoritmen diskret gitt funksjon på gitt intervall(på en gitt periode) med antall startpoeng

D gnist Fourier-transformasjon

Som et resultat av transformasjonen får vi de reelle og imaginære verdiene til funksjonen, som er definert på frekvensområdet.

Den omvendte diskrete Fourier-transformen assosieres frekvensfunksjon, som er definert av K-fold-spekteret på frekvensdomenet, en annen funksjon , som er definert på tidsdomenet.

N ˗ antall signalverdier målt per periode, samt mangfoldet av frekvensspekteret;

k ˗ frekvensindeks.

Som allerede nevnt transformeres den diskrete Fourier til N-punkter diskret signal assosierer N-komplekse spektralprøver av signalet med . N operasjoner kreves for å beregne én spektralprøve kompleks multiplikasjon og tillegg. Dermed er beregningskompleksiteten til den diskrete Fourier-transformasjonsalgoritmen kvadratisk, med andre ord kreves komplekse multiplikasjons- og addisjonsoperasjoner.

Fouriertransformasjon - en transformasjon som sammenligner funksjonene til en reell variabel. Denne operasjonen utføres hver gang vi oppfatter forskjellige lyder. Øret utfører en automatisk "beregning", som vår bevissthet er i stand til å utføre bare etter å ha studert den aktuelle delen. høyere matematikk. Det menneskelige høreorganet bygger en transformasjon, som et resultat av at lyden ( oscillerende bevegelse betingede partikler i elastisk medium, som forplanter seg i en bølgeform i et fast, flytende eller gassformig medium) er gitt i form av et spekter av påfølgende verdier av volumnivået til toner i forskjellige høyder. Etter det snur hjernen seg denne informasjonen til en kjent lyd.

Matematisk Fourier Transform

transformasjon lydbølger eller andre oscillerende prosesser (fra lysstråling og havvann til stjerne- eller solaktivitet) kan også utføres ved hjelp av matematiske metoder. Så ved å bruke disse teknikkene kan du utvide funksjonene ved å presentere oscillerende prosesser et sett med sinusformede komponenter, det vil si bølgende kurver som går fra minimum til maksimum, så tilbake til minimum, som havbølge. Fouriertransformasjon - en transformasjon hvis funksjon beskriver fasen eller amplituden til hver sinusoid som tilsvarer en viss frekvens. Fasen er utgangspunktet for kurven, og amplituden er dens høyde.

Fourier-transformasjonen (eksempler er vist på bildet) er et veldig kraftig verktøy som brukes i ulike vitenskapsfelt. I enkeltsaker det brukes som et middel til å løse ganske komplekse ligninger som beskriver dynamiske prosesser som skjer under påvirkning av lys, varme eller elektrisk energi. I andre tilfeller lar det deg bestemme de vanlige komponentene i komplekse oscillerende signaler, takket være hvilke du kan tolke forskjellige eksperimentelle observasjoner i kjemi, medisin og astronomi riktig.

Historisk referanse

Den første personen som brukte denne metoden var fransk matematiker Jean Baptiste Fourier. Transformasjonen, senere oppkalt etter ham, ble opprinnelig brukt til å beskrive mekanismen for varmeledning. Fourier brukte hele sitt voksne liv på å studere varmes egenskaper. Han ga et stort bidrag til matematisk teori definisjoner av røttene til algebraiske ligninger. Fourier var professor i analyse ved Polyteknisk skole, sekretær for Institute of Egyptology, var i den keiserlige tjenesten, der han utmerket seg under byggingen av veien til Torino (under hans ledelse ble mer enn 80 tusen kvadratkilometer med malaria-sumper drenert). Men all denne kraftige aktiviteten hindret ikke forskeren i å matematisk analyse. I 1802 utledet han en ligning som beskriver fordelingen av varme i faste stoffer. I 1807 oppdaget en forsker en metode for å løse gitt ligning, som kalles Fourier-transformasjonen.

Termisk konduktivitetsanalyse

Forskeren brukte en matematisk metode for å beskrive mekanismen for varmeledning. Et praktisk eksempel, der det ikke er noen vanskeligheter med å beregne, er forplantningen av termisk energi gjennom en jernring, en del nedsenket i ild. For å utføre eksperimenter varmet Fourier opp en del av denne ringen rødglødende og begravde den inn fin sand. Etter det tok han temperaturmålinger på motsatt side av den. Til å begynne med er varmefordelingen uregelmessig: en del av ringen er kald og den andre er varm, og en skarp temperaturgradient kan observeres mellom disse sonene. Men i prosessen med varmeutbredelse over hele overflaten av metallet, blir det mer ensartet. Så snart tar denne prosessen form av en sinusoid. Til å begynne med øker grafen jevnt og avtar også jevnt, nøyaktig i henhold til lovene for endring av cosinus- eller sinusfunksjonen. Bølgen jevner seg gradvis ut, og som et resultat blir temperaturen den samme over hele overflaten av ringen.

Forfatteren av denne metoden foreslo at den innledende uregelmessige fordelingen kan dekomponeres i en serie med elementære sinusoider. Hver av dem vil ha sin egen fase (utgangsposisjon) og sitt eget temperaturmaksimum. I dette tilfellet endres hver slik komponent fra et minimum til et maksimum og tilbake med full sving rundt ringen et heltall antall ganger. En komponent med en periode ble kalt den grunnleggende harmoniske, og en verdi med to eller flere perioder ble kalt den andre, og så videre. Så, matematisk funksjon, som beskriver temperaturmaksimum, fase eller posisjon kalles Fourier-transformasjonen av fordelingsfunksjonen. Forskeren samlet en enkelt komponent som er vanskelig å matematisk beskrivelse, til et brukervennlig verktøy - serie med cosinus og sinus, oppsummering for å gi den originale distribusjonen.

Essensen av analysen

Bruk av denne analysen til transformasjon av varmeutbredelse langs hard gjenstand, som har en ringformet form, begrunnet matematikeren at en økning i periodene til den sinusformede komponenten ville føre til dens raske forfall. Dette sees tydelig i de grunnleggende og andre harmoniske. I sistnevnte når temperaturen sitt maksimum to ganger og minimumsverdier på ett pass, og i det første - bare en gang. Det viser seg at avstanden dekket av varme i den andre harmoniske vil være halvparten av den i hovedtonen. I tillegg vil gradienten i den andre også være dobbelt så bratt som i den første. Derfor, siden den mer intense varmestrømmen går en avstand dobbelt så kort, vil denne harmoniske avta fire ganger raskere enn den fundamentale som funksjon av tid. I fremtiden vil denne prosessen gå enda raskere. Matematikeren mente at denne metoden lar deg beregne prosessen med den innledende fordelingen av temperatur over tid.

Utfordring til samtiden

Fourier Transform Algoritmen har blitt en utfordring teoretiske grunnlag datidens matematikk. På begynnelsen av det nittende århundre godtok ikke de mest fremtredende forskere, inkludert Lagrange, Laplace, Poisson, Legendre og Biot, hans uttalelse om at den innledende temperaturfordelingen er dekomponert i komponenter i form av en grunnleggende harmonisk og høyere frekvenser. Imidlertid kunne Vitenskapsakademiet ikke ignorere resultatene oppnådd av matematikeren, og tildelte ham en pris for teorien om lovene for varmeledning, samt sammenligne det med fysiske eksperimenter. I Fouriers tilnærming var hovedinnvendingen det faktum at den diskontinuerlige funksjonen er representert ved summen av flere sinusformede funksjoner som er kontinuerlige. Tross alt beskriver de revet rette og buede linjer. Samtidige til forskeren møtte aldri lignende situasjon, Når diskontinuerlige funksjoner beskrevet av en kombinasjon av kontinuerlig, for eksempel kvadratisk, lineær, sinus eller eksponentiell. I tilfelle matematikeren hadde rett i sine uttalelser, bør summen av en uendelig rekke av en trigonometrisk funksjon reduseres til en nøyaktig trinnvis. På den tiden virket en slik uttalelse absurd. Men til tross for tvil, har noen forskere (f.eks. Claude Navier, Sophie Germain) utvidet omfanget av forskning og tatt dem utover analysen av fordelingen av termisk energi. I mellomtiden fortsatte matematikere å pine seg over spørsmålet om summen av flere sinusformede funksjoner kan reduseres til en nøyaktig representasjon av en diskontinuerlig.

200 år med historie

Denne teorien har utviklet seg over to århundrer, i dag har den endelig dannet seg. Med sin hjelp er romlige eller tidsmessige funksjoner delt inn i sinusformede komponenter, som har sin egen frekvens, fase og amplitude. Denne transformasjonen oppnås av to forskjellige matematiske metoder. Den første av dem brukes når den opprinnelige funksjonen er kontinuerlig, og den andre - når den er representert av et sett med diskrete individuelle endringer. Hvis uttrykket er hentet fra verdier som er definert av diskrete intervaller, kan det deles inn i flere sinusformede uttrykk med diskrete frekvenser - fra den laveste og deretter to ganger, tre ganger og så videre høyere enn den viktigste. En slik sum kalles Fourier-serien. Hvis innledende uttrykk gitt verdi for hver ekte nummer, så kan den dekomponeres i flere sinusformede frekvenser med alle mulige frekvenser. Det kalles vanligvis Fourier-integralet, og løsningen innebærer integrerte transformasjoner funksjoner. Uavhengig av hvordan konverteringen oppnås, må to tall angis for hver frekvens: amplitude og frekvens. Disse verdiene er uttrykt som Samlet teori uttrykk for komplekse variabler, sammen med Fourier-transformasjonen, gjorde det mulig å utføre beregninger ved konstruksjon av ulike elektriske kretser, analyse mekaniske vibrasjoner, studerer mekanismen for bølgeutbredelse og mer.

Fourier-transformasjon i dag

I dag er studiet av denne prosessen hovedsakelig redusert til å finne effektive metoder overgang fra en funksjon til dens transformerte form og omvendt. Denne løsningen kalles den direkte og inverse Fourier-transformasjonen. Hva betyr det? For å produsere en direkte Fourier-transform kan man bruke matematiske metoder, eller analytiske. Til tross for at visse vanskeligheter oppstår ved bruk av dem i praksis, er de fleste integraler allerede funnet og inkludert i matematiske oppslagsverk. Ved hjelp av numeriske metoder kan man beregne uttrykk hvis form er basert på eksperimentelle data, eller funksjoner hvis integraler ikke er i tabellene og er vanskelige å presentere i analytisk form.

Før bruken av datateknologi var beregningene av slike transformasjoner veldig kjedelige, de krevde manuell utførelse av et stort antall aritmetiske operasjoner, som var avhengig av antall punkter som beskrev bølgefunksjon. For å lette beregningene finnes det i dag spesielle programmer som gjorde det mulig å implementere nye. Så i 1965 opprettet James Cooley og John Tukey programvare, kjent som "Fast Fourier Transform". Den lar deg spare tid for beregninger ved å redusere antall multiplikasjoner i analysen av kurven. Den raske Fourier-transformmetoden er basert på å dele kurven med stort antall enhetlige prøveverdier. Følgelig halveres antall multiplikasjoner med samme reduksjon i antall poeng.

Bruk av Fourier-transformasjonen

Denne prosessen brukes i ulike vitenskapsfelt: innen fysikk, signalbehandling, kombinatorikk, sannsynlighetsteori, kryptografi, statistikk, oseanologi, optikk, akustikk, geometri og andre. De rike mulighetene for bruken er basert på en rekke nyttige funksjoner, som kalles "egenskapene til Fourier-transformasjonen". La oss vurdere dem.

1. Transformasjonen av en funksjon er en lineær operator og, med passende normalisering, er den enhetlig. Denne eiendommen kjent som Parsevals teorem, eller generelt Plancherel-teoremet, eller Pontryagins dualisme.

2. Transformasjonen er reversibel. Dessuten har det omvendte resultatet nesten samme form som i den direkte løsningen.

3. Sinusformede baseuttrykk er native differensierte funksjoner. Dette betyr at en slik representasjon endres med en konstant koeffisient til vanlige algebraiske.

4. I henhold til "convolution"-teoremet, transformeres denne prosessen kompleks operasjon til elementær multiplikasjon.

5. Den diskrete Fourier-transformasjonen kan raskt beregnes på en datamaskin ved hjelp av den "raske" metoden.

Varianter av Fourier-transformasjonen

1. Oftest dette semesteret brukes til å betegne en kontinuerlig transformasjon som gir et hvilket som helst kvadrat-integrerbart uttrykk som en sum av komplekse eksponentielle uttrykk med spesifikke vinkelfrekvenser og amplituder. Denne typen har flere ulike former, som kan variere konstante koeffisienter. Den kontinuerlige metoden inkluderer en konverteringstabell, som finnes i matematiske oppslagsverk. Det generaliserte tilfellet er brøkkonvertering, ved hjelp av hvilken denne prosessen kan heves til den nødvendige reelle kraften.

2. Den kontinuerlige måten er en generalisering tidlig teknikk Fourierrekker definert for ulike periodiske funksjoner eller uttrykk som eksisterer i et begrenset område og representerer dem som serier av sinusoider.

3. Diskret Fourier-transformasjon. Denne metoden brukes i datateknologi for vitenskapelige beregninger og for digital signalbehandling. For å utføre denne typen beregninger er det nødvendig å ha funksjoner som definerer individuelle punkter, periodiske eller avgrensede områder på et diskret sett i stedet for kontinuerlige Fourier-integraler. Signaltransformasjonen i dette tilfellet er representert som summen av sinusoider. Samtidig gjør bruken av den «raske» metoden det mulig å søke diskrete løsninger for enhver praktisk oppgave.

4. Vinduet Fourier-transformasjon er en generalisert form av den klassiske metoden. I motsetning til standard løsning, når den brukes som tas over hele eksistensområdet til en gitt variabel, her er bare den lokale frekvensfordelingen av spesiell interesse, forutsatt at den opprinnelige variabelen (tiden) er bevart.

5. Todimensjonal Fourier-transformasjon. Denne metoden brukes til å jobbe med todimensjonale datamatriser. I dette tilfellet utføres transformasjonen først i én retning, og deretter i den andre.

Konklusjon

I dag er Fourier-metoden solid forankret i ulike vitenskapsfelt. For eksempel ble skjemaet åpnet i 1962 dobbel DNA-helix ved å bruke Fourier-analyse i kombinasjon med sistnevnte, fokuserte de på krystallene av DNA-fibre, som et resultat ble bildet som ble oppnådd ved strålingsdiffraksjon registrert på film. Dette bildet ga informasjon om verdien av amplituden ved bruk av Fourier-transformasjonen til en gitt krystallstruktur. Fasedata ble oppnådd ved å sammenligne DNA-diffraksjonskartet med kartene oppnådd fra analysen av lignende kjemiske strukturer. Som et resultat har biologer gjenopprettet krystallstrukturen - den opprinnelige funksjonen.

Fourier-transformasjoner spiller en stor rolle i studiet av det ytre rom, halvleder- og plasmafysikk, mikrobølgeakustikk, oseanografi, radar, seismologi og medisinske undersøkelser.

Disse transformasjonene er funksjonelle fordi de transformerer en funksjon av en variabel til en helt annen funksjon av en variabel, og omvendt.

Fourier-transformasjoner har formen:

Integralligningen (4.34) kalles den direkte, og ligningen (4.35) kalles invers Fourier-transformasjon. Stenografi for disse ligningene

Fourier-integralet (direkte Fourier-transformasjon) lar deg utvide en ikke-periodisk funksjon som har egenskapen absolutt integrerbarhet innenfor gitte grenser til en uendelig rekke harmoniske som danner et kontinuerlig spektrum av frekvenser i området fra til med et uendelig lite frekvensintervall mellom tilstøtende harmoniske (dvs. i grensen

Fourier-transformasjonsmetoden er uegnet for initiale (eller grense)forhold som ikke er null. Denne metoden kan bare brukes når de ønskede funksjonene har et Fourier-bilde, dvs. for absolutt integrerbare tidsfunksjoner som tilfredsstiller ulikheten

De vanligste funksjonene i kontrollteori er enhetstrinnfunksjonen (1.44) og produktet av en sinusformet funksjon ved identitetsfunksjon(1,51). Fourier-transformasjonen er ikke anvendelig for noen av disse funksjonene, siden betingelse (4.38) ikke er oppfylt.

Disse manglene begrenser bruken av Fourier-transformasjonsmetoden.

For å anvende Fourier-integralet er det nødvendig å velge en funksjon som er tilstrekkelig nær den som studeres, for eksempel til en trinnfunksjon ved endelige verdier, men som samtidig tilfredsstiller betingelsen (4.38). Denne funksjonen kan oppnås ved å multiplisere

trinnfunksjon på hvor c er en tilstrekkelig liten positiv verdi. Den nyoppnådde hjelpefunksjonen

Ved å la c ha en tendens til null og gå over til grensen, kan vi gå fra hjelpefunksjonen til hovedfunksjonen. I tillegg, hvis vi begrenser oss til funksjoner som er identisk lik null for så vil betingelse (4.38) gjelde for en stor klasse av funksjoner og vi kan finne frekvensspekteret til funksjonen ved hjelp av uttrykk (4.34) . I stedet introduserer vi en ny notasjon, siden denne mengden nå også avhenger av c:

Putting med finne

Denne formelen sammenfaller med den direkte Laplace-transformasjonen (4.9).

Det følger at Fourier-transformasjonen kan sees på som spesielt tilfelle Laplace forvandler seg.

Transformasjonsmetodene beskrevet ovenfor lar oss trekke følgende konklusjoner:

1) integro-differensialligninger erstattes av algebraiske ligninger;

2) operasjonen med å bestemme integrasjonskonstantene elimineres, siden startforholdene tas i betraktning helt fra begynnelsen når du finner bildet av ønsket verdi;

3) operasjonen med å bestemme røttene karakteristisk ligning er fullstendig bevart.

Den mest praktiske for å løse praktiske problemer er Laplace-transformasjonsmetoden. I en litt modifisert form kan den brukes på studiet av diskret ACS (se kapittel 7).

Vurder bruken av Laplace-transformmetoden for å løse en differensialligning av formen

Vi transformerer denne differensiallikningen ved å bruke den direkte Laplace-transformasjonen (4.9) og setning 1 og 2. Som et resultat får vi algebraisk ligning, skrevet for bilder:

hvor er summen av alle vilkårene som inneholder startbetingelsene.

Herfra er bildet av ønsket funksjon

På null Innledende forhold uttrykk (4.41) og (4.42) er forenklet:

Når du kjenner bildet av ønsket funksjon, kan du finne originalen, for eksempel fra bildetabeller.

Hvis bildet av ønsket verdi er en rasjonell algebraisk brøk, så prøver de å skrive det som en sum enkle brøker med konstante koeffisienter. Omvendt transformasjon for hver av disse enkle brøkene kan hentes fra tabellene, og det endelige uttrykket til originalen presenteres som summen av de individuelle verdiene som er funnet. Du kan også bruke dekomponeringsteoremet for å bestemme originalen.

Hvis Laplace-bildet er en rasjonell algebraisk brøkdel av formen

Tenk på de grunnleggende egenskapene til Fourier-transformasjonen.

Linearitet. Vurder funksjonene og
med spektre
Og
:

(12)

Da vil spekteret til deres lineære kombinasjon være:

Tidsforsinkelse. Vi antar at spekteret er kjent
signal

(14)

La oss beregne spekteret til det tidsforskyvede signalet:
. Angi funksjonsargumentet til den nye variabelen
, Deretter
Og

Fikk den signalforsinkelsen en stund fører til multiplikasjon av spekteret med
.

Skalaendring. Vi antar at spekteret er kjent
signal
som gjennom
signalspekteret uttrykkes
. Vi introduserer en ny variabel
, endrer vi integrasjonsvariabelen
.

(16)

Multiplikasjon med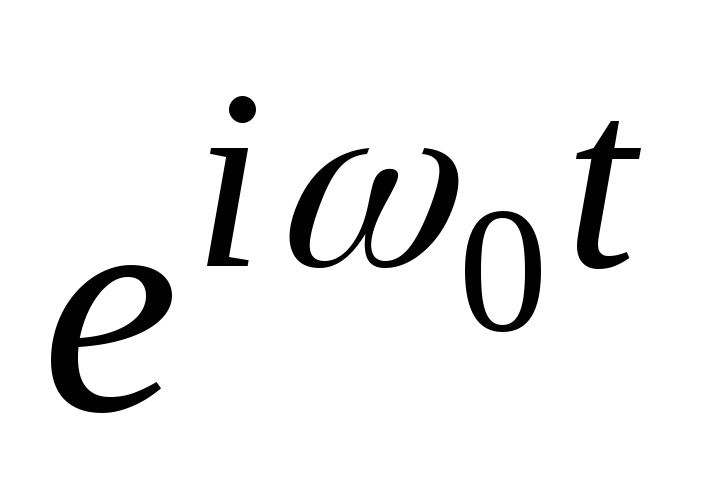
. Som i forrige tilfelle antar vi at spekteret er kjent
signal
. Finn spekteret til dette signalet, multiplisert med
.

Dermed multipliseres signalet med
fører til en forskyvning av spekteret ved .

Derivert spektrum. I denne saken nøkkelpunktet er funksjonens absolutte integrerbarhet. Av det faktum at integralet av modulen til en funksjon må være avgrenset, følger det at ved uendelig må funksjonen ha en tendens til null. Integralet til den deriverte av funksjonen er tatt i deler, de resulterende ikke-integrale leddene er lik null, siden funksjonen har en tendens til null ved uendelig.

(18)

Spektrum av integralet. La oss finne spekteret til signalet
. Og det vil vi anta
, det vil si at signalet ikke har en konstant komponent. Dette kravet er nødvendig for at leddene utenfor integralet er lik null når integralet tas av deler.

(19)

Konvolusjonsteorem. Det er kjent at
Og
funksjonsspektre
Og
hhv. Det kreves å uttrykke konvolusjonsspekteret
gjennom
Og
. For å gjøre dette, i Fourier-integralet av konvolusjon, vil en av funksjonene bli erstattet av variabelen
, så kan eksponenten erstattes
. Som et resultat av en slik utskifting vil dobbeltintegralet være er lik produktet to Fourier-integraler.

(20)

Fourier-transformasjonen av konvolusjonen av to signaler gir produktet av spektrene til disse signalene.

Produksjon av signaler. Det er kjent at
Og
er spektra av funksjoner
Og
hhv. Det er nødvendig å uttrykke spekteret til produktet
gjennom spektre
Og
. La oss bytte inn i Fourier-integralet i stedet for et av signalene, for eksempel
, dets uttrykk i form av den inverse Fourier-transformasjonen, og endre deretter rekkefølgen for integrasjon.

(21)

Spekteret til produktet av signaler er konvolusjonen av spektrene til disse signalene.

Diskret signalspektrum

Spesiell oppmerksomhet bør rettes mot diskrete signaler, siden slike signaler brukes i digital behandling. Et diskret signal, i motsetning til et kontinuerlig, er en tallsekvens som tilsvarer verdiene til et kontinuerlig signal på bestemte tidspunkter. Et betinget diskret signal kan betraktes som et kontinuerlig signal, som til visse tider antar noen verdier, og til andre tider er lik null. Altså for eksempel diskret
signalet kan gis som et produkt av et kontinuerlig signal
på en sekvens av periodisk repeterende rektangulære pulser
- tidsstyringspulser (fig. 1).

Ris. 1. Signaldiskretisering.

(22)

Rektangulære pulser har varighet , repetisjonsperiode :

(23)

Pulsamplituden velges slik at integralet til pulsen over perioden er lik . I dette tilfellet er klokkepulsene dimensjonsløse. Vi utvider sekvensen av slike impulser til en trigonometrisk serie:

(24)

For å få umiddelbare signalavlesninger
, er det nødvendig å rette pulsvarigheten til null:
. Vi kaller et slikt klokkesignal ideelt. I dette tilfellet, ekspansjonskoeffisienten
i Fourier-serien vil alle være lik 1.

(25)

Nøyaktig samme form har utvidelsen i Fourier-serien av funksjonen:

(26)

Utvidelseskoeffisienter til en trigonometrisk serie av klokkesignalet
:

(27)

Da vil det diskrete signalet se slik ut:

Når vi beregner Fourier-transformasjonen til et diskret signal, bytter vi operasjonen av summering og integrasjon, og bruker deretter egenskapen δ - Funksjoner:

Spekteret til et diskret signal er en periodisk funksjon. Tenk på eksponenten i hotellbegrepet
som en funksjon av frekvens. Gjentakelsesperioden er . Mest stor periode repetisjoner i form av tall
, og dette vil følgelig være repetisjonsperioden for hele spekteret. Det er spekteret til et diskret signal har en repetisjonsperiode lik kvantiseringsfrekvensen
.

La oss få et nytt show
. Fordi
er et produkt av funksjoner
Og
, spekteret til det diskrete signalet
beregnes som en konvolusjon av spektrene til et kontinuerlig signal
og spekteret til klokkesignalet
.

(30)

Beregn
ved å bruke (25). Fordi
periodisk funksjon, dens spektrum er diskret.

Så konvolusjon (30)

Det følger av uttrykk (32) at spekteret til det diskrete signalet er en periodisk repeterende funksjon
.

Selve det faktum at det skjer kvalitative endringer i signalspekteret som et resultat av sampling antyder at det opprinnelige signalet kan bli forvrengt, siden det er fullstendig bestemt av spekteret. På den annen side introduserer ikke den periodiske repetisjonen av det samme spekteret i seg selv noe nytt i spekteret, derfor kan du under visse forhold, ved å kjenne signalverdiene på individuelle tidspunkter, finne hvilken verdi dette signalet tok på et hvilket som helst annet tidspunkt, det vil si få originalt kontinuerlig signal. Dette er betydningen av Kotelnikov-teoremet, som setter en betingelse for valget av kvantiseringsfrekvensen i samsvar med den maksimale frekvensen i signalspekteret.

Hvis denne betingelsen brytes, vil et periodisk repeterende spektrum etter digitaliseringen av signalet bli overlagret (fig. 2). Spekteret som resulterer fra overlegget vil tilsvare et annet signal.

Ris. 2. Spektra overlapper hverandre.

Denne serien kan også skrives som:

(2),
Hvor , k-te kompleks amplitude.

Forholdet mellom koeffisientene (1) og (3) uttrykkes med følgende formler:

Merk at alle disse tre representasjonene av Fourier-serien er helt likeverdige. Noen ganger, når du arbeider med Fourier-serier, er det mer praktisk å bruke eksponentene til det imaginære argumentet i stedet for sinus og cosinus, det vil si å bruke Fourier-transformasjonen i kompleks form. Men det er praktisk for oss å bruke formel (1), der Fourier-serien er representert som en sum av cosinusbølger med tilsvarende amplituder og faser. I alle fall er det feil å si at resultatet av Fourier-transformasjonen av det virkelige signalet vil være de komplekse amplitudene til harmoniske. Som wikien korrekt sier, "Fourier-transformasjonen (?) er en operasjon som kartlegger en funksjon av en reell variabel til en annen funksjon, også av en reell variabel."

Total:
Det matematiske grunnlaget for spektralanalysen av signaler er Fourier-transformasjonen.

Fouriertransformasjonen lar oss representere kontinuerlig funksjon f(x) (signal) definert på segmentet (0, T) som summen av endelig antall(uendelig rad) trigonometriske funksjoner(sinus og/eller cosinusbølger) med visse amplituder og faser, også vurdert på segmentet (0, T). En slik serie kalles en Fourier-serie.

Vi noterer oss noen flere punkter, hvor forståelsen er nødvendig for riktig anvendelse av Fourier-transformasjonen til signalanalyse. Hvis vi vurderer Fourier-serien (summen av sinusoider) på hele X-aksen, så kan vi se at utenfor segmentet (0, T), vil funksjonen representert av Fourier-serien periodisk gjenta funksjonen vår.

For eksempel, i grafen i fig. 7 er den opprinnelige funksjonen definert på segmentet (-T \ 2, + T \ 2), og Fourier-serien representerer en periodisk funksjon definert på hele x-aksen.

Dette er fordi sinusoidene i seg selv er henholdsvis periodiske funksjoner, og summen deres vil være en periodisk funksjon.

fig.7 Representasjon av en ikke-periodisk opprinnelig funksjon ved en Fourier-serie

Dermed:

Vår opprinnelige funksjon er kontinuerlig, ikke-periodisk, definert på et eller annet intervall med lengde T.
Spekteret til denne funksjonen er diskret, det vil si at den presenteres som en uendelig serie av harmoniske komponenter - Fourier-serien.
Faktisk er en viss periodisk funksjon definert av Fourier-serien, som sammenfaller med vår på segmentet (0, T), men denne periodisiteten er ikke avgjørende for oss.

Periodene til de harmoniske komponentene er multipler av segmentet (0, T) som den opprinnelige funksjonen f(x) er definert på. Med andre ord er de harmoniske periodene multipler av varigheten av signalmålingen. For eksempel perioden for den første harmoniske av Fourier-serien lik intervallet T som funksjonen f(x) er definert på. Perioden til den andre harmoniske av Fourier-serien er lik intervallet T/2. Og så videre (se fig. 8).

fig.8 Perioder (frekvenser) for de harmoniske komponentene i Fourier-serien (her T = 2?)

Følgelig er frekvensene til de harmoniske komponentene multipler av 1/T. Det vil si at frekvensene til de harmoniske komponentene Fk er lik Fk= k\T, hvor k varierer fra 0 til?, for eksempel k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (ved null frekvens - konstant komponent).

La vår opprinnelige funksjon være et signal registrert i T=1 sek. Da vil perioden til den første harmoniske være lik varigheten av signalet vårt T1=T=1 sek og frekvensen til overtonen er 1 Hz. Perioden til den andre harmoniske vil være lik varigheten av signalet delt på 2 (T2=T/2=0,5 sek) og frekvensen er 2 Hz. For den tredje harmoniske T3=T/3 sek og frekvensen er 3 Hz. Og så videre.

Steget mellom harmoniske i dette tilfellet er 1 Hz.

Dermed kan et signal med en varighet på 1 sek dekomponeres til harmoniske komponenter (for å oppnå et spektrum) med en frekvensoppløsning på 1 Hz.
For å øke oppløsningen med 2 ganger til 0,5 Hz, er det nødvendig å øke målevarigheten med 2 ganger - opptil 2 sekunder. Et signal med en varighet på 10 sekunder kan dekomponeres til harmoniske komponenter (for å oppnå et spektrum) med en frekvensoppløsning på 0,1 Hz. Det er ingen andre måter å øke frekvensoppløsningen på.

Det er en måte å kunstig øke varigheten av signalet ved å legge til nuller til utvalget av prøver. Men det øker ikke den reelle frekvensoppløsningen.

3. Diskrete signaler og diskret Fouriertransformasjon

Med utviklingen av digital teknologi har også måtene å lagre måledata (signaler) på endret seg. Hvis signalet tidligere kunne tas opp på båndopptaker og lagres på bånd i analog form, digitaliseres signalene nå og lagres i filer i datamaskinens minne som et sett med tall (teller).

Det vanlige opplegget for måling og digitalisering av et signal er som følger.

fig.9 Skjema for målekanalen

Signalet fra måletransduseren ankommer ADC i løpet av en tidsperiode T. Signalsamplene (sample) som oppnås i løpet av tiden T overføres til datamaskinen og lagres i minnet.

fig.10 Digitalisert signal - N avlesninger mottatt i tid T

Hva er kravene til parametere for signaldigitalisering? En enhet som konverterer et analogt inngangssignal til en diskret kode (digitalt signal) kalles en analog-til-digital-omformer (ADC, engelsk analog-til-digital-omformer, ADC) (Wiki).

En av hovedparametrene til ADC er den maksimale samplingshastigheten (eller samplingshastigheten, engelsk samplingsfrekvens) - frekvensen for å ta prøver av et signal kontinuerlig i tid under samplingen. Målt i hertz. ((Wiki))

I følge Kotelnikov-teoremet, hvis et kontinuerlig signal har et spektrum begrenset av frekvensen Fmax, kan det gjenopprettes fullstendig og unikt fra dets diskrete prøver tatt med tidsintervaller , dvs. med frekvens Fd ? 2*Fmax, hvor Fd - samplingshastighet; Fmax - maksimal frekvens for signalspekteret. Med andre ord må signalsamplingsfrekvensen (ADC samplingshastighet) være minst 2 ganger den maksimale frekvensen til signalet vi ønsker å måle.

Og hva vil skje hvis vi tar avlesninger med en lavere frekvens enn det som kreves av Kotelnikov-teoremet?

I dette tilfellet oppstår effekten av "aliasing" (aka stroboskopisk effekt, moiré-effekt), der høyfrekvente signalet etter digitalisering blir til et lavfrekvent signal som faktisk ikke eksisterer. På fig. 5 høyfrekvent rød sinusbølge er det virkelige signalet. Den lavere frekvensen blå sinusbølge er et dummy-signal som er et resultat av at mer enn en halv periode med et høyfrekvent signal har tid til å passere i løpet av samplingstiden.

Ris. 11. Utseendet til et falskt lavfrekvent signal når samplingshastigheten ikke er høy nok

For å unngå effekten av aliasing, plasseres et spesielt anti-aliasing-filter foran ADC - LPF (lavpassfilter), som sender frekvenser under halvparten av ADC-samplingsfrekvensen, og kutter av høyere frekvenser.

For å beregne spekteret til et signal fra dets diskrete sampler, brukes den diskrete Fourier-transformasjonen (DFT). Vi bemerker nok en gang at spekteret til et diskret signal er "per definisjon" begrenset av frekvensen Fmax, som er mindre enn halvparten av samplingsfrekvensen Fd. Derfor kan spekteret til et diskret signal representeres av summen av et endelig antall harmoniske, i motsetning til den uendelige summen for Fourier-serien til et kontinuerlig signal, hvis spektrum kan være ubegrenset. I følge Kotelnikov-teoremet må den maksimale harmoniske frekvensen være slik at den står for minst to sampler, så antallet harmoniske er lik halvparten av antallet samples av det diskrete signalet. Det vil si at hvis det er N sampler i samplet, vil antallet harmoniske i spekteret være lik N/2.

Tenk nå på den diskrete Fourier-transformasjonen (DFT).

Sammenligner med Fourier-serien

Vi ser at de er sammenfallende, bortsett fra at tiden i DFT er diskret og antall harmoniske er begrenset til N/2 – halvparten av antallet sampler.

DFT-formlene er skrevet i dimensjonsløse heltallsvariabler k, s, der k er antallet signalprøver, s er antallet spektralkomponenter.
Verdien av s viser antall fullsvingninger av harmonikken i perioden T (varigheten av signalmålingen). Den diskrete Fourier-transformasjonen brukes til å finne amplitudene og fasene til harmoniske numerisk metode, dvs. "på datamaskinen"

Gå tilbake til resultatene som ble oppnådd i begynnelsen. Som nevnt ovenfor, når man utvider en ikke-periodisk funksjon (vårt signal) til en Fourier-serie, tilsvarer den resulterende Fourier-serien faktisk en periodisk funksjon med periode T. (Fig. 12).

fig.12 Periodisk funksjon f(x) med periode Т0, med måleperiode Т>T0

Som man kan se i fig. 12, er funksjonen f(x) periodisk med periode Т0. På grunn av det faktum at varigheten av måleprøven T ikke sammenfaller med perioden til funksjonen T0, har funksjonen oppnådd som en Fourier-serie en diskontinuitet i punktet T. Som et resultat vil spekteret til denne funksjonen inneholde et stort nummer av høyfrekvente harmoniske. Hvis varigheten av måleprøven T falt sammen med perioden til funksjonen T0, ville bare den første harmoniske (en sinusoid med en periode lik prøvevarigheten) være tilstede i spekteret oppnådd etter Fourier-transformasjonen, siden funksjonen f. (x) er en sinusformet.

Med andre ord, DFT-programmet "vet ikke" at signalet vårt er en "bit av en sinusbølge", men prøver å representere en periodisk funksjon som en serie, som har et gap på grunn av inkonsistensen til de enkelte delene av sinusbølgen.

Som et resultat dukker det opp harmoniske i spekteret, som totalt sett skal representere funksjonens form, inkludert denne diskontinuiteten.

Altså for å få det "riktige" spekteret til signalet, som er summen av flere sinusoider med ulike perioder, er det nødvendig at et helt antall perioder av hver sinusoid passer på signalmåleperioden. I praksis kan denne betingelsen oppfylles for en tilstrekkelig lang varighet av signalmålingen.

Fig.13 Et eksempel på funksjonen og spekteret til signalet for den kinematiske feilen til girkassen

Med kortere varighet vil bildet se "verre" ut:

Fig.14 Et eksempel på funksjonen og spekteret til rotorens vibrasjonssignal

I praksis kan det være vanskelig å forstå hvor de "virkelige komponentene" er og hvor er "artefaktene" forårsaket av ikke-mangfoldet av periodene til komponentene og varigheten av signalprøven eller "hopp og pauser" av bølgeformen. Ordene "ekte komponenter" og "artefakter" er selvfølgelig ikke sitert forgjeves. Tilstedeværelsen av mange harmoniske på spektrumgrafen betyr ikke at signalet vårt faktisk "består" av dem. Det er som å tenke at tallet 7 «består» av tallene 3 og 4. Tallet 7 kan representeres som summen av tallene 3 og 4 – dette er riktig.

Det samme er vårt signal ... eller rettere sagt, ikke engang "vårt signal", men en periodisk funksjon kompilert ved å gjenta signalet vårt (sampling) kan representeres som en sum av harmoniske (sinusoider) med visse amplituder og faser. Men i mange tilfeller som er viktige for praksis (se figurene ovenfor), er det faktisk mulig å relatere harmoniske oppnådd i spekteret til virkelige prosesser som er sykliske i naturen og gir et betydelig bidrag til signalformen.

Noen resultater

1. Det virkelige målte signalet, varighet T sek, digitalisert av ADC, det vil si representert av et sett med diskrete sampler (N stykker), har et diskret ikke-periodisk spektrum, representert av et sett med harmoniske (N/2 stykker) ).

2. Signalet er representert av et sett med reelle verdier og spekteret er representert av et sett med reelle verdier. De harmoniske frekvensene er positive. Det faktum at det er mer praktisk for matematikere å representere spekteret i en kompleks form ved bruk av negative frekvenser, betyr ikke at "det er riktig" og "det bør alltid gjøres på denne måten".

3. Signalet målt på tidsintervallet T bestemmes kun på tidsintervallet T. Hva som skjedde før vi begynte å måle signalet, og hva som vil skje etter det - dette er ukjent for vitenskapen. Og i vårt tilfelle - det er ikke interessant. DFT til et tidsbegrenset signal gir det "virkelige" spekteret, i den forstand at det under visse forhold lar deg beregne amplituden og frekvensen til komponentene.

Brukte materialer og andre nyttige materialer.